Fatigue Parameter Based on the Assessment of Stress Components in all Material Planes

A new fatigue parameter is proposed, which provides a new way of thinking to assess fatigue damage problems. The complete stress state at a certain material point, i.e., taking into account any material plane at that point, is included in the method. The influence of tension and compression state and also the mean stress are also included. Some experiments with different materials and loading conditions are used to validate the capabilities of the proposed method. The results show that the method provides good predictions for axial cyclic and/or torsion cyclic conditions with zero or nonzero mean stresses, in-phase and out-of-phase, different shapes of the specimen, loading waveform and loading path.

Introduction

Fatigue is one of the most common damage mechanisms in engineering components. The methods used for the evaluation of fatigue damage can be split into three main categories according to the mechanical magnitudes used in the definition of various criteria, i.e. stress-based, strain-based, and energy-based methods. As a general rule, the stress-based methods are used for high-cycle fatigue, the strain-based methods are used in low-cycle fatigue and can also be used for high-cycle fatigue, and the energy-based methods can be used for both high- and low-cycle fatigue because they contain contributions of both stress and strain magnitudes. Basically, in the stress/strain-based methods, the maximum normal or shear stress/strain is used in the case of tension fatigue or torsion fatigue and then some simple modifications, such as amplitude, mean value, separation between the elastic/ plastic components are used. The stress invariants, like J₂, hydrostatic pressure σ_H, or some equivalent stress/strain states, such as Mises, Tresca, etc. are also used to predict fatigue damage.

More complex formulations assume that fatigue damage should take into account the stress or strain components (typically, normal and shear components) that can be active in different planes at a given material point. Thus, a fatigue parameter (FP) given by Δγ_max/2+SΔεn, where Δγ_max is the range of maximum shear strains, Δεn is the range of normal strains in the plane of maximum range of shear strains, and S is a material constant, was proposed in [1]. It is therefore assumed that both shear and normal strains can affect fatigue damage, the shear strain is the predominant factor in the course of crack formation and in the first stages of crack development, while the normal strain is predominant during macrocrack propagation. In [2], the authors modified the Kandil method as follows: Δγ_max/2+(1–σ_n/2σ_y)Δεn, where σ_n is a normal stress in the plane of maximum shear-strain range and σ_y is the yield limit. In this modification, the influence of normal stresses can be taken into consideration. The influence of normal loading was considered in [3] with the help of the maximum normal stress ${\sigma}_n^{\mathrm{max}}$ in the form 0.5Δγ_max[1+k${\sigma}_n^{\mathrm{max}}$/σ_y], where k is a material constant. In this method, it is assumed that the fatigue damage is mainly affected by the maximum shear strain range; the maximum normal stress is only used as a correcting term to revise the influence of the maximum shear strain range. In the energy-based methods, it is assumed that the fatigue damage is controlled by the energy dissipation in cyclic loading represented by the hysteretic loop in the stress-strain plot. A fatigue parameter ${\sigma}_1^{\mathrm{max}}$Δε₁/2, where ${\sigma}_1^{\mathrm{max}}$ is the maximum principal stress and Δε₁, is the range of principal strains, is presented in [4]. Note that it represents the tractive part of a sort of hysteretic loop in a fully reversed cycle. In this approach, the normal energy is used to calculate fatigue damage, which is accurate when tensile failure of the material is predominant. The fatigue parameter in the form

$$ 0.25\varDelta {\gamma}_{12}\left[1/\left(1-{\sigma}_{12}^{\mathrm{max}}/{\sigma}_f^{\hbox{'}}\right)+1/\left(1-{\sigma}_{22}^{\mathrm{max}}/{\sigma}_f^{\hbox{'}}\right)\right], $$

where Δγ₁₂ is the range of shear strains, Δσ₁₂ is the range of shear stress, $\varDelta {\sigma}_{12}^{\mathrm{max}}$ is the maximum shear stress, $\varDelta {\sigma}_{22}^{\mathrm{max}}$ is the maximum normal stress, and τ′_f and σ′_f are the shear and normal fatigue strength limits, is defined in [5]. In this method, it is assumed that the shear energy makes the main contribution to the fatigue damage and, at the same time, both the maximum shear and normal stresses exert some influence on the fatigue damage.In [6], the authors combine the two methods proposed above and suggest the following parameter:

$$ \varDelta {\varepsilon}_1\varDelta {\sigma}_1+ k\varDelta {\gamma}_1\varDelta {\tau}_1, $$

where Δσ₁ and Δτ₁ are the ranges of normal and shear stresses, respectively, Δγ₁ and Δε₁ are the ranges of shear and normal strains, respectively, and k is a material constant. In this method, it is assumed that both shear and normal energy can affect the fatigue damage and that the relative contribution of shear and normal energy is quantified by the parameter k. Further modifications were proposed in [7] as follows:

$$ \varDelta {\sigma}_n\varDelta {\varepsilon}_n/{\sigma}_f^{\hbox{'}}{\varepsilon}_f^{\hbox{'}}+\left(1+{\sigma}_n^m/{\sigma}_f^{\hbox{'}}\right)\left(\varDelta {\tau}_{\mathrm{max}}\varDelta \left(0.5{\gamma}_{\mathrm{max}}\right)\right)/{\tau}_f^{\hbox{'}}{\gamma}_f^{\hbox{'}}, $$

where ${\sigma}_n^m$ is the mean normal stress, τ′_f and σ′_f are the shear and normal coefficients of fatigue strength, and ε′_f and γ ′_f are the normal and shear fatigue ductility coefficients, respectively. In this method, the influence of mean normal stress ${\sigma}_n^m$ is taken into account.

A Proposed New Fatigue Parameter

The different approaches to the evaluation of fatigue damage reviewed in the previous section indicate that the stress/strain-based methods are essentially based on normal/shear, stress/strain, and some modifications, such as those caused by the range (maximum and mean), or on a combination of some of these (the methods based on energy magnitudes may serve as an example). The proposed approach is based on the generalization of the idea that the normal and shear components of stresses and strains are different in different planes at a certain material point, in addition to the simple combination of maximum stress or strain values. The definition of the new fatigue parameter is described in what follows. The well-known Mohr’s circle representation of the stress (or strain) state is used to illustrate the main ideas of the proposed method.

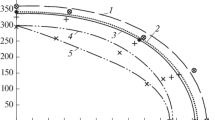
In Fig. 1, we present the Mohr’s stress circle for the 3D stress state (Fig. 1a) and the 2D stress state (Fig. 1b). The dark symbol in the figure corresponds to the normal and shear stress components in a certain material plane. In the methods sketched in the previous section only some stress/strain components at a certain point (or, maybe, at two points) are used to compute the fatigue damage. Although the stress (strain) state at a material point is completely described by Mohr’s representation, the fatigue damage, generally speaking, depends on the normal and shear stress (or strain) components in a given plane. Therefore, we need a method to quantify the amount of damage in each plane. It is also necessary to find a procedure of weighing with an aim to define the equivalent fatigue damage parameter at this point. The possible combinations of normal/shear stresses are represented by the shadowed region in the 3D Mohr’s stress circle displayed in Fig. 1a, and by the entire circumference for the plane-stress conditions (Fig. 1b). The new fatigue parameter is defined as follows:

Fig. 1.

Mohr’s stress circle: (a) 3D stress; (b) 2D stress.

$$ FP=\frac{\sum \varDelta D.\varDelta P}{P}, $$

(1)

where ΔD is the fatigue damage in a certain material plane for a certain material point, which is a function of σ and τ, and ΔP is the contribution of each material plane to the total set of possible planes; the summation is extended to all material planes and P is the summation of all ΔP. In this way, all stress/strain components at a certain material point can be taken into account. It is not necessary to choose certain specific components as the representative components to calculate the fatigue damage. This overcomes a shortcoming of the methods outlined above. The mathematical form of Eq. (1) for the 3D and 2D stress (strain) states can be rewritten as Eq. (2), where ΔS/S is an area element in the 3D Mohr’s stress circle and ΔL/L is an arc-length element in the plane of Mohr’s stress circle:

$$ {\displaystyle \begin{array}{c} FP=\frac{\sum \varDelta D.\varDelta S}{S};\\ {} FP=\frac{\sum \varDelta D.\varDelta L}{L}.\end{array}} $$

(2)

Since the stress components in a certain material plane can be reduced to the normal and shear components, we define the fatigue damage ΔD as follows:

$$ \varDelta D=\mu \left(A\left|\sigma \right|+B\left|\tau \right|\right), $$

(3)

where A and B are coefficients used to describe the influence of normal and shear stress components, respectively, on the fatigue damage. In order to make sure that the effects of both normal and shear stress are positive, A and B should be greater than zero.

In the present paper, it is assumed that the effects of normal and shear stresses are identical, i.e., A = B. In this case, we use the absolute value of τ in view of the top-bottom symmetry of τ in Mohr’s circle; otherwise, the mean influence of τ becomes equal to zero as a result of averaging. In order to make sure that the fatigue damage is positive, we use the absolute value of σ; at the same time, μ is used to reflect the different influence of tension and compression loads and is defined as follows:

$$ \mu ={\displaystyle \begin{array}{c}+1\\ {}-1.\omega \end{array}}...{\displaystyle \begin{array}{c}{\sigma}_m\ge 0,\\ {}{\sigma}_m<0,\end{array}} $$

(4)

where σ_m is the mean stress and ω is the coefficient used to describe the influence of compression. In what follows, the value of ω is assumed to be equal to 1. This means that tension and compression exert the same influence. Under the conditions of multiaxial loading, the FP can be found as follows:

$$ \mathrm{F}P=\mathrm{F}{P}_{\mathrm{max}}-\mathrm{F}{P}_{\mathrm{min}}, $$

(5)

where FP_max and FP_min are the maximum and minimum values of the FP in a cycle. According to this new method, we can consider three cases of evaluation of the fatigue parameter both for the 3D stressed state and for the 2D stressed state depending on the sign of the principal stresses (see Fig. 2). The first case corresponds to the situation where the minimum principal stress is greater than or equal to zero as in Figs. 2a and d. The second case is realized when the maximum principal stress is less than or equal to zero as in Figs. 2b and e. In the third case, the maximum principal stress is greater than zero and the minimum principal stress is smaller than zero as in Figs. 2c and f.

Fig. 2.

Different stress states for the 3D and 2D stress states: (a–c) three 3D cases. (d–f) three 2D cases.

Sensitivity Analysis

We now consider some simple cases to show the influence of the variations of principal stresses on the FP according to the proposed method. We use Figs. 2d and e as examples to reveal the influence of principal stresses. In this discussion, we assume that only one principal stress is variable in order to be able to compare different degrees of influence of changes in each of the different principal stresses. For the case depicted in Fig. 2d, we get the following rates of variation of the FP (the details of calculations can be found in the appendix):

$$ \frac{\partial FP}{\partial {\sigma}_1}=\frac{A}{2}+\frac{B}{\pi },\kern0.5em \frac{\partial FP}{\partial {\sigma}_2}=\frac{A}{2}+\frac{B}{\pi }. $$

(6)

Similarly, for the case depicted in Fig. 2e, we get

$$ {\displaystyle \begin{array}{cc}\frac{\partial FP}{\partial {\sigma}_2}=\frac{A}{2}+\frac{B}{\pi },& \frac{\partial FP}{\partial {\sigma}_3}=\frac{A}{2}+\frac{B}{\pi }.\end{array}} $$

(7)

Note that, for the case in Fig. 2d in which A and B are greater than zero, the value of the FP increases with σ₁, and the influence of σ₁ on the FP is stronger than the influence of σ₂. The value of σ₂ exerts only positive influence on the FP when the value of A/B is larger than 2/π. For the case in Fig. 2e, the influence of σ₂ is stronger than the influence of σ₃ and, moreover, σ₃ always negatively affects the value of FP. In addition, when the value of A/B is smaller than 2/π, σ₂ exerts a positive influence on the value of FP. In the other cases, the influence of variations of the principal stresses is more complicated and each case should be analyzed separately. Some other special cases, such as fully reversed torsion, fully reversed biaxial tension-compression, and fully reversed axial loading with the same stress amplitudes are depicted in Fig. 3. It can be seen that, according to the new parameter proposed in this paper, the degrees of fatigue damage in the cases of fully reversed torsion and biaxial opposite tension-compression with the same stress amplitude are identical. At the same time, in the case of fully reversed axial loading, the degree of fatigue damage is different.

Fig. 3.

Some cases with identical stress amplitudes: (a) fully reversed torsion; (b) fully reversed biaxial tension-compression; (c) fully reversed axial loading.

Results and Experimental Verification

In order to check the capabilities of the proposed new fatigue parameter, we used some experimental resultsm obtained for different materials subjected to different loading conditions. In Figs. 4a–c, we present the data of fatigue tests obtained under the conditions of axial and torsion loading. The tests shown in Fig. 4a were carried out in the fully reversed axial and fully reversed torsion loading modes with zero mean stresses. The tests depicted in Fig. 4b correspond to the axial and torsion loading modes with zero or nonzero mean stresses. The tests in Fig. 4c were performed under the axial and torsion loading conditions with zero mean stresses and for different specimen shapes. It is worth noting that, in the single axial (or single torsion) loading modes for different materials, different shapes of the specimens, and zero or nonzero mean stresses, the predictions performed by using the new fatigue parameter are quite good.

Fig. 4.

Dependences of the FP on the number of cycles (N) for different materials: (a) S355 J2 [8], (b) SNCM630 [9], (c) AW-2007 [10] [(Ο) reversed axial (experiment); (––) reversed axial loading (prediction); (□) reversed torsion (experiment); (− −  − −) reversed torsion (prediction)]; (d) Haynes 188 [11] [(Ο) in/out of phase axial-load+torsion (experiment); (––) in/out of phase axial-load +torsion (prediction)]; (e) 42CrMo [12] [(Ο) complex loading (experiment); (––) complex loading (prediction)]; (f) AW-2007 [10] [(Ο) complex loading (experiment), (––) complex loading (fitting), (− −  − −) complex loading (prediction)].

There are experimental data on the differences between the axial and torsion curves of fatigue damage [8, 10] regarded as a clear indication of the fact that fatigue damage depends on the loading conditions. Most of the available experimental results are for the axial and torsion loads. In order to predict the fatigue damage under more complicated loading conditions, such as axial-torsion loading, in-phase and out-of-phase loading, and even random loading that contain various combinations of normal and shear stresses, we assume that the fatigue-damage curve under complex loading conditions F(FP_c, N_c) can be predicted as an axial fatigue damage curve Q(FP_a, N_a) and a shear fatigue damage curve W(FP_t, N_t):

$$ F\left(\mathrm{F}{P}_c,{N}_c\right)=f\left(\xi Q,\zeta W\right). $$

(8)

The parameters ξ and ζ represent the influence of the axial and torsion loading conditions. These parameters reflect the relative contributions of the axial and torsion loading conditions, respectively, to the fatigue damage curve obtained under the condition of complex loading. Thus, if ξ/ζ = 1, then the fatigue damage curve obtained under complex loading conditions is the bisector of an angle between the fatigue damage curves plotted under the axial and torsion loading conditions.

The results of the tests shown in Fig. 4d were obtained for the in-phase and out-of-phase axial-torsion loading conditions for different values of the mean stresses, different phase differences, and different shapes of the loading waveform. Since both axial and torsional loads are included in these loading conditions, we can use these data to plot the fatigue damage curve directly for the complex loading conditions. It can be seen that the proposed method provides good agreement. The tests in Fig. 4e correspond to more complicated loading conditions with different shapes of the load path. It can be seen that the results are also good, to within a factor of two, accepted as reasonable in the fatigue tests.

The tests in Fig. 4f correspond to the same material as in Fig. 4c, but the loading conditions are more complicated and containing different load paths. First, we use Eq. (8) to predict the fatigue damage curve under the complex loading conditions with the help of the axial and torsion fatigue damage curves but without using the data generated for the complex loading conditions. Then the experimental data on fatigue under complex loading conditions are compared with the predicted fatigue damage curve. The complex loading conditions have different loading paths but all load paths satisfy the equation ε_max/γ_max=3^0.5. Therefore, it is assumed that the influence coefficient ξ/ζ=3^0.5. This means that the fatigue curve in this particular complex loading mode is closer to the fatigue damage curve under the conditions of axial loading. It can be seen that the predicted fatigue damage curve almost coincides with the curve based on the direct fitting of the experimental data.

Conclusions

In the present paper, we propose a new fatigue parameter, which suggests a new way of thinking to tackle the fatigue damage problems. The difference between this new method and the other existing methods is that there is no need to choose certain stresses, strains, or energy components in a certain material plane as representative parameters to compute the fatigue damage. The stress components in each material plane at a certain material point are averaged and included in the method, which can show all features of the stress state at a certain material point. In this new method, the difference between the tension and compression states and the influence of the mean stress are taken into account.

Some experiments with different materials and different loading conditions are used to validate the capabilities of the proposed method both for the data representation and for the life prediction. The loading conditions considered in the procedure of validation include reversed axial, reversed torsion, axial cycling with nonzero mean stress, and torsion cycling with nonzero mean stress. We also studied different types of the specimens, different shapes of the loading waveform, in-phase and out-of-phase load, and different loading paths. The accumulated results show that the proposed method provides good correlations and predictions for all investigated materials and loading conditions.

Appendix

For the case in Fig. 2d, the FP is computed as follows:

$$ \mathrm{FP}=\frac{\oint \left(A|\sigma |+B|\tau |\right). ds}{L}. $$

The integral is taken with respect to the angle that describes Mohr’s circle, between 0 and π, in view of the symmetry of τ in Mohr’s circle as explained earlier. Thus, we obtain

$$ \mathrm{FP}=\frac{2\underset{0}{\overset{\pi }{\int }}\left[A\left(\frac{\sigma_1-{\sigma}_2}{2}\cos \theta +\frac{\sigma_1+{\sigma}_2}{2}\right)+B\frac{\sigma_1-{\sigma}_2}{2}\sin \theta \right]\frac{\sigma_1-{\sigma}_2}{2} d\theta}{\pi \left({\sigma}_1-{\sigma}_2\right)}. $$

Finally, we get

$$ {\displaystyle \begin{array}{cc}\frac{\mathrm{\partial FP}}{\partial {\sigma}_1}=\frac{A}{2}+\frac{B}{\pi },& \frac{\mathrm{\partial FP}}{\partial {\sigma}_2}\end{array}}=\frac{A}{2}+\frac{B}{\pi }. $$