1 Introduction

The flow in a channel with non-parallel walls was firstly discussed by Jeffery [1] and Hamel [2] in 1915. Therefore, it is also called Jeffery–Hamel flow. Researchers are still showing interest in the work done by these two and have extended the scope to study different variations of velocity and temperature under varying conditions.

Due to the industrial, medical, biomedical and engineering applications, till now, many studies have been carried out, which show that the variation in flow behavior is possible with a change in angle between the walls [3–7]. All these studies were carried out considering the Newtonian nature of the fluid, and no one attempted to extend the idea to non-Newtonian fluids other than Hayat et al. [8] and Asadullah et al. [9]. They used non-Newtonian fluids and studied the effects of angle opening and other involved parameters on velocity and temperature profiles.

These days, nanotechnology is gaining more importance due to the applications in engineering, real life, medical sciences and other applicable areas. The idea is to add a part of nanoparticles to some base fluids. It not only enhances the thermal properties of the fluids but also affects the velocity of the fluids. Different models have been used to analyze the various thermal and physical properties of nanofluids. Among others, one of the models is presented by Choi [10, 11]. Hamilton and Crosser model [12] is also one of these models presented. Later on, Buongiorno [13] presented a comprehensive model that incorporated both Brownian motion and thermophoresis into account. Xue [14] noticed that the existing models consider only the spherical or rotational elliptical nature of the nanoparticles. Also, these models do not account for the effect of the space distribution of the CNTs on thermal conductivity. Based on Maxwell theory [15], Xue proposed a theoretical model that considered the rotational elliptical nanotubes with very large axial ratio and compensating the effects of the space distribution on CNTs. Some of the studies available in open literature can be found in [16–25] and references therein. Jeffery–Hamel flow is also a part of these studies. Some studies related to Jeffery–Hamel flow of nanofluids can be seen in [26–29].

At the end of twentieth century, Iijima [30] discussed the potential applications of carbon nanotubes (CNTs) for various devices, solar cells, ultra-capacitors, gas storage, etc. [31, 32]. Different types of carbon nanotubes are available. Normally, we characterize these to two types, i.e., single-walled (SWCNTs) and multi-walled (MWCNTs). In single-walled CNTs, there is only one layer or wall holding the particles together. On the other hand, in MWCNTs there is a collection of nested tubes that continue to increase in diameter. MWCNTs may contain one inner tube and one outer tube called double-walled tubes to 100 tubes. These CNTs result in more enhanced thermal properties of base fluids as compared to any other nanoparticles. In a study, Murshed et al. [33] concluded that carbon nanotubes may increase the thermal conductivity of the base fluid as much as 6 times. Many studies are available using CNTs to analyze the flow behavior and heat transfer in different geometries.

To the best of our knowledge, no one has ever attempted to study the flow of CNT-based nanofluids between non-parallel walls. Using model presented by Xue, equations governing the flow are transformed to a set of nonlinear ordinary differential equations. Due to the nonlinearity and abstract nature of the problem, an exact solution is unlike; hence, a numerical solution using Runge–Kutta–Fehlberg method is obtained. Investigation is carried out by taking the velocity slip effects into consideration. Effects of the nanoparticle volume fraction, inclination angle, Reynolds number and Eckert number on the temperature profile are presented with the help of graphs. A comprehensive discussion is presented to highlight the certain aspects of analysis. A comparative study with already existing results backs the results presented in current study.

2 Governing equations

Consider the flow of a fluid commenced by the presence of a source or sink at the intersection of two rigid planer plates. The walls make an angle 2α with each other (see Fig. 1). A radial and symmetric nature of the flow is taken. The plates are embedded in a nanofluid medium filled with SWCNTs and MWCNTs as nanoparticles. There is a thermal equilibrium between the base fluid (water) and the nanoparticles (CNTs). A velocity slip at the walls of the channel is assumed. Under the above assumptions, the velocity field takes the form V = [\(\hat{u}_{r}\), 0, 0], where \(\hat{u}_{r}\) is a function of r and θ both.

Fig. 1
figure 1

Schematic diagram for the flow problem

Full size image

In the absence of body forces, the equations governing the flow are written in the form [34]

$$\frac{1}{r}\frac{\partial }{\partial r}(r\hat{u}_{r} ) = 0,$$
(1)
$$\rho_{nf} \left( {\hat{u}_{r} \frac{{\partial \hat{u}_{r} }}{\partial r}} \right) = - \frac{\partial p}{\partial r} + \mu_{nf} \left[ {\frac{{\partial^{2} \hat{u}_{r} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial \hat{u}_{r} }}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} \hat{u}_{r} }}{{\partial \theta^{2} }} - \frac{{\hat{u}_{r} }}{{r^{2} }}} \right],$$
(2)
$$- \frac{1}{{\rho_{nf} r}}\frac{\partial p}{\partial \theta } + \frac{2}{{r^{2} }}\frac{{\mu_{nf} }}{{\rho_{nf} }}\frac{{\partial \hat{u}_{r} }}{\partial \theta } = 0,$$
(3)
$$\hat{u}_{r} \frac{{\partial \hat{T}}}{\partial r} = \frac{{k_{nf} }}{{\left( {\rho C_{p} } \right)_{nf} }}\left[ {\frac{{\partial^{2} \hat{T}}}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial \hat{T}}}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} \hat{T}}}{{\partial \theta^{2} }}} \right] + \mu_{nf} \left[ {4\left( {\frac{{\partial \hat{u}_{r} }}{\partial r}} \right)^{2} + \frac{1}{{r^{2} }}\left( {\frac{{\partial \hat{u}_{r} }}{\partial \theta }} \right)^{2} } \right].$$
(4)

Boundary conditions for the problem are,

$$\begin{array}{lll} {\hat{u}_{r} = U,} & {\frac{{\partial \hat{u}_{r} }}{\partial \theta } = 0,} & {\frac{{\partial \hat{T}}}{\partial \theta } = 0} \\ {\hat{u}_{r} = - \gamma_{1} \frac{{\partial \hat{u}_{r} }}{\partial \theta },} & {\hat{T} = \hat{T}_{w} } & {} \\ \end{array} \quad {\text{at}}\;\begin{array}{l} {\theta = 0,} \\ {\theta = \alpha .} \\ \end{array}$$
(5)

In above equations, \(\hat{u}_{r}\) is the component of the velocity, γ 1 is the velocity slip parameter and \(\hat{T}\) is the temperature of the base fluid. Further, ρ nf , μ nf , (ρC p ) nf and k nf denote the density, dynamic viscosity, heat capacity and thermal conductivity of the fluid, respectively [14, 37–39], where

$$\upsilon_{nf} = \frac{{\mu_{nf} }}{{\rho_{nf} }},\quad \mu_{nf} = \frac{{\mu_{f} }}{{\left( {1 - \phi } \right)^{2.5} }},\quad \alpha_{nf} = \frac{{k_{nf} }}{{\left( {\rho C_{p} } \right)_{nf} }},\quad \rho_{nf} = \left( {1 - \phi } \right)\rho_{f} + \phi_{\text{CNT}} ,$$
(6)
$$\left( {\rho C_{p} } \right)_{nf} = \left( {1 - \phi } \right)\left( {\rho C_{p} } \right)_{f} + \phi \left( {\rho C_{p} } \right)_{\text{CNT}} ,$$
(7)
$$\frac{{k_{nf} }}{{k_{f} }} = \frac{{1 - \phi + 2\phi \left( {\frac{{k_{\text{CNT}} }}{{k_{\text{CNT}} - k_{f} }}} \right)\ln \left( {\frac{{k_{\text{CNT}} + k_{f} }}{{2k_{f} }}} \right)}}{{1 - \phi + 2\phi \left( {\frac{{k_{f} }}{{k_{\text{CNT}} - k_{f} }}} \right)\ln \left( {\frac{{k_{\text{CNT}} + k_{f} }}{{2k_{f} }}} \right)}}.$$
(8)

Here, μ f is the viscosity of base fluid and ϕ is the nanoparticle volume fraction. k f and k CNT are the thermal conductivities, and ρ f and ρ CNT are densities of base fluid and CNT, respectively.

Equation (1) can also be written as

$$f(\theta ) = r\hat{u}_{r} \left( {r,\theta } \right)$$
(9)

Employing the similarity transform, above equations can be reduced to following dimensionless form

$$F(\eta ) = \frac{f(\theta )}{{f_{\hbox{max} } }},\quad \eta = \frac{\theta }{\alpha },\quad \varTheta \left( \eta \right) = \frac{{\bar{T}}}{{\bar{T}_{w} }}.$$
(10)

By eliminating the pressure p from Eqs. (2) and (3) and using Eqs. (9) and (10), the above system gets reduced to a system of nonlinear ordinary differential equations in terms of velocity and temperature profiles as under

$$F^{'''} (\eta ) + 2\alpha Re\left( {1 - \phi } \right)^{2.5} \left( {\left( {1 - \phi } \right) + \phi \frac{{\rho_{\text{CNT}} }}{{\rho_{f} }}} \right)F(\eta )F^{'} (\eta ) + 4\alpha^{2} F^{'} (\eta ) = 0,$$
(11)
$$\frac{{k_{nf} }}{{k_{f} }}\varTheta^{''} \left( \eta \right) + \frac{EcPr}{{\left( {1 - \phi } \right)^{2.5} }}\left( {\left( {1 - \phi } \right) + \phi \frac{{\left( {\rho C_{p} } \right)_{\text{CNT}} }}{{\left( {\rho C_{p} } \right)_{f} }}} \right)\left[ {4\alpha^{2} F^{2} \left( \eta \right) + \left( {F^{'} \left( \eta \right)} \right)^{2} } \right] = 0.$$
(12)

After implementing the similarity transform, boundary conditions also get reduced to

$$\begin{aligned} F(0) = 1,\quad F^{'} (0) = 0,\quad F(1) = - \frac{\gamma }{{\left( {1 - \phi } \right)^{2.5} }}F^{'} (1) \hfill \\ \varTheta^{'} \left( 0 \right) = 0, \quad \varTheta \left( 1 \right) = 0. \hfill \\ \end{aligned}$$
(13)

Here, Re is Reynolds number defined as:

$$Re = \frac{f}{\upsilon } = \frac{Ur\alpha }{\upsilon }\left( \begin{aligned} {\text{Divergent}}\;{\text{Channel}}:\alpha > 0,U > 0 \hfill \\ {\text{Convergent}}\;{\text{Channel}}:\alpha < 0,U < 0 \hfill \\ \end{aligned} \right).$$
(14)

Further, \(Ec = \frac{{\mu c_{p} }}{k}\), \(Pr = \frac{{U^{2} }}{{c_{p} T_{w} }}\) and \(\gamma = \frac{{\gamma_{1} }}{\alpha }\) are Eckert number, Prandtl number and the velocity slip parameter, respectively. Quantities of physical interest are skin friction coefficient and Nusselt number defined as:

$$C_{F} = \frac{{\mu_{nf} \left( {\tau_{r\theta } } \right)_{\eta = 1} }}{{\rho_{nf} U^{2} }},$$
$$Nu = \frac{{ - lk_{f} \left( {q_{w} } \right)_{\eta = 1} }}{{kT_{w} }}.$$

Dimensionless form of the same quantities can be written as

$$Re_{r} C_{f} = \frac{1}{{\left( {1 - \phi } \right)^{2.5} \left( {\left( {1 - \phi } \right) + \phi \frac{{\rho_{\text{CNT}} }}{{\rho_{f} }}} \right)}}F^{'} (1),$$
(15)
$$\alpha Nu = - \frac{{k_{nf} }}{{k_{f} }}\varTheta^{'} \left( 1 \right).$$
(16)

3 Solution procedure

Equations (11) and (12) together with the boundary conditions (13) represent a two-point boundary value problem. We solve it using a well-known numerical method called Runge–Kutta–Fehlberg technique. Nonlinear boundary value problem is firstly converted into a system of initial value problems using the shooting technique, and then, the solutions is obtained by using Runge–Kutta–Fehlberg method. Step size is taken as Δη = 0.01, and a tolerance level of 10−6 is restricted to obtained the asymptotically convergent results.

4 Results and discussion

In this section, the main focus is to discuss the behavior of non-dimensional velocity and temperature profiles under the influence of varying parameters. In Table 1, the properties of physical and thermal interest linked to the base fluid and nanoparticles are given. These properties are used to explore the changes emerging in velocity and temperature profiles subject to the variations in different parameters. For the said purpose, two subsections are presented: one for the diverging channel and the other for the converging channel.

Table 1 Physical and thermal properties of base fluid and CNTs [35–37]
Full size table

4.1 Diverging channel

Figures 2, 3, 4, 5, 6, 7, 8, 9 and 10 are plotted to discuss the variations in velocity and temperature profiles. Figure 2 gives a graphical description of the flow under the variation in angle α for diverging channel. With an increase in opening angle α, velocity is seen to be declining. At the centerline of the channel, the velocity bears a maximum value, while, on moving toward the walls, drop in velocity is observed. Slightly higher values of the velocity for MWCNTs are clearly perceived. A decrease in the velocity profile for increasing Reynolds number is depicted in Fig. 3. A curvy profile for the velocity is observed at the center of the channel. This clearly shows that, for the dominate velocity, Reynolds number tends to get higher values, which in result causes the velocity to decelerate. Also, with the rising values of Reynolds number, there comes a point where some backflow regions may emerge near the walls. MWCNTs tend to get higher values for increasing Re as compared to SWCNTs.

Fig. 2
figure 2

Velocity profile for variation in α

Full size image
Fig. 3
figure 3

Velocity profile for variation in Re

Full size image
Fig. 4
figure 4

Velocity profile for variation in ϕ

Full size image
Fig. 5
figure 5

Velocity profile for variation in γ

Full size image
Fig. 6
figure 6

Temperature profile for variation in α

Full size image
Fig. 7
figure 7

Temperature profile for variation in Re

Full size image
Fig. 8
figure 8

Temperature profile for variation in ϕ

Full size image
Fig. 9
figure 9

Temperature profile for variation in γ

Full size image
Fig. 10
figure 10

Temperature profile for variation in Ec

Full size image

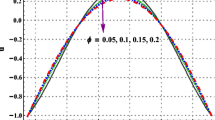
The behavior of the velocity profile for increasing nanoparticle volume fraction is depicted in Fig. 4. An increase in the amount of nanoparticles considerably changes the velocity near the walls; however, minor effect at the mid-portion of the channel is observed. Evidently, SWCNTs have a slightly lower velocity than MWCNTs, which is due to the higher density values for SWCNTs. Velocity slip parameter provides an accelerated flow near the walls as shown in Fig. 5. No effect of the said parameter is seen at the center of the channel. This is obviously due to the slip condition acting at the wall. Slip condition has no effect on the velocity near the central region of the channel. This means that near the walls, slip conditions raise the velocity of the fluid that causes the fluid to regain its original velocity at the central portion of the channel.

Figures 6, 7, 8, 9 and 10 are plotted to show the impacts of channel opening, Reynolds number, Eckert number and γ on the temperature profile. Since water is used as a base fluid, Prandtl number needs to be fixed at 6.2. Effects of increasing angle α are portrayed in Fig. 6. As we increase the opening, higher values of the temperature are observed. This phenomenon is more prominent at the center of the channel. MWCNTs tend to have higher values of temperature than the SWCNTs. Higher thermal conductivity of MWCNTs is a major factor behind this. An analogous behavior of the temperature profile for increasing Reynolds number can be seen in Fig. 7. The only difference is the higher thermal values in the case of Re. This means, higher the viscous forces, higher the temperature of the fluid.

In Fig. 8, the variations in temperature due to an increment in nanoparticle volume fraction are plotted. A certain decrement in temperature is seen for the case of diverging channel. Almost identical values for both SWCNTs and MWCNTs are observed. Velocity slip parameter is seen to affect the temperature profile quite significantly. Lower values of temperature are seen with the increasing values of slip parameter as depicted in Fig. 9. Major variations are at the centerline of channel for both the nanoparticle volume fraction and velocity slip parameter. In Fig. 10, the main outcomes following increasing Eckert number on temperature profile are portrayed. A sudden upsurge in temperature of the fluid is observed near the centerline of channel. Since the dissipation function Ec is the ratio of specific heat to the thermal conductivity, it causes the temperature profile to rise quite significantly. Again, MWCNTs have a slightly higher value of temperature as compared to SWCNTs.

4.2 Converging channel

As painted in Figs. 11 and 12, the change in α and Re for converging channel results in a quite opposite behavior of velocity to the one seen in diverging channel. A constant value of velocity is observed at the mid of the channel, and as we move near the walls, a steep decrease clearly exhibits the boundary layer character of the flow. For increasing nanoparticle volume fraction, an increment in the velocity is observed in Fig. 13 for the case of converging channel. For all the above cases, MWCNTs have a slightly lower velocity value as compared to SWCNTs. Slip parameter γ effects the velocity profile in an almost similar manner as it does in diverging channel, i.e., an increase in the velocity is witnessed (Fig. 14). However, for converging channel, the change is quite rapid near the walls.

Fig. 11
figure 11

Velocity profile for variation in α

Full size image
Fig. 12
figure 12

Velocity profile for variation in Re

Full size image
Fig. 13
figure 13

Velocity profile for variation in ϕ

Full size image
Fig. 14
figure 14

Velocity profile for variation in γ

Full size image

Figures 15, 16, 17, 18 and 19 are portrayed to analyze the behavior of temperature profile under varying angle, Reynolds number, nanoparticle volume fraction, slip velocity parameter γ and Eckert number Ec, respectively. Clearly, \(\varTheta \left( \eta \right)\) declines with a growth in α, Re and ϕ. The observed behavior is quite opposite to the one seen in diverging channel. Almost identical temperature profile for the velocity slip parameter γ is seen. Slightly higher temperature values for MWCNTs are observed. To see the effects of Eckert number Ec, Fig. 19 is plotted. Alike behavior of the temperature profile for both converging and diverging channels is a major observation. Also, \(\varTheta \left( \eta \right)\) attains its extreme value near the center of the plates for all the parameters involved.

Fig. 15
figure 15

Temperature profile for variation in α

Full size image
Fig. 16
figure 16

Temperature profile for variation in Re

Full size image
Fig. 17
figure 17

Temperature profile for variation in ϕ

Full size image
Fig. 18
figure 18

Temperature profile for variation in γ

Full size image
Fig. 19
figure 19

Temperature profile for variation in Ec

Full size image

A comparison of the solution obtained by Runge–Kutta–Fehlberg method with some of already existing solutions (of the limited cases of the same problem) is provided in Table 2. An exceptionally well agreement has been found, which supports out results.

Table 2 Comparative study of present results to the already existing solutions in the literature for ϕ = γ = 0
Full size table

Behavior of the skin friction coefficient and the rate of heat transfer at the wall (Nusselt number) under varying different emerging parameters for both converging and diverging channels is provided in the form of figures. For the said purpose, Figs. 20, 21, 22, 23, 24, 25, 26, 27, 28 and 29 are portrayed. From Figs. 20 and 21, it can clearly be observed that for increasing values of velocity slip parameter, the skin friction tends to decrease for both diverging and converging channels. However, the skin friction has relatively higher values for converging channels. From the applications point of view, velocity slip can play a major role to reduce the effects of skin friction near the walls. Angle opening α affects the skin friction in diverging channel in a way opposite to the converging channels as shown in Figs. 21 and 22. An increase in the skin friction is seen for the case of converging channel, while for diverging it tends to decrease with increasing α. Also, MWCNTs tend to have higher values as compared to SWCNTs for both the parameters.

Fig. 20
figure 20

Skin friction for varying γ (diverging channel)

Full size image
Fig. 21
figure 21

Skin friction for varying γ (converging channel)

Full size image
Fig. 22
figure 22

Skin friction for varying α (diverging channel)

Full size image
Fig. 23
figure 23

Skin friction for varying α (converging channel)

Full size image
Fig. 24
figure 24

Skin friction for varying Re (diverging channel)

Full size image
Fig. 25
figure 25

Skin friction for varying Re (converging channel)

Full size image
Fig. 26
figure 26

Nusselt number for varying α (diverging channel)

Full size image
Fig. 27
figure 27

Nusselt number for varying (converging channel)

Full size image
Fig. 28
figure 28

Nusselt number for varying γ (diverging channel)

Full size image
Fig. 29
figure 29

Nusselt number for varying λ (converging channel)

Full size image

In Figs. 23 and 24, the variations in the skin friction for altering Re are plotted. An increased skin friction is seen for the converging channel, while for the diverging channel, a drop in skin friction coefficient is observed. Higher values of the skin friction at the wall for MWCNTs in diverging channel are a major difference as compared to the lower values in converging channel.

Variations in Nusselt number for different parameters are plotted in Figs. 26, 27, 28 and 29. One can easily observe the increment in Nusselt number for varying angles. The rate of heat transfer at the wall is perceived to be higher for diverging channel as compared to the converging channel. For slip parameter, similar effects on Nusselt number are seen for both the channels. Slip velocity tends to increase the rate of heat transfer at the wall for both channels.

5 Conclusions

The present study is devoted to formulate Jeffery–Hamel flow for the case of carbon nanotubes suspended nanofluid flow with heat transfer considering the velocity slip effects. Non-dimensional form of the equations governing the flow is obtained by using a similarity transform. Obtained results are plotted in the graphs, and variations in velocity and thermal profiles are discussed comprehensively. Comparative study is also presented to authenticate the obtained solutions by using existing solutions in the literature. Effects of involved parameters have been discussed above, and in short the following conclusions can be established:

  • The obtained numerical solution leads to reliable and easily computable results.

  • Increase in angle opening and Reynolds number forms backflow regimes for the case of divergent channel.

  • The nanoparticle volume fraction tends to decrease the velocity and temperature profiles for both convergent and divergent channels.

  • Velocity slip parameter increases the velocity profile for both convergent and divergent channels. However, the temperature profile decreases for diverging channel with increasing slip parameter and increases for converging channel.

  • The slip increases the velocity profile for both the converging and diverging channels while the temperature is seen to be decreasing with an increase in slip parameter.

  • Dissipation effect increases the temperature of the fluid for both divergent and convergent channels.

  • Numerical values of the skin friction coefficient are on a higher side for convergent channel as compared to the divergent channel.

  • SWCNTs have higher rate of heat transfer at the walls of the channel for increasing α in the case of diverging channel and lower values for α in the case of converging channel, while for some other parameters, rate of heat transfer has no change for SWCNTs and MWCNTs.

  • For diverging channel, the value of skin friction is greater for MWCNTs as compared to SWCNTs.