1 Introduction

Understanding liquid transport in nanoscale confinements is important for a variety of applications including water filtration and desalination (Hinds et al. 2004), modeling of oil and water transport in shale reservoirs (Bernard et al. 2012) and investigation of drug transport across biological cell membranes (Park et al. 2009). Dominated by the large surface area-to-volume ratio, liquids inside nanoscale confinements experience wall force field effects and exhibit substantially different physics than what is observed in larger scales. It is essential to understand the nanoscale transport phenomena, which can be investigated using molecular dynamics (MD) simulations (Koplik and Banavar 1995; Karniadakis and Beskok 2005; Li et al. 2010). Knowing the limitations of continuum-based approaches in nanoscale transport problems is equally important, since continuum models are computationally cheaper and easier to use in engineering applications.

Navier–Stokes equations are based on the assumptions of isotropy, local thermodynamic equilibrium, and linear constitutive laws such as the Newton’s law of viscosity and Fourier law of heat conduction. Liquid–wall interactions in nanoscale channels influence hydrodynamics of the system in several ways. Density layering near the surfaces induces inhomogeneity of the liquid normal to the surface. In addition, no-slip, slip or stick (liquid adsorption) can be observed at the liquid–wall interface, depending on the liquid–wall interaction strength (Nagayama and Cheng 2004). Moreover, local thermodynamic equilibrium of the system, macroscopic definitions of density and velocity distributions (Travis et al. 1997a; Hartkamp and Luding 2010), and the constitutive laws (Travis and Gubbins 2000; Xu and Zhou 2003) might breakdown.

It is a well-known fact that liquid density in nanoscale confinements results in an average density lower than the bulk value (Travis and Gubbins 2000; Wu et al. 2013; Wang and Hadjiconstantinou 2015), and the average density decreases with decreasing channel height (Raghunathan et al. 2007; Suk and Aluru 2013; Bhadauria and Aluru 2013). MD simulations of force-driven liquid flows have shown that density profiles in nano-channels are independent of the magnitude of the driving force (Travis et al. 1997a; Sokhan et al. 2002; Toghraie Semiromi and Azimian 2010). However, nano-confinements may induce significant changes in liquid viscosity. In order to investigate viscosity variations, it is possible to define an apparent viscosity μ a as a characteristic of the flow field which can be different than the thermodynamic viscosity μ td. While experimental research has contradicting findings about the relation between the apparent and thermodynamic viscosities (Debye and Cleland 1959; Chan and Horn 1985; Israelachvili 1986; Gee et al. 1990), theoretical works extract viscosity using equilibrium and non-equilibrium MD. In the former method, diffusion coefficient for liquid molecules is found from Green–Kubo relation (Allen and Tildesley 1987), and Einstein relation (Heyes 1998) is used to calculate the viscosity (Meier et al. 2004; Thomas and McGaughey 2008; Thomas et al. 2010; Suk and Aluru 2013), while the latter method predicts apparent viscosity using a parabolic fit to the streaming velocity profile (Sokhan et al. 2002; Suk and Aluru 2013). MD results indicate viscosity dependence on the near-wall liquid distribution and wall structure. Literature shows both viscosity decrease (Sokhan et al. 2002; Thomas and McGaughey 2008) and viscosity increase (Suk and Aluru 2013) with the reduced channel height.

The second critical aspect that changes the hydrodynamics of the system in nanoscale confinement is slip at the liquid–wall interface, which consequently influences the mass flow rate. Experimental and computational results for slip length and flow rate variations in nanoscale confinements have been reviewed in Karniadakis and Beskok (2005). Regarding the velocity slip, several investigators focused on validating the no-slip condition (Koplik et al. 1988, 1989), while others defined a general boundary condition at the interface (Thompson and Troian 1997). Effects of different parameters such as pressure (Liang and Keblinski 2015), channel size (Liu and Li 2011; Suk and Aluru 2013), nanotube diameter (Sokhan et al. 2002; Thomas and McGaughey 2008, 2009), as well as different surface wettability conditions (Bhadauria and Aluru 2013) on slip length, and mass flow rate have been investigated. Some MD studies also show nonlinear variations in the slip length, including unbounded slip values beyond a critical shear rate (Thompson and Troian 1997). Such results were obtained under extreme shear rates, where variations in the fluid viscosity and other transport properties and performance of the utilized thermostat must be investigated. Reported slip lengths also show sensitivity to atomistic modeling of solid surfaces using cold or thermally interacting wall models (Bernardi et al. 2010). It is important to describe MD results by carefully choosing and maintaining the thermodynamic state despite the wall force field effects. Unfortunately, few studies in the literature delineate or differentiate their results as a function of the local thermodynamic state of liquid, which could be the reason of contradicting results in the literature.

In this paper, we investigate mass and momentum transport in force-driven liquid flows both in nanoscale periodic domains and in nanoscale channels. Our objectives are to systematically investigate the effects of nano-confinement on liquid and flow properties and identify deviations from the classic continuum solution for Poiseuille flow. In order to establish this, we first quantify viscosity of liquid argon at a known thermodynamic state in a periodic domain. Then, we investigate the variations in liquid density, viscosity, velocity, slip length, shear stress and mass flow rate in different sized nano-channels as a function of the channel height. Our study distinguishes itself from the literature by carefully fixing and maintaining liquid argon at a known thermodynamic state for a wide range of channel sizes.

This work is organized as follows: In Sects. 2 and 3, we describe the theoretical background and MD simulation parameters for nanoscale force-driven flows, respectively. In Sect. 4, we present viscosity calculation in nanoscale periodic domains and investigate the effects of simulation box size, periodic dimension size, and the Lennard-Jones cutoff distance on simulation results. Section 5 presents investigations of local velocity, density, viscosity, slip length, mass flow rate, and shear stress as a function of the channel height and examine the validity of continuum solution. Conclusions are presented in Sect. 6.

2 Theoretical background and model description

Boundary conditions at the solid–liquid interface and the smallest length scale that allows continuum transport description are crucial for investigation of mass, momentum and energy transport in nanoscale confinements (Karniadakis and Beskok 2005). Molecular dynamics simulations of force-driven flows with a constant force applied on each liquid molecule have been used to investigate the fluid viscosity (Travis et al. 1997b), slip length and mass flow rate (Suk and Aluru 2013) in nano-channels. Considering steady, incompressible, force-driven, fully developed flow confined between two parallel plates with separation h, Navier–Stokes equations in the stream-wise direction can be reduced to:

$$\frac{{d^{2} u\left( z \right)}}{{dz^{2} }} = - \frac{f}{\mu }$$
(1)

where µ is the apparent viscosity and f is the body force applied on the system (N/m3). For macroscopic channels, apparent viscosity in Eq. 1 is equivalent to the absolute viscosity at a given thermodynamic state. Boundary conditions at the liquid–solid interface (\(z = 0\) and z = h) consider velocity slip described by a Navier-type slip condition (Lamb 1932)

$$u_{l} - u_{w} = \beta \frac{{{\text{d}}u}}{{{\text{d}}z}}$$
(2)

where u l is the liquid velocity, u w is the wall velocity, and β is the slip length. Solution of Eq. 1 subject to slip conditions results in the following velocity profile

$$u\left( z \right) = \frac{{ - fh^{2} }}{2\mu }\left( {\left( {\frac{z}{h}} \right)^{2} - \left( {\frac{z}{h}} \right)} \right) + \frac{hf\beta }{2\mu }$$
(3)

First term on the right-hand side is the parabolic velocity profile typical of no-slip solution, while the second term is due to velocity slip. The no-slip and slip velocity terms will be used to determine the liquid viscosity and slip length, respectively. Integration of the velocity profile across the channel by assuming constant density and uniform channel width (W) gives the mass flow rate:

$$\dot{m} = \rho W\mathop \int \limits_{0}^{h} u\left( z \right){\text{d}}z = \frac{{\rho wh^{3} f}}{12\mu }\left( {1 + 6\frac{\beta }{h}} \right)$$
(4)

For a known thermodynamic state, one can easily predict the velocity profile and mass flow rate using Eqs. 3 and 4. Knowing the limitations of these equations is crucial in nanoscale fluids engineering, since one needs to rely on costly molecular-level calculations only if there is a need.

3 Methodology and simulation details

We used molecular dynamics code LAMMPS (Large-Scale Atomic/Molecular Massively Parallel Simulator) to simulate a planar force-driven liquid argon flow in periodic rectangular domains and in gold channels with heights, h, varying from 3.26 to 35.89 nm. All simulations were performed at 119.8 K temperature and 1411.5 kg/m3 density (ρ* = 0.84), where argon is compressed liquid with absolute viscosity of 240.74 µPa s (Stewart and Jacobsen 1989).

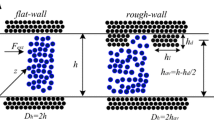
The periodic box simulations were performed in domains that are 2h in height and utilized two equal body forces acting in opposite directions within half of the domain. These resulted in two parabolic velocity profiles that connect on the periodic sides and at the center of the domain, naturally satisfying the no-slip conditions in the absence of walls. Objectives of the periodic domain simulations were to assess the effects of domain periodicity, cutoff distance and simulation box size on the absolute viscosity of liquid argon at specified thermodynamic state. These simulations were essentially used for verification of the methodology that will be used to predict the apparent viscosity in nano-channels. The second set of simulations focused on liquid argon flow in gold channels (Fig. 1). For all simulations, a constant force in the stream-wise direction is added to each molecule. The domain is constructed using 2028 gold molecules with 6 wall layers on each side. Gold molecules are 0.204 nm apart and form face-centered cubic (FCC) structure with (100) plane facing argon. Wall molecules are fixed at their initial location and do not have wall–wall molecular interactions (i.e., cold wall model). Different number of argon molecules are used for different channel/domain sizes, as shown in Table 1. Periodic boundary conditions are applied in the stream-wise and span-wise directions kept at 5.3 nm length and width. Flow parameters are obtained using 0.2267 Å tall slab-bins.

Fig. 1
figure 1

Schematic and dimensions of the simulation domain a. A snapshot of Argon molecules bounded by the FCC gold walls b

Full size image
Table 1 Fluid domain information for different sized channels
Full size table

Body force applied on each molecule is chosen carefully to result in a maximum fluid velocity less than 25 m/s to eliminate nonlinear behaviors shown in the literature (Thompson and Troian 1997; Xu and Zhou 2003). Mass of an argon molecule is \(m_{\text{Ar}} \,= 6.63 \times 10^{ - 26}\,{\text{kg}}\), its molecular diameter is \(\sigma_{\text{Ar}} \,= 0.3405\,{\text{nm}}\) and the depth of the potential well \(\in_{\text{Ar}} \,= 1.65399 \times 10^{ - 21}\,{\text{J}}\), while parameters for gold molecules are as \(m_{\text{Au}} \,= 3.27 \times 10^{ - 25}\,{\text{kg}}\), \(\sigma_{\text{Au}} \,= 0.2934\,{\text{nm}}\), \(\in_{\text{Au}} \,= 2.7096 \times 10^{ - 22}\,{\text{J}}\). Interatomic interactions between Au and Ar are obtained using Kong mixing rule (Sutmann et al. 2002) and result in \(\sigma_{{{\text{Au}} - {\text{Ar}}}} = 0.3227\,{\text{nm}}\) and \(\in_{{{\text{Au}} - {\text{Ar}}}} = 5.9142 \times 10^{ - 22}\,{\text{J}}\). Both Ar and Au atoms interact via Lennard-Jones interatomic potential defined by:

$$V\left( {r_{ij} } \right) = \left\{ {\begin{array}{*{20}l} {4 \in \left[ {\left( {\frac{\sigma }{{r_{ij} }}} \right)^{12} - \left( {\frac{\sigma }{{r_{ij} }}} \right)^{6} } \right] - V\left( {r_{\text{c}} } \right) } & { r \le r_{\text{c}} } \\ 0 & {r > r_{\text{c}} } \\ \end{array} } \right.$$
(5)

where r ij is the interatomic distance, r c is the cutoff distance, and V(r c) is the value of interatomic potential at r = r c.

Simulations are started from the Maxwell–Boltzmann velocity distribution for liquid argon molecules at 119.8 K and ran for different time periods for each case to reach fully developed flow using 1 fs time steps. The time scale for momentum diffusion is estimated in each domain using t d ≈ h 2/ν, where ν is the kinematic viscosity and h is the channel/domain height. To ensure that simulations have reached a steady state, each case is run for \(16\,{{t}}_{\text{d}}\), after which, the results were averaged for 16 ns (16 × 106 time steps) using canonical NVT ensemble. Nose–Hoover thermostat is applied on the liquid domain to maintain it at 119.8 K. Results are recorded every 1 × 104 time steps (10 ps), resulting in 1600 data sets to obtain the time-averaged results. To determine the standard deviation in averaged quantities, we first obtain the average of each 80 data sets and then calculate the standard deviation for 20 cumulative sets of data.

4 Periodic domain with no physical boundaries

Viscosity of the fluid is a key parameter that determines the flow characteristics. Therefore, it is critical to develop a methodology to obtain the viscosity accurately. Following Backer et al. (2005), we subdivided the spatially periodic domain into two equal systems and applied an equal body force in opposing directions, which resulted in two counter-flowing planar force-driven flows without explicit boundaries. Applying external forces cause viscous heating in the system, and this heat should be removed to fix the temperature at a desired value. In this work, we first remove the bias velocity from the liquid molecules and then apply Nose–Hoover thermostat (Evans and Holian 1985) to control the temperature. Figure 2 shows the velocity profile for a periodic box of 2h = 6.53 nm at 119.8 K and 1411.5 kg/m3. To determine the liquid viscosity, we calculate four different viscosities and calculate their average. First, we fit a second-order polynomial for the velocity profile in the form of u = az 2 + bz + c, on each side of the periodic box, which has been labeled as “velocity polynomial fit” in Fig. 2. Then, we use the “a” coefficients in the two velocity fits to calculate \(\mu_{1 }\) and μ 2 using μ = −f/2a. Second, we use the maximum velocity, u max, that occurs at the center of each section and find coefficient “a” from u = az(z − h) as \(a = - \left| {\frac{{4u_{ \hbox{max} } }}{{h^{2} }}} \right|\) for each section and then calculate viscosities μ 3 and μ 4 from μ = −f/2a. Finally, the liquid viscosity is defined as the average of these four values and indicated as μ av.

Fig. 2
figure 2

Force-driven flow of liquid argon in a periodic box of 2h = 6.53 and 5.3 nm in the stream-wise and span-wise directions. Argon is maintained at 119.8 K and 1411.5 kg/m3. Coefficient of determination R 2 = 0.999 for both left and right polynomial fits

Full size image

Table 2 shows scale effects on the calculated viscosity from counter-flowing planar force-driven flows in a periodic domain. The maximum error and standard deviation (SD) in the apparent viscosity are about 3 and 5 %, respectively and occur for the smallest channel. The SD values in Table 2 are standard deviations of the four different viscosity data obtained for each simulation case. The results clearly show that liquid argon in a periodic box attains the local thermodynamic viscosity in the absence of physical boundaries, and the methodology used in determining the apparent viscosity is valid in domains as small as 1.43 nm.

Table 2 Scale effect on the calculated viscosity from counter-flowing force-driven flow
Full size table

In addition to the domain dimensions, we also investigated the effects of Lennard-Jones cutoff distance on liquid viscosity and have observed that using cutoff distance of r c = 3.2 σ, which is approximately equal to 1.09 nm for Ar molecules, is sufficient to maintain the desired thermodynamic viscosity. The study of cutoff distance is important since the choice of an inappropriate cutoff can introduce simulation artifacts. Another set of simulations of the periodic case were used to investigate the effect of the periodic dimension size on the viscosity. We ran case d1 in periodic domains that extend 5.3, 10.6 and 21.2 nm in the span-wise and stream-wise directions and have observed that maintaining the periodic dimensions at 5.3 nm was sufficient (Results not shown for brevity).

5 Nano-channel flows

Molecular dynamics simulations of force-driven flows in seven different nano-channels with heights varying from 3.26 to 35.89 nm are performed. For all cases, wall location is defined as the boundary line at the center of aligned wall molecules at the first wall layer facing the liquid molecules. In the following, density and velocity profiles, apparent viscosity and slip length are described.

Figure 3 shows the density and velocity profiles obtained in 3.26- and 35.89-nm channels. For the specified Ar–Au interaction parameters, the first 9 bins are empty of Ar molecules for all cases, and locations of the density peaks are independent of the channel size. The first density peak is 13 bins away from the wall. Density profiles show well-known density layering near the walls (Koplik et al. 1988, 1989). For large channels, the density layering subsides sufficiently away from each wall and the density converges to its bulk value. Since the average density within the density layering region is smaller than the desired thermodynamic state value (ρ td), bulk density (ρ bulk) in the middle of the channel often exceeds ρ td, creating difficulties in setting the correct thermodynamic state for simulations. This spurious density increase can be corrected in two separate ways. For large enough channels where one can observe a constant bulk density region, the correct thermodynamic density can be set using two consecutive simulations. The first simulation using an initial number of molecules (N initial) results in ρ bulk and yields an average density of

$$\rho_{\text{av}} = \frac{2}{h}\mathop \int \limits_{0}^{L} \left( {\rho - \rho_{\text{bulk}} } \right){\text{d}}z + \rho_{\text{bulk}}$$
(6)

where h is the channel height and L is the distance from wall where density oscillations subside. For current simulations, L is approximately 3 nm. The average density is related to the initial number density since ρ av = mN initial/V, where V is the domain volume and m is the molecular mass. One can predict the correct number of molecules (N td ) that would lead to the desired thermodynamic density using N td  = N initial(ρ td/ρ bulk).

Fig. 3
figure 3

Density and velocity profiles in h = 3.26 nm (a) and h = 35.89 nm (b) channels. MD simulation data are shown by lines; “velocity polynomial fit” is the second-order polynomial fitted to the MD velocity data, while “velocity from Eq. 2” is Eq. 2 plotted using thermodynamic viscosity and a constant slip length (β ≈ 1.1 nm) obtained for the largest channel case. R 2 = 0.96 and 0.995 for curve fits in the smallest and largest channels, respectively

Full size image

For smaller channels where a bulk region cannot be observed, we fix the local thermodynamic state by inserting the small channel in a large periodic box (see Fig. 4a). Due to periodicity and the channel geometry, this situation resembles an array of nano-channels with different heights. We employ equilibrium MD simulations to obtain the density distribution. Figure 4b shows density profiles across middle of the simulation domain. While density layers overlap at the interior of the channel, the desired thermodynamic density is achieved about 3 nm away from the walls. Equilibrium MD simulations are conducted for a sufficiently long time scale that allows equilibration between inside and outside portions of the channel. We estimate the proper number density simply by counting the liquid molecules in a region sufficiently away from the channel inlet and outlets (shown by the rectangular box in Fig. 4a). Once number density for the small channel is found, we simulate force-driven flow in the small channels using a domain similar to Fig. 1b. Since flow does not affect the local density distribution, comparison of density profiles between the equilibrium MD and flow cases yields perfectly matching density profiles as shown in Fig. 4b for h = 3.26 nm case. Results prove that the liquid density and temperature inside smaller channels are in equilibrium with a larger domain that maintains the desired thermodynamic state.

Fig. 4
figure 4

A snapshot of the molecules in the array of channels used to find the number density inside the h = 3.26-nm channel (a). Density profiles inside the single channel and an array of channels show perfect match (b)

Full size image

In order to investigate the viscosity, slip length and mass flow rate in the channel, we curve fit the MD velocity data. Since curve fitting is very sensitive to the selected part of the velocity data, we fit a parabolic velocity profile between the first density peaks on opposing walls. Velocity profiles obtained for the smallest and largest channels and their parabolic fits are also shown in Fig. 3. As can be seen, parabolic velocity profiles model MD data with reasonable accuracy, and the velocity profiles show finite slip on the walls. Velocity profiles predicted using Eq. 3 with thermodynamic absolute viscosity (240.74 µPa s) and the slip length predicted from the largest channel simulation (β ≈ 1.1 nm) are shown with solid lines. While Eq. 3 estimates the velocity profile in 35.89-nm channel accurately, it overestimates the MD profile in 3.26-nm channel.

After fitting a parabolic velocity profile on the velocity data for each channel in the form of u = az 2 + bz + c, liquid viscosity is calculated using \(\mu = - f/2a\) (See Sect. 4 for details), while the slip length is found using β = 2 cμ/hf. Apparent viscosity for each channel is calculated, and its variation as a function of the channel height is shown by triangles in Fig. 5. MD data show decreased viscosity with decreased channel size, where the apparent viscosity in the nano-channel is lower than the expected thermodynamic state value for channel sizes lower than 25 nm. Figure 5 also shows variation of channel average density (calculated using Eq. 6) as a function of the channel size (circles), which shows density decrease with decreased channel height. Because of density layering region that has lower density than the bulk density region, the average density in all nano-channels is smaller than the desired thermodynamic value. This effect is present even for the 60-nm channel. Such behavior was shown earlier in nanotubes (Wang and Hadjiconstantinou 2015). Figure 5 also shows argon viscosity at 119.8 K and the local average density (squares) obtained using thermodynamic tables (Stewart and Jacobsen 1989). Although the apparent viscosity and thermodynamic viscosity at average density both show reduction in decreased channel heights, they are not correlated with each other. Behavior of the apparent viscosity is due to increasing importance of wall effects, manifested by density layering, since simulations in similarly sized periodic domains resulted in recovery of absolute viscosity at the specified thermodynamic state. Figure 6 shows liquid viscosity and the slip length for 7 different sized channels, where the methodology for calculating the error bars is explained in Sect. 3. Evidently, the slip lengths are almost constant for all channel sizes and it is about 1.1 nm.

Fig. 5
figure 5

Viscosity, average density and thermodynamic viscosity at the average density for different sized channels. The desired thermodynamic viscosity and density are 240.7 μPa s and 1411.5 kg/m3, respectively

Full size image
Fig. 6
figure 6

Liquid viscosity and slip length for different sized channels

Full size image

Figure 7 shows the mass flow rate ratio which is calculated as the mass flow rate from MD simulations normalized by predictions from Eq. 4. It is crucial to state that we utilized ρ Ar = 1411.5 kg/m3, β = 1.1 nm and the thermodynamic viscosity of 240.7 μPa s for all analytical calculations. The mass flow rate ratio is unity for channels larger than 9 nm. However, this ratio decreases with decreased channel height. An interesting aspect of this behavior is that decrease in the mass flow rate ratio is visible only below 9 nm, while both the average density and fluid viscosity decrease from their expected values even at larger scales. The key observation here is that mass flow rate is proportional to the average density, while it is inversely proportional to the apparent viscosity. Therefore, decrease in both quantities with decreased channel dimensions cancels each other’s effects up to 9 nm height, after which, continuum-based mass flow rate formula (Eq. 4) overpredicts the mass flow rate.

Fig. 7
figure 7

Variation of the MD-based mass flow rate as a function of the channel height normalized by the predictions from Eq. 4 using β = 1.1 nm and ρ Ar = 1411.5 kg/m3 and μ = 240.7 μPa s

Full size image

Investigation and validation of the constitutive laws that determine the stress tensor and heat flux vector are crucial for continuum-based approximations. In a previous study, we validated Fourier law of heat conduction for liquid argon confined in a nano-channel (Kim et al. 2009). Here, we investigate the relevance of MD-computed shear stress with the analytically predicted shear rate and the apparent viscosity. Components of stress tensor are calculated using Irvin-Kirkwood relation, which has contributions from kinetic terms and virial terms. The latter is associated with the molecular spacing and the intermolecular forces imposed on each atom from its neighbors. Naturally, the virial terms have contributions due to Ar–Ar interactions (liquid virial) and due to wall force field (wall virial) (Thompson et al. 2009). Figure 8 shows the shear stress (τ) obtained in a periodic box of 2h = 6.53 nm. Since we observe two opposing parabolic velocity profiles, the shear stress first increases and then decreases in the domain. Due to 1-D flow, constitutive law for shear stress is given by τ = μ(du/dz), which can predict MD-based calculations very accurately using μ = 240.7 μPa s. In the absence of walls, shear stress is dominated by the liquid virial, and the results validate Newton’s law of viscosity for Newtonian fluids.

Fig. 8
figure 8

Shear stress from the MD simulation and predictions of the constitutive law in the periodic box of 2h = 6.53 nm. Viscosity used in the constitutive law is equal to 240.7 μPa s

Full size image

Shear stress variations in the nano-channel are shown in Fig. 9 for the h = 3.26-nm case. Figure 9a shows kinetic and virial contributions to shear stress, which exhibits oscillations toward the walls due to local variations in liquid virial induced by density layering and by the wall force field. Based on a linear momentum balance in the stream-wise direction, wall shear stress is determined by the applied body force. Shear stress variation based on the constitutive law is also shown with a dashed line, which varies linearly due to parabolic velocity profile and uses the apparent viscosity in the channel. Using this simplified relation closely mimics MD data in the middle of the channel, but cannot predict shear stress variations in the near-wall region.

Fig. 9
figure 9

Density distribution, virial, kinetic and total shear stress from MD simulation, and total shear stress from constitutive law (a). Total shear stress divided by density from MD data and shear stress from constitutive law divided by the average density in h = 3.26-nm channel (b)

Full size image

Figure 9b shows shear stress divided by the local density from MD data and shear stress from the constitutive law divided by the average density in h = 3.26-nm channel, which exhibit reduced fluctuations compared to Fig. 9a. To investigate this further, we divide apparent viscosity with the average density for each channel and compare these with the kinematic viscosity at the desired thermodynamic state. Table 3 shows the calculated kinematic viscosity and error for each channel case. The maximum error in kinematic viscosity is about 2 %, which indicates that kinematic viscosity in the nano-channels remains nearly constant for channels as small as 3.2 nm. This observation may have significant implications for the development of continuum-based transport models in nano-channels.

Table 3 Calculated kinematic viscosity (ν) for different sized channels
Full size table

6 Conclusions

Molecular dynamics simulations of force-driven liquid argon in nanoscale periodic domains and in gold nano-channels were performed to investigate the wall effects and length scales that result in deviations from classic Poiseuille flow solution. All simulations used Lennard-Jones interactions between Ar–Ar and Ar–Au interactions, where the interaction parameters for Ar–Au were determined using Kong mixing rule. Liquid argon in nano-channels was kept at a fixed thermodynamic state by carefully maintaining its density with respect to a larger system in thermodynamic equilibrium and by fixing its temperature using Nose–Hoover thermostat. Simulations were performed for parallel-plate channel and domain heights varying between 3.26 and 35.89 nm. Based on the parameters used in this paper, our findings can be summarized as follows:

  1. 1.

    Local thermodynamic equilibrium can be maintained under force-driven flows in periodic domains as small as 4 molecular diameters (h ≈ 1.43 nm), where liquid argon behaves as a Newtonian fluid. Simulation results in periodic domains verify that deviations from continuum solution observed in nano-channels are solely due to nano-confinement effects.

  2. 2.

    In nano-channels, density layering near the walls reduces average density below the thermodynamic value, which is observable for h < 60 nm.

  3. 3.

    Apparent viscosity in nano-channels starts decreasing and deviating from the viscosity at the local thermodynamic state for h < 25 nm.

  4. 4.

    Slip length in the nano-channel is fixed at β = 1.1 nm.

  5. 5.

    Continuum-based mass flow rate predictions using the density and viscosity at a given thermodynamic state and constant slip length become inaccurate for h < 9 nm. This surprising behavior is due to decrease in the apparent viscosity and average density in nano-confinements, whose effects cancel each other for h > 9 nm.

  6. 6.

    Local shear stress correlates well with the constitutive law for a Newtonian fluid for channel heights as small as h ≈ 3.26 nm. However, liquid–liquid virial terms due to density fluctuations and liquid–wall virial due to wall force field induce deviations in the near-wall region. Despite these variations in the shear stress, constant apparent viscosity with a parabolic velocity profile reasonably matches MD results till h ≈ 3.26 nm.

  7. 7.

    Kinematic viscosity in the nano-channel observed to be a constant for channel heights as small as h ≈ 3.26 nm.

Although current results are valid for a specific liquid–wall pair and the fluid–wall interaction parameters determined based on Kong mixing rule, the methodology in this work can be used for systematic investigations of the limitations of continuum solution for other liquid–wall combinations. Knowing these limits for nanoscale flows will allow simple yet reliable predictions of engineering parameters without a need for costly molecular calculations, when applicable. Our future work will include investigation of these limits for combined mass and heat transport using thermally interacting walls for Lennard-Jones fluids and water in various nano-channels and nanotubes.