1 Introduction

When a single spherical particle moves with a steady translational velocity in the fluid, the flow fields around can be obtained by solving Stokes equation, and therefore the drag force acting on the sphere. The force is proportional to the velocity of the particle, and the coefficient is 3πμd p, where μ is the dynamic viscosity of the fluid and d p is the diameter of the sphere (Batchelor 1967). The well-known Stokes’ law of resistance is valid for viscous force dominated flow Re < 0.5 without separation, where Re is the Reynolds number. The formula has been used widely in the two-phase flow study, even though it is different from the reality. Considering the impact of the weakly nonlinear fluid inertia, second- and higher-order approximation by singular perturbation approach can be obtained. Stokes’ drag formula is also valid for the extreme dilute suspensions. Experiments show that, when the volume fraction of the particles is less than 2 %, the dilute suspension can be approximated with the dual-sphere model. Various interactions between the two spheres have been considered, such as van der Waals force, electric force, and fluid dynamic force between the spheres. Due to the random Brownian motion of suspended particles, it is convenient to use statistical theory describing the process, however, which will encounter the difficulties of solving the pair-distribution equation and the occurrence of divergent integrals. Batchelor made the integrals convergent; the main contribution to the change in drag force comes from the backflow induced by surrounding spheres, and afterward, they overcome the difficulty of obtaining the pair-distribution function and established the statistical theory for polydisperse system (Wen 1996). In fact, the theory did not consider the impact of the interaction between the particles and was an ultimate theory, and therefore, there existed some discrepancy with reality. In order to predict the drag of particles under the dynamic interaction between particle clouds and the fluid, many researchers performed numerous experiments and summarized empirical expressions for the drag force (Crowe et al. 2012). As the experiments were conducted for different flow conditions and particle properties, the many discrepancies between them have never been resolved.

The adsorption between the nanoparticles and the liquid molecules can be regarded as a special reaction, which formed the activated complex with low mobility; meanwhile, the adsorbed liquid lost a degree of freedom. The thickness of the liquid layer is closely related to the chemical potential of the absorbing liquid and its pressure. For the monomolecular liquid layer in the suspension with low concentration, the adsorbed molecules on particle surface are in a hexagonal close-packed arrangement. Many studies have shown that the interfacial layer is typically 1–5 atomic molecular thickness (Wang et al. 2012). One the basis of the electron density profile at the liquid layer, the interfacial layer thickness on the particle surface can be given as \(\delta = \sqrt {2\pi } \sigma\), where σ characterizes the diffuseness of interfacial boundary and lies within 0.2–0.8 nm (Murshed et al. 2008). However, there is no exact theoretical model available in determining the liquid layer thickness on the particle surface. As ordered liquid molecules lie in the middle, the crystalline layer exhibits physical behavior between liquid and solid. More investigations need to be performed on the detailed characteristics of the nanolayer. The arrangement of molecules in the liquid layer, the mobility, mechanical properties and thermal conductivity of the layer can be analyzed to identify the impact of liquid layer on the flow and heat transfer of the nanofluid. Attentions have been focused on heat conduction of the liquid layer; however, its impact on the interaction force between phases has not been studied before.

Numerous theoretical and experimental studies have shown that the thermal performance of heat transfer devices can be enhanced by adding nanoparticles to the base fluid. Wang et al. (2012) summarized potential mechanisms of heat conduction in nanofluids proposed by previous investigators. They presented their experimental work and concluded that the key contributor to the enhancement of thermal conductivity was nanoparticle clustering. Lee et al. (2010) studied the models for the thermal conductivity of nanofluids and analyzed the proposed mechanisms as well as the discrepancies between experimental data. Grosan and Pop (2011) analyzed the mixed convection boundary layer flow of a nanofluid past a vertical cylinder and found that small fraction of nanoparticles caused significant change in the skin friction coefficient. Mahian et al. (2013) investigated the application of nanofluids in solar energy engineering and discussed the impacts of nanofluids on the performance of solar devices. Ghadimi et al. (2011) reviewed on the research progress of stabilization methods as well as different instruments for stability inspection. Based on a discrete phase model, Kondaraju et al. (2011) performed simulations on nanofluids flow and heat transfer by solving the Navier–Stokes equations with source terms. The effect of polydispersity on the effective thermal conductivity of nanofluids was investigated. They suggested that the deviation of thermal conductivity was increased with the increase in the size variation. Wen et al. (2009) simulated laminar nanofluid flow by a combined Euler and Lagrange method. The acting forces included contributions from hydrodynamic forces, Brownian force, thermophoresis force and virtual mass force. The particles concentration is unsteady and highly nonuniform inside the channel. However, temperature equation of nanoparticles was not solved. In the simulation on the movement of nanoparticles performed by many previous researchers, the drag force model they adopted was Stokes’ resistance law.

Considering the interaction of multi-particle and the fluid, a new drag force model has been developed. The viscosity behavior of the liquid layer absorbed on nanoparticles is analyzed, and the radial distribution of viscosity in the nanolayer is present. The new model has been employed to simulate nanofluid flow in a circular dish, and the numerical results have been discussed.

2 New drag force model

2.1 Drag in dispersed particle systems

For determining the viscous drag force exerted on a cloud of particles, the typical analysis is to solve the flow equations around multi-particles; however, due to the complexity of the unsteady flow conditions, it is difficult to give the corresponding theoretical formula. If the problem is modeled as a particle embedded in a porous medium, it will also encounter the difficulties of complex boundaries. Based on the differences between the drag force on the particles with uniform distribution and the Stokes resistance for a single particle, the contribution of an individual particle to the drag of the reference particle is given, in which the factors of angle, distance, and velocity have been taken into account, and then applied to calculate the drag on the reference particle in real particle clouds.

The classic expression for particle drag with specified volume fraction φ is

$$6\pi \mu a\left[ {\frac{{4 + 3\varphi + 3\sqrt {(8\varphi - 3\varphi^{2} )} }}{{(2 - 3\varphi )^{2} }}} \right]U,$$
(1)

where a is the radius of the particle and U is the relative velocity between the particle and the fluid. The same formula was derived by different researchers through analysis utilizing different approaches, which showed good agreement with the experimental data (Damiano et al. 2004). The corresponding analysis will be conducted as below. The velocity distribution in the Stokes flow around a particle is

$$u_{\theta } = - U\sin \theta \left[ {\frac{3}{4}\frac{a}{r} + \frac{1}{4}\left( \frac{a}{r} \right)^{3} } \right],\quad u_{r} = U\cos \theta \left[ {\frac{3}{2}\frac{a}{r} - \frac{1}{2}\left( \frac{a}{r} \right)^{3} } \right],$$
(2)

and the magnitude of velocity varies sinusoidally with period π around the particle, where θ and r denote the angular and radial coordinate, respectively. As the drag force is proportional to velocity approximately in the considered case, thus the contribution of circumferential particles to the particle drag is assumed to show a sinusoidal phase modulation similarly. As θ = 0 corresponds to the maximum value, the extracted contribution to the drag per unit length can be given as

$$F_{{\bar{r}}} = \frac{1}{2}F_{o} \sin 2\left( {\theta + \frac{\pi }{4}} \right) + \overline{F} ,$$
(3)

where the circumferential average

$$\overline{F} = 6\pi \mu a\left[ {\frac{{4 + 3\varphi + 3\sqrt {\left( {8\varphi - 3\varphi^{2} } \right)} }}{{\left( {2 - 3\varphi } \right)^{2} }} - 1} \right]\frac{U}{{2\pi \bar{r}}} = \frac{3\mu aU}{{\bar{r}}}\left[ {\frac{{4 + 3\varphi + 3\sqrt {\left( {8\varphi - 3\varphi^{2} } \right)} }}{{\left( {2 - 3\varphi } \right)^{2} }} - 1} \right],$$

and the fluctuation magnitude \(F_{o} = \left[ {u_{r} (0) - u_{\theta } \left( {\frac{\pi }{2}} \right)} \right]\frac{6\pi \mu a}{{2\pi \bar{r}}} = \frac{9\mu aU}{{4\bar{r}}}\left( {\frac{a}{r} - \frac{{a^{3} }}{{r^{3} }}} \right),\)where \(\bar{r}\) represents the averaged distance between particles.

The variation in the surrounding particles impact on the drag with the distance is analyzed as follows. From the circumferential averaged velocity \(\overline{{\sqrt {u_{\theta }^{2} + u_{r}^{2} } }}\), the force varies approximately as \(F \propto r^{ - 1}\); however, through analysis on the results of the long-range forces between the particles, it follows closely \(F \propto r^{ - 2}\). Here, the impact of the distance on the drag is considered the same as the mechanism for the viscosity of the suspensions \(F \propto \mu_{\text{eff}}\), taking the Brownian motion into account, the effective viscosity of the suspensions is expressed by \(\mu_{\text{eff}} = (1 + 2.5\varphi + 6.2\varphi^{2} )\mu_{\text{f}}\) (Batchelor 1977), so the actual contribution to the drag force

$$F_{{r{\prime }}} = \frac{{(1 + 2.5\varphi {\prime } + 6.2\varphi {\prime }^{2} )}}{{(1 + 2.5\varphi + 6.2\varphi^{2} )}}F_{{\bar{r}}} ,$$
(4)

where φ′ is the volume fraction corresponding to the specific distance r′ between an individual particle and the reference particle.

As the direction of the velocities of the impacted particles and the specified particle is not entirely consistent, the velocity components in parallel and perpendicular direction need to be analyzed, respectively. The lateral force is caused by the perpendicular velocity component, which changes the velocity direction of the reference particle; therefore, the complexity of the evolution process for the particle distribution is increased. Due to the asymmetric particle distribution with reference to the specified particle and the difference in particle velocity directions, the distribution of fluid velocity and pressure in the vicinity of the particle is nonsymmetrical, and this will cause the direction inconsistence between the particle velocity and the resistance of the particle, which is suitable even for particles with symmetric shape moving in the overall symmetrical flows, which may be one of the reasons for dispersion of measurement data on particle drag.

In actual computations, as the influence of particles far away from the analyzed particle is negligible, particles within 1.5 times the averaged distance are selected. In the two-dimensional case, the position (θ′, r′) and the parallel velocity U′ of the particles relative to the reference particle are known. The equivalent range influenced by the particle interaction is \(\Delta\theta = \frac{2\pi }{n}\), and the contribution of a particle to the drag \(F_{{{\text{D}}{\prime }}} = \int_{{\theta {\prime } - \frac{\pi }{n}}}^{{\theta {\prime } + \frac{\pi }{n}}} {F_{{r{\prime }}} \bar{r}} {\text{d}}\theta\), where \(n = \frac{{\pi r_{c}^{2} \varphi }}{{\pi a^{2} }}\). Considering the comprehensive contribution of all particles to the drag force component in the direction parallel and perpendicular to the velocity of the reference particle, the drag on the reference particle is obtained by

$$\overrightarrow {{F_{\text{D}} }} = \sum\limits_{{n{\prime }}} {\overrightarrow {{F_{{{\text{D}}{\prime }}} }} } ,$$
(5)

where n′ is the number of particles for computation, and the velocity used in the real calculation represents the velocity difference between the particles and the local fluid.

2.2 Viscosity distribution of the liquid layer

As shown in Fig. 1 (Jang and Choi 2004), the thickness of the liquid layer can be analyzed through the methods in physical chemistry of surfaces. For instance, in a dilute suspension, the thickness can be estimated by Langmuir monolayer adsorption model \(\delta = \frac{1}{\sqrt 3 }\left( {\frac{4M}{{\rho_{\text{f}} N_{\text{A}} }}} \right)^{1/3}\)(Wang et al. 2003), where M represents the molecular weight of the liquid, ρ f is the density of the liquid, and N A is the Avogadro constant (6.022 × 1023/mol). For the thermal conductivity of the nanolayer, if the distribution inside the layer varies linearly (Kamalvand and Karami 2013), the expression for the average thermal conductivity can be derived as \(k_{\text{l}} = \frac{{k_{\text{f}} M_{\text{l}}^{2} }}{{(M_{\text{l}} - \gamma )\ln (1 + M_{\text{l}} ) + \gamma M_{\text{l}} }}\), where \(M_{\text{l}} = \varepsilon_{\text{p}} (1 + \gamma ) - 1\), \(\varepsilon_{\text{p}} = k_{\text{p}} /k_{\text{f}}\), \(\gamma = \delta /a\), in which k p and k f, respectively, represent the thermal conductivity of the particle and fluid. For particles in the compressible fluid, such as argon atoms around the copper nanoparticle, it was observed that the density of argon in the liquid layer is about 1.5 times the density outside (Li et al. 2010). For particles in the liquid, due to the impact of the surface adsorption, the pressure in the liquid layer has increased, and the space between molecules decreases and their interactions will be enhanced, so the viscosity is revealed to be increased near the layer. Thus, the increased viscosity in the liquid layer is suggested to have a significant role in predicting the effective viscosity of nanofluids as the experimental data are larger than the previous theoretical prediction, while no one has considered this effect.

Fig. 1
figure 1

Sketch of a particle with nanolayer in a liquid

Full size image

Theoretical analysis can be performed on the radial distribution of viscosity in the nanolayer as follows. If the solid viscosity is considered to be very large, the fluid within the layer has low mobility, the viscosity within the structure of a few molecular layers is different from the viscosity of the surrounding ordinary fluid, which is similar to the atmosphere of the Earth, and thus, it will cause the noncontinuous spatial distribution of viscosity. For convenience, we assume that the viscosity μ l shows the continuous exponential variation

$$\frac{{\mu_{l} }}{\mu } = \frac{\delta }{r}{\text{e}}^{ - B(a/\delta )r/\delta + a/\delta } + 1,$$
(6)

and the influenced range of the nanolayer outer boundary on both sides is the same, which satisfied the constraints r = 0, \(\frac{{\mu_{l} }}{\mu } \to \infty\) and r = 2δ, \(\frac{{\mu_{l} }}{\mu } \to 1\), thus when \(r = \delta\), \(\frac{{\mu_{\text{l}} }}{\mu } = {\text{e}}^{(1 - B)(a/\delta )} + 1\). If the outer boundary is considered as a case similar to the mixture of ice and water, according to the viscosity variation in water with the temperature, for instance, the viscosity at the freezing point is approximately 2 times that at the room temperature, so the coefficient B is taken as 1 for the water-based nanofluid. In addition, the viscosity in this layer may be analyzed from the view of the viscous properties of viscoelastic fluids.

3 Verification of drag force model

In order to examine the accuracy of the new force model, the drag force computed by the simulation of particles motion is compared with the existing result. The movement of one and a half thousand particles has been presented, and the mean drag coefficient for particles is determined via calculating the statistical average. The drag force coefficient variation for particles as given by previous investigators has been shown in Fig. 2, where \(F_{\text{D}}^{*} = \frac{{F_{\text{D}} - 6\pi \mu aU}}{6\pi \mu aU}\). It can be observed that the simulation results are in good agreement with the classical predictions (Tam 1969; van der Hoef et al. 2005).

Fig. 2
figure 2

Variation in drag force coefficient versus volume fraction

Full size image

4 Application in nanofluid flow

Flow and heat transfer of a nanofluid in a confined zone with constant temperature at the wall–liquid interface has been considered. The medium is a water-based nanofluid containing alumina nanoparticles. According to its physical characteristics, a theoretical approach has been used to predict nanofluid as two-phase mixtures. It is considered that the base fluid and the nanoparticles are coupled with momentum and heat transfer. The numerical simulation is performed based on a combined Euler and Lagrange method.

4.1 Mathematical modeling and numerical approach

Discrete phase model is used to study the nanofluid flow with nanoparticles determined by the Lagrangian trajectory method. For the continuous fluid phase, the flow and heat transfer behaviors are governed by the equations according to the laws of conservation of mass, momentum, and energy (Warsi 2006).

It is convenient to define the following dimensionless variables before solving the problem.

$$\begin{gathered} \vec{x}^{ * } = \frac{{\vec{x}}}{R},\quad \overrightarrow {V}^{ * } = \frac{{\overrightarrow {V} }}{{V_{\infty } }},\quad t^{ * } = \frac{{V_{\infty } t}}{R},\quad p^{ * } = \frac{p}{{\rho V_{\infty }^{2} }},\quad \rho^{ * } = \frac{\rho }{{\rho_{\infty } }},\quad \hfill \\ T^{ * } = \frac{{T - T_{\infty } }}{{T_{\text{s}} - T_{\infty } }},\quad \overrightarrow {{F_{\text{p}} }}^{*} = \frac{{\overrightarrow {{F_{\text{p}} }} R}}{{V_{\infty }^{2} }},\quad q_{\text{p}}^{*} = \frac{{q_{\text{p}} R}}{{V_{\infty } (T_{\text{s}} - T_{\infty } )}} \hfill \\ \end{gathered}$$
(7)

where \(\vec{x}\)and \(t\)denote the space and time coordinates, \(\overrightarrow {V}\), p, ρ, and T represent respectively the velocity, pressure, density and temperature of the fluid, \(\overrightarrow {{F_{\text{p}} }}\)and \(q_{\text{p}}\)are source terms, and these variables are normalized by the characteristic quantities as \(R\)for the spatial variable, \(V_{\infty }\)for velocity, ρ ∞ for density, T s and T ∞ for temperature.

Considering the laminar, unsteady regime of the model, the incompressible Navier–Stokes equations with source terms for the fluid flow can be expressed in the dimensionless variables as below (Kondaraju et al. 2011).

$$\nabla \cdot \overrightarrow {V}^{*} = 0,$$
(8)
$$\frac{{\partial \overrightarrow {V}^{*} }}{{\partial t^{*} }} + (\overrightarrow {V}^{*} \cdot \nabla )\overrightarrow {V}^{*} = - \nabla p^{*} + \frac{1}{Re}\nabla^{2} \overrightarrow {V}^{*} + \overrightarrow {{F_{p} }}^{*} ,$$
(9)
$$\frac{{\partial T^{*} }}{{\partial t^{*} }} + \overrightarrow {V}^{*} \cdot \nabla T^{*} = \frac{1}{Re\Pr }\nabla^{2} T^{*} + q_{p}^{*} ,$$
(10)

where the Reynolds number \(Re = \frac{{\rho U_{\infty } R}}{\mu }\), the Prandtl number \(\Pr = \frac{\nu }{\alpha }\), \(\alpha = \frac{{k_{\text{f}} }}{{\rho_{\text{f}} c_{\text{pf}} }}\), in which \(\nu\), α are kinematic viscosity and thermal diffusion coefficient of the fluid, respectively, c pf represents the specific heat of the fluid. The source terms \(\overrightarrow {{F_{\text{p}} }}\)and q p representing the momentum and energy transfer between the fluid and particles are given by (Bianco et al. 2009)

$$\overrightarrow {{F_{\text{p}} }} = \frac{1}{{\rho_{\text{f}} }}\sum\limits_{{n_{\text{p}} }} {\frac{{m_{\text{p}} }}{\delta V}} \frac{{{\text{d}}\overrightarrow {{V_{\text{p}} }} }}{{{\text{d}}t}},\quad q_{\text{p}} = \frac{1}{{\rho_{\text{f}} }}\sum\limits_{{n_{\text{p}} }} {\frac{{m_{\text{p}} }}{\delta V}} c_{\text{pp}} \frac{{{\text{d}}T_{\text{p}} }}{{{\text{d}}t}},$$
(11)

where δV is the cell volume, n p is the number of nanoparticles within a cell volume, m p, c pp, and T p denote respectively the mass, the specific heat, and the temperature of the particle. \(\frac{{{\text{d}}\overrightarrow {{V_{\rm{p}} }} }}{{{\rm{d}}t}}\)and \(\frac{{{\rm d}T_{\text{p}} }}{{{\rm d}t}}\)respectively represent instantaneous change rate of velocity and the temperature for particles to be discussed below.

In the Lagrangian frame of reference, the movement equation of nanoparticles is given by

$$\frac{{{\text{d}}\overrightarrow {{V_{\text{p}} }} }}{{{\text{d}}t}} = \overrightarrow {{F_{\text{D}} }} + \overrightarrow {{F_{\text{B}} }} + \overrightarrow {{F_{\text{T}} }} + \overrightarrow {{F_{\text{L}} }} ,$$
(12)

The main force terms on the right-hand side include the drag force, Brownian force, the thermophoretic force and Saffman’s lift force.

The drag force \(\overrightarrow {{F_{\text{D}} }}\)exerted on the particle by the surrounding fluid is calculated by Eq. 5, and the viscosity used is μ l(δ).

\(\overrightarrow {{F_{\text{B}} }}\)is the Brownian force expressed as (Li and Ahmadi 1992)

$$\overrightarrow {{F_{\text{B}} }} = \xi_{i} \sqrt {\frac{{\pi S_{0} }}{\Delta t}} ,$$
(13)

where ξ i is the unit variance Gaussian random number with zero mean. The spectral intensity \(S_{0} = \frac{{216\nu k_{\text{B}} T}}{{\pi^{2} \rho_{\text{f}} d_{\text{p}}^{5} \left( {\frac{{\rho_{\text{p}} }}{{\rho_{\text{f}} }}} \right)^{2} C_{\text{c}} }}\), where \(k_{\text{B}}\)is the Boltzmann constant, C c is known as the Cunningham correction factor, ρ p and d p represent the density and the diameter of the particle, respectively.

The thermophoretic force \(\overrightarrow {{F_{\text{T}} }}\)due to the temperature gradient on the particle surface in Eq. 8 can be calculated by (Wen et al. 2009)

$$\overrightarrow {{F_{\text{T}} }} = - \frac{{6\pi d_{\text{p}} \mu^{2} C_{\text{s}} (K + C_{\text{t}} Kn)}}{{\rho (1 + 3C_{\text{m}} Kn)(1 + 2K + 2C_{\text{t}} Kn)}}\frac{1}{T}\nabla T,$$
(14)

where the thermal slip coefficient \(C_{s} = 1.17\), the thermal exchange coefficient C t = 2.18 and C m = 1.14, the ratio of thermal conductivity K = k f/k p.

The expression for Saffman’s lift force due to the shear is given by (Saffman 1965)

$$\overrightarrow {{F_{L} }} = \frac{{2K_{s} \nu^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \rho d_{ij} }}{{\rho_{p} d_{p} (d_{lk} d_{kl} )^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0pt} 4}}} }}(\overrightarrow {V} - \overrightarrow {{V_{p} }} ),$$
(15)

where K s = 2.594 and d ij is the deformation tensor.

The time-dependent temperature equation for particle is expressed as (Kondaraju et al. 2010)

$$\frac{{{\text{d}}T_{\text{p}} }}{{{\text{d}}t}} = \frac{{6k_{\text{f}} Nu_{\text{p}} }}{{\rho_{\text{p}} c_{\text{pp}} d_{\text{p}}^{2} }}(T - T_{\text{p}} ),$$
(16)

Nu p is the Nusselt number for nanoparticles calculated by Ranz–Marshall correlation \(Nu_{\text{p}} = 2 + 0.6\,Re_{\text{p}}^{1/2} \Pr^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}}\), where \(Re_{\rm p} = \frac{{\rho_{\rm f} d_{\rm p} \left| {\overrightarrow {{V_{\rm p} }} - \overrightarrow {V} } \right|}}{\mu }\).

Physical and thermal properties of solid nanoparticles and water at reference temperature are listed in Table 1 (Abu-Nada et al. 2008).

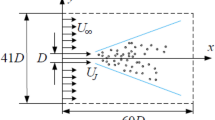
Table 1 Thermo physical properties of base fluid and alumina nanoparticle
Full size table

In the present study, the characteristic-based split (CBS) algorithm (Zienkiewicz et al. 2005) is used to simulate the incompressible fluid flow in a dish. Discrete phase equations are solved by the momentum and energy balance on the particles. Due to two-dimensional flow features, the governing equations for the fluid flow are 2-D unsteady N–S equations. As shown in Fig. 3, the domain of the present simulation is a circular dish rotated clockwise with dimensionless angular velocity being from 1.0 to 5.0. It consists of 9,109 nodes and 17,929 triangular elements. In the dish, 7,825 alumina nanoparticles move with the same velocity and temperature as water initially. As the Knudsen number Kn < 0.001 is valid for the nanofluid flow, no slip velocity and isothermal boundary conditions are applied on dish walls. Constant higher temperature T s = 323 K is applied to the wall, and the initial fluid temperature is T ∞ = 298 K. The diameter of the nanoparticles is selected to be 30 nm.

Fig. 3
figure 3

Elements in the circular domain

Full size image

In order to validate the numerical algorithm, different flow regimes are selected to demonstrate the precision of the Fortran program. The numerical data from the present computation for a case of fluid flow at low Reynolds numbers (Re = 100) is compared with previous data. The averaged Nusselt number obtained by the present code is 5.07, the corresponding result of the experimental work is 5.19 (Khiabani et al. 2010), and the numerical data carried out by Mettu et al. (2006) are 5.08. The comparison of the present result and the previous data shows satisfactory agreement. Figure 4 shows the temperature profile of alumina–water nanofluid with 4 % volume fraction. The present result is found to agree well with the numerical data of Yang and Lai (2011).

Fig. 4
figure 4

Temperature distribution for alumina-water nanofluid with 4 % volume fraction

Full size image

4.2 Results and discussions

Figure 5 presents the comparison of the drag force on particles simulated respectively with Stokes drag model for single particle and the modified model, where t′ is the number of computational time and F D′ = F DΔt, in which Δt represents the time step. The three typical particles selected are located close to the boundary, near the center part and approximately in the middle between them. It can be observed that the obviously larger enhanced fluctuations simulated by multi-particle model, the enhanced complexity in frequency with low- and high-frequency components, and the results of the single-particle model approximately fluctuate up and down symmetrically around the average value with relatively simple frequency. As the effect of particles interactions with fluid is in analogy to the increased particle size, the impact range of the flow field on the particle becomes larger, which is equivalent to the movement of a enlarged particle in the larger local area; the effect of variation in the flow field is enhanced, so the fluctuation has been enlarged with more complex frequencies. The difference in the above comparisons is similar to the Brownian motion of different-sized particles.

Fig. 5
figure 5

Variation in drag force exerted on particles simulated with a Stokes drag model b present model

Full size image

The trajectories of particles within a square domain in the vicinity of the central part are shown in Fig. 6, the geometry of trajectory is more regular approximating arc as the distance from the dish center increases, and the effect of Brownian motion stands out near the central part with trajectories fluctuating significantly. Note that the circular dish rotates clockwise in the simulation.

Fig. 6
figure 6

Trajectories of nanoparticles in the circular dish

Full size image

The distribution of the instantaneous velocity magnitude of the fluid within the dish at Re = 5 is illustrated in Fig. 7. Obvious fluctuations can be seen in the contours, and the velocity in the middle is lower than that close to the boundary, due to the disturbance of the particles, the fluid velocity near the wall may be slightly larger than that on the dish boundary.

Fig. 7
figure 7

Fluid velocity contours in the dish

Full size image

Figure 8 presents the instantaneous distribution of the nanoparticles in the dish rotating with constant and varied angular. As the flow in the rotating dish exhibits special feature, so the particles are approximately uniformly dispersed and the intermediate hollow space is gradually enlarged; the centripetal force provided by fluid pressure gradient is not sufficient for the change in the velocity direction of particles. Moreover, as shown in the actual computation, the lateral force is of a lower order than the drag force component in the direction of movement for particles. The velocity of particles on the outer side is high than that on the inner side of the reference particle, so it makes a larger contribution to the lateral force and then the diffusion process of particles. When the rotation of the dish speeds up, it first drives the accelerated movement of the particles near the boundary, thus will cause a significant change in the arrangement of the particles.

Fig. 8
figure 8

Nanoparticle distribution in the circular dish a uniform rotating b accelerated rotating

Full size image

5 Conclusions

Based on the viewpoint of multi-particle interactions, the circumferential distribution function of the contribution to the drag on particle is constructed, combined its variation with the distance; the improved expression for the calculation of the drag force is presented. The computed drag is not parallel with the direction of the particle velocity, and the impact of the lateral force increases the complexity for the transport process of particles. For the ordered structure adsorbed on the surface of nanoparticles, the viscosity behavior in and near the nanolayer has been analyzed for the first time. The increased viscosity of the interfacial layer is suggested to be the main reason why the experimental result for the effective viscosity of nanofluids is larger than the theoretical prediction. Considering the multi-particle effect and the characteristic of the crystalline layer, a new model for the drag exerted on a nanoparticle has been proposed and applied to simulate the nanofluid flow in rotary dish. Different simulation results with the traditional drag model is investigated, and the instantaneous distribution of nanoparticles as well as the velocity of the fluid has been analyzed. If we could obtain the precise solution of the flow field in the vicinity of nanoparticles, a more accurate model for the drag force will be presented.