1 Introduction

The flow past a circular cylinder is a classical problem in fluid mechanics and it also represents an idealisation of many flows of practical significance. Typical examples include flow in tubular heat exchanger, instrumentation technology in hot-wire anemometry, flow past dividers in polymer processing, piping installations, and offshore cylindrical drilling rigs, etc. A wealth of information [1–3] on the flow past a cylinder has accumulated over the years on various aspects of this flow configuration. Numerous experimental and numerical investigations have been carried out aimed at understanding the dynamics of the flow by evaluating the global parameters to characterize the flow, such as wake length, separation angle, drag and lift coefficients, Strouhal number (St), and Nusselt number (Nu w ). Indeed, a variety of flow phenomena may be encountered depending upon the value of the Reynolds number (Re) and whether the flow is confined or unconfined. Thus for instance, the flow past an unconfined circular cylinder may be divided into different regimes depending upon the value of Re. For Re ∼ 1, the flow is fore and aft symmetric, divides at the front stagnation point and reunites smoothly behind the cylinder. As the value of Re increases above 5, the flow separation takes place on the downstream side with the formation of two symmetric vortices, which are stable and remain attached to the cylinder. However, such symmetric vortices grow in size as Re is progressively increased. At about Re ∼ 46 [4], the stability of the flow is lost, and the oscillations of vortices give rise to the well-known von Karman vortex street. The discrete vortices are regularly placed behind the cylinder, with St characterizing the frequency of oscillation of the vortices. In this flow regime, St increases with Re. This regime continues up to about Re=180 at which the flow transits to one consisting of complex three-dimensional flow structure [5]. However, when the circular cylinder is confined in a plane channel, with a parabolic velocity profile of the oncoming fluid, the nature and stability of the resulting flow differ greatly owing to the blockage effect induced by the stationary walls of the plane channel. Due to additional dissipation at the confining walls, the transition from the steady to unsteady flow is somewhat delayed and occurs at somewhat higher Re than that for an unconfined cylinder [6]. The effect of blockage on the stability of the flow may also vary depending upon whether the cylinder is confined symmetrically or asymmetrically [7]. Evidently, such changes in the flow patterns are also reflected in the values of the drag (C D) and lift (C L) coefficients, St, and Nu w . This work sets out to elucidate the effect of blockage ratio (β) and gap ratio (γ) on momentum and heat transfer characteristics from an asymmetrically confined circular cylinder in a plane channel. The related literature is briefly presented here to emphasize the salient findings of the past studies, while a detailed description is available elsewhere [8].

Following the early numerical study of Thom [9], Kawaguti and Jain [10] solved the field equations for Re=1–100. They presented the results on the recirculation length, separation angle, total drag, surface pressure and vorticity distribution as a function of time thereby showing their approach to steady state values. The time dependent numerical simulation of the Navier–Stokes equations for the unsteady flow past a circular cylinder in cross flow was first carried out by Payne [11] for Re=40 and 100, followed by Ingham [12] for Re=100 in which the evolution of flow characteristics like drag and recirculation length with time was presented. The flow past an impulsively started circular cylinder was studied numerically by Collins and Dennis [13] by integrating the time dependent Navier-Stokes equations for Re=40, 100, 200 and 500. Patel [14] has presented the semi-analytical solutions for the flow past an impulsively started circular cylinder for Re=60, 100, 200, 500, 550 and 600. Over this range of Re, it appears that steady state conditions were not realized as the wake length continued to grow with the appearance of the secondary vortex on the surface of the cylinder for Re=500, 550, and 600.

The main limitation of all the above-mentioned numerical simulations was that it was assumed that the flow reached steady state after a long time or the solutions were presented for short times at which flow remained steady. This assumption is clearly at odds with the available experimental results. Braza et al. [15] have solved the time dependent Navier–Stokes equations for the flow past an unconfined cylinder by a finite volume second order accurate scheme and an alternating direction implicit procedure for Re=100, 200 and 1,000. They have shown that the flow reaches steady state symmetric pattern after a shorter or longer establishment period even at Re=1,000 and it was attributed to the fact that in case of numerical simulations the destabilizing factors like non-uniform inlet conditions, irregularity of the boundary conditions, vibrations and surface roughness that are present in experimental conditions are absent as the boundary conditions and initial conditions are symmetric which lead to the steady symmetric solution of the Navier–Stokes equations. Therefore, they used a perturbation method to generate vortex shedding from cylinder, by introducing rotation of the circular cylinder in clockwise direction followed by its rotation in anticlockwise direction for a short period of time and then keeping the cylinder stationary for subsequent calculations. The secondary eddies appeared in the vicinity of each primary eddy above Re=200 and had significance presence in the near wake at Re=1,000. Jackson [4] used the finite element method to locate the symmetry breaking Hopf bifurcation, which characterizes the onset of vortex shedding, i.e., the transition from steady to unsteady flow. The critical Re, at which flow becomes periodic was determined to be ∼ 46.

The two-dimensional, unsteady Navier–Stokes equations for the flow past a circular and a square cylinder were solved by Franke et al. [16] for Re≤5,000 for the circular cylinder case and Re≤300 for the square cylinder case; the development of the vortex shedding from the cylinder was examined as the flow velocity increased from zero to free stream value following a sine function. No disturbance was introduced to obtain vortex shedding. The vortex shedding was automatically triggered by round-off errors and numerical diffusion.

On the other hand, the flow past a cylinder confined in a plane channel has received much less attention [6–8, 17–20]. Chakraborty et al. [8] have extensively studied the effect of walls on the steady, two-dimensional flow past a circular cylinder confined symmetrically in a plane channel by numerical simulations for Re between 0.1 and 200 and for β between 0.05 and 0.65. For a fixed value of Re, the total drag was found to increase with increasing β, and for a fixed β, decrease with increasing Re. The recirculation length and separation angle were found to decrease with β, both of which are consistent with the available experimental results [17, 18]. The experiments all seem to suggest the critical Re at which the vortex shedding occurs to increase with β. The upper limit of Re at which twin vortices are stable and adhere to the cylinder was determined to be 39.5. The stability of the flow past a circular cylinder confined symmetrically in a plane channel has also been studied by Chen et al. [6]. Steady flow past the circular cylinder was perturbed slightly by the rotation of the circular cylinder for a short period of time. The time dependent motion following the rotation was examined to determine the critical Re, at which the perturbation was amplified leading to unsteady flow. The critical Re for β=0.2 was found to be 69. Numerical bifurcation studies, similar to those carried out by Jackson [4], were carried out to determine the critical Re for various β ranging from 0.1 to 0.7. It was showed that stability is lost through a symmetry breaking Hopf bifurcation. The critical Re was found to increase with β up to 0.5 and then to decrease with β from 0.5 to 0.7.

The loss of stability of the flow past a circular cylinder confined asymmetrically in a rectangular plane channel for β=0.2 was studied by Zovatto and Pedrizzetti [7] using a finite element method based on the vorticity–stream function formulation. The flow was assumed to start impulsively and at the inlet a parabolic velocity profile was specified. The critical Re at which the flow became periodic was found to increase as the cylinder approached one of the two confining walls. For a fixed Re, the drag coefficient and the non-dimensional time period of the oscillations was found to show an inverse dependence on the gap between the cylinder and the wall. Similarly, Khan et al. [19] have investigated the effect of β on fluid flow and heat transfer from a circular cylinder confined in a plane channel for isothermal and isoflux boundary conditions using a boundary layer approximation. They presented correlations for drag coefficient and heat transfer coefficient as functions of Re, Pr and β. The mean Nusselt number, Nu w , and drag were found to increase with β and the mean Nu w for the isoflux boundary condition was found to be higher than that for the isothermal boundary condition. Some experimental studies [21–25] have also been carried out to elucidate the effect of a plane boundary near the circular cylinder at high Re. All these studies clearly show that the presence of the wall significantly affects the forces and vortex shedding from the cylinder. However, the situation considered in the present study is very different from these experiments due to the confinement of the cylinder in a plane channel.

From the aforementioned discussion, it is fair to conclude that little work is available on the momentum and heat transfer characteristics from an asymmetrically confined circular cylinder [7] and heat transfer from a symmetrically confined cylinder [19] in a plane channel. There has been no study in the literature regarding the heat transfer from an asymmetrically confined cylinder in a plane channel. Therefore, the main objective of the present work is to study the momentum and heat transfer characteristics from an asymmetrically confined circular cylinder in a plane channel for 10≤Re≤500. The two-dimensional simulations were carried up to Re=500, even though it is well known that the unconfined flow becomes three-dimensional at Re>180 [5]. The motivation for carrying out the simulations up to Re=500 was to study the effect of wall proximity on the vortex shedding from the cylinder and it was assumed that the transition to three-dimensional flow may be possibly delayed in the presence of confining walls.

2 Problem statement and formulations

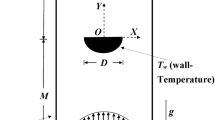
Consider the unsteady, two-dimensional and non-isothermal flow of a viscous incompressible Newtonian fluid past a circular cylinder confined in a plane channel, as shown schematically in Fig. 1. Two plane walls, separated by a distance, H, confine a circular cylinder of diameter d whose position is defined by a gap ratio, γ, defined as Δ/(H/2−d/2) where Δ is the minimum distance from the surface of the cylinder to the nearest wall. The value of γ is equal to 1 when the cylinder is placed symmetrically between the plane walls and 0 when it touches one of the walls. The cylinder is located at 15 d and 40 d from the inlet and outlet, respectively, which are sufficient to obtain domain independent results [7]. The length of the cylinder in the z-direction is assumed to be sufficiently long to have insignificant end effects, and thereby implying that there is no flow in z-direction and that no flow variables depend upon z-coordinate. The fluid at a temperature of T ∞ enters at the velocity inlet boundary AC with a parabolic velocity profile and leaves at the outflow boundary BD. The confining walls are at free stream temperature (T ∞) whereas the cylinder is at a temperature of T w . The effect of variation in density and viscosity due to temperature is neglected.

Fig. 1
figure 1

Schematic for the flow past an asymmetrically confined circular cylinder in a plane channel

Full size image

Under these conditions, the equations of continuity, momentum and energy reduce to: Continuity:

$$\frac{{\partial V_{x}}}{{\partial x}} + \frac{{\partial V_{y}}}{{\partial y}} = 0$$
(1)

x-momentum:

$$\rho \left({\frac{{\partial V_{x}}}{{\partial t}} + V_{x} \frac{{\partial V_{x}}}{{\partial x}} + V_{y} \left. {\frac{{\partial V_{x}}}{{\partial y}}} \right)} \right. = - \frac{{\partial p}}{{\partial x}} + \mu {\left({\frac{{\partial ^{2} V_{x}}}{{\partial x^{2}}} + \frac{{\partial ^{2} V_{x}}}{{\partial y^{2}}}} \right)}$$
(2)

y-momentum:

$$\rho \left({\frac{{\partial V_{y}}}{{\partial t}} + V_{x} \frac{{\partial V_{y}}}{{\partial x}} + V_{y} \left. {\frac{{\partial V_{y}}}{{\partial y}}} \right)} \right. = - \frac{{\partial p}}{{\partial y}} + \mu {\left({\frac{{\partial ^{2} V_{y}}}{{\partial x^{2}}} + \frac{{\partial ^{2} V_{y}}}{{\partial y^{2}}}} \right)}$$
(3)

Energy equation:

$$\rho \hat{C}_{p} {\left({\frac{{\partial T}}{{\partial t}} + V_{x} \frac{{\partial T}}{{\partial x}} + V_{y} \frac{{\partial T}}{{\partial y}}} \right)} = K{\left({\frac{{\partial ^{2} T}}{{\partial x^{2}}} + \frac{{\partial ^{2} T}}{{\partial y^{2}}}} \right)}$$
(4)

The appropriate boundary conditions for this flow are as follows:

Inlet boundary at AC: The fluid is assumed to enter the inlet plane with a parabolic velocity profile and at the free stream temperature of T∞.

$$V_{x} = U_{\rm max} (1 - (y/H/2))^{2};\quad V_{y}= 0\;\hbox{and}\; T = T_{\infty}$$
(5)

Outflow boundary at BD: The zero diffusion flux condition for all variables is implemented at the outlet boundary. This implies that the conditions of the outflow plane are extrapolated from within the domain and have no impact on the upstream flow. This is tantamount to the fully developed flow assumption.

Walls AB and CD: The usual no slip condition is applied at the confining walls, AB and CD and these walls are at free stream temperature of T∞.

$$V_{x} = 0;\quad V_{y} = 0\;\hbox{and}\; T = T_{\infty}$$
(6)

Surface of the cylinder: At the surface of the cylinder, no slip boundary condition is applied and the cylinder is at a temperature of T w .

$$V_{x} = 0;\quad V_{y} = 0\;\hbox{and}\; T = T_{w}$$
(7)

Drag: The total drag coefficient is defined as

$$C_{\rm D} = \frac{F_{\rm D}}{\frac{1}{2}\rho \bar{u}^{2}_{d} d}$$
(8)

where, FD is the drag force per unit length of the cylinder and \(\bar{u}_{d}\) is the average velocity based on the diameter of the cylinder given by

$$\bar{u}_{d} {\left({\beta, \gamma} \right)} = \frac{1}{d}{\int\limits_{d_{2}}^{d_{1}} {u_{{\max}}}}{\left({1 - {\left({\frac{y}{\frac{H}{2}}}\right)}^{2}} \right)}\hbox{d}y$$
(9)

where, d1 and d2 are the y-coordinates of the cylinder and are functions of β and γ as given below

$$d_{1} = \frac{d}{{2\beta}}{\left({\gamma {\left({1 - \beta} \right)} - 1} \right)} + d$$
(10)
$$d_{2} = \frac{d}{{2\beta}}{\left({\gamma {\left({1 - \beta} \right)} - 1} \right)}$$
(11)

Lift: The lift coefficient is defined as

$$C_{\rm L} = \frac{F_{\rm L}}{\frac{1}{2}\rho \bar{u}^{2}_{d} d}$$
(12)

where, FL is the lift force per unit length of the cylinder.

Strouhal number: The non-dimensional frequency of the oscillations is defined as

$$St = \frac{f}{\bar{u}_{d}/d}$$
(13)

where, f is the vortex shedding frequency.

Nusselt Number: Nu w =hd/k, where h is the local surface heat transfer coefficient \(\overline{Nu}_{w} = \bar{h}d/k,\) where \(\bar{h}\) is the heat transfer coefficient averaged over the surface of the cylinder.

3 Numerical methodology

FLUENT (version 6.1) employs a finite volume based numerical method to solve the governing flow and energy equations. In the present case, unstructured computational cells were created with a fine mesh near the cylinder and coarse mesh away from the cylinder with the help of successive ratio scheme in GAMBIT. The grid independence study was carried out for each case by refining the grid size until the variation in C D and Nu w was less than 0.5%. Unsteady segregated solver was used with second order upwinding scheme for the convective terms in the momentum equation. Pressure implicit with splitting of operators (PISO) scheme was used for pressure–velocity coupling. A convergence criterion of 1×10−9 was applied to the residuals of the continuity, the momentum and energy equations.

4 Results and discussion

Before solving the problem of interest, the code has been validated by using the prior results available in the literature to establish the level of the accuracy of the new results obtained in this work. This is accomplished by making detailed comparisons of the present results with the published data for the steady and unsteady momentum and heat transfer from a circular cylinder under confined and unconfined conditions.

4.1 Validation of \(\bar{C}_{\rm D},\) C L, St and \(\overline{Nu}_{w}\)

For the validation of our results with the published data, a circular geometry with a circular outer boundary located at 112 radii way from the surface of the cylinder is chosen. A grid size of 90×60 previously used by Chakraborty et al. [8] is also employed in this work. The present values of C D are compared with the published results [8, 10, 26, 27] in Table 1. The maximum deviation from the literature values is 8.2% at Re=40, which is due to the smaller outer boundary (r∞/r=29) used by Sucker and Brauer [26]. The corresponding validation for heat transfer from an unconfined cylinder has been carried out using a circular domain (500 d). The values of \(\overline{{Nu}}_{w}\) for the range of Re between 0.01 and 40 are compared with the published results [28–30] in Table 1. A maximum deviation of 4.1% from the literature value is observed at Re=40. Table 2 presents a similar comparison of \(\bar{C}_{\rm D}\) (time average), C L and St for the range of Re from 50 to 500 with the literature values. The maximum deviation in \(\bar{C}_{\rm D}\) from the literature values is 5.3% at Re=500 whereas the correspondence in the values of C L and St is seen to be good.

Table 1 Comparison of C D and \(\overline{{Nu}} _{w} \) values with the published data for the steady flow range
Full size table
Table 2 Comparison of \(\bar{C}_{\rm D},\) C L and St values with the published data for the unsteady flow range
Full size table

The results for momentum and heat transfer for an asymmetrically confined circular cylinder in plane channel are validated with the published data of Zovatto and Pedrizzetti [7] for β=0.2 and γ=0.375 as shown in Table 3 and are found to be in good agreement with the data. The maximum deviation in \(\bar{C}_{\rm D}\) is 5.8% at Re=40. Since the published data available in the literature for an asymmetrically confined cylinder is limited, the model was also validated with the data of Khan et al. [19] for heat transfer from a symmetrically confined cylinder in a plane channel for β=0.1 and 0.2 as shown in Table 4. The present values of \(\overline{{Nu}}_{w}\) are in close agreement, with a maximum deviation of 4.7% at Re=20 at β=0.1.

Table 3 Comparison of \(\bar{C}_{\rm D} \) values for β=0.2 and γ =0.375
Full size table
Table 4 Comparison of \(\bar{C}_{\rm D} \) and \(\overline{{Nu}} _{w} \) (Pr=0.7441) values for β=0.1 and β=0.2
Full size table

4.2 Validation of critical Re

Chen et al. [6] have determined the critical Re at which the flow becomes unsteady for a symmetrically confined cylinder for β=0–0.7. Table 5 shows a typical comparison between their and the present results for β=0–0.4 and the two results are seen to be in good agreement. For determining critical Re, the flow is disturbed by the rotation of the cylinder and the ensuing time dependent motion is examined to check whether the disturbance is decayed or amplified leading to vortex shedding. Zovatto and Pedrizzetti [7] have determined the critical Re for a cylinder confined asymmetrically between the plane walls for β=0.2 and γ=1–0.125. A good match with their results is evident in Table 5.

Table 5 Comparison of Re C and St values at various blockage ratios and Re C values for various γ (β=0.2)
Full size table

From these comparisons, it is perhaps fair to say that the present values of \(\bar{C}_{\rm D},\) C L, St and \(\overline{{Nu}}_{w}\) obtained using this code are reliable within 3–4%.

4.3 Variation of critical Re with β and γ

The variation of critical Re with γ for β=0.1–0.4 is determined using time dependent numerical simulations. While determining the critical value of Re, the value of Re was increased in steps of 4 in the simulations. The effect of β and γ on critical Re is shown in Fig. 2. For a given β, the critical Re increases with a decrease in γ implying that the transition of the flow is delayed as the cylinder moves closer to one of the confining walls. However, the critical Re increases steeply for γ<0.5. The increase is more pronounced at higher values of β. For example, at β=0.3, the critical Re increases from 120 to 276 as γ decreases from 0.5 to 0.25. This may be attributed to the fact that as the cylinder approaches the wall, the interaction of the boundary layer of the wall with that of the cylinder suppresses the vortex shedding from the cylinder resulting in the stability of the flow. The critical Re increases with increase in β for a given γ, which is in agreement with the previous results [6] due to the suppression of vortex shedding.

Fig. 2
figure 2

Variation of critical Re with β and γ

Full size image

4.4 Effect of β on \(\bar{C}_{\rm D},\) St, C L and \(\overline{{Nu}}_{w}\) for a symmetrically confined cylinder

Figure 3a presents the effect of β on \(\bar{C}_{\rm D}\) for different Re. As expected, \(\bar{C}_{\rm D}\) increases with β from 0 (unbounded flow) to 0.1 for Re<50. For Re≥50 the effect of increase in β from 0 to 0.1 on \(\bar{C}_{\rm D} \) is negligible. It may also be observed from the figure that as the value of β increased from 0.1 to 0.4, \(\bar{C}_{\rm D}\) also increased for a fixed value of Re. The increase in \(\bar{C}_{\rm D}\) with increase in β is attributed to the fact that as the walls approach closer to the cylinder, the obstruction to the flow increases. Therefore, the velocity gradients become steeper resulting in relatively higher drag force on the cylinder. However, increase in \(\bar{C}_{\rm D} \) is more pronounced only at low Re. The significant increase in \(\bar{C}_{\rm D} \) is caused by the large boundary layer thickness at low Re i.e. the effect of viscous forces extends to larger distances from the cylinder resulting in the interaction with the walls.

Fig. 3
figure 3

Effect of blockage ratio (β) on \(\bar{C}_{\rm D},\) St, \(\overline{{Nu}}_{w}\) and C L for γ=1

Full size image

Figure 3b illustrates the effect of increase in β on St. For all values of β, except at 0.4, S, increases with Re, which is consistent with the literature [15]. The change in St as β increases from 0 to 0.2 is negligible for Re≤300, whereas it decreases for Re≥400. For example, at Re=500 the decrease in St is 3.7% as β increases from 0 to 0.2. However, as β increases from 0.2 to 0.4, St increases significantly for a fixed Re. The increase in St from β=0.2 to 0.4 at Re=400 is 31%. The effect of β on\(\overline{{Nu}} _{w}\) is illustrated in Fig. 3c. The effect of β<0.3 on \(\overline{{Nu}}_{w}\) is negligible at Re>100, whereas at Re<100 as β increases from 0.3 to 0.4, the mean Nusselt number \(\overline{{Nu}} _{w}\) increases for all values of Re. For example, at Re=100 increase in \(\overline{{Nu}} _{w}\) is 7.78%, corresponding to increase in β from 0.3 to 0.4.

Figure 3d illustrates the trajectories of \(\bar{C}_{\rm D}\) and C L at Re=200 for a symmetrically confined cylinder during one period of oscillation of the alternating vortices. The amplitude of oscillations in C L decreases with increasing β. The double rings in the trajectories show that the time period of oscillations of C L is twice that of \(\bar{C}_{\rm D}.\) The frequency of the oscillation of C D is twice that of C L due to the contribution of upper and lower alternating vortices to the oscillation in C D.

4.5 Effect of γ on \(\bar{C}_{\rm D}\) for an asymmetrically confined cylinder.

Owing to asymmetry, the dynamics of flow differs due to the presence of the stationary wall closer to the cylinder surface. Figure 4 illustrates the effect of γ on \(\bar{C}_{\rm D}\) for β=0.1, 0.2, 0.3, and 0.4. It is clearly seen that, at β=0.1, as γ decreases, i.e., the cylinder approaches one of the confining walls for fixed Re, \(\bar{C}_{\rm D}\) increases, though the change in \(\bar{C}_{\rm D}\) is small as γ decreases from 1 to 0.75. For a fixed Re<200, \(\bar{C}_{\rm D}\) increases as γ decreases from 0.75 to 0.25 and the change in \(\bar{C}_{\rm D}\) is negligible at Re≥200. For example, at Re=20 increase in \(\bar{C}_{\rm D} \) is 21% as γ decreases from 0.75 to 0.25. The effect of decrease in γ on \(\bar{C}_{\rm D}\) is more pronounced only at low Re and the effect vanishes at Re≥200. Also, for β=0.2, 0.3, and 0.4, drag coefficient increases with a decrease in γ. At higher Re and blockage ratios, the increase in \(\bar{C}_{\rm D} \) as γ decreases from 1 to 0.25 is large. For example, at β=0.1 and Re=100, the increase in \(\bar{C}_{\rm D}\) as γ decreases from 1 to 0.25 is 8%, whereas at β=0.4 increase in \(\bar{C}_{\rm D}\) is 38%. When the cylinder is closer to the wall, the gap between the cylinder and the wall is filled by the boundary layers of the cylinder and on the wall where viscous forces are dominant. In this case the viscous and pressure forces exerted on the cylinder increase resulting in increase in the total drag coefficient.

Fig. 4
figure 4

Effect of γ on \(\bar{C}_{\rm D}\) and St for various blockage ratios (β)

Full size image

4.6 Effect of γ on vortex shedding from an asymmetrically confined cylinder

Both the presence of the stationary walls and asymmetry significantly affect the value of St. The effect of γ on St is shown in Fig. 4. For given values of β and Re, the value of St increases with decrease in γ. At β=0.1, this increase in St at Re=200 is 14.3% as γ decreases from 1 to 0.25. It may also be observed from the figure that for a fixed γ and Re, St increases with increase in β.

Figure 5 illustrates the effect of β and γ on vortex shedding from the cylinder at Re=200, where the instantaneous vorticity contours are presented to show the effect of asymmetrical confinement of the cylinder. For β=0.1, when the cylinder is symmetrically confined in the plane channel, the vortex street consists of positive (shed from the bottom) and negative (shed from the top) vortices. As the cylinder approaches one of the confining walls the regular structure and the symmetry of the vortices is distorted. It may also be observed from this figure that at β=0.1 and γ=1, the vortex structure consists of double row of vortices shed from the cylinder. However, at γ=0.75, the positive vortices shed from the cylinder are significantly distorted due to interaction with the wall which results in the formation of vortex street with a single row of vortices. At γ=0.5 and 0.25, the effect is more pronounced with weak positive vortices shed from the bottom side of the cylinder. In this case the vortex street has almost become a single row of vortices. Figure 5 also illustrates the effect of γ on vortex shedding for β=0.2 at Re=200. As seen from the figure, when the cylinder is symmetrically confined in the plane channel, the structure of vortex street is well defined, with regularly placed positive and negative vortices. However, when compared to the symmetrically confined case at β=0.1, the vortex shedding structure is relatively irregular. Also, as the cylinder approaches one of the confining walls the double row of vortices converges to a single row of vortices. At γ=0.125, i.e., when the cylinder is present very close to the bottom wall, the vortex shedding is completely suppressed. The vortex shedding is gradually suppressed as the cylinder approaches one of the confining walls at β=0.3 and 0.4. At γ=0.25, the vortex shedding is completely suppressed in both cases.

Fig. 5
figure 5

Snapshots of instantaneous vorticity contours at Re=200 for various β and γ

Full size image

Figure 6 illustrates the effect of γ on\(\bar{C}_{\rm L} \) for various β. For a fixed Re, the mean lift coefficient \(\bar{C}_{\rm L}\) decreases as γ decreases for a fixed β. \(\bar{C}_{\rm L}\) is zero when the cylinder is symmetrically confined in a plane channel. However, at smaller values of γ the oscillations the values of the lift coefficient are not symmetric about zero. Therefore, \(\bar{C}_{\rm L} \) has a non-zero value in the asymmetrically confined case. Due to the relatively larger amplitude of the oscillations in the lift coefficient in the negative direction, \(\bar{C}_{\rm L}\) is negative. The amplitude of \(\bar{C}_{\rm L}\) increases in the negative direction and decreases in the positive direction as the cylinder moves closer to the bottom wall of the plane channel. The trend is reversed when the cylinder is present sufficiently close to the cylinder which is observed for β=0.2, 0.3 and 0.4 at low Re. The mean lift is positive at low Re and at low γ. However, the mean lift becomes negative at higher Re. At β=0.1, the cylinder is not sufficiently close to the wall so as to result in the mean positive lift.

Fig. 6
figure 6

Effect of γ on \(\bar{C}_{\rm L}\) for various blockage ratios (β)

Full size image

4.7 Effect of γ on \(\overline{{Nu}} _{w} \) for an asymmetrically confined cylinder

Figure 7 describes the effect of γ on \(\overline{{Nu}} _{w}.\) The effect of γ on \(\overline{{Nu}} _{w}\) is observed to be negligible for all β. The variation of the local Nu w on the surface of the cylinder with γ is also shown in Fig. 7 at Re=200. For all β, change in the distribution of local Nu w on the surface of the cylinder is negligible with decrease in γ, except some distortion in the distribution when the cylinder is present very close to the bottom wall. The distortion is more pronounced at high β. However, the corresponding change in the surface averaged values of Nu w is negligible with a decrease in γ for each β.

Fig. 7
figure 7

Effect of γ on average and local Nusselt number for various blockage ratios (β)

Full size image

5 Conclusions

In this work, unsteady numerical computations have been carried out for the momentum and heat transfer from an asymmetrically confined circular cylinder in a plane channel for the range of Re between 10 and 500 and β between 0.1 and 0.4, and γ between 0.125 and 1. The transition of flow past a cylinder confined in a plane channel is characterized as a function of β and γ.

The critical Re at which the transition takes place from a steady to unsteady flow increases with a decrease in γ for a fixed β. For a given Re, \(\bar{C}_{\rm D}\) and St were found to increase with a decrease in γ. The amplitude of the oscillations in the C L decreases as β increases at a fixed Re. The oscillations in the lift coefficient increase in the negative direction as γ decreases at a fixed Re and β. The oscillations in the C L are completely suppressed when the cylinder is very close to one of the confining walls, and under these conditions, the mean lift coefficient was found to be positive. The effect of decrease in γ on \(\overline{{Nu}}_{w}\) was found to be negligible for all β investigated.