1 Introduction

Microscale gas flows can be found extensively in and around the channels of certain micro-electromechanical systems (MEMS), such as micro-turbines and pumps, micro-motors, micro-bearings and nanotubes, which has emerged as an interesting area for prying into the fundamental physical phenomena in such micro-devices (Ho and Tai 1998; Li et al. 2014; Osman et al. 2012; Wang and Li 2004; Zhang et al. 2012). In general, when the characteristic scale in such confined channels can be comparable to gaseous mean free path, rarefaction effect would become significant and insufficient collisions to equilibrate the process of heat and momentum transport make it challenging to simulate micro-flows accurately, especially through continuum methods where the linear laws of Navier–Stokes–Fourier (NSF) are not available any longer for non-equilibrium transport.

Much effort has been put into the theoretical tools to get the real physical solution of the challenging confined flow problems of which NSF equations fail in description. Boltzmann equation provides a significant option to describe the dilute gas flows at all degrees of rarefaction. However, the highly nonlinear particle collision term in the right-hand side of the Boltzmann equation entailing great mathematical complexity has prevented any attempt of direct solutions. One of the most successful methods for the solution of the Boltzmann equation has to be direct simulation Monte Carlo (DSMC) method based on a probabilistic procedure of tracking statistically representative particles, which was first proposed by Bird (1994). However, subject to its statistical fluctuation, it is expensive both in computational time and memory requirements, particularly for low-speed flows in MEMS (Oran et al. 1998). In order to reduce the computational consumption, Fan and Shen (2001) proposed information preservation method (IP) and have gained its success to simulate low-speed gas flows in microscale. Another route for the solution of Boltzmann equation is to simplify or discrete the collision term, such as linearized Boltzmann equation (Grad 1963), modeling equation methods (BGK, ES-BGK and Shakhov models) (Bhatnagar et al. 1954; Holway 1966; Shakhov 1968), discrete velocity methods (DVM), discrete ordinate method (DOM) (Broadwell 2006; Yang et al. 2016) and unified gas-kinetic scheme (UGKS) (Xu and Huang 2010), etc.

The micro-Couette flow in MEMS can be regarded as a benchmark case for the investigation on a crucial physical layer of few free paths away from the solid surface, which is defined as the Knudsen layer. Extended hydrodynamic equations (EHE) have provided potent tools in capturing these microscale flows with acceptable computational efficiency. However, the underlying physical phenomena of the Knudsen layer behind the Couette flow, such as nonlinear velocity profile, larger temperature difference, smaller shear stress, nonzero normal stress, tangential heat flux and non-intuitive velocity gradient singularity (Lilley and Sader 2007) have not been predicted accurately by existing macroscopic hydrodynamic methods (Lockerby et al. 2005), which seem to be a challenging task. For example, Burnett-type equations that originate from the second-order Chapman–Enskog expansion (Chapman and Cowling 1953) and Grad’s moment equations (Grad 1949) have manifested their defective capacity in capturing high-speed and low-density flow physics (Grad 1952; Rosenau 1989). Thankfully continuum description of microscale flows has seen many new recent advancements including regularization of Grad equations (Gu and Emerson 2009; Torrilhon 2016; Torrilhon and Struchtrup 2008) and Onsager–Burnett equations (Singh and Agrawal 2016; Singh et al. 2017). Moreover, a set of generalized hydrodynamic equations (GHE) proposed by Eu (1980, 1992, 2002; Eu and Ohr 2001; Mazen Al-Ghoul and Eu 1997) also seems to provide a feasible solution in non-equilibrium transport problem. On the basis of GHE, an efficient non-Newton–Fourier computational model (nonlinear coupled constitutive relations, NCCR) was proposed by Myong (1999, 2001, 2004, 2009) and has attained well-pleasing results in 1-D shock wave structures and multidimensional hypersonic rarefied flows (Jiang et al. 2016, 2017; Zhao et al. 2016). In Myong’s recent work (Myong 2016, 2011a), analytical solutions of the Couette flow have been derived for acquiring better understanding of non-equilibrium effects inside the Knudsen layer.

Moreover, gas–surface molecular interaction also plays a dominant role in guaranteeing the accuracy of solutions in the micro-Couette flow. Nonslip boundary conditions are no longer valid because of the existence of a tiny gap of velocity and temperature between the near-wall gas and surface. Slip boundary conditions should be implemented under rarefied conditions. For 13 moment equations and Burnett-type equations, a complete theory of boundary conditions is still lacking (Struchtrup and Taheri 2011), which is also true for Eu’s GHE. The number of boundary conditions needs to be figured out firstly in all high-order boundary value problems for Burnett equations, R13 equations (Gu and Emerson 2007; Torrilhon 2016; Torrilhon and Struchtrup 2008) or R26 equations (Gu and Emerson 2009). As a contrast, the NCCR method is indeed a reduced model which shares a similar feature with NSF constitutive relations as a closure of stress and heat flux, since it doesn’t necessarily consider the substantial derivative of non-conserved variables and higher-order moments in Eu’s GHE on the basis of adiabatic approximation. To some extent, we don’t have to consider the solution of a hyperbolic system of non-conserved variables as aforementioned 13 moment methods. Therefore, the NCCR model does not require additional numerical boundary conditions theoretically and all non-conserved variables on the wall can be evaluated from conserved variables during the solution. However, it is worthwhile noting that enhanced boundary conditions suitable for NCCR model with more accuracy can be achieved probably if based on a more precise physical description of the gas–surface interaction.

In present wok, we intend to apply the NCCR model to confined flows and investigate this set of non-Newton–Fourier constitutive relations’ capability by numerical approaches. Considering the complex solution of the NCCR model, an unusual numerical strategy has been adopted in our approach with reserving the velocity component perpendicular to the wall as a dummy unknown variable and using an unsteady time-marching numerical scheme with a coupled iterative method for approaching final steady solution. This numerical strategy provides a convenient framework for adopting different kinds of wall boundary conditions. With regard to the investigation on a variety of existing boundary conditions and seeking for a well-posed one for NCCR model, emphasis is also placed on the derivation of a new form of enhanced boundary conditions on the basis of Maxwell wall boundary theory and nonlinear stress/strain rate relationship. Finally, the accuracy and effectiveness of combining the NCCR model and enhanced boundary conditions for investigating the micro-Couette flow are assessed extensively.

2 Generalized hydrodynamics

2.1 Conventional hydrodynamic model: the Navier–Stokes–Fourier constitutive relations

Conservation laws, namely mass, momentum and energy conservation laws could be derived from the Boltzmann equation directly. By differentiating the conserved invariants of density \(\rho\), momentum \(\rho {\mathbf{u}}\) and internal energy density \(\rho e\) with time, there follows a set of evolution equations without external force for the lowest order conserved moments:

$$\frac{\partial \rho }{\partial t} + \nabla \cdot \rho {\mathbf{u}} = 0,$$
(1)
$$\frac{{\partial \rho {\mathbf{u}}}}{\partial t} + \nabla \cdot \rho {\mathbf{uu}} + \nabla \cdot {\varvec{\Pi}} = - \nabla \left( {p + \Delta } \right),$$
(2)
$$\frac{\partial \rho e}{\partial t} + \nabla \cdot \rho e{\mathbf{u}} + \nabla \cdot {\mathbf{Q}} = - \left( {p + \Delta } \right)\nabla \cdot {\mathbf{u}} - {\varvec{\Pi}}:\nabla {\mathbf{u}},$$
(3)

where \({\varvec{\Pi}}\), \(\Delta\), \({\mathbf{Q}}\) and \(p\) denote the shear stress, excess normal stress, heat flux and gas pressure, respectively. Obviously, these non-conserved variables given in (2) and (3) are higher-order moments and this set of equations need additional relations to close. One of the classical methods is through linear viscosity and heat conduct laws.

However, the conventional Navier–Stokes–Fourier constitutive relations do not take the excess normal stress \(\Delta\) into account under Stokes’ hypothesis that the bulk viscosity for the excess normal stress \(\Delta\) vanishes. The Navier–Stokes–Fourier (NSF) constitutive relations can also be obtained through Chapman–Enskog expansion of distribution function in terms of Knudsen number around the Maxwellian distribution. The zeroth-order approximation yields Euler equations and the first-order expansion gives the NSF constitutive relations as

$${\varvec{\Pi}}_{0} = - 2\eta \left[ {\nabla {\mathbf{u}}} \right]^{\left( 2 \right)} ,\quad \Delta_{0} = - \eta_{b} \nabla \cdot {\mathbf{u}} = 0,\quad {\mathbf{Q}}_{0} = - \lambda \nabla T,$$
(4)

in which \(\eta_{b}\) denotes the bulk viscosity. The bracket symbol \(\left[ {\;\;} \right]^{\left( 2 \right)}\) represents the traceless symmetric part of the second-rank symmetric tensor. For instance, \(\left[ {\mathbf{A}} \right]^{\left( 2 \right)}\) is equal to \({{\left( {{\mathbf{A}} + {\mathbf{A}}^{t} } \right)} \mathord{\left/ {\vphantom {{\left( {{\mathbf{A}} + {\mathbf{A}}^{t} } \right)} 2}} \right. \kern-0pt} 2} - {{{\mathbf{I}}Tr{\mathbf{A}}} \mathord{\left/ {\vphantom {{{\mathbf{I}}Tr{\mathbf{A}}} 3}} \right. \kern-0pt} 3}\). Finally, the NSF model (4) could be substituted into the evolution Eqs. (1)–(3) to yield traditional hydrodynamic equations, i.e., the NSF equations, which are applicable in continuum regime.

2.2 Generalized hydrodynamic equations: the Eu’s modified moment method

As Knudsen number increases, the NSF constitutive relations would fail in description of the gas flows removed far away from equilibrium due to insufficient molecular collisions. Therefore, high-order moments should be involved to get an accurate physical description of the non-equilibrium flows. A general velocity moment of order \(l\) can be defined as

$$\varPhi^{{\left( {abc \ldots l} \right)}} = \langle mC_{a} C_{b} C_{c} \ldots C_{l} f\left( {{\mathbf{v}},{\mathbf{r}},t} \right)\rangle ,$$
(5)

where \(C\) represents the peculiar velocity. Differentiating the general moment (5) with time and substituting it into the Boltzmann equation for the time derivative of distribution function gives the evolution equation for the general velocity moment \(\varPhi^{{\left( {abc \ldots l} \right)}}\):

$$\begin{aligned} \frac{\partial }{\partial t}\varPhi^{{\left( {abc \ldots kl} \right)}} & = - \nabla \cdot \left( {\varPhi_{i}^{{\left( { \cdot ab \ldots l} \right)}} + {\mathbf{u}}\varPhi_{i}^{{\left( {ab \ldots l} \right)}} } \right) - \sum\limits_{{{\text{all}}\;{\text{terms}}}} {\left( {\frac{{{\text{d}}{\mathbf{u}}}}{{{\text{d}}t}}} \right)_{a} \varPhi_{i}^{{\left( {bc \ldots l} \right)}} } \\ & \quad - \sum\limits_{{{\text{all}}\;{\text{terms}}}} {\varPhi_{i}^{{\left( { \cdot bc \ldots l} \right)}} \cdot \nabla u_{a} + } \sum\limits_{{{\text{all}}\;{\text{terms}}}} {F_{ia} \varPhi_{i}^{{\left( {bc \ldots l} \right)}} + \varLambda_{i}^{{\left( \varPhi \right)\left( {abc \ldots kl} \right)}} } , \\ \end{aligned}$$
(6)

where the dissipation term is expressed as

$$\varLambda^{{\left( \varPhi \right)\left( {abc \ldots kl} \right)}} = \left\langle {mC_{a} C_{b} C_{c} \ldots C_{l} \Re \left( f \right)} \right\rangle .$$
(7)

And the subscript and superscript dot \(\left( \cdot \right)\) in the formula, such as \(\varPhi^{{\left( { \cdot bc \ldots l} \right)}} = \langle C_{ \cdot } C_{b} C_{c} \ldots C_{l} f\rangle\), designates contraction with \(\nabla\) by a scalar product.

Eu (1992, 2002) truncated the infinite non-conserved moments to the second- and third-order set which can be denoted by a unified symbol as

$$\varPhi^{\left( k \right)} = \left\langle {h^{\left( k \right)} f({\mathbf{v}},{\mathbf{r}},t)} \right\rangle ,$$
(8)

where \(\varPhi^{\left( 1 \right)}\) denotes the shear stress \({\varvec{\Pi}}\), \(\varPhi^{\left( 2 \right)}\) the excess normal stress \(\Delta\), \(\varPhi^{\left( 3 \right)}\) the heat flux \({\mathbf{Q}}\) and their microscopic expressions are correspond to

$$h^{\left( 1 \right)} = [m{\mathbf{CC}}]^{(2)} ,\quad h^{\left( 2 \right)} = \frac{1}{3}mC^{2} - p/n,\quad h^{\left( 3 \right)} = \left( {\frac{1}{2}mC^{2} + H_{rot} - \hat{h}m} \right){\mathbf{C}}.$$
(9)

In above expressions, \(n\) represents the number density of molecules and \(\hat{h}\) is the enthalpy density per unit mass. \(H_{\text{rot}}\) denotes the rotational Hamiltonian of molecular. Substituting the stress and heat flux expressions into Eq. (6), a set of evolution equations for the non-conserved moments of interest could be derived as

$$\rho \frac{\text{d}}{{{\text{d}}t}}\hat{\varPhi }^{(\alpha )} = Z^{\left( \alpha \right)} + \varLambda^{\left( \alpha \right)} ,$$
(10)

where

$$\hat{\varPhi }^{\left( \alpha \right)} = \varPhi^{\left( \alpha \right)} /\rho ,$$
(11)
$$\varLambda^{\left( \alpha \right)} = \left\langle {h^{\left( \alpha \right)} \Re \left( f \right)} \right\rangle ,$$
(12)
$$Z^{\left( \alpha \right)} = - \nabla \cdot \psi^{\left( \alpha \right)} + \left\langle {f\left( {d_{t} + C \cdot \nabla + {\mathbf{F}} \cdot \nabla_{\upsilon } } \right)h^{\left( \alpha \right)} } \right\rangle .$$
(13)

In formula (13), \(\psi^{\left( \alpha \right)}\) represents the flux of higher-order moments, namely \(\psi^{\left( \alpha \right)} = \left\langle {Ch^{\left( \alpha \right)} f} \right\rangle\). Explicit forms for the kinematic term \(Z^{\left( \alpha \right)}\) are summarized in literature (Eu 2002), which can be listed below as

$$Z^{\left( 1 \right)} = - {\mathbf{\nabla }} \cdot \psi^{\left( 1 \right)} - 2\left[ {{\varvec{\Pi}} \cdot \left[ {\nabla {\mathbf{u}}} \right]^{\left( 2 \right)} } \right]^{\left( 2 \right)} + \left[ {{\varvec{\Pi}},{\varvec{\upomega}}} \right] - 2\left( {p + \Delta } \right)\left[ {\nabla {\mathbf{u}}} \right]^{\left( 2 \right)} - \frac{2}{3}{\varvec{\Pi}}\nabla \cdot {\mathbf{u}},$$
(14)
$$Z^{\left( 2 \right)} = - {\mathbf{\nabla }} \cdot \psi^{\left( 2 \right)} - \frac{2}{3}{\varvec{\Pi}}:\left[ {\nabla {\mathbf{u}}} \right]^{\left( 2 \right)} - \frac{2}{3}\Delta \nabla \cdot {\mathbf{u}} - pd_{t} \ln \left( {\frac{p}{{\rho^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0pt} 3}}} }}} \right),$$
(15)
$$\begin{aligned} Z^{\left( 3 \right)} & = - \nabla \cdot \psi^{\left( 3 \right)} - d_{t} {\mathbf{u}} \cdot \left( {{\mathbf{P}} - p{\mathbf{\rm I}}} \right) + {\mathbf{Q}} \cdot \left( { - \left[ {\nabla {\mathbf{u}}} \right]^{\left( 2 \right)} - {\varvec{\upomega}} - \frac{1}{3}{\mathbf{\rm I}}\nabla \cdot {\mathbf{u}}} \right) \\ & \quad + \varphi^{\left( 3 \right)} :\left( { - \left[ {\nabla {\mathbf{u}}} \right]^{\left( 2 \right)} - {\varvec{\upomega}} - \frac{1}{3}{\mathbf{\rm I}}\nabla \cdot {\mathbf{u}}} \right){\mathbf{ - }}{\mathbf{P}} \cdot {\mathbf{\nabla }}\hat{h}, \\ \end{aligned}$$
(16)

where the higher-order moment \(\varphi^{\left( 3 \right)}\) is defined as \(\left\langle {m{\mathbf{CCC}}f} \right\rangle\) and \({\varvec{\upomega}}\) is the vorticity tensor defined by

$${\varvec{\upomega}} = \frac{1}{2}\left[ {\nabla {\mathbf{u}} - \left( {\nabla {\mathbf{u}}} \right)^{t} } \right].$$

It forms an antisymmetric tensor with \({\varvec{\Pi}}\) by

$$\left[ {{\varvec{\Pi}},{\varvec{\upomega}}} \right] = {\varvec{\Pi}} \cdot {\varvec{\upomega}} - {\varvec{\upomega}} \cdot {\varvec{\Pi}}.$$

Note that these formulas (10)–(16) are still an open set of evolution equations because the dissipation terms are still unknown. In Eu’s modified moment method (Eu 1980, 1992), a distribution function is expressed by

$$f = f^{\left( 0 \right)} \exp \left[ { - \beta \left( {H^{\left( 1 \right)} - \mu + \mu^{0} } \right)} \right].$$
(17)

In above expression, \(f^{\left( 0 \right)}\) denotes the local equilibrium distribution function as \(\exp \left[ { - \beta \left( {H - \mu^{0} } \right)} \right]\) where \(\beta = {1 \mathord{\left/ {\vphantom {1 {k_{\text{B}} T}}} \right. \kern-0pt} {k_{\text{B}} T}}\) and the normalization factors \(\mu^{0}\) in local equilibrium can be obtained by \(\exp \left( {\beta \mu^{0} } \right) = n^{0} \left( {{{m\beta } \mathord{\left/ {\vphantom {{m\beta } {2\pi }}} \right. \kern-0pt} {2\pi }}} \right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}}\). And the factor \(\mu\) comes from

$$\exp \left( { - \beta \mu } \right) = \left( {n^{0} } \right)^{ - 1} \left\langle {\exp \left[ { - \beta \left( {H + H^{\left( 1 \right)} } \right)} \right]} \right\rangle ,$$

where \(H = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}mC^{2}\) and \(H^{\left( 1 \right)} = \sum\nolimits_{k = 1}^{\infty } {X_{k} h^{\left( k \right)} }\) represents the non-equilibrium contribution. The \(X_{k}\) are underdetermined functions in implicit forms of macroscopic variables, which evolve by the constraint of the Boltzmann equation and the second law of thermodynamics. By Substitution of this distribution function (17) into the dissipation term (12) with the introduction of cumulant expansion (Kubo 1962), the dissipation terms can be obtained in a nonlinear form as

$$\varLambda^{\left( 1 \right)} = - \left( {{p \mathord{\left/ {\vphantom {p \eta }} \right. \kern-0pt} \eta }} \right){\varvec{\Pi}}{{\sinh \kappa } \mathord{\left/ {\vphantom {{\sinh \kappa } \kappa }} \right. \kern-0pt} \kappa },$$
(18)
$$\varLambda^{\left( 2 \right)} = - \left( {{{2p} \mathord{\left/ {\vphantom {{2p} {3\eta_{b} }}} \right. \kern-0pt} {3\eta_{b} }}} \right)\Delta {{\sinh \kappa } \mathord{\left/ {\vphantom {{\sinh \kappa } \kappa }} \right. \kern-0pt} \kappa },$$
(19)
$$\varLambda^{\left( 3 \right)} = - \left( {{{p\hat{h}} \mathord{\left/ {\vphantom {{p\hat{h}} {\lambda T}}} \right. \kern-0pt} {\lambda T}}} \right){\mathbf{Q}}{{\sinh \kappa } \mathord{\left/ {\vphantom {{\sinh \kappa } \kappa }} \right. \kern-0pt} \kappa },$$
(20)

where \(\kappa\) is given by the Rayleigh–Onsager dissipation function

$$\kappa = \frac{{\left( {mk_{\text{B}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0pt} 4}}} }}{\sqrt 2 d}\frac{{T^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0pt} 4}}} }}{p}\left[ {\frac{{{\varvec{\Pi}}:{\varvec{\Pi}}}}{2\eta } + \gamma^{\prime}\frac{{\Delta^{2} }}{{\eta_{b} }} + \frac{{{\mathbf{Q}} \cdot {\mathbf{Q}}}}{\lambda T}} \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} .$$
(21)

Combination of the formulas (10), (14), (16), (18) and (20) yields Eu’s generalized hydrodynamic equations finally.

2.3 A generalized hydrodynamic model: nonlinear coupled constitutive relations

However, the set of generalized hydrodynamic equations is still an open system of partial differential equations involving higher-order moments. Before any attempt of using it to describe non-equilibrium gas transport mechanism, a closure should be taken into account firstly. Eu et al. (Bhattacharya and Eu 1987; Eu and Ohr 2001; Mazen Al-Ghoul and Eu 1997) took a basic closure tenet that only a few moments are sufficient for the description of gas transport mechanism of interest and the higher-order moments should not be calculated in terms of lower-order moments to reduce the computational cost. Since there exists no single closure theory founded on a firm theoretical justification, Eu proposed the following closure different from Grad’s:

$$\psi^{\left( 1 \right)} = \psi^{\left( 2 \right)} = \psi^{\left( 3 \right)} = 0.$$
(22)

Furthermore, Eu (2002) also observed that the higher-order moments decay faster than the conserved variables in experiments, which backed up the closure tenet. It means that the non-conserved variables have already attained steady state when the conserved variables no longer change. Compared with the evolution timescale of conserved variables, the timescale of non-conserved variables are negligible. This approximation is named as adiabatic approximation by Eu, which is similar with the center manifold approximation (Knobloch and Wiesenfeld 1983) used in nonlinear dynamics. Note that the term related to a third-rank tensor \(\varphi^{\left( 3 \right)}\) in Eq. (16) has also been omitted in accordance with 13 moment methods. Therefore, on basis of the adiabatic approximation, the steady form of generalized hydrodynamic equations, which is nonlinear coupled constitutive relations (NCCR) called by Myong (2009, 2011a, 2016), are obtained as

$$- 2\left[ {{\varvec{\Pi}} \cdot \nabla {\mathbf{u}}} \right]^{\left( 2 \right)} - \frac{p}{\eta }{\varvec{\Pi}}q\left( \kappa \right) - 2(p + \Delta )\left[ {\nabla {\mathbf{u}}} \right]^{\left( 2 \right)} = 0,$$
(23)
$$- 2\gamma^{\prime}(\Delta {\mathbf{I}} + {\varvec{\Pi}}):\nabla {\mathbf{u}} - \frac{2}{3}\gamma^{\prime}p\nabla \cdot {\mathbf{u}} - \frac{2}{3}\gamma^{\prime}\frac{p}{{\eta_{b} }}\Delta q\left( \kappa \right) = 0,$$
(24)
$$- {\varvec{\Pi}} \cdot c_{p} \nabla T - {\mathbf{Q}} \cdot \nabla {\mathbf{u}} - \frac{{pc_{p} }}{\lambda }{\mathbf{Q}}q\left( \kappa \right) - (p + \Delta )c_{p} T\nabla \ln T = 0,$$
(25)

where \(q\left( \kappa \right)\) denotes \({{\sinh \kappa } \mathord{\left/ {\vphantom {{\sinh \kappa } \kappa }} \right. \kern-0pt} \kappa }\) and \(\gamma^{\prime}\) is equal to \({{\left( {5 - 3\gamma } \right)} \mathord{\left/ {\vphantom {{\left( {5 - 3\gamma } \right)} 2}} \right. \kern-0pt} 2}\) in which \(\gamma\) represents the specific heat ratio.

3 Wall boundary conditions

3.1 Langmuir slip and Maxwell–Smoluchowski models

Before the investigation for the NCCR model in micro-Couette flows, wall boundary conditions need to be elucidated theoretically. There are two common gas–surface molecular interaction models available in literatures (Langmuir 1916; Maxwell 1879): one is Langmuir’s surface adsorption theory and the other is Maxwell’s scattering theory. The former mainly focuses on the processes of adsorption and desorption and the latter considers the processes of incidence and reflection.

Following the basic idea of Langmuir (1916), a practicable slip model was firstly developed by Eu et al. (Bhattacharya and Eu 1987; Eu et al. 1987) and Myong et al. (Myong 2001, 2003; Myong et al. 2005) and has been extensively used in LBM (Chen and Tian 2010; Kim et al. 2007). In this model, the velocity and temperature of the fluid adjacent to the wall could be expressed as a weighted mean between the value of the wall and the gas at a mean free path away from the wall or at the free-stream as follows in dimensional form:

$$u = \alpha u_{w} + \left( {1 - \alpha } \right)u_{g} ,$$
(26)
$$T = \alpha T_{w} + \left( {1 - \alpha } \right)T_{g} ,$$
(27)

where the fraction \(\alpha\) is equal to \({{\beta p} \mathord{\left/ {\vphantom {{\beta p} {\left( {1 + \beta p} \right)}}} \right. \kern-0pt} {\left( {1 + \beta p} \right)}}\) for monatomic gases and \({{\sqrt {\beta p} } \mathord{\left/ {\vphantom {{\sqrt {\beta p} } {1 + \sqrt {\beta p} }}} \right. \kern-0pt} {1 + \sqrt {\beta p} }}\) for diatomic gases. \(\beta\) can be calculated by \({{A\bar{l}\exp \left( {{{D_{e} } \mathord{\left/ {\vphantom {{D_{e} } {k_{\text{B}} T_{w} }}} \right. \kern-0pt} {k_{\text{B}} T_{w} }}} \right)} \mathord{\left/ {\vphantom {{A\bar{l}\exp \left( {{{D_{e} } \mathord{\left/ {\vphantom {{D_{e} } {k_{\text{B}} T_{w} }}} \right. \kern-0pt} {k_{\text{B}} T_{w} }}} \right)} {k_{\text{B}} T_{w} }}} \right. \kern-0pt} {k_{\text{B}} T_{w} }}\), where these coefficients \(A\), \(D_{e}\), \(\bar{l}\) have specific definitions in literatures (Bhattacharya and Eu 1987; Myong 2004). Eu et al. (1987) took \({L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0pt} 2}\) as the value of \(\bar{l}\) for the case of sufficiently rarefied gases in the micro-Couette flow. Considering the cases we intend to investigate, we take \(\bar{l} = {l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0pt} 2}\) for the low-Knudsen number cases and switch to \({L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0pt} 2}\) for \(Kn \ge 0.5\) cases in our research.

Comparing with Langmuir slip model, Maxwell–Smoluchowski (M/S) model is more common to estimate the slip effect on the wall under rarefied conditions (Gad-el-Hak 1999):

$$u - u_{\text{wall}} = C_{m} l\left( {\frac{\partial u}{\partial y}} \right)_{w} + C_{s} \frac{\mu }{\rho T}\left( {\frac{\partial T}{\partial x}} \right)_{w} ,$$
(28)
$$T - T_{\text{wall}} = C_{t} l\left( {\frac{\partial T}{\partial y}} \right)_{w} ,$$
(29)

where the coefficient \(C_{m}\) can be expressed by \({{\left( {2 - \sigma_{u} } \right)} \mathord{\left/ {\vphantom {{\left( {2 - \sigma_{u} } \right)} {\sigma_{u} }}} \right. \kern-0pt} {\sigma_{u} }}\), \(C_{t}\) by \({{\left( {2 - \sigma_{T} } \right)} \mathord{\left/ {\vphantom {{\left( {2 - \sigma_{T} } \right)} {\sigma_{T} \cdot {{2\gamma } \mathord{\left/ {\vphantom {{2\gamma } {\left( {\gamma + 1} \right)Pr}}} \right. \kern-0pt} {\left( {\gamma + 1} \right)Pr}}}}} \right. \kern-0pt} {\sigma_{T} \cdot {{2\gamma } \mathord{\left/ {\vphantom {{2\gamma } {\left( {\gamma + 1} \right)Pr}}} \right. \kern-0pt} {\left( {\gamma + 1} \right)Pr}}}}\). Here, \(\sigma_{u}\) and \(\sigma_{T}\) are the accommodation coefficients. The slip velocity calculated by DSMC in the Couette flow is proved to be close to \(l{{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial y}}} \right. \kern-0pt} {\partial y}}\) (Bird 1994), which attracted various researchers to investigate these slip and thermal creep coefficients \(C_{m}\), \(C_{t}\), \(C_{s}\) through molecule dynamics, DSMC or experiments. However, how to choose these free coefficients is still an open question (Zhang et al. 2012).

Another route for capturing the slip velocity and jump temperature phenomenon accurately at large Knudsen numbers is to propose higher-order theoretical models or modifications. Beskok and Karniadakis (1999) attempted to expand the first-order M/S model into higher orders by using Taylor series expansion:

$$u - u_{\text{wall}} = C_{m} \left[ {l\left( {\frac{\partial u}{\partial y}} \right)_{w} + \frac{{l^{2} }}{2!}\left( {\frac{{\partial^{2} u}}{{\partial y^{2} }}} \right)_{w} + \frac{{l^{3} }}{3!}\left( {\frac{{\partial^{3} u}}{{\partial y^{3} }}} \right)_{w} + \cdot \cdot \cdot } \right],$$
(30)
$$T - T_{\text{wall}} = C_{t} \left[ {l\left( {\frac{\partial T}{\partial y}} \right)_{w} + \frac{{l^{2} }}{2!}\left( {\frac{{\partial^{2} T}}{{\partial y^{2} }}} \right)_{w} + \frac{{l^{3} }}{3!}\left( {\frac{{\partial^{3} T}}{{\partial y^{3} }}} \right)_{w} + \cdot \cdot \cdot } \right].$$
(31)

The second-order approximation of M/S model could be truncated so straightforwardly that the second-order M/S-type boundary conditions should yield better results than the first-order one. However, the fact is opposite against the original intuition (Bao et al. 2007; Lockerby and Reese 2003; Zhao 2014), which indicates the physical inaccuracy in the second-order M/S-type model.

Hsia and Domoto (1983) proposed another high-order expansion through experimental investigation, which contains negative even-order derivatives compared with the positive ones in Eqs. (30) and (31):

$$u - u_{\text{wall}} = C_{m} \left[ {l\left( {\frac{\partial u}{\partial y}} \right)_{w} - \frac{{l^{2} }}{2!}\left( {\frac{{\partial^{2} u}}{{\partial y^{2} }}} \right)_{w} + \frac{{l^{3} }}{3!}\left( {\frac{{\partial^{3} u}}{{\partial y^{3} }}} \right)_{w} - \cdots } \right].$$
(32)

Similar derivations are made for the temperature jump boundary condition,

$$T - T_{\text{wall}} = C_{t} \left[ {l\left( {\frac{\partial T}{\partial y}} \right)_{w} - \frac{{l^{2} }}{2!}\left( {\frac{{\partial^{2} T}}{{\partial y^{2} }}} \right)_{w} + \frac{{l^{3} }}{3!}\left( {\frac{{\partial^{3} T}}{{\partial y^{3} }}} \right)_{w} - \cdots } \right].$$
(33)

The second-order Hsia–Domoto (H/D) boundary conditions has been adopted successfully in Burnett-type equations and proves its accuracy in predicting wall shear stress and heat flux in the Couette flow (Bao et al. 2007; Zhao 2014). The distinction between the second-order M/S and H/D models reflects that the positive second-order term may overcorrect the slip velocity and jump temperature values. The second-order H/D boundary conditions can be written as

$$u - u_{\text{wall}} = C_{m} \left[ {l\left( {\frac{\partial u}{\partial y}} \right)_{w} - \frac{{l^{2} }}{2!}\left( {\frac{{\partial^{2} u}}{{\partial y^{2} }}} \right)_{w} } \right],$$
(34)
$$T - T_{\text{wall}} = C_{t} \left[ {l\left( {\frac{\partial T}{\partial y}} \right)_{w} - \frac{{l^{2} }}{2!}\left( {\frac{{\partial^{2} T}}{{\partial y^{2} }}} \right)_{w} } \right].$$
(35)

3.2 Enhanced NCCR-based boundary conditions

Comparing above gas–surface molecular interaction models, the Maxwell–Smoluchowski model and the Langmuir slip model, they both depend on the concept of accommodation or adjustable coefficients to describe the slip phenomenon on the wall accurately. Since there is no special superiority between these two models, we will propose a set of enhanced boundary conditions from the high-order M/S model in present work.

The NCCR model reduced from the generalized hydrodynamic equations ought to be a higher-order approximation (Rana et al. 2016) than the NSF constitutive relations for the Boltzmann equation. The Maxwell-type boundary conditions based on the linear stress/strain rate relation, which are suitable for the NSF equations, may be short of reflecting the second-order characteristics in the NCCR model. Lockerby and Reese (Lockerby and Reese 2008) mentioned that one of the main shortcomings of the Maxwell-type boundary conditions is that they did not consider the nonlinear stress/strain rate relationship when being applied for high-order constitutive relations. They (Lockerby et al. 2004) clarified and brought back the general form of the first-order Maxwell slip expression, which should be expressed in terms of stress rather than strain rate:

$$u - u_{\text{wall}} = - C_{m} \frac{l}{\eta }\varPi - C_{s} \frac{\gamma - 1}{\gamma }\frac{Pr}{p}Q_{x} ,$$
(36)

where \(\varPi\) and \(Q_{x}\) denote the tangential shear stress and the heat flux along the surface, respectively, \(p\) is the gas pressure nearest to the wall. Similar derivations for the temperature jump boundary condition can be shown in the following expression:

$$T - T_{\text{wall}} = - C_{t} \frac{l}{\lambda }Q_{y} ,$$
(37)

where \(\lambda\) is the coefficient of heat conduction and \(Q_{y}\) is the heat flux perpendicular to the surface. Note that the significant distinction and relationship between these two sets of boundary conditions (28), (29) and (36), (37) would be the substitution of the linear Newton–Fourier constitutive relations (4) into the latter. It means that the boundary conditions (36) and (37) are more general than the common scalar forms (28) and (29) which match with linear constitutive relations’ accuracy. Lockerby et al. (2004) proposed Maxwell–Burnett boundary conditions based on above general forms and Burnett constitutive relations. Reasonable agreement with experimental data for the Poiseuille flow was also achieved.

Based on the first-order Maxwell’s general boundary conditions (36) and (37), a set of nonlinear velocity slip and temperature jump boundary conditions has been proposed to manifest nonlinear characteristics with the NCCR model on the wall (Myong 2011b, 2016). However, the effect of the second-order terms on the velocity slip and temperature jump components should be both taken into account when the flows are removed far away from equilibrium (Hsia and Domoto 1983; Lockerby and Reese 2008). Although the exact effect due to the second-order terms is not easy to assess, the ratio between the second-order and the first-order dimensionless terms may give preliminary evaluation of the relative magnitude, i.e.,

$$r = {\raise0.7ex\hbox{${ - \frac{{Kn^{2} }}{2!}\frac{{\partial^{2} u}}{{\partial y^{2} }}}$} \!\mathord{\left/ {\vphantom {{ - \frac{{Kn^{2} }}{2!}\frac{{\partial^{2} u}}{{\partial y^{2} }}} {Kn\frac{\partial u}{\partial y}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${Kn\frac{\partial u}{\partial y}}$}}\quad {\text{or}}\quad {\raise0.7ex\hbox{${ - \frac{{Kn^{2} }}{2!}\frac{{\partial^{2} T}}{{\partial y^{2} }}}$} \!\mathord{\left/ {\vphantom {{ - \frac{{Kn^{2} }}{2!}\frac{{\partial^{2} T}}{{\partial y^{2} }}} {Kn\frac{\partial T}{\partial y}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${Kn\frac{\partial T}{\partial y}}$}}.$$
(38)

For the purpose of comparison only, the analytical NSF solutions to the constant-viscosity Couette flow can be used. For simplicity, take temperature profile (62) of Couette flow with the same wall temperature to deduce the ratio on the wall. The ratio defined by (38) becomes as follows:

$$r_{y = 0} = {\raise0.7ex\hbox{${ - \frac{{Kn^{2} }}{2!}\frac{{\partial^{2} T}}{{\partial y^{2} }}}$} \!\mathord{\left/ {\vphantom {{ - \frac{{Kn^{2} }}{2!}\frac{{\partial^{2} T}}{{\partial y^{2} }}} {Kn\frac{\partial T}{\partial y}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${Kn\frac{\partial T}{\partial y}}$}} = Kn.$$
(39)

It could be found that the ratio on the wall is nothing but the local Knudsen number, and the second-order effect on temperature component can no longer be neglected without justification especially when the local Knudsen number approaches unity. Furthermore, the second-order effect on velocity component is also kept to be examined in our present work.

Therefore, since the second-order H/D boundary conditions are more physical than the second-order MS one, we propose a new enhanced form of the second-order NCCR-based boundary conditions based on the former one:

$$u - u_{\text{wall}} = C_{m} \left[ {\frac{l}{ - \eta }\varPi_{\text{NCCR}} + \frac{{l^{2} }}{2\eta }\frac{{\partial \varPi_{\text{NCCR}} }}{\partial y}} \right] + C_{s} \frac{\gamma - 1}{\gamma }\frac{\Pr }{p}\left( { - Q_{{x{\text{NCCR}}}} } \right),$$
(40)
$$T - T_{\text{wall}} = C_{t} \left[ {\frac{l}{ - \lambda }Q_{{y{\text{NCCR}}}} + \frac{{l^{2} }}{2\lambda }\frac{{\partial Q_{{y{\text{NCCR}}}} }}{\partial y}} \right].$$
(41)

Considering strong rarefaction effect would give rise to the heat flux along the solid surface in the micro-Couette flow, the thermal creep term is also taken into account in present work. The thermal creep coefficient \(C_{s}\) is recommended to be 0.75 in general. All stress and heat flux at the right-hand side of Eqs. (40) and (41) are resolved iteratively from the nonlinear coupled constitutive relations (NCCR) near the wall.

4 Numerical method

4.1 Control equations for Couette flow

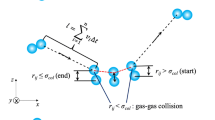
A schematic for the Couette flow is illustrated in Fig. 1, where two infinite solid walls with constant wall temperatures \(T_{L}\) and \(T_{0}\) are moving parallel to the x-direction with constant opposite speeds \(u_{L}\) and \(u_{0}\). The distance between the two plates is \(L\) and the degree of rarefaction effect is defined by the global Knudsen number as \(Kn = {l \mathord{\left/ {\vphantom {l L}} \right. \kern-0pt} L}\).

Fig. 1
figure 1

Schematic of the micro-Couette flow

Full size image

Actually, the micro-Couette flow is quasi-one-dimensional for the linear NSF model, but includes multidimensional effect on the stress tensor and heat flux in the NCCR model. Therefore, it could be considered as a two-dimensional shear flow which is homogeneous in z-direction and its reserved non-conserved variables are given by

$${\varvec{\Pi}} = \left[ {\begin{array}{*{20}l} {\varPi_{xx} } \hfill & {\varPi_{xy} } \hfill & 0 \hfill \\ {\varPi_{xy} } \hfill & {\varPi_{yy} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & { - \varPi_{xx} - \varPi_{yy} } \hfill \\ \end{array} } \right],\quad {\mathbf{Q}} = \left( {\begin{array}{*{20}l} {Q_{x} ,} \hfill & {Q_{y} ,} \hfill & 0 \hfill \\ \end{array} } \right).$$

Note that a special motion feature induced by two infinite parallel plates in x-direction can lead to no variation of flow parameters along this direction under no pressure gradient, namely \({\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-0pt} {\partial x}} = 0\). By combining the conservation law of mass, a simple relation \(v = 0\) can be obtained. However, the velocity component \(v\) is still reserved in present work as a dummy unknown variable for the solution of the coupled system. Moreover, different from conventional steady methods solving the Couette flow, an unsteady time-marching strategy is established by introducing the time derivatives of conserved variables into the governing equations. The final convergent solution will approach to the steady result after a long enough evolution time. The control equations can be summarized as

$$\begin{aligned} & \frac{\partial \rho }{\partial t} + v\frac{\partial \rho }{\partial y} + \rho \frac{\partial v}{\partial y} = 0, \\ & \frac{\partial u}{\partial t} + v\frac{\partial u}{\partial y} + \frac{1}{\rho }\frac{{\partial \varPi_{yx} }}{\partial y} = 0, \\ & \frac{\partial v}{\partial t} + v\frac{\partial v}{\partial y} + \frac{1}{\rho }\frac{{\partial \left( {\varPi_{yy} + \Delta + p} \right)}}{\partial y} = 0, \\ & \frac{\partial T}{\partial t} + v\frac{\partial T}{\partial y} + \frac{1}{{\rho c_{v} }}\varPi_{yx} \frac{\partial u}{\partial y} + \frac{1}{{\rho c_{v} }}\left( {\varPi_{yy} + \Delta + p} \right)\frac{\partial v}{\partial y} + \frac{1}{{\rho c_{v} }}\frac{{\partial Q_{y} }}{\partial y} = 0. \\ \end{aligned}$$
(42)

Actually, this numerical strategy avoids handling extra integration conditions, such as \(\varPi_{yx} = c_{1}\) and \(\varPi_{yy} + \Delta + p = c_{2}\), where \(c_{1}\) and \(c_{2}\) are unknown integration constants. Lockerby and Xue (Lockerby and Reese 2003; Xue et al. 2001) assumed that the constant is independent of the \(Kn\) number and had to take the pressure \(p_{NS}\) at \(Kn = 0\) as an approximated value of \(c_{2}\) in the study for the Burnett equations.

In present work, the dimensionless flow variables and properties are utilized as follows:

$$\begin{aligned} & y^{*} = \frac{y}{L},\quad t^{*} = \frac{t}{{{L \mathord{\left/ {\vphantom {L {a_{L} }}} \right. \kern-0pt} {a_{L} }}}},\quad u^{*} = \frac{u}{{a_{L} }},\quad v^{*} = \frac{v}{{a_{L} }},\quad p^{*} = \frac{p}{{\rho_{L} a_{L}^{2} }},\quad T^{*} = \frac{T}{{T_{L} }},\quad \eta^{*} = \frac{\eta }{{\eta_{L} }},\quad \eta_{b}^{*} = \frac{{\eta_{b} }}{{\eta_{L} }},\quad \lambda^{*} = \frac{\lambda }{{\lambda_{L} }}, \\ & R^{*} = \frac{R}{{a_{L}^{2} /T_{L} }} = \frac{1}{\gamma },\quad c_{v}^{*} = \frac{{c_{v} }}{{a_{L}^{2} /T_{L} }} = \frac{1}{{\gamma \left( {\gamma - 1} \right)}},\quad {\varvec{\Pi}}^{*} = \frac{{\varvec{\Pi}}}{{{{\eta_{L} a_{L} } \mathord{\left/ {\vphantom {{\eta_{L} a_{L} } L}} \right. \kern-0pt} L}}},\quad \Delta^{*} = \frac{\Delta }{{{{\eta_{L} a_{L} } \mathord{\left/ {\vphantom {{\eta_{L} a_{L} } L}} \right. \kern-0pt} L}}},\quad {\mathbf{Q}}^{*} = \frac{{\mathbf{Q}}}{{\lambda_{L} T_{L} /L}}, \\ \end{aligned}$$

where the subscript \(L\) represents the gas property evaluated at the upper plate of the microchannel. \(\eta\), \(\eta_{b}\) and \(\lambda\) denote the coefficients of viscosity, bulk viscosity and heat conduction. The asterisks denote dimensionless parameters and will be omitted below for notational brevity. Here, a composite number \(N_{\delta }\) is defined as

$$N_{\delta } = \frac{{\eta_{L} }}{{\rho_{L} a_{L} L}} = \frac{{Ma_{L} }}{{Re_{L} }}.$$
(43)

After inserting the ideal gas equation of state into Eq. (42), unsteady-state evolution equations can be expressed in the following dimensionless form:

$$\frac{{\partial {\mathbf{U}}}}{\partial t} + {\mathbf{A}}\frac{{\partial {\mathbf{U}}}}{\partial y} + N_{\delta } {\mathbf{B}}\frac{{\partial {\mathbf{G}}_{v} }}{\partial y} = 0,$$
(44)

where

$$\begin{aligned} & {\mathbf{U}} = \left[ {\begin{array}{*{20}c} {\ln \rho } \\ u \\ v \\ T \\ \end{array} } \right],\quad {\mathbf{G}}_{v} = \left[ {\begin{array}{*{20}c} 0 \\ {\varPi_{yx} } \\ {\varPi_{yy} + \Delta } \\ {Q_{y} } \\ \end{array} } \right],\quad {\mathbf{B}} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & {\frac{1}{\rho }} & 0 & 0 \\ 0 & 0 & {\frac{1}{\rho }} & 0 \\ 0 & 0 & 0 & {\frac{\varepsilon }{{\rho c_{v} }}} \\ \end{array} } \right], \\ & {\mathbf{A}} = \left[ {\begin{array}{*{20}c} v & 0 & 1 & 0 \\ 0 & v & 0 & 0 \\ {\frac{T}{\gamma }} & 0 & v & {\frac{1}{\gamma }} \\ 0 & {N_{\delta } \frac{{\varPi_{yx} }}{{\rho c_{v} }}} & {N_{\delta } \frac{{\varPi_{yy} + \Delta }}{{\rho c_{v} }} + \frac{T}{{\gamma c_{v} }}} & v \\ \end{array} } \right]. \\ \end{aligned}$$

A similar process for the simplification of the constitutive relations is conducted by reserving all terms including the velocity component \(v\). As a result, the NCCR model for the micro-Couette flow is reduced to the following system of seven algebraic equations:

$$q\left( {c\hat{R}} \right)\left[ {\begin{array}{*{20}c} {\hat{\varPi }_{xx} } \\ {\hat{\varPi }_{yy} } \\ {\hat{\varPi }_{zz} } \\ {\hat{\varPi }_{xy} } \\ {\hat{\Delta }} \\ {\hat{Q}_{x} } \\ {\hat{Q}_{y} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left( {1 + \hat{\Delta } + \hat{\varPi }_{yy} } \right)\hat{\varPi }_{xx0}^{{v_{y} }} + \left( {{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0pt} 3}} \right)\hat{\varPi }_{xy} \hat{\varPi }_{xy0}^{{u_{y} }} } \\ {\left( {1 + \hat{\Delta } + \hat{\varPi }_{yy} } \right)\hat{\varPi }_{yy0}^{{v_{y} }} - \left( {{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}} \right)\hat{\varPi }_{xy} \hat{\varPi }_{xy0}^{{u_{y} }} } \\ {\left( {1 + \hat{\Delta } + \hat{\varPi }_{yy} } \right)\hat{\varPi }_{zz0}^{{v_{y} }} - \left( {{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}} \right)\hat{\varPi }_{xy} \hat{\varPi }_{xy0}^{{u_{y} }} } \\ {\left( {1 + \hat{\Delta } + \hat{\varPi }_{yy} } \right)\hat{\varPi }_{xy0}^{{u_{y} }} + \left( {{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0pt} 4}} \right)\hat{\varPi }_{xy} \hat{\varPi }_{yy0}^{{v_{y} }} } \\ {\left( {1 + 3\hat{\varPi }_{yy} + 3\hat{\Delta }} \right)\hat{\Delta }_{0}^{{v_{y} }} + 3f_{b} \hat{\varPi }_{yx} \hat{\varPi }_{xy0}^{{u_{y} }} } \\ {\hat{\varPi }_{xy} \hat{Q}_{y0} + {{\hat{Q}_{y} \hat{\varPi }_{xy0}^{{u_{y} }} } \mathord{\left/ {\vphantom {{\hat{Q}_{y} \hat{\varPi }_{xy0}^{{u_{y} }} } {Pr}}} \right. \kern-0pt} {Pr}}} \\ {\left( {1 + \hat{\Delta } + \hat{\varPi }_{yy} } \right)\hat{Q}_{y0} + \left( {{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0pt} 4}} \right){{\hat{Q}_{y} \hat{\varPi }_{yy0}^{{v_{y} }} } \mathord{\left/ {\vphantom {{\hat{Q}_{y} \hat{\varPi }_{yy0}^{{v_{y} }} } {Pr}}} \right. \kern-0pt} {Pr}}} \\ \end{array} } \right],$$
(45)

where

$$\begin{aligned} & \hat{\varPi }_{xx} = \frac{{N_{\delta } }}{p}\varPi_{xx} ,\quad \hat{\Delta } = \frac{{N_{\delta } }}{p}\Delta ,\quad \hat{Q}_{x} = \frac{{N_{\delta } }}{p}\frac{{Q_{x} }}{{\sqrt {{T \mathord{\left/ {\vphantom {T {\left( {2\varepsilon } \right)}}} \right. \kern-0pt} {\left( {2\varepsilon } \right)}}} }},\quad \hat{\varPi }_{xy0}^{{u_{y} }} = \frac{1}{2}\frac{{\partial \hat{u}}}{\partial y},\quad \frac{{\partial \hat{u}}}{\partial y} = - 2\eta \frac{{N_{\delta } }}{p}\frac{\partial u}{\partial y}, \\ & \hat{R} = \left[ {\left( {\hat{\varPi }_{xx}^{2} + \hat{\varPi }_{yy}^{2} + \hat{\varPi }_{zz}^{2} + 2\hat{\varPi }_{xy}^{2} } \right) + \frac{{2\gamma^{\prime}}}{{f_{\text{b}} }}\hat{\Delta }^{2} + \left( {\hat{Q}_{x}^{2} + \hat{Q}_{y}^{2} } \right)} \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} ,\quad \gamma^{\prime} = \frac{(5 - 3\gamma )}{2},\varepsilon = \frac{1}{Pr(\gamma - 1)}. \\ \end{aligned}$$

The nonlinear factor \(q\left( {c\hat{R}} \right)\), defined as \({{\sinh \left( {c\hat{R}} \right)} \mathord{\left/ {\vphantom {{\sinh \left( {c\hat{R}} \right)} {c\hat{R}}}} \right. \kern-0pt} {c\hat{R}}}\), represents the physical effect of nonlinear energy dissipation occurring through molecular collisions. \(f_{\text{b}}\) is the ratio of bulk viscosity to shear viscosity. If the inverse power law (46) is adopted for gaseous viscosity,

$$\eta = \frac{{5\left( {{{mk_{\text{B}} T} \mathord{\left/ {\vphantom {{mk_{\text{B}} T} \pi }} \right. \kern-0pt} \pi }} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}{{8A_{2} \left( \nu \right)\varGamma \left[ {4 - {2 \mathord{\left/ {\vphantom {2 {\left( {\nu - 1} \right)}}} \right. \kern-0pt} {\left( {\nu - 1} \right)}}} \right]}}\frac{1}{{d^{2} }},$$
(46)

the constant \(c\), given by

$$c = \frac{{\left( {mk_{\text{B}} T_{r} } \right)^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0pt} 4}}} }}{{2d_{r} \eta_{r}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }},$$
(47)

reduces to a function of the exponent \(\nu\) as

$$c = \left[ {\frac{2\sqrt \pi }{5}A_{2} \left( \nu \right)\varGamma \left[ {4 - {2 \mathord{\left/ {\vphantom {2 {\left( {\nu - 1} \right)}}} \right. \kern-0pt} {\left( {\nu - 1} \right)}}} \right]} \right]^{{\frac{1}{2}}} ,$$

where \(\varGamma\) is the gamma function and the values of function \(A_{2} \left( \nu \right)\) can be obtained from Table 1.

Table 1 Values of \(A_{2} \left( \nu \right)\) for the inverse power laws
Full size table

Similarly we also do the scaling for our enhanced NCCR-based boundary conditions. The dimensionless forms are divided into three parts of slip velocity and two parts of jump temperature so that the contribution of each term will be analyzed easily later, which can be rewritten as follows,

$$u - u_{\text{wall}} = \underbrace {{C_{m} \frac{Kn}{ - \eta }\varPi_{\text{NCCR}} }}_{{U_{\text{slip}}^{A} }} + \underbrace {{C_{m} \frac{{Kn^{2} }}{2\eta }\frac{{\partial \varPi_{\text{NCCR}} }}{\partial y}}}_{{U_{\text{slip}}^{B} }} + \underbrace {{C_{s} \frac{{N_{\delta } }}{\gamma p}\left( { - Q_{{x{\text{NCCR}}}} } \right)}}_{{U_{\text{slip}}^{C} }},$$
(48)
$$T - T_{\text{wall}} = \underbrace {{C_{t} \frac{Kn}{ - \lambda }Q_{{y{\text{NCCR}}}} }}_{{T_{\text{jump}}^{A} }} + \underbrace {{C_{t} \frac{{Kn^{2} }}{2\lambda }\frac{{\partial Q_{{y{\text{NCCR}}}} }}{\partial y}}}_{{T_{\text{jump}}^{B} }}.$$
(49)

4.2 Numerical solutions

In present work, the MacCormack method is adopted to discretize Eq. (44) by forward differencing in a prediction step and backward differencing in a correcting step. Viscous term is recommended to be discretized by central difference schemes in both steps. A prediction step yields

$$\left( {\frac{{\partial {\mathbf{U}}}}{\partial t}} \right)_{i}^{t} = - \left( {{\mathbf{A}}_{i}^{t} \frac{{{\mathbf{U}}_{i + 1}^{t} - {\mathbf{U}}_{i}^{t} }}{\Delta y} + N_{\delta } {\mathbf{B}}_{i}^{t} \frac{{\left( {{\mathbf{G}}_{v} } \right)_{i + 1}^{t} - \left( {{\mathbf{G}}_{v} } \right)_{i - 1}^{t} }}{2\Delta y}} \right).$$
(50)

The time derivative terms in Eq. (50) are utilized to compute the estimated values of conserved variables at \(t + \Delta t\) as follows

$${\bar{\mathbf{U}}}_{i}^{t + \Delta t} = {\mathbf{U}}_{i}^{t} + \left( {\frac{{\partial {\mathbf{U}}}}{\partial t}} \right)_{i}^{t} \Delta t.$$
(51)

And then a correcting step is taken by using the estimated values to calculate the values of time derivatives at \(t + \Delta t\) as

$$\left( {\overline{{\frac{{\partial {\mathbf{U}}}}{\partial t}}} } \right)_{i}^{t + \Delta t} = - \left( {{\bar{\mathbf{A}}}_{i}^{t + \Delta t} \frac{{{\bar{\mathbf{U}}}_{i}^{t + \Delta t} - {\bar{\mathbf{U}}}_{i - 1}^{t + \Delta t} }}{\Delta y} + N_{\delta } \overline{{\mathbf{B}}}_{i}^{t + \Delta t} \frac{{\left( {{\bar{\mathbf{G}}}_{v} } \right)_{i + 1}^{t + \Delta t} - \left( {{\bar{\mathbf{G}}}_{v} } \right)_{i - 1}^{t + \Delta t} }}{2\Delta y}} \right).$$
(52)

The average values of time derivatives can be obtained by

$$\left( {\frac{{\partial {\mathbf{U}}}}{\partial t}} \right)_{av} = \frac{1}{2}\left[ {\left( {\frac{{\partial {\mathbf{U}}}}{\partial t}} \right)_{i}^{t} + \left( {\overline{{\frac{{\partial {\mathbf{U}}}}{\partial t}}} } \right)_{i}^{t + \Delta t} } \right].$$
(53)

Finally, the values of conserved variables at \(t + \Delta t\) can be acquired by

$${\mathbf{U}}_{i}^{t + \Delta t} = {\mathbf{U}}_{i}^{t} + \left( {\frac{{\partial {\mathbf{U}}}}{\partial t}} \right)_{av} \Delta t.$$
(54)

The traditional time step in the NS equations is turned out to be stable and available for the NCCR model in the Couette flows as

$$\Delta t = \hbox{min} \left( {{\text{CFL}}\frac{\Delta y}{{\sqrt {\left( {u_{i}^{t} } \right)^{2} + \left( {v_{i}^{t} } \right)^{2} } + a_{i}^{t} }}} \right).$$
(55)

At every time step of marching, an additional process is required to solve the nonlinear algebraic Eqs. (45) to obtain the stress and heat flux in the NCCR model. Note that there is a strong coupled relationship among these non-conserved variables in Eq. (45). A computational strategy is utilized to merge the nonlinear coupled Eqs. (45) into one formulation through the Rayleigh–Onsager dissipation function \(\hat{R}\) which serves as an interim parameter below

$$\hat{R}^{2} q\left( {c\hat{R}} \right) = F,$$
(56)

where

$$F = \frac{3}{2}\left( {1 + \hat{\Delta } + \hat{\varPi }_{yy} } \right)\hat{\varPi }_{yy} \hat{\varPi }_{yy0}^{{v_{y} }} + 2\left( {1 + \hat{\Delta } + 3\gamma^{\prime}\hat{\Delta } + \hat{\varPi }_{xx} + \hat{\varPi }_{yy} } \right)\hat{\varPi }_{xy} \hat{\varPi }_{xy0}^{{u_{y} }} + \frac{3}{2}\hat{\varPi }_{xy}^{2} \hat{\varPi }_{yy0}^{{v_{y} }} + \frac{{2\gamma^{\prime}}}{{f_{b} }}\left( {1 + 3\hat{\varPi }_{yy} + 3\hat{\Delta }} \right)\hat{\Delta }\hat{\Delta }_{0}^{{v_{y} }} + \hat{\varPi }_{xy} \hat{Q}_{x} \hat{Q}_{y0} + \frac{1}{\Pr }\hat{Q}_{x} \hat{Q}_{y} \hat{\varPi }_{xy0}^{{u_{y} }} + \left( {1 + \hat{\Delta } + \hat{\varPi }_{yy} } \right)\hat{Q}_{y} \hat{Q}_{y0} + \frac{3}{4\Pr }\hat{Q}_{y}^{2} \hat{\varPi }_{yy0}^{{v_{y} }} .$$
(57)

An iterative method is adopted to solve the algebraic Eq. (56) for the interim parameter \(\hat{R}\):

$$\begin{aligned} \hat{R}_{n} = \left[ {\left( {\hat{\varPi }_{xxn}^{2} + \hat{\varPi }_{yyn}^{2} + \hat{\varPi }_{zzn}^{2} + 2\hat{\varPi }_{xyn}^{2} } \right) + \frac{{2\gamma^{\prime}}}{{f_{b} }}\hat{\Delta }_{n}^{2} + \left( {\hat{Q}_{xn}^{2} + \hat{Q}_{yn}^{2} } \right)} \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \hfill \\ \hat{R}_{n + 1} = \frac{1}{c}\sinh^{ - 1} \left( {\frac{{cF_{n} }}{{\hat{R}_{n} }}} \right). \hfill \\ \end{aligned}$$
(58)

And then, all values of the stress and heat flux terms at \(n + 1\) time step are updated through the interim parameter.

$$\begin{aligned} & \left( {\hat{\varPi }_{xx} } \right)_{n + 1} = \left[ {\left( {1 + \hat{\Delta }_{n} + \hat{\varPi }_{yyn} } \right)\hat{\varPi }_{xx0}^{{v_{y} }} + \frac{4}{3}\hat{\varPi }_{xyn} \hat{\varPi }_{xy0}^{{u_{y} }} } \right]\frac{{\hat{R}_{n} \hat{R}_{n + 1} }}{{F_{n} }} \\ & \left( {\hat{\varPi }_{yy} } \right)_{n + 1} = \left[ {\left( {1 + \hat{\Delta }_{n} + \hat{\varPi }_{yyn} } \right)\hat{\varPi }_{yy0}^{{v_{y} }} - \frac{2}{3}\hat{\varPi }_{xyn} \hat{\varPi }_{xy0}^{{u_{y} }} } \right]\frac{{\hat{R}_{n} \hat{R}_{n + 1} }}{{F_{n} }} \\ & \left( {\hat{\varPi }_{zz} } \right)_{n + 1} = \left[ {\left( {1 + \hat{\Delta }_{n} + \hat{\varPi }_{yyn} } \right)\hat{\varPi }_{zz0}^{{v_{y} }} - \frac{2}{3}\hat{\varPi }_{xyn} \hat{\varPi }_{xy0}^{{u_{y} }} } \right]\frac{{\hat{R}_{n} \hat{R}_{n + 1} }}{{F_{n} }} \\ & \left( {\hat{\varPi }_{xy} } \right)_{n + 1} = \left[ {\left( {1 + \hat{\Delta }_{n} + \hat{\varPi }_{yyn} } \right)\hat{\varPi }_{xy0}^{{u_{y} }} + \frac{3}{4}\hat{\varPi }_{xyn} \hat{\varPi }_{yy0}^{{v_{y} }} } \right]\frac{{\hat{R}_{n} \hat{R}_{n + 1} }}{{F_{n} }} \\ & \left( {\hat{\Delta }} \right)_{n + 1} = \left[ {\left( {1 + 3\hat{\varPi }_{yyn} + 3\hat{\Delta }_{n} } \right)\hat{\Delta }_{0}^{{v_{y} }} + 3f_{b} \hat{\varPi }_{yxn} \hat{\varPi }_{xy0}^{{u_{y} }} } \right]\frac{{\hat{R}_{n} \hat{R}_{n + 1} }}{{F_{n} }} \\ & \left( {\hat{Q}_{x} } \right)_{n + 1} = \left[ {\hat{\varPi }_{xyn} \hat{Q}_{y0} + \frac{1}{\Pr }\hat{Q}_{yn} \hat{\varPi }_{xy0}^{{u_{y} }} } \right]\frac{{\hat{R}_{n} \hat{R}_{n + 1} }}{{F_{n} }} \\ & \left( {\hat{Q}_{y} } \right)_{n + 1} = \left[ {\left( {1 + \hat{\Delta }_{n} + \hat{\varPi }_{yyn} } \right)\hat{Q}_{y0} + \frac{3}{4\Pr }\hat{Q}_{yn} \hat{\varPi }_{yy0}^{{v_{y} }} } \right]\frac{{\hat{R}_{n} \hat{R}_{n + 1} }}{{F_{n} }}. \\ \end{aligned}$$
(59)

The whole iterative process is considered to be converged according to the criteria \(\left| {\hat{R}_{n + 1} - \hat{R}_{n} } \right| \le 10^{ - 5}\). Before the iteration, the linear values of the non-conserved variables from the NSF model are assigned as the initial values for the stress and heat flux terms in Eqs. (58) and (59):

$$\begin{aligned} \hat{R}_{0} = \left[ {\left( {\hat{\varPi }_{xx0}^{2} + \hat{\varPi }_{yy0}^{2} + \hat{\varPi }_{zz0}^{2} + 2\hat{\varPi }_{xy0}^{2} } \right) + \frac{{2\gamma^{\prime}}}{{f_{b} }}\hat{\Delta }_{0}^{2} + \left( {\hat{Q}_{x0}^{2} + \hat{Q}_{y0}^{2} } \right)} \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \hfill \\ \hat{\varPi }_{xx1} = \frac{{\sinh^{ - 1} \left( {c\hat{R}_{0} } \right)}}{{c\hat{R}_{0} }}\hat{\varPi }_{xx0} ,\quad \hat{\varPi }_{yy1} = \frac{{\sinh^{ - 1} \left( {c\hat{R}_{0} } \right)}}{{c\hat{R}_{0} }}\hat{\varPi }_{yy0} ,\quad \hat{\varPi }_{zz1} = \frac{{\sinh^{ - 1} \left( {c\hat{R}_{0} } \right)}}{{c\hat{R}_{0} }}\hat{\varPi }_{zz0} \hfill \\ \hat{\Delta }_{1} = \frac{{\sinh^{ - 1} \left( {c\hat{R}_{0} } \right)}}{{c\hat{R}_{0} }}\hat{\Delta }_{0} ,\quad \hat{Q}_{x1} = \frac{{\sinh^{ - 1} \left( {c\hat{R}_{0} } \right)}}{{c\hat{R}_{0} }}\hat{Q}_{x0} ,\quad \hat{Q}_{y1} = \frac{{\sinh^{ - 1} \left( {c\hat{R}_{0} } \right)}}{{c\hat{R}_{0} }}\hat{Q}_{y1} . \hfill \\ \end{aligned}$$
(60)

In order to accelerate above numerical convergence process further, the analytical solutions of the linear NSF model to the conventional constant-viscosity and nonslip-jump Couette flow are adopted to provide initial conditions for the numerical computation

$$u = \left( {Ma_{L} - Ma_{0} } \right)y + Ma_{0} ,$$
(61)
$$T = \frac{{T_{0} }}{{T_{L} }} + \left( {1 - \frac{{T_{0} }}{{T_{L} }}} \right)y + \frac{{\left( {Ma_{L} - Ma_{0} } \right)^{2} }}{{{2 \mathord{\left/ {\vphantom {2 {Pr(\gamma - 1)}}} \right. \kern-0pt} {Pr(\gamma - 1)}}}}y\left( {1 - y} \right),$$
(62)

where the Mach numbers of the moving plates are defined as \(Ma_{L} = {{u_{L} } \mathord{\left/ {\vphantom {{u_{L} } a}} \right. \kern-0pt} a}\), \(Ma_{0} = {{u_{0} } \mathord{\left/ {\vphantom {{u_{0} } a}} \right. \kern-0pt} a}\) and \(a\) denotes the sound speed. Furthermore, to avoid the drastic change of the velocity slip and temperature jump values during the iterative computational process, a relaxation method (Bao et al. 2007; Lockerby and Reese 2003; Zhao 2014) is utilized for the wall boundary conditions as follows

$$u_{s}^{\text{relaxation}} = u_{s}^{n} + R_{f} \left( {u_{s}^{n + 1} - u_{s}^{n} } \right),$$
(63)
$$T_{j}^{\text{relaxation}} = T_{j}^{n} + R_{f} \left( {T_{j}^{n + 1} - T_{j}^{n} } \right),$$
(64)

where the relaxation factor \(R_{f}\) is recommended as \(2 \times 10^{ - 6}\) for all cases.

4.3 Convergence and grid independence

Figure 2 shows convergence process of the computed temperature, velocities in x- or y-direction, density and pressure profiles by the NCCR model as time advances. It can be seen that all profiles converge to final steady result after \(8n\) times the evolution time step. The deviation of temperature and velocity in x-direction profiles from linear NSF’s analytical solution implies that nonslip boundary conditions are no longer suitable for the micro-Couette flow at \(Kn = 0.1\). Notice that after a big perturbation at the beginning, the profile of velocity \(v\) finally converges to zero as theoretical deduction predicts. It proves that the strategy of keeping velocity component \(v\) as a dummy unknown variable is practicable and reliable.

Fig. 2
figure 2

Evolution of different variable profiles with time for the Couette flow (\(Ma_{0} = -\, 0.74\), \(Ma_{L} = 0.74\), \(Kn = 0.1\), \(T_{0} = T_{L} = 273\;{\text{K}}\), diatomic nitrogen gas). a Temperature, b velocity in x-direction, c velocity in y-direction, d density, e pressure

Full size image

In present work, grid independence study is carried out before taking any investigations. Figure 3 shows the density and temperature profiles predicted by uniform Grid 1 (20 grid points in y-direction), Grid 2 (100 grid points) and Grid 3 (500 grid points) across the domain. Notice that the Grid 2 and 3 give almost the same results while the Grid 1 yields obvious deviation for all profiles. It means that 100 grid points will be enough for the resolution of the current flow and could be used for the rest cases.

Fig. 3
figure 3

Grid independence study test (\(Ma_{0} = - 0.74\), \(Ma_{L} = 0.74\), \(Kn = 0.1\), \(T_{0} = T_{L} = 273{\text{K}}\), diatomic nitrogen gas). a Density profile, b temperature profile

Full size image

5 Results and discussion

In this section, an important emphasis is placed on seeking for a well-posed wall boundary condition suitable for the NCCR model in confined flows. DSMC results are always used to assess the capability of hydrodynamic models as a canonical substitute due to the lack of reliable experimental data in microfluidics. The utility of three different wall boundary conditions, such as the Langmuir (LM) slip conditions (26)–(27), the first-order Maxwell–Smoluchowski (M/S) slip conditions (28)–(29) and the enhanced NCCR-based boundary conditions (40)–(41), is investigated firstly in this section. Figure 4 shows the comparison of velocity slip and temperature jump values obtained by the DSMC (Ejtehadi et al. 2013) and NCCR method using different boundary conditions for diatomic nitrogen gas. The viscosity of gas is evaluated as

$$\eta = \eta_{\text{ref}} \left( {\frac{T}{{T_{\text{ref}} }}} \right)^{s} ,$$
(65)

where \(s = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2} + {2 \mathord{\left/ {\vphantom {2 {\left( {\nu - 1} \right)}}} \right. \kern-0pt} {\left( {\nu - 1} \right)}}\) and \(\nu\) is the exponent of the inverse power laws. The gas properties of nitrogen used in computations are given in Table 2.

Fig. 4
figure 4

Variation of velocity slip and temperature jump nearest to the wall predicted by DSMC (dots) and NCCR model (lines) over a range of Knudsen numbers for the Couette flow (\(u_{0} = - 250\;{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-0pt} {\text{s}}}\), \(u_{L} = 250\;{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-0pt} {\text{s}}}\), \(T_{0} = T_{L} = 273\;{\text{K}}\), diatomic nitrogen)

Full size image
Table 2 Physical gas properties of Nitrogen
Full size table

Fully diffuse reflection has been assumed on the wall with the tangential/thermal accommodation coefficient \(\sigma_{u}\) and \(\sigma_{T}\) equal to unity for diatomic cases. In Fig. 4, the values of velocity slip and temperature jump increase rapidly for Kn up to about 0.4, but the increase rate slows down as the Kn continues to increase. The solutions of the Langmuir (LM) slip conditions have weak agreement with the DSMC data while the other two show better quantitative approximation to some extent. Note that although Langmuir’s adsorption theory gives nice adsorption isothermal of the gas–surface interaction, it does not necessarily give good predication of the slip velocity and jump temperature. Comparing the detail profiles of the first-order M/S and our enhanced conditions, both of them provide good prediction for the slip across the full range of Knudsen numbers. However, the 1st-order M/S conditions will diverge rapidly from the temperature jump values predicted by DSMC after \(Kn = 0.25\), while our enhanced conditions still continue to provide close agreement with DSMC up to \(Kn = 1\).

Furthermore, a noteworthy phenomenon can be seen in Fig. 4 that the first-order M/S for NCCR solution underpredict the jump temperature and overpredict the slip velocity while the enhanced boundary conditions slightly overestimate both the values. It is therefore much desirable to examine what part contributes most. A deep analysis has been done in Fig. 5 to see the specific contributions from these different parts in our enhanced NCCR-based boundary conditions (48)–(49). As is shown in Fig. 5, the 2nd-order term \(U_{\text{slip}}^{B}\) and the thermal creep term \(U_{\text{slip}}^{C}\) do not give too much influence on the slip compared to the 1st-order term \(U_{slip}^{A}\). But the 2nd-order term \(T_{\text{jump}}^{B}\) in temperature jump starts making difference from the beginning of transition regime at \(Kn = 0.1\) and reaches to the same order of magnitude of the 1st-order part \(T_{\text{jump}}^{A}\) at about \(Kn = 0.9\). The 2nd-order term \(T_{\text{jump}}^{B}\) drives our enhanced temperature jump values move from the 1st-order M/S toward the DSMC solutions, as is depicted in Fig. 4. This may be used to account for the reason why the change is more pronounced in temperature jump due to the enhanced BC and less in velocity slip compared to the 1st-order M/S for such a simple flow. But on the whole, our enhanced NCCR-based boundary conditions demonstrate better capability than the first-order M/S and LM boundary conditions, particularly for capturing the temperature jump on the solid surface over a large range of transition regime.

Fig. 5
figure 5

Comparison of the contributions from different parts of the enhanced boundary conditions with the 1st-order M/S over a range of Knudsen numbers for the Couette flow (\(u_{0} = -\,250\;{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-0pt} {\text{s}}}\), \(u_{L} = 250\;{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-0pt} {\text{s}}}\), \(T_{0} = T_{L} = 273\;{\text{K}}\), diatomic nitrogen)

Full size image

In order to demonstrate the capability of above wall boundary conditions again in the monatomic NCCR model, the flow profiles of macroscopic variables along the y-direction are also compared in argon gas flows. The viscosity of argon is computed by Sutherland’s law as

$$\eta = \eta_{\text{ref}} \left( {\frac{T}{{T_{\text{ref}} }}} \right)^{1.5} \frac{{T_{\text{ref}} + T_{s} }}{{T + T_{s} }}.$$
(66)

The other properties of argon used in computations are given in Table 3.

Table 3 Physical gas properties of Argon
Full size table

Attention should be paid on the variation of the general NCCR model (45) for monatomic gases with the excess normal stress \(\Delta = 0\), which is given by

$$q\left( {c\hat{R}} \right)\left[ {\begin{array}{*{20}c} {\hat{\varPi }_{xx} } \\ {\hat{\varPi }_{yy} } \\ {\hat{\varPi }_{zz} } \\ {\hat{\varPi }_{xy} } \\ {\hat{Q}_{x} } \\ {\hat{Q}_{y} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left( {1 + \hat{\varPi }_{yy} } \right)\hat{\varPi }_{xx0}^{{v_{y} }} + \left( {{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0pt} 3}} \right)\hat{\varPi }_{xy} \hat{\varPi }_{xy0}^{{u_{y} }} } \\ {\left( {1 + \hat{\varPi }_{yy} } \right)\hat{\varPi }_{yy0}^{{v_{y} }} - \left( {{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}} \right)\hat{\varPi }_{xy} \hat{\varPi }_{xy0}^{{u_{y} }} } \\ {\left( {1 + \hat{\varPi }_{yy} } \right)\hat{\varPi }_{zz0}^{{v_{y} }} - \left( {{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}} \right)\hat{\varPi }_{xy} \hat{\varPi }_{xy0}^{{u_{y} }} } \\ {\left( {1 + \hat{\varPi }_{yy} } \right)\hat{\varPi }_{xy0}^{{u_{y} }} + \left( {{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0pt} 4}} \right)\hat{\varPi }_{xy} \hat{\varPi }_{yy0}^{{v_{y} }} } \\ {\hat{\varPi }_{xy} \hat{Q}_{y0} + {{\hat{Q}_{y} \hat{\varPi }_{xy0}^{{u_{y} }} } \mathord{\left/ {\vphantom {{\hat{Q}_{y} \hat{\varPi }_{xy0}^{{u_{y} }} } {Pr}}} \right. \kern-0pt} {Pr}}} \\ {\left( {1 + \hat{\varPi }_{yy} } \right)\hat{Q}_{y0} + \left( {{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0pt} 4}} \right){{\hat{Q}_{y} \hat{\varPi }_{yy0}^{{v_{y} }} } \mathord{\left/ {\vphantom {{\hat{Q}_{y} \hat{\varPi }_{yy0}^{{v_{y} }} } {Pr}}} \right. \kern-0pt} {Pr}}} \\ \end{array} } \right],$$
(67)

and the related bulk viscosity is no longer considered. Overall, the computation of the monatomic NCCR model (67) shares similar process with the formulas (56)–(60).

Figure 6 shows the predicted temperature profiles of the argon gas flows for \(Kn = 0.012,\;0.1,\;0.25,\;0.5,\;0.75\) and \(1.0\). The DSMC and R13 results used as comparisons are obtained from Gu and Emerson’s simulations (Gu and Emerson 2007, 2009). The NCCR solutions are acquired by employing above three different wall boundary conditions, and the linear NSF equations are also solved with the 1st-order M/S conditions. Comparing their influence on the monatomic NCCR model, the LM boundary conditions consistently underestimate the temperature jump in the transition regime except the continuum regime at \(Kn = 0.012\). It should also be pointed out that subject to the low-order characteristics, the 1st-order M/S conditions do not distinguish the nonlinear high-order capability of the NCCR model from the linear NSF model for \(Kn\) above \(0.25\), as shown in Fig. 6c–f. The enhanced NCCR-based conditions yield good results in better agreement with temperature jump values on the wall predicted by DSMC than the other two wall boundary conditions. Moreover, the R13 and NCCR profiles are closer to the DSMC data than the linear NSF results, although their results start to diverge from the DSMC profiles at \(Kn = 0.25\) with the R13 overestimating and the NCCR underestimating the temperature in the central region of the Couette flow.

Fig. 6
figure 6

Temperature profiles over a range of Knudsen numbers in the micro-Couette flow (\(u_{0} = - 50\;{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-0pt} {\text{s}}}\), \(u_{L} = 50\;{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-0pt} {\text{s}}}\), \(T_{0} = T_{L} = 273\;{\text{K}}\), monatomic argon gas)

Full size image

Since the improvement of the NCCR results by the enhanced boundary conditions is pronounced in above results, the capability still deserves to be investigated more carefully. The computed profiles of tangential velocity, normal heat flux and shear stress by DSMC, R13, NSF and NCCR models are presented in Figs. 7 and 8. Considering the symmetry characteristic, only upper-half distributions of the heat flux and shear stress in the flow is plotted in Fig. 8. At \(Kn = 0.012\) and \(0.1\), Figs. 7a, b and 8a show that the R13, NCCR and NSF models all yield tangential velocity, normal heat flux and shear stress in excellent agreement with the DSMC results. However, as the degree of rarefaction is increased, some non-negligible discrepancies turn up with all three models underestimating the normal heat flux and overestimating the velocity slip as well as the shear stress. In the transition regime, the predicted velocity profiles from the DSMC approach indicate an underlying non-equilibrium phenomenon (nonlinear velocity profile) in the micro-Couette flow, as illustrated in Fig. 7d–f. Unfortunately, all three models including the R13, NCCR and NSF fail to capture this special feature of the velocity profile. But on the whole, the values including the velocity and heat flux predicted by the R13 and NCCR models are closer to DSMC results than those by NSF model. It is also worthwhile mentioned that the NCCR yields close results with the R13 for these profiles. Remembering that NCCR serves as similar constitutive relations to close the original five conserved moments rather than the evolution equations of 13 moments as the R13 equations, it is acceptable and admired to obtain the consistent capability with R13 from the NCCR model under the limit of less degree of freedom. Figure 8 also presents constant shear stresses across the domain for the planar Couette flow. The deviation between the three continuum-based hydrodynamic models and the DSMC method is enlarging as the flow departures from the thermal equilibrium with about 7% overestimation at \(Kn = 0.25,\;0.5\) and 9% overestimation at \(Kn = 1.0\). Because the current NCCR model is reduced from Eu’s generalized hydrodynamic equations with simplifications, it indicates the necessity for improving this model further, which has been our ongoing research content.

Fig. 7
figure 7

Velocity profiles over a range of Knudsen numbers in the micro-Couette flow (\(u_{0} = -\,50\;{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-0pt} {\text{s}}}\), \(u_{L} = 50\;{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-0pt} {\text{s}}}\), \(T_{0} = T_{L} = 273\;{\text{K}}\), monatomic argon)

Full size image
Fig. 8
figure 8

Predicted profiles of normal heat flux and shear stress in the micro-Couette flow (\(u_{0} = -\, 50\;{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-0pt} {\text{s}}}\), \(u_{L} = 50\;{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-0pt} {\text{s}}}\), \(T_{0} = T_{L} = 273\;{\text{K}}\), monatomic argon)

Full size image

Moreover, hard-sphere and Maxwell gas flows are also investigated in order to further pry into the potential of the combination of the 2nd-order non-Newton–Fourier model (NCCR) with our enhanced NCCR-based conditions on the description of the underlying mechanisms in the Knudsen layer. The viscosities of the hard-sphere (\(s = 0.5\), \(c = 1.1908\)) and Maxwell molecules (\(s = 1.0\), \(c = 1.0138\)) are evaluated by the inverse power laws (65). And other reference properties used in computations are given in Table 4. In Figs. 9 and 11, the slip and jump coefficients are adjustable to be assumed as \(C_{m} = 0.8\), \(C_{t} = 2.25\) for both continuum theories as the best fit to the DSMC solutions (Bird 1994) with diffusive wall conditions.

Table 4 Physical gas properties of the hard-sphere and Maxwell gases
Full size table
Fig. 9
figure 9

Predicted profiles of tangential and normal heat fluxes \({{Q_{x,y} } \mathord{\left/ {\vphantom {{Q_{x,y} } {p_{{{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0pt} 2}}} u_{L} }}} \right. \kern-0pt} {p_{{{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0pt} 2}}} u_{L} }}\) in the micro-Couette flow (\(Ma_{0} = -\, 1.0\), \(Ma_{L} = 1.0\), \(T_{0} = T_{L} = 273\;{\text{K}}\), \(Kn = 0.25\), hard-sphere molecule)

Full size image

As shown in Fig. 9, the tangential heat flux without the presence of temperature gradient, namely non-gradient-transport mechanism, turns up for the hard-sphere gas in the micro-Couette flow. The NCCR model is able to capture this significant non-equilibrium phenomenon in quantitative agreement with the DSMC results (Marques and Kremer 2001; Myong 2016), even although both the linear NSF and the nonlinear model (NCCR) could predict the normal heat flux quite well. Similar phenomena can also be found for the Maxwellian gas at the upper limit of slip regime (\(Kn = 0.1\)) and in transition regime (\(Kn = 1.0\)), as illustrated in Fig. 10. Myong’s analytical solutions (Myong 2016) to NCCR model are also presented in comparison with our numerical solutions in Figs. 10 and 11. It could be found that our solutions are in qualitative agreement with those from Myong’s, which indicates that our numerical strategy could provide another practicable and efficient option of resolving the NCCR model. The slight difference in normal and shear stresses implies a significant improvement, which can be explained by the different wall boundary conditions adopted. It also means that the enhanced boundary conditions are well-fit to the NCCR model. It is also worthwhile mentioning that another significant non-equilibrium feature highlighted in Fig. 11 is the nonzero values of the normal components of stress \(\varPi_{xx}\) and \(\varPi_{yy}\) for the planar Couette flow in the states away from thermal equilibrium. The NCCR model is capable of predicting this characteristic of the non-equilibrium flow, while the linear NSF model describes none of the abnormal non-equilibrium properties. In contrast, the shear stress predicted by the NCCR model is closer to that from DSMC solution than that by the linear NSF laws, as illustrated in Fig. 11. Overall, all the behavior of the NCCR model in conjunction with the enhanced boundary conditions in depicting the underlying mechanism of the Knudsen layer demonstrates its outstanding capability and indicates a better choice than the linear NSF model with the 1st-order M/S conditions for non-equilibrium flows.

Fig. 10
figure 10

Predicted profiles of tangential and normal heat fluxes \({{Q_{x,y} } \mathord{\left/ {\vphantom {{Q_{x,y} } {p_{{{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0pt} 2}}} u_{L} }}} \right. \kern-0pt} {p_{{{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0pt} 2}}} u_{L} }}\) in the micro-Couette flow (\(Ma_{0} = -\, 0.8\), \(Ma_{L} = 0.8\), \(T_{0} = T_{L} = 273{\text{K}}\), \(Kn = 0.1\), \(1.0\), Maxwellian molecules)

Full size image
Fig. 11
figure 11

Predicted profiles of normal and shear stresses \({{\varPi_{xx,yy,xy} } \mathord{\left/ {\vphantom {{\varPi_{xx,yy,xy} } {p_{{{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0pt} 2}}} }}} \right. \kern-0pt} {p_{{{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0pt} 2}}} }}\) in the micro-Couette flow (\(Ma_{0} = -\, 0.8\), \(Ma_{L} = 0.8\), \(T_{0} = T_{L} = 273\;{\text{K}}\), \(Kn = 0.1\), \(1.0\), Maxwellian molecules)

Full size image

Last but not least, a quick comparison of our self-contained numerical solution by NCCR model with the analytical solutions (Singh et al. 2014) by other well-known non-Newton–Fourier models such as Augmented Burnett, Super Burnett and R13 equations, is done in Fig. 12, where the zoomed view in velocity profiles in Knudsen layer near the wall has been plotted. These analytical solutions for \(kn = 0.3\) start deviating from the beginning of Knudsen layer at the location \({Y \mathord{\left/ {\vphantom {Y L}} \right. \kern-0pt} L} = 0.7\), while the NCCR solution follows the DSMC data up to about \({Y \mathord{\left/ {\vphantom {Y L}} \right. \kern-0pt} L} = 0.93\). The maximum deviation among these models is found to be nearly 18% in Augmented Burnett profile. In general, NCCR model performs better compared to these models.

Fig. 12
figure 12

Zoomed in view of the velocity profiles in Knudsen layer near the wall as obtained from the various non-Newton–Fourier models for \(kn = 0.3\)

Full size image

6 Conclusions

The paper has presented a numerical strategy of the NCCR model reduced from Eu’s generalized hydrodynamic equations for the micro-Couette flow and the contrastive analysis of the influence of three wall boundary conditions (the 1st-order M/S, Langmuir slip and NCCR-based model) employed for this model. It is clear from the contrastive results that both the 1st-order M/S boundary conditions and the Langmuir slip conditions fail to keep the same accuracy with the 2nd-order NCCR model. Subject to their low-order accuracy, the NCCR model’s potential in the confined flows fails to be expressed near the wall. However, the utilization of the enhanced NCCR-based boundary conditions has brought significant improvements for both diatomic and monatomic gases, particularly in describing the temperature profiles across the domain and the exact value of temperature jump on the wall. Furthermore, the significance of the 2nd-order temperature jump term in boundary conditions is manifested, while the 2nd-order slip term and the thermal creep term are less important in micro-Couette flow.

The capability of the combination of this non-Newton–Fourier model with the enhanced NCCR-based boundary conditions has also been investigated further for both Maxwell and hard-sphere gas. The computational results of the micro-Couette flow show that the combination can not only recover the linear NSF solution in continuum regime, but also performed much better than the NSF model, even some Burnett-type equations for the prediction of the Knudsen layer in transition regimes at large Knudsen numbers above 0.1. Overall, the present NCCR model is capable of capturing the nonzero normal stress and tangential heat flux phenomena of the Knudsen layer in transition regimes in qualitative agreement with DSMC and higher-order moment methods such as R13 equations. Notice that the present numerical solutions of the NCCR model are self-contained in the sense that there is no need for adjustment to obtain reasonable results by using external results from DSMC or experiments, which is founded in many previous studies (Gu and Emerson 2007; Lockerby and Reese 2003; Xue and Ji 2003). Therefore, the present results obtained by the NCCR model are fairly practical under the consideration of computational efficiency.

Certainly, some limitations are also observed in the current model during the analysis because it does not contain the evolutional terms of the higher-order non-conserved moments as other moment methods do. Regardless of the well-pleasing results that have been obtained, improving research is still necessary in our further work.