1 Introduction

Flows through micro-channels have recently gained intense attention both because of fundamental scientific issues and of technological applications in bio-chemical devices, bio-assays, micro-sensors, -actuators, -reactors, etc. (Karniadakis et al. 2005). Other important micro-nano-fluidic devices comprise Winchester-type hard disk drives, with air gaps of less than 50 nm, handling air flows at very high speeds. A variety of Micro Electro Mechanical Systems (MEMS) devices also contain micro-channel flows, such as electro static comb micro drives (Tai et al. 1989), and electro statically side-driven micromotor (Mehregany et al. 1990; Trimmer 1997). In all of these micro-devices, increased mass flow rates are measured when compared with corresponding flow rates predicted by the classical Navier–Stokes equations. From the fluid mechanics point of view, the anomalous mass flow rates through micro-channels are of particular interest (Arkilic et al. 1994; Maurer et al. 2003), both because of their importance in fundamental studies and their technological applications in MEMS.

Micro-channel gas flows offer the possibility of directly testing the theoretical limitations of the basis of the classical Navier–Stokes equations. Early studies on micro-channel gas flow had already concluded that the theoretical predictions, using the Navier–Stokes equations and no slip velocity at the wall as boundary condition, under-predicted the experimental mass flow rates (Arkilic et al. 1997). The resultant discrepancies are often compensated by introducing the Maxwellian slip velocity boundary condition (Maxwell 1879) that was originally proposed for atomically smooth walls.

To get agreement with the experimental measurements, several different wall-slip models of varying complexity, containing freely adjustable parameters, have been proposed (Schamberg 1947; Sreekanth 1969; Beskok and Karniadakis 1999; Dongari et al. 2007). However, it may be noted that the models, introducing wall-slip as boundary condition, are not truly predictive, but need adjustable parameters which are often postulated to have some functional dependence on Knudsen number (Kn = λ/h, where λ is the mean free path of molecules and h is the height of the channel). The model parameters have to be determined by fitting the experimental data to the simulation results (Karniadakis et al. 2005). An example of slip model (Beskok and Karniadakis 1999) that is claimed to be rather successful in correlating the experimental data is:

$$ U_{s} = U_{w} + \frac{2 - \sigma }{\sigma }\frac{Kn}{1 - B(Kn)Kn}\left( {\frac{{{\text{d}}U}}{{{\text{d}}n}}} \right) $$
(1)

where σ is the percentage of molecules that are reflected from the wall diffusively (i.e., with average tangential velocity corresponding to that of the wall, i.e., U w ). Furthermore, U s is the so-called Maxwell slip velocity, U w the wall velocity, (dU/dn) is the velocity gradient perpendicular to the wall. It is to be noted that B(Kn) is the above mentioned fitting parameter which needs to be determined by comparing predicted results with the Direct Simulation Monte Carlo (DSMC) method or with reliable experimental data.

Recent theoretical studies (Brenner 2005, 2006; Durst et al. 2006) have pointed out the importance of inclusion of additional terms into the classical Navier–Stokes equations resulting in the so called extended Navier–Stokes equations. The key idea is that a strong density gradient for a compressible fluid acting in the direction of flow adds an additional diffusive mode of mass transport. It is interesting that the approach to use extended equations obviates the need for an ad hoc introduction of Maxwellian slip to explain flow phenomena such as thermophoresis (Brenner 2005), thermal transpiration (Bielenberg and Brenner 2006) and structure of shock waves (Greenshields and Reese 2007). It is thus expected that density gradient driven diffusion may also contribute to micro-channel gas flows with small channel heights (h), as the convective pressure driven flow increases proportional to h 3 (Arkilic et al. 1997), whereas the diffusive flux scales linearly with the height h.

The present paper shows, however, that the most dramatic breakdown of the classical Navier-Stokes predictions occurs in the Knudsen regime (Kn > 1), where the density gradient driven diffusive mass flux assumes paramount importance vis-à-vis the pressure driven convection. The purpose of this paper is to explore the applications of the extended Navier–Stokes equations, including the axial diffusion, to explain the enhanced flow in micro-channels without invoking the Maxwellian wall slip velocity. A uniform treatment is proposed for all values of the Knudsen number by a modification of the diffusivity by undertaking the Knudsen diffusion phenomenon in the free-molecular regime (Knudsen 1909; Kennard 1938; Malek and Coppens 2003). In this treatment, the diffusive transport also introduces a slip-kind of wall velocity, but in a somewhat natural way as the diffusive flux depends only on the axial pressure gradient, which is uniform across the channel cross-section.

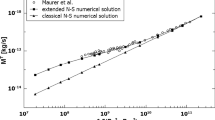
Another objective of this study lies in exploring the underlying physics of the so called Knudsen paradox (Knudsen 1909). The Knudsen paradox relates to the presence of a minimum when the mass flow rate normalized by the pressure difference is plotted against the Knudsen number (Knudsen 1909; Gaede 1913). Generally speaking, the exploration of Knudsen paradox and its full understanding also requires consideration of the entire transport regimes (Fig. 1) from small to large values of the Knudsen number. The results of the extended Navier–Stokes are compared with the available experimental data, with Boltzmann simulations and also with the exact simulations that do not assume a model for the wall-slip, such as the DSMC method over a large range of Knudsen number. It is also worth noting that even for higher Knudsen numbers, the theories (Beskok and Karniadakis 1999; Dongari et al. 2007) based on continuum assumptions in conjunction with the higher order slip boundary conditions have been employed to investigate gas flows through micro-channels.

Fig. 1
figure 1

Classification of flow regimes with Knudsen number

Full size image

A brief literature study pointing out those papers which are most relevant to the present problem of the theoretical treatment of micro-channel flows is presented in Sect. 2. The governing equations and the results of the extended Navier–Stokes treatment are presented in Sect. 3. The results are then compared with the experimental and DSMC data, showing a good agreement and pointing out the importance of diffusive contribution to the mass transport in gas flow through micro-channel.

In order to be precise and avoid any confusion, we shall use the term “Navier–Stokes equations” to refer to the classical Navier–Stokes equations without any diffusive effects. The term “present theory” or the term “modified Navier–Stokes equations” refers to the modified Navier–Stokes equations proposed by Durst et al. (2006) which include extra diffusive terms. The diffusive term itself can be classical diffusion at lower Knudsen numbers or the Knudsen diffusion at higher values of the Knudsen number. It may also be noted that in the case of isothermal gas flows considered here, Brenner (2005, 2006) notion of volume-diffusion and Durst et al. (2006) notion of self-mass diffusion in fact result in identical expressions for the extra diffusive flux driven by the density gradient. See “Appendix” for more detailed discussion.

2 Theory of micro-channel gas flows: a background

Referring to available knowledge, the conventional no-slip boundary condition was claimed to apply to solid-fluid interfaces when the wall roughness is of the order of the mean free path of gas molecules or larger. Studies to support this were carried out by Richardson (1973) and Mo and Rosenberger (1990). However, the validity of this boundary condition has been questioned for gaseous flows in micro-channels by many researchers (Gad-el-Hak 1999). The questioning was based on differences observed between the experiments and theoretical results, the latter being based on the classical Navier–Stokes equations and the application of the no-slip boundary condition at walls. It has been thought that the applied no-slip wall boundary condition is responsible for these deviations. Maxwell (1879) first proposed a first order slip model to calculate the slip velocity at the wall for atomically smooth walls. Later many other heuristic extended slip models have been proposed even for atomically rough walls and are comprehensively summarized by Karniadakis et al. (2005). Various values of the slip-coefficients and the methods of their determination have been applied (Schamberg 1947; Deissler 1964; Sreekanth 1969; Beskok and Karniadakis 1999; Pan et al. 1999; Colin 2005; Dongari et al. 2007). Fitting of the experimental results, with the help of theoretical results based on a slip-model, often necessitates postulating various dependences of the slip coefficient on the Knudsen number and the geometry of a considered channel. A number of these slip coefficients are summarized in Colin (2005) and Dongari et al. (2007). The logic for the choice of a particular slip-model is not really described in the above cited papers.

Brenner (2005, 2006) and Durst et al. (2006) have recently proposed modifications to the Navier–Stokes equations that relate to volume diffusion (Brenner 2005) or self-mass diffusion (Durst et al. 2006) occurring in fluids that would be significant for flows with high density gradients. It is shown that for strong local temperature and/or density gradients, diffusive transport of momentum, heat, and mass gives rise to additional terms in the constitutive relationships. The resultant modifications gave good predictions of the viscous structure of shock waves (Greenshields and Reese 2007) in the range Mach numbers 1.0–12.0 (while conventional Navier–Stokes equations are known to fail above about Mach number 2). The modified equations are also found to be successful in explaining phenomena such as thermophoresis (Brenner 2005), thermal transpiration (Bielenberg and Brenner 2006). In this paper, we therefore utilize these modified forms of Navier–Stokes equations (Durst et al. 2006) to investigate gas flows through micro-channel without using the no-slip boundary condition.

Hence, the main objective of this paper is to extend the applicability of the continuum based equations in conjunction with the diffusive mass flux to predict the flows operating at high Knudsen numbers as the studies of gas flows in the transition regime (0.1 < Kn < 10, refer to Fig. 1) are certainly interest to researchers in many areas of physics, chemistry and engineering technology, and in the Knudsen regime (Kn > 10) covering from traditional heterogeneous catalytic processes over porous catalysts, to molecular transport processes in nano-structured materials, to rarefied gas processes in atmosphere and space.

There are several simulations of the micro-flows independent of the Navier–Stokes treatment. For example, semi-analytical and numerical solutions of the linearized Boltzmann equations for rarefied flow for channels (or) pipe in both transition and free-molecular regimes have been obtained. Linearized Lattice-Boltzmann treatment by Cercignani and Daneri (1963) addressed the problem of the so-called Knudsen paradox. In such studies, simplifications for the collision integral based on the BGK model were extensively used under the assumptions of small pressure gradients and isothermal condition. Other investigators derived solutions based on the hard-sphere and Maxwellian models for the collision integral (Huang et al. (1997), Sone (1989) and Ohwada et al. (1989)). Using the slip model given in Eq. 1, within the context of slip-models, Beskok and Karniadakis (1999) have provided some results for the transition regime (Kn ~ 1), and early free-molecular regime (Kn ~ 10). The slip models encompassing the free-molecular regime are postulate based, rather than physics based, and thus the extensions of the original Maxwell’s slip model and also the values of model parameters have to be determined by DSMC simulations for various Knudsen number regimes and various geometries.

As noted before, the diffusive effects are likely to become very important in the free-molecular regime (Kn > 10), where the bulk diffusivity (or Fickian diffusion coefficient, Hosticka et al. 1998) also becomes modified because of the increased frequency of molecular wall collisions. When the ratio of mean free path to the confining channel dimensions becomes large (Kn ≫ 1), the situation is described as the Knudsen regime (Malek and Coppens 2003). In this regime, diffusion is described by the Knudsen diffusivity rather than the bulk diffusivity.

From the brief presentation above, it can be concluded that the approach to micro-channel flows, based on the classical Navier–Stokes equations, is limited to the use of postulate based wall slip models for which various parameters are determined either empirically or by comparisons with independent simulations. The slip-models become even more complex when the transition and Knudsen regimes of flow are considered. On the other hand, the recently developed extended Navier–Stokes equations including the diffusive mode of transport are beginning to successfully address the problems such as thermophoresis that were historically also formulated by postulating a wall slip. In view of these, we propose to test the predictions of the extended Navier–Stokes approach for the problem of micro-channel flows without introducing a model of the wall slip a priori.

3 Theory and results

3.1 Extended Navier–Stokes equations

It needs to be emphasized for the present study that fluid motions can occur by both convection and diffusion where the latter has its origin in the thermal motion of molecules (Brenner 2005, 2006; Durst et al. 2006). When both motions are taken into account, the total fluid velocity can be written as,

$$ \hat{U}_{i} = U_{i} + \bar{u}_{i}^{D} $$
(2)

where \( \hat{U}_{{i}} = {\text{total}}\;{\text{velocity}} \), U i  = convection velocity and \( \bar{u}_{{i}}^{D} = {\text{diffusion}}\;{\text{velocity}} \), see Kennard (1938). Hence both convective and diffusive motions need to be treated accurately when dealing with flow situations where high gradients of the thermodynamic properties occur in a flow field, i.e., high gradients of the density ρ, temperature T or pressure P.

The modified continuity and the momentum equations, including the molecular mass transport and the molecular momentum transport, derived by Durst et al. (2006) are given below:

$$ \frac{\partial \rho }{\partial t} + \frac{{\partial (\rho \hat{U}_{{i}} )}}{{\partial x_{{i}} }} = 0 \Rightarrow \frac{\partial \rho }{\partial t} + \frac{{\partial (\rho U_{{i}} )}}{{\partial x_{{i}} }} = - \frac{{\partial (\dot{m}_{{i}}^{{D}} )}}{{\partial x_{{i}} }} $$
(3)

local diffusive mass transport can be derived from the kinetic theory of gases:

$$ \dot{m}_{{i}}^{{D}} = \rho \bar{u}_{{i}}^{{D}} = - \rho D\frac{\partial }{{\partial x_{{i}} }}\left[ {\ln \left( {\rho \sqrt T } \right)} \right] $$
(4)

where \( \dot{m}^{D} \) is the mass flux induced due to molecular self diffusion, \( D = \left( {1/3} \right)\bar{u}_{{M}} \lambda \) and ρD = μ in accordance with the transport theory for ideal gases. Here D is defined as the diffusivity of the gas,\( \bar{u}_{M} \) is the molecular mean velocity and μ is the viscosity of the gas.

$$ \left\{ {\frac{{\partial \left[ {(\rho )U_{j} } \right]}}{\partial t} + \frac{{\partial \left[ {(\rho U_{i} )U_{j} } \right]}}{{\partial x_{i} }}} \right\} = - \frac{\partial P}{{\partial x_{j} }} - \frac{{\partial \tau_{ij} }}{{\partial x_{i} }} + \rho g_{j} $$
(5)
$$ \tau_{ij} = - \mu \left( {\frac{{\partial U_{j} }}{{\partial x_{i} }} + \frac{{\partial U_{i} }}{{\partial x_{j} }}} \right) + \frac{2}{3}\mu \delta_{ij} \frac{{\partial U_{k} }}{{\partial x_{k} }} + \dot{m}_{i}^{D} \,U_{j} + \dot{m}_{j}^{D} \,U_{i} - \frac{2}{3}\delta_{ij} \dot{m}_{k}^{D} U_{k} $$
(6)

The general governing equations simplify to the form given below if the following imposed flow conditions relevant for a micro-channel flow are taken into account: (a) The flow is assumed to be steady, two-dimensional, locally fully developed, i.e., the transverse velocity can be neglected; (b) The flow conditions are isothermal, as the Mach number of flow analyzed in the present paper is assumed to be very low (Ma ≪ 1) and hence, the energy equation does not need to be solved; (c) The channel is long, and the entry and exit effects are negligible, i.e., the fully developed channel flow is treated.

$$ \left( {\frac{{\partial (\rho (U_{1} )^{2} )}}{{\partial x_{1} }}} \right) = - \frac{{{\text{d}}P}}{{{\text{d}}x_{1} }} - \frac{{\partial \tau_{11} }}{{\partial x_{1} }} - \frac{{\partial \tau_{21} }}{{\partial x_{2} }} $$
(7)

Using the above mentioned assumptions, the expressions for τ 11 and τ 21 can be derived from Eq. (6) to yield the following momentum transport relationships:

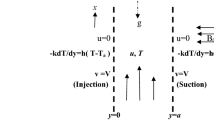
$$ \tau_{11} = - \mu \left( {\frac{4}{3}\frac{{\partial U_{1} }}{{\partial x_{1} }}} \right) + \frac{4}{3}\dot{m}_{1}^{D} U_{1} \quad {\text{and}}\quad \tau_{21} = - \mu \left( {\frac{{\partial U_{1} }}{{\partial x_{2} }}} \right) $$
(8)

In this work, it is also assumed that the channel height, h is much smaller than the channel width, w, so that the fluid essentially sees two infinite parallel plates, separated by h. Hence the assumption of two-dimensionality introduced to derive the final equations is valid, refer to Fig. 2 for the channel geometry.

Fig. 2
figure 2

Channel geometry, with the system of coordinates

Full size image

The Reynolds numbers of all the flows studied in micro-channels are usually very low, i.e., Re < 1, and hence it becomes very important to incorporate the physically correct molecular diffusion into any analysis to treat micro-channels flows. Our detailed solutions of the governing equations yielded the following simple and physically justified insights: (a) The additional mass diffusion given by \( \dot{m}_{1}^{D} \)in Eq. 4 is important and needs to be taken into account in the continuity equation; (b) The additional momentum terms τ 11 and \( \left( {\frac{{\partial (\rho (U_{1} )^{2} )}}{{\partial x_{1} }}} \right) \)are small in comparison to the gradient driven term τ 21, given in Eq. 8. Because of this, τ 11 is neglected for the results presented in this paper; (c) the last but not least, it should be mentioned, that the convective part of the velocity profile is assumed to be parabolic. The assumption of the convective part of velocity profile being parabolic is also in agreement with the numerical data available in the literature (Beskok and Karniadakis 1999; Agrawal and Agrawal 2006; Agrawal et al. 2005; Pan et al. 1999; Arkilic et al. 1997).

3.2 Analytical treatment of micro-channel gas flow

The governing equations of fluid motions in Sect. 3.1 suggest that the actual total mass flux through the channel is made up of two parts, the convective motion, driven by the imposed pressure difference between inlet and outlet, and the motion caused by the self-diffusive mass transport. Hence the same pressure difference that drives the convective motion also induces a diffusive motion, which for isothermal condition can be written as follows using Eq. 4

$$ \dot{m}_{1}^{D} = - \rho D\left( {\frac{1}{\rho }\frac{{{\text{d}}\rho }}{{{\text{d}}x_{1} }}} \right) $$
(9)

Using the ideal gas law one can also write:

$$ \frac{1}{\rho }\frac{{{\text{d}}\rho }}{{{\text{d}}x_{1} }} = \frac{1}{P}\frac{{{\text{d}}P}}{{{\text{d}}x_{1} }}\quad {\text{and}}\quad \dot{m}_{1}^{D} = - \rho D\left( {\frac{1}{P}\frac{{{\text{d}}P}}{{{\text{d}}x_{1} }}} \right) $$
(10)

In spite of the fact that the governing differential equations for the velocity profile are non-linear, e.g., see Eq. 7, closer considerations of the magnitude of the various terms in Eq. 7 suggest that the convective and diffusive motions of the gas are not coupled and can thus be treated independently.

Using Eqs. 9 and 10, one can write the expression for the induced mass flow rate, due to self diffusion, as follows:

$$ \dot{M}^{D} \, = \,\dot{m}^{D} wh\, = \, - \mu \,\frac{1}{P}\,\frac{dP}{{dx_{1} }}\,wh $$
(11)

where w and h are the width and height of the channel respectively.

By integrating Eq. 11 from inlet to outlet, one can obtain the following relationship for diffusion mass flow rate \( (\dot{M}^{D} ) \)

$$ \dot{M}^{D} = \frac{\mu wh}{L}\,\ln \left( {\frac{{P_{\rm in} }}{{P_{\rm out} }}} \right) $$
(12)

where L is the length of the channel

The analytical expression for the mass flow rate for compressible flows using the Navier–Stokes equations and the no-slip wall velocity boundary conditions, can be given by the equation below, e.g., see also Arkilic et al. (1997):

$$ \dot{M}^{C} = \frac{{h^{3} w\left( {P_{\rm in}^{2} - P_{\rm out}^{2} } \right)}}{24\mu LRT} $$
(13)

Hence, the total mass flow rate through a micro-channel can be expressed as the sum of \( \dot{M}^{D} \) and \( \dot{M}^{C} \) yielding:

$$ \dot{M}^{T} = \frac{{h^{3} w\left( {P_{{\rm in}}^{2} - P_{\text{out}}^{2} } \right)}}{24\mu LRT} + \frac{\mu wh}{L}\,\ln \left( {\frac{{P_{\text{in}} }}{{P_{\text{out}} }}} \right) $$
(14)

To compare results obtained with the present theory, the experimental data of Maurer et al. (2003) were selected as a basis because his results cover a wide Kn-number range, from the continuum regime up to the early transition regime shown in Fig. 1. More importantly, Maurer’s experimental studies report all the conditions of the experiments that are required for the authors’ theoretical computations.

Figure 3 shows the present theory results and compares them with the experimental data. The comparisons of the experimental data of Maurer et al. (2003) and the corresponding theoretical results show good agreement for small differences in the square of pressures, i.e., for high Knudsen numbers. At the high end of the square of the pressures, i.e., for small Knudsen numbers, the theoretical solution, as expected, converges to the corresponding Navier–Stokes solution with the no-slip velocity boundary condition, whereas the experimental data (Maurer et al. 2003) data shows some deviation. This must be due to small experimental errors, which may have resulted from the errors in estimating the effective or “fluid mechanically felt” channel height. With this assumption one can correct the data yielding an offset to the theory at low Kn numbers. After incorporating this correction, the results shown in Fig. 4 were obtained. This figure shows excellent agreement of the measurements with the theory. This confirms that predictions of micro-channel flow rates can be carried out, based on the Navier–Stokes equations in conjunction with the diffusive flux, together with the conventional no-slip wall velocity as a boundary condition. Wherever the flow conditions for the results present in this paper are not mentioned explicitly, one has to note that the authors used the information provided in the Table 1 to compute the results.

Fig. 3
figure 3

Comparison of mass flow rate as a function of composite pressure drop (difference in squares of pressures), for helium, against the experimental data of Maurer et al. (2003)

Full size image
Fig. 4
figure 4

Comparison of mass flow rate as a function of composite pressure drop (difference of squares of pressures), for helium, against the experimental data by Maurer et al. (2003)

Full size image
Table 1 Imposed flow conditions and physical properties of helium gas
Full size table

It is a well known fact that the mass flow rate is directly proportional to the pressure drop for high Knudsen numbers, i.e., for Kn → ∞ covering the free-molecular regime (Kennard 1938). However, by inspection of Figs. 3 and 4, one can notice that the mass flow rate solution obtained using the extended Navier–Stokes equations approaches a constant value in the free-molecular regime, which is in contradiction with the free-molecular theory. One can explain this deviation of extended Navier–Stokes equations by introducing the Knudsen diffusion phenomenon into the treatment of diffusive motion of fluids. As pointed out before, the bulk diffusivity \( (D = \left( {1/3} \right)\bar{u}_{M} \lambda ) \) (or Fickian diffusion coefficient, Hosticka et al. 1998) becomes modified because of the increased frequency of molecular wall collisions in the rarefied Knudsen regime Kn → ∞. When the ratio of mean free path to the confining channel dimensions becomes large, the situation is described as the Knudsen regime of micro-channel flows (Malek and Coppens 2003). More detailed discussions on Knudsen diffusion and the corresponding results are presented in the section below.

3.3 Flow rates in free molecular and transition regime

Knudsen’s experimental study of rarefied gas flow through capillaries, which he initiated around 1907, was among the first designed to test the consequences of the kinetic theory of gases. Bulk diffusion given by Eqs. 4, 9 and 11 occurs when the mean free path (λ) is relatively short compared to the channel size (h). However, for large Knudsen numbers, relatively few gas molecules collide with each other compared to the number of collisions between molecules and the wall of the channel. This leads to the occurrence of so-called Knudsen diffusion when the mean free path is relatively large compared to the channel size, i.e., such as height of the channel, so the molecules collide frequently with the channel walls. Knudsen diffusion is more dominant compared to the molecular diffusion for the Knudsen numbers greater than 1. For fully developed Knudsen diffusion, the mass flux can be expressed as follows (Knudsen 1909; Kennard 1938):

$$ \dot{M}^{K} = \frac{{wh^{2} }}{3}\sqrt {\frac{8}{\pi RT}} \,\frac{{{\text{d}}P}}{{{\text{d}}x_{1} }} $$
(15)

where R is the specific gas constant

By taking into account the linear variation of pressure variation in the flow in the free-molecular regime, one can deduce from Eq. 15 the following relationship:

$$ \dot{M}^{K} = \frac{{wh^{2} }}{3L}\sqrt {\frac{8}{\pi RT}} \,P_{\text{out}} \left( {P_{r} - 1} \right) $$
(16)

Here P r = P in/P out, where as P in and P out are the inlet and outlet pressure, respectively.

From the above Eq. 16, one can notice that the difference between Eqs. 4, 9 and 11 and Eq. 16 lies in the fact that the mean free path (λ) in the bulk diffusion Eq. 11 is replaced by the height of the channel (h) (Note: \( \mu = \left( {1/3} \right)\rho \bar{u}_{M} \lambda \)). This finding also indicates that the molecular transport term for mass (Durst et al. 2006) (Eq. 11), should be incorporated in the classical continuity equation. The bulk diffusion which is given in Eq. 11 is dominant when the mean free path is relatively short compared to the channel dimensions, i.e., for small Knudsen numbers (Kn → 0). Figure 5 presents the graphical sketch of the both kinds of diffusion.

Fig. 5
figure 5

Sketch showing the different kind of diffusive modes of transport of fluids (a) molecular diffusion (b) fully developed Knudsen diffusion

Full size image

The theory for free-molecular regime (Kn > 10), continuum and to some extend the slip flow regime (0 < Kn < 0.1), is well developed. However, the operational regime of many microsystems at standard temperature and pressure can be in the transition regime (0.1 < Kn < 10) (Karniadakis et al. 2005). It is thus necessary to carry out investigations in the transition regime. In the transition regime, the diffusion has properties of both Knudsen and bulk diffusion. The exact theoretical basis to fundamentally describe diffusion in transition regime, however, remains unclear. It is instructive to read Knudsen’s own attempts to understand it and his dissatisfaction with his own explanations (Knudsen 1909). It is however clear that the transition regime is a mixture of both the free and the confined modes of diffusion to a varying degree depending on the magnitude of the Knudsen number. Using Eq. 4 one can obtain the bulk diffusivity (D b = D) as follows

$$ D^{b} = \left( {\frac{1}{3}} \right)\bar{u}_{M} \lambda = \left[ {\left( {\frac{1}{3}} \right)\bar{u}_{M} h_{{}} } \right]Kn $$
(17)

Hence, using Eq. 17 and by replacing λ with h, one can write the Knudsen diffusivity as follows (D K)

$$ D^{K} = \left( {\frac{1}{3}} \right)\bar{u}_{M} h $$
(18)

Eqs. 17 and 18 can be rewritten as

$$ \mathop {\lim }\limits_{{Kn \to_{{}} 0}} \left( {D^{e} } \right) = D^{K} Kn $$
(19)
$$ \mathop {\lim }\limits_{{Kn \to_{{}} \infty }} \left( {D^{e} } \right) = D^{K} $$
(20)

where D e is the effective diffusivity

One can notice that D K remains constant for a given gas, channel height (h) and temperature.

The effective diffusivity (D e) should smoothly vary between the two limits of bulk diffusion (Kn → 0) to fully developed Knudsen diffusion (Kn → ∞). Since the asymptotic behaviors of D e in both low and high Knudsen numbers regimes is known, the suggestions of Churchill and Usagi (1972) and the work of Durst et al. (2005) on the development lengths of laminar pipe and channel flows can be employed to get the simplest interpolation which correctly reproduces these asymptotic cases. The behavior in the transition regime can be interpolated by:

$$ D^{e} = \left[ {\left( {D^{b} } \right)^{c} + \left( {D^{K} } \right)^{c} } \right]^{1/c} $$
(21)

Here c is interpolation constant.

One can clearly deduce from Eq. 19 that when Kn → 0, the effect of Knudsen diffusion term is negligible and for high Knudsen numbers (Kn → ∞) the effect of molecular diffusion is negligible, which is possible only when c < 0. Figure 6 shows the variation of normalized effective diffusion (\( D^{{e^{*} }} = D^{e} /D^{K} \)) against the Knudsen number for different values of c.

Fig. 6
figure 6

Variation of normalized effective diffusivity against Knudsen number

Full size image

Using Eqs. 12, 16 and 21, the effective diffusive mass flow rate can be written as given below

$$ \dot{M}_{e}^{D} = \left[ {\left( {\dot{M}^{D} } \right)^{c} + \left( {\dot{M}^{K} } \right)^{c} } \right]^{1/c} $$
(22)

Hence, using Eqs. 22 and 13 the effective total mass flow rate can be written as:

$$ \dot{M}_{e}^{T} = \dot{M}_{e}^{C} + \left[ {\left( {\dot{M}^{D} } \right)^{c} + \left( {\dot{M}^{K} } \right)^{c} } \right]^{1/c} $$
(23)

here \( \dot{M}_{e}^{C} \) is the effective convective mass flow rate that is similar to the expression given in Eq. 13, except the fact that μ is replaced with μ e (effective viscosity), which is obtained using the effective diffusivity.

As seen in Fig. 6, the effective diffusivity (D e) matches both the asymptotes smoothly for −2 < c < −1. The best fit to the experimental data (Maurer et al. 2003) on the mass flow rate is obtained using equation (23) with c = −1.6. As shown in Fig. 7, the agreement is very good and the present theory also converges to the free-molecular and continuum theories in the asymptotic cases. Thus, the exponent c = −1.6 is used for interpolation in the transition regime. However, for typical values of c ranging from −2 to −1, negligible differences were observed between the predicted values of mass flow rate. Thus, a value of c = −1 may be chosen without much loss of accuracy. It may also be noted that other intuitive simpler interpolation schemes such as, given in Eq. 24, work nearly equally well in describing the experimental data of normalized flow rate (Q), see Eq. 25. However, these computations are not shown in Figs. 8 and 9 to avoid the overcrowding of data displayed.

Fig. 7
figure 7

Variation of mass flow rate against the average of difference of square of pressures from the continuum to the free-molecular regime and its comparison with experimental data (Maurer et al. 2003)

Full size image
Fig. 8
figure 8

Variation of normalized volume flow rate against Knudsen number and comparisons with experimental data (Dong 1956) and Lattice Boltzmann equations (Cercignani et al. 2004) in the transition regime (0.1 < Kn < 10)

Full size image
Fig. 9
figure 9

Variation of normalized volume flow rate against Knudsen number and comparisons with DSMC data (Karniadakis et al. 2005) and other existing theories over the continuum to free molecular regimes (0 < Kn < 100). Existence of the minimum at Kn ~ 1 is referred to as the Knudsen paradox

Full size image
$$ \dot{M}_{e}^{D} \, = \,\frac{{\dot{M}^{D} + Kn\,\dot{M}^{K} }}{1 + Kn} $$
(24)

One can notice from Eq. 24 that when Kn → 0, the effect of the Knudsen diffusion term is negligible and for high Knudsen numbers (Kn → ∞) the effect of molecular diffusion is negligible. The results based on the present theory and their matching with the experimental and simulation data are not much sensitive to a reasonable interpolation scheme used.

3.4 Normalized flow rate and Knudsen’s Paradox: comparisons with experiments

To further study the use of the extended Navier–Stokes equations, one can turn ones attention to the normalized volume flow rate (Q) defined in Eq. 22 as given in Dongari et al. (2007), where c s represents the speed of sound. It is known from Knudsen’s (1909) and Gaede’s (1913) experiments in the transition flow regime that there is a minimum in the normalized flow rate in pipe and channel flows. Knudsen observed this minimum at about approximately Kn ~ 1. This behavior has been investigated by many researchers both theoretically (Cercignani and Daneri 1963; Loyalka and Hamoodi 1990) and experimentally (Dong 1956; Tison 1993). It was first shown by Knudsen that in the free-molecular regime, a diffusive transport process proportional to the pressure gradient but independent of density is observed; see also Eq. 15.

The normalized volume flow rate can be obtained as:

$$ {\text{Q }} = \frac{{ - \rho c_{s} \int_{0}^{h} {\hat{U}{\text{d}}y} }}{{h^{2} \left( {{\text{d}}P/{\text{d}}x} \right)}} $$
(25)

Figure 8 presents comparison of normalized mass flow rate as a function of Knudsen number through the micro-channel obtained from the present theory against the semi-analytical solution obtained using linearized Boltzmann equations of Cercignani et al. (2004) and the experimental data of Dong (1956). The present theory agrees very well with Cercignani et al. (2004) for Kn less than about 0.1, which corresponds approximately to the end of the slip flow regime. The Boltzmann solution diverges from the experimental data in the early transition flow regime (Kn > 0.1). However, the present theory matches fully with the experimental data in the entire transition flow regime (0.1 < Kn < 10). One has to note that this excellent agreement is achieved without incorporating any kind of complex and adjustable slip models. This suggests that the extended Navier–Stokes equations with appropriate treatment of diffusive mode of transport, in conjunction with the conventional no-slip boundary condition at the wall, indeed form a suitable framework to explain all the details of the micro-channel flows.

Figure 9 shows the variation of normalized mass flow rate against Knudsen number (Kn). In this figure, the extended Navier–Stokes results are compared over a larger range of Knudsen number with the second order slip flow theory (Dongari et al. 2007), Boltzmann solution (Cercignani and Daneri 1963) and DSMC simulation results (Karniadakis et al. 2005). One can notice from Fig. 9 that the second order slip flow theory deviates from all other theoretical approaches at Knudsen number around 2 and diverge away at high Knudsen numbers. The linearized Boltzmann solution has good agreement with the extended Navier–Stokes equations solution up to Kn = 10. However, in the limit of high Kn numbers, the flow rate predicted by the lattice Boltzmann approach increases asymptotically to a value proportional to (1/π)1/2 ln (Kn). On the other hand DSMC results match the Boltzmann solution quite well up to Kn = 10. But beyond this value, the DSMC results are close to our extended Navier–Stokes solution and subsequently approach a constant value in the free-molecular regime, rather than increasing logarithmically. It is important to note that Knudsen (1909) mentioned that the normalized volume flow rate (Q) reaches a constant value in the Knudsen regime (Kn → ∞).

One can deduce by looking at Eqs. 15 and 23 and Fig. 7 that the normalized volume flow rate must converge towards a finite limit for large Knudsen numbers (Kn → ∞). As discussed above, this inability to approach the free-molecular regime at high Kn numbers indicates a limitation of the Boltzmann approach. However, DSMC simulations seem to correctly capture this regime.

4 Design of micro-channel flow studies

To give a further example of the usage of the above equations, in the considerations below, the Knudsen paradox is treated. For this purpose, the conductance \( C\, = \,\dot{M}_{e}^{T} \,/\,\left( {P_{\text{in}} \, - \,P_{\text{out}} } \right) \) is expressed as follows by using Eqs. 12, 13, 16 and 24:

$$ C = \frac{{\dot{M}_{e}^{T} }}{{P_{\text{in}} - P_{\text{out}} }} = \frac{{h^{3} wP_{\text{out}} \left( {P_{r} + 1} \right)}}{{\left( {24\mu LRT} \right)}} + \frac{\mu wh}{L(Kn + 1)}\left[ {\frac{{\ln \left( {P_{r} } \right)}}{{\left( {P_{r} - 1} \right)P_{\text{out}} }}} \right] + \frac{{wh^{2} Kn}}{3L(Kn + 1)}\sqrt {\frac{8}{\pi RT}} $$
(26)

One can relate the outlet pressure (P out) to the outlet mean free path of the gas molecules as follows:

$$ P_{\text{out}} = \frac{K}{{\lambda_{\text{out}} }},\,\quad {\text{with}} \; K \; {\text{being }}K = \frac{RT}{{\sqrt 2 \Uppi d^{2} N_{A} }} $$
(27)

Here R is the gas constant, T temperature, d molecular diameter and N A , the Avogadro number. Differentiating Eq. 26 with respect to the mean free path (λout), and making dC/dλout = 0, one can obtain the following expression for Knudsen number (Kn), where the conductance minimum occurs:

$$ Kn = \frac{1}{\sqrt Z - 1} $$
(28)
$$ Z = \left[ {\frac{{\mu \ln \left( {P_{r} } \right)}}{(\Pr - 1)K} + \frac{1}{3}\sqrt {\frac{8}{\pi RT}} } \right]\left[ {\frac{24\mu RT}{K(\Pr + 1)}} \right] $$
(29)

One can clearly deduce from Eqs. 23 and 26 that the change in curvature of conductance, i.e., the occurrence of minimum, happens when the diffusive mass flow rate \( (\dot{M}_{e}^{D} ) \) starts to dominate the convective mass flow rate \( (\dot{M}^{C} ). \) Knudsen (1909) mentioned that the “Knudsen paradox” will occur for a Knudsen number of approximately 1. But the above equation shows that the occurrence of the minimum has a dependence on the physical properties of the gas and the pressure ratio. This is in agreement with the results present in Fig. 10, which were computed using the extended Navier–Stokes equations.

Fig. 10
figure 10

Comparison of conductance versus Knudsen number for different gases at different pressure ratios

Full size image

To the best of our knowledge, there is no appropriate theoretical treatment of micro-channel flows available that permits the minimum of conductance to be predicted and also to be physically explained, i.e., theoretical treatments using linear slip models do not yield the “Knudsen paradox” as a result. Though it is appreciated that higher order slip models capture this phenomenon, e.g., see Beskok and Karniadakis (1999), Karniadakis et al. (2005) and Dongari et al. (2007), but at the same time “higher order Maxwell slip wall velocity boundary conditions” do not result in convergence for high Knudsen numbers, e.g., see Karniadakis et al. (2005). On the other hand, the present treatment shows that the minimum of the conductance is not really a paradox, but rather a consequence of the different scaling for the convective and diffusive fluxes. In particular, the diffusive flux begins to dominate for Kn > 1. It can be theoretically predicted and the results also yield the dependence of the minimum on the properties of the employed gas and pressure ratio, see Figs. 10 and 11. These two figures show that the minimum moves towards smaller Kn-numbers, if the pressure ratio is decreased. The considered Knudsen-minimum is also more pronounced for Helium than for air. It can be explained by the fact that the Helium molecules diffuse faster compared to the air molecules for a given pressure ratio.

Fig. 11
figure 11

The location of the Knudsen minimum for different pressure ratios for air and helium

Full size image

All the above reported computational results were obtained for a constant channel height and the pressure was varied to obtain the Kn-number variation shown in Figs. 10 and 11. All other parameters employed in the theoretical predictions can be taken from Table 1. The results in this section show that the present theory is consistent with previous experimental data. Further, we emphasize the prediction of Knudsen paradox using the extended Navier–Stokes equations without imposing any slip boundary condition at the wall could be obtained.

5 Conclusions

In this paper, studies of gas flows through micro-channel have been carried out theoretically from the continuum to the Knudsen regime and a uniform treatment is proposed for all values of Knudsen number. The investigation employs the continuum Navier–Stokes equations together with the incorporation of diffusive flux by considering the Knudsen diffusion phenomenon and the conventional no-slip boundary condition at the wall. In the current treatment, the diffusive mode of transport also introduces a slip-kind of wall velocity but in a somewhat natural way as the diffusive flux depends only on the axial pressure gradient, which is uniform across the channel cross-section. Analytical expressions for mass flow rate and normalized volume flow rate could be derived for this important class of flows. The results provide a insight into the physics of the particular behaviors of micro-channel gas flows over the entire Knudsen number range.

Figures 8 and 9 convey that the predictions based on the continuum Navier–Stokes equations together with the incorporation of diffusive flux, but without any wall-slip postulate, do agree rather remarkably with the experimental data. Further, the results of such an approach also match the results of the Boltzmann equations (up to transition regime) and the DSMC simulations (in all regimes including the free-molecular regime, i.e., for large range of Knudsen number. These results not only provide a theoretical treatment for the underlying physics of micro-channel gas flows, but also offer a simple analytical scheme that circumvents the difficulties of precise micro-flow measurements and complex simulations valid over a limited range of parameters. The theoretical treatment presented here can be readily extended to other more complex geometries as well and suggests better design and interpretation of the micro-channel flow studies as discussed below. Indeed, one has to notice that this excellent agreement is obtained with the experiments, other theoretical approaches and simulations without invoking any kind of complex models and/or adjustable parameters.

The underlying physics of the Knudsen’s minima, or so called Knudsen’s paradox, has also been clarified based on the inclusion of axial diffusion. The occurrence of minimum flux is caused by the fact that the diffusive mode of transport begins to dominate the convective mode at the higher Knudsen numbers. The dependence of the location of the Knudsen’s minima on the physical properties of the gas and the pressure ratio has been derived analytically. We also show that the normalized volume flow rate reaches a constant value for Kn → ∞ which is in turn in agreement with the Knudsen’s finding (Knudsen 1909). The new insights gained through this theoretical approach can be used to design new sets of experiments in the field of micro-fluid mechanics to prove (or disprove) results obtained with the help of the extended Navier–Stokes equations.