1 Introduction

Rarefied gas flows through pipes of different forms are very important in practice. Many industrial apparatuses such as microducts, microturbines or vacuum equipment are the examples of small devices involving the gas flow at an arbitrary Knudsen number. Recently, various numerical methods were developed and applied to rarefied gas flows through capillaries. Such flows through pipe of simple forms, e.g., circular tube, plane channel, were profoundly studied by many researchers. A critical review and recommended data on this topic can be found in Sharipov and Seleznev (1998).

Recently, some results on gas flows through a rectangular channel obtained by the discrete velocity method were reported in Sharipov (1999a, b). Numerical schemes applied in these papers are suitable just only for the specific pipe cross section, i.e., for circle or for rectangle. However, the wide diversity of the pipe forms used in practice requires a further development of the existing approaches so that it would be possible to calculate gas flows through pipes of arbitrary form, e.g., ellipse, triangle, trapezoid etc. Some results obtained by the integro-moment method based on the linearized BGK equation for tubes with various cross sections are reviewed in Aoki (1989). According to this review, a rarefied gas flow through a tube with an elliptical cross section was calculated in Hasegawa and Sone (1988) only for one value of the aspect ratio by the integro-moment method. Some new results related to internal flows in pipes of various cross sections based on the numerical solution of the BGK kinetic equation may be found in Breyiannis et al. (2008), Naris and Valougeorgis (2008). Recently, an approach based on the discrete velocity method, but extended to the tubes of the elliptical cross section, is proposed in Graur and Sharipov (2007), where only isothermal flow was considered on the basis of the BGK kinetic equation.

The present paper is the extension of the work (Shakhov 1968), where the discrete velocity method was generalized to case of the tubes of the elliptical cross sections. Here, non-isothermal flows through pipes of the elliptical cross section are considered using the S-model kinetic equation. The mass flow rates due to the pressure and temperature gradients are calculated over the whole range of the Knudsen number and in a wide range of the pipe section aspect ratio. The case of arbitrary pressure and temperature ratios is simulated. A special attention is paid to the thermal transpiration effect. The flow driven only by a temperature gradient is considered and the corresponding pressure distribution is obtained for several values of the section aspect ratio. The coefficient of the thermomolecular pressure difference is obtained and the influence of the aspect ratio on this coefficient is studied.

2 Statement of the problem

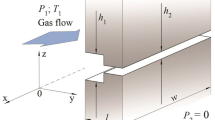
Consider a tube connecting two reservoirs containing the same gas. The tube cross section is elliptical as is shown in Fig. 1, where 2b is the maximal tube dimension in the y direction, 2a is the maximal dimension in the x direction. Without loss of generality, we consider that b ≤ a. The pressure and temperature in the left and right reservoirs are equal to p 1 and T 1, p 2 and T 2, respectively. We are going to calculate the mass flow rate through this tube assuming that:

  • The tube length L is significantly larger than the dimension a of the tube cross section, i.e., a ≪ L. This assumption allows us to neglect the end effects and to consider only the longitudinal component of the bulk velocity and heat flux vector, which depend only on x and y coordinates.

  • The pressure and temperature depend only on the longitudinal coordinate z′ and their gradients are small, i.e.,

    $$ \xi_P={\frac{b}{p}}{\frac{\hbox{d}p}{\hbox{d}z^\prime}}, \quad |\xi_P|\ll 1, $$
    (1)
    $$ \xi_T={\frac{b}{T}}{\frac{\hbox{d}T}{\hbox{d}z^\prime}}, \quad |\xi_T|\ll 1. $$
    (2)

    This assumption allows us to linearize the kinetic equation.

Fig. 1
figure 1

Tube cross section and coordinates

Full size image

The gas rarefaction is characterized by the parameter

$$ \delta= {\frac{bp}{\mu v_m}}, \quad v_m=\left({\frac{2kT}{m}}\right)^{1/2}, $$
(3)

where μ is the shear viscosity, v m is the most probable molecular speed, m is the molecular mass of the gas, and k is the Boltzmann constant. Since the viscosity is proportional to the molecular mean free path, the rarefaction parameter δ is inversely proportional to the Knudsen number.

It is convenient to express the final results in terms of the dimensionless flow rate G * through a cross section defined as

$$ G_*={\frac{1}{\pi a b p}}\sqrt{{\frac{2kT}{m}}}\dot M, $$
(4)

where \({\dot M}\) is the mass flow rate, p = p(z′) is the local pressure in the cross section and T = T(z′) is the local temperature in the same section. Since the pressure and temperature gradients are small the reduces flow rate G * can be decomposed as

$$ G_*=-\xi_P G_P+\xi_T G_T, $$
(5)

where the coefficients G P and G T do not depend on the gradients ξ P and ξ T , but only on the rarefaction parameter δ. The first one G P is called the Poiseuille coefficient, while the second one G T is called the thermal creep coefficient. They are introduced so that to be always positive.

3 Kinetic equation

To calculate the coefficients G P and G T in the transition regime the Boltzmann equation should be solved. This equation provides reliable numerical data but requires great computational effort. To reduce this effort the collision integral may be simplified remaining its main properties. In the present paper we apply the S-model kinetic equation (Shakhov 1968), which provides the correct Prandtl number. For a steady flow it reads

$$ {{\mathbf{v}}}\cdot {\frac{\partial f}{\partial {{\mathbf{r}}}^\prime}}= {\frac{f^S-f}{\tau}}, $$
(6)

where f is the one particle distribution function, r′ is the position vector, v is the molecular velocity, f S is given as

$$ f^{S}(n,T, {{\mathbf{u}}}^{\prime}) = f^{\rm M}\left[ 1+{\frac{2m}{15 n({{\mathbf{r}}}^{\prime}) (kT({{\mathbf{r}}}^{\prime}))^2}} {{\mathbf{V}}}\cdot {{\mathbf{q}}}'({{\mathbf{r}}}^{\prime}) \left({\frac{m V^2}{2kT({{\mathbf{r}}}^{\prime})}}-{\frac{5}{2}}\right) \right], $$
(7)

and f M is the local Maxwellian distribution function:

$$ f^{\rm M} (n,T,{{\mathbf{u}}}^{\prime})= n({{\mathbf{r}}}^{\prime})\left({\frac{m}{2\pi k T({{\mathbf{r}}}^{\prime})}}\right)^{3/2} \exp\left[-{\frac{m({{\mathbf{v}}}- {{\mathbf{u}}}^{\prime}({{\mathbf{r}}}^{\prime}))^2}{2kT({{\mathbf{r}}}^{\prime})}}\right], $$
(8)

n is the number density, u′ is the bulk velocity, V = v−u′(r′) is the peculiar velocity, q′ is the heat flux vector. The relaxation time expression

$$ \tau={\frac{\mu}{p}} $$
(9)

provides the best agreement with the exact Boltzmann equation. The bulk velocity u′ and the heat flux q′ are defined as

$$ {{\mathbf{u}}}^{\prime}({{\mathbf{r}}}^{\prime})={\frac{1}{n}}\int\limits_{- \infty}^{+\infty}{{\mathbf{v}}} f({{\mathbf{r}}}^{\prime}, {{\mathbf{v}}}) \hbox {d} {{\mathbf{v}}}, \quad {{\mathbf{q}}}^{\prime}({{\mathbf{r}}}^{\prime})={\frac{m}{2}}\int\limits_{- \infty}^{+\infty}{{\mathbf{V}}} V^2 f({{\mathbf{r}}}^{\prime}, {{\mathbf{v}}})\hbox {d}{\bf v}. $$
(10)

Under the assumptions of the small local pressure and temperature gradients (1), (2) the distribution function f can be linearized as

$$ f({{\mathbf{r}}}, {{\mathbf{c}}})=f^0\left[1+h(x,y,{{\mathbf{c}}})+\xi_P z+\left(c^2-\frac{5}{2}\right)\xi_T z\right], $$
(11)

where c = v/v m , h is the perturbation function and

$$ f^0= n_0\left({\frac{m}{2\pi k T_0}}\right)^{3/2}\exp\left[-{\frac{m v^2}{2kT_0}}\right] $$
(12)

is the absolute Maxwellian with the equilibrium number density n 0 and the equilibrium temperature T 0. In the case of week nonequilibrium the local Maxwellian distribution function (8) can be related to the absolute Maxwellian (12) as

$$f^M(n,T,{{\mathbf{u}}}^{\prime})=f^0\left[1+{\frac{n-n_0}{n_0}}+ {\frac{m}{k T_0}}{{\mathbf{v}}} \cdot {\bf u^{\prime}}+{\frac{T-T_0}{T_0}}\left(c^2-{\frac{3}{2}}\right)\right]. $$
(13)

The f S distribution function (7) is given as

$$ \begin{aligned} f^S(n,T,{{\mathbf{u}}}^{\prime})&=f^0\left[1+{\frac{n- n_0}{n_0}}+{\frac{m}{k T_0}}{{\mathbf{v}}} \cdot {{\mathbf{u}}}^{\prime}+{\frac{T-T_0}{T_0}}\left(c^2- {\frac{3}{2}}\right)\right. \\ &\quad\left.+\;{\frac{2m}{15 n_0 (kT_0)^2}}{{\mathbf{v}}} \cdot {{\mathbf{q}}}^{\prime} \left(c^2-{\frac{5}{2}}\right) \right]. \end{aligned} $$
(14)

Substituting the relations (11) and (14) into Eq. (6), using the notation (9), and after some simplifications one obtains

$$ \begin{aligned} &{{\mathbf{c}}} \cdot {\frac{\partial}{\partial {{\mathbf{r}}}}} \left[h(x,y,{{\mathbf{c}}})+\xi_P z+\left(c^2-{\frac{5}{2}}\right)\xi_T z\right] \\ &\quad=\delta\left[2{{\mathbf{c}}} \cdot {{\mathbf{u}}}+ {\frac{4}{15}} {{\mathbf{c}}} \cdot {{\mathbf{q}}}\left(c^2-{\frac{5}{2}}\right)-h(x,y,{{\mathbf{c}}})\right], \end{aligned} $$
(15)

where the following dimensionless quantities have been introduced

$$ \begin{aligned} &x={\frac{x^{\prime}}{b}}, \quad y={\frac{y^{\prime}}{b}}, \quad z={\frac{z^{\prime}}{b}}, \\ &{{\mathbf{u}}}={\sqrt{{\frac{m}{2kT_0}}}{{\mathbf{u}}}^{\prime}}, \quad {{\mathbf{q}}}={\frac{2}{n_0 m}}\left({\frac{m}{2kT_0}}\right)^{3/2}{{\mathbf{q}}}^{\prime}. \end{aligned} $$
(16)

Here we assume the bulk velocity u′ and the heat flow vector q′ to have the z-component only, so the subscript z is omitted in the dimensionless notations u and q.

From Eq. (15) and using notations (16) we obtain the linearized S-model equation in the dimensionless form

$$ \begin{aligned} c_x {\frac{\partial h}{\partial x}}+c_y{\frac{\partial h}{\partial y}}&=\delta \left[2c_z u+{\frac{4}{15}} c_z q\left(c^2-{\frac{5}{2}}\right)- h(x,y,{{\mathbf{c}}})\right] \\ &\quad- c_z\left[\xi_P+\left(c^2-{\frac{5}{2}}\right)\xi_T\right], \end{aligned} $$
(17)

where

$$ u(x,y)={\frac{1}{\pi^{3/2}}} \int\limits_{-\infty}^{+\infty} c_z \hbox {e}^{-c^2} h(x,y,{{\mathbf{c}}}) \hbox {d}{{\mathbf{c}}}, $$
(18)
$$ q(x,y)= {\frac{1}{\pi^{3/2}}} \int\limits_{-\infty}^{+\infty}c_z \left(c^2-{\frac{5}{2}}\right) \hbox {e}^{-c^2}h(x,y,{{\mathbf{c}}}) \hbox {d}{{\mathbf{c}}}. $$
(19)

Then, the reduced mass flow rate G * defined by (4) can be calculated via the reduced velocity u(x,y) as

$$ G_*=-{\frac{2}{\pi}}{\frac{b}{a}}\int\limits_{-1}^{1} \int\limits_{-a/b\sqrt{1-y^2}}^{a/b\sqrt{1-y^2}} u(x,y) \hbox {d} x \hbox {d} y. $$
(20)

Since the pressure and temperature gradients are supposed to be small, therefore the solution of the linear equation (17) can be split in two parts

$$ h=h_P \xi_P+h_T \xi_T. $$
(21)

Substituting expression (21) into (18), (19) one can see that the distribution function moments can be also split as

$$ u=u_{P} \xi_P+u_{T} \xi_T, \quad q=q_{P} \xi_P+q_{T} \xi_T. $$
(22)

Substituting the first relation of (22) into (20) one obtains the coefficients G P and G T introduced by Eq. (5), expressed via the bulk velocities u P and u T as

$$G_P=-{\frac{2}{\pi}}{\frac{b}{a}}\int\limits_{-1}^{1} \int\limits_{-a/b\sqrt{1-y^2}}^{a/b\sqrt{1-y^2}} u_{P}(x,y) \hbox {d} x \hbox {d} y, $$
(23)
$$ G_T=\frac{2}{\pi}{\frac{b}{a}}\int\limits_{-1}^{1} \int\limits_{-a/b\sqrt{1-y^2}}^{a/b\sqrt{1-y^2}} u_{T}(x,y) \hbox {d} x \hbox {d} y. $$
(24)

Using the Onsager relation (Loyalka 1971; Sharipov 1994a, b)

$$ \int\limits_{-1}^{1} \int\limits_{-a/b\sqrt{1-y^2}}^{a/b\sqrt{1-y^2}} u_{T}(x,y) {d} x {d} y= \int\limits_{-1}^{1} \int\limits_{-a/b\sqrt{1-y^2}}^{a/b\sqrt{1-y^2}} q_{P}(x,y) \hbox {d} x \hbox {d} y, $$
(25)

we may express G T via q P as

$$ G_T=\frac{2}{\pi}{\frac{b}{a}}\int\limits_{-1}^{1} \int\limits_{-a/b\sqrt{1-y^2}}^{a/b\sqrt{1-y^2}} q_{P}(x,y) \hbox {d} x \hbox {d} y. $$
(26)

Therefore, to calculate the reduced mass flow rate G * defined by Eq. (4) it is enough to obtain the solution h P . Further, we assume that ξ P  = 1 and ξ T  = 0 in Eq. (17), implying that h = h P , u = u P and q = q P .

Multiplying Eq. (17) by \(\frac{c_z}{\sqrt{\pi}}\hbox {e}^{-c_z^2}\) and by \(\frac{c_z^3}{\sqrt{\pi}}\hbox {e}^{-c_z^2}\) and integrating it with respect to d c z we obtain two equations

$$ \begin{aligned} &c_x {\frac{\partial \phi}{\partial x}}+c_y{\frac{\partial \phi}{\partial y}}= \delta \left[u+{\frac{2}{15}}q\left(c_x^2+c_y^2-1\right)-\phi(x,y,c_x, c_y)\right]- {\frac{1}{2}}, \\ &c_x {\frac{\partial \psi}{\partial x}}+c_y{\frac{\partial \psi}{\partial y}} = \delta \left[{\frac{3}{2}}u+{\frac{1} {5}}q\left(c_x^2+c_y^2\right)-\psi(x,y,c_x,c_y)\right]- {\frac{3}{4}}, \end{aligned} $$
(27)

where the functions ϕ and ψ are introduced in order to eliminate the variable c z

$$ \phi(x,y)={\frac{1}{\sqrt{\pi}}}\int\limits_{-\infty}^{+\infty} c_z \hbox {e}^{-c_z^2} h \hbox {d} c_z, \quad \psi(x,y)={\frac{1} {\sqrt{\pi}}}\int\limits_{-\infty}^{+\infty} c_z^3 \hbox {e}^{-c_z^2} h \hbox {d} c_z. $$
(28)

The Cartesian coordinates in the velocity space (c x ,c y ) in Eq. (27) may be replaced by the polar coordinates (c p , φ), i.e.,

$$ c_x=c_p \cos \varphi, \quad c_y=c_p \sin \varphi, \quad 0\le\varphi \le 2 \pi. $$
(29)

Equations (27) may be now rewritten in the new variables as

$$ \begin{aligned} &-c_p{\frac{\partial \phi}{\partial s}}= \delta \left[u+{\frac{2}{15}}q\left(c_p^2-1\right)-\phi(x,y,c_p, \varphi)\right]- {\frac{1}{2}}, \\ &-c_p{\frac{\partial \psi}{\partial s}}= \delta \left[{\frac{3}{2}}u+{\frac{1}{5}}q c_p^2-\psi(x,y,c_p, \varphi)\right]- {\frac{3}{4}}, \end{aligned} $$
(30)

where s is the characteristic. The bulk velocity and the heat flux are expressed as

$$ u=\frac{4}{\pi} \int\limits_0^{\pi/2}\int\limits_0^{\infty}\phi(c_p, \varphi) \hbox {e}^{-c_p^2}c_p \hbox {d}c_p \hbox {d}\varphi, $$
(31)
$$ q={\frac{4}{\pi}} \int\limits_0^{\pi/2}\int\limits_0^{\infty}\left[(c_p^2-{\frac{5}{2}})\phi(c_p, \varphi)+\psi(c_p, \varphi)\right] \hbox {e}^{-c_p^2}c_p \hbox {d}c_p \hbox {d}\varphi. $$
(32)

So, in order to obtain the reduced mass flow rate the system of two equations (30) must be solved.

We assume the complete accommodation of molecules on the tube walls. It means that h(x,y,c p ,ϕ) = 0 at the walls for the reflected particles in Eq. (17). Consequently, the conditions ϕ = 0 and ψ = 0 for the reflected particles are used as the boundary conditions for the system (30).

4 Limit solutions

In the free molecular regime (δ = 0) Eq.(17) is significantly simplified and can be solved analytically. After its splitting into two parts according to (21) and assuming ξ T  = 0 the analytical expression for G P may be easily found (Graur and Sharipov 2007). The corresponding numerical values are presented in the first row of Table 1. Furthermore, assuming ξ P  = 0 in Eq. (17) and after the integration one obtains \(u_T=-\frac{1}{2}u_P,\) so

$$ G_T={\frac{1}{2}}G_P \quad {at} \quad \delta=0. $$
(33)

The values of G T are shown in the first row of Table 2.

Table 1 Reduced flow rate G P versus rarefaction parameter δ and aspect ratio a/b
Full size table
Table 2 Reduced flow rate G T versus rarefaction parameter δ and aspect ratio a/b
Full size table

In the hydrodynamic flow regime (δ → ∞) the gas flow is described by the Stokes equation. The analytical solution of this equation for u P with the non-slip boundary condition may be found in Landau and Lifshitz (1989), Graur and Sharipov (2007), while the thermal creep velocity u T is equal to 0. Therefore the mass flow rates take the form

$$ G_{P}={\frac{\delta}{2}}\,{\frac{a^2}{a^2+b^2}}, \quad G_T=0 \quad \hbox {at} \quad \delta \rightarrow \infty. $$
(34)

A moderate rarefaction of the gas can be taken into account applying the velocity slip boundary condition (Sharipov 2003) to the Stokes equation. In other words, we consider that the tangential component of the bulk velocity near the wall is proportional to its normal gradient and to the longitudinal temperature gradient, i.e.,

$$ u=\sigma_{{\rm P}} \ell {\frac{\partial u}{\partial \eta^{\prime}}}+{\frac{\sigma_{{\rm T}}}{2}}\ell{\frac{\partial \ln T} {\partial z^{\prime}}},\quad \hbox {at}\quad \eta^{\prime}=0, $$
(35)

where η′ is the normal coordinate with its origin at the tube wall and directed toward to the gas, z′ is the coordinate tangential to the surface in the flow direction, \(\sigma_{{\rm P}}\) is the viscous slip coefficient, σ T is the thermal slip coefficient, ℓ = μv m /p is the equivalent free path.

In Graur and Sharipov (2007) the following expression of the flow rate due to the pressure gradient was obtained by the numerical integration of the Stokes equation with the velocity slip boundary condition (35)

$$ G_P={\frac{\delta}{2}}\,{\frac{(a/b)^2} {(a/b)^2+1}}+\sigma_{{\rm P}} \left[1-0.6976{\frac{1-(a/b)^2}{1.951+(a/b)^2}}\right] \quad \hbox {at } \delta \gg 1. $$
(36)

Using the thermal slip boundary condition (second term in (35)) one obtains the constant velocity over cross section (Sharipov and Seleznev 1998)

$$ u_T={\frac{\sigma_{{\rm T}}}{2 \delta}}. $$
(37)

Substituting (37) in (24) we obtain the thermal creep coefficient G T as

$$ G_T={\frac{\sigma_{{\rm T}}}{\delta}} \quad \hbox {at} \quad \delta \gg 1. $$
(38)

Note, this coefficient does not depends on the aspect ratio a/b.

The expressions (36) and (38) are valid for any values of the slip coefficients σ P and σ T which depend on the accommodation coefficients (Sharipov 2003). For the diffuse gas–surface interaction assumed here the slip coefficients are given by

$$ \sigma_P=1.018,\quad \sigma_T=1.175\;. $$
(39)

5 Numerical results

The system of the kinetic equations (30) was solved by the discrete velocity method and the details of the numerical algorithm may be found in Graur and Sharipov (2007), where a non-uniform grid adapted to the elliptic cross section was introduced in the physical space.

The numerical calculations were carried out in the range of the rarefaction parameter δ from 0.01 to 20 and for several values of the aspect ratio a/b in the range from 1 to 100. The flow rates G P and G T were calculated with the numerical error less than 0.1%. The accuracy was estimated by comparing numerical results obtained for different parameters of the numerical grid. An analysis showed that to reach the accuracy of 0.1% the grid in the physical space should be 1,000 × 1,000 points and the parameter N φ should be equal to 100 for all values of δ, while the parameter N c depends on δ. In the range 0 ≤ δ ≤ 0.1 the value N c  = 25 should be used and for δ > 0.1 the smaller value, viz. N c  = 12, is enough.

The numerical results on the flow rates G P and G T are presented in Tables 1 and 2, respectively. In the case a/b = 1, i.e, circular cross section of the tube, the results of the present work are compared with those obtained from the S-model equation by the discret velocity method in Sharipov (1996). It can be seen that the discrepancy with this work does not exceed the numerical accuracy.

One can see the Knudsen minimum (for the mass flow rate G P ) presenting for all aspect ratio around δ∼0.2−0.5. This minimum becomes more apparent for the large aspect ratio a/b = 100 and is shallow for the circular cross-section.

In the fourth columns of Tables 1 and 2 the results corresponding to a small deviation from the circular tube are shown, i.e., for a/b = 1.1. Note, in the all regimes the relative difference of the flow rate G P , due to the deviation in the aspect ratio from unity, is about (a/b − 1), while for the flow rate G T this relative difference is smaller then (a/b − 1), especially in hydrodynamic regime.

When the aspect ratio increases, i.e., at a/b → ∞, both flow rates G P and G T tend to constant values in the hydrodynamic regime (δ ≫ 1). The same conclusion can be made from the slip solution (36), where G P tends to the constant value \(\frac{\delta} {2}+ 1.6076\sigma_P\) when a/b tends to infinity, and the slip solution G T also is given by the constant value (38).

Comparing the values of G P corresponding to δ = 20 in Table 1 with those calculated by Eq.(36) it can be seen that the relative difference does not exceed 0.5%. Thus, Eq. (36) can be successfully used for δ > 20. However, a comparison of the values of G T given in the last row of Table 2 with the expression (38) shows that the difference is about 7%.

Near the free molecular regime δ ≪ 1 the flow rates increase by increasing the aspect ratio. If one compares the values of both G P and G T in the free molecular regime (δ = 0) with the corresponding values at δ = 0.01, one will see that the difference between them is small only for the small aspect ratios, i.e., at a/b ≤ 2, while for the large aspect ratios the difference is significant. In other words, for a/b≥5 the flow does not reach the free-molecular regime even at δ = 0.01. In order to be free-molecular the condition δa/b ≪ 1 must be satisfied.

6 Arbitrary pressure and temperature drop

The solutions of the S-model kinetic equation, presented above, are obtained under the conditions (1) and (2), of the smallness of the pressure and temperature gradients. However, in practice these gradients are usually large, when the pressure and temperature ratios p 2/p 1 and T 2/T 1 between inlet and outlet reservoirs are arbitrary. One way of the application of the developed approach to the arbitrary pressure and temperature gradients are proposed in Sharipov (1996). When the tube length is significantly larger that its cross section size, i.e., L ≫ b, the pressure and temperature gradients, estimated as follows

$$ \xi_P \sim {\frac{b(p_2-p_1)}{L p_{av}}}, \quad \xi_T\sim {\frac{b(T_2-T_1)}{L T_{av}}}, $$
(40)

where

$$ p_{av}={\frac{1}{2}}\left(p_1+p_2\right), \quad T_{av}=\frac{1} {2}\left(T_1+T_2\right), $$
(41)

are obviously small. Hence one can apply the developed approach to the cases of the arbitrary pressure and temperature ratios using the reduced mass flow rates G P (δ) and G T (δ) given in Tables 1 and 2.

When the pressure and temperature ratios are large, δ varies significantly along the channel. This rarefaction parameter depends on the local pressure and temperature according to relation (3). Assuming the hard sphere model of molecules we can express the local rarefaction parameter as a function of the local values of the pressure and temperature and of their values in the inlet reservoir

$$ \delta(p,T)=\delta_1{\frac{p(z)}{p_1}}{\frac{T_1}{T(z)}}. $$
(42)

Let us introduce a reduced mass flow rate as

$$ G={\frac{L}{\pi a b^2 p_1}}\sqrt{{\frac{2k T_1}{m}}} \dot M, $$
(43)

which does not depend of the local rarefaction parameter δ(z′), unlike the reduced mass flow rate G * defined by Eq. (4).

Substituting relations (1), (2), (4) and (43) in (5) we obtain the following differential equation

$$ G\,{\frac{p_1}{p}}\sqrt{{\frac{T}{T_1}}}\,{\frac{b}{L}}=-{\frac{1}{p}}\, {\frac{\hbox{d}p}{\hbox{d}z}}G_P(\delta)+{\frac{1}{T}}\,{\frac{\hbox{d}T}{\hbox{d}z}}G_T(\delta). $$
(44)

Since the thermal conductivity of the channel wall is essentially greater than that of the gas, and in addition, the characteristic dimension of the channel cross section is usually small compared to its of the channel wall, so the temperature distribution of the gas along the cannel is determined by the wall temperature distribution. We suppose here that the wall temperature distribution is linear, that is a good approximation when the wall thermal conductivity does not depend of the temperature.

When the temperature distribution is known, the following differential equation for the pressure distribution may be solved

$$ {\frac{1}{p_1}}\,{\frac{\hbox{d}p}{\hbox{d}z}}={\frac{p(z)}{p_1}}\,{\frac{1} {T}}\,{\frac{\hbox{d}T}{\hbox{d}z}}\,{\frac{G_T(\delta)}{G_P(\delta)}}-{\frac{G} {G_P(\delta)}}{\frac{b}{L}}\sqrt{{\frac{T}{T_1}}}. $$
(45)

At the inlet (z = 0) and outlet (z = L/b) boundaries the pressure is equal to the inlet p 1 and to the outlet p 2 reservoirs pressure accordingly. The reduced mass flow rate G is the parameter of the differential equation (45). This equation is solved numerically, assuming the linear temperature distribution along the channel, using the expression of the local rarefaction parameter (42) and the values of G P (δ) and G T (δ) given in Tables 1 and 2. The reduced mass flow rate G for one temperature ratio T 2/T 1 = 3.8 and two pressure ratios p 2/p 1 = 1 and p 2/p 1 = 100 are given in Tables 3 and 4. Note, the ratio T 2/T 1 = 3.8 corresponds to the typical situation when one reservoir is maintained at the liquid nitrogen temperature, while the second one is maintained at the room temperature.

Table 3 Reduced flow rate G versus rarefaction parameter δ1 and aspect ratio a/b at p 2/p 1 = 1 and T 2/T 1 = 3.8
Full size table
Table 4 Reduced flow rate G versus rarefaction parameter δ1 and aspect ratio a/b at p 2/p 1 = 100 and T 2/T 1 = 3.8
Full size table

For the first case the pressure ratio is equal to 1 (Table 3), so the flow is driven only by the temperature gradient from the cold reservoir toward to the hot one (the mass flow rate is positive). The mass flow rate decreases when the rarefaction parameter δ1 increases. The mass flow rate remains still constant for δ1 greater than 1 when aspect ratio varies from 10 to 100. Note that, in spite of the pressure ratio p 2/p 1 = 1 the pressure gradient still arises in the channel. The pressure distributions along a channel for three aspect ratios a/b = 1,10,100 are shown in Fig. 2. It can be seen that the pressure is 15% higher in the tube middle compared with its value at the tube ends. It is explained by the fact that the temperature at z = 0 is lower than that at z = L/b. Since the first term in the right hand side of Eq. (45) is inversely proportional to the temperature, it is larger than the second term at the tube entrance z = 0. Hence, the pressure derivative is positive at the entrance, while it is negative at the exit z = L/b, where the first term becomes smaller than the second one.

Fig. 2
figure 2

Pressure distribution along the tube, p 2/p 1 = 1, T 2/T 1 = 3.8, δ1 = 0.01

Full size image

In the case of the pressure ratio p 2/p 1 = 100 the flow properties changed completely: the reduced mass flow rate is negative, so the gas flows from the hot reservoir, where the pressure is higher, to the cold one, where the pressure is lower. The reduced mass flow rate increases when the rarefaction parameter δ1 increases.

7 Thermomolecular pressure difference

Let us assume two reservoirs maintained by the temperatures T 1 and T 2 and the pressures in both reservoirs are initially the same. This case is different from that considered in the previous section where the same pressures p 2/p 1 = 1 are maintained in both reservoirs. If these reservoirs are connected by a pipe the gas begins to flow from the cold reservoir to the hot one, then the pressure in the hot reservoir begins to increase until the mass flow rate vanishes.

The relation between p 1, p 2, T 1 and T 2 in the stationary state can be written in the following form

$$ {\frac{p_2}{p_1}}=\left({\frac{T_2}{T_1}}\right)^{\gamma}, $$
(46)

where the coefficient γ depends on many factors: pipe length-to-radius ratio, type of the gas, properties of the gas-surface interaction. In order to calculate this coefficient, let us consider differential equation (44). When the reduced mass flow rate G is equal to zero, this equation is reduced to

$$ {\frac{1}{p}}\,{\frac{\hbox{d}p}{\hbox{d}z}}G_P(\delta)={\frac{1}{T}}\,{\frac{\hbox{d}T}{\hbox{d}z}}G_T(\delta). $$
(47)

If we introduce the non-dimensional pressure and temperature as

$$ \tilde p={\frac{p}{p_1}}, \quad \tilde T={\frac{T}{T_1}}, $$
(48)

the rarefaction parameter in any section (42) may be expressed as

$$ \delta(p,T)=\delta_1{\frac{\tilde p}{\tilde T}}. $$
(49)

Then Eq. (47) reads

$$ {\frac{\hbox{d} \tilde{p}}{\hbox{d} \tilde T}}={\frac{\tilde p}{\tilde T}}{\frac{G_T(\delta_1 \tilde p/\tilde T)}{G_P(\delta_1 \tilde p/\tilde T)}}. $$
(50)

It is possible to consider Eq. (50) as a differential equation for a pressure as a function of a temperature \({\tilde p}({\tilde T})\) with the boundary condition \({\tilde p}=1\) at \({\tilde T}=1.\) The unknown value is the pressure ratio \(p_2/p_1={\tilde p}(T_2/T_1).\) Note that in Eq. (50) the dimensionless temperature \({\tilde T}\) is an independent variable, so the function \({\tilde p}({\tilde T})\) depends only on the ratio T 2/T 1 and on the rarefaction parameter δ1 and does not depend of the temperature distribution in the pipe (Sharipov and Seleznev 1998), unlike the case considered in Sect. 6. The coefficient γ is calculated from Eq. (46) as

$$ \gamma={\frac{\ln (p_2/p_1)}{\ln (T_2/T_1)}}. $$
(51)

The differential equation (50) was solved numerically. The calculations have been carried out for the same value of the temperature ratio T 2/T 1 as in Section 6. The coefficients G P (δ) and G T (δ) as functions of δ1 (Tables 1 and 2) have been used. The results of the calculations are given in Table 5. In the first column the coefficient γ calculated in Sharipov (1996) for the tube of the circular cross section a/b = 1 is presented. To solve Eq. (50) an interpolation of the coefficients G P (δ) and G T (δ) at the intermediate points of δ (between the values given in Tables 1, 2) is used. Therefore, the small difference with the present results (second column) is due to the fact that in Sharipov (1996) 33 values of G P and G T are used to interpolate these coefficients instead of 12 in the present paper. The coefficient γ depends essentially from the rarefaction parameter: when δ1 increases then γ decreases. The coefficient γ depends also on the pipe aspect ratio: the smaller values of γ correspond to the larger values of the aspect ratio.

Table 5 Thermomolecular pressure difference exponent γ (Eq. (46)) versus rarefaction parameter δ1 and aspect ratio a/b
Full size table

8 Examples of application

In order to illustrate how the present results can be applied a specific example is given here. Consider a gas flow through a pipe of the elliptic cross section with the characteristic dimension b = 0.217 μm, the ration a/b = 2, at the pressure P = 105 Pa and at temperature T = 293 K. Under such conditions the gas viscosity is μ = 19.73· 10−6 Pa s and the most probable speed is v m = 1.10 × 103 m/s. The rarefaction parameter δ defined by (3) is equal to unity. According to Table 1 for δ = 1 and a/b = 2 the coefficient G P is equal to 2.0323. Let us assume the dimensionless pressure gradient ξ P  = −0.01, see Eq. (1), to be maintained along the pipe and we consider the isothermal flow. Using Eqs. (4) and (5) the mass flow rate is calculated as \({\dot M}=0.546 {\times}10^{-12}\) kg/s.

9 Conclusion

The mass flow rate through a tube with the elliptical cross section driven by both pressure and temperature gradients is calculated over the whole range of the rarefaction parameter varying from the free molecular regime to the hydrodynamic one. Various aspect ratios of the tube axis a/b are considered. The analysis of the numerical data shows the significant influence of this aspect ratio on the mass flow rate due to the pressure gradient. The Knudsen minimum in the transitional regime exists at any aspect ratio a/b. It is becomes deeper by the decreasing ratio a/b. The influence of the section aspect ratio on the mass flow rate driven by temperature gradient is significant in the transitional and free molecular regimes, but in the slip and hydrodynamic regimes the aspect ratio practically does not influence the mass flow rate.

The case of the arbitrary pressure and temperature ratios is considered. The thermomolecular pressure difference is calculated and its dependence on the rarefaction parameter and on the aspect ratio of the pipe cross section is shown.