Nonisothermal Rarefied Gas Flow through a Long Cylindrical Channel under Arbitrary Pressure and Temperature Drops

Abstract

The problem of rarefied gas flow through a long cylindrical channel as a function of the pressure and the temperature maintained at the channel ends is considered on the basis of the S-model of the Boltzmann kinetic equation. The pressure and temperature drops between the channel ends vary from small values at which the linear transport theory is valid to large values at which the gas molecule mean free path ceases to be constant along the channel. The solution to the model kinetic equation is found by means of the collocation method using the Chebyshev polynomials and rational functions. The mass flow and the pressure in the channel are obtained. Isobaric and isothermal flows are investigated.

The investigations of rarefied gas flows through micro- and nano-channels are essential to many practical applications [1–3]. Such flows can be correctly described on the basis of the kinetic Boltzmann equation or the model kinetic equation [1]. For example, a series of investigations [5–10] were carried out for the cylindrical channel using the S-model of the kinetic Boltzmann equation [4]. In [5–7] numerical solutions of the problem of steady-state nonisothermal rarefied gas flow through a long circular cross-section pipe were obtained without regard for the end effects on the basis of the linearized S-model. In [5–7] the gas temperature and pressure distributions along the channel were assumed to be linear. In the complete formulation without simplifying assumptions the problem was solved in [8–10] for fairly long pipes using the finite difference method in the entire flow region. In particular, in [9] the effect of the pipe length on the distributions of macroscopic quantities (density, temperature, mass velocity, and gas mass flow) along the pipe axis was analyzed when gas flows out from the high-pressure section into a vacuum and a comparison with the results obtained in accordance with the methods presented in [1] was carried out. Using these methods (see, e.g., [2, 12]) the end effects, including the processes proceeding in the containers, are neglected. The gas mass flow is determined locally in each of the pipe cross-sections from the linear theory of infinite pipe and the pressure distribution along the pipe is determined by integrating the one-dimensional continuity equation with the boundary conditions of equality of the pressure to the corresponding pressures in the containers connected by the pipe under consideration. In this case the temperature distribution is assumed to be specified by the boundary conditions. In [9] it was shown that the simplified formulation of the problem without regard for one or both boundary conditions at the pipe ends and the approximate method for calculating the gas mass flow can be used only for fairly long pipes and fairly rarefied gases. The applicability criterion is determined by the ratio of the rarefaction parameter to the dimensionless channel length.

The aim of the present study is to solve the problem of steady-state nonisothermal gas flow through a long circular cross-section pipe at given pressures and temperatures at the pipe ends in the simplified formulation [1] with the use of the semianalytic method. In the present study the S-model is used as the basic equation and the diffuse reflection model is used as the boundary condition on the channel walls. In the formulation [6] the solution of the linear problem with the diffuse boundary conditions is found using the collocation method for the Chebyshev polynomials and rational functions [13, 14], the gas mass and heat fluxes caused by the gas pressure and temperature gradients in the channel are calculated over the entire Knudsen number range, and the comparison with the results of [2, 5–7, 11] is carried out. The solution of the nonlinear problem of the pressure distribution is found numerically using the Runge–Kutta method for a given linear temperature distribution which holds when the wall thermal conductivity and thickness do not vary along the channel. A particular attention is payed to recovery of the gas pressure distribution in the channel. As follows from the numerical calculations performed, the semianalytic method proposed makes it possible to diminish significantly the calculation volume due to the preliminary elaboration of construction of the solution of the model equation.

1. FORMULATION OF THE PROBLEM. KINETIC EQUATION

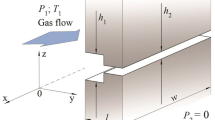
We will consider rarefied gas flow from one container to another when the containers are connected by a long cylindrical channel of radius $R'$. In the first and second containers the pressure and the temperature remain constant and are equal to ${{p}_{1}}$, ${{T}_{1}}$ and ${{p}_{2}}$, ${{T}_{2}}$, respectively. We will assume that ${{p}_{2}} > {{p}_{1}}$ and ${{T}_{2}} > {{T}_{1}}$. The $z'$ axis is directed along the channel axis. We will consider gas flow in the middle part of channel. We will assume that the channel length $L' \gg R'$. The temperature distribution in the channel is determined by the wall temperature [1]. The dimensionless gas pressure and temperature gradients are assumed to be small in absolute value:

$${{G}_{p}} = \frac{{R'}}{{{{p}_{0}}}}\frac{{dp}}{{dz'}},\quad {\text{|}}{{G}_{p}}{\text{|}} \ll 1,\quad {{G}_{T}} = \frac{{R'}}{{{{T}_{0}}}}\frac{{dT}}{{dz'}},\quad {\text{|}}{{G}_{T}}{\text{|}} \ll 1,$$

(1.1)

where ${{p}_{0}}$ and ${{T}_{0}}$ are the gas pressure and temperature at a certain point taken as the origin. The radius $R'$ of the cylindrical channel is taken as the dimensional length scale. In what follows, the dimensional quantities will be denoted without prime. In the linear approximation for the gas pressure and temperature as functions of z we obtain the following expressions:

$$p(z) = {{p}_{0}}(1 + {{G}_{p}}z),\quad T(z) = {{T}_{0}}(1 + {{G}_{T}}z).$$

We will determine the state of rarefied gas at the point whose radius-vector ${\mathbf{r}}$ has the coordinates $\rho$, $\varphi$, and $z$ in the cylindrical coordinate system in configuration space using the gas molecule distribution function $f({\mathbf{r}},{\mathbf{C}})$, where ${\mathbf{C}} = {{\beta }^{{1/2}}}{\mathbf{v}}$ is the dimensionless molecular velocity, $\beta = m{\text{/}}(2{{k}_{{\text{B}}}}{{T}_{0}})$, ${{k}_{{\text{B}}}}$ is the Boltzmann constant, and m is the gas molecular mass. In the velocity space we will also use the cylindrical coordinates $({{C}_{ \bot }},\psi ,{{C}_{z}})$: ${{C}_{\rho }} = {{C}_{ \bot }}\cos\psi$, ${{C}_{\varphi }} = {{C}_{ \bot }}\sin\psi$, and C_z. Since the dimensionless pressure and temperature gradients are small, in the linear approximation the distribution function $f({\mathbf{r}},{\mathbf{C}})$ takes the form [15]:

$$f({\mathbf{r}},{\mathbf{C}}) = {{f}_{0}}(C)\left( {1 + {{G}_{T}}\left( {{{C}^{2}} - \frac{5}{2}} \right)z + {{G}_{p}}z + h(\rho ,{\mathbf{C}})} \right),$$

(1.2)

where ${{f}_{0}}(C) = {{n}_{0}}{{(\beta {\text{/}}\pi )}^{{3/2}}}\exp( - {{C}^{2}})$ is the absolute Maxwellian distribution function and n₀ is the gas number density at the origin. The perturbation function $h(\rho ,{\mathbf{C}})$ can be represented as the sum in which the terms are related to ${{G}_{p}}$ and ${{G}_{T}}$:

$$h(\rho ,{\mathbf{C}}) = {{G}_{p}}{{h}_{1}}(\rho ,{\mathbf{C}}) + {{G}_{T}}{{h}_{2}}(\rho ,{\mathbf{C}}).$$

(1.3)

Following [1, 16], we introduce the dimensionless components of the mass velocity of gas and the heat flux vector

$${{U}_{z}} = {{\beta }^{{1/2}}}{{u}_{z}},\quad {{q}_{z}} = \frac{{{{\beta }^{{1/2}}}}}{{{{p}_{0}}}}q_{z}^{'}.$$

(1.4)

Here, ${{u}_{z}}$ and $q_{z}^{'}$ denote the corresponding dimensional quantities [16]

$${{u}_{z}}({\mathbf{r}}) = \frac{1}{{n(z)}}\int {{{v}_{z}}f({\mathbf{r}},{\mathbf{C}}){{d}^{3}}{\mathbf{v}}} ,$$

(1.5)

$$q_{z}^{'}({\mathbf{r}}) = \frac{m}{2}\int {\left( {{{v}_{z}} - {{u}_{z}}} \right){{{\left( {v - u} \right)}}^{2}}f({\mathbf{r}},{\mathbf{C}}){{d}^{3}}{\mathbf{v}}} ,$$

(1.6)

where $n(z)$ is the gas molecular number density.

Substituting (1.2) in (1.5) and (1.6) and taking (1.3) into account, for the dimensionless components (1.4) we obtain

$${{U}_{z}}(\rho ) = {{G}_{p}}{{U}_{{z,1}}}(\rho ) + {{G}_{T}}{{U}_{{z,2}}}(\rho ),\quad {{q}_{z}}(\rho ) = {{G}_{p}}{{q}_{{z,1}}}(\rho ) + {{G}_{T}}{{q}_{{z,2}}}(\rho ),$$

$${{U}_{{z,i}}}(\rho ) = \frac{1}{{{{\pi }^{{3/2}}}}}\int {\exp( - {{C}^{2}}){{C}_{z}}{{h}_{i}}(\rho ,{\mathbf{C}}){{d}^{3}}{\mathbf{C}}} ,\quad i = 1,2,$$

(1.7)

$${{q}_{{z,i}}}(\rho ) = \frac{1}{{{{\pi }^{{3/2}}}}}\int {\exp( - {{C}^{2}}){{C}_{z}}\left( {{{C}^{2}} - \frac{5}{2}} \right){{h}_{i}}(\rho ,{\mathbf{C}}){{d}^{3}}{\mathbf{C}}} ,\quad i = 1,2.$$

(1.8)

Here, ${{U}_{{z,1}}}$ and ${{q}_{{z,1}}}$ determine the mass velocity and the component of the heat flux vector as a result of the presence of the pressure gradient for isothermal gas channel flow, while ${{U}_{{z,2}}}$ and ${{q}_{{z,2}}}$ represent their values for isobaric flow caused by the temperature gradient.

In the first stage of investigation our aim is to find the reduced gas mass and heat fluxes which depend on G_p and ${{G}_{T}}$

$$\begin{gathered} {{J}_{M}} = \frac{{J_{M}^{'}}}{{\pi R{\kern 1pt} {{'}^{2}}{\kern 1pt} p(z)}}\sqrt {\frac{{2{{k}_{{\text{B}}}}T(z)}}{m}} = {{G}_{p}}{{J}_{{M,1}}} + {{G}_{T}}{{J}_{{M,2}}} \\ {{J}_{Q}} = \frac{{2J_{Q}^{'}}}{{\pi R{\kern 1pt} {{'}^{2}}{\kern 1pt} p(z)}}\sqrt {\frac{m}{{2{{k}_{{\text{B}}}}T(z)}}} = {{G}_{p}}{{J}_{{Q,1}}} + {{G}_{T}}{{J}_{{Q,2}}} \\ \end{gathered} $$

(1.9)

Here, primes denote the dimensional fluxes. The coefficients ${{J}_{{M,i}}}$ and ${{J}_{{Q,i}}}$ (i = 1, 2) are the dimensionless factors of proportionality between the fluxes across a channel cross-section and the local pressure and temperature gradients G_p and G_T

$${{J}_{{M,i}}} = 4\int\limits_0^1 \,{{U}_{{z,i}}}(\rho )\rho d\rho ,\quad {{J}_{{Q,i}}} = 4\int\limits_0^1 \,{{q}_{{z,i}}}(\rho )\rho d\rho ,\quad i = 1,2.$$

(1.10)

As the basic equation that describes kinetics of the processes, we will use the S-model of the kinetic Boltzmann equation in the cylindrical coordinate system [6, 17]

$$\begin{gathered} \left( {\frac{{\partial h}}{{\partial \rho }}\cos\psi - \frac{{\partial h}}{{\partial \psi }}\frac{{\sin\psi }}{\rho }} \right){{C}_{ \bot }} + {{G}_{T}}\left( {{{C}^{2}} - \frac{5}{2}} \right){{C}_{z}} + {{G}_{p}}{{C}_{z}} + \delta h(\rho ,{\mathbf{C}}) \\ = \frac{\delta }{{{{\pi }^{{3/2}}}}}\int {K({\mathbf{C}},{\mathbf{C}}')\exp( - {{C}^{{'2}}})h(\rho ,{\mathbf{C}}'){{d}^{3}}{\mathbf{C}}'} \\ \end{gathered} $$

(1.11)

where $\delta = {\text{K}}{{{\text{n}}}^{{ - 1}}}$ is the gas rarefaction parameter, ${\text{Kn}} = {{l}_{g}}{\text{/}}R'$ is the Knudsen number, ${{l}_{g}} = {{\eta }_{g}}{{\beta }^{{ - 1/2}}}{\text{/}}p$ is the molecular mean free path, ${{\eta }_{g}}$ is the dynamic gas viscosity, and $K({\mathbf{C}},{\mathbf{C}}')$ is the kernel of this equation [17]

$$K({\mathbf{C}},{\mathbf{C}}') = \frac{4}{{15}}{\mathbf{CC}}'\left( {{{C}^{{'2}}} - \frac{5}{2}} \right)\left( {{{C}^{2}} - \frac{5}{2}} \right) + 2{\mathbf{C}}'{\mathbf{C}} + \frac{2}{3}\left( {{{C}^{{'2}}} - \frac{3}{2}} \right)\left( {{{C}^{2}} - \frac{3}{2}} \right) + 1.$$

We will multiply the left- and right-hand sides of Eq. (1.11) by $C_{z}^{k}\exp( - C_{z}^{2}){\text{/}}\sqrt \pi$ (k = 1, 3) and integrate it with respect to C_z from $- \infty$ to $+ \infty$. With regard to (1.3), (1.7), and (1.8) the equations thus obtained can be reduced to two independent systems of equations. For restoration of the mass velocity ${{U}_{{z,1}}}(\rho )$ and the component of the heat flux vector ${{q}_{{z,1}}}(\rho )$ the system of equations takes the form:

$$\left( {\frac{{\partial {{Z}_{{1,1}}}}}{{\partial \rho }}\zeta + \frac{{\partial {{Z}_{{1,1}}}}}{{\partial \zeta }}\frac{{(1 - {{\zeta }^{2}})}}{\rho }} \right){{C}_{ \bot }} + \delta {{Z}_{{1,1}}}(\rho ,{{C}_{ \bot }},\zeta ) + \frac{1}{2} = \delta \left( {{{U}_{{z,1}}}(\rho ) + \frac{2}{{15}}{{q}_{{z,1}}}(\rho )(C_{ \bot }^{2} - 1)} \right),$$

(1.12)

$$\left( {\frac{{\partial {{Z}_{{2,1}}}}}{{\partial \rho }}\zeta + \frac{{\partial {{Z}_{{2,1}}}}}{{\partial \zeta }}\frac{{(1 - {{\zeta }^{2}})}}{\rho }} \right){{C}_{ \bot }} + \delta {{Z}_{{2,1}}}(\rho ,{{C}_{ \bot }},\zeta ) + \frac{3}{4} = \delta \left( {\frac{3}{2}{{U}_{{z,1}}}(\rho ) + \frac{1}{5}{{q}_{{z,1}}}(\rho )C_{ \bot }^{2}} \right),$$

(1.13)

where $\zeta = \cos\psi$ and

$${{Z}_{{1,i}}}(\rho ,{{C}_{ \bot }},\zeta ) = \frac{1}{{\sqrt \pi }}\int\limits_{ - \infty }^{ + \infty } \,\exp( - C_{z}^{2}){{C}_{z}}{{h}_{i}}(\rho ,{\mathbf{C}})d{{C}_{z}},$$

(1.14)

$${{Z}_{{2,i}}}(\rho ,{{C}_{ \bot }},\zeta ) = \frac{1}{{\sqrt \pi }}\int\limits_{ - \infty }^{ + \infty } \,\exp( - C_{z}^{2})C_{z}^{3}{{h}_{i}}(\rho ,{\mathbf{C}})d{{C}_{z}},\quad i = 1,2.$$

(1.15)

The components ${{U}_{{z,i}}}(\rho )$ and ${{q}_{{z,i}}}(\rho )$ (i = 1, 2) can be expressed in terms of the functions introduced above ${{Z}_{{k,i}}}(\rho ,{{C}_{ \bot }},\zeta )$ ($k,i = 1,2$) as follows:

$${{U}_{{z,i}}}(\rho ) = \frac{2}{\pi }\int\limits_0^{ + \infty } \,\exp( - C_{ \bot }^{2}){{C}_{ \bot }}\int\limits_{ - 1}^1 \,\frac{1}{{\sqrt {1 - {{\zeta }^{2}}} }}{{Z}_{{1,i}}}(\rho ,{{C}_{ \bot }},\zeta )d\zeta d{{C}_{ \bot }},$$

(1.16)

$$\begin{gathered} {{q}_{{z,i}}}(\rho ) = \frac{2}{\pi }\int\limits_0^{ + \infty } \,\exp( - C_{ \bot }^{2}){{C}_{ \bot }}\int\limits_{ - 1}^1 \,\frac{1}{{\sqrt {1 - {{\zeta }^{2}}} }}{{Z}_{{2,i}}}(\rho ,{{C}_{ \bot }},\zeta )d\zeta d{{C}_{ \bot }} - \frac{5}{2}{{U}_{{z,i}}}(\rho ) \\ \, + \frac{2}{\pi }\int\limits_0^{ + \infty } \,\exp( - C_{ \bot }^{2})C_{ \bot }^{3}\int\limits_{ - 1}^1 \,\frac{1}{{\sqrt {1 - {{\zeta }^{2}}} }}{{Z}_{{1,i}}}(\rho ,{{C}_{ \bot }},\zeta )d\zeta d{{C}_{ \bot }}. \\ \end{gathered} $$

(1.17)

For restoration of ${{U}_{{z,2}}}(\rho )$ and ${{q}_{{z,2}}}(\rho )$ the system of equations take the form:

$$\left( {\frac{{\partial {{Z}_{{1,2}}}}}{{\partial \rho }}\zeta + \frac{{\partial {{Z}_{{1,2}}}}}{{\partial \zeta }}\frac{{(1 - {{\zeta }^{2}})}}{\rho }} \right){{C}_{ \bot }} + \delta {{Z}_{{1,2}}}(\rho ,{{C}_{ \bot }},\zeta ) + \frac{{C_{ \bot }^{2} - 1}}{2} = \delta \left( {{{U}_{{z,2}}}(\rho ) + \frac{2}{{15}}{{q}_{{z,2}}}(\rho )(C_{ \bot }^{2} - 1)} \right),$$

$$\left( {\frac{{\partial {{Z}_{{2,2}}}}}{{\partial \rho }}\zeta + \frac{{\partial {{Z}_{{2,2}}}}}{{\partial \zeta }}\frac{{(1 - {{\zeta }^{2}})}}{\rho }} \right){{C}_{ \bot }} + \delta {{Z}_{{2,2}}}(\rho ,{{C}_{ \bot }},\zeta ) + \frac{{3C_{ \bot }^{2}}}{4} = \delta \left( {\frac{3}{2}{{U}_{{z,2}}}(\rho ) + \frac{1}{5}{{q}_{{z,2}}}(\rho )C_{ \bot }^{2}} \right).$$

As the boundary condition on the channel surface Γ, we will use the diffuse reflection model [16]

$${{f}^{ + }}({{{\mathbf{r}}}_{\Gamma }},{\mathbf{C}}) = {{f}_{\Gamma }}({{{\mathbf{r}}}_{\Gamma }},{\mathbf{C}}),\quad {\mathbf{C}}{{{\mathbf{e}}}_{n}} > 0.$$

Here, ${{f}^{ + }}({{{\mathbf{r}}}_{\Gamma }},{\mathbf{C}})$ is the distribution function of the gas molecules reflected from the channel surface, e_n is the unit vector normal to this surface directed towards the gas, and ${{f}_{\Gamma }}({{{\mathbf{r}}}_{\Gamma }},{\mathbf{C}})$ is the locally equilibrium distribution function [18]

$${{f}_{\Gamma }}({{{\mathbf{r}}}_{\Gamma }},{\mathbf{C}}) = {{n}_{\Gamma }}(z)\mathop {\left( {\frac{m}{{2\pi {{k}_{B}}{{T}_{\Gamma }}(z)}}} \right)}\nolimits^{3/2} \exp\left( { - \frac{{{{T}_{0}}}}{{{{T}_{\Gamma }}(z)}}{{{\mathbf{C}}}^{2}}} \right),$$

(1.18)

where ${{T}_{\Gamma }}(z)$ is the gas temperature on the channel surface and ${{n}_{\Gamma }}(z)$ is the gas molecular number density in the neighborhood of the channel walls. In view of smallness of ${{G}_{p}}$ and ${{G}_{T}}$, we will linearize (1.9) the function (1.18) about the absolute Maxwellian distribution function ${{f}_{0}}(C)$ [1]. As a result, taking (1.2) and (1.3) into account, for the functions ${{Z}_{{k,i}}}(\rho ,{{C}_{ \bot }},\zeta )$ (k, i = 1, 2) we obtain the following boundary conditions:

$${{Z}_{{k,i}}}(1,{{C}_{ \bot }},\zeta ) = 0,\quad \zeta < 0,\quad i,k = 1,2.$$

(1.19)

2. SOLUTION TO THE BOUNDARY-VALUE PROBLEM. GAS FLOWS AT SMALL PRESSURE AND TEMPERATURE DROPS

We will find the solution to the system of equations (1.12) and (1.13) with the boundary conditions (1.19). We will expand the unknown function ${{Z}_{{1,i}}}(\rho ,{{C}_{ \bot }},\zeta )$ (i = 1, 2) in a series in the Chebyshev polynomials and rational functions

$${{Z}_{{1,i}}}(\rho ,{{C}_{ \bot }},\zeta ) = \sum\limits_{{\mathbf{j}} = 0}^\infty \,a_{{\mathbf{j}}}^{{(i)}}{{T}_{{{{j}_{1}}}}}({{\rho }^{*}}){{T}_{{{{j}_{2}}}}}(\zeta ){{T}_{{{{j}_{3}}}}}(C_{ \bot }^{*}),$$

(2.1)

$$\rho {\text{*}} = 2\rho - 1,\quad C_{ \bot }^{*} = \frac{{{{C}_{ \bot }} - 1}}{{{{C}_{ \bot }} + 1}},$$

(2.2)

where ${\mathbf{j}} = ({{j}_{1}},{{j}_{2}},{{j}_{3}})$. In order to determine ${{T}_{j}}(x)$ in expansion (2.1) we will use the recurrence relations [13]

$${{T}_{0}}(x) = 1,\quad {{T}_{1}}(x) = x,\quad {{T}_{j}}(x) = 2x{{T}_{{j - 1}}}(x) - {{T}_{{j - 2}}}(x),\quad j \geqslant 2.$$

Restricting our attention in expansion (2.1) to the terms with the numbers ${{j}_{k}} \leqslant {{n}_{k}}$ ($k = \overline {1,3}$), we obtain

$${{Z}_{{1,i}}}(\rho ,{{C}_{ \bot }},\zeta ) = \sum\limits_{{\mathbf{j}} = 0}^{\mathbf{n}} \,{{a}_{{\mathbf{j}}}}{{T}_{{{{j}_{1}}}}}(\rho {\text{*}}){{T}_{{{{j}_{2}}}}}(\zeta ){{T}_{{{{j}_{3}}}}}(C_{ \bot }^{*}) = {{{\mathbf{T}}}_{1}}(\rho {\text{*}}){\mathbf{Q}}(\zeta ){\mathbf{W}}(C_{ \bot }^{*}){{{\mathbf{A}}}_{{\mathbf{i}}}},\quad i = 1,2.$$

(2.3)

Here, ${\mathbf{n}} = ({{n}_{1}},{{n}_{2}},{{n}_{3}})$ and $n_{k}^{'} = {{n}_{k}} + 1$ ($k = \overline {1,3}$)

$${{{\mathbf{T}}}_{{\mathbf{k}}}} = {{{\mathbf{T}}}_{{1 \times n_{k}^{'}}}},\quad {{{\mathbf{T}}}_{{1 \times n}}}(x) = \left( {{{T}_{0}}(x){{T}_{1}}(x) \ldots {{T}_{n}}(x)} \right),$$

(2.4)

${\mathbf{Q}}(\zeta )$ and ${\mathbf{W}}({{C}_{ \bot }})$ are the block diagonal matrices

$${\mathbf{Q}}(\zeta ) = {{\Phi }_{{n_{1}^{'} \times n_{1}^{'}n_{2}^{'}}}}(\zeta ),\quad {\mathbf{W}}(C_{ \bot }^{*}) = {{\Phi }_{{n_{1}^{'}n_{2}^{'} \times n_{1}^{'}n_{2}^{'}n_{3}^{'}}}}(C_{ \bot }^{*}),$$

(2.5)

$${{\Phi }_{{m \times mn}}}(x) = {\text{diag}}\left( {{{{\mathbf{T}}}_{{1 \times n}}}(x),{{{\mathbf{T}}}_{{1 \times n}}}(x), \ldots {{{\mathbf{T}}}_{{1 \times n}}}(x)} \right),$$

(2.6)

and ${{{\mathbf{A}}}_{{\mathbf{i}}}} = {{{\mathbf{A}}}_{{{\mathbf{i}}n_{1}^{'}n_{2}^{'}n_{3}^{'} \times 1}}}$ is the unknown column matrix ($i = 1,2$)

$${{{\mathbf{A}}}_{{\mathbf{i}}}} = \mathop {(a_{{000}}^{{(i)}}a_{{001}}^{{(i)}} \ldots a_{{00{{n}_{3}}}}^{{(i)}} \ldots a_{{{{n}_{1}}{{n}_{2}}0}}^{{(i)}}a_{{{{n}_{1}}{{n}_{2}}1}}^{{(i)}} \ldots a_{{{{n}_{1}}{{n}_{2}}{{n}_{3}}}}^{{(i)}})}\nolimits^T .$$

(2.7)

The derivatives of ${{{\mathbf{T}}}_{1}}(\rho {\text{*}})$ with respect to the variable ρ and of ${{{\mathbf{T}}}_{2}}(\zeta )$ with respect to ζ can be determined as follows:

$$\frac{{d{{{\mathbf{T}}}_{1}}(\rho {\text{*}})}}{{d\rho }} = 2{{{\mathbf{T}}}_{1}}(\rho {\text{*}}){{{\mathbf{J}}}_{1}},\quad \frac{{d{{{\mathbf{T}}}_{2}}(\zeta )}}{{d\zeta }} = {{{\mathbf{T}}}_{2}}(\zeta ){{{\mathbf{J}}}_{2}},$$

(2.8)

where ${{{\mathbf{J}}}_{{\mathbf{k}}}} = {{{\mathbf{J}}}_{{n_{k}^{'} \times n_{k}^{'}}}}$ is the matrix (k = 1, 2) whose nonzero elements can be calculated from the following formulas [19]

$${{({{J}_{k}})}_{{i,j + 1}}} = \left\{ \begin{gathered} j,\quad i = 1\;\;(j\;{\text{is}}\,{\text{odd}}) \hfill \\ 2j,\quad j > i - 1\;\;(i\;{\text{is}}\,{\text{even}},j\;{\text{is}}\,{\text{even}}) \hfill \\ 2j,\quad j > i - 1,\quad i > 1\;\;(i\;{\text{is}}\,{\text{odd}},j\;{\text{is}}\,{\text{odd}}). \hfill \\ \end{gathered} \right.$$

(2.9)

For example, in accordance with (2.9), for ${{n}_{1}} = 5$$(n_{1}^{'} = 6)$ we obtain

$${{{\mathbf{J}}}_{1}} = \left( {\begin{array}{*{20}{c}} 0&1&0&3&0&5 \\ 0&0&4&0&8&0 \\ 0&0&0&6&0&{10} \\ 0&0&0&0&8&0 \\ 0&0&0&0&0&{10} \\ 0&0&0&0&0&0 \end{array}} \right).$$

Substituting (2.3) in (1.16) and (1.17), for the components ${{U}_{{z,1}}}(\rho {\text{*}})$ and ${{q}_{{z,1}}}(\rho {\text{*}})$ we arrive at the following expressions:

$${{U}_{{z,1}}}(\rho {\text{*}}) = 4{{{\mathbf{P}}}_{1}}(\rho {\text{*}}){{{\mathbf{A}}}_{1}},$$

(2.10)

$${{q}_{{z,1}}}(\rho {\text{*}}) = 4\left( {{{{\mathbf{P}}}_{3}}(\rho {\text{*}}) - \frac{5}{2}{{{\mathbf{P}}}_{1}}(\rho {\text{*}})} \right){{{\mathbf{A}}}_{1}} + 4{{{\mathbf{P}}}_{1}}(\rho {\text{*}}){{{\mathbf{A}}}_{2}}.$$

(2.11)

Here, P_i (i = 1, 3) are the $1 \times n_{1}^{'}n_{2}^{'}n_{3}^{'}$ matrices whose nonzero elements can be determined as follows:

$$\begin{gathered} {{({{P}_{i}})}_{{1,n_{2}^{'}n_{3}^{'}{{j}_{1}} + {{j}_{3}} + 1}}}(\rho {\text{*}}) = {{I}_{{i,{{j}_{3}}}}}{{({{T}_{1}})}_{{1,{{j}_{1}} + 1}}}(\rho {\text{*}}),\quad {{j}_{{1,3}}} = \overline {0,{{n}_{{1,3}}}} , \\ 2{{I}_{{i,{{j}_{3}}}}} = \int\limits_0^{ + \infty } \,\exp( - C_{ \bot }^{2})C_{ \bot }^{i}{{T}_{{{{j}_{3}}}}}(C_{ \bot }^{*})d{{C}_{ \bot }}. \\ \end{gathered} $$

(2.12)

Expression (2.12) is obtained with regard to orthogonality of the polynomials $\{ {{T}_{{{{j}_{2}}}}}(\zeta )\}$ (${{j}_{2}} = \overline {0,{{n}_{2}}}$). The integrals ${{I}_{{i,{{j}_{3}}}}}$ (i = 1, 2, ${{j}_{3}} = \overline {0,{{n}_{3}}}$) can be found numerically from the formula

$${{I}_{{i,{{j}_{3}};n}}} = \frac{4}{n}{{\sum\limits_{k = 0}^n }}{''{\tau }_{{{\text{ex}}}}}({{\hat {C}}_{{ \bot ,k}}},n){{w}_{i}}({{\hat {C}}_{{ \bot ,k}}}){{T}_{{{{j}_{3}}}}}({{\hat {C}}_{{ \bot ,k}}}),\quad {{\tau }_{{{\text{ex}}}}}(C_{ \bot }^{*},n) = {{\sum\limits_{j = 0}^{n/2} }}{''\frac{{{{T}_{j}}({{{\hat {C}}}_{ \bot }})}}{{1 - 4{{j}^{2}}}}},$$

(2.13)

$${{w}_{i}}(C_{ \bot }^{*}) = \frac{{\exp\left( { - \tfrac{{{{{(1 + C_{ \bot }^{*})}}^{2}}}}{{{{{(1 - C_{ \bot }^{*})}}^{2}}}}} \right){{{(1 + C_{ \bot }^{*})}}^{i}}}}{{{{{(1 - C_{ \bot }^{*})}}^{{i + 2}}}}},$$

$${{\hat {C}}_{{ \bot ,k}}} = \cos\left( {\frac{{\pi (n - k)}}{n}} \right),\quad k = \overline {0,n} ,$$

where ${{\sum\limits_{k = 0}^{n}{''}}}$ is meant the sum in which the first and last terms are multiplied by 1/2.

In (2.13) n is even. For n = 40 the absolute difference of the values of ${{I}_{{i,{{j}_{3}}}}}$ (i = 1, 3, ${{j}_{3}} = \overline {0,{{n}_{3}}}$) obtained with the use of (2.13) and the Gauss method is not greater than 10^–9.

Expressing the variables $\rho$ and ${{C}_{ \bot }}$ from equalities (2.2) in terms of $\rho {\text{*}}$ and $C_{ \bot }^{*}$ and taking into account (2.3)–(2.11), we can transform the system of equations (1.12) and (1.13) to the form:

$${{\Lambda }_{1}}(\rho {\text{*}},\zeta ,C_{ \bot }^{*}){{{\mathbf{A}}}_{1}} + {{\Lambda }_{2}}(\rho {\text{*}},C_{ \bot }^{*}){{{\mathbf{A}}}_{2}} = - \frac{1}{2},$$

(2.14)

$${{\Delta }_{1}}(\rho {\text{*}},C_{ \bot }^{*}){{{\mathbf{A}}}_{1}} + {{\Delta }_{2}}(\rho {\text{*}},\zeta ,C_{ \bot }^{*}){{{\mathbf{A}}}_{2}} = - \frac{3}{4}.$$

(2.15)

Here, the matrices ${{\Lambda }_{{\mathbf{i}}}}$ and ${{\Delta }_{{\mathbf{i}}}}$ (i = 1, 2) are of the $1 \times n_{1}^{'}n_{2}^{'}n_{3}^{'}$ dimension and can be determined as follows:

$$\begin{gathered} {{\Lambda }_{1}}(\rho {\text{*}},\zeta ,C_{ \bot }^{*}) = \left( {{{\Psi }_{1}}(\rho {\text{*}},\zeta ) + \frac{{C_{ \bot }^{*} + 1}}{{1 - C_{ \bot }^{*}}}{{\Psi }_{2}}(\rho {\text{*}},\zeta )} \right){\mathbf{W}}(C_{ \bot }^{*}) \\ \, - 4\delta {{{\mathbf{P}}}_{1}}(\rho {\text{*}}) + \frac{4}{3}\delta \left( {\frac{{{{{(C_{ \bot }^{*} + 1)}}^{2}}}}{{{{{(1 - C_{ \bot }^{*})}}^{2}}}} - 1} \right)\left( {{{{\mathbf{P}}}_{1}}(\rho {\text{*}}) - \frac{2}{5}{{{\mathbf{P}}}_{3}}(\rho {\text{*}})} \right), \\ \end{gathered} $$

$${{\Psi }_{1}}(\rho {\text{*}},\zeta )\delta {{{\mathbf{T}}}_{1}}(\rho {\text{*}}){\mathbf{Q}}(\zeta ),\quad {{\Psi }_{2}}(\rho {\text{*}},\zeta ) = 2\zeta {{{\mathbf{T}}}_{1}}(\rho {\text{*}}){{{\mathbf{J}}}_{1}}{\mathbf{Q}}(\zeta ) + \frac{{2(1 - {{\zeta }^{2}})}}{{\rho {\text{*}} + 1}}{{{\mathbf{T}}}_{1}}(\rho {\text{*}}){\mathbf{Q}}'(\zeta ),$$

$${\mathbf{Q'}}(\zeta ) = {\text{diag}}\left( {{{{\mathbf{T}}}_{2}}(\zeta ){{{\mathbf{J}}}_{2}},{{{\mathbf{T}}}_{2}}(\zeta ){{{\mathbf{J}}}_{2}}, \ldots {{{\mathbf{T}}}_{2}}(\zeta ){{{\mathbf{J}}}_{2}}} \right),$$

$${{\Lambda }_{2}}(\rho {\text{*}},C_{ \bot }^{*}) = \frac{8}{{15}}\delta \left( {1 - \frac{{{{{(C_{ \bot }^{*} + 1)}}^{2}}}}{{{{{(1 - C_{ \bot }^{*})}}^{2}}}}} \right){{{\mathbf{P}}}_{1}}(\rho {\text{*}}),$$

$${{\Delta }_{1}}(\rho {\text{*}},C_{ \bot }^{*})\frac{{2\delta {{{(C_{ \bot }^{*} + 1)}}^{2}}}}{{{{{(1 - C_{ \bot }^{*})}}^{2}}}}\left( {{{{\mathbf{P}}}_{1}}(\rho {\text{*}}) - \frac{2}{5}{{{\mathbf{P}}}_{3}}(\rho {\text{*}})} \right) - 6\delta {{{\mathbf{P}}}_{1}}(\rho {\text{*}}),$$

$${{\Delta }_{2}}(\rho {\text{*}},\zeta ,C_{ \bot }^{*}) = \left( {{{\Psi }_{1}}(\rho {\text{*}},\zeta ) + \frac{{C_{ \bot }^{*} + 1}}{{1 - C_{ \bot }^{*}}}{{\Psi }_{2}}(\rho {\text{*}},\zeta )} \right){\mathbf{W}}(C_{ \bot }^{*}) - \frac{{4\delta {{{(C_{ \bot }^{*} + 1)}}^{2}}}}{{5{{{(1 - C_{ \bot }^{*})}}^{2}}}}{{{\mathbf{P}}}_{1}}(\rho {\text{*}}).$$

The boundary conditions (1.19) can be written in the form:

$$\Omega (1,\zeta ,C_{ \bot }^{*}){{{\mathbf{A}}}_{{\mathbf{j}}}} = 0,\quad {{\Omega }_{{1 \times n_{1}^{'}n_{2}^{'}n_{3}^{'}}}}(1,\zeta ,C_{ \bot }^{*}) = {{{\mathbf{T}}}_{1}}(1){\mathbf{Q}}(\zeta ){\mathbf{W}}(C_{ \bot }^{*}),\quad \zeta < 0,\quad j = 1,2.$$

(2.16)

We now multiply Eqs. (2.14), (2.15), and (2.16) by ${{w}_{i}}(C_{ \bot }^{*})$ ($i = \overline {0,{{n}_{3}}}$) and integrate with respect to $C_{ \bot }^{*}$ from –1 to 1. As a result, we obtain

$$\Lambda _{{1,{\mathbf{i}}}}^{'}(\rho {\text{*}},\zeta ){{{\mathbf{A}}}_{1}} + \Lambda _{{2,{\mathbf{i}}}}^{'}(\rho {\text{*}}){{{\mathbf{A}}}_{2}} = - \frac{1}{2}{{I}_{{i,0}}},\quad i = \overline {0,{{n}_{3}}} ,$$

(2.17)

$$\Delta _{{1,{\mathbf{i}}}}^{'}(\rho {\text{*}}){{{\mathbf{A}}}_{1}} + \Delta _{{2,{\mathbf{i}}}}^{'}(\rho {\text{*}},\zeta ){{{\mathbf{A}}}_{2}} = - \frac{3}{4}{{I}_{{i,0}}},\quad i = \overline {0,{{n}_{3}}} ,$$

(2.18)

$$\Omega _{{\mathbf{i}}}^{'}(1,\zeta ){{{\mathbf{A}}}_{{\mathbf{j}}}} = 0,\quad \Omega _{{\mathbf{i}}}^{'}(1,\zeta ) = {{{\mathbf{T}}}_{1}}(1){\mathbf{Q}}(\zeta ){\mathbf{W}}_{{\mathbf{i}}}^{'},\quad \zeta < 0,\quad j = 1,2;\quad i = \overline {0,{{n}_{3}}} .$$

(2.19)

Here,

$$\Lambda _{{1,{\mathbf{i}}}}^{'}(\rho {\text{*}},\zeta ) = {{\Psi }_{1}}(\rho {\text{*}},\zeta ){\mathbf{W}}_{{\mathbf{i}}}^{'} + {{\Psi }_{2}}(\rho {\text{*}},\zeta ){\mathbf{W}}_{{{\mathbf{i}} + 1}}^{'} + \frac{4}{3}\delta {{{\mathbf{P}}}_{1}}(\rho {\text{*}})({{I}_{{i + 2,0}}} - 4{{I}_{{i,0}}}) + \frac{8}{{15}}\delta {{{\mathbf{P}}}_{3}}(\rho {\text{*}})({{I}_{{i,0}}} - {{I}_{{i + 2,0}}}),$$

$$\Lambda _{{2,{\mathbf{i}}}}^{'}(\rho {\text{*}}) = \frac{8}{{15}}\delta ({{I}_{{i,0}}} - {{I}_{{i + 2,0}}}){{{\mathbf{P}}}_{1}}(\rho {\text{*}}),$$

$$\Delta _{{1,{\mathbf{i}}}}^{'}(\rho {\text{*}}) = 2\delta {{{\mathbf{P}}}_{1}}(\rho {\text{*}})({{I}_{{i + 2,0}}} - 3{{I}_{{i,0}}}) - \frac{4}{5}\delta {{{\mathbf{P}}}_{3}}(\rho {\text{*}}){{I}_{{i + 2,0}}},$$

$$\Delta _{{1,{\mathbf{i}}}}^{'}(\rho {\text{*}},\zeta ) = {{\Psi }_{1}}(\rho {\text{*}},\zeta ){\mathbf{W}}_{{\mathbf{i}}}^{'} + {{\Psi }_{2}}(\rho {\text{*}},\zeta ){\mathbf{W}}_{{{\mathbf{i}} + 1}}^{'} - \frac{4}{5}\delta {{{\mathbf{P}}}_{1}}(\rho {\text{*}}){{I}_{{i + 2,0}}},$$

$${\mathbf{W}}_{{{\mathbf{i}}n_{1}^{'}n_{2}^{'} \times n_{1}^{'}n_{2}^{'}n_{3}^{'}}}^{'} = {\text{diag}}\left( {{{{\mathbf{I}}}_{{\mathbf{i}}}},{{{\mathbf{I}}}_{{\mathbf{i}}}} \ldots {{{\mathbf{I}}}_{{\mathbf{i}}}}} \right),\quad {{{\mathbf{I}}}_{{{\mathbf{i}}1 \times n_{{13}}^{'}}}} = \left( {{{I}_{{i,0}}},{{I}_{{i,2}}}, \ldots {{I}_{{i,{{n}_{3}}}}}} \right).$$

As the collocation points, in Eqs. (2.17)–(2.19) we will use the roots of the polynomials ${{T}_{{n_{i}^{'}}}}(x)$ ($i = 1,2$) on the segment $[ - 1;1]$

$${{x}_{{i,k}}} = \cos\left( {\frac{{\pi (2{{n}_{i}} - 2{{k}_{i}} + 1)}}{{2({{n}_{i}} + 1)}}} \right),\quad {{k}_{i}} = \overline {0,{{n}_{i}}} ,\quad i = 1,2,$$

(2.20)

where ${{x}_{{1,k}}} = \rho _{{{{k}_{1}}}}^{*}$ and ${{x}_{{2,k}}} = {{\zeta }_{{{{k}_{2}}}}}$.

Substituting (2.20) in (2.17), we arrive at the system of linear $n_{1}^{'}n_{2}^{'}n_{3}^{'}$ equations in which we replace the equations with $\rho {\text{*}} = \rho _{{{{n}_{1}}}}^{*}$ and $\zeta = {{\zeta }_{{{{k}_{2}}}}}$ by the equations following from the boundary condition (2.19) for Z_{1, 1} with the values of variables ρ* = 1 and $\zeta = {{\zeta }_{{{{k}_{2}}}}}$ (${{k}_{2}} = \overline {0,k_{2}^{'}}$). Here, $k_{2}^{'}$ is the subscript such that ${{\zeta }_{{k_{2}^{'}}}} < 0$ and ${{\zeta }_{{k_{{2 + 1}}^{'}}}} \geqslant 0$, i.e., $k_{2}^{'} = {{n}_{2}}{\text{/}}2 - 1$, if n₂ is even and $k_{2}^{'} = ({{n}_{2}} - 1){\text{/}}2$ otherwise.

As a result, we obtain

$${{{\mathbf{B}}}_{1}}{{{\mathbf{A}}}_{1}} + {{{\mathbf{B}}}_{2}}{{{\mathbf{A}}}_{2}} = {{{\mathbf{F}}}_{1}},$$

where ${{B}_{j}}$ (j = 1, 2) are the $n_{1}^{'}n_{2}^{'}n_{3}^{'} \times n_{1}^{'}n_{2}^{'}n_{3}^{'}$ matrices and F₁ is the column ($n_{1}^{'}n_{2}^{'}n_{3}^{'} \times 1$) matrix

$${{{\mathbf{B}}}_{1}} = \left( {\begin{array}{*{20}{c}} {\Lambda _{{1,0}}^{'}(\rho _{0}^{*},{{\zeta }_{0}})} \\ {\Lambda _{{1,1}}^{'}(\rho _{0}^{*},{{\zeta }_{0}})} \\ \ldots \\ {\Lambda _{{1,{{{\mathbf{n}}}_{3}} - 1}}^{'}(\rho _{{{{n}_{1}} - 1}}^{*},{{\zeta }_{{{{n}_{2}}}}})} \\ {\Lambda _{{1,{{{\mathbf{n}}}_{3}}}}^{'}(\rho _{{{{n}_{1}} - 1}}^{*},{{\zeta }_{{{{n}_{2}}}}})} \\ \ldots \\ {\Omega _{0}^{'}(1,{{\zeta }_{0}})} \\ {\Omega _{1}^{'}(1,{{\zeta }_{0}})} \\ \ldots \\ {\Omega _{{{{{\mathbf{n}}}_{3}}}}^{'}(1,{{\zeta }_{{k_{2}^{'}}}})} \\ {\Lambda _{{1,0}}^{'}(\rho _{{{{n}_{1}}}}^{*},{{\zeta }_{{k_{2}^{'} + 1}}})} \\ \ldots \\ {\Lambda _{{1,{{{\mathbf{n}}}_{3}} - 1}}^{'}(\rho _{{{{n}_{1}}}}^{*},{{\zeta }_{{{{n}_{2}}}}})} \\ {\Lambda _{{1,{{{\mathbf{n}}}_{3}}}}^{'}(\rho _{{{{n}_{1}}}}^{*},{{\zeta }_{{{{n}_{2}}}}})} \end{array}} \right),\quad {{{\mathbf{B}}}_{2}} = \left( {\begin{array}{*{20}{c}} {\Lambda _{{2,0}}^{'}(\rho _{0}^{*},{{\zeta }_{0}})} \\ {\Lambda _{{2,1}}^{'}(\rho _{0}^{*},{{\zeta }_{0}})} \\ \ldots \\ {\Lambda _{{2,{{{\mathbf{n}}}_{3}} - 1}}^{'}(\rho _{{{{n}_{1}} - 1}}^{*},{{\zeta }_{{{{n}_{2}}}}})} \\ {\Lambda _{{2,{{{\mathbf{n}}}_{3}}}}^{'}(\rho _{{{{n}_{1}} - 1}}^{*},{{\zeta }_{{{{n}_{2}}}}})} \\ \ldots \\ 0 \\ 0 \\ \ldots \\ 0 \\ {\Lambda _{{2,0}}^{'}(\rho _{{{{n}_{1}}}}^{*},{{\zeta }_{{k_{2}^{'} + 1}}})} \\ \ldots \\ {\Lambda _{{2,{{{\mathbf{n}}}_{3}} - 1}}^{'}(\rho _{{{{n}_{1}}}}^{*},{{\zeta }_{{{{n}_{2}}}}})} \\ {\Lambda _{{2,{{{\mathbf{n}}}_{3}}}}^{'}(\rho _{{{{n}_{1}}}}^{*},{{\zeta }_{{{{n}_{2}}}}})} \end{array}} \right),\quad {\mathbf{F}} = - \frac{1}{2}\left( {\begin{array}{*{20}{c}} {{{I}_{{0,0}}}} \\ {{{I}_{{1,0}}}} \\ \ldots \\ {{{I}_{{{{n}_{3}} - 1,0}}}} \\ {{{I}_{{{{n}_{3}},0}}}} \\ \ldots \\ 0 \\ 0 \\ \ldots \\ 0 \\ {{{I}_{{0,0}}}} \\ \ldots \\ {{{I}_{{{{n}_{3}} - 1,0}}}} \\ {{{I}_{{{{n}_{3}},0}}}} \end{array}} \right).$$

Similarly, substituting (2.20) in (2.18), we arrive at the system of linear $n_{1}^{'}n_{2}^{'}n_{3}^{'}$ equations in which we replace the equations with $\rho {\text{*}} = \rho _{{{{n}_{1}}}}^{*}$ and $\zeta = {{\zeta }_{{{{k}_{2}}}}}$ by the equations following from the boundary condition (2.19) for Z_{2, 1} with the values of variables ρ* = 1 and $\zeta = {{\zeta }_{{{{k}_{2}}}}}$ (${{k}_{2}} = \overline {0,k_{2}^{'}}$). As a result, we obtain

$${{{\mathbf{D}}}_{1}}{{{\mathbf{A}}}_{1}} + {{{\mathbf{D}}}_{2}}{{{\mathbf{A}}}_{2}} = {{{\mathbf{F}}}_{2}},$$

(2.21)

where ${{{\mathbf{F}}}_{2}} = 3{\text{/}}2{{{\mathbf{F}}}_{1}}$ and the matrices D₁ and D₂ are determined similarly to B₂ and B₁ in which $\Lambda _{{2,{\mathbf{i}}}}^{'}$ and $\Lambda _{{1,{\mathbf{i}}}}^{'}$ are replaced by $\Delta _{{1,{\mathbf{i}}}}^{'}$ and $\Delta _{{2,{\mathbf{i}}}}^{'}$ ($i = \overline {0,{{n}_{3}}}$), respectively.

For finding A₁ we obtain the equation

$$({{{\mathbf{B}}}_{1}} - {{{\mathbf{B}}}_{2}}{\mathbf{D}}_{2}^{{ - 1}}{{{\mathbf{D}}}_{1}}){{{\mathbf{A}}}_{1}} = {{{\mathbf{F}}}_{1}} - {{{\mathbf{B}}}_{2}}{\mathbf{D}}_{2}^{{ - 1}}{{{\mathbf{F}}}_{2}},$$

(2.22)

where ${\mathbf{D}}_{2}^{{ - 1}}$ is the inverse matrix for D₂.

The solution of Eq. (2.22) can be found by means of the LU-method in the software of computer algebra Maple. In accordance with (2.10), on the basis of the obtained elements of the matrix A₁ we obtain an expression for ${{U}_{{z,1}}}(\rho {\text{*}})$. Substituting (2.10) in (1.10), we have

$${{J}_{{M,1}}} = 4\int\limits_{ - 1}^1 \,{{{\mathbf{P}}}_{1}}(\rho {\text{*}})({{T}_{0}}(\rho {\text{*}}) + {{T}_{1}}(\rho {\text{*}}))d\rho {\text{*}}{{{\mathbf{A}}}_{1}} = 8\sum\limits_{{{i}_{3}} = 0}^{{{n}_{3}}} \,{{I}_{{1,{{i}_{3}}}}}\left( {\sum\limits_{{{i}_{1}} = 0}^{[{{n}_{1}}/2]} \,\frac{{a_{{2n_{2}^{'}n_{3}^{'}{{i}_{1}} + {{i}_{3}} + 1,1}}^{{(1)}}}}{{1 - 4i_{1}^{2}}} + \sum\limits_{{{i}_{1}} = 0}^{[n_{1}^{'}/2] - 1} \,\frac{{a_{{n_{2}^{'}n_{3}^{'}(2{{i}_{1}} + 1) + {{i}_{3}} + 1,1}}^{{(1)}}}}{{4 - {{{(2{{i}_{1}} + 1)}}^{2}}}}} \right).$$

(2.23)

In Table 1 we have given the values of $- {{J}_{{M,1}}}$ obtained from formulas (2.23) at $n{\text{*}} = {{n}_{1}} = 2{{n}_{{2,3}}}$ for $\delta < 0.5$ and at $n{\text{*}} = {{n}_{1}} = 2{{n}_{{2,3}}}$ for $\delta \geqslant 0.5$. For the sake of comparison, in the same table we have given the values of the components ${{J}_{{M,1}}}$ borrowed from [2, 5–7, 11]. The results in [2, 5, 6] were obtained on the basis of solving the linearized S-model using the methods of discrete velocities and ordinates. In [7] the spectral method was applied to finding the solution with the use of cubic splines (δ = 0.1, 0.5, and 1), and in [11] the conservative method was used. This method represents the implicit second-order scheme on non-structured grids. As can be seen, already at n* = 10 the method proposed gives, in whole, the acceptable results for $\delta > 0.02$. In the free-molecular limit (δ = 0) the value of J_{M, 1} is equal to $- 1.5026$ at n* = 10 and ${{J}_{{M,1}}} = - 1.5045$ at $n{\text{*}} = 12$. This corresponds to the value $- 8{\text{/}}(3\sqrt \pi )$ calculated analytically [1].

Table 1.

δ	–JM, 1
	(2.23)		[2]	[5]	[6, 7]	[11]
	n* = 10	n* = 20
0.01	1.4861	1.4798	1.4781	1.4800	1.4770	1.4765
0.02	1.4710	1.4631	1.4617	1.4636	1.4616	1.4611
0.05	1.4386	1.4334	1.4330	1.4339	1.4334	1.4329
0.1	1.4097	1.4090	1.4086	1.4101	1.4090	1.4085
0.2	1.3892	1.3899	1.3891	1.3911	–	1.3893
0.5	1.3986	1.4008	1.3996	1.4011	1.4005	1.3998
1.0	1.4740	1.4768	1.4748	1.4758	1.4764	1.4731
2.0	1.6749	1.6784	1.6772	1.6799	1.6779	1.6757
5.0	2.3615	2.3664	2.3646	2.3666	2.3655	2.3619
10.0	3.5726	3.5778	3.5752	3.5749	3.5762	3.5674

The matrix A₂ can be found from Eq. (2.21). In accordance with (2.11), on the basis of the obtained elements of the matrices ${{{\mathbf{A}}}_{{\mathbf{i}}}}$ ($i = 1,2$) we can restore the component ${{q}_{{z,1}}}(\rho {\text{*}})$. Expression (1.10) for ${{J}_{{Q,1}}}$ can be reduced to the form:

$$\begin{gathered} {{J}_{{Q,1}}} = 8\sum\limits_{{{i}_{3}} = 0}^{{{n}_{3}}} \,{{I}_{{3,{{i}_{3}}}}}\left( {\sum\limits_{{{i}_{1}} = 0}^{[{{n}_{1}}/2]} \,\frac{{a_{{2n_{2}^{'}n_{3}^{'}{{i}_{1}} + {{i}_{3}} + 1,1}}^{{(1)}}}}{{1 - 4i_{1}^{2}}} + \sum\limits_{{{i}_{1}} = 0}^{[n_{1}^{'}/2] - 1} \,\frac{{a_{{n_{2}^{'}n_{3}^{'}(2{{i}_{1}} + 1) + {{i}_{3}} + 1,1}}^{{(1)}}}}{{4 - {{{(2{{i}_{1}} + 1)}}^{2}}}}} \right) \\ \, + 8\sum\limits_{{{i}_{3}} = 0}^{{{n}_{3}}} \,{{I}_{{1,{{i}_{3}}}}}\left( {\sum\limits_{{{i}_{1}} = 0}^{[{{n}_{1}}/2]} \,\frac{{a_{{2n_{2}^{'}n_{3}^{'}{{i}_{1}} + {{i}_{3}} + 1,1}}^{{(2)}}}}{{1 - 4i_{1}^{2}}} + \sum\limits_{{{i}_{1}} = 0}^{[n_{1}^{'}/2] - 1} \,\frac{{a_{{n_{2}^{'}n_{3}^{'}(2{{i}_{1}} + 1) + {{i}_{3}} + 1,1}}^{{(2)}}}}{{4 - {{{(2{{i}_{1}} + 1)}}^{2}}}}} \right) - \frac{5}{2}{{J}_{{M,1}}}. \\ \end{gathered} $$

(2.24)

In Table 2 we have given the values of ${{J}_{{Q,1}}}$ obtained from formula (2.24) for the same values of n which were used earlier for obtaining ${{J}_{{M,1}}}$. We will use the approach proposed above for finding the components ${{U}_{{z,2}}}(\rho {\text{*}})$ and ${{q}_{{z,2}}}(\rho {\text{*}})$ and calculating the values of the corresponding reduced fluxes. In this case the system of equations (1.14) and (1.15) with the boundary conditions (1.19) can be reduced to the form:

$${{{\mathbf{B}}}_{1}}{\mathbf{A}}_{1}^{*} + {{{\mathbf{B}}}_{2}}{\mathbf{A}}_{2}^{*} = {\mathbf{F}}_{1}^{*},$$

$${{{\mathbf{D}}}_{1}}{\mathbf{A}}_{1}^{ * } + {{{\mathbf{D}}}_{2}}{\mathbf{A}}_{2}^{ * } = {\mathbf{F}}_{2}^{ * },$$

where the unknown matrices ${\mathbf{A}}_{{\mathbf{k}}}^{*}$ (k = 1, 2)

$${{Z}_{{2,j}}}(\rho ,{{C}_{ \bot }},\zeta ) = {{{\mathbf{T}}}_{1}}(\rho {\text{*}}){\mathbf{Q}}(\zeta ){\mathbf{W}}(C_{ \bot }^{*}){\mathbf{A}}_{{\mathbf{j}}}^{*},\quad j = 1,2$$

and the column matrices ${\mathbf{F}}_{1}^{*}$ and ${\mathbf{F}}_{2}^{*}$ can be determined similarly to ${{{\mathbf{F}}}_{1}}$ and ${{{\mathbf{F}}}_{2}}$, in which ${{I}_{{i,0}}}$ should be replaced by ${{I}_{{i + 2,0}}} - {{I}_{{i,0}}}$ and ${{I}_{{i + 2,0}}}$ ($i = \overline {0,{{n}_{3}}}$), respectively.

Table 2.

δ	JQ, 1 = JM, 2							–JQ, 2
	(2.23)		[2]	[5]	[6, 7]	[11], JM, 2	[11], JQ, 1	(2.23)		[6, 7]
	n* = 10	n* = 10						n* = 10	n* = 20
0.01	0.7301	0.7238	0.7223	0.7243	0.7210	0.7188	0.7207	3.3074	3.2912	3.2848
0.02	0.7112	0.7033	0.7022	0.7042	0.7020	0.6998	0.7016	3.2390	3.2197	3.2166
0.05	0.6678	0.6629	0.6627	0.6637	0.6630	0.6609	0.6626	3.0750	3.0636	3.0638
0.1	0.6214	0.6208	0.6469	0.6206	0.6209	0.6192	0.6189	0.6205	2.8799	2.8800
0.2	0.5663	0.5672	0.5896	0.5667	–	0.5653	0.5668	2.6159	2.6190	–
0.5	0.4777	0.4785	0.4953	0.4780	0.4784	0.4767	0.4780	2.1334	2.1363	2.1360
1.0	0.3961	0.3969	0.4087	0.3962	0.3968	0.3947	0.3946	1.6723	1.6749	1.6745
2.0	0.3022	0.3028	0.3095	0.3022	0.3027	0.3020	0.3020	1.1778	1.1797	1.1794
5.0	0.1757	0.1763	0.1781	0.1759	0.1762	0.1759	0.1759	0.6175	0.6186	0.6186
10.0	0.1012	0.1020	0.1024	0.1018	0.1020	0.1019	0.1023	0.3403	0.3411	0.3410

In Table 2 we have given the values of ${{J}_{{M,2}}}$ and ${{J}_{{Q,2}}}$ as functions of δ. From Tables 1 and 2 it can be seen that rapid convergence in the mean is observed with increase in ${{n}_{{1,2,3}}}$. It is necessary to note that coincidence of the values of ${{J}_{{M,2}}}$ and ${{J}_{{Q,1}}}$ is confirmed by the Onzager relation [1] and serves as an additional criterion of the accuracy of the results obtained.

3. GAS FLOWS AT ARBITRARY PRESSURE AND TEMPERATURE DROPS

We will now describe the second stage of the problem, namely, we will be find the mass fluxes as functions of the pressures ${{p}_{1}}$ and ${{p}_{2}}$ and the temperatures ${{T}_{1}}$ and ${{T}_{2}}$ at the channel ends. In the case of small temperature and pressure drops at the channel ends, the temperature and pressure distributions along the channel can be assumed to be linear [1]. In this case the temperature and pressure gradients can be determined from the formulas [1]

$${{G}_{T}} = \frac{{{{T}_{2}} - {{T}_{1}}}}{{L{{T}_{{{\text{av}}}}}}},\quad {{G}_{p}} = \frac{{{{p}_{2}} - {{p}_{1}}}}{{L{{p}_{{{\text{av}}}}}}},$$

where $L = L'{\text{/}}R'$, ${{T}_{{{\text{av}}}}} = ({{T}_{2}} + {{T}_{1}}){\text{/}}2$, ${{p}_{{{\text{av}}}}} = ({{p}_{2}} + {{p}_{1}}){\text{/}}2$ and the temperature and pressure drops are small: $({{T}_{2}} - {{T}_{1}}) \ll {{T}_{1}}$ and $({{p}_{2}} - {{p}_{1}}) \ll {{p}_{1}}$. In this case the quantity J_M remains constant. If the ratios ${{T}_{2}}{\text{/}}{{T}_{1}}$ and ${{p}_{2}}{\text{/}}{{p}_{1}}$ are large, then the pressure distribution ceases to be linear and the quantity J_M varies along the channel.

We introduce the new reduced flux whose value does not vary along the channel as [1]

$$J_{M}^{*} = \frac{L}{{\pi {{R}^{{'2}}}{{p}_{1}}}}J_{M}^{'}\sqrt {\frac{{2{{k}_{{\text{B}}}}{{T}_{1}}}}{m}} .$$

(3.1)

Expressing $J_{M}^{'}$ from (1.9) and substituting in (3.1), with regard to (1.1) we obtain

$$J_{M}^{*} = \frac{{L\sqrt {{{T}_{1}}} }}{{{{p}_{1}}}}\left( {\frac{1}{{\sqrt T }}{{J}_{{M,1}}}\frac{{dp}}{{dz}} + \frac{p}{{{{T}^{{3/2}}}}}{{J}_{{M,2}}}\frac{{dT}}{{dz}}} \right).$$

(3.2)

Let $z{\text{*}} = z'{\text{/}}L' = z{\text{/}}L$, $T{\text{*}} = T{\text{/}}{{T}_{1}}$, and $p{\text{*}} = p{\text{/}}{{p}_{1}}$, then expression (3.2) can be written in the form:

$$J_{M}^{*} = \frac{1}{{\sqrt {T{\text{*}}} }}{{J}_{{M,1}}}\frac{{dp{\text{*}}}}{{dz{\text{*}}}} + \frac{{p{\text{*}}}}{{{{T}^{{*3/2}}}}}{{J}_{{M,2}}}\frac{{dT{\text{*}}}}{{dz{\text{*}}}}.$$

(3.3)

It should be noted that, as distinct from $J_{M}^{*}$ which does not vary along the channel, the quantities ${{J}_{{M,1}}}$ and ${{J}_{{M,2}}}$ depend on z. This dependence manifests itself implicitly in terms of the parameter δ. For the hard-sphere model we have the following relations [1]:

$$\delta = \frac{{p{{T}_{i}}}}{{{{p}_{i}}T}}{{\delta }_{i}},\quad {{\delta }_{i}} = \frac{{R'{{p}_{i}}}}{{{{\eta }_{g}}({{T}_{i}})}}\sqrt {\frac{m}{{2{{k}_{{\text{B}}}}{{T}_{i}}}}} ,\quad i = 1,2.$$

(3.4)

We will consider isothermal flow. In this case $T{\text{*}} = 1$ (${{T}_{1}} = {{T}_{2}}$) and equation (3.3) takes the form:

$$J_{M}^{*}dz{\text{*}} = {{J}_{{M,1}}}dp{\text{*}}{\text{.}}$$

(3.5)

Expressing p* from (3.4) and substituting in (3.3), we will integrate the left- and right-hand sides of (3.5). Taking into account the fact that $J_{M}^{*}$ is independent of $dz{\text{*}}$, we obtain

$$J_{M}^{*} = \int\limits_1^{{{p}_{2}}/{{p}_{1}}} \,{{J}_{{M,1}}}dp{\text{*}} = \frac{1}{{{{\delta }_{1}}}}\int\limits_{{{\delta }_{1}}}^{{{\delta }_{2}}} \,{{J}_{{M,1}}}d\delta .$$

(3.6)

In (3.6) the values of the integral can be found numerically from the formula

$$J_{M}^{*} = \frac{{2({{\delta }_{2}} - {{\delta }_{1}})}}{{m{{\delta }_{1}}}}\sum\limits_{k = 0}^m{''{\tau}_{{ex}}}(\delta _{k}^{*},m){{J}_{{M,1}}}({{\delta }^{{(k)}}}),$$

(3.7)

$${{\delta }^{{(k)}}} = \left( {\frac{{{{\delta }_{2}} - {{\delta }_{1}}}}{2}} \right)\delta _{k}^{*} + \frac{{{{\delta }_{1}} + {{\delta }_{2}}}}{2},\quad \delta _{k}^{*} = \cos\left( {\frac{{\pi (m - k)}}{m}} \right),\quad k = \overline {0,m} ,$$

(3.8)

where the function ${{\tau }_{{{\text{ex}}}}}(\delta _{k}^{*},m)$ is defined above in (2.13). The values of ${{J}_{{M,1}}}({{\delta }^{{(k)}}})$ in (3.7) can be found using the expansion of this quantity in a series in terms of the Chebyshev polynomials on the interval $\delta \in [0,10]$ [13], where we take points (3.8) as the interpolation nodes in calculating the function (2.23). The calculations show that absolute value of the error is of the order of ${{10}^{{ - 3}}}$ for the number of series terms equal to 33. In the third, fourth, and fifth columns of Table 3 we have given the values of $- J_{M}^{*}$ obtained from formulas (3.7) for m = 2, 4, and 8 on the intervals $[0.1,\;1]$, $[0.1,\;10]$, and $[1,\;10]$. In the sixth column of Table 3 we have given the values calculated from the mean value theorem: $- J_{M}^{*} = {{\kappa }_{p}}{{J}_{{M,1}}}(\delta ')$, where κ_p = $({{\delta }_{1}} - {{\delta }_{2}}){\text{/}}{{\delta }_{1}}$ and $\delta ' = ({{\delta }_{1}} + {{\delta }_{2}}){\text{/}}2$. In the last column we have given the values of $J_{M}^{*}$ obtained in [20] on the basis of the BGK model of the kinetic equation. From Table 3 we can see that rapid convergence in the mean is observed for small values of m in (3.7), the intermediate value of ${{J}_{{M,1}}}(\delta ')$ being close to the arithmetical mean. This corresponds to the assumption in [1].

Table 3.

–$J_{M}^{*}$ at T* = 1							$J_{M}^{*}$ at p* = 1 and $T_{2}^{*}$ = 3.8
δ1	δ2	(3.7)			κpJM, 1(δ')	[20]	δ1	(3.11)			(κTJM, 2(δ')
		m = 2	m = 4	m = 8				m = 2	m = 4	m = 8
0.1	1.0	12.7720	12.7499	12.7494	12.6628	12.6270	0.1	0.6426	0.6375	0.6376	0.6007
1.0	10	22.4956	22.4719	22.4711	22.3691	22.3200	1.0	0.4579	0.4533	0.4535	0.4191
0.1	10	239.2577	237.5450	237.4764	235.4562	235.8180	10	0.1674	0.1630	0.1630	0.1376

Using the values of the parameter $J_{M}^{*}$ found from formula (3.6), from (3.5) with regard to (3.4) we can obtain the differential equation for $p{\text{*}}(z{\text{*}})$

$$\frac{{dp{\text{*}}}}{{dz{\text{*}}}} = \frac{{J_{M}^{*}}}{{{{J}_{{M,2}}}({{\delta }_{1}}p{\text{*}}(z{\text{*}}))}}$$

with the boundary condition $p{\text{*}}( - 1{\text{/}}2) = 1$.

In Figs. 1 and 2 we have given the distributions $p{\text{*}}(z{\text{*}})$ obtained by the Runge–Kutta method for the values of δ₁ and δ₂ given in Table 3. These are, respectively, curves 1 and 2 for ${{\delta }_{1}} = 0.1$ and 1 and ${{\delta }_{2}} = 1$ and 10 in Fig. 1 and curve for ${{\delta }_{1}} = 0.1$ and ${{\delta }_{2}} = 10$ in Fig. 2. From Figs. 1 and 2 it can be seen that for ${{\delta }_{1}}$ = 0.1 and ${{\delta }_{2}} = 1$ the distribution $p{\text{*}}(z{\text{*}})$ approaches the linear distribution (curve 1).

Fig. 1.

Pressure distribution $p{\text{*}}(z{\text{*}})$ in the isothermal gas channel flow regime: curves 1 and 2 correspond to $({{\delta }_{1}},\;{{\delta }_{2}}) = (0.1,\;1)$ and $(1,\;10)$, respectively.

Fig. 2.

Pressure distribution $p{\text{*}}(z{\text{*}})$ in the isothermal gas channel flow regime: $({{\delta }_{1}},\;{{\delta }_{2}}) = (0.1,\;10)$.

We will consider isobaric flow. In this case p* = 1 (${{p}_{1}} = {{p}_{2}}$) and equation (3.3) can be reduced to the form:

$$J_{M}^{*}dz{\text{*}} = T{{{\text{*}}}^{{ - 3/2}}}{{J}_{{M,2}}}dT{\text{*}}{\text{.}}$$

(3.9)

We will integrate (3.9). Taking (3.4) into account, we obtain

$$J_{M}^{*} = \int\limits_1^{{{T}_{2}}/{{T}_{1}}} \,T{{{\text{*}}}^{{ - 3/2}}}{{J}_{{M,2}}}dT{\text{*}} = - \delta _{1}^{{ - 1/2}}\int\limits_{{{\delta }_{1}}}^{{{\delta }_{2}}} \,{{\delta }^{{ - 1/2}}}{{J}_{{M,2}}}d\delta .$$

(3.10)

The values of integral (3.10) can be found numerically from the formula

$$J_{M}^{*} = \frac{{2({{\delta }_{1}} - {{\delta }_{2}})}}{{\sqrt {{{\delta }_{1}}} m}}\sum\limits_{k = 0}^{m''}{{\tau }_{{{\text{ex}}}}(\delta _{k}^{*},m)\frac{{{{J}_{{M,2}}}({{\delta }^{{(k)}}})}}{{\sqrt {{{\delta }^{{(k)}}}}}}},$$

(3.11)

where ${{\tau }_{{{\text{ex}}}}}(\delta _{k}^{*},m)$, $\delta _{k}^{*}$, and ${{\delta }^{{(k)}}}$ are determined in accordance with (2.13) and (3.8). In Table 3 we have represented the values of $J_{M}^{*}$ calculated from formula (3.11) at m = 2, 4, and 8 for $T_{2}^{*} = 3.8$ and ${{\delta }_{1}} = 0.1$, $1$, and $10$. The temperature ratio $T_{2}^{*} = 3.8$ corresponds to the room temperature ${{T}_{2}} = 293$ К maintained in the second container and the liquid nitrogen temperature ${{T}_{1}} = 77.2$ К in the first container [2]. For the values of ${{\delta }_{1}}$ shown in Table 3 the intervals of $\delta$ are contained on the interval $[0,10]$; therefore, as in the case of isothermal gas flow, we use the Chebyshev polynomials for the interpolated function ${{J}_{{M,2}}}(\delta )$. In the last column in Table 3 we have given the values of $J_{M}^{*} = ({{\kappa }_{T}}{{J}_{{M,2}}})(\delta ')$ calculated from the mean value theorem for the integral, where ${{\kappa }_{T}}(\delta ) = ({{\delta }_{2}} - {{\delta }_{1}}){{(\delta {{\delta }_{1}})}^{{ - 1/2}}}$ and $\delta ' = ({{\delta }_{1}} + {{\delta }_{2}}){\text{/}}2$.

Using the values of the parameter $J_{M}^{*}$ found in this case from formula (3.10), we obtain from (3.9) with regard to (3.4) the differential equation for $T{\text{*}}(z{\text{*}})$

$$\frac{{dT{\text{*}}}}{{dz{\text{*}}}} = \frac{{J_{M}^{*}T{{{\text{*}}}^{{3/2}}}(z{\text{*}})}}{{{{J}_{{M,1}}}\left( {\tfrac{{{{\delta }_{1}}}}{{T{\text{*}}(z{\text{*}})}}} \right)}}$$

with the boundary condition $T{\text{*}}( - 1{\text{/}}2) = 1$.

In Fig. 3 we have plotted the distributions $T{\text{*}}(z{\text{*}})$ obtained by the Runge–Kutta method at $T_{2}^{*} = 3.8$ and the values of ${{\delta }_{1}}$ from Table 3. These are curves 1–3, respectively. From Fig. 3 we can see that with increase in ${{\delta }_{1}}$ the distribution $T{\text{*}}(z{\text{*}})$ approaches to the linear distribution (curve 3).

Fig. 3.

Temperature distribution $T{\text{*}}(z{\text{*}})$ for $T_{2}^{*} = 3.8$ in the isobaric gas channel flow regime: curves 1–3 correspond to ${{\delta }_{1}} = 0.1$, 1, and 10, respectively.

We will now consider flow at T* and p* different from unity. In this case we will assume that the wall heat conductivity and thickness do not vary along the channel. Then the temperature distribution can be considered to be linear [2]: $T{\text{*}}(z{\text{*}}) = (T_{2}^{*} - 1)z{\text{*}} + (1 + T_{2}^{*}){\text{/}}2$. The pressure distribution is not known in advance and must be found as a result of solving Eq. (3.3) in which $J_{M}^{*}$ is a parameter. The values of $p{\text{*}}( - 1{\text{/}}2) = 1$ and $p{\text{*}}(1{\text{/}}2) = {{p}_{2}}{\text{/}}{{p}_{1}}$ determine the boundary conditions. Let $\tau = \sqrt {T{\text{*}}}$, then equation (3.3) can be reduced to

$$\frac{{dp{\text{*}}}}{{d\tau }} = 2\left( {\frac{{J_{M}^{*}{{\tau }^{2}}}}{{(T_{2}^{*} - 1){{J}_{{M,1}}}}} - \frac{{p{\text{*}}{{J}_{{M,2}}}}}{{\tau {{J}_{{M,1}}}}}} \right)$$

(3.12)

with the boundary conditions $p{\text{*}}(1) = 1$ and $p{\text{*}}(\sqrt {{{T}_{2}}{\text{/}}{{T}_{1}}} ) = {{p}_{2}}{\text{/}}{{p}_{1}}$.

In the free-molecular regime ($\delta = 0$) we have ${{J}_{{M,2}}} = - {{J}_{{M,1}}}{\text{/}}2$ and the general solution of the differential equation (3.12) takes the form:

$$p{\text{*}}(\tau ) = \left( {\frac{{J_{M}^{*}{{\tau }^{2}}}}{{{{J}_{{M,1}}}(T_{2}^{*} - 1)}} + C} \right)\tau ,$$

(3.13)

where C is the integration constant. Substituting the boundary conditions $p{\text{*}}(1) = 1$ and $p{\text{*}}({{\tau }_{2}}) = p_{2}^{*}$ in (3.13), we arrive at a system of equations for determining C and $J_{M}^{*}$. As a result, we obtain

$$J_{M}^{*} = \left( {\frac{{p_{2}^{*}}}{{{{\tau }_{2}}}} - 1} \right){{J}_{{M,1}}},\quad C = \frac{{p_{2}^{*} - \tau _{2}^{3}}}{{(1 - \tau _{2}^{2}){{\tau }_{2}}}}.$$

(3.14)

In the free-molecular regime for the cylindrical channel we have ${{J}_{{M,1}}} = - 8{\text{/}}(3\sqrt \pi ) = - 1.5045$. At $T_{2}^{*}$ = 3.8 for $p_{2}^{*} = 100$ and $p_{2}^{*} = 1$ the values of $J_{M}^{*}$ found in accordance with (3.14) are equal to –75.6747 and 0.7327, respectively.

Substituting (3.14) in (3.13) and taking into account that $\tau = \sqrt {T{\text{*}}(z{\text{*}})}$ and T*(z*) = $(T_{2}^{*} - 1)z{\text{*}}\, + \,(1 + T_{2}^{*}){\text{/}}2$, we obtain the pressure distribution along the channel $p{\text{*}}(z{\text{*}})$

$$p{\text{*}}(z{\text{*}}) = \left( {\frac{1}{2}\left( {\frac{{p_{2}^{*}}}{{\sqrt {T_{2}^{*}} }} - 1} \right)z{\text{*}} + \frac{1}{4}\left( {\frac{{p_{2}^{*}}}{{\sqrt {T_{2}^{*}} }} + 1} \right)} \right)\sqrt {4(T_{2}^{*} - 1)z{\text{*}} + 2(T_{2}^{*} + 1)} .$$

(3.15)

In Figs. 4 and 5 the distributions $p{\text{*}}(z{\text{*}})$ obtained from (3.15) at $T_{2}^{*} = 3.8$ for $p_{2}^{*} = 100$ and $p_{2}^{*} = 1$ are shown by broken curve (curve 4).

Fig. 4.

Pressure distribution $p{\text{*}}(z{\text{*}})$ at $p_{2}^{*} = 100$ and $T_{2}^{*} = 3.8$: curves 1–4 correspond to ${{\delta }_{1}} = 0.1$, 1, 10, and 0, respectively.

Fig. 5.

Pressure distribution $p{\text{*}}(z{\text{*}})$ at $p_{2}^{*} = 1$ and $T_{2}^{*} = 3.8$: curves 1–4 correspond to ${{\delta }_{1}} = 0.1$, 1, 10, and 0, respectively.

In the intermediate regime ${{J}_{{M,1}}}$ and ${{J}_{{M,2}}}$ depend on the parameter δ whose values vary from δ₁ to δ₂. Taking into account that $p{\text{*}} = p{\text{/}}{{p}_{1}}$, we can express p* from (3.4) and differentiate the equality obtained. As a result, we have

$$p{\text{*}} = \frac{{\delta {{\tau }^{2}}}}{{{{\delta }_{1}}}},\quad \frac{{dp{\text{*}}}}{{d\tau }} = {{\delta }_{1}}\left( {\frac{{d\delta }}{{d\tau }}{{\tau }^{2}} + 2\delta \tau } \right).$$

(3.16)

Substituting (3.16) in (3.12), we obtain the differential equation for $\delta (\tau )$

$$\frac{{d\delta }}{{d\tau }} = \frac{{2J_{M}^{*}{{\delta }_{1}}}}{{(T_{2}^{*} - 1){{J}_{{M,1}}}(\delta )}} - \frac{{2\delta }}{\tau }\left( {\frac{{{{J}_{{M,2}}}(\delta )}}{{{{J}_{{M,1}}}(\delta )}} + 1} \right)$$

(3.17)

with the boundary condition $\delta (1) = {{\delta }_{1}}$. The solution of this equation can be found by the Runge–Kutta method taking the parameter $J_{M}^{*}$ so that $\delta (\sqrt {{{T}_{2}}{\text{/}}{{T}_{1}}} ) = {{\delta }_{2}}$ with the absolute error not greater than 10^–4. As the initial value of $J_{M}^{*}$, we use the solution of the equation

$${{\delta }_{2}} - {{\delta }_{1}} = \frac{{2J_{M}^{*}{{\delta }_{1}}}}{{(T_{2}^{*} - 1){{J}_{{M,1}}}(\delta ')}}({{\tau }_{2}} - {{\tau }_{1}}) - 2\delta 'ln\left( {\frac{{{{\tau }_{2}}}}{{{{\tau }_{1}}}}} \right)\left( {\frac{{{{J}_{{M,2}}}(\delta ')}}{{{{J}_{{M,1}}}(\delta ')}} + 1} \right),$$

(3.18)

where $\delta ' = ({{\delta }_{1}} + {{\delta }_{2}}){\text{/}}2$.

In Table 4 we have represented the values of $J_{M}^{*}$ obtained from (3.18) and (3.17) at $p_{2}^{*} = 100$ and $p_{2}^{*} = 1$ for $T_{2}^{*} = 3.8$ and ${{\delta }_{1}} = 0.1$, 1, and 10. In (3.17) for the interpolated functions ${{J}_{{M,1}}}(\delta )$ and ${{J}_{{M,2}}}(\delta )$ we used the Chebyshev polynomials (m = 8). In Table 4 we have given the values borrowed from [2] in the last column.

Table 4.

δ1	–$J_{M}^{*}$ × 10–2 at $p_{2}^{*}$ = 100 and $T_{2}^{*}$ = 3.8			$J_{M}^{*}$ at $p_{2}^{*}$ = 1 and $T_{2}^{*}$ = 3.8
	(3.18)	(3.17)	[2]	(3.18)	(3.17)	[2]
0.1	0.8974	0.9712	0.971	0.5871	0.6340	0.6324
1.0	2.8557	3.8326	3.818	0.3389	0.4312	0.4315
10	22.6028	33.2470	32.82	–0.2360	0.1474	0.1496

Taking into account the fact that $\tau = \sqrt {T{\text{*}}(z{\text{*}})}$ and $T{\text{*}}(z{\text{*}}) = (T_{2}^{*} - 1)z{\text{*}} + (1 + T_{2}^{*}){\text{/}}2$, in accordance with (3.16) we obtain the pressure distribution $p{\text{*}}(z{\text{*}})$ along the channel. In Figs. 4 and 5 we have represented the distributions $p{\text{*}}(z{\text{*}})$ at $p_{2}^{*} = 100$ and $p_{2}^{*} = 1$ for $T_{2}^{*} = 3.8$ and the values of δ₁ from Table 4.

SUMMARY

The problem of mass- and heat-transfer in rarefied gas in a long cylindrical channel at arbitrary pressure and temperature drops at the channel ends is solved within the framework of the kinetic approach. The expressions for the mass and heat fluxes as functions of the pressure and temperature gradients are obtained on the basis of the S-model of the Boltzmann kinetic equation using the Chebyshev polynomials and rational functions. The mass and heat fluxes across the transverse channel cross-section are calculated for various rarefaction parameters. A comparison with similar results obtained by other authors is carried out. The values of the mass gas fluxes are obtained in the intermediate and free-molecular flow regimes as functions of the pressure and temperature at the channel ends and isothermal and isobaric rarefied gas flows are investigated. The graphs of the gas pressure distribution along the channel are plotted. For isothermal and non-isothermal gas flows, the difference between the corresponding pressure profiles along the channel axis is demonstrated. The technique proposed can be also applied to the channels of other transverse cross-sections and another model of the surface interaction between the gas molecules and the channel walls.