Introduction

Natural granular flows like rock falls, avalanches, debris flows, and landslides may initiate huge impulsive waves, called landslide-generated waves (LGWs) or landslide tsunamis (Ward 2001). when they occur in the borders of a water body (e.g., dam reservoirs, lakes, rivers, oceans). LGWs are highly destructive due to the nature of having long wavelength and short wave period or high velocity (Titov 1997). They may impose serious damages to dam bodies, offshore and onshore constructions, and human possessions or cause fatalities with a huge runup, overtopping, or following flood (Panizzo et al. 2005; Ataie-Ashtiani and Malek-Mohammadi 2007; Ataie-Ashtiani and Malek-Mohammadi 2008). A massive landslide may also decrease effective capacity of water reservoirs or change the bed topography and natural morphology of the affected area. The biggest recorded LGW in the world is a 180-m impulsive wave with velocity of about 160 km/h caused by a 40 Mm3 rockslide in Lituya Bay, Alaska, in 1958 (Thurman and Trujillo 2003; Fritz et al. 2009). Accordingly, it has significant importance to analyze the LGW risks of probable landslide hazard all over the world in order to minimize their potential damages.

A large number of numerical studies have been performed regarding LGWs. Three distinguished stages in numerical simulation of impulsive waves are the generation, the propagation, and the runup/overtopping stages (Ataie-Ashtiani and Yavari-Ramshe 2011). Researchers have achieved considerable advances in simulation of the propagation stage using Boussinesq-type equations with high orders of wave non-linearity and dispersion ( e.g., Ataie-Ashtiani and Najafi-Jilani 2007; Ataie-Ashtiani and Yavari-Ramshe 2011; Lynett 2002; Watts et al. 2003; Lynett and Liu 2005; Dutykh and Kalisch 2013). With proper estimation of positive wave amplitudes near the borders of the water body, wave runup can also be appropriately calculated either numerically or with empirical equations (e.g., Ataie-Ashtiani and Malek-Mohammadi 2008; Dodd 1998; Hubbard and Dodd 2002; Liu et al. 2005; Lynett and Liu 2005; Schüttrumpf et al. 2009). The key challenge concerning numerical modeling of LGWs is the generation stage. Correct prediction of LGWs near the source is the key to the accurate simulation of the propagation and the runup/overtopping stages. Recent experimental works (Fritz 2002; Enet and Grilli 2005, 2007; Grilli and Watts 2005; Liu et al. 2005; Najafi-Jilani and Ataie-Ashtiani 2008; Ataie-Ashtiani and Nik-Khah 2008) exhibit a complex three-phase system (water-air-soil) contributing in the landslide wave generation stage, especially for subaerial cases.

The wave generation phase is including the processes of the slide initiation, motion, and interaction with water. Slide triggering, which is beyond the scope of this paper, requires the information of seismology, geology, and geophysics (Grilli et al. 2009). Regarding landslide motion, two general approaches have been typically applied. The majority of available numerical models consider landslide as a solid body with predefined kinematics using a semi-empirical equation, e.g., describing the center of mass motion as a time variable bottom boundary (Noda 1971; Mader 1973; Raney and Butler 1975; Goto and Ogawa 1992; Sander and Hutter 1996; Grilli et al. 1999; Grilli et al. 2002; Lynett 2002; Synolakis et al. 2002; Saut 2003; Yuk et al. 2006; Ataie-Ashtiani and Najafi-Jilani 2007; Serrano-Pacheco et al. 2009a; Cecioni and Bellotti 2010). This approach is commonly applied for submarine landslides, although some researchers proposed new ideas for subaerial cases (Lynett and Liu 2005; Yavari-Ramshe and Ataie-Ashtiani 2009; Ataie-Ashtiani and Yavari-Ramshe 2011). In the second approach, the sliding mass is treated as a general deformable mass. Recent experimental and numerical studies confirm the significant effects of landslide deformations on LGW characteristics (Abadie et al. 2008; Ataie-Ashtiani and Najafi-Jilani 2008; Ataie-Ashtiani and Nik-Khah 2008; Mohammed and Fritz 2012; Heller and Spinneken 2013). They have confirmed that landslide rheological behavior should be properly described and included in numerical simulations to predict LGW characteristics more accurately. With considering landslide as a rigid body, LGW properties (e.g., wave amplitudes, velocities, and periods) have been generally overestimated (Grilli and Watts 2005; Abadie et al. 2008; Sælevik et al. 2009; Heller and Kinnear 2010; Ataie-Ashtiani and Yavari-Ramshe 2011).

A list of numerical studies which follow the second approach, i.e., deformable landslide, is summarized in Table 1. The related models generally describe the combination of water and landslide as a mixture, a multiphase, or a multilayer flow model. Mixture models consider the blend of water, soil grains, and air as a single-phase flow having variable mixture density and velocity in time and space (Manninen et al. 1996). In these models, landslide may be described as an inviscid (Heinrich et al. 1998) or viscous fluid (Ma et al. 2013) with various rheological models like Bingham (Assier Rzadkiewicz et al. 1997) or Coulomb (Mangeney et al. 2000). In multiphase models, water, air, and grain soils are separately considered as either inviscid or viscous fluids whose interfaces are tracked by a proper technique like volume of fluid (VOF) (Abadie et al. 2010; Abadie et al. 2008; Biscarini 2010; Horrillo et al. 2013). level set (LS) (Pastor et al. 2009; Zhao et al. 2015). or smoothed particle hydrodynamic (SPH) (Ataie-Ashtiani and Shobeyri 2008; Capone et al. 2010; Cremonesi et al. 2011) method. Finally, the third group is multilayer models which consider landslide as a separate layer beneath a layer of water while each layer may include a multiphase flow. In some early research works, a two-layer shallow flow model was developed considering submarine landslide as a laminar layer of viscous fluid (Jiang and Leblond 1992) or a layer of inviscid fluid (Imamura and Imteaz 1995). Thomson et al. (2001) modified the two-layer model of Jiang and Leblond (1992) for including subaerial landslides. Later, different rheological flow models (e.g., bilinear, Bagnold, Bingham, Herschel-Bulkley, or Coulomb) were applied to describe the behavior of viscid or inviscid granular layer (e.g., Heinrich et al. 2001; Imran et al. 2001; Serrano-Pacheco et al. 2009b). Shigihara et al. (2006) considered landslide as a layer of viscous fluid having shear stress on the interface and bottom defined by the Manning equation. Recently, some researchers have described the landslide layer as a two-phase solid–fluid mixture with different rheologies (e.g., Fernández-Nieto et al. 2008; Shakeri Majd and Sanders 2014). The same hypothesis is applied in the present model.

Table 1 A list of the numerical models of LGWs considering a deformable landslide
Full size table

In this study, a fully coupled two-layer flow model is developed which is composed of a layer of two-phase granular medium moving beneath an inviscid and homogeneous layer of water. Water and granular material are supposed to be immiscible. Landslide behavior is conceptualized based on the Savage–Hutter (SH) assumptions (Savage and Hutter 1989; Savage and Hutter 1991) as the best-tested and the most parsimonious model for cohesion-less granular mixtures (Iverson and Vallance 2001; Denlinger and Iverson 2001; Greve and Hutter 1993; Hungr and Morgenstern 1984; Hutter and Koch 1991; Koch et al. 1994; Mangeney et al. 2003; Pitman and Le 2005; Toni and Scotton 2005; Wieland et al. 1999; Yavari-Ramshe et al. 2015). In real landslide events, the two-phase nature of the granular mass including sand grains and interstitial water cannot be neglected (Hungr 1995; Iverson and Denlinger 2001; Iverson and Vallance 2001; Pitman and Le 2005; Pudasaini et al. 2005). particularly, when landslide happens in the borders of a water body or triggers by a heavy rain.

To consider the two-phase nature of the landslide, the sliding material is described as a granular medium filled with water, called the Coulomb mixture, where the dissipation within its solid phase is described by a Coulomb-type friction law (Iverson and Denlinger 2001; Pudasaini et al. 2005). Both phases are supposed to have the same velocity, for simplicity (Fernández-Nieto et al. 2008).

The same assumptions applied by Fernández-Nieto et al. (2008) are implemented in the present model regarding the effects of bottom curvature. Incompressible Euler equations are transferred to a local coordinate system along the bottom to take the bed curvature effects into account, under the hypothesis of small variation of the bed curvature proposed by Bouchut et al. (2003). To discretize the system of model equations, a well-balanced Roe-type finite volume method (FVM) introduced by Yavari-Ramshe et al. (2015) is applied. This scheme has been applied in a one-layer numerical model to study natural granular-type flows and is generalized for the present two-layer model.

The core objectives of this paper are to introduce an applicable two-layer two-phase landslide tsunami model using a proposed state-of-the-art FVM formulation and to study the effects and importance of landslide rigidity on LGW characteristics and two-phase solid–liquid nature of granular material on both landslide deformations and water surface fluctuations. This is the first time that a detailed sensitivity analysis is performed on the effects of each phase of landslide on both LGW characteristics and landslide deformations based on comparison with two sets of experimental data. The importance of landslide deformations on LGW characteristics is also investigated with comparing the model predictions with experimental measurements and numerical results of a Boussinesq-type model considering a rigid slide. For the sake of simplicity, the problems are simulated in one dimension. However, the proposed scheme can be extended for more general one- or multidimensional flows.

The paper is organized as follows: “Mathematical model equations” section provides the governing mathematical equations. In “Numerical model formulations” section, the proposed well-balanced Roe-type finite volume scheme is introduced and applied to discretize the system of model equations. “Numerical results” section is devoted to illustration of numerical results including model verification, sensitivity analysis, and comparison with a simpler numerical model regarding landslide rigidity. Finally, the concluding results will be discussed in the last section.

Mathematical model equations

The system of model equations is derived from the following incompressible Euler equations (Toro 1999).

$$ \left\{\begin{array}{l}\nabla .{V}_i^{\prime }=0\\ {}{\rho}_i{\partial}_t{V}_i^{\prime }+{\rho}_i{V}_i^{\prime }.\nabla {V}_i^{\prime }=-\nabla .{P}_i+{\rho}_i\nabla \left(\overrightarrow{g}\;.\;\overrightarrow{X}\right)\end{array}\right. $$
(1)

Index i = 1 represents the upper layer, composed of a homogeneous inviscid fluid (water) with constant density ρ 1, and i = 2 denotes the second layer, composed of a granular mass with constant density ρ 2. As it is mentioned in the first section, the second layer is considered to be a solid–fluid mixture, a grain medium with density ρ s and porosity ψ 0 which its pores are filled with the upper layer fluid. Accordingly, the granular layer density is calculated as (Terzaghi et al. 1996)

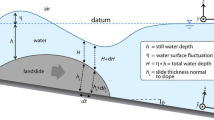
$$ {\rho}_2=\left(1-{\psi}_0\right){\rho}_s+{\psi}_0{\rho}_1 $$
(2)

V ′ i  = (u i , v i )is the velocity vector of each layer with the horizontal and the vertical components u i and v i . \( {P}_i=\left[\begin{array}{cc}\hfill {P}_{i,xx}\hfill & \hfill {P}_{i,xz}\hfill \\ {}\hfill {P}_{i,zx}\hfill & \hfill {P}_{i,zz}\hfill \end{array}\right] \) is the normal stress tensor of each layer with P i,xz  = P i,zx . \( \overrightarrow{g}=\left(0,-g\right) \) is the vector of gravitational acceleration. \( \overrightarrow{X}=\left(x,z\right) \) represents Cartesian coordinate. \( \nabla =\left(\frac{\partial }{\partial x},\frac{\partial }{\partial z}\right) \) is the gradient vector. t is time and ∂ t  = ∂/∂t. It should be noticed that for a dry subaerial landslide, ρ 1 substitutes with ρ a which represents the air density. The model parameters are illustrated in Fig. 1.

Fig. 1
figure 1

Schematic definition of the present model parameters

Full size image

It is supposed that both phases of the second layer have the same velocity (Iverson and Denlinger 2001). The pressure tensor of the Coulomb mixture can be decomposed as

$$ {P}_2={P}_2^s+{P}_2^f $$
(3)

where P s2 and P f2 are the pressure tensors of the solid phase and the fluid phase, respectively (Fernández-Nieto et al. 2008).

Then, Eq. 1 is transferred to a local coordinate system over the non-erodible bed defined by z = b(x), based on the following transformation matrix (Fernández-Nieto et al. 2008)

$$ \begin{array}{ll}{\nabla}_{\overrightarrow{X}}\left(X,Z\right)=\frac{1}{J}\left(\begin{array}{cc}\hfill \cos \theta \hfill & \hfill \sin \theta \hfill \\ {}\hfill -J \sin \theta \hfill & \hfill J \cos \theta \hfill \end{array}\right),\hfill & J=1-Z{d}_X\theta \hfill \end{array} $$
(4)

X and Z represent the components of the local coordinate system. X denotes the curve length of the bottom, and Z is measured perpendicular to the bed (Fig. 1). J is the Jacobian of the change of variables. For a non-erodible bed, the flow depth, h ′1  + h ′2 , should be less than the local radius of the bed curvature so that J ≠ 0 (Savage and Hutter 1991). θ represents the local bed slope angle.

The kinematic (K.C.) and boundary (B.C.) conditions applied in the model are (Fernández-Nieto et al. 2008).

  • At the free water surface, i.e., Z = S = H 1 + H 2

    $$ \left\{\begin{array}{l}{\partial}_tS+{U}_1{\partial}_XS-{V}_1=0\kern2.74em K.C.\\ {}{P}_1.{n}_S=0\kern7.5em B.C.\end{array}\right. $$
    (5)

  • At the layers interface, i.e., Z = H 2

    $$ \left\{\begin{array}{l}{\partial}_t{H}_2+{U}_i{\partial}_X{H}_2-{V}_i=0\kern2.74em K.C.\\ {}{n}_i.\left({P}_1-{P}_2\right){n}_i=0\kern5.36em B.C.\end{array}\right. $$
    (6)

  • At the bottom, i.e., Z = 0

    $$ \left\{\begin{array}{ll}{V}_2=0\hfill & K.C.\hfill \\ {}{P}_2.{n}_b-{n}_b\left({n}_b.{P}_2.{n}_b\right)=-\left({U}_b/\left|{U}_b\right|\right)\left({n}_b.\left({P}_2-{P}_1\right).{n}_b\right) \tan \delta \hfill & B.C.\hfill \end{array}\right. $$
    (7)

n s , n i , and n b are the exterior unit normal vectors of the free water surface, the interface of two layers, and the bottom, respectively. H i is the thickness of each layer normal to the bed. The second equation of Eq. 7 describes the interactions between the granular flow and the non-erodible bottom based on a Coulomb-type friction law (Savage and Hutter 1989). U and V are the flow velocity components in the X and Z directions, respectively. In this relation, U b is the sliding velocity along the stationary bed and δ is the basal friction angle.

In the next step, a dimensional analysis is performed on the system of model equations, K.C.s and B.C.s, using two characteristic lengths of L and H′ in the X and Z directions, respectively. The non-dimensional variables (\( \tilde{.} \)) are (Fernández-Nieto et al. 2008) as follows:

$$ \begin{array}{l}\\ {}\begin{array}{ll}\left(X,Z,t\right)=\left(L\overset{\sim }{X},{H}^{\prime}\overset{\sim }{Z},\sqrt{L/g}\overset{\sim }{t}\right),\hfill & \left({U}_i,{V}_i\right)=\sqrt{Lg\;}\left({\overset{\sim }{U}}_i,\varepsilon {\overset{\sim }{V}}_i\right),\hfill \\ {}\left({P}_{iXX},{P}_{iZZ}\right)=gH^{\prime}\left({\tilde{P}}_{iXX},{\overset{\sim }{P}}_{iZZ}\right),\hfill & \begin{array}{ll}{P}_{iXZ}=gH^{\prime }{\mu}_i{\overset{\sim }{P}}_{iXZ},\hfill & {H}_i=H^{\prime }{\overset{\sim }{H}}_i\hfill \end{array}\hfill \end{array}\end{array} $$

where μ 1 = 1 and μ 2 = tan δ 0 (Fernández-Nieto et al. 2008). δ 0 is the angle of repose of the granular material (Fernández-Nieto et al. 2008). ε = H′/L is a small parameter due to considering a shallow domain.

Next, the system of model equations is averaged in perpendicular direction to the bottom. d X θ is considered to be Ο (ε) (Bouchut et al. 2003). therefore, J = 1 − Zd X θ ≈ 1 (Fernández-Nieto et al. 2008). The Coulomb friction term is also assumed to be of the order of a small parameter γ ∈ (0 , 1), introduced by Gray (2001). so that tan δ 0 = Ο(ε γ) (Fernández-Nieto et al. 2008).

Depth-averaging the system of model equations, K.C.s and B.C.s, with considering d X θ to be Ο(ε) (Bouchut et al. 2003) results in the following relations up to order ε (Fernández-Nieto et al. 2008).

$$ {P}_{1ZZ}={\rho}_1\left(S-Z\right) \cos \theta $$
(8)
$$ {P}_{2ZZ}={P}_{2ZZ}^S+{P}_{2ZZ}^f={\rho}_1{h}_1 \cos \theta +{\rho}_2\left({h}_2-Z\right) \cos \theta $$
(9)

P 2ZZ is the total pressure on the second layer normal to the bottom. P S2ZZ and P f2ZZ are the normal pressures of the grain and the fluid phase on the second layer, respectively (Fernández-Nieto et al. 2008). With considering the landslide as a fluid–solid mixture, a proper constitutive relation is required for both phases. Iverson and Denlinger (2001) and Pudasaini et al. (2005) have considered linear normal stresses perpendicular to the non-erodible bottom since the flow is considered to be shallow. They have introduced a factor Λ f which distributes the normal stress between fluid and solid phases. Fernández-Nieto et al. (2008) consider two factors λ 1 and λ 2 for allocating the normal stresses to the fluid and solid phases in the flow interface and within the Coulomb mixture layer, respectively. The present model follows the same definition for these two pressure terms as

$$ \left\{\begin{array}{l}{P}_{2ZZ}^f={\lambda}_1{\rho}_1{h}_1 \cos \theta +{\lambda}_2{\rho}_1\left({h}_2-Z\right) \cos \theta \\ {}{P}_{2ZZ}^S=\left(1-{\lambda}_1\right){\rho}_1{h}_1 \cos \theta +\left({\rho}_2-{\lambda}_2{\rho}_1\right)\left({h}_2-Z\right) \cos \theta \end{array}\right. $$
(10)

λ 1 and λ 2should be determined by calibration. These coefficients are estimated for both subaerial and submarine landslides based on comparison with the experimental data of Ataie-Ashtiani and Nik-Khah (2008) and Ataie-Ashtiani and Najafi-Jilani (2008) in “Numerical results” section. Based on Eq. 10, λ 1 controls the distribution of the pressure at the interface (P 1ZZ (H 2) = ρ 1 H 1 cos θ) between two phases of the second layer (Fernández-Nieto et al. 2008). λ 2 determines what percent of the normal pressure comes from each phase through the second layer (Fernández-Nieto et al. 2008; Iverson and Denlinger 2001). As a result, λ 1 = 1 is equivalent to the continuity of the pressure of the fluid phase of the second layer with the fluid of the first layer and λ 1 = 0 means that the pore fluid is isolated from the first layer fluid (Fernández-Nieto et al. 2008).

Following constitutive relations are also considered to relate normal and longitudinal stresses of each layer and each phase (Iverson and Denlinger 2001). An isotropic stress is defined for homogeneous fluid of the first layer and the same pore fluid, i.e., P 1XX  = P 1ZZ and \( {P}_{{}_{2XX}}^f={P}_{{}_{2ZZ}}^f \). For anisotropic solid phase of the Coulomb mixture, the normal and longitudinal stresses are related through the proportionality factor K (\( {P}_{{}_{2XX}}^s=K{P}_{{}_{2ZZ}}^s \)) which represents the earth pressure coefficient calculated as (Savage and Hutter 1989)

$$ {K}_{act/ pass}=2\left(1-\operatorname{sgn}\left(\frac{\partial {U}_2}{\partial X}\right)\sqrt{1-{\left(\frac{ \cos \varphi }{ \cos \delta}\right)}^2}\right)/{ \cos}^2\varphi -1 $$
(11)

φ represents the internal friction angle of the granular material. The “active” and “passive” states of the earth pressure coefficient are corresponding to the maximum and minimum values of K which are distinguished by the sign of the longitudinal strain (∂U 2/∂X) (Savage and Hutter 1989). Classic SH model considers negligible depth gradients due to shallow flow assumption of parallel flow lines. The curved flow lines caused by a significant depth gradient, e.g., dam-break problems, create a pressure component non-parallel to the bed (Hungr 2008). This pressure component originates additional shear stresses close to the bottom which are not considered in original SH model and the model developed by Fernández-Nieto et al. (2008). The present model overcomes this deficiency using the proposed method of Hungr (2008). He has modified the definition of the resisting shear stress at the flow by reducing the basal friction angle as a fraction of these extra stresses as

$$ \tan {\delta}_{\mod{}}= \tan \delta -{\lambda}^{\prime }K\left(\frac{\partial {H}_2}{\partial X}\right) $$
(12)

In this relation, δ mod is the modified (reduced) basal friction angle, λ′ is an empirical coefficient validated as about 0.333, and ∂H 2/∂X is the granular flow depth gradient (Hungr 2008). Then, K is calculated by Eq. 13 using the modified value δ mod. Without reducing δ dynamically, the granular flow tail (ensuing flow) moves very slowly in comparison with experiments (Yavari-Ramshe et al. 2015). The tail motion is important when dealing with LGWs. The slide trailing motion continuously generates trailing wave trains, which may become significant especially in dam reservoirs, lakes, and closed bays. Hunger’s modification also improves the numerical prediction of the slide tail deformations and velocities.

Based on the considered constitutive relations, normal pressure of the second layer is (Fernández-Nieto et al. 2008)

$$ {P}_{2XX}=K{P}_{2ZZ}^S+{P}_{2ZZ}^f={H}_1 \cos \theta {\rho}_1\left({\lambda}_1+K\left(1-{\lambda}_1\right)\right)+\left({H}_2-Z\right) \cos \theta \left({\lambda}_2{\rho}_1+K\left({\rho}_2-{\lambda}_2{\rho}_1\right)\right) $$
(13)

Finally, the system of model equations is rewritten with original variables and is retransferred to the Cartesian coordinate system using the following relations (Fernández-Nieto et al. 2008)

$$ \begin{array}{lll}\partial /\partial X= \cos \theta \partial /\partial x,\hfill & {h}_i={H}_i/ \cos \theta, \hfill & {q}_i={h}_i{u}_i\hfill \end{array} $$

Consequently, the final system of model equations will be (Fernández-Nieto et al. 2008)

$$ \left\{\begin{array}{l}{\partial}_t{h}_1+{\partial}_x\left({q}_1 \cos \theta \right)=0\\ {}{\partial}_t\left({q}_1\right)+{\partial}_x\left({h}_1{u_1}^2 \cos \theta +g\frac{{h_1}^2}{2}{ \cos}^3\theta \right)=-g{h}_1 \cos \theta {d}_xb+g\frac{h_1^2}{2} \sin \theta { \cos}^2\theta {d}_x\theta -g{h}_1 \cos \theta {\partial}_x\left({h}_2{ \cos}^2\theta \right)\\ {}{\partial}_t{h}_2+{\partial}_x\left({q}_2 \cos \theta \right)=0\\ {}{\partial}_t\left({q}_2\right)+{\partial}_x\left({h}_2{u_2}^2 \cos \theta +g{\varLambda}_2\frac{{h_2}^2}{2}{ \cos}^3\theta \right)=-g{h}_2 \cos \theta {d}_xb+g\frac{h_2^2}{2} \sin \theta { \cos}^2\theta {d}_x\theta \\ {}\kern1em -r{\varLambda}_1g{h}_2 \cos \theta {\partial}_x\left({h}_1{ \cos}^2\theta \right)+\frac{\Im }{ \cos \theta}\end{array}\right. $$
(14)

where r = ρ 1/ρ 2. The terms of order ε 1 + γ are neglected, and the flow velocity is considered to have a constant profile (Fernández-Nieto et al. 2008). ℑ represents the Coulomb friction term defined as (Fernández-Nieto et al. 2008)

$$ \left\{\begin{array}{ll}\Im =-\left(g\left(1-r\right){h}_2{ \cos}^2\theta +{h}_2{u}_2^2 \cos \theta {d}_x\left( \sin \theta \right)\right)\frac{q_2}{\left|{q}_2\right|} \tan \delta \hfill & \left|\Im \right|\ge {\sigma}_c\hfill \\ {}{q}_2=0\hfill & \left|\Im \right|<{\sigma}_c\hfill \end{array}\right. $$
(15)

where σ c is the basal critical stress which is defined based on the angle of repose of the sliding mass as σ c  = g(1 − r)h 2 cos θ tan δ 0 (Fernández-Nieto et al. 2008). Based on Eq. 15, when the basal friction term is less than the critical basal stress, |ℑ| < σ c , the granular mass stops moving, u 2 = 0. This happens when the granular mass angle is smaller than its angle of repose. With this assumption, the model is able to capture the sudden appearance of the flowing/static regions along the granular flow path. Moreover, Λ 1 = λ 1 + K(1 − λ 1) and Λ 2 = rλ 2 + K(1 − rλ 2) (Fernández-Nieto et al. 2008) (for more details about the mathematical formulations, see Fernández-Nieto et al. 2008).

Numerical model formulations

In this section, the system of model Eq. (14) is discretized using a modified Q-scheme of Roe proposed by Yavari-Ramshe et al. (2015). This scheme, which was developed for a one-layer granular-type flow model, is generalized for the present two-layer model. In this scheme, the non-homogeneous source terms concerning the bed level and the bed curvature are upwinded in the same way of numerical fluxes. The Coulomb friction term is discretized using a two-step semi-implicit method.

As it is mentioned, the system of model equations is transferred to a local coordinate system along the non-erodible bottom to consider the effects of the bed curvature on the sliding mass deformations. As a result, numerical fluxes depend not only on horizontal distance x but also on the bed curvature changes which makes it difficult to define an exact well-balanced scheme (Castro et al. 2007; Fernández-Nieto et al. 2008). In this regard, we have followed the special finite volume solver introduced by Castro et al. (2007) for two-layer shallow-water equations which preserves water at rest while also verifies an entropy inequality. Finally, the main difference between the one-layer and the two-layer system of model equations is regarding the non-conservative coupling term which is discretized based on the proposed method of Dal Maso et al. (1995) and applied by Fernández-Nieto et al. (2008). The general hyperbolic form of model equations is

$$ {\partial}_tW+{\partial}_xF\left(\theta, W\right)={G}_1\left(x,W\right)+{G}_2\left(x,W\right)+B(W){\partial}_xW+T $$
(16)

where F is the numerical fluxes as a conservative product. B is the coupling term. G 1, G 2, and T are three source terms corresponding to the bed level, the bed curvature and the coupling term, and the basal friction, respectively. These terms are defined as follows:

$$ \begin{array}{l}\begin{array}{ll}W=\left[\begin{array}{l}{h}_1\\ {}{q}_1\\ {}{h}_2\\ {}{q}_2\end{array}\right],\hfill & F\left(\theta, W\right)=\left[\begin{array}{l}{q}_1 \cos \theta \\ {}\frac{{q_1}^2}{h_1}{ \cos}^2\theta +gK\frac{{h_1}^2}{2}{ \cos}^3\theta \\ {}{q}_2 \cos \theta \\ {}\frac{{q_2}^2}{h_2}{ \cos}^2\theta +g{\varLambda}_2K\frac{{h_2}^2}{2}{ \cos}^3\theta \end{array}\right]\hfill \end{array}\hfill \\ {}\begin{array}{lll}{G}_1=\left[\begin{array}{l}0\\ {}-g{h}_1 \cos \theta {d}_xb\\ {}0\\ {}-g{h}_2 \cos \theta {d}_xb\end{array}\right],\hfill & {G}_2=\left[\begin{array}{l}0\\ {}-g\left(\frac{{h_1}^2}{4}+{h}_1{h}_2\right) \cos \theta\;{\partial}_x\left({ \cos}^2\theta \right)\\ {}0\\ {}-g\left(\frac{{h_2}^2}{4}+r{\varLambda}_1{h}_1{h}_2\right) \cos \theta\;{\partial}_x\left({ \cos}^2\theta \right)\end{array}\right] and\hfill & T=\left[\begin{array}{l}0\\ {}0\\ {}0\\ {}\Im / \cos \theta \end{array}\right]\hfill \end{array}\hfill \\ {}B(W)=\left[\begin{array}{cccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill -g{h}_1{ \cos}^3\theta \hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill -r{\varLambda}_1g{h}_2{ \cos}^3\theta \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]\hfill \end{array} $$

The computational domain is subdivided into constant intervals of size Δx as shown in Fig. 2. The ith grid cell is denoted by I i  = [x i − 1/2, x i + 1/2] (LeVeque 2002). For the sake of simplicity, the time step, Δt, is also supposed to be constant and t n = nΔt. x i + 1/2 = iΔx and x i  = (i − 1/2)Δx are the centers of the cell I i . W n i denotes the numerical approximation of the average value over the ith cell at time t n as (LeVeque 2002)

Fig. 2
figure 2

Computational domain discretization in x–t space; the cell average W n i is updated using the intermediate values of fluxes F n + 1/2 i ± 1/2 at the cell edges

Full size image
$$ {W}_i^n\cong \frac{1}{\varDelta x}{\displaystyle {\int}_{x_{i-1/2}}^{x_{i+1/2}}W\left(x,{t}^n\right)dx} $$
(17)

The proposed scheme is a two-step Roe-type FVM upwinding the source terms (Yavari-Ramshe et al. 2015). In the first step, the vectors of unknowns, W, are predicted as W *. Then, in the second step, the predicted values of the granular layer velocities, u 2, are corrected based on the effects of the bottom friction.

First step

The predicted values W * = [h 1 * u 1 * h 2 * u 2 *] are defined by the following scheme at the first step (Yavari-Ramshe et al. 2015).

$$ {W}_i^{*}={W}_i^n+{r}_c\left(d{f}_{i-1/2}^{n+1/2,+}-d{f}_{i+1/2}^{n+1/2,-}\right) $$
(18)

where W * i  = [h *1,i   u *1,i   h *2,i   u *2,i ], W i  = [h 1,i   u 1,i   h 2,i   u 2,i ], and r c  = dt/dx. The generalized numerical fluxes df n + 1/2,∓ i ± 1/2  = df ∓ i ± 1/2 (W n i , W n i ± 1 , W n + 1/2 i , W n + 1/2 i ± 1 ) are computed as

$$ d{f}_{i+1/2}^{n+1/2,\mp }=\frac{1}{2}\left\{\pm {F}_{i+1}^{n+1/2}\mp {F}_i^{n+1/2}\pm {S}_{i+1/2}^n\pm {B}_{i+1/2}^nd{W}_{i+1/2}^n-{P}_{1,i+1/2}d{W}_{i+1/2}^{n+1/2}+{P}_{2,i+1/2}\left({S}_{i+1/2}^n+{T}_{i+1/2}^ndx\right)\right\} $$
(19)

W n + 1/2 i is the vector of intermediate values of unknowns (\( {W}_i^{n+1/2}={W}_i^n+\frac{r_c}{2}\left(d{f}_{i-1/2}^{n,+}-d{f}_{i+1/2}^{n,-}\right) \)) computed at dt/2. Furthermore, S i + 1/2 = S 1,i + 1/2 + S 2,i + 1/2 + S 3,i + 1/2 + S 4,i + 1/2 where

$$ \begin{array}{l}{S}_{1,i+1/2}=\left[\begin{array}{l}0\\ {}-g{h}_{1,i+1/2} \cos {\theta}_{i+1/2}\\ {}0\\ {}-g{h}_{2,i+1/2} \cos {\theta}_{i+1/2}\end{array}\right]d{b}_{i+1/2},\hfill \\ {}{S}_{2,i+1/2}=\left[\begin{array}{l}0\\ {}-g\left({h}_{1,i+1/2}^2/4+{h}_{1,i+1/2}{h}_{2,i+1/2}\right) \cos {\theta}_{i+1/2}\\ {}0\\ {}-g\left({h}_{2,i+1/2}^2/4+r{\varLambda}_1{h}_{1,i+1/2}{h}_{2,i+1/2}\right) \cos {\theta}_{i+1/2}\end{array}\right]d{\left({ \cos}^2\theta \right)}_{i+1/2},\hfill \\ {}\begin{array}{ll}{S}_{3,i+1/2}=\left[\begin{array}{l}0\\ {}-3g{h_{1,i+1/2}}^2/4 \cos {\theta}_{i+1/2}\\ {}0\\ {}-3g{\varLambda}_2{h_{2,i+1/2}}^2/4 \cos {\theta}_{i+1/2}\end{array}\right]d{\left({ \cos}^2\theta \right)}_{i+1/2},\hfill & {S}_{4,i+1/2}=\left[\begin{array}{l}-{q}_{1,i+1/2}\\ {}-{q}_{1,i+1/2}^2/{h}_{1,i+1/2}\\ {}-{q}_{2,i+1/2}\\ {}-{q}_{2,i+1/2}^2/{h}_{2,i+1/2}\end{array}\right]d{\left( \cos \theta \right)}_{i+1/2}\hfill \end{array}\hfill \end{array} $$

and db i + 1/2 = b i + 1 − b i , d(cos θ) i + 1/2 = cos θ i + 1 − cos θ i , and d(cos2 θ) i + 1/2 = cos2 θ i + 1 − cos2 θ i . Moreover, P 1,i + 1/2 = κ i + 1/2|D i + 1/2|κ − 1 i + 1/2 is the Roe correction term (Yavari-Ramshe et al. 2015). |D i + 1/2| is a diagonal matrix defined as (Yavari-Ramshe et al. 2015)

$$ \left|{D}_{i+1/2}\right|=\left[\begin{array}{cccc}\hfill \left|{\lambda}_{1,i+1/2}\right|\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill \left|{\lambda}_{2,i+1/2}\right|\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill \left|{\lambda}_{3,i+1/2}\right|\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \left|{\lambda}_{4,i+1/2}\right|\hfill \end{array}\right] $$

λ l,i + 1/2, l = 1, 2, 3, 4, represents the local eigenvalues of the Jacobean matrix A or the coefficient matrix of the system of model Eq. (14) which is defined as \( {A}_{i+1/2}=\left[\begin{array}{cc}\hfill {J}_{i+1/2}^1\hfill & \hfill {B}_{i+1/2}^1\hfill \\ {}\hfill {B}_{i+1/2}^2\hfill & \hfill {J}_{i+1/2}^2\hfill \end{array}\right] \) where

$$ \begin{array}{l}{J}_{i+1/2}^1=\left[\begin{array}{cc}\hfill 0\hfill & \hfill \cos {\theta}_{i+1/2}\hfill \\ {}\hfill -{\overline{u}}_{1,i+1/2}^2 \cos {\theta}_{i+1/2}+{c}_{1,i+1/2}^2{ \cos}^2{\theta}_{i+1/2}\hfill & \hfill 2{\overline{u}}_{1,i+1/2} \cos {\theta}_{i+1/2}\hfill \end{array}\right]\hfill \\ {}{J}_{i+1/2}^2=\left[\begin{array}{cc}\hfill 0\hfill & \hfill \cos {\theta}_{i+1/2}\hfill \\ {}\hfill -{\overline{u}}_{2,i+1/2}^2 \cos {\theta}_{i+1/2}+{\varLambda}_2{c}_{2,i+1/2}^2{ \cos}^2{\theta}_{i+1/2}\hfill & \hfill 2{\overline{u}}_{2,i+1/2} \cos {\theta}_{i+1/2}\hfill \end{array}\right]\hfill \\ {}\begin{array}{ll}{B}_{i+1/2}^1=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ {}\hfill {c}_{1,i+1/2}^2{ \cos}^2{\theta}_{i+1/2}\hfill & \hfill 0\hfill \end{array}\right],\hfill & {B}_{i+1/2}^2=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ {}\hfill r{\varLambda}_1{c}_{2,i+1/2}^2{ \cos}^2{\theta}_{i+1/2}\hfill & \hfill 0\hfill \end{array}\right]\hfill \end{array}\hfill \end{array} $$

and κ i + 1/2 is the matrix whose columns are the local eigenvectors associated with each local eigenvalue λ l,i + 1/2. The coefficient matrix A is evaluated at the Roe’s intermediate states which are calculated as (Yavari-Ramshe et al. 2015; Fernández-Nieto et al. 2008)

$$ \begin{array}{l}\begin{array}{lll}{\overline{u}}_{k,i+1/2}=\frac{\sqrt{h_{k,i+1}}{u}_{k,i+1}+\sqrt{h_{k,i}}{u}_{k,i}}{\sqrt{h_{k,i+1}}+\sqrt{h_{k,i}}},\hfill & {h}_{k,i+1/2}=\frac{h_{k,i+1}+{h}_{k,i}}{2},\hfill & \cos {\theta}_{i+1/2}=\frac{ \cos {\theta}_i+ \cos {\theta}_{i+1}}{2},\hfill \end{array}\hfill \\ {}{ \cos}^2{\theta}_{i+2}=\frac{{ \cos}^2{\theta}_i+{ \cos}^2{\theta}_{i+1}}{2}\hfill \end{array} $$

for k = 1, 2. \( {c}_{{}_{k,i+1/2}}^n=\sqrt{g{h}_{k,i+1/2} \cos {\theta}_{i+1/2}} \) stands for the characteristic wave velocity and dW i + 1/2 = W i + 1 − W i .

P 2,i + 1/2 = κ i + 1/2 sgn(D i + 1/2)κ − 1 i + 1/2 is the correction part of the projection matrixes applied for upwinding the source terms (Yavari-Ramshe et al. 2015). sgn(D i + 1/2) is a diagonal matrix defined as follows (Yavari-Ramshe et al. 2015)

$$ \operatorname{sgn}\left({D}_{i+1/2}\right)=\left[\begin{array}{cccc}\hfill \operatorname{sgn}\left({\lambda}_{1,i+1/2}\right)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill \operatorname{sgn}\left({\lambda}_{2,i+1/2}\right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill \operatorname{sgn}\left({\lambda}_{3,i+1/2}\right)\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \operatorname{sgn}\left({\lambda}_{4,i+1/2}\right)\hfill \end{array}\right] $$

The coupling term B and the Coulomb friction matrix T are defined as (Fernández-Nieto et al. 2008)

$$ {B}_{i+1/2}=\left[\begin{array}{cc}\hfill 0\hfill & \hfill {B}_{i+1/2}^1\hfill \\ {}\hfill {B}_{i+1/2}^2\hfill & \hfill 0\hfill \end{array}\right]\kern0.5em \mathrm{and}\kern0.5em {T}_{i+1/2}=\left[\begin{array}{c}\hfill 0\hfill \\ {}\hfill 0\hfill \\ {}\hfill 0\hfill \\ {}\hfill {\Im}_{i+1/2}/ \cos {\theta}_{i+1/2}\hfill \end{array}\right] $$

where

$$ \begin{array}{l}{\Im}_{i+1/2}=\left\{\begin{array}{l}{\Im}_{1,i+1/2}+{\Im}_{2,i+1/2}\kern1em \left|{q}_{2,i+1/2}\right|>\frac{\varDelta t{\sigma}_{c,i+1/2}}{ \cos {\theta}_{i+1/2}}\\ {}{\tau}_{crit,i+1/2}\kern4em Otherwise\end{array}\right.\hfill \\ {}{\Im}_{1,i+1/2}=-{c}_{2,i+1/2} \cos {\theta}_{i+1/2}\left(1-r\right)\operatorname{sgn}\left({\overline{u}}_{2,i+1/2}\right) \tan \delta \hfill \\ {}{\Im}_{2,i+1/2}=-{h}_{2,i+1/2}{\overline{u}}_{2,i+1/2}^2\frac{ \sin {\theta}_{i+1}- \sin {\theta}_i}{\varDelta x}\operatorname{sgn}\left({\overline{u}}_{2,i+1/2}\right) \tan \delta \cos {\theta}_{i+1/2}\hfill \\ {}{\sigma}_{c,i+1/2}=\left(1-r\right){c}_{2,i+1/2}^2 \cos {\theta}_{i+1/2} \tan {\delta}_0\hfill \\ {}\begin{array}{l}{\tau}_{crit,i+1/2}={c}_{2,i+1/2}^2 \cos {\theta}_{i+1/2}\left\{\left({\varLambda}_2-r{\varLambda}_1\right)\left({b}_{i+1}-{b}_i+{h}_{2,i+1}{ \cos}^2{\theta}_{i+1}-{h}_{2,i}{ \cos}^2{\theta}_i\right)/\varDelta x\right.\\ {}\kern4em +\left(1-{\varLambda}_2\right)\left(\left({b}_{i+1}-{b}_i\right)/\varDelta x+\left({h}_{2,i+1/2}/4\right)\left({ \cos}^2{\theta}_{i+1}-{ \cos}^2{\theta}_i\right)/\varDelta x\right\}\end{array}\hfill \end{array} $$

At the first step, T is only included in the uncentered part of the scheme. The actual effects of the Coulomb friction term on the granular layer velocities are reflected in the second step (Fernández-Nieto et al. 2008). The vector of unknowns, \( {W}_{{}^i}^{*} \), calculated by Eq. 18, is predicted without considering the interaction between the granular material and the non-erodible bed. In the second step, the flow thicknesses and the first layer velocities remain the same, i.e., h n + 1 k,i  = h * k,i (k = 1,2) and q n + 11,i  = q *1,i , but the predicted values of q *2,i will be modified based on the effects of the Coulomb friction to compute the state values corresponding to the next time step, \( {W}_{{}^i}^{n+1} \).

Second step

In this step, the state values, \( {W}_{{}^i}^{*} \), predicted in the first step, are applied to calculate the updated values of granular layer velocity q n + 12 , based on the following equations (Fernández-Nieto et al. 2008).

$$ {q}_{2,i}^{n+1}=\left\{\begin{array}{l}\left({q}_i^{*}+\left({\Im}_{1,i}^{*}+{\Im}_{2,i}^{*}\right)\varDelta t/ \cos {\theta}_i\right.\kern1em \left|{q}_{2,i}^{*}\right|>\frac{\sigma_c^{*}\varDelta t}{ \cos {\theta}_i}\\ {}0\kern11em \mathrm{Otherwise}\end{array}\right. $$
(20)

where

$$ \begin{array}{l}{\Im}_{1,i}^{*}=-\left(1-r\right)\frac{{\left({c}_{2,i-1/2}^{*}\right)}^2+{\left({c}_{2,i+1/2}^{*}\right)}^2}{2} \cos {\theta}_i\operatorname{sgn}\left({q}_{2,i}^{*}\right) \tan \delta \hfill \\ {}{\Im}_{{}_{2,i}}^{*}=-\frac{h_{2,i-1/2}^{*}+{h}_{2,i+1/2}^{*}}{2}{{\overline{u}}_i^{*}}^2\frac{ \sin {\theta}_{i+1/2}- \sin {\theta}_{i-1/2}}{\varDelta x}\operatorname{sgn}\left({q}_{2,i}^{*}\right) \tan \delta \cos {\theta}_i\hfill \\ {}\begin{array}{ll}{\sigma}_{{}_{c,i}}^{*}=\left(1-r\right)\frac{{\left({c}_{2,i-1/2}^{*}\right)}^2+{\left({c}_{2,i+1/2}^{*}\right)}^2}{2} \cos {\theta}_i \tan {\delta}_0,\hfill & {c}_{{}_{2,i+1/2}}^{*}=\sqrt{g\frac{h_{2,i}^{*}+{h}_{2,i+1}^{*}}{2} \cos {\theta}_{i+1/2}}\hfill \end{array}\hfill \end{array} $$

Based on Eq. 20, when the Coulomb friction term is less than the critical resistance of the bottom against the flow, |T| < σ c , the granular material stops moving, q n + 12  = 0. It shows that the numerical treatment of the Coulomb friction term acts like a predictor-corrector method.

Numerical model properties

The followings are some properties of the present model regarding the system of model equations and its discretization.

  • The Courant–Friedrichs–Lewy (CFL) condition is applied in the present model as one of the stability requirements (Courant et al. 1928).

    $$ \max \kern0.5em \left\{{\left\Vert {\lambda}_{l,i\pm 1/2}\right\Vert}_{\infty },\kern1em 1\le l\le 4,\kern1em 0\le i\le m\right\}\frac{\varDelta t}{\varDelta x}\le \gamma $$
    (21)

    where 0 < γ ≤ 1 is a constant, λ l,i ± 1/2 are the local eigenvalues of the Jacobean matrix A, and m is the number of computational cells.

  • The present model is a well-balanced scheme. It satisfies all the stationary solutions regarding water at rest and no movement for the granular layer when its angle is less than the angle of repose of the granular material (Yavari-Ramshe et al. 2015). The steady state corresponding to water at rest over a stationary sediment layer is equivalent to the following condition,

    $$ \left\{\begin{array}{l}b+\left({h}_1+{h}_2\right){ \cos}^2\theta =cst\\ {}\left|\left({\varLambda}_2-r{\varLambda}_1\right){\partial}_x\left(b+{h}_2{ \cos}^2\theta \right)+\left(1-{\varLambda}_2\right)\left({\partial}_xb+\frac{h_2}{4}{\partial}_x{ \cos}^2\theta \right)\right|\le \left(1-r\right) \tan {\delta}_0\\ {}{u}_1={u}_2=0\end{array}\right. $$
    (22)

    The second inequality in Eq. 22 is equivalent to stationary state of the second layer when its angle is less than the angle of repose. This inequality is obtained from the momentum conservation equation of the second layer considering u 2 = 0 where ℑ < σ c  = gh 2 cos2 θ tan δ 0. When the angle of granular layer is less than the angle of repose, this inequality is satisfied and the second layer will remain stationary (Yavari-Ramshe et al. 2015; Fernández-Nieto et al. 2008).

  • In Roe-type schemes, the fluxes may not be computed correctly when one of the eigenvalues of the Jacobean matrix A vanishes (Castro et al. 2003). In this situation, the numerical viscosity of the scheme disappears which may cause inappropriate numerical behavior (Castro et al. 2003). One practical example of this condition is when the flow is critical. A proper solution, applied in the present model, is increasing the near-zero eigenvalues in critical cells based on the right, λ R, and the left, λ L, eigenvalues of the critical cell as

    $$ {\left|\lambda \right|}^{*}=\frac{\lambda^2}{\varDelta \lambda }+\frac{\varDelta \lambda }{4}\kern0.5em \mathrm{When}\kern0.5em -\varDelta \lambda /2<\lambda <\varDelta \lambda /2 $$
    (23)

    where Δλ = 4(λ R − λ L) (Van Leer et al. 1989). Then, the flux terms are computed based on these modified eigenvalues |λ|*.

  • The present model is able to deal with various situations of wet/dry transitions applying a modified wet/dry treatment (Yavari-Ramshe et al. 2015) based on the non-linear method of Castro et al. (2005b) where only one of the layers is involved in the wet/dry situation. This wet/dry algorithm is modified by Yavari-Ramshe et al. (2015) to deal with the bed curvature changes in the present model. When both layers are engaged in a wet/dry front, solving a non-linear Riemann problem happens to be complicated. In these situations, the wet/dry fronts are treated by an approximation of the present wet/dry algorithm proposed by Castro et al. (2005a).

Numerical results

In this section, the present model is applied to simulate two sets of available experimental data performed by Ataie-Ashtiani and Najafi-Jilani (2008) and Ataie-Ashtiani and Nik-Khah (2008) on submarine and subaerial LGWs, respectively. Their experimental setup is briefly explained in the following. The model parameters are calibrated for both submarine and subaerial landslides including an unconfined mass of sand. A sensitivity analysis is performed to investigate the effects of two-phase nature of the landslide based on constitutive structure of the slide on landslide deformations and induced water surface fluctuations. Afterward, the effects of the sliding mass deformability on generated wave characteristics are studied in comparison with the experiments and the numerical results of LS3D model (Ataie-Ashtiani and Najafi-Jilani 2007). LS3D is a two-dimensional depth-averaged Boussinesq-type model developed by Ataie-Ashtiani and Najafi-Jilani (2007) to study submarine LGWs. The model has been extended for simulating subaerial real world cases by Ataie-Ashtiani and Yavari-Ramshe (2011). In LS3D, landslide has a rigid hyperbolic-shaped geometry described using a truncated hyperbolic secant function as a time-variable bottom boundary (Ataie-Ashtiani and Najafi-Jilani 2007).

Experimental setup

Two series of 120 experiments were performed in a part of a 25-m-long, 2.5-m-wide, and 1.8-m-deep flume at Sharif University of Technology (SUT). Figure 3 shows a schematic of this experimental setup. The flume contained two frictionless inclined planes with slopes adjustable from 15° to 60°: one applied as a sliding slope and the other as a wave runup surface. Eight wave gauges, the Validyne DP15 differential pressure transducers, were located at eight points along the central axis of the tank, St. 1 to St. 8, shown on Fig. 3, to record the water surface fluctuations. In these experiments, the spatial and temporal changes of the induced wave properties, such as amplitude and period, are studied. Furthermore, the effects of the bed slope angle, the still water depth, the initial depth of the slide mass center, and the slide geometry and rigidity on LGWs are investigated. Further information on the experiments can be found in Ataie-Ashtiani and Najafi-Jilani (2008), Ataie-Ashtiani and Nik-Khah (2008), and Najafi-Jilani and Ataie-Ashtiani (2008).

Fig. 3
figure 3

Schematics of the experimental setup for LGWs. All dimensions are in centimeter (Ataie-Ashtiani and Nik-Khah 2008)

Full size image

The sliding masses are either rigid, made of 2-mm-thick steel sheet with various dimensions and shapes (wedge, cubic, and hyperbolic shaped) or deformable, sand grains with mean diameter, D 50, of about 0.8 cm and density of about 1.9 g/cm3. Deformable slides have two different categories. In the first group, the slides are made of unconfined lump of sand representing frictional material, materials with negligible cohesion like loose sands. The second set contained confined sand in a softly deformable lace representing cohesive material such as saturated muds and clays (Ikari and Kopf 2011). In each set of experiments, 18 tests were performed using deformable slides, including 9 tests on each type (unconfined and confined masses) with the same initial wedge shape but three different values of the slope angle θ (30°, 45°, and 60°) and three different values of initial position of the sliding mass (h 0C) for each θ. The still water depth, h 0, for all deformable tests is the constant value of 0.8 m. The experimental parameters and the initial profile of deformable slides are illustrated in Fig. 4. Based on the SH assumptions applied in the present model, the sliding mass is considered to have negligible cohesion. Accordingly, the experimental data of the first group of deformable slides, i.e., unconfined masses, are appropriate to be simulated by the present model.

Fig. 4
figure 4

Schematics of the experimental parameters and the initial wedge-shaped profile of deformable slides. All dimensions are in centimeter

Full size image

Sensitivity analysis

In the following, the effects of the two-phase nature of landslide on induced water surface fluctuations (“Water surface fluctuations” section) and the sliding mass deformations (“Sliding mass deformations” section) are investigated based on different values of λ 1and λ 2 which represents the role of each phase in constitutive structure of the landslide layer. Then, these two parameters are calibrated based on the comparison between numerical and experimental results regarding both the time histories of water surface fluctuations and landslide deformations.

From Eq. 9, the normal stress of the second layer (P 2ZZ  = P S2ZZ  + P f2ZZ  = ρ 1 h 1 cos θ + ρ 2(h 2 − Z)cos θ) is described as the sum of the normal stresses of the solid (P S 2ZZ ) and the fluid (P f 2ZZ ) phases defined by Eq. 10. If λ 1 = λ 2 = 0, then P f2ZZ  = 0 and P 2ZZ  = P S2ZZ . It means that no contribution is considered for the fluid phase in definition of the normal pressures and, consequently, longitudinal stresses along the Coulomb mixture. On the other hand, if λ 1 = λ 2 = 1, then P f2ZZ  = ρ 1 h 1 cos θ + ρ 1(h 2 − Z)cos θ and P S2ZZ  = (ρ 2 − ρ 1)h 2 cos θ. This condition may represent complete liquefaction as the pore water is carrying the entire load of the first layer. Following comparisons confirm the importance of each phase in defining the second-layer stresses such that ignoring each phase causes large differences between numerical and experimental LGWs.

In all the simulated cases, the computational parameters are supposed to be dx = 0.02 m, dt = 0.004 s, and r c = dt/dx = 0.2 satisfying CFL condition. The sliding surface is lubricated to be frictionless which is equivalent to δ ≈ 0. The landslide porosity is calibrated as ψ 0  = 0.3. The second layer density or the Coulomb mixture density can be calculated based on Eq. 2 using the water density of ρ 1 = 1.0 g/cm3 and the sand grain density of ρ s = 1.9 g/cm3 as ρ 2 = 1.63 g/cm3. Accordingly, r = ρ 1/ρ 2 ≈ 0.6135.

Water surface fluctuations

In the following sensitivity analysis, the experimental and numerical results regarding the time history of water surface fluctuations recorded by St. 1 in Fig. 3 are compared. Specifically, the predicted values of the maximum positive amplitude (a p,max) and the maximum negative amplitude (a n,max) of the first LGW are compared with experimental measurements for different values of λ 1and λ 2 to investigate the effects of each phase of landslide on landslide tsunami generation.

Due to considering a small variation of the bed curvature in the present model, i.e., d x θ = Ο(ε), experiment no. 103 of Ataie-Ashtiani and Najafi-Jilani (2008) with the smallest value of incline (θ = 30°) is selected to be simulated by the present model. This experiment is including the release of an unconfined mass of sand through a 30° incline from the first location of h 0C = 0.2751 m. The measured values of a p,max and a n,max of the first LGW are 0.0059 and 0.0279 m, respectively. The numerical results regarding the simulation of experiment 103 of Ataie-Ashtiani and Najafi-Jilani (2008) can be observed in Fig. 5.

Fig. 5
figure 5

a a n,max and a p,max of the first LGW against λ 1 (λ 2 = 0.7) and b their relative errors. c a n,max and a p,max against λ 2 (λ 1 = 0.5) and d their relative errors. Experiment no. 103 of Ataie-Ashtiani and Najafi-Jilani (2008)

Full size image

Based on Fig. 5a, as λ 1 is increased, an impulsive wave with a smaller negative height and a bigger positive height is generated. Larger λ 1 means that the fluid phase is more linked to the water layer and burdens a higher percentage of the first layer pressure at the interface. Figure 5b illustrates the relative errors regarding the prediction of a p,max and a n,max calculated as

$$ Err=\frac{\left|{a}_{\mathrm{n}/\mathrm{p},\mathrm{predicted}}-{a}_{\mathrm{n}/\mathrm{p},\mathrm{measured}}\right|}{a_{\mathrm{n}/\mathrm{p},\mathrm{measured}}} $$
(24)

where a n/p,predicted is the numerical prediction of a n,max or a p,max and a n/p,measured is the equivalent experimental measurement. According to this figure, the relative errors of both a n,max and a p,max are mostly less than 5 % for 0.2 ≤ λ 1 ≤ 0.5. It means that about 35 % of the water layer pressure is applied on the liquid phase and about 65 % on the solid part. Therefore, the pore fluid is not isolated from the first layer and it bears about 35 % of water pressure at the interface. Although with ignoring the contribution of fluid phase (λ 1 = 0), a n,max and a p,max are estimated with the relative error of about 4 % for this case with ψ 0  = 0.3 but for a more porous media (ψ 0 > 0.5). The relative errors increase up to about 50 %. This fact confirms the importance of considering the independent role of each phase of the Coulomb mixture in numerical modeling.

Figure 5c illustrates the sensitivity analysis performed on the LGW properties against λ 2 with λ 1 = 0.5. In contrast with λ 1, as λ 2 is increased, the first LGW has a bigger a n,max and a smaller a p,max. Based on Fig. 5d, for 0.7 ≤ λ 2 ≤ 0.9, there is a good agreement between the experimental and the numerical impulsive waves. From Eq. 10, The second-layer stresses without the water layer pressure are equal to ρ 2(h 2 − Z)cos θ. For this simulated case with ρ 1 = 1.0 g/cm3, ρ 2 = 1.63 g/cm3, and λ 2 ≈ 0.8, P f2ZZ  = 0.8(h 2 − Z)cos θ and P S2ZZ  = 0.83(h 2 − Z)cos θ. It means that each phase burdens about 50 % of the normal stresses of the second layer. This fact confirms that not only the fluid phase is not isolated from the water layer and burdens about 35 % of the first layer pressure, but also it has an important and independent contribution in definition of the Coulomb mixture stresses. Without fluid-phase contribution (λ 2 = 0), a n,max of the first LGWs is about 70 % underestimated. The relative error of about 10 % in estimation of a p,max for 0.7 ≤ λ 2 ≤ 0.9 in Fig. 5d is due to considering λ 1 = 0.5. To have a more accurate estimation, λ 1 should be reduced which is also another verification of its importance.

A possible simplification is considering a same value for λ 1 and λ 2 (Fernández-Nieto et al. 2008). As a result, the fluid phase P f2ZZ  = λ 1 ρ 1(h 1 + h 2 − Z)cos θ will be independent of the solid phase. A more generalization is considering λ 1 = λ 2 = ψ 0 (Fernández-Nieto et al. 2008). In this case, the normal stresses of the solid phase, P S2ZZ  = (1 − ψ 0)(ρ 1 h 1 + ρ s (h 2 − Z))cos θ, depend on the density of the solid part ρ s not the mixture ρ 2. Figure 6 shows that how a n,max and a p,max change against porosity when λ 1 = λ 2 = ψ 0. Based on Fig. 6, both a n,max and a p,max grow as the porosity decreases. From Eq. 2 and ρ s = 1900 kg/m3, lower porosity means having a heavier and consequently more devastative slide that causes bigger waves. The best agreements between numerical and experimental induced waves are obtained for 0.3 ≤ ψ 0 ≤ 0.4. However, sensitivity analysis shows that for having a more accurate estimation, λ 1 and λ 2 should be determined as two independent variables.

Fig 6
figure 6

a Maximum negative (a n,max) and positive (a p,max) amplitudes of the first LGW against different values of porosity ψ 0 and b their relative errors. Experiment no. 103 of Ataie-Ashtiani and Najafi-Jilani (2008)

Full size image

Sliding mass deformations

The landslide deformations are compared with the pictures of landslide depth profiles at 0.3/0.6 and 0.4/0.8 s after releasing the slide for the experiment no. 106 of each submarine and subaerial cases, respectively. These pictures are quantified to be compared with the predicted profiles of the second layer. In experiment 106 of Ataie-Ashtiani and Najafi-Jilani (2008). a mass of sand is released along a 45° inclined plane from the initial position of h 0C = 0.1654 m.

Figure 7 illustrates landslide predicted depth profiles for different values of λ 1 and λ 2 at 0.3 and 0.6 s after releasing the granular mass. With proper definition of the Coulomb mixture parameters like δ, φ, ψ 0, λ 1, and λ 2, various types of cohesion-less landslide materials from dry granular masses to loose mud can be simulated by the present model. When ψ 0, λ 1, and λ 2 are supposed to be zero, P f2ZZ  = 0 and P S2ZZ  = ρ 1 h 1 cos θ + ρ s (h 2 − Z)cos θ which represents a dry granular mass. In this condition, the slide deformations are approximately similar to the illustrated profiles for ψ 0 = 0.3, λ 1 = 0 and λ 2 = 0.2 in Fig. 7a, b. The slide shapes a thick front edge followed by a thin ensuing flow. Besides, the mixture moves very slowly such that it almost preserves its initial shape. When λ 1 = 0 and ψ 0 = 0.3, increasing λ 2 slows the slide elongation; although the numerical flux of the second layer is slightly increased due to the increase of Λ 2 = rλ 2 + K(1 − rλ 2).

Fig. 7
figure 7

Landslide depth profiles for different values of λ 1 and λ 2 at two different times, 0.3 and 0.6 s after releasing the sliding mass. Experiment 106 of Ataie-Ashtiani and Najafi-Jilani (2008)

Full size image

As λ 1 is increased, e.g., Fig. 7c, d, the sliding mass elongates faster and the second layer velocity increases. Large values of λ 1 in combination with a large value of λ 2 may represent complete liquefaction or loose materials like debris/muddy flows or even sediment transports with considering a high porosity, ψ 0. Finally, when λ 1 is supposed to be more than about 0.8 (e.g., Fig. 7e, f), for small values of λ 2, the sliding mass illustrates the same behavior of having a thick front followed by a thinner tail. These results are in agreement with the numerical results of Sassa and Sekiguchi (2010, 2012) who developed a code called LIQSEDFLOW to predict the flow of sediment–water mixtures caused by liquefaction or fluidization under dynamic environmental loading with considering the multiphase nature of submarine sediment gravity flows. They emphasize on the important role of the two-phase physics of subaqueous gravity flows in modeling the simultaneous processes of flow stratification, deceleration, and redeposition. They results show that considering more sediment concentration (equivalent to smaller λ 2) in a fluidized (high λ 1) granular flow decreases its flow-out potential. Nevertheless, as λ 2 is also increased, the second layer tends to show a dam-break type or fluidic behavior which elongates more rapidly, e.g., the depth profiles regarding the values 0.6 and 0.8 of λ 2 in Fig. 7f. This case can be physically interpreted as a complete liquefaction where the slide moves faster, has the most elongations, and travels the maximum distances.

As a result, when the solid phase of the sliding mass is more effective than the fluid phase (small values of λ 1), the granular flow front gets thicker than the ensuing flow. As λ 1 is increased, the granular layer forms a more symmetric hyperbolic-shaped profile. A large number of available numerical models consider a rigid body with a hyperbolic-shaped geometry as the sliding mass (e.g., Ataie-Ashtiani and Najafi-Jilani 2007; Grilli et al. 1999; Watts et al. 2003). Based on the present numerical results, this idea is proper for a uniform grain sized mass with average values of granular parameters, e.g., 0.3 < λ 1, λ 2 < 0.7, on a constant slope. In these conditions, the slide steadily forms a hyperbolic-shaped profile which progressively elongates along its path. But, it is not suitable for real hazards where there is a general topography; a slide with non-uniform grain size; or loose, fluidic, and liquefied slides. Finally, for a large value of λ 1, the liquefied granular layer shows a dam-break-like behavior where the flow front is thinner than the trailing flow.

Regarding the simultaneous interactions between landslide deformations and water surface fluctuations, a more liquefied granular layer for high values of λ 1 and λ 2 moves fast and elongates rapidly (Fig. 7e, f). This is like a sudden withdrawal beneath the water layer which generates a wave with high a n,max followed by a small a p,max (Fig. 5c). For a more solid slide, where λ 1 and λ 2 are small, the dense landslide elongates slowly (Fig. 7a) but applies a more strong impact to the water body. Therefore, the generated wave has larger a p,max with a smaller a n,max (Fig. 5a).

Therefore, both solid and fluid phases play an important contribution in describing the constitutive structure of the second layer as a two-phase flow. With a single-phase landslide and ignoring the effects of pore fluid or solid phase, accurate prediction of landslide deformations and water surface fluctuations simultaneously and as a coupled system is very unlikely. With considering a single-phase landslide, either water wave properties or landslide deformations or both may have huge differences with experimental measurements. Therefore, for having a more accurate estimation of both layer’s characteristics at the same time, two-phase nature of landslide should be considered in simulations as well as its rheological behavior.

For real LGW hazards, the model parameters can be initially considered as λ 1 = λ 2 = ψ 0. Then, the formation patterns of both LGWs and landslide deformations should be compared with recorded data. If landslide moves very fast or a p,max is underestimated, λ 1 and λ 2 should be reduced. On the other hand, underestimated landslide velocity or overestimated a p,max shows that pore water has a more prominent role in the constitutive structure of the landslide and λ 1 and λ 2 should be increased. For potential landslide hazards with no recorded data, a probabilistic analysis may be performed or different landslide scenarios can be considered including the worst and the safest landslide scenarios (Ataie-Ashtiani and Yavari-Ramshe 2011; Ataie-Ashtiani and Malek-Mohammadi 2007, 2008).

Finally, the experimental depth profiles of landslide at t = 0.3 s and t = 0.6 s for test no. 106 of Ataie-Ashtiani and Najafi-Jilani (2008) are shown in Fig. 12. Two distinct properties can be deduced from these photos regarding the slide deformations. The sliding mass is moving very slowly, its front edge has traveled a short distance of about 7 cm along the inclined surface after 0.6 s. Besides, the slide profile has a thick front followed by a thin trailing flow. These two properties are more corresponding to the computed profiles in Fig. 7a, b. It shows that the best agreements between the experimental and the numerical results regarding landslide deformations obtain with λ 1 less than about 0.4 and λ 2 more than about 0.7, which are in agreement with the estimated intervals in “Water surface fluctuations” section.

Calibration of the model parameters

To calibrate λ 1 and λ 2 for the submarine experiments of Ataie-Ashtiani and Najafi-Jilani (2008). the complete time history of water surface fluctuations recorded at St. 1 and landslide depth profiles are compared with numerical results for tests 103 and 106, respectively. Based on the performed sensitivity analysis, λ 1 and λ 2 are changed within the approximate ranges of 0.2 ≤ λ 1 ≤ 0.5 and 0.7 ≤ λ 2 ≤ 0.9. To quantify the following comparisons between the numerical and the experimental LGWs, the computational error, Err c , is calculated as

$$ Er{r}_C=\frac{{\displaystyle \sum_{i=1}^n\left|\frac{\eta_{\mathrm{numerical}}-{\eta}_{\mathrm{experimental}}}{\eta_{\mathrm{experimental}}}\right|}}{n+1} $$
(25)

in a specified time period of T s , where η represents the water surface fluctuations from still water level and n = T s /Δt. The computational error of landslide depth profiles is calculated with the same equation where η is replaced with h 2 and n is the number of mesh points. Figure 8a illustrates the predicted time histories of LGWs for a number of λ 1 and λ 2 combinations which result in the computational errors less than 5 % in comparison with the experimental measurements. The best agreement is related to the values of 0.45 and 0.75 for λ 1 and λ 2, respectively.

Fig. 8
figure 8

a Water surface fluctuations at the generation stage (St. 1) for experiment 103 of Ataie-Ashtiani and Najafi-Jilani (2008) for different values of λ 1 and λ 2. b Comparison of the slide front location versus time for experiment 106 of Ataie-Ashtiani and Najafi-Jilani (2008) for different values of λ 1 and λ 2

Full size image

The second criterion to adjust the best values of λ 1 and λ 2 is comparing the estimated landslide depth profiles with the equivalent experimental data for test 106 of Ataie-Ashtiani and Najafi-Jilani (2008). Besides the lack of recorded data on landslide deformations, the second difficulty in this regard is related to the initial geometry of the slide in experiment 106 of Ataie-Ashtiani and Najafi-Jilani (2008). The front face of the wedge-shaped landslides (Fig. 3) stands vertical on 30° or 60° inclines but not on the 45° sliding surface of experiment 106. This makes the definition of the initial landslide geometry hard for numerical code. In the present simulations, the slide front face is considered to be vertical also on 45° inclines. The numerical and experimental results of the landslide depth profiles at t = 0.3 s and t = 0.6 s and the temporal landslide front locations are compared for the case 106 of Ataie-Ashtiani and Najafi-Jilani (2008). The slide front locations, x f , versus time are illustrated in Fig. 8b for the same combinations of λ 1 and λ 2 applied in Fig. 8a. The best fitted results are obtained for the same values of λ 1 = 0.45 and λ 2 = 0.75 regarding both landslide depth profiles and front velocities with computational errors less than about 8 and 1 %, respectively. The complete details regarding the comparison of the numerical and the experimental depth profiles of landslide are discussed in “Submarine landslides” section and Fig. 12.

Model verification

Now that all the model parameters are calibrated based on the experimental data, the effects of the slide deformability on induced water wave properties are investigated and compared with the experimental measurements and the LS3D numerical results for both submarine and subaerial cases in the following.

Submarine landslides

The calibrated values of model parameters for submarine LGWs are as follows: λ 1 = 0.45, λ 2 = 0.75, φ = 35°, and ψ 0 = 0.3. The basal friction angle is negligible on the lubricated inclined parts of the flume and about δ = 15° through the horizontal section. Using these values, the numerical results of water surface fluctuations at the generation stage (St. 1 in Fig. 3) are illustrated in Fig. 9 for experiment 103 of Ataie-Ashtiani and Najafi-Jilani (2008). The numerical and experimental results are in a good agreement with a computational error less than about 4 %. The relative errors between the numerical and experimental values of a n,max and a p,max are also less than 5 %.

Fig. 9
figure 9

Water surface fluctuations at the generation stage (St. 1) for experiments 4, 103, and 112 of Ataie-Ashtiani and Najafi-Jilani (2008); comparison between the present model, LS3D model, and the experimental measurements for different slide rigidity

Full size image

To compare the effects of landslide rigidity on induced water waves, water surface fluctuations of experiments 4 and 112 of Ataie-Ashtiani and Najafi-Jilani (2008) are also illustrated in Fig. 9. These three experiments have the same conditions regarding the free surface level, the sliding slope, the slide initial position, geometry, and density. In experiment 4 of Ataie-Ashtiani and Najafi-Jilani (2008). the sliding mass is a rigid body while in experiments 103 and 112 of Ataie-Ashtiani and Najafi-Jilani (2008). it is an unconfined and confined deformable mass of sand, respectively. As it is expected, the numerical LGWs predicted by the present model are in a better agreement with the experimental waves caused by an unconfined mass of sand (Exp. 103) than a rigid (Exp. 4) or confined deformable (Exp. 112) mass.

The present numerical results are also compared with the numerical results of LS3D model in Fig. 9. The water surface fluctuations predicted by LS3D are closer to the experimental measurements of test 4 which are generated by a rigid mass. It is due to considering a time variable bottom boundary with a solid hyperbolic-shaped geometry as the sliding mass (Ataie-Ashtiani and Najafi-Jilani 2007). Besides, limiting the geometry of the rigid landslide to a hyperbolic shape in LS3D model causes a relative error of about 9 % in estimating the a n,max of LGW which is generated with a rigid wedge-shaped body. It is a considerable point which can be also deduced from “Sensitivity analysis” section. It seems that the maximum negative amplitudes of LGWs are more sensitive to landslide deformations than the positive wave height. Based on Fig. 5, a p,max remains in a close range of less than about 20 % to experimental measurements while a n,max changes widely for different values of λ1 and λ2. Therefore, with considering a proper rheological behavior for the sliding mass, the generated wave amplitudes get more than 30 % closer to the measurements.

To examine the ability of the present model in predicting the propagation stage of the LGWs, the predicted time history of water surface fluctuations is compared with the experimental data recorded at the location of the second gauge (St. 2 in Fig. 3) for the same case of experiment 103 of Ataie-Ashtiani and Najafi-Jilani (2008). The numerical and experimental results are illustrated in Fig. 10. The numerical results properly follow the same formation patterns of the experimental data with a computational error of about 10 %. As it can be observed in Fig. 10, the numerical model overestimates the wave amplitudes within the propagation stage. There is also a time phase difference of about 10–15 % between the numerical and the experimental results which makes the numerical wave steeper than the experimental wave. Both observed differences grow with distance from the slide source. These differences are mainly due to the wave dispersion which cannot be properly modeled with the shallow-water-type equations applied in the present model and gradually makes the numerical results far from the experimental data. The secondary factor affecting the accuracy of the numerical results is the one-dimensional simulation of an actual three-dimensional experimental condition. The lateral propagation of LGWs along the flume width magnifies wave dispersion within the propagation stage.

Fig. 10
figure 10

Water surface fluctuations at the propagation stage (St.2) for experiment 103 of Ataie-Ashtiani and Najafi-Jilani (2008); comparison between the present model and the experimental measurements

Full size image

The same comparisons are also performed for experiment 106 of Ataie-Ashtiani and Najafi-Jilani (2008) in Fig. 11. The experimental data of case numbers 13, 106, and 115 are compared with the numerical results of the present model. These three experiments also have the same conditions but different rigidity including a rigid, unconfined deformable, and confined deformable sliding mass, respectively. The numerical and experimental waves are in a good agreement with a computational error less than about 5 %. The relative errors between numerical and experimental values of a p,max and a n,max are about 5 and 1 %, respectively.

Fig. 11
figure 11

Water surface fluctuations at the generation stage (St.1) for experiments 13, 106, and 115 of Ataie-Ashtiani and Najafi-Jilani (2008); comparison between the present model and the experimental measurements for different slide rigidity

Full size image

Finally, the second-layer depth profiles, 0.3 and 0.6 s after releasing the sliding mass are compared with the related experimental results in Fig. 12. As it mentioned in “Calibration of the model parameters” section, the initial landslide profile is numerically defined with a vertical front face while in the real experimental conditions, it has an inclined front face. This explains the computational errors of about 10 % between numerical and experimental depth profiles at both t = 0.3 and t = 0.6  s. To have a more accurate prediction of landslide deformations, a more proper method should be applied to define the initial landslide geometry. One solution which is applied by Savage and Hutter (1989) is considering the initial geometry of landslide the same as the recorded landslide profile at a short time after the beginning of its motion. It is possible if there is a detailed experimental data regarding landslide motion. The relative errors of landslide front locations illustrated in Fig. 8b are about 0.4 and 1.1 % at t = 0.3 and t = 0.6  s, respectively.

Fig. 12
figure 12

Comparison between numerical and experimental depth profiles of landslide, 0.3 and 0.6 s after releasing the slide for experiment 106 of Ataie-Ashtiani and Najafi-Jilani (2008)

Full size image

Subaerial landslides

In this section, the model is applied to simulate the experimental data of Ataie-Ashtiani and Nik-Khah (2008) for LGWs caused by subaerial landslides. The model parameters are calibrated for subaerial cases in the same way of submarine landslides. The experiments include releasing a dry mass of sand from a specified distance outside the water (h 0C) which hits the water surface, enters the flume, and moves beneath the surface until it comes to rest again. Above the water surface, the slide is dry, but when it enters the water, it gets wet. Accordingly, the optimum values of model parameters in this case are different outside and inside the water body. As long as the slide is on the aerial part, there is no fluid phase in the second layer. Therefore, λ 1 and λ 2 are supposed to be zero. Once the sliding mass enters the water, its pores start to be filled with water. The calibrated values of λ 1, λ 2, and ψ 0 for the underwater part of the slide movement are 0.4, 0.7, and 0.4, respectively. Besides, the internal friction angle of the granular material should be reduced to 25° for having more accurate numerical results. Outside the water, there is no surrounded water pressure on the sliding mass. Therefore, grain segregation occurs faster which may decrease the frictional resistance of the grains against each other.

Experiment 105 of Ataie-Ashtiani and Nik-Khah (2008) is simulated with the present model. In this experiment, the initial distance of the slide from the still water surface, h 0C, is 0.5 m over a 30° slope. The model parameters are Δx = 0.02 m and r c = 0.1. Figure 13 illustrates the predicted water surface fluctuations at St. 1, compared with the experimental data of tests 6, 105, and 114 of Ataie-Ashtiani and Nik-Khah (2008) with the same conditions but different slide rigidity including a rigid, unconfined deformable, and confined deformable mass, respectively. The numerical results of LS3D model for the same case are also shown in this figure. As it can be observed in Fig. 13, the present numerical results are in a very good agreement with experiment 105 with a computational error less than 5 %. The present model is more consistent with unconfined deformable mass (Exp. 105) while LS3D model is showing a more rigid behavior (more consistent with Exp. 6). a n,max and a p,max are predicted with the relative errors of less than about 1 and 5 %, respectively. The observed difference between the predicted and measured a p,max around t = 3.5 s is probably due to the intrinsic limitation of shallow-water-type equations in wave dispersion modeling and also one-dimensional simulation of the actual three-dimensional experiments.

Fig. 13
figure 13

Water surface fluctuations at the generation stage (St.1) for experiments 6, 105, and 114 of Ataie-Ashtiani and Nik-Khah (2008); comparison between the present numerical model, LS3D model, and the experimental measurements with different slide rigidity

Full size image

Submarine and subaerial LGWs have different pattern of formation. As it can be observed in Figs. 9 and 11, submarine LGWs start with negative amplitude followed by a positive wave which are the maximum negative and positive wave heights. On the other hand, subaerial LGWs start with a positive wave followed by a negative height and the maximum positive and negative amplitudes generally appear as the second generated wave (Ataie-Ashtiani and Yavari-Ramshe 2011). One intricacy regarding the extended version of LS3D model from submarine to subaerial landslide is that the predicted LGWs by LS3D model always show a submarine LGW pattern even though the waves are induced by a subaerial landslide hazard (Ataie-Ashtiani and Yavari-Ramshe 2011). It is due to applying a submarine formulation for the sliding mass with modified values of acceleration and terminal velocity for subaerial cases (Ataie-Ashtiani and Yavari-Ramshe 2011). In Fig. 13, for both cases 6 and 105, the second negative height is the maximum one, but the LS3D results show the first negative wave amplitude as its maximum negative height. This fact confirms the importance of landslide rheology not only for predicting the landslide deformations and the topographical changes of the bottom but also for more accurate estimation of LGW generation patterns and characteristics.

The only drawback regarding the simulation of subaerial cases is when they have strong vertical accelerations and velocities which is an intrinsic limitation of shallow-water equations (Abadie et al. 2010). When the sliding slope increases to 45° or 60° and subaerial mass released from a big initial distance, it may reach to high vertical accelerations which cannot be considered in shallow flow models. Moreover, when the subaerial slide strikes the water surface, a splash zone composed of a three-phase mixture (water-air-soil) happens. In this area, gas phase may have noticeable effects on the generated wave properties. Finally, in some cases, a strong vorticity may also happen in near field which can only be modeled applying fully non-linear Navier–Stokes equations.

Conclusions

A two-layer shallow-water-type model is developed including a granular-type layer moving beneath a layer of water to study LGWs as a fully coupled system. Landslide is modeled as a two-phase solid–fluid Coulomb mixture, a granular medium filled with water where the dissipation within its solid phase is described by a Coulomb-type friction law and normal and longitudinal stresses of the solid phase are related by factor K representing the earth coefficient pressure. A modified definition of K introduced by Hungr (2008) is applied based on dynamic reduction of basal friction angle which improves the numerical treatment of a large depth gradient and the spreading velocity of granular flow tail. The effects of both solid and fluid phases are considered in definition of normal stresses within the second layer by distributer factors λ 1 and λ 2. The numerical model also considers the bed curvature effects by transferring the system of model equations to a local coordinate system connected to the non-erodible bed.

A second-order Roe-type FVM is proposed to solve the model equations as a coupled system. The scheme treats wet/dry transitions numerically based on a modified non-linear method. The proposed method is fully well balanced and satisfies steady-state solutions concerning water at rest and no movement for the granular layer when its angle is less than the angle of repose. The synchronized appearances of flowing/static states can also be captured by model along the landslide path.

The proposed model is applied to investigate the effects and importance of landslide rheology and two-phase nature on both slide deformations and LGW characteristics by comparing the numerical results with the experimental data of Ataie-Ashtiani and Najafi-Jilani (2008) for submarine LGWs and Ataie-Ashtiani and Nik-Khah (2008) for subaerial LGWs. The numerical simulations verify that for proper estimation of both landslide deformation and water surface fluctuations simultaneously, the effects of both phases of landslide should be considered in defining the constitutive structure of the second layer. Ignoring each phase may result in the relative errors up to about 30 % for maximum positive and about 70 % for maximum negative wave amplitudes. Two-phase landslide consideration is especially important for accurate prediction of landslide characteristics including landslide deformation patterns, temporal depth profiles and velocities, and maximum traveling distances. Finally, with appropriate definition of Coulomb mixture parameters including λ 1, λ 2, ψ 0, δ, and φ, the model is able to predict a diversity of landslide hazards and LGWs from dry granular material to loose flows and even sediment transport.

Regarding landslide rheology, numerical results are compared with experimental measurements and a numerical model which considers a rigid moving landslide. Comparisons reveal the importance of a proper rheological behavior to predict the consequent tsunamis accurately. With considering a rigid slide, impulsive wave properties are often overestimated and the patterns of impulsive wave formations are incorrect. With a proper rheological model, numerical results are about 30 % closer to the experiments. It is been observed that maximum negative wave amplitudes are more affected by landslide rigidity than maximum positive amplitudes. It should be noticed that predicting the topographical changes of the seabed after landslide, which is an important matter in continental morphology and geophysics, requires landslide deformations to be forecasted.

The calibrated model is able to predict both landslide deformations and induced surface water fluctuations with computational errors less than about 5 % for both submarine and subaerial cases. The only drawback is for subaerial cases with strong vertical accelerations which are in contrast with shallow flow assumption. The developed and verified model can be applied to study real cases. Authors’ future work focuses on the application of the numerical model for a real case setup to explore the influences of the landslide physical characteristics such as the following: partial submergence, shapes, and geotechnical properties on LGW characteristics.