Introduction

Subaerial landslides entering confined water bodies such as lakes, fjords, and reservoirs may generate large waves that can cause fatalities and serious damage to offshore and onshore property (Roberts et al. 2014). Two well-known examples of subaerial landslides that generated large, damaging waves are the 1963 Vajont disaster in Italy, where a landslide-generated wave overtopped a hydroelectric dam by approximately 70 m and caused more than 2000 fatalities in downstream towns (Müller 1964) and the 1958 Lituya Bay event in Alaska, where the wave generated by an earthquake-triggered rockslide ran up more than 520 m above the shoreline (Miller 1960). Therefore, it is important to predict and manage the risks associated with landslide-generated waves to minimize their potential damage (Oppikofer et al. 2016).

In recent decades, a large number of 2D and 3D numerical models have been developed to simulate landslide-generated waves triggered by subaerial and subaqueous failures (Yavari-Ramshe and Ataie-Ashtiani 2016). Two general approaches have typically been adopted. One is to treat the landslide as a rigid block with predefined shape and kinematic conditions (Heinrich 1992; Grilli and Watts 1999; Wang et al. 2011). This approach may be integrated into an advanced hydrodynamic model such as a Boussinesq-type model, in which both nonlinear and dispersive effects on waves can be well described by considering the vertical structure of the flow (Lynett and Liu 2002; Ataie-Ashtiani and Najafi-Jilani 2007). Since the landslide is often treated as a moving bottom boundary with its motion given a priori, such a model tends to overestimate wave heights and run-ups due to its inaccuracy in capturing the deformation features of the landslide (Ataie-Ashtiani and Yavari-Ramshe 2011; Miller et al. 2017; Yavari-Ramshe and Ataie-Ashtiani 2017). An alternative approach is to treat the landslide as a deformable mass with a specific rheology (Heinrich et al. 2001; Quecedo et al. 2004). Experimental and numerical studies have confirmed that landslide deformation has a significant effect on the impact velocity and frontal shape of the landslide body and, in turn, on wave generation (Fritz et al. 2003; Mohammed and Fritz 2012; Heller and Spinneken 2013). The most widely applied among these deformable mass models are the so-called multilayer models that treat the landslide as a lower layer of fluidized granular material flowing beneath an upper layer of inviscid fluid (Fernández-Nieto et al. 2008; Kelfoun et al. 2010; Ma et al. 2015; Xiao et al. 2015). Various rheological flow models have been used to describe the behavior of the lower granular landslide layer (Heinrich et al. 2001; Gauer et al. 2005; Cremonesi et al. 2011).

To apply the multilayer model, both fully 3D Navier–Stokes equations and depth-averaged equations have been used to simulate the entire process of the landslide motion, its interaction with water and the subsequent wave generation, propagation, and run-up. Since great computational efforts are often required, fully 3D models can only be applied to the simulation of laboratory experiments, or cases with idealized topography (Quecedo et al. 2004; Abadie et al. 2010). In comparison, depth-averaged models have been more widely used to simulate real-world events because they achieve a better balance between acceptable accuracy and moderate computation time (Zweifel et al. 2007; Kelfoun et al. 2010; Giachetti et al. 2011; Cannata et al. 2012; Pastor et al. 2015; Yavari-Ramshe and Ataie-Ashtiani 2017).

Due to the complicated interaction between a landslide and water upon impact, accurate simulation of landslide motion and wave generation, propagation, and run-up using depth-averaged numerical models remains challenging. Most simulations using the depth-averaged approach are based on calibration of rheological parameters to match either the observed landslide run-out or the wave run-up (Cannata et al. 2012; Wang et al. 2015; Wang et al. 2016). To the authors’ knowledge, results that match both the landslide run-out and wave run-up have not previously been achieved in a full-scale case. Furthermore, in most depth-averaged models, a hydrostatic pressure assumption is used at the landslide-water interface during the wave generation phase. However, some experiments and 3D numerical simulation results have shown that the water pressure during impact varies dynamically (Ma et al. 2015; Heller et al. 2016). As discussed in a recent review on studies of landslide-generated waves (Yavari-Ramshe and Ataie-Ashtiani 2016), incorporating non-hydrostatic corrections in depth-averaged models is a key to capturing the complex interaction between the deforming granular mass and water.

In this paper, we develop a fully coupled two-layer flow model comprising a layer of deformable, granular landslide material moving beneath an inviscid and homogeneous layer of water. We integrate some features of the dynamic landslide analysis model DAN3D (Hungr 1995; McDougall and Hungr 2004; McDougall 2006; Hungr and McDougall 2009) and the open-source tsunami analysis model COMCOT (Cornell Multi-grid Coupled Tsunami Model) (Wang and Power 2011; Wang et al. 2016). Both models have been widely used to simulate, respectively, landslides (e.g., McDougall and Hungr 2004; Aaron and Hungr 2016) and tsunamis (e.g., Wu and Huang 2009; Xing et al. 2016). However, they have never been combined to simulate the entire landslide-generated wave process from landslide initiation to wave run-up. In contrast to rigid body models (Wu and Huang 2009; Huang et al. 2016), the present model accounts for the influence of the shape and velocity profile of the landslide upon impact. An empirical formula is introduced to estimate the dynamic water pressure at the interface between the landslide and the water. The resulting coupled two-layer, depth-averaged model with non-hydrostatic pressure is used to simulate waves generated by the rock avalanche that occurred at Chehalis Lake, British Columbia, Canada on December 4, 2007.

The paper is organized as follows. The second section presents the theoretical basis for the two-layer model. The governing equations for the granular landslide and its interaction with the surrounding water are presented. The third section reviews the Chehalis Lake event and the observations and measurements collected after the event. The fourth section shows the numerical results and compares them with documented landslide run-out and wave run-up. The fifth section presents an analysis of  the sensitivity of the results to different landslide rheologies and other key parameters. The last section provides conclusions and a discussion of potential future model improvements.

Two-layer deformable landslide-generated wave model

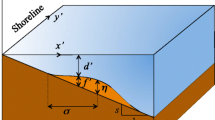
Our model uses COMCOT as a basic framework and incorporates some features developed for the advanced modeling of landslides from DAN3D, namely, the techniques to deal with complex terrain, which are not directly included in COMCOT. A non-hydrostatic pressure correction is also embedded in the model to simulate the landslide-water interaction. Landslide motion, wave generation and propagation are separately formulated, but they form a coupled system. A sketch of the model with the spatial frames of reference is shown in Fig. 1. The landslide motion is solved in a bed-normal coordinate system \( \left(\tilde{x},\tilde{y},\tilde{z}\right) \) with \( \tilde{z} \) oriented upward and perpendicular to the slope. The landslide-generated wave motion is solved in the traditional Cartesian coordinate system with z oriented vertically upward against gravity and the pre-impact, still water surface lying in the (x, y) plane.

Fig. 1
figure 1

Schematic showing the two different frames of reference that are used in the model: a bed-normal orientation for the landslide component and b vertical orientation for the wave component

Full size image

Landslide model

Basic equations and boundary conditions

Assuming that the density of the landslide material is spatially and temporally invariant and the landslide is incompressible, the following continuity Eq. (1) and momentum equation (2) govern the motion and the deformation of the landslide in general:

$$ \nabla \cdot \mathbf{v}=0 $$
(1)
$$ {\rho}_s\left[\frac{\partial \mathbf{v}}{\partial t}+\nabla \cdot \left(\mathbf{vv}\right)\right]=-\nabla \cdot \mathbf{T}+{\rho}_s\mathbf{g} $$
(2)

where ρ s is the landslide density; \( \mathbf{v}\left({v}_{\tilde{x}},{v}_{\tilde{y}},{v}_{\tilde{z}}\right) \) is the vector of landslide velocity; T is the stress tensor; and g is the vectorized acceleration of gravity.

When the landslide is subaerial, the shear stress on the top surface is considered to be negligible and the normal stress is equal to the atmospheric pressure (Hungr 1995). After the landslide enters the water, however, the normal pressure at the water-landslide interface is given by:

$$ {p}^{\left(\mathrm{i}\right)}={\rho}_f gH+{q}^{\left(\mathrm{i}\right)} $$
(3)

where the superscript (i) denotes values at the water-landslide interface (i.e., at \( \tilde{z}={h}_s \) or z =  − h); ρ f is the water density; H is the instantaneous water depth as shown in Fig. 1; g is the acceleration of gravity; and q is the hydrodynamic pressure. The first term on the right side of Eq. (3) is the hydrostatic pressure and the second term is the non-hydrostatic correction. Accurate evaluation of q (i) is challenging. For a heuristic understanding, we consider the conservation of momentum as the landslide impacts the water, as follows:

$$ {m}_e\Delta \mathbf{v}={\mathbf{q}}^{\left(\mathrm{i}\right)}\Delta A\Delta t $$
(4)

where Δv is the velocity variation of the landslide as it enters the water, m e is the effective mass of the landslide, ΔA is a representative cross-sectional area of the landslide in the flow direction, q (i) is the averaged hydrodynamic pressure acting on the landslide, and Δt is a characteristic time interval. A recent experimental study on landslide-generated waves by Miller et al. (2017) shows that, for long and thin granular flows, only the leading portion of the landslide mass contributes to the generation of the leading and highest wave. Therefore, we assume that the effective mass m e  = ρ s s i b i Δl, in which Δl is an effective length of the landslide and s i and b i are, respectively, the frontal thickness and width of the landslide. The change in the velocity of the landslide is assumed to be Δv = α v, in which v is the mean velocity of the landslide and α is a coefficient of proportionality. The time interval can be approximately expressed as Δt = Δl/|v|. As a result, q (i) = m e Δv/(ΔAΔt) = αρ s s i b i v|v|/ΔA. Considering the energy loss during the impact period and the isotropy of the water pressure, q (i) can thus be related to the square of the velocity of the landslide after introducing a dynamic pressure coefficient C p (Kelfoun et al. 2010):

$$ {q}^{\left(\mathrm{i}\right)}={C}_p{\rho}_s{\left|\mathbf{v}\right|}^{\boldsymbol{2}} $$
(5)

Equation (5) is consistent with the conclusions of previous studies (Jiang and LeBlond 1992; Tinti et al. 2006; Kelfoun et al. 2010) in that the absolute water depth has no influence on the dynamic part of the interactive force between the water and the underlying landslide.

We estimate the shear stress τ d at the water-landslide interface based on Manning’s formula and the relative velocity between the landslide and the water (Zweifel et al. 2007; Wang et al. 2016):

$$ {\boldsymbol{\tau}}_d^{\left(\mathrm{i}\right)}={\rho}_f{gn}^2{H}^{-1/3}\left|\mathbf{u}-\mathbf{v}\right|\left(\mathbf{u}-\mathbf{v}\right) $$
(6)

where u is the velocity of the water and n is the Manning coefficient.

It is assumed that the landslide-water interface is immiscible (i.e., mixing at the interface can be ignored) (Ma et al. 2015). The kinematic boundary condition at the interface then requires:

$$ {v}_{\tilde{z}}^{\left(\mathrm{i}\right)}=\frac{\partial {h}_s}{\partial t}+{v}_{\tilde{x}}^{\left(\mathrm{i}\right)}\frac{\partial {h}_s}{\partial \tilde{x}}+{v}_{\tilde{y}}^{\left(\mathrm{i}\right)}\frac{\partial {h}_s}{\partial \tilde{y}} $$
(7)

The bed-normal stress at the base of the landslide equals the bed-normal component of the total weight of material above. The basal shear stress depends on the rheology of the landslide and will be discussed later. Ignoring possible entrainment of material at the base of the landslide, the kinematic boundary condition at the base is:

$$ {v}_{\tilde{z}}^{\left(\mathrm{b}\right)}=0 $$
(8)

where the superscript (b) denotes values at the base of the landslide.

Depth-averaged equations

A depth-integrated model for the landslide motion can be derived by integrating Eqs. (1) and (2) over the landslide thickness; it is formulated as:

$$ \frac{\partial {h}_s}{\partial t}+\frac{\partial \left({\overline{v}}_{\tilde{x}}{h}_s\right)}{\partial \tilde{x}}+\frac{\partial \left({\overline{v}}_{\tilde{y}}{h}_s\right)}{\partial \tilde{y}}=0 $$
(9)
$$ {\displaystyle \begin{array}{l}{\rho}_s\left[\frac{\partial \left({h}_s{\overline{v}}_{\tilde{x}}\right)}{\partial t}+\frac{\partial \left({h}_s{\overline{v}}_{\tilde{x}}^2\right)}{\partial \tilde{x}}+\frac{\partial \left({h}_s{\overline{v}}_{\tilde{x}}{\overline{v}}_{\tilde{y}}\right)}{\partial \tilde{y}}\right]\\ {}\kern1.25em ={\rho}_s{h}_s{g}_{\tilde{x}}-\left[\frac{\partial \left({\overline{\sigma}}_{\tilde{x}}{h}_s\right)}{\partial \tilde{x}}+\frac{\partial \left({\overline{\tau}}_{\tilde{y}\tilde{x}}{h}_s\right)}{\partial \tilde{y}}-{\sigma}_{\tilde{x}}^{\left(\mathrm{i}\right)}\frac{\partial {h}_s}{\partial \tilde{x}}-{\tau}_{\tilde{y}\tilde{x}}^{\left(\mathrm{i}\right)}\frac{\partial {h}_s}{\partial \tilde{y}}+{\tau}_{\tilde{z}\tilde{x}}^{\left(\mathrm{i}\right)}-{\tau}_{\tilde{z}\tilde{x}}^{\left(\mathrm{b}\right)}\right]\end{array}} $$
(10)
$$ {\displaystyle \begin{array}{l}{\rho}_s\left[\frac{\partial \left({h}_s{\overline{v}}_{\tilde{y}}\right)}{\partial t}+\frac{\partial \left({h}_s{\overline{v}}_{\tilde{x}}{\overline{v}}_{\tilde{y}}\right)}{\partial \tilde{x}}+\frac{\partial \left({h}_s{\overline{v}}_{\tilde{y}}^2\right)}{\partial \tilde{y}}\right]\\ {}\kern1.25em ={\rho}_s{h}_s{g}_{\tilde{y}}-\left[\frac{\partial \left({\overline{\tau}}_{\tilde{x}\tilde{y}}{h}_s\right)}{\partial \tilde{x}}+\frac{\partial \left({\overline{\sigma}}_{\tilde{y}}{h}_s\right)}{\partial \tilde{y}}-{\tau}_{\tilde{x}\tilde{y}}^{\left(\mathrm{i}\right)}\frac{\partial {h}_s}{\partial \tilde{x}}-{\sigma}_{\tilde{y}}^{\left(\mathrm{i}\right)}\frac{\partial {h}_s}{\partial \tilde{y}}+{\tau}_{\tilde{z}\tilde{y}}^{\left(\mathrm{i}\right)}-{\tau}_{\tilde{z}\tilde{y}}^{\left(\mathrm{b}\right)}\right]\end{array}} $$
(11)
$$ {\displaystyle \begin{array}{l}{\rho}_s\left[\frac{\partial \left({h}_s{\overline{v}}_{\tilde{z}}\right)}{\partial t}+\frac{\partial \left({h}_s{\overline{v}}_{\tilde{x}}{\overline{v}}_{\tilde{z}}\right)}{\partial \tilde{x}}+\frac{\partial \left({h}_s{\overline{v}}_{\tilde{y}}{\overline{v}}_{\tilde{z}}\right)}{\partial \tilde{y}}\right]\\ {}\kern1.25em ={\rho}_s{h}_s{g}_{\tilde{z}}-\left[\frac{\partial \left({\overline{\tau}}_{\tilde{x}\tilde{z}}{h}_s\right)}{\partial \tilde{x}}+\frac{\partial \left({\overline{\tau}}_{\tilde{y}\tilde{z}}{h}_s\right)}{\partial \tilde{y}}-{\tau}_{\tilde{x}\tilde{z}}^{\left(\mathrm{i}\right)}\frac{\partial {h}_s}{\partial \tilde{x}}-{\tau}_{\tilde{y}\tilde{z}}^{\left(\mathrm{i}\right)}\frac{\partial {h}_s}{\partial \tilde{y}}+{\sigma}_{\tilde{z}}^{\left(\mathrm{i}\right)}-{\sigma}_{\tilde{z}}^{\left(\mathrm{b}\right)}\right]\end{array}} $$
(12)

where the overbars denote depth-averaged values.

Further simplification of Eq. (12) is achieved by assuming that the thickness of the landslide varies gradually and is small relative to its length and width, which is generally true for most landslide types. The terms containing shear stresses \( {\tau}_{\tilde{x}\tilde{z}} \) and \( {\tau}_{\tilde{y}\tilde{z}} \) in the momentum equation along the \( \tilde{z} \) direction are thus small relative to the total bed-normal stress at the base of the landslide and can be neglected (Savage and Hutter 1989; Ma et al. 2015). When the landslide is in contact with the bed, its bed-normal curvature is identical to the bed-normal curvature of the sliding surface. Therefore, the material derivative of \( {v}_{\tilde{z}} \) is equal to the centripetal acceleration due to the bed-normal curvature of the sliding surface in the direction of motion:

$$ \frac{D{\overline{v}}_{\tilde{z}}}{Dt}=\frac{{\left|\mathbf{v}\right|}^2}{R} $$
(13)

where R is the bed-normal radius of curvature of the sliding surface in the direction of motion, which is considered to be positive for a concave surface. The \( \tilde{z} \) direction component of gravity is

$$ {g}_{\tilde{z}}=-g\cos \theta $$
(14)

where θ is the ground slope angle. Substituting Eqs. (13) and (14) into Eq. (12) and neglecting the relatively small shear stresses, we obtain the following expression for the total bed-normal stress at the base:

$$ {\sigma}_{\tilde{z}}^{\left(\mathrm{b}\right)}=\left({\rho}_f gH+{C}_p{\rho}_s{\left|\mathbf{v}\right|}^2\right)+{\rho}_s{h}_s\left(g\cos \theta +\frac{{\left|\mathbf{v}\right|}^2}{R}\right) $$
(15)

allowing Eq. (12) to be replaced by Eq. (15).

Further simplifications of the momentum Eqs. (10) and (11) are possible by adopting a conventional practice in soil mechanics. According to Savage and Hutter (1989), who assumed that all stresses increase linearly with depth below the landslide surface, it is possible to normalize the stress state with respect to the total bed-normal stress by virtue of the stress coefficient, denoted by k ap :

$$ {\overline{\sigma}}_{\tilde{x}}={\overline{\sigma}}_{\tilde{y}}={k}_{ap}{\overline{\sigma}}_{\tilde{z}} $$
(16)

where k ap is the earth pressure coefficient. If the internal shear strength of the landslide is frictional, k ap can be expressed as in Iverson (1997) as:

$$ {k}_{ap}=2\frac{1\pm {\left[1-{\mathrm{cos}}^2{\varphi}_c\left(1+{\mathrm{tan}}^2\varphi \right)\right]}^{1/2}}{{\mathrm{cos}}^2{\varphi}_c}-1 $$
(17)

where φ c is the internal angle of friction of the landslide and φ is the basal friction angle. Equation (17) is valid for φ < φ c . The sign ± is positive (i.e., k ap is the passive earth pressure coefficient) where the local flow is convergent and is negative (i.e., k ap is the active earth pressure coefficient) where the local flow is divergent. If, on the other hand, φ ≥ φ c , k ap must be determined by:

$$ {k}_{ap}=\frac{1+{\mathrm{sin}}^2{\varphi}_c}{1-{\mathrm{sin}}^2{\varphi}_c} $$
(18)

Substituting the stress boundary conditions at the top and bottom of the landslide (i.e., Eqs. (3), (6), and (15)) into Eq. (10) and neglecting the relatively small terms containing transverse stress and spatial derivatives of k ap (Gray et al. 1999), the depth-averaged momentum equation in the \( \tilde{x} \) direction can finally be derived:

$$ {\displaystyle \begin{array}{l}{\rho}_s\left[\frac{\partial \left({h}_s{\overline{v}}_{\tilde{x}}\right)}{\partial t}+\frac{\partial \left({h}_s{{\overline{v}}_{\tilde{x}}}^2\right)}{\partial \tilde{x}}+\frac{\partial \left({h}_s{\overline{v}}_{\tilde{x}}{\overline{v}}_{\tilde{y}}\right)}{\partial \tilde{y}}\right]\\ {}\kern1.25em ={\gamma \rho}_f{h}_s{g}_{\tilde{x}}+{\rho}_f\left( gH+\gamma {C}_p{\left|\mathbf{v}\right|}^2\right)\frac{\partial {h}_s}{\partial \tilde{x}}+{\rho}_f{gn}^2{H}^{-1/3}\left({u}_x-{v}_{\tilde{x}}\cos {\theta}_{\tilde{x}}\right)\left|\mathbf{u}-\mathbf{v}\right|+{\tau}_{\tilde{z}\tilde{x}}^{\left(\mathrm{b}\right)}\\ {}\kern1.25em -{\rho}_f{k}_{ap}\left\{\frac{\partial {h}_s}{\partial \tilde{x}}\left[ gH+\gamma {C}_p{\left|\mathbf{v}\right|}^2+\gamma {h}_s\left(g\cos \theta +\frac{{\left|\mathbf{v}\right|}^2}{R}\right)\right]+{h}_s\left(g\frac{\partial H}{\partial \tilde{x}}+\gamma {C}_p\frac{\partial {\left|\mathbf{v}\right|}^2}{\partial \tilde{x}}\right)\right\}\end{array}} $$
(19)

where γ = ρ s /ρ f is the specific density of the landslide. Terms on the right side of Eq. (19) are grouped according to the type of stress: the first term represents the driving force due to the gravity; the second term represents the effect of the water pressure acting on the interface between the water and the landslide; the third term represents the drag force on the landslide surface; the fourth term is the basal shear stress; and the last term represents differential longitudinal normal stresses within the landslide (the hydrodynamic effect included in this term does not apply before the landslide enters the water). The depth-integrated momentum equation in the \( \tilde{y} \) direction can be derived from Eq. (11) in a similar way. Therefore, a closed system of equations for h s , \( {v}_{\tilde{x}} \), and \( {v}_{\tilde{y}} \) is obtained once the basal shear stress \( {\tau}_{\tilde{z}\tilde{x}}^{\left(\mathrm{b}\right)} \) is evaluated.

Basal shear resistance

The basal shear stress opposes motion of the landslide. The magnitude of \( {\tau}_{\tilde{z}\tilde{x}}^{\left(\mathrm{b}\right)} \) is governed by a basal rheology that may be different from the internal rheology. In this study, two different basal rheologies, frictional and Voellmy, are used to describe the basal shear stress acting on the landslide.

The frictional effect commonly plays an important role in granular materials and generally must be considered when real landslide motions are simulated (Denlinger and Iverson 2004; Aaron and Hungr 2016). Frictional basal resistance is proportional to the effective bed-normal stress at the base of the landslide, \( {\widehat{\sigma}}_{\tilde{z}}^{\left(\mathrm{b}\right)} \), which is the difference between the total bed-normal stress at the base, \( {\sigma}_{\tilde{z}}^{\left(\mathrm{b}\right)} \), and the pore fluid pressure at the base, ξ (b):

$$ {\tau}_{\tilde{z}\tilde{x}}^{\left(\mathrm{b}\right)}=-\left({\sigma}_{\tilde{z}}^{\left(\mathrm{b}\right)}-{\xi}^{\left(\mathrm{b}\right)}\right)\tan \varphi \cdot \frac{v_{\tilde{x}}}{\left|\mathbf{v}\right|}=-{\widehat{\sigma}}_{\tilde{z}}^{\left(\mathrm{b}\right)}\tan \varphi \cdot \frac{v_{\tilde{x}}}{\left|\mathbf{v}\right|} $$
(20)

The component of the basal shear stress along \( \tilde{y} \) direction can be derived in a similar way as Eq. (20). Pore fluid pressure could arise at the base of the landslide by two mechanisms. One is that a thin layer of water could become trapped between the landslide and the substrate due to a lifting effect, which has been observed experimentally (Mohrig et al. 1999) and explained theoretically (Wang et al. 2011). The other mechanism involves the generation of excess pore fluid pressure in the substrate as the landslide overrides it (Hungr and Evans 2004). Pore fluid pressure can be related to the total bed-normal stress by introducing a pore pressure ratio, \( {r}_{\xi }=\xi /{\sigma}_{\tilde{z}} \) (Hungr 1995; McDougall 2006). Then:

$$ {\tau}_{\tilde{z}\tilde{x}}^{\left(\mathrm{b}\right)}=-{\sigma}_{\tilde{z}}^{\left(\mathrm{b}\right)}\left(1-{r}_{\xi}^{\left(\mathrm{b}\right)}\right)\tan \varphi \cdot \frac{v_{\tilde{x}}}{\left|\mathbf{v}\right|} $$
(21)

The Voellmy resistance model combines frictional and velocity-dependent effects and may be expressed as:

$$ {\tau}_{\tilde{z}\tilde{x}}^{\left(\mathrm{b}\right)}=-\left({\sigma}_{\tilde{z}}^{\left(\mathrm{b}\right)}f\left(1-{r}_{\xi}^{\left(\mathrm{b}\right)}\right)+\frac{\rho_sg{\left|\mathbf{v}\right|}^2}{\lambda}\right)\cdot \frac{v_{\tilde{x}}}{\left|\mathbf{v}\right|} $$
(22)

where f is the friction coefficient and λ is a turbulence-effect parameter. The first term on the right side of Eq. (22) accounts for the frictional component of resistance and has the same form as Eq. (21) (i.e., f is analogous to tanφ). The second term accounts for the potential sources of velocity-dependent resistance.

Water wave model

We next apply the depth-averaged nonlinear shallow water equations to model the water waves generated by a landslide. The conventional shallow water equations (Liu et al. 1998), however, must be modified to include the non-hydrostatic effect when depth-averaging the pressure over the moving landslide. Specifically, a direct integration of the pressure term in the Navier–Stokes equations, from the bottom wall boundary of the water layer to the free surface, yields:

$$ {\int}_{-h}^{\eta}\frac{\partial p}{\partial x} dz=\frac{\partial }{\partial x}{\int}_{-h}^{\eta } pdz-{p}^{\left(\mathrm{s}\right)}\frac{\partial \eta }{\partial x}-{p}^{\left(\mathrm{w}\right)}\frac{\partial h}{\partial x} $$
(23)

where p is the total water pressure including both hydrostatic and hydrodynamic parts; η and h are defined in Fig. 1; the superscripts (s) and (w) are values taken, respectively, at the free surface (i.e., at z = η) and at the bottom wall boundary of the water layer (i.e., at z =  − h). Note that the pressure is no longer hydrostatic over the landslide. Interaction between the landslide and the water is accounted for by imposing pressure p (i) at the interface, according to Eq. (3), p (i) = ρ f gH + C p ρ s |v|2.

Assuming that the water pressure increases linearly with depth below the water surface, the pressure at any depth in the water can be expressed by:

$$ p={\rho}_f\left( gH+\gamma {C}_p{\left|\mathbf{v}\right|}^2\right)\frac{\eta -z}{H} $$
(24)

Substituting Eq. (24) and the stress free boundary conditions (relative to the atmosphere pressure) at the free surface of the water into Eq. (23) leads to:

$$ {\int}_{-h}^{\eta}\frac{\partial p}{\partial x} dz={\rho}_f gH\frac{\partial \eta }{\partial x}+\frac{1}{2}{C}_p{\rho}_s{\left|\mathbf{v}\right|}^2\frac{\partial H}{\partial x}+{C}_p{\rho}_sH\left|\mathbf{v}\right|\frac{\partial \left|\mathbf{v}\right|}{\partial x}-{C}_p{\rho}_s{\left|\mathbf{v}\right|}^2\frac{\partial h}{\partial x} $$
(25)

The first term on the right side of Eq. (25) represents the hydrostatic part of the water pressure, and the other three terms represent the hydrodynamic part.

In contrast to our approach, some existing models ignore the hydrodynamic pressure and assume a hydrostatic law to represent the interactive pressure over the landslide surface (Zweifel et al. 2007; Wang et al. 2011; Cannata et al. 2012). That practice is not, however, supported by known experimental results, which show that the pressure along the interface of the water and the landslide varies dynamically and is related to the impact velocity of the landslide on the water surface (Heller et al. 2016). For a given landslide impact velocity, the impulsive wave height and run-up would be underestimated if only the hydrostatic water pressure is considered.

Neglecting the relatively small diffusion effects, the governing equations for the landslide-induced wave motion in the Cartesian coordinates (x,  y,  z) can be written as:

$$ \frac{\partial \eta }{\partial t}+\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\right)=-\frac{\partial h}{\partial t} $$
(26)
$$ \frac{\partial P}{\partial t}+\frac{\partial }{\partial x}\left(\frac{P^2}{H}\right)+\frac{\partial }{\partial y}\left(\frac{PQ}{H}\right)+ gH\frac{\partial \eta }{\partial x}+{f}_x=0 $$
(27)
$$ \frac{\partial Q}{\partial t}+\frac{\partial }{\partial x}\left(\frac{PQ}{H}\right)+\frac{\partial }{\partial y}\left(\frac{Q^2}{H}\right)+ gH\frac{\partial \eta }{\partial y}+{f}_y=0 $$
(28)

where P = Hu x and Q = Hu y denote the volume flux components in the x and y directions, and u x and u y are vertically averaged horizontal velocity components in, respectively, the x and y directions. Additionally, f = (f x ,  f y ) represents the shear stress on the water-landslide interface and does not apply before the landslide impacts the water. In this study, f is split into two parts: we let f = f d  + f p , with f d being the drag force parallel to the landslide surface and f p being the hydrodynamic pressure acting on the landslide surface. Using Manning's law, f d is estimated in terms of the relative velocity between the landslide and the water, as given by Eq. (6):

$$ {f}_{dx}={gn}^2{H}^{-1/3}\left({u}_x-{v}_{\tilde{x}}\cos {\theta}_{\tilde{x}}\right)\left|\mathbf{u}-\mathbf{v}\right| $$
(29)
$$ {f}_{dy}={gn}^2{H}^{-1/3}\left({u}_y-{v}_{\tilde{y}}\cos {\theta}_{\tilde{y}}\right)\left|\mathbf{u}-\mathbf{v}\right| $$
(30)

The second component of f, f p is a result of Eq. (25):

$$ {f}_{px}=\gamma {C}_p\left(\frac{1}{2}{\left|\mathbf{v}\right|}^2\frac{\partial H}{\partial x}+H\left|\mathbf{v}\right|\frac{\partial \left|\mathbf{v}\right|}{\partial x}-{\left|\mathbf{v}\right|}^2\frac{\partial h}{\partial x}\right) $$
(31)
$$ {f}_{py}=\gamma {C}_p\left(\frac{1}{2}{\left|\mathbf{v}\right|}^2\frac{\partial H}{\partial y}+H\left|\mathbf{v}\right|\frac{\partial \left|\mathbf{v}\right|}{\partial y}-{\left|\mathbf{v}\right|}^2\frac{\partial h}{\partial y}\right) $$
(32)

Conceptually, there are two important mechanisms involved in the wave generation by the landslide: 1) the pushing effect in response to the landslide momentum and 2) the bottom-rising effect as a result of significant differences in the bottom geometry. In the present wave model, the first mechanism is represented by the hydrodynamic pressure over the moving landslide, and the second mechanism is included in the varying position and thickness of the landslide.

Numerical implementation of the present model utilizes COMCOT. At each time step, dt, the displacement and thickness of the landslide are first computed along the bed-normal coordinates using Eqs. (9) and (19), and the \( \tilde{y} \) direction counterpart to Eq. (19). The effect of variations in the thickness of the landslide dh s , on the water surface elevation is then calculated from Eq. (26). Finally, the water motion is computed by Eqs. (27) and (28). The equations governing the landslide motion are solved with the explicit upwind finite difference schemes proposed by Kelfoun and Druitt (2005), although with more general quadrilateral grids to discretize the terrain surface. The modified explicit staggered leap-frog finite difference scheme in Wang and Liu (2011) is utilized to solve the nonlinear shallow water equations. A detailed description of the numerical scheme can be found in the literature (Kelfoun and Druitt 2005; Wang and Power 2011).

Overview of the landslide-generated wave at Chehalis Lake

On December 4, 2007, a rock avalanche entered the northwest part of Chehalis Lake, which is located in the southern Coast Mountains 80 km east of Vancouver, British Columbia. The failure involved quartz diorite underlying a steep slope at elevations ranging from approximately 530 to 820 m above sea level (a.s.l.); the head scarp is about 210 m wide (Brideau et al. 2012). The elevation of the lake surface was 221 m a.s.l.

After detaching, the rock mass slid obliquely into a steep bedrock gully, fragmented and traveled a horizontal distance of about 800 m, with an elevation drop of approximately 550 m, before impacting Chehalis Lake (Roberts et al. 2013). Based on the distribution of the rock avalanche deposit on the lake floor (Fig. 2 in Roberts et al. 2013), the landslide appears to have decelerated rapidly upon impact; the debris limit detected by bathymetric surveys conducted following the event does not extend more than 350 m from the western shoreline. The waves generated by the landslide propagated across the lake, ran up the opposite shoreline to an approximate maximum height of 38 m and traveled down the lake to its outlet over 7.5 km away (Roberts et al. 2013).

Fig. 2
figure 2

Overview of the Chehalis Lake landslide. a Location of Chehalis Lake within Chehalis Valley. Elevation data from CDEM. b Overview of the northern end of Chehalis Lake, where run-up, inundation, and geomorphic modification by the landslide-generated wave were greatest. The lake shoreline used in the numerical simulations is 221 m a.s.l. and derived from the CDEM. High-resolution satellite image (31 July 2016) from GoogleEarth. c View to the northwest of the Chehalis Lake landslide (photo taken by N. Roberts in May 2009). The yellow region is the landslide source area

Full size image

The initial failure geometry and travel path are shown in Fig. 2. Based on a comparison of pre-failure and post-failure digital topographic data obtained, respectively, from Canadian Digital Elevation Model (CDEM) and aerial Light Detection and Ranging (LiDAR) data, we estimate the volume of the failed rock mass as 2.2 to 2.5 Mm3. The distribution of the rock avalanche mass above and beneath the lake, derived from orthophotos, LiDAR, and SONAR data sets (Brideau et al. 2012; Roberts et al. 2013), provides precise constraints for the landslide simulation.

Wave run-up, inundation, erosion, and deposition along the shorelines were systematically measured during a 2-week lakeshore survey conducted 18 months after the event (see Roberts et al. 2013). The landslide-generated waves stripped vegetation, soil, and surficial sediment up to tens of meters above the shoreline, leaving a prominent trimline that is still visible today (Fig. 3). The trimline generally decreases in elevation to the north and south away from the landslide impact point, but increases again near the lake outlet, likely due to convergence and amplification of waves in the relatively narrow and shallow southern reach of the lake.

Fig. 3
figure 3

Trimline and wave damage along the shoreline of Chehalis Lake a across the lake from the landslide (photo taken by P. Si in May 2016) and b adjacent to the landslide (photo taken by N. Roberts in May 2009). Note ~3-m-high boat (circled) for scale in (b). Elevations denote the highest evidence of run-up above lake level and, in most cases, extend several meters above the obvious vegetation trimline (for details see Roberts et al. 2013). Photo locations are shown in Fig. 2b

Full size image

Numerical results

Landslide simulation results

We use the field data described in the “Overview of the Landslide-Generated Wave at Chehalis Lake” section to demonstrate the two-layer depth-averaged model proposed in this study. We adjusted the basal rheological parameters by trial and error, taking into consideration published values from comparable case studies (e.g., Sosio et al. 2008), to achieve the best fit with the observed subaqueous run-out of the landslide deposit. The main parameters of the landslide used in the simulation are summarized in Table 1.

Table 1 Input data for the Chehalis landslide-generated wave simulation
Full size table

The simulated landslide volume was V s = 2.2 × 106 m3. Based on field observations, the sliding surface is almost a smooth rock plane and the bedrock gulley down which the rock avalanche traveled contained limited colluvium. Consequently, we assumed erosion/entrainment to be negligible. To best fit the trimline elevations and landslide thicknesses documented at the site by Roberts et al. (2013) following the event, a basal friction angle of 25° was used with the frictional model, along with an internal friction angle of φ c = 35°. The pore pressure ratio at the basal surface, \( {r}_{\xi}^{\left(\mathrm{b}\right)} \), typically ranges between 0 and 1, where the latter represents total liquefaction (Dutto et al. 2015; Pastor et al. 2015). In the present model, the pore pressure ratio was taken to be 0 when the landslide is above the water and 0.7 when the landslide is below the water. The time required to generate this excess pore pressure after impact was neglected. After the landslide impacts the lake, the interactive force between the fragmented debris and the water must be calculated. In the present model, according to published values, a Manning coefficient of n = 0.013, which is appropriate for the interaction of water and the top surface of the landslide (Zweifel et al. 2007; Wang et al. 2016), was used and a dynamic pressure coefficient of C p  = 0.3 was calibrated to match the simulated and observed run-out of the landslide deposit.

In order to simulate the entire processes of the Chehalis Lake event, a computational domain of 3800 m × 8800 m was discretized using a regular grid of 5 m × 5 m in the present study. The time step Δt was automatically determined during the computation to satisfy the Courant–Friedrichs–Lewy (CFL) stability condition for the numerical scheme. The computation was implemented on a desktop computer with a single CPU of 2.6 GHz. It required a total computational time of about 4 h to complete the simulation of a 10-min landslide-generated wave event.

The landslide simulation results are shown in Fig. 4. About 10 s after initiation, the rock mass slides obliquely into the deep gully and rapidly disintegrates. About 22 s after initiation, the disintegrated rock mass impacts the lake with a velocity slightly greater than 40 m/s. When the landslide impacts the lake, most of the momentum is transferred to the water body. The simulated landslide then decelerates rapidly; the frontal velocity is reduced to approximately 5 m/s 30 s after the landslide impacts the water (i.e., roughly 50 s after initiation of the landslide). The frontal depth of the landslide increases dramatically due to the interactive force between the landslide and the water. Unlike some existing numerical models that simulate a relatively long landslide run-out under the water (Wang et al. 2015), the simulated landslide in our model ran out only about 315 m from the shoreline onto the flat lake bottom. This result is consistent with the extent of the deposit documented in the bathymetric survey. After about 80 s, the landslide comes to rest and leaves relatively thick debris in places above the water, especially in the deep gully (Fig. 4d), also consistent with field observations (Fig. 2c) and the LiDAR data. Based on field measurements, the maximum depth of the deposit is approximately 37.5 m, nearly identical to our numerical result of 39 m.

Fig. 4
figure 4

Simulation of landslide motion using a frictional rheological model a 10 s, b 22 s, c 50 s, and d 80 s after initial failure (see Table 1 for model parameters). The landslide stopped at roughly t = 80 s. The solid blue line and dashed black line show, respectively, the lake shoreline and the observed landslide limit. Contour lines are elevations above the lake surface derived from the CDEM. For interpretation of color patterns, the reader is referred to the web version of this article

Full size image

The pre-failure topography and the simulated final landslide profile along section A-A’-A” (Fig. 2b) are shown in Fig. 5 in comparison with topographic data acquired after the event. The simulated maximum depth of debris on the slope outside the deep gully is approximately 20 m at a point about 100 m above the lake surface. The inset in Fig. 5 shows the simulated landslide velocity distribution along section A-A’ before the landslide impacts the water. The landslide velocity fluctuates along section A-A’ due to the complex topography. The velocity increases rapidly at the landslide front, reaching approximately 42 m/s just prior to impact. The simulated frontal thickness at the impact site is approximately 6 m. Experimental studies (Mohammed and Fritz 2012; Heller and Spinneken 2013) show that landslide thickness and velocity at impact are two of the most important parameters governing the generated wave height, as discussed below.

Fig. 5
figure 5

Simulated landslide deposit along section A-A’-A" based on the same frictional model as in Fig. 4 (see Table 1 for parameters). The blue line shows the initial lake surface (221 m a.s.l.). The inset shows the simulated velocity distribution along A-A’ before the landslide impacts the lake

Full size image

Wave simulation results

When the simulated landslide impacts the lake, it pushes and lifts the water surface approximately 50 m above the initial water level. A large wave then propagates across the lake, and runs up the opposite shoreline. Figure 6 shows the simulated wave propagation at different times during wave initiation, propagation, and run-up. About 30 s after the landslide impacts the lake (i.e., 50 s after initiation of of the landslide), the leading wave reaches the east shoreline of Chehalis Lake and runs up to a maximum height of approximately 38 m (Fig. 6b). Meanwhile, waves along the west and east shorelines propagate both up and down the lake, stripping vegetation up to tens of meters above the shoreline (Fig. 3b). At t = 80 s (Fig. 6c), the simulated waves arrive at Skwellepil Fan, with a run-up of approximately 15 m, and at the Chehalis River delta at the north end of the lake, where many trees and a campground were destroyed. The wave energy dissipates rapidly in the shallow and narrow channel off Skwellepil Fan. After 6 min and approximately 8 km of travel (Fig. 6e), the simulated waves reach the south end of Chehalis Lake. Due to funneling and shoaling near this end of the lake, the simulated wave run-ups increase up to 6 m. After eight minutes, the lake surface is more stable with simulated wave amplitudes less than 3 m.

Fig. 6
figure 6

Simulated wave generation and propagation a 30 s, b 50 s, c 80 s, d 180 s, e 340 s, and f 480 s after initial failure. The black line shows the lake shoreline

Full size image

Figure 7 shows simulated wave run-up along both the east and west shorelines compared with field-measured values. The observed wave heights are well simulated by accounting for the hydrodynamic pressure on the landslide-water interface during the wave generation phase. Simulated wave run-ups decrease up and down the lakeshore from the landslide impact point. Waves in the northern part of the lake decay faster than those to the south because they rapidly reach the Chehalis River delta and dissipate most of their energy. In the southern part of the lake, the simulated waves decay more slowly and their heights vary with distance due to water depth changes and shoreline complexity.

Fig. 7
figure 7

Comparison of simulated and observed wave run-up (Roberts et al. 2013) along the east and west shorelines of Chehalis Lake. C p is the dynamic pressure coefficient. The horizontal axis shows the distance along shoreline from the landslide travel path

Full size image

To examine the influence of the non-hydrostatic component of pressure on wave generation, we performed a comparative study by considering only the hydrostatic pressure (i.e., C p  = 0), which corresponds to the conventional practice using existing models, including COMCOT (Zweifel et al. 2007; Wang et al. 2016). The simulated maximum run-up on the east and the west shorelines, as shown in Fig. 7, is approximately 12 and 9 m, respectively, in this case, which is much lower than the observed run-up. Based on the numerical results under various conditions, it is actually possible to demonstrate that the hydrostatic model not only underestimates the wave run-ups along the lake shorelines, but also fails to correctly reproduce the observed landslide trimline and the subaqueous run-out of the landslide deposit. Recently proposed models that make this hydrostatic pressure assumption may be able to simulate the bulk characteristics of landslide-generated waves, but they may not be able to simulate the entire physical process, including reasonably accurate simulations of landslide velocities and landslide deposit distributions both above and below the water.

Analysis and discussion

The major characteristics of the complex landslide-generated wave event at Chehalis Lake are well simulated by the non-hydrostatic two-layer depth-averaged model using the frictional rheology along the base of the landslide. The simulated landslide run-out and wave run-up around the lake shorelines both closely match values measured in the field. The parameters used in the model have been calibrated to match simulated and observed landslide deposit distributions, but are consistent with those used in the previous studies reporting successful back-analyses of rock avalanches (Sosio et al. 2008; Castleton et al. 2016; Grämiger et al. 2016; Aaron et al. 2017; Moore et al. 2017). In this section, the influence of the landslide internal strength and the different basal rheological assumptions on generated waves are discussed.

Influence of internal strength

In some published landslide-generated wave models, a hydrostatic law is assumed to govern the internal stresses in the landslide (i.e., the internal friction angle equals zero) to simplify the numerical computations (Heinrich et al. 2001; Wang et al. 2016). This assumption, however, is unrealistic for fluid-like landslides composed of granular materials that have internal shear strength (Savage and Hutter 1989; Iverson 1997; McDougall 2006; Hungr 2008; Aaron and Hungr 2016). In fact, many studies (McDougall 2006; Wu et al. 2015) have emphasized the effect of internal strength on the spreading behavior of the landslide mass. To highlight the importance of accounting for internal strength using Eq. (17), we ran a simulation of the Chehalis Lake event with the internal friction angle set to zero. The basal resistance parameters are the same as those used in the frictional model with internal strength as described in the “Numerical results” section. The main parameters used in the simulation and the simulation results are summarized in Table 2.

Table 2 Input data and simulation results using frictional rheology with and without internal strength
Full size table

Figure 8a shows the distribution of the landslide debris when it impacts the water, and Fig. 8b shows the final run-out and deposit of the landslide with no internal strength. Compared to the results shown in Fig. 4, it is found that the frontal width is narrower, the impact area is much smaller, the impact velocity is lower, and the frontal thickness is higher when the landslide impacts the lake surface. As a result, the simulated wave is smaller, with a maximum run-up of 28 m on the east shore of the lake, about 10 m lower than the results when internal strength is considered. The longitudinal profiles of the landslide in the deep gully (profile A-A’) when the landslide impacts the lake, are shown in Fig. 9. The figure shows that most of the landslide simulated with no internal strength concentrates in the gully, with a maximum thickness of approximately 75 m. Furthermore, the landslide decelerates more slowly when it enters the lake and stops about 100 s after initiation, resulting in an extra run-out of approximately 60 m under water. The landslide finally forms a relatively narrow deposit, inconsistent with the deposit documented in the bathymetric survey (Fig. 2 in Roberts et al. 2013).

Fig. 8
figure 8

Simulation results of landslide motion without internal strength (φ c  = 0∘) a 22 s and b 100 s after landslide initiation. The dashed black line shows the observed limit of the landslide. The landslide stopped at about t = 100 s

Full size image
Fig. 9
figure 9

Profile of landslide thickness variations along cross-section A-A’ for the frictional rheology model with and without internal strength

Full size image

Comparison between different landslide rheological models

Various rheological models, including frictional, Voellmy, Bingham, and Herschel–Bulkley, have been used to describe the diverse behavior of natural landslides. They have also been integrated into different numerical models for simulating landslide-generated waves. Yavari-Ramshe and Ataie-Ashtiani (2016) reviewed a large number of these numerical models and found that the frictional and Voellmy rheologies are the most widely used, accounting for about 70% of the total models they surveyed. To examine the sensitivity of numerical results to these two widely used rheologies, we compared the frictional results documented in the “Numerical results” section with the results of a simulation using the Voellmy rheology (i.e. Eq. (22)).

The input parameters for the Voellmy rheology were obtained by trial and error to match the observed landslide data. The best match was produced with f = 0.32 and λ = 900 m/s2. These values are within the range of Voellmy parameters reported in previous successful back-analyses of similar landslide events (e.g., Castleton et al. 2016; Manzanal et al. 2016). The other parameters (φ c , C p , n, and \( {r}_{\xi}^{\left(\mathrm{b}\right)} \)) were kept the same as those used with the frictional rheology. For the subaqueous portion of the landslide, \( {r}_{\xi}^{\left(\mathrm{b}\right)}=0.7 \) results in a bulk basal friction coefficient of f = 0.1. This value was then used to reproduce the observed landslide impact area. Previous back-analyses of rock avalanches that overrode saturated substrate suggested a similar bulk friction coefficient when using the Voellmy rheology (e.g., Hungr and Evans 1996; McDougall et al. 2006; Aaron and Hungr 2016). The reduction of basal resistance in the subaqueous portion of the landslide could also be explained by rapid undrained loading of the saturated lake bottom materials, a mechanism for subaerial rock avalanches described in Hungr and Evans (2004). The main parameters that were used with the different rheologies and the relevant simulation results are summarized in Table 3.

Table 3 Input data and simulation results using Voellmy rheology
Full size table

The simulated maximum wave run-up using the Voellmy rheology is similar to the results using the frictional rheology (Table 3). However, as shown in Tables 2 and 3, the frontal velocity and profile of the landslide at the time of impact are different. The simulated landslide velocity distributions are shown in Fig. 10. Using the Voellmy rheology, the simulated velocity before the landslide enters the water is less than the velocity obtained using the frictional rheology. The reason for this difference is that the velocity-dependent term in Eq. (22) dominates basal resistance when the landslide has a relatively high velocity, thus limiting the flow velocities. When the landslide enters the water, it decelerates rapidly and the Voellmy rheology degenerates to the frictional rheology as the velocity-dependent term ρ s g|v|2/λ reduces to zero. Accordingly, the frictional term in Eq. (22) determines the final motion of the landslide under the water. Since the friction coefficient f = 0.32 ≈ tan 18∘ is smaller than the frictional angle φ = 25∘that was used with frictional rheology, the simulation with the Voellmy rheology moves for a longer time, and the final run-out under water is farther, than the simulation using frictional rheology.

Fig. 10
figure 10

Landslide velocity evolution for two different rheologies assuming C p  = 0.3, \( {r}_{\xi}^{\left(\mathrm{b}\right)}=0.7 \), n = 0.013. a frictional rheology with φ = 25∘, φ c  = 35∘. b Voellmy rheology with f = 0.32, λ = 900 m/s2. The dashed line shows the observed limit of the landslide

Full size image

The longitudinal impact profiles of the simulated landslide using the two rheological models are presented in Fig. 11. The simulated landslide using the frictional rheology concentrated in the deep gully (along profile A-A’) and has a maximum thickness of approximately 60 m at the rear of the profile. The simulated landslide using the Voellmy rheology spreads more widely across the slope, and the frontal thickness at the impact site is approximately 4 m greater than the simulation using the frictional rheology. Overall, the frictional rheology better simulates features of the landslide deposit. However, the landslide-generated waves simulated by the two rheologies are not very different in terms of their size, likely because the effect of a lower simulated impact velocity in the Voellmy case is offset by the effect of a higher simulated impact thickness. This result is supported by experimental results, which indicate that the amplitude of generated waves correlates strongly with impact velocity and frontal thickness (Heller and Hager 2010; Mohammed and Fritz 2012).

Fig. 11
figure 11

Profile of landslide thickness variations along cross-section A-A’ for two different rheologies

Full size image

By changing the turbulence parameter λ from 900 to 500 m/s2, the impact velocity decreases to approximately 34 m/s and the impact thickness decreases by approximately 3 m. These changes result in a much smaller wave run-up (approximately 28 m), which shows the important influence of the velocity-dependent term on generated waves.

Conclusion

In this paper, we present a two-layer depth-averaged model that takes into account non-hydrostatic pressure on the landslide-water interface. We apply the model to the rock avalanche-generated wave in Chehalis Lake in 2007. The simulation results using the frictional rheology model and accounting for internal strength of the landslide match field data for the landslide deposit both above and below the lake surface, as well as wave run-up along the shoreline. This work demonstrates the potential usefulness of the two-layer depth-averaged approach in modeling real landslide-generated wave events. Sensitivity analyses demonstrate the important influence of landslide internal strength, dynamic water pressure, and different landslide rheologies on the generated waves. All other factors being equal, maximum wave run-up is underestimated when internal strength or the dynamic component of pressure at the landslide-water interface is neglected, potentially resulting in underestimation of hazard and risk along shorelines.

Calibrated simulation results using the frictional and Voellmy rheologies can produce similar wave run-up results, although the frictional rheology tends to produce high impact velocities and a tapered flow front, whereas the Voellmy rheology tends to produce relatively lower impact velocities and a blunt flow front. In real-world cases, the appropriate rheology should be chosen based on calibration back-analyses of previous landslides that are similar to the landslide in question. Efforts are ongoing to create a database of calibrated back-analyses from which parameters can be estimated for true predictive analyses. The successful simulation of the Chehalis Lake rock avalanche-generated wave event contributes to this database.