Designing a rain gauge network: utilizing satellite-derived precipitation data with geostatistical multivariate techniques

Abstract

Although numerous studies have investigated the validity of satellite-derived precipitation datasets, there has been a lack of emphasis on their practical applications. This study aims to explore the implications of such datasets in designing rain gauge networks, which are essential for acquiring reliable precipitation data. Initially, four satellite-derived precipitation datasets (PERSIANN, PERSIANN-CDR, PERSIANN-CCS, and TRMM 3B43 V.7) were statistically compared to ground-based observations from 23 synoptic stations within the Fars province in southwestern Iran, the designated study area, to assess their validity. Furthermore, to provide a technical comparison, the degree of spatial independence (variogram) derived from these datasets was compared to that obtained from ground-based observations. To meet the study's objectives, a detrending process was implemented to render the datasets isotropic and bounded. Among the aforementioned satellite-derived datasets, PERSIANN-CCS and TRMM 3B43 V.7 demonstrated promise for enhancement to be utilized in rain gauge network design through a hybrid method combining multivariate analysis incorporating factor analysis and a geostatistical approach incorporating ordinary (point and block) kriging. Based on the PERSIANN-CCS and TRMM 3B43 V.7 satellite-derived datasets, rain gauge grids containing 70 and 56 rain gauges were initially proposed using a scree diagram. However, after considering a predetermined level of accuracy (block variance of residuals set to 10 ${mm}^{2}$), the numbers were subsequently reduced to 56 and 28 rain gauges, respectively. Consequently, this research sheds light on the practical utility of satellite-based precipitation datasets in the development of rain gauge networks in regions with insufficient data coverage or for evaluating existing networks.

Introduction

Evaluating the efficiency of open- or closed-loop systems, including hydrological models, requires monitoring the input signals and measuring the quantity and quality indicators of the output products. Rainfall monitoring, being the most significant process in the water cycle, plays a crucial role in enhancing the efficiency of applied hydrological models such as flood forecasting and control operators, and water resources management programs (Chahine 1992; Georgakakos and Kavvas 1987; Worden et al. 2007). Precipitation measurement instruments, such as ground rain gauges, radars, and satellites, are the monitoring technologies used in various rainfall-related environmental models (Joss et al. 1990; Michaelides et al.) 2009; Tapiador et al. 2012.

Satellite-derived precipitation products have become widely used for monitoring rainfall, among other methods (Joseph et al. 2009; Khojand et al. 2022; New et al. 2001; Pettorelli et al. 2005; Xie and Arkin 1995). While there are both advantages and disadvantages to using this type of data, including concerns about reliability and validity (Loew et al. 2017), one major benefit is the ability to access continuously updated measurements at small spatiotemporal scales. However, to generate rainfall data from signals sent by the satellites, secondary inference algorithms are required to convert primary signals and images into related values such as depth and intensity. The accuracy and reliability of these algorithms and input signals can affect the validity and reliability of satellite-derived precipitation data. Despite the availability of comprehensive satellite-derived precipitation data, which is made publicly accessible by individuals, institutions, and governments for scientific promotion, using this data alone in hydrological models is not yet entirely reliable (Chen et al. 2022).

Compared to satellite-derived precipitation data, ground-based rainfall measurement using rain gauges is considered the most reliable method for estimating rainfall, and the quantities obtained from them are widely used in hydrological models and water resources management (Chen et al. 2018). The main advantage of using rain gauges is that they provide direct measurement without the need for inference algorithms or significant modifications. Rain gauges range from traditional standard tools to modern remote devices and are the most common tool for directly estimating point precipitation at ground level. However, measuring the accuracy of the rainfall may be compromised by environmental conditions such as evaporation, wind (Zhou et al. 2019), and wetting, in addition to topographic setting (flat, rolling, and mountainous) of the site location (Shi et al. 2020) and accessibility to the stations. To solve these issues and expand the spatial range of measurement, a network of rain gauges called a "rain gauge network" is used.

Designing a rain gauge network requires not only collection of hydrological data but also application of computational and statistical principles to derive reliable rainfall attributes, such as rainfall depth, duration, and hyetographs (Abu Salleh et al. 2019; Shaghaghian and Abedini 2013). Computational principles, including optimization algorithms such as exhaustive search (Bastin et al. 1984), tabu search (Ming-Hsu, et al. 2006), genetic algorithms (ADIB, A. and M. MOSLEMZADEH 2016), and simulated annealing (Pardo-Igúzquiza 1998), as well as objective functions such as entropy (Su and You 2014; Wang et al. 2019; Wei et al. 2014; Xu et al. 2015), variance (Adhikary et al. 2015; Cheng et al. 2008; Huynh, et al. 2021; Krajewski 1987; Mohd Aziz, et al. 2019), and fractal dimension (Korvin et al. 1990; Mazzarella and Tranfaglia 2000), are essential in establishing the basic structure of rainfall monitoring network design procedures. Environmental data, such as spatiotemporal distribution of precipitation over the study area, must be fed into the design procedures to adapt the existing conditions to the model. Therefore, easy access and ensured reliability of environmental data are critical requirements for the rain gauge design methods for proper performance of the process.

The combined use of satellite data and rain gauges has proven to be common and beneficial. One example is the calibration of satellite-derived precipitation algorithms using ground-based observations. The TMPA 3B42-V7 algorithm, for instance, utilizes the Global Precipitation Climatology Centre (GPCC) gauge analyses to improve the integration of estimates (Liu 2015; Yong et al. 2014; Yong et al. 2013). Additionally, satellite-based products have been employed to compensate for the limitations of ground-based observations. Studies have applied satellite-based products to enhance data gathered from rain gauges (Akbari and Torabi Haghighi 2020; Khoshchehreh et al. 2020; Li and Shao 2010). Due to the scarcity of databases with regular high spatiotemporal resolutions, remotely sensed meteorological measurements, particularly satellite-derived precipitation products, have recently garnered increased attention in rain gauge network design (Bradley et al. 2002; Dai et al. 2017; Yeh et al. 2017). Various methodologies have been proposed for designing rain gauge networks, which incorporate satellite-derived precipitation products. These range from analyzing data in ungauged catchments (Liu et al. 2021) to incorporating them into existing design algorithms (Contreras et al. 2019; Huang et al. 2020).

Overall, in the past two decades, numerous studies have been conducted to assess the accuracy and validity of satellite-derived data. As a result, this field of study has become saturated. Now, it is crucial to progress and apply this type of data in practical scenarios. Despite the existence of some studies in this field (Liu et al. 2021; Gadhawe et al. 2021), there are still some aspects that need to be explored, indicating that this vision is not entirely new. This article is part of a series that discusses the utilization of satellite-derived precipitation data in hydrometeorological applications. In the first paper (Khojand et al. 2022), the examination focused on the impact of climate indices on the validity, reliability, and certainty of satellite-derived precipitation data. Building upon this research, the current paper concentrates on the integration of satellite-derived precipitation data into a commonly used model for rain gauge network design (Shaghaghian and Abedini 2013). This novel approach has the potential to enhance the creation of new rain gauge networks and evaluate existing monitoring systems in the study area. The findings from this study have significant implications and can provide valuable insights for various hydrometeorological applications.

Study area and data

Study area

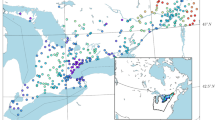
The Fars province, located in the southwest region of Iran (27˚-32˚ N, 50˚-55˚ E), has an arid and semiarid climate which encompasses mountainous areas and dry plains. The study area spans a total of 122,608 ${km}^{2}$ (Fig. 1), primarily composed of mountainous regions situated in the northern and northwestern sectors of the province. Approximately, 54% of the area is covered by elevations greater than 1500m above M.S.L. However, the southern and eastern parts of the study area are characterized by flat lands, including southern coastal plains and eastern deserts, where average slopes are less than 5% and elevation is less than 1000 $m$ above M.S.L. Thus, the study area has a diverse range of landforms. The area is influenced by three main air masses: Mediterranean, which is the most active and impacts most parts of the study area; continental tropical (also known as Sudan), which enters from the south and affects the entire study area (with the southern part being impacted the most); and maritime tropical which causes summer rainfall over the southeast of the study area. The Mediterranean and continental tropical air masses are dominant from December to March, known as the wet period, while the maritime tropical air mass occasionally supplies moisture from the Arabian Sea and the Indian Ocean to the southeast and south of the study area during July and August, which are part of the dry period.

Fig. 1

Spatial distribution of available ground-based and satellite-based observation, regional climate division, and direction of air masses affecting the study area (Khojand et al. 2022)

Dataset

Available rain gauge network

The reference dataset employed in the present work is based on the daily rainfall observations derived from 23 synoptic stations. The synoptic station data were provided by Iran Meteorological Organization (IMO), and the recording period of the stations varied in duration, but all had data from 2000 to 2020 which temporally covers the satellite-derived datasets. The spatial distribution of the synoptic gauge stations over the study area is shown in Fig. 1.

Satellite-derived precipitation datasets

The primary goal of this study is to employ a readily available dataset of satellite-derived precipitation to design a network of ground-based rain gauges. While numerous satellite-derived datasets are available, they must be properly organized to generate values over an extended period of time. As such, the following datasets have been selected and adjusted to suit the objectives of this study:

PERSIANN family

The study utilizes three satellite-derived datasets from the PERSIANN family, which are PERSIANN, PERSIANN-CCS, and PERSIAN-CDR. These datasets incorporate artificial neural network models to assess rainfall rate utilizing a combination of satellite data and ground-based rain gauge observations. These datasets have spatial quasi-global coverage of 60°N to 60°S at a spatial resolution of 0.25° from the turn of the millennium. While PERSIANN and PERSIANN-CCS have hourly temporal resolution data, PERSIANN-CDR has lower temporal resolution data (daily) due to the data preparation procedure. The long-term temporal resolution dataset used in this study was obtained directly from the following website https://chrsdata.eng.uci.edu. As an example, Fig. 2 displays the spatial distribution of annual precipitation in the study area in 2019 using data from three PERSIANN family satellite-derived precipitation datasets. To mitigate inconsistencies between spatial resolutions of some of the datasets used in this study, slight improvements have been made on some of them.

Fig. 2

Spatial distribution of annual precipitation over the study area in 2019 utilizing PERSIANN, PERSIANN-CDR, and PERSIANN-CCS satellite-derived precipitation datasets, sourced from https://chrsdata.eng.uci.edu

TRMM 3B43 Version 7

The TRMM 3B43 Version 7 is a monthly satellite-derived dataset that has been processed and calibrated with the GPCC's gauge-based observations. It is one of the TMPA products and can be downloaded from NASA's Earth Observing System Data and Information System (https://disc.gsfc.nasa.gov/datasets/trmm_3b43_7). This dataset covers the latitude belt from 50°N to 50°S at a spatial resolution of 0.25° and spans from 1998 to 2020. To suit our needs, we accumulated the monthly data to obtain the annual total precipitation by summing up the twelve values for each grid point in every year. We then calculated the mean annual precipitation and assigned it to each grid point.

Overall, Table 1 offers a concise summary of the characteristics of the datasets used in this study.

Table 1 Overview of the characteristics of the datasets used in the current study

Methodology

In this research, a procedure for designing a ground-based rainfall monitoring network is proposed. The procedure combines satellite-derived precipitation data with a clustering strategy based on the correlation structure of the regionalized variable used in the model, following a method used in previous studies (Shaghaghian and Abedini 2013). The two main components of the proposed method are a reliable satellite-derived dataset and the clustering strategy. Below is a brief overview of the procedure's components.

Satellite-derived annual precipitation data

The rainfall monitoring network's objective should align with the temporal-scale of the satellite-derived precipitation data used in the design process. For example, flood routing methods require high temporal resolution precipitation data, such as minutely data, which may not be available from the above-mentioned satellite-derived datasets. However, the current datasets can provide long-term rainfall data, which is adequate for determining a region's prevailing climate conditions, as this study's purpose. Hence, the initial phase of the rain gauge network design algorithm necessitates preparing a mean annual precipitation (MAP) dataset at every available point.

Besides the temporal-scale characteristics, low reliability can also pose a practical barrier to the effectiveness of satellite-derived datasets. Hence, in the rain gauge network design algorithm, the second step involves assessing the reliability and validity of satellite-derived precipitation data. Satellite-derived precipitation datasets verification employs several indicators, and the following five parameters are typically used to gauge the accuracy of satellite-derived data:

$${\text{Pearson correlation coefficient}}:\rho = \frac{{{\text{cov}} (S,G)}}{{\sigma_{S} \sigma_{G} }}$$

(1)

$${\text{Spearman's}}\;{\text{rank}}\;{\text{correlation}}\;{\text{coefficient}}: \, \rho_{r} = \frac{{{\text{cov}}(S_{r} ,G_{r} )}}{{\sigma_{{S_{r} }} \sigma_{{G_{r} }} }}$$

(2)

$$E_{i} = S_{i} - G_{i} {\text{ Mean Error }}\left( {{\text{ME}}} \right):\overline{E}$$

(3)

$${\text{Mean Absolute Error }}\left( {{\text{MAE}}} \right): \left| {\overline{E}} \right|$$

(4)

$${\text{Relative Bias }}\left( {{\text{RB}}} \right):\frac{{\overline{E}}}{G} \times 100$$

(5)

where $S$ and $G$ are Satellite-derived precipitation data and the ground-based observations, ${S}_{r}$ and ${G}_{r}$ are rank variables of the previously-mentioned parameters, and ${S}_{i}$ and ${G}_{i}$ are corresponding annual Satellite-derived precipitation data and the rain gauge observations.

In order to assess the effectiveness of the proposed rain gauge network design algorithm using satellite-derived datasets, a method for comparing the structure of the regionalized variable (variogram) obtained from Satellite-derived precipitation data with rain gauge observations is utilized. This comparison will be further explained in the upcoming sections when variogram modeling is discussed.

Variogram modeling

A variogram model represents the extent of spatial dependence of a regionalized random variable. In the process of variogram modeling, the experimental variogram is a mathematical expression that determines the correlation between two points in terms of their distance and direction. This expression is computed from observed data as follows:

$$\gamma \left({h}_{\theta }\right)=\frac{1}{2N\left({h}_{\theta }\right)}\sum_{i=1}^{N\left({h}_{\theta }\right)}{\left[Z\left({x}_{i}\right)-Z\left({x}_{i}+{h}_{\theta }\right)\right]}^{2}$$

(6)

where $N\left({h}_{\theta }\right)$ is the number of sample data points separated by a distance $h$ in the direction of angle $\theta$ from a fixed axis; ${x}_{i}$ and $\left({x}_{i}+{h}_{\theta }\right)$ are sampling locations separated by a distance $h$ in direction $\theta$; $Z\left({x}_{i}\right)$ and $Z\left({x}_{i}+{h}_{\theta }\right)$ are values of the observed variable $Z$, measured at the corresponding locations ${x}_{i}$ and $\left({x}_{i}+{h}_{\theta }\right)$, respectively. After deriving the unprocessed variogram from the observed data, which is an experimental variogram that may not have the necessary mathematical properties for direct use, the next step is to fit a permissible theoretical variogram for practical applications in geostatistical models. In the field of hydrology, three theoretical bounded models¹ have gained significant attention: exponential, Gaussian, and spherical variogram models. These models are expressed as follows:

$$\begin{gathered} \gamma_{t} \left( {h_{\theta } } \right) = N_{0} + S_{\theta } \left[ {1 - e^{{ - \frac{{\sqrt 3 h_{\theta } }}{{r_{\theta } }}}} } \right]{\text{Exponential}} \hfill \\ \gamma_{t} \left( {h_{\theta } } \right) = N_{0} + S_{\theta } \left[ {1 - e^{{ - \frac{{3h_{\theta }^{2} }}{{r_{\theta }^{2} }}}} } \right]{\text{Gaussian}} \hfill \\ \gamma_{t} \left( {h_{\theta } } \right) = N_{0} + S_{\theta } \left[ {1.5\frac{{h_{\theta } }}{{r_{\theta } }} - 0.5\frac{{h_{\theta }^{3} }}{{r_{\theta }^{3} }}} \right]{\text{Spherical}} \hfill \\ \end{gathered}$$

(7)

where ${N}_{0}$, ${r}_{\theta }$ and $\left({{N}_{0}+S}_{\theta }\right)$, commonly called as variogram parameters in $\theta$ direction, are nugget, range and sill, respectively. When these parameters do not vary with direction, the variogram is said to be isotropic, and spatial dependence only changes with distance between locations. On the other hand, if the variogram parameters vary with direction, the variogram is considered anisotropic. There are three types of anisotropy: geometric anisotropy, which is characterized by varying ranges at different angles; zonal anisotropy, where only the sill values vary in different directions; and mixed anisotropy, where both range and sill values vary in multiple directions.

To model theoretical variogram, the next step is to approximate its parameters. There are two methods for estimating the parameters: fitting the best curve to the experimental variogram and using cross-validation in the kriging method. In the first method, the parameters (nugget, sill, and range coefficients) are iteratively changed to minimize the root mean square error² (RMSE) as specified in Eq. 8. The latter method involves changing the parameters to minimize the error³ index and achieve the best prediction in the kriging model. It is important to note that the type of fit influences the estimation error, $E$, which is proportional to Eq. 8.

$${\text{Root Mean Square Error (RMSE)}}:\sqrt {\sum {(E)^{2} } }$$

(8)

Ordinary point and block kriging

One crucial aspect of designing a rainfall monitoring network involves utilizing kriging methods, including simple, ordinary, and universal kriging, in either point or block formats. These methods are closely linked to the use of spatially-related variables. When considering such variables, a randomly assigned value, such as the annual rainfall depth recorded at specific locations, can be seen as a manifestation of a random function, $P\left(x,y\right)$. This function can be broken down into deterministic and stochastic components, as follows:

$$P\left(x,y\right)=m\left(x,y\right)+W\left(x,y\right)$$

(9)

where $m\left(x,y\right)$ and $W\left(x,y\right)$ are algebraic trend model and small-scale variations with zero expectation, respectively. Moreover, in linear simulation, the estimated value ($\widehat{P}$) at spatial location $\left({x}_{0},{y}_{0}\right)$ is obtained as a linear combination of the observed values ($P$) at spatial locations $\left({x}_{i},{y}_{i}\right)$:

$$\widehat{P}\left({x}_{0},{y}_{0}\right)={\sum }_{i=1}^{N}{\lambda }_{i}P\left({x}_{i},{y}_{i}\right)$$

(10)

where the weight factors ${\lambda }_{i}$ correspond to the observed values at $\left({x}_{i,}{y}_{i}\right)$, and $N$ refers to the total number of points with observed values. Various methods are available for determining the weight factors by minimizing the residual (estimation error) and making assumptions about estimating the deterministic component of the regionalized random variable. These methods give rise to different types of kriging.

Equation 11 defines the residual as the discrepancy between the predicted value and the actual value. Equation 12 demonstrates that minimizing residuals and assuming a mean of zero are two fundamental principles in kriging models.

$$R\left( {x_{0} ,y_{0} } \right) = P\left( {x_{0} ,y_{0} } \right) - \hat{P}\left( {x_{0} ,y_{0} } \right)$$

(11)

$$\begin{gathered} \mathop \sum \limits_{i = 1}^{N} \lambda_{i} \gamma \left( {x_{i} ,y_{i} ;x_{j} ,y_{j} } \right) - m\left( {x_{0} ,y_{0} } \right) = \gamma \left( {x_{0} ,y_{0} ;x_{j} ,y_{j} } \right){ }Vj = 1,2, \ldots ,N \hfill \\ \mathop \sum \limits_{i = 1}^{N} \lambda_{i} = 0 \hfill \\ \end{gathered}$$

(12)

In a typical point kriging model, the value of $m(x,y)$ is assumed constant across the entire domain, denoted as $m$. This value, referred to as the Lagrange multiplier, is typically unknown and calculated during the solution of the model equations. Similarly, in ordinary block kriging, the Lagrange multiplier for the block is usually determined by calculating the arithmetic mean of the estimated values of the discrete grid points within the domain. As a result, the weight values for the equations, as well as the $m$ value, are derived by solving a system of linear equations, as presented in Eq. 13 and Eq. 14, for ordinary point and block kriging, respectively.

$$\begin{gathered} \mathop \sum \limits_{i = 1}^{N} \lambda_{i}^{OK} \gamma \left( {x_{i} ,y_{i} ;x_{j} ,y_{j} } \right) - m = \gamma \left( {x_{0} ,y_{0} ;x_{j} ,y_{j} } \right){ }Vj = 1,2, \ldots ,N \hfill \\ \mathop \sum \limits_{i = 1}^{N} \lambda_{i}^{OK} = 1 \hfill \\ \end{gathered}$$

(13)

$$\begin{gathered} \mathop \sum \limits_{i = 1}^{N} \lambda_{i}^{BK} \gamma \left( {x_{i} ,y_{i} ;x_{j} ,y_{j} } \right) - m = \frac{1}{M}\mathop \sum \limits_{k = 1}^{M} \gamma \left( {x{^{\prime}}_{k} ,y{^{\prime}}_{k} ;x_{j} ,y_{j} } \right){ }Vj = 1,2, \ldots ,N \hfill \\ \mathop \sum \limits_{i = 1}^{N} \lambda_{i}^{BK} = 1 \hfill \\ \end{gathered}$$

(14)

where $M$ is the number of discretized points inside a typical block, and apostrophes corresponds to them. After deriving the weights (${\lambda }_{i}^{OK}$ and ${\lambda }_{i}^{BK}$), the variance of the block residual is obtained as follows:

$$VAR\left( R \right) = - m + \frac{1}{M}\mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{M} \lambda_{i}^{BK} \gamma \left( {x^{\prime}_{j} ,y^{\prime}_{j} ;x_{i} ,y_{i} } \right) - \frac{1}{{M^{2} }}\mathop \sum \limits_{i = 1}^{M} \mathop \sum \limits_{j = 1}^{M} \gamma \left( {x^{\prime}_{j} ,y^{\prime}_{j} ;x^{\prime}_{i} ,y^{\prime}_{i} } \right)$$

(15)

Factor analysis

The present study also utilizes factor analysis to process satellite-derived data. Factor analysis is a highly beneficial multivariate statistical technique that reorganizes and streamlines the original variables ($N$ variables) into fewer underlying non-correlated factors ($A$ factors where $A<N$), denoted as ${F}_{1},{F}_{2},\dots ,{F}_{A}$ (also known as common factors), to preserve as much information contained in the original variables as possible. In this analysis, each variable is deemed a linear combination of a group of unobserved, underlying, and latent variables plus an error component. To ensure uniformity among the original variables, standardized variables are employed as the first step. Thus, if such variables are considered random regionalized variables, we have:

$$\overline{P}\left( {x_{i} ,y_{i} } \right) = \mathop \sum \limits_{j}^{A} L_{ij} F_{j} + \varepsilon_{i} \;\;\;i = 1, 2, \ldots , N$$

(16)

where $\overline{P }\left({x}_{i},{y}_{i}\right)$ represents the standardized original regionalized random variable, ${L}_{ij}$ is the loading coefficient of the $j$ th common factor, and ${\varepsilon }_{i}$ is the uncorrelated component that cannot be accounted for by the common factors.

The next step in factor analysis is to determine the loading coefficient of common factors by using the correlation pattern between the main data. Geostatistical calculations can simplify elements of the correlation matrix to terms of loading coefficients (Eq. 17). While the number of equations is not the same as the number of loading coefficients, extra assumptions are needed to determine these coefficients. One well-known method for this is the principal component method (PCM), which ignores the variance of unrelated components (${\psi }_{i}$). By merging this method with eigen-decomposition of the correlation matrix (${\text{\rm P}}_{N\times N}$), $N$ original random variables can be factorized and truncated into $A$ significant common factors. Equation 18 shows the eigen-decomposition, where ${V}_{N\times A}$ is the truncated modal matrix constructed with the most significant eigenvectors (${\overrightarrow{V}}_{1},{\overrightarrow{V}}_{2},\dots ,{\overrightarrow{V}}_{A}$) corresponding to the $m$ largest eigenvalues (${\lambda }_{1},{\lambda }_{1},\dots ,{\lambda }_{A}$). Additionally, ${\Lambda }_{A\times A}$ is a diagonal matrix that includes these eigenvalues.

$$\rho_{ij} = COV\left[ {\overline{P}\left( {x_{i} ,y_{i} } \right),\overline{P}\left( {x_{j} ,y_{j} } \right)} \right] = \mathop \sum \limits_{k = 1}^{A} L_{ik} L_{jk} + \psi_{i} \Rightarrow P_{N \times N} = L_{N \times A} L_{N \times A}^{T}$$

(17)

$${\text{COV}}\left[ {\overline{P}\left( {x_{i} ,y_{i} } \right),\overline{P}\left( {x_{j} ,y_{j} } \right)} \right] = {\text{\rm P}}_{N \times N} = V_{N \times A} {\Lambda }_{A \times A} V_{N \times A}^{T}$$

(18)

The correlation matrix used in factor analysis is derived from the semi-positive theoretical variogram, resulting in eigenvalues that are either zero or positive. As a result, according to Eq. 17 and Eq. 18, the correlation between the $i$ th original value and the $j$ th common factor (${L}_{ij}$) is represented as ${V}_{ij}\sqrt{{\lambda }_{i}}$, where ${V}_{ij}$ is the $j$ th element of ${\overrightarrow{V}}_{i}$, and ${L}_{ij}$ ranges from $-1$ to $+1$. To improve the correlation between the main variables and a number of common factors while making them independent of the rest, $L$ can be rotated to maximize certain elements while others approach zero. This rotation is intended to maximize the shared variance among items, resulting in more discrete representations of how the data correlates with each principal component. Maximizing the variance involves increasing the squared correlation of items related to one factor while decreasing correlations on any other factor. This type of rotation is known as varimax rotation, which simplifies the item loadings by eliminating insignificant factors and identifying the factors that the data is more closely related to.

Clustering method

In the proposed rain gauge network design algorithm mentioned in this study, the dataset used, as well as the study area, exhibit spatial clustering. Clustering refers to grouping primary data into classes based on their similar characteristics. The utilization of clustering in the rain gauge network design procedures has the implication of narrowing down the search space and reducing the computational effort needed to explore potential solutions, allowing for the identification of more optimal outcomes.

A combination of factor analysis and the kriging method is an innovative and practical approach utilized in this research (Shaghaghian and Abedini 2013; Shyu et al. 2011; Venkatramanan et al. 2016). In brief, the weight factors obtained from Eq. 13 and Eq. 14 determine the coefficients of each known variable (observed value) in an algebraic linear combination equation. This equation is used to compute the variance of residuals, which serves as the objective function for the rainfall monitoring network. Since there may be some correlation among the known variables, factor analysis aids in identifying common information derived from these variables and categorizes them into clusters. Mathematically, the $j$ th factor holds significance in the calculation of the objective function (Eq. 15).

$$\beta_{j} = \mathop \sum \limits_{i = 1}^{N} \lambda_{i}^{BK} L\prime_{ij}$$

(19)

where $L\prime_{ij}$ is the rotated loading coefficient of $j$ th common factor. Therefore, higher values of ${\beta }_{j}$ can be selected as the more significant factors which are here interpreted as clusters. Moreover, $\lambda_{i}^{BK} L\prime_{ij}$ can also be considered as the share of the $i$ th observation in the $j$ th cluster, and according to this contribution, the observation can also be relatively clustered.

Rain gauge network design strategy

The approach to rain gauge network design in this study draws inspiration from numerous established methods. However, a significant distinction lies in the primary data source utilized, which predominantly comprises satellite-derived precipitation datasets. Moreover, the proposed strategy can be delineated into the following two phases:

• 1- In the initial phase, it is essential to establish the spatial pattern of precipitation variability within the region. This determination necessitates access to rainfall data from various locations. Satellite-derived precipitation data is utilized in this study to delineate this pattern. Notably, for the proposed methodology, summarizing temporal variations in precipitation calls for a simplified index. Hence, the average annual precipitation at each location serves as the basis. The structure of spatial precipitation variation is represented as a bounded and isotropic variogram model. Therefore, it becomes imperative to examine the feasibility of attaining an isotropic bounded variogram by eliminating the deterministic component.

• 2- In the subsequent stage, following the construction of an isotropic bounded variogram, one of the traditional approaches can be employed to configure the rain gauge network. In this investigation, a geostatistical multivariate analysis technique (Shaghaghian and Abedini 2013) is utilized to divide the area into uncorrelated clusters. By refining the search area, the configuration is then carried out individually for each cluster. This design may involve the addition or removal of rain gauge stations from the current set or the creation of a rain gauge network within the cluster without regard to the existing stations.

Processing utilized datasets to generate relevant and actionable data, in addition to the design strategy, necessitates specific computational procedures outlined in detail in Fig. 3.

Fig. 3

Flowchart illustrating the process of designing a rain gauge network using a satellite-derived precipitation dataset

Results and discussion

Satellite-derived precipitation datasets can aid in mitigating data deficiencies and difficulties encountered in hydrological modeling. However, it is crucial to process the data efficiently to derive necessary model parameters. Once processed, the data is inputted into the model to generate outputs that are valuable in hydrological application and further modeling. In this section, we assess four annual precipitation datasets that are obtained from satellite-based databases through statistical and geostatistical comparisons with ground-based observations. Based on this evaluation, we select more appropriate satellite-derived precipitation datasets, and use them in designing an effective ground-based rain gauge network. Finally, we analyze and compare the performance of both the proposed and the available rain gauge networks.

Assessing validity of annual satellite-derived precipitation

The reliability of satellite-based hydrological models is heavily dependent on the accuracy of the input data. It is necessary for the input data to be consistent with the ground-based observations or improved to ensure consistency. Table 2 and Fig. 4 provide statistical comparison metrics for the evaluation of four satellite-derived precipitation datasets. The TRMM 3B43 V.7 dataset exhibits the highest compatibility with the ground-based observations among the evaluated satellite-based datasets in Fars. According to Table 2, moderate correlation ($0.35<\rho \le 0.67$) is observed between datasets derived from the PERSIANN family and the ground-based observations, while strong correlation ($0.67<\rho \le 1.00$) is observed between TRMM 3B43 V.7 and ground-based observations (Hemphill 2003; Schober et al. 2018; Taylor 1990). In addition to the correlation coefficient, the coefficient of determination (${R}^{2}$) also indicates a higher level of agreement between TRMM 3B43 V.7 and ground-based observations than the agreement between datasets derived from the PERSIANN family and ground-based observations (Galbraith et al. 1991). However, some conflicting interpretations are associated with other error metrics calculated for the satellite-derived datasets. The mean error ($ME$) and relative bias ($RB$) values suggest that, in comparison to datasets derived from PESIANN and PERSIANN-CDR, the TRMM 3B43 V.7 and PERSIANN-CCS overestimate the annual rainfall rates over the study period in the study area. The closeness of the aforementioned values to zero for the dataset derived from PERSIANN-CCS attests to its higher precision, but as shown in Fig. 4, this may be due to the inappropriate temporal distribution of data.

Table 2 Summary of error metrics used to validate the PERSIANN, PERSIANN-CDR, PERSIANN, and TRMM 3B43 V.7 with respect to ground-based observations of annual mean precipitation over Fars province, Iran

Fig. 4

Scatterplots of Mean Annual SDPD and RGBO over the study area

Numerous studies have been carried out in the study area to evaluate the reliability of satellite-derived precipitation data using probability distributions as a tool (Khojand et al. 2022; Salmani-Dehaghi and Samani 2019). While these studies have found that data aligns with ground-based observations, there have been some discrepancies in the results. For instance, certain research suggests that TRMM family products are more dependable than the PERSIANN family in the Fars region of Iran (Khojand et al. 2022; Moazami et al. 2013), which is consistent with this research's findings. In contrast, other studies that compared three members of the PERSIANN family differed from the outcomes of this research (Salmani-Dehaghi and Samani 2019).

Variogram and correlation model for mean annual satellite-derived precipitation data and ground-based observations

Many rain gauge network design strategies rely on analyzing the spatial discrepancy, or variogram, of rainfall data. In this study, the first step in variogram modeling involves creating an experimental variogram. This type of variogram plots the averaged semivariogram of mean annual satellite-derived precipitation data and ground-based rainfall observations for pairs of points located at specific intervals against the Euclidean distance using Eq. 6. The resulting diagrams can detect any non-random trend or anisotropy present in the spatial datasets. It is important to note that most geostatistical-based methods in rain gauge network design assume stationary and isotropic spatial datasets, which can be represented by bounded variograms. Therefore, the next step is to remove any disturbing components from the data. The resulting semivariogram, which corresponds to the processed data after removing these components, should be best fitted by an appropriate theoretical variogram.

Figure 5 illustrates the experimental variograms acquired from various datasets, including PERSIANN, PERSIAN-CDR, PERSIAN-CCS, TRMM 3B43 V.7 satellite-derived datasets, as well as ground-based observations. The variograms are shown for both the original (unprocessed) datasets and the detrended datasets which will be explained in detail later. The variograms are presented for three directions: east–west ($\theta =0^\circ$), northwest-southeast ($\theta =-60^\circ$), and northeast-southwest ($\theta =+60^\circ$) across the study area. Diagrams derived from original datasets reveal the presence of non-random trends and directional dependency, which are significant limitations if they are directly used in rain gauge design strategies. Additionally, Fig. 6 provides a visual representation of the distribution of mean annual rainfall in the study area using the four satellite-derived precipitation datasets and ground-based observations. Most datasets exhibit noticeable trends, with the PERSIANN satellite-derived dataset showing a decreasing trend from northwest to southeast. This information can help in understanding the spatial patterns of rainfall in the study area.

Fig. 5

Experimental variogram modeling (using original and detrended data) for PERSIANN group and TRMM 3B43 V. 7 satellite-derived datasets

Fig. 6

Three-dimensional graphical representation of spatial variation of the long-term satellite-derived precipitation data and ground-based rainfall observation over the study area

Unbounded variograms display an increasing level of variability as distance increases, suggesting the existence of a continuous variation trend in a particular direction beyond the examined area. The power model is a commonly used unbounded variogram model. In this model, the coefficient represents the intensity of the process, while the power parameter describes the curvature and must be between 0 and 2 (excluding these limits). If the power is lower than 1, the curve is convex upwards. If it equals 1, the variance increases linearly with distance. On the other hand, if the power is greater than 1, the curve is concave upwards. Therefore, in the fitted power variogram model, the value of the power serves as an indicator of the presence of an underlying oriented trend. This trend should be removed for the purposes of the study.

Table 3 presents the power values for the power model variogram of the original satellite-derived and ground-based datasets, along with the processed datasets where first- and second-order polynomials are removed as non-random components. It is evident from the table that the power values decrease as the first- and second-order polynomials are removed from the original datasets. To meet our design strategy with an acceptable value of 1, the PERSIANN-CCS dataset is initially suitable, while the PERSIANN and PERSIANN-CDR datasets require a first-order polynomial detrend to be applicable in the current study. Additionally, addressing this issue requires a second-order polynomial detrend for the TRMM 3B43 V.7 satellite-derived dataset.

Table 3 Non-stationarity index for variograms fitted to the original and deterended SDPD

In this study, the variograms for the processed datasets (referred to as trend removed datasets) are also displayed in Fig. 5. It is evident that the variograms exhibit isotropy, as they are assumed to be the same and bounded in multiple directions. Thus, the omnidirectional variogram, where the semivariogram is solely a function of the distance between two points, is used due to its independence from direction. This allows for the utilization of the bounded theoretical variograms described in Eq. 7 for variogram modeling. The variogram parameters and fitting index values are shown in Table 4 for one member of the PERSIANN family (PERSIANN-CCS), TRMM 3B43 V.7, and ground-based observed data. The PERSIANN-CCS dataset is selected due to its highest trend-free and random characteristics. The variogram models and their corresponding fitting curves are presented in Fig. 7. According to the fitting index (Root Mean Squared Error, RMSE, defined in Eq. 8), all of the models appear to have acceptable fits. However, the Gaussian model exhibits a unique characteristic where the rate of variogram increases within a specific interval, and the variogram is convex upward within this interval. This distinct feature is clearly observed in the experimental semivariograms. Therefore, among the proposed models, the Gaussian model seems to be slightly more suitable and is recommended for further variogram modeling.

Table 4 Variogram parameters for 'detrended' ground-based rainfall observations and datasets obtained from chosen satellite-derived products

Fig. 7

Theoretical variogram modeling (Exponential, Gaussian and Spherical) for ground-based observations and two satellite-based datasets (PERSIANN-CCS and TRMM 3B43 V. 7)

The final step in this stage entails developing a correlation model. In the context of a bounded variogram, the sill represents the overall covariance of spatial data. Consequently, calculating the covariance between variables separated by distance 'h' can be achieved by subtracting the variogram values from the sill value. Moreover, the correlation can be easily computed by dividing the covariance by the sill value.

Rain gauge network design

In geostatistical-based rain gauge network design algorithms, the spatial dependency structure of precipitation plays a critical role. In this study, the comparison between four satellite-derived datasets and ground-based observations was conducted to evaluate their suitability for determining this dependency structure. Two datasets, one from the TRMM family and another from the PERSIANN family, were identified as suitable for further investigation. Theoretical variograms derived from these datasets will be used as the basis for designing the rain gauge network strategy in this study.

In this research, the algorithm used to design the rain gauge monitoring network combines geostatistical concepts and multivariate analysis. The study area is divided into sub-regions, and if the amount of rainfall in these sub-regions is not dependent on each other, a monitoring gauge is assigned to each sub-region to track the rainfall for the entire region. In the first step of this research, several rain gauge grids with different densities are compared. Figure 8 illustrates the relationship between the explained variance ratio and the rain gauge cover area for ground-based observation and two selected satellite-derived observations. The explained variance ratio is calculated by summing the values of the elements of the characteristic vector of the correlation matrix that are greater than 1 and dividing it by the total number of elements. This value can be obtained from the scree graph of the correlation matrix. Figure 9 shows an example of this graph for five types of grids based on ground-based observations. For instance, in the case of a 1600 km2 grid (40 km by 40 km), the correlation matrix contains 25 elements, out of which 10 are significant (greater than 1). The sum of these 10 elements is 14.8, indicating that 59% of the overall variance can be explained by selecting 10 rain gauges out of the available 25 gauges.

Fig. 8

Impact of rain gauge network density on explained variance ratios resulted from ground-based observations, TRMM 3B43 V. 7 and PERSIANN-CCS satellite-derived datasets

Fig. 9

Scree diagrams generated from correlation matrices obtained from ground-based observations for 5 grid network scenarios

The figures mentioned above serve as the basis for our rain gauge design strategy. Prior to utilizing these figures, users need to determine the desired accuracy of their design network, which is measured by explained variance. This accuracy factor influences the density of the rain gauge network. Additionally, the model correlation structure of the data is crucial. Table 4 provides the parameters for the Gaussian model, which is recommended among other variogram models. The correlation-distance relations for ground-based observations, PERSIANN-CCS, and TRMM 3B43 V. 7 satellite-derived datasets are determined as $\uprho \left(\text{h}\right)=\text{exp}\left(-2.96\times {10}^{-3}{\text{h}}^{2}\right)$, $\uprho \left(\text{h}\right)=\text{exp}\left(-0.40\times {10}^{-3}{\text{h}}^{2}\right)$, and $\uprho \left(\text{h}\right)=\text{exp}\left(-0.55\times {10}^{-3}{\text{h}}^{2}\right)$ respectively. With these assumptions in mind, it becomes feasible to establish an initial network for our purpose. For instance, referring to Fig. 8, if the goal is to account for 75% of the total variance of precipitation over the study area, using the correlation (variogram) function obtained from the PERSIANN-CCS satellite-derived dataset indicates that each rain gauge should cover an area of 222.9 ${km}^{2}$. On the other hand, for TRMM 3B43 V. 7, this value increases to 1290.7 ${km}^{2}$, which is closer to the 942.7 ${km}^{2}$ calculated from the correlation function derived from ground-based observations.

In addition to the aforementioned procedure, this method can be compared to a widely used algorithm at this stage, which investigates the impact of reducing the variance of residuals by increasing the number of rain gauges (Bastin et al. 1984). Figure 10 illustrates the variations in residual variance of a gridded rain gauge network based on the considered coverage area for each rain gauge, using ground-based observations and the two satellite-derived datasets mentioned earlier. As expected, the variance of residuals increases with the expansion of the rain gauge coverage area (resulting in a decrease in gauge density) for all cases. To illustrate the concept, let's consider the design of a gridded rain gauge network using variograms derived from either ground-based observations, TRMM 3B43 V.7, or PERSIANN-CCS satellite-derived datasets. The objective is to reduce the variance of residuals to 10 ${mm}^{2}$. For this purpose, each rain gauge within the gridded network should cover specific areas: 1955.6, 2204.9, and 1776.1 square kilometers, respectively. To achieve this, a grid network of either 44.2 by 44.2, 46.9 by 46.9, or 42.1 by 42.1 is required, corresponding to the aforementioned area sizes.

Fig. 10

Impact of rain gauge network density on block variance of residual (accuracy) resulted from ground-based observations, TRMM 3B43 V. 7 and PERSIANN-CCS satellite-derived datasets

Up until this point in the study, a grid rain gauge network has been proposed using only multivariate analysis and a geostatistical approach. The spatial dependency/independency structures were determined based on ground-based observations and two satellite-derived datasets. The next step involves improving the design strategy by incorporating these two concepts. Previous studies have commonly used a hybrid method, but the variograms employed in those studies were derived solely from ground-based observations (Shaghaghian and Abedini 2013). The hybrid method offers a significant advantage in making dense grids sparser by eliminating redundant rain gauges that can be covered by others. This means that a dense rain gauge network can be initially designed and then effectively sparsened using this hybrid method.

After developing a dense grid network where each node represents a potential rain gauge, the total variance resulting from these nodes is taken into account. The study area is then clustered using a hybrid method, and a rain gauge is assigned to each cluster, establishing a rain gauge network. Figure 11 illustrates the decreasing variance of residuals as the number of clusters (represented by rain gauges) increases. This process is carried out using three previously described datasets: ground-based observations, PERSIANN-CCS, and TRMM 3B43 V. 7 satellite-derived datasets. To elaborate further, in order to achieve a residuals variance of 10 ${mm}^{2}$, it is necessary to have a rain gauge network consisting of 35, 56, and 28 rain gauges for these respective datasets. Comparing these values with the grid network designed initially, which indicated a need for 62, 70, and 56 rain gauges (by dividing the study area, which spans 122,608 ${km}^{2}$, by the rain gauge coverage area), the effectiveness of the hybrid method for the rain gauge network becomes apparent.

Fig. 11

Impact of number of rain gauges on the block variance of residuals (accuracy) in rain gauge networks designed using ground-based observations, TRMM 3B43 V. 7, and PERSIANN-CCS satellite-derived datasets

All available methods used to observe rain gauge networks can only identify redundant rain gauges or, at best, identify areas with a lack of rain gauges. Our approach to designing a rain gauge network is centered on utilizing satellite-derived precipitation datasets, which are distributed across the study area in grids (e.g., 0.25° × 0.25° for TRMM satellite-derived precipitation datasets as illustrated in Fig. 1, or with higher density for PERSIANN-CCS). As a result, the resulting rain gauge network should be structured in a grid pattern. The optimization of this grid, such as relocating some stations closer to accessible locations, is a challenge that has not been addressed in this study. Therefore, Fig. 12 showcases the proposed rain gauge network based on TRMM 3B43 V. 7 satellite-derived datasets, with a detailed explanation of the design process provided in preceding paragraphs.

Fig. 12

Rain gauge network designed utilizing TRMM 3B43 V. 7 and PERSIANN-CSS satellite-derived precipitation datasets

In summary, the main goal of the article is to utilize satellite-derived precipitation datasets for creating ground-based rain gauge networks. Out of the four datasets examined, two were selected and improved: TRMM 3B43 V. 7 and PERSIANN-CCS. Based on statistical comparisons conducted in this study and findings from other research, it can be concluded that TRMM satellite-derived precipitation datasets are more reliable for the study area (Khojand et al. 2022; Salmani-Dehaghi and Samani 2019). However, the detrended version of PERSIANN-CCS can also be used for designing a rain gauge network in this study. The effectiveness of satellite-derived datasets depends on the desired level of accuracy. For instance, if a highly accurate rain gauge network is needed, PERSIANN-CCS suggests a denser network compared to TRMM-CCS. However, an optimized network derived from ground-based observations falls between these two options.

Concluding remarks

Developing an effective rain gauge network requires accurate precipitation data. However, obtaining reliable precipitation data depends on having a well-designed rain gauge network. This creates a challenging paradox. One potential solution to this dilemma is using satellite-derived precipitation data. In this study, we evaluate four satellite-derived precipitation datasets, namely, PERISANN, PESIANN-CDR, PERSIANN-CCS, and TRMM 3B43 V. 7, to determine their suitability for rain gauge network design algorithms. Among these datasets, PERSIANN-CCS, and TRMM 3B43 V. 7 show promise for improvement. After enhancing these datasets and modeling a bounded variogram, the resulting models are incorporated into a geostatistical multivariate rain gauge network design approach. The study concludes by proposing an optimized rain gauge network based on the findings. Furthermore, according to the findings of this study, the following conclusions can be drawn:

• 1- The geostatistical multivariate approach for rain gauge network design has the benefit of attenuating characteristics. It can be effectively employed to optimize the design of rain gauge networks, whether they are being newly implemented or already exist, with the aim of improving their cost-effectiveness.

• 2- The effectiveness of using satellite-derived precipitation datasets for rain gauge network design cannot be solely determined through statistical comparison with ground-based observations. For example (as illustrated in Table 2), the comparison between the two datasets reveals that the PERSIANN-CCS satellite-derived dataset exhibits a weaker correlation with the observations from ground rain gauge stations compared to other satellite-derived datasets. However, following some straightforward adjustments to the spatial datasets (specifically, removing the overall trend), this dataset was able to accurately model the spatial variations of rainfall values. Moreover, the variability does not escalate infinitely; after trend removal, a bounded variogram is obtained, as depicted in Fig. 5. As a result of these findings, the PERSIANN-CCS dataset has been effectively utilized in the algorithm for designing rain gauge networks.

• 3- The accuracy of information obtained from rain gauge networks can be assessed using two methods: "explained variance" and "block variance of residuals." The use of explained variance is suitable for conducting multivariate analysis techniques, while the block variance of residuals is more appropriate for geostatistical-based approaches.

• 4- The primary purpose of establishing a rain gauge network is to monitor the spatial and temporal variations in rainfall across a particular area. Consequently, a higher degree of spatial variability necessitates a more extensive deployment of rain gauges within this network. As illustrated in Fig. 6, the spatial variability in mean annual precipitation derived from the PERSIANN-CCS satellite dataset surpasses that of the TRMM 3B43 V. 7 satellite dataset. Therefore, it is anticipated that to achieve a similar level of precision, the rain gauge network derived from the PERSIANN-CCS satellite dataset would require a denser distribution of gauges compared to the network derived from the TRMM 3B43 V. 7 satellite dataset. For instance, as depicted in Fig. 11, if we set the accuracy threshold for the rain gauge network at 10 ${mm}^{2}$ based on block variance residuals, the network resulting from the PERSIANN-CCS dataset would necessitate 56 rain gauges, whereas the network derived from the TRMM 3B43 V. 7 dataset would only require 28 rain gauges.

As a recommendation for further studies, the suggested rain gauge network in this research aims to capture long-term precipitation parameters across the study area. The findings could prove valuable for macro-scale water management purposes. However, it is important to consider situations where lower temporal resolution of precipitation data is needed, such as for flood forecasting. In such cases, it is recommended to design the rain gauge network while taking this issue into account. Satellite-derived datasets like TRMM 3B42 RT, which provides semi-hourly data, can be utilized for rain gauge network design in these instances.