The long-term characteristics of GNSS signal distortion biases and their empirical corrections

Abstract

Global Navigation Satellite System (GNSS) precise data processing depends on the accurate processing of various errors. However, the distorted GNSS live signals will result in systematic biases in pseudorange observations, namely, signal distortion bias (SDB). Studies have shown that GNSS SDBs are stable over a short time and can be well modeled according to receiver brands and models. Thus, we focus on analyzing the long-term characteristics of SDB and establishing their empirical corrections based on many GNSS observations from 2017 to 2019. The results show that the SDBs differ among different satellite system. For example, the SDBs are within ± 1 ns for all the signals of GPS and BDS-2 while they are within ± 0.5 ns for Galileo and QZSS. Also, most of the SDBs remained very stable even as the firmware version of the receiver was being upgraded during the 3 years. The portion of SDB STDs over 3-year series and within 0.1 ns are 93.2, 99.9, and 86.7% for GPS, Galileo, and QZSS, respectively. As for BDS-2, the SDB STDs within 0.1 ns and 0.2 ns are 70.0% and 96.8% due to the poor quality of pseudorange observations. Thus, the estimated GNSS SDBs are given as constant values for each satellite-receiver-group pair and signals in SINEX BIAS format. The validations show that both pseudorange residuals and STEC extraction of zero-baselines show about 1 ns systematic biases without SDB corrections. However, the RMS of pseudorange residuals decreases by 28.26 to 51.18% while the RMS of double-differenced STEC decreases by 12.5 to 49.2% for different satellite systems with SDB corrections. The results from 2017 to 2019 validate that most GNSS SDBs could be treated as constants if there is no update of satellite and receiver hardware. Also, it should be noted that SDB corrections may not be applicable for individual satellites and receivers when there are satellite signal fault or flex power. Therefore, it should be routine to calibrate the GNSS SDBs with the replacement of satellite and update of receiver brands and models.

Introduction

In traditional Global Navigation Satellite System (GNSS) data processing, the hardware delays are generally split into a sum of satellite- and receiver- dependent parts for Code Division Multiple Access (CDMA) satellite system. The satellite part is the same for all users, while the receiver part is the same for satellites of the same navigation system and they are both treated as constant values for a specific time session (Montenbruck et al. 2017). Based on this assumption, the Differential Code Biases (DCB), Uncalibrated Phase Bias (UPD) are estimated for each satellite and receiver (Montenbruck et al. 2014; Wang et al. 2016; Geng et al. 2019). However, the existence of receiver-related pseudorange bias caused by signal distortion validates that the satellite-plus-receiver hardware delay cannot be rigorously split into a sum of two independent parts (Gong et al. 2018).

The chip shapes of the GNSS signals are assumed to be rectangular theoretically. However, due to the influence of the radio frequency filter at the transmitting and receiving end, the live signal will produce distortion (Phelts et al. 2000). Such distorted GNSS signals will cause the receiver’s correlation function to deviate from its ideal triangular shape, which will lead to a shift in the tracking point and thus cause a bias in the pseudorange observation (Hauschild and Montenbruck 2016). GNSS Pseudorange observations also suffer the effect of group delay variations (Wanninger and Beer 2015; Lou et al. 2017) and temperature-related hardware variations (Zhang et al. 2017). In order to distinguish them from other pseudorange biases and to facilitate writing, the pseudorange bias caused by signal distortion is uniformly called signal distortion bias (SDB). The SDB will reach up to several nanoseconds among different receiver types and limit GNSS data processing accuracy with inhomogeneous types of receivers (Gong et al. 2021). Over the last few decades, much research has been carried out to study the mechanism, characteristics, effects of data processing, and correction method of SDBs in detail.

Mechanism and characteristics

In March 1993, it was reported that GPS differential solution was biased by 3–8 m depending on different types of user equipment when GPS PRN 19 was included in the solution (Edgar et al. 1999). It was then validated that these biases were caused by the C/A code signal distortion of different receiver configurations, i.e., code correlator spacing and RF front-end bandwidths (Mitelman et al. 2000). Further studies indicated that both anomaly and nominally healthy satellites were affected by signal distortion biases (Mitelman et al. 2004). Since then, more research has focused on the characteristics of signal distortions to reproduce the distorted chip shape (Pini et al. 2005; Phelts and Akos 2006; Wong et al. 2010; Aerts et al. 2010), and the tracking errors caused by signal distortion (Wong et al. 2011; Lestarquit et al. 2012; Vergara et al. 2016). A comprehensive experiment with a special receiver firmware validated that SDB depended on the receiver front-end bandwidth and correlator design for both live and simulated signals (Hauschild and Montenbruck 2016).

To analyze the characteristics of GNSS SDBs, various co-located geodetic receivers of different brands were established. The studies proved that zero-baseline differential code bias residuals were close to zero for identical receiver hardware with identical settings. However, non-zero residuals emerged once the receivers of zero-baseline were set with different correlator spacing for multipath mitigation (Hauschild and Montenbruck 2016). Following a similar idea, it was observed that SDB of GPS, BDS-2, and Galileo mainly depended on the receiver brands and models for receivers demonstrated with abundant data from various GNSS networks, i.e., multi-GNSS experiment campaign (MGEX) (Montenbruck et al. 2017), the crustal movement observation network of China (CMONOC, Chen 1998), the National BDS Augmentation Service System (NBASS, Shi, et al. 2017), the Curtin GNSS CORS and the Hong Kong SatRef GPS Network stations (Gong et al. 2018, 2021; Mao et al. 2021). Generally, the SDBs of Galileo among different receiver types are smaller than those of GPS and BDS-2, which may be attributed to different signal modulation methods. Besides, SDB of BDS B1I is larger than that of BDS B1C and GPS L1C/A, while the SDB of GPS L2C is larger than that of BDS B3I and B2a (Tang et al. 2020).

Effects on GNSS precise data processing

Ignoring these biases among different receiver types will reduce the accuracy of GNSS data processing. Research demonstrates that discrepancy of up to ± 3 ns and ± 1.5 ns would arise among different receiver types for satellite clock and satellite DCB, respectively (Hauschild et al. 2019; Wang et al. 2020). Also, the discrepancy of wide-lane ambiguity resolution success rate among different receiver types can exceed 20%. For example, the GPS wide-lane ambiguity resolution success rate of TPS LEGACY is about 96%, while it is only 70% for LEICA GR50 (Villiger and Dach 2019). In addition, the positioning accuracy will be reduced by about 1 m if the receiver configuration differs much from the receivers used for group delay estimation (Tang et al. 2020). All of the above studies validated that ignoring the SDB among different receiver types will reduce the accuracy of GNSS data processing.

Correction of SDB

In view of the influence of SDB on GNSS precise data processing, much research has been carried out to eliminate or reduce the effect of SDB. For GNSS data processing, an ideal solution is to eliminate these biases at the signal processing stage. The GPS Interface Control Documents (ICD) specifies that the broadcast group delay differential correction terms should be applied to an ideal correlation receiver with a bandwidth of 20.46 MHz and a correlator spacing of 97.75 ns. Another possible way is to optimize the receiver algorithm when capturing the GNSS signal (Kou and Wu 2021). However, it seems that the receiver manufacturers currently can hardly satisfy these requirements. Since different receivers may be equipped with different configurations, another solution is to model these SDBs based on data from various receivers at the data processing stage.

Gong et al. (2018) estimated corrections for each receiver group classified according to the receiver brands and models. The results demonstrate that the signal distortion bias of most stations can be well modeled according to receiver groups for GPS, Galileo, and BDS-2 (Gong et al. 2018, 2021). Then, empirical corrections for more than 20 receiver types are estimated and provided, and the results show that the consistency of satellite clock, satellite DCB estimated from different receiver types greatly improved with these corrections. Meanwhile, the accuracy of positioning and success rate of ambiguity resolution improve when mixed receiver types are used (Zheng et al. 2019). Following a similar method, it is validated that multi-GNSS real-time satellite clock estimation, single point positioning, precise point positioning, and real-time kinematic positioning can improve as well (Chen et al. 2021a, 2021b; Zhang et al. 2021). In addition, the root mean square (RMS) errors of 24 h precise orbit determination overlap corresponding to the radial, cross-track, and along-track components improve by 1.4, 2.7, and 12.7%, respectively, after correcting the inter-receiver SDB. The standard deviations of the SLR residuals of satellites C01, C13, and C11 are reduced from 30.7, 7.1, and 3.5 cm to 30.2, 6.8, and 2.9 cm, respectively (Li et al. 2021). However, all experiments are validated with a short-time session. Thus, the long-term characteristics of SDBs should be further studied to determine an appropriate correction model.

With the update of SINEX_BIAS version 1.00, generalizations, extensions, and a considerable number of added detailed definitions, descriptions, and examples were added, which greatly enriches the use of GNSS biases (Schaer 2016). We aim at reviewing the GNSS SDBs and investigate the stability of SDBs among inhomogeneous receiver types. First, we introduce the methods used for SDBs calibration. Then, experiments based on observations from MGEX network are used to analyze the characteristics of GPS/BDS-2/Galileo/QZSS SDBs. Next, the corrections of GNSS signal distortion biases provided in SINEX Bias format together with the validation of zero-baselines are presented. Finally, some conclusions are given.

GNSS SDB estimated from network

This section uses GNSS observations from the MGEX network to estimate SDB since the stations are equipped with various receiver brands and models. The method of SDB estimation with a GNSS network is given first. Then, the experiments with data from 2017 to 2019 are carried out to analyze the long-term characteristics of GNSS SDBs and establish empirical corrections.

Methods

In traditional GNSS data processing, hardware delay is generally divided into two parts: receiver-specific and satellite-specific (Montenbruck et al. 2017). Thus, the raw GNSS observations can be described as:

$$\left\{ {\begin{array}{*{20}l} {P_{r,sig}^{s} = \rho + c \cdot \left( {Clk_{r} + b_{r,sig} - Clk^{s} - b_{sig}^{s} } \right) + \alpha^{s} \cdot T^{z} + \beta_{sig} \cdot I^{s} } \hfill \\ {{\Phi }_{r,sig}^{s} = \rho + c \cdot \left( {t_{r} + B_{r,sig} - t^{s} - B_{sig}^{s} } \right) + \alpha^{s} \cdot T^{z} - \beta_{sig} \cdot I^{s} + \lambda_{sig} \cdot N_{sig} } \hfill \\ \end{array} } \right.$$

(1)

where $P_{{r,{\text{ }}sig}}^{s}$ and $\Phi _{{r,{\text{ }}sig}}^{s}$ represent the pseudorange and carrier-phase measurements on sig (sig = C1C, C1W, C2W, etc.) from receiver r to satellite s (s = 1, 2, …, m), m is the number of satellites tracked by receiver r; ρ is the geometric distance with antenna phase center corrections; c denotes the speed of radio waves in vacuum; Clk_r and Clk^s are receiver and satellite clock error, respectively; T_z is the zenith tropospheric delay that can be converted to slant with the mapping function α^s; $b_{r,sig }$ and $b_{{sig}}^{s}$ are the receiver-specific and satellite-specific pseudorange hardware delay, respectively; $B_{r,sig }$ and $B_{{{ }sig}}^{{\text{s}}}$ are the receiver-specific and satellite-specific phase hardware delay, respectively; I^s denotes the line-of-sight total electron content with the frequency-dependent factor ${\beta }_{sig}$; $\lambda_{sig}$ and $N_{sig}$ are wavelength and integer ambiguity of carrier phase observation, respectively. However, due to the existence of SDB, the raw GNSS pseudorange observation should be modified as follow (Zheng et al. 2019):

$$P_{r,sig}^{s} =\, \rho + c \cdot \left( {Clk_{r} + b_{r,sig} - Clk^{s} - b_{sig}^{s} + b_{group\left( r \right),sig}^{s} } \right) + \alpha^{s} \cdot T^{z} + \beta_{sig} \cdot I^{s}$$

(2)

where $b_{{group(r),sig}}^{s}$ is the SDB related to satellite-receiver-type, which means $b_{group\left( r \right),sig}^{s}$ is same for stations equipped with receivers of the same type. Obviously, $b_{group\left( r \right),sig}^{s}$ is linearly dependent on $b_{r,sig}$ and $b_{sig}^{s}$.

To eliminate the effect of ionospheric delay on SDB calibration, the ionospheric-free (IF) combination, Hatch-Melbourne-Wübbena combination (HMW, Hatch 1982; Melbourne 1985; Wübbena 1985), and pseudorange ionospheric- and geometry-free (IFGF) combination are proposed in Zheng et al. (2019):

$$\left\{ \begin{gathered} P_{{r,IF,sig\left( {i,j} \right)}}^{s} = f_{IF1} \cdot P_{r,sig\left( i \right)}^{s} - f_{IF2} \cdot P_{r,sig\left( j \right)}^{s} \hfill \\ HMW_{{r,sig\left( {i,j} \right)}}^{s} = \frac{{f_{HMW1} \cdot P_{r,sig\left( i \right)}^{s} + f_{HMW2} \cdot P_{r,sig\left( j \right)}^{s} }}{{\lambda_{{HMW,sig\left( {i,j} \right)}} }} - \left( {\frac{{{\Phi }_{r,sig\left( i \right)}^{s} }}{{\lambda_{sig\left( i \right)} }} - \frac{{{\Phi }_{r,sig\left( j \right)}^{s} }}{{\lambda_{sig\left( j \right)} }}} \right) \hfill \\ IFGF_{{r,sig\left( {i,j,k} \right)}}^{s} = \left( {f_{IF1} - f_{IF3} } \right)P_{r,sig\left( i \right)}^{s} - f_{IF2} P_{r,sig\left( j \right)}^{s} + f_{IF4} P_{r,sig\left( k \right)}^{s} \hfill \\ \end{gathered} \right.$$

(3)

where $P_{{IF,sig\left( {i,j} \right)}}$, $HMW_{{sig\left( {i,j} \right)}}$ and $IFGF_{{sig\left( {i,j,k} \right)}}$ are IF pseudorange observation, HMW combination and IFGF pseudorange combination, respectively; $f_{HMW1} = \frac{{f_{sig\left( i \right)} }}{{f_{sig\left( i \right)} + f_{sig\left( j \right)} }}$, $f_{HMW2} = \frac{{f_{sig\left( j \right)} }}{{f_{sig\left( i \right)} + f_{sig\left( j \right)} }}$,$f_{IF1} = \frac{{f_{sig\left( i \right)}^{2} }}{{f_{sig\left( i \right)}^{2} - f_{sig\left( j \right)}^{2} }}$, $f_{IF2} = \frac{{f_{sig\left( j \right)}^{2} }}{{f_{sig\left( i \right)}^{2} - f_{sig\left( j \right)}^{2} }}$, $f_{IF3} = \frac{{f_{sig\left( i \right)}^{2} }}{{f_{sig\left( i \right)}^{2} - f_{sig\left( k \right)}^{2} }}$ and $f_{IF4} = \frac{{f_{sig\left( k \right)}^{2} }}{{f_{sig\left( i \right)}^{2} - f_{sig\left( k \right)}^{2} }}$; $\lambda_{{HMW,sig\left( {i,j} \right)}}$ is the wavelength of HMW combination. Substituting carrier-phase observation from (1) and pseudorange observation from (2) into (3), then (3) can be rewritten as:

$$\begin{gathered} P_{{r,IF,sig\left( {i,j} \right)}}^{s} = \rho + c \cdot \left( {Clk_{r} - Clk^{s} + f_{IF1} \cdot Bias_{sig\left( i \right)} - f_{IF2} \cdot Bias_{sig\left( j \right)} } \right) + \alpha^{s} \cdot T_{r}^{z} \hfill \\ HMW_{{r,sig\left( {i,j} \right)}}^{s} = \frac{{f_{HMW,sig\left( i \right)} \cdot Bias_{sig\left( i \right)} + f_{HMW,sig\left( j \right)} \cdot Bias_{sig\left( j \right)} }}{{\lambda_{{MW,sig\left( {i,j} \right)}} }} - \left( {B_{{r,sig\left( {i,j} \right)}}^{s} + N_{{r,sig\left( {i,j} \right)}}^{s} } \right) \hfill \\ IFGF_{{r,sig\left( {i,j,k} \right)}}^{s} = \left( {f_{IF1} - f_{IF3} } \right) \cdot Bias_{sig\left( i \right)} - f_{IF2} \cdot Bias_{sig\left( j \right)} + f_{IF4} \cdot Bias_{sig\left( k \right)} \hfill \\ \end{gathered}$$

(4)

where $Bias_{sig\left( i \right)} = {{c}} \cdot \left( {b_{r,sig\left( i \right)} - b_{sig\left( i \right)}^{s} + b_{group\left( r \right),sig\left( i \right)}^{s} } \right){;}$ $B_{{r,sig\left( {i,j} \right)}}^{s} = c \cdot \left( {\frac{{B_{r,sig\left( i \right)} - B_{sig\left( i \right)}^{s} }}{{\lambda_{sig\left( i \right)} }} - \frac{{B_{r,sig\left( j \right)} - B_{sig\left( j \right)}^{s} }}{{\lambda_{sig\left( j \right)} }}} \right)$ is phase hardware delay of HMW combination; $N_{{r,sig\left( {i,j} \right)}}^{s}$ is the wide-lane ambiguity.

To estimate the biases from (4), as for IF pseudorange combination, the station coordinate, satellite orbit, and clock should be fixed by using post-processed precise products to calculate the residual of IF pseudorange combination. As for HMW combination, the wide-lane ambiguity can be eliminated by integer rounding. Then, based on these combinations, we can derive three combinations as follows:

$$\left\{ \begin{aligned} &Bias_{{r,IF,sig\left( {i,j} \right)}}^{s} &= P_{cal} - P_{{r,IF,sig\left( {i,j} \right)}}^{s} \hfill \\ &= \frac{{\left( {f_{IF1} \cdot Bias_{IF,sig\left( i \right)} - f_{IF2} \cdot Bias_{IF,sig\left( j \right)} } \right)}}{c} \hfill \\ &Bias_{{r,HMW,sig\left( {i,j} \right)}}^{s} = \lambda_{{HMW,sig\left( {i,j} \right)}} \cdot (HMW_{{r,sig\left( {i,j} \right)}}^{s} - Round\left( {\left( {HMW_{{r,sig\left( {i,j} \right)}}^{s} } \right)} \right) \hfill \\ &= \lambda_{{MW,sig\left( {i,j} \right)}} \cdot \frac{{f_{HMW,sig\left( i \right)} \cdot Bias_{HMW,sig\left( i \right)} + f_{HMW,sig\left( j \right)} \cdot Bias_{HMW,sig\left( j \right)} }}{c} \hfill \\ &Bias_{{r,IFGF,sig\left( {i,j,k} \right)}}^{s} = \frac{{\left( {f_{IF1} - f_{IF3} } \right) \cdot Bias_{sig\left( i \right)} - f_{IF2} \cdot Bias_{sig\left( j \right)} + f_{IF4} \cdot Bias_{sig\left( k \right)} }}{c} \end{aligned} \right.$$

(5)

where $P_{cal} = \rho + c \cdot \left( {Clk_{r} - Clk^{s} } \right) + \alpha^{s} \cdot T_{r}^{z}$ is the calculated distance between satellite and receiver, including precise geometry distance, satellite clock, receiver clock, tropospheric delay; $Bias_{IF,sig\left( i \right)} = b_{IF,r,sig\left( i \right)} - b_{IF,sig\left( i \right)}^{s} + b_{group\left( r \right),sig\left( i \right)}^{s}$, $Bias_{HMW,sig\left( i \right)} = b_{HMW,r,sig\left( i \right)} - b_{HMW,sig\left( i \right)}^{s} + b_{group\left( r \right),sig\left( i \right)}^{s}{;}$ Round(*) represent the rounding operation. As for IF combinations, since satellite and receiver clock also contain hardware delays, most of the receiver-specific, and satellite-specific hardware can be eliminated. $b_{IF,r,sig\left( i \right)} {\text{ and }}b_{IF,sig\left( i \right)}^{s}$ represent the residual of receiver-specific and satellite-specific hardware, respectively. As for HMW combinations, $b_{HMW,r,sig\left( i \right)} = b_{r,sig\left( i \right)} + \frac{{B_{r,sig\left( i \right)} }}{{\lambda_{sig\left( i \right)} \cdot f_{HMW,sig\left( i \right)} }}$ and $b_{HMW,sig\left( i \right)}^{s} = b_{sig\left( i \right)}^{s} + \frac{{B_{sig\left( i \right)}^{s} }}{{\lambda_{sig\left( i \right)} \cdot f_{HMW,sig\left( i \right)} }}$ consist of phase and pseudorange hardware delays. Thus, based on (5), the raw biases of different frequencies can be determined without being affected by the ionospheric error:

$$\left\{ \begin{gathered} Bias_{sig\left( i \right)} = \frac{{f_{sig\left( j \right)} }}{{f_{sig\left( i \right)} }}Bias_{{HMW,sig\left( {i,j} \right)}} + \frac{{f_{sig\left( i \right)} - f_{sig\left( j \right)} }}{{f_{sig\left( i \right)} }}Bias_{{IF,sig\left( {i,j} \right)}} \hfill \\ Bias_{sig\left( j \right)} = \frac{{f_{sig\left( i \right)} }}{{f_{sig\left( j \right)} }}Bias_{{HMW,sig\left( {i,j} \right)}} - \frac{{f_{sig\left( i \right)} - f_{sig\left( j \right)} }}{{f_{sig\left( j \right)} }}Bias_{{IF,sig\left( {i,j} \right)}} \hfill \\ Bias_{sig\left( k \right)} = \frac{{f_{sig\left( i \right)}^{2} - f_{sig\left( k \right)}^{2} }}{{f_{sig\left( k \right)}^{2} }}Bias_{{IFGF,sig\left( {i,j,k} \right)}} + \frac{{f_{sig\left( i \right)} f_{sig\left( j \right)} }}{{f_{sig\left( k \right)}^{2} }}Bias_{{HMW,sig\left( {i,j} \right)}} \hfill \\ \quad\quad \quad\quad+ \frac{{f_{sig\left( k \right)}^{2} - f_{sig\left( i \right)} f_{sig\left( j \right)} }}{{f_{sig\left( k \right)}^{2} }}Bias_{{IF,sig\left( {i,j} \right)}} \hfill \\ \end{gathered} \right.$$

(6)

As for those signals at the same frequency, such as C1C and C1W on L1, C2W, C2X, C2L, and C2S on L2, additional combinations between these observations should be added for SDB analysis:

$$\begin{aligned} \Delta P_{{r,sig\left( {i,j} \right)}}^{s} &= P_{r,sig\left( i \right)}^{s} - P_{r,sig\left( j \right)}^{s} \hfill \\ &= \Delta b_{{r,sig\left( {i,j} \right)}} - \Delta b_{{sig\left( {i,j} \right)}}^{s} + \Delta b_{{group\left( r \right),sig\left( {i,j} \right)}}^{s} \hfill \\ \end{aligned}$$

(7)

where $\Delta P_{{r,sig\left( {i,j} \right)}}^{s}$ is single difference pseudorange between two signals. Based on (6) and (7), biases of each frequency can be determined. However, these biases consist of three parts, i.e., satellite-specific, receiver-specific, and satellite-receiver-type parts. The observation equation can be described as:

$${\mathbf{v}} = {\mathbf{B}} \cdot \left[ {\begin{array}{lll} {{\mathbf{Bias}}_{r} } & {{\mathbf{Bias}}^{{\mathbf{s}}} } & {{\mathbf{Bias}}_{group\left( r \right)}^{s} } \\ \end{array} } \right] - {\mathbf{L}}$$

(8)

where ${\mathbf{B}}$ and L are design matrix and Observation-Minus Calculation (OMC) matrix, respectively; ${\mathbf{Bias}}_{r}$, ${\mathbf{Bias}}^{{\mathbf{s}}}$ and ${\mathbf{Bias}}_{group\left( r \right)}^{s}$ are receiver-specific, satellite-specific and satellite-receiver-type biases:

$$\left\{ {\begin{array}{l} {B = \left[ {\begin{array}{*{20}c} {{\mathbf{U}}_{n} \otimes {\mathbf{u}}_{m} } & {{\mathbf{u}}_{n} \otimes {\mathbf{U}}_{m} } & {{\mathbf{u}}_{n} \otimes {\mathbf{U}}_{l} } \\ \end{array} } \right]} \\ {L = \left[ {\begin{array}{*{20}c} {{\mathbf{Bias}}_{{1,{\varvec{sig}}\left( {\varvec{i}} \right)}} } & \cdots & {{\mathbf{Bias}}_{{{\varvec{n}},{\varvec{sig}}\left( {\varvec{i}} \right)}} } \\ \end{array} } \right]^{{\varvec{T}}} } \\ \end{array} } \right.$$

(9)

$$\left\{ {\begin{array}{l} {{\mathbf{u}}_{n} = \left( {\begin{array}{*{20}c} 1 & {1 \cdots } & 1 \\ \end{array} } \right)^{T} } \\ {{\mathbf{U}}_{n} = \left( {\begin{array}{*{20}c} 1 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & 1 \\ \end{array} } \right)} \\ \end{array} } \right.$$

(10)

$$\left\{ {\begin{array}{l} {{\mathbf{Bias}}_{r} = \left[ {\begin{array}{*{20}c} {Bias_{1} } & {Bias_{2} \cdots } & {Bias_{n} } \\ \end{array} } \right]} \\ {{\mathbf{Bias}}^{s} = \left[ {\begin{array}{*{20}c} {Bias^{1} } & {Bias^{2} \cdots } & {Bias^{m} } \\ \end{array} } \right]} \\ {{\mathbf{Bias}}_{group\left( r \right)}^{s} = \left[ {\begin{array}{*{20}c} {{\mathbf{Bias}}_{1}^{s} } & {{\mathbf{Bias}}_{2}^{s} \cdots } & {{\mathbf{Bias}}_{l}^{s} } \\ \end{array} } \right]} \\ {{\mathbf{Bias}}_{r}^{s} = \left[ {\begin{array}{*{20}c} {Bias_{r}^{1} } & {Bias_{r}^{2} \cdots } & {Bias_{r}^{m} } \\ \end{array} } \right]} \\ \end{array} } \right.$$

(11)

where ${\mathbf{U}}_{n}$ is a n-dimensional unit matrix and ${\mathbf{u}}_{n}$ is a n-dimensional column vector with an element of 1; m is the number of satellites, n is the number of sites, l is the number of receiver groups.

To separate these three parts, additional equations should be added for each signal. The first one is the sum of satellite-specific biases, which is zero. Also, the SDB of a specific receiver type is set as zero to eliminate the rank defect, e.g., TRIMBLE receiver (Gong et al. 2018). Currently, since the precise data processing of most International GNSS Service (IGS) Analysis Centers (ACs) are based on different receiver types, the products contain the average of SDBs from different receiver types. Thus, the constraint used in Gong et al. (2018) will result in a large systematic bias between SDB corrections and current IGS products. Therefore, to make the SDB corrections as compatible as possible with existing IGS products, we add the constraint that the sum of all satellite-receiver-type biases for the same satellite is zero:

$$\left\{ {\begin{array}{*{20}c} {\mathop \sum \limits_{s = 0}^{s = m} Bias_{i,sig\left( j \right)}^{s} = 0} \\ {\mathop \sum \limits_{i = 0}^{i = l} Bias_{i,sig\left( j \right)}^{s} = 0} \\ \end{array} } \right.$$

(12)

Since SDB is linearly related to $b_{{r,sig{ }}}$ and ${{ b}}_{{{ }sig}}^{{{s}}}$, different constraints result in different estimations of SDB and thus the value of $b_{{r,sig{ }}}$ and ${{ b}}_{{{ }sig}}^{{{s}}}$. However, as long as SDB, $b_{{r,sig{ }}}$ and ${{ b}}_{{{ }sig}}^{{{s}}}$ are estimated on the same basis, no error will be introduced based on the zero-mean condition for users.

Experiments and results

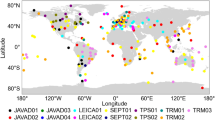
With the construction and development of the MGEX network, the number of GNSS stations has increased from about 170 in 2017 to about 300 in 2019. Figure 1 presents the distribution of MGEX stations at DOY 365, 2019. Among these approximately 300 stations, all of them can track GPS signals and about 90% of stations can track Galileo signals. As for BDS-2 and QZSS, the number of stations that provide their observations is about 85 and 40%, respectively. In addition, all these observations are downloaded from the IGS data center of Wuhan University (ftp://igs.gnsswhu.cn) and the time session is 3 years covering DOY 001, 2017 to DOY 365, 2019. At the same time, the experiments were performed with the FUSING (FUSing IN GNSS) software (Gu et al. 2020; Shi et al. 2019). The FUSING software was developed for high precision real-time GNSS data processing and multi-sensor navigation and atmospheric modeling (Luo et al. 2021).

Fig. 1

Distribution of MGEX stations used for GNSS SDB estimation at DOY 365, 2019

According to previous results of Gong et al. (2018, 2021) and Zhang et al. (2021), most SDBs corrections can be divided into different groups according to receiver brands and models except for some stations equipped with receiver TRIMBLE and JAVAD. Thus, we divide all the SDB corrections into 13 groups and the details of classification criteria are given in Table 1. Then, the daily SDB of each group can be estimated based on (5–12).

Table 1 Receiver groups classification according to receiver brands and models

Figure 2 presents the update of firmware versions for receivers equipped with different receiver brands. From the figure, there are many changes in receiver firmware versions. For example, there are total 20 types of firmware versions for JAVAD and the firmware versions are mainly 3.6.3, 3.6.6, and 3.6.7 at the beginning of year 2017. With the update of receivers, the firmware versions change to 3.7.5 and 3.7.6 for most JAVAD receivers. Similarly, the firmware versions of other receiver brands have also changed significantly, such as from 4.02 to 4.30 for LEICA, from 5.15 to 5.37 for TRIMBLE. Also, the numbers of different receiver types also change during the 3 years, where the numbers of receiver JAVAD, TRIMBLE, and SEPT increase significantly.

Fig. 2

Number of stations with different firmware versions from 2017 to 2019

To investigate the long-term characteristics of SDB, Fig. 3 presents the GPS C2W-C2L SDB series from stations CHU2 and DAR4. Over the 3-year time series, there are two receiver hardware updates. One is receiver model change from TPS NET-G3A to TPS NET-G5 and the other is firmware version change from TPS NET-G5 5.1 to TPS NET-G5 5.2.2. As for the first hardware update, the SDB of satellite G15 is changed from − 0.5 ns to − 1.1 ns, which means the receiver model change will result in SDB jumps. However, there is almost no change of SDBs for satellite G07 at both two stations, which may be due to the fact that G07 satellite SDBs of TPS NET-G3A 3.6 and TPS NET-G5 5.1 are closer. This also proves that SDB values are different among different satellites of the same receiver. As for the second hardware update, there is no change in receiver brand and model, except the firmware versions are updated from 5.1 to 5.2.2. Thus, the SDB is basically unchanged, i.e., the change of firmware version will not cause a change of SDB. On the one hand, the results confirm that SDBs are mainly related to receiver brand and model and have little correlation with firmware versions. On the other hand, it is proved that SDB is quite stable during the 3 years if there is no update of receiver hardware.

Fig. 3

C2W-C2L SDB series of satellites G07 and G15 from stations CHU2 and DAR4. The dash lines represent the receiver hardware update where the first hardware update is from TPS NET-G3A 3.6 to TPS NET-G5 5.1 and the second hardware update is from TPS NET-G5 5.1 to TPS NET-G5 5.2.2

It has been proved that signal faults change the hardware biases (Shallberg et al. 2017), which results in larger positioning errors than that of nominally healthy satellites (Edgar et al. 1999). Thus, it should be noted that the SDBs estimated for nominally healthy satellites cannot be applied for anomaly satellites. In addition, the flex power of the signal will also change the hardware biases (Xiang et al. 2020). Figure 4 presents the G01 and G32 differenced bias between two days for constant power and flex power. According to the results, the differenced biases between two days are concentrated around zero when signals are transmitted at constant power. However, when there is a flex power, the average biases of G01 and G32 satellites are shifted about 0.2 ns and 0.1 ns, respectively. In addition, the biases shift of most receivers is close except for JAVAD TRE_G3TH DELTA receiver in version “3.6.6 APR, 27, 2016” (the red cycles in the gray area). This indicates that although the hardware biases are changed, SDBs of most receivers are still consistent when there is a flex power of the signal. But it also suggests that SDB corrections may not be applicable to individual satellites and receivers when there is flex power of the signal.

Fig. 4

C1C-C1W differenced bias between two days of G01 and G32. The black squares represent differenced bias between January 25 and 26, 2017; The red cycles represent differenced bias between January 26 and 28, 2017; The red cycles in the gray area are results of JAVAD TRE_G3TH DELTA receiver in version “3.6.6 APR, 27, 2016”

Figure 5 presents the SDB correction series of GPS, BDS-2, Galileo, and QZSS part signals from 2017 to 2019. Also, SDBs are calculated based on the average SDBs of 7-day solutions to reduce the impact of noises. According to the figure, except for the SDB corrections of G063 C1C signal of JAVAD03 receiver group show an annual cycle of about ± 0.3 ns, SDB correction series of most signals and receiver groups are stable over the 3-year time session. According to Fig. 2, the firmware versions and number of stations change during the 3-year for different receiver brands. Thus, the results validate that SDB corrections are mainly affected by receiver brands and models but barely affected by firmware versions of the receiver. In addition, the SDBs of Galileo are smaller than that of GPS and BDS, which is consistent with the results of Hauschild and Montenbruck (2016) and Gong et al. (2021). This may be related to the different signal structures adopted for different satellite systems.

Fig. 5

SDB correction series of GPS, BDS-2, Galileo, and QZSS part signals based on 7-day solutions from 2017 to 2019

To analyze the long-term stability of GNSS SDB, STDs of all signals are calculated in this part. We can get a STD value for each satellite and signal based on a 3-year series for each receiver group. Figure 6 presents the distribution of GNSS SDB STDs from MGEX network. From the figure, the portions of SDB STDs within 0.1 ns are 93.2, 99.9, and 86.7% for GPS, Galileo, and QZSS, respectively. As for BDS-2, the SDB STDs within 0.1 ns and 0.2 ns are 70.0 and 96.8%, respectively. The STDs of BDS-2 SDBs are a little larger than that of GPS, Galileo, and QZSS mainly due to the limited accuracy of satellite orbit and clock and multipath of GEO satellites. Overall, the STDs of SDBs estimated from MGEX network are quite small compared with the estimated SDB corrections values given in the appendix. The results show that GNSS SDBs are quite stable and can be treated as constant values from the year 2017 to 2019. Thus, the GNSS SDB corrections are estimated as constant value and given in SINEX BIAS format for the convenience of users (https://www.researchgate.net/project/GNSS-Biases).

Fig. 6

STDs of GPS, BDS-2, Galileo, and QZSS pseudorange biases estimated from MGEX network based on 7-day solutions over 3-year series

Validation of zero-baselines

To validate the SDB corrections estimated, the 3-year data of 8 zero-baselines from DOY 001, 2017 to DOY 365, 2019 is used in this section for residual analysis and slant total electron content (STEC) extraction.

Data collection

Table 2 gives detailed information on the 8 zero-baselines, including receiver brand and models. For baseline 8, the receiver model is updated from LEICA GR25 to LEICA GR50 after MJD 58,099. As for other baselines, there was no change in receiver brands and models during the experiment.

Table 2 Information of zero-baseline

Residuals of zero-baselines

As for zero-baseline, geometry-related and atmosphere delay can be eliminated by differential operation between two stations. Thus, the single difference pseudorange observation between stations r₁ and r₂ can be described as:

$$\begin{gathered} \Delta P_{r1,r2,sig}^{s} = P_{r1,sig}^{s} - P_{r2,sig}^{s} \hfill \\\quad = c \cdot \left( {Clk_{r1} + b_{r1,sig} - Clk_{r2} - b_{r2,sig} + b_{{group\left( {r1} \right),sig}}^{s} - b_{{group\left( {r2} \right),sig}}^{s} } \right) \hfill \\\quad = c \cdot \left( {\Delta Clk_{r1,r2} + \Delta b_{r1,r2,sig} + \Delta b_{{group\left( {r1,r2} \right),sig}}^{s} } \right) \hfill \\ \end{gathered}$$

(13)

where $\Delta$ represent single difference operator; $\Delta Clk_{r1,r2} = Clk_{r1} - Clk_{r2}$, $\Delta b_{r1,r2,sig} = b_{r1,sig} - b_{r2,sig}$, $\Delta b_{{group\left( {r1,r2} \right),sig}}^{s} = b_{{group\left( {r1} \right),sig}}^{s} - b_{{group\left( {r2} \right),sig}}^{s}$ are single difference receiver clocks, receiver-specific hardware, and SDBs, respectively. The receiver clocks and receiver-specific hardware are determined by the average of single difference pseudorange observations $\Delta P_{r1,r2,sig}^{s}$ for all visible satellites,

$$\begin{gathered} \Delta SDB_{r1,r2,sig\left( i \right)}^{s} = \Delta P_{r1,r2,sig}^{s} - \frac{1}{m} \cdot \mathop \sum \limits_{s = 1}^{s = m} \Delta P_{r1,r2,sig}^{s} \hfill \\ \quad= c \cdot \left( {\Delta b_{{group\left( {r1,r2} \right),sig}}^{s} - \frac{1}{m} \cdot \mathop \sum \limits_{s = 1}^{s = m} \Delta b_{{group\left( {r1,r2} \right),sig}}^{s} } \right) \hfill \\ \end{gathered}$$

(14)

where $\Delta SDB_{r1,r2,sig}^{s}$ is single difference signal distortion bias. Obviously, if the signal distortion biases of two receivers from zero baselines are same, $\Delta SDB_{r1,r2,sig}^{s}$ should be zero. Otherwise, $\Delta SDB_{r1,r2,sig}^{s}$ would be non-zero.

Figure 7 presents the 3-year time series of GPS C1C and C2W pseudorange residuals with or without SDB corrections. For the results without SDB corrections, C1C and C2W pseudorange residuals show systematic biases for different satellites. The systematic biases are quite stable over 3 years except for observation noises and can reach about ± 1 ns. When the SDB corrections are corrected, the systematic biases of GPS pseudorange residuals greatly decrease. Both C1C and C2W pseudorange residuals are close to zero.

Fig. 7

GPS pseudorange residual series of zero-baseline 4. The top two panels represent pseudorange residuals without SDB corrections and the bottom two panels represent pseudorange residuals with SDB corrections

Figure 8 presents the 3-year time series of BDS-2 C2I and C7I pseudorange residuals with or without SDB corrections. Similarly, the BDS-2 C2I and C7I pseudorange residuals show systematic biases without SDB corrections. But the systematic biases of C7I are quite smaller than that of C2I due to BDS-2 C7I SDB corrections of TRIMBLR NETR9 and SEPT POLARXS are close. As the results of GPS, the systematic biases of BDS-2 C2I and C7I pseudorange residuals are quite stable over 3 years and greatly decrease with SDB corrections.

Fig. 8

BDS-2 pseudorange residual series of zero-baseline 4. The top two panels represent pseudorange residuals without SDB corrections and the bottom two panels represent pseudorange residuals with SDB corrections

According to Figs. 7 and 8, the daily pseudorange residuals show a large noise. Thus, the average residuals are calculated based on a 3-year series according to each satellite of each baseline. Figure 9 shows the distribution of GNSS average pseudorange residuals without and with SDB corrections. According to the figure, the pseudorange residuals with SDB corrections are more concentrated near zero than those without SDB corrections. For example, the percentage of Galileo pseudorange residuals within ± 0.03 ns improves from 74.01 to 90.82%. Also, the RMS of pseudorange residuals without SDB corrections are 0.297, 0.224, 0.042, and 0.092 ns for GPS, BDS-2, Galileo, and QZSS, respectively. However, the RMS of pseudorange residuals with SDB corrections decreases to 0.145, 0.120, 0.022, and 0.066 ns for GPS, BDS-2, Galileo, and QZSS, respectively. Moreover, it seems the quality of Galileo pseudorange observation is better than that of GPS, BDS-2, and QZSS since the pseudorange residuals are smaller than those of other satellite system. Generally, the SDB corrections can reduce the systematic biases of GPS/BDS-2/Galileo/QZSS pseudorange observations among different receiver types. What’s more, the SDB corrections are validated to be useful over 3 years, which indicates that these corrections can be used as empirical correction models to reduce the effects of GNSS SDB.

Fig. 9

Distribution of GNSS average pseudorange residuals of 8 zero-baselines based on 3-year series; blue and red bars represent residuals without and with SDB corrections, respectively

STEC extraction

In addition to the pseudorange residuals, the difference of slant ionospheric delay of zero-baseline can also be used to verify the validity of GNSS SDB corrections. The STEC can be determined by the smoothed pseudorange geometry-free (GF) combination (Hernández-Pajares et al. 2009). Since the satellite pierce points are the same for two receivers in a zero-baseline, the single-differenced geometry-free observation between two receivers will eliminate all the STEC and satellite DCB. Thus, the residuals only contain the receiver hardware and observation noises. If the SDB corrections are valid, the single-differenced GF observation among different satellites should be consistent. Otherwise, there will be systematic biases among different satellites.

Since the accuracy of STEC extraction is greatly affected by the noise of pseudorange observation, the cutoff elevation of STEC extraction is set as 20°, and the minimum smoothed time is set as 10 min in this section. Figure 10 presents the single-differenced STEC series of different satellite systems. Among them, the results of a few Galileo satellites are given due to the lack of receiving satellites. Like previous SDB results, the consistency of Galileo and QZSS single-differenced STEC is better than that of GPS and BDS-2 due to the small SDB of Galileo and QZSS. However, as for GPS and BDS-2, the single-differenced STEC shows large systematic biases even after a long smoothing period among different satellites without SDB corrections. For example, the STEC bias between GPS G03 and G29 can reach up to 8 TECU, while the STEC bias between C02 and C13 is about 5 TECU. Similar to the results of pseudorange residuals, the systematic biases of STEC from zero-baseline among different satellites greatly decrease when SDB corrections are corrected.

Fig. 10

Single-differenced STEC of zero-baseline 3. The left 4 panels represent STEC without SDB corrections and the right 4 panels represent STEC with SDB corrections

Table 3 gives the average RMS of double-differenced STEC of all zero-baselines, from which, we can know that the RMS of double-differenced STEC decreases for GPS/BDS-2/Galileo/QZSS from 12.5 to 49.2%. Among them, the maximum improvement is the results of GPS and the RMS decrease from 1.28 TECU to 0.65 TECU. The minimum improvement is the results of Galileo with an improvement of 12.5% due to the small SDBs for Galileo observations. As for BDS-2, the poor accuracy in the convergence stage will affect the statistical results since the whole arcs of STEC are used for RMS calculation. Thus, the RMS of double differenced STEC with SDB corrections is still 0.85 TECU, which is the largest in all satellite systems. Generally, the SDB corrections given here can reduce the effect of SDBs on STEC extraction for all satellite systems.

Table 3 Average RMS of double-differenced STEC of all zero-baselines (TECU)

Conclusion and discussion

The distorted GNSS signals will shift the tracking point and thus cause a bias in the pseudorange observation, namely SDB. It has been widely validated that GNSS SDB will result in the inconsistency of data processing among inhomogeneous receivers, such as satellite clock estimation and satellite DCB estimation. Also, previous research has shown that SDBs are stable over a short time period and related to receiver brands and models; thus they can be well modeled.

Many GNSS observations from 2017 to 2019 are collected from nearly 300 MGEX stations to analyze the long-term characteristics of GNSS SDB. The results show that the SDBs of GPS and BDS-2 are larger than those of Galileo and QZSS. Generally, the SDBs are within ± 1 ns for all the signals of GPS and BDS-2 while they are within ± 0.5 ns for Galileo and QZSS. Besides, most of the GNSS SDBs are quite stable for the satellite-receiver pair without the update of satellite and receiver brand and model. The proportion of SDB STDs over a 3-year series within 0.1 ns are 93.2, 99.9, and 86.7% for GPS, Galileo, and QZSS, respectively. As for BDS-2, the SDB STDs within 0.1 ns and 0.2 ns are 70.0 and 96.8% due to the poor quality of pseudorange observations. Overall, the GNSS SDBs can be treated as constant corrections from 2017 to 2019. Thus, the estimated GNSS SDBs are given as empirical corrections for each satellite-receiver-group pair and signal.

As for validation, pseudorange residuals and STEC extraction of zero-baseline are adopted. The 3-year results show that both pseudorange residuals and STEC extraction of zero-baseline show large systematic biases without SDB corrections, especially for GPS and BDS-2. However, the systematic biases greatly decrease with SDB corrections. The RMS of pseudorange residuals decreases by 28.26 to 51.18%, while the RMS of double differenced STEC decreases by 12.5 to 49.2% for different satellite systems. The results show that the empirical SDB corrections are validated over the 3-year time session.

Based on the analysis above, the SDBs are calibrated as a constant value according to SVN of satellite and receiver types for each signal. Moreover, SDBs are presented in SINEX BIAS format to be compatible with other bias products, such as DCB and OSB. With the replacement of satellites and an update of receiver models, calibration of SDBs is suggested to be a routine in the future.

Appendix: GNSS SDB corrections

Figures 11, 12, 13, and 14 are the values of GPS/BDS-2/Galileo/QZSS SDB corrections. According to these figures, the SDBs of GPS and BDS-2 are larger than those of Galileo and QZSS. Generally, the SDBs are within ± 1 ns for all signals of GPS and BDS-2 while they are within ± 0.5 ns for Galileo and QZSS.

Fig. 11

SDB corrections of GPS multi-frequency signals; Y-axis represents different satellite SVN numbers and X-axis represents different receiver groups and signals; the different colors represent SDB values (unit ns)

Fig. 12

SDB corrections of BDS-2 multi-frequency signals; Y-axis represents different satellite SVN numbers and X-axis represents different receiver groups and signals; the different colors represent SDB values (unit ns)

Fig. 13

SDB corrections of Galileo multi-frequency signals; Y-axis represents different satellite SVN numbers and X-axis represents different receiver groups and signals; the different colors represent SDB values (unit ns)

Fig. 14

SDB corrections of QZSS multi-frequency signals; Y-axis represents different satellite SVN numbers and X-axis represents different receiver groups and signals; the different colors represent SDB values (unit ns)