On the short-term temporal variations of GNSS receiver differential phase biases

Abstract

As a first step towards studying the ionosphere with the global navigation satellite system (GNSS), leveling the phase to the code geometry-free observations on an arc-by-arc basis yields the ionospheric observables, interpreted as a combination of slant total electron content along with satellite and receiver differential code biases (DCB). The leveling errors in the ionospheric observables may arise during this procedure, which, according to previous studies by other researchers, are due to the combined effects of the code multipath and the intra-day variability in the receiver DCB. In this paper we further identify the short-term temporal variations of receiver differential phase biases (DPB) as another possible cause of leveling errors. Our investigation starts by the development of a method to epoch-wise estimate between-receiver DPB (BR-DPB) employing (inter-receiver) single-differenced, phase-only GNSS observations collected from a pair of receivers creating a zero or short baseline. The key issue for this method is to get rid of the possible discontinuities in the epoch-wise BR-DPB estimates, occurring when satellite assigned as pivot changes. Our numerical tests, carried out using Global Positioning System (GPS, US GNSS) and BeiDou Navigation Satellite System (BDS, Chinese GNSS) observations sampled every 30 s by a dedicatedly selected set of zero and short baselines, suggest two major findings. First, epoch-wise BR-DPB estimates can exhibit remarkable variability over a rather short period of time (e.g. 6 cm over 3 h), thus significant from a statistical point of view. Second, a dominant factor driving this variability is the changes of ambient temperature, instead of the un-modelled phase multipath.

1 Introduction

It has long been known that the space-borne and ground-based Global Navigation Satellite System (GNSS) data are a rich source of information for retrieving various ionospheric parameters (e.g. slant total electron content, sTEC) (Dettmering et al. 2011; Hernández-Pajares et al. 1999; Komjathy et al. 2012; Li et al. 2015; Liu and Gao 2004; Mannucci et al. 1998; Tang et al. 2015). The first essential task serving the purpose of sTEC retrieval is to extract the ionospheric observables from every continuous arc of GNSS code and phase observations, involving the following three sequential steps (Dyrud et al. 2008; Liu and Wan 2016; Ping et al. 2002; Stephens et al. 2011).

Consider a given arc that generally covers a time span of a few (say, 3–7) hours. The first step consists of epoch-wise differencing the code observations at two different frequencies, giving rise to the code geometry-free observations. This shall fully eliminate the frequency-independent effects on the code observations, leaving only the sTEC and the satellite and receiver differential code biases (DCB) (Sardon et al. 1994; Xue et al. 2015; Li et al. 2016). Along similar lines one can construct the phase geometry-free observations, encompassing the sTEC, the satellite and receiver differential phase biases (DPB) and the ambiguity that remains constant as long as no cycle slip occurs. In the second step, one needs to compute the so-called leveling bias through (weighted) averaging the differences between the phase and the code geometry-free observations over all the epochs. The leveling bias is thereby a linear combination of the DCB, the DPB and the ambiguity, thus arc-dependent. The third step refers to the application of the leveling bias computed to the phase geometry-free observations, eventually leading to the ionospheric observables of interest.

It is important to note some implications in the descriptions above.

First, the ionospheric observables so obtained are not unbiased; they have an interpretation of the sTEC plus the (scaled) satellite and receiver DCB, thereby necessitating the isolation of sTEC from DCB by means of sophisticated ionospheric models (e.g. thin-layer or tomographic) (Brunini and Azpilicueta 2010; Chen et al. 2016; Debao et al. 2015; Yao et al. 2013). We remark here that the satellite and receiver DCB combined may attain a maximum magnitude of 100 total electron content units (TECu) (Ciraolo et al. 2007; Yunbin et al. 2015), thus deserving a careful treatment.

Second, leveling errors in the ionospheric observables may arise in the leveling bias computation process, having multiple causes including the multipath in the code geometry-free observations and the intra-day variability of the receiver DCB (Brunini and Azpilicueta 2009; Ciraolo et al. 2007; Coster et al. 2013; Kao et al. 2013; Zhong et al. 2015); both effects are non-random and thus cannot be reasonably averaged out, in particular for rather short arcs. Several researchers have demonstrated numerically that, in the worst case, the leveling errors induced solely by the code multipath (time-varying receiver DCB) can reach sizes of up to 5.3 (8.8) TECu (Ciraolo et al. 2007).

The primary goal of this paper is to bring to light another possible cause of the leveling errors, that is, the variations of receiver DPB over relatively short time intervals (ranging from one entire day down to a few hours). For this purpose we borrow from related studies in other fields the idea of characterising receiver DPB based on zero and/or short baselines (Bruyninx et al. 1999; Wang and Gao 2001), and extend it in essentially two respects. First, we develop a theoretically rigorous method, enabling epoch-wise estimation of between-receiver DPB (BR-DPB) from a single epoch of (inter-receiver) single-differenced, phase-only GNSS observations. This method will give rise to high-precision, epoch-wise BR-DPB estimates that are free of code multipath-induced errors, provided that the phase-only observations in use are accurate to millimetre levels, as is often the case. It is expected that from these estimates the actual time-varying characteristics of receiver DPB can be inferred to the greatest extent possible. Second, whereas those previous studies focused merely on global positioning system (GPS, US GNSS), in this study we also pay attention to the newly emerging BeiDou Navigation Satellite System (BDS, Chinese GNSS) (Shi et al. 2012; Yang et al. 2011). Unlike the GPS whose constellation consists only of medium earth orbit (MEO) satellites, the BDS constellation is comprised of MEO, geostationary orbit (GEO) as well as Inclined geosynchronous orbit (IGSO) satellites (Montenbruck et al. 2013). Nowadays, the use of the BDS to study the ionosphere is continuously expanding (Jin et al. 2016; Li et al. 2012; Tang et al. 2014; Xue et al. 2015; Zhang et al. 2015).

2 Methods

In seeking to clarify the mechanism of the leveling errors, this section starts with a theoretical outline on the use of GNSS phase and code geometry-free observations for ionospheric observable retrieval. We then describe in detail our proposed method for the epoch-wise estimation of BR-DPB, with special attention paid to the elimination of discontinuities that may show up in the estimates.

2.1 Retrieval of ionospheric observables

Our point of departure is to model the code (phase) geometry-free observable $p_\mathrm{r,gf}^\mathrm{s}$ ($\phi _\mathrm{r,gf}^\mathrm{s}$) associated with satellite s and receiver r as

$$\begin{aligned} p_\mathrm{r,gf}^\mathrm{s}= & {} \left( {\mu _2 -\mu _1 } \right) \iota _\mathrm{r}^\mathrm{s} +d^\mathrm{s}+d_\mathrm{r} +\varepsilon _{\mathrm{r},p}^\mathrm{s} \nonumber \\ \phi _\mathrm{r,gf}^\mathrm{s}= & {} \left( {\mu _2 -\mu _1 } \right) \iota _\mathrm{r}^\mathrm{s} +\delta ^\mathrm{s}+\delta _\mathrm{r} +z_\mathrm{r,gf}^\mathrm{s} +\varepsilon _{\mathrm{r},\phi }^\mathrm{s} \end{aligned}$$

(1)

with $p_\mathrm{r,gf}^\mathrm{s} =p_{\mathrm{r},2}^\mathrm{s} -p_{\mathrm{r},1}^\mathrm{s}$ ($\phi _\mathrm{r,gf}^\mathrm{s} =\phi _{\mathrm{r},1}^\mathrm{s} -\phi _{\mathrm{r},2}^\mathrm{s}$) and where $p_{\mathrm{r},j}^\mathrm{s}$ ($\phi _{\mathrm{r},j}^\mathrm{s}$) is the code (phase) observable at frequency $f_j$ with $j=1,2$. Here, we assume that a number of corrections including satellite and receiver phase centre offsets and variations (PCO and PCV) and phase wind-up are applied to the observables. We denote the first-order effect of the sTEC on $p_{\mathrm{r},j}^\mathrm{s}$ by $\mu _j \cdot \iota _\mathrm{r}^\mathrm{s}$, with $\mu _j =\frac{f_1^2 }{f_j^2 }$ and $\iota _\mathrm{r}^\mathrm{s}$ the sTEC at $f_1$. The offset between two satellite code (phase) instrumental delays at $f_1$ and $f_2$ accounts for the existence of the satellite DCB (DPB), denoted using $d^\mathrm{s}$ ($\delta ^\mathrm{s}$); likewise, we can arrive at a definition for the receiver DCB (DPB), denoted using $d_\mathrm{r}$ ($\delta _\mathrm{r}$). $\varepsilon _{\mathrm{r},p}^\mathrm{s}$ ($\varepsilon _{\mathrm{r},\phi }^\mathrm{s}$) is the un-modelled error due to code (phase) noise and multipath. $z_\mathrm{r,gf}^\mathrm{s}$ is the combination of two integer ambiguities $z_{\mathrm{r},j}^\mathrm{s}$ in $\phi _{\mathrm{r},j}^\mathrm{s}$, which reads

$$\begin{aligned} z_\mathrm{r,gf}^\mathrm{s} =\lambda _1 \cdot z_{\mathrm{r},1}^\mathrm{s} -\lambda _2 \cdot z_{\mathrm{r},2}^\mathrm{s} \end{aligned}$$

(2)

where $\lambda _j =\frac{c}{f_j }$ is the wavelength, with c the speed of light in vacuum. All quantities in above two equations are expressed in units of length, except for $z_{\mathrm{r},j}^\mathrm{s}$ that are expressed in cycles.

We shall now compute the leveling bias $L_\mathrm{r}^\mathrm{s}$ by (weighted) averaging a continuous arc of $( {p_\mathrm{r,gf}^\mathrm{s} -\phi _\mathrm{r,gf}^\mathrm{s} })$. Thus we have, assuming the arc considered here covers a total of t epochs,

$$\begin{aligned} L_\mathrm{r}^\mathrm{s}= & {} {\sum _{i=1}^t {( {p_\mathrm{r,gf}^\mathrm{s} -\phi _\mathrm{r,gf}^\mathrm{s} } )\cdot w_i}}\Big /{\sum _{i=1}^t {w_i}}\nonumber \\= & {} d^\mathrm{s}-\delta ^\mathrm{s}+d_\mathrm{r} -\delta _\mathrm{r} -z_\mathrm{r,gf}^\mathrm{s} +\varepsilon _{\mathrm{r},L}^\mathrm{s} \end{aligned}$$

(3)

with i the epoch index, $w_i$ the (non-normalised) weight and $\varepsilon _{\mathrm{r},L}^\mathrm{s}$ the error in $L_\mathrm{r}^\mathrm{s}$.

Note, in Eq. (3), that, $w_i$ quantifies the contribution of $({p_\mathrm{r,gf}^\mathrm{s} -\phi _\mathrm{r,gf}^\mathrm{s} })$ at epoch i to the resulted $L_\mathrm{r}^\mathrm{s}$. Generally, we choose the weighting scheme as a function of elevation and/or signal-to-noise ratio (Hartinger and Brunner 1999). The presence of $\varepsilon _{\mathrm{r},L}^\mathrm{s}$ can be primarily attributed to the multipath component of $\varepsilon _{\mathrm{r},p}^\mathrm{s}$, normally $100\times$ greater than that of $\varepsilon _{\mathrm{r},\phi }^\mathrm{s}$ (Georgiadou and Kleusberg 1988). Furthermore, the tacit assumption is that, $d^\mathrm{s}$, $\delta ^\mathrm{s}$, $d_\mathrm{r}$ and $\delta _\mathrm{r}$ are time-invariant over t epochs. In fact, however, this assumption might not hold true, thus partially accounting for $\varepsilon _{\mathrm{r},L}^\mathrm{s}$ as well. As mentioned earlier in this paper, other researchers found that $d_\mathrm{r}$ could indeed exhibit striking intra-day variability. A natural continuation of this work is the extension to $\delta _\mathrm{r}$. This is the aim of the present paper. It is possible, though not usual, that the changes in $d^\mathrm{s}$ and/or $\delta ^\mathrm{s}$ occur over a period of time as short as a few hours (Li et al. 2013; Montenbruck et al. 2012). Such a consideration falls, however, outside the scope of the present paper.

Applying $L_\mathrm{r}^\mathrm{s}$ to $\phi _\mathrm{r,gf}^\mathrm{s}$ finally yields

$$\begin{aligned} \bar{{\iota }}_\mathrm{r}^\mathrm{s}= & {} \alpha ( {L_\mathrm{r}^\mathrm{s} +\phi _\mathrm{r,gf}^\mathrm{s} } ) \nonumber \\= & {} \iota _\mathrm{r}^\mathrm{s} +\alpha ( {d^\mathrm{s}+d_\mathrm{r} } )+\varepsilon _{\mathrm{r},\bar{{\iota }}}^\mathrm{s} \end{aligned}$$

(4)

with $\bar{{\iota }}_\mathrm{r}^\mathrm{s}$ the ionospheric observable, $\alpha =\frac{1}{\mu _2 -\mu _1 }$ the scaling factor that is about 1.55 for GPS and 1.49 for BDS, and $\varepsilon _{\mathrm{r},\bar{{\iota }}}^\mathrm{s} =\alpha ( {\varepsilon _{\mathrm{r},L}^\mathrm{s} +\varepsilon _{\mathrm{r},\phi }^\mathrm{s} }$) the leveling error.

Equation (4) succeeds in clarifying that, $\varepsilon _{\mathrm{r},L}^\mathrm{s}$, after being amplified by a factor of $\alpha$, has been translated into $\bar{{\iota }}_\mathrm{r}^\mathrm{s}$, and thus tends to be a particularly dominating component of $\varepsilon _{\mathrm{r},\bar{{\iota }}}^\mathrm{s}$.

2.2 Epoch-wise estimation of BR-DPB

Consider a zero or short baseline configuration, for which one can safely assume no differential ionospheric effects. The difference between two phase geometry-free observables $\phi _{a,\mathrm{gf}}^\mathrm{s}$ and $\phi _{b,\mathrm{gf}}^\mathrm{s}$ simultaneously measured at two receivers (called a and b) reads

$$\begin{aligned} \phi _{ab,\mathrm{gf}}^\mathrm{s} =\delta _{ab} +z_{ab,\mathrm{gf}}^\mathrm{s} +\varepsilon _{ab,\phi }^\mathrm{s} \end{aligned}$$

(5)

with $(\cdot )_{ab} =(\cdot )_a -(\cdot )_b$ the (inter-receiver) single-differencing operator.

Table 1 An overview of GNSS data sets used in this study

Equation (5) represents a rank-deficient system since the BR-DPB $\delta _{ab}$ and the ambiguity $z_{ab,\mathrm{gf}}^\mathrm{s}$ are not individually estimable. To cope with this problem, we need to assign one satellite (say, $s=1$) as pivot, whose ambiguity $z_{ab,\mathrm{gf}}^1$ plays its role as the datum. Consequently we have the re-parametrised variant of Eq. (5), written as

$$\begin{aligned} \phi _{ab,\mathrm{gf}}^1= & {} \bar{{\delta }}_{ab} +\varepsilon _{ab,\phi }^1 \nonumber \\ \phi _{ab,\mathrm{gf}}^\mathrm{s}= & {} \bar{{\delta }}_{ab} +z_{ab,\mathrm{gf}}^{s1} +\varepsilon _{ab,\phi }^\mathrm{s} \end{aligned}$$

(6)

with $s\ne 1$ and where $\bar{{\delta }}_{ab} =\delta _{ab} +z_{ab,\mathrm{gf}}^1$ is the estimable (but biased) BR-DPB. $z_{ab,\mathrm{gf}}^{s1} =z_{ab,\mathrm{gf}}^\mathrm{s} -z_{ab,\mathrm{gf}}^1$, the estimable ambiguity, is in essence the geometry-free combination of two integer double-differenced ambiguities $z_{ab,1}^{s1}$ and $z_{ab,2}^{s1}$ at $f_1$ and $f_2$, that is, $z_{ab,\mathrm{gf}}^{s1} =\lambda _1 \cdot z_{ab,1}^{s1} -\lambda _2 \cdot z_{ab,2}^{s1}$. This fact motivates us to estimate the $\bar{{\delta }}_{ab}$ through the following two steps.

Based on the double-differenced code and phase observables, the first step is to resolve for the integer-values of $z_{ab,1}^{s1}$ and $z_{ab,2}^{s1}$ for all independent satellite pairs throughout the whole observation period. We consider this task to be rather easy to accomplish, particularly because these observables from the zero or short baseline are close to error-free, thereby leading to fast (potentially even instantaneous) ambiguity resolution (Teunissen et al. 1997). With $z_{ab,1}^{s1}$ and $z_{ab,2}^{s1}$ successfully resolved, it allows us to calculate the $z_{ab,\mathrm{gf}}^{s1}$ deterministically.

The second step takes $z_{ab,\mathrm{gf}}^{s1}$ calculated in step one for $s\ne 1$ as deterministic corrections and apply them to $\phi _{ab,\mathrm{gf}}^\mathrm{s}$, thus yielding

$$\begin{aligned} \begin{aligned} \phi _{ab,\mathrm{gf}}^1&=\bar{{\delta }}_{ab} +\varepsilon _{ab,\phi }^1 \\ \bar{{\phi }}_{ab,\mathrm{gf}}^\mathrm{s}&=\bar{{\delta }}_{ab} +\varepsilon _{ab,\phi }^\mathrm{s} \end{aligned} \end{aligned}$$

(7)

with $\bar{{\phi }}_{ab,\mathrm{gf}}^\mathrm{s} =\phi _{ab,\mathrm{gf}}^\mathrm{s} -z_{ab,\mathrm{gf}}^{s1}$. We conclude this step by solving for the $\bar{{\delta }}_{ab}$ epoch-wise using the least-squares estimator.

Recall that $\bar{{\delta }}_{ab} =\delta _{ab} +z_{ab,\mathrm{gf}}^1$, where the datum ambiguity $z_{ab,\mathrm{gf}}^1$ corresponds to the pivot satellite $s=1$. In general, one pivot satellite can be visible (that is, in the common view of two zero or short baseline receivers) only for a few hours, in particular if it is a MEO satellite. When the observation period exceeds a few tens of hours, as is our case, assigning multiple satellites as pivot would be inevitable. As long as pivot satellite alters, for instance, from $s=1$ to $s=2$, two datum ambiguities $z_{ab,\mathrm{gf}}^1$ and $z_{ab,\mathrm{gf}}^2$ are highly expected to be different in size, thereby introducing one abrupt jump in the epoch-wise estimates of $\bar{{\delta }}_{ab}$ that can be derived as $z_{ab,\mathrm{gf}}^{21} =z_{ab,\mathrm{gf}}^2 -z_{ab,\mathrm{gf}}^1$. Bearing this in mind, we shall proceed to correct such a jump by taking advantage of the exact magnitude of $z_{ab,\mathrm{gf}}^{21}$ that is available at no extra computational cost, as it was already computed during the integer ambiguity resolution phase.

Finally, we make two remarks concerning the BDS constellation. First, the occurrence of jump(s) caused by the changing pivot satellite is possibly avoidable, if use has been made of one GEO satellite that is known to be constantly visible as pivot. Second, suppose that a and b are two BDS-enabled receivers from different manufacturers. Special care should then be taken to account for the non-zero phase Inter-Satellite-Type Bias (ISTB) problem (Nadarajah et al. 2013), leading to the dependence of the BR-DPB $\delta _{ab}$ upon satellite types. Fortunately for us, we can deal with this problem by applying the tabulated phase ISTB values published by that work to the BDS phase observations used in our experiments.

3 Results and discussion

3.1 Experiment setup

Table 1 summarises the relevant characteristics of the experimental data sets considered for this study, including the station name, receiver and antenna type, approximate location of the receivers and time period of the observations.

The first two pairs of receivers, participating in the International GNSS Service (IGS) network (http://www.igs.org/), create two short baselines. These receivers acquire GPS (phase and code) observations at both L1 (1575.42 MHz) and L2 (1227.60 MHz) frequencies. According to their modip latitude (Azpilicueta et al. 2006), the two receivers LCK3/4 ($27.45{^\circ }\hbox {N}$) with approximate distance of 4.5 m are located in the low-latitude ionospheric region, while the other two receivers KERG/KRGG ($56.40{^\circ }\hbox {S}$) separated by approximately 8.5 m are situated at the mid-latitude ionospheric region. This set of experimental data corresponds to the period from 19 to 23 June 2015. The first 3 days are a quiet geomagnetic period (daily Kp sum 6−, 1$+$ and 12−), whereas the remaining 2 days were characterised by highly disturbed geomagnetic conditions (daily Kp sum 35$+$ and 42−).

Fig. 1

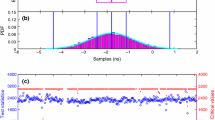
One-day time series of BR-DPB estimates (in m) associated with GPS, LCK3–LCK4 and day 174: before (blue, left y axis) and after (green, left y axis) eliminating the jumps. Red line (right y axis) indicates the visibility of each pivot satellite, and as an example the eclipse specifies the time period covered by the first pivot satellite (PRN 1)

In addition, from a network of five receivers deployed at the main campus of Curtin University in Perth (Australia), we collected GPS observations at L1 and L2 frequencies, along with BDS ones at B1 (1561.098 MHz) and B2 (1207.14 MHz) frequencies, during the whole April 2015. We classify these receivers according to whether or not they have been connected to a common antenna. The three receivers CUT0/1/3, sharing one antenna (TRM59800.00), were installed in the roof-top plant room of building 402, where the inside temperature varies in accordance with the changing outside temperatures. A few hundred (358) metres away from this antenna, another antenna of the same type was connected via a splitter to receivers SPA5/7 that were placed in an air-conditioned room of building 407. It is worth mentioning that the air-conditioning system operates every day between 9:00 and 21:30 Local Time (LT, UTC$+$8 hours), maintaining room temperatures as near 25 $^\circ$C as possible. Moreover, we recorded the ambient environmental temperatures to which these five receivers were exposed over 3 days (from 24 to 26 April 2015) with a time resolution of 1 min or less.

In all the cases, the sampling interval of experimental GNSS observations is 30 s and the cut-off elevation mask is 10$^\circ$. These observations, each weighted according to the elevation of the satellite, were processed into BR-DPB estimates on a baseline-by-baseline and epoch-by-epoch basis. During this process, the integer ambiguity resolution was performed using the least-squares ambiguity decorrelation adjustment (LAMBDA) method (Teunissen 1995). For the sake of brevity, we shall restrict ourselves to the analysis of BR-DPB estimates obtained for a selected set of baselines during some of the experimental days. These results are representative of all the experimental results that we obtained.

3.2 Alignment of epoch-wise BR-DPB estimates

As stated before, abrupt jumps may very likely be present in the epoch-wise BR-DPB estimates covering a long period of time (e.g. 24 h). Prior to our analysis, proper handling of these jumps should be in place. We address this issue by considering a representative example (depicted in Fig. 1), which concerns two time series of epoch-wise BR-DPB estimates (in metres) determined using GPS phase observations collected at two short baseline receivers LCK3/4 on day 174 of 2015. The first time series (blue line, left y axis) contains ten jumps with sizes ranging from a few centimetres to several metres. This, taken together with the red line (right y axis) which shows the pivot satellites chosen during different time periods of the day, confirms that each jump occurs immediately at the instant when the current pivot satellite sets and a new pivot satellite comes into view. Fortunately, the use of integer resolved double-differenced ambiguities permits us to eliminate those 10 jumps, resulting in the second time series (green line, left y axis) that is jump-free, and can therefore later be used for our further analysis. As one can see by comparing the two time series, they coincide with each other only during the time period when the first pivot satellite (i.e. PRN 1) remains active, further implying that the datum ambiguity affecting the second time series (green line) refers uniquely to PRN 1.

Fig. 2

One-day time series of BR-DPB estimates (in m), shifted vertically by an amount equal to the value of the estimate at 00:00 (GPST). Four plots, arranged in two rows and two columns, depict the results for two short baselines (upper row, LCK3–LCK4; bottom row, KERG-KRGG) and for two consecutive days (left column, day 170; right column, day 171). Note that LCK3 and LCK4 use antennas of the same type, while KERG and KRGG use antennas of different types

3.3 Characterisation of BR-DPB estimates

As a point of interest, Fig. 2 seeks to illustrate the intra-day variability as well as the between-day repeatability of BR-DPB estimates using four representative cases; each is shown in a separate plot, including a whole day of BR-DPB estimates determined for one short baseline. For better visibility, we have shifted each one-day time series vertically, such that they all start with zero at GPS time (GPST) 00:00 (i.e. the first epoch).

We pay attention, first of all, to the two cases depicted in Fig. 2a, b, from which two conclusions can be drawn. First, the magnitude of variability in the time series within a few hours may not fall within the noise level (generally below 1 cm) and can thus be considered to be statistically significant. Take, for example, the first case (Fig. 2a). It follows that this time series exhibits a sharp reduction in size (up to approximately 5 cm) within the first 3–4 h. Second, by comparing two figures, we further find that the two time series show very distinct variability patterns. We take this fact as an indication that, phase multipath, widely known to repeat at approximately a sidereal day (236 s less than 1 solar day), cannot account for the major cause of that variability; otherwise, one can expect that one time series should follow the same variability pattern as the other.

From Fig. 2c, d, depicting the remaining two cases, we confirm and extend our above findings. Importantly, the leading cause underlying the noticeable intra-day variability in BR-DPB estimates, although still unclear up to this point, appears to be dependent at least upon the receiver location and the experimental day. Given this fact, it is entirely natural to suspect that such a cause has something to do with the environmental conditions surrounding the receivers. In what follows, we shall focus primarily on the verification of this hypothesis.

Figure 3a, b show, respectively, for GPS and BDS, the 3-day time series of BR-DPB estimates in relation to two zero baseline receivers SPA5/7. Interestingly, it is found that both time series are slightly different in the magnitude, but remarkably similar in the trend. The difference can be attributed to the fact that the receiver bias value usually depends, in addition to other factors such as hardware and antenna, on the GNSS constellation (Zhang and Teunissen 2015). On the other hand, the similarity lies particularly in the fact that the same (or, at least, close to the same) oscillating behaviour is simultaneously present in both time series and that oscillation occurs every day between 01:00 GPST (09:00 LT) and 13:30 GPST (21:30 LT), corresponding exactly to the time interval when the air-conditioning system is on. This motivates us to examine the ambient temperatures to which the two receivers SPA5/7 were exposed (as depicted in Fig. 3c or 4c) on the same days. We note that the correlation between the time series of BR-DPB estimates (Fig. 3a or b) and that of temperatures (Fig. 3c or 4c) is quite striking, thereby suggesting that the intra- as well as between-day variability in BR-DPB estimates is, or should be, a direct response to the changes of ambient temperature. We further support this finding by showing more results. The panels (a) and (b) of Fig. 4 are analogous to those of Fig. 3 but refer to another pair of receivers (CUT0 and SPA7) creating a short baseline. Figure 4d, the analogue to Fig. 3c or 4c, depicts the ambient temperatures experienced by the receivers CUT0/1/3. Taken together, these results demonstrate again that the variability at different time scales in each time series (Fig. 4a or b) can be traced almost exclusively to the temperature factor (Fig. 4c, d); in this case, interestingly, the changing temperatures of receiver CUT0 (Fig. 4d) and that of receiver SPA7 (Fig. 3c or 4c) are found to be responsible, respectively, for the overall variability pattern and the oscillations in each time series (Fig. 4a or b).

Fig. 3

a Three-day time series of BR-DPB estimates (in m) determined using GPS phase data from the zero baseline SPA5–SPA7; these estimates have been shifted vertically by an amount equal to the value of the estimate at 00:00 (GPST) on the first day; b BDS counterpart; c 3-day time series of ambient environmental temperatures (in $^\circ$C) measured in the air-conditioned room of building 407 where receivers SPA5/7 are located. A data gap lasting 1 h or less occurs on day 115 due to the temporary failure of temperature sensor

Fig. 4

a, b Analogous to those of Fig. 3, except that they refer to the short baseline CUT0–SPA7; c same as that of Fig. 3; d 3-day time series of ambient environmental temperatures (in $^\circ$C) measured in the roof-top plant room of building 402 where receivers CUT0/1/3 are located

Fig. 5

Upper (bottom) scatter plot displays BR-DPB estimates depicted in Fig. 4a (Fig. 4b) versus ambient temperatures depicted in Fig. 4d. The time period covered by these estimates and temperatures corresponds to 9:00–21:30 local time on days 114–116 of 2015, during which receiver SPA7 is subject to stable temperature and, consequently, insignificant DPB variability. Superimposed on each scatter plot is the least-squares regression line in red

Returning to Fig. 2, it follows that the peak-to-peak value that each time series reaches ranges from almost 8 cm (Fig. 2b), down to 5 cm (Fig. 2d). These values are expected to lead to levelling errors up to 0.5 TECu in the ionospheric observables (1 TECu contributes to a path delay of approximately 16 cm at the L1 GPS frequency). Consider other error sources that are known to be relevant to ionospheric studies, in particular, receiver PCO and PCV, phase wind-up and intra-day variability of receiver DCB. In general, the effect that each of them has on the ionospheric observables is at the level of ${\le }3$ cm (0.2 TECu), ${\le }2$ cm (0.1 TECu) and ${\le }8.8$ TECu. This means that, intra-day variability of receiver DCB is the largest error source, followed in descending order by that of receiver DPB (which is the focus of this study), receiver PCO and PCV, and phase wind-up.

We shall recall the fact that ionospheric studies rely primarily on zero-differenced (instead of inter-receiver single-differenced) GNSS observables. Hence, it is desirable to quantitatively analyse the effect of temperature on DPB estimates for individual receivers. We execute such an analysis based on the data sets shown in Fig. 4. We turn first to Fig. 5a, in which a scatter plot is shown of the close-to-linear dependence of the BR-DPB estimates (taken from Fig. 4a, but expressed in units of nanoseconds) upon the corresponding temperatures (see Fig. 4d). These estimates and temperatures correspond to the period when one of the receivers, SPA7, is operating in a controlled temperature environment, and as such, is subject to fairly constant DPB. This relation is statistically significant, because the Pearson Correlation Coefficient (PCC) between the two variables is equal to 0.75; for a statistical sample size greater than 100, as is the case here, the absolute PCC greater than 0.25 is rated significant. Drawn through these data points is the least-squares regression line, whose slope reflects the change rate of GPS DPB of receiver CUT0, shown to be on the order of 0.004 ns, or, 4 ps per $^\circ$C. This value is of statistical significance as its formal error is about 0.3 ps. Likewise, shown in Fig. 5b is a scatter plot representing the relation between the same set of temperature data as considered in Fig. 5a and the BR-DPB estimates (in nanoseconds) taken from Fig. 4b. Again, we see that this relation is strongly linear over the range of temperatures studied (with PCC of 0.92). At the same time, the non-zero slope of the calculated regression line suggests that, in this case, the change rate of BDS DPB of receiver CUT0 amounts to 9 ps per $^\circ$C (with formal error of 0.3 ps). To handle the significant sensitivity of the receiver DPB to the temperature effect, it makes better sense to model the receiver DPB as a linear function of ambient temperatures measured, than to assume them to be time-invariant.

4 Conclusions

In this paper, we have developed a method for between-receiver differential phase bias (BR-DPB) estimation. This method has the following characteristics, which make it well suited for use in disclosing short-term temporal variations, if any, in GNSS receiver differential phase biases. First, advantage has been taken of the zero or short baseline setup, thereby enabling an adequate cancellation of the sources of error that are common to both receivers. Second, use has been made of epoch-wise, (inter-receiver) single-differenced, phase geometry-free observations. In doing so, the resultant BR-DPB estimates of high precision (generally better than 1 cm) turn out to be immune to the effect of code multipath. Third, care has been taken of the integer nature of double-differenced ambiguities. This ensures the full exploitation of the phase observations employed, and, more importantly, the reasonable elimination of the jumps very likely present in BR-DPB estimates.

We applied the method detailed above to a number of sets of GPS and BDS data, covering a broad range of receiver and antenna types, receiver locations and observation periods. According to the experimental results, we found that the BR-DPB estimate could indeed vary rapidly as a function of time. In a particular case (see, for example, Fig. 2a), it is shown that this variability over a period of a few hours (e.g. from 00:00 to 00:03 GPST) is statistically significant, as it reaches a peak-to-peak value of 5 cm, much higher than the noise level. Moreover, we identified the leading cause underlying the occurrence of this variability as the changes in ambient temperature to which both receivers were exposed. Finally, we demonstrated for what is to our knowledge the first time that the change rate of receiver DPB with respect to ambient temperature can be on the order of a few ps per $^\circ$C. Therefore, we suggest taking into account this important issue when extracting the ionospheric observables from GNSS data collected by receiver(s) subject to extreme temperature fluctuations, such that the leveling errors can be expected to be further reduced.