Introduction

Global navigation satellite systems (GNSSs) can provide all-weather worldwide positioning service, and have been widely used in various fields. However, in some challenging situations, GNSSs cannot provide precise and reliable positioning service. For example, when GNSS satellites are not visible due to occlusion, the accuracy of GNSS positioning service is significantly reduced, or even completely unavailable.

Ground-based positioning systems broadcasting GNSS-like signals can enhance the performance of GNSS, or even provide stand-alone positioning service, as a supplement or backup (Wang 2002). A large number of such systems have been designed for various applications, including aircraft landing (Cobb 1997; Kiran and Bartone 2004; Lee et al. 2008), land/marine vehicle navigation (Jiang et al. 2015; Montillet et al. 2014), and indoor positioning (Guo et al. 2018; Jiang et al. 2014; Kee et al. 2003; Lee et al. 2010).

These systems include a number of base stations and provide regional positioning services. The concept of base stations in this research is different from that in GNSS augmentation systems. The base stations can be transmitters broadcasting navigation signals. In some systems, the base stations include receivers for wireless time synchronization.

Some ground-based systems work without GNSS and provide stand-alone precise positioning service, such as Locata (Barnes et al. 2003). In precise point positioning, the carrier phase measurements need to be used, for which ambiguity resolution (AR) is a key issue. Existing AR methods for ground-based systems usually follow those in GNSS precise positioning, such as antenna swap methods, known-point-initialization (KPI) methods, and on-the-fly (OTF) methods (Ge et al. 2008; Gourevitch et al. 1995; Hofmann-Wellenhof and Remondi 1988; Teunissen 1995).

Among them, the KPI methods and OTF methods have been widely used for single point positioning in stand-alone ground-based systems. The KPI methods require other measuring instruments to obtain accurate initial coordinates, based on which the receiver resolves the integer ambiguities (Montillet et al. 2009). Due to its stringent requirements for accurate initial coordinates, however, the KPI method is quite limited in practice.

The dynamic key point initialization (DKPI) method requires a number of initial points and determines ambiguities via the change of geometry (Guo et al. 2018). Unlike the KPI methods, the DKPI method allows approximate coordinates of initial points. It can be said that the more accurate initial points a method requires, the more inconvenient it will be. In this regard, the DKPI method is more convenient than the KPI methods.

The OTF methods resolve ambiguities via geometric changes. OTF methods do not depend on a priori information obtained by measuring instruments, and so are very convenient in practice. There have been a number of related research studies for ground-based systems. Amt (2006) and Bertsch et al. (2009) proposed OTF-AR methods based on the nonlinear batch least squares estimation. AR methods based on an extended Kalman filter are proposed in Jiang et al. (2013) and Lee et al. (2005). Some OTF-AR methods have been verified by experiments, which demonstrate that ground-based systems are able to provide high-precision positioning services (Jiang et al. 2013; Montillet et al. 2009).

For existing OTF methods, the AR problem is usually considered to be a nonlinear integer-mixed problem. The approximated linear expansion is widely used, based on initial position estimation obtained from code measurements. As a result, the performance of existing OTF-AR methods depends greatly on the accuracy of code measurements. On the one hand, due to the much closer distance between the receiver and the base stations than in GNSS, the nonlinear effect is quite significant in ground-based positioning (Dai et al. 2001). Therefore, if the accuracy of the initial position estimation is poor, the nonlinear error caused by linearization can be severe.

On the other hand, multi-path effects are more severe in ground-based positioning than in GNSS, so the error of the code measurement could be relatively large, resulting in a low-accuracy initial position estimation. In this case, existing OTF methods will suffer from convergence difficulties, thereby limiting their application (Jiang et al. 2013).

It must be pointed out that the discussion in Amt (2006) and Bertsch et al. (2009) assumes accurate time synchronization and integer values of ambiguities. However, the DKPI method allows ambiguities that are not integers and was verified with an experimental system without accurate synchronization in Guo et al. (2018). We will consider both cases.

Recently, an OTF method with the idea of double differencing and squaring is proposed in Wang et al. (2018), which avoids using code measurements. However, in their system model, a transceiver is required to perform two-way ranging to eliminate the clock differences of the rover and base stations. The additional transceiver increases the size, expense and power consumption of the user equipment and the total number of users is limited by the communication capacity. In this regard, such a system is not desirable for practical applications and quite different from others (Amt 2006; Bertsch et al. 2009; Guo et al. 2018; Jiang et al. 2014; Montillet et al. 2009).

We present a new double difference square (DDS) observation model of carrier phase measurement for ground-based navigation systems without two-way ranging, based on which a new OTF-AR method only involving the carrier phase measurement is proposed for precise point positioning. With a clock model introduced, the proposed method obtains the linear DDS observation model by double differencing and squaring, and then solves it to obtain an initial solution with decimeter-level accuracy. Based on this solution, the float solution with higher accuracy can be solved, which only requires the frequency synchronization of base stations. Further, if the clock differences of base stations are accurately calibrated, the fixed solution can be obtained by employing the LAMBDA algorithm.

The performance of the proposed method is first validated by numerical simulations, and then a point positioning experiment is carried out with an in-house-developed prototype ground-based positioning system. The results show that the positioning accuracy of the proposed method can achieve centimeter-level accuracy and enable precise point positioning in situations without reliable code measurements or other measuring instruments.

First, a basic system model is introduced and the single difference (SD) observation of carrier phase measurement is reviewed. Then, the DDS model is established, based on which a new OTF-AR method is proposed. The proposed method is verified by numerical simulations. In addition, with an in-house-developed prototype ground-based navigation system, a real-world experiment is conducted to demonstrate the proposed method. Conclusions and future work are summarized in the last section.

Basic system model

A typical ground-based positioning system usually consists of a number of base stations and receivers. Generally, the base stations are stationary and broadcast GNSS-like ranging signals. For the proposed method, the base stations do not have to be accurately synchronized in time, although frequency synchronization is required. The base stations can simply be transmitters if they share a common clock source by a wire connection. Otherwise, the synchronization can be realized by wireless links and the base station would then need to include a receiver.

Receivers process signals broadcast by base stations and obtain the carrier phase measurements, which are used to determine positions. At the kth epoch, the carrier phase measurement \(\phi _{k}^{i}\) between the ith base station and the receiver is expressed as

$$\phi _{k}^{i}={\lambda ^{ - 1}}\left\| {{{\mathbf{s}}_i} - {{\mathbf{u}}_k}} \right\|+{N_i} - {f_{\mathbf{c}}}\delta {t_i}+{f_{\mathbf{c}}}\delta t_{k}^{u}+w_{k}^{i},$$
(1)

where si represents the coordinates of the ith base station and uk represents the receiver’s coordinates at kth epoch. \(\lambda\) and fc denote the carrier wavelength and frequency, respectively. Ni denotes the ambiguity values. It is assumed that all base stations are frequency synchronized and there is no loss of signal lock and cycle slip, so Ni is considered to be constant. \(\delta {t_i}\) and \(\delta t_{k}^{u}\) represent the clock biases of the ith base station and the kth receiver, respectively. The base stations are assumed to be synchronized, so \(\delta {t_i}\) is also considered to be constant. For ground-based navigation systems, the observation is free of ionospheric delay. \(w_{k}^{i}\) represents other unmodeled errors, including thermal noise and multipath error.

The term \(\delta t_{k}^{u}\) can be eliminated by differencing between base stations, and the SD observation \(\Delta \phi _{k}^{{ij}}\) between the ith and jth base stations is defined as

$$\Delta \phi _{k}^{{ij}}=\phi _{k}^{i} - \phi _{k}^{j}={\lambda ^{ - 1}}\left( {\left\| {{{\mathbf{s}}_i} - {{\mathbf{u}}_k}} \right\| - \left\| {{{\mathbf{s}}_j} - {{\mathbf{u}}_k}} \right\|} \right)+{N_{ij}} - {f_{\mathbf{c}}}\delta {t_{ij}}+w_{k}^{{ij}},$$
(2)

where \({N_{ij}}={N_i} - {N_j}\), \(\delta {t_{ij}}=\delta {t_i} - \delta {t_j}\), and \(w_{k}^{{ij}}=w_{k}^{i} - w_{k}^{j}\).

To utilize the SD observation, one of the key issues is to resolve integer ambiguities Nij. Existing ambiguity initialization methods usually require an initial position estimation which can be obtained by measuring instruments or code measurements (Jiang et al. 2013; Montillet et al. 2009). Then, based on the initial position estimation, the approximated expansion is performed to resolve ambiguities.

As stated previously, a relatively large error in the initial position estimation will make existing algorithms difficult to converge. This means that existing methods will fail if measuring instruments are unavailable or the code measurements have a large error.

To solve this problem, a new AR method involving only carrier phase measurements is proposed for ground-based precise positioning. The proposed positioning method introduces a new DDS observation model, which is the core innovation.

Precise point positioning methods based on DDS model

In this section, we first propose a double difference square (DDS) observation model, which only involves carrier phase measurements and is proven to be linear. Based on the initial solution obtained from the DDS model, the float solution and a fixed solution with higher accuracy are obtained. The complete algorithm is then summarized.

DDS observation model

The DDS model is defined as

$$\nabla {\Delta ^2}\phi _{{km}}^{{ij}}=\left[ {{{\left( {\phi _{k}^{i}} \right)}^2} - {{\left( {\phi _{k}^{j}} \right)}^2}} \right] - \left[ {{{\left( {\phi _{m}^{i}} \right)}^2} - {{\left( {\phi _{m}^{j}} \right)}^2}} \right].$$
(3)

With the above definition, the derivation of the DDS model is explained in the following. First, the original carrier measurements are squared as follows:

$${\left[ {\phi _{k}^{i} - ({N_i} - {f_{\text{c}}}\delta {t_i}+{f_{\text{c}}}\delta t_{k}^{u}+w_{k}^{i})} \right]^2}={\lambda ^{ - 2}}{\left\| {{\mathbf{s}_i} - {\mathbf{u}_k}} \right\|^2}.$$
(4)

In (4), the clock bias of the receiver \(\delta t_{k}^{u}\) can be further modeled as

$$\delta t_{k}^{u}=\delta t_{0}^{u}+\tau k+{e_{{t_k}}},$$
(5)

where \(\delta t_{0}^{u}\) is the initial clock bias and \({e_{{t_k}}}\) is the unmodeled error. In addition, \(\tau ={f_{\text{e}}}{T_{\text{s}}},\) where fe is the clock drift and Ts is the sampling interval. Although this model is relatively simple, it has been proven in later experiments that it is sufficient to help resolve ambiguities.

It should be noted that it is not necessary to obtain the specific receiver clock bias. In (5), \(\delta t_{0}^{u}\) is a constant term and will be incorporated in the ambiguities in the following discussion. Therefore, the specific value of \(\delta t_{0}^{u}\) is not required.

However, the estimate of \(\tau\) is important. If the base stations are frequency synchronized, \(\tau\) can be obtained from the carrier Doppler frequency when the receiver is static.

A generalized ambiguity zi is defined as

$${z_i}={N_i} - {f_{\text{c}}}\delta {t_i}+{f_{\text{c}}}\delta t_{0}^{u}.$$
(6)

Putting (5) and (6) into (4), it can be shown that

$${\left[ {\phi _{k}^{i} - ({z_i}+{f_{\text{c}}}\tau k+{f_{\text{c}}}{e_{{t_k}}}+w_{k}^{i})} \right]^2}={\lambda ^{ - 2}}{\left\| {{\mathbf{s}_i} - {\mathbf{u}_k}} \right\|^2}.$$
(7)

Then, with some manipulations, it can be shown that

$${\left( {\phi _{k}^{i}} \right)^2}={\lambda ^{ - 2}}{\left\| {{\mathbf{s}_i} - {\mathbf{u}_k}} \right\|^2}+2\phi _{k}^{i}\left( {{z_i}+{f_{\text{c}}}\tau k} \right) - {\left( {{z_i}+{f_{\text{c}}}\tau k} \right)^2}+2\left( {\phi _{k}^{i} - {z_i} - {f_{\text{c}}}\tau k} \right)\left( {w_{k}^{i}+{f_{\text{c}}}{e_{{t_k}}}} \right).$$
(8)

Here, the higher order terms of \({e_{{t_k}}}\) and \(w_{k}^{i}\) are ignored since they are considered to be far less than the true distance. As seen from (6), two clock difference terms are absorbed into zi, and as a result, the generalized ambiguity zi is not an integer.

Through the double difference defined in (3), the square terms of uk and zi which are unknown can be eliminated. Through the difference between the different base stations, we have:

$$\begin{aligned} {\left( {\phi _{k}^{i}} \right)^2} - {\left( {\phi _{k}^{j}} \right)^2} & ={\lambda ^{ - 2}}\left[ {\mathbf{s}_{i}^{{\text{T}}}{\mathbf{s}_i} - \mathbf{s}_{j}^{{\text{T}}}{\mathbf{s}_j} - 2({\mathbf{s}_i} - {\mathbf{s}_j}){\mathbf{u}_k}} \right]+2(\phi _{k}^{i}+{f_{\text{c}}}\tau k){z_i} - 2(\phi _{k}^{j}+{f_{\text{c}}}\tau k){z_j} \\ & \quad +2\phi _{k}^{{ij}}{f_{\text{c}}}\tau k - z_{i}^{2} - z_{j}^{2}+n_{k}^{{ij}}, \\ \end{aligned}$$
(9)

where \(\phi _{k}^{{ij}}=\phi _{k}^{i} - \phi _{k}^{j}\) and \(n_{k}^{{ij}}=2\left( {\phi _{k}^{i} - {z_i} - {f_{\text{c}}}\tau k} \right)\left( {w_{k}^{i}+{f_{\text{c}}}{e_{{t_k}}}} \right) - 2\left( {\phi _{k}^{j} - {z_j} - {f_{\text{c}}}\tau k} \right)\left( {w_{k}^{j}+{f_{\text{c}}}{e_{{t_k}}}} \right)\). It can be seen that the square term of uk has been eliminated in (9).

Further, through differencing across positions, the square terms of zi and zj are eliminated and the DDS observation can be written as

$$\begin{aligned} \nabla {\Delta ^2}\phi _{{km}}^{{ij}} & = - 2{\lambda ^{ - 2}}{({\mathbf{s}_i} - {\mathbf{s}_j})^{\text{T}}}({\mathbf{u}_k} - {\mathbf{u}_m})+2\left[ {\phi _{{km}}^{i} - {f_{\text{c}}}\tau (k - m)} \right]{z_i} - 2\left[ {\phi _{{km}}^{j} - {f_{\text{c}}}\tau (k - m)} \right]{z_j} \\ & \quad +2{f_{\text{c}}}\tau (\phi _{k}^{{ij}}k - \phi _{m}^{{ij}}m)+n_{{km}}^{{ij}}, \\ \end{aligned}$$
(10)

where \(\phi _{{km}}^{i}=\phi _{k}^{i} - \phi _{m}^{i}\), and \(n_{{km}}^{{ij}}=n_{k}^{{ij}} - n_{m}^{{ij}}\).

It is not hard to show that the unknown terms in (10) are \({\mathbf{u}_k} - {\mathbf{u}_m}\), zi and zj, which means the DDS observation model is linear. Therefore, by combining DDS observations between multiple base stations and the receiver’s locations, all generalized ambiguities \({z_1},{z_2}, \ldots ,{z_L}\) can be estimated. It should be noted that according to the definition (6), \({z_1},{z_2}, \ldots ,{z_L}\) are not necessarily integers. In other words, the estimate given by the DDS model should be float values.

It should be pointed out that the presented DDS model is different from the one in Wang et al. (2018), although the idea of double difference and square has similarities. In addition to the receiver, the system in Wang et al. (2018) requires a transceiver for the user equipment, and the clock differences are eliminated by two-way ranging.

However, in this research, we are dealing with general receivers and the clock differences are taken into account. If the method in Wang et al. (2018) is simply adopted, the unknown clock differences will be multiplied by the unknown ambiguities, resulting in a nonlinearity of the model.

To solve this problem, we introduced the clock model in (5) and defined the generalized ambiguities incorporating a part of the clock differences in (6). Hence, the DDS model (10) including \(\tau\) and the generalized ambiguities is more complicated than that in Wang et al. (2018).

Solution of DDS model

Without loss of generality, let \(j=1\) and \(m=1\), and then at the kth epoch, the \(L - 1\) observations are written in vector form as

$${\mathbf{y}_k}={\mathbf{A}_k}\mathbf{z}+{\mathbf{B}_k}{\mathbf{x}_k}+{\mathbf{n}_k},$$
(11)

where \({\mathbf{y}_k}=\left[ {\begin{array}{*{20}{c}} {\nabla {\Delta ^2}\phi _{{k1}}^{{21}} - 2{f_{\text{c}}}\tau (\phi _{k}^{{21}}k - \phi _{1}^{{21}})} \\ {\nabla {\Delta ^2}\phi _{{k1}}^{{31}} - 2{f_{\text{c}}}\tau (\phi _{k}^{{31}}k - \phi _{1}^{{31}})} \\ \vdots \\ {\nabla {\Delta ^2}\phi _{{k1}}^{{L1}} - 2{f_{\text{c}}}\tau (\phi _{k}^{{L1}}k - \phi _{1}^{{L1}})} \end{array}} \right]\), \({\mathbf{A}_k}=2\left[ {\begin{array}{*{20}{c}} { - \phi _{{k1}}^{1}+{f_{\text{c}}}\tau (k - 1)}&{\phi _{{k1}}^{2} - {f_{\text{c}}}\tau (k - 1)}&{}&{}&{} \\ { - \phi _{{k1}}^{1}+{f_{\text{c}}}\tau (k - 1)}&{}&{\phi _{{k1}}^{3} - {f_{\text{c}}}\tau (k - 1)}&{}&{} \\ { - \phi _{{k1}}^{1}+{f_{\text{c}}}\tau (k - 1)}&{}&{}& \ddots &{} \\ { - \phi _{{k1}}^{1}+{f_{\text{c}}}\tau (k - 1)}&{}&{}&{}&{\phi _{{k1}}^{L} - {f_{\text{c}}}\tau (k - 1)} \end{array}} \right]\), \({\mathbf{z}}={\left[ {\begin{array}{*{20}{c}} {{z_1}}&{{z_2}}& \cdots &{{z_L}} \end{array}} \right]^{\text{T}}}\), \({{\mathbf{B}}_k}= - 2{\lambda ^{ - {\text{2}}}}{\left[ {\begin{array}{*{20}{c}} {{{\mathbf{s}}_2} - {{\mathbf{s}}_1}}&{{{\mathbf{s}}_3} - {{\mathbf{s}}_1}}& \cdots &{{{\mathbf{s}}_L} - {{\mathbf{s}}_1}} \end{array}} \right]^{\text{T}}}\), \({{\mathbf{x}}_k}={{\mathbf{u}}_k} - {{\mathbf{u}}_1}\), and \({{\mathbf{n}}_k}{\text{=}}{\left[ {\begin{array}{*{20}{c}} {n_{{k{\text{1}}}}^{{{\text{21}}}}}&{n_{{k{\text{1}}}}^{{{\text{31}}}}}& \cdots &{n_{{k{\text{1}}}}^{{L1}}} \end{array}} \right]^{\text{T}}}\).

As can be seen from (10), if the receiver’s position is unchanged, i.e., \({{\mathbf{u}}_k} - {{\mathbf{u}}_m}={\mathbf{0}}\), the DDS observation \(\nabla {\Delta ^2}\phi _{{km}}^{{ij}}\) is trivial. That is to say, observations obtained at a single position are not sufficient to solve (11). Similar to other OTF-AR methods, the geometric changes between the receiver and base stations are quite important. The receiver needs to move, and multiple DDS observations at different positions can constitute a solvable problem.

Assuming that during the receiver’s motion, KL original carrier phase measurements are obtained at K different positions. Then, the total number of DDS observations is \((L - 1)(K - 1)\), and all DDS observations can be written in vector form as

$$\mathbf{y}=\mathbf{A}\mathbf{z}+\mathbf{B}\mathbf{x}+\mathbf{n},$$
(12)

where \({\mathbf{y}}={\left[ {\begin{array}{*{20}{c}} {{\mathbf{y}}_{2}^{{\text{T}}}}&{{\mathbf{y}}_{3}^{{\text{T}}}}& \cdots &{{\mathbf{y}}_{K}^{{\text{T}}}} \end{array}} \right]^{\text{T}}}\), \({\mathbf{A}}={\left[ {\begin{array}{*{20}{c}} {{\mathbf{A}}_{2}^{{\text{T}}}}&{{\mathbf{A}}_{3}^{{\text{T}}}}& \cdots &{{\mathbf{A}}_{K}^{{\text{T}}}} \end{array}} \right]^{\text{T}}}\), \({\mathbf{B}}=\left[ {\begin{array}{*{20}{c}} {{{\mathbf{B}}_2}}&{}&{}&{} \\ {}&{{{\mathbf{B}}_{\text{3}}}}&{}&{} \\ {}&{}& \ddots &{} \\ {}&{}&{}&{{{\mathbf{B}}_K}} \end{array}} \right]\), \({\mathbf{x}}={\left[ {\begin{array}{*{20}{c}} {{\mathbf{x}}_{2}^{{\text{T}}}}&{{\mathbf{x}}_{3}^{{\text{T}}}}& \cdots &{{\mathbf{x}}_{K}^{{\text{T}}}} \end{array}} \right]^{\text{T}}}\), and \({\mathbf{n}}={\left[ {\begin{array}{*{20}{c}} {{\mathbf{n}}_{2}^{{\text{T}}}}&{{\mathbf{n}}_{3}^{{\text{T}}}}& \cdots &{{\mathbf{n}}_{K}^{{\text{T}}}} \end{array}} \right]^{\text{T}}}\).

Therefore, the generalized ambiguities can be estimated by solving the following equation:

$${\mathbf{\hat {z}}}=\mathop {\arg \hbox{min} }\limits_{{\{ {\mathbf{z}},{\mathbf{x}}\} }} {\left\| {{\mathbf{y}} - {\mathbf{Az}} - {\mathbf{Bx}}} \right\|^2}.$$
(13)

For D-dimensional positioning, the unknown values include L generalized ambiguities and \(D(K - 1)\) difference coordinates. Then, the solvability condition for a DDS model is obtained as

$$\left( {L - 1} \right)\left( {K - 1} \right) \geq L+D\left( {K - 1} \right).$$
(14)

This condition can be decomposed into two inequalities:

$$L \geq D+2,$$
(15)
$$K \geq \frac{L}{{L - D - 1}}+1.$$
(16)

It can be seen that to make the DDS model solvable, the minimum number of base stations is \(D+2\).

It should be pointed out that the data incorporation procedure here is more sophisticated than that in Wang et al. (2018), in which case the problem is simply composed by the double difference and square. However, in our method, the receiver needs to estimate \(\tau\) first in the static state, and this procedure is necessary since the coefficient matrix Ak in (11) is related to \(\tau\). Then, as shown in (11), some terms related to \(\tau\) are subtracted from the DDS observations.

Float solution and fixed solution

In Wang et al. (2018), the float solution and fixed solution can be directly obtained since the clock differences are eliminated by two-way ranging. However, due to the square and double difference, the noise level increases, and most of the error comes from the clock model in this research. To improve the performance of the ambiguity resolution, the float solution and fixed solution are then obtained from single difference observations.

According to (6), due to the clock bias, the generalized ambiguity values \({\mathbf{\hat {z}}}\) obtained from (13) are float values. After the single differencing in (2), the clock difference of the receiver can be eliminated, and the SD observation is rewritten as

$$\Delta \phi _{k}^{{ij}}={\lambda ^{ - 1}}\left( {\left\| {{{\mathbf{s}}_i} - {{\mathbf{u}}_k}} \right\| - \left\| {{{\mathbf{s}}_j} - {{\mathbf{u}}_k}} \right\|} \right)+{z_{ij}}+w_{k}^{{ij}},$$
(17)

where \({z_{ij}}\) is the SD generalized ambiguity.

$${z_{ij}}={z_i} - {z_j}={N_{ij}} - {f_c}\delta {t_{ij}}.$$
(18)

Denote the generalized ambiguity in vector form as

$${{\mathbf{z}}_{sd}}{\text{=}}{\left[ {\begin{array}{*{20}{c}} {{z_{{\text{21}}}}}&{{z_{31}}}& \cdots &{{z_{L1}}} \end{array}} \right]^{\text{T}}}.$$
(19)

With \({\mathbf{\hat {z}}}\) obtained from (13), the initial solution of zij can be directly obtained. Then, the receiver’s coordinates at the kth epoch are determined by iteratively solving the following equation:

$${{\mathbf{\hat {u}}}_k}{\text{=}}\mathop {\arg \hbox{min} }\limits_{{{{\mathbf{u}}_k}}} \left\| {{{\mathbf{\varphi }}_k} - {{\mathbf{\rho }}_k}({{\mathbf{u}}_k}) - {{{\mathbf{\hat {z}}}}_{sd}}} \right\|_{{{{\mathbf{R}}_k}}}^{2},$$
(20)

where \({{\mathbf{\varphi }}_k}={\left[ {\begin{array}{*{20}{c}} {\Delta \phi _{k}^{{21}}}&{\Delta \phi _{k}^{{31}}}& \cdots &{\Delta \phi _{k}^{{L1}}} \end{array}} \right]^{\text{T}}}\), \({{\mathbf{\rho }}_k}({{\mathbf{u}}_k}){\text{=}}{\left[ {\begin{array}{*{20}{c}} {\left\| {{{\mathbf{s}}_{\text{2}}} - {{\mathbf{u}}_k}} \right\| - \left\| {{{\mathbf{s}}_{\text{1}}} - {{\mathbf{u}}_k}} \right\|}&{\left\| {{{\mathbf{s}}_3} - {{\mathbf{u}}_k}} \right\| - \left\| {{{\mathbf{s}}_1} - {{\mathbf{u}}_k}} \right\|}& \cdots &{\left\| {{{\mathbf{s}}_L} - {{\mathbf{u}}_k}} \right\| - \left\| {{{\mathbf{s}}_1} - {{\mathbf{u}}_k}} \right\|} \end{array}} \right]^{\text{T}}}\), \(\left\| \cdot \right\|_{{\mathbf{P}}}^{2}{\text{=}}{\left( \cdot \right)^{\text{T}}}{{\mathbf{P}}^{ - 1}}\left( \cdot \right)\) and \({{\mathbf{R}}_k}\) denotes the covariance matrix. If the covariance of the SD observations is assumed to be half the autocovariance, \({{\mathbf{R}}_k}\) can be deduced to be:

$${{\mathbf{R}}_k}=\frac{1}{2}\left[ {\begin{array}{*{20}{c}} {2\sigma _{{\Delta \phi }}^{2}}&{\sigma _{{\Delta \phi }}^{2}}& \cdots &{\sigma _{{\Delta \phi }}^{2}} \\ {\sigma _{{\Delta \phi }}^{2}}&{2\sigma _{{\Delta \phi }}^{2}}& \cdots &{\sigma _{{\Delta \phi }}^{2}} \\ \vdots & \vdots & \ddots & \vdots \\ {\sigma _{{\Delta \phi }}^{2}}&{\sigma _{{\Delta \phi }}^{2}}& \cdots &{2\sigma _{{\Delta \phi }}^{2}} \end{array}} \right].$$
(21)

It is worth noting that the ambiguity values are invariant as long as there are no cycle slips or loss of signal lock. Therefore, all SD observations can be incorporated into a joint equation. Then, using \({{\mathbf{\hat {z}}}_{sd}}\) and \({{\mathbf{\hat {u}}}_k}\)as the initial input, the following equation can be solved iteratively:

$$\left\{ {{{{\mathbf{\tilde {z}}}}_{sd}},\;{\mathbf{\tilde {u}}}} \right\}=\mathop {\arg \hbox{min} }\limits_{{\left\{ {{{\mathbf{z}}_{sd}},\;{\mathbf{u}}} \right\}}} \left\| {\varvec{\upvarphi} - {\mathbf{\rho }}\left( {\mathbf{u}} \right) - {{\mathbf{z}}_{sd}}} \right\|_{{\mathbf{R}}}^{2},$$
(22)

where \({\mathbf{\varphi }}={\left[ {{\mathbf{\varphi }}_{1}^{{\text{T}}},{\mathbf{\varphi }}_{2}^{{\text{T}}}, \cdots ,{\mathbf{\varphi }}_{K}^{{\text{T}}}} \right]^{\text{T}}}\), \({\mathbf{u}}={\left[ {{\mathbf{u}}_{1}^{{\text{T}}},{\mathbf{u}}_{2}^{{\text{T}}}, \cdots ,{\mathbf{u}}_{K}^{{\text{T}}}} \right]^{\text{T}}}\), \({\mathbf{\rho }}\left( {\mathbf{u}} \right)={\left[ {{\mathbf{\rho }}_{1}^{{\text{T}}}\left( {\mathbf{u}} \right),{\mathbf{\rho }}_{2}^{{\text{T}}}\left( {\mathbf{u}} \right), \cdots ,{\mathbf{\rho }}_{K}^{{\text{T}}}\left( {\mathbf{u}} \right)} \right]^{\text{T}}}\) and

$${\mathbf{R}}=\left[ {\begin{array}{*{20}{c}} {{{\mathbf{R}}_{\text{1}}}}&{}&{}&{} \\ {}&{{{\mathbf{R}}_{\text{2}}}}&{}&{} \\ {}&{}& \ddots &{} \\ {}&{}&{}&{{{\mathbf{R}}_K}} \end{array}} \right].$$
(23)

The float solution \({{\mathbf{\tilde {z}}}_{sd}}\) obtained from (22) has higher accuracy than the initial solution \({{\mathbf{\hat {z}}}_{sd}}\).

If base stations are accurately time synchronized, then we have \(\delta {t_{ij}}=0\) for all \(i\) and\(j\). In this case, it can be seen from (18) that \({z_{ij}}={N_{ij}}\) and \({z_{ij}}\) are integer values. Then, a fixed solution can be further obtained by employing integer ambiguity searching methods, such as the LAMBDA method (Teunissen 1995).

It is worth noting that even though the base stations are not accurately synchronized, i.e., they are frequency synchronized but the clock differences \(\delta {t_{ij}}\) are nonzero, the float solution \({{\mathbf{\tilde {z}}}_{sd}}\) can still be used to determine positions, which is similar to the DKPI method (Guo et al. 2018). The proposed method allows the base stations to be only frequency synchronized. The following simulations and experiments will prove that the float solution has high accuracy and can be directly used for precise point positioning.

Here, we summarize the proposed method in the following algorithm.

Algorithm 1

 

Initialization

The receiver remains stationary for a short period of time to estimate \(\tau\)

DDS model

The receiver moves and obtains the DDS observations from original carrier phase measurements. Then, solve (13) that integrates all the DDS observations by the least squares method

Initial solution

The initial solution \({{\mathbf{\hat {z}}}_{sd}}\) is obtained directly from the previous result

Float solution

With the results of the previous two steps, the float solution \({{\mathbf{\tilde {z}}}_{sd}}\) is obtained by solving (22)

Fixed solution

If accurate time synchronization is achieved between all base stations, the search for the fixed solution is performed

Numerical simulations

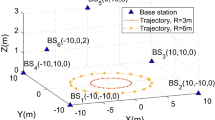
In this section, the proposed method is verified by numerical simulations. Six base stations located in the space of 20 m by 20 m by 4 m are marked by blue triangles with coordinates shown in Fig. 1.

Fig. 1
figure 1

Diagram of the receiver trajectory and position of base stations

Full size image

The trajectory of the receiver is a horizontal circle centered at (10, 10, 0), and the receiver is assumed to traverse the trajectory one time. To study the influence of geometric changes on the accuracy of ambiguity solutions, 100 trials were carried out with various R.

The minimum radius for R is 3 m, depicted by the red dashed line in Fig. 1, and in this case, the ranges of HDOP and VDOP are 0.89–0.94 and 2.6–4.0, respectively. The maximum value of R is 6 m, depicted by the yellow dashed line with stars in the figure, and HDOP ranges from 0.88 to 1.0, while VDOP ranges from 1.9 to 4.8. R is increased in 0.5-m increments and there are seven different radii.

In addition, the square trajectory circumscribed to each circular trajectory described above is simulated. The smallest square trajectory is indicated by a purple solid line in Fig. 1, and HDOP ranges from 0.89 to 0.95 while VDOP ranges from 2.5 to 4.2. The largest square is represented by dotted green line and HDOP ranges from 0.88 to 1.0, while VDOP ranges from 1.9 to 5.2.

The signal carrier frequency is set to 2465.43 MHz, which means the carrier wavelength is about 12.2 cm. It is assumed that the standard deviation (STD) of the carrier measurement noise in (1) is 0.05 cycle. For the clock model (5), the STD of the unmodeled error is assumed to be 0.05 cycle, and the parameter \(\tau\) is randomly generated in each trial. For a specific trajectory, 100 trials are performed and, in each trial, 100 evenly distributed observations are used for resolving ambiguities.

Comparison of float solution accuracy

First, the root mean square error (RMSE) of the initial solution is shown in Fig. 2. It is clearly shown that, as the trajectory radius increases, i.e., the geometric change increase, the accuracy of the initial solutions significantly improves. When the receiver’s trajectory radius is greater than 5 m, the estimation error is less than one cycle. Even in the worst case with R = 3 m, the RMSE of the initial solutions is still no larger than 3.5 carrier cycles, which means a decimeter-level accuracy.

Fig. 2
figure 2

RMSE of the initial solution for each SD ambiguity using circle trajectories

Full size image

Another phenomenon is that the base station positions have some impact on the accuracy of the initial solutions and the float solutions. In Fig. 2, the RMSE of initial solution for z51, which is marked by violet bars, is the largest, and when R = 3 m, it is about 3.2 cycles. More importantly, the RMSE of the initial solution for z31 is obviously lower than that of the others, and it is always less than 0.5 cycles when the radius is changed from 3 to 6 m.

Further, the estimation error of the float solutions is given in Fig. 3. As can be seen, compared with the initial solution, the accuracy of the float solution is significantly improved. The RMSE of the float solution is within 0.1 cycles in all cases. In other words, the float solutions achieve centimeter-level accuracy. As shown in the figure, similar to the initial solution, the estimation accuracy of the float solution significantly improves with increasing trajectory radius. In addition, the accuracy of z51 and z61 with R = 6 m is worse than that with R = 5.5 m, but the difference is not obvious. This may be due to the fact that the VDOP is poor when the trajectory is closer to the edge, which can be seen from the parameter description of the simulation. The specific impact of trajectory geometry is still a problem to be studied.

Fig. 3
figure 3

RMSE of the float solution for each SD ambiguity using circle trajectories

Full size image

The above results are also observed in the simulation using square trajectories. It can be seen from Figs. 4 and 5 that the accuracy improves as the trajectory expands. Furthermore, the base station positions have some impact on accuracy.

Fig. 4
figure 4

RMSE of the initial solution for each SD ambiguity using square trajectories

Full size image
Fig. 5
figure 5

RMSE of the float solution for each SD ambiguity using square trajectories

Full size image

By comparing Figs. 2 and 4, it can be seen that the accuracy using a circle trajectory is slightly worse than that using the circumscribed square trajectory. Similar conclusions can be drawn by comparing Figs. 3 and 5. This is mainly because the square trajectory is slightly larger, which can be clearly seen in Fig. 1.

Comparison of positioning accuracy

The horizontal and vertical positioning error of the initial, float, and fixed solutions are compared in Figs. 6 and 7. It should be mentioned that for all trials, the proposed method correctly obtains fixed solutions.

Fig. 6
figure 6

Comparison of the horizontal error of the initial, float and fixed solutions

Full size image
Fig. 7
figure 7

Comparison of the vertical errors of the initial, float and fixed solutions

Full size image

As shown in Figs. 6 and 7, although the positioning accuracy of the initial solutions can only reach the decimeter level, both the float and the fixed solutions achieve centimeter-level accuracy. Moreover, the accuracy of the float solution is only slightly lower than that of the fixed solution.

It can be seen that in most cases, the positioning accuracy using the square trajectory is better than that using the circle trajectory. This is consistent with the previous discussion on the accuracy of ambiguity solutions. However, when R = 6 m, the vertical error using the square trajectory is worse. In fact, in addition to the accuracy of ambiguity solutions, the DOP value will influence the positioning accuracy. The largest square trajectory has poor DOP values since it is close to the edge of the field.

As mentioned at the end of the previous section, when the base stations are not accurately synchronized, i.e., the clock differences \(\delta {t_{ij}}\) are nonzero, the float solutions can be used in precise positioning. Here, our simulations show that, compared with the fixed solution, the accuracy of the float solution does not decrease significantly, which means that the proposed method allows the base stations to be only frequency synchronized.

In summary, geometric change has a key influence on the performance of the proposed method. With an increase of the trajectory radius, the accuracy of the ambiguity solution significantly improves. To test the practical performance of the proposed method, a real-world experiment is conducted and the results are introduced in the next section.

Experiments

The real-world experiment was conducted based on an in-house-developed prototype ground-based navigation system deployed on the rooftop of a building in Beijing, in June 2018. The simplified system configuration is depicted in Fig. 8. A base station can receive signals from other stations and the time synchronization is realized by the wireless links. Figure 9 shows the main hardware of six base stations, BS1–BS6, except for their antennas. The signal carrier frequency is set to 2465.43 MHz. As shown in Fig. 10, the receiver is installed on a wheeled robot. The output rate of observations is 10 Hz, i.e., the epoch interval is 0.1 s.

Fig. 8
figure 8

Simplified system configuration of the real-world experiment. The base stations can send and receive signals in S-band and maintain time synchronization over the wireless links

Full size image
Fig. 9
figure 9

Main hardware of the six base stations. A computer serves as the display and control unit

Full size image
Fig. 10
figure 10

Wheeled robot with a receiver installed on it

Full size image

Figure 11 depicts the robot’s trajectory and the experiment configuration. The antennas of the six base stations are marked by the blue triangle in Fig. 11, for which the coordinates are measured by reference to the total station and listed in Table 1. The experimental environment is shown in Fig. 12, in which the antennas of BS2, BS3 and BS6 are identified by yellow arrows. In Fig. 11, the robot’s trajectory during the ambiguity resolution process and the subsequent precise point positioning are marked by the red dotted line and the solid orange line, respectively.

Fig. 11
figure 11

Experiment configuration and the robot’s trajectory

Full size image
Fig. 12
figure 12

Experiment environment and antennas of several base stations

Full size image
Table 1 Coordinates of the six base stations
Full size table

In the experiment, four reference points are measured by reference to the total station to validate the proposed method and evaluate positioning accuracy. These reference points are identified by P1–P4 in Fig. 11 and their coordinates and DOP values are given in Table 2.

Table 2 Coordinates and DOP values of the four reference points
Full size table

The robot’s moving process is as follows:

  1. 1.

    First, at the starting point shown in Fig. 11, the receiver performed the initialization step to estimate \(\tau\). The fitting residual is shown in Fig. 13. As can be seen from the figure, the fitting residual is no larger than 0.15 cycles, and the fitting RMSE is about 0.056 cycle.

  2. 2.

    Subsequently, the robot started to move clockwise and obtained the initial, float and fixed solutions. This was completed in the first lap marked by the red dotted line in Fig. 11.

  3. 3.

    To evaluate the positioning accuracy, the robot moved to the four reference points P1–P4 in turn, and these points are marked by the squares in Fig. 11. When the robot was stationary near a predetermined point, we used the total station to measure its coordinates. The trajectory during this process is marked by the solid orange line in Fig. 11.

At each reference point, the positioning results were recorded for at least 30 s and compared with the true position. During the robot’s movement, HDOP changes were between 1.46 and 2.00, while VDOP changes were between 4.55 and 8.99.

Fig. 13
figure 13

Fitting residual of carrier phase measurements at the start point

Full size image
Fig. 14
figure 14

Absolute error of the initial solution for each SD generalized ambiguity

Full size image

From 100 to 330 s, the robot was always moving and its trajectory is the first lap marked by the red dotted line in Fig. 11. During this process, the receiver continues resolving ambiguities. Figures 14 and 15 show the absolute error of the initial solution and the float solution, and logarithmic coordinates are used for ease of observation.

Fig. 15
figure 15

Absolute error of the float solution for each SD generalized ambiguity

Full size image

As can be seen from Figs. 14 and 15, with the robot’s motion, the error of both solutions decreases rapidly until about 150 s. However, the robot’s motion after 150 s does not bring significant improvement as it had done before. It can be said that at the beginning, the geometry changes can effectively improve the accuracy of solutions.

The error of the initial solution seems to be quite small at 200 s but increases slightly latter. It is a coincidence that the signs of the errors changed at about 200 s, which is not shown by the absolute values.

After 250 s, the error of the two solutions varies slightly with the robot’s motion. At the end of the first lap, the error of the initial solution is about several cycles, while that of the float solution is less than one cycle.

The east, north and elevation positioning errors at the four points P1–P4 are given in Figs. 16, 17 and 18, respectively. The blue dotted lines indicate the positioning error of the float solutions, while the red solid lines indicate that of the fixed solutions. The statistical results are given in Tables 3 and 4, and the bold and underlined numbers indicate the largest RMSE.

Fig. 16
figure 16

East positioning errors of the float solutions and fixed solutions at the four reference points

Full size image
Fig. 17
figure 17

North positioning errors of the float solutions and fixed solutions at the four reference points

Full size image
Fig. 18
figure 18

Elevation errors of the float solution and fixed solution at the four reference points

Full size image
Table 3 Positioning error of the float solution at four measured points (unit: cm)
Full size table
Table 4 Positioning error of the fixed solution at four measured points (unit: cm)
Full size table

From these data, it can be said that both the positioning results of the float solutions and the fixed solutions are of high accuracy. As can be seen from Table 3, the worst RMSE in the north direction is about 3 cm, while that in the east direction is about 1.67 cm. The horizontal results show better accuracy than the vertical results, and the worst RMSE in elevation is about 22 cm, which occurred at P3. This is because the VDOP is larger than the HDOP.

By contrast, the positioning results of the fixed solution have better positioning accuracy. As can be seen from Table 4, the fixed solutions achieve centimeter-level positioning accuracy at all four known points. The worst vertical RMSE of the fixed solutions is about 8 cm, which occurred at P3.

The positioning results of the initial solution and the fixed solution are compared for the whole trajectory, and their differences are shown in Fig. 19. It can be seen that the differences in both north and east directions are no more than 2 cm, while the differences in elevation range from 5 to 15 cm.

Fig. 19
figure 19

Differences between the positioning results of the float solutions and the fixed solutions

Full size image

The test results at the four reference points show that the positioning accuracy varies at these points. As shown in Table 2, the maximum DOP value is at P4, but the largest positioning error of both the float solution and the fixed solution is at P3. It is believed that this is most likely due to the multipath effect on carrier measurements, which is more obvious in ground-based positioning than GNSS. Our future work will try to improve the system’s ability to resist the multipath effect. In addition to the receiver’s algorithms, solutions by taking advantage of the flexible design of transmitters and signals will also be considered.

In conclusion, this experiment demonstrates that the proposed method is able to resolve ambiguities by only using carrier phase measurements and is not dependent on code or other measurements. It is also proven that in practical applications, with a fixed solution, our system can achieve centimeter-level positioning accuracy. Even if the base stations are not accurately synchronized, the float solution, whose accuracy is slightly lower than the fixed solution, can also be used in precise positioning.

Conclusions

We present a new OTF-AR method for ground-based positioning systems, which is based on a new DDS observation model that solely relies on carrier phase measurements without two-way ranging. The new DDS observation model is proposed with a definition of generalized ambiguities. One of the important advantages of our method is that it applies to cases where code or other measurements are unavailable or not sufficiently accurate.

The proposed method is validated by numerical simulations and a real-world experiment. The results show that geometric changes have a significant impact on its performance. In the experiment, the proposed method was successfully applied to an in-house-developed prototype ground-based navigation system, and the positioning accuracy achieved centimeter-level accuracy. This work enables ground-based precise positioning to be applied in situations where no reliable code measurements or other measuring instruments are available and allows the base stations to be only frequency synchronized.