1 Introduction

Precise point positioning (PPP) can achieve centimeter to decimeter positioning accuracy globally, and has been recognized as a powerful tool for various applications such as those of geophysics and meteorology (Zumberge et al. 1997; Kouba and Héroux 2001; Bisnath and Gao 2007; Dow et al. 2009). However, traditional PPP requires an initialization time longer than 30 min to achieve positioning accuracy of within 10 cm, which greatly inhibits its industrial application. To shorten the initialization time and improve the accuracy, integer ambiguity resolution (IAR) approaches for PPP have been developed in recent years (Gabor and Nerem 1999; Mervart et al. 2008; Ge et al. 2008; Collins et al. 2008; Laurichesse et al. 2009; Bertiger et al. 2010; Li et al. 2011; Lannes and Prieur 2013).

The main factors that inhibit PPP ambiguity resolution are the receiver- and satellite-dependent fractional cycle biases (FCBs), which are absorbed into the undifferenced ambiguities, destroying their integer nature. The receiver FCB can be eliminated by single differencing between satellites (SDBS), while the satellite FCB must be derived in advance from a network of reference stations to recover the integer properties of ambiguities (Gabor and Nerem 1999). Mervart et al. (2008) proposed a phase-only method for PPP-IAR. Ge et al. (2008) used the SDBS model to eliminate the receiver FCB, then both the wide-lane (WL) and narrow-lane (NL) SDBS FCBs for a satellite pair should be identical for all tracking stations and thus allowing the FCBs to be estimated by averaging over all tracking stations. The integer property of PPP ambiguity was recovered by sequentially correcting the satellite WL and NL FCBs. However, as shown by Teunissen and Khodabandeh (2015), the method of Ge et al. (2008) is not optimal, since averaging over stations will result in a bias in the FCB solutions. Alternatively, Bertiger et al. (2010) delivered all undifferenced (UD) ambiguity estimates that contain the FCBs to users for PPP ambiguity resolution. Collins et al. (2008) and Laurichesse et al. (2009) directly fixed the UD ambiguities to integers and used the clock estimates to absorb the UD NL FCBs. Their WL FCB determination is similar to that of Ge et al. (2008) but on a UD level, while the NL UPDs are not determined but assimilated into the clock estimates. Lannes and Prieur (2013) proposed a closure-ambiguity approach to solve the rank defect when estimating the UD FCBs. Li et al. (2013) proposed a method of estimating the UD FCBs of L1 and L2 observations, and this is based on the previously generated WL and NL FCBs, which is similar to the method of Laurichesse et al. (2009). Odijk et al. (2015) presented a PPP-IAR method based on UD and uncombined observations, and used S-system theory to make the model full rank by constraining a minimum set of parameters. Meanwhile, Gu et al. (2015) employed both an a priori ionosphere correction model and its spatio-temporal correlation as constraints to improve the ambiguity resolution. By applying S-system theory, Teunissen and Khodabandeh (2015) provided a good description of such methods and did not identify important differences among them.

Although great achievements have been made for ambiguity resolution, PPP still suffers from a long initialization time of 30 min needed for the first ambiguity-fixed solution (Geng et al. 2011). With the full operation of GLONASS with 24 satellites since the end of 2011, and the improved quality of GLONASS orbits and clocks (IGS, http://www.igs.org/; Dow et al. 2009), it is worth investigating the performance of GPS+GLONASS PPP ambiguity resolution, especially the improvements of the initial fixing time (IFT) and the correct fixing rate (CFR) of ambiguities, comparing with GPS-only solutions.

Liu et al. (2016a) showed that, the fixing percentage in kinematic PPP with solo GPS is 17.6% within 10 min, while improved singnificantly to 42.8% when adding BDS IGSO and MEO satellites. Tolman et al. (2010) and Cai and Gao (2013) showed that adding GLONASS satellites to GPS-only PPP solutions can improve either the convergence time or solution accuracy when there are only a few GPS satellites available. However, their studies are based on float PPP, and the contribution of adding GLONASS observation to the IFT of ambiguity-fixed PPP has not been studied. Jokinen et al. (2013) studied IFT improvements made by adding GLONASS observations to improve solo-GPS PPP ambiguity resolution. They assigned a much lower weight to both the GLONASS code and phase observations, and the results showed that adding GLONASS reduces the IFT by approximately 5% compared with the GPS-only solution. Li and Zhang (2014) used an SDBS combined PPP model where the noise in GLONASS code measurements can be ignored, and found that the average IFT can be shortened by 27.4% from 21.6 to 15.7 min in static mode and by 42.0% from 34.4 to 20.0 min in kinematic mode. However, the signal establishment system of GLONASS is frequency division multiple access (FDMA), which will cause both code and carrier-phase inter-frequency bias (IFB) in the receiver terminal. As a result, the ambiguity of GLONASS satellites is not fixed in Jokinen et al. and Li and Zhang’s studies. Although Trimble’s RTX system has used Trimble NetR9 receivers to provide the GPS+GLONASS ambiguity-fixed PPP service, it still requires 18.4 min to achieve a horizontal accuracy of better than 4 cm (90%) (Landau et al. 2013). While it should be pointed out that, their products were computed based on 100 globally distributed stations, which might be response for the long initialization time. Liu et al. (2016b) used a network of Trimble NetR8 receivers to perform GLONASS FCB estimation and PPP ambiguity, and gave a very preliminary result for GLONASS only static PPP.

In PPP, the WL ambiguity is resolved by the Hatch–Melbourne–Wübbena (HMW) (Hatch 1982; Melbourne 1985; Wübbena 1985) combination of code and carrier-phase observations, so both code and carrier-phase IFBs will affect the WL ambiguity resolution. Generally, GLONASS carrier-phase IFB can be calibrated with a linear model of frequency (Wanninger and Wallstab-Freitag 2007; Wanninger 2012). However, code IFB behaves abnormally, and there is no general model with which to correct it (Kozlov et al. 2000; Yamada et al. 2010; Al-Shaery et al. 2013; Chuang et al. 2013). Uncalibrated code IFB will cause the WL fractional parts from different receivers to contradict each other and fail the FCB estimation. Banville et al. (2013) selected two GLONASS reference satellites with adjacent frequency channels for the definition of HMW integer ambiguity to remove the linear dependency of the NL code IFB on the frequency channel number. Unfortunately, this method alone is not sufficient to recover the integer properties of GLONASS WL ambiguities, and Banville et al. separated stations into clusters to better isolate GLONASS WL FCB. Later, Banville (2016) formed an ionosphere-free combination with a wavelength of approximately 5 cm for GLONASS PPP ambiguity resolution. Because of the rather short wavelength, only limited improvements were made to the initial convergence period for kinematic PPP. Reussner and Wanninger (2011) proposed the use of a precise ionospheric model to help the WL combination of L1 and L2 observations in directly fixing the WL ambiguity. However, this method depends on a precise ionospheric delay model (precise enough to fix the WL ambiguity with a wavelength of \(\sim \)86 cm), which devalues its application. Geng and Bock (2015) adopted Reussner and Wanninger (2011)’s idea and found that 92.4% of all fractional parts of GLONASS WL ambiguities agree well within ±0.15 cycles. However, due to the limited number of high-elevation GLONASS satellites and the modest 2–8 TECU accuracy of a global ionosphere map (GIM) (Hernández-Pajares et al. 2009), only hourly static PPP-IAR is performed. The efficiency of PPP-IAR for GLONASS is not as high as that for the GPS: only 63% of hourly solutions are fixed for GLONASS while 97% for GPS (Geng and Bock 2015).

From the above cited studies, the main problem with current PPP-IAR is that, it requires a long time (over 20 min) to achieve the first fixing. Hence, it is of great value to study the potential contribution of adding GLOANSS to PPP-IAR with the traditional HMW WL-fixing method, because the HMW method is both geometry-free and ionosphere-free for fixing the WL ambiguity and the decomposed NL ambiguity has a relatively long wavelength of \(\sim \)10cm. In the present paper, to assess the contribution of adding GLONASS, we used a network of homogeneous receivers to estimate GLONASS WL FCBs and the integer satellite clock. The effects of the different wavelengths for GLONASS satellites on FCB estimation and PPP ambiguity resolution are discussed in detail. GPS+GLONASS PPP ambiguity resolution is then applied, and numerical results based on data from 41 rover stations for a period of 21 days are analyzed to show the improvements in the IFT and CFR compared with GPS-only solutions. To resolve GLONASS PPP ambiguity across heterogeneous receivers, we also used GIMs to assist the WL carrier-phase combination in directly fixing the WL ambiguity. A network of 40 stations with receivers produced by four different manufactures is used to analyze the performance of the GIM-aided method of Reussner and Wanninger (2011).

2 Methods

The GLONASS code and carrier-phase observations on frequency \(g(g=1,2)\) at a particular epoch between receiver i and satellite k can be written as

$$\begin{aligned} \begin{array}{l} P_{g,i}^k =\rho _i^k +c\mathrm{d}t_i -c\mathrm{d}t^{k}+\mu _i^k /(f_g^k )^{2}+b_{g,i} -b_g^k +F_{g,i}^k \\ L_{g,i}^k =\rho _i^k +c\mathrm{d}t_i -c\mathrm{d}t^{k}-\mu _i^k /(f_g^k )^{2}+B_{g,i} -B_g^k +\lambda _g^k N_{g,i}^k, \end{array}\nonumber \\ \end{aligned}$$
(1)

where \(P_{g,i}^k \) and \(L_{g,i}^k \) are code and carrier-phase observations with corresponding wavelength \(\lambda _g^k \) and frequency \(f_g^k \). \(\rho _i^k \) is the sum of the geometric delay and tropospheric delay. \(\mathrm{d}t_i \) and \(\mathrm{d}t^{k}\) are the receiver and satellite clock biases. c is the speed of light in vacuum. \(\mu _i^k /(f_g^k )^{2}\) denotes the slant ionospheric delay. \(N_{g,i}^k \) denotes the integer ambiguity. \(b_{g,i}\) and \(B_{g,i}\) denote the code and carrier-phase hardware bias, respectively, for the receiver, whereas \(b_g^k \) and \(B_g^k \) denote those for the satellite. \(F_{g,i}^k \) is the code IFB, which is not separable from the receiver clock and is defined as the difference with respect to satellite R11 (having a frequency index of zero). Errors resulting from the offset and variation of the antenna phase center, tidal displacements, relativity and phase wind-up at the satellite antenna are assumed to have been corrected by models and are ignored here. For clarity, we neglect unmodeled errors and noise.

In GNSS data processing, it is commonly assumed that the code and carrier phase share the same receiver clock. However, this was proven to be false by Sleewaegen et al. (2012), because the code-phase bias (CPB) can exceed a few hundred nanoseconds. This will do no harm to CDMA GNSS systems (e.g., GPS, Galileo, and BeiDou), while for FDMA-based GLONASS, the CPB will cause carrier-phase IFB for both L1 and L2 observations (Sleewaegen et al. 2012):

$$\begin{aligned} \Delta L_{1,i}^k =\Delta L_{2,i}^k =\mathrm{CPB}_i \cdot 105264\cdot 10^{-9}\cdot k, \end{aligned}$$
(2)

where \(k=[-7,-4,-3,\ldots 0\ldots 6]\) is the GLONASS satellite frequency number (http://www.glonass-center.ru), and the unit of CPB is nanoseconds. Equation (2) reveals how the carrier-phase IFB is introduced, where the properties are exactly the same as those observed by Wanninger (2012). The CPB is the same for most receivers of the same brand, and can be calculated with the carrier-phase IFB given in Wanninger (2012), as shown in Table 1. While for some stations, the CPB may differ significantly from Table 1, so it is best to estimate a CPB correction for each station, such that, applying these station-specific CPB corrections to the carrier phase, the carrier-phase IFB (or CPB) will not exist in our processing.

Table 1 CPB corrections for GLONASS receivers of nine different brands derived from the values given by Wanninger (2012)
Full size table

In PPP processing, the well-known ionosphere-free (IF) combination is usually used to eliminate the first-order ionosphere delays, and the IF form of Eq. (1) can be written as

$$\begin{aligned} P_{\mathrm{IF},i}^k= & {} \alpha \Delta P_{1,i}^k -\beta \Delta P_{2,i}^k\nonumber \\= & {} \rho _i^k +c\mathrm{d}t_i -c\mathrm{d}t^{k}+b_{\mathrm{IF},i} -b_{\mathrm{IF}}^k +F_{\mathrm{IF},i}^k \nonumber \\ L_{\mathrm{IF},i}^k= & {} \alpha \Delta L_{1,i}^k -\beta \Delta L_{2,i}^k \nonumber \\= & {} \rho _i^k +c\mathrm{d}t_i -c\mathrm{d}t^{k}+B_{\mathrm{IF},i} -B_{\mathrm{IF}}^k +\lambda _1^k N_{\mathrm{IF},i}^k , \end{aligned}$$
(3)

where \(\alpha =f_1^{k2}/(f_1^{k2}-f_2^{k2}),\beta =f_2^{k2}/(f_1^{k2}-f_2^{k2})\), and \(N_{\mathrm{IF},i}^k \) is the IF ambiguity with corresponding wavelength \(\lambda _1^k \). The IF ambiguity is usually expressed as the combination of WL and NL ambiguities and fixed sequentially:

$$\begin{aligned} N_{\mathrm{IF},i}^k =\frac{f_1^k f_2^k }{f_1^{k2}-f_2^{k2}}N_{w,i}^k +\frac{f_1^k }{f_1^k +f_2^k }N_{1,i}^k , \end{aligned}$$
(4)

where \(N_{w,i}^k \) and \(N_{1,i}^k \) are the WL and NL ambiguities, respectively. In PPP, the case is more complicated than that of Eq. (4), since the FCBs destroy the integer nature of WL and NL ambiguities, which must be estimated at the server end such that PPP users can retrieve the integer nature of WL and NL ambiguities and thus fix the ambiguities to integers.

2.1 UD WL FCB estimation

The WL ambiguity is usually derived with the geometry-free HMW combination of carrier-phase and code observations as

$$\begin{aligned} \mathrm{HMW}_i^k= & {} \left( {\frac{L_{1,i}^k }{\lambda _1^k }-\frac{L_{2,i}^k }{\lambda _2^k }} \right) -\left( {\frac{f_1^k P_{1,i}^k +f_2^k P_{2,i}^k }{(f_1^k +f_2^k )\lambda _w^k }} \right) \nonumber \\= & {} N_{w,i}^k +\phi _{w,i} -\phi _w^k -H_{w,i}^k \end{aligned}$$
(5)

where \(\lambda _w^k =\frac{c}{f_1^k +f_2^k }\) is the WL wavelength. \(\phi _{w,i} =\left( \frac{B_{1,i} }{\lambda _1^k }\right. \left. -\frac{B_{2,i} }{\lambda _2^k }-\frac{f_1^k b_{1,i} +f_2^k b_{2,i}}{(f_1^k +f_2^k )\lambda _w^k } \right) \) and \(\phi _w^k =\left( {\frac{B_1^k }{\lambda _1^k }-\frac{B_2^k }{\lambda _2^k }-\frac{f_1^k b_1^k +f_2^k b_2^k }{(f_1^k +f_2^k )\lambda _w^k }} \right) \) are receiver and satellite WL FCBs, respectively. \(H_{w,i}^k =\frac{f_1^k F_{1,i}^k +f_2^k F_{2,i}^k }{(f_1^k +f_2^k )\lambda _w^k }\) is the receiver WL IFB. The integer nature of the WL ambiguity is destroyed by the existence of the WL FCB and WL IFBs, which must be properly accounted for to recover the integer nature of the WL ambiguity.

Although the receiver WL FCB has no bias resulting from the satellite, the frequency and wavelength are different for each GLONASS satellite, meaning that the receiver WL FCB will also be different. To further investigate this, we reformulate the receiver WL FCB as

$$\begin{aligned} \phi _{w,i}= & {} \frac{f_1^{k2}}{(f_1^k +f_2^k )\cdot c}(B_{1,i} -b_{1,i} )+\frac{f_1^k f_2^k }{(f_1^k +f_2^k )\cdot c}(B_{1,i} -B_{2,i} )\nonumber \\&+\frac{f_1^k f_2^k }{(f_1^k +f_2^k )\cdot c}(b_{1,i} -b_{2,i} )-\frac{f_2^{k2}}{(f_1^k +f_2^k )\cdot c}(B_{2,i} -b_{2,i} )\nonumber \\ \end{aligned}$$
(6)

According to Eq. (2) and neglecting the hardware-induced CPBs, we can get \(B_{1,i} -b_{1,i} =B_{2,i} -b_{2,i} =\mathrm{CPB}_i \) and \(B_{1,i} -B_{2,i} =b_{1,i} -b_{2,i} =\mathrm{DCB}_i \). Here \(\mathrm{DCB}_i \) is the differential code hardware bias for receiver i. Equation (6) can thus be reformulated as \(\phi _{w,i} =\frac{f_1^k -f_2^k }{c}\mathrm{CPB}_i +2\times \frac{f_1^k f_2^k }{(f_1^k +f_2^k )\cdot c}\mathrm{DCB}_i \). The coefficients \(\frac{f_1^k -f_2^k }{c}\) and \(\frac{f_1^k f_2^k }{(f_1^k +f_2^k )\cdot c}\) depend on the satellite frequency, but the maximum differences between different satellites are less than 0.006 and 0.011, respectively. Additionally, after applying station-specific CPB and DCB corrections, we can assume that the residual \(\mathrm{CPB}_i\) and \(\mathrm{DCB}_i \) are less than 3 m (10 ns). The maximum difference in the receiver WL FCB between different satellites can then be assumed to be within \(0.00\hbox {6}\times 3+0.0\hbox {11}\times 2\times 3=\hbox {0.084}\) cycles. We therefore assume that the receiver WL FCB is only dependent on the receiver and will not affect the WL ambiguity resolution.

It is noted that the receiver WL IFB in Eq. (5) depends also on the satellite and receiver, which will affect the WL FCB estimation. If we use homogeneous receivers for FCB estimation and PPP ambiguity fixing, we can assume the same (or comparable) code IFB, and the WL IFB for a particular satellite will be the same for all involved receivers and can be grouped into the satellite FCBs. Equation (5) can therefore be rewritten as

$$\begin{aligned} \mathrm{HMW}_i^k =N_{w,i}^k +\phi _{w,i} -\tilde{\phi }_w^k , \end{aligned}$$
(7)

where \(\tilde{\phi }_w^k =\phi _w^k +H_w^k \). Since the WL IFB is identical for all receivers, the subscript i is dropped. With the above reformulation, the receiver IFB has no effect on the WL FCB estimation. On the basis of Eq. (7), the UD WL FCB can be estimated following the procedures proposed by Laurichesse et al. (2009).

2.2 Integer satellite clock estimation

Satellite clock estimation is based on Eq. (3), where station coordinates and satellite orbits are usually known and fixed. Because the carrier-phase observation is ambiguous, the absolute clocks can only be determined by the code observation. The satellite and receiver clock estimation will therefore absorb the code hardware bias originating at the satellite and receiver. Because we use receivers with the same code IFB, the IF code IFB \(F_{\mathrm{IF},i}^k \) for satellite k will be the same for all stations. We can therefore drop the subscript i and merge the code IFB into the satellite clocks. Equation (3) can thus be rewritten as

$$\begin{aligned} P_{\mathrm{IF},i}^k= & {} \rho _i^k +c\mathrm{d}\tilde{t}_i -c\mathrm{d}\tilde{t}^{k} \nonumber \\ L_{\mathrm{IF},i}^k= & {} \rho _i^k +c\mathrm{d}\tilde{t}_i -c\mathrm{d}\tilde{t}^{k}+\lambda _1^k \tilde{N}_{\mathrm{IF},i}^k, \end{aligned}$$
(8)

where \(c\mathrm{d}\tilde{t}_i \hbox { }=c\mathrm{d}t_i +b_{\mathrm{IF},i}\), \(c\mathrm{d}\tilde{t}^{k}=c\mathrm{d}t^{k}+b_{\mathrm{IF}}^k -F_{\mathrm{IF}}^k \). \(\lambda _1^k \tilde{N}_{\mathrm{IF},i}^k =\tilde{B}_{\mathrm{IF},i} -\tilde{B}_{\mathrm{IF}}^k +\lambda _1^k N_{\mathrm{IF},i}^k \) is the float IF ambiguity, with \(\tilde{B}_{\mathrm{IF},i} =B_{\mathrm{IF},i} -b_{\mathrm{IF},i}\) and \(\tilde{B}_{\mathrm{IF}}^k \hbox { }=B_{\mathrm{IF}}^k -b_{\mathrm{IF}}^k +F_{\mathrm{IF}}^k \).

After fixing the WL ambiguity and by considering Eq. (4), we get the expression of the float IF ambiguity:

$$\begin{aligned} \lambda _1^k \tilde{N}_{\mathrm{IF},i}^k= & {} \tilde{B}_{\mathrm{IF},i} -\tilde{B}_{\mathrm{IF}}^k +\frac{c}{f_1^k +f_2^k }N_{1,i}^k +\frac{cf_2^k }{f_1^{k2}-f_2^{k2}}N_{w,i}^k \nonumber \\= & {} \frac{c}{f_1^k +f_2^k }(\phi _{n,i} -\phi _n^k +N_{1,i}^k )+\frac{cf_2^k }{f_1^{k2}-f_2^{k2}}N_{w,i}^k,\nonumber \\ \end{aligned}$$
(9)

where \(\phi _{n,i}^ =\frac{f_1^k +f_2^k }{c}\tilde{B}_{\mathrm{IF},i},\phi _n^k =\frac{f_1^k +f_2^k }{c}\tilde{B}_{\mathrm{IF}}^k \) are the receiver and satellite NL FCBs, respectively, which must be separated to recover the integer nature of the NL ambiguity. It is noted that although the receiver NL FCB has no bias originating at the satellite, the satellite-specific frequencies will cause the receiver NL FCB to be different for each satellite. The maximum difference of the coefficient \(\frac{f_1^k +f_2^k }{c}\) is less than \(\hbox {0.043}\); therefore, after applying the station-specific CPB correction, we can assume the receiver NL FCB \(\phi _{n,i}\) to be within \(\hbox {0.043}\times 3=\hbox {0.129}\) cycles. We thus assume that the receiver NL FCB depends only on the receiver and will not affect the NL ambiguity resolution.

By further fixing the NL ambiguity in Eq. (9), we get the final observation equation for integer satellite clock estimation:

$$\begin{aligned} P_{\mathrm{IF},i}^k= & {} \rho _i^k +c\mathrm{d}\tilde{T}_i -c\mathrm{d}\tilde{T}^{k} \nonumber \\ L_{\mathrm{IF},i}^k= & {} \rho _i^k +c\mathrm{d}\tilde{T}_i -c\mathrm{d}\tilde{T}^{k}+\frac{c}{f_1^k +f_2^k }N_{1,i}^k +\frac{cf_2^k }{f_1^{k2}-f_2^{k2}}N_{w,i}^k ,\nonumber \\ \end{aligned}$$
(10)

where \(c\mathrm{d}\tilde{T}_i =c\mathrm{d}\tilde{t}_i +\tilde{B}_{\mathrm{IF},i} ,c\mathrm{d}\tilde{T}^{k}=c\mathrm{d}\tilde{t}^{k}+\tilde{B}_{\mathrm{IF}}^k \) are the receiver and satellite clocks that have absorbed the receiver and satellite FCB, respectively. The UD clock estimation is made according to Eq. (8), getting the float IF ambiguity that can be fixed with the procedures proposed by Laurichesse et al. (2009). After fixing the ambiguity, the integer satellite clock estimation can be made using Eq. (10). It is noted from Eq. (8) that the satellite code hardware bias and the code IFB for each satellite are absorbed by the satellite clock, which will be consistent for PPP users with the same type of receiver and will not affect the precision of code observations.

2.3 GPS+GLONASS PPP ambiguity resolution strategy

With the WL FCB and the integer clock produced by the server, GPS+GLONASS PPP ambiguity resolution can be performed at the user end. If the same type of receiver is used, float PPP can be performed using Eq. (8), getting the float IF ambiguity with integer nature. WL and NL ambiguity resolution can then be performed sequentially.

The WL ambiguity is resolved by rounding (Dong and Bock 1989; Blewitt 1989; Ge et al. 2008). For rapid PPP ambiguity resolution, the NL ambiguities will have a strong correlation, and the LAMBDA method is thus adopted to search for the integers (Teunissen 1995) and the well-known ratio test is used to validate the ambiguity resolution. The criterion used for the ratio test will be discussed in the experiment section.

2.3.1 WL ambiguity fixing

The estimate \(\hat{{N}}_{w,i}^k \) and variance \(\sigma _{\hat{{N}}_{w,i}^k }^2 \) of a float WL ambiguity can be obtained using Eq. (7). After applying satellite WL FCB corrections, the same receiver WL FCB still exists in all WL ambiguity estimates, and it can be obtained by averaging the fractional parts of all WL ambiguities. Note that the averaging is not a trivial operation because of the cyclical nature of FCBs (Gabor and Nerem 1999; Ge et al. 2008), which means −0.5 cycles are identical to +0.5 cycles. This problem can be solved using the formulation of Gabor and Nerem (1999):

$$\begin{aligned} \phi _{w,i}^R= & {} \hbox {atan}2\left( {\frac{\sum \nolimits _M {\cos (\mathop {\overline{\mathrm{HMW}}_i^k } 2\pi )} }{M},\frac{\sum \nolimits _M {\sin (\mathop {\overline{\mathrm{HMW}}_i^k } 2\pi )} }{M}} \right) /2\pi \nonumber \\ \mathop \sigma \nolimits _{\phi _{w,i}^R }^2= & {} \frac{\left<(\mathop {{\overline{\mathrm{HMW}}}_i^k } -[\mathop {\overline{\mathrm{HMW}}_i^k } ]-\phi _{w,i}^R )^{2}\right>}{M}, \end{aligned}$$
(11)

where \({{\overline{\mathrm{HMW}}}_i^k } \) is the satellite-FCB-corrected HMW combination and M is the number of float WL ambiguity estimates for all satellites. Note that the result of the first expression of Eq. (11) will be biased because the first expression is a nonlinear operator. To mitigate the influence of the biasness, we use the result as an initial value, and the cyclical problem can be solved by adjusting all the float WL ambiguities to be near the initial estimate of the WL receiver FCB. Then the averaging can be directly applied to get the estimate and variance of the receiver WL FCB. The receiver FCB \(\phi _{w,i}^G \) and its variance \(\mathop \sigma \nolimits _{\phi _{w,i}^G }^2 \) can be derived for the GPS in the same way as for GLONASS. Once the WL receiver FCB is obtained, it can be used to further correct the WL ambiguity estimates in retrieving their integer properties. Specifically, an integer WL ambiguity can be retrieved with

$$\begin{aligned}&N_{w,i}^k ={{\overline{\mathrm{HMW}}}_i^k } -\phi _{w,i}^R \nonumber \\&N_{w,i}^j ={{\overline{\mathrm{HMW}}}_i^k } -\phi _{w,i}^G . \end{aligned}$$
(12)

The variance is \(\sigma _{N_{w,i}^k }^2 =\sigma _{\hat{{L}}_{w,i}^k }^2 +\sigma _{\phi _{w,i}^R }^2 ,\sigma _{N_{w,i}^j }^2 =\sigma _{\hat{{L}}_{w,i}^j }^2 +\sigma _{\phi _{w,i}^G }^2 \). Here, k and j represent a GLONASS and GPS satellite, respectively. The WL ambiguity fixing decision can then be made according to the probability (fixation to the nearest integer), which is calculated, for example, with the formula proposed by Dong and Bock (1989) or that proposed by Blewitt (1989). The estimated receiver WL FCB is only needed for the WL fixing and not for deriving the NL ambiguities and reconstructing the fixed IF ambiguities. As the WL wavelength is \(\sim \)86 cm, the accuracy requirement for receiver WL FCB is not so high, fixing is enough.

2.3.2 Effect of the bias in the receiver WL FCB

It is noted from Eq. (6) that the receiver WL FCB is determined by the difference between the code and carrier-phase hardware delays, which has an integer part plus a fractional part. However, we can only estimate the fractional part, and all the fixed WL ambiguity will therefore be biased by a common integer offset. Assuming the common integer offset to be \(\Delta N_{w,i}^R \) and \(\Delta N_{w,i}^G \) for GLONASS and GPS, respectively, we know from Eq. (4) that the common offset will be absorbed entirely into the corresponding NL ambiguity, while the IF ambiguity remains unchanged. The NL ambiguity will thus be biased by

$$\begin{aligned}&\Delta N_{1,i}^k =\frac{f_2^k }{f_1^k -f_2^k }\Delta N_{w,i}^R , \end{aligned}$$
(13)
$$\begin{aligned}&\Delta N_{1,i}^j =\frac{f_2^G }{f_1^G -f_2^G }\Delta N_{w,i}^G . \end{aligned}$$
(14)

For GLONASS, the two frequencies of each satellite have the relationship of\(f_1^k /f_2^k =9/7\), and we thus have

$$\begin{aligned} \Delta N_{1,i}^k =3.5\Delta N_{w,i}^R . \end{aligned}$$
(15)

According to Eqs. (14) and (15), the common offset in the WL ambiguity will produce a common offset in the NL ambiguity for all GPS or GLONASS satellites. The integer part of the common NL offset will be absorbed by the NL ambiguity, while the fractional part is the same for all satellites and can be grouped into the receiver NL FCB and will not affect the final fixing of the NL ambiguity. Moreover, since the IF ambiguities are unchanged, the positioning result will not be affected either. Note that the WL ambiguity fixing strategy is also applicable to the reference stations when estimating the integer satellite clocks.

2.3.3 NL ambiguity fixing

After fixing the WL ambiguity, the NL ambiguity and its variance–covariance can be obtained using Eq. (4). There is a strong linear correlation between the receiver clock bias and the NL ambiguities on the integer level, and a singularity thus exists in the integer least-squares adjustment. This problem does not exist for the single-differencing approach of Ge et al. (2008), where the receiver clock has been eliminated by the difference between satellites. To remove this singularity, a reference ambiguity must be chosen and fixed to an appropriate value, for GLONASS and GPS separately. Before applying the LAMBDA method, we choose the reference ambiguity with the highest satellite elevation angle and fix it to the nearest integer. Assuming the selected reference ambiguity is \(N^R \) and \(N^G \) and can be rounded to \(N_0^R \) and \(N_0^G \) for GLONASS and GPS, respectively. Then the contribution of the reference ambiguity can be expressed as an artificial observation as

$$\begin{aligned}&N^R =N_0^R ,P_0^R \in \infty \nonumber \\&N^G =N_0^G ,P_0^G \in \infty , \end{aligned}$$
(16)

where \(P_0^G \) and \(P_0^R \) are the weights of the reference ambiguity.

Fig. 1
figure 1

Distribution of used homogeneous stations in China; blue dots denote reference stations while red dots denote rover stations

Full size image

2.3.4 Effect of the bias in the NL reference ambiguity

With a few minutes of data, it is inevitable for the reference ambiguity to be biased because of the low precision of the float ambiguity. For GLONASS, assuming the reference ambiguity is biased by \(\Delta N_0^R \) and considering the NL ambiguities are not separable with the receiver clock, the fixed values for all NL ambiguities will be shifted by the common value of \(\Delta N_0^R \lambda _n^k \). The ambiguity (in meters) of another GLONASS satellite p can then be expressed as (Habrich et al. 1999)

$$\begin{aligned} \lambda _n^p N_n^p +\lambda _n^k \Delta N_0^R =\lambda _n^p (N_n^p +\Delta N_0^R )+\Delta N_0^R (\lambda _n^k -\lambda _n^p ), \end{aligned}$$
(17)

where \(N_n^p \) is the “real” ambiguity of satellite p, and \(N_n^p +\Delta N_0^R \) is the biased ambiguity of satellite p. It is noted that the second term on the right of Eq. (17), namely \(\Delta N_0^R (\lambda _n^k -\lambda _n^p )\), affects the integer nature of the final ambiguity of satellite p. The maximum difference in the NL wavelength between two GLONASS satellites is less than 0.0005 m. Therefore, for \(\Delta N_0^R (\lambda _n^k -\lambda _n^p )\) to remain within 0.01 m, \(\Delta N_0^R \) needs to be less than 20 cycles (2 m). With several minutes of data, GPS+GLONASS PPP can easily converge to an accuracy of within 1 m (or even better for most occasions), which will satisfy the precision requirement of the reference ambiguity. We can thus safely assume that the bias in the reference ambiguity will not affect the NL ambiguity fixing of other ambiguities. Meanwhile, for GPS, since the wavelength is the same for each satellite, the second term on the right side of Eq. (17) is always zeros, and the bias in the GPS reference ambiguity will thus do no harm to the ambiguity fixing for other satellites. It is noted that the above discussions are also applicable to the reference stations when estimating the integer satellite clocks.

3 Data and processing strategy

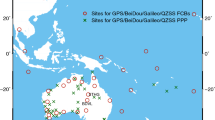
We selected 67 stations with identical hardware configurations from the Crustal Movement Observation Network of China to assess the contribution of adding GLONASS to the GPS-only solution. All these stations are equipped with Trimble NetR8 receivers (firmware version Nav 4.XX Boot 3.) and the same antenna type of TRM59800.00 SCIS, and we assume that these receivers have comparable code IFB and that the unit variations can be neglected. Observations with a sampling interval of 30 s covering days of year (DOYs) 1–21 in 2013 are used. Twenty-six stations are used as reference stations to generate integer satellite clocks while another 41 stations are used as user stations to perform PPP ambiguity fixing with the clock products. The distribution of stations is shown in Fig. 1.

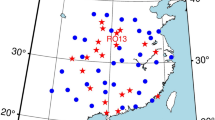
We have also adopted Wanninger’s (2011) method to investigate the GLONASS FCB estimation and PPP ambiguity resolution with heterogeneous receivers. We use a reference network with 40 stations covering DOYs 1–7 in 2013. It consists of 12 Topcon, 11 Trimble, 10 Leica and 7 Ashtech receivers located within a circular area having a radius of 300 km. The distribution of the sites is shown in Fig. 2. We use this relatively small area so that the ionosphere pierce points (IPPs) for each satellite will be concentrated within a small area, where we anticipate moderate or minimal ionosphere variations in space.

Fig. 2
figure 2

Distribution of used stations with heterogeneous receivers in France

Full size image

The positioning and navigation data analyst (PANDA) software (Shi et al. 2008), developed at Wuhan University, is modified to process GPS+GLONASS data. We apply the absolute phase centers (Rebischung et al. 2012) correction, the phase wind-up effects (Wu et al. 1993), and the station displacement models proposed by IERS conventions 2003 (McCarthy and Petit 2003). For both GPS and GLONASS, a cut-off angle of 7\({^{\circ }}\) is used, a priori precision of 1 and 0.01 m are used for code and carrier-phase observations, respectively, and an elevation-dependent weighting strategy is applied to weight measurements. Respective receiver clocks are estimated for GPS and GLONASS, and a common zenith tropospheric delay (ZTD) is estimated as being piecewise constant every 60 min. The final orbit products of the European Space Agency IGS analysis center are used. Since there is no accurate C1–P1 DCB product for GLONASS satellites, we use C1 and P2 code observations for GLONASS. To assess the benefits of ambiguity resolution when using GPS+GLONASS, the daily rover observations are divided into 24 pieces of hourly sets; and both kinematic and static PPP-IAR is performed for each hourly data. We assume that the ambiguities can be fixed to the correct integers with daily observations, and the PPP ambiguities are then compared with the daily “truth” to check the correctness.

4 Results and discussions

4.1 Experimental results with homogeneous receivers

4.1.1 Quality of the WL FCB and the integer clock estimation

The WL FCB and the integer clock estimates are critical for PPP ambiguity resolution. It is therefore necessary to ensure these products are of high quality. Firstly, the quality of the WL estimates is evaluated by examining the a posteriori residuals of the float ambiguities. A statistical histogram of the residuals of daily WL float ambiguity is shown in Fig. 3. For GPS satellites, 95.8% of all WL residuals are within \(\pm 0.15\) cycles, and 98.8% within \(\pm 0.25\) cycles. For GLONASS satellites, the residuals are a little larger in that only 83.0% of the WL residuals are within \(\pm 0.15\) cycles, which might be due to the unit variations of the code IFB. Meanwhile, 96.6% of the GLONASS residuals are within \(\pm 0.25\) cycles, which is comparable to that for GPS and meets the WL ambiguity resolution goal. Therefore, using homogeneous receivers, we can neglect the unit variations of the GLONASS code IFB among receivers, and achieve high consistency between all float WL ambiguities and FCB estimates.

Fig. 3
figure 3

Distribution of a posteriori residuals of the daily WL float ambiguities

Full size image

To validate the integer clock estimates, we examine a posteriori residuals of the fixed NL ambiguities, the statistical histogram of which is shown in Fig. 4. Generally, 94.5 and 94.4% of the NL residuals are within 0.1 cycles for GPS and GLONASS, respectively, while 97.7 and 97.8% are within 0.2 cycles. It is seen that, although the WL residuals of GLONASS are larger than those of GPS, the NL residuals of GLONASS are of the same magnitude as those of GPS. It is confirmed that the code IFB is very similar for each selected receiver and will not affect the WL FCB estimation or integer clock estimation.

Fig. 4
figure 4

Distribution of a posteriori residuals of the NL float ambiguities

Full size image

4.1.2 Selection of the critical values in ratio test

Although ratio test is very popular for ambiguity validation, different critical values have been proposed in the literature (Han and Rizos 1996a, b; Wei and Schwarz 1995; Leick et al. 2015). A higher critical value means a more confident result at the cost of unnecessary rejections, so the selection of the ratio value is thus a critical issue relating to PPP-IAR.

We refer to the percentage of epochs for which a correct ambiguity is accepted as the correct-fixing rate (CFR) and analyze the CFR at different critical values for GPS-only and GPS+GLONASS kinematic PPP solutions. The results are shown in Fig. 5. For a critical value of 2.0, the CFR is only 75.2% for the GPS alone but as large as 98.8% for GPS+GLONASS. The CFR increases with the critical value. For a critical value of 6, the CFR is 99.6% for GPS+GLONASS and only 96.8% for GPS alone.

Fig. 5
figure 5

CFR at different ratio values for GPS-only and GPS+GLONASS kinematic PPP

Full size image
Fig. 6
figure 6

CFR with different ratio values for solo GPS and GPS+GLONASS static PPP

Full size image
Fig. 7
figure 7

GPS-only kinematic PPP-IAR results for the XNIN station on DOY 1 of 2013

Full size image

We also analyzed the CFR with different critical values for static PPP; the results are shown in Fig. 6. Compared with kinematic PPP, for GPS alone, the CFR with a critical value of 2.0 improves to 85.3%, while it is 98.4% with a critical value of 6.0. However, all CFR values are smaller than the corresponding values of GPS+GLONASS in kinematic PPP.

When comparing with kinematic PPP, the improvement of the CFR at each critical value in static PPP is very little, less than 1%, for GPS+GLONASS. This is because the addition of GLONASS has increased the model strength sufficiently, such that very little is added by using a static model that constrains the position parameters between epochs. At a critical value of 2.0, the CFR for GPS+GLONASS kinematic PPP is as high as 98.8%, and there is no appreciable improvement when increasing the critical value or using the static model, and we therefore propose using a critical value of 2.0 for GPS+GLONASS PPP. Meanwhile, for solo GPS, to compare the positioning performance with that of GPS+GLONASS, we again use a critical value of 2.0 in the following PPP ambiguity resolution analysis.

4.1.3 PPP ambiguity resolution results

As an example, Figs. 7 and 8 present the position errors for GPS-only and GPS+GLONASS kinematic PPP at the XNIN station. We clearly see how the position filter converges and how the ambiguity is fixed for each coordinate component. The float PPP converges more quickly for the combined GPS+GLONASS processing in most sessions. For the ambiguity-fixed solution, there are three sessions in which the IFT exceeds 30 min and one session in which ambiguity resolution is not achieved. When using GPS+GLONASS, the IFT improves appreciably to within 15 min for all sessions. As can be seen, the combined GPS+GLONASS PPP has a better IFT than the GPS-only PPP solutions.

Fig. 8
figure 8

GPS+GLONASS kinematic PPP-IAR results for the XNIN station on DOY 1 of 2013

Full size image

To comprehensively analyze the contribution of adding GLONASS to the IFT improvement, the ambiguity-fixed PPP solution is applied to all hourly observations of the 41 rover stations made over 21 days in both kinematic and static mode. The IFT of each hourly solution is recorded and analyzed. We calculate the fixing percentage of all the hourly solutions for different observation lengths; results are shown in Fig. 9. It is seen that, when adding GLONASS, the fixing percentage improves appreciably for short observation lengths. The improvement decreases with the observation length, and very little improvement is achieved when the observation length is 60 min. As typical values, Table 2 gives the fixing percentages for observation lengths of 5, 10 and 15 min. Within 5 min, the fixing percentage for the GPS-only solution is only 11.70%; when adding GLONASS, the fixing percentage improves appreciably to 73.71%. For observation lengths of 10 and 15 min, the fixing percentage is, respectively, 46.80 and 68.48% for GPS-only solution and 95.83 and 98.59% for GPS+GLONASS solution. We see that, when adding GLONASS, the fixing percentage appreciably improves for the short time span.

Fig. 9
figure 9

Fixing percentage at different observation lengths for GPS-only and GPS+GLONASS kinematic PPP

Full size image
Table 2 Fixing percentage at different observation lengths for GPS-only and GPS+GLONASS kinematic PPP
Full size table
Fig. 10
figure 10

Fixing percentage at different observation lengths for GPS-only and GPS+GLONASS static PPP

Full size image
Table 3 Fixing percentage at different observation lengths for GPS-only and GPS+GLONASS static PPP
Full size table

The fixing percentage for the static model with different observation lengths is given in Fig. 10, while typical values for observation lengths of 5, 10 and 15 min are given in Table 3. Compared with kinematic PPP, for GPS-only solutions, the fixing percentage within 5, 10 and 15 min improves appreciably to 21.77, 69.74 and 88.18%, respectively. However, all these percentages are smaller than the corresponding percentages for GPS+GLONASS kinematic PPP solutions. Compared with the case for GPS-only solutions, the improvement from kinematic PPP to static PPP in the fixing percentage is very little for GPS+GLONASS solutions; the improvements are 6.07, 1.66 and 0.50%, respectively. This might be because the model strength is good enough for GPS+GLONASS, and using the static model does not contribute much to the model strength.

Figure 11 shows the fixing percentage in kinematic PPP within 15 min for each station with respect to the station latitude. In the case of GPS alone, the fixing percentage varies considerably for each station, ranging from 53 to 86%. Additionally, the figure reveals a trend that the fixing percentage increases with latitude. This might be due to the higher ionosphere irregularity at low latitude. In the case of GPS+GLONASS, the fixing percentage exceeds 93.8% for each station and has an average of 98.4% across all stations. Additionally, there is no relation between the fixing percentage and the station latitude for GPS+GLONASS.

Fig. 11
figure 11

Fixing percentage of GPS-only and GPS+GLONASS kinematic PPP within 15 min for each station

Full size image
Fig. 12
figure 12

Fixing percentage of GPS-only and GPS+GLONASS kinematic PPP within 15 min on each day

Full size image

We also calculate the fixing percentage in kinematic PPP within 15 min on each day, as shown in Fig. 12. The figure shows that, for the GPS-only solution, the fixing percentage varies considerably for each day, ranging from 55 to 75%. Additionally, there is a trend that the fixing percentage decreases the higher the ionospheric delay. Meanwhile, for GPS+GLONASS, the fixing percentage exceeds 97.0% for each day and has a mean of 98.4% across all days.

Fig. 13
figure 13

Fixing percentage of GPS-only and GPS+GLONASS kinematic PPP within 15 min at different values of the \(K_{\mathrm{p}}\) index

Full size image

To confirm the speculation from Figs. 11 and 12 that, for the GPS alone, the fixing percentage decreases with increasing ionosphere delay, we classify each hourly solution by the corresponding hourly \(K_{\mathrm{p}}\) index value. We then calculate the fixing percentage within 15 min for each value of the \(K_{\mathrm{p}}\) index; results are plotted in Fig. 13. The figure reveals that the fixing percentage for the GPS alone is affected by the ionosphere. However, nearly no such effect on GPS+GLONASS PPP is observed in Fig. 13. We speculate this may be caused by that, different satellites will experience different levels of higher-order ionosphere delay, which will cause them to be biased by different amounts of higher ionosphere delay and to experience different amounts of cycle slips. If we use GPS+GLONASS observations, because more satellites are used, we will have many more satellites experiencing low higher-order ionosphere delay, which will improve the performance of PPP-IAR with GPS-only observations.

Fig. 14
figure 14

Distribution of a posteriori residuals of the WL float ambiguities

Full size image
Fig. 15
figure 15

Distribution of a posteriori residuals of the NL float ambiguities

Full size image

4.2 Experimental results with heterogeneous receivers

In this section, we used the GIM to assess Reussner and Wanninger’s (2011) method and estimated the WL and NL FCBs with all the 40 reference stations at 5-min intervals. We analyze the a posteriori residuals of WL float ambiguity on seven days; the statistical histogram is shown in Fig. 14. For GPS satellites, 90.2% of all WL residuals are within \(\pm 0.15\) cycles and 94.8% are within \(\pm 0.25\) cycles. For GLONASS satellites, the residuals are comparable with those of GPS: 88.6 and 93.4% are within \(\pm 0.15\) cycles and \(\pm 0.25\) cycles, respectively. Figure 15 shows the distribution of the residuals in the NL FCB estimation. Generally, 98.2 and 95.2% of the NL residuals are within \(\pm 0.1\) cycles for the GPS and GLONASS, respectively, while 99.1 and 97.6% are within \(\pm 0.15\) cycles. It is seen, when using the GIM-corrected WL combination, the effect of the code IFB on the WL FCB estimation has been greatly diminished, and both WL and NL FCB estimations can be made across a variety of receiver types.

However, it is noted that more than 5% of the WL residuals are larger than 0.25 cycles for both GPS and GLONASS, and this is somehow a much larger number than the results in Fig. 3. To further investigate this finding, Fig. 16 shows the time series of a posteriori residuals of the WL and NL float ambiguities for four satellites on DOY 6 in 2013. It is seen that, because of the low precision of the GIM, the WL residuals of the four satellites are very large during the convergence stage. Meanwhile, for the NL ambiguity, because the ionosphere delay has been eliminated, the NL residuals are within \(\pm 0.2\) cycles for all stations. It is thus demonstrated that the precision of the GIM is critical to WL FCB estimation based on WL combination. The large ionosphere delay will also affect the WL ambiguity resolution of PPP.

Fig. 16
figure 16

Time series of a posteriori residuals of the WL float ambiguities on DOY 6 in 2013. The first line is for G17, the second for G21, the third for R06 and the fourth for R14

Full size image

With the WL and NL FCB estimates, the GPS+GLONASS kinematic PPP-IAR solution is applied to all hourly observations for the 40 reference stations that made observations over 7 days. For comparison, we also calculate GPS WL and NL FCBs using the traditional HMW method and performed GPS-only kinematic PPP-IAR with these FCB products for all 40 stations. We calculate the fixing percentage for different observation lengths; results are shown in Fig. 17. It is seen that the fixing percentage is even lower than that of the GPS-only solutions obtained with the HMW method. It is also noted that Geng and Bock (2015) realized this idea in an uncombined way where the GIM is used as the external constraint for GLONASS static PPP ambiguity resolution, and they could only fix 69% of the GLONASS ambiguity for hourly static PPP. Considering this point and the analysis of Fig. 16, we believe that the low fixing percentage is due to the low precision of the GIM.

5 Conclusions

This paper presented recent progress made for PPP ambiguity resolution using GPS+GLONASS observations. With a network of homogeneous receivers, it was demonstrated that the WL FCB and integer satellite clock can be estimated with comparable precision for GPS and GLONASS satellites: 98.8% of a posteriori residuals of the WL ambiguities are within \(\pm 0.25\) cycles for the GPS and 96.6% for GLONASS. Meanwhile, 94.5 and 94.4% of the NL residuals are within 0.1 cycles for GPS and GLONASS, respectively.

We first analyzed the CFR in ratio tests for different critical values. At a critical value of 2.0, the CFR is only 75.2% for GPS-only kinematic PPP while it is as high as 98.8% for GPS+GLONASS kinematic PPP. Additionally, there is no appreciable further improvement when increasing the critical value or using a static model, and we thus propose using a value of 2.0 as the critical value for GPS+GLONASS PPP. Meanwhile, for GPS-alone solutions, to compare the positioning performance with that of GPS+GLONASS, we also use a value of 2.0 for the PPP ambiguity resolution analysis.

Fig. 17
figure 17

Fixing percentage at different observation lengths for GPS-only and GPS+GLONASS kinematic PPP

Full size image

The contribution of GLONASS observations to the IFT of PPP was investigated. Numerical results show that for kinematic PPP, the fixing percentage within 5 min for solo GPS alone is only 11.70%. When adding GLONASS observations, the percentage improves appreciably to 73.71%. In the cases of observation lengths of 10 and 15 min, the fixing percentage is, respectively, 46.80 and 68.48% for the GPS-only solution and 95.83 and 98.59% for the GPS+GLONASS solution. For GPS-only static PPP, the fixing percentages within 5, 10 and 15 min improve appreciably to 21.77, 69.74 and 88.18%, respectively. However, all these percentages are smaller than corresponding percentages for GPS+GLONASS kinematic PPP solutions. Meanwhile, the improvement of the fixing percentage from kinematic PPP to static PPP is very small for GPS+GLONASS solutions. This might be because of the model strength is good enough for GPS+GLONASS, and using a static model does not contribute much to the model strength. On average, the RMS position error is 0.53 and 0.46 cm for the GPS alone in the north and east directions, respectively; values are 0.40 and 0.39 cm for GPS+GLONASS, showing an improvement of 24.5 and 15.2%. The precision in the up direction appreciably improves with the increasing observation time length and when the time is extended to 30 min, the RMS error is 1.76 and 1.54 cm for GPS-only and GPS+GLONASS.

For GLONASS PPP ambiguity resolution with heterogeneous receivers, we also used the GIM model to assist the WL ambiguity resolution with the WL carrier-phase combination, where the effect of the code IFB is eliminated. For WL FCB estimation, 94.8 and 93.4% of the residuals are within \(\pm 0.25\) cycles for GPS and GLONASS, respectively. Meanwhile, for the NL FCB estimation, 98.2 and 95.2% of the NL residuals are within \(\pm 0.1\) cycles for GPS and GLONASS, respectively. It is confirmed that, employing this method, both the WL and NL FCB estimation can be achieved across a variety of receiver types. However, because of the relatively low accuracy of current GIMs, the fixing percentage of GIM-aided GPS+GLONASS PPP ambiguity resolution is very low.