Introduction

The traditional carrier phase tracking loops, such as the phase lock loop (PLL), are designed in the frequency domain for a Global Navigation Satellite System (GNSS) receiver. The parameters of the PLL can be determined by the theory of Wiener filter (WF) (Jaffe and Rechtin 1955). The PLL has been widely employed in the GNSS receiver (Ward et al. 2006). However, it is a challenge for the PLL to keep lock-in when a receiver is in a high dynamic environment or the signals are very weak (Jwo 2001). To keep tracking the GNSS signals in such situations, a Kalman filter (KF) carrier phase tracking loop has been proposed. Psiaki (2001a, b) designed a KF to estimate the attitude of a turntable and a Kalman smoother to track the received global positioning system (GPS) signal. Later, the KF was applied to track the weak GNSS signals (Psiaki and Jung 2002; Ziedan and Garrison 2003). Meanwhile, the various KFs were implemented in the cascaded vector tracking receivers to track the high dynamic GNSS signals (Petovello and Lachapelle 2006; Won et al. 2009). For example, the I/Q outputs were treated as the pre-filtering measurements of white noises with the nonlinear measurement equations. This implementation can improve the receiver accuracy. In other implementations, the discriminator outputs were treated as the pre-filtering measurements with the linear measurement equations, but of non-white measurement noises. Under the assumption of quasi-Gaussian distribution, a robust implementation can be achieved.

Since both the PLL and the KF can be applied in the GNSS tracking loops, it is worthwhile to compare the two tracking methods numerically. A steady KF can be equivalent to a filter in the frequency domain so that the equivalent noise bandwidth can be obtained, which makes the KF and the PLL comparable by their noise bandwidths (O’Driscoll and Lachapelle 2009). Salem et al. (2012) proposed an experimental method to design an equivalent PLL for a given extended Kalman filter (EKF). Patapoutian (1999) deduced the equivalent 2nd-order PLL of a steady KF. However, the equivalence of the general 3rd-order PLL to a steady KF has not been investigated yet. Moreover, the factors that affect the performance of the KF also need to be sorted out.

For the traditional tracking loops, the rule-of-thumb analysis method that was verified by the Monte Carlo simulations had been widely applied to design the loops (Ward et al. 2006; Ward 1997). However, there is no counterpart in the field of the KF tracking loop in the literature. Therefore, the rule-of-thumb analysis method for the KF tracking loop is presented.

We address the problems mentioned above. It proves the equivalence of the 3rd-order PLL and the steady KF, which makes the PLL and the KF loops comparable. The factors impacting the performance of the KF tracking loop are investigated, which can guide in tuning the KF for better performance. The rule-of-thumb threshold for the KF tracking loop is calculated upon the covariance analysis of the suboptimal KF. The method is verified by the Monte Carlo simulations.

KF tracking model

The continuous and the discrete models for the KF tracking loops are presented in this section. Similar models with the different states can be found in the literature (O’Driscoll and Petovello 2011). The continuous model is to prove the equivalence of the steady KF tracking to the traditional one, and the discrete model is to investigate the impact of some factors on the KF tracking quantitatively.

Continuous model

The system equations can be modeled as,

$$ {\dot{\mathbf{x}}}\left( t \right) = {\mathbf{Fx}}\left( t \right) + {\mathbf{Gw}}\left( t \right) $$
(1)

where the state vector \( {\mathbf{x}}\left( t \right) = \left[ {\begin{array}{*{20}c} {\Delta \phi } & {\Delta \omega } & {\Delta \alpha } \\ \end{array} } \right]^{\text{T}} \) is the errors of carrier phase, carrier frequency, and carrier frequency rate, respectively; \( {\mathbf{F}} \) is the state dynamics matrix, given by,

$$ {\mathbf{F}} = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{array} } \right] $$
(2)

\( {\mathbf{G}} \) is the process noise matrix; and \( {\mathbf{w}}\left( t \right) \) is the process noise.

If the effect of the receiver oscillator and the line-of-sight (LOS) jerk is taken into account, \( {\mathbf{w}}\left( t \right) = [\begin{array}{*{20}c} {w_{b} } & {w_{d} } & {w_{\alpha } } \\ \end{array} ]^{\text{T}} \), where w b , w d , and w α are the zero-mean white noises with the power spectral density (PSD) of q b , q d , and q α, respectively. With the known Allan parameters of the receiver oscillator noise, q b and q d can be written as (Brown and Hwang 2012),

$$ \begin{aligned} & q_{b} = \frac{{h_{0} }}{2} \\ & q_{d} = 2\pi^{2} h_{ - 2} \\ \end{aligned} $$
(3)

where h 0 and h −2 are the Allan parameters. Their typical values of the temperature-compensated crystal oscillator (TCXO) and oven-controlled crystal oscillator (OCXO) are listed in Table 1 (Brown and Hwang 2012).

Table 1 Allan parameters of TCXO and OCXO
Full size table

The value of q α can be determined by the LOS jerk (Salem 2012). The process noise matrix \( {\mathbf{G}} \) is written as,

$$ {\mathbf{G}} = {\text{diag}}\left[ {\begin{array}{*{20}c} {\omega_{rf} } & {\omega_{rf} } & {{{\omega_{rf} } \mathord{\left/ {\vphantom {{\omega_{rf} } {\text{c}}}} \right. \kern-0pt} {\text{c}}}} \\ \end{array} } \right] $$
(4)

where ω rf is the nominal frequency of the carrier, for the GPS L1, \( \omega_{rf} = 2\pi \times 1575.42 \times 1 0^{6} \;{{\text{rad}} \mathord{\left/ {\vphantom {{\text{rad}} {\text{s}}}} \right. \kern-0pt} {\text{s}}} \); \( {\text{c}} = 2.99792458 \times 10^{8} \,{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-0pt} {\text{s}}} \) is the speed of light in vacuum space; and \( {\text{diag}}\left[ \bullet \right] \) denotes the diagonal matrix. The process noise covariance is,

$$ {\mathbf{Q}} = {\text{E}}\left[ {{\mathbf{Gww}}^{\text{T}} {\mathbf{G}}^{\text{T}} } \right] = {\text{diag}}\left[ {\begin{array}{*{20}c} {\omega_{rf}^{2} q_{b} } & {\omega_{rf}^{2} q_{d} } & {{{\omega_{rf}^{2} q_{\alpha } } \mathord{\left/ {\vphantom {{\omega_{rf}^{2} q_{\alpha } } {{\text{c}}^{2} }}} \right. \kern-0pt} {{\text{c}}^{2} }}} \\ \end{array} } \right] $$
(5)

where \( {\text{E}}\left( {\mathbf{x}} \right) \) is the expectation of \( {\mathbf{x}} \). Equations (1)–(5) form the system model of the KF.

The measurement equation is written as,

$$ z\left( t \right) = \tilde{\phi } = {\mathbf{Hx}}\left( t \right) + v\left( t \right) $$
(6)

where \( \tilde{\phi } \) is the output of a Costas phase discriminator, \( {\mathbf{H}} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ \end{array} } \right] \), v(t) is a zero-mean white noise with the PSD of σ 2 ϕ T, and T is the coherent integration period. The measurement noise covariance is,

$$ \begin{aligned} & R = {\text{E}}\left[ {v^{2} \left( t \right)} \right] = \sigma_{\phi }^{2} T \\ & \sigma_{\phi }^{2} = \frac{1}{{2{c \mathord{\left/ {\vphantom {c {n_{0} T}}} \right. \kern-0pt} {n_{0} T}}}}\left( {1 + \frac{1}{{2{c \mathord{\left/ {\vphantom {c {n_{0} T}}} \right. \kern-0pt} {n_{0} T}}}}} \right) \\ \end{aligned} $$
(7)

where \( {c \mathord{\left/ {\vphantom {c {n_{0} }}} \right. \kern-0pt} {n_{0} }} = 10^{{\tfrac{{\left( {{C \mathord{\left/ {\vphantom {C {N_{0} }}} \right. \kern-0pt} {N_{0} }}} \right)_{\text{dB - Hz}} }}{10}}} \) and C/N 0 are the carrier-to-noise ratio expressed in Hz and in dB-Hz, respectively.

Discrete model

The discrete state equations can be obtained from (1) as follows (Psiaki and Jung 2002),

$$ {\mathbf{x}}_{k + 1} = {\mathbf{\varPhi x}}_{k} + {\varvec{\Gamma}}_{k} {\mathbf{w}}_{k} $$
(8)

where \( {\mathbf{x}}_{k} \) is the value of \( {\mathbf{x}} \) at k time and \( {\mathbf{x}}_{k} = \left[ {\begin{array}{*{20}c} {\Delta \phi_{k} } & {\Delta \omega_{k} } & {\Delta \alpha_{k} } \\ \end{array} } \right]^{\text{T}} \); the state transition matrix \( {\varvec{\Phi}} \) is,

$$ {\varvec{\Phi}} = \left[ {\begin{array}{*{20}c} 1 & T & {{{T^{2} } \mathord{\left/ {\vphantom {{T^{2} } 2}} \right. \kern-0pt} 2}} \\ 0 & 1 & T \\ 0 & 0 & 0 \\ \end{array} } \right] $$
(9)

and the process noise covariance \( {\mathbf{Q}}_{k} \) is,

$$ \begin{aligned} & {\mathbf{Q}}_{k} = {\varvec{\Gamma}}_{k} {\text{E}}\left[ {{\mathbf{w}}_{k} {\mathbf{w}}_{k}^{\text{T}} } \right]{\varvec{\Gamma}}_{k}^{\text{T}} \\ & \quad = \left( {\frac{{\omega_{rf} }}{c}} \right)^{2} q_{\alpha } \left[ {\begin{array}{*{20}c} {{{T^{5} } \mathord{\left/ {\vphantom {{T^{5} } {20}}} \right. \kern-0pt} {20}}} & {{{T^{4} } \mathord{\left/ {\vphantom {{T^{4} } 8}} \right. \kern-0pt} 8}} & {{{T^{3} } \mathord{\left/ {\vphantom {{T^{3} } 6}} \right. \kern-0pt} 6}} \\ {{{T^{4} } \mathord{\left/ {\vphantom {{T^{4} } 8}} \right. \kern-0pt} 8}} & {{{T^{3} } \mathord{\left/ {\vphantom {{T^{3} } 3}} \right. \kern-0pt} 3}} & {{{T^{2} } \mathord{\left/ {\vphantom {{T^{2} } 2}} \right. \kern-0pt} 2}} \\ {{{T^{3} } \mathord{\left/ {\vphantom {{T^{3} } 6}} \right. \kern-0pt} 6}} & {{{T^{2} } \mathord{\left/ {\vphantom {{T^{2} } 2}} \right. \kern-0pt} 2}} & T \\ \end{array} } \right] + \omega_{rf}^{2} q_{d} \left[ {\begin{array}{*{20}c} {{{T^{3} } \mathord{\left/ {\vphantom {{T^{3} } 3}} \right. \kern-0pt} 3}} & {{{T^{2} } \mathord{\left/ {\vphantom {{T^{2} } 2}} \right. \kern-0pt} 2}} & 0 \\ {{{T^{2} } \mathord{\left/ {\vphantom {{T^{2} } 2}} \right. \kern-0pt} 2}} & T & 0 \\ 0 & 0 & 0 \\ \end{array} } \right] + \omega_{rf}^{2} q_{b} \left[ {\begin{array}{*{20}c} T & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right] \\ \end{aligned} $$
(10)

where \( {\mathbf{w}}_{k} \) and \( {\varvec{\Gamma}}_{k} \) are the discrete process noise and its matrix, respectively.

The measurement equation is,

$$ z_{k} = {\mathbf{H}}_{k} {\mathbf{x}}_{k} + v_{k} $$
(11)

where z k is the output of a Costas phase discriminator, v k a zero-mean white noise with the variance R k  = σ 2 ϕ , and \( {\mathbf{H}}_{k} = \left[ {\begin{array}{*{20}c} 1 & { - {T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0pt} 2}} & {{{T^{2} } \mathord{\left/ {\vphantom {{T^{2} } 6}} \right. \kern-0pt} 6}} \\ \end{array} } \right]. \)

Equivalence of the steady KF tracking to the traditional tracking

If only the LOS jerk is taken into account and the oscillator noise is neglected, \( {\mathbf{Q}} \) in (5) will be simplified as,

$$ {\mathbf{Q}} = {\text{diag}}\left[ {\begin{array}{*{20}c} 0 & 0 & Q \\ \end{array} } \right] $$
(12)

where \( {{Q = \omega_{rf}^{2} q_{\alpha } } \mathord{\left/ {\vphantom {{Q = \omega_{rf}^{2} q_{\alpha } } {{\text{c}}^{2} }}} \right. \kern-0pt} {{\text{c}}^{2} }} \). The Riccati equation (Gelb 1974) for a continuous KF is,

$$ {\dot{\mathbf{P}}} = {\mathbf{FP}} + {\mathbf{PF}}^{\text{T}} + {\mathbf{Q}} - {\mathbf{PH}}^{\text{T}} {\mathbf{HPR}}^{ - 1} $$
(13)

and the gain matrix is,

$$ {\mathbf{K}} = {\mathbf{PH}}^{\text{T}} {\mathbf{R}}^{ - 1} $$
(14)

The steady covariance and its gain matrix can be derived from (12) to (14) as below (Jwo 2001).

$$ {\mathbf{P}}_{\infty } = \left[ {\begin{array}{*{20}c} {2Q^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0pt} 6}}} R^{{{5 \mathord{\left/ {\vphantom {5 6}} \right. \kern-0pt} 6}}} } & {2Q^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} R^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} } & {Q^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} R^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \\ {2Q^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} R^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} } & {3Q^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} R^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } & {2Q^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} R^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} } \\ {2Q^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} R^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} } & {2Q^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} R^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} } & {2Q^{{{5 \mathord{\left/ {\vphantom {5 6}} \right. \kern-0pt} 6}}} R^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0pt} 6}}} } \\ \end{array} } \right] $$
(15)
$$ {\mathbf{K}}_{\infty } = \left[ {\begin{array}{*{20}c} {2\left( {{Q \mathord{\left/ {\vphantom {Q R}} \right. \kern-0pt} R}} \right)^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0pt} 6}}} } \\ {2\left( {{Q \mathord{\left/ {\vphantom {Q R}} \right. \kern-0pt} R}} \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} } \\ {\left( {{Q \mathord{\left/ {\vphantom {Q R}} \right. \kern-0pt} R}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {2\omega_{n} } \\ {2\omega_{n}^{2} } \\ {\omega_{n}^{3} } \\ \end{array} } \right] $$
(16)

where ω n  = (Q/QR.R)1/6. The corresponding transfer function H(s) to the steady KF is,

$$ H\left( s \right) = \frac{{2\omega_{n} s^{2} + 2\omega_{n}^{2} s + \omega_{n}^{3} }}{{s^{3} + 2\omega_{n} s^{2} + 2\omega_{n}^{2} s + \omega_{n}^{3} }} $$
(17)

Equations (15)–(17) are the same as the model of the traditional third-order PLL (Jaffe and Rechtin 1955). However, the PLL is the closed-form quasi-optimal filter derived from the WF. Hence, the following remarks can be made:

  1. 1.

    The steady KF is equivalent to the PLL based on the WF, which makes the KF and the PLL comparable.

  2. 2.

    The KF has a better transient and dynamic performance than the PLL although they have the same level of the steady accuracy.

  3. 3.

    Although it is a trade-off in the KF design between the improvement of the dynamic range of the tracking loop and the mitigation of the tracking loop noise, the time-variant gain matrix of the KF is similar to the adaptive bandwidth of the traditional tracking loop (Won et al. 2012). Hence, a well-designed KF will have a larger dynamic range and higher sensitivity than a traditional PLL (Tang et al. 2013; Won and Eissfeller 2013).

  4. 4.

    Both Q and R impact on the state estimation accuracy according to (15), which is not as reported in Tang et al. (2014) that Q has no effect on the estimation accuracy of the carrier phase and the carrier frequency.

If taking into account both the LOS jerk and the oscillator noise, the steady gain matrix can be similarly derived as,

$$ {\mathbf{K}}_{\infty } = \left[ {\begin{array}{*{20}c} \lambda & {\frac{1}{2}\left( {\lambda^{2} - \rho_{b} } \right)} & {\sqrt {\rho_{\alpha } } } \\ \end{array} } \right]^{\text{T}} $$
(18)

where \( \lambda > \sqrt {\rho_{b} } \) is a positive real root of the quartic equation,

$$ \left( {\lambda^{2} - \rho_{b} } \right)^{2} - 8\sqrt {\rho_{\alpha } } \lambda - 4\rho_{d} = 0 $$
(19)

and

$$ \begin{aligned} & \rho_{\alpha } = \frac{{\omega_{rf}^{2} q_{\alpha } }}{{{\text{c}}^{2} \sigma_{\phi }^{2} T}} \\ & \rho_{d} = \frac{{\omega_{rf}^{2} q_{d} }}{{\sigma_{\phi }^{2} T}} \\ & \rho_{b} = \frac{{\omega_{rf}^{2} q_{b} }}{{\sigma_{\phi }^{2} T}} \\ \end{aligned} $$
(20)

Equations (18)–(20) are the same as those of the traditional tracking loop derived from the WF (O’Driscoll and Petovello 2011). Hence, the aforementioned remarks on the KF and the traditional PLL still hold.

Factors impacting the KF tracking

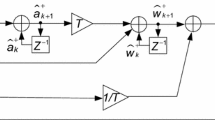
In order to numerically evaluate the effect of the factors on the performance of the KF tracking loop, a covariance analysis can be made on the discrete KF model by simulations. Both error budgeting and suboptimal analysis are conducted herein. Figure 1 depicts the flowchart of the analyses.

Fig. 1
figure 1

Flowchart of performance analysis in simulations

Full size image

In Fig. 1, the superscripts ‘+’ and ‘−’ denote the values after and before the measurement updating. The superscript ‘*’ denotes the designed KF parameters. As long as the values of C/N 0, q b , q d , and q α are determined, \( {\mathbf{R}}_{k}^{*} \) and \( {\mathbf{Q}}_{k}^{*} \) can be calculated by (7), (10), and (11) accordingly. Then, the KF for the tracking loop can be designed. \( {\mathbf{K}}_{k}^{*} \), which is used to calculate the covariance matrix \( {\mathbf{M}} \) in the following analysis, is the gain matrix of the designed KF. If the values of \( {\mathbf{R}}_{k} \), \( {\mathbf{Q}}_{k} \), and \( {\mathbf{P}}_{0}^{ - } \) are different from those of \( {\mathbf{R}}_{k}^{*} \), \( {\mathbf{Q}}_{k}^{*} \), and \( {\mathbf{P}}_{0}^{* - } \), both \( {\mathbf{P}}_{k} \) and \( {\mathbf{M}}_{k} \) are suboptimal in Fig. 1. For example, the KF for the carrier tracking loop is designed to meet the requirement of the lowest value of C/N 0 but the received signals in applications are not always so weak that the KF is suboptimal. It should be noted that \( {\mathbf{M}} \) is linear with \( {\mathbf{R}} \), \( {\mathbf{Q}} \), and \( {\mathbf{M}}_{0}^{ - } \) when \( {\mathbf{K}}_{k}^{*} \) is determined. Hence, the impact of the factors (such as \( {\mathbf{Q}} \)) and their components (such as q α ) on the performance of the KF can be investigated independently (Farrell 2008).

In the following analysis, the first diagonal element of \( {\mathbf{M}}_{k}^{ + } \) is assumed as the variance of Δϕ k , σ 2Δϕ . Both the transient and the steady values of σ Δϕ will be studied in the error budgeting analysis, while only the steady value of σ Δϕ will be studied in the suboptimal analysis.

Error budgeting analysis

Figure 2 depicts the transient process of σ Δϕ with the factors. The simulation conditions are given that \( {\mathbf{P}}_{0}^{* - } \) = diag[(2π)2 (2π × 1000)2 0], T = 0.02 s, C/N 0 = 35 dB-Hz, the parameters in Table 1 are used, q α  = (0.2)2m2/s5, and the total simulation time is 1 s. In the figure, \( {\mathbf{P}}_{0}^{* - } \) contributes the most to σ Δϕ at first, but its contribution decays so quickly that its effect can be neglected after several iterations. The contributions of the other four factors, q b , q d , q α , and R k , to σ Δϕ keep increasing with the number of iterations, but they become stable after 0.5 s. Since the OCXO parameters are used in Fig. 2 (top), the impact of q b and q d on σ Δϕ is less than that of q α and R k on σ Δϕ , but the contribution of q b and q d to σ Δϕ increases significantly in Fig. 2 (bottom) since the TCXO parameters are used. Hence, it is helpful to reduce the steady value of σ Δϕ by improving the accuracy of the local oscillator and reducing the LOS jerk and the measurement noise.

Fig. 2
figure 2

Impact of the factors on the transient process of σ Δϕ with OCXO (top) and TCXO (bottom). The solid line, the dash line, the plus sign line, the dot line, and the point line indicate the errors derived by the oscillator noise PSDs q b and q d , the LOS jerk PSD q α , the measurement noise variance R, and \( {\mathbf{P}}_{0} \), respectively

Full size image

In the following, the effect of the LOS jerk and C/N 0 on the steady value of σ Δϕ will be explored further by simulations. Since the effect of \( {\mathbf{P}}_{0}^{* - } \) on the steady value of σ Δϕ can be neglected, it is assumed that \( {\mathbf{P}}_{0}^{* - } = {\mathbf{0}}_{3 \times 3} \) in the simulations. The value of C/N 0 will be 25 dB-Hz or 45 dB-Hz and that of q α will be (0.001 g/s)2/Hz or (30 g/s)2/Hz. The OCXO parameters are used herein. The other simulation conditions are the same as above. Figure 3 depicts the steady value of σ Δϕ and the contributions of the factors. The abscissa shows the test cases 1–4 in the simulations. The simulation conditions corresponding to the four cases are listed in Table 2. This table lists the percentages of the errors due to the factors in the steady value of σ 2Δϕ . It is similar to the above simulations that the effect of OCXO on the steady value of σ Δϕ is very limited while both the LOS jerk and R k play the important role in the steady value of σ Δϕ . As expected, the steady value of σ Δϕ is the largest when the value of C/N 0 is small and that of q α is large; on the contrary, the steady value of σ Δϕ is the smallest when the value of C/N 0 is large and that of q α is small. In the former three cases, R k contributes more to the steady value of σ Δϕ than q α . However, in the fourth case, q α contributes more to the steady value of σ Δϕ than R k on the contrary. Hence, it is more efficient to reduce the steady value of σ Δϕ by reducing the value of R k in the former three cases, while it is more efficient by reducing the value of q α in the fourth case.

Fig. 3
figure 3

Steady value of σ Δϕ and the contributions of the factors. The dark blue, the dark cyan, and the yellow parts represent the errors derived by q b  + q d , q α , and R, respectively

Full size image
Table 2 Percentages of the errors due to the factors in σ 2Δϕ
Full size table

Suboptimal analysis

As mentioned above, the designed KF will be suboptimal if the actual values of its parameters in applications are not the same as their designed. Herein, the performance of the designed KF is compared with that of the optimal KF. The total carrier phase error σ Δϕ with C/N 0 is depicted in Fig. 4. σ Δϕ with the LOS jerk is depicted in Fig. 5, where the results of the designed KF and the optimal KF are shown in the lines with circles and with asterisks, respectively. In the optimal KF, the actual values of \( {\mathbf{Q}}_{k} \) and R k are used. As shown in Figs. 4 and 5, in addition to the design point where the designed KF has the same performance as the optimal KF (because the designed KF is optimal at this point), on the other points the designed KF has a poorer performance. The optimal KF is slightly more sensitive than the designed KF in Fig. 4. In Fig. 5, the designed KF loses its lock of the signals when the LOS jerk is greater than 27 g/s, while the optimal KF can still keep in lock of the signals even with a LOS jerk more than 100 g/s. Hence, it aims to estimate \( {\mathbf{Q}}_{k} \) and R k in real time as accurate as possible for the KF-based tracking loop.

Fig. 4
figure 4

Carrier phase uncertainty σ Δϕ versus C/N 0 with the jerk of 10 g/s. The asterisk and the circle curves depict the performances of the optimal filter with the actual C/N 0 and the designed filter with \( {C \mathord{\left/ {\vphantom {C {N_{0} }}} \right. \kern-0pt} {N_{0} }} = 30\;{\text{dB - Hz}} \), respectively

Full size image
Fig. 5
figure 5

Carrier phase uncertainty σ Δϕ versus jerk (\( {C \mathord{\left/ {\vphantom {C {N_{0} }}} \right. \kern-0pt} {N_{0} }} = 35\;{\text{dB - Hz}} \)). The asterisk and the circle curves depict the optimal filter with the actual jerk and the designed filter with the jerk of 10 g/s, respectively

Full size image

Rule-of-thumb analysis method for the tracking loops

The rule-of-thumb analysis method is an indispensable tool for the traditional tracking loop design. A similar rule-of-thumb analysis method is proposed for the KF-based tracking loop design. Two methods are presented hereinafter.

Rule-of-thumb PLL analysis method

The 3-sigma rule-of-thumb threshold for a PLL tracking loop with a Costas discriminator to keep lock-in is (Ward et al. 2006),

$$ 3\sigma_{\text{PLL}} = 3\sqrt {\sigma_{{{\text{PLL}}t}}^{2} + \sigma_{{\nu}{\text{i}}}^{2} + \sigma_{\text{A}}^{2} } + \theta_{e} \le 45^{ \circ } $$
(21)

where \( \sigma_{{{\text{PLL}}t}} \) is the PLL thermal noise, \( \sigma_{{\nu}{\text{i}}} \) is the vibration-induced oscillator jitter, \( \sigma_{\text{A}} \) is the Allan variance-induced oscillator jitter, and θ e is the dynamic stress error. If the oscillator-related noises are neglected, Eq. (21) can be simplified as

$$ \sigma_{\text{PLL}} = \sigma_{{{\text{PLL}}t}} + {{\theta_{e} } \mathord{\left/ {\vphantom {{\theta_{e} } 3}} \right. \kern-0pt} 3} \le 15^{ \circ } $$
(22)

In (22), the PLL thermal noise and the oscillator-related noises are treated as random noises while the dynamic stress error is assumed as a bias. Hence, the root mean square (RMS) of the noise is added with the bias in (22). However, if the dynamic stress error is a random noise rather than a bias (Ward 1998), Eq. (22) should be modified accordingly, which is the case encountered in the KF.

Rule-of-thumb KF tracking analysis method

In the KF, the dynamic stress error is modeled as a white noise. As mentioned above, the dynamic stress error should also be taken into account of the RMS threshold since the thermal noise and the oscillator-related noises are random too. Hence, the 1-sigma rule-of-thumb threshold for the KF is,

$$ \sigma_{\Delta \phi } = \sqrt {\sigma_{{\Delta \phi_{{{\text{KF}}t}} }}^{2} + \sigma_{{\Delta \phi_{Et} }}^{2} } \le 15^{ \circ } $$
(23)

where \( \sigma_{{\Delta \phi_{{{\text{KF}}t}} }} \) and \( \sigma_{{\Delta \phi_{Et} }} \) represent the KF thermal noise and the dynamic stress noise, respectively. The oscillator-related noises are neglected in (23).

Simulations

In order to validate the proposed rule-of-thumb analysis method for the KF, four KF-based tracking loops are designed with the conditions listed in Table 3 in the simulations. Filters 1 and 4 are suitable for tracking weak GNSS signals and high dynamic GNSS signals, respectively. The performances of Filters 2 and 3 are in the middle between Filters 1 and 4.

Table 3 Parameters for the four designed KF tracking loops
Full size table

Figure 6 depicts the estimated phase jitter of the four filters according to the proposed rule-of-thumb analysis with C/N 0 in the range from 15 to 35 dB-Hz. The level line is the threshold for the four filters according to (23). In the figure, the loss-of-lock thresholds for the four filters are 15.8, 19.0, 22.6, and 26.6 dB-Hz, respectively.

Fig. 6
figure 6

Carrier phase uncertainty σ Δϕ versus C/N 0. The level line is the threshold of 15°. The curves depict the performances of the filters using the rule-of-thumb KF tracking analysis method

Full size image

In order to assess the proposed method, the following Monte Carlo simulations are performed. As an example, the trajectory with the maximum jerk of 10 g/s for Filter 4 is shown in Fig. 7, where the range of C/N 0 is from 15 to 30 dB-Hz. The trajectories for Filters 1, 2, and 3 are similar but of the maximum jerks of 0.01, 0.1, and 1 g/s, respectively. The code loop is a first-order DLL with the bandwidth of 0.8 Hz for all the four tracking loops. The DLL is aided by the KF-based carrier tracking loop. The cos (2δϕ) carrier phase lock detector (Van Dierendonck 1996) is used, and its output is smoothed by a low-pass filter. The simulation is run 100 times for each value of C/N 0 to acquire the probability of tracking. The probability threshold for the filters is set as 50 %. The simulation with 100 runs can acquire the confidence of 90 % statistically (Brown and Hwang 2012), which can make the simulation result comparable to the benchmark of the traditional loops, e.g., Ward (1997, 1998).

Fig. 7
figure 7

Dynamic trajectory with the maximum jerk of 10 g/s for Filter 4 Monte Carlo simulations

Full size image

Figure 8 depicts the probability of tracking for the four designed filters. The level line is the probability threshold of tracking 50 %. As shown in the figure, the filters can always track the GNSS signals with a high C/N 0. However, the filters completely lose their lock of the signals with a very low C/N 0. The rule-of-thumb thresholds in Fig. 6 and the Monte Carlo simulations in Fig. 8 are summarized in Table 4, which shows that the proposed rule-of-thumb analysis for the KF is valid. The rule-of-thumb thresholds are coincided with the simulation thresholds for Filters 2, 3, and 4, but the two thresholds for Filter 1 have a difference as large as 2.1 dB-Hz. The reason is that such weak GNSS signals lead to a very noisy phase lock detector that cannot detect the tracking status successfully (Jin et al. 2013).

Fig. 8
figure 8

Probability of tracking by the Monte Carlo simulations. The level line is the probability of 50 %

Full size image
Table 4 Thresholds of the four filters
Full size table

Conclusions

Both the continuous and the discrete models are presented to investigate the impact of the LOS jerk, the oscillator error, and the measurement error on the performance of the KF-based tracking loop. The derivation of the continuous model proves that the steady KF is equivalent to the PLL, which makes the PLL and the KF comparable. The simulation results show that the oscillator error, the LOS jerk, and the measurement error affect the steady tracking error significantly while the impact of \( {\mathbf{P}}_{0}^{ - } \) on the value of σ Δϕ attenuates quickly. If an accurate oscillator, such as an OCXO, is used, the effect of the oscillator error on the steady value of σ Δϕ is very limited. It is necessary to reduce the measurement noise and/or the receiver dynamics to improve the KF accuracy, which is similar to the requirements of the traditional tracking loop. However, the KF outperforms the equivalent PLL since its time-variant gain matrix is adaptive. The rule-of-thumb analysis method for a KF tracking loop is proposed further. The dynamic stress error and the thermal noise are taken into account of the total carrier phase error in the rule-of-thumb threshold for the KF. The Monte Carlo simulations have validated the rule-of-thumb analysis method.