Introduction

The primary objective of a Global Navigation Satellite System (GNSS) receiver is to synchronize the local signal with the incoming signal of the space vehicle (SV) and to decode the navigation data message to calculate the final position, velocity and time (PVT). In modern GNSS receivers, this process normally involves three logical stages that are acquisition, tracking, and PVT calculation (Parkinson and Spilker 1996). The tracking loop is the key stage that keeps the receiver locked to the incoming Doppler frequency shift and code delay in both static and dynamic situations. In conventional digital receiver designs, the tracking loop consists of a frequency lock loop (FLL), a phase lock loop (PLL) and a delay lock loop (DLL), which are responsible of estimating the carrier frequency, phase and code delay of the received signal. In the previous years, most digital receivers just inherited the lock loop architectures from analog counterparts in which the three loops were designed separately rather than in one integrated loop (Kaplan and Hegarty 2006).

Recently, several studies focusing on the combination of these loops have been presented and compared with the traditional ones (Kaplan and Hegarty 2006; Roncagliolo et al. 2012; Lashley et al. 2009; Abbott and Lillo 2003; Psiaki 2001). Among these solutions, the loop structure known as FLL-assisted PLL/DLL is widely adopted as it can reduce locking time and avoid false locks (Roncagliolo et al. 2012). Other solutions that have been proposed to enhance the tracking robustness are the so-called vector tracking (Lashley et al. 2009; Abbott and Lillo 2003) and Kalman filter (KF)-based tracking (Psiaki 2001). In the vector tracking architectures, the navigation solution is fed back into the tracking loop with a consequential enhancement of the sensitivity and robustness of the tracking part. In the KF-based tracking loop design, both the FLL/PLL and DLL are substituted by a unique KF that is in charge of estimating all the unknown parameters in a coupled manner (Florence and Petovello 2010). The literature demonstrates that KF-based tracking loop outperforms traditional one in multiple aspects. For instance, Won et al. (2009) compared the performance of different designs of tracking loops, demonstrating that KF-based tracking can work in lower carrier-to-noise density ratio (C/N 0) situations and obtain more accurate parameter estimates in comparison with traditional ones. Similarly, in Petovello and Lachapelle (2006), three different KF implementation options have been investigated with particular emphasis given to the carrier phase in the frame of ultra-tight GPS/INS integration. The advantage of extended Kalman filter (EKF)-based tracking in terms of positioning accuracy has been confirmed by comparison with a professional-grade receiver (Tang et al. 2013). Furthermore, the usage of EKF-based tracking has been also analyzed in weak signal situations in Psiaki and Jung (2002) and Ziedan and Garrison (2003).

However, even though a lot of effort has been made in the past to the design of a KF at the level of the tracking stage and many studies have been done to evaluate a posteriori the performance of such new tracking architecture, less attention has been paid to the in-depth theoretical analysis of the KF-based tracking loop itself and KF tuning. In O’Driscoll and Lachapelle (2009), the Kalman system is analyzed by simply comparing its equivalent noise bandwidth with the traditional tracking loop only in steady state. In Salem et al. (2012), an experimental methodology is proposed to decide the equivalent PLL for a given EKF-based tracking loop. Furthermore, Won et al. (2012) offer a more comprehensive and sensible analysis, comparing the discrete time domain expressions of a traditional second-order PLL and KF system model and deriving the mathematical relationships between them. However, they simplify the analysis by considering the KF model with only two states and an approximated observation matrix, which is only suitable in case of low dynamics, short integration time and small frequency error. In addition, the values of initial error covariance, process noise covariance and measurement noise covariance are set in an empirical way.

Therefore, in order to overcome the aforementioned issues, a new approach is proposed to link the KF-based tracking loop and the traditional one. This allows us to derive a detailed mathematical description that gives a better insight into such new tracking loop design and a clear understanding of the benefits gained by the KF-based tracking loop. At first, we derive an equivalent control system model of the Kalman system through its discrete time mathematical expressions. After that, the corresponding transfer function is obtained, so that the dynamic responses in the whole process can be analyzed in a mathematical way. Furthermore, the response to the KF tuning parameters including initial error covariance, process and measurement noise covariance is investigated in details in order to derive a proper set of criteria to optimally drive the tuning of the filter parameters.

In first section, the Kalman-based tracking loop architecture is briefly introduced, and a control system model is derived from the mathematical description of Kalman system. In the next section, the influence of initial settings of the KF is discussed from the perspective of a control system. A reasoned tuning process of noise covariances in dynamic conditions is also obtained and practical implementation criteria are identified. Finally, a summary is provided and conclusions are drawn.

System model

In a KF-based tracking loop, there are generally two fundamental implementation options, named EKF-based and linear KF-based tracking loop. The main difference between these two architectures is in the type of measurements, which in case of EKF are the accumulated output of the correlators in their in-phase (I) and quadrature (Q) components, while in linear KF case, they are the outputs of the discriminators. In order to the subject simple, we focus hereafter on the analysis of the linear KF-based tracking loop only, and the following analysis strategy can also be applicable to EKF.

Linear Kalman-based tracking loop

A linear KF-based tracking model is typically used to estimate the following parameters: code phase error \( \Delta \tau \) (unit: chips), carrier phase error \( \Delta \theta \) (unit: radians), carrier frequency error \( \Delta f \) (unit: Hz) and carrier frequency rate error \( \Delta \alpha \) (unit: Hz/s). The system model (error-state) in discrete time domain can be described as:

$$ \left[ {\begin{array}{*{20}c} {\Delta \tau } \\ {\Delta \theta } \\ {\Delta f} \\ {\Delta \alpha } \\ \end{array} } \right]_{{k + 1}} = \left[ {\begin{array}{*{20}c} 1 & 0 & {\beta T} & {\frac{{\beta T^{2} }}{2}} \\ 0 & 1 & {2\pi T} & {\pi T^{2} } \\ 0 & 0 & 1 & T \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\Delta \tau } \\ {\Delta \theta } \\ {\Delta f} \\ {\Delta \alpha } \\ \end{array} } \right]_{k} + w_{k} $$
(1)

where the coefficient β is used to convert the units of cycles to units of chips, e.g., for GPS L1 β = 1/1,540, T represents the integration time, and W k represents the process noise vector. The subscript \( k \in {\mathbb{N}} \) indicates the discrete time instant.

In this KF-based vector tracking model, the output of two discriminators, i.e., carrier phase discriminator output \( \overline{\delta \varphi } \) and code phase discriminator output \( \overline{\delta \tau } \) are utilized as measurements. Then, the measurement model can be written as:

$$ \left[ {\begin{array}{*{20}c} {\overline{{\delta \varphi }} } \\ {\overline{{\delta \tau }} } \\ \end{array} } \right]_{{k + 1}} = \left[ {\begin{array}{*{20}c} 0 & 1 & { - \pi T} & {\frac{{\pi T^{2} }}{3}} \\ 1 & 0 & { - \frac{{\beta T}}{2}} & {\frac{{\beta T^{2} }}{6}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\Delta \tau } \\ {\Delta \theta } \\ {\Delta f} \\ {\Delta \alpha } \\ \end{array} } \right]_{{k + 1}} + V_{k} $$
(2)

where V k is the measurement noise vector, \( \overline{\delta \varphi } \) and \( \overline{\delta \tau } \) are average values rather than instantaneous values because they are obtained through an integration over time T. Hereafter, this will be termed as “averaging effect.”

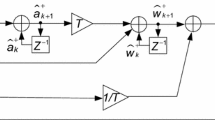
From the system model (1) and measurement model (2), we can observe that the whole system is the combination of two similar systems, namely code phase tracking loop and carrier tracking loop. Without loss of generality, we focus on the carrier phase tracking loop, which can be described as:

$$ \left\{ \begin{gathered} \left[ {\begin{array}{*{20}c} {\Delta \theta } \\ {\Delta f} \\ {\Delta \alpha } \\ \end{array} } \right]_{{k + 1}} = \left[ {\begin{array}{*{20}c} 1 & {2\pi T} & {\pi T^{2} } \\ 0 & 1 & T \\ 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\Delta \theta } \\ {\Delta f} \\ {\Delta \alpha } \\ \end{array} } \right]_{k} + W_{k}^{\prime } \hfill \\ \overline{{\delta \varphi }} _{{k + 1}} \left[ {\begin{array}{*{20}c} 1 & { - \pi T} & {\frac{{\pi T^{2} }}{3}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\Delta \theta } \\ {\Delta f} \\ {\Delta \alpha } \\ \end{array} } \right] + V_{k}^{\prime } \hfill \\ \end{gathered} \right. $$
(3)

and a similar approach can also be used to analyze the code tracking loop. The KF theory indicates that we can get an a posteriori state estimate \( \widehat{X}_{k} \) by incorporating the measurement Z k in the predicted state (a priori state estimate) (Brown and Hwang 1997) as follows:

$$ \widehat{X}_{k + 1} = \widehat{X}_{k + 1}^{ - } + K_{k + 1} \cdot \left( {Z_{k + 1} - H_{k + 1} \cdot \widehat{X}_{k + 1}^{ - } } \right) $$
(4)

where \( \widehat{X}_{k + 1}^{ - } \) is the a priori state estimate obtained by propagating in time the state estimate \( \widehat{X}_{k + 1}^{ - } = A_{k + 1} \cdot \widehat{X}_{k} \), with \( A_{k + 1} \) being state propagation matrix, \( K_{k + 1} \) is the Kalman gain, and \( H_{k + 1} \) is the observation matrix that connects the measurements with the current states.

Comparing (3) and (4) and defining

$$ \begin{gathered} \widehat{X} = \left[ {\Delta \theta ,\;\Delta f,\;\Delta \alpha } \right]_{k}^{T} \hfill \\ Z_{{k + 1}} = {\text{Measurements}}\;{\text{at}}\;{\text{time}}\left( {k + 1} \right) \hfill \\ H_{{k + 1}} = \left[ {\begin{array}{*{20}c} 1 & { - \pi T} & {\frac{{\pi T^{2} }}{3}} \\ \end{array} } \right] \hfill \\ A_{{k + 1}} = \left[ {\begin{array}{*{20}c} 1 & {2\pi T} & {\pi T^{2} } \\ 0 & 1 & T \\ 0 & 0 & 1 \\ \end{array} } \right] \hfill \\ \end{gathered} $$
(5)

the corresponding a posteriori state estimate can be written as:

$$ \left[ \begin{gathered}\Delta \theta \hfill \\\Delta f \hfill \\\Delta \alpha \hfill \\ \end{gathered} \right]_{k + 1} = A_{k} \cdot\,\left[ \begin{gathered}\Delta \theta \hfill \\\Delta f \hfill \\\Delta \alpha \hfill \\ \end{gathered} \right]_{k} + \left[ \begin{gathered} k_{1} \hfill \\ k_{2} \hfill \\ k_{3} \hfill \\ \end{gathered} \right]_{k + 1} \cdot\,\left( {Z_{k + 1} - H_{k + 1} \cdot A_{k + 1} \cdot\,\left[ \begin{gathered}\Delta \theta \hfill \\\Delta f \hfill \\\Delta \alpha \hfill \\ \end{gathered} \right]_{k} } \right) $$
(6)

where \( K_{k + 1} = \left[ {k_{1} ,\;k_{2} ,\;k_{3} } \right]_{k + 1}^{T} ,\;H_{k + 1} \cdot A_{k + 1} = \left[ {1,\;\;\pi T,\;\;\frac{{\pi T^{2} }}{3}} \right] \), and we can denote \( \left( {Z_{k + 1} - H_{k + 1} \cdot A_{k + 1} \cdot\,\left[ \begin{gathered}\Delta \theta \hfill \\\Delta f \hfill \\\Delta \alpha \hfill \\ \end{gathered} \right]_{k} } \right) = e_{z} \) as shown in Fig. 1. It is important to note that in Won et al. (2012), the observation matrix \( H_{k + 1} \) for a second-order system is set approximately as

$$ H_{{k + 1\left( {2{\text{nd}}\;{\text{order}}} \right)}} = [1\;\;0\;] $$
(7)

without considering the influence of frequency error or frequency rate error on the discriminator output. In this sense, expression (7) can only work well for short integration time and small frequency or frequency rate error. In our approach, the influence of averaging effect (Petovello and Lachapelle 2006) in the discriminator has been taken into account as shown in (5). Finally, the KF system can be illustrated as shown in Fig. 1 where the averaging effect has been highlighted.

Fig. 1
figure 1

Block diagram of the Kalman filter tracking loop. z −1 represents one-step delay in the z domain. k 1, k 2, and k 3 are Kalman gains

Full size image

Equivalent control system

Based on the diagram depicted in Fig. 1, we can derive the corresponding equivalent control system model to facilitate the analysis of KF-based tracking loop. It is known that an integrator in the continuous time domain

$$ \dot{u}\left( t \right) = f\left( t \right) $$
(8)

and sampled every \( T \) seconds can be expressed as

$$ u\left( {\left( {k + 1} \right)T} \right) = u\left( {kT} \right) + \int_{kT}^{{\left( {k + 1} \right)T}} {f\left( t \right){\text{d}}t} $$
(9)

A mathematical discrete approximation can be applied to (9) so as to obtain

$$ u\left( {k + 1} \right) \approx u\left( k \right) + f\left( k \right) \cdot T $$
(10)

whose corresponding transfer function in the z domain is

$$ H\left( z \right) = \frac{{Tz^{ - 1} }}{{1 - z^{ - 1} }} $$
(11)

Finally, the equivalent control system of the KF represented in Fig. 1 is obtained as shown in Fig. 2 by substituting the Laplace operator 1/s to the z-transfer function (11).

Fig. 2
figure 2

System of the Kalman filter tracking loop in the continuous time domain

Full size image

According to Mason’s gain formula (MGF) (Newnes 1998), the following transfer function in the s domain can be easily derived for the system in Fig. 2,

$$ \frac{{\varphi_{\text{out}}^{ - } \left( s \right)}}{{\varphi_{\text{in}} \left( s \right)}} = \frac{{\left( {\frac{{T\pi k_{3} }}{3} + \pi k_{2} + \frac{{k_{1} }}{T}} \right)s^{2} + \left( {2\pi k_{3} + \frac{{2\pi k_{2} }}{T}} \right)s + \frac{{2\pi k_{3} }}{T}}}{{s^{3} + \left( {\frac{{T\pi k_{3} }}{3} + \pi k_{2} + \frac{{k_{1} }}{T}} \right)s^{2} + \left( {2\pi k_{3} + \frac{{2\pi k_{2} }}{T}} \right)s + \frac{{2\pi k_{3} }}{T}}} $$
(12)

which conforms to the expression of optimal third-order phase lock loop in Jaffe and Rechtin (1955). According to Brown and Hwang (1997), the corresponding noise bandwidth can be computed as

$$ B_{n} = \frac{{m_{1} \cdot m_{2}^{2} + m_{1}^{2} - m_{2} \cdot m_{0} }}{{4\left( {m_{1} \cdot m_{2} - m_{0} } \right)}} = \frac{{m_{2} }}{4} + \frac{{m_{1}^{2} }}{{4\left( {m_{1} \cdot m_{2} - m_{0} } \right)}} $$
(13)

where

$$ \left\{ \begin{gathered} m_{0} = \frac{{2\pi k_{3} }}{T} \hfill \\ m_{1} = 2\pi k_{3} + \frac{{2\pi k_{2} }}{T} \hfill \\ m_{2} = \frac{{T\pi k_{3} }}{3} + \pi k_{2} + \frac{{k_{1} }}{T} \hfill \\ \end{gathered} \right. $$
(14)

It can be concluded that the equivalent noise bandwidth of KF B n is actually decided by the Kalman gain vector K k and integration time T. Simply put, it evolves over time with K k .

Reasoned criteria to tune the Kalman filter

When using a KF architecture, there are three covariance matrices that have to be tuned in order to achieve proper performances, namely the initial estimate error covariance P ini, the process noise covariance Q and the measurement noise covariance R. Once P ini, Q and R are set, the Kalman gain vector K k can be determined as:

$$ \begin{gathered} P_{k}^{ - } = A_{k} P_{k - 1} A_{k}^{\rm T} + Q_{k} \hfill \\ K_{k} = P_{k}^{ - } H_{k}^{T} \left( {H_{k} P_{k}^{ - } H_{k}^{T} + R_{k} } \right)^{ - 1} \hfill \\ P_{k} = \left( {I - K_{k} H_{k} } \right)P_{k}^{ - } \hfill \\ \end{gathered} $$
(15)

where Q k is the discrete time equivalent of Q, and R k represents the time evolution of R. An alternative expression of (15) can be written as (Stephens and Thomas 1995)

$$ \begin{gathered} P_{k}^{ - 1} = \left( {A_{k} P_{k - 1} A_{k}^{T} + Q_{k} } \right)^{ - 1} + \left( {H_{k}^{T} H_{k} } \right)/R_{k} \hfill \\ K_{k} = \left( {P_{k} H_{k}^{T} } \right)/R_{k} \hfill \\ \end{gathered} $$
(16)

For the state system considered in (3), the measurement covariance matrix R k reduces to a scalar, which can be computed as (Parkinson and Spilker 1996)

$$ R_{k} = \sigma_{{\Delta \varphi }}^{2} = \frac{1}{{2T \cdot \left( {C/N_{0} } \right)_{k} }}\left( {1 + \frac{1}{{2T \cdot \left( {C/N_{0} } \right)_{k} }}} \right)\;\;\;({\text{rad}}^{2} ) $$
(17)

Considering the general cases in the following simulations, C/N 0 is set equal to 38 dBHz as a typical value. Meanwhile, the value of Q k can be expressed as follows (Brown and Hwang 1997):

$$ Q_{k} \approx \frac{1}{2}\left[ {A_{k} \cdot Q + Q \cdot A_{k}^{T} } \right] \cdot T $$
(18)

However, the main practical issue is the setting of Q, since a complete knowledge of the noise input is not generally available. For this reason, the influence of Q will be analyzed from a different perspective and will be presented in section “Steady-state segment.” On the other hand, the setting of the initial phase error covariance P ini is strongly related to the accuracy of the prior information including carrier phase and frequency estimates provided by the acquisition stage. If given an accurate prior information, P ini could be set quite small as, for instance equal to Q k and the tracking will be in lock nearly with no transient (Stephens and Thomas 1995).

Generally, during the very initial stage of the tracking, the uncertainty about the frequency and phase estimates necessitates a much larger P ini than Q k to leave enough space for state corrections. Eventually, in terms of error covariance matrix P k and Kalman gain K k , the KF system will converge progressively to a stable solution. The time period consumed by the filter to reach a steady state is called transition segment. From that moment on, the filter works in steady segment. In the following sections, we will investigate the effects of KF’s parameters including P, Q and R in both segments.

Criteria based on the transition segment

As mentioned before, in case of non-perfect a priori initialization of the tracking loop, the transition segment should allow the system to correct relatively large estimates errors. Tausworthe (1971) proposed a second/third-order hybrid approach that can be adopted in this temporal segment. In principle, the initial second-order loop is exploited for a fast refinement of the parameter estimates with “wide bandwidth” during the transient time, and then, the system switches to a “narrow bandwidth” third-order loop in the steady segment.

In the case of tracking-based on the KF approach, at the first processing step, we set the initial error covariance as

$$ P_{{{\text{ini}}}} = \left[ {\begin{array}{*{20}c} {P_{{i,1}} } & {} & {} \\ {} & {P_{{i,2}} } & {} \\ {} & {} & {P_{{i,3}} } \\ \end{array} } \right] $$
(19)

where P i,1, P i,2, P i,3 indicate the initial error covariance of the state parameters within the system (3). Typically, we have:

$$ \left[ {P_{\text{ini}} } \right]_{{\left( {jj} \right)}} \gg \left[ {Q_{1} } \right]_{{\left( {jj} \right)}} $$
(20)

which means that Q k can be ignored at the beginning. So, for the first step, by using (5) and (15), the initial estimate error covariance P can be simplified as:

$$ \begin{aligned} P_{1}^{ - } & = A_{1} \cdot P_{{ini}} \cdot A_{1}^{T} + Q_{1} \\ & \approx A_{1} \cdot P_{{ini}} \cdot A_{1}^{T} \\ & = \left[ {\begin{array}{*{20}c} {P_{{i,1}} + 4\pi ^{2} T^{2} P_{{1,3}} } & {2\pi TP_{{i,2}} + \pi T^{3} P_{{i,3}} } & {\pi T^{2} P_{{i,3}} } \\ {2\pi TP_{{i,2}} + \pi T^{3} P_{{i,3}} } & {P_{{i,2}} + T^{2} P_{{i,3}} } & {TP_{{i,3}} } \\ {\pi T^{2} P_{{i,3}} } & {TP_{{i,3}} } & {P_{{i,3}} } \\ \end{array} } \right] \\ \end{aligned} $$
(21)

and

$$ H_{1} P_{1}^{ - } H_{1}^{T} = P_{i,1} + \pi^{2} T^{2} P_{i,2} + \frac{{\pi^{2} T^{4} P_{i,3} }}{9} $$
(22)

Then the KF gain can be stated as

$$ \begin{aligned} K_{1} & = P_{1}^{ - } H_{1}^{T} \left( {H_{1} P_{1}^{ - } H_{1}^{T} + R_{1} } \right)^{{ - 1}} \\ & = \left[ {\begin{array}{*{20}c} {k_{1} } \\ {k_{2} } \\ {k_{3} } \\ \end{array} } \right]_{1} \\ & = \left[ {\begin{array}{*{20}c} {P_{{i,1}} + 2\pi ^{2} T^{2} P_{{i,2}} + \frac{{\pi ^{2} T^{4} }}{3}P_{{i,3}} } \\ {\pi TP_{{i,2}} + \frac{{\pi T^{3} }}{3}P_{{i,3}} } \\ {\frac{{\pi T^{2} }}{3}P_{{i,3}} } \\ \end{array} } \right] \cdot \frac{1}{{P_{{i,1}} + 2\pi ^{2} T^{2} P_{{i,2}} + \frac{{\pi ^{2} T^{4} P_{{i,3}} }}{9} + R_{1} }} \\ \end{aligned} $$
(23)

Based on (23), the setting of P i,1 and P i,3 can be derived first as follows.

Setting of P i,1 and P i,3

In order to make the system (3) equivalent to a second-order loop, k 3 in (12) should be close to zero during the transition segment that can be achieved through an appropriate selection of P i,1 and P i,3. The choice of P i,2 will be analyzed based on another set of considerations in the following subsection.

In order to guarantee k 3 = 0 and keep a setting of P ini following its physical meaning (Brown and Hwang1997), from (23) and (17), we can set

$$ P_{i,1} = 1 \gg R_{k} $$
(24)
$$ P_{i,3} \ll \frac{1}{{T^{2} }} $$
(25)

We set P i,3 equal to 10 for simplicity so that

$$ \begin{gathered} \;\frac{{\pi T^{2} }}{3}P_{i,3} \ll 1 \hfill \\ P_{i,1} + \pi^{2} T^{2} P_{i,2} + \frac{{\pi^{2} T^{4} P_{i,3} }}{9} + R_{k} > 1 \hfill \\ \;\frac{{\pi T^{2} }}{3}P_{i,3} \ll P_{i,1} + \pi^{2} T^{2} P_{i,2} + \frac{{\pi^{2} T^{4} P_{i,3} }}{9} + R_{k} \hfill \\ \end{gathered} $$
(26)

Therefore, at the beginning,

$$ k_{3} = \;\frac{{\frac{{\pi T^{2} }}{3}P_{i,3} }}{{P_{i,1} + \pi^{2} T^{2} P_{i,2} + \frac{{\pi^{2} T^{4} P_{i,3} }}{9} + R_{k} }} \approx 0 $$
(27)

As a consequence, expression (12) turns to a second-order loop with s domain transfer function

$$ \frac{{\varphi_{\text{out}}^{ - } \left( s \right)}}{{\varphi_{\text{in}} \left( s \right)}} = \frac{{\left( {\pi k_{2} + \frac{{k_{1} }}{T}} \right)s + \left( {\frac{{2\pi k_{2} }}{T}} \right)}}{{s^{2} + \left( {\pi k_{2} + \frac{{k_{1} }}{T}} \right)s + \left( {\frac{{2\pi k_{2} }}{T}} \right)}} $$
(28)

and the corresponding second-order system can be described as

$$ \left\{ \begin{aligned} \left[ {\begin{array}{*{20}c} {\Delta \theta } \\ {\Delta f} \\ \end{array} } \right]_{{k + 1}} & = \left[ {\begin{array}{*{20}c} 1 & {2\pi T} \\ 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\Delta \theta } \\ {\Delta f} \\ \end{array} } \right]_{k} + W_{{2k}}^{\prime } \\ \overline{{\delta \varphi }} _{{k + 1}} & = \left[ {\begin{array}{*{20}c} 1 & {} \\ \end{array} - \pi T} \right]\left[ {\begin{array}{*{20}c} {\Delta \theta } \\ {\Delta f} \\ \end{array} } \right]_{{k + 1}} + V_{{2k}}^{\prime } \\ \end{aligned} \right. $$
(29)

Furthermore, the process noise error Q k can be ignored at the beginning due to (20) and consequently (16) changes to (Patapoutian 1999)

$$ \begin{gathered} P_{k}^{ - 1} = A_{k}^{ - T} P_{k - 1}^{ - 1} A_{k}^{ - 1} + \left( {H_{k}^{T} H_{k} } \right)/R_{k} \hfill \\ \;\;\;\;\; = \left( {A_{k}^{ - T} } \right)^{k} P_{ini}^{ - 1} \left( {A_{k}^{ - 1} } \right)^{k} + \frac{{\sum\limits_{j = 0}^{k} {\left( {A_{k}^{ - T} } \right)^{j} H_{k}^{T} H_{k} A_{k}^{ - j} } }}{{R_{k} }} \hfill \\ K_{k} = \left( {P_{k} H_{k}^{T} } \right)/R_{k} \hfill \\ \end{gathered} $$
(30)

From (30), it can be concluded that once the system is determined, and then, in the transition segment, the Kalman gain is actually decided by the time evolution of P ini. However, it is hard to infer the relationship between Kalman gain K k and initial error variance P ini directly by inspection of (30). For this reason, numerical evaluations of (30) are useful at this point to get insight into the KF evolution during the initial steps, in particular into the evolution of K k as a function of the initialization P ini.

In the following experiments, the simulation parameters are set as: C/N 0 = 38 dB-Hz, T = 0.001 s. Then, from (17), it can be computed that \( R_{k} = 0.0855\quad \forall {\mkern 1mu} k \in {\mathbb{N}} \). Based on (24) and (25), it is possible to observe the time evolution of the Kalman gain parameters k 1 and k 2 as shown in Fig. 3.

Fig. 3
figure 3

Illustration of Eq. (30) by numerical evaluation

Full size image

Setting of P i,2

With respect to the choice of P i,2, several factors have to be considered, namely the potential ambiguity problem of the discriminator output, the response of the tracking loop to the system dynamics, the stability and the true noise bandwidth. They will be discussed in the following part.

Factor 1: the potential ambiguity problem of discriminator output

The design of PLL follows a linear model, which implies that no issues of nonlinearity or ambiguity should occur over the full operating range (Stephens and Thomas 1995). In order to guarantee this assumption, at the very beginning of a KF-based tracking loop, we also have to deal with the potential ambiguity problem of the discriminator output in the case of a large initial frequency error. The initial steps of the KF system are illustrated in Fig. 4, where

$$ x_{T0} = \left[ \begin{gathered}\Delta \theta_{0} \hfill \\\Delta f_{0} \hfill \\ \end{gathered} \right] $$
(31)

is the assumed true initial state vector, containing the true values of initial phase error \( \Delta \theta_{0} \), a value in the range \( ( - \pi ,\;\pi ) \) and frequency error \( \Delta f_{0} \). Without any a priori accurate information, the initial state vector is traditionally set to zero:

$$ \widehat{x}_{0} = \left[ \begin{gathered} 0 \hfill \\ 0 \hfill \\ \end{gathered} \right] $$
(32)
Fig. 4
figure 4

Initial steps for KF system

Full size image

Without considering the influence of noise, due to the pull-in range of a two-quadrant phase discriminator which is \( \left( { - \pi /2,\pi /2} \right) \), the first phase measurement error obtained by a discriminator can be expressed as:

$$ Z_{1} =\Delta \theta_{0} + \pi\Delta f_{0} T \pm n\pi $$
(33)

where nπ represents the potential ambiguity and n is an integer number. In the first measurement update, we will have

$$ \widehat{x}_{1}^{ - } = \left[ {\begin{array}{*{20}c} {\Delta \widehat{\theta }_{1}^{ - } } \\ {\Delta \widehat{f}_{1}^{ - } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & {2\pi T} \\ 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {k_{1} } \\ {k_{2} } \\ \end{array} } \right]_{1} Z_{1} $$
(34)

and then, both \( \Delta \widehat{\theta }_{1}^{ - } \) and \( \Delta \widehat{f}_{1}^{ - } \) will be used to update the local NCO including phase and phase rate update (Tang et al. 2013).

As shown in (33), the discriminator output Z may involve ambiguity issues due to the uncertainty of \( \Delta \theta_{0} \) and \( \Delta f_{0} \). Therefore, the first measurement update can be used to solve the aforementioned problem by the following two considerations:

  1. 1.

    From (33), the initial uncertain phase error \( \Delta \theta_{0} \) should be removed from the discriminator output, and then only \( \Delta f_{0} \) needs to be considered in the next step in order to guarantee nonexistence of ambiguity in the following discriminator outputs. For this reason, in the first measurement update, k 1 should be equal to 1 as shown in (35).

  2. 2.

    In the first measurement update, ideally the value of k 2 should be close to zero in (34) to make sure the initial large frequency error will not be enlarged due to the uncertainty of Z 1. Otherwise, the enlarged frequency error will increase the possibility of false frequency lock, as shown in Fig. 5 (Stensby 2002) where a big k 2 Z 1 can lead to a wrong estimation of the frequency.

    Fig. 5
    figure 5

    Result of the first experiment (large initial frequency error equal to 150 Hz, C/N 0 = 38 dB-Hz, T = 1 ms)

    Full size image

Hence, in (34), the Kalman gain in the first step can be set as

$$ \left[ \begin{gathered} k_{1} \hfill \\ k_{2} \hfill \\ \end{gathered} \right]_{1} = \left[ \begin{gathered} 1 \hfill \\ 0 \hfill \\ \end{gathered} \right] $$
(35)

then,

$$ \left[ {\begin{array}{*{20}c} {k_{1} } \\ {k_{2} } \\ \end{array} } \right]_{1} Z_{1} = \left[ {\mathop {\Delta \theta _{0} + \pi \Delta f_{0} T \pm n\pi }\limits_{0} } \right] $$
(36)

After the first NCO update, if \( \Delta f_{0} \) can be considered approximately constant in two consecutive epochs, the true value of state vector becomes

$$ x_{T1} = \left[ \begin{gathered} \pi\Delta f_{0} T \mp n\pi \hfill \\\Delta f_{0} \hfill \\ \end{gathered} \right] $$
(37)

In the following step, the measurement can be expressed as

$$ Z_{2} = 2\pi\Delta f_{0} T \pm n\pi $$
(38)

in order to remove the potential ambiguity problem in (38), \( 2\pi\Delta f_{0} T \) should be located within the pull-in range of the phase discriminator:

$$ - \frac{\pi }{2} \,\le\, 2\pi\Delta f_{0} T \,\le \,\frac{\pi }{2} $$
(39)

Given T = 1 ms, then

$$ - 250\;{\text{Hz}}\, \le\,\Delta f_{0} \,\le \,250\;{\text{Hz}} $$
(40)

upon condition (40), the value of n in (37) and (38) is equal to zero. Then, the true value of the state vector and the discriminator output can be rewritten as

$$ \left\{ \begin{gathered} x_{T1} = \left[ \begin{gathered} \pi\Delta f_{0} T \hfill \\\Delta f_{0} \hfill \\ \end{gathered} \right] \hfill \\ Z_{2} = 2\pi\Delta f_{0} T \hfill \\ \end{gathered} \right. $$
(41)

In addition, the Kalman gain K k is always positive during the whole operating process

$$ K_{k} > 0 $$
(42)

which can guarantee that starting from the second step, the NCO frequency update (k 2 Z) can eventually decrease the frequency error without any ambiguity involved. In presence of noise, considering 2σ bound, the condition (40) can be changed to

$$ \left| {\Delta f_{0} } \right| < \left( {250 - \frac{{\sigma _{{\Delta \varphi }} }}{{\pi T}}} \right)\;{\text{Hz}} $$
(43)

where \( \sigma_{{\Delta \varphi }} \) can be computed in (17).

With the proper setting as shown in (35), it can be concluded that the KF system can avoid the potential risk of ambiguity in the estimation of the carrier frequency from the second step onward, since the first step is used to remove the potential ambiguity problem of Z 1. From this perspective, based on Fig. 3,

$$ P_{i,1} = 1\;{\text{and}}\;P_{i,2} \le 1.4e3 $$
(44)

can approximately satisfy the requirement, and \( P_{i,1} = 1\;{\text{and}}\;P_{i,2} = 1.4e3 \) can be treated as the boundary value in this condition.

Factor 2: the response of the KF loop to a ramp input

As mentioned before, the main objective of the transition segment is to refine parameters estimates in a fast manner. According to Kaplan and Hegarty (2006) and Jaffe and Rechtin (1955), the optimal transfer function of a second-order system concerning PLL is

$$ \varPhi \left( s \right) = \frac{{2\zeta w_{n} s + w_{n}^{2} }}{{s^{2} + 2\zeta w_{n} s + w_{n}^{2} }} $$
(45)

Comparing (28) and (45), it can be obtained that

$$ \left\{ \begin{gathered} w_{n}^{2} = \frac{{2\pi k_{2} }}{T} \hfill \\ 2\zeta w_{n} = \pi k_{2} + \frac{{k_{1} }}{T} \hfill \\ \end{gathered} \right. $$
(46)

and the corresponding noise bandwidth can be computed as

$$ \begin{aligned} B_{n} & = \frac{{w_{n} }}{2}\left( {\zeta + \frac{1}{{4\zeta }}} \right) \\ & = \frac{{k_{1} k_{2} \pi }}{{4T}} + \frac{{\pi k_{2} }}{{2\left( {T\pi k_{2} + k_{1} } \right)}} \\ \end{aligned} $$
(47)

which is plotted in Fig. 6

Fig. 6
figure 6

Equivalent noise bandwidth and damping ratio

Full size image

In order to analyze the loop response in dynamic conditions, suppose there is a ramp input

$$ \varphi_{\text{ramp}} =\Delta f_{0} \cdot t $$
(48)

Then, the output of the system (28) in s domain will be

$$ \begin{aligned} \varphi _{{{\text{out}}}}^{ - } \left( s \right) & = \frac{{2\zeta w_{n} s + w_{n}^{2} }}{{s^{2} + 2\zeta w_{n} s + w_{n}^{2} }} \cdot \frac{{\Delta f_{0} }}{{s^{2} }} \\ & = \frac{{\Delta f_{0} }}{{s^{2} }} - \frac{{\Delta f_{0} }}{{s^{2} + 2\zeta w_{n} s + w_{n}^{2} }} \\ \end{aligned} $$
(49)

In the time domain, the output can be expressed as

$$ \varphi_{\text{out}}^{ - } \left( t \right) =\Delta f_{0} t - \frac{{\Delta f_{0} }}{{w_{n} \sqrt {1 - \zeta^{2} } }}e^{{ - \zeta w_{n} t}} \sin \left( {w_{n} \sqrt {1 - \zeta^{2} } t} \right) $$
(50)

In (50), once the damping ratio ζ is fixed, the bigger the w n , the faster the output of the system will catch up with the ramp input signal, which also means the system can correct the frequency error more quickly. From (46), it can observed that w n is directly proportional to k 2; therefore, the bigger we choose k 2 the shorter the response of the whole system. In Fig. 3, we have plotted different values of k 2 with different P i,2. After this analysis and by keeping in mind the upper bound expressed in (43) to avoid frequency ambiguities as stated in (44), it appears convenient to select the highest possible P i,2 to speed up the convergence of the KF. Therefore, in the context of transition segment, the best choice can be

$$ P_{i,1} = 1,\quad P_{i,2} = 1.4e3 $$
(51)

Otherwise, in case of large initial frequency error, if w n is too small, such as when \( P_{i,1} = 1\;{\text{and}}\;P_{i,2} = 1e2, \) the system will enter into a false frequency lock (Stensby 2002) as shown in Fig. 5 (triangle-marked line). However, if the initial frequency error is small such as 20 Hz, a correspondingly small w n can also work as shown in Fig. 7. Generally, since we have no idea in real situations how big the frequency error is, a good trade-off that has been proved through several experiments is to follow the criteria stated in (51), which can make the system capable of correcting frequency errors in the range of the one expressed in (43) when T = 0.001 s.

Fig. 7
figure 7

Result of the second experiment (small initial frequency error equal to 20 Hz, C/N 0 = 38 dBHz, T = 1 ms)

Full size image

Since w n is proportional to B n , which represents the amount of noise within the loop. Therefore, the values of P i,1 and P i,2 in (51) must be validated with an analysis of the performance in the corresponding noise equivalent bandwidth as shown in Factor 3 analysis.

Factor 3: stability and true noise bandwidth

According to Stephens and Thomas (1995), a large product B n T can possibly make the loop diverge from the expected behavior or cause instability. In order to prevent such issues, the choice in (51) has to be evaluated both in terms of stability and true noise bandwidth. Based on (11), (28) and (46), the second-order model in the discrete time domain can be expressed as

$$ \varPhi \left( Z \right) = \frac{{2\zeta w_{n} TZ + w_{n}^{2} T^{2} - 2\zeta w_{n} T}}{{Z^{2} + \left( {2\zeta w_{n} T - 2} \right)Z + 1 - 2\zeta w_{n} T + w_{n}^{2} T^{2} }} $$
(52)

As shown in Fig. 5, the first ten steps are very critical in terms of frequency error correction, additionally with the previous conclusion stated in Factor 1 analysis that the system really starts working from step 2, we can mainly evaluate the average performance in the two initial parts based on the different equivalent noise bandwidth as shown in Fig. 6, one part is from step 2 to 6, and a second part is from 6 to 11. In the first part (step 2–6), the average nominal noise bandwidth is \( B_{{{\text{na}}1}} = 300\;{\text{Hz}} \), and the damping ratio is \( \zeta = 0.87 \) according to (52). The evaluation result is shown in Fig. 8. Similarly, in the second part (step 6–11), the average nominal noise bandwidth is \( B_{{{\text{na}}2}} = 169\;{\text{Hz}} \), and damping ratio is \( \zeta = 0.83 \). The evaluation result is shown in Fig. 9.

Fig. 8
figure 8

Bode plot of both continuous and discrete systems, and pole-zero plot of discrete system (First part)

Full size image
Fig. 9
figure 9

Bode plot of both continuous and discrete systems, and pole-zero plot of discrete system (Second part)

Full size image

As Figs. 8 and 9 show, there is a minor difference between the real noise bandwidth and input one, which implies the coherence between real noise bandwidth and the input “loop parameter bandwidth B n ”. Meanwhile, the system always keeps stable, both for the first and second part (Thomas 1989). This means the solution in (51) can be a convenient choice for the transition segment in case T = 0.001 s and the acceptable initial frequency error within the range in (43).

Summary of the tuning criteria based on the performance in the transient segment

In order to summarize the above considerations referred to the transient segment of the KF tracking process, the suggested criteria for the setting of P ini in the absence of accurate prior information can be stated as follows:

  1. 1.

    Independently of the uncertainty of the initial phase error, the acceptable initial frequency error is expressed in (43) when a two-quadrant phase discriminator is adopted.

  2. 2.

    \( P_{i,1} \gg R_{k} \) where R k can be computed using (17).

  3. 3.

    \( P_{i,3} \ll P_{i,1} /T^{2} \) where Tis the integration time.

  4. 4.

    P i,2 depends on the evaluation of the system in terms of factor 1, 2, and 3, respectively. When T = 1 ms, then \( P_{i,2} /P_{i,1} \le 1.4e3 \), and without any accurate prior information, the choice \( P_{i,2} /P_{i,1} = 1.4e3 \) represents the best trade-off in terms of stability, rapidity of convergence and the avoidance of carrier phase ambiguity.

Steady-state segment

The previous discussion proved that during the transient segment, the influence of coefficient k 3 can be ignored and KF-based loop (3) is comparable to a second-order traditional PLL if properly initialized. However, as k 3 increases with the time, as shown in Fig. 10, the role of k 3 can no longer be ignored, which means that the system transitions fast to a third-order system termed steady-state segment. In steady state, based on (16), the values of the error variance P s and Kalman gain K s can be computed from the solution of the following system of equations:

$$ \left\{ \begin{gathered} P_{s}^{ - 1} = \left( {A_{k} P_{s} A_{k}^{T} + Q_{k} } \right)^{ - 1} + \left( {H_{k}^{T} H_{k} } \right)/R_{k} \hfill \\ K_{s} = \left( {P_{s} H_{k}^{T} } \right)/R_{k} \hfill \\ \end{gathered} \right. $$
(53)

where A k and H k are fixed once the KF system is given. R k can be computed using (17) and Q k can be computed as in (18). Both depend on C/N 0. Therefore, once the system is determined, the loop behavior in steady state is substantially driven by the values assigned to the entries of the process noise error covariance matrix Q of (18) and R k . Indeed, to some degree, K s in (53) is proportional to Q and inversely proportional to R k .

Fig. 10
figure 10

Value of Kalman gain K and corresponding equivalent noise bandwidth

Full size image

As far as the setting of Q is concerned, it can be computed following the definition of the KF model, where Q(1,1) and Q(2,2) can be obtained from the involved clock model (Petovello and Lachapelle 2006; Brown and Hwang 1997). On the other side, from the perspective of a control system as shown in Figs. 1, 2, the value of Kalman gain K is related to the variance of corresponding parameter estimates and is approximately proportional to Q in steady state. Hereafter, we mainly analyze the tuning of Q from the perspective of the equivalent control system. Since in our experiments the simulated clock error is very small, we have given the initial approximate value of Q as

$$ Q = \left[ {\begin{array}{*{20}c} {10^{{ - 3}} } & {} & {} \\ {} & {10^{{ - 2}} } & {} \\ {} & {} & 1 \\ \end{array} } \right] $$
(54)

From (18), Q k can be computed as:

$$ \begin{aligned} Q_{k} & \approx \frac{1}{2}\left[ {A_{k} \cdot Q + Q \cdot A_{k}^{T} } \right] \cdot T \\ & = \left[ {\begin{array}{*{20}c} {10^{{ - 6}} } & {3.14 \times 10^{{ - 8}} } & {1.57 \times 10^{{ - 9}} } \\ {3.14 \times 10^{{ - 8}} } & {10^{{ - 5}} } & {5 \times 10^{{ - 7}} } \\ {1.57 \times 10^{{ - 9}} } & {5 \times 10^{{ - 7}} } & {10^{{ - 3}} } \\ \end{array} } \right] \\ \end{aligned} $$
(55)

With Q k and R k ready, we can start the advanced analysis of the system in different conditions as follows.

Loop response evolution in dynamic conditions

We now present a set of numerical results showing the influence of the choice of Q according to the evolution of KF-based loop response in dynamics conditions. In PLL applications, the phase input is usually modeled in the form

$$ \theta \left( t \right) = \left( {a + bt + ct^{2} + \cdots } \right)u\left( t \right) $$
(56)

where a, b and c are constants and u(t) is the unit step function. If the highest order of PLL is n, then the PLL can track n terms of (56) with zero steady-state phase error.

Case-study 1: Doppler frequency variations at constant rate

In the first experiment, the parameters are set as follows: (C/N 0)dB = 38 dB-Hz, T = 0.001 s. f error,ini = 150 Hz, and Doppler rate \( v_{f} = 100\;{\text{Hz}}/{\text{s}} \). Based on the analysis in section “Criteria based on the transition segment,” we can set P ini \( P_{\text{ini}} \) as

$$ P_{{{\text{ini}}}} = \left[ {\begin{array}{*{20}c} 1 & {} & {} \\ {} & {1.4e3} & {} \\ {} & {} & {10} \\ \end{array} } \right] $$
(57)

During the transition segment, the system follows the performance of a second-order system (29), with

$$ P_{{{\text{ini,2order}}}} = \left[ {\begin{array}{*{20}c} 1 & {} \\ {} & {1.4e3} \\ \end{array} } \right],\;Q_{{{\text{2order}}}} = \left[ {\begin{array}{*{20}c} {10^{{ - 3}} } & {} \\ {} & {10^{{ - 2}} } \\ \end{array} } \right] $$
(58)

From Figs. 10, 11, we can see that during the transition segment a third-order (3) and a second-order (29) systems have the same performance. However, when the KF enters into the steady segment, the role of k 3 is no longer negligible and the advantage of the third-order tracking loop becomes evident, since it can track a signal with a frequency rate equal to 100 Hz/s while the estimate from the second-order system deviates from the correct value. In steady state, for third-order system, the solution of (53) is:

$$ K_{s} = \left[ {\begin{array}{*{20}c} {0.0189} \\ {0.0276} \\ {0.1071} \\ \end{array} } \right],\;P_{s} = \left[ {\begin{array}{*{20}c} {0.0016} & {0.0024} & {0.0092} \\ {0.0024} & {0.0057} & {0.0279} \\ {0.0092} & {0.0279} & {0.2567} \\ \end{array} } \right] $$
(59)
Fig. 11
figure 11

Error of frequency estimate

Full size image

In conclusion, if the value of P ini satisfies (27) and is initialized properly, then we can state that the KF-based PLL is a combination of two different models: a second-order model is used within the transition segment in order to speed up lock of carrier frequency, then the KF eventually transitions to a third-order model to make the system more robust to the dynamic stress.

Case-study 2: variable Doppler rate

It is well known that in high dynamic situations where the frequency rate changes quickly, the loop noise bandwidth (13) has to be enlarged correspondingly to be able to track the signal. However, at the same time, we may have to keep k 1 and k 2 small to guarantee the low variance of phase and frequency estimates. From this perspective, based on (13) and (14), we can achieve the goal only by increasing Q(3,3) without degrading the accuracy of phase and frequency estimates significantly. If we set the parameters as:

$$ \begin{gathered} P_{{{\text{ini}}}} = \left[ {\begin{array}{*{20}c} 1 & {} & {} \\ {} & {1.4e3} & {} \\ {} & {} & {10} \\ \end{array} } \right],\;\;Q = \left[ {\begin{array}{*{20}c} {10^{{ - 3}} } & {} & {} \\ {} & {10^{{ - 2}} } & {} \\ {} & {} & {Q\left( {3,3} \right)} \\ \end{array} } \right] \hfill \\ T = 0.001\;{\text{s}},\;\left( {C/N_{0} } \right)_{{{\text{dB}}}} = 38\;{\text{dBHz}} \hfill \\ \end{gathered} $$
(60)

we can get the results reported in Fig. 12 about the influence of Q(3,3) on the value of Kalman gain and equivalent noise bandwidth. The figure shows that the equivalent noise bandwidth is enlarged when Q(3,3) increases. On the contrary, k 1 and k 2 do not change in a significant way.

Fig. 12
figure 12

Influence of Q(3,3)

Full size image

In order to observe the time evolution of the loop response with the parameters reported in (60), we feed the loop with a carrier signal with f dop = 40sin(2πt) Hz and f error,ini = 100 Hz. Two different values of Q(3,3) are considered in Fig. 13.

Fig. 13
figure 13

Comparison of the performance with two different Q(3,3)

Full size image

Figure 13 shows that when Q(3,3) = 1, the system cannot work correctly in high-order dynamic case, but it can track the signal correctly for a short amount of time at the beginning. On the other hand, when Q(3,3) is increased up to 103, the KF system is able to work in a proper way even though from A to B, the frequency rate is nearly 160 Hz/s, and there are “sudden” changes in point A and B.

In conclusion, in high dynamic situations, Q(1,1), Q(2,2) are set small in order to maintain the low variance of phase and frequency estimate, while Q(3,3) is enlarged to keep the loop capable of tracking signals in high dynamics. Actually, at the same time, the drawback is that the variance of frequency rate error estimate \( \Delta \alpha \) will increase, but this fact will not affect the accuracy of phase and frequency estimate that we are concerned with normally.

Summary of the tuning criteria based on the performance in the steady-state segment

The performance of the system mainly depends on the value of Q and R in steady state. Intuitively, Q and R could be computed following the definition of KF system: For instance, R can be computed by (17) and the values of Q(1,1) and Q(2,2) can also be obtained through the clock model, while the value of Q(3,3) depends on the knowledge of frequency rate. Given the value of R k computed by (17), the tuning criteria for Q can also be given from the perspective of a control model. Briefly Q(1,1) and Q(2,2) are set small values to guarantee the small variance of phase and frequency estimates, and Q(3,3) can be enlarged to adapt the system to high dynamics.

Summary and future works

We have analyzed the KF-based tracking loop in depth. First, the equivalent control model is derived based on the mathematical expression of Kalman system with the main focus on the carrier tracking only. Based on the control model, the influence of initial error variance matrix P ini, process noise covariance Q, and measurement noise covariance R is analyzed. Briefly, P ini mainly decides the performance of the transition segment, while Q and R have influence on the steady-state segment. In the transition segment, with the pre-conditions stated in (20) and (27), the system can be equalized to a second-order system that can lock the frequency quickly. Moreover, the setting of P i,2 is discussed in details with the main consideration of three factors in order to avoid false lock issue, speed up the convergence and guarantee the stability of the system. As far as the steady segment is concerned, the KF can be equivalent to a third-order tracking loop. At this stage, the performance mainly depends on the settings of Q and R: Q(1,1) and Q(2,2) are set small to guarantee the accuracy of phase and frequency estimate, while Q(3,3) is enlarged to adapt the system to higher order dynamic situations. In conclusion, the Kalman system actually integrates all the parameters into one single unity, which can decide the overall tracking performance, and, at the same time, inside this unity, each value of the Kalman gain k 1, k 2, k 3 has influence on the variance of Kalman states separately.

Understanding the KF-based tracking loop itself in depth can also provide the insights into different research fields such as the design of different integrated navigation system (Petovello and Lachapelle 2006), adaptive tracking loop (Won and Eissfeller 2013) and vector tracking techniques (Lin et al. 2011). Additionally, in the future, the work can be extended to other important promising aspects including how to design optimal systems corresponding to different noise models such as Gauss–Markov model in case of multipath, how to include the analysis of filter stability and sensitivity and real-time implementation of a KF-based tracking loop.