Assigned and unassigned distance geometry: applications to biological molecules and nanostructures

Abstract

Considering geometry based on the concept of distance, the results found by Menger and Blumenthal originated a body of knowledge called distance geometry. This survey covers some recent developments for assigned and unassigned distance geometry and focuses on two main applications: determination of three-dimensional conformations of biological molecules and nanostructures.

1 Introduction

Distance Geometry (DG) is the study of geometry based on the notion of distance, where its mathematical foundations were established by Menger (1928) and Blumenthal (1953). In the majority of applications, the input data of the related problem consists of an incomplete list of distances between object pairs, and the output is a set of positions in some Euclidean space realizing those given distances. In some applications, distances are pre-assigned to pairs of objects; in others, this information must be found and is part of the output.

Let V be a set of n objects and

$$\begin{aligned} x : V \rightarrow {\mathbb {R}}^K \end{aligned}$$

be the function that assigns positions (coordinates) in a Euclidean space of dimension $K>0$ to the n objects belonging to the set V, whose elements are called vertices. The function x is referred to as a realization function.

Let ${\mathcal {D}} = ( d_1, d_2, \ldots , d_m )$ be a finite sequence consisting of m distances, called a distance list, where repeated distances, $d_i = d_j$, are allowed. Distances in ${\mathcal {D}}$ can be represented either with a nonnegative real number (when the distance is exact) or by an interval $[\underline{d},\bar{d}]$, where $0 < \underline{d} < \bar{d}$.

Considering the set of all possible unordered pairs $\{u,v\}$ of vertices in V, called $\hat{E}$, we define an injective function $\ell$, called assignment function, given by

$$\begin{aligned} \ell : \{1,2,\ldots , m \} \longrightarrow \hat{E} \end{aligned}$$

that relates an index of an element of the distance list ${\mathcal {D}}$ to an unordered pair of vertices of V. Thus, $\ell (j) = \{u,v\}$ means that the j-th entry of $\mathcal{D}$ is assigned to $\{u,v\}$ and we denote its corresponding edge weight by $d(u,v) = d_{\ell ^{-1}(\{u,v\})} = d_j$.

From the assignment function $\ell$, we can define the edge set E as the image of $\ell$, that is $E = \ell (\{1,\ldots ,m\}) \subset \hat{E}$. The edge weight function $d:E \rightarrow \{d_1, \ldots , d_m \}$ is given, also from the assignment function, by

$$\begin{aligned} d(u,v) = d_{\ell ^{-1}(\{u,v\})}. \end{aligned}$$

Using $V,\,E,\,d$ we define a simple weighted undirected graph $G = (V,E,d)$.

Definition 1

(Duxbury et al. 2016) Given a list ${\mathcal {D}}$ of m distances, the unassigned Distance Geometry Problem (uDGP) in dimension $K>0$ asks to find an assignment function $\ell : \{1,\ldots ,m\} \rightarrow \hat{E}$ and a realization $x: V \rightarrow {\mathbb {R}}^K$ such that

$$\begin{aligned} \forall \{u,v\} \in \ell (\{1,\ldots ,m\}) \, : \, d(u,v) = d_ {\ell ^{-1}(\{u,v\})}, \,\, \Vert x(u) - x(v) \Vert = d(u,v). \end{aligned}$$

(1)

Let $d_{uv}$ be the short notation for d(u, v). Since precise values for distances may not be available, the equality constraint in (1) becomes

$$\begin{aligned} \underline{d}_{uv} \le \Vert x(u) - x(v) \Vert \le \bar{d}_{uv}, \end{aligned}$$

where $\underline{d}_{uv}$ and $\overline{d}_{uv}$ are, respectively, the lower and upper bounds on the distance $d_{uv}$ ($\underline{d}_{uv} = \overline{d}_{uv}$ when $d_{uv}$ is an exact distance).

When distances are already assigned to pairs of vertices, we can assume that the associated graph G is known a priori. The following definition can be derived immediately from Definition 1:

Definition 2

(Liberti et al. 2014a) Given a weighted undirected graph $G=(V,E,d)$, the assigned Distance Geometry Problem (aDGP) in dimension $K>0$ asks to find a realization $x : V \rightarrow {\mathbb {R}}^K$ such that

$$\begin{aligned} \forall \{ u,v \}\,\in \, E, \, \,\, \Vert x(u) - x(v) \Vert = d_{uv} . \end{aligned}$$

(2)

As in Definition 1, the equality constraint in (2) is actually an inequality constraint when interval distances are considered.

We point out that several methods for uDGP and aDGP are based on a global optimization approach, where a penalty function is defined with the aim of having all distance constraints satisfied (Liberti et al. 2014a). When all distances are exact, one possible penalty function related to the constraints (2) is

$$\begin{aligned} \mathcal{L}(x\,;\,d, \ell ) = \sum _{\{u,v\} \in E} \left( \Vert x(u) - x(v) \Vert ^2 - d_{uv}^2 \right) ^2. \end{aligned}$$

(3)

In the following, we will employ the acronym DGP when referring to the general problem, and we will use the acronyms uDGP and aDGP when it will be important to specify the class of DGP we are referring to.

A recent and wide survey on the DGP is given in Liberti et al. (2014a); an edited book and a journal special issue completely devoted to DGP solution methods and its applications can be found in Mucherino et al. (2013) and Mucherino et al. (2015), respectively. The reader can find a discussion on the history of the DGP in Liberti and Lavor (2015).

The DGP has several interesting applications (see Liberti et al. (2014a) and citations therein, and Juhás et al. (2006)). In dimension $K=2$, the sensor network localization problem is the one of finding the positions of the sensors of a given network by using the available relative distances. Such distances can be estimated by measuring the power for a 2-way communication between pairs of sensors. In dimension $K=3$, molecular conformations can be obtained by exploiting information about distances between atom pairs. In many cases, distances can be either derived from the chemical structure of the molecule, or estimated by Nuclear Magnetic Resonance (NMR) experiments. This problem is also referred to as Molecular DGP (MDGP). X-ray or neutron scattering experiments may be used to find a set of interatomic distances, though the distances are not assigned to atom pairs. In Sect. 5, we will consider cases where it is necessary to identify conformations of biological molecules or nanostructures using lists of interatomic distances.

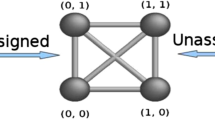
The aDGP is NP-hard (Saxe 1979). The uDGP class is particularly challenging because the graph structure and the graph realization both need to be determined at the same time. In contrast, the DGP usually solved in the context of molecular conformations using NMR data starts from a known graph structure and proceeds to find a graph realization. However, the information that is actually given by the NMR experiments consists of a list ${\mathcal {D}}$ of distances, that are only subsequently assigned to atom pairs (Almeida et al. 2013). Therefore, the MDGP can also be considered as a uDGP. Figure 1 gives a schematic illustration of the input data for a uDGP, as well as for an aDGP.

Fig. 1

(Color online) Differences between uDGP and aDGP problems for a simple case. Image from PhD thesis of Saurabh Gujarathi

The uDGP is not new to mathematics and has been previously studied in various contexts. In an early paper (Skiena et al. 1990) the problem of “reconstructing point sets from interpoint distances” was discussed, though their work and the subsequent literature focuses predominantly on one-dimensional integer problems (Jaganathan and Hassibi 2013). Problems such as the turnpike problem and the beltway problem are in this class and are motivated by DNA sequencing problems often called “digest” problems.

This is one of the first literature surveys that is concerned with both uDGP and aDGP (see Dokmanic et al. (2015), for a distance matrix approach to these problems). Our survey will begin with an overview on graph rigidity and on the conditions for unique realization in Sect. 2. Section 3 will present a state of the art on methods for the uDGP. The discretization of the aDGP will be discussed in Sect. 4, and details about some important implications of the discretization will be provided. Finally, Sect. 5 will be devoted to two main applications of the DGP: identification of three-dimensional conformations of biological molecules such as proteins and nanostructures. The discussion of nanostructures is more extensive as it has not been surveyed in the context of DGPs before. Section 6 will conclude the survey.

2 Graph rigidity and unique embeddability

Our aim is to find a set of n positions for a given set of objects (vertices in V), in the Euclidean space having dimension $K>0$, that are consistent with a given list ${\mathcal {D}}$ of distances (see Introduction). In other words, we are interested in finding a realization x for which a list of distances, pre-assigned or not to pairs of vertices, is satisfied. The first question we may ask ourselves is related to the uniqueness of the solution to the DGP. Given a list ${\mathcal {D}}$, is there more than one realization?

Clearly, if only a few (compatible) distances are given, many solutions can be found that are consistent with the distance constraints. The opposite extreme case is the one where the full set of $n(n-1)/2$ distances is given. The number of translational degrees of freedom of an embedding of n vertices in ${\mathbb {R}}^K$ is nK, while $K(K+1)/2$ is the number of degrees of freedom associated with translations and rotations of a rigid body in K dimensions. As a consequence, when all available distances are exact, since $n(n-1)/2 \gg nK - K(K+1)/2$ for large values of n, it is a likely event to have a unique realization.

A related question was raised by Patterson (1944) in his early work considering the determination of crystal structures from scattering data, and there is a large subsequent literature (Gommes et al. 2012). An important result is that there is a subclass of instances that are homometric, which means that elastic scattering data, and hence the full set of interpoint vector distances, is not sufficient to determine a unique realization (Jain and Trigunayat 1977; Schneider et al. 2010). Patterson’s original paper discussed the vector separations $x(u)-x(v)$, whereas the uDGP considers the distances $||x(u)-x(v)||$. Two distinct point sets are weakly homometric when their complete sets of interpoint distances are the same (Senechal 2008), where point sets related by rigid rotations, translations or reflections are not distinct within the context of this discussion. Weakly homometric point sets are of interest in the uDGP and in a variety of contexts (Skiena et al. 1990; Boutin and Kemper 2007; Senechal 2008). Figure 2 shows two three-dimensional conformations that are weakly homometric with a hexagon. When the distance list has a large number of entries in comparison to the number of degrees of freedom, the probability of having homometric variants decreases rapidly, though no rigorous tests are available. We concentrate on distance lists that are not weakly homometric (NWH), and hence have a unique realization.

Fig. 2

(Color online) The hexagon has three distinct distances with degeneracies $(6-grey,6-blue,3-green)$. The two three-dimensional conformations in the figure are weakly homometric with the hexagon (from Juhás et al. 2006)

A beautiful and rich literature on uniqueness of structures is based on the theory of generic graph rigidity. The beauty of this theory is based on the fact that generic graph rigidity is a topological property where the rigidity of all graph realizations that are generic is dependent only on the graph connectivity and not on the specifics of the realization (Connelly 1991; Hendrickson 1992; Graver et al. 1993). Conditions for a unique graph realization have been determined precisely for generic cases, where it has been proven that a unique solution exists if and only if the kernel of the stress matrix has dimension $K+1$, the minimum possible (Connelly 1991; Hendrickson 1992; Connelly 2005; Jackson and Jordan 2005; Gortler et al. 2010). A second approach is to use rigorous constraint counting methods that have associated algorithms based on bipartite matching. Combinatorial algorithms of this type to test for generic global rigidity (Hendrickson 1992; Connelly 2013), based on Laman’s theorem (Laman 1970; Lovász and Yemini 1982) and its extensions (Tay 1984; Connelly 2013), are also efficient for testing the rigidity of a variety of graphs relevant to materials science, statistical physics and the rigidity of proteins (Jacobs and Thorpe 1995; Jacobs and Hendrickson 1997; Moukarzel and Duxbury 1995; Moukarzel 1996; Thorpe and Duxbury 1999; Rader et al. 2002; Whiteley 2005).

In the following, we will concentrate on constructing graph realizations using Globally Rigid Build-up (GRB) methods that have sufficient distance constraints to ensure generic global rigidity at each step in the process; or on less constrained cases where a binary tree of possible structures is developed using build up strategies and branch and prune methods (iBP) (Lavor et al. 2013). These buildup procedures can be applied to both generic and non-generic cases. GRB methods have been developed for the aDGP case (Dong and Wu 2002; Eren et al. 2004; Wu and Wu 2007; Voller and Wu 2013), and more recently for the uDGP case (Gujarathi et al. 2014; Duxbury et al. 2016). Both of these GRB methods iteratively add a site and $K+1$ (or more) edges to an existing globally rigid structure. In two dimensions this approach is called trilateration Eren et al. (2004). GRB methods for NWH problems are polynomial for the case of precise distance lists satisfying the additional condition that all substructures are unique, for both aDGP and uDGP (see Sect. 3), in contrast to the most difficult DGP cases defined by Saxe (Saxe 1979), where the DGP is NP-hard. The NP-hard instances of DGP with precise distances correspond to families of locally rigid structures that are consistent with an exponentially growing number of different nanostructures as the size of the structure grows (Liberti et al. 2014b). If global rigidity is only imposed at the final step in the process, the algorithm must search an exponential number of intermediate locally rigid structures from which the final unique structure is selected, for example using the iBP algorithm (see Sect. 4). If globally rigid substructures occur at intermediate steps however, the complexity of the search can be reduced, as has been demonstrated in recent branch and prune approaches (Liberti et al. 2014a).

Significant extensions of GRBs are required to fully treat imprecise distance lists that occur in experimental data. One promising approach, the LIGA algorithm, utilizes a stochastic build-up heuristic with backtracking and tournament strategies to mitigate experimental errors (Juhás et al. 2006, 2008). LIGA has been used to successfully reconstruct $C_{60}$ and several crystal structures using distance lists extracted from experimental X-ray or neutron scattering data (Juhás et al. 2006, 2008; Juhas et al. 2010).

Theorems 1–5 below summarize the results necessary for polynomial-time build-up algorithms for the exact distance cases of the aDGP and the uDGP. This theory also provides useful background in understanding other algorithms for finding nanostructure from experimental data (see Sect. 5.3), including simulated annealing methods and the LIGA algorithm (see Sects. 3.2, 5.4), and algorithms for the molecular distance geometry problem.

Before stating the theorems, we give key definitions.

Definition 3

A bar-joint framework consists of rigid bars connecting point-like joints. These bars impose distance constraints but they are freely rotatable around the joints. For an embedding in K dimensions, each free joint has K translational degrees of freedom.

Most of the discussion below is for structures represented by bar-joint frameworks. In many models that are studied computationally, each bar is replaced by a simple spring that has a natural length, $x_0$ and a spring constant k, so that the energy of the spring is $\frac{1}{2} k ||x-x_0||^2$, where $||x-x_0||$ is the extension of the spring. For physical springs k and $x_0$ are positive.

Definition 4

A body-bar framework consists of rigid bars connecting extended rigid objects called bodies. The bars impose distance constraints but they are freely rotatable around the joints, where the joints are located on the surfaces of the bodies. An additional condition is that only one bar is incident to each joint in a body-bar framework.

The restriction to at most one bar incident to a joint enables considerable mathematical progress in the area of rigorous constraint counting. In contrast, bar-joint frameworks may have many bars incident to a joint, and this leads to special cases which cause difficulties for constraint counting methods. For an embedding in K dimensions, each free body has K translational degrees of freedom and $K(K-1)/2$ rotational degrees of freedom, so that each free body has a total of $K(K+1)/2$ degrees of freedom.

Definition 5

A flexible structure is a structure that allows at least one continuous internal deformation of one or more of its vertices or bodies, under the application of an infinitesimal general force.

A flexible structure has at least one zero eigenvalue in its dynamical matrix, $\mathbf {D}$. For a bar-joint framework with joints i (${=}1,2,\ldots ,n$) at position $\mathbf {r}_i$, the dynamical matrix is found by replacing each bar in the framework by a simple spring, so that the elastic energy, $E_S$, of the framework is given by,

$$\begin{aligned} {E_S} = \sum _{\{i,j\} \in E} k_{ij} \left( ||\mathbf {r}_i - \mathbf {r}_j|| - d_{ij}\right) ^2, \end{aligned}$$

(4)

where $k_{ij}$ is a positive parameter characterizing the stiffness of the spring placed between vertices i and j, and $d_{ij}$ is the natural (unperturbed) length of that spring. We consider a small distortion of each vertex, $\mathbf {\delta r}_i$. A second order expansion of the elastic energy yields a quadratic form in the small distortions

$$\begin{aligned} \delta E_S = \delta \mathbf {r}^T \mathbf {D} \delta \mathbf {r}, \end{aligned}$$

(5)

where $\delta \mathbf {r}$ is a vector of length nK containing the small distortions of each vertex in the framework, and $\delta \mathbf {r}^T$ is its transpose. $\mathbf {D}$ is the dynamical matrix.

The eigenvalues of the dynamical matrix give the frequencies of the vibrational modes of the structure. If there is a continuous distortion of the framework that has no restoring force, there is an associated zero frequency mode of the dynamical matrix. In the physics literature, a zero eigenvalue of the dynamical matrix is called a “floppy” mode or “soft” mode, and these modes play an important role in the analysis of structural phase transitions.

Definition 6

A redundant bar can be removed from a structure without increasing the number of floppy modes in the structure.

Definition 7

An isostatic or locally rigid structure has no floppy modes and no redundant bars. Each bar in an isostatic structure removes one degree of freedom of the vertices or bodies in the structure. An isostatic structure has a restoring force to a general infinitesimal distortion, i.e. to any linear combination of the distortions $\delta \mathbf {r}_i$.

Note however that an isostatic structure is in general not globally rigid as there may be more than one realization consistent with its distance matrix (see Theorem 1 below). Locally rigid structures are not necessarily unique and in the worst case the number of possible structures consistent with the distance matrix of an isostatic structure grows exponentially in the number of vertices or bodies in the framework.

Definition 8

A globally rigid structure has no floppy modes and the distance matrix of the structure has a unique realization.

In the applications to nanostructures and proteins, bar-joint models are common where the joints usually correspond to the atoms in the structure. In sensor networks, the joints correspond to sensors. The GRB methods described in Sect. 3 apply to globally rigid bar-joint frameworks, while the branch and prune methods for the discretizable DGP described in Sect. 4 apply to bar-joint frameworks that can have isostatic domains.

The theory of graph rigidity leads to the following important results.

Theorem 1

(Connelly 1991; Hendrickson 1992; Connelly 2005; Jackson and Jordan 2005; Gortler et al. 2010) The following statements hold for generic graphs:

• A unique realization exists if and only if the graph is globally rigid.

• Each bar (edge) in a globally rigid graph is redundant.

• The stress matrix, $\Omega$, of a globally rigid realization has kernel of dimension $K+1$.

The stress matrix, $\Omega$, is derived from the coefficients appearing in the stress energy (Connelly 1991; Hendrickson 1992; Connelly 2005; Jackson and Jordan 2005; Gortler et al. 2010)

$$\begin{aligned} \mathcal{S}(\mathbf{r}) = \sum _{{i,j}\in E} {\upomega }_{ij} \left( \mathbf {r}_i - \mathbf {r}_j\right) ^2, \end{aligned}$$

that satisfy the related force equations for each vertex at equilibrium

$$\begin{aligned} \sum _j {\upomega }_{ij} \left( \mathbf {r}_j - \mathbf {r}_i\right) = 0. \end{aligned}$$

The elements of the stress matrix are $\Omega _{ij} = - {\upomega }_{ij}$ for off diagonal elements, and the diagonal elements are $\Omega _{ii} = \sum _j {\upomega }_{ij}$ so that the row sum is zero for all rows of $\Omega$. Furthermore, the stress matrix block diagonalizes into a separate block for each dimension, as the force components in each dimension are independent. The energy used in the calculation of the stress matrix corresponds to a set of springs that have zero natural length, and the coefficients ${\upomega }_{ij}$ that look like spring constants have the peculiar property that they may be either positive (for tension) or negative (for compression). It is remarkable that this construction yields general results about the global rigidity of generic graphs. The minimum number of zero frequency modes of the stress matrix are due to the fact that the stress energy is unaltered by a shift of the origin (leading to K zero frequency modes), and by the fact that the unit vector is an eigenfunction of the stress matrix, with zero eigenvalue. This leads to $K+1$ trivial zero frequency modes of the stress matrix. If other zero frequency modes exist they indicate non-uniqueness of realizations of the distance list of the structure.

Theorem 2

(Hendrickson 1992; Jackson and Jordan 2005) Generic 3-connected graphs in the plane are globally rigid.

For a restricted subclass of graphs satisfying the molecular conjecture (Whiteley 2005), this result extends to three dimensions.

Theorem 3

(Based on Whiteley 2005) Generic 4-connected graphs in spatial dimension 3 are globally rigid if they satisfy the molecular conjecture.

The molecular conjecture applies to molecular structures in three dimensions when there is a strong restoring force to bond angle changes, as occurs for protein or polymer backbones and in many nanostructures.

A GRB process that ensures global rigidity for systems that are not weakly homometric at each step of the algorithm is stated in Theorems 4 and 5 below. We need the following definition.

Definition 9

We say that a distance list ${\mathcal {D}}$ contains compatible distances if a solution to the corresponding aDGP exists.

Theorem 4

(Follows from Dong and Wu 2002) A GRB algorithm in ${\mathbb {R}}^2$ that adds three compatible distances connecting a new site to an existing globally rigid structure yields a structure that is globally rigid, if the three sites of the existing structure at which the three added distances connect are not on the same line.

Theorem 5

(Dong and Wu 2002) A GRB algorithm in ${\mathbb {R}}^3$ that adds four compatible distances connecting a new site to an existing globally rigid structure yields a structure that is globally rigid, if the four sites of the existing structure at which the four distances connect are not in the same plane.

GRB algorithms using distances that satisfy Theorems 4 and 5 provide sufficient conditions for generating globally rigid NWH structures, and hence a unique embedding, by ensuring uniqueness at each step in the buildup. Section 3 discusses extension of these results to the unassigned distance geometry problem.

3 State of the art on algorithms for the uDGP

In some applications, the information about the pairs of vertices that corresponds to a given known distance is not provided. In other words, while the distance is known, the identity of the two vertices having such a relative distance is not. In this case, the graph G is actually unknown, and the only input is the list ${\mathcal {D}}$ of distances (see Definition 1 and Fig. 1). This is the uDGP and it has received much less attention than the aDGP. In this section we survey two algorithms that have recently been developed for uDGPs. The first is based on a GRB approach that is based on extensions of the results of Theorems 4 and 5 to the uDGP case. The second algorithm is also a build-up approach, however it is stochastic and relies on backtracking to resolve incorrect structures generated during buildup. To develop the GRB approach, we start with a definition and a theorem [full details are found in Duxbury et al. (2016)].

Definition 10

Let ${\mathcal {D}}$ be a distance list with m elements. Amongst all the possible assignments of $\mathcal{D}$ to the set $\hat{E}$ of the underlying graph, $\ell : \{1,\ldots ,m\} \rightarrow \hat{E}$, there is one assignment that corresponds to the structure from which the distance list was calculated. We call that assignment the true assignment (TA).

In general, for distance lists containing precise and compatible distances, assignments different from the TA leading to a feasible aDGP may exist. However, for a NWH distance list, the only assignment that leads to a aDGP having a solution is the TA.

Theorem 6

The smallest generic graph that has a redundant edge and is globally rigid in dimensions $K=2,3$ is the clique of size $K+2$.

Proof

Cliques in three dimensions satisfy the molecular conjecture so constraint counting can be used (Laman 1970; Connelly 2013). By constraint counting, a generic graph with n vertices, having no floppy modes and $n(n-1)/2$ edges has one redundant edge if:

$$\begin{aligned} n(n-1)/2 = nK - K(K+1)/2 + 1, \end{aligned}$$

(6)

which gives $n = K+2$. nK is the number of degrees of freedom of the nodes in the structure, while $K(K+1)/2$ is the set of global degrees of freedom that occur for any rigid body and is not affected by the edge constraints.$\square$

Theorem 6 states that the smallest globally rigid structure in two dimensions has four vertices and in three dimensions has five vertices, as presented in Fig. 3. We call these structures the core of the buildup, and in order to start a build-up procedure, a core compatible with the input distance list must be found. This is the most time consuming step in the reconstruction for uDGPs. If the distances are imprecise, larger cores should be used for the buildup process to reduce the chances of incorrect starting structures.

Fig. 3

(Color online) Examples of cores in $K=2$ (left) and $K = 3$ (right). A core is the smallest cluster that contains a redundant bond in a generic graph rigidity sense. For the two dimensional case (left figure), the horizontal bond is the base (in black), the bonds below it (in blue) make up the base triangle while those above it (in red) make up the top triangle. The vertical bond is the bridge bond (in green). The extension to $K = 3$ requires a base triangle (black), feasible tetrahedra compatible with the base triangle (blue, red) and finally a bridging bond (green) that is consistent with the target distance list (from Duxbury et al. 2016)

3.1 GRB for uDGPs (TRIBOND)

The input to the TRIBOND algorithm consists of a distance list ${\mathcal {D}}$ and the number n of vertices to be embedded. The first step in the algorithm is finding a core, and from Theorem 6 we know that a core in two dimensions has four sites and in three dimensions five sites. The procedures that TRIBOND uses to find cores are illustrated in Fig. 3. Once a core has been found, build-up is carried out utilizing Theorems 4 or 5 to ensure that the conformation remains globally rigid at each step in the process.

A sketch of the TRIBOND algorithm is given in Algorithm 1. The framework F is the structure that is built, starting with the CORE and increased in size by adding one vertex position at a time. In this discussion, it is assumed that the distance list is complete and precise, so that there are $n(n-1)/2$ precise distances in ${\mathcal {D}}$.

If TRIBOND runs to completion it generates the correct unique structure for distance lists that are NWH. However, during buildup, incorrect “decoy” positions may be generated leading to failure of buildup. A decoy position is a vertex position that is consistent with the input distance list at an intermediate stage of the buildup, but which fails to be part of a correct completed structure. Although for cases that we have studied decoy positions are unlikely, distance lists leading to decoy positions can be constructed. A restricted set of distance lists has no intermediate decoy positions, and we define such distance lists to be strongly generic.

Definition 11

A distance list is strongly generic if it is NWH and if all of the compatible globally rigid substructures that can be formed from this distance list are also part of the final unique structure.

Strongly generic distance lists have no decoy positions and for these cases, for a list ${\mathcal {D}}$ of exact distances, TRIBOND runs deterministically to completion. Moreover, we find that in practice distance lists of random point sets can be reconstructed in polynomial time (see below), though random restarts are needed in some cases. Due to the need for random restarts in general TRIBOND is a combinatorial heuristic algorithm. For strongly generic distance lists, it is straightforward to find a polynomial upper bound on TRIBOND by estimating the worst-case computational time for core-finding and for buildup. Since the number of ways of choosing six distances from the set of $m = n(n-1)/2$ unique distances is ${m\atopwithdelims ()6}$, a brute force search would find a core in computational time $\tau _{core} < {m\atopwithdelims ()6} \sim n^{12}$, which demonstrates that the algorithm is polynomial in two dimensions. Similar arguments show that TRIBOND is polynomial in any embedding dimension for strongly generic distance lists, though the polynomial exponent is large.

These arguments are useful to show that the computational complexity of TRIBOND is polynomial for strongly generic distance lists for any K (Gujarathi et al. 2014; Duxbury et al. 2016), however these upper bounds on the algorithmic efficiency are loose. In practice, the scaling of the computational time with the size of random point sets in the plane is approximately $n^{3.3}$ (Fig. 4), and point sets with over 1000 sites have been reconstructed on a laptop. As can be seen from the figure, core-finding is the most time consuming part of the procedure. Extensions to three dimensions look promising, and strategies to treat imprecise distances have also been demonstrated. For the case of imprecise distances it is especially important to find a reliable substructure that has at least the size of the core in order to have a reliable buildup and reconstruction. A large starting substructure increases the chances of having multiple redundant bond checks (pruning distances) to validate any addition of a new vertex to the conformation.

Fig. 4

Experimental results for a series of reconstructions from distance lists generated from random point sets in two dimensions. The mean computational cost (bridge bond checks) for finding the core, performing buildup and their total is presented as a function of the number of points in the structure. The plots for the total and core finding steps are nearly indistinguishable because core finding takes an order of magnitude more time than buildup. Each point on the plots is an average over 25 different instances of random point sets. We find that the mean total computational time scales as $\tau _{total} \sim N^{3.3}$. From Gujarathi et al. (2014)

3.2 LIGA: a robust heuristic

The LIGA heuristic is efficient for precise and imprecise uDGPs with a relatively low number of distinct distances. The input of the algorithm may only consist of the distance list ${\mathcal {D}}$. In some cases, the number of vertices, n, in the solution is given as well; in other cases, only approximate information about the number of vertices may be given. Using LIGA, the structure of $C_{60}$ and a range of crystal structures (Juhás et al. 2006, 2008; Juhas et al. 2010) have been solved using distances extracted from X-ray or neutron scattering experiments (see Sect. 5.3). This algorithm uses a combination of ideas from dynamic programming with backtracking, and tournaments as illustrated in Fig. 5, and in the pseudocode Algorithm 2. The input to LIGA is the ordered distance list ${\mathcal {D}}$, the number of vertices n, and the size of the population s that is kept for each cluster size in the algorithm. LIGA builds up a candidate structure by starting with a single vertex and adding additional vertices one at a time. The algorithm keeps a population of candidate structures at each size and uses promotion and relegation procedures to move toward higher quality nanostructures.

Fig. 5

Schematic of the operation of the LIGA algorithm. A population of structures at all sizes is kept. Smaller substructures are increased in size by addition of a vertex and edges. If the cost of a vertex addition is low, then the addition is kept with a probability that depends on the cost. The substructure is then bigger and is promoted to a higher level. This initiates demotion of an existing substructure of larger size by removing a vertex from it, the most expensive vertex in the substructure. The process is carried out iteratively until low cost structures of the target size are generated. From Juhás et al. (2008)

A key feature of the LIGA algorithm is the choice of a cost function. If we have n vertices and m distances in ${\mathcal {D}}$, with $m \le n(n-1)/2$, then the cost of constructing a model substructure with label i is the following:

$$\begin{aligned} c_i = \min _{\ell } \frac{1}{m} \sum _{\{u,v\}} \left( d^{model}_{uv} - t_{\ell ^{-1}(\{u,v\})}\right) ^2, \end{aligned}$$

(7)

where $d^{model}_{uv}$ is a distance in the model and $t_{\ell ^{-1}(\{u,v\})}$ is a distance in ${\mathcal {D}}$. The minimum is taken over all ways of assigning model distances to nearest distances and the sum is over all distances in the model. A pseudocode for LIGA is given in Algorithm 2.

Promotion is the process of changing the level of a candidate substructure (also called “cluster”) by adding one or more vertices to it. LIGA generates possible positions for new vertices using three different methods:

• 1. Line trials. This method places new sites in-line with two existing vertices in the cluster.

• 2. Planar trials. This method adds vertices in plane to account for occurrence of vertex planes in crystal structures.

• 3. Pyramid trials. Three vertices in a subcluster are randomly selected based on their fitness to form a base for a pyramid of four vertices. The remaining vertex is constructed using three randomly chosen lengths from the list of distances. As there are 3! ways of assigning three lengths to three vertices, and because a pyramid vertex can be placed above or below the base plane, this method generates 12 candidate positions.

Each of these methods is repeated many times (typically, 10,000 times in our trials) to provide a large pool of possible positions for a new vertex. For each of the generated sites, LIGA calculates the associated cost increase for the enlarged candidate and filters the ‘good’ positions with the new cost in a low cost window. The positions outside the cost window are discarded and the winner is chosen randomly from the remaining possibilities with a probability proportional to 1 / cost (the cost of a vertex is the contribution to Eq. (7) of the edges incident to the vertex). The winner vertex is added to the candidate substructure, and the distances it uses are removed from ${\mathcal {D}}$. The costs of other vertices in the pool are recalculated with respect to the new candidate subcluster and the shortened distance table. If the candidate has fewer than n vertices and there are any vertices inside the cost window, a new winner is selected and added. This can lead to an avalanche of added vertices, potentially reducing the long-term overhead associated with generating larger high-quality candidates.

Each level is set to contain a fixed number of candidates, but at the beginning they are completely or partially empty. When a winner for promotion is selected from a level that is not full it adds a copy of itself to that level in addition to being promoted. Similarly, when a loser is selected for relegation from a division that is not full it adds a copy of itself to that division before being relegated. Finally, after a winner is promoted it checks to see if there are any empty levels below its new level. If this is the case then it adds an appropriately relegated clone of itself to those empty levels.

4 Discretizing aDGP instances without GRB

This section considers cases where the number of available distances is too small to guarantee global rigidity at each step in the buildup procedure, as is typical in problems such as protein structure determination. However, discretization of the search space is still possible if the number of distances available ensures that isostatic conditions are preserved during buildup.

As remarked in Sect. 2, GRB methods are able to find solutions to DGP instances with exact distances in polynomial time. In fact, at every iteration of the related algorithms, the unique position for the current vertex can be computed. In other words, the search space is discretized and reduced to one singleton per vertex. In order to do that in three dimensions, it is necessary that the current vertex has known distance from at least four other non-coplanar vertices to which a position has already been assigned.

The work in Carvalho et al. (2008) showed for the first time that weaker assumptions are actually necessary for performing a discretization of the search space. These weaker assumptions make it possible to consider real-life instances of the aDGP relevant to several applications, including determination of protein and other molecular structures. In this context, an important theoretical contribution consisted in formalizing the concept of discretization orders (Lavor et al. 2012a; Cassioli et al. 2015b). We will focus our discussion on the case $K=3$.

aDGP instances need to satisfy the following assumptions in order to have a discrete search space. The main requirement is that the vertices need to be sorted in a way that there are at least three reference vertices for each of them, aside, obviously, from the first three. This ensures that the isostatic condition is preserved. We say that a vertex u is a reference for another vertex v when u precedes v in the given vertex order, and the distance $d_{uv}$. In such a case, indeed, candidate positions for v belong to the sphere centered in u and having radius $d_{uv}$ ($d_{uv}$ is called a reference distance).

The interval Branch and Prune (iBP) algorithm performs a recursive search on the tree which represents the domain of the aDGP after the discretization (Lavor et al. 2013). Let us suppose that there exists an order for the vertices $v \in V$, so that we can assign a numerical label $i \in \{1,2,\ldots ,|V|\}$ to each of them. At each recursive call of the iBP algorithm, candidate positions for the current vertex i are computed using the positions of and distances to the previously placed reference vertices.

The subproblem which needs to be solved at each iBP recursive call is the following. Suppose there are three previous vertices, say $\{ i_3, i_2, i_1 \}$, whose positions are already available, as well as the distances between the current vertex i and these three reference vertices.

When the distances between i and its references are exact, in order to determine $\mathrm{x}_i$, it is necessary to intersect three spheres centered at $\mathrm{x}_{i_3}$, $\mathrm{x}_{i_2}$ and $\mathrm{x}_{i_1}$, and having radius $d_{i_3,i}$, $d_{i_2,i}$ and $d_{i_1,i}$, respectively. If the reference vertices $\{ i_3, i_2, i_1 \}$ are not collinear (see assumption (b.3) in Definition (12)), then such an intersection results in at most two points. When this situation is verified for all vertices $i > 3$, then the search domain has the structure of a binary tree (Lavor et al. 2012b).

However, if one of the three reference distances, say $d_{i_3,i}$, is an interval, then the two spheres centered at $\mathrm{x}_{i_1}$ and $\mathrm{x}_{i_2}$ need to be intersected with a spherical shell centered at $\mathrm{x}_{i_3}$. As a result, the intersection gives two candidate arcs (see Fig. 6). These arcs are over the dashed circle ${\mathcal {C}}$ defined by the intersection of the two spheres. They are symmetric with respect to the plane defined by $\{ i_3, i_2, i_1 \}$. When the intersection consists of two arcs, a finite number D of sample positions can be selected from each arc (Lavor et al. 2013). This way, we still have a discrete set of possible positions for the vertex i.

Fig. 6

The two feasible arcs obtained by intersecting two spheres and one spherical shell

We give the following definition of discretizable DGP, in the case where the distances are supposed to be pre-assigned to pairs of vertices (i.e., the associated graph G is known).

Definition 12

The interval Discretizable DGP in dimension 3 (iDDGP$_3$).

Let $G=(V,E,d)$ be a simple weighted undirected graph and $E'$ be the set of edges related to exact distances. We say that G represents an instance of the iDDGP$_3$ if there exists a vertex order on V having the following conditions:

• (a) $G_C = (C,E_C) \equiv G[\{1,2,3 \}]$ is a clique and $E_C \subset E'$;

• (b) $\forall i \in \{ 4,\ldots ,|V| \}$, there exists $\left\{ i_1,i_2,i_3\right\}$ such that

  • 1. $i_3< i$, $i_2 < i$, $i_1< i$;

  • 2. $\left\{ (i_2,i),(i_1,i)\right\} \subset E'$ and $(i_3,i) \in E$;

  • 3. $d_{i_1,i_3} < d_{i_1,i_2} + d_{i_2,i_3}$.

Assumption (a) allows us to place the first 3 vertices uniquely, avoiding consideration of congruent solutions that can be obtained by rotations and translations. Assumption (b.1) ensures the existence of three reference vertices for every $i > 3$, and assumption (b.2) ensures that at most one of the three reference distances may be represented by an interval. Finally, assumption (b.3) prevents the references vertices from being collinear. Under these assumptions, the aDGP can be discretized.

A sketch of the iBP algorithm is given in Algorithm 3. Given a vertex order on V satisfying the assumptions in Definition 12, the algorithm calls itself recursively in order to explore the tree of candidate positions. Every time a new position is computed, it defines a new branch of the tree. This phase in iBP is named the branching phase. For every computed position, its feasibility is verified by checking the constraints (2), up to the current layer, or other additional feasibility criteria (Mucherino et al. 2011; Cassioli et al. 2015a). This phase in iBP is named the pruning phase, and the criteria are called pruning devices (see line 3 of Algorithm 3).

Even if the search tree grows exponentially in the worst case, the pruning devices allow iBP to focus the search on the feasible parts of the tree. The easiest and probably most efficient pruning device is the Direct Distance Feasibility (DDF) criterion (Lavor et al. 2012b), which consists in verifying the $\epsilon$-feasibility of constraints involving distances between the current vertex i and previously placed vertices:

$$\begin{aligned} \underline{d}(k,i) - \epsilon \le \Vert \mathrm{x}_k - \mathrm{x}_i \Vert \le \overline{d}(k,i) + \epsilon , \quad \forall (k,i) \in E {\setminus } \{ i_3,i_2,i_1 \}, \text { with } k<i. \end{aligned}$$

(8)

The distances defining the above constraints are called pruning distances.

In the algorithm call, i is the current vertex for which the candidate positions are searched, n is the total number of vertices, d is the pre-assigned distance list, and D is the discretization factor, i.e. the number of sample points that are taken from the arcs in case the distance $d_{i_3,i}$ is represented by an interval. In the algorithm (see lines 3 and 3), we make use of a list L of positions and arcs, from which candidate positions are extracted.

A necessary preprocessing step for solving aDGPs by this discrete approach is finding suitable discretization orders. In previous works, discretization orders have been either handcrafted (Lavor et al. 2013), or designed by exploring pseudo de Bruijn graphs formed by cliques of G (Mucherino 2015), or even automatically obtained by a greedy algorithm (Lavor et al. 2012a; Mucherino 2013). In this work, we will consider a discretization order particularly designed for protein backbones (see Sect. 5.1).

It is interesting to mention that if an instance of iDDGP$_3$ has only exact distances such that for each vertex $i>4$ there are at least four reference distances to four previous non-coplanar vertices then the iBP reduces to a variant of the Geometric Build-up (Dong and Wu 2002; Wu and Wu 2007; Voller and Wu 2013), where a vertex order is pre-defined.

A fundamental step in both methods is how to compute the candidate positions for the next vertex i by solving a sphere intersection subproblem:

$$\begin{aligned} || \mathrm{x}_i - \mathrm{x}_j ||^2 = d_{ij}^2, \quad \forall j \in J \subset \{1, \ldots , i-1 \}. \end{aligned}$$

4.1 Computing Cartesian coordinates

While looking for candidate vertex positions for the vertex i (we use the notation in Definition 12), it is supposed that the reference vertices $\left\{ i_3,i_2,i_1\right\}$ are already positioned and they define a local coordinate system centered at $i_1$ (Gonçalves and Mucherino 2014). Once this coordinate system has been identified, each candidate position for the vertex i can be represented by two angles, to which we will refer with the symbols $\theta _i$ and ${\upomega }_i$.

In detail, we will use the symbol $\theta _i$ in order to refer to the angle formed by the two segments $(i,i_1)$ and $(i_1,i_2)$. When dealing with molecules, this angle is also referred to as the bond angle. Moreover, we will use the symbol ${\upomega }_i$ for referring to the angle formed by the two planes defined by the two triplets $(i_3,i_2,i_1)$ and $(i_2,i_1,i)$. Similarly, when the focus is on molecules, this angle is generally named the torsion angle. We warn the reader that, even if we will use the terms “bond angle” and “torsion angle” in the following, as in molecular biology, the angles that are used here may not be equivalent to the ones generally considered for molecules such as proteins. The angles $\theta _{i}$ and ${\upomega }_{i}$ can be computed by exploiting the positions of the previous vertices $i_1$, $i_2$ and $i_3$, as well as the available distances $d_{i_1,i}$, $d_{i_2,i}$ and $d_{i_3,i}$ (see Fig. 6).

When the three reference distances are all exact, three spheres can be defined, whose intersection gives 2 points, with probability 1 (Lavor et al. 2012b). The two points $\mathrm{x}_i^+$ and $\mathrm{x}_i^-$ for vertex i are symmetric with respect to the plane defined by the reference vertices. When one of the three distances is instead represented by an interval (see Definition 12), the third sphere becomes a spherical shell, and the intersection yields two arcs (see Fig. 6). These two arcs correspond to two intervals, $[\underline{{\upomega }}_i^+, \overline{{\upomega }}_i^+]$ and $[\underline{{\upomega }}_i^-, \overline{{\upomega }}_i^-]$, for the angle ${\upomega }_i$. In order to discretize these intervals, a certain finite set of points can be chosen from the two arcs. From a computational point of view, this can be implemented by choosing a certain subset of distances from the available interval, and by intersecting the three spheres several times, while the third one changes its radius in the given interval: by selecting D equidistant angles in $[\underline{{\upomega }}_i^+, \overline{{\upomega }}_i^+]$ and other D equidistant angles in $[\underline{{\upomega }}_i^-, \overline{{\upomega }}_i^-]$, $2\,D$ positions for i can be computed. At each recursive call of iBP, therefore, the main subproblem is the one of finding the points given by one or several sphere intersections.

Suppose that we need to place the vertex i: let $i_1$, $i_2$ and $i_3$ be the three reference vertices for i. From the equations of the spheres in the three-dimensional space, we can deduce that the intersection points can be obtained by solving the following system of quadratic equations:

$$\begin{aligned} \left\{ \begin{array}{lcl} || \mathrm{x}_i - \mathrm{x}_{i_1} ||^2 &{} = &{} d_{i,i_1}^2 \\ || \mathrm{x}_i - \mathrm{x}_{i_2} ||^2 &{} = &{} d_{i,i_2}^2 \\ || \mathrm{x}_i - \mathrm{x}_{i_3} ||^2 &{} = &{} d_{i,i_3}^2 \end{array} \right. . \end{aligned}$$

(9)

Instead of attempting the solution of a quadratic system, another method can be considered where the solutions to the quadratic system are found by solving two linear systems. This method was implemented in conjunction with the iBP for instances consisting of exact distances only, but it was shown that it can lead to strong numerical instabilities (Mucherino et al. 2012).

An alternative method for solving (9) which exploits internal coordinates is proposed in (Gonçalves and Mucherino 2014). In order to avoid considering solutions that can be obtained by translations and rotations, we can fix the vertices that belong to the initial clique (see assumption (a) in Definition 12). The first vertex is placed in the origin of the Cartesian system of coordinates, the second one is in the negative x-axis, and the third vertex is placed on the 1st (or 2nd) quadrant of the xy-plane.

If we consider consecutive reference vertices, so that $i_3 = 1$, $i_2 = 2$ and $i_1 = 3$, in order to position the 4th vertex, we need to compute the torsion angle ${\upomega }_{4}$ defined by the first four consecutive vertices. As described in Lavor et al. (2012b, 2015), the cosine of ${\upomega }_{4}$ can be computed from the distances between pairs of vertices in the quadruplet. The cosine of the torsion angle, together with distances and angles between segments, can be used for identifying the two positions given by the sphere intersections. For a general vertex $i>3$, candidate positions can be computed by multiplying $4 \times 4$ matrices, whose elements depend on distances, bond and torsion angles. If we assume that $i_3=i-3$, $i_2=i-2$ and $i_1=i-1$, for each $i>3$, then the Cartesian coordinates of the candidate positions, for vertex i, can be obtained by:

$$\begin{aligned} \mathrm{x}_i = \left[ \begin{array}{r} x_{i} \\ y_{i} \\ z_{i} \\ 1\end{array} \right] =B_{1}B_{2}B_3\ldots B_{i}\left[ \begin{array}{r} 0 \\ 0 \\ 0 \\ 1\end{array} \right] , \end{aligned}$$

(10)

where the matrices $B_i$ are defined inductively as:

$$\begin{aligned} B_1= & {} \left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \end{array} \right] , B_2 = \left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} -1 &{} 0 &{} 0 &{} -d_{12} \\ 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \end{array} \right] , \nonumber \\ B_3= & {} \left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} -\cos \theta _3 &{} \sin \theta _3 &{} 0 &{} -d_{23}\cos \theta _3 \\ \sin \theta _3 &{} -\cos \theta _3 &{} 0 &{} d_{23}\sin \theta _3 \\ 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \end{array} \right] , \end{aligned}$$

(11)

$$\begin{aligned} B_i= & {} \left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} -\cos \theta _{i} &{} -\sin \theta _{i} &{} 0 &{} -d_{i-1,i}\cos \theta _{i} \\ \sin \theta _{i} \cos {\upomega }_{i} &{} -\cos \theta _{i} \cos {\upomega }_{i} &{} -\sin {\upomega }_{i} &{} d_{i-1,i} \sin \theta _{i} \cos {\upomega }_{i} \\ \sin \theta _{i} \sin {\upomega }_{i} &{} -\cos \theta _{i} \sin {\upomega }_{i} &{} \cos {\upomega }_{i} &{} d_{i-1,i} \sin \theta _{i} \sin {\upomega }_{i} \\ 0 &{} 0 &{} 0 &{} 1\end{array} \right] . \end{aligned}$$

(12)

This procedure is very efficient and works well in practice (Mucherino et al. 2011; Lavor et al. 2012b, 2013). It requires, however, that the reference vertices $i_3$, $i_2$ and $i_1$ are the ones that immediately precede i (this condition is named the consecutivity assumption). In previous publications, therefore, orders on V satisfying this assumption were strongly required. However, finding an order satisfying this assumption is NP-Hard (Cassioli et al. 2015b), while orders that do not satisfy the consecutivity assumption can be obtained automatically in polynomial time (see Lavor et al. (2012a); Mucherino 2013)). More recently, in (Gonçalves and Mucherino 2014), the procedure defined by Eqs. (10)–(12), has been generalized, so that the consecutivity assumption is not necessary anymore. This procedure allows us to generate accurate Cartesian coordinates, while orders satisfying weaker assumptions can be employed.

In order to present this generalized procedure, we start with analyzing the meaning of the matrices $B_i$ [see Eq. (12)]. The first three elements of the last column of the matrix correspond to the spherical coordinates of a vertex position in a system of coordinates described as follows. The vertex $i_1$ is the center of this coordinate system. The x-axis is defined in such a way that $i_2$ is on its negative side. The y-axis (orthogonal to the x-axis) is defined such that the vertex $i_3$ is on the xy-plane and has negative y coordinate. We remark that this definition allows us to have a clockwise orientation for torsion angles, in a way that the minimum distance between $i_3$ and i is achieved when ${\upomega }_i = 0$ (equivalently, we have the maximal distance achieved when ${\upomega }_i = {\uppi }$). Naturally, the z-axis is normal to the xy-plane (see Fig. 8). We will refer to this coordinate system as the system defined in $i_1$.

When it is supposed that the reference vertices $i_3$, $i_2$ and $i_1$ are the ones that immediately precede i in the total ordering, i.e. $i_3 = i - 3$, $i_2 = i - 2$ and $i_1 = i - 1$, then the Cartesian coordinates of a certain position in the system of coordinates defined in i can be expressed in the system of coordinates defined in the vertex $i_1 = i-1$ through the equation:

$$\begin{aligned} \left[ \begin{array}{r} x' \\ y' \\ z' \end{array} \right] = \left[ \begin{array}{lll} -\cos \theta _{i} &{}\quad -\sin \theta _{i} &{}\quad 0 \\ \sin \theta _{i} \cos {\upomega }_{i} &{}\quad -\cos \theta _{i} \cos {\upomega }_{i} &{}\quad -\sin {\upomega }_{i} \\ \sin \theta _{i} \sin {\upomega }_{i} &{}\quad -\cos \theta _{i} \sin {\upomega }_{i} &{}\quad \cos {\upomega }_{i} \end{array} \right] \left[ \begin{array}{r} x \\ y \\ z \end{array} \right] + \left[ \begin{array}{r} -d_{i-1,i} \cos \theta _{i} \\ d_{i-1,i} \sin \theta _{i} \cos {\upomega }_{i} \\ d_{i-1,i} \sin \theta _{i} \sin {\upomega }_{i} \end{array} \right] , \end{aligned}$$

or equivalently $(x',y',z',1)^{T} = B_i (x,y,z,1)^{T}$. In particular, the coordinates of the vertex i in the system of coordinates defined in $i_1 = i-1$ is given by

$$\begin{aligned} \left[ \begin{array}{r} x'_{i} \\ y'_{i} \\ z'_{i} \\ 1 \end{array} \right] = B_i \left[ \begin{array}{r} 0 \\ 0 \\ 0 \\ 1 \end{array} \right] = \left[ \begin{array}{r} -d_{i-1,i} \cos \theta _{i} \\ d_{i-1,i} \sin \theta _{i} \cos {\upomega }_{i} \\ d_{i-1,i} \sin \theta _{i} \sin {\upomega }_{i} \\ 1 \end{array} \right] . \end{aligned}$$

We can point out therefore that the role of each matrix $B_i$ is to change the basis from the coordinate system in the vertex i to the coordinate system in $i-1 = i_1$. Since the canonical system of coordinates is defined by the vertex having rank 1, when the vertices $1,2,\ldots ,i-1,i$ are placed consecutively, i.e. we have $i_3=i-3, i_2=i-2, i_1=i-1$ for each i, the matrix product $B_1 B_2 \ldots B_{i-1} B_i$ plays the role of changing the basis from the one in the vertex i to the canonical basis. This explains Eq. (10).

Figure 7 shows how this procedure strongly depends on the consecutivity assumption. In Fig. 7a, we have a path defined by the matrices $B_i$ where the consecutivity assumption is always satisfied. In this case, as explained above, every matrix is able to step from one coordinate system to another, by making reference to the coordinate system defined by the previous vertex $i-1$ in the order. In Fig. 7b, instead, we have a path where the consecutivity assumption is broken at vertex 6, because the three reference vertices are the vertices 4, 3 and 2. In this case, the matrix $B_6$ should not be multiplied by the previous cumulative product $B_1 \ldots B_5$, because it is not necessary to pass through the coordinate system defined at the vertex 5. In general, therefore, in the absence of the consecutivity assumption, different paths for the matrices $B_i$ (i.e. different sequences of basis transformations) can be defined. This can lead to the definition of a tree of possible paths (such as the one in Fig. 7b), which would make the implementation of this procedure cumbersome.

Fig. 7

A tree of possible paths for computing coordinates in the canonical system

The main idea for the generalized procedure for computing candidate vertex positions is to avoid to accumulate matrices every time we step from one vertex to another. Instead, we introduce a new matrix that we will denote by the symbol $U_{i_1}$. If $\hat{x}$, $\hat{y}$ and $\hat{z}$ are the three unit vectors describing the coordinate system defined in $i_1$, then

$$\begin{aligned} U_{i_1} = \left( \begin{array}{c@{\quad }c@{\quad }c} \hat{x}_1 &{} \hat{y}_1 &{} \hat{z}_1 \\ \hat{x}_2 &{} \hat{y}_2 &{} \hat{z}_2 \\ \hat{x}_3 &{} \hat{y}_3 &{} \hat{z}_3 \\ \end{array} \right) . \end{aligned}$$

(13)

This matrix is able to convert directly vertex positions from the coordinate system defined in $i_1$ to the canonical system. This conversion is possible independently of whether the reference vertices are consecutive or not.

Recall that, along the current branch of the iBP tree, the Cartesian coordinates for the reference vertices $i_1$, $i_2$ and $i_3$ are supposed to be already available. The coordinate system in $i_1$, and hence the matrix $U_{i_1}$, can be defined as follows. Let $v_1$ be the vector from $i_2$ to $i_1$. Equivalently, let $v_2$ be the vector from $i_2$ to $i_3$. The x-axis for the system in $i_1$ can be defined by $v_1$: $\hat{x}$ is the unit vector related to $v_1$. Moreover, the vectorial product $v_1 \times v_2$ gives another vector that defines the z-axis, whose corresponding unit vector is $\hat{z}$. Finally, the vectorial product $\hat{x} \times \hat{z}$ provides the vector that defines the y-axis (let the unit vector be $\hat{y}$). Figure 8 shows the coordinate system defined by the three unit vectors $(\hat{x},\hat{y},\hat{z})$.

Fig. 8

The reference vertices $i_3$, $i_2$ and $i_1$ induce a system of coordinates

The three obtained vectors $\hat{x}$, $\hat{y}$ and $\hat{z}$ can be used for defining the columns of the matrix $U_{i_1}$, as specified in Eq. (13), which is a unitary rotation matrix. Once $U_{i_1}$ has been computed, the canonical Cartesian coordinates for a candidate position for the vertex i can be obtained by:

$$\begin{aligned} {\mathrm{x}}_i ({\upomega }_i) = \left[ \begin{array}{r} x_{i} \\ y_{i} \\ z_{i} \end{array} \right] = \left[ \begin{array}{r} x_{i_1} \\ y_{i_1} \\ z_{i_1} \end{array} \right] + U_{i_1} \left[ \begin{array}{r} -d_{i_1,i} \cos \theta _{i} \\ d_{i_1,i} \sin \theta _{i} \cos {\upomega }_{i} \\ d_{i_1,i} \sin \theta _{i} \sin {\upomega }_{i} \end{array} \right] . \end{aligned}$$

(14)

Recall that $\cos \theta _{i}$ and $\cos {\upomega }_{i}$ can be computed by exploiting the available distances $d_{i_1,i}$, $d_{i_2,i}$ and $d_{i_3,i}$, as well as the positions of the previous vertices $i_1$, $i_2$ and $i_3$.

Notice that Eq. (14) is equivalent to Eq. (10), in the sense that they both depend on bond angles and torsion angles, and they both provide the same result. However, there is no need to accumulate products of matrices in Eq. (14), so that the consecutivity assumption is not necessary.

As shown in Gonçalves and Mucherino (2014), the generalized procedure for the computation of vertex coordinates in the iBP algorithm, based on Eq. (14), is very stable when working on aDGP instances related to real proteins. Moreover, Eq. (14) is also at the basis of an important technique that can be used to reduce the feasible arcs obtained by the intersection of two spheres with one spherical shell (continuous subsets of ${\upomega }_i$ are obtained, rather than two distinct real values). This technique for arc reduction was firstly proposed in Gonçalves et al. (2014), and it is detailed in Sect. 4.2.

4.2 Reducing the feasible arcs by exploiting pruning distances

When candidate vertex positions, at each recursive call of the iBP algorithm, are computed by intersecting two spheres with one spherical shell, a continuous set of positions is obtained and generally corresponds to two disjoint arcs. In terms of torsion angles ${\upomega }_i$, these arcs correspond to two intervals for the torsion angle values. In Lavor et al. (2013), it is simply selected a predefined number of samples from the arcs (i.e., a certain number of torsion angle values from the available intervals). This technique relies on at least one of such samples being able to fulfill the pruning distance constraints on the current layer. This, however, may not be the case: pruning distances at the same layer could be infeasible with all selected positions. In practice, the region on the arcs that can be compatible with other available distances may be contained between two selected samples, but not cross any of them. The procedure detailed below overcomes this issue for pruning distances at the current tree layer.

Let D be the predefined number of samples to be taken from the arcs obtained with the sphere intersection. Naturally, the value given to D plays a critical role, because the number of generated positions (and hence the number of branches added to the tree) can be relatively large and lead to a combinatorial explosion. On the one hand, too large D values can drastically increase the width of the tree; on the other hand, too small values can generate trees where no solutions can be found (all branches are pruned, because all positions, at a certain layer, are not compatible with pruning distances).

During a typical run of the algorithm, every time the reference distance $d_{i_3,i}$ is represented by an interval (it defines a spherical shell), D equidistant samples are taken from each arc. As a consequence, $2 \times D$ positions are generated in total, and $2 \times D$ new branches are added to the tree, at the current layer, for every branch at the upper level. After their computation, the feasibility of each position is verified. There are two extreme situations. All computed positions may be feasible: a smaller D value might be considered without harming the computations. Otherwise, all positions may be infeasible. In this case, since D samples on the arcs are taken, the latter information does not allow us to discriminate between “the two arcs are infeasible” and “the chosen samples are infeasible”. In Gonçalves et al. (2014), an adaptive scheme was proposed for tailoring the branching phase of the iBP algorithm so that all computed candidate positions are feasible at the current layer. The idea is to identify, before the branching phase of the algorithm, the subset of positions on the two candidate arcs that is feasible with respect to all pruning distances to be verified on the current layer.

Let us suppose that, at the current layer i, the distance $d_{i_3,i}$ is represented by the interval $[\underline{d}_{i_3,i}, \overline{d}_{i_3,i}]$. Two arcs on the circle $\mathcal{C}$ can be identified (see Fig. 6, and refer to Eq. (14) in Sect. 4.1), which correspond to the two intervals of the torsion angles $[\underline{{\upomega }}^+, \overline{{\upomega }}^+] \subset [0,{\uppi }]$ and $[\underline{{\upomega }}^-, \overline{{\upomega }}^-] \subset [{\uppi },2{\uppi }]$ (from now on, we will omit the subscripts of the angles $\theta _i$ and ${\upomega }_i$ in order to simplify notation). All points in those two arcs satisfy the interval distance $[\underline{d}_{i_3,i},\overline{d}_{i_3,i}]$, as well as the two exact distances $d_{i_2,i}$ and $d_{i_1,i}$, by construction. However, there can be other distances between the already placed vertex and i that we could exploit for tightening these two arcs. Let us suppose there is an $h \in \{ j<i \ |\ j \notin \{i_3,i_2,i_1 \} \}$ such that the distance $d_{h,i}$ is known. Solutions to the equation

$$\begin{aligned} d_{h,i} = \left\| \mathrm{x}_{h} - \mathrm{x}_i({\upomega })\right\| \end{aligned}$$

(15)

give the values for the angle ${\upomega }$ that are compatible with the distance $d_{h,i}$. From Eqs. (15) and (14) and using the fact that $U_{i_1}$ is an orthogonal matrix, we obtain

$$\begin{aligned} d_{h,i}^2= & {} \left\| \mathrm{x}_h - \mathrm{x}_i({\upomega })\right\| ^2 = \left\| v \right\| ^2 + d_{i_1,i}^2 \\&- \,2 \left\langle v , \left( -d_{i_1,i} \cos \theta \right) \,\hat{x} + \left( d_{i_1,i} \sin \theta \cos {\upomega }\right) \,\hat{y} + \left( d_{i_1,i} \sin \theta \sin {\upomega }\right) \,\hat{z} \right\rangle , \end{aligned}$$

where $\langle \cdot ,\cdot \rangle$ denotes the inner product between two vectors, $v = \mathrm{x}_h - \mathrm{x}_{i_1}$ and $\hat{x},\hat{y},\hat{z}$ are the columns of $U_{i_1}$. If we define

$$\begin{aligned} \begin{array}{ll} A = 2\langle v, \hat{y} \rangle \left( d_{i_1,i} \sin \theta \right) , &{} \ \ \ \ B = 2\langle v, \hat{z} \rangle \left( d_{i_1,i} \sin \theta \right) , \\ \ \\ \Delta = \left\| v \right\| ^2 + d_{i_1,i}^2 + 2 \langle v , \hat{x} \rangle \left( d_{i_1,i} \cos \theta \right) , &{} \ \ \ \ C = \Delta - d_{h,i}^2, \end{array} \end{aligned}$$

(16)

we obtain the following equation:

$$\begin{aligned} A \cos {\upomega }+ B \sin {\upomega }= C. \end{aligned}$$

(17)

A discussion about how to solve Eq. (17) is presented in detail in Gonçalves et al. (2014). Solutions to Eq. (17) provide the points where the sphere, centered at $\mathrm{x}_h$ and with radius $d_{h,i}$, intersects the circle ${\mathcal {C}}$ in Fig. 6. When $d_{h,i}$ is given by an interval $[\underline{d}_{h,i}, \overline{d}_{h,i}]$, we solve Eq. (17) for the bounds $\underline{d}_{h,i}$ and $\overline{d}_{h,i}$:

$$\begin{aligned} A \cos {\upomega }+ B \sin {\upomega }= & {} \Delta - \underline{d}_{h,i}^2 , \end{aligned}$$

(18)

$$\begin{aligned} A \cos {\upomega }+ B \sin {\upomega }= & {} \Delta - \overline{d}_{h,i}^2. \end{aligned}$$

(19)

The solutions of (18) and (19) are the extreme points of the feasible arcs: they define feasible intervals for the angle ${\upomega }$.

The feasible positions for the vertex i can be therefore obtained by intersecting the two previously computed arcs (in bold in Fig. 6) and several spherical shells, each of them defined by considering one pruning distance between i and $h < i$. In order to perform this intersection, the Eqs. (18) and (19) need to be solved for every pruning distance $d_{h,i}$.

When Eqs. (18) and (19) have solutions, values for ${\upomega }$ can be computed that are able to identify new arcs on the circle $\mathcal{C}$, which was previously obtained by intersecting two spheres. If both equations admit solutions, two pairs of angle values can be identified: $\underline{{\upomega }}^l$ and $\overline{{\upomega }}^l$, using lower bound on the distance (Eq. 18), and $\underline{{\upomega }}^u$ and $\overline{{\upomega }}^u$, using its upper bound (Eq. 19). The two intervals $[\underline{{\upomega }}^l, \overline{{\upomega }}^l]$ and $[\underline{{\upomega }}^u, \overline{{\upomega }}^u]$ are able to identify two arcs on $\mathcal{C}$, which are compatible, evidently, with the considered pruning distance, as well as with the two exact distances previously employed for defining $\mathcal{C}$. These two arcs need therefore to be intersected with the arcs related to the discretization distance $d_{i_3,i}$. Moreover, if other pruning distances are available, other pairs of Eqs. (18) and (19) can be defined and new arcs on the circle $\mathcal{C}$ may be identified. The final subset of $\mathcal{C}$ which is compatible with all available distances can be obtained by intersecting the arcs obtained for each pruning distance with the arcs related to the distance $d_{i_3,i}$.

For a given pruning distance $d_{h,i}$, if both Eqs. (18) and (19) have no solutions, then the final set of feasible positions on $\mathcal{C}$ is either empty, or it corresponds to the entire $\mathcal{C}$. It is sufficient to test any value of ${\upomega }$ in one of the candidate arcs to state that

$$\begin{aligned} \underline{d}^2_{h,i} < \left\| \mathrm{x}_h - \mathrm{x}_i({\upomega })\right\| ^2 < \overline{d}^2_{h,i} , \end{aligned}$$

or not.

Moreover, for a given distance $d_{h,i}$, only one of the two Eqs. (18) and (19) may have solutions. In this case, only one arc can be identified on the circle $\mathcal{C}$. In order to find the right orientation of such an arc on the circle ${\mathcal {C}}$, we define the function

$$\begin{aligned} F({\upomega }) = \Vert \mathrm{x}_h - \mathrm{x}_i({\upomega })\Vert ^2 = \Delta - A \cos {\upomega }- B \sin {\upomega }, \end{aligned}$$

and we consider its derivative

$$\begin{aligned} F'({\upomega }) = A \sin {\upomega }- B \cos {\upomega }. \end{aligned}$$

(20)

The correct orientation at an extreme point (solution of (18)) is the one for which $F({\upomega })$ increases, which can be obtained from Eq. (20). Notice that we might need to add $2{\uppi }$ to one of the extreme points in order to have $\overline{{\upomega }} > \underline{{\upomega }}$. The analysis for the case in which only Eq. (19) has solutions is analogous.

After considering all pruning distances, i.e., after performing all intersections, the final result provides a list of arcs on ${\mathcal {C}}$ that are feasible with all the distances that can be verified at the current layer. All positions that can be taken from these arcs are feasible at the current layer: all of them generate a new branch and may serve as a reference for computing new candidate positions on deeper layers of the tree. In order to integrate the iBP algorithm with this adaptive scheme, there are two main changes to be performed. On line 3, the adaptive scheme needs to be invoked for taking into consideration the information about the pruning distances. Moreover, if DDF is the only pruning device employed, lines 3–3 may be removed, because this verification becomes unnecessary.

5 Applications

5.1 DGP in biological molecules

The distance information from NMR experiments are distances between nuclei in proteins (Almeida et al. 2013; Crippen and Havel 1988; Wuthrich 1989; Hendrickson 1995; Nilges and O’Donoghue 1998). Since they may contain errors, they are treated as restraints rather than constraints (Clore and Gronenborn 1997; Brunger et al. 1998; Nilges and O’Donoghue 1998; Berger et al. 2011). Recently, a variety of other approaches to distance measurements in biological and inorganic materials have been developed and there is considerable promise for continuing progress in this area (Guerry and Herrmann 2011; Bouchevreau et al. 2013). Considerable experimental work is carried out to determine the pair of nuclei assigned to each distance extracted from the NMR data, allowing the problem to be represented by a graph $G=(V,E,d)$, where V represents the set of atoms and E is the set of atom pairs for which a distance is available.

As pointed out in Sect. 4, it is a fundamental pre-processing step for the solution of aDGPs to identify a suitable discretization order for the vertices of G. We consider a model for the protein backbone as depicted in Fig. 9. With the backbone atoms N, H, $C_{{\upalpha }}$, $H_{{\upalpha }}$ and C, we have included only $C_{{\upbeta }}$ and $H_{{\upbeta }}$ to represent the side chain R of each amino acid. The backbone model of Fig. 9 has only 3 amino-acids but it can be extended for a longer protein chain, thanks to the regular pattern of the protein backbone.

Fig. 9

A model for the protein backbone and a possible discretization order

From Fig. 9, we can derive a discretization order, where the first three atoms $N-C_{{\upalpha }}-H_{{\upalpha }}$ of the first amino-acid can be used as initial clique (see assumption (a) in Definition 12) because the involved distances are related to bond lengths that can be considered as exact (Crippen and Havel 1988). Taking into account the peptide plane distances and the distances between hydrogens provided by NMR, it is not hard to verify that assumptions (b.1)–(b.2) of Definition 12 are satisfied by the order given in Fig. 9. Other discretization orders are given in Lavor et al. (2011, 2013) and Costa et al. (2014).

On the basis of the model in Fig. 9, it is possible to conceive other pruning devices (Mucherino et al. 2011) to be integrated with DDF (see, Eq. (8)), based on chirality constraints and rigid parts (peptide planes and tetrahedrons around $C_{{\upalpha }}$’s) of the protein chain.

Although, in general, the cost of exploring the search tree of a iDDGP$_3$ after discretization grows exponentially, it is important to mention that this is not the case for sets of exact distances with periodic pruning distances. In Liberti et al. (2013), it is shown that this situation is likely to happen in proteins, where the iBP algorithm presents a polynomial behavior, being able to find realizations for proteins with thousands of atoms in less than a minute.

Additionally, the iBP algorithm can potentially enumerate all incongruent conformations of a molecular iDDGP$_3$ instance. This is a clear advantage, allowing exploration of different shapes that a protein can assume inside cells. In Fig. 10, we present 2 incongruent realizations for the protein 2PPZ, whose distance information was extracted from the PDB. For this instance, we assume that all distances below 4.4Å  are exact. In fact, the iBP found 4 incongruent conformations, but 2 of them were pruned by chirality. Notice that the realizations in Fig. 10 differ by a partial reflection.

Fig. 10

Two incongruent conformations for protein 2PPZ from PDB that differ by partial reflection. Only distances below 4.4Å  were considered

When interval distances come into play, the iBP algorithm may become an heuristic (for a fixed number of equidistant samples D). The main difficulties arise from the discretization of the arcs (see Sect. 4) and the fact that interval pruning distances cannot guide the search in a effective way. Some recent efforts, like the scheme presented in Sect. 4.2, have been done in order to overcome these barriers (Gonçalves et al. 2014; Gonçalves and Mucherino 2014; Lavor et al. 2015), where preliminary results suggest new investigations.

Figure 11 shows a conformation found by iBP for the protein instance 2ERL, against the true conformation deposited in PDB. Here, only distances below 5Å  are considered, where the ones related to hydrogen pairs are represented by an interval of width 1Å. Although the RMSD (Root Mean Squared Deviation) is 0.86Å, it seems that the iBP could capture the global fold of the protein.

Fig. 11

Superimposition of a conformation found by iBP (red) and the target 2ERL from PDB (blue). The RMSD between the structures is 0.86Å

Improvements in handling interval distances may allow the use of iBP as an exploratory tool for finding incongruent approximate conformations for proteins based on NMR distance information.

5.2 DGP in nanostructures

The Nanostructure Problem is the problem of finding, at high precision, the atomic positions of molecular, biomolecular or solid state systems when it is difficult or impractical to grow a single crystal or even a polycrystal sample (Billinge and Levin 2007). The meaning of high precision is context dependent, however a typical requirement in a solid state system is the determination of the positions of all atoms in a nanostructure to better than 2 % for each interatomic distance in the nanostructure, and in some cases even higher resolution is necessary. High resolution is required as the function of nanostructured materials and complex molecules is highly sensitive to small changes in the interatomic distances, making it essential to determine nanostructure to high precision to enable understanding and design of materials. Nanostructure problems are encountered in a wide variety of materials, including complex molecules, nanoparticles, polymers, proteins, non-crystalline motifs embedded in a crystalline matrix and many others (see Fig. 12 for three examples). We consider single phase problems where one nanostructure is dominant, though extensions to multiphase nanostructures are possible once the single phase case can be solved efficiently.

Fig. 12

(Color online) Examples of nanostructured materials. a Nanostructured bulk materials. b Intercalated mesoporous materials. c Discrete nanoparticles. In each case, ball-and-stick renditions of possible structures are shown on the top, and TEM images of examples are shown on the bottom. From Billinge and Levin (2007)

The pair-distribution function (PDF) method is a versatile and readily available approach to probing the local atomic structure of nanostructured materials (Egami and Billinge 2012). PDF results can be extracted from X-ray, neutron or electron total scattering data and in many cases the data can be collected efficiently. The major bottleneck in PDF analysis is the extraction of nanostructures from the data, as standard techniques are based on either refinement from a good initial guess (Farrow et al. 2007); or on simulated annealing (McGreevy and Pusztai 1988; Evrard and Pusztai 2005; Tucker et al. 2007).

A more systematic approach to finding good starting structures is a high priority in the field and provides the motivation for developing ab-initio DG approaches (Gujarathi et al. 2014; Juhás et al. 2006). Alternative experimental approaches such as high resolution transmission electron microscopy (see Fig. 12) are very useful for larger scale morphological studies, but they do not yield the high precision atomic structures available from diffraction and scattering approaches. Local structural information can also be found using extended X-ray absorption fine-structure (EXAFS) and related near-edge absorption spectroscopies, solid-state NMR, and scanning probe methods at sample surfaces. An innovative emerging approach utilizes ultrafast X-ray laser pump-probe “diffract and destroy” methods which require a separate suite of analysis algorithms (Gaffney and Chapman 2007).

A longer term goal in the field is to develop modeling frameworks incorporating all of the available experimental probes to yield consensus best local atomic structures (see Fig. 13), and the most recent software packages are moving in this direction. Here, we focus on the determination of local atomic structure from PDF data.

Fig. 13

(Color online) Schematic of the concept of combining experimental data and ab-initio modeling to deduce a consensus best atomic structure. From Billinge (2010)

The ideal PDF contains a list of the interatomic distances in a material for both crystalline or non-crystalline cases (see the next subsection). There is a very extensive literature describing PDF experiments on a wide range of complex nanostructured materials (Egami and Billinge 2012). Nanostructures consistent with the experimental PDF data are usually discovered using one of two approaches: (1) By using physical intuition or theoretical modeling to propose a starting structure, followed by structure refinement (Farrow et al. 2007) or (2) Use of global optimization methods to find structures, most often using a simulated annealing approach that in this literature is called Reverse Monte Carlo (RMC) (McGreevy and Pusztai 1988; Tucker et al. 2007). Nanostructures found to be consistent with the PDF data are then tested further by checking their properties against known results from other experimental structural characterization approaches such as TEM, STM etc, and experimental results for electrical, mechanical, thermodynamic, optical, magnetic and other physical properties. Quantum mechanical calculations to predict the structure and properties of complex materials are utilized in making these comparisons. Though the RMC method is a global optimization approach it is of limited use in finding unique nanostructures, due to the strong metastability of the nanostructure optimization problem. However, RMC is widely utilized to find populations of local nanostructures consistent with materials with varying local atomic structures, such as structural glasses and liquids.

Attempts at finding unique global minimum nanostructures of solid state materials using DG approaches is recent (see Sect. 3), despite the long history of finding global minimum atomic structures using Bragg diffraction from single crystals. This is partly due to the fact that only recently PDF methods have become sufficiently refined to provide distances lists of sufficient quality to enable extraction of high quality distance lists.

5.3 The pair distribution function

The distances between atoms in a material are contained in the pair distribution function (PDF). The PDF is found by taking a Fourier transform of the structure factor (see Eq. 22 below) which is extracted from the experimentally measured total scattering of X-rays, neutrons or electrons from a sample (Egami and Billinge 2012; Billinge and Kanatzidis 2004). The PDF method is widely used to study nanostructures (Egami and Billinge 2012; Billinge and Kanatzidis 2004; Billinge and Levin 2007) and several software packages to find atomic structures that are consistent with PDF data are available (Evrard and Pusztai 2005; Farrow et al. 2007; Tucker et al. 2007). Despite the successes of these methods, finding high quality nanostructures from experimental PDF data remains challenging and subject to interpretation. There is a need for efficient computational methods that have a stronger mathematical foundation and performance guarantees. DG methods provide one avenue to achieve these more rigorous approaches to nanostructure determination. As we show below, a perfect PDF would yield all of the interatomic distances in the sample. However there are many limitations in the real PDF data. First, the data is truncated at an upper interatomic distance that is typically 3.5 nm or less, and the data is imprecise leading to overlap of peaks and hence difficulty in extracting distances that are close in length.

The ideal pair distribution function is defined by

$$\begin{aligned} g(r)= {1\over r} \frac{1}{ N \left( \langle f \rangle \right) ^2} \sum _{j\ne l} f^*_j f_l \delta \left( r-r_{jl}\right) . \end{aligned}$$

(21)

The delta function in this expression yields a set of peaks in g(r), that are located at the values of the interatomic distances. Here, $r_{jl}$ is the distance between atoms j and l located at positions $\mathbf {r}_j$ and $\mathbf {r}_l$ so that $r_{jl} = ||\mathbf {r}_l-\mathbf {r}_j||$. N is the total number of atoms in the structure, where $j=1,\ldots ,N$ and $l=1,\ldots ,N$. $f_j$ is the scattering power of the atom at position $\mathbf {r}_j$, and $f_j^*$ is its complex conjugate. The scattering power is found by taking a Fourier transform of the electron charge density (for X-ray or electron scattering) or the nuclear potential (neutron scattering) (see  Sivia (2011) for details).

The measured structure factor, extracted from scattering experiments in the kinematical limit where multiple scattering is ignored, is given by (see Sivia (2011) Chapter 3)

$$\begin{aligned} S(\mathbf Q ) \propto \sum _{j,l} f^*_j f_l e^{i \mathbf Q \cdot \left( \mathbf {r}_j - \mathbf {r}_l\right) }, \end{aligned}$$

(22)

where $\mathbf Q = \mathbf k - \mathbf k '$ is the scattering wavevector which is the difference of the incoming and outgoing wavevectors of the particle that is scattered. For elastic scattering, the magnitudes of the scattering wavevectors are the same, $k = k'$, where k is the magnitude of $\mathbf k$. The term $j=l$ is called the self-scattering term, and is usually treated separately and normalized in the following way,

$$\begin{aligned} S(\mathbf Q ) = 1 + \frac{1}{N (\langle f \rangle )^2} \sum _{j\ne l} f^*_j f_l \, \exp \left( i \mathbf Q \cdot \mathbf {r}_{jl}\right) . \end{aligned}$$

(23)

$(\langle f \rangle )^2$ is the mean square averaged scattering power, where the average is taken over all scatterers in the system. PDF analysis is usually used when the material samples are amorphous or powders so that the scattering is independent of sample orientation and an average over the scattering angles yields

$$\begin{aligned} S (Q)= 1+ \frac{1}{ N (\langle f \rangle )^2}\sum _{j\ne l} f^*_j f_l \, \frac{\sin \left( {Q \, r_{jl}}\right) }{Qr_{jl}}, \end{aligned}$$

(24)

where Q is the magnitude of $\mathbf Q$ and $r_{jl}$ is the magnitude of $\mathbf {r}_{jl}$.

For convenience in comparing different materials, the PDF above is often normalized so that it approaches one at large distances. From the relations (21) and (24), it is easy to see that the structure factor (the experimentally measured quantity) is related to the pair distribution function through

$$\begin{aligned} g(r) = {2\over {\uppi }} \int _0^{\infty } Q [ S(Q) - 1] sin(Qr) dQ. \end{aligned}$$

(25)

From the point of view of DG, the key feature of the pair distribution function as defined in Eq. (21) is that it contains a list of interatomic distances without any specific reference to the particular atoms at the endpoints of each distance, so finding atomic structure from the PDF requires solution to a uDGP.

The experimental PDF does not have delta function peaks as occurs in the ideal PDF of Eq. 21. The experimental peak width is determined by both physical processes and experimental resolution (Egami and Billinge 2012). A high resolution X-ray PDF for a crystalline sample of Ni is presented in Fig. 14, and interatomic distances extracted from this PDF are indicated. In structures with high symmetry, such as Ni which crystallizes into a face-centered cubic structure, distances of the same length occur frequently and the degeneracy of each distance can be estimated from the area of each peak. Extraction of high quality distance lists requires high purity samples, high resolution detectors and careful data analysis.

Fig. 14

(Color online) High quality PDF for FCC Ni. The bottom figure indicates distances that have been extracted from this experimental PDF (G(r)). The radial distribution function R is especially useful for extracting distance lists, and it is related to G(r) through $R(r) = r (G(r) - G_{bg}(r))$, where $G_{bg}(r)$ is a background subtraction that depends on the shape of the sample. The experiments actually measure the structure factor S(Q), and the experimental PDF, G(r), is found by carrying out the integral Eq. 25. Since the experimental data is over a bounded range of Q, and it has finite resolution $\delta Q$, the experimental PDF has ripples and other artifacts that have to be understood. The LIGA algorithm efficiently reconstructs the local FCC structure from the distances extracted from this experimental data (Juhás et al. 2006)

5.4 Reverse Monte Carlo (RMC) and structure refinement (PDFGui)

Reverse Monte Carlo (RMC) methods (McGreevy and Pusztai 1988; Tucker et al. 2007) consider models with atomic positions $\mathbf {r}_i$, $i=1,\ldots ,n$. The starting model is a configuration of these points that are often chosen to be either random or ordered, and it is a good practice to check that the final results are robust to the choice of the initial model. Monte Carlo based methods, such as simulated annealing, are used to move the atomic positions of the model in order to minimize the residual,

$$\begin{aligned} R = \sum _i^P \left( p_{i}^{model} - p_i^{exp.}\right) ^2, \end{aligned}$$

(26)

where $p_{i}^{model}$ is the PDF calculated from the model positions, using Eq. 21 convolved with a Gaussian to represent the experimental uncertainty in the distances. $p_i^{exp.}$ is the experimental data that may be extracted from X-ray, neutron or electron scattering experiments. P is the number of data points used to represent the PDF. The PDF is calculated from distance $r=0$ to a maximum $r_{max}$, so the resolution in real space is $\delta r = r_{max}/P$. The experimental resolution in reciprocal space is $\delta q$ and it is important to take account of any oversampling issues in interpreting features in the PDF. The simulated annealing algorithm used in RMC is a global optimizer, though convergence inefficiencies mean that in many RMC studies, particularly on crystalline materials using RMC-profile, it is being used as a local optimizer. Additional terms can be added to the expression for R above to treat other experimental data.

RMC was developed to capture populations of local atomic structures occurring in glasses and liquids (McGreevy and Pusztai 1988), and the number of degrees of freedom in the models used for that purpose is typically much higher than the number of points used in the residual, so the model is underconstrained. Unless further constraints are applied, the models found by RMC using underconstrained models may fit the experimental data extremely well, yet be non-unique and not necessarily correct. Physical or chemical constraints should be added to the RMC procedure to capture known properties of the target nanostructure. A new RMC code, called RMCProfile, is public and maintained predominantly by the theory group at ISIS in the Rutherford labs (Tucker et al. 2007). It has the capability to include a variety of constraints, a variety of experimental data, and in the case of crystalline systems it has different procedures to treat both the total scattering and the Bragg peaks.

PDFGui requires the assumption of a reference structure, and the residual Eq. 26 is minimized with respect to candidate distortions that are also input by the user. PDFGui is maintained predominantly by the Billinge group at Brookhaven and Columbia (Farrow et al. 2007). Distortions of the reference structure are described by a set of parameters, and a minimization of the residual Eq. 26 is taken over the parameter set. The number of parameters used in the minimization is usually much smaller than the number of degrees of freedom in the data, so the models are overconstrained. Minimization is often taken using standard downhill methods such as Levenberg–Marquardt. PDFgui is part of the Diffpy complex modeling package, Diffpy-CMI (http://diffpy.org), which does contain global optimization methods and is a software implementation of a complex modeling paradigm, illustrated in Fig. 13. In the case of nanoparticles, assumptions must also be made about the reference structure of the surface and other defects.

5.5 Solution to uDGP for a fullerene molecule

An illustration of the solution to the $C_{60}$ fullerene using the LIGA algorithm for uDGP is presented in Fig. 15, showing that it is possible to reconstruct interesting nanostructures from unassigned distance lists extracted from real experimental PDF data. A large number of other structures have been reconstructed using LIGA using precise distance lists and also from experimental data (Juhas et al. 2010). LIGA works well when structures have high symmetry leading to a limited number of unique distances. However, LIGA has difficulty with structures that have a large number of different distances due to the stochastic nature of its vertex addition procedures. The emergence of DGP GRB methods, such as those used in TRIBOND, provide new avenues for improving LIGA (see Sect. 3.2).

Fig. 15

Reconstruction of a buckeyball from experimental neutron scattering data. a–c Various forms of the experimental data, starting with the raw structure factor data. The imprecise distance list of d extracted from this data is the only information that is used to find the correct structure. From Juhás et al. (2006, 2008)

When the distance list ${\mathcal {D}}$ is obtained from experimental PDF data (see Sect. 5.3), they may contain significant errors in the multiplicity and values of the distances (see Fig. 15). This is a problem especially because underestimated multiplicities may greatly increase the cost of the correct structure. Under such circumstances it is advantageous to relax or even ignore multiplicities altogether. In the first case, the distance table is constructed with distance multiplicities increased by a fixed percentage, and thus it contains more lengths than actually present in the searched structure. In the second case, the program allows any distance to be compared with the model structure an arbitrary number of times. This is in effect the same as setting infinite multiplicities for all lengths in the target set. It is also possible to relax the condition of a fixed target size N, in which case the largest cluster size keeps growing. However since the distances have a fixed maximum length, the cost of the large structures grows significantly, indicating the true largest cluster consistent with the input distance list.

One clear lesson emerging from experiences with the TRIBOND and LIGA algorithms, and which has also been emphasized in recent work on BP methods for DGPs, is that the ordering of vertices used in reconstruction from distance information is very important. In TRIBOND this is illustrated in Fig. 4 which shows that finding a reliable core is the most time consuming step in reconstruction. This leads to the viewpoint that it is more effective to find a smaller number of high precision distances in a core, than it is to find a larger number of low precision distances that are not closely related.

6 Conclusion

We reviewed some methods for the assigned and the unassigned DGP (aDGP and uDGP) that determine graph embeddings by iteratively growing substructures. Starting with a general discussion on graph rigidity, we have presented two main approaches to the DGP. The first approach, for the uDGP, is strongly based on the concept of finding unique substructures during iterative growth of a final unique realization. The second, initially conceived for the aDGP, reduces the search space to a discrete one having the structure of a tree, for systems that do not have a unique realization at each step in the build up. We focused our attention on two particular applications: the identification of conformations of biological molecules and determining the nanostructures of complex materials.

It is worth emphasizing that globally rigid substructures should be used if possible, as each redundant bond in such a substructure provides a check on the correctness of the reconstruction. This is not true of substructures that are not globally rigid. For precise distance lists, the smallest substructure in three dimensions containing a redundant bond is a clique with five vertices. One strategy to solve macromolecular structure from a set of distance constraints is then to identify and reconstruct the most redundant, in a graph rigidity sense, substructures first. Moreover, concentrating experimental and theoretical efforts on finding the precise structure of small subunits of a large protein or nanostructure will enable a solid base from which to build larger structures, using for example tree search methods such as iBP. This approach will also help to mitigate the effects of errors and uncertainties in the distance lists while taking advantage of problem structure. An important theoretical challenge is to extend the understanding of a core size to cases where the distances are imprecise. In the imprecise case, it would be very useful to have bounds on the probability that a substructure is unique, given the substructure size, the number of distances used and the errors in those distances.

As this survey shows, two emerging research lines, one originally developed for the aDGP and the other for the uDGP, have several common and several complementary features. Utilization of these two approaches in combination should yield interesting methods for tackling the general DGP and its many applications.