Assessing interbank contagion using simulated networks

Abstract

This paper presents a new approach to randomly generate interbank networks while overcoming shortcomings in the availability of bank-by-bank bilateral exposures. Our model can be used to simulate and assess interbank contagion effects on banking sector soundness and resilience. We find a strongly non-linear pattern across the distribution of simulated networks, whereby only for a small percentage of networks the impact of interbank contagion will substantially reducoe average solvency of the system. In the vast majority of the simulated networks the system-wide contagion effects are largely negligible. The approach furthermore enables to form a view about the most systemic banks in the system in terms of the banks whose failure would have the most detrimental contagion effects on the system as a whole. Finally, as the simulation of the network structures is computationally very costly, we also propose a simplified measure—a so-called Systemic Probability Index—that also captures the likelihood of contagion from the failure of a given bank to honour its interbank payment obligations but at the same time is less costly to compute. We find that the SPI is broadly consistent with the results from the simulated network structures.

1 Introduction

The inception of the euro created a large and integrated euro area money market, allowing euro area banks to lend and fund themselves via other euro area banks; also across national borders. This helped ease financial transactions and facilitate trade among euro area countries. This success notwithstanding, the global financial crisis erupting in mid-2007 led to heavy losses at many financial institutions and to severe disruptions in the interbank markets as individual institutions lost confidence in the soundness of their peers. This was reinforced by a string of bank failures in the ensuing years, the most prominent being the one of Lehman Brothers (the US investment bank) in September 2008. More recently, the euro area sovereign debt crisis was also accompanied by a number of bank failures and bailouts and raised substantial concerns about the risk of pernicious contagion effects among euro area banks (and their sovereigns).

These events have highlighted the systemic risks to the financial system of individual bank failures via the interlinkages that exist between banks; especially in the unsecured interbank market. Particular attention has been paid to potential counterparty risks banks are exposed to via their bilateral interbank exposures.¹ This in turn has led to a flurry of academic research to help understand, measure and assess the impact of contagion within the network of banks and other institutions that constitute the financial system. In addition, a number of policy initiatives have been introduced in recent years to counter the potential contagion risks of interlinked banking networks; especially exemplified by the additional capital requirements on globally systemic institutions (G-SIBs).

The academic literature analysing financial contagion has followed different strands. One area of research has focused on capturing contagion using financial market data. Kodres and Pritsker (2002) provide a theoretical model whereby in an environment of shared macroeconomic risks and asymmetric information asset price contagion can occur even under the assumption of rational expectations. On the empirical side, some early studies attempted to capture contagion using event studies to detect the impact of bank failures on stock (or debt) prices of other banks in the system.² The evidence from these studies was, however, rather mixed. This may be due to the fact that stock price reactions typically observed during normal periods do not capture well the non-linear and more extreme asset price movements typically observed during periods of systemic events where large-scale contagion effects could be expected. In this light, some more recent market data studies have applied extreme-value theory to better capture such extraordinary events.³ In a similar vein, Polson and Scott (2011) apply an explosive volatility model to capture stock market contagion measured by excess cross-sectional correlations. Other studies have tried to capture the conditional spillover probabilities at the tail of the distribution by using quantile regressions.⁴ Diebold and Yilmaz (2011) proposes in turn to use variance decompositions as connectedness measures to construct networks among financial institutions based on market data.

A different strand of the literature has been based on balance sheet exposures (such as interbank exposures and bank capital) with the aim of conducting counterfactual simulations of the potential effects on the network of exposures if one or more financial institutions encounter problems. This may overcome some of the deficiencies of the market data-based literature, such as the fact that asset prices can be subject to periods of significant mis-pricing which may distort the signals retrieved from the analysis. The starting point to analyse bank contagion risks and interconnectedness on the basis of balance sheet data is having reliable information on interbank networks. One can view a financial exposure or liability within a network as a relationship (or edge) of an institution (node) vis-à-vis another whereby the relationship portrays a potential channel of shock transmission among institutions. Mutual exposures of financial intermediaries are generally beneficial as they allow for a more efficient allocation of financial assets and liabilities and are a sign of better diversified financial institutions.⁵ At the same time, when large shocks hit the financial system, financial networks—especially if exposures are concentrated among a few main players—can act as an accelerator of the shock’s initial impact by propagating it throughout the financial system via network links. As emphasized by Allen and Gale (2000) the underlying structure of the network determines how vulnerable it is to contagion.⁶ For example, Allen and Gale (2000) emphasize the contagion risk prevailing in incomplete networks. ⁷ It is furthermore emphasized in the literature that in the presence of asymmetric information about the quality of counterparties and of the underlying collateral, adverse selection problems may arise which can render interbank networks dysfunctional in periods of distress.⁸

The financial contagion literature is furthermore related to complex network analysis in other academic fields (transportation, medicine and physics in particular). It thus relates to the so-called “robust yet fragile” network characterisation, by which networks are found to be resilient to most shocks but can be susceptible to pernicious contagion effects when specific nodes are targeted.⁹ Recent models of the interbank market that incorporates this knife-edge character of financial networks include Nier et al. (2007), Iori et al. (2008) and Georg (2011).

To model how shocks to one (or more) financial entity can have contagious effects throughout the financial system a dynamic network modelling approach is warranted. This involves imposing certain characteristics, or behavioural assumptions, on the nodes to allow for translating shocks to specific nodes into propagation channels affecting other nodes in the network via the bilateral relationships.

In reality, however, network analysis is constrained by the fact that data on bilateral interbank exposures are generally not available to other than supervisors and market oversight authorities. To counter such difficulties, this paper proposes an alternative approach to construct interbank networks. Our approach makes use of individual banks’ aggregate interbank exposures to simulate a wide range of possible interbank networks. Once the interbank interconnectedness structures have been simulated, a dynamic analysis of how and to what extent shocks to different entities propagate throughout the banking system can be conducted. Such analysis is, for example, useful in a macro stress test context to gauge the impact on specific banks or the banking system as a whole from shocks to one or more banks.

The simulation approach to analysing contagion within interbank networks proposed in this paper is related to the so-called Stochastic Block Modeling of networks, as for instance suggested by Lu and Zhou (2010), whereby link prediction algorithms are used to produce the missing links between agents (nodes) in a given network.¹⁰ Our dynamic network modelling is also related to the literature on shock transmissions, which asserts that the transmission depends on the probability distribution governing whether nodes have contact with each other and can occur through “knock-on” cascading effects (see e.g. Newman (2005)).

Notably, our approach differs from networks based on entropy methods and based on real-time data, which are typically capturing one particular snapshot of the network structure. Instead, we simulate a large number of possible networks contingent on the underlying exposure data and imposed behavioural characteristics.¹¹ This produces a very dynamic pattern of interbank networks, which reflects well the volatile nature of financial network structures (see e.g. Garratt et al. 2011; Gabrieli 2011). It also aims to circumvent the averaging bias characteristic of entropy measures, which tend to produce too much averaging at the tails and thus may underestimate contagion risk (see e.g. Mistrulli 2011).

The main contributions of the paper to the growing literature on network analysis are threefold: first, we propose a robust method to construct interbank networks without necessarily having access to bank-by-bank bilateral connections. Second, our model allows to randomly generate a wide distribution of possible networks which in turn can be used to dynamically analyse the likelihood and size of shock propagations throughout the interbank network. In this context, we also allow for the impact of fire sales, which is shown to exacerbate the contagion.¹². Third, we derive a “contagion index” that provides a robust proxy for the simulated networks but is computationally easier to handle. In our view, the model will be useful for regular financial stability analysis, as conducted in central banks in particular. First of all, it provides a convenient tool for assessing the systemic risk of individual banks in the system and to calculate the systemic impact (and likelihood) of shocks hitting one or more banks. As such, it can also be linked to outcomes of traditional top-down macro stress tests to illustrate the contagion effects from different macro-financial scenarios. A final contribution compared to the previous literature relates to the geographical coverage. Whereas most interbank contagion studies refer to specific country settings, in our paper we create networks between large banks in the EU as a whole.¹³ This allows to also address the importance of cross-border interbank contagion as compared to contagion solely within the national borders. In an ever more globalized financial system, such cross-border contagion may be expected to become increasingly relevant; as also the financial crisis erupting in 2007 amply illustrated.

Some caveats to our modelling approach should be mentioned. First, drawing random networks from a uniform distribution does not necessarily lead to the core-periphery structure often observed in real world network data. This notwithstanding, the behavioural characteristics that we impose upon the nodes (e.g. whether banks are internationally or mainly domestically-oriented) before randomly drawing our networks would in fact be expected to imply a priori some degree of core-periphery structure. Moreover, owing to the substantial size differences of the interbank assets and liabilities across banks in our sample (and hence the amount of assets/liabilities of individual banks to be distributed within the system) the procedure would generally result in the emergence of large money centre banks in our simulated systems. Second, the fact that the drawing of interbank loans follows a sequential approach whereby the loan volume is drawn as a random fraction of the remaining total exposure may have significant implications for the overall distribution of loans held by individual banks in the generated networks. While this bias is averaged out at the level of individual loans among banks $(i,j)$ once many simulations are considered, when considering the overall distribution of loan volumes the bias may remain. It is for example rather unlikely that, in a particular simulation, a bank would have a large number of loans of roughly equal size—a case which may plausibly occur for money centres. Finally, the network structures resulting from our simulations are contingent on the specific characteristics we impose on the nodes—in other words, the probability that two banks are linked to each other. Ultimately, the validity of the network structures randomly generated would need to be cross-checked against real world network data.

The paper is organised as follows: Sect. 2 describes the baseline model and the various steps involved in the derivation of the simulated networks. Section 3 in turn presents the contagion index, and some possible model extensions. Results are discussed in Sects. 4 and 5 concludes.

2 Baseline model

The structure of our model of the interbank contagion consists of a random interbank networks in which we apply a shock to one bank (or a set of banks) that is subsequently transmitted within this interbank system. The network is generated in a random way based on the banks’ balance sheet data on their total interbank placements and deposits and on the assessment of banks’ geographical breakdown of activities. There are 89 banks in the analysed sample, mostly from euro area countries. These are banks included in the EU-wide stress tests conducted by the European Banking Authority (EBA), but the data used to parametrise the model are taken from Bureau van Dijk’s Bankscope and banks’ financial reports. Notably, we do not have data on the individual banks’ bilateral exposures, which are instead derived based on their total interbank placements and deposits; as described below. The shock is simply meant to be a given bank’s default on all its interbank payments. It then spreads across the banking system transmitted by the interbank network of the simulated bilateral exposures.

There are three main building blocks of the model. First, the probability map that a bank in a given country makes an interbank placement to a bank in another (or the same) country was proposed; second, an iterative procedure to generate interbank networks by randomly picking a link between banks and accepting it with probability taken from the probability map. Finally, the algorithm of clearing payments proposed by Eisenberg and Noe (2001) on the interbank market in two versions was applied: without and (modified) with a “fire sales” mechanism.

2.1 Probability map

Bank-by-bank bilateral interbank exposures are not readily available. For that reason, to define the probability structure of the interbank linkages (a probability map), as a starting point the EBA disclosures on the geographical breakdown of individual banks’ activities (here measured by the geographical breakdown of exposures at default) were employed.¹⁴ The probabilities were defined at the country level, i.e. the exposures were aggregated within a country and the fraction of these exposures towards banks in a given country was calculated. These fractions were assumed to be probabilities that a bank in a given country makes an interbank placement to a bank in another (or the same) country. Banks were grouped into two subcategories within countries: with domestic scope of activities and with international activity, respectively. Banks within the same group were assigned similar probabilities in the probability map. The classification was based on a ratio calculated as the share of cross-border intra-EU exposures to total exposures. With respect to the definition of internationally active banks we experimented with different threshold values and found the most robust specification to be a share of international exposures to total exposures equal to 25 per cent.

The probability map based on the EBA disclosures is an arbitrary choice contingent on the very limited availability of data about interbank market structures. An idea of market fragmentation along the national borders while treating separately the internationally active banks seems to be justified. Nevertheless, the results (structure of the network and the contagion spreading) are dependent on the particular probability structure (geographical proximity matters). In results Sect. 4 we perform some sensitivity analysis of the systemic importance of banks if the probability map is distorted.

2.2 Interbank network

The network is generated randomly based on the probability map which is based on the geographical breakdown of exposures. This probability is represented by a matrix $P^{geo}$, such that $P^{geo}_{ij}\in [0,1]$ indicates a probability that bank $j$ has an interbank exposure vis-à-vis bank $i$ or, in other words, bank $i$ has liability towards bank $j$. The proposed procedure generating the interbank system is a version of the “Accept–Reject” scheme. A possible interbank network (realisation from a distribution of networks given by the probability map) is generated in the following way. A pair of banks is randomly drawn (all pairs have equal probability) and the pair is kept as an edge (link) in the interbank network with a probability given by the probability map. If the drawn link is kept as an interbank exposure, then the random number is generated (from the uniform distribution on $[0,1]$) indicating what percentage of reported interbank liabilities ($l$) of the first bank in the pair comes from the second bank in the pair (the amount is appropriately truncated to account for the reported interbank assets ($a$) of the second bank). If not kept, then the next pair is drawn (and accepted with a corresponding probability or not). Ultimately, the stock of interbank liabilities and assets is reduced by the volume of the assigned placement. The procedure is repeated until no more interbank liabilities are left to be assigned as placements from one bank to another.

For one realisation of the network structure obtained by the proposed algorithm, the size of the linkage between a given pair $(i,j)$ of banks depends on order of drawn linkages. The first drawn link would on average be allocated 50 % of total liabilities of $j$, the second—25 % and so on. This bias related to linkages between banks $i$ and $j$ is averaged out if many interbank structures are considered. The first drawn pair in one realisation of the algorithm may be any $\text{ n }{\mathrm{th}}$ pair in the next realisation. We construct 20,000 structures for the purpose of our contagion analysis. Analysing many different interbank structures instead of just one specific (either observed at the reporting date or—if not available—estimated e.g. by means of entropy measure) accounts for a very dynamic, unstable nature of the interbank structures confirmed by many studies (see e.g. Garratt et al. 2011; Gabrieli 2011). The way in which linkages are drawn may still be an issue for the distribution of the whole network. It may underestimate the probability of networks in which nodes have many linkages of similar size. However, the algorithm does not exclude such configurations, which are typical for the real interbank networks with money centers.

Figure 1 illustrates one realisation from the whole distribution of network structures for the EU banking sector generated using the random network modelling approach. The width of the arrows indicates the size of exposures (logarithmic scale) and the colouring scale (from light to dark green) denotes the probability (inferred from the interbank probability map) that a given bank grants an interbank deposit to the other bank. Most of the connections are between banks from the same country but the connectivity between the biggest domestic banking systems is also quite high (the German, Spanish and British banking systems, in particular).

Fig. 1

Generated interbank network. An arrow between bank A and B indicates an interbank deposit of bank B placed in bank A; the width of an arrow reflects the size of the exposure; the lighter the green color of an arrow, the lower the probability is that the arrow joins a given pair of banks (color figure online)

The very general characteristics of the network and of the role played by the particular nodes can be performed by means of some standard network measures. The simulated network approach gives the whole distribution of measures that, further statistically analysed, may indicate some candidate banks to be systemically important. Following ECB (2012), we looked at three centrality measures—i.e. degree, closeness and betweenness, which inform about network activity, independence of nodes and nodes’ control of activity in the network respectively. We also calculated a very simple measure of network density, i.e. the ratio of the number of linkages to total possible interbank connections (which is ${N \atopwithdelims ()2}$ for $N$ banks in the system). In our context, betweeness seems to most appropriately address an issue of identification of systemic nodes, i.e. causing and transmitting most sizable contagion. The centrality measures applied to the simulated networks are discussed in Sect. 4, in particular with a reference to the entropy maximising networks broadly considered in the literature (see Mistrulli (2011) about the entropy maximising networks). Additionally, we verify if the network measures can explain the size of the simulated contagion losses in the banking system.¹⁵

2.3 Contagion mechanism

The assessment of the size of the interbank contagion is based on the so-called interbank clearing payments vector, derived by Eisenberg and Noe (2001) and which is define in our modification by the vector $p^{*}$ solving the following equation

$$\begin{aligned} p^{*}=\min \left\{ \max \{C-a+l+\sum _{i=1}^N\pi ^{\top }p^{*},0\},l\right\} \end{aligned}$$

(1)

where:

• $C$ - vector of banks’ regulatory capital. It reflects the full absorption capacity of banks;

• $a$ - vector of interbank assets;

• $l$ - vector of interbank liabilities;

• $\pi ^{\top }$ - transposed matrix of the relative interbank exposures with $\pi _{ij}$ entry defined as bank $i$ interbank exposure towards bank $j$ divided by the total interbank exposure of bank $i$.

The expression $C - a + l$ can be interpreted as banks’ own funding sources adjusted by the net interbank exposures; the ultimate interbank payments are derived as the equilibrium of flows in the interbank network. The contagious default on the interbank deposits is detected by comparing $l_i$ and $p^{*}$ – if the difference is greater than 0 then it means that bank $i$ defaults on its interbank payments. The loss for the interbank creditors is calculated as

$$\begin{aligned} loss = \pi ^{\top }(l-p^{*}) \end{aligned}$$

In order to compare the interbank losses in a standardised way across the banking system, we calculate an impact of the losses on a capital adequacy measure (CAR) defined as the Core Tier 1 capital divided by the risk weighted assets. Consequently, the CAR reduction of bank $i$ as a result of losses incurred on the interbank exposures is defined as

$$\begin{aligned} \Delta \mathrm{CAR}_i=100\cdot \left( \frac{\mathrm{CT}1_i-loss_i}{\mathrm{RWA}_i}-\mathrm{CAR}_i\right) \end{aligned}$$

where CT1 is Core Tier 1 capital and RWA denoted risk-weighted assets. The equilibrium payments vector is calculated in an iterative (sequential) procedure. Namely, let us define a function $F:[0,l_1]\times \dots \times [0,l_N]\rightarrow [0,l_1]\times \dots \times [0,l_N]$ as

$$\begin{aligned} F(p)=\min \left\{ \max \{C-a+l+\sum _{i=1}^N\pi ^{\top }p,0\},l\right\} \end{aligned}$$

(2)

The value of $F$ for a given $p$ can be interpreted as the vector of the interbank payment given banks receive back as much as $\pi ^{\top }p$ of their interbank assets. It can be shown that a sequence $(p^n)$ defined as $p^0=l$ and $p^n = F(p^{n-1})$ converges to the clearing payments vector $p^{*}$.¹⁶

The clearing payments vector approach to study the contagion effect is one of two common strands present in the literature. The other one is a cascade approach (see e.g. van Lelyveld and Liedorp 2006; Nier et al. 2007) that analyses sequences of banks’ defaults. Unlike in models of the cascade defaults, interbank clearing payments do not reflect any dynamics of contagion spreading. In the clearing payments theory, the equilibrium resolves immediately after an external shock affects a group of bank in a system (eg. in form of default on the interbank liabilities $\pi _{ij}\cdot l_i$ or reduction of the capital base $C_i$). As such, the sequence $(p^n)$ cannot be interpreted as a dynamic model of defaults but is rather a technical way to compute the equilibrium payments in an efficient way.

In an event-driven concept of contagion it is interesting to decompose the first and second round effects of contagion. First, we introduce a notion of a triggering bank, i.e. a bank that initially defaults on their interbank deposits (due to some exogenous shock not encompassed by the model). Second, we define the first round effects as those related purely to the default of banks on their interbank payments given

• default of a triggering bank or a group of triggering banks on all its interbank deposits,

• all other banks declaring to pay back all their interbank debts.

Third, the default of other banks following bank-triggers’ inability to pay back their interbank debts would be classified as second round contagion effects if

• they would pay back all their debts if all non-triggering banks which are their debtors returned their debts,

• they are not capable of paying back part of their interbank deposits in the clearing payments equilibrium.

In other words, first round effects describe the knock-on results nearest to the triggering banks in the network. The second round effects thus refer to all subsequent rounds of shock propagation. Formally, let us denote by $\mathcal J$ the set of triggering banks, i.e. $\mathcal J \subset \{1,\dots ,N\}$, and define $N\times 1$ vector $l(\mathcal J )$ as

$$\begin{aligned} l_i(\mathcal J ):=\left\{ \begin{array}{ll} l_i&{}\quad \text{ if } i\notin \mathcal J \\ 0&{}\quad \text{ if } i\in \mathcal J \\ \end{array}\right. \end{aligned}$$

It can be interpreted as an indicator for which banks are assumed not to pay back their interbank liabilities. Formally, the decomposition is defined as:

$$\begin{aligned} l-p^{\infty }=\underbrace{l-F\left( l(\mathcal J )\right) }_{\text{ I } \text{ round }}+\underbrace{F\left( l(\mathcal J )\right) -p^{\infty }}_{\text{ II } \text{ round }}, \end{aligned}$$

(3)

where $p^{\infty }$ is the limit of the iteration $p^n = F(p^{n-1})$ with $p^0=l(\mathcal J )$.

2.4 Fire sales of illiquid portfolio

The concept of the sequence $(p^n)$ is helpful in introducing the “fire sales” mechanism to the interbank equilibrium. In order to meet their obligations, banks may need to shed part of their securities portfolio; the less interbank assets they receive back, the higher is the liquidation need. This may adversely affect the mark-to-market valuation of their securities portfolios and further depress their capacity to pay back their interbank creditors. Consequently, this mechanism may lead to a spiral effect of fire sales of securities (as, for example, suggested in recent papers by Geanakoplos 2009 and Brunnermeier 2009.

Banks may respond in different ways to the losses on the interbank exposures depending on their strategies and goals. In order to cover the resultant liquidity shortfall, they may simply shed some assets. However, the sell-off may be much more severe for banks targeting their leverage ratio (see also Adrian and Shin 2010). In the latter case, the usually double digit ratio of “$x$” would translate into securities disposal of “$x*\mathrm loss$”. We account for both cases in our modeling framework of the “fire sales”.

Covering liquidity shortfall from interbank losses. We assume that the depth of the devaluation of securities portfolios is related to the share of the liquidated securities to the total volume of securities held by banks. In order to quantify this “fire sales” mechanism we introduce an auxiliary measure of the conditional amount of securities sold (SecSold) by bank $i$ given all banks pay back $p$ units of their interbank deposits, i.e.:

$$\begin{aligned} \mathrm SecSold (p)=\sum _{i=1}^N\min \{S_i,(p_i-l_i)^-\} \end{aligned}$$

(4)

where $S_i$ denotes the stock of securities held in the assets of bank $i$ and $a^-:=-\min (a,0)$, called a negative part of $a$.

The above formula sums up the volume of all the securities needed to cover the difference between interbank assets (equal to $(\pi ^{\top })_ip$ given banks pay back $p$ of their interbank debts, where $(A)_i$ denotes the $i$-th raw of a given matrix $A$) and interbank liabilities $l_i$. Obviously, a natural cap for that volume is the total volume of securities portfolio.

The new equilibrium interbank payments vector can be computed with a new loss absorption capacity which is equal to the initial capital level less the devaluation of the securities. Let TS denote the aggregate volume of securities held by the banks in the analysed system. Following the idea of Cifuentes et al. (2005), in order to relate the price of securities to the supply of these securities (equal to the volume of the “fire sales”) we introduce the $\alpha >0$ elasticity factor. Then the market value of securities is defined as $S(p):=S\exp \left( -\alpha \mathrm SecSold (p)/\mathrm TS \right)$. Hence, the equilibrium interbank payments vector $p^{*}$ satisfies

$$\begin{aligned} p^{*}\!=\!\min \{\max \{C\!-\!S\cdot \left( 1\!-\!\exp \left( \!-\!\alpha \frac{\mathrm{SecSold}(p^{*})}{\mathrm{TS}}\right) \right) -a+l\!+\!\sum _{i=1}^N\pi ^{\top }p^{*},0\},l\} \end{aligned}$$

(5)

The term $S\cdot \left( 1-\exp \left( -\alpha \mathrm SecSold (p^{*})/\mathrm TS \right) \right)$ reflects the negative impact of selling of securities at “fire sale” prices on the loss absorption capacity of banks. A discussion of some results of contagion in case of “fire sales” in the securities portfolio can be found in ECB (2012).

Target leverage ratio. The “fire sales” can be more pronounced if banks aim to maintain the target leverage ratio, i.e. the ratio of assets to the amount of capital. This strategy is usually an outcome of the optimal funding structure given the risk tolerance of the shareholders. Fulfilling that strategy, any loss, which depresses the capital base, would trigger asset sales bringing the leverage ratio to the assumed level. Should the banking system react in this way, the depth of asset disposal were typically 10 or 20 times higher than the interbank losses.

$$\begin{aligned} \mathrm{SecSold}^L(p)=\sum _{i=1}^N\min \left\{ S_i, \frac{\mathrm{TA}_i}{CT1_{i}}\left( p_{i}-l_{i}\right) ^{-}\right\} , \end{aligned}$$

(6)

where $\mathrm{TA}_i$ denotes total assets of bank $i$.

The existence of the equilibrium payments vector in both versions of the “fire sales” model follows application of the famous Tarski–Knaster’s theorem about fixed points of an isotone mapping (see a similar application by Hałaj 2012).

2.5 Advantages–disadvantages

The proposed simulation procedure, apparently of a Monte Carlo type, may potentially give results of any predefined accuracy but at a cost of long, even enormously long, computational time. Let the following parametrisation serve as an example. If 20,000 networks are to be generated, and for each of them the clearing payments be calculated (with and without “fire sales” mechanism) then a parallel mode computing in Matlab on 8 processor unit lasts $\sim$8 h.

The computational burden prompted us to try defining a simplified measure of a systemic importance of bank that would be far easier and faster to calculate. Obviously, the simplifying assumptions are likely to distort the results but that trade-off is unavoidable. We would treat a simplification as viable if the simplified model detects the same group of the most systemically important banks.

3 Systemic Probability Index

The main goal of the section is to define a measure of systemic fragility in the system, measure that reflects the losses generated via clearing payments vectors in the simulated networks. We have four general objectives:

• building an index (called: Systemic Probability Index) measuring the contagion risk stemming form the interbank structure rather than the risk related to an external shock;

• taking into account the whole range of possible interbank structures accounting for the probability map introduced in Sect. 2.1;

• designing it in such a way that it is easy and fast to compute for large interbank systems, at least substantially reducing the time of Monte Carlo simulations;

• providing consistent results with the most systemically important banks indicated by the losses derived upon the clearing payments method for the simulated network.

The Systemic Probability Index (SPI) reflects the likelihood of the contagion spreading across the banking system after a default of a given bank on its interbank debt. Therefore, it is a bank-specific measure, depending on the distribution of the interbank deposits and placements among banks and on the probability map. The rest of the section is devoted to describing the sufficient assumptions needed to satisfy the objectives listed above and leading to a particular definition of the Index. The performance of SPI is assessed in Sect. 4 by comparing the sets of systemically important banks indicated by SPI and clearing payments approach, and more quantitatively, by measuring correlation of the index with the interbank losses in the simulated networks.

Our starting point was to use a probability structure based on the simulated interbank networks to construct a measure of how likely, how broad and how fast is the interbank contagion spreading after a given bank defaults on all its interbank payments. Let us suppose that a node $I$ defaults on its interbank payments. What is the probability that node $j$ defaults? It can be expressed as

$$\begin{aligned} P^{(1)}_{Ij}=\mathbf P \left( G_{Ij}\pi _{Ij}l_I>C_j\right) , \end{aligned}$$

where $G_{Ij}$ is a random variable taking values from the set $\{0,1\}$, where 1 occurs with probability $P^{geo}_{Ij}$ (defined in Sect. 2.1). The relative exposure $\pi _{Ij}$ can formally be characterised by the joint probability of the whole matrix $\pi$. The algorithm of random networks in the Sect. 2.2 suggests a uniform distribution on a set of matrices with predefined sum of columns (given by $a$) and rows (given by $l$).

What is the impact of a default at round $k$ on the probability of default at round $k+1$? More precisely, what is the relationship between probability of default at $k$ and $k+1$? Let us assume that the default at $k$ means that the whole volume of debt is not returned back by the defaulted bank to its creditors. Thus,

$$\begin{aligned} P^{(k+1)}_{Ij}=\mathbf P \left( \sum _{i=1}^NG_{ij}\pi _{ij}\cdot P^{(k)}_{Ii}l_{i}>C_j\right) \end{aligned}$$

(7)

is the probability of default of the bank $j$ at time $k+1$ given that the probabilities of default of banks at time $k$ are $P^{k}_{Ij}$.

In order to calculate the probability index $P$ the distribution of the sum of $K$ independent uniform random variables $X_1,\dots ,X_K$ on intervals $[0,x_1], [0,x_2],\ldots , [0,x_K]$ has to be determined. However, even the simplest known to us characterisation of the distribution given by Bradley and Gupta (2002) leads to intractable recursion 7.¹⁷ All in all, this prompted us to consider a different distribution on edges, with an invariance property as far as summation is concerned.

The basic idea behind the simplification of the interbank network distribution refers to the flexibility with which the sum of normally distributed random variables can be handled. For that reason we replace the uniform distribution on edges of the network with normal distribution preserving some key characteristics of these edges. The simplification is summarised in the following assumption.

Assumption 1 For a given sequence of coefficients $(b_1,\dots ,b_N)$, the weighted sum of bank’s $j$ interbank relative exposures $\sum _{i=1}^Nb_iG_{ij}\pi _{ij}$ is approximated by the sum of normally distributed components $(\pi ^G_{ij})_{i\in \{1,\dots ,N\}}$ weighted by $b_i$s. The mean and standard deviation of the approximate relative exposure ratios $\pi ^G$ is

$$\begin{aligned} \mathbf E [\pi ^G_{ij}]=P^{geo}_{ij}\min (1,\frac{a_j}{l_i})/2, \quad \sigma (\pi ^G_{ij})=\frac{\sqrt{3}}{6}P^{geo}_{ij} \min (1,\frac{a_j}{l_i}) \end{aligned}$$

The assumption has a statistical justification based on central limit theorems. Namely, for a sufficiently large number of components, the sum of uniformly distributed variables can be quite accurately approximated by the normal distribution (see an extensive, but rather technical discussion in a working paper version Hałaj and Kok 2013). Most importantly, the approximation may understate the tail probabilities of network configurations that are crucial from the systemic risk perspective. We checked that the distribution of the original sum tends to have a systematically “fatter” right tail. Therefore, based on the Berry–Esseen theorem, we propose a correction term in the definition of the systemic probability index accounting for the maximum possible error in the approximation of the sum of uniform distributions, which is defined as (detailed explanation in Hałaj and Kok 2013):

$$\begin{aligned} \omega (P^{geo}_{\cdot j},d_{\cdot j},b^{(k)}_I)= 6\sqrt{3}\frac{\sum _{i=1}^N\left( \frac{(P^{geo}_{ij})^2}{16}+P^{geo}_{ij} \left( 1-\frac{P^{geo}_{ij}}{2}\right) ^4+\frac{(1-P^{geo}_{ij}) (P^{geo}_{ij})^3}{2}\right) (d_{ij}b^{(k)}_{Ii})^3}{\left( \sqrt{\sum _{i=1}^N\left( P^{geo}_{ij}d_{ij} b^{(k)}_{Ii}\right) ^2}\right) ^3} \end{aligned}$$

(8)

$\Phi (\cdot )$ is the cumulative probability function of the standard normal distribution and $d_{ij}:=\min (1,a_j/l_i)$. The coefficient $b^{(k)}_{Ii}$ can be interpreted as the size of the expected, $k$-round default of bank $i$ on its interbank payments. Namely, in a general case of a recovery ratio $R_i$ of the interbank losses, $b_{Ii}^{(k)}=P^{(k)}_{Ii}(1-R_i)l_i$.¹⁸ For brevity of notation, let us define a loss ratio $L_i=1-R_i$.

Summarising, we define the individual bank systemic indices in the following way:

Let $\gamma >0, b^{(k)}_I=[P^{(k)}_{I1}L_1l_1\, \dots \,P^{(k)}_{IN}L_Nl_N]^{\top }$ and

$$\begin{aligned} \omega _{Ij}^{(k)}=\omega (P^{geo}_{\cdot j},d_{\cdot j},b^{(k)}_I)K_1/\left( 1+|\frac{C_j-b^{(k)}_I\cdot \mathbf E [\pi ^G_{\cdot j}]}{\sqrt{(b_{I}^{(k)})^2\cdot D^2[\pi ^G_{\cdot j}]}}|^3\right) \end{aligned}$$

Define $\Sigma ^{(k)}_j:=\sum _{i=1}^N\pi ^G_{ij}\cdot P^{(k)}_{Ii}L_il_{i}$. Then, for all $k\in \mathbb N$ $P^{(k)}_{II}=1$. If $j\ne I$, then

$$\begin{aligned} P^{(1)}_{Ij}&= \left\{ \begin{array}{ll} \mathbf P (\pi ^G_{Ij}L_Il_I>C_j) &{}\quad \mathrm if \quad \mathbf P (\pi ^G_{Ij}L_Il_I>C_j)>\gamma \\ \min (\gamma ,\omega _{Ij}^{(1)}+\mathbf P (\pi ^G_{Ij}L_Il_I>C_j)) &{}\quad \mathrm if \quad \mathbf P (\pi ^G_{Ij}L_Il_I>C_j)\le \gamma \\ \end{array}\right. \nonumber \\ P^{(k+1)}_{Ij}&= \left\{ \begin{array}{ll} \mathbf P (\Sigma ^{(k)}_j>C_j) &{}\quad \mathrm if \quad \mathbf P (\Sigma ^{(k)}_j>C_j)>\gamma \\ \min (\gamma ,\omega _{Ij}^{(k)}+\mathbf P (\Sigma ^{(k)}_j>C_j)) &{}\quad \mathrm if \quad \mathbf P (\Sigma ^{(k)}_j>C_j)\le \gamma \\ \end{array}\right. \end{aligned}$$

(9)

The recursive formula 9 is complicated enough to deserve detailed explanations. First, $P^{(1)}_{Ij}$ indicates probability that bank’s $I$ default on interbank payments triggers losses in bank $j$ that are higher than capital of bank $j$. Therefore, bank $I$ is a triggering bank. The $\gamma$ fraction should be relatively low in order to account for the tail correction $\omega$. Second, the lion share of the distribution lies ex definitione within the admissible ranges. If the link between banks $i$ and $j$ is certain according to the probability map, i.e. $P^{geo}_{ij}=1$, then precisely $1-2\Phi (2\sqrt{3})\simeq 99.97~\%$ of the distribution belongs to the range $[0,\min (1,\frac{a_j}{l_i})]$. Third, the distribution is centered around $P^{geo}_{ij}\min (1,\frac{a_j}{l_i})/2$. Therefore, the lower the probability $P^{geo}$ of the link, the lower values are sampled from the distribution in Assumption 1 (with the vanishing link if $P^{ij}$ approaches 0). The main, unquestionable advantage of the index is a substantial reduction of the computational burden comparing with the Monte Carlo simulation; practically, the recursion can be explicitly solved. The first visible drawback of the index is the infinite support of the distribution which allows for realisations higher then 1 (the share in total exposures higher then 100 %). However, it happens with marginal probability. The same reasoning applies to equally probable shares of the distribution that are negative.

Summerising, the normal distribution simplifies the system a lot. This is shown in the following corollary:

Corollary 3.1

Let $m_{ij}:=\mathbf E [\pi _{ij}], \Delta l^{(k)}_i:=P^{(k)}_{Ii}L_il_{i}$. Then

$$\begin{aligned} \Sigma ^{(k)}_j\sim \mathcal N \left( \sum _{i=1}^Nm_{ij}\Delta l^{(k)}_i,\left[ \sum _{i=1}^N\left( m_{ij}\Delta l^{(k)}_i\right) ^2\right] ^{\frac{1}{2}}\right) \end{aligned}$$

A vector measure $P^{(k)}_{I\cdot }$ should be aggregated across the banking system to obtain a scalar and comparable measure of bank’s default impact on the interbank system, i.e. Systemic Probability Index. It can be done in many ways and we propose 2: one reflecting the limit (equilibrium) probability index and the other accounting for the speed with which the index stabilises at the equilibrium. In order to define the former, we weigh the individual indices at their limits by banks’ total assets. i.e.:

$$\begin{aligned} \mathrm SPI _I=\frac{\sum _{j=1}^N\mathrm TA _jP^{(\infty )}_{Ij}}{\sum _{j=1}^N\mathrm TA _j} \end{aligned}$$

(10)

The index representing the second mentioned type is computed in two steps. First, the individual path $P^{(1)}_{Ij}, P^{(2)}_{Ij},\ldots P^{(K)}_{Ij}$, for some large $K$ is averaged using the decreasing weights $\exp (-1\beta ), \exp (-2\beta ),\ldots \exp (-K\beta )$, with $\beta >0$ as a given decay factor. Second, as in the former case we weigh the resulting time weighted indices by banks’ total assets and define a time weighted average of individual indices in the following way:

$$\begin{aligned} P^w_{Ij}=\frac{\sum _{k=1}^{\infty } e^{-\beta k}P^{(k)}_{Ij}}{\sum _{k=1}^{\infty } e^{-\beta k}}=(e^{\beta }-1)\sum _{k=1}^{\infty } e^{-\beta k}P^{(k)}_{Ij} \end{aligned}$$

It depends on $\beta$ which measures how we weigh the importance of the outcomes from the early stages of the recursion 9. Consequently, the weighted Systemic Probability Index is defined as

$$\begin{aligned} \mathrm SPI ^w_I=\frac{\sum _{j=1}^N\mathrm TA _jP^w_{Ij}}{\sum _{j=1}^N\mathrm TA _j} \end{aligned}$$

(11)

Convergence It is not a priori obvious, that the Systemic Probability Index is well-defined. Namely, the individual probabilities $P_{Ij}^{(k)}$ may not be convergent as $k$ tends to infinity, what would lead to an ambiguity in the definition. However, it is not the case if only for some $k, P^{(k)}_{Ij}\ge \gamma$.

Theorem 3.1

For every $I\in \{1,\dots ,N\}$ and every $i\in \{1,\dots ,N\}$, the sequences $(P^{(k)}_{Ii})_{k\in \mathbb N }$ either converge, with the limit denoted $P_{Ii}^{(\infty )}$ or stay within a (narrow) band $[0,\gamma ]$ (with the limit defined in this case as ${\lim \sup }_kP^{(k)}_{Ii}$).

Proof

(rather technical and postponed to the Appendix)$\square$

Remark 3.1

The convergence is unconditional of $\gamma$ if no tail-correction is introduced. Then, the proof simplifies substantially.

4 Results

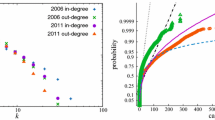
The very first conclusion about how reasonable is the simulated network approach rather than approaches focusing just on one particular network structure can be inferred from the topological properties of the simulated networks. For that purpose, we calculate the distribution of the betweenness measures for all nodes in the 20,000 simulated networks and compare those with the entropy maximising network (using the efficient RAS algorithm Mistrulli 2011) and the average network (described by the sum of all the simulated relative exposure matrices $\pi$ divided by 20,000). The results shown in Fig. 2. The complex shape of the resulting distributions suggests that none of the two calculated special networks are far from approximating the set of simulated networks. In addition, the study of systemically important nodes in the two special network cases could be misleading. For example, it is counterintuitive that (as indicated by the entropy maximising network) the Hungarian bank in our sample should be more systemically important than all the German banks in the sample or (as pointed out by the average network) that the default of one of the Irish banks may induce higher contagion than any of the German banks. Summing up, the simulated networks allow for analysing much richer structures related to the probability map of the geographical breakdown of banks’ activities than just the usually available (or estimated) one period snapshots. Otherwise, one ignores some very useful information about probabilities of the interbank links which is helpful in studying the tail contagion risk related to the variety of possible formation of the interbank structures.

Fig. 2

Betweenness-centrality measures: distribution on the simulated networks vs the average network. Blue line distribution on the simulated networks, red (vertical) line measure for the average simulated network, green (vertical) line measure for the entropy maximising network (color figure online)

Against this background, we now turn to discuss the contagion results based on our simulated networks. First, to illustrate the outcome of the network simulation, we compute—for each simulated network—the average Capital Adequacy Ratio reduction (i.e. average $\Delta \mathrm CAR _i$) in the event of one bank failing on its interbank liabilities. Figure 3 shows the distribution of average CAR reductions across all the simulated networks; with and without “fire sale” losses. It is observed that for the large majority of simulated networks the average solvency implications are relatively muted. In other words, contagious bank default is a tail-risk phenomenon. Broadly speaking, in 99 % of the scenarios the CAR reduction is negligible, while only in 1 percentage point of the network realisations the CAR reduction surpasses 0.2 percentage point. This suggests that the interbank network structures are overall fairly robust against idiosyncratic shocks to the system, which thus serves the purpose of diversifying risks among the banks. This notwithstanding, we also observe substantial non-linear effects in terms of contagion as for some, albeit limited in number, network structures the impact on overall banking sector capitalisation turns out to be much larger than for the vast majority of the networks.

Fig. 3

Distribution of the average CAR reduction (in p.p.)

It is furthermore noticeable from Fig. 4 that when including a fire sale mechanism the interbank contagion will increase the CAR reduction. It is, however, also observed that the additional contagion impact compared to the case without any fire sales is relatively limited under the “liquid assets” assumption described in Sect. 2.4. The fire sale impact is considerably more pronounced if banks instead are assumed to sell assets in order to retain a specific target leverage ratio, as the implications of contagious bank defaults now kick-in at substantially lower percentiles of the distribution of simulated networks (see Fig. 4). This finding is consistent with theoretical predictions about the potential for substantial and long-lasting spillover effects when financial intermediaries aim at controlling their leverage metrics.¹⁹ It also suggests that bank-specific characteristics are crucial determinants for contagion risk (see e.g. Nier et al. 2007).

Fig. 4

Distribution of the average CAR reduction with target leverage ratio (in p.p.)

Another notable feature of the simulated networks we observed is that in the vast majority of cases there are no substantial differences between the contagion effects derived using the probability map to simulate the networks and those derived without averaging out the cross-border exposures (i.e. disaggregate map).

We can also decompose the CAR reductions into first-round and second-round contagion effects; as proposed in Eq. 3 (see Fig. 5). We observe that while the first-round, or direct, effects are clearly dominating the overall impact across all banks, at least for some banks also the second-round shock propagation adds to the overall losses in the system. This shows that when analysing interbank contagion one needs to look beyond the direct exposures between the banks in the network, but also needs to consider potential knock-on effects once the first round impact of bank defaults has been accumulated.

Fig. 5

Decomposition of the distribution of individual banks’ CAR reduction into first and second round contagion (in p.p.). Blue area aggregate effect of first round contagion, red area (above the blue one) second round contagion (color figure online)

Turning now to the results based on the SPI, Fig. 6 shows the bank-by-bank SPI index values for the two different probability maps that we consider; i.e., one where banks are grouped into international and domestically-oriented institutions and another where no distinction is made between the different types of banks. We observe that according to the SPI only around a dozen of banks (mainly from Germany, France and Spain) out of the sample of 89 banks appear to be systemic in nature whereby a failure of one of these banks is attached with a high likelihood of spreading to the rest of the interbank network.

Fig. 6

SPI index for two different probability maps (for grouped banks into domestic/internationally active banks and for disaggregate data). SPI total assets weighted average of $P^{(\infty )}_i$s

It is furthermore noticeable that for the large majority of the banks the SPI based on the international/domestic grouping and the SPI based on the disaggregate measure (i.e. no grouping) are broadly the same. In other words, the same set of banks appear systemically relevant, according to the index, independent of the aggregation method. Only in a few cases, mainly pertaining to the French banking groups, we find that the “disaggregate” SPI lies significantly above the “grouped” SPI. For those few banks it thus appears that grouping banks according to their international activities matters, as their systemic relevance is somewhat “averaged out” taking into account the international dimension. In this sense, using the international/domestic grouping of banks is useful as it allows for detecting outliers.

With a view to using the SPI to identify the systemic nature of a bank, we find some indication that there is a clearly visible positive relationship between the SPI and the failure results from our simulated network (Fig. 7). The only exception concerns three German banks for which the SPI is relatively high compared to the simulated results. A simplistic method to quantify the positive relationships discerned in Fig. 7 is to calculate the correlation coefficient. Correlation of the index with the average CAR reductions related to the 10 % worst contagion losses is at the level of 64 % (see Table 1). Overall, this gives us confidence that the trade-off between computational simplicity and precision in the results does not compromise the SPI.

Fig. 7

Probability Index (SPI, y-axis) vs results of the simulation (log scale, x-axis). SPI total assets weighted average of $P^{(\infty )}_i$s; results of the simulation presented as the average of the 10 % worst losses induced by a given banks default on its interbank deposits

Table 1 Correlation between SPI, weighted SPI and average banks’ CAR reductions for a given percentile of distribution of the simulated networks

The results of the simulations and SPI can be compared also in a time dimension. For that purpose, we collected end of 2010 data on interbank assets and liabilities and capital from banks’ balance sheets and we performed an analogues exercise as for the 2011 data in order to calculate CAR reduction due to contagion losses and values of SPI indices. We used the same probability map as in the case of 2011 simulations. The results are presented in Fig. 8. There are two important conclusions that can be drawn from this comparison. First, at the end of 2011 the contagion risk measured by SPI increases (the 2011 line lies above the corresponding 2010 line on the upper part of the figure, except for one Dutch bank). Second, this observation is mostly confirmed by the $\Delta$CAR showing a general consistency between results of the simulation and SPI (apart from one French and one British bank).

Fig. 8

Comparison of results (simulation vs SPI) for 2010 and 2011 data. CAR reduction $=$ average of 10 % worst $\Delta$CAR (in pp)

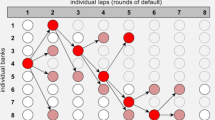
The importance of controlling for (especially French) banks’ international activities is also discernible when looking at the cascading effects on other banks conditioned on individual bank defaults. Thus, Fig. 9 illustrates the extent to which individual bank defaults trigger contagion to other banks when using the probability map, while Fig. 10 shows the same cascades but using the disaggregate map.

Common for both examples is that the knock-on effects of bank defaults on other banks tend to affect other domestic banks (red lines) first, and only subsequently (if at all) the shock propagates to foreign banks (green lines). Notably, the international contagion is more visible (especially for French banks, but also for German and UK banks) when applying the disaggregate map.

In general, it is notable that many banks only display contagion to other domestic entities whereas cross-border contagion appears to be substantially more limited. This may reflect that apart from a few large players the EU interbank market is still very much fragmented along national lines.

Fig. 9

Convergence of SPI index components for bank-triggers

Fig. 10

Convergence of SPI index components for bank-triggers with disaggregate probability map

The probability map was constructed defining internationally active banks as those with cross-border exposures exceeding an arbitrary threshold of 25 % of their total exposures. Checking the robustness of this assumption, in Fig. 11 the SPI impact of incrementally shocking the probability map entries are shown. We observe that for the large majority of banks marginally changing the probability map does not materially alter the results; especially in terms of the relative ranking of the banks. In other words, varying the thresholds for when a bank is internationally active does not materially affect the assessment of which banks are systemically relevant: systemic banks remain systemic, while non-systemic ones remain non-systemic.

Fig. 11

$\mathrm SPI$ and $\mathrm SPI ^w$ indices under various scenarios of $P^{geo}$. The original $P^{geo}$ matrix entries were randomly shocked by adding to each entry a number drawn from uniform distribution on interval $[-0.05,0.05]$ (100 scenarios considered)

So far, in our simulated networks we did not restrict the size of exposures a bank is allowed to hold against another bank. However, in practice banks are constrained by so-called “large exposure limits”.²⁰ To account for such regulations, we impose two conditions:

• 1. the sum of all exposures that (individually) exceed 10 per cent of the capital should not exceed 800 % of capital;

• 2. each exposure should not exceed 25 % of the total regulatory capital.

Figure 12 illustrates the implications in terms of CAR reductions when imposing such “large exposure limits”. As expected, this has the effect of substantially reducing the overall contagion impact across the networks compared to the situation without any limits to counterparty exposures (see Fig. 3).

Fig. 12

Distribution of the average CAR reduction for networks satisfying large exposure limits (in p.p.)

Having analysed the topological properties of the simulated networks and the distribution of losses induced by the networks it is natural to ask about any formal relationship between network measures and network related losses. More specifically, the question is whether there is a relationship between any of the centrality measures and the size of the losses. We tested measures like in- and out-degree, betweenness, clustering coefficient and—the very simple one—the average number of nodes. We have found (see Table 2) that the only insignificant correlation is between clustering measure and SPI or losses obtained from the clearing payments. Other statistical measures are positively correlated with the results of our model but the strength of the correlation differs substantially among the calculated network statistics and does not exceed 50 % (except for out-degree correlation with the SPI). This comparison proves that clearing payment losses (expressed in CAR reduction) and consequently SPI are complementary measures to the standard network statistics. They provide additional information about nodes’ systemic importance.

Table 2 Correlation between network statistics and the two simulated network measures (in %)

5 Conclusions

We propose two new tools to study the contagion risk in the banking system based on the simulated networks concept. Both abstract from the usual snapshot perspective in most contagion studies. The first tool allows for generating many possible interbank structures and for analysing distribution of clearing payments vector á la Eisenberg and Noe (2001). Since the simulation of the random networks is computationally costly we propose a second tool which is the so called SPI. It is based on the same set of information as the random networks (publicly available data and EBA disclosures on the geographical breakdown of banks’ activities) but is substantially easier to compute. Both tools give consistent results measured in terms of inclusion of the sets of systemic banks, i.e. banks that are found to be systemic in the random network tool (generate highest contagion losses in the interbank system) are confirmed to be systemic by the SPI.

The simulations that we performed confirm that contagion is heterogenous across the banking system and strongly non-linear. We found that there are banks that pose much higher contagion risk to the banking system than other banks. At the same time, a small fraction of possible network structures may spread relatively sizable contagion losses across the system, thus highlighting the non-linear nature of shock propagation effects. Contagion is very much a tail risk problem.

Our simulated networks approach (either in form of random networks or the SPI allows for comparison of the tail risk networks. Although, all of the simulated structures on average can transmit contagion of only very limited size, the impact of bank-triggers on the system may substantially differ in extreme cases. This is both confirmed by the simulations of contagion losses and by the SPI.

There is a couple of interesting extensions of the analysis presented in the article. We can group them into theoretical and empirical strands.

Sensitivity of contagion related to the changes of interbank activity and changes in capitalisation of nodes banks in the system is one research path that seems to be interesting to follow. Theoretically necessary conditions for a system to remain resilient to systemic risk would have interesting policy implications as far as simple monitoring of the system’s proneness to contagion risk is concerned. As far as the SPI is concerned, there is a couple of technical extensions to follow in order to bring the probability structure closer to the initial sum of uniform random variables (see working paper version Hałaj and Kok 2013 for some details). They may increase the accuracy of the SPI-based results, although at a higher computational cost, however still manageable.

The answer to the question about how realistic are the simulated networks could be obtained based on the interbank exposures extracted from the payment systems. An ideal source of data for the European banking system is the overnight interbank payments data. Not only can the simulated and the true structures be compared but the probability map could be estimated from the time series of the observed networks. Even if such the highly confidential data are not available for such the analysis, one could still study empirically the development of the contagion risk in time. For that purpose, at least a time series of the balance sheet interbank exposures should be gathered to verify how changes in other systemic risk measures (see Holló et al. 2012) correlate with the contagion losses in the simulated random networks or with changes in SPI.

Appendix

1.1 Proof of theorem 3.1

We focus on the triggering bank $I$. Let us define a mapping $\Psi _I:[0,1]^N\rightarrow [0,1]^N$ as

$$\begin{aligned} \Psi _{Ij}(z)=\left\{ \begin{array}{ll} \mathbf P ((\pi ^{\top })_I\cdot A(z)>C_j),&{}\mathbf P ((\pi ^{\top })_I\cdot A(z)>C_j)>\gamma \\ \min \left\{ \gamma ,B(z)+\mathbf P ((\pi ^{\top })_I\cdot A(z)>C_j)\right\} ,&{}\mathbf P ((\pi ^{\top })_I\cdot A(z)>C_j)\le \gamma \\ \end{array}\right. \end{aligned}$$

where $A(z)$ is an isotone, positive mapping and $B(z)$ a given mapping (in $\mathbb R$).

Suppose that $z_1\in [0,1]^N$ is such that $z_{1i}\ge \gamma$ and $z_1\succ z_2$. Then, $\Psi _I(z_1)\succ \Psi _I(z_2)$. It follows from the fact that $A(\cdot )$ is isotone and positive. In fact, $A(\cdot )$ and $B(\cdot )$ both depend on $j$ but we drop the index for brevity. Let us notice, that for $e$ being a unit vector (e.g. $e^{(k)}:=[\underbrace{0\dots 0}_{k}\ 1\ \underbrace{0\dots \ 0}_{N-k-1}]$), $e^{(k)}\preceq \Psi _I(e^{(k)})$, since by definition $\Phi _I$ is bounded by 0 and 1. If $\Psi _Ij(e^{(k)})\ge \gamma$, then the sequence $\Psi _Ij(e^{(k)}),\ \Psi _Ij\circ \Psi _Ij(e^{(k)}),\dots ,\ \Psi _Ij\circ \dots \circ \Psi _Ij(e^{(k)}),\dots$ is non-decreasing and, since is bounded by 1, it converges. It is, then, sufficient to prove the theorem by showing that $\Psi _I$ is isotone if $A(z)$ is replaced by $[z_1L_1l_1,\dots ,z_NL_Nl_N]^{\top }$. But trivially, $A_j(z)$ is increasing in every $z_i$. This completes the proof.

Remark 6.1

Why $(P_{Ij}^{(k)})$ may not be globally convergent? Set $b:\!=\![z_1L_1l_1\,\dots \,z_N$ $L_Nl_N]^{\top }$. Let $B(z)$ be replaced by

$$\begin{aligned} \left[ \begin{array}{cc} \omega (P^{geo}_{\cdot 1},d_{\cdot 1},b)\frac{K_1}{1+\left| \frac{C_1-b\cdot \mathbf E [\pi ^G_{\cdot 1}]}{\sqrt{b^2\cdot D^2[\pi ^G_{\cdot 1}]}}\right| ^3}\\ \vdots \\ \omega (P^{geo}_{\cdot N},d_{\cdot N},b)\frac{K_1}{1+\left| \frac{C_N-b\cdot \mathbf E [\pi ^G_{\cdot N}]}{\sqrt{(b)^2\cdot D^2[\pi ^G_{\cdot N}]}}\right| ^3}\\ \end{array}\right] . \end{aligned}$$

Let us represent $B$ in the following way (we slightly abuse the notation introducing $z$ to power $n^{\text{ th }}$, i.e. $z^n:=[z_1^n,\dots ,x_N^n]^{\top }$):

$$\begin{aligned} B(z)=B^1(z)B^2(z) \end{aligned}$$

where

$$\begin{aligned} B^1(z)&= \frac{Q^{(21)}\cdot z^3}{\sqrt{Q^{(22)}\cdot z^2}^3}\\ B^2(z)&= \frac{1}{1+\frac{C_j-Q^{(23)}\cdot z}{\sqrt{Q^{(24)}\cdot z^2}}} \end{aligned}$$

for positive vectors $Q^{(21)}, Q^{(22)}, Q^{(23)}$ and $Q^{(24)}$. We determine a region where $B$ is increasing. Namely, differentiating $B^1$ with respect to $z_i$ (in the set $\{z|\mathbf P ((\pi ^{\top })_I\cdot A(z)>C_j)<\gamma \}$), one observes that it is increasing if

$$\begin{aligned} 3Q^{(21)}_iz_i^2\sqrt{Q^{(22)}\cdot z^2}^3-3Q^{(21)}\cdot z^3\sqrt{Q^{(22)}\cdot z^2}Q^{(22)}_iz_i>0. \end{aligned}$$

It happens for $z$ bounded from $0^N$, i.e. for all $i\in \{1,\dots ,N\}$ satisfying

$$\begin{aligned} z_i>\frac{Q^{(22)}_i\sum _{m\ne i}Q^{(21)}_mz_m^3}{Q^{(21)}_i\sum _{m\ne i}Q^{(22)}_mz_m^2}. \end{aligned}$$

In case of $B^2$ the differentiation with respect to $z_i$ brings us to the following inequality

$$\begin{aligned} Q^{(23)}_iz_i\sqrt{Q^{(24)}\cdot z^2}+(C_j-Q^{(23)}\cdot z)\frac{Q^{(24)}_iz_i}{\sqrt{Q^{(24)}\cdot z^2}}>0 \end{aligned}$$

that translates into increasing $B^2$. The sufficient condition for the inequality to hold is $C_j-Q^{(23)}\cdot z>0$.