Random-intercept misspecification in generalized linear mixed models for binary responses

Abstract

We study properties of maximum likelihood estimators of parameters in generalized linear mixed models for a binary response in the presence of random-intercept model misspecification. Further exploiting the test proposed in an existing work initially designed for detecting general random-effects misspecification, we are able to reveal how the true random-intercept distribution deviates from the assumed. Besides this advance compared to the existing methods, we also provide theoretical insights on when and why the proposed test has low power to identify certain forms of misspecification. Large-sample numerical study and finite-sample simulation experiments are carried out to illustrate the theoretical findings.

1 Introduction

Cluster data arise naturally in a host of applications. For instance, in longitudinal studies, each subject is followed at multiple time points, producing repeated measures for each subject; or, at a fixed time point, measures of multiple traits of each subject are collected; in animal experiments, data on animals in each litter are recorded, with a cluster referring to a litter of animals. It is important in statistical analyses of such data to account for the correlation among observations within a cluster. When the response of interest is discrete, generalized linear mixed models (GLMM) provide a practically useful and mathematically flexible platform for analyzing cluster data. Random effects in GLMM are hypothetical, unobservable quantities that play the key role in characterizing cluster-specific features and introducing correlation among observations within a cluster. Molenberghs and Verbeke (2005), Jiang (2007), and McCulloch et al. (2008) provide comprehensive reviews on theories of GLMM and abundant examples of its application.

Most off-the-shelf statistical software carry out analyses of cluster data modeled by GLMM under the assumption that random effects follow normal distributions. There is a sizable collection of literature concerning statistical inference drawn based on this normality assumption when the assumption is violated. Some researchers reported empirical evidence along with theoretical explanations suggesting that likelihood-based inference can be compromised in the presence of random-effects model misspecification (Ten Have et al. 1999; Heagerty and Kurland 2001; Agresti et al. 2004; Litière et al. 2007, 2008). On the other hand, some studies showed that the bias in covariate (fixed) effects estimation due to this type of misspecification is usually small (Butler and Louis 1992; Neuhaus et al. 1992; McCulloch and Neuhaus 2011a, b; Neuhaus et al. 2013), although loss of efficiency in these estimators and an inflated Type I error when testing a covariate effect are observed. The consent among these existing works is that random-effects misspecification has non-negligible adverse effects on the estimators of variance components and the fixed intercept. Misleading inference on variance components and the intercept are unattractive in many fields of research. For example, in genetics, reliable inference for variance components are important to scientists (Scurrah et al. 2000); for many models in the item response theory, the intercept represents the item difficulty, a quantity very much of interest to psychometricians (Woods 2008). More importantly, random-effects distributions themselves are the focal point of studies in many applications. These applications include surrogate marker evaluation and psychometric properties evaluation, as well as pharmachokenetics (PK) and pharmechodynamics (PD), where mixed effects models are often used to characterize a PK/PD process with practically meaningful random effects that scientists wish to understand.

Relaxing model assumptions on random effects in GLMM is one way to avoid some of the aforementioned adverse effects. This motivates semi/non-parametric modeling for random effects in GLMM, such as those proposed by Follmann and Lambert (1989), Butler and Louis (1992), Zackin et al. (1996), Magder and Zeger (1996), Kleinman and Ibrahim (1998), Chen et al. (2002), Caffo et al. (2007), Lee and Thompson (2008), Komàrek and Lesaffre (2008), Wang (2010), Papageorgiou and Hinde (2012), and Lesperance et al. (2014). In the study presented in this article, we aim at exploiting informative diagnostic methods to assess the adequacy of an assumed random-effect distribution. Many existing methods sharing the same goal as ours are designed to estimate the random effects or their distributions (Ritz 2004; Pan and Lin 2005; Waagepetersen 2006). There exists a collection of Hausman-type tests constructed based on contrasting a statistic that is robust to such misspecification with another one that is sensitive to it (White 1982; Tchetgen and Coull 2006; Alonso et al. 2008; Bartolucci et al. 2015), following the general idea of the specification tests pioneered in Hausman (1978). A very similar idea of comparing two statistics is employed in Bartolucci et al. (2015) to detect time-variant unobserved heterogeneity in generalized linear models (GLM) for panel data, with one feature distinguishing it from the aforementioned Hausman-type tests, which is that both statistics can be sensitive to the time-invariant assumption. Claeskens and Hart (2009) considered order selection-type goodness-of-fit (GOF) tests in the framework of linear mixed models (LMM), which entails nesting the normal distribution for random effects within a bigger, thus more flexible, class of distributions, and then testing for normality against a higher-order, i.e., more complicated, model in the class. In theory, this idea is applicable to GLMM, but the lack of closed-form likelihood functions in general for GLMM discourages its use. Also, most GOF tests are not informative enough to shed light on how the true distribution differs from normal. Verbeke and Molenberghs (2013) proposed an exploratory diagnostic tool based on the gradient function, which can give certain indication of how the true random-effects distribution deviates from normal. Efendi et al. (2014) further constructed a test statistic based on this idea and developed a bootstrap procedure to estimate the p value associated with the test. Drikvandi et al. (2016) proposed yet another test based on the gradient function that outperforms the test in Efendi et al. (2014), who also derived the asymptotic null distribution of the proposed test statistic. A different aspect of informativeness is achieved by the diagnostic method proposed by Huang (2009), which can distinguish model misspecification on a random intercept from that on a random slope (among possibly multiple random slopes), but it can not tell how the true distribution deviates from the assumed. In this article, we further exploit her test statistic within the subclass of GLMMs where the random intercept is the only random effect, allowing one to gain more information on the direction of deviation of the true random-intercept distribution from an assumed distribution.

Standing in stark contrast to the Hausman-type diagnostic methods, which require some component of robust (to random-effects model assumptions) inference, our method does not require robust estimators, which free us from seeking for consistent inferential methods in the presence of model misspecification. The key ingredient that frees us from robust inference is the grouped data induced from the observed cluster data, which is described in Sect. 2 following the model formulated for the observed data. In Sect. 3, effects of random-intercept misspecification on maximum likelihood estimators (MLE) based on the raw data and the MLEs based on the grouped data are investigated. We revisit the test statistics in Huang (2009) in Sect. 4 to facilitate assessing an assumed random-intercept distribution. Following this review, we seek theoretical explanations for when and why the test has low power to detect certain types of misspecification. Implementation and performance of the proposed diagnostic method are illustrated via simulation in Sect. 5, where we compare our method with that in Tchetgen and Coull (2006) and two tests proposed in Alonso et al. (2008). In Sect. 6, we apply the proposed method to two real-life applications. We conclude the article with discussions on the contributions of our study and future research directions in Sect. 7.

2 Data and models

Denote by $\mathbf {Y}_i=(Y_{i1}, \ldots , Y_{in_i})^t$ the vector of observed binary responses from cluster i, and by $\mathbf {X}_i$ the $n_i \times p$ matrix of the associated covariates, with the jth row being $\mathbf {X}_{ij}$, for $i=1, \ldots , m, j=1, \ldots , n_i$. Suppose that the conditional mean of $Y_{ij}$ given the covariates and the random effect is

$$\begin{aligned} E\left( Y_{ij}| \mathbf {X}_{ij}, b_{i0}; \varvec{\beta }\right) = h\left( \mathbf {X}_{ij} \varvec{\beta }+ b_{i0} \right) , \text { for }\quad i=1, \ldots , m, \quad j=1, \ldots , n_i, \end{aligned}$$

(1)

where $\varvec{\beta }$ is the $p\times 1$ vector of fixed effects, $b_{i0}$ is the cluster-specific random intercept, and $h(\cdot )$ is a known inverse link function. Under the assumed model of $b_{i0}$, which is specified by the probability density function (pdf) indexed by parameter(s) $\tau$, $f_b(b_{i0}; \tau )$, the contribution of cluster i to the observed-data likelihood is $f_{\mathbf {Y}} ( \mathbf {Y}_i | \mathbf {X}_i; \varvec{\beta }, \tau ) = \int f_b(b_{i0}; \tau ) \prod _{j=1}^{n_{i}} h(\mathbf {X}_{ij} \varvec{\beta }+ b_{i0})^{Y_{ij}} \left\{ 1-h(\mathbf {X}_{ij}\varvec{\beta }+ b_{i0})\right\} ^{1-Y_{ij}}db_{i0}$, for $i=1, \ldots , m$. Note that the cluster-specific nature of $b_{i0}$ (in the true and assumed GLMMs) rules out scenarios with endogeneity, where a random effect depends on (or is correlated with) within-cluster covariates or where there is a time-varying unobserved individual effect as considered in Bartolucci et al. (2015).

To implement the proposed diagnostic method, another data set induced from the above observed data is needed. To create this induced data set, one partitions cluster i into $G_i$ groups and define grouped responses as $Y_{ig}^*=\max _{j \in I_{ig}}Y_{ij}$, where $I_{ig}$ is the index set such that $j\in I_{ig}$ indicates that observation j is in group g within cluster i, for $i=1, \ldots ,m$, $g=1, \ldots . G_i$. We defer discussions on some practical and theoretical consideration of the actual implementation of such partition to Sect. 7. Using the grouped data, letting $\mathbf {Y}_i^*=(Y^*_{i1}, \ldots , Y^*_{iG_i})^t$, one has the contribution of cluster i to the grouped-data likelihood as $f_{\mathbf {Y}^*}( \mathbf {Y}^*_i| \mathbf {X}_i; \varvec{\beta }, \tau )= \int f_b( b_{i0}; \tau ) \prod _{g=1}^{G_i} [1-\prod _{j\in I_{ig}} \{1-h(\mathbf {X}_{ij} \varvec{\beta }+b_{i0})\}]^{Y_{ig}^*} [\prod _{j\in I_{ig}}\{1-h(\mathbf {X}_{ij}\varvec{\beta }+b_{i0})\}]^{1-Y_{ig}^*} db_{i0}$, for $i=1, \ldots , m$.

Due to its appeal to practitioners, we consider for the majority of the article a normal assumed model for $b_{i0}$, where $\tau$ denotes the standard deviation of $b_{i0}$, and $f_b(b_{i0}; \tau )=\tau ^{-1}\phi (b_{i0}/\tau )$, with $\phi (\cdot )$ being the standard normal pdf. In addition, we also consider another assumed model for $b_{i0}$ that has aroused a great deal of interest among statisticians since its proposal in Wang and Louis (2003), namely the bridge distribution. The pdf of a mean-zero bridge distribution (for $b_{i0}$) is given by $f_b(b_{i0};\tau )=\sin (\tau \pi )/[2 \pi \{\cosh (\tau b_{i0})+\cos (\tau \pi ) \}]$, where $\tau \in (0, 1)$ and the standard deviation of $b_{i0}$ now becomes $\pi \sqrt{(\tau ^{-2}-1)/3}$. Like a normal distribution, the pdf of a bridge distribution is symmetric and bell-shaped but with a heavier tail. The appealing feature of a bridge distribution for $b_{i0}$ is that, if the link function in a GLMM is the logit link and $b_{i0}$ is the only random effect (as in our study), then the logit link is retained in the marginal model of $Y_{ij}$ (given $\mathbf {X}_{ij}$).

Define $\varvec{\varOmega }=(\varvec{\beta }^t, \tau )^t$ as the vector of all unknown parameters in the assumed GLMM, and denote by $\hat{\varvec{\varOmega }}$ the MLE of $\varvec{\varOmega }$ derived under the assumed model based on the observed data, and by $\hat{\varvec{\varOmega }}^*$ as the counterpart MLE based on the grouped data. In the next section, we look into the limits of $\hat{\varvec{\varOmega }}$ and $\hat{\varvec{\varOmega }}^*$ as $m\rightarrow \infty$ (with $\max _{1\le i \le m} n_i$ bounded) when the true distribution of $b_{i0}$ deviates from the assumed model in different ways. Throughout the article, the notational conventions used to denote the (limiting) MLEs of $\varvec{\varOmega }$ based on the observed/grouped data are also adopted for individual parameters in $\varvec{\varOmega }$.

3 Limits of maximum likelihood estimators

By invoking the Kullback–Leibler (KL) divergence between the true model and an assumed model, White (1982) established that $\hat{\varvec{\varOmega }}$ converges almost surely to

$$\begin{aligned} \tilde{\varvec{\varOmega }}=\arg \min _{\varvec{\varOmega }} \lim _{m \rightarrow \infty } m^{-1} E_{\mathbf {Y}|\mathbf {X}}\left\{ \log \frac{g_{\mathbf {Y}}(\mathbf {Y}|\mathbf {X};\varvec{\varOmega }_0)}{f_{\mathbf {Y}}(\mathbf {Y}|\mathbf {X};\varvec{\varOmega })}\right\} , \end{aligned}$$

(2)

where $g_{\mathbf {Y}} (\mathbf {Y}|\mathbf {X}; \varvec{\varOmega }_0)$ is the likelihood function of $\mathbf {Y}=\{\mathbf {Y}_i\}_{i=1}^m$ given $\mathbf {X}=\{\mathbf {X}_i\}_{i=1}^m$ under the correct model evaluated at the true parameter value $\varvec{\varOmega }_ 0$, $f_{\mathbf {Y}}(\mathbf {Y}|\mathbf {X};\varvec{\varOmega })$ is the observed-data likelihood under the assumed model, and the expectation is taken with respect to the true model of $\mathbf {Y}$ given $\mathbf {X}$. Similarly, $\hat{\varvec{\varOmega }}^*$ converges almost surely to

$$\begin{aligned} \tilde{\varvec{\varOmega }}^*=\arg \min _{\varvec{\varOmega }} \lim _{m \rightarrow \infty } m^{-1} E_{\mathbf {Y}^*|\mathbf {X}}\left\{ \log \frac{g_{\mathbf {Y}^*}(\mathbf {Y}^*|\mathbf {X};\varvec{\varOmega }_0)}{f_{\mathbf {Y}^*}(\mathbf {Y}^*|\mathbf {X};\varvec{\varOmega })}\right\} , \end{aligned}$$

(3)

where $g_{\mathbf {Y}^*} (\mathbf {Y}^*|\mathbf {X}; \varvec{\varOmega }_0)$ is the true-model likelihood of grouped data $\mathbf {Y}^*=\{\mathbf {Y}^*_i\}_{i=1}^m$, $f_{\mathbf {Y}^*}(\mathbf {Y}^*|\mathbf {X};\varvec{\varOmega })$ is the grouped-data likelihood under the assumed model, and the expectation is taken with respect to the true model of $\mathbf {Y}^*$ given $\mathbf {X}$.

In the upcoming two subsections, we first focus on a specific GLMM with the logit link, under which we are able to evaluate the KL divergence appearing in (2) and (3) nearly exactly. We then switch to a similar GLMM but with the probit link and the true distribution of $b_{i0}$ being a skew normal, which allows for more analytic derivations to reveal some properties of the MLEs under a misspecified random-intercept model.

3.1 Logistic GLMM

Consider a logistic regression model for $Y_{ij}$ given by, for $i=1, \ldots , m$ and $j=1, \ldots , 8$,

$$\begin{aligned} E\left( Y_{ij}| \mathbf {X}_{ij}, b_{i0}\right) = \left\{ 1+\exp \left( -\beta _0-\beta _1 X_{ij,1}-\beta _2 X_{ij,2}-\beta _3 X_{ij,1}X_{ij,2}-b_{i0}\right) \right\} ^{-1}, \end{aligned}$$

(4)

where $X_{ij,1}=x_{i}$ with $x_{i}$ equal to either 0 or 1, $X_{ij,2}=(j-1)/7$, and the true fixed effects values are $\varvec{\beta }=(\beta _0, \, \beta _1, \ \beta _2, \, \beta _3)^t=(-2, \, 1, \, 0.5, \, -0.25)^t$. With $n_i=8$ for $i=1, \ldots , m$, the sample space of $\mathbf {Y}_i$ consists of $256({=}2^8)$ distinct binary-valued $8 \times 1$ vectors, $\{\varvec{y}_l\}_{l=1}^{256}$. And, under the current covariates setting, $\mathbf {X}_i$ is equal to either $\mathbf {X}^{(1)}=[\varvec{1}\, \varvec{0}\, \mathbf {S}\, \varvec{0}]$ or $\mathbf {X}^{(2)}=[\varvec{1}\, \varvec{1}\, \mathbf {S}\, \mathbf {S}]$, where $\varvec{1}$ is the $8 \times 1$ vector of ones, $\varvec{0}$ is the $8 \times 1$ vector of zeros, and $\mathbf {S}=(0, \, 1, \ldots , 7)^t/7$. Now specifying $g_{\mathbf {Y}}(\mathbf {Y}_i|\mathbf {X}_i; \varvec{\varOmega }_0)$ boils down to finding two sets of probabilities, $\{\pi ^{(k)}(\varvec{y}_l)\}_{l=1}^{256}$, for $k=1, 2$, where $\pi ^{(k)}(\varvec{y}_l)=g_{\mathbf {Y}}(\varvec{y}_l|\mathbf {X}^{(k)}; \varvec{\varOmega }_0)$, for $l=1, \ldots , 256$. Because deriving these $512(=2\times 256)$ probabilities explicitly is infeasible even when the true distribution of $b_{i0}$ is normal, we use empirical probabilities observed from a large sample generated from the true model to approximate these true-model probabilities. More specifically, for each fixed-effect design matrix $\mathbf {X}^{(k)}$ ($k=1, 2$), we generate a random sample $\{\mathbf {Y}_i\}_{i=1}^{10^6}$ from the true model with $\mathbf {X}_i=\mathbf {X}^{(k)}$ for $i=1, \ldots , 10^6$, and use the observed proportion of $\varvec{y}_l$ to approximate $\pi ^{(k)}(\varvec{y}_l)$ for $l=1, \ldots , 256$. We further assume that $\mathbf {X}_i$ takes $\mathbf {X}^{(1)}$ or $\mathbf {X}^{(2)}$ equally likely across the entire sample. Once we obtain the two sets of true-model probabilities, finding $\tilde{\varvec{\varOmega }}$ defined in (2) is equivalent to maximizing

$$\begin{aligned} \sum ^{256}_{l=1}\sum _{k=1}^2 \pi ^{(k)}(\varvec{y}_l)\log f_{\mathbf {Y}}\left( \varvec{y}_l|\mathbf {X}^{(k)}; \varvec{\varOmega }\right) \end{aligned}$$

(5)

over $\varvec{\varOmega }$, where the integral that defines $f_{\mathbf {Y}}\left( \varvec{y}_l|\mathbf {X}^{(k)}; \varvec{\varOmega }\right)$, for $k=1, 2$ and $l=1, \ldots , 256$, is numerically solved using the M-point Gauss–Hermite quadrature, with a suitably large M. This recipe of finding $\tilde{\varvec{\varOmega }}$ follows the idea of artificial sample proposed by Rotnitzky and Wypij (1994), which was employed by Heagerty and Kurland (2001) and Huang (2009) to numerically obtain limiting MLEs under misspecified models. The accuracy of the resulting $\tilde{\varvec{\varOmega }}$ has been shown to be satisfactory in these existing works.

To fix the idea of grouped data, we set $G_i=2$, for $i=1, \ldots , m$, and split each cluster right at the middle according to the sorted values in $X_{ij,2}$. We then repeat the same exercise as above to find $\tilde{\varvec{\varOmega }}^*$ by maximizing the objective function, $\sum ^{4}_{l=1} \sum _{k=1}^2 \pi ^{(k)}(\varvec{y}^*_l)\log f_{\mathbf {Y}^*}\left( \varvec{y}^*_l|\mathbf {X}^{(k)}; \varvec{\varOmega }\right)$, over $\varvec{\varOmega }$, where $\pi ^{(k)}(\varvec{y}^*_l)=g_{\mathbf {Y}^*}(\varvec{y}^*_l|\mathbf {X}^{(k)}; \varvec{\varOmega }_0)$, for $k=1, 2$ and $l=1, \ldots , 4$.

With the theoretical formulations needed to numerically obtain $\tilde{\varvec{\varOmega }}$ and $\tilde{\varvec{\varOmega }}^*$ in position, we handpick the following four mean-zero true random-intercept distributions to pair with either the normal distribution or the bridge distribution as the assumed model for $b_{i0}$: (I) the standard normal distribution (when the assumed model is normal) or the bridge distribution with $\tau =0.5$ (when the assumed model is a bridge distribution); (II) a Student’s t distribution with degrees of freedom 8/3, resulting in a standard deviation of 2; (III) a shifted (via centering) and scaled (via multiplying $-2$) left-skewed gamma distribution with standard deviation 2, based on a gamma distribution with shape and scale parameters both equal to 1 (before shifting and scaling); (IV) a shifted and scaled right-skewed gamma distribution that is symmetric of (III). Table 1 presents $\tilde{\varvec{\varOmega }}$ and $\tilde{\varvec{\varOmega }}^*$ under different true models for $b_{i0}$ when one assumes a normal $b_{i0}$ (upper half of Table 1) and when one assumes $b_{i0}$ follow a bridge distribution (lower half of Table 1).

Table 1 Limiting MLEs based on the observed data, $\tilde{\varvec{\varOmega }}$, and limiting MLEs based on the grouped data, $\tilde{\varvec{\varOmega }}^*$, under different combinations of true/assumed models for $b_{i0}$

Results regarding $\varvec{\beta }$ shown in Table 1 are in line with the finding in Neuhaus et al. (1992), who concluded that the bias in the MLEs of the fixed effects is usually small, and $\tilde{\beta }_0$ can differ more from the truth when the true distribution of $b_{i0}$ is skewed. We reach a similar conclusion for $\tilde{\varvec{\beta }}^*$, which is not considered in the existing literature. Results regarding $\tau$ shown in Table 1 are more intriguing. When the true distribution of $b_{i0}$ is symmetric around zero but different from the assumed, a small or moderate amount of bias is present in $\tilde{\tau }$ and $\tilde{\tau }^*$, but the relative change from $\tilde{\tau }$ to $\tilde{\tau }^*$ is minimal. In contrast, when the true random-intercept distribution is skewed, although the bias in $\tilde{\tau }$ and $\tilde{\tau }^*$ may be small or moderate, the relative change from $\tilde{\tau }$ to $\tilde{\tau }^*$ is much more substantial. More interestingly, after translating $\tilde{\tau }$ and $\tilde{\tau }^*$ to the corresponding limiting MLEs of the standard deviation of $b_{i0}$, denoted by $\tilde{\sigma }$ and $\tilde{\sigma }^*$ respectively, we observe that $\tilde{\sigma }-\tilde{\sigma }^*<0$ when the true distribution of $b_{i0}$ is left-skewed, whereas $\tilde{\sigma }-\tilde{\sigma }^*>0$ when the true model is right-skewed. This pattern is observed under both assumed models for $b_{i0}$. The same clean contrast between $\tilde{\sigma }$ and $\tilde{\sigma }^*$ is also observed when the true model is multimodal with different directions of skewness (results omitted here). Later, in Sect. 4.2, we will provide some theoretical insight on the reason for this tantalizing phenomenon. Besides the skewness of the true random-intercept distribution, Alonso et al. (2008) provided empirical evidence showing that how much the MLEs are affected by random-intercept misspecification also depends on the variance of the true random-intercept distribution. Bearing this finding in mind, we purposefully set the variance of distributions (II), (III), and (IV) above to be the same across these three cases, which all correspond to scenarios where the assumed random-intercept model (either normal or bridge) deviates from the true model. With this common variance changed to other values (results not included in Table 1), the relative change from $\tilde{\sigma }$ to $\tilde{\sigma }^*$ remains substantial when the true model is skewed, with the sign of $\tilde{\sigma }-\tilde{\sigma }^*$ reflecting the direction of skewness.

Intrigued by the pattern of the limiting MLEs of $\tau$, we propose to use $\hat{\tau }-\hat{\tau }^*$ as the basis of an informative diagnostic test to reveal the direction of skewness of the true random-intercept distribution. Before we present a formal test statistic for this purpose, we wish to look more closely into the dependence of $\tilde{\varvec{\varOmega }}-\tilde{\varvec{\varOmega }}^*$ (and individual limiting MLEs) on the skewness of the true random-intercept distribution without being distracted by other features of the true distribution. This close inspection is made possible by considering a probit GLMM with the true model of $b_{i0}$ specified by a skew normal pdf, as elaborated in the next subsection.

3.2 Probit GLMM

Consider a probit regression model for $Y_{ij}$, $E(Y_{ij}| \mathbf {X}_{ij}, b_{i0}) = \varPhi (\mathbf {X}_{ij}\varvec{\beta }+b_{i0})$, for $i=1, \ldots , m$ and $j=1, \ldots , n_i$, where $\varPhi (\cdot )$ is the standard normal cumulative distribution function (cdf). Suppose that one assumes normal $b_{i0}$, but the true distribution of $b_{i0}$ is a skew normal (SN, Azzalini 1985) with mean zero and variance $\sigma ^2$, of which the pdf is $g_b (b_{i0}; \sigma , \, \alpha )=(2/\omega )\phi \{(b_{i0}+\alpha d \sigma )/\omega \} \varPhi \{(\alpha /\omega )(b_{i0}+\alpha d\sigma )\},$ where $\alpha$ is the shape parameter, $d = \sqrt{2/\{\pi (1+\alpha ^2)-2\alpha ^2\}}$, and $\omega = \sigma \sqrt{\pi (1+\alpha ^2)/\{\pi (1+\alpha ^2)-2\alpha ^2\}}$. Note that $\alpha <0$ results in a left-skewed distribution, $\alpha >0$ leads to a right-skewed distribution, and $\alpha =0$ yields a normal distribution.

With the probit regression model in conjunction with the SN random intercept, integrals used to define the true/assumed observed-data likelihood can be derived analytically up to the point where one only needs to evaluate the cdf of a multivariate normal. As shown in Appendix S1 of the supplementary material, the true observed-data likelihood for cluster i is, for $i=1, \ldots , m$,

$$\begin{aligned} g_{\mathbf {Y}}\left( \mathbf {Y}_i|\mathbf {X}_i; \varvec{\varOmega }\right) = 2P\left\{ V_{i0}\le 0, \, V_{ij} \le (-1)^{Y_{ij}} \left( -\mathbf {X}_{ij} \varvec{\beta }+ \alpha d \sigma \right) , \, j=1, \ldots , n_i \right\} , \end{aligned}$$

(6)

where $\mathbf {V}_i=(V_{i0}, \, V_{i1}, \ldots , V_{in_i})^t \sim N_{n+1}(\varvec{0}, \, \mathbf {S}_{\mathbf {V}_i})$, in which

$$\begin{aligned} \mathbf {S}_{\mathbf {V}_i}= \begin{bmatrix} 1+\alpha ^2&(-1)^{Y_{i1}+1}\alpha \omega&(-1)^{Y_{i2}+1}\alpha \omega&\ldots&(-1)^{Y_{in_i}+1}\alpha \omega \\ (-1)^{Y_{i1}+1}\alpha \omega&1+\omega ^2&(-1)^{Y_{i1}+Y_{i2}}\omega ^2&\ldots&(-1)^{Y_{i1}+Y_{in_i}}\omega ^2 \\ (-1)^{Y_{i2}+1}\alpha \omega&(-1)^{Y_{i1}+Y_{i2}} \omega ^2&1+\omega ^2&\ldots&(-1)^{Y_{i2}+Y_{in_i}}\omega ^2 \\ \vdots&\vdots&\vdots&\ddots&\vdots \\ (-1)^{Y_{in_i}+1}\alpha \omega&(-1)^{Y_{i1}+Y_{in_i}} \omega ^2&(-1)^{Y_{i2}+Y_{in_i}} \omega ^2&\ldots&1+\omega ^2 \end{bmatrix}. \end{aligned}$$

(7)

The observed-data likelihood function under the assumed model can be obtained by setting $\alpha =0$ in (6) and (7), resulting in the following likelihood evaluated at $\tilde{\varvec{\varOmega }}$, for $i=1, \ldots , m$,

$$\begin{aligned} f_{\mathbf {Y}}\left( \mathbf {Y}_i|\mathbf {X}_i; \tilde{\varvec{\varOmega }}\right) = 2P\left\{ W_{i0}\le 0, \, W_{ij}\le (-1)^{Y_{ij}+1}\mathbf {X}_{ij} \tilde{\varvec{\beta }}, \, j=1, \ldots , n_i\right\} , \end{aligned}$$

(8)

where $\mathbf {W}_i=(W_{i0}, \, W_{i1}, \ldots , W_{in})^t \sim N_{n+1}(\varvec{0}, \, \mathbf {S}_{\mathbf {W}_i})$ with

$$\begin{aligned} \mathbf {S}_{\mathbf {W}_i}= \begin{bmatrix} 1&0&0&\ldots&0 \\ 0&1+\tilde{\sigma }^2&(-1)^{Y_{i1}+Y_{i2}}\tilde{\sigma }^2&\ldots&(-1)^{Y_{i1}+Y_{in_i}}\tilde{\sigma }^2 \\ 0&(-1)^{Y_{i1}+Y_{i2}} \tilde{\sigma }^2&1+\tilde{\sigma }^2&\ldots&(-1)^{Y_{i2}+Y_{in_i}}\tilde{\sigma }^2 \\ \vdots&\vdots&\vdots&\ddots&\vdots \\ 0&(-1)^{Y_{i1}+Y_{in_i}} \tilde{\sigma }^2&(-1)^{Y_{i2}+Y_{in_i}} \tilde{\sigma }^2&\ldots&1+\tilde{\sigma }^2 \end{bmatrix}. \end{aligned}$$

(9)

Similarly, integrals that define the true/assumed grouped-data likelihood can also be greatly simplified, as elaborated in Appendix S1 of the supplementary material.

Having the aforementioned four (nearly) explicit likelihood functions not only improves the transparency of the numerical search for $\tilde{\varvec{\varOmega }}$ and $\tilde{\varvec{\varOmega }}^*$ as maximizers of the corresponding objective functions (such as (5)), but also allows analytic exploration of the dependence of these limiting MLEs on $\alpha$. In particular, because $\tilde{\varvec{\varOmega }}$ is the point in the r-dimensional parameter space that makes the wrong-model likelihood “look like” the truth-model likelihood evaluated at the true parameter values, one may compare (6)–(7) with (8)–(9) to get a sense of how $\tilde{\varvec{\varOmega }}$ differs from $\varvec{\varOmega }_0$. For example, to simplify the comparison, we approximate (8) by setting $(\tilde{\beta }_1, \, \tilde{\beta }_2, \, \tilde{\beta }_3)$ at the true parameter values, $(\beta _1, \, \beta _2, \, \beta _3)$. This approximation is not far-fetched because, as shown in Neuhaus et al. (1992), $(\hat{\beta }_1, \, \hat{\beta }_2, \, \hat{\beta }_3)^t$ are very close to being consistent in the presence of most random-intercept model misspecification. With this approximation, one can heuristically compare $\tilde{\beta }_0$ with the truth, $\beta _0$, by matching the upper bounds involved in the cdf in (6) with those in (8), that is, setting $(-1)^{Y_{ij}}(-\mathbf {X}_{ij}\varvec{\beta }+\alpha d \sigma )\approx (-1)^{Y_{ij}+1} \mathbf {X}_{ij}\tilde{\varvec{\beta }}$, resulting in $\tilde{\beta }_0 \approx \beta _0-\alpha d \sigma$. Because d, $\sigma >0$, this approximation for $\tilde{\beta }_0$ indicates positive bias in $\tilde{\beta }_0$ when $\alpha <0$, negative bias when $\alpha >0$, and zero bias when $\alpha =0$ (as expected).

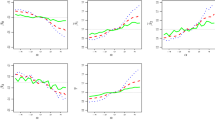
Using the same true values of $\varvec{\beta }$ and covariates setting as those in Sect. 3.1, fixing $\sigma$ at 1 in the true SN pdf and varying $\alpha$ from $-15$ to 15 at increments of 0.5, we obtain $\tilde{\varvec{\varOmega }}$ and $\tilde{\varvec{\varOmega }}^*$ as functions of $\alpha$. Figure 1 shows these functions and Fig. 2 depicts $\tilde{\varvec{\varOmega }}-\tilde{\varvec{\varOmega }}^*$. Note that the direction of bias in $\tilde{\beta }_0$ demonstrated in Fig. 1 reconciles with the above heuristic arguments about $\tilde{\beta }_0$. Figure 2 highlights the interesting phenomenon, partly underscored in Sect. 3.1, that the sign of $\tilde{\theta }-\tilde{\theta }^*$ solely depends on the sign of $\alpha$, where $\theta$ denotes generically a parameter in $\varvec{\varOmega }$; and the absolute difference, $|\tilde{\sigma }-\tilde{\sigma }^*|$, is much larger than that associated with any other parameter when $\alpha \ne 0$.

Fig. 1

Limiting MlEs of $\varvec{\varOmega }$ based on the observed (dashed lines)/grouped (solid lines) data versus $\alpha$ for probit GLMM with skew normal $b_{i0}$. The horizontal dotted reference line in each panel refers to the true value of the corresponding parameter

Fig. 2

Plot of $\tilde{\varvec{\varOmega }}-\tilde{\varvec{\varOmega }}^*$ versus $\alpha$ for probit GLMM with skew normal $b_{i0}$. Horizontal dotted reference lines signify the value zero

4 Model diagnostics

4.1 Revisit Huang’s test

Properties of limiting MLEs revealed in Sect. 3 suggest the following test statistic to facilitate diagnosing random-intercept model misspecification,

$$\begin{aligned} t_{\tau }=\left( \hat{\tau }-\hat{\tau }^*\right) /\hat{\nu }_\tau , \end{aligned}$$

(10)

where $\hat{\nu }_\tau$ is an estimator of the standard error of $\hat{\tau }-\hat{\tau }^*$. Recall that, if one assumes a normal random intercept, $\tau$ is the standard deviation of $b_{i0}$, i.e., $\sigma$; if one assumes a bridge distribution for $b_{i0}$, $\tau$ is the only parameter in the bridge distribution, of which $\sigma$ is a decreasing function. As implemented in Huang (2009), where more general GLMMs that include random slopes are considered, one may certainly construct test statistics like (10) associated with other parameters estimated along with $\tau$. That is, denoting by $\theta$ a generic element in $\varvec{\varOmega }$ and by $\hat{\mathbf {U}}$ an estimator of the variance–covariance matrix of $\hat{\varvec{\varOmega }}-\hat{\varvec{\varOmega }}^*$, one may consider $t_{\theta }=(\hat{\theta }-\hat{\theta }^*)/\hat{\nu }_\theta$, where $\hat{\nu }_\theta$ is the square root of the diagonal element of $\hat{\mathbf {U}}$ corresponding to $\theta$. One may also combine $t_{\theta }$’s for all parameters in $\varvec{\varOmega }$ in the following test statistic, $T^2=(m-r)\{r(m-1)\}^{-1}(\hat{\varvec{\varOmega }}-\hat{\varvec{\varOmega }}^*)^t \hat{\mathbf {U}}^{-1}(\hat{\varvec{\varOmega }}-\hat{\varvec{\varOmega }}^*)$, where r is the number of parameters in $\varvec{\varOmega }$. The estimator $\hat{\mathbf {U}}$ is derived from the influence-function approximation of $\hat{\varvec{\varOmega }}-\hat{\varvec{\varOmega }}^*$, as elaborated in Huang (2009). It is also shown there that, under the null hypothesis (to be stated momentarily), $T^2\sim F(r, m-r)$ and $t_{\theta }\sim \text {Student's }t$ with $m-r$ degrees of freedom asymptotically, and significant deviation from zero of any one of these test statistics signals some form of model misspecification.

Strictly speaking, these test statistics do not directly test $H_0:\, b_{i0}\sim N(0, \tau ^2)$ or $H_0:\, b_{i0}\sim {\text {bridge}}(\tau )$ versus an alternative. Instead, take $t_\tau$ as an example, it merely tests $H^*_0:\, \tilde{\tau }-\tilde{\tau }^*=0$ versus an alternative such as $H^*_a:\, \tilde{\tau }-\tilde{\tau }^* \ne 0$. As observed in the large-sample numerical studies in Sect. 3, $\tilde{\tau }-\tilde{\tau }^*$ can be very close to zero even if the true random-intercept distribution is neither normal nor a bridge distribution yet is also symmetric. Hence, $t_{\tau }$ (or even $T^2$) typically lacks power to distinguish two symmetric distributions for $b_{i0}$. This is the price we pay for letting go of robust inference, i.e., not requiring consistent estimators in the presence of model misspecification, in return for a more flexible and informative diagnostic test. More importantly, this is not surprising because of the intrinsic arbitrariness in random-effects modeling according to Verbeke and Molenberghs (2010), who concluded that “$\ldots$to any given model an entire class of (random-effects) models can be assigned, with all of its members producing the same fit to the observed data$\ldots$”. To look deeper into this “gray area” of the test, in the next subsection, we search for theoretical explanations for when and why $\tilde{\tau }-\tilde{\tau }^*\approx 0$. A byproduct of this search is an explanation for the relationship between the sign of $\tilde{\sigma }-\tilde{\sigma }^*$ and the skewness direction of the true random-intercept distribution observed in Sect. 3.

4.2 Local effects of skewness

We begin with formulating the true random-intercept distribution by contaminating the assumed distribution as $G_b=(1-\epsilon )F_{b,\tau _0}+\epsilon G^c_b$, where $G_b$ is the cdf of the true random-intercept distribution, $F_{b, \tau _0}$ is the cdf of the assumed distribution evaluated at the true parameter value(s) $\tau _0$, and $G^c_b$ can be viewed as the contaminating distribution that, along with the weight $\epsilon \in [0, 1]$, contributes to the discrepancy between the truth and the assumed model. This is also the formulation used in Gustafson (1996) when studying the so-called local effect of misspecification. Similar to the assumptions made in Gustafson (1996), to retain the interpretability of $\tau$ even in the wrong-model inference so that, for example, it is always meaningful to estimate the variance of $b_{i0}$, it is assumed that $F_b$ is parameterized in terms of moments of $b_{i0}$, and $G_b^c$ belongs to a class of distributions that have the same first two moments as those of $F_{b, \tau _0}$. This is a large enough class of contaminating distributions to keep the investigation of model misspecification interesting and practically well motivated, and also a sensible class to consider now that we wish to detect random-intercept misspecification mainly based on the difference between two estimators of the second moment of $b_{i0}$, $\hat{\sigma }-\hat{\sigma }^*$. To adapt to the context of Sect. 3, $F_{b, \tau _0}$ is assumed to correspond to a mean-zero symmetric distribution. Consequently, the direction of skewness of $G_b$ is fully determined by that of $G_b^c$ unless $\epsilon =0$.

Because $\epsilon$ partly controls the severity of distributional misspecification on $b_{i0}$, it is of interest to study $\tilde{\varvec{\varOmega }}$ and $\tilde{\varvec{\varOmega }}^*$ both as functions of $\epsilon$. Now, considering a first-order Taylor expansion of $\tilde{\varvec{\varOmega }}(\epsilon )$ and $\tilde{\varvec{\varOmega }}^*(\epsilon )$ around $\epsilon =0$, while noting that $\tilde{\varvec{\varOmega }}(0)=\tilde{\varvec{\varOmega }}^*(0)=\varvec{\varOmega }_0$, one can see that $\epsilon \tilde{\varvec{\varOmega }}'(0)$ and $\epsilon \tilde{\varvec{\varOmega }}^{*'}(0)$ are the first-order asymptotic bias of $\tilde{\varvec{\varOmega }}(\epsilon )$ and $\tilde{\varvec{\varOmega }}^*(\epsilon )$, respectively. This motivates us to derive the first derivative, $\tilde{\varvec{\varOmega }}'(0)$ and $\tilde{\varvec{\varOmega }}^{*'}(0)$. Like in Gustafson’s derivations, all derivatives evaluated at zero are right derivatives. Unlike Gustafson’s goal of study, we are less interested in each first-order bias term and more interested in the difference between these two bias terms for the purpose of model diagnostics. With details provided in Appendix S2 of the supplementary material, we first derive $\tilde{\varvec{\varOmega }}'(0)-\tilde{\varvec{\varOmega }}^{*'}(0)$, of which the element associated with $\sigma$ is of most interest. Based on this difference and assuming that both random-intercept distributions specified by $F_{b, \tau _0}$ and $G_b^c$ have pdf’s tail off as $b_{i0}$ (or b for short) deviates from zero, so that, under both $F_{b, \tau _0}$ and $G_b^c$, the majority of probability mass is assigned at a neighborhood of $b=0$, we show that

$$\begin{aligned} \tilde{\sigma }-\tilde{\sigma }^* = (\epsilon /6) \varDelta _\sigma ^{(3)}(0, \varvec{\varOmega }_0) E_{g^c}(b^3)+O(b^4), \end{aligned}$$

(11)

where $E_{g^c}(b^3)$ is the third moment of $G_b^c$, which determines the skewness of $G_b^c$; $\varDelta _\sigma ^{(3)}(0, \varvec{\varOmega }_0)$ is the third-order partial derivative of $\varDelta _\sigma (b, \varvec{\varOmega }_0)$ with respect to b evaluated at $b=0$, and $\varDelta _\sigma (b, \varvec{\varOmega }_0)$ denotes the element in the following $r\times 1$ vector corresponding to $\sigma$,

$$\begin{aligned} E_{\mathbf {X}} \left\{ \mathbf {I}^{-1}_{f*} \sum _{l=1}^4 \mathbf {s}^*(\varvec{y}_l^*; \mathbf {X}, \varvec{\varOmega }_0) f_{\mathbf {Y}^*}(\varvec{y}^*_l| \mathbf {X}, b; \varvec{\varOmega }_0) - \mathbf {I}^{-1}_f \sum _{l=1}^{2^n} \mathbf {s}(\varvec{y}_l; \mathbf {X}, \varvec{\varOmega }_0) f_{\mathbf {Y}}(\varvec{y}_l| \mathbf {X}, b; \varvec{\varOmega }_0) \right\} , \end{aligned}$$

(12)

in which $\mathbf {s}(\varvec{y}_l; \mathbf {X}, \varvec{\varOmega }_0)$ is the observed-data score function associated with the assumed model evaluated at $\varvec{\varOmega }_0$ and $\varvec{y}_l$, $\mathbf {s}^*(\varvec{y}^*_l; \mathbf {X}, \varvec{\varOmega }_0)$ is the counterpart grouped-data score function evaluated at $\varvec{y}^*_l$, $\mathbf {I}_f$ and $\mathbf {I}_{f^*}$ are the negative Fisher information matrices associated with these two scores, respectively. Looking at (11), one may conclude that the sign of $\tilde{\sigma }-\tilde{\sigma }^*$ is dominated by the sign of $\varDelta _\sigma ^{(3)}(0, \varvec{\varOmega }_0) E_{g^c}(b^3)$. Hence, it is expected that, if $G_b^c$ is symmetric and thus $E_{g^c}(b^3)=0$, $\tilde{\sigma }-\tilde{\sigma }^*\approx 0$, resulting in the aforementioned gray area of our test based on $t_\tau$. Given (12), it is numerically straightforward to compute $\varDelta _\sigma ^{(3)}(0, \varvec{\varOmega }_0)$ given any true parameter configuration (i.e., the value of $\varvec{\varOmega }_0$) and design matrix configuration (i.e., the distribution of $\mathbf {X}$). And we observe $\varDelta _\sigma ^{(3)}(0, \varvec{\varOmega }_0)\ge 0$ for a broad range of these configurations (see Appendix S2 for a pictorial demonstration). This explains the connection between the sign of $\tilde{\sigma }-\tilde{\sigma }^*$ and the skewness direction of $G_b$, which is fully determined by the sign of $E_{g^c}(b^3)$.

The phenomenon that $t_\tau$ has low power when $G_b$ is symmetric should not cause much concern as, after all, both $\hat{\varvec{\beta }}$ and $\hat{\varvec{\beta }}^*$ are practically unaffected by this type of misspecification. The informativeness of $t_\tau$ when $G_b$ is skew deserves more attention (and celebration) as this is the case where wrong-model inference suffers more. The information revealed by $t_\tau$ can be further exploited in choosing a more adequate model for the random intercept that is flexible yet constrained to reflect the direction of skewness. Imposing this constraint can improve the efficiency of inference compared to when one assumes a bigger class of flexible distribution family without the constraint imposed. Admittedly, such informativeness of $t_\tau$ can be partly due to the fact that we focus on the subclass of GLMMs where $b_{i0}$ is the only random effect, which is undoubtedly an important subclass that has been the topic of great interest among many researchers (Neuhaus et al. 1992; Wang and Louis 2003, 2004; Tchetgen and Coull 2006; Caffo et al. 2007, etc.). The operating characteristics of $t_\tau$ in the presence of random slope(s), whose distribution(s) may be misspecified, are among the topics of our follow-up investigation.

The last step of the derivations outlined above (and elaborated in Appendix S2) leading to (11) requires the assumption that the pdf associated with $G_b$ tails off outside a neighborhood of zero. We discuss in Appendix S3 of the supplementary material implication and consequences of violation of this assumption. The take-home message there is that $t_\tau$ can have some power to detect model misspecification when the pdf associated with $G_b$, although symmetric, does not tail off as b deviates from zero.

5 Empirical evidence

We realize that the test statistics defined in Sect. 4.1 have a similar structure as the test statistic proposed by Tchetgen and Coull (2006). Their method is applicable for GLMMs with at least one within-cluster covariate. Denote by $\varvec{\beta }^{W}$ the $q\times 1$ subvector of $\varvec{\beta }$ corresponding to the within-cluster covariate(s). Then an estimator of $\varvec{\beta }^{W}$ can be obtained based on the conditional distribution of a sufficient statistic for $\varvec{\beta }^{W}$ given a sufficient statistic for the random effects derived in Sartori and Severini (2004). Denote this estimator as $\hat{\varvec{\beta }}^{W}_{C}$, where the subscript “C” signifies that this estimator originates from a conditional likelihood rather than the marginal likelihood used to obtain the MLE of $\varvec{\beta }^{W}$, $\hat{\varvec{\beta }}^{W}$. Note that the term “conditional distribution/likelihood” in Tchetgen and Coull (2006) should not be confused with the conditional model of the response given random effect(s) as in, say, (1). By construction, $\hat{\varvec{\beta }}^{W}_{C}$ is robust to model assumptions on random effects. Making use of this feature, Tchetgen and Coull (2006) proposed to diagnose random-effects misspecification via the following test statistic that follows a $\chi _q^2$ asymptotically in the absence of model misspecification,

$$\begin{aligned} D=m\left( \hat{\varvec{\beta }}^W_C-\hat{\varvec{\beta }}^W \right) ^t \hat{\varvec{\varSigma }}^{-1}\left( \hat{\varvec{\beta }}^W_C-\hat{\varvec{\beta }}^W\right) , \end{aligned}$$

(13)

where $\hat{\varvec{\varSigma }}$ is the estimator for the variance-covariance matrix of $\hat{\varvec{\beta }}^{W}_{C}-\hat{\varvec{\beta }}^{W}$ derived based on influence functions corresponding to the two estimators, $\hat{\varvec{\beta }}^{W}_{C}$ and $\hat{\varvec{\beta }}^{W}$. We include their test as a competing method in the simulation study presented next.

In addition, we also implement two determinant tests developed by Alonso et al. (2008). These determinant tests exploit the equivalence between the inverse Fisher’s information matrix and the sandwich variance-covariance matrix in the absence of model misspecification (White 1982). The two test statistics are $\delta _{d1}=\log |\mathbf {B}(\hat{\varvec{\varOmega }})\{-\mathbf {A}^{-1}(\hat{\varvec{\varOmega }})\}|$ and $\delta _{d2}=|\mathbf {B}(\hat{\varvec{\varOmega }})||-\mathbf {A}^{-1}(\hat{\varvec{\varOmega }})|$, where $\mathbf {A}(\varvec{\varOmega }) = m^{-1}\sum _{i=1}^m \partial ^2 \log f_\mathrm{{\tiny \mathbf {Y}}}(\mathbf {Y}_i|\mathbf {X}_i; \varvec{\varOmega })/(\partial \varvec{\varOmega }\partial \varvec{\varOmega }^t)$, and $\mathbf {B}(\varvec{\varOmega }) = m^{-1}\sum _{i=1}^m (\partial \log f_\mathrm{{\tiny \mathbf {Y}}}(\mathbf {Y}_i|\mathbf {X}_i; \varvec{\varOmega })/\partial \varvec{\varOmega })(\partial \log f_\mathrm{{\tiny \mathbf {Y}}}(\mathbf {Y}_i|\mathbf {X}_i; \varvec{\varOmega })/\partial \varvec{\varOmega })^t$. The authors showed that, with $\hat{\varvec{\varOmega }}$ replaced by $\varvec{\varOmega }_0$ in these two test statistics, under regularity conditions (including that the score function is normally distributed), the asymptotic null distributions of $m\delta ^2_{d1}/(2r)$ and $m(\delta _{d2}-1)^2/(2r)$ are both $\chi ^2_1$. In what follows, we consider two simulation settings, with the first one closely mimicking that in Tchetgen and Coull (2006). Both R code and SAS IML code that implement the proposed method are available from the correspondence author upon request. Computing D, as well as the test proposed by Bartolucci et al. (2015), involves the conditional MLE of within-cluster fixed effects. Computing our test statistics only involves the marginal MLEs, which are less readily available in standard software when it comes to grouped data than conditional MLEs.

[Setting I]: In this experiment, given a realization of $\{b_{i0}\}_{i=1}^m$, binary responses $\{Y_{ij}, \, j=1, \ldots , n\}_{i=1}^m$ are generated according to the model considered in the accompanying technical report of Tchetgen and Coull (2006) at http://www.bepress.com/harvardbiostat/. In particular, this model is the same as that given in (4) but with the linear predictor being $\beta _0+\beta _1 X_{ij,2}+\beta _2 X_{ij,1}X_{ij,2}+b_{i0}$, where $\varvec{\beta }=(\beta _0,\, \beta _1,\, \beta _2)^t=(-0.5, \, 0.2, \, 0.5)^t$, the between-cluster covariate is $X_{ij,1}=x_i$, with $\{x_i\}_{i=1}^m$ simulated from Bernoulli(0.5), and the within-cluster covariate is $X_{ij, 2}=5(j-1)/(n-1)$, for $i=1, \ldots , m$, $j=1, \ldots , n$. We set $m=150, 300, 600$, and, at each level of m, four levels of n (3, 5, 8, 10) are considered. When creating grouped data, we set $G_i=2$ for $i=1, \ldots , m$, and partition each cluster into two subgroups according to the sorted values of $X_{ij,2}$. Fixing the assumed model of $b_{i0}$ at $N(0, \, \tau ^2)$, we consider the following five true models for $b_{i0}$ when generating $\{b_{i0}\}_{i=1}^m$: (I) N(0, 1); (II) a t distribution with standard deviation 2; (III) a shifted and scaled right-skewed gamma with standard deviation 2; (IV) a mixture normal specified by $\lambda N (2.0, \, 0.5)+ (1-\lambda )N(-0.86,\, 0.5)$, where $\lambda \sim {\text {Bernoulli}}(0.3)$; (V) $b_{i0}|X_{ij,1} \sim N\{0, \, (1+2X_{ij,1})^2\}$. For each simulation configuration, we generate 300 Monte Carlo (MC) replicates (to be consistent with the scale of simulations in Tchetgen and Coull (2006)), resulting in 300 sets of $t_\theta$ from our proposed method, 300 realizations of D defined in (13), and 300 realizations of $(\delta _{d1}, \, \delta _{d2})$. To compute Tchetgen and Coull’s D, we employ the SAS code provided in their technical report, implemented using PROC LogXact 7.0 for SAS 9.2 (Cytel Software, Inc. 2012). To compute our test statistics, we only need to go through two rounds of relatively more straightforward marginal, as opposed to conditional, maximum likelihood estimation. And quantities needed to compute the two determinant test statistics are readily available as byproducts from computing $\hat{\nu }_\theta$ involved in our test statistics.

Table 2 Rejection rates (in percentage) of our proposed test ($t_\theta$), the test proposed by Tchetgen and Coull (2006) (D), and the two determinant tests ($\delta _{d1}$, $\delta _{d2}$) in Alonso et al. (2008) across 300 MC replicates generated from the true model under Setting I in Sect. 5

Table 3 Rejection rates (in percentage) of our proposed test ($t_{\theta }$), the test proposed by Tchetgen and Coull (2006) (D), and two determinant tests ($\delta _{d1}$, $\delta _{d2}$) in Alonso et al. (2008) when $b_{i0}$ is assumed to follow a normal distribution across 900 MC replicates generated from the true model in Setting II in Sect. 5

Table 2 presents the proportions of tests among 300 MC replicates from each method that reject $H^*_0$, thus also reject $H_0: \, b_{i0}\sim N(0, \tau ^2)$, at significance level 0.05. Considering the “directional” nature of our test statistic, and now that we do know the sign of $\tilde{\tau }-\tilde{\tau }^*$ based on the skewness of the true distribution of $b_{i0}$, we also report rejection rates of our test assuming a one-sided alternative under cases (III) and (IV), besides the rejection rates associated with a two-sided alternative $H_a^*: \, \tilde{\tau }-\tilde{\tau }^*\ne 0$. Empirical evidence here suggest that our test confers the right size when the assumed random-intercept model coincides with the true model; and when the true model is skew, our test has comparable or higher power than Tchetgen and Coull’s test, especially when $n>3$. When the true model is symmetric as in case (II), where $b_{i0}$ follows a t distribution, the determinant tests have moderate power to reject the normality assumption when m and n are large. For case (V) with $b_{i0}|X_{ij,1} \sim N\{0, \, (1+2X_{ij,1})^2\}$, our $t_\tau$ performs like that under cases (I) and (II), which is not surprising because the true marginal distribution of $b_{i0}$ is symmetric, like those under cases (I) and (II). However, as seen in Table 2 under case (V), the test statistic $t_{\beta _2}$ sends strong signals to indicate model misspecification. This phenomenon of $t_\theta$, where $\theta$ is one of the fixed effects, is explored in Huang (2009) and Huang (2011), where more general GLMMs and more different types of random-effects misspecification are considered. This observation motivates inspection of $t_\theta$ for all parameters in $\varvec{\varOmega }$ if one wishes to discover existence of model misspecification besides the type we focus on in this article. When multiple $t_\theta$’s are used simultaneously for model diagnosis, one should address the issue of multiple testing, say, by using the Bonferroni correction.

[Setting II]: Note that both fixed effects in the model considered in Setting I are associated with within-cluster covariates, that is, $\varvec{\beta }^{W}=(\beta _1, \, \beta _2)^t$, and there is no fixed effect associated with the between-cluster covariate. We now consider another GLMM that includes a between-cluster covariate by itself so that $\varvec{\beta }$ contains a fixed effect ($\beta _1$) associated with the between-cluster covariate. This GLMM is specified by (4) with $\varvec{\beta }=(\beta _0, \, \beta _1, \beta _2, \beta _3)^t=(-2, \, 1, \, 0.5, \, -0.25)^t$. Except for that $X_{ij,2}=(j-1)/(n-1)$, the configurations of $X_{ij,1}$, the sizes of m and n, as well as the way to create grouped data, are the same as those in Setting I. Interestingly, with a between-cluster covariate by itself in the GLMM besides two within-cluster covariates, Tchetgen and Coull’s test (implemented using the authors’ SAS code applied to the model in Setting II) gives nearly no power in all considered configurations to detect random-intercept misspecification. Table 3 provides the rejection rates of our tests associated with a two-sided $H_a^*$, Tchetgen and Coull’s test, and the determinant tests when assuming a normal $b_{i0}$ across 900 MC replicates. Except when the true random-intercept distribution is a Student’s t, the proposed test mostly outperforms the competing tests. Table 4 shows the empirical power of the aforementioned tests when one assumes $b_{i0}$ follows a bridge distribution. To pair up with the assumed bridge distribution, we use the same five true distributions as in Setting I except that we replace the t distribution in (II) with the bridge distribution in order to monitor the size of the tests. The size of the determinant tests are severely inflated in this scenario (and thus their rejection rates in the presence of model misspecification in Table 4 are omitted). We again observe promising power of our test except when the true distribution is symmetric, while retaining the right size in the absence of model misspecification.

Table 4 Empirical size (in percentage) of our proposed test ($t_{\theta }$), the test proposed by Tchetgen and Coull (2006) (D), and two determinant tests ($\delta _{d1}$, $\delta _{d2}$) proposed by Alonso et al. (2008) in the absence of model misspecification, and rejection rates associated with $t_{\theta }$ and D in the presence of model misspecification when $b_{i0}$ is assumed to follow a bridge distribution across 900 MC replicates generated from the true model in Setting II in Sect. 5

Up to this point, the assumed random-intercept distribution has always been symmetric in our theoretical anlyses and simulation studies, a feature playing a key role especially in Sect. 4.2 where we establish analytically the connection between the skewness of the true random-intercept distribution and the sign of $\tilde{\sigma }-\tilde{\sigma }^*$. Keeping the model of $Y_{ij}$ given $\mathbf {X}_{ij}$ and $b_{i0}$ under Setting II, assuming that $b_{i0}$ follows a SN distribution specified by two parameters, $\alpha$ and $\sigma$, as introduced in Sect. 3.2, we compute $t_\sigma$ as we vary the true $b_{i0}$-distribution. Recall that the family of SN includes normal distributions as well as (unimodal) skewed distributions. To violate the model assumption, we consider generating $b_{i0}$ from three bimodal mixture normals given by a symmetric mixture normal, $0.5N(-1, 0.25)+0.5N(1, 0.25)$, a left-skewed mixture normal, $0.2N(-2, 0.16)+0.8N(0.5, 0.16)$, and a right-skewed mixture normal, $0.2N(2, 0.16)+0.8N(-0.5, 0.16)$. To monitor the size of the test, we also simulate $b_{i0}$ from N(0, 1). Figure 3 presents the rejection rates across 300 MC replicates when the cluster size is 10. The comparison between $\tilde{\sigma }$ and $\tilde{\sigma }^*$ when the assumed $b_{i0}$-distribution is skewed no longer follows the arguments in Sect. 4.2. But we still observe some empirical power from this experiment, suggesting that, this type of discrepancy between the assumed and the truth (unimodality versus bimodality) can lead to significant disagreement between the MLE of the variance component based on the raw data and the MLE from the grouped data. In this particular case, the estimated shape parameter of the assumed SN model can provide a clue on the direction of the skewness of the underlying truth.

Fig. 3

Plot of rejection rates (in percentage) of $t_{\sigma }$ when $b_{i0}$ is assumed to follow a skew normal distribution across 300 MC replicates generated from the true model in Setting II in Sect. 5. The true distribution is (I) N(0, 1), (II) a symmetric mixture normal, (III) a left-skewed mixture normal, and (IV) a right-skewed mixture normal, respectively

6 Real-data examples

In what follows, we entertain two real-life examples where cluster data are collected and modeled by GLMMs. For illustration purposes, we focus on using the proposed test to assess the adequacy of a GLMM with a random intercept, of which the distribution is assumed to be normal or a bridge distribution. Two-sided tests are considered in both examples when computing p-values associated with the tabulated test statistics.

Example 1

(Respiratory infection data): In this study 275 preschool children were examined every three months for 18 months for the presence of respiratory infection (Lin and Carroll 2001). Besides the binary response as an indicator of the presence/absence of a child’s infection status, each child’s age at the beginning of the study and the season when the examination took place were also recorded. We start from a relatively simple GLMM given by, for $i=1, \ldots , 275$, $j=1, \ldots , n_i$, with $n_i$ ranging from 4 to 6,

$$\begin{aligned} E\left( Y_{ij}| \mathbf {X}_{ij}, b_{i0}; \varvec{\beta }\right) = \left\{ 1+\exp \left( -\beta _0-\beta _1 X_{ij,1}-\beta _2 X_{ij,2}-b_{i0}\right) \right\} ^{-1}, \end{aligned}$$

(14)

where $X_{ij,1}$ is defined as $[\{{\text {baseline age (in months)}}-36\}/12]^3$, and $X_{ij,2}$ takes values 1, 2, 3, 4, representing the season of the jth examination for child i. The inclusion of a cubic term of baseline age in (14) is supported by Lin and Carroll (2001), who found that this term is highly statistically significant. To create grouped data, we leave the clusters with $n_i<3$ as they are, and for clusters with $n_i\ge 3$, we create two subgroups within each cluster according to the sorted values of $X_{ij,2}$. Using the raw observed data and the grouped data, we carry out maximum likelihood estimation to obtain $\hat{\varvec{\varOmega }}$ and $\hat{\varvec{\varOmega }}^*$ twice, first assuming $b_{i0}\sim N(0, \, \tau ^2)$, and second assuming $b_{i0}\sim {\text {bridge}}(\tau )$. For completeness, under each random-intercept assumed model, we compute $t_{\theta }$ for all parameters as well as $T^2$. The MLEs and the corresponding test results are tabulated in Table 5 (upper half of the table).

Table 5 Maximum likelihood estimates of $\varvec{\varOmega }$ and values of the corresponding test statistics computed in Example 1 (upper half of the table) and Example 2 (lower half of the table) in Sect. 6

According to Table 5, the test based on $t_{\tau }$ under neither assumed random-intercept model suggests significant discrepancy between $\hat{\tau }$ and $\hat{\tau }^*$, although the tests based on $t_{\beta _0}$ and $t_{\beta _2}$ show border-line significant evidence of model misspecification. Referring back to our observations in the simulation study, one may conclude that, the true distribution of $b_{i0}$ may have a variance component that depends on $X_{ij,2}$ and the marginal distribution of $b_{i0}$ (after “marginalizing out” $X_{ij,2}$) may be approximately symmetric. Additionally, we notice that the values of $t_{\beta _0}$, $t_{\beta _2}$, and $T^2$ under the normal assumed model for $b_{i0}$ are slightly more significant than those under the bridge-distribution assumption. This could be evidence that the true (marginal) distribution of $b_{i0}$ has a heavier tail, like that of a bridge distribution, than a normal distribution. Refitting the GLMM assuming other heavy-tailed distributions for $b_{i0}$ can be a follow-up model building exercise, which we do not further pursue in this example.

Example 2

(Toenail infection data): This data set is from a multi-center study, in which two oral treatments for toenail infection are compared (Fitzmaurice et al. 2004). In the study, each patient was scheduled to be evaluated for the degree of onycholysis seven times, although in the end only 224 out of a total of 294 patients provided the complete set of seven follow-up measures. The onycholysis outcome variable is the binary response of interest, with 0 representing none or mild infection and 1 indicating moderate or severe infection. Besides the response, recorded information of each patient include the treatment indicator, $X_{ij,1}$, and the time point (in months) when a measure was taken, $X_{ij,2}$, for $i=1, \ldots , 294$ and $j=1, \ldots , n_i$, where $n_i$ varies from 1 to 7. We adopt the GLMM considered in Molenberghs and Verbeke (2005, Chapter 14) given by $E\left( Y_{ij} | \mathbf {X}_{ij}, b_{i0}; \varvec{\beta }\right) = \left\{ 1+\exp \left( -\beta _0-\beta _1 X_{ij,1}-\beta _2 X_{ij,2}-\beta _3 X_{ij,1}X_{ij,2}-b_{i0}\right) \right\} ^{-1}$, where, as in Example 1, we first assume $b_{i0}\sim N(0, \, \tau ^2)$ and then assume $b_{i0}\sim {\text {bridge}}(\tau )$. To implement the proposed test, we partition each cluster of size greater than 2 into two groups according to the sorted values of $X_{ij,2}$, and leave the other smaller clusters as they are. Using the raw observed data and the induced grouped data, we obtain $\hat{\varvec{\varOmega }}$ and $\hat{\varvec{\varOmega }}^*$, along with the corresponding test statistics, under each assumed distribution for $b_{i0}$. These results are presented in Table 5 (lower half of the table).

Under both assumed models for $b_{i0}$, besides the overall test based on $T^2$, $t_\tau$ stands out as highly significant in Table 5, which is a strong signal suggesting that both assumed models for $b_{i0}$ are questionable. Moreover, because the value of $t_\tau$ is positive (negative) when a normal (bridge) random intercept is assumed, this test provides sufficient evidence that the true random-intercept distribution is right-skewed. We notice that, in Verbeke and Molenberghs (2013) where this data set is analyzed using the same GLMM, they estimated the distribution of $b_{i0}$ using a mixture normal, and the estimated density (Verbeke and Molenberghs 2013, Fig. 1(c)) is indeed right-skewed, matching up with our conclusion based on $t_\tau$. To follow up, we repeat our tests when $b_{i0}$ is assumed to follow a two-component mixture normal, with a common standard deviation $\tau$ in the two components. Now we obtain a p-value of 0.465 associated with $t_\tau$, suggesting that a mixture normal is likely a more adequate model for $b_{i0}$ than a normal distribution. Although in principle the proposed test can be used to check the adequacy of any assumed random-intercept distribution, we discourage its use on a complicated assumed distribution that is flexible at the price of involving many parameters. This is because the proposed test requires one to infer all unknown parameters using the less informative grouped data, which can be inefficient and in turn compromise the power of the test.

7 Discussion

In this study we are able to reveal more information of the true model and gain further insight of the diagnostic test in Huang (2009) when applying to GLMM with a random intercept $b_{i0}$ as the only random effect. Focusing on this class of GLMM, we discover an interesting connection between the discrepancy of the two limiting MLEs, $\tilde{\sigma }-\tilde{\sigma }^*$, and the skewness of the true random-intercept distribution, where $\sigma$ is the standard deviation of $b_{i0}$. We provide theoretical explanations for this connection, as well as other observed properties of MLEs. We find reasons for the low power of the proposed test in the presence of certain misspecification. With closed-form likelihood functions rarely available for GLMM, such theoretical development are important contributions that can advance the understanding of likelihood-based inference in the framework of GLMM in the presence of random-effects model misspecification.

Besides being able to detect random-intercept misspecification of the type that can substantially compromise inference, the test based on $t_\tau$ can reveal in what direction the true random-intercept distribution deviates from the assumed. Such valuable information is attained without estimating $b_{i0}$ or its pdf (as being attempted by many researchers). This advantage of the proposed method is achieved by drawing wrong-model inference twice, starting from the same assumed GLMM (with the same assumption on $b_{i0}$), first using the raw observed data and then using an induced grouped data set. It may be surprising, albeit expected after some in-dept theoretical exploration, that repeated wrong-model analyses can be more fruitful than exploitation of some robust/consistent inference in developing diagnostic methods. And the key to an informative diagnostic method based on wrong-model analyses is to understand how such analyses based on different types of data compare with each other, rather than how each round of wrong-model analysis is affected by model misspecification. This is a fresh view we have not seen in the existing literature on the topic of model diagnosis. To recap, when it comes to assessing model assumptions, making use of wrong-model analyses repeatedly can be a more fruitful direction than many traditional routes.

We have not addressed some practical issues related to creating grouped data. In all examples in this article, we set $G_i=2$ as long as $n_i\ge 2$, and we partition each cluster according to the sorted values of the within-cluster covariate. The motivation of partitioning according to the sorted values of a within-cluster covariate is to maximize the between-group variation of such covariate, which yields more informative groups within a cluster compared to groups randomly formed. Setting $G_i=2$ is mainly for simplicity, although one may legitimately concern about the information loss with such a small $G_i$ (compared to a bigger $G_i$). Noticing that the raw observed data is a special case of the grouped data with $G_i=n_i$, one may wish to distinguish $G_i$ from $n_i$ as much as possible (i.e., making $G_i$ as small as possible) so that the grouped data differ from the observed data more, which typically leads to more discrepancy between $\hat{\varvec{\varOmega }}$ and $\hat{\varvec{\varOmega }}^*$ (at least in limit) in the presence of model misspecification. However, with a smaller $G_i$, the variability of $\hat{\varvec{\varOmega }}^*$ is higher since more information are lost with fewer groups per cluster. Hence, there is a trade-off between $\tilde{\varvec{\varOmega }}-\tilde{\varvec{\varOmega }}^*$ and $\hat{\mathbf {U}}$. And the interplay of “discrepancy between limiting MLEs” and “finite-sample variability” is reflected in $t_\theta$ and $T^2$ constructed in Sect. 4.1. In other words, these test statistics are designed to balance these two factors by “standardizing” the discrepancy on the numerator, which weakens the dependence of the test statistics on $G_i$. Hence, in practice, one does not need to be too concerned about the choice of $G_i$. After all, the power of the proposed tests mainly depends on, first, the type of model misspecification, and second, the observed data structure, neither of which one can manipulate at the testing stage.

The above discussion leads to the awareness that forming grouped data is like a one-trick pony in the sense that one does not have many options to create grouped data that can influence the amount or the type of information one can obtain from the test statistics. This trick is useful enough for the subclass of GLMM considered in this article. It will be interesting to look into how the operating characteristics of the proposed tests are affected by co-existence of other model misspecification in a bigger class of GLMM. When there are multiple sources of model misspecification, we conjecture that more flexible ways of creating induced data from the observed data are needed to disentangle different inappropriate model assumptions. Rather than this one-trick pony considered in the current study, we have started looking into creating missing data within each cluster as a mechanism of constructing induced data, based on which wrong-model analyses are carried out (repeatedly). This direction has been shown to be promising in detecting model misspecification in LMM (Huang 2013). A referee brought up the possibility of applying the proposed idea to detect time-varying latent individual effects in GLM for panel data as those considered in Bartolucci et al. (2015). Although this context is beyond the scope of the current study, where exogeneity is imposed, we conjecture that some modification of the proposed test with a more careful design of the grouped data can yield tests for detecting time-varying unobserved heterogeneity. Lastly, we would like to point out that the presented study is in the frequentist framework, and the consideration of random-effects specification in the Bayesian framework is fundamentally different, as discussed in Grilli and Rampichini (2015). There, a complete specification of a random-effect distribution involves a conditional distribution of the random effect given $\tau$, and a prior for $\tau$.