Improved wrong-model inference for generalized linear models for binary responses in the presence of link misspecification

Abstract

In the framework of generalized linear models for binary responses, we develop parametric methods that yield estimators for regression coefficients less compromised by an inadequate posited link function. The improved inference are obtained without correcting a misspecified model, and thus are referred to as wrong-model inference. A byproduct of the proposed methods is a simple test for link misspecification in this class of models. Impressive bias reduction in estimators for the regression coefficients from the proposed methods and promising power of the proposed test to detect link misspecification are demonstrated in simulation studies. We also apply these methods to a classic data example frequently analyzed in the existing literature concerning this class of models.

1 Introduction

Since the seminal paper of Nelder and Wedderburn (1972), the class of generalized linear models (GLM) has received wide acceptance in a host of applications (McCullagh and Nelder 1989). It provides a practically interpretable and mathematically flexible platform for studying the association between a non-normal response and covariates of interest. In this study we focus on GLM for a binary response. The most popular GLM for binary responses assume a logit link, or probit, complementary log-log, etc., mainly due to ease of interpretation and convenient implementation using standard software. However, it has come to practitioners’ attention that a symmetry link, such as logit and probit, may not be reasonable in many applications; and the asymmetric complementary log-log link only allows a fixed negative skewness, making it too rigid for many scenarios. Many theoreticians concur with this concern regarding routine use of these popular links. For instance, Czado and Santner (1992) considered GLM for binary responses and showed that the maximum likelihood estimators (MLE) of regression coefficients obtained under an inappropriate link can be biased and inefficient.

There are two ways to avoid an inadequate link function. The more explored way is employing a flexible class of link functions (Aranda-Ordaz 1981; Guerrero and Johnson 1982; Morgan 1983; Whittemore 1983; Stukel 1988; Kim et al. 2007; Jiang et al. 2013). With a nonstandard link involved, inference results from methods along this line are usually harder to interpret than those from methods that use a standard link function. But, when a standard link is inadequate, methods adopting flexible links can better preserve certain integrity of covariate effects. This is especially important when the question of interest is whether or not there exists a significant covariate effect. Another way is to stick to one of the routinely used links, such as the logit link, and assume a more flexible functional form through which covariates enter the conditional mean model of the response. This approach can be unattractive to practitioners when a specific simple form of the linear predictor in GLM is desirable for meaningful interpretations of a covariate effect. This is the case in, for example, models in the item response theory as discussed in Samejima (2000). There, the author showed that the MLE for regression coefficients based on a logistic regression produces results that contradict with the psychological reality. As a remedy, she proposed a family of models with asymmetric links without revising the functional form of the linear predictor.

In this study, we develop parametric methods to achieve estimators for regression coefficients less compromised by link misspecification without correcting the assumed link or adopting a nonlinear predictor. Similar to methods that employ flexible link functions, the main benefit of the proposed methods is to avoid distorting inference for covariate effects due to a misspecified link, even though one sacrifices simple interpretation for the estimated covariate effects. To gain insight on the impact of link misspecification on regression coefficients estimation, we investigate asymptotic bias in the MLE for regression coefficients in the presence of link misspecification in Sect. 2. Results from the bias analysis motivate the first proposed bias reduction method we present in Sect. 3, followed by a second proposed method that also leads to substantial bias reduction in the MLE for regression coefficients in the presence of link misspecification. Section 4 reports simulation studies designed to illustrate the implementation and performance of the proposed methods. In Sect. 5, a simple yet powerful test for link misspecification is developed using byproducts of the proposed estimation methods, which unifies parameter estimation and model verification in one round of analysis based on maximum likelihood. The bias reduction methods and the new test for link misspecification are applied to a classic real-life data example in Sect. 6. Finally, we address some practical considerations, refinement of the proposed methods, and future research agenda in Sect. 7.

2 Effects of local link misspecification

2.1 Models and data

Suppose that one has a random sample consisting of n realizations of the response-covariate pair, (Y, X), and the mean of the binary response Y given X is $E(Y_i|X_i)=G(\beta _0+\beta _1 X_i)$, for $i=1, \ldots , n$, where the regression coefficients $\varvec{\beta }=(\beta _{0}, \beta _{1})^{{ \mathrm {\scriptscriptstyle T} }}$ are of central interest, and G(t) is a non-decreasing differentiable link function. Denote by H(t) the link one assumes for the mean model $E(Y_i|X_i)$ that differs from G(t). For notational simplicity, we assume a scalar covariate in this section. Generalization to multivariate regression models will be addressed in the next two sections.

Denoted by ${\tilde{\varvec{\beta }}}=({\tilde{\beta }}_0, {\tilde{\beta }}_1)^{ \mathrm {\scriptscriptstyle T} }$ the naive MLE for $\varvec{\beta }$ resulting from the misspecified model. To obtain an estimator less biased than ${\tilde{\varvec{\beta }}}$, we propose two strategies making use of a reclassified response $Y^*$ generated according to

$$\begin{aligned} P(Y^*=Y|Y, X)=\pi . \end{aligned}$$

(1)

In principle, one may let $\pi$ depend on (Y, X). For simplicity, a constant $\pi$ is used in the sequel. Combining (1) and the assumed GLM, one has the assumed model for $Y^{*}$ given X specified by $E(Y^*_i|X_i) = (2\pi -1)H(\beta _0+\beta _1 X_i)+1-\pi$, for $i=1, \ldots , n$. It has been shown that $\pi$ and $\varvec{\beta }$ are identifiable using the reclassified data $\{(Y^*_i, X_i)\}_{i=1}^n$ when $\pi \ne 0.5$ (Carroll et al. 2006, Section 15.3). Denote by ${\hat{\pi }}$ and ${\hat{\varvec{\beta }}}(\pi )$ the resulting MLEs for $\pi$ and $\varvec{\beta }$ based on the assumed model, respectively.

Since $\pi$ is a known constant in the user-designed reclassification model, one can literally see the finite sample bias in ${\hat{\pi }}$. Moreover, ${\hat{\pi }}$ and ${\hat{\varvec{\beta }}}(\pi )$ are entwined in the sense that the bias in one estimator correlates with the bias in the other estimator. This connection is the gateway to an estimator for $\varvec{\beta }$ that is less biased than ${\tilde{\varvec{\beta }}}$. We develop the first bias reduction strategy by exploiting this connection explicitly. Our second proposed strategy makes use of this connection implicitly. In particular, the first strategy is developed based on the following bias analysis of ${\hat{\varvec{\beta }}}(\pi )$ under mild link misspecification.

2.2 Asymptotic bias

Denote by p and $\varvec{b}=(b_0, b_1)^{ \mathrm {\scriptscriptstyle T} }$ the limiting MLEs for $\pi$ and $\varvec{\beta }$, respectively, under the assumed model based on the reclassified data as $n\rightarrow \infty$. According to the theories of MLEs resulting from misspecified models (White 1982), under regularity conditions, $(p, \varvec{b})$ is the point in the parameter space associated with $(\pi , \varvec{\beta })$ where the Kullback-Leibler distance between the true model likelihood and the assumed model likelihood for the reclassified data is minimized. Equivalently, $(p, \varvec{b})$ solves the following normal score equations, which we derive in the “Appendix”,

$$\begin{aligned} E\left( \frac{\mu _0-\mu }{\mu (1-\mu )} \begin{bmatrix} 2H(\eta )-1 \\ H'(\eta ) \\ H'(\eta )X \end{bmatrix} \right) ={\varvec{0}}, \end{aligned}$$

(2)

where the expectation is with respect to the distribution of X, $\eta =b_0+b_1X$, $H'(\eta )=(d/d\eta )H(\eta )$,

$$\begin{aligned} \mu =(2p-1)H(\eta )+1-p, \end{aligned}$$

(3)

is the mean of $Y^*$ given X under the assumed model evaluated at the limiting MLEs, $(p, b_0, b_1)$, and

$$\begin{aligned} \mu _0=(2\pi -1)G(\eta _0)+1-\pi \end{aligned}$$

(4)

is the mean of $Y^*$ given X under the correct model evaluated at the true parameter values, $(\pi , \beta _0, \beta _1)$, in which $\eta _0=\beta _0+\beta _1 X$.

To gain insight on the properties of $\varvec{b}$, we first consider a local model misspecification where the link misspecification is mild. More specifically, suppose that the true link relates to the assumed link via

$$\begin{aligned} G(t)=(1-\epsilon )H(t)+\epsilon G_c(t), \end{aligned}$$

(5)

for some small $\epsilon \in [0, 1]$, where $G_c(t)$ can be interpreted as the contamination link. In the presence of outliers in data, (5) can be interpreted as that, had there been no outliers (corresponding to $\epsilon =0$), H(t) would be an adequate link function in a GLM characterizing the data; with more extreme outliers (corresponding to a larger $\epsilon$), one has to modify one’s favorite link function, such as the logit link, to construct a less popular link G(t) in order to better capture the data with outliers as a whole. Following this interpretation, one essentially alleviates influence of outliers on regression coefficient estimation when one reduces bias in ${\tilde{\varvec{\beta }}}$, and the resultant bias-reduced covariate effect estimators can be interpreted in the same way as if the logit link, or other assumed H(t) one chooses, were the true link for outlier-free data.

Under the formulation of (5), $G_c(t)$ and $\epsilon$ together control the discrepancy between the true link and the assumed link. To signify the dependence of p and $\varvec{b}$ on the severity of link misspecification and the level of data coarsening, one may view these limiting MLEs as functions of $\epsilon$ and $\pi$, denoted by $p(\epsilon , \pi )$ and $\varvec{b}(\epsilon , \pi )$, respectively. Because setting $\epsilon =0$ in (5) gives $G(t)=H(t)$, i.e., the case without link misspecification, one has $p(0, \pi )=\pi$ and $\varvec{b}(0, \pi )=\varvec{\beta }$. With a small $\epsilon$ in the presence of a mild link misspecification, we consider a first order Taylor expansion of the two elements in $\varvec{b}(\epsilon , \pi )$, $b_0(\epsilon , \pi )$ and $b_1(\epsilon , \pi )$, around $\epsilon =0$,

$$\begin{aligned} \begin{aligned} b_0(\epsilon , \pi )&= \beta _0+b_0'(0, \pi )\epsilon +o(\epsilon ),\\ b_1(\epsilon , \pi )&= \beta _1+b_1'(0, \pi )\epsilon +o(\epsilon ), \end{aligned} \end{aligned}$$

(6)

where $b_0'(0, \pi )$ is equal to $(\partial /\partial \epsilon ) b_0(\epsilon , \pi )$ evaluated at $\epsilon =0$, which can be interpreted as a first order bias factor associated with $b_0$, and thus an asymptotic first order bias factor associated with $\hat{\beta }_0(\pi )$; $b_1'(0, \pi )$ is similarly defined and has a similar interpretation relating to $b_1$ and ${\hat{\beta }}_1 (\pi )$. We next derive these two bias factors by exploring an approximated solution to (2).

Solving (2) for $(p, \varvec{b})$ cannot be done explicitly in general. To simplify the equations to be solved, we assume that $(p, \varvec{b})$ is a point in the parameter space such that $\mu _0-\mu =0$ with probability one over the support of X. Such point may not exist in the parameter space except in some special model settings. This assumption is made for the sole purpose of envisioning an approximated solution to (2) that allows one to obtain some approximated first order bias factors in (6), which can shed some light on the effects of link misspecification. Following this assumption and defining $\delta =p-\pi$, one has

$$\begin{aligned} 0&= \mu _0-\mu \\&= (2\pi -1) G(\eta _0)+1-\pi -\left\{ (2p -1) H(\eta )+1-p \right\} , \text { by }(3) \text { and }(4), \\&= (2\pi -1)\{(1-\epsilon )H(\eta _0)+\epsilon G_c(\eta _0)-H(\eta )\}-2\delta H(\eta )+\delta , \text { by } (5), \\&= (2\pi -1)\left[ \epsilon \{G_c(\eta _0)-H(\eta _0)\}+H(\eta _0)-H(\eta )\right] +\left\{ 1-2H(\eta )\right\} \delta . \end{aligned}$$

(7)

Bearing in mind the dependence of $(p, \varvec{b})$ on $(\epsilon , \pi )$, we differentiate (7) with respect to $\epsilon$ to yield

$$\begin{aligned} 0&= (2\pi -1)\{G_c(\eta _0)-H(\eta _0)\}+\{1-2H(\eta )\}\frac{\partial p(\epsilon , \pi )}{\partial \epsilon }+H'(\eta )\left\{ \frac{\partial b_0(\epsilon , \pi )}{\partial \epsilon }\right. \\&\quad \left. +\frac{\partial b_1(\epsilon , \pi )}{\partial \epsilon }X\right\} (1-2p). \end{aligned}$$

(8)

Setting $\epsilon =0$ in (8) gives

$$\begin{aligned} 0&= (2\pi -1)\left\{ G_c(\eta _0)-H(\eta _0)\right\} +\left\{ 1-2H(\eta _0)\right\} p'(0, \pi ) \\&\quad +H'(\eta _0)\left\{ b_0'(0, \pi )+b_1'(0, \pi ) X \right\} (1-2\pi ), \end{aligned}$$

(9)

where $p'(0, \pi )$ is equal to $(\partial /\partial \epsilon )p(\epsilon , \pi )$ evaluated at $\epsilon =0$. Now that it is assumed that (9) holds with probability one over the support of X, one may evaluate X at any value in the support in this equation. Suppose that the support contains zero and one. By first setting $X=0$ and then setting $X=1$ in (9), one obtains the two bias factors in (6) given by

$$\begin{aligned} b_0'(0, \pi )&=\frac{G_c(\beta _0)-H(\beta _0)}{H'(\beta _0)}+\frac{\left\{ 1-2H(\beta _0)\right\} p'(0, \pi )}{(2\pi -1)H'(\beta _0)}, \end{aligned}$$

(10)

$$\begin{aligned} b_1'(0, \pi )&= \frac{G_c(\beta _0+\beta _1)-H(\beta _0+\beta _1)}{H'(\beta _0+\beta _1)}+\frac{\{1-2H(\beta _0+\beta _1)\}p'(0, \pi )}{(2\pi -1)H'(\beta _0+\beta _1)}-b_0'(0, \pi ). \end{aligned}$$

(11)

These first order bias factors can reveal some effects of link misspecification on the MLE for $\varvec{\beta }$. For instance, if $\beta _0=0$ and H(t) is a symmetric link, then (10) reduces to $b_0'(0, \pi )=\{G_c(0)-0.5\}/H'(0)$, for all $\pi$. This simple result of $b_0'(0, \pi )$ suggests that, if $G_c(t)$ is left-skewed (right-skewed), then $b_0'(0, \pi )<0 (>0)$, and thus $b_0$ tends to be smaller (bigger) than the truth. If G(t) is also symmetric, which means that $G_c(t)$ has to be symmetric unless $\epsilon =0$, then $b_0'(0, \pi )=0$, suggesting that the asymptotic bias in ${\hat{\beta }}_0(\pi )$ is of order $o(\epsilon )$ for all $\pi$. These patterns of $b_0$ are indeed observed for ${\hat{\beta }}_0(\pi )$, as well as ${\tilde{\beta }}_0$, in our simulation study. Moreover, according to (11), $\beta _1=0$ implies $b_1'(0,\pi )=0$ for all $\pi$. This is in line with the well established fact that $\beta _1=0$ implies $b_1=0$ even in the presence of link misspecification. Besides these implications on the direction of bias in ${\hat{\varvec{\beta }}}(\pi )$ and ${\tilde{\varvec{\beta }}}$, these bias factors along with (6) reveal a bias correction method we elaborate next.

3 Bias reduction using reclassified data

3.1 Explicit bias reduction

Evaluating (10) at two different values of $\pi$, $\pi _1$ and $\pi _2$, and forming the difference between the two resultant equations yields

$$\begin{aligned} b'_0(0, \pi _1)-b'_0(0, \pi _2) = \frac{\left\{ 1-2H(\beta _0)\right\} }{H'(\beta _0)}\left\{ \frac{p'(0, \pi _1)}{2\pi _1-1}-\frac{p'(0, \pi _2)}{2\pi _2-1} \right\} , \end{aligned}$$

hence, by (6),

$$\begin{aligned} b_0(\epsilon , \pi _1)-b_0(\epsilon , \pi _2)\approx & {} \frac{\left\{ 1-2H(\beta _0)\right\} }{H'(\beta _0)}\left\{ \frac{p'(0, \pi _1)}{2\pi _1-1}-\frac{p'(0, \pi _2)}{2\pi _2-1} \right\} \epsilon \\\approx & {} R(\beta _0)\left( \frac{p_1-\pi _1}{2\pi _1-1}-\frac{p_2-\pi _2}{2\pi _2-1} \right) , \end{aligned}$$

(12)

where $R(\beta _0)=\{1-2H(\beta _0)\}/H'(\beta _0)$, $p_k=p(\epsilon , \pi _k)$, for $k=1, 2$, and the substitution leading to the last equation is based on a first order Taylor expansion of $p(\epsilon , \pi )$ around $\epsilon =0$, $p(\epsilon , \pi )=\pi +p'(0, \pi )\epsilon +o(\epsilon )$. Inspired by (12), we propose the following estimator for $\beta _0$,

$$\begin{aligned} {\hat{\beta }}^{(1)}_0 = R^{-1}\left[ \left\{ {\hat{\beta }_0}(\pi _1)-{\hat{\beta }}_0(\pi _2)\right\} \left( \frac{{\hat{\pi }}_1-\pi _1}{2\pi _1-1}-\frac{{\hat{\pi }}_2-\pi _2}{2\pi _2-1}\right) ^{-1}\right] , \end{aligned}$$

(13)

where ${\hat{\beta }}_0(\pi _k)$ is the MLE for $\beta _0$ under the assumed model based on the reclassified data with $\pi =\pi _k$, for $k=1, 2$, and $R^{-1}(\cdot )$ is the inverse function of $R(\beta _0)$. For instance, if the assumed link H(t) is the logit function, then $R^{-1}(s)=\log 2-\log (\sqrt{s^2+4}+s)$.

Using (11) and following similar derivations that inspire ${\hat{\beta }}^{(1)}_0$, we construct the following estimator for $\beta _1$,

$$\begin{aligned} {\hat{\beta }}^{(1)}_1 = R^{-1}\left[ \left\{ {\hat{\beta }}_0(\pi _1)-{\hat{\beta }}_0(\pi _2)+{\hat{\beta }}_1(\pi _1)-{\hat{\beta }}_1(\pi _2)\right\} \left( \frac{{\hat{\pi }}_1-\pi _1}{2\pi _1-1}-\frac{{\hat{\pi }}_2-\pi _2}{2\pi _2-1}\right) ^{-1}\right] - {\hat{\beta }}^{(1)}_0, \end{aligned}$$

(14)

where ${\hat{\beta }}_1(\pi _k)$ is the MLE for $\beta _1$ under the assumed model based on the reclassified data with $\pi =\pi _k$, for $k=1, 2$.

How effectively the first proposed estimator $\hat{\varvec{\beta }}^{(1)}=({\hat{\beta }}^{(1)}_0, {\hat{\beta }}^{(1)}_1)^{ \mathrm {\scriptscriptstyle T} }$ reduces bias in ${\tilde{\varvec{\beta }}}$ depends on how severe the link misspecification is, since the construction of ${\hat{\varvec{\beta }}}^{(1)}$ originates from the Taylor expansion around $\epsilon =0$ in (6). In addition, ${\hat{\varvec{\beta }}}^{(1)}$ is derived based on the assumption that the solution to (2) solves a much simpler equation, $\mu _0-\mu =0$. This assumption allows us to derive the approximated bias factors in (10) and (11) without directly finding or approximating the solution to (2). If the so-obtained bias factors are misleading representations of the direction or magnitude of the true bias, ${\hat{\varvec{\beta }}}^{(1)}$ can be more biased than ${\tilde{\varvec{\beta }}}$. This can happen, for example, when X is a vector covariate, making the assumption that $\mu _0-\mu =0$ with probability one over the support of X further from reality. However, when X is a scalar whose support contains zero and one, ${\hat{\varvec{\beta }}}^{(1)}$ can substantially improve over ${\tilde{\varvec{\beta }}}$ as evidenced in the simulation study in Sect. 4.

3.2 Implicit bias reduction

The connection between ${\hat{\varvec{\beta }}}(\pi )$ and ${\hat{\pi }}$ is only marginally exploited in the first proposed estimator because ${\hat{\varvec{\beta }}}^{(1)}$ only uses two levels of reclassification, $\pi _1$ and $\pi _2$. More substantial bias reduction can be achieved by more fully exploiting the relationship between ${\hat{\varvec{\beta }}}(\pi )$ and ${\hat{\pi }}$, or, equivalently, the connection between ${\hat{\varvec{\beta }}}(\pi )$ and $d={\hat{\pi }}-\pi$. Instead of viewing ${\hat{\varvec{\beta }}}$ as a function of $\pi$, now it is more helpful to view it as a function of d, writing it as ${\hat{\varvec{\beta }}}(d)$. Since $\pi$ is a user-specified parameter in the reclassification model, one can empirically explore the connection between ${\hat{\varvec{\beta }}}(d)$ and d by setting $\pi$ at a sequence of K values over (0.5, 1), denoted by $\{\pi _k\}_{k=1}^K$, and computing $d_k={\hat{\pi _k}}-\pi _k$ and ${\hat{\varvec{\beta }}}(d_k)$ for each $k \in \{1, \ldots , K\}$. Using the sequence, $\{{\hat{\varvec{\beta }}}(d_k), d_k\}_{k=1}^K$, one may apply an extrapolant on ${\hat{\varvec{\beta }}}(d)$ to extrapolate to ${\hat{\varvec{\beta }}}(0)$. This extrapolation is intuitively sensible if one believes that ${\hat{\pi }}$ is inconsistent for $\pi$ unless the model for $Y^*$ given X is correctly specified, in which case ${\hat{\varvec{\beta }}}(d)$ is also consistent for $\varvec{\beta }$. In what follows, we summarize this proposed method in an algorithm that leads to our second proposed estimator for $\varvec{\beta }$, denoted by ${\hat{\varvec{\beta }}}^{(2)}=({\hat{\beta }}^{(2)}_0, {\hat{\beta }}^{(2)}_1)^{ \mathrm {\scriptscriptstyle T} }$.

• RC-1 For each $(j, k)\in \{1, \ldots , J\}\times \{1, \ldots , K\}$, generate reclassified responses $\{Y^*_{ijk}, i=1, \ldots , n\}_{j=1}^J$ according to (1) with $\pi =\pi _k$.

• RC-2 For each $(j, k)\in \{1, \ldots , J\}\times \{1, \ldots , K\}$, compute the MLEs for $\pi$ and $\varvec{\beta }$ based on data $\{(Y^*_{ijk}, X_i)\}_{i=1}^n$, resulting in estimates denoted by ${\hat{\pi }}_{k,j}$ and ${\hat{\varvec{\beta }}}_{k,j}$. Compute $\hat{\pi }_k=J^{-1}\sum _{j=1}^J {\hat{\pi }}_{k,j}$, $d_k={\hat{\pi }}_k-\pi _k$, and ${\hat{\varvec{\beta }}}(d_k)=J^{-1}\sum _{j=1}^J{\hat{\varvec{\beta }}}_{k,j}$, for $k=1, \ldots , K$.

• RC-3 View $\{{\hat{\varvec{\beta }}}(d_k), \, d_k\}_{k=1}^K$ as K realizations of the response-predictor pair $({\hat{\varvec{\beta }}}(d), d)$. Use these realizations to carry out regression analysis assuming a user-specified regression function.

• RC-4 Use the regression results from RC-3 to extrapolate the response ${\hat{\varvec{\beta }}}(d)$ at $d=0$, leading to the proposed estimate for $\varvec{\beta }$, ${\hat{\varvec{\beta }}}^{(2)}$.

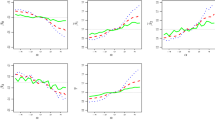
Figure 1 gives a pictorial illustration of the rationale behind this implicit bias reduction method. To produce plots in the upper panels, we fix the true model, from which a data set of size $n=600$ is generated, as a GLM with the link $G(t)=1/[1+\exp \{-h(t)\}]$, in which $h(t)=10 \{\exp (\alpha _1 t)-1\}I(t\ge 0)-10 \log (1+\alpha _2 t)I(t<0)$ with $(\alpha _1, \alpha _2)=(0.1, -0.1)$. This link function is depicted (as the dashed curve) in contrast to the logit link (as the solid curve) in Fig. 2. It is an example of generalized logit links (Stukel 1988) to be introduced more formally in Sect. 4. The true values of the regression coefficients are $\varvec{\beta }=(-1, 1)^{ \mathrm {\scriptscriptstyle T} }$. The upper panels show MLEs for $\varvec{\beta }$ and $\pi$ based on reclassified data induced from this one raw data set with $\pi$ varying over the range $[0.1, 0.4]\cup [0.6, 0.9]$, while always assuming a logistic model for Y given X. The nearly symmetric pattern with respect to the center point of the presented range of the horizontal axis shown these estimates indicates that varying $\pi$ over only the upper region above 0.5, such as [0.6, 0.9], can lead to a simpler and more effective extrapolation. More importantly, $\pi =0.5$ is a singularity where $\varvec{\beta }$ is not identifiable based on the corresponding reclassified data, even though the scatter plot of ${\hat{\pi }}$ versus $\pi$ suggests that ${\hat{\pi }}$ approaches 0.5 (the truth) as $\pi$ tends to 0.5, and hence $d={\hat{\pi }}-\pi$ approaches zero. This is consistent with the implication of the estimating equations in (2). By (4), $\mu _0=E(Y^*|X=x; \varvec{\beta })=0.5$ for all x and $\varvec{\beta }$; and thus, by (3), $p=0.5$ in conjunction with any value for $\varvec{b}$ solves (2) for all $\varvec{\beta }$. This is why ${\hat{\varvec{\beta }}}$ becomes ill-behaved as d approaches zero (due to $\pi$ approaching 0.5). Despite this singularity point of $\pi =0.5$, the first two upper panels do imply certain dependence of ${\hat{\varvec{\beta }}}$ on d that motivates the implicit bias reduction method. To show such dependence from a different angle, we design another experiment where we fix $\pi$ at 0.9 when generating reclassified data, and vary the true GLM from which the raw binary responses are simulated, where the link functions in these models are generalized logit links with $(\alpha _1, \alpha _2)=(a, -a)$, in which a varies from 0 to 0.5. As pointed out in Sect. 4, the generalized logit link with $(\alpha _1, \alpha _2)=(0, 0)$ is simply the logit link, producing a case where the assumed logistic model coincides with the true model. Using the reclassified data induced from each raw data set at a fixed a-level, we obtain the MLEs for $\varvec{\beta }$ and $\pi$ shown in the lower panels in Fig. 1. Like those seen in the upper panels, the dependence of ${\hat{\varvec{\beta }}}$ on d is evident, and the former becomes closer to the truth as d gets closer to zero, but without the concern of ill-behaved ${\hat{\varvec{\beta }}}$ near the singularity point of $\pi =0.5$ observed in the upper panels.

Certainly, in a given application with one observed data set for (Y, X), one cannot vary the underlying true model as we did to create plots in the lower panels in Fig. 1. In order to empirically manifest the dependence of ${\hat{\varvec{\beta }}}$ on d, one creates movements in d by varying $\pi$ when generating reclassified data based on one given raw data set while avoiding the singularity point of $\pi =0.5$. One concern of extrapolating at $d=0$ in RC-4 is that this direction of extrapolation is equivalent to pushing $\pi$ towards 0.5. Although this is a legitimate concern, the hope here is that the dependence of ${\hat{\varvec{\beta }}}$ on d observed in the lower panels of Fig. 1 can be preserved well enough over the majority of the lower or upper half range of $\pi$ so that one can utilize the preserved dependence over such range to learn the underlying dependence of ${\hat{\varvec{\beta }}}$ and d as model misspecification diminishes (corresponding to a shrinks to zero in the lower panels of Fig. 1.)

Fig. 1

Upper panels show ${\hat{\varvec{\beta }}}$ versus $d=\hat{\pi }-\pi$ and ${\hat{\pi }}$ versus $\pi$ based on reclassified data induced from a data set of size $n=600$ generated according to a GLM with a generalized logit link with $(\alpha _1, \alpha _2)=(0.1, -0.1)$, where the reclassified data correspond to $\pi$ varying over the range $[0.1, 0.4]\cup [0.6, 0.9]$. Lower panels show ${\hat{\varvec{\beta }}}$ versus d and ${\hat{\pi }}$ versus a as a varies within [0, 0.5] based on one reclassified data with $\pi =0.9$ at each level of a induced from a data set of size $n=600$ generated from a GLM with the generalized logit link with $(\alpha _1, \alpha _2)=(a, -a)$. In the four panels regarding ${\hat{\varvec{\beta }}}$, solid lines imposing on the scatter plots result from the loess fit, red dotted lines are the reference lines highlighting $d=0$ and the truth of $\varvec{\beta }$. The solid line in the plot of ${\hat{\pi }}$ versus $\pi$ is a $45^\circ$ reference line. The solid line in the plot of ${\hat{\pi }}$ versus a is the reference line signifying the true value of $\pi$, 0.9

This proposed method shares some similarity with a bias reduction method well received in the measurement error community, known as the simulation extrapolation (SIMEX) method (Cook and Stefanski 1994; Stefanski and Cook 1995). Consider a more general setting where one has a method to consistently estimate a parameter, say, $\theta$, based on data $\{(Y_i, X_i)\}_{i=1}^n$. Suppose that $\{X_i\}_{i=1}^n$ are unobserved, and the actual observed covariate values are $\{W_i\}_{i=1}^n$, where $W_i=X_i+U_i$, in which $U_i$ is the nondifferential measurement error (Carroll et al. 2006, section 2.5) for $i=1,\ldots , n$. If one ignores measurement error, one would apply the same estimation method to data $\{(Y_i, W_i)\}_{i=1}^n$ to estimate $\theta$, resulting in a naive estimator denoted by ${\tilde{\theta }}$, which is typically inconsistent. To reduce bias in ${\tilde{\theta }}$, the SIMEX method exploits further contaminated covariate data as in the following algorithm, where $\lambda _1<\lambda _2<\ldots <\lambda _{\mathrm{K}}$ are a sequence of user-specified positive constants.

• SM-1 For each $(j, k)\in \{1, \ldots , J\}\times \{1, \ldots , K\}$, generate further contaminated covariate data, $\{W^*_{ijk}=W_i+\sqrt{\lambda _k}U^*_{ij}, \, i=1, \ldots , n\}_{j=1}^J$, where $\{U^*_{ij}\}_{i=1}^n$ are user-simulated pseudo errors that follow the same distribution as $\{U_i\}_{i=1}^n$, and are independent across $j=1, \ldots , J$.

• SM-2 For each $(j, k)\in \{1, \ldots , J\}\times \{1, \ldots , K\}$, compute the naive estimate for $\theta$ using data $\{(Y_i, W^*_{ijk})\}_{i=1}^n$, denoted by ${\hat{\theta }}_{k,j}$. Compute $\hat{\theta }(\lambda _k)=J^{-1}\sum _{j=1}^J{\hat{\theta }}_{k,j}$, for $k=1, \ldots , K$.

• SM-3 View $\{{\hat{\theta }}(\lambda _k), \, \lambda _k\}_{k=0}^K$ as $K+1$ realizations of the response-predictor pair $(\hat{\theta }(\lambda ), \lambda )$, where $\lambda _0=0$ and $\hat{\theta }(0)={\tilde{\theta }}$. Use these realizations to carry out regression analysis assuming a user-specified regression function.

• SM-4 Use the regression results from SM-3 to extrapolate the response ${\hat{\theta }}(\lambda )$ at $\lambda =-1$, leading to a SIMEX estimate for $\theta$.

Heuristically, the case with $\lambda =-1$ is of interest because $\text {Var}(W_i+\sqrt{\lambda }U^*_{ij}|X_i)=(1+\lambda )\text {Var}(W_i|X_i)$, which is equal to zero at $\lambda =-1$, corresponding to data without measurement error. Thus, with a well chosen extrapolant, ${\hat{\theta }}(-1)$ is expected to resemble the consistent estimate one would obtain had one used data $\{(Y_i, X_i)\}_{i=1}^n$ to estimate $\theta$.

Both SIMEX and the implicit bias reduction method can be easily generalized to models with a vector covariate X, with more caution when choosing an extrapolant, since the extrapolant is typically unknown. In the practice of SIMEX, simple extrapolant such as the quadratic extrapolant has shown to work well in many scenarios. Plots of ${\hat{\varvec{\beta }}}$ in Fig. 1 along with the fitted loess curve (Cleveland and Devlin 1988) also suggest that a quadratic extrapolant may be adequate in RC-3 and RC-4 in the proposed implicit bias reduction algorithm. This will be the extrapolant used in our second proposed method in the simulation study. The proposed method differs from SIMEX in two aspects. First, in SM-1, in order to simulate pseudo measurement error, one needs to estimate the distribution of $\{U_i\}_{i=1}^n$ based on external data or replicate measures. In contrast, in RC-1, one knows the right model according to which coarsened data are induced from the original data. Second, the absence of measurement error translates to a correct model specification in the context of SIMEX; but model misspecification remains even if one eliminates data coarsening (by setting $\pi =1$) in our context. This, along with the fact that $\lambda$ is not estimated in SIMEX but $\pi$ is estimated along with $\varvec{\beta }$ in our method, makes it more challenging to develop an estimator for the variance of ${\hat{\varvec{\beta }}}^{(2)}$ following the strategy for SIMEX estimators proposed in Stefanski and Cook (1995). One may adopt bootstrap methods to estimate the variance of ${\hat{\varvec{\beta }}}^{(2)}$, even though we do not pursue this issue in the current study.

4 Simulation study

4.1 Finite sample performance of ${\hat{\varvec{\beta }}}^{(1)}$

A simulation study is conducted to compare the first proposed estimator ${\hat{\varvec{\beta }}}^{(1)}$ with the naive estimator ${\tilde{\varvec{\beta }}}$ when one assumes a logistic model whereas the truth is a generalized logistic model (Stukel 1988), with $\varvec{\beta }=(-1, 1)^{ \mathrm {\scriptscriptstyle T} }$. Here, $H(t)=1/\{1+\exp (-t)\}$ and $G(t)=1/[1+\exp \{-h(t)\}]$, where

$$\begin{aligned} h(t)= \left\{ \begin{array}{ll} \alpha _1^{-1}\{\exp (\alpha _1t)-1\}I(\alpha _1>0)+tI(\alpha _1=0)-\alpha _1^{-1}\log (1-\alpha _1 t)I(\alpha _1<0), &{} \text { if }t \ge 0,\\ -\alpha _2^{-1}\{\exp (-\alpha _2t)-1\}I(\alpha _2>0)+tI(\alpha _2=0)+\alpha _2^{-1}\log (1+\alpha _2 t)I(\alpha _2<0), &{} \text { if }t<0. \end{array} \right. \end{aligned}$$

Note that, if $\alpha _1=\alpha _2=0$, G(t) reduces to the logit link; if $\alpha _1=\alpha _2$, G(t) is symmetric; otherwise, G(t) is asymmetric. The generalized logit link with $(\alpha _1, \alpha _2)=(-0.1, 0.2)$ used in this experiment is depicted as the dotted curve in Fig. 2. We consider three covariate distributions, all with mean zero and variance one: N(0, 1), $\text {uniform}(-\sqrt{3}, \sqrt{3})$, and a shifted gamma distribution with skewness equal to $\sqrt{2}$. These covariate distribution configurations encompass symmetric and asymmetric distributions, as well as distributions with bounded support and unbounded support. Given the simulated covariate values $\{X_i\}_{i=1}^n$, $\{Y_i\}_{i=1}^n$ are generated from the generalized logistic model, where $n=400$, 600, 800, 1000. Based on each simulated data set $\{(Y_i, X_i)\}_{i=1}^n$, we carry out logistic regression to obtain ${\tilde{\varvec{\beta }}}$; then two reclassified data sets are generated according to (1) with $(\pi _1, \pi _2)=(0.7, 0.9)$. Using these two coarsened data sets, ${\hat{\varvec{\beta }}}^{(1)}$ is computed according to (13) and (14). This experiment is repeated 1000 times at each simulation setting.

Fig. 2

Three generalized logit links, with $(\alpha _1, \alpha _2)=(0.1, -0.1)$ (dashed line), $(-0.1, 0.2)$ (dotted line), and $(-0.5, 0.5)$ (dot-dashed line), contrasting with the logit link (solid line)

Table 1 presents summary statistics of the simulation results, including Monte Carlo averages of the considered estimates, mean absolute deviations (MAD) of these estimates from the corresponding truth, and empirical coverage probabilities (CP) of 95% confidence intervals. The 95% confidence intervals for $\beta _0$ based on ${\tilde{\beta }}_0$ is obtained by invoking the asymptotic normality of MLE, leading to ${\tilde{\beta }}_0\pm 1.96\times \text {s.e.}({\tilde{\beta }}_0)$ as the interval bounds, where $\text {s.e.}({\tilde{\beta }}_0)$ is the estimated standard error of ${\tilde{\beta }}_0$ resulting from the sandwich variance estimation for M-estimators (Boos and Stefanski 2013, section 7.2.1). A 95% confidence internal for $\beta _1$ based on ${\tilde{\beta }}_1$ is similarly obtained using each simulated data set. Also assuming asymptotic normality for ${\hat{\varvec{\beta }}}^{(1)}$, we construct 95% confidence intervals based on the first proposed estimate, with estimated standard errors associated with each point estimate obtained via a bootstrap method involving 100 bootstrap samples. Under the current designed link misspecification, ${\tilde{\varvec{\beta }}}$ is noticeably compromised, and ${\hat{\varvec{\beta }}}^{(1)}$ exhibits impressive bias reduction, at the price of inflated variability. Due to the inflated variability, the MAD associated with ${\hat{\varvec{\beta }}}^{(1)}$ is typically around three times as high as that associated with $\tilde{\varvec{\beta }}$ in the current simulation settings. Thanks to the bias correction, and also in part due to the inflated variability, the confidence intervals based on ${\hat{\varvec{\beta }}}^{(1)}$ stay much closer to the nominal level compared to those based on ${\tilde{\varvec{\beta }}}$, of which coverage probabilities drop quickly as sample size increases.

As discussed in Sect. 3.1, ${\hat{\varvec{\beta }}}^{(1)}$ can deteriorate in the presence of severe link misspecification, and its quality depends on factors irrelevant to the primary model configuration, such as the distribution of X and the choice of $(\pi _1, \pi _2)$. Among all three covariate distributions experimented in the presented simulation study, we see the proposed estimator achieve bias reduction to some extent. When choosing $(\pi _1, \pi _2)$, we suggest selecting two values in (0.5, 1) so that the reclassified responses do not lose too much information in the original responses. Another guideline we have found practically useful in the empirical study is to choose $(\pi _1, \pi _2)$ so that the common denominator appearing in (13) and (14), i.e., $({\hat{\pi }}_1-\pi _1)/(2\pi _1-1)-(\hat{\pi }_2-\pi _2)/(2\pi _2-1)$, is not too close to zero, say, is above 0.01. Even with the above practical considerations one needs to bear in mind when applying the proposed explicit bias reduction method, it is still an appealing and convenient way to correct the naive estimates for bias because of the closed-form expressions for such correction once the naive estimates are computed via straightforward maximum likelihood estimation.

Table 1 Averages of parameter estimates for $\varvec{\beta }$, denoted by ${\tilde{\varvec{\beta }}}$, and the corresponding mean absolute deviations (MAD) and empirical coverage probabilities (CP) of 95% confidence intervals across 1000 Monte Carlo replicates when assuming a logistic model for Y given X, and the counterpart quantities associated with the proposed explicit bias-reduced estimates, ${\hat{\varvec{\beta }}}^{(1)}$. The true parameter values are $\varvec{\beta }=(-1, 1)^{ \mathrm {\scriptscriptstyle T} }$. Numbers in parentheses are Monte Carlo standard errors (s.e.) associated with the averages

Even though all derivations in Sects. 2.2 and 3.1 still go through when $\beta _1$ is a vector slope parameter, with Taylor approximation in (6) and other derivations relating to $\beta _1$ done elementwise, we do not recommend generalizing the explicit bias reduction method to models with a vector covariate for reasons pointed out at the end of Sect. 3.1.

4.2 Finite sample performance of ${\hat{\varvec{\beta }}}^{(2)}$

To demonstrate the performance of the implicit bias reduction method, we carry out simulation experiments under similar settings as those in Sect. 4.1, except that the true link function in the data generating process takes a sequence of generalized logit links. More specifically, we consider true links as generalized logit link G(t) with $(\alpha _1, \alpha _2)=(-a, a),$ where a varies from 0.1 to 0.5 at increments of 0.1. The generalized logit link that deviates from the logit link the most in this sequence, at $a=0.5$, is shown in Fig. 2. When implementing this method, we estimate $\varvec{\beta }$ based on reclassified data generated according to (1) with $\pi$ varying from 0.6 to 0.9 at increments of 0.005, with $J=100$ in the algorithm described in Sect. 3.2; and we use the quadratic extrapolant in RC-3 and RC-4 to obtain ${\hat{\varvec{\beta }}}^{(2)}$. Based on 1000 Monte Carlo replicates, Fig. 3 provides pictorial comparisons between ${\hat{\varvec{\beta }}}^{(2)}$ and ${\tilde{\varvec{\beta }}}$ when $n=800$, with covariate $X\sim N(0, 1)$. Figure 4 shows the same comparisons when X follows a shifted gamma distribution with mean zero, variance one, and skewness $\sqrt{2}$. The substantial bias reduction achieved by ${\hat{\varvec{\beta }}}^{(2)}$ using a quadratic extrapolant is evident in both figures. Although, like ${\hat{\varvec{\beta }}}^{(1)}$, ${\hat{\varvec{\beta }}}^{(2)}$ is more variable than ${\tilde{\varvec{\beta }}}$ (but much less variable than ${\hat{\varvec{\beta }}}^{(1)}$), which is expected when coarsened data are used to compute the bias-reduced estimator and an additional parameter needs to be estimated simultaneously. Accounting for both bias and variance, the mean squared error (MSE) of ${\hat{\varvec{\beta }}}^{(2)}$ is significantly lower than that of ${\tilde{\varvec{\beta }}}$.

Fig. 3

Upper panels show Monte Carlo averages of relative bias of ${\hat{\varvec{\beta }}}^{(2)}$ (dashed line) and those of ${\tilde{\varvec{\beta }}}$ (solid line). Lower panels show MSE of ${\hat{\varvec{\beta }}}^{(2)}$ (dashed line) and MSE of ${\tilde{\varvec{\beta }}}$ (solid line). True links are generalized logit links with $(\alpha _1, \alpha _2)=(-a, a)$. The covariate X follows N(0, 1)

Fig. 4

Upper panels show Monte Carlo averages of relative bias of ${\hat{\varvec{\beta }}}^{(2)}$ (dashed line) and those of ${\tilde{\varvec{\beta }}}$ (solid line). Lower panels show MSE of ${\hat{\varvec{\beta }}}^{(2)}$ (dashed line) and MSE of ${\tilde{\varvec{\beta }}}$ (solid line). True links are generalized logit links with $(\alpha _1, \alpha _2)=(-a, a)$. The covariate X follows a shifted gamma distribution with mean zero, variance one, and skewness $\sqrt{2}$

Applying the implicit bias reduction method to regression models with multiple covariates does not add extra complication, even though a larger sample size is needed to obtain improved inference. Figure 5 shows the comparison of ${\hat{\varvec{\beta }}}^{(2)}$ and ${\tilde{\varvec{\beta }}}$ obtained from logistic regression with two covariates. In particular, we generate 300 Monte Carlo replicate data sets, each of size $n=1000$, from the true models with the aforementioned sequence of generalized logit models, which involves one continuous covariate $X_1\sim N(0, 1)$ and one binary covariate $X_2$ that takes value one with probability 0.5. The true regression coefficients are $\varvec{\beta }=(\beta _0, \beta _1, \beta _2)^{ \mathrm {\scriptscriptstyle T} }=(-1, 0.5, 0.5)^{ \mathrm {\scriptscriptstyle T} }$. In this case, the proposed method with the quadratic extrapolant shows signs of over correcting ${\tilde{\varvec{\beta }}}$ for bias when the link misspecification is mild (when $a=0.1$ and 0.2), producing estimates more biased than ${\tilde{\varvec{\beta }}}$. This may suggest the need to explore a different extrapolant. In practice, we recommend one plot ${\hat{\varvec{\beta }}}^{(2)}(d)$ (elementwise) versus d to gain some visual hints on the choice of an extrapolant. Regardless, using the quadratic extrapolant in this experiment, the gain from the proposed method again stand out once the link misspecification is more severe (e.g., when $a>0.2$).

Fig. 5

Upper panels show Monte Carlo averages of relative bias of ${\hat{\varvec{\beta }}}^{(2)}$ (dashed line) and those of ${\tilde{\varvec{\beta }}}$ (solid line). Lower panels show MSE of ${\hat{\varvec{\beta }}}^{(2)}$ (dashed line) and MSE of ${\tilde{\varvec{\beta }}}$ (solid line). True links are generalized logit links with $(\alpha _1, \alpha _2)=(-a, a)$. The covariates $X_1$ follows N(0, 1) and $X_2$ follows Bernoulli(0.5)

Up to this point, the true links G(t) in the data generating processes in the simulation studies for the two proposed methods are all asymmetric. In “Appendix A” in the supplementary materials we present additional simulation study where symmetric generalized logit links are used in the data generating process. These additional results provide convincing empirical evidence that both proposed methods yield estimators less biased than ${\tilde{\varvec{\beta }}}$ when the assumed link and the true link are both symmetric.

5 A test for link misspecification

Here we propose a simple t test for link misspecification using byproducts of the proposed bias reduction methods. Hosmer et al. (1997) compared nine tests for link misspecification in the context of logistic regression and found none of them exhibit satisfactory power. Among these tests, eight of them are goodness-of-fit (GOF) tests in nature constructed based on prediction error, and one is Stukel’s score test based on fitting a generalized logit model (Stukel 1988). This score test is a test of $H_0: \, (\alpha _1, \alpha _2)=(0, 0)$, where the score is the normal score derived from the likelihood of a generalized logistic model. Compared with the eight GOF tests, Stukel’s score test exhibits the highest power to detect link misspecification. We believe the reason for this is that, although inference on covariate effects can be very misleading in the presence of link misspecification, the impact on predictions is often more subtle. Hence, a residual-based GOF test tends to be less sensitive to link misspecification.

A more sensitive indicator of link misspecification is readily available from the proposed estimation procedures for $\varvec{\beta }$, which is simply ${\hat{\pi }}$, since ${\hat{\pi }}$ inconsistently estimate $\pi$ in the presence of link misspecification. Hence, fixing $\pi$ at a value one chooses, one can easily construct a t test with test statistic $t=({\hat{\pi }}-\pi )/{\hat{\nu }}$, where ${\hat{\nu }}$ is the sandwich standard error estimator associated with ${\hat{\pi }}$. Following the asymptotic theory of MLE, it is straightforward to show that the null distribution of the test statistic is a t distribution with $n-\text {dim}(\varvec{\beta })-1$ degrees of freedom, where $\text {dim}(\varvec{\beta })$ denotes the dimension of $\varvec{\beta }$. A test statistic value that deviates significantly from zero indicates an inadequate assumed link.

Like Stukel’s score test, our proposed test is not based on prediction error. To compare the operating characteristics of Stukel’s test and our test, we carry out simulation study under settings similar as those in the experiments in Sect. 4, with the sample size n varying from 200 to 1000 at increments of 200. We consider four true links in this experiment, including the logit link and three generalized logit links with $(\alpha _1, \alpha _2)=(-0.5, 0.5), (0.5, 0.5), (1, 1)$. The setting with the logit link as the truth allows one to assess the size of a test. We let $\pi =0.9$ in the t test. Setting the significance level at 0.05, Fig. 6 depicts the empirical power defined by the rejection rate across 1000 MC replicates associated with each test versus n under each of the true link configurations. Clearly, our test outperforms the Stukel’s test in all scenarios, and both retain the right size. Stukel’s test appears to be more promising when the true link is asymmetric, whereas the proposed t test is more powerful in the presence of more severe link misspecification even when the true link is also symmetric as the assumed link. “Appendix B” in the supplementary materials provides QQ plots of the test statistics collected from the case without link misspecification, which suggest close agreement between the claimed null distribution of the proposed test statistic and a t distribution. Due to the typically moderate to large sample size n when comparing with the dimension of $\varvec{\beta }$ in most applications where this proposed test is designed for, one may simply view the standard normal as the null distribution of the test statistic in practice.

Fig. 6

Rejection rates of Stukel’s test (solid lines) and the proposed t test (dashed lines) across 1000 Monte Carlo replicates versus the sample size n when the true link is logit (in (a)) and when the true link is a generalized logit link with three different configurations for $(\alpha _1, \alpha _2)$ (in (b), (c), (d))

6 A real data example

We now entertain a classic data example reported in Bliss (1935) that has been analyzed by many researchers since then, who were mostly concerned about the adequacy of the logistic model for this date set. The data were collected in an experiment where the association between mortality of adult beetles and exposure to gaseous carbon disulfide is of interest. In particular, the data include logarithm (with base 10) of dosages of carbon disulfide exposure for a total of 481 adult beetles, and the status (being killed or surviving) of each beetle after five hours’ exposure. Let $Y_i$ denote the indicator of being killed after exposure to carbon disulfide for the ith beetle, and denote by $X_i$ the $\hbox {log}_{{10}}$dose this beetle was exposed to, for $i=1, \ldots , 481$. Pregibon (1980) applied his test for link specification and found strong evidence to support an asymmetric link as opposed to the logit link. Aranda-Ordaz (1981) showed that the complementary log-log link is more appropriate for the data. Stukel (1988) first used the likelihood ratio GOF test, resulting in a p-value of 0.0815; she then followed up with her score test and found stronger evidence against the logit link, with a p-value of 0.0125; lastly, she used the likelihood ratio test to compare the logistic model and her proposed skewed generalized logistic model for this data, and obtained a p-value of 0.0077.

Using our test proposed in Sect. 5, with $\pi =0.95$, we also reject the assumed logit link, with p-value equal to 0.0001. We then repeatedly estimate $\varvec{\beta }$ assuming the logit link and using reclassified data simulated from the raw data according to (1) with $\pi$ ranging from 0.75 to 0.95 at increments of 0.001. Applying a quadratic extrapolant on the sequence of $\hat{\varvec{\beta }(d)}$ leads to ${\hat{\varvec{\beta }}}^{(2)}=(-57.99, 32.62)^{ \mathrm {\scriptscriptstyle T} }$, with the estimated (via bootstrap) standard errors equal to (10.23, 5.41). In Stukel’s analysis based on a generalized logistic model, her estimates of $\beta _0$ and $\beta _1$ are $-47.4$ (6.47) and 26.6 (3.66), respectively, with the corresponding estimated standard error in parentheses. And the standard logistic regression gives ${\tilde{\varvec{\beta }}}=(-60.71, 34.27)^{ \mathrm {\scriptscriptstyle T} }$, with the estimated standard errors equal to (5.18, 2.91). In comparison, ${\hat{\varvec{\beta }}}^{(2)}$ lies between ${\tilde{\varvec{\beta }}}$ and that obtained by Stukel, who attempted to correct for the potentially inadequate logit link. This can suggest that the implicit bias reduction method effectively reduce some bias in ${\tilde{\varvec{\beta }}}$ even though we still analyze the (reclassified) data assuming a logit link. We did not apply the explicit bias reduction method to this data because the support of X excludes zero and one, the two values one evaluates X at when deriving ${\hat{\varvec{\beta }}}^{(1)}$.

7 Discussion

The conventional model building and inference routine is to first test suspicious assumptions in a posited model using some diagnostic tools; and if inadequate model assumptions are detected, one makes attempts to correct the model and draw inference again using the updated model. If one has little ground for verifying or correcting the posited model, one often resorts to semi-/non-parametric methods to draw inference. As rich as the body of existing semi-/non-parametric methods, most of them are computationally demanding and can be inefficient. In this study we present a different take on parametric inference that leads to more reliable inference even without guessing the “right” model. Moreover, we unify parametric inference and model diagnosis under the same framework based on simulated reclassified data. If the test for the assumed link does not reject the null, one has some reassurance for ${\tilde{\varvec{\beta }}}$; otherwise, one may adopt the proposed bias-reduced estimates. In fact, we would not recommend one use the proposed bias reduction methods when one lacks sufficient evidence to indicate presence of model misspecification. The first bias reduction estimator for $\beta _0$ in (13) comes from (12), which becomes an identity that sheds no light on $\beta _0$ when the assumed model is not misspecified since now one has, on the left-hand side of (12), $b_0(0, \pi _1)-b_0(0, \pi _2)=0$ for all $\pi _1$ and $\pi _2$, and the factor following $R(\beta _0)$ on the right-hand side is also zero. Consequently, (13) does not yield a sensible estimator for $\beta _0$. For the second bias reduction estimator for $\varvec{\beta }$, the problem with it in the absence of model misspecification lies in the fact that $d_k$ is expected to be close to zero for all k’s, and the sequence $\{{\hat{\varvec{\beta }}}(d_k), d_k\}_{k=1}^K$ will provide little information on the dependence of ${\hat{\varvec{\beta }}}$ on d, and thus regressing ${\hat{\varvec{\beta }}}(d_k)$ on $d_k$ can be subject to high variability.

We provide in “Appendix C” in the supplementary materials the SAS PROC IML code for implementing the proposed estimation methods and the test. Computationally, the implicit bias reduction method is more demanding than the explicit bias reduction method mainly because the former entails computing the MLEs of unknown parameters for a large number of times. This makes using bootstrap methods, such as those described in Section A.9.4 in Carroll et al. (2006), to estimate the variance of ${\hat{\varvec{\beta }}}^{(2)}$ more cumbersome. To develop new variance estimation methods for these estimators that are computationally less burdensome is among our upcoming research agenda.

Although we consider the assumed link in GLM as the source of model misspecification in the current study, the implicit bias reduction method and the proposed t test are also applicable when a different model assumption is violated, such as those considered in Hosmer et al. (1997). To illustrate the rationale of the proposed methods, we keep the reclassification mechanism as simple as (1), but different data coarsening mechanisms are certainly worth systematic investigation. This is especially needed in order to generalize these methods to GLM for responses other than a binary response. Even in the context of our study, different coarsening mechanisms that lead to induced data allowing stronger identificability of $\pi$ can be beneficial, as Copas (1988) pointed out, who used a missclassification model similar to ours, that $\pi$ is hard to estimate unless when n is very large. This inherent weak identifiability of $\pi$ causes little numerical difficulty in implementing the proposed methods when one uses the true value of $\pi$ as the starting value when obtaining its MLE, which is feasible since the truth is known for this user-specified parameter. But, for a more complex GLM when such parameter becomes harder to estimate, one may generate coarsened data that allow part of the raw data free of error to alleviate the nonidentifiability issue. This is similar in spirit to having validation data or external data to allow identifiability of measurement error distributions. Furthermore, with the reclassfication mechanism given by (1), the proposed t test can be improved by using $\sup _{\pi \in (0.5, 1)} (|\hat{\pi }-\pi |/{\hat{\nu }})$ as the test statistic, instead of fixing $\pi$ at one value as is done in Sects. 5 and 6. The drawback of this supreme-type test statistic is that its null distribution is no longer as trivial as before, which may need to be estimated using some simulation-based methods. For instance, one may approximate the null distribution of $t_\pi =|{\hat{\pi }}-\pi |/{\hat{\nu }}$ by a Gaussian process indexed by $\pi$, and use some bootstrap method to obtain an estimate for the covariance function under an assumed covariance structure for the process.

The introduction of an extraneous parameter as a device to calibrate estimates for parameters of interest can be applied to other models more complex than GLM, which can be more vulnerable to model misspecification. Since “...all models are wrong but some are useful...” (George Box), rather than attempting to guess the right model, a more productive approach to draw inference is to embrace a useful wrong model and then strive for inference results that remain reliable under the wrong model. This is the very philosophy we follow in this study and also in our follow-up research.

Appendix: Proof of equation (2)

Because the assumed GLM is specified by $P(Y=1|X)=H(\eta )$, where $\eta =\beta _0+\beta _1 X$, and the reclassified response is generated according to $P(Y^*=Y|Y, X)=\pi$, one has

$$\begin{aligned} P(Y^*=1|X)&= P(Y^*=1, Y=0|X)+P(Y^*=1, Y=1|X) \\&= P(Y=0|X)P(Y^*\ne Y|Y, X)+P(Y=1|X)P(Y^*=Y|Y, X) \\&= \{1-H(\eta )\}(1-\pi )+H(\eta )\pi \\&= (2\pi -1)H(\eta )+1-\pi . \end{aligned}$$

(15)

It follows that the likelihood function based on the assumed primary model for $Y^*$ evaluated at one data point $(Y^*, X)$ is $L(\pi , \varvec{\beta })=P(Y^*=1|X)^{Y^*}\{1-P(Y^*=1|X)\}^{1-Y^*}$, and the log-likelihood function is $\ell (\pi , \varvec{\beta })=Y^*\log P(Y^*=1|X)+(1-Y^*)\log \{1-P(Y^*=1|X)\}$.

Differentiating (15) with respect to each element in $(\pi , \varvec{\beta })$ gives

$$\begin{aligned} \begin{aligned} \frac{\partial P(Y^*=1|X)}{\partial \pi }&=2H(\eta )-1, \\ \frac{\partial P(Y^*=1|X)}{\partial \beta _0}&=(2\pi -1)H'(\eta ), \\ \frac{\partial P(Y^*=1|X)}{\partial \beta _1}&=(2\pi -1)H'(\eta )X. \end{aligned} \end{aligned}$$

(16)

Using (16), one can show that the three normal score functions associated with $\ell (\pi , \varvec{\beta })$ are given by

$$\begin{aligned} \frac{\partial \ell (\pi , \varvec{\beta })}{\partial \pi }&= Y^*\frac{2H(\eta )-1}{P(Y^*=1|X)}-(1-Y^*)\frac{2H(\eta )-1}{1-P(Y^*=1|X)},\\ \frac{\partial \ell (\pi , \varvec{\beta })}{\partial \beta _0}&= Y^*\frac{(2\pi -1)H'(\eta )}{P(Y^*=1|X)}-(1-Y^*)\frac{(2\pi -1)H'(\eta )}{1-P(Y^*=1|X)}, \\ \frac{\partial \ell (\pi , \varvec{\beta })}{\partial \beta _1}&= Y^*\frac{(2\pi -1)H'(\eta )X}{P(Y^*=1|X)}-(1-Y^*)\frac{(2\pi -1)H'(\eta )X}{1-P(Y^*=1|X)}. \end{aligned}$$

To further simplify notations, let $\mu =P(Y^*=1|X)$. The above three score functions can be re-expressed as

$$\begin{aligned} \begin{aligned} \frac{\partial \ell (\pi , \varvec{\beta })}{\partial \pi }&= \frac{Y^*-\mu }{\mu (1-\mu )}\{2H(\eta )-1\}, \\ \frac{\partial \ell (\pi , \varvec{\beta })}{\partial \beta _0}&= \frac{Y^*-\mu }{\mu (1-\mu )}(2\pi -1)H'(\eta ), \\ \frac{\partial \ell (\pi , \varvec{\beta })}{\partial \beta _1}&= \frac{Y^*-\mu }{\mu (1-\mu )}(2\pi -1)H'(\eta )X. \end{aligned} \end{aligned}$$

(17)

The expectation of the first score in (17) with respect to the true distribution of $(Y^*, X)$ is

$$\begin{aligned} E\left[ \frac{Y^*-\mu }{\mu (1-\mu )}\{2H(\eta )-1\}\right]&= E\left( E\left[ \left. \frac{Y^*-\mu }{\mu (1-\mu )}\{2H(\eta )-1\}\right| X\right] \right) \\&= E\left[ \frac{\mu _0-\mu }{\mu (1-\mu )}\{2H(\eta )-1\}\right] , \end{aligned}$$

where $\eta _0$ is equal to $\eta$ evaluated at the true value of $\varvec{\beta }$, and $\mu _0 =(2\pi -1)G(\eta _0)+1-\pi$, as defined in (4), is the mean of $Y^*$ given X under the correct model evaluated at the true parameter values. Setting this expectation equal to zero gives the first estimating equation in (2). Similarly, the expectations of the second and the third score functions in (17) with respect to the true distribution of $(Y^*, X)$ are given by

$$\begin{aligned} E\left[ \frac{Y^*-\mu }{\mu (1-\mu )}(2\pi -1)H'(\eta )\right]&= E\left[ \frac{\mu _0-\mu }{\mu (1-\mu )}H'(\eta )\right] (2\pi -1), \\ E\left[ \frac{Y^*-\mu }{\mu (1-\mu )}(2\pi -1)H'(\eta )X\right]&= E\left[ \frac{\mu _0-\mu }{\mu (1-\mu )}H'(\eta )X\right] (2\pi -1), \end{aligned}$$

respectively. Setting these two expectations equal to zero gives the second and the third equations in (2).