Numerical simulation of a single cell passing through a narrow slit

Abstract

The narrow slit between endothelial cells that line the microvessel wall is the principal pathway for tumor cell extravasation to the surrounding tissue. To understand this crucial step for tumor hematogenous metastasis, we used dissipative particle dynamics method to investigate an individual cell passing through a narrow slit numerically. The cell membrane was simulated by a spring-based network model which can separate the internal cytoplasm and surrounding fluid. The effects of the cell elasticity, cell shape, nucleus and slit size on the cell transmigration through the slit were investigated. Under a fixed driving force, the cell with higher elasticity can be elongated more and pass faster through the slit. When the slit width decreases to 2/3 of the cell diameter, the spherical cell becomes jammed despite reducing its elasticity modulus by 10 times. However, transforming the cell from a spherical to ellipsoidal shape and increasing the cell surface area by merely 9.3 % can enable the cell to pass through the narrow slit. Therefore, the cell shape and surface area increase play a more important role than the cell elasticity in cell passing through the narrow slit. In addition, the simulation results indicate that the cell migration velocity decreases during entrance but increases during exit of the slit, which is qualitatively in agreement with the experimental observation.

1 Introduction

Most cancer-related deaths are due to metastasis. Metastasis is a complex, multistep processes including the detachment of cancer cells from the primary tumor and the migration to distant targeted organs through blood and/or lymphatic circulations. During hematogenous metastasis (through blood), the emigration of tumor cells from the blood stream through the vascular wall into the tissue involves arrest in the microvasculature, or adhesion to the endothelial cells forming the microvessel wall and transmigration to the tissue through the endothelial barrier termed as extravasation (Reymond et al. 2013; Strell and Entschladen 2008; Wirtz et al. 2011). Cell adhesion to vessel wall has been investigated both computationally and experimentally (Rejniak 2012; Yan et al. 2012). However, little is known about how adherent tumor cells physically penetrate the vascular wall.

Fig. 1

Schematic diagram of tumor cell extravasation including three states: adhesion, transmigrating and transmigrated. EC represents endothelial cell and TC represents tumor cell (revised from Fan and Fu 2015)

Microvessel walls mainly consist of endothelial cells. There are four primary pathways observed in the microvessel wall by using electron microscopy: intercellular clefts, transcellular pores, vesicles and fenestrae (Sugihara-Seki and Fu 2005). The inter-endothelial cleft is not only widely believed to be the main pathway for water and hydrophilic solute transport under normal physiological conditions but also suggested to be the pathway for the transport of tumor cell across microvessel walls in disease. Endothelial cells of some tumor vessels overlap one another, have luminal projections, and give rise to abluminal sprouts. The size of the intercellular openings is less than $2\,\upmu \hbox {m}$ in diameter (McDonald and Baluk 2002). For a tumor cell transmigration of the endothelial monolayer, it was observed clearly that there are three states it has to experience: adhesion, transmigrating and transmigrated, as shown in Fig. 1 (Fan and Fu 2015). By using confocal microscopy (Fan and Fu 2015), we have observed the transmigration of a malignant breast tumor cell through the endothelial monolayers, as shown in Fig. 2. In this observation, the transmigration occurs at the bi-joint between endothelial cells. From the biochemical and molecular biological investigations, an endothelial retraction is currently a favorable model for tumor cell transendothelial migration (Miles et al. 2008; Voura et al. 1998). Next, tumor cells undergo dramatic shape changes, driven by a significant rearrangement of the cell cytoskeleton (Sugihara-Seki and Fu 2005). Also, invasive cancer cells can disrupt the endothelial barrier through regulating the biomechanical properties of endothelial cells (Mierke 2011, 2012). In addition, it is found that metastatic cancer cells are softer than their normal or benign counterparts, which may facilitate cancer cell extravasation from the blood stream (Cross et al. 2007; Suresh 2007). To understand how tumor cells undergo large elastic deformation during penetrating the vascular wall, it is necessary to analyze this process from the mechanical point of view.

Fig. 2

Tumor cell (red, labeled “T”) transmigration through the junction between two endothelial cells (labeled “E”). The green lines are the EC borders. Blues are cell nuclei. (From Fan and Fu 2015, with permission)

The passage of cell through a narrow channel, slit or small pore has attracted much attention since 1980s. Freund (2013) numerically investigated the flow of red blood cells (RBCs) through a narrow slit and observed that the cells infold in the slit due to high velocity or high cytosol viscosity, which might provide a mechanism for jamming. Omori et al. (2014) revealed that the transit time increases nonlinearly with the viscosity ratio when RBCs pass through a thin micropore. Wu and Feng (2013) explored malaria-infected RBCs transit through microchannel in terms of the cell deformability. Li et al. (2014) and Quinn et al. (2011) simulated a single RBC flowing through a narrow cuboid channel using dissipative particle dynamics and found that the cell deformation and transit time depend on cross-sectional geometry and cell size. These studies on RBC passage through a confined geometry provide important insights into a tumor cell’s journey through the inter-endothelial cleft. As for the studies on tumor cell transmigration, cell deformation in microfluidic device offers effective measurement means to quantify cell mechanical properties in vitro (Chaw et al. 2007; Leong et al. 2011). It is found that the surface area of cancer cells increases by more than 3 fold during the cell deformation through 10 $\upmu \hbox {m}$ microgap (Chaw et al. 2007). Moreover, high-resolution time-lapse microscopy was employed to investigate the dynamic nature of tumor cell extravasation in an in vitro microvascular network platform. The findings showed that the tumor cell extrudes firstly through the formation of a small opening ($\sim$1–2 $\upmu \hbox {m}$) between endothelial cells and the opening grows to form a pore $\sim$8–10 $\upmu \hbox {m}$ in diameter to allow for nuclear transmigration (Chen et al. 2013). Finally, the numerical study on the circulating tumor cells passing through a 3D micro-filtering channel shed lights on the importance of channel geometry on deformability-based cancer cell separation (Zhang et al. 2014).

Since cell deformability plays an important role in passing through the slit, we are particularly interested in the effects of changes in the cell elasticity and cell surface area on the behavior of cell passing through narrow slit in this study. We firstly described the spring-based network cell model and briefly introduced the numerical method—dissipative particle dynamics (DPD). Then we reported the deformation of a cell through a narrow slit and presented results for cell passing through the slit with different sizes. The effects of cell elasticity, cell shape, slit size and cell nucleus on cell transit were discussed. Lastly, the conclusions drawn from this work were made.

2 Physical model and numerical method

2.1 Cell membrane model

A spring-based network model was first proposed and further developed as discrete description of RBCs at the spectrin protein level by Boey et al. (1998) and Li et al. (2005). On the basis of this, Pivkin and Karniadakis (2008) developed a systematic coarse-graining procedure to reduce the number of degrees of freedom dramatically. This coarse-grained model was improved by Fedosov et al. (2010), yielding accurate mechanical response. This spring-based network model has been employed to simulate the deformation and margination of white blood cells (Fedosov and Gompper 2014), which have similar process of extravasation as tumor cells. The total energy of the network is defined as

$$\begin{aligned} E(\{\mathbf{r}_{i} \})=E_{\text {in-plane}} +E_\mathrm{bending} +E_\mathrm{area} +E_\mathrm{volume} \end{aligned}$$

(1)

where $\mathbf{r}_{i}$ represents the vertex coordinates and the in-plane elastic energy is given by

$$\begin{aligned} E_{\text {in-plane}} =\sum _\mathrm{alledges} {E_\mathrm{WLC} } +\sum _\mathrm{alledges} {E_ \mathrm{p} } \end{aligned}$$

(2)

Each edge in the network is a spring consisting of two potentials—a worm-like model with elastic energy $E_\mathrm{WLC}$ and a power function potential with energy $E_\mathrm{P}$, as follows:

$$\begin{aligned}&E_\mathrm{WLC} =\frac{k_\mathrm{B} Tl_{\max } }{4p}\frac{3x_l ^{2}-2x_l ^{3}}{1-x_l } \end{aligned}$$

(3)

$$\begin{aligned}&E_\mathrm{P} =\frac{k_\mathrm{p} }{(m-1)l^{m-1}} \end{aligned}$$

(4)

where $x_l =l/l_{\max } \in (0,1)$, l is the instantaneous spring length, $l_{\max }$ is the maximum spring extension, which is equal to 2.2 times (Fedosov et al. 2010) equilibrium spring length for the WLC model, p is the persistence length, $k_\mathrm{B}$ is Boltzmann constant and T is temperature of the system, which is equal to 310 K. $k_\mathrm{p}$ is a spring constant and m is a specified exponent, here we set it to 2 (Fedosov et al. 2010).

The bending energy is given by

$$\begin{aligned} E_\mathrm{bending} =\sum _{\text {all triangle adjacents}} {k_\mathrm{bend} \left[ {1-\cos (\theta _{\alpha \beta } -\theta _0 )} \right] } \end{aligned}$$

(5)

where $k_\mathrm{bend}$ is a bending modulus; $\theta _{\alpha \beta }$ is the instantaneous angle formed between the outer normal vectors of two adjacent triangles $\alpha$, $\beta$ sharing the common edge; $\theta _0$ is the spontaneous angle.

The area and volume conservation constraints are

$$\begin{aligned}&E_\mathrm{area} =\frac{k_\mathrm{area}^\mathrm{tot} (A^\mathrm{tot}-A_0^\mathrm{tot} )^{2}}{2A_0^\mathrm{tot} }+\sum _{\text {all triangles}} {\frac{k_\mathrm{area} (A-A_0 )^{2}}{2A_0 }} \nonumber \\\end{aligned}$$

(6)

$$\begin{aligned}&E_\mathrm{volume} =\frac{k_\mathrm{volume} (V-V_0^\mathrm{tot} )^{2}}{2V_0^\mathrm{tot} } \end{aligned}$$

(7)

where $k_\mathrm{area}^\mathrm{tot}$, $k_\mathrm{area}$ and $k_\mathrm{volume}$ are constraint constants for global area, local area, and volume; $A^\mathrm{tot}$ and V are the instantaneous membrane area and the cell volume; $A_{0}^\mathrm{tot}$ and $V_{0}^\mathrm{tot}$ are their respective specified total area and volume values. A, $A_{0}$ are the instantaneous and initial local areas.

Nodal forces are derived from the total energy as follows:

$$\begin{aligned} \mathbf{F}_i ^\mathrm{membrane}=-\partial E\{(\mathbf{r}_{i} )\}/\partial \mathbf{r}_{i} \end{aligned}$$

(8)

2.2 Cell mechanical properties

The elasticity of the network is based on the linear analysis of a two-dimensional sheet of springs built with equilateral triangles (Dao et al. 2006). The linear shear modulus of the WLC-POW model is

$$\begin{aligned} \mu _0= & {} \frac{\sqrt{3}k_\mathrm{B} T}{4pl_{\max } x_0 }\left( \frac{x_0 }{2(1-x_0 )^{3}}-\frac{1}{4(1-x_0 )^{2}}+\frac{1}{4}\right) \nonumber \\&+\frac{\sqrt{3}k_\mathrm{p} (m+1)}{4l_0 ^{m+1}},x_0 =l_0 /l_{\max } \end{aligned}$$

(9)

where $l_0$ is the equilibrium length of the spring.

The linear area-compression modulus (Fedosov et al. 2010) is defined as

$$\begin{aligned} K=2\mu _0 +k_\mathrm{area}^\mathrm{tot} +k_\mathrm{area} \end{aligned}$$

(10)

The Young’s modulus Y for the two-dimensional sheet can be expressed through the shear and area-compression moduli as follows

$$\begin{aligned} Y=\frac{4K\mu _0 }{K+\mu _0 } \end{aligned}$$

(11)

The Poisson’s ratio $\nu$ is given by

$$\begin{aligned} \nu =\frac{K-\mu _0 }{K+\mu _0 } \end{aligned}$$

(12)

Based on the incompressibility assumption, we set $k_\mathrm{area}^\mathrm{tot} +k_\mathrm{area} >>\mu _0$, so $Y \rightarrow 4\mu _0$ and $\nu \rightarrow 1$. The dimensionless parameters $G_\mathrm{D} =K/\mu _0 =1000$ and $G_\mathrm{V} =k_\mathrm{volume} /\mu _0 =1000$ ensure that membrane area and cell volume variation within 1 % (Ye et al. 2014) during the cell deformation, respectively.

Table 1 DPD parameters used in the simulations

The relationship between bending modulus $k_\mathrm{bend}$ and the macroscopic membrane bending rigidity $k_\mathrm{c}$ is derived for the case of a spherical shell in the Helfrich bending energy (Helfrich 1973), as follows:

$$\begin{aligned} k_\mathrm{bend} =\frac{2}{\sqrt{3}}k_\mathrm{c} \end{aligned}$$

(13)

2.3 Dissipative particle dynamics (DPD) method

DPD as a mesoscopic simulation technique has been used widely for computing the flow of complex fluids (Fan et al. 2006; Soares et al. 2013; Warren 2003). Introductions to DPD method have been presented in detail in previous studies (Espanol 1995; Groot and Warren 1997; Hoogerbrugge and Koelman 1992). In brief, each DPD particle i represents a soft lump of atoms and interacts with surrounding particles, denoted by j with three simple pairwise additive forces: conservative (repulsive) force, $\mathbf{F}_{ij}^\mathrm{C}$, dissipative (friction) force, $\mathbf{F}_{ij}^\mathrm{D}$, and random (Brownian) force, $\mathbf{F}_{ij}^\mathrm{R}$.

$$\begin{aligned} \mathbf{F}_{ij}^\mathrm{C}= & {} F_{ij}^\mathrm{C} (\mathrm{r}_{ij} )\hat{{\mathbf{r}}}_{ij} , \nonumber \\ \mathbf{F}_{ij}^\mathrm{D}= & {} -\gamma \omega ^\mathrm{D}(r_{ij} )(\mathbf{v}_{ij} \cdot \hat{{\mathbf{r}}}_{ij} )\hat{{\mathbf{r}}}_{ij} , \nonumber \\ \mathbf{F}_{ij}^\mathrm{R}= & {} -\sigma \omega ^{R}(r_{ij} )\cdot \frac{\xi _{ij} }{\sqrt{\hbox {d}t}}\cdot \hat{{\mathbf{r}}}_{ij} , \end{aligned}$$

(14)

where $\hat{{\mathbf{r}}}_{ij} =\mathbf{r}_{ij} /r_{ij}$, $\mathbf{r}_{ij} =\mathbf{r}_i -\mathbf{r}_j$ and $\mathbf{v}_{ij} =\mathbf{v}_i -\mathbf{v}_j$. The coefficients $\gamma$ and $\sigma$ define the strength of dissipative and random forces, respectively. In addition, $\omega ^\mathrm{D}$ and $\omega ^\mathrm{R}$ are weight functions, and $\xi _{ij}$ is a normally distributed random variable with zero mean, unit variance, and $\xi _{ij} =\xi _{ji}$. All forces are truncated beyond the cutoff radius $r_c$, which defines the length scale in the DPD system. The conservative force is given by

$$\begin{aligned} F_{ij}^\mathrm{C} (r_{ij} )=\left\{ {{\begin{array}{lll} {a_{ij} (1-r_{ij} /r_\mathrm{c} )} &{}{\text{ for }}&{} {r_{ij} \le r_\mathrm{c} } \\ 0 &{}{ \text{ for }} &{} {r_{ij} >r_\mathrm{c} } \\ \end{array} }} \right. \end{aligned}$$

(15)

where $a_{ij}$ is the conservative force coefficient between particles i and j.

The random and dissipative forces form a thermostat and must satisfy the fluctuation-dissipation theorem in order for the DPD system to maintain equilibrium temperature T. This leads to:

$$\begin{aligned} \omega ^\mathrm{D}(r_{ij} )=\left[ {\omega ^\mathrm{R}(r_{ij} )} \right] ^{2}, \sigma ^{2}=2\gamma k_\mathrm{B} T \end{aligned}$$

(16)

The choice for the weight functions is as follows

$$\begin{aligned} \omega ^\mathrm{R}(r_{ij} )=\left\{ {{\begin{array}{lll} {(1-r_{ij} /r_\mathrm{c} )^{1/4}} &{} {for} &{} {r_{ij} \le r_\mathrm{c} } \\ 0 &{} {for} &{} {r_{ij} >r_\mathrm{c} } \\ \end{array} }} \right. \end{aligned}$$

(17)

where the value of exponent affects the viscosity of the DPD fluid, lower values typically result in a higher viscosity (Fan et al. 2006).

The conservative force reflects the compressibility of the fluid, the dissipative force mainly captures the viscosity of the fluid and the random force ensures that the fluid temperature remains constant.

When the cell model is immersed into the DPD fluid, the total force exerted on a membrane particle is given by

$$\begin{aligned} \mathbf{F}_i =\mathbf{F}_i ^\mathrm{membrane}+\sum _{j\ne i} {\mathbf{F}_{ij}^\mathrm{C} +\mathbf{F}_{ij}^\mathrm{D} +\mathbf{F}_{ij}^\mathrm{R} } \end{aligned}$$

(18)

While for a fluid particle, the total force is expressed by

$$\begin{aligned} \mathbf{F}_i =\sum _{j\ne i} {\mathbf{F}_{ij}^\mathrm{C} +\mathbf{F}_{ij}^\mathrm{D} +\mathbf{F}_{ij}^\mathrm{R} } +f_x \mathbf{e}_x \end{aligned}$$

(19)

where $f_x$is the value of body force along x direction. The mass of the individual particle is set to 1 and particle motion is governed by Newton’s equations of motion:

$$\begin{aligned} \mathrm{d}{} \mathbf{r}_i= & {} \mathbf{v}_i \mathrm{d}t \nonumber \\ \mathrm{d}{} \mathbf{v}_i= & {} \mathbf{F}_i \mathrm{d}t \end{aligned}$$

(20)

The above equations of motion were integrated using the modified velocity-Verlet algorithm (Espanol 1995; Groot and Warren 1997; Hoogerbrugge and Koelman 1992)

$$\begin{aligned} \mathbf{r}_i (t+\Delta t)= & {} \mathbf{r}_i (t)+\Delta t\mathbf{v}_i (t)+\frac{1}{2}(\Delta t)^{2}{} \mathbf{F}_i (t) \nonumber \\ \tilde{\mathbf{v}}_i (t+\Delta t)= & {} \mathbf{v}_i (t)+\lambda \Delta t\mathbf{F}_i (t) \nonumber \\ \mathbf{F}_i (t+\Delta t)= & {} \mathbf{F}_i (\mathbf{r}_i (t+\Delta t),\tilde{\mathbf{v}}_i (t+\Delta t)) \nonumber \\ \mathbf{v}_i (t+\Delta t)= & {} \mathbf{v}_i (t)+\frac{1}{2}\Delta t[\mathbf{F}_i (t)+\mathbf{F}_i (t+\Delta t)] \end{aligned}$$

(21)

where $\tilde{\mathbf{v}}_i (t+\Delta t)$ is the prediction of the velocity at time $t+\Delta t$ and $\lambda$ is an empirically introduced parameter, which accounts for the additional effects of the stochastic interactions, and is set to 0.65. The velocity is first predicted to obtain the force and then corrected in the last step.

DPD parameters used in the simulations of interactions among particles representing inner fluid $(\hbox { S}_\mathrm{i})$, external fluid $(\hbox { S}_\mathrm{o})$, cell vertices (C) and walls (W) are shown in Table 1.

2.4 Model and physical units scaling

The scaling procedure has been presented (Fedosov et al. 2010), which relates the model’s non-dimensional units to physical units. In order to keep the simulation system consistent with the real system, the physical properties should be mapped onto the dimensionless properties in the model. The length scale is adapted:

$$\begin{aligned} L^\mathrm{S}=\frac{D_0^\mathrm{P} }{D_0^\mathrm{M} } \end{aligned}$$

(22)

where the superscript M and P denote “model” and “physical”. The energy scale is provided as follows

$$\begin{aligned} E^\mathrm{S}=\frac{Y^\mathrm{P}}{Y^\mathrm{M}}\left( \frac{D_0^\mathrm{P} }{D_0^\mathrm{M} }\right) ^{2} \end{aligned}$$

(23)

The force scale is defined by

$$\begin{aligned} N^\mathrm{S}=\frac{Y^\mathrm{P}}{Y^\mathrm{M}}\frac{D_0^\mathrm{P} }{D_0^\mathrm{M} } \end{aligned}$$

(24)

The scaling between model and physical times is defined as follows

$$\begin{aligned} \tau ^\mathrm{S}=\frac{Y^\mathrm{M}}{Y^\mathrm{P}}\frac{D_0^\mathrm{P} }{D_0^\mathrm{M} }\frac{\eta ^\mathrm{P}}{\eta ^\mathrm{M}} \end{aligned}$$

(25)

where $\eta ^\mathrm{P}$ is the physical fluid viscosity, the surrounding fluid and cytoplasm are considered as incompressible Newtonian fluid.

The scaling between model and physical body force is expressed

$$\begin{aligned} f^\mathrm{S}=\frac{Y^\mathrm{P}}{Y^\mathrm{M}}\left( \frac{D_0^\mathrm{M} }{D_0^\mathrm{P} }\right) ^{2}\frac{n}{\rho } \end{aligned}$$

(26)

where n is the number of density in the simulation system, in this study we set $\textit{n}\,=\,6$. The density of the surrounding fluid, $\rho$, is set to be $10^{3}\,\hbox {kg}/\hbox {m}^{3}$. Simulation (in DPD units) and physical (in SI units) parameters for fluid and cell membrane are shown in Table 2.

Table 2 Simulation (in DPD units) and physical (in SI units) parameters

3 Results and discussion

3.1 Model geometry and parameter values

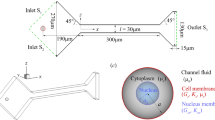
The geometry of the model slit is schematically depicted in Fig. 3. The slit has a rectangular cross section of width $\hbox { w}_\mathrm{c}$, length of 2  $\upmu \hbox {m}$ and height of 14 $\upmu \hbox {m}$. The spherical cell with diameter of 9 $\upmu \hbox {m}$ is located at $\hbox { x}= -5.6\,\upmu \hbox {m}$ initially. The computational domain is triply periodic as labeled, and the origin of the coordinate is located in the center of the slit. The vessel walls are regarded as rigid bodies, and the cell nuclei are not taken into consideration for simplicity. In order to simulate a pressure-driven flow through the slit, a uniform body force is applied to the fluid particles located at $\hbox { x} \ge 15\,\upmu \hbox {m}$. The pressure gradient in the region around the slit is not constant, which voids the validity of application of the uniform body force in that area. In order to control the density fluctuations of the fluid near the wall boundaries, an adaptive boundary condition is adopted, which has been applied on the measurement of red blood cell large deformation in a microfluidic system (Li et al. 2014). To prevent the particles from penetrating into the solid wall and the cell membrane and ensure no-slip condition, bounce-back reflection is enforced on them. It should be pointed out that due to the soft potential in DPD, the body force driven flow passing through obstacle usually results in a vacuum area in the downstream. The conservative force deriving from this soft potential tries to capture the effects of the “pressure” between different particles. Because of the soft interaction between fluid particles, the “speed of sound” in the DPD fluid is low (Pan et al. 2013) and consequently the Mach number is very high even at very low Reynolds number, resulting in a significant compressibility effect. The “speed of sound” in DPD fluid at constant temperature (Espanol 1995) has been derived as $c^{2}={\partial p}/{\partial \rho }=k_\mathrm{B} T+\pi {\text{ anr }}_c ^{4}/15$. An alternative approach to avoid the density rarefaction after the cell is to employ a large conservative coefficient (Ye et al. 2014), thus the “speed of sound” can be enhanced to ensure the Mach number less than 0.3. The fluid particles in Fig. 4 are found to be distributed uniformly.

Fig. 3

Schematic illustration of a spherical cell near a slit at initial time from the front view (a) and the left side view (b)

An important non-dimensional parameter, the capillary number is introduced, which represents the ratio between the flow viscous traction force and the elastic resistance of the membrane. A local capillary number can be defined as

$$\begin{aligned} {\text{ Ca }}=\frac{\eta _o U}{Y } \end{aligned}$$

(27)

where $\eta _0$ is the viscosity of the plasm, a characteristic velocity $U={\rho f_x w_c ^{2}}/{8\eta _0 }$. In the following results to be presented, a fixed body force $f_x =88.29\,\hbox {m}/\hbox {s}^{2}$ is applied to drive the flow. According to the optical measurements of cell deformability by a microfluidic optical stretcher, cancer cells were found to stretch approximately five times more than normal cells, and metastatic cells were found to stretch about twice as much as non-metastatic cancer cells (Lincoln 2004). The elasticity modulus of tumor cells from cancer patients was measured and yielded average value of about 0.5 kPa (Cross et al. 2007). The atomic force microscopy indentation study found that the average Young’s modulus for malignant breast cells ranged from 300 to 600 Pa at different loading rates (Li et al. 2008). As the cell membrane is only about 7–9 nm thick, which is much smaller than the diameter of the cell, the Young’s modulus for two-dimensional sheet-based cell membrane model was approximately by the average cell stiffness multiplied by the membrane thickness (Hou et al. 2009). So Young’s modulus ranges from 2.1 to $5.4\,\upmu \hbox {N}/\hbox {m}$ and Ca lies between 0.123 and 0.336. The Reynolds number $R_e ={\rho Uw_c }/{\eta _0 }$ varies from 0.002384 between 0.00565, and the Mach number computed by $\mathrm{Ma}=U/c$ lies between 0.077 and 0.137 in current study.

Fig. 4

Cross section of a deformed spherical cell passing through the slit $(\hbox { w}_\mathrm{c}=8\,\upmu \hbox {m})$ for body force $\hbox { f}_{ x}=88.29\,\hbox {m}/\hbox {s}^{2}$ exerted on the fluid particles located on $\hbox { x}>15\,\upmu \hbox {m}$ and $\hbox { x}<-15\,\upmu \hbox {m}$. a t = 7.275 ms, b t = 16.975 ms, c t = 26.675 ms, d t = 38.315 ms. The model consists of four types of particles: wall particles (black), fluid particles (blue), membrane particles (red), and cytoplasm particles (green)

Fig. 5

a Cell centroid trajectories and b the elongation indexes for three resolutions, n = 3, 6, 9 during passing through the narrow slit $(\hbox { w}_\mathrm{c}=8\,\upmu \hbox {m})$

Figure 4 visualizes the cell deformation during passing through the narrow slit. Since initially a cell has a diameter of $9\,\upmu \hbox {m}$, which is larger than the slit width, the cell would experience compression deformation. As the cell enters the slit, the front end of the cell membrane is gradually stretched along the flow direction, while the rear side maintains its sphericity, as shown in Fig. 4a. When the cell reaches the center of the slit, it is elongated to the longest, as can be seen in Fig. 4b. During exiting from the slit, the cell gradually recovers its initial spherical shape, see Fig. 4d.

To investigate the numerical convergence with respect to spatial resolution, cell passage through the narrow slit $\hbox { w}_\mathrm{c} \,{=}\, 8\,\upmu \hbox {m})$ for three resolutions, $n\,{=}\,3$, 6, 9 have been compared. As shown in Fig. 5a, the cell centroid trajectories for $n=6$ and $n=9$ agree with each other very well, but there is a large discrepancy for $n=3$. We have further checked the cell elongation index, which is defined in the following section, and the difference between $n=6$ and $n=9$ are not very large. Therefore, n = 6 is chosen for all calculations.

Fig. 6

Cell displacement along flow direction (a) and the elongation index (b) during passing through the narrow slit $(\hbox { w}_\mathrm{c}=8\,\upmu \hbox {m})$ at different values of the Young’s modulus

3.2 Effects of the cell membrane elasticity

In this section, the effect of Young’s modulus as an important factor to the elasticity of a cell is examined, with values varying from 0.416 to $4.16\,\upmu \hbox {N}/\hbox {m}$ which enclose the values from the measurement (Hou et al. 2009). Figure 6a shows the distance between the cell front, rear end and their respective initial positions. It can be seen that the cells with different elasticity experience the same trend of motion. As the cell enters into the slit, the line chart begins with a steep slope in the displacement of front end and this gradually decreases, which is qualitatively in agreement with experiment (Lincoln 2004). Also, the dashed line represents the distance between the exit and the initial position of cell rear end in Fig. 6a. Once the displacement of the rear end exceeds the dashed line, it means that the cell passes the slit completely and the time spent is defined by the transit time. The displacement of the front end is slightly greater than that of rear end initially, but then it is exceeded by the latter, which means the cell is stretched first and then shrinks. Obviously, with the decrease of modulus, it takes less time for the cell to pass through the slit, which can be seen in Fig. 6a. The malignant breast cancer cells was found to have a Young’s modulus which is 1/1.8–1/1.4 that of their non-malignant counterparts (Lincoln 2004). The study on the deformability of breast cancer cells has shown that the non-malignant cells have longer entry time than the malignant counterparts through the microchannel, where the entry time is defined as the time taken for the cell to deform and enter completely into the microchannel (Lincoln 2004). In order to characterize the deformation of the cell, elongation index is introduced. It is the ratio of the cell elongated length $(L_{x})$ in the flow direction to its initial diameter (D). In Fig. 6b, the cell elongates first and then shrinks gradually, which is corresponding to the displacements of rear end and front end. Apparently, it is faster to recover its original sphere shape and easier to deform for a softer cell.

A bending modulus for the breast cancer cell membrane was calculated to be $1.35\times 10^{-19}$ J (Guo 2004), which is in the same order as that for the red blood cell membrane. Based on the investigation on the transit of cells with different bending rigidities through the slit, it takes longer time for the stiffer cell to transit through the slit, but there is almost no difference in the trajectories of cell centroid when the bending rigidity reduces by an order magnitude, as can be seen in Fig. 7. So the bending rigidity has little effect on the cell transit time. Based on the ratio between the bending forces to membrane spring forces expressed by $\xi =k_\mathrm{bend} /YR^{2}$, where R is the cell radius, it reaches the order of $10^{-3}$ so that the deformation due to bending forces is negligible compared to the deformation caused by elastic force.

Overall, under the condition of cell surface area-preserving, Young’s modulus is only related to shear modulus determined by the wormlike chain spring forces and plays a key role in the membrane elasticity.

Fig. 7

Centroid trajectories of cells passing through the narrow slit $(\hbox { w}_\mathrm{c}=8\,\upmu \hbox {m})$ at different values of bending rigidities with $\hbox { Y} =4.16\,\upmu \hbox {N}/\hbox {m}$

3.3 Cell entry into the narrow slits with decreasing size

With the decrease in the slit size, the cell enters more slowly and protrudes less and less into the slit, then it becomes blocked, just as shown in Fig. 8, the two dash lines indicate the positions of cell centroid entry and exit. Compared with the entry into the slit with a width of $\hbox { w}_\mathrm{c }= 6\,\upmu \hbox {m}$, the cell in the slit with $\hbox { w}_\mathrm{c}= 7\,\upmu \hbox {m}$ moves faster and produces a longer protrusion. In fact, for a fixed pressure drop, the narrower the slit is, the lower the Ca. The supplied body force is not large enough to produce sufficient viscous traction force to deform the cell in face of the resistance from the confinement of the narrower slit.

Fig. 8

Centroid trajectories of cell passing through slits with different sizes

Fig. 9

The protrusion length comparison for blocked cells in the slit $(\hbox { w}_\mathrm{c}= 6\,\upmu \hbox {m})$ at different values of Young’s modulus

As the elasticity affects largely the cell deformability, cells with different values of the Young’s modulus squeezing into the slit of 6 $\upmu \hbox {m}$ width are compared in Fig. 9. It illustrates the steady-state shape of the cell after obstruction. The length of protrusion is indicated by $l_{t}$, the distance between the cell front end and the entry of the slit. As seen from Fig. 9, reducing the elasticity modulus by 10 times can double the protrusion length, but still does not enable the cell to pass the narrow slit.

3.4 Effects of the cell shape

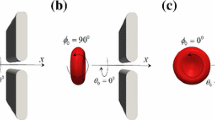
The cell surface-to-volume ratio is a determinant of the static deformability of the cells. Cancer cells exhibit various kind of shapes, including round, oval elongated and clusters (Park et al. 2014). The shape transformation from sphere to flat ellipsoid largely increases the surface-to-volume ratio. In this subsection, spherical and ellipsoidal cell with the same volume and mechanical properties passing through the narrow slit $(w_\mathrm{c} = 6\,\upmu \hbox {m})$ are compared in terms of the deformation. The effects of initial orientation of ellipsoidal cell on its transit through the slit are investigated. Information about different cell shapes is listed in Table 3.

Table 3 Geometrical properties about different shapes of cells

In order to characterize the cell deformation, the expression of local strain has been introduced in the previous study (Chen et al. 2013). Based on this definition, the average deformation $\gamma _{i }$ for the membrane particle i is expressed as follows:

$$\begin{aligned} \gamma _i =\sqrt{\frac{\sum _{j=1}^{N_i } {\left( \frac{l_{ij} }{l_{ij,0} }-1\right) ^{2}} }{N_i }} \end{aligned}$$

(28)

where $N_{i }$ represents the number of springs which is connected by particle i, $l_{ij}$ and $l_{ij,0}$ are the instantaneous and spontaneous lengths of springs, respectively. The local deformation contour for each membrane particle is plotted in Fig. 10. When the spherical cell protrudes the slit, its forefront suffers large deformation but the rear end does not nearly deform. The middle part of the cell located in the slit retains to be stretched with local $\gamma$ reaching 80 % after blockage, as shown in Fig. 10a. But for an ellipsoidal cell, the deformation depends on its initial orientation. When its seminor axis is parallel to y axis at initial time, the cell can pass through the slit easily, which can be seen in Fig. 10b, as the length of seminor axis is comparable to the slit. When the cell enters the slit, its front end is stretched initially. With the increase in protrusion length, the extruded part of cell expands and middle part maintains to be stretched, while the rear end almost keeps its original shape. After exiting from the slit, the forefront of the cell is stretched largely, while the rear end is compressed. But if the cell rotates $90^{\circ }$ around z or x axis at initial time, the size of cell is nearly double the slit width. Therefore, the cell should compress itself when traversing the narrow slit, which produces large deformation. As its centroid reaches the center of the slit, the extruded part expands largely and local $\gamma$ can attain 70 %, while the exposed part has not been squeezed into the slit shrinks and even some wrinkles appear on the membrane, as can be seen in Fig. 10c, d. When the cell exits from the slit, it enfolds within the slit. After passing through the slit, the expanding part gradually shrinks and the shrinking one expands slowly.

In fact, before transmigrating through the slit between two endothelial cells, a tumor cell has to adhere to the endothelium. Then, the adherent spherical cell would spread out into a flat shape before extravasation (Albelda et al. 1994; Dewitt and Hallett 2007; Stoletov et al. 2010; Zhu et al. 2000). This shape change enables tumor cells transmigrate through a much narrower slit. Next, effect of initial orientation on ellipsoidal cell transit time is investigated. Firstly, the transit time, entry time and exit time are defined as

$$\begin{aligned} \Delta t=t_\mathrm{out} , \Delta t_\mathrm{entry} =t_{x_\mathrm{c} =0} , \Delta t_\mathrm{exit} =t_\mathrm{out} -t_{x_\mathrm{c} =0} , \end{aligned}$$

(29)

where $t_\mathrm{out} =t({\mathop {\mathrm{min}}\nolimits _{x\in s}}\, x=1)$ and $t_{x_\mathrm{c} =0}$ is the time when the cell centroid approaches the middle of the slit. Figure. 11 compares the cell transit time, entry time and exit time for three different orientations. For all cases, the entry time is longer than the time spent on exit from the slit. It takes less time to pass through the slit for the cell with initial seminor axis parallel to flow direction. This may because that the cross section of the cell perpendicular to the flow direction is largest compared to the other two cases. The initial layout that the seminor axis is parallel to z axis has the longest transit time and enlarges the difference between entry time and exit time, due to the fact that the cell needs longer time to deform itself to adapt to the slit when entering into the slit. To conclude, initial orientation plays an important role in the ellipsoidal cell transit through the narrow slit

Fig. 10

Snapshots of the cell deformation for different relaxed shapes through the narrow slit $(\hbox { w}_\mathrm{c}=6\,\upmu \hbox {m})$ from the front view (the upper row) and the top view (the lower row) separately. A / V is 0.667 in a, 0.730 in b, c and d. b, c and d represent that the seminor axis of the cell is parallel to y, x and z axis, respectively

A quantitative observation of tumor cell deformation using microfluidic device pointed out that during the transition through the microgap, the cancer cell (15–18 $\upmu \hbox {m}$) deformed from a spherical to ellipsoidal shape and the cell’s surface area increased by 8.8- and 3.7-fold across the $3\upmu \hbox {m}$ and $10\upmu \hbox {m}$ gaps, respectively (Chaw et al. 2007, 2006). The cell membrane would confront with the resulting increase in surface tension as it deforms across a narrower slit and its deformability affects its survivability. In addition, for undeformed leukocytes, there are many folds and wrinkles on the membrane, which provide more than 80 % excess surface area (Dewitt and Hallett 2007; Schmidschonbein et al. 1980). Likewise, a physically unrestrained circulating cancer cell is assumed to have a pleated surface and the membrane unpleating could occur and the cell surface area would increase largely when cells enter capillaries (Weiss et al. 1988). Therefore, transformation from spherical to flat ellipsoidal shape can increase cell deformability largely and facilitates the cancer cell extravasation.

3.5 Effect of nucleus on cell transit across the slit

The above-mentioned results are based on the deformation of cell without nucleus. In this subsection the ellipsoidal cells with and without nucleus passing through the narrow slit $(\hbox { w}_\mathrm{c} = 4\,\upmu \hbox {m})$ are investigated. The seminor axis of cell is parallel to the y axis initially. The nucleus is assumed to have a spheroidal shape with diameter of $\,3\,\upmu \hbox {m}$ and Young’s modulus $41.6\,\upmu \hbox {N}/\hbox {m}$. In order to enable the cell to pass through the narrower slit, the external body force increases three times.

Figure 12 plots the trajectories of the ellipsoidal cells with and without nucleus. Admittedly, under the same condition, the cell without nucleus can completely pass through the slit while having the nucleus blocks the contraction. The nucleus with weaker deformability indirectly constrains the membrane deformation when cell enters into the slit, which further leads to the cell blockage. Therefore, to a certain extent, the presence of nucleus reduces the deformability of the cell when its size is comparable to the slit.

4 Conclusion

In this study, a cell passing through a narrow slit was numerically investigated using dissipative particle dynamics (DPD) combined with a spring-based network model for the cell membrane. The effects of the cell elasticity, cell shape as well as the slit size on the cell passage through the slit were discussed. It was found that although the elasticity as an important factor to deformability affects cell transit across the slit, reducing the elasticity modulus by 10 times cannot enable a spherical cell to pass the slit with the width 2/3 of its diameter. However, transforming the cell from a spherical into ellipsoidal shape, with the surface area increased only by 9.3 %, the cell can pass the slit. Also, the effect of initial orientation of ellipsoidal cell on its passage through the slit including cell deformation and transit time has been investigated. The findings showed that it takes less time for the cell with larger cross-sectional perpendicular to the flow direction. Furthermore, the effect of nucleus on cell transit through the slit with $4\,\upmu \hbox {m}$ in width was examined. It demonstrated that when the cell nucleus is comparable with the slit size, it would slow down the cell passage and even lead to cell blockage. In conclusion, the cell shape and surface area increase plays a more vital role than the cell elasticity in improving cell deformability, which facilitates the cell to pass through the narrower slit. Moreover, the nucleus indirectly reduces the deformability of cell during cell passage through the slit when its size is comparable to the slit.

Fig. 11

The transit time, entry time and exit time of the ellipsoidal cell for the three kinds of initial orientations: A, B and C represent that the seminor axis of the cell is parallel to y, x and z axis, respectively

Fig. 12

Trajectories of the ellipsoidal cell with and without nucleus passing through the narrow slit $(\hbox {w}_\mathrm{c} = 4 \upmu \hbox {m})$. Blue represents cell nucleus

Nevertheless, several limitations of the model in this study should be mentioned. Firstly, tumor transmigration is a complex process including the interaction between endothelial cells, blood cells and tumor cell, which has not been considered in this study. Secondly, the slit geometry is simple, while in reality the inter-endothelial cleft is irregular and flexible, which has a great effect on tumor cell transmigration. Finally, for simplicity, the blood vessel wall is regard as rigid. The effect of vessel wall elasticity on the cell transit across the slit should be investigated in the future research.