1 Introduction

The migration of malignant tumor cells to distant targeted organs is often achieved by blood circulation. The tumor cell entered into the bloodstream is called the circulating tumor cell (CTC). Its motion largely depends on the local blood hydrodynamic conditions such as shear stress and viscosity. The tumor cell must suffer the hydrodynamic shear stresses and local forces due to neighboring biological cells, which may lead to the arrest of cell movement in larger vessels. In order to escape from the circulatory system, the tumor cell must first bind to a blood vessel wall by molecular interactions between the tumor cells and the endothelial cells forming the inner wall of the blood vessels. A series of in vivo experiments demonstrated that the curved portion and bifurcations in microvasculature serve as the major sites of tumor cell adhesion (Guo et al. 2014; Zhang et al. 2016). Most of the flexible tumor cells were arrested at postcapillary venule–postcapillary venule intersections (Guo et al. 2014). Experimental investigation using a confocal micro-PIV system showed that cancer cells frequently adhered to the inner of the bifurcation (Ishikawa et al. 2011). The precise mechanism of this phenomenon is not yet clear, but it is obvious that the tumor cell deformability together with the presence of RBCs and localized hydrodynamic conditions should contribute to this preferred adhesion of tumor cells. Simulations that can explain cell adhesion under complex flow conditions in microcirculation would be of great help in quantifying the relationship between adhesion molecules and complex shear stresses.

Previous numerical findings have reported that red blood cells tend to slow down and aggregate around the apex of the diverging bifurcation (Barber et al. 2011; Li et al. 2020; Wang et al. 2016; Ye and Peng 2019). The simulation results showed that cells preferentially enter the daughter branch of a larger flow ratio or the wider branch when the branches are different in size (Barber et al. 2011; Hyakutake and Nagai 2015; Wang et al. 2016). However, if the daughter branches are symmetric, the cells would flow through a branch depending on the deflection of the cell centroid at the apex of the bifurcation (Barber et al. 2011; Li et al. 2012; Ye et al. 2018). In addition, the deformability of cells has a considerable influence on the motion of cells at the bifurcations. The stiffer cells may block the vessel when traversing the daughter branches (Barber et al. 2011; Tang et al. 2015; Ye and Peng 2019; Ye et al. 2019). Most of the previous studies focused on tumor cells’ motion in straight channels with uniformly-sized rectangular or cylindrical cross sections (Rejniak 2012; Takeishi et al. 2015). The flow mode of a CTC is largely affected by its size relative to the diameter of the blood vessel. A transition from train formation to margination occurred at (R − a)/tR≈1, where R is the vessel radius, a is the cell radius, and tR is the thickness of RBCs (Takeishi et al. 2015). In our previous study on the motion of a tumor cell in a straight circular microvessel, the presence of RBC would also be the major factor for cell adhesion at low flow rates (Xiao et al. 2017). Numerical study on the moition of leukocyte-inspired microroller in blood flow showed that shear-induced collisions between RBCs and the microroller can affect the motion of the microroller (Qi et al. 2021). Previous study on the migration of tumor cells in a real microvascular network revealed that tumor cells probably extravasate at the bifurcations when the flow rate is relatively low and the hematocrit is moderate (Wang et al. 2021). A numerical study on the motion of a tumor cell in a curved microvessel revealed that vessel curvature has a significant influence on cell adhesion (Xiao et al. 2020b). It is necessary to further study the motion of tumor cells in a bifurcated microvessel and investigate how the bifurcations influence the adhesion of CTC.

In this study, 3D simulations of the motion of a tumor cell in a symmetric bifurcated microvessel were carried out by using the dissipative particle dynamics method coupled with a spring-based network cell model. Then, the effects of the initial position of CTC at the upstream of diverging bifurcation, externally-applied acceleration as well as the intercellular interaction between flowing RBC and adherent CTC on the motion of CTC in the bifurcated microvessel were investigated. Finally, summary and conclusions were presented.

2 Models and methods

The blood flow dynamics is solved by the dissipative particle dynamics method, which has been adopted in our previous studies. Introductions to the DPD method have been presented in detail (Espanol 1995; Groot and Warren 1997; Hoogerbru and Koelma 1992). In brief, each DPD particle characterizes a soft lump of atoms and interacts with surrounding particles by three simple pairwise additive forces: conservative force, dissipative force, and random force. Particle motion is governed by Newton’s equations of motion.

$$\begin{aligned} {\text{d}}{\mathbf{r}}_{i} = & {\mathbf{v}}_{i} {\text{d}}t \\ m_{i} {\text{d}}{\mathbf{v}}_{i} = & \sum\limits_{{j \ne i}} {\left( {F_{{ij}}^{C} - \gamma \left[ {\omega \left( {r_{{ij}} } \right)} \right]^{2} \left( {{\mathbf{v}}_{{ij}} \cdot {\mathbf{\hat{r}}}_{{ij}} } \right){\mathbf{\hat{r}}}_{{ij}} + \sigma \omega \left( {r_{{ij}} } \right)\frac{{\xi _{{ij}} }}{{\sqrt {{\text{d}}t} }}{\mathbf{\hat{r}}}_{{ij}} } \right)} {\text{d}}t + {\mathbf{F}}_{{{\text{ext}}}} {\text{d}}t \\ \end{aligned}$$
(1)

where \({\mathbf{r}}_{i}\), \({\mathbf{v}}_{i}\) and \(m_{i}\) are the location, velocity, and mass of the ith particle, the mass of the individual particle is set to 1; t is the time. \({\mathbf{F}}_{{i{\kern 1pt} j}}^{C}\) is the conservative force between particle i and j. γ and σ reflect the strength of dissipative and random forces, respectively. \(\omega (r_{ij} )\) is a distance-dependent weight function. \({\hat{\mathbf{r}}}_{ij} = {\mathbf{r}}_{{{\mathbf{i}}j}} /r_{ij}\), \({\mathbf{r}}_{ij} = {\mathbf{r}}_{i} - {\mathbf{r}}_{j}\) and \({\mathbf{v}}_{ij} = {\mathbf{v}}_{i} - {\mathbf{v}}_{j}\). \(\xi_{ij}\) is a normally distributed random variable with zero mean, unit variance, and \(\xi_{ij} = \xi_{ji}\); dt is the time step. \({\mathbf{F}}_{ext}\) is the external force acted on particle i.

The cell membrane is modeled as a collection of particles connected by elastic springs. These springs comprise a network, which is endowed with in-plane and bending energy as well as constraint of surface area and volume. The details of the RBC membrane model and the scaling procedure have been described in previous studies (Boey et al. 1998; Fedosov et al. 2010; Pivkin and Karniadakis 2008; Xiao et al. 2020a, 2016, 2017). The total energy of the network is defined as

$$ E(\{ {\mathbf{r}}_{i} \} ) = E_{{\text{in - plane}}} + E_{{{\text{bending}}}} + E_{{{\text{area}}}} + E_{{{\text{volume}}}} $$
(2)

The deformation forces are derived from the total energy as follows:

$$ {\mathbf{F}}_{i}^{membrane} = - \partial E\{ ({\mathbf{r}}_{i} )\} /\partial {\mathbf{r}}_{i} $$
(3)

A detailed description of the four types of energies can be found in the previous work(Fedosov et al. 2010). Based on linear analysis of a hexagonal system built with equilateral triangles (Dao et al. 2006), the macroscopic properties of the simulated cell were presented. The linear shear modulus of the WLC-POW model is

$$ G = \frac{{\sqrt 3 k_{B} T}}{{4pl_{\max } x_{0} }}\left( {\frac{{x_{0} }}{{2(1 - x_{0} )^{3} }} - \frac{1}{{4(1 - x_{0} )^{2} }} + \frac{1}{4}} \right) + \frac{{\sqrt 3 k_{p} (m + 1)}}{{4l_{0}^{m + 1} }},\quad x_{0} = l_{0} /l_{\max } $$
(4)

where \(l_{{0}}\) and \(l_{\max }\) are equilibrium spring length and the maximum spring extension, p is the persistence length, \(k_{B}\) T is the Boltzmann temperature of the system. \(k_{p}\) is a POW force coefficient and m is a specified exponent.

The linear area dilation modulus is approximated as

$$ K = 2G + k_{{{\text{area}}}}^{{{\text{tot}}}} + k_{{{\text{area}}}} $$
(5)

where \(k_{{{\text{area}}}}^{{{\text{tot}}}}\), \(k_{{{\text{area}}}}\) are constraint constants for the global area and local area.

The Young’s modulus Y for the two-dimensional sheet can be expressed as

$$ Y = \frac{{4{\text{KG}}}}{K + G} $$
(6)

The relationship between bending modulus \(k_{{{\text{bend}}}}\) and the macroscopic membrane bending rigidity \(k_{c}\) is derived for the case of a spherical shell in the Helfrich bending energy, as follows:

$$ k_{{{\text{bend}}}} = \frac{2}{\sqrt 3 }k_{c} $$
(7)

2.1 CTC adhesion model

A major conceptual development is the recognition that under the shear flow, CTC adhesion to vascular endothelium is often mediated via a surprisingly small number of receptor-ligand bonds (Zhu et al. 2000), where receptors and ligands are distributed on the surface of the cell and the endothelial cells, respectively. The formation and dissociation of bonds between receptors and ligands are controlled by the probabilistic model developed by Hammer and Apte (1992). The probabilities of bond formation and disassociation in a time interval \(\Delta t\) are given by

$$ P_{{{\text{on}}}} = \left\{ \begin{gathered} \hfill 1 - e^{{ - k_{{{\text{on}}}} \Delta t}} ,l^{b} < d_{{{\text{on}}}} \\ \hfill 0,l^{b} \ge d_{{{\text{on}}}} \\ \end{gathered} \right.,\quad P_{{{\text{off}}}} = \left\{ \begin{gathered} \hfill 1 - e^{{ - k_{{{\text{off}}}} \Delta t}} ,l^{b} < d_{{{\text{off}}}} \\ \hfill 0,l^{b} \ge d_{{{\text{off}}}} \\ \end{gathered} \right. $$
(8)

where \(k_{{{\text{on}}}}\) and \(k_{{{\text{off}}}}\) are the formation and dissociation rates of a bond. At a given time instance, two random numbers \(\xi_{1}\) and \(\xi_{2}\) with uniform distribution in [0, 1] are generated. If an existing bond breaks, the condition \(\xi_{1} < P_{{{\text{off}}}}\) should be satisfied. A new bond is allowed to form if \(P_{{{\text{on}}}} > \xi_{2}\) under the condition that the distance between a receptor and a free ligand is less than the reactive distance. A free ligand refers to that it is not bound to any receptors. Reversely, a pre-existing bond may break with off-rate \(k_{{{\text{off}}}}\) or if its length exceeds the rupture distance \(d_{{{\text{off}}}}\). The rates \(k_{{{\text{on}}}}\) and \(k_{{{\text{off}}}}\) are defined as:

$$ \begin{gathered} k_{{{\text{on}}}} = k_{{{\text{on}}}}^{0} \exp \left( { - \frac{{\sigma_{{{\text{on}}}} (l^{b} - l_{0}^{b} )^{2} }}{{2k_{B} T}}} \right), \hfill \\ k_{{{\text{off}}}} = k_{{{\text{off}}}}^{0} \exp \left( {\frac{{\sigma_{{{\text{off}}}} (l^{b} - l_{0}^{b} )^{2} }}{{2k_{B} T}}} \right) \hfill \\ \end{gathered} $$
(9)

where \(k_{{{\text{on}}}}^{0}\) and s are the unstressed reaction rates at the distance \(l^{b} = l_{0}^{b}\) between a receptor and a ligand with the equilibrium spring length \(l_{0}^{b}\). The effective on and off strengths \(\sigma_{{{\text{on}}}}\) and \(\sigma_{{{\text{off}}}}\) define a decrease or an increase in the corresponding rates within the interaction lengths \(d_{{{\text{on}}}}\) and \(d_{{{\text{off}}}}\). Bonds are supposed to behave as elastic springs, which obey the Hooke’s law

$$ F(l^{b} ) = k_{s} (l^{b} - l_{0}^{b} ) $$
(10)

where \(k_{s}\) is the spring constant. The binding force can be derived as \({\mathbf{F}}_{i}^{{{\text{bond}}}} = F(r_{ij} ){\hat{\mathbf{r}}}_{ij}\).

Adhesive dynamics of CTC depends on several factors, such as densities of the available receptors and ligands, bond formation/dissociation rates, bond strength,cell properties and flow conditions. The densities of the physical receptors and ligands found in experiments are larger than those in simulations, and a coarse-grained model of a CTC is adopted. Thus, a receptor-ligand binding site in simulations may represent several physical bonds.

2.2 Model and physical unit scaling

To relate the model’s non-dimensional units to the physical parameters, a scaling procedure has been presented by Fedosov et al. (2010), which ensures that the modeling system is consistent with the physical system. The length scale is given by:

$$ L^{S} = \frac{{D_{0}^{P} }}{{D_{0}^{M} }} $$
(11)

where the superscripts M and P denote “model” and “physical”. The energy scale is provided as follows:

$$ E^{S} = \frac{{Y^{P} }}{{Y^{M} }}\left( {\frac{{D_{0}^{P} }}{{D_{0}^{M} }}} \right)^{2} $$
(12)

The force scale is defined by

$$ N^{S} = \frac{{Y^{P} }}{{Y^{M} }}\frac{{D_{0}^{P} }}{{D_{0}^{M} }} $$
(13)

The scaling between model and physical times is defined as follows:

$$ \tau^{S} = \frac{{Y^{M} }}{{Y^{P} }}\frac{{D_{0}^{P} }}{{D_{0}^{M} }}\frac{{\eta^{P} }}{{\eta^{M} }} $$
(14)

3 Simulation setup and modeling parameters

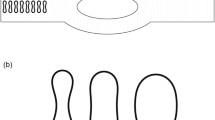
The motion of a circulating tumor cell under plasma flow in a symmetric diverging-converging bifurcated microvessel was simulated. The microvessel is of right-left symmetric geometry, and each symmetric part consists of a straight parent elliptical tube and two daughter branches with a circular cross section. This bifurcated microvessel is an ideal model, representing the basic unit of a real microvascular network. The schematic model of the bifurcation is illustrated in Fig. 1. The parent tube bifurcates into two branches, forming a Y-shaped tube. A mirror-image Y-shaped microvessel with confluence is created on the right domain. The length of the parent tube is \(L_{{\text{p}}} = {5}6\,{\mu m}\) and the semi-major and semi-minor axes of the elliptical cross section are \(a = {7}\sqrt {2} \,{\mu m}\) and \(b = 7\,{\mu m}\). The length and diameter of the two branches are \(L_{{\text{d}}} = {5}6\,{\mu m}\) and \(D_{{\text{d}}} = 7\,{\mu m}\). The angle between the two daughter branches is \(\alpha = {\pi \mathord{\left/ {\vphantom {\pi {3}}} \right. \kern-\nulldelimiterspace} {3}}\). An adaptive boundary method is applied to guarantee the vessel wall impenetrability and no-slip condition(Lin et al. 2019). A periodic boundary condition is assumed at the left and right boundary of the microvessel along the x-direction. To drive the flow, an external acceleration is applied to all free particles along the centerline of the microvessel, which is equivalent to the pressure gradient \(\Delta P{/}L = \rho {\text{g}}\), where ∆P is the pressure drop over the tube length and ρ is the suspension’s mass density.

Fig. 1
figure 1

Schematic illustration of a 3D symmetric bifurcated microvessel with diverging and converging bifurcations

Full size image

Different types of circulating tumor cells vary in size. Measurement of biopsy slides of small cell lung carcinoma showed that these cells are on average 7.2 to 10 µm in diameter(Harouaka et al. 2013). The circulating tumor cells of prostate cancer isolated by a microfluidic device are 8–16 µm in diameter, and three-dimensional imaging showed that the circulating tumor cells appeared spherical (Stott et al. 2010). CTCs from clinical samples can be smaller than tumor cell lines. The flexible tumor cell with a spherical shape has a diameter of 9 µm, which has been adopted in previous numerical studies(Xiao et al. 2016, 2017; Yan et al. 2010). It is constructed by 1174 particles. For simplicity, the nucleus is neglected in this study. Initially, the CTC is released in the parent tube before the diverging bifurcation. When the flow begins, the tumor cell moves with it from left to right and enters the bifurcations. Bounce-back reflection is exerted on the surface of the cell membrane to ensure its impenetrability. The parameters of plasma and CTC are listed in Table 1.

Table 1 Simulation parameters for cell membrane and plasma
Full size table

4 Results and discussion

4.1 Fluid flows in a bifurcated microvessel

In this section, a Poiseuille flow in the absence of cells in the bifurcated microvessel was firstly simulated. In this DPD model, an external acceleration is 100 m/s2, which is equivalent to a pressure gradient of \(\Delta P/L = \rho g = 0.1{\text{Pa}}/\mu {\text{m}}\). The generated mean velocity for the flow of the parent tube in absence of cells is 0.51 mm/s and the Reynolds number is \({\text{Re}} = \rho u_{m} D/\mu = 5.95 \times 10^{ - 3}\), which is the typical value for the arterioles with a diameter of 15 µm (Popel and Johnson 2005). Figure 2 illustrates the distribution of velocity vectors and contours for the cross section of the flow. It seems that the flow velocity distribution is upper-lower symmetric. The adherent CTC was arrested in blood flow with a relatively low velocity of less than 1 mm/s at the postcapillary venule (Guo et al. 2014).

Fig. 2
figure 2

The distribution of axial velocity magnitude contours and velocity vectors for the cross section of the flow without CTC in a bifurcated microvessel

Full size image

4.2 Effects of the initial position of CTC on its motion in the bifurcated microvessel

The effect of the initial position of the CTC on the motion, deformation, and adhesion of the cell is investigated. The CTC firstly is arranged close to the left boundary and at the center of the parent tube. The blood is first assumed to be an incompressible, Newtonian plasma with constant density and viscosity, which are given in Table 1. The cell’s motion and shape evolution in the bifurcated microvessel is shown in Fig. 3(a). The CTC moves along the centerline of the parent vessel before the bifurcation. When it enters into the conjunction of the two branches, as shown in Fig. 3(b), it moves slowly and deviates from the centerline gradually before approaching the apex of the diverging bifurcation. On reaching the flow divider between the two branches, the cell contacts the inter-sectional vessel wall of two daughter branches, and ligand-receptor bonds form on its surface. As the residence time at the bifurcation apex prolongs, the number of bonds increases rapidly and the cell rotates more slowly. The spherical cell deforms to make a flat contact area with the vessel wall. Finally, it slides into the upper branch and meanwhile, the contact area enlarges and the rolling motion temporarily stops. Under the combined influence of the cell deformation, hydrodynamic force, and stochastic bond kinetics, some new receptor-ligand bonds form in the front end and several formed bonds are ruptured in the rear end. The adherent cell presents as a ‘tear drop’ shape, which promotes the formation of more receptor-ligands in the front end of the tumor cell. The hydrodynamic wall-directed force is so weak that the cell is ultimately arrested by the tethering of receptors (see Fig. 3(c)).

Fig. 3
figure 3

Trajectory of the tumor cell which is initially released at the tube centerline a and the variation of number of receptor-ligand bonds formed on the surface of CTC and the trajectories of x and y centroid of the CTC b and the hydrodynamic force and total adhesive force toward the wall c under the condition of an externally-applied acceleration g = 100 m/s.2

Full size image

When the cell locates near the vessel wall initially, its motion, deformation, and adhesion in the bifurcated microvessel are shown in Fig. 4. It first binds to the wall by the receptor-ligand bond formation. When the flow starts, the plasma begins to flow and the adherent tumor cell rolls along the vessel wall of the parent tube. During the transformation of the CTC from a sphere to a ‘tear drop’ shape, the contact area increases so that the number of bonds grows up slightly. During its rolling on the vessel wall, the formation rate of the number of bonds is smaller than the breakage rate under the influence of increasing hydrodynamic shear force, the number of ligand-receptor bonds decreases gradually and the cell moves away from the vessel. Before reaching the flow divider between the two branches, the cell moves near the vessel wall and its centroid deflects to the lower branch. Consequently, the cell cannot contact the apex of the bifurcation, so it will not be arrested by the vessel wall. Instead, the cell enters into the lower daughter branch and it moves along the center of the vessel and recovers to nearly spherical shape. Finally, it passes through the top daughter branch and enters into the parent vessel.

Fig. 4
figure 4

Trajectory of the tumor cell which is initially released at the bottom of the parent tube a and the variation of number of receptor-ligand bonds formed on the surface of CTC and the trajectories of x and y centroid of the CTC b under the condition of an externally-applied acceleration g = 100 m/s.2

Full size image

4.3 Effects of external acceleration on the motion of the CTC in the bifurcated microvessel

The effect of external acceleration on the motion and adhesion of the CTC is studied. When the CTC is released from the center of the parent tube initially, it would be arrested by the diverging bifurcation under the condition of an external acceleration of g = 100 m/s2. If the externally-applied acceleration increases to 150 m/s2, the adherent CTC at the apex of the bifurcation also slides into the upper branch and extends along the flow direction under the increasing shear force acted by the plasma fluid so that the contact area increases, as shown in Fig. 5(a), resulting in a rapidly growing number of ligand-receptor bonds (see Fig. 5(b)). The adherent CTC rolls slowly when the number of ligand-receptor bonds reaches its peak value of about 50. Since cell motion is affected by the combination of cell deformation, hydrodynamic force, and stochastic bond kinetics. Affected by the persistent streamwise force, the bond formation rate is lower than the bond breakage rate, leading to a gradual decline in the number of ligand-receptor bonds. The CTC moves slowly away from the vessel and travels with the plasma flow. After passing through the joint position of the diverging and converging bifurcations, the CTC moves near the outer wall of the daughter branch influenced by the inertial force. Then the CTC migrates toward the centerline and exits from the branch to the parent tube.

Fig. 5
figure 5

Trajectory of the tumor cell which is initially released at the tube centerline a and the variation of number of receptor-ligand bonds formed on the surface of CTC and the trajectories of x and y centroid of the CTC b under the condition of an externally-applied acceleration g = 150 m/s.2

Full size image

For the case of the tumor cell released from the centerline of the parent tube, the effect of externally-applied acceleration on the number of ligand-receptor is investigated when the tumor cell is passing through the diverging bifurcation. As shown in Fig. 6, when the externally-applied acceleration decreases from 100 m/s2 to 50 m/s2, the adherent CTC at the apex of the diverging bifurcation deforms less and a fewer number of ligand-receptors. Subsequently, the hydrodynamic shear force acted by the plasma is not strong enough to peel off the tethered CTC and the cell stops at the vessel wall of the top branch. However, if the acceleration increases to 150 m/s2, even though the peak value of the number of bonds increases by 50%, the adherent CTC would detach from the vessel wall in the upper daughter branch. But when the acceleration continues to rise to 200 m/s2, the maximum value of the number of the bonds falls to approximately 30, which may be ascribed to shorter residence time. In addition, the tethered CTC peels off the wall earlier.

Fig. 6
figure 6

The number of receptor-ligand bonds formed on the surface of CTC when the CTC that is released at the tube centerline moves to the diverging bifurcation for the flow at different external accelerations

Full size image

The effect of initial location on cell transit time through the bifurcations is investigated. Here, the transit time, the entry time, and exit time are defined as \(\Delta t_{{1}} = t_{{x_{c} = 0}} - t_{{x_{c} = - {56}}}\) and \(\Delta t_{{2}} = t_{{x_{c} = {56}}} - t_{{x_{c} = 0}}\), where \(t_{{x_{c} = 0}}\) is the time instant that the cell centroid approaches the joint position of the diverging and converging bifurcations, \(t_{{x_{c} = - {56}}}\) refers to the time when the cell centroid reaches the intersection of two daughter branches, which is at the upstream of the diverging bifurcation and \(t_{{x_{c} = {56}}}\) means the time instant that the cell centroid exits from the converging bifurcation. Obviously, the tumor cell located at the centerline of the parent tube initially experiences a longer entry time and a shorter exit time. From Fig. 7, it can be found that the CTC spends about 80% of entry time on the adhesion and detachment from the vessel wall. This means that the CTC moving freely in the parent tube would experience a long residence time at the apex of the bifurcation under low flow rates, which facilitates firm adhesion and further extravasation from the bloodstream into the surrounding tissue.

Fig. 7
figure 7

Transit time through the diverging and converging bifurcations, indicated by Δt1 and Δt2, respectively, for the CTC initially released at the parent tube centerline (labeled by “initial free CTC”) under the external conditions of g = 150 m/s2 and g = 200 m/s2and at nearly the vessel wall (labeled by “initial adherent CTC”) under the external conditions of g = 100 m/s2, g = 150 m/s2and g = 200 m/s.2

Full size image

4.4 Effects of RBCs on the motion of CTC in the bifurcated microvessel

As the main blood constituents, RBCs are not distributed uniformly in the small blood vessels, the size of which is not negligible compared with the diameter of the blood vessel. So they behave like elastic objects suspended in plasma and affect the transport of the CTC. Here, the blood is treated as a suspension of RBCs. Previous findings showed that the collision between the flowing RBCs and marginated WBCs in a small vessel not only enlarges the streamwise forces, impairing the WBC binding but also causes an average wall-directed force, which is expected to enhance binding (Isfahani and Freund 2012). In this section, eight RBCs are initially located coaxially with the centerline of the parent tube in the downstream of the converging bifurcation, and the CTC is released at the tube centerline. Subjected to an externally-applied acceleration of g = 100 m/s2, the cells are transported by the suspending fluid, as shown in Fig. 8. To investigate how the flowing RBCs affect the motion of CTC, the trajectories of two RBCs closest to the CTC are traced, which are labeled by ‘orange’ RBC and ‘green’ RBC, respectively, (see Fig. 8).

Fig. 8
figure 8

Motion of a file of 8 RBCs and a CTC in the symmetric bifurcated microvessel at time instants a t = 0 ms, b t = 4 ms, c t = 40 ms, d t = 80 ms, e t = 120 ms, f t = 160 ms, g t = 200 ms, and h t = 232 ms under the condition of an externally-applied acceleration g = 100 m/s2. Two RBCs closest to the CTC are labeled by ‘orange’ RBC and ‘green’ RBC to investigate how the flowing RBCs affect the adherent CTC

Full size image

The RBCs deform into a parachute shape when flowing in the parent tube. Meanwhile, the CTC moves along the centerline of the parent vessel and arrives at the apex of the bifurcation at t = 40 ms. As time elapses, the CTC attaches to the vessel wall entering into the upper daughter branch, and the following RBCs aggregate around the apex and are separated into branches at t = 80 ms. At this moment, the orange RBC is flowing past the adherent CTC and colliding with the tumor cell, the wall-directed force generated by which acts upon the tumor cell and further promotes cell binding(see Fig. 9(b)). At the same time, the green RBC is moving at the upstream of the tethered CTC, the intercellular force exerted by which drives the CTC to peel off the vessel wall. Although more receptor-ligand bonds are formed (see Fig. 9(a)), the difference in the increase of ligand-receptor bond number is not obvious, compared with Fig. 3. When the orange RBC and green RBC move to the upper branch and cross over the adherent CTC, they block the vessel easily and the flow rate may decrease significantly. So the rest of the RBCs approaching the branch point of the bifurcation would travel into the lower branch with a high flow rate, as shown in Fig. 8(e). After the green RBC crosses over the adherent CTC at t = 160 ms, the number of ligand-receptor bonds grows up again, increasing from 32 to 45 in Fig. 9(a). To conclude, the presence of RBCs would facilitate firm adhesion of the adherent CTC.

Fig. 9
figure 9

Variation of the number of receptor-ligand bonds formed on the surface of CTC and the trajectories of x and y centroid position of the CTC, green RBC and orange RBC a, and the hydrodynamic force and total adhesive force toward the wall b under the condition of an externally-applied acceleration g = 100 m/s.2

Full size image

5 Conclusions

The motion, deformation, and adhesion of a CTC flowing in a symmetric bifurcated microvessel are studied using dissipative particle dynamics. The effects of initial cell location, externally-applied acceleration (flow rate), and the presence of RBCs on the motion of CTCs are investigated. The results showed that the initial position of CTC has a significant influence on the trajectory of CTC in the flow. The CTC located near the vessel wall initially has a tendency to enter the nearest branch, whereas the CTC released at the parent tube centerline would move slowly and attach to the vessel wall at the branch point, finally sliding into a daughter branch depending on the deviating of the cell centroid at the apex of the diverging bifurcation. At relatively low flow rates, the rolling CTC on the vessel wall of the daughter branch deforms to a teardrop and the number of ligand-receptor increases significantly and subsequently the cell is arrested due to the increasing binding force. When the flow is applied by an increased external acceleration, the adherent CTC deforms largely under the higher shear force to induce a large contact area, leading to more ligand-receptor bonds formed at the surface of the cell membrane. But if the externally-applied acceleration continues to increase, the number of ligand-receptor bonds would decrease, which is caused by the reduced residence time. Introducing a file of RBCs in the bloodstream at lower flow rates, the collision between the adherent CTC and flowing RBCs increases the wall-directed force, prolonging the contact time and further promoting the firm adhesion of CTC. These results are expected to understand the mechanical mechanism of cell adhesion, and further predict the location where the CTCs are arrested and then escape away from the bloodstream. Meanwhile, it may provide some valuable insights into the development of approaches to cancer diagnosis and therapy.

Although DPD method naturally couples flow with microscopic cells, this method is based on a low degree of particle-to-particle continuity and requires larger numbers of particles to accurately represent sharp cell features in the simulation of cell adhesion. To avoid the high computational cost, a coarse-grained model was adopted to roughly describe the phenomenon of cell adhesion, which reduces the accuracy. To solve this problem, a hybrid method coupling the advantages of both the mesh-based method and DPD may be one alternative solution in the future.