1 Introduction

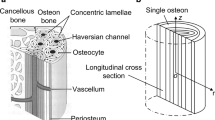
Trabeculae are microstructural components of cancellous bone that maintain a three-dimensional network structure based on the applied mechanical loading. The arrangement of the trabeculae is continually reorganized owing to bone remodeling to satisfy mechanical demands. Figure 1 shows the schematic of the hierarchical bone structure from the cellular level to the organ level. Bone tissue is renewed by osteoclastic bone resorption and osteoblastic bone formation on individual trabecular surfaces, which is called the remodeling cycle (Parfitt 1994). Although the well-ordered cellular behavior during the process of the remodeling cycle is still unclear, osteocytes buried in calcified bone matrix are believed to be responsible for regulating the activities of osteoclasts and osteoblasts (Tatsumi et al. 2007; Bonewald 2011; Nakashima et al. 2011). From an anatomical point of view, the osteocyte network via slender cell processes housed in a lacuno-canalicular porosity is considered to be suitable for sensing the surrounding mechanical environment (Cowin et al. 1991; Sugawara et al. 2005; Himeno-Ando et al. 2012).

Fig. 1
figure 1

Hierarchical bone structure from the cellular to the organ level. The individual trabeculae in cancellous bone contain a lamellar bone matrix and interstitial fluid in a lacuno-canalicular porosity

Full size image

Experimental and theoretical studies have shown that the flow of interstitial fluid in a lacuno-canalicular porosity is likely to be a mechanical cue initiating an osteocytic response (Weinbaum et al. 1994; Burger and Klein-Nulend 1999; Price et al. 2011; Kameo and Adachi 2014). The interstitial fluid flow is triggered by deformation of the bone matrix under external loading, which is typically cyclic because of locomotion and the maintenance of posture (Weinbaum et al. 1994). As shown in Fig. 1, the bone matrix of trabeculae has a lamellar structure comprising mineral crystals and collagen fibers (Martin et al. 1998), formed by repeated remodeling cycles. Thus, the mechanical properties of the bone matrix are directional and different for each lamella. Indeed, the dispersion in the measured values of the bone material properties (e.g., Turner et al. 1999) suggests that these properties can vary spatially even in the same bone tissue. Among the various material properties, the heterogeneous distribution of permeability, which measures the ability of a porous material to transmit fluid, can significantly influence the behavior of interstitial fluid in the lacuno-canalicular porosity within the individual trabeculae (Beno et al. 2006; Kameo et al. 2010; Pereira and Shefelbine 2014).

For quantitative evaluation of the interstitial fluid flow in bone tissue, Biot’s poroelastic theory (Biot 1941, 1955) has been widely used (Cowin 1999). Poroelasticity is a continuum theory that considers the mechanical behavior of fluid-saturated porous media based on the interaction between the deformation of the solid matrix and the flow of the internal fluid. A number of analytical studies on fluid-saturated bones have employed the poroelastic approach that considers bone tissue as an isotropic material (Zhang and Cowin 1994; Zeng et al. 1994) or a transversely isotropic material (Rémond and Naili 2005). In other studies, a poroelastic finite element method has been applied to quantify the fluid pressure behavior in bone tissue (Manfredini et al. 1999; Rémond et al. 2008; Pereira and Shefelbine 2014). Rémond et al. (2008) considered the spatial distribution of bone mechanical properties in finite element simulations to solve the poroelastic problem associated with a hollow cylindrical osteon. In our previous work, we derived an analytical solution containing both transient and steady-state responses for the interstitial fluid pressure in a two-dimensional trabecula when subjected to cyclic loading (Kameo et al. 2008, 2009). In our analytical study, the trabecula was assumed to be a homogeneous and isotropic material for simplicity, despite the fact that the bone matrix is made of several lamellae.

The purpose of the present study is to clarify the effect of the lamellar structure of the bone matrix—i.e., variations in material properties—on the fluid flow stimuli to osteocytes embedded in trabeculae. We used an analytical approach to investigate the response of the interstitial fluid pressure in the lacuno-canalicular porosity within the single trabecula to applied cyclic loading. We focused on variations in permeability because it is a key factor for characterizing the interstitial fluid flow. In our developed model, a single trabecula is idealized as a two-dimensional poroelastic slab composed of multiple layers, where each layer is an isotropic material and has a different value of permeability. We present an analytical solution for the interstitial fluid pressure in the single trabecula as a summation of the transient and steady-state parts by solving the governing equations for the quasi-static poroelasticity. Based on the obtained solution, we demonstrate how variations in permeability influence the pressure and seepage velocity of interstitial fluid, which are associated with the mechanical stimuli to osteocytes.

2 Poroelastic analysis

2.1 Governing equations

We used the linear poroelasticity (Detournay and Cheng 1993; Wang 2000; Coussy 2004) to describe the solid–fluid interaction in a single trabecula under the assumption of small perturbations. In particular, we focused on the quasi-static mechanical behavior because the bone tissue within a living body is usually subjected to low-frequency cyclic loading from activities of daily living.

For an isotropic poroelastic material, the total stress tensor \(\sigma _{ij}\) and fluid pressure p satisfy the diffusion equation obtained from the fluid continuity equation:

$$\begin{aligned} c\nabla ^{2}\left( {\sigma _{kk} +\frac{3}{B}p} \right) =\frac{\partial }{\partial t}\left( {\sigma _{kk} +\frac{3}{B}p} \right) , \end{aligned}$$
(1)

where \(\nabla ^{2}\) represents the Laplace operator and the summation convention on repeated indices is adopted. In the above equation, the diffusion coefficient c and Skempton coefficient B are given by

$$\begin{aligned}&c=\frac{k}{\mu }\left[ {\frac{2GB^{2}\left( {1-\nu } \right) \left( {1+\nu _u } \right) ^{2}}{9\left( {1-\nu _u } \right) \left( {\nu _u -\nu } \right) }} \right] \end{aligned}$$
(2)
$$\begin{aligned}&B=\frac{1/K-1/{K_s }}{\phi /{K_f }+1/K-{\left( {1+\phi } \right) }/{K_s }}, \end{aligned}$$
(3)

where \(G, \nu \), and K are, respectively, the shear modulus, Poisson’s ratio, and the bulk modulus under the drained condition, satisfying \(K={2G\left( {1+\nu } \right) }/{3\left( {1-2\nu } \right) }\). \(K_{s}\) is the solid bulk modulus, \(K_{f}\) is the fluid bulk modulus, \(\phi \) is the porosity, k is the intrinsic permeability, and \(\mu \) is the dynamic viscosity of the fluid. The undrained Poisson’s ratio \(\nu _{u}\) can be expressed in the following form:

$$\begin{aligned} \nu _u =\frac{3\nu +\alpha B\left( {1-2\nu } \right) }{3-\alpha B\left( {1-2\nu } \right) }, \end{aligned}$$
(4)

where \(\alpha \) is the Biot–Willis coefficient given by

$$\begin{aligned} \alpha =1-\frac{K}{K_s }, \end{aligned}$$
(5)

Another relationship between the sum of the three normal stresses \(\sigma _{kk}\) and the fluid pressure p can be obtained from the strain compatibility equations:

$$\begin{aligned} \nabla ^{2}\left[ {\sigma _{kk} +\frac{2\alpha \left( {1-2\nu } \right) }{\left( {1-\nu } \right) }p} \right] =0. \end{aligned}$$
(6)

Equations (1)–(6) constitute the set of governing equations to be solved. Seven independent material properties are required for the poroelastic analysis: the permeability k, fluid viscosity \(\mu \), drained shear modulus G, drained Poisson’s ratio \(\nu \), solid bulk modulus \(K_{s}\), fluid bulk modulus \(K_{f}\), and porosity \(\phi \).

2.2 Formulation

For the model of a single lamellar trabecula indicated by the red square in Fig 1, we considered a two-dimensional poroelastic slab consisting of n layers with a width of L in the x-direction and a unit thickness, as shown in Fig. 2. This model represents the longitudinal cross section of an individual cylindrical trabecula, which is a typical trabecula in cancellous bone. To impose uniform external loadings, two rigid and impermeable plates were placed at the top and bottom of this sample in reference to Mandel’s problem (Wang 2000; Coussy 2004) and our previous studies (Kameo et al. 2008, 2009). Mandel’s problem is a classical problem associated with the compression of a poroelastic slab. In this study, each layer of the poroelastic slab is assumed to be an isotropic material with the same material properties except for the permeability k. The physical quantities associated with the i-th layer are identified by the subscript i. In addition to the global coordinate system (x, y), a local coordinate \(x_{i}\) is employed by taking the origin at the left side of the i-th layer with a width of \(l_{i}\), as shown in Fig. 2.

Fig. 2
figure 2

Model of a single lamellar trabecula subjected to cyclic loading. The trabecula is idealized as a two-dimensional poroelastic slab consisting of n layers. This model represents the longitudinal cross section of a cylindrical trabecula

Full size image

A cyclic uniaxial load along the y-direction \(F\left( t \right) =-L\sigma _0 \sin \omega t\) is applied to the trabecular model through the plates at time \(t = 0\). Considering the problem symmetry, the stress components \(\sigma _{ij}\) and fluid pressure p depend only on x (or \(x_{i}\)) and t. Assuming no shear stresses throughout the poroelastic slab, i.e., \(\sigma _{xy} = 0\), and that the slab edges \(x = 0, L\) are stress free, the stress equilibrium in the x-direction requires \(\sigma _{xx} = 0\). For poroelastic analysis of a single trabecula, the term containing the fluid pressure p in Eq. (6) is negligible because the bone matrix supports much more of the mechanical load than the interstitial fluid (Weinbaum et al. 1994; Kameo et al. 2008). Therefore, under a plane stress condition in the z-direction, i.e., \(\sigma _{zz} = 0\), the sum of the three normal stresses \(\sigma _{kk}\) is written as follows:

$$\begin{aligned} \sigma _{kk} =\sigma _{yy} =-\sigma _0 \sin \omega t. \end{aligned}$$
(7)

Substituting Eqs. (7) into (1) provides the diffusion equation for the i-th layer:

$$\begin{aligned} c_i \frac{\partial ^{2}p_i }{\partial x_i^2 }-\frac{\partial p_i }{\partial t}=-\frac{B}{3}\sigma _0 \omega \cos \omega t. \end{aligned}$$
(8)

When the slab edges at \(x = 0, L\) are drained, the initial and boundary conditions for the fluid pressure p can be expressed in the following form:

$$\begin{aligned}&t=0;\quad p_i =0 \left( {i=1\sim n} \right) \end{aligned}$$
(9)
$$\begin{aligned}&x_1 =0;\quad p_1 =0 \end{aligned}$$
(10)
$$\begin{aligned}&x_i =l_i , x_{i+1} =0;\quad p_i =p_{i+1} , \nonumber \\&\quad -\frac{k_i }{\mu }\frac{\partial p_i }{\partial x_i}=-\frac{k_{i+1} }{\mu }\frac{\partial p_{i+1} }{\partial x_{i+1} } \quad \left( {i=1\sim n-1} \right) \end{aligned}$$
(11)
$$\begin{aligned}&x_n =l_n ;\quad p_n =0, \end{aligned}$$
(12)

where we consider the continuity of the fluid pressure and fluid flux at the boundaries of the layers.

By introducing the following dimensionless values

$$\begin{aligned} x_i^*= & {} \frac{x_i }{L}, t^{*}=\frac{c_0 t}{L^{2}}, p_i^*=\frac{p_i }{{B\sigma _0 }/3}, \nonumber \\ l_i^*= & {} \frac{l_i }{L}, k_i^*=\frac{k_i }{k_0 }=\frac{c_i }{c_0 }, \varOmega =\frac{L^{2}\omega }{c_0 } , \end{aligned}$$
(13)

with the diffusion equation and the initial and boundary conditions, Eqs. (8)–(12) are rewritten as follows:

$$\begin{aligned}&k_i^*\frac{\partial ^{2}p_i^*}{\partial x_i^{*2} }-\frac{\partial p_i^*}{\partial t^{*}}=-\varOmega \cos \varOmega t^{*} \end{aligned}$$
(14)
$$\begin{aligned}&t^{*}=0;\quad p_i^*=0 \quad \left( {i=1\sim n} \right) \end{aligned}$$
(15)
$$\begin{aligned}&x_1^*=0;\quad p_1^*=0 \end{aligned}$$
(16)
$$\begin{aligned}&x_i^*=l_i^*, x_{i+1}^*=0;\quad p_i^*=p_{i+1}^*,\nonumber \\&\quad k_i^*\frac{\partial p_i^*}{\partial x_i^*}=k_{i+1}^*\frac{\partial p_{i+1}^*}{\partial x_{i+1}^*} \quad \left( {i=1\sim n-1} \right) \end{aligned}$$
(17)
$$\begin{aligned}&x_n^*=l_n^*; p_n^*=0. \end{aligned}$$
(18)

In Eq. (13), \(k_{0}\) and \(c_{0}\) represent typical values of the permeability and diffusion coefficient that satisfy Eq. (2). Henceforth, we omit the asterisk (*) from the dimensionless values to simplify the notation.

2.3 Solution

We solve the initial and boundary value problems shown in Eqs. (14)–(18) analytically by making use of the Laplace transform technique. By taking the Laplace transform of Eq. (14) with respect to time under the initial condition Eq. (15), the fundamental solution for the fluid pressure can be obtained as follows:

$$\begin{aligned} \tilde{p}_i =A_i \cosh \sqrt{\frac{s}{k_i }}x_i +B_i \sinh \sqrt{\frac{s}{k_i }}x_i +\frac{\varOmega }{s^{2}+\varOmega ^{2}}, \end{aligned}$$
(19)

where the tilde \((^{\sim })\) signifies the Laplace transform and \(A_{i}\) and \(B_{i}\) are unknown coefficients to be determined from the boundary conditions, Eqs. (16)–(18). By substituting Eq. (19) into Eqs. (16)–(18) after taking the Laplace transform, these equations can be expressed in matrix form:

$$\begin{aligned} \left[ {a_{kl} } \right] \left\{ {\begin{array}{l} A_1 \\ B_1 \\ \vdots \\ A_n \\ B_n \\ \end{array}} \right\} =\frac{\varOmega }{s^{2}+\varOmega ^{2}}\left\{ {\begin{array}{l} f_1 \\ 0 \\ \vdots \\ 0 \\ f_{2n} \\ \end{array}} \right\} \quad \left( {k, l=1\sim 2n} \right) , \end{aligned}$$
(20)

where the nonzero elements among \(a_{kl}\) and \(f_{k}\) are given by

$$\begin{aligned}&a_{11} =1 \nonumber \\&a_{2i, 2i-1} =\cosh \sqrt{\frac{s}{k_i }}l_i , a_{2i, 2i} =\sinh \sqrt{\frac{s}{k_i }}l_i , a_{2i, 2i+1} =-1 \nonumber \\&a_{2i+1, 2i-1} =\sqrt{k_i s}\sinh \sqrt{\frac{s}{k_i }}l_i , a_{2i+1, 2i} =\sqrt{k_i s}\cosh \sqrt{\frac{s}{k_i }}l_i , \nonumber \\&a_{2i+1, 2i+1} =-\sqrt{k_{i+1} s} \left( {i=1\sim n-1} \right) \nonumber \\&a_{2n, 2n-1} =\cosh \sqrt{\frac{s}{k_n }}l_n , a_{2n, 2n} =\sinh \sqrt{\frac{s}{k_n }}l_n \nonumber \\&f_1 =-1, f_{2n} =-1. \end{aligned}$$
(21)

By applying Cramer’s rule to the system of equations in Eq. (20), the fluid pressure solution in the Laplace transformed domain is obtained as follows:

$$\begin{aligned} \tilde{p}_i =\frac{\varOmega }{\varDelta \left( {s^{2}+\varOmega ^{2}} \right) }\left( {\bar{{A}}_i \cosh \sqrt{\frac{s}{k_i }}x_i +\bar{{B}}_i \sinh \sqrt{\frac{s}{k_i }}x_i +\varDelta } \right) , \end{aligned}$$
(22)

where \(\varDelta \) is the determinant of the matrix \(\left[ {a_{kl} } \right] \) and \(\bar{{A}}_i \) and \(\bar{{B}}_i \) are the determinants of the matrix formed by replacing the (2\(i - 1\))-th and 2i-th columns, respectively, of the matrix \(\left[ {a_{kl} } \right] \) by the column vector \(\left\{ {f_k } \right\} \). The inverse Laplace transform of Eq. (22) from using the residue theorem eventually provides the solution to the fluid pressure in the form of the summation of the steady-state solution \(p_i^\mathrm{steady}\) and transient solution \(p_i^\mathrm{trans} \):

$$\begin{aligned} p_i =p_i^\mathrm{steady} +p_i^\mathrm{trans} , \end{aligned}$$
(23)

where the first term is the sum of the residues corresponding to the simple poles \(s=\pm i\varOmega \) and the second term is the sum of the residues corresponding to the roots of \(\varDelta =0\). The steady-state solution \(p_i^\mathrm{steady}\) can be derived as follows:

$$\begin{aligned}&p_i^\mathrm{steady}\nonumber \\&\quad =\hbox {Im}\left[ {\frac{\left. {\bar{{A}}_i } \right| _{s=i\varOmega } \cosh \sqrt{\frac{i\varOmega }{k_i }}x_i +\left. {\bar{{B}}_i } \right| _{s=i\varOmega } \sinh \sqrt{\frac{i\varOmega }{k_i }}x_i +\left. \varDelta \right| _{s=i\varOmega } }{\left. \varDelta \right| _{s=i\varOmega } }e^{i\varOmega t}} \right] , \end{aligned}$$
(24)

where Im gives the imaginary part of the complex number.

To obtain the transient solution \(p_i^\mathrm{trans} \), it is convenient to put \(s=-\lambda ^{2} \left( {\lambda >0} \right) \). By using this notation, Eqs. (19)–(22) are rewritten in the following form:

$$\begin{aligned}&\tilde{p}_i ={A}'_i \cos \frac{\lambda }{\sqrt{k_i }}x_i +{B}'_i \sin \frac{\lambda }{\sqrt{k_i }}x_i +\frac{\varOmega }{\lambda ^{4}+\varOmega ^{2}} \end{aligned}$$
(25)
$$\begin{aligned}&\left[ {e_{kl} } \right] \left\{ {\begin{array}{l} {A}'_1 \\ {B}'_1 \\ \vdots \\ {A}'_n \\ {B}'_n \\ \end{array}} \right\} =\frac{\varOmega }{\lambda ^{4}+\varOmega ^{2}}\left\{ {\begin{array}{l} f_1 \\ 0 \\ \vdots \\ 0 \\ f_{2n} \\ \end{array}} \right\} \quad \left( {k, l=1\sim 2n} \right) \end{aligned}$$
(26)
$$\begin{aligned}&e_{11} =1 \nonumber \\&e_{2i, 2i-1} =\cos \frac{\lambda }{\sqrt{k_i }}l_i , e_{2i, 2i} =\sin \frac{\lambda }{\sqrt{k_i }}l_i , e_{2i, 2i+1} =-1 \nonumber \\&e_{2i+1, 2i-1} =-\lambda \sqrt{k_i }\sin \frac{\lambda }{\sqrt{k_i }}l_i , e_{2i+1, 2i} =\lambda \sqrt{k_i }\cos \frac{\lambda }{\sqrt{k_i }}l_i , \nonumber \\&e_{2i+1, 2i+1} =-\lambda \sqrt{k_{i+1} } \left( {i=1\sim n-1} \right) \nonumber \\&e_{2n, 2n-1} =\cos \frac{\lambda }{\sqrt{k_n }}l_n , e_{2n, 2n} =\sin \frac{\lambda }{\sqrt{k_n }}l_n \nonumber \\&f_1 =-1, f_{2n} =-1 \end{aligned}$$
(27)
$$\begin{aligned}&\tilde{p}_i =\frac{\varOmega }{D\left( {\lambda ^{4}+\varOmega ^{2}} \right) }\left( {{\bar{{A}}}'_i \cos \frac{\lambda }{\sqrt{k_i }}x_i +{\bar{{B}}}'_i \frac{\lambda }{\sqrt{k_i }}x_i +D} \right) , \end{aligned}$$
(28)

where D is the determinant of the matrix \(\left[ {e_{kl} } \right] \) and \({\bar{{A}}}'_i \) and \({\bar{{B}}}'_i \) are the determinants of the matrix formed by replacing the (\(2i - 1\))-th and 2i-th columns, respectively, of the matrix \(\left[ {e_{kl} } \right] \) by the column vector \(\left\{ {f_k } \right\} \). By taking the inverse Laplace transform of Eq. (28) with the help of the residue theorem, the transient solution of fluid pressure \(p_i^\mathrm{trans}\) can be derived as the sum of the residues corresponding to the roots of \(D=0\) as follows:

$$\begin{aligned} p_i^\mathrm{trans}= & {} \sum _{j=1}^\infty \frac{-2\lambda _j e^{-\lambda _j^2 t}}{\left. {\frac{dD}{d\lambda }} \right| _{\lambda =\lambda _j } }\Bigg [ \left. {{\bar{{A}}}'_i } \right| _{\lambda =\lambda _j } \cos \frac{\lambda _j }{\sqrt{k_i }}x_i\nonumber \\&+\left. {{\bar{{B}}}'_i } \right| _{\lambda =\lambda _j } \sin \frac{\lambda _j }{\sqrt{k_i }}x_i \Bigg ]\frac{\varOmega }{\lambda _j^4 +\varOmega ^{2}} , \end{aligned}$$
(29)

where \(\lambda _{j}\) is the j-th positive roots of \(D\left( \lambda \right) =0\). For the calculation of the derivative in Eq. (29), the following relation can be used:

$$\begin{aligned} \left. {\frac{dD}{d\lambda }} \right| _{\lambda =\lambda _j } =\sum _{m=1}^{2n} {M_m } , \end{aligned}$$
(30)

where \(M_{m}\) is the determinant of the matrix formed by replacing the m-th column of the matrix \(\left[ {e_{kl} } \right] \) by the derivative of the same column with respect to \(\lambda \).

2.4 Single trabecular model

Table 1 lists the material properties used in the poroelastic modeling of a single trabecula (Smit et al. 2002; Beno et al. 2006). Among these material constants, the intrinsic permeability \(k_{0}\) and porosity \(\phi \) are especially important factors that influence the interstitial fluid pressure and seepage velocity. Because the values of these two factors are more sensitive to changes in lacuno-canalicular morphology compared with those of the other five constants, it is essential to set \(k_{0}\) and \(\phi \) appropriately in order to quantify the fluid flow stimuli for osteocytes. While there is generally a positive correlation between permeability and porosity (Kameo et al. 2010), we considered variations in only permeability and ignored variations in porosity for simplicity.

Table 1 Material properties of trabecula as poroelastic material (Smit et al. 2002; Beno et al. 2006)
Full size table

By using seven independent material properties in Table 1, the poroelastic constants defined in Sect. 2.1 (i.e., the Biot–Willis coefficient \(\alpha \) [Eq. (5)], undrained Poisson’s ratio \(\nu _{u}\) [Eq. (4)], Skempton coefficient B [Eq. (3)], and typical value of the diffusion coefficient \(c_{0}\) [Eq. (2)]) are, respectively, derived as follows: \(\alpha = 0.15, \nu _{u} = 0.33, B = 0.35\), and \(c_{0} = 3.9 \times 10^{-8} \hbox {m}^{2}/\hbox {s}\). Considering that an individual trabecula in vivo has a typical width of \(L = 200\,\upmu \hbox {m}\) and is subjected to 1–20 Hz cyclic loading (Weinbaum et al. 1994), the range of the dimensionless frequency \(\varOmega \) defined in Eq. (13) is estimated to be between 6.5 and 130. Therefore, we set two different values of \(\varOmega (\varOmega = 10\hbox { and }100)\) to investigate the role of the loading frequency.

The total number of layers that constitute a single trabecula was selected as \(n = 6\), which is within the physiological range. Each layer was assumed to have the same width. The spatial variations in trabecular permeability are difficult to determine because the size of the lacuno-canalicular porosity can vary according to osteocytic remodeling of the perilacunar and pericanalicular matrix (Qing and Bonewald 2009). Therefore, in order to investigate their effect on the behavior of interstitial fluid, we considered three cases, all of which have the same average permeability. Case 1 deals with a single trabecula in which the permeability is linearly distributed from the first layer to the sixth layer and has the following settings: \(k_{1} = 0.5, k_{2} = 0.7, k_{3} = 0.9, k_{4} = 1.1, k_{5} = 1.3\), and \(k_{6} = 1.5\). In the equilibrium state of bone remodeling, an individual cylindrical trabecula may have an axisymmetrical lamellar structure. In order to account for such conditions, the other two cases consider the trabeculae with a symmetrical distribution of permeability about the central axis \(x=L/2\): in Case 2, \(k_{1} = 0.5, k_{2} = 1.0, k_{3} = 1.5, k_{4} = 1.5, k_{5} = 1.0\), and \(k_{6} = 0.5\); in Case 3, \(k_{1} = 1.5, k_{2} = 1.0, k_{3} = 0.5, k_{4} = 0.5, k_{5} = 1.0\), and \(k_{6} = 1.5\). In Case 2, the interstitial fluid around the center of trabecula can flow through more easily than the fluid close to the trabecular surfaces, while Case 3 represents the reverse condition. Table 2 summarizes the settings of the trabecular permeability in the above three cases.

Table 2 Settings of trabecular permeability for poroelastic analysis
Full size table

3 Results

3.1 Fluid pressure

The fluid pressure in a single trabecula under cyclic loading was calculated according to Eqs. (24) and (29). Figure 3 shows the fluid pressure distributions along the x-direction in Case 1, where the permeability was linearly distributed (see Table 2). Figure 3a, b corresponds to the steady-state responses for the dimensionless frequencies \(\varOmega = 10\) and 100, respectively, plotted for eight equal-length phase points in a period. Figure 3c, d corresponds to the transient responses for \(\varOmega = 10\) and 100, respectively, plotted at \(t^{*} = 0, 0.01, 0.1\), and 1. All of the figures exhibit asymmetrical fluid pressure distributions about the central axis \(x^{*} = 0.5\) owing to the spatial gradient of permeability. As shown in Fig. 3a, b, increasing the dimensionless frequency \(\varOmega \) caused the fluid pressure profile in steady state to transform from a parabolic shape to a trapezoidal shape. Thus, the fluid pressure gradient around the trabecular surfaces built up because of the increase in \(\varOmega \). The fluid pressure gradient at the edge \(x^{*} = 0\), where the value of permeability was smaller, was larger than that at the other edge \(x^{*} = 1\) when the loading frequency was constant.

Fig. 3
figure 3

Fluid pressure distribution along x-direction in Case 1 (\(k_1^*= 0.5, k_2^*= 0.7, k_3^*= 0.9, k_4^*= 1.1, k_5^*= 1.3, k_6^*= 1.5\)). Steady-state response: a \(\varOmega = 10\), b \(\varOmega = 100\). Transient response: c \(\varOmega = 10\), d \(\varOmega = 100\)

Full size image

As shown in Fig. 3c, d, the transient stage was observed after cyclic loading was applied, and it decayed within the time \(t^{*} = 1\). The magnitude of the transient response was related to the fluid pressure profile in steady state at the phase point 0 because the sum of the transient and steady-state fluid pressures at \(t^{*} = 0\) must be null by the initial conditions, Eqs. (9), (15). Figure 3c, d indicates that the effect of the transient response is more important at low loading frequencies than at high loading frequencies.

Figures 4 and 5 show the fluid pressure distributions in the steady state along the x-direction in Cases 2 and 3, respectively, where the permeability was symmetrically distributed (see Table 2). In these figures, part (a) corresponds to the result for the dimensionless frequency \(\varOmega = 10\) and part (b) corresponds to the result for \(\varOmega = 100\). As shown in Figs. 4a and 5a, the maximum values of both the fluid pressure and its spatial gradient for \(\varOmega = 10\) were larger in Case 2, where the value of permeability close to the trabecular surfaces was less than that around the center of trabecula. On the other hand, for the loading frequency \(\varOmega = 100\), the peak values of the fluid pressure in Cases 2 and 3 were almost the same, whereas the fluid pressure gradient around the trabecular surfaces was larger in Case 2 than in Case 3, as shown in Figs. 4b and 5b.

Fig. 4
figure 4

Fluid pressure distribution in steady state along x-direction in Case 2 (\(k_1^*= 0.5, k_2^*= 1.0, k_3^*= 1.5, k_4^*= 1.5, k_5^*= 1.0, k_6^*= 0.5\)): a \(\varOmega = 10\) and b \(\varOmega = 100\)

Full size image
Fig. 5
figure 5

Fluid pressure distribution in steady state along x-direction in Case 3 (\(k_1^*= 1.5, k_2^*= 1.0, k_3^*= 0.5, k_4^*= 0.5, k_5^*= 1.0, k_6^*= 1.5\)): a \(\varOmega = 10\) and b \(\varOmega = 100\)

Full size image

3.2 Seepage velocity

The seepage velocity in poroelastic materials is one of the mechanical properties that quantifies the fluid flow at the macroscopic scale. In the context of bone poroelasticity, the seepage velocity represents the average velocity of interstitial fluid in a lacuno-canalicular porosity and is closely associated with the mechanical stimuli to osteocytes during the bone remodeling process. According to Darcy’s law, the x component of the seepage velocity for the i-th layer \(v_{i}\) is given by

$$\begin{aligned} v_i =-\frac{1}{\phi }\frac{k_i }{\mu }\frac{\partial p_i }{\partial x_i }. \end{aligned}$$
(31)

If we introduce the following dimensionless seepage velocity

$$\begin{aligned} v_i^*=\frac{v_i }{{B\sigma _0 k_0 }/{3\mu L\phi }}, \end{aligned}$$
(32)

this quantity can be expressed as

$$\begin{aligned} v_i^*=-k_i^*\frac{\partial p_i^*}{\partial x_i^*}. \end{aligned}$$
(33)

By substituting Eqs. (23) into (33) with the help of Eqs. (24) and (29), the solution for the dimensionless seepage velocity can be obtained. In this study, we focused only on the seepage velocity behavior in the steady state.

Figure 6 shows the seepage velocity distributions in the steady state along the x-direction in Cases 1–3 at the fluid pressure peak. Figure 6a corresponds to the result for the dimensionless frequency \(\varOmega = 10\), and Fig 6b corresponds to the result for \(\varOmega = 100\). In both parts of the figure, the profile of the seepage velocity in the single trabecula with constant permeability, i.e., \(k_i^*=1.0 \left( {i=1\sim 6} \right) \), is presented as a reference result. As shown in Fig. 6a, the seepage velocity for \(\varOmega = 10\) was almost linearly distributed across the trabecula, and its maximum value was observed at the edge \(x^{*} = 1\) in Case 1. When the loading frequency was \(\varOmega = 100\), as shown in Fig. 6b, the seepage velocity around the center of trabecula was negligible for all permeability values. The distribution curves in Cases 1 and 2 overlapped near the edge \(x^{*} = 0\), and the curves in Cases 1 and 3 also overlapped in the neighborhood of the other edge \(x^{*} = 1\). The maximum seepage velocity was larger in Case 3 than in Case 2, in contrast to the results for the fluid pressure gradient presented in the previous section.

Fig. 6
figure 6

Seepage velocity distribution in steady state along x-direction for a \(\varOmega = 10\) and b \(\varOmega = 100\): Case 1 (\(k_1^*= 0.5, k_2^*= 0.7, k_3^*= 0.9, k_4^*= 1.1, k_5^*= 1.3, k_6^*= 1.5\)); Case 2 (\(k_1^*= 0.5, k_2^*= 1.0, k_3^*= 1.5, k_4^*= 1.5, k_5^*= 1.0, k_6^*= 0.5\)); Case 3 (\(k_1^*= 1.5, k_2^*= 1.0, k_3^*= 0.5, k_4^*= 0.5, k_5^*= 1.0, k_6^*= 1.5\)) and constant permeability \(k_i^*=1.0 \left( {i=1\sim 6} \right) \) as reference

Full size image

4 Discussion

We developed an analytical solution for the interstitial fluid pressure in the lacuno-canalicular porosity within a single trabecula modeled as a two-dimensional multilayered poroelastic material subjected to cyclic loading, in which each layer has a different value of permeability. Based on the obtained transient and steady-state solutions, we investigated the effect of variations in permeability on the behavior of interstitial fluid. Poroelastic analysis showed that a heterogeneous distribution of permeability produces remarkable variations in the fluid pressure and seepage velocity in the cross section of the individual trabecula.

The trabecular permeability depends on both the dimensions of the lacuno-canalicular porosity and its microstructure, such as the tortuosity, bifurcation, and the density of the pericellular matrix (Beno et al. 2006; Kameo et al. 2010). Measuring the exact value of the intrinsic permeability is extremely difficult because the lacuno-canalicular porosity has a complex three-dimensional structure with a diameter of only several hundred nanometers. Despite extensive research to determine the bone permeability, the estimated range based on theoretical and experimental approaches is quite broad: from \(10^{-26}\) to \(10^{-18}\hbox { m}^{2}\) (Zhang et al. 1998; Smit et al. 2002; Beno et al. 2006; Oyen 2008; Gailani et al. 2009; Kameo et al. 2010). In our study, we set the approximate median value of \(k_{0} = 1.1\times 10^{-21}\hbox { m}^{2}\) as the representative permeability, which was determined based on the method proposed by Beno et al. (2006). The magnitude of the trabecular permeability \(k_{0}\) is reflected in the dimensionless frequency \(\varOmega \), as shown in Eqs. (2) and (13). As the order of magnitude of permeability increases or the dimensionless frequency \(\varOmega \) decreases, the peak fluid pressure decreases due to rapid leakage from the trabecular surfaces. On the other hand, as the order of permeability decreases or \(\varOmega \) increases, the fluid pressure response approaches undrained behavior; this leads to no flow in the whole region except for the neighborhood of the trabecular surfaces.

Computer simulations have been utilized in order to understand how the bone permeability affects mechanical stimuli at the cellular level (Manfredini et al. 1999; Rémond et al. 2008; Pereira and Shefelbine 2014). Rémond et al. (2008) investigated the effect of spatial gradients of the permeability on the interstitial fluid flow using poroelastic finite element analysis of an osteon in cortical bone. They reported that permeability gradients do not cause a notable variation of the fluid velocity distribution, in contrast to our results shown in Fig. 6. Although this has interesting implications for cellular mechanosensing, such behavior of the interstitial fluid can only be observed when the permeability is sufficiently large (\({\sim }10^{-18}\hbox { m}^{2}\)), i.e., under nearly drained conditions. As shown in Fig. 6, the seepage velocity is generally influenced by the permeability distribution, and its sensitivity depends on the rate of loading relative to the permeability, which was defined as the dimensionless frequency \(\varOmega \) in this study.

The seepage velocity of the interstitial fluid can be considered as a characteristic of the mechanical stimuli to osteocytes embedded in trabeculae. This quantity is related to the fluid pressure gradient, which is a driving force of the fluid flow according to Eq. (31). As noted in the previous section, the distribution of the seepage velocity in the single trabecula does not coincide with that of the fluid pressure gradient because the permeability is not constant. The applied loading frequency is one of the most important factors that affect the behavior of the interstitial fluid. Figure 6 shows that as the dimensionless frequency \(\varOmega \) increases, the seepage velocity and thus the mechanical stimuli to osteocytes close to the trabecular surfaces increases, while the flow around the center of trabecula decreases. Considering the in vivo experimental results, which showed that a more significant bone ingrowth was induced at higher loading rates (Goldstein et al. 1991), the results obtained in the current analytical study imply that osteocytes buried in the neighborhood of the trabecular surfaces primarily work as mechanosensory cells during the bone remodeling process.

Comparing the seepage velocity near the surfaces between three cases of trabeculae in Fig. 6 indicates that the maximum seepage velocity and thus the maximum fluid flow stimuli to osteocytes are mostly governed by the value of permeability in the neighborhood of the trabecular surfaces if there is no difference in the average permeability in a single trabecula. In particular, large mechanical stimuli for osteocytes could be found around trabecular surfaces with relatively large permeability. According to the Frost’s mechanostat theory (Frost 1987, 2003), the single trabecula in Case 3, i.e., the trabecula in which the permeability close to the trabecular surfaces is relatively large, has a higher potential for bone formation via trabecular surface remodeling. These results suggest that the bone resorption and formation on the trabecular surface can be influenced by the changes in the dimension and microstructure of the neighboring lacuno-canalicular porosity as well as the changes in the trabecular volume or external loads. Even as the capability of osteocytes to remove old mineral and to deposit new mineral is still under discussion (Qing and Bonewald 2009), it is possible that osteocyte mechanotransduction via interstitial fluid flow and the subsequent trabecular bone adaptation to the mechanical loads is regulated to some extent by osteocytic remodeling of the lacuno-canalicular porosity. Indeed, significant differences in the structural architecture of the osteocyte networks in the parietal bone (flat bone) and tibia (long bone) have been previously noted (Himeno-Ando et al. 2012); and this experimental fact suggests a strong correlation between the architecture of the lacuno-canalicular porosity and the physiological loading patterns to these bones.

In the present analysis, we modeled a single trabecula as a two-dimensional poroelastic slab with isotropic material properties, for the sake of simplicity. However, an individual trabecula in vivo has a cylindrical morphology, and the mechanical behavior can be regarded as transversely isotropic (Turner et al. 1999; Rémond and Naili 2005; Rémond et al. 2008) owing to the component mineral crystals and collagen fibers. Furthermore, we assumed only that permeability is not constant among the poroelastic material properties listed in Table 1, even though the permeability k is closely related to the porosity \(\phi \) (Kameo et al. 2010). Nevertheless, this poroelastic analysis provides fundamental knowledge on interstitial fluid behavior under physiological cyclic loading when permeability is spatially distributed in a single trabecula. By setting the appropriate distribution of permeability in an individual trabecula based on experimental findings, the current theoretical analysis would help understand the relationship between the macroscopic loads applied to the trabecula and the resulting microscopic mechanical environment of osteocytes within the trabecula, which is in turn associated directly with bone remodeling.