Multiscale two-way embedding schemes for free-surface primitive equations in the “Multidisciplinary Simulation, Estimation and Assimilation System”

Abstract

We derive conservative time-dependent structured discretizations and two-way embedded (nested) schemes for multiscale ocean dynamics governed by primitive equations (PEs) with a nonlinear free surface. Our multiscale goal is to resolve tidal-to-mesoscale processes and interactions over large multiresolution telescoping domains with complex geometries including shallow seas with strong tides, steep shelfbreaks, and deep ocean interactions. We first provide an implicit time-stepping algorithm for the nonlinear free-surface PEs and then derive a consistent time-dependent spatial discretization with a generalized vertical grid. This leads to a novel time-dependent finite volume formulation for structured grids on spherical or Cartesian coordinates, second order in time and space, which preserves mass and tracers in the presence of a time-varying free surface. We then introduce the concept of two-way nesting, implicit in space and time, which exchanges all of the updated fields values across grids, as soon as they become available. A class of such powerful nesting schemes applicable to telescoping grids of PE models with a nonlinear free surface is derived. The schemes mainly differ in the fine-to-coarse scale transfers and in the interpolations and numerical filtering, specifically for the barotropic velocity and surface pressure components of the two-way exchanges. Our scheme comparisons show that for nesting with free surfaces, the most accurate scheme has the strongest implicit couplings among grids. We complete a theoretical truncation error analysis to confirm and mathematically explain findings. Results of our discretizations and two-way nesting are presented in realistic multiscale simulations with data assimilation for the middle Atlantic Bight shelfbreak region off the east coast of the USA, the Philippine archipelago, and the Taiwan–Kuroshio region. Multiscale modeling with two-way nesting enables an easy use of different sub-gridscale parameterizations in each nested domain. The new developments drastically enhance the predictive capability and robustness of our predictions, both qualitatively and quantitatively. Without them, our multiscale multiprocess simulations either were not possible or did not match ocean data.

1 Introduction

Ocean dynamics is now known to involve multiple scales and dynamical interactions with inherent transient effects and intense localized gradients. Sources of interacting scales and intermittent behavior include internal nonlinear dynamics, steep bathymetries, complex geometries, and remote and boundary forcing. To predict such dynamics, ocean modeling systems must be capable of multiresolution, multiscale, and multidynamic numerical simulations. A major objective of our present research is to derive and study robust and accurate two-way embedding (nesting) schemes for telescoping ocean domains governed by primitive equation (PE) dynamics with a nonlinear free surface. The intent is to resolve tidal-to-mesoscale dynamics over large multiresolution domains with complex coastal geometries from embayments and shallow seas with strong tidal flows to the steep shelfbreaks and the deep ocean with frontal features, jets, eddies, and other larger-scale current systems.

Most structured-grid models have been developed to be general, with applications in varied ocean regions (e.g., 1995; Mooers 1999). These modeling systems include Modular Ocean Model (Griffies et al. 2007, 2010), Navy Layer Ocean Model/Deep-ocean Assessment and Reporting of Tsunamis (Carnes et al. 1996; Wallcraft et al. 2003), Regional Ocean Model System (Haidvogel et al. 2000; Shchepetkin and McWilliams 2005), Princeton Ocean Model (POM; 1987; Mellor 2004), Parallel Ocean Program (Smith et al. 1992), MIT General Circulation Model (Marshall et al. 1997), Terrain-following Ocean Modeling System (Ezer et al. 2002; Arango et al. 2010), Hybrid Coordinate Ocean Model (HYCOM; Bleck 2002; Chassignet et al. 2009), and Harvard Ocean Prediction System (HOPS; Robinson 1999; Haley et al. 1999). Examples of applications of these models as well as others include for the US eastern coastal oceans (Signell et al. 2000; Lynch et al. 2001; Robinson et al. 1999, 2001), northwestern Atlantic (Chassignet et al. 2000; Chassignet and Malanotte-Rizzoli 2000), Atlantic Ocean (Chassigne et al. 2003; 2000), Pacific Ocean and US western coastal oceans (de Szoeke et al. 2000; Chao et al. 2009), Mediterranean Sea (Pinardi and Woods 2002; Onken et al. 2003, 2008), European North Seas (Berntsen and Svendsen 1999), and basins and the global ocean (Semtner 2000; Dutay et al. 2002; Marshall et al. 1997; Gent et al. 1998). More recently, unstructured algorithms have been applied to simulate multiscale ocean dynamics and processes (Deleersnijder and Lermusiaux 2008a, b). Here we focus only on the use of conservative structured and embedded grid approaches to multiscale dynamics that are ubiquitous around the world: tidal-to-mesoscale dynamics at shelfbreaks, including interactions with shallow seas, complex coastal geometries, and deep oceans.

To our knowledge, none of the above structured models includes fully implicit two-way embedding schemes for nonlinear free-surface PEs. With fully implicit and two-way embedding, all of the updated field values are exchanged across scales among nested domains, as soon as they become available, within the same time step. This is challenging but found most valuable with nonlinear free-surface PEs. Major contributions of this manuscript are to derive a class of such embedding schemes, implicit in space and time, to compare them to alternatives using simulations and theoretical truncation error analysis, and to illustrate them in a set of realistic applications. Another contribution is a time-dependent spatial discretization of the nonlinear free-surface PEs, including generalized vertical coordinates. These computational algorithms are derived and developed next. Specific new developments include a nonlinear formulation of the free surface and its boundary conditions, a modification of an implicit time-stepping algorithm (Dukowicz and Smith 1994) to handle the nonlinear formulation, a consistent spatial discretization for a time-dependent finite volume method, a generalized vertical grid, and a fully implicit two-way nesting scheme for the nonlinear free-surface PE. Implicit two-way nesting schemes are shown to have truncation errors of higher order than other nesting schemes across the multiresolution domains. Two-way nesting also enables us to easily use different parametrizations for the sub-gridscale physics in each nested domain. The additions of these improvements are shown to drastically enhance the predictive capability and robustness of our ocean prediction system. Without them, our multiscale multiprocess simulations were either not possible or their predictions did not match ocean data.

All of the above new computational schemes have been derived and implemented as part of our MIT Multidisciplinary Simulation, Estimation and Assimilation System (MSEAS; MSEAS Group 2010). This allowed us to evaluate robustness in several ocean regions, including the middle Atlantic Bight, Californian coast around Monterey Bay, Philippine archipelago, and Taiwan–Kuroshio region of the eastern Pacific (e.g., see Section 5). These applications utilized various components of MSEAS including our free-surface generalization of the original rigid-lid PE model of the HOPS (see “Appendix 3” and Haley et al. 1999); a coastal objective analysis scheme based on fast-marching methods (Agarwal and Lermusiaux 2010); uncertainty estimation, data assimilation, and adaptive sampling schemes (Lermusiaux 1999, 2002, 2007; Lermusiaux et al. 2000, 2002); a stochastic representation for sub-gridscale processes (Lermusiaux 2006); nested tidal inversion schemes (Logutov and Lermusiaux 2008); multiple biological models (Tian et al. 2004); and several acoustic models (Lam et al. 2009; Lermusiaux and Xu 2010).

A recent and comprehensive review of nesting algorithms can be found in Debreu and Blayo (2008), including discussions on time-stepping and time-splitting issues. They review methods for the conservation of quantities across the nesting interface and compare a variety of schemes for the transfer of information between grids. They conclude with a review of methods to control noise, including relaxation methods, sponge layers and open boundary conditions suitable for nesting. One-way nesting and two-way nesting with PE models are relatively common (e.g., Spall and Holland 1991; Fox and Maskell 1995; Sloan 1996; Penven et al. 2006; Haley et al. 2009; Mason et al. 2010), and we refer to Debreu and Blayo (2008) for a review. Focusing on scheme comparisons, Cailleau et al. (2008) contrasted methods to control the open boundaries of a modeling domain (Bay of Biscay embedded in a North Atlantic domain), specifically one-way nesting, two-way nesting, and “full coupling based on domain decomposition” (Schwarz method: Martin 2003, 2004). They found that this “full coupling” gave the most regular solutions at interfaces but was computationally much more expensive (a factor of 5) than two-way nesting, without demonstrating significant improvements. Other recent examples include Barth et al. (2005) who use nesting and the free-surface GHER model (Beckers 1991; Beckers et al. 1997) to obtain high-resolution simulations in the Ligurian Sea nested in Mediterranean domains. A new feature of their nesting algorithm is their interpolation of normal velocities from the coarse-to-fine domains. They employ a constrained minimization of the second derivatives to obtain smoothly continuous boundary fields while maintaining the conservation of volume. In Barth et al. (2007), this same setup is coupled with an ensemble-based data assimilation algorithm to assimilate sea surface temperature (SST) and sea surface height (SSH). Estournel et al. (2009) applied “scale-oriented” one-way multimodel nesting to the northwestern Mediterranean Sea (MFSTEP: Pinardi et al. 2002), using a variational scheme to ensure mass balance. Guo et al. (2003) used one-way nesting and the POM for their studies of the Kuroshio, using three telescoping domains. They found that higher resolution not only improved bathymetry reproduction but also JEBAR (joint effect of baroclinicity and relief: Sarkisya and Ivanov 1971) and the Kuroshio dynamics. Other developments include attempts at using improved physics in the refined nested domain. Shen and Evans (2004) developed such a modeling system based on a semi-Lagrangian scheme: A fully nonhydrostatic simulation can be embedded in a larger weakly nonhydrostatic simulation which, in turn, can be embedded in a still larger compatible hydrostatic simulation. Maderich et al. (2008) developed a system to model the transport and mixing of industrial cooling water in freshwater and marine environments, combining free-surface hydrostatic physics with a buoyant jet model or a nonhydrostatic model, using buffer zones to reduce noise due to physics mismatches.

The nesting schemes in all above works fall under the categories we define as “explicit” or “coarse-to-fine implicit” nesting. As shown in Fig. 1, in explicit two-way nesting, the coarse and fine domain fields are only exchanged at the start of a discrete time integration or time step: The two-way exchanges are explicit. In “coarse-to-fine implicit” two-way nesting, the coarse domain feeds the fine domain during its time step: Usually, fine domain boundary values are computed from the coarse domain integration, but the fine domain interior values are only fed back at the end of the coarse time step. In “fine-to-coarse implicit” two-way nesting, it is the opposite; fine domain updates are fed to the coarse domain during its integration but the coarse domain feedback only occur at the end of the fine domain discrete integration. In this paper, we derive two-way nested schemes, fully implicit in space and time: The fine and large domains exchange all updated information during their time integration, as soon as updated fields become available. A type of such scheme consists of computing fine domain boundary values from the coarse domain but with feedback from the fine domain. Some of the algorithmic details of our multiscale fully implicit two-way nesting schemes are specific to MSEAS, but the approach and schemes are general and applicable to other modeling systems.

Fig. 1

Schematic of a explicit, b coarse-to-fine implicit, c fine-to-coarse implicit, and d fully implicit two-way nesting. Green arrows sketch coarse-to-fine transfers; red arrows sketch fine to coarse. The left arrow indicates discrete time integrations or time steps (n − 1, n, and n + 1). Nesting transfers occur before (explicit) or during (implicit) discrete time step n. If the time steps of two nested models are not equal, the duration of step n would in general be the longest of the two

In what follows, in Section 2, we give the equations of motion, provide an implicit time discretization for the nonlinear free-surface PEs, and develop a time-dependent, spatial discretization of the PEs. In Section 3, we derive and describe our fully implicit two-way nesting scheme and contrast it from traditional explicit and coarse-to-fine implicit schemes. In Section 4, we compare nesting schemes and show that for nesting with free surfaces, the most accurate schemes are those with stronger implicit couplings among grids, especially for the velocity components. We also complete a theoretical truncation error analysis to mathematically confirm and explain our findings. In Section 5, we illustrate the use of our novel discretization and nesting schemes in the middle Atlantic Bight, Philippine archipelago, and Taiwan–Kuroshio region of the eastern Pacific. Conclusions are in Section 6. Details on vertical and horizontal discretizations and fluxes, open boundary conditions, and conservation properties are in “Appendix 1”. Multiscale nesting procedures for setting up multigrid domains and bathymetries, for multiresolution initialization, for tidal forcing, and for solving the free-surface equation are given in “Appendix 2”. Our original two-way nesting scheme for rigid-lid PEs is outlined in “Appendix 3”.

2 Formulation of a new scheme for free-surface primitive equation modeling

In this section, we derive the discretized equations of motion for our new nested nonlinear free-surface ocean system. We have encoded both the spherical and Cartesian formulations (see “Appendix 1”) and most often use the spherical one, but for ease of notation, we present the equations in only one form, the Cartesian one. In Section 2.1, we give the differential form of the free-surface PEs. In Section 2.2, we recast these equations in their integral control volume form in order to easily derive a mass preserving scheme. In Section 2.3, we introduce our novel implicit time discretization of these PEs. Finally, in Section 2.4, we derive the corresponding time-dependent, spatial discretization which preserves mass and tracers in the presence of a time-varying free surface.

2.1 Continuous free-surface primitive equations

The equations of motion are the PEs, derived from the Navier–Stokes equations under the hydrostatic and Boussinesq approximations (e.g., Cushman-Roisin and Beckers 2010). Under these assumptions, the state variables are the horizontal and vertical components of velocity (u, w), the temperature (T), and the salinity (S). Denoting the spatial positions as (x,y,z) and the temporal coordinate with t, the PEs are:

$$ \label{Eq:PEpdeContinuity} {\rm Cons.\ Mass} \quad \nabla \cdot \mathbf{u} + \frac{\partial w}{\partial z} = 0 , $$

(1)

$$ \label{Eq:PEpdeHorizMomentum} {\rm Cons.\ Horiz.\ Mom.} \quad \frac{D \mathbf{u}}{D t} + f \hat k \times \mathbf{u}= -{1 \over \rho_0} \nabla p + {\bf F} , $$

(2)

$$ \label{Eq:PEpdeVertMomentum} {\rm Cons.\ Vert.\ Mom.} \quad \frac{\partial p}{\partial z} = -\rho g, $$

(3)

$$ \label{Eq:PEpdeConsvHeat} {\rm Cons.\ Heat} \quad \frac{D T}{D t} = F^T , $$

(4)

$$ \label{Eq:PEpdeConsvSalt} {\rm Cons.\ Salt} \quad \frac{D S}{D t} = F^S , $$

(5)

$$ \label{Eq:PEpdeEqofState} {\rm Eq.\ of\ State} \quad \rho = \rho (z,T,S) $$

(6)

where $\frac{D}{Dt}$ is the 3D material derivative, p is the pressure, f is the Coriolis parameter, ρ is the density, ρ ₀ is the (constant) density from a reference state, g is the acceleration due to gravity, and $\hat k$ is the unit direction vector in the vertical direction. The gradient operators, $\nabla$, in Eqs. 1 and 2 are 2D (horizontal) operators. The turbulent sub-gridscale processes are represented by F, F ^T, and F ^S.

Since we are considering free-surface applications in regions with strong tides, we need a prognostic equation for the evolution of the surface elevation, η. We integrate Eq. 1 over the vertical column and apply the kinematic conditions at the surface and bottom to arrive at the nonlinear free-surface transport constraint

$$ \label{Eq:FreeSurface} \frac{\partial \eta}{\partial t} + \nabla \cdot \left( \int^\eta_{-H} {\bf u} \, dz \right) = 0 $$

(7)

where H = H(x,y) is the local water depth in the undisturbed ocean.

We decompose the horizontal velocity into a depth averaged (“barotropic”) component, U, and a remainder (“baroclinic”), u ^′

$$ \label{Eq:VelDecomp} {\bf u} = { \mathbf{u}^\prime} + {\bf U} \;\, ; \quad {\bf U} = \frac{1}{H+\eta} \int^\eta_{-H} \mathbf{u} \, dz . $$

(8)

To further isolate the effects of the free surface, we decompose the pressure into a hydrostatic component (employing the terminology of Dukowicz and Smith 1994), p _h, and a surface component, p _s:

$$ \begin{array}{lll} \label{Eq:PressDecomp} &&{\kern-6pt} p = p_{\rm s} + p_{\rm h} \; ; \; p_{\rm h}(x,y,z,t) = \int^\eta_{z} g \rho \, d\zeta \; ; \;\\ &&{\kern-6pt} p_{\rm s}(x,y,t) = \rho_0 g \eta . \end{array} $$

(9)

Note that the definition of the hydrostatic pressure automatically enforces Eq. 3. Using Eqs. 8 and 9, we split Eq. 2 into two equations, one for U obtained by taking the vertical average of Eq. 2 and one for u ^′ by removing the vertical average from Eq. 2:

$$ \frac{\partial {\mathbf{U}}}{\partial t} - \frac{\left.{\mathbf{u}^\prime}\right|_\eta}{H+\eta} \frac{\partial \eta}{\partial t} + f \hat k \times {\mathbf{U}} = \overline{\widehat{\cal F}} -g \nabla \eta $$

(10)

$$ \frac{\partial {\mathbf{u}^\prime}}{\partial t} + \frac{\left.{\mathbf{u}^\prime}\right|_\eta}{H+\eta} \frac{\partial \eta}{\partial t} + f \hat k \times {\mathbf{u}^\prime} = \widehat{\cal F} - \overline{\widehat{\cal F}} . $$

(11)

In Eqs. 10 and 11, we now have additional terms of the form $\frac{\left.{\mathbf{u}^\prime}\right|_\eta}{H+\eta} \frac{\partial \eta}{\partial t}$. These small terms are often neglected but are kept here since our dynamical focus ranges from the deep ocean to the very shallow ocean with strong tides. In Eqs. 10 and 11, we have introduced the following notation for the terms we group on the RHS:

$$ \widehat{\cal F} = -{1 \over \rho_0} \nabla p_h - {\boldsymbol{\Gamma}}(\mathbf{u}) + \mathbf{F} \;\, ; \quad \overline{\widehat{\cal F}} = \frac{1}{H+\eta} \int^\eta_{-H} \widehat{\cal F} \, dz $$

and for the advection operator

$$ \boldsymbol \Gamma(\mathbf{u}) = \left( \begin{array}{c} \Gamma(u) \\ \Gamma(v)\end{array}\right) \;\, ; \quad \Gamma(\phi) = u \frac{\partial \phi}{\partial x} + v \frac{\partial \phi}{\partial y} + w \frac{\partial \phi}{\partial z}. $$

Note that instead of directly solving for u ^′ using Eq. 11, we instead solve for u using Eq. 2 recast in the following form

$$ \label{Eq:pdePEmomFullXY} \frac{\partial {\mathbf{u}}}{\partial t} + f \hat k \times {\mathbf{u}} = \widehat{\cal F} - g \nabla \eta , $$

(12)

then obtain u ^′ from definition 8. By using Eqs. 12 and 8 instead of Eq. 11, we reduce the truncation error for our time-splitting procedure in Section 2.3.1.

2.2 Control volume formulation of the free-surface primitive equations

We now rewrite the governing Eqs. 1, 4, 5, and 12 in a conservative integral formulation. With this transformation at the continuous level, it is easier to derive a new discrete system that correctly accounts for the temporal changes in the ocean volume due to a moving free surface.

We integrate Eq. 1 and the conservative forms of Eqs. 4, 5, and 12 over a control volume $\cal V$ and use the divergence theorem to arrive at the following system of equations:

$$ \label{Eq:PEcontinuity} \int_{\cal S} \left( \mathbf{u} , w\right) \cdot d{\boldsymbol{\cal A}} = 0 , $$

(13)

$$ \label{Eq:PEmomFullXY} \frac{\partial}{\partial t} \left( \int_{\cal V} {\mathbf{u}} \, d{\cal V} \right) + \int_{\cal V} f \hat k \times {\mathbf{u}} \, d{\cal V} = \widetilde{\cal F} - g \nabla \eta , $$

(14)

$$ \label{Eq:UclinDef} {\mathbf{u}^\prime} = \mathbf{u} - \frac{1}{H+\eta} \int^\eta_{-H} \mathbf{u} \, dz , $$

(15)

$$ \label{Eq:PEmomTropXY} \frac{\partial {\mathbf{U}}}{\partial t} - \frac{\left.{\mathbf{u}^\prime}\right|_\eta}{H+\eta} \frac{\partial \eta}{\partial t} + f \hat k \times {\mathbf{U}} = \overline{\widetilde{\cal F}} -g \nabla \eta , $$

(16)

$$ \label{Eq:ConsHeat} \frac{\partial}{\partial t} \left(\int_{\cal V} T \, d{\cal V}\right) + \tilde\Gamma(T) = \int_{\cal V} F^T \, d{\cal V} , $$

(17)

$$ \label{Eq:ConsSalt} \frac{\partial}{\partial t} \left(\int_{\cal V} S \, d{\cal V}\right) + \tilde\Gamma(S) = \int_{\cal V} F^S \, d{\cal V} , $$

(18)

$$ \label{Eq:EqState} \rho = \rho (z,T,S) , $$

(19)

$$ \label{Eq:FreeSurfaceUbaro} \frac{\partial \eta}{\partial t} + \nabla \cdot \left[ \left( H + \eta \right) \mathbf{U} \right] = 0 $$

(20)

where

$$ \widetilde{\cal F} = -{1 \over \rho_0} \int_{\cal S} p_h \, \hat n_h \cdot d{\boldsymbol{\cal A}} - {\boldsymbol{\tilde\Gamma}}(\mathbf{u}) + \int_{\cal V} \mathbf{F} \, d{\cal V} , $$

$$ \overline{\widetilde{\cal F}} = \frac{1}{H+\eta} \int^\eta_{-H} \widetilde{\cal F} \, dz , $$

$\cal S$ is the surface of the control volume, and $d{\boldsymbol{\cal A}}$ is an infinitesimal area element vector pointing in the outward normal direction to $\cal S$. In Eqs. 14–18, we have introduced the following notation for the surface advective fluxes:

$$ {{\boldsymbol{\tilde\Gamma}}(\mathbf{u})} = \left( \begin{array}{c} \tilde\Gamma(u) \\ \tilde\Gamma(v)\end{array}\right) \;\, ; \quad \tilde\Gamma(\phi) = \int_{\cal S} \phi \, \left({\mathbf u} , w \right) \times d{\boldsymbol{\cal A}} $$

where $\phi \, \left(\mathbf u , w \right)$ denotes the local advective flux of ϕ.

2.3 Temporal discretization

We now derive our novel implicit time discretization for the nonlinear free-surface PEs (Eqs. 13–20). Using the following discrete time notation:

$$ t_n = n \, \Delta t \;\, ; \quad \phi\left(t_n\right) = \phi^n $$

where Δt is the discrete time step, and using the second-order leap-frog time differencing operator:

$$ \delta(\phi) = \phi^{n+1} - \phi^{n-1} , $$

we obtain the following temporal discretization of Eqs. 13–20

$$ \label{Eq:PEcontTimeDisc} \int_{{\cal S}^n} \left( \mathbf u^n , w^n\right) \cdot d{\boldsymbol{\cal A}} = 0 , $$

(21)

$$ \begin{array}{rll} \label{Eq:TimeDiscFullPeMomentumXY} \frac{1}{\tau} \, \delta\left( \int_{\cal V} \mathbf{u} \, d{\cal V} \right) &+& \left(\int_{\cal V} f \hat k \times \mathbf{u} \, d{\cal V}\right)^\alpha = \widetilde{\cal F}^{n,n-1}\\ &-& \left(\int_{\cal V} g \nabla \eta \, d{\cal V}\right)^\alpha , \end{array} $$

(22)

$$ \label{Eq:TimeDiscUclinDef} {\mathbf{u}^\prime}^{n+1} = \mathbf{u}^{n+1} - \frac{1}{H+\eta^{n+1}} \int^{\eta^{n+1}}_{-H} \mathbf u^{n+1} \, dz , $$

(23)

$$ \label{Eq:TimeDiscBarotropicPeMomentumXY} \frac{\delta({\mathbf{U}})}{\tau} - \frac{\left.{\mathbf{u}^\prime}^n\right|_\eta}{H+\eta^n} \frac{\delta \eta}{\tau} + f \hat k \times {\mathbf{U}}^\alpha = \overline{\widetilde{\cal F}^{n,n-1}} - g \nabla \eta^\alpha , $$

(24)

$$ \label{Eq:TimeDiscConsHeat} \frac{1}{\tau} \, \delta\left( \int_{\cal V} T \, d{\cal V} \right) = \int_{{\cal V}^n} {F^T}^n \, d{\cal V} - \tilde{\Gamma}(T^n) , $$

(25)

$$ \frac{1}{\tau} \, \delta\left( \int_{\cal V} S \, d{\cal V} \right) = \int_{{\cal V}^n} {F^S}^n \, d{\cal V} - \tilde{\Gamma}(S^n) , $$

(26)

$$ {{\eta^{n+1} - \eta^n} \over {\Delta t}} + \nabla \cdot \left[ \left(H+\eta^n\right) \mathbf{U}^\theta \right] = 0 $$

(27)

where

$$ \begin{array}{rll} \widetilde{\cal F}^{n,n-1} &= &-{1 \over \rho_0} \int_{{\cal S}^n} p^n_h \, \hat n_h \cdot d{\boldsymbol{\cal A}} - {\boldsymbol{\tilde{\Gamma}}}(\mathbf u^n)\\ &&+ \int_{{\cal V}^n} \mathbf F^n \, d{\cal V} + \int_{{\cal V}^{n-1}} \mathbf F^{n-1} \, d{\cal V} ,\\ \overline{\widetilde{\cal F}^{n,n-1}} & = & \frac{1}{H+\eta^n} \int^{\eta^n}_{-H} \left\{ -{1 \over \rho_0} \int_{{\cal S}^n} p^n_h \, \hat n_h \cdot d{\boldsymbol{\cal A}} - {\boldsymbol{\tilde{\Gamma}}}(\mathbf u^n)\right. \\ && {\kern60pt}\left. + \int_{{\cal V}^n} \mathbf F^n \, d{\cal V} \right\} \, dz \\ &&+ \frac{1}{H+\eta^{n-1}} \int^{\eta^{n-1}}_{-H} \left\{ \int_{{\cal V}^{n-1}} \mathbf F^{n-1} \, d{\cal V} \right\} \, dz , \end{array} $$

and τ = 2 Δt is twice the time step. Following the results of the stability analyses in Dukowicz and Smith (1994), we have introduced semi-implicit time discretizations for the Coriolis force

$$ \phi^\alpha = \alpha \phi^{n+1} + (1 - 2 \alpha) \phi^n + \alpha \phi^{n-1} $$

and for the barotropic continuity:

$$ \phi^\theta = \theta \phi^{n+1} + (1 - \theta) \phi^n . $$

In practice, we run using the stabilizing choices $\alpha=\frac{1}{3}$ (C. Lozano and L. Lanerolle, private communication) and θ = 1 (Dukowicz and Smith 1994). A stability analysis of the explicit leap-frog algorithm can be found in Shchepetkin and McWilliams (2005), while Dukowicz and Smith (1994) analyze the linearized implicit algorithm. Note that even though our discretization parallels Dukowicz and Smith (1994), we do not make the linearizing assumption η ≪ H in Eqs. 8, 9, and 27. This generalization allows our system to be deployed in littoral regions of high topographic variations and strong tides.

A couple of observations are worth making. First, we are considering the case in which the control volume is time dependent. Therefore, in the new time discretizations (Eqs. 21–26), all terms involving control volume integrals must be evaluated at the proper discrete times as a whole, not just the integrands. The second is that Eqs. 22–24 and 27 form a coupled system of equations to solve for u ^n + 1, u ^{′ n + 1}, U ^n + 1, and η ^n + 1. We decouple these equations using a time-splitting algorithm. Another approach would have been to use an iterative method (e.g., Newton solver). However, time-splitting is usually more efficient and for their similar time-splitting approach, Dukowicz and Smith (1994) showed that no significant physics was lost, provided fΔt ≤ 2. Our time steps are always much smaller than that limit.

2.3.1 Time-splitting procedure

Similar to Dukowicz and Smith (1994), we employ a time-splitting approach by first introducing the splitting variables, $\widehat{\left(\int_{\cal V} {\mathbf{u}} \, d{\cal V}\right)}^{n+1}$ and ${\hat {{\bf U}}}^{n+1}$:

$$ \label{Eq:Definitionuhat} \widehat{\left(\int_{\cal V} {\bf u} \, d{\cal V}\right)}^{n+1} \equiv {\left(\int_{\cal V} {\bf u} \, d{\cal V}\right)}^{n+1} + \alpha \tau \delta\left( \int_{\cal V} g \nabla \eta \, d{\cal V} \right), $$

(28)

$$ \label{Eq:DefinitionUhat} {\hat {\bf U}}^{n+1} \equiv {\bf U}^{n+1} + \alpha \tau g \nabla \delta \eta - \frac{\left.{\bf u^\prime}^n\right|_\eta}{H+\eta^n}\delta \eta. $$

(29)

The novel portions of this, needed to deal with the full nonlinear free-surface dynamics, are the introduction of Eq. 28 and the last term in Eq. 29. Substituting Eqs. 28 and 29 into Eqs. 22 and 24, we obtain

$$ \begin{array}{rll} && \hat \delta \left(\int_{\cal V} {\bf u} \, d{\cal V}\right) + \alpha \tau \hat \delta \left(\int_{\cal V} f \hat k \times {\bf u} \, d{\cal V}\right) \\ && \;\; =\tau \widetilde{\cal F}^{n,n-1} - \tau \left(\int_{\cal V} g \nabla \eta \, d{\cal V}\right)^{\tilde \alpha} - \tau \left( \int_{\cal V} f \hat k \times {\bf u} \, d{\cal V}\right)^{\tilde \alpha }\\ && \;\; + \alpha^2 \tau^2 \delta \left( \int_{\cal V} f \hat k \times \nabla \eta \, d{\cal V}\right) , \end{array} $$

(30)

$$ \begin{array}{rll} \hat \delta {\bf U} + \alpha f \tau \hat k \times \hat \delta {\bf U} &=& \tau \left\{{\boldsymbol{\cal F}}^{n,n-1} - g \nabla \eta^{\tilde \alpha} \right\}\\ & & +\, \alpha^2 g f \tau^2 \hat k \times \nabla \delta \eta + \alpha f \tau \delta \eta \hat k \\ &&\times \frac{\left.{{\bf u}^\prime}^n\right|_\eta}{H+\eta^n} , \end{array} $$

(31)

where we have introduced the following notation

$$ \phi^{\tilde \alpha} = (1-2\alpha) \phi^n + 2\alpha \phi^{n-1} , $$

$$\begin{array}{rll} &&{\kern-6pt}\hat \delta {\bf U} = {\hat {\bf U}}^{n+1} - {\bf U}^{n-1} \quad; \\ &&\hat \delta \left(\int_{\cal V} {\bf u} \, d{\cal V}\right) = \widehat{\left(\int_{\cal V} {\bf u} \, d{\cal V}\right)}^{n+1} - {\left(\int_{\cal V} {\bf u} \, d{\cal V}\right)}^{n-1} , \end{array} $$

$$\begin{array}{rll} \label{Eq:DukSmTimeDiscBaroMomRHS} {\boldsymbol{\cal F}}^{n,n-1} & = & \frac{1}{H+\eta^n} \int^{\eta^n}_{-H} \left\{ -{1 \over \rho_0} \int_{{\cal S}^n} p^n_h \, \hat n_h \cdot d{\boldsymbol{\cal A}} - {\boldsymbol{\tilde{\Gamma}}}(\mathbf u^n)\right. \\ && {\kern60pt} \left.+ \int_{{\cal V}^n} \mathbf F^n \, d{\cal V} \right\} \, dz \\ && +\, \frac{1}{H+\eta^{n-1}} \int^{\eta^{n-1}}_{-H} \left\{ \int_{{\cal V}^{n-1}} \mathbf F^{n-1} \, d{\cal V} \right\} \, dz\\ & & -\, f \hat k \times \mathbf{U}^{\tilde \alpha} . \end{array} $$

To decouple Eqs. 30–31, we first notice that the last term in Eq. 30 and the second to last term in Eq. 31 are both $O\left(\tau^2 \delta \eta\right)$. These terms are the same order as the second-order truncation errors already made and hence can be discarded. The last term in Eq. 31 is $O\left(\tau \delta \eta\right)$. Although this represents a first-order error term in the free-surface elevation, it is still comparable to the error in the free-surface integration scheme (Eq. 27). Furthermore, the term is divided by H + η, meaning that it is $O\left(\frac{\tau\delta\eta}{H+\eta}\right)$ which is never larger than $O\left(\frac{\tau\delta\eta}{\eta}\right)$ in a single time step and often much smaller. Hence, we discard this term too. Discarding these terms results in the following decoupled momentum equations

$$ \begin{array}{rll} \label{Eq:TimeDiscFullHatPeMomentumXY} &&{\kern-6pt}\hat \delta \left(\int_{\cal V} \mathbf u \, d{\cal V}\right) + \alpha \tau \hat \delta \left(\int_{\cal V} f \hat k \times \mathbf u \, d{\cal V}\right) \\ &&= \tau \widetilde{\cal F}^{n,n-1}- \tau \left(\int_{\cal V} g \nabla \eta \, d{\cal V}\right)^{\tilde \alpha} - \tau \left( \int_{\cal V} f \hat k \times \mathbf u \, d{\cal V}\right)^{\tilde \alpha} , \\ \end{array} $$

(32)

$$ \label{Eq:TimeDiscUhat} \hat \delta \mathbf U + \alpha f \tau \hat k \times \hat \delta \mathbf U = \tau \left\{{\boldsymbol{\cal F}}^{n,n-1} - g \nabla \eta^{\tilde \alpha} \right\} , $$

(33)

To finish the decoupling, we take Eq. 27, average it with itself evaluated a time step earlier, and substitute Eq. 29 for U ^n + 1. The result is the following decoupled equation for η ^n + 1

$$ \begin{array}{rll} \label{Eq:TimeDiscFreeSurface} &&{\kern-6pt}\alpha \theta g \tau \nabla \cdot \left[ \left(H+\eta^n\right) \nabla \delta \eta \right] - \theta \nabla \cdot \left(\left.\mathbf{u^\prime}^n\right|_\eta \delta \eta \right) - {{2 \delta \eta} \over \tau} \\ &&= \nabla \cdot \left[ \left(H+\eta^n\right) \left( \theta {\hat {\bf U}}^{n+1} + \mathbf U^n + (1 - \theta) \mathbf U^{n-1} \right) \right] \end{array} $$

(34)

In conclusion, the new elements of temporal discretization are in Eqs. 28, 29, 32, and 34. In particular, the nonlinear free-surface parametrization is maintained by the H + η ⁿ factors in the divergences in Eq. 34 and by the second term on the left-hand side of Eq. 34.

Note that it is this decoupling procedure that inspired us to keep the full momentum equation (Eq. 12) instead of the baroclinic equation (Eq. 11; see Section 2.1). Had we worked with the baroclinic momentum equation directly, the barotropic equations (Eqs. 29, 31, and 33) would have been unchanged; however, the truncation term in going from Eqs. 30 to 32 would have been $\alpha \tau f \delta \left(\int_{\cal V} \frac{\hat k \times \left.\mathbf{u^\prime}^n\right|_\eta}{H+\eta^n} \eta \, d{\cal V}\right)$ instead of the higher-order term we obtained in Eq. 30. Further, the error term in Eq. 30 is more uniform, while the error term that would have been obtained from the baroclinic equations would have grown as the topography shoaled.

2.4 Time-dependent, nonlinear “distributed-σ” spatial discretization of the free-surface primitive equations

Using temporal discretization (Eqs. 21, 23, 25, 26, and 32–34), we can derive our new, time-dependent, spatial discretization. This discretization distributes with depth the temporal volume changes in the water column due to the time-variable free surface. We found that these variations of cell volumes must all be accounted for to avoid potentially large momentum and tracer errors in regions of strong tides and shallow topography.

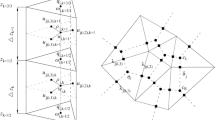
Following Bryan (1969), we discretize Eqs. 21, 23, 25, 26, and 32–34 on the staggered Arakawa B-grid (Arakawa and Lamb 1977). We retain the B-grid of the PE model of HOPS based on its ability to simulate geostrophy and any potentially marginally resolved fronts and filaments in our multiscale simulations (Webb et al. 1998; Griffies et al. 2000; Wubs et al. 2006). We employ a finite volume discretization in which the average of a variable over the volume is approximated by the value of the variable at the center of the finite volume (see Section 4.7.1). As shown in Fig. 2, the tracers and free surface (T, S, η) are horizontally located at the centers of “tracer cells” while velocities (u ^′, U, ${\hat {\bf U}}$) are located at the centers of “velocity cells” which are offset $\frac{1}{2}$ grid-point to the northeast from the “tracer cells”. In the vertical, the 3D tracers and velocities (T, S, u ^′) are, again, located at the centers of their respective cells, while the vertical velocities are calculated at the tops of the tracer and velocity cells. By choosing this type of discretization, the control volumes of Eqs. 21, 23, 25, 26, and 32–34 become structured-grid finite volumes.

Fig. 2

B-grid indexing scheme. a Horizontal lay-out. Here T stands for variables centered in tracer cells (T, S, η) and u represents variables centered in velocity cells (u, u ^′, U). b Vertical lay-out. Tracer cells are shown, velocity cells have the same lay-out, merely shifted $\frac{1}{2}$ grid-point, and w represents the vertical velocity

In the vertical, our new time-dependent, terrain-following coordinates are defined as follows: First, the terrain-following depths for the (undisturbed) mean sea level, $z^{\rm MSL}_{i,j,k}$, are set (see “Appendix 1.1”). We then define the time variable model depths such that the change in cell thickness is proportional to the relative thickness of the original (undisturbed) cell. Hence, along model level k, the depths can be found from

$$ \label{Eq:ZdefFreeSurface} z_k (x,y,t) = \eta (x,y,t) + \left(1 + \frac{\eta (x,y,t)}{H (x,y)} \right) z^{\rm MSL}_k (x,y) . $$

(35)

By distributing the temporal change in the free surface across all the model levels, we simplify the discretization in shallow regions with large tides (e.g., we avoid requiring that the top level be thick enough to encompass the entire tidal swing, which in the case of very shallow depth can mean most of the total depth). An additional computational benefit is that the time dependence of the computational cell thickness decouples from the vertical index. This provides us the following properties:

$$ \begin{array}{rll} \frac{1}{H+\eta^n} \sum^K_{k=1} \phi^n_{i,j,k} dz^n_{i,j,k}& =& \frac{1}{H} \sum^K_{k=1} \phi^n_{i,j,k} dz^{\rm MSL}_{i,j,k} ; \notag\\ \frac{\Delta {\cal V}^n_{i,j,k}}{\Delta {\cal V}^{\rm MSL}_{i,j,k}}& =& 1 + \frac{\eta^n_{i,j}}{H_{i,j}} \end{array} $$

both of which are used to derive Eq. 39 below.

Since our vertical grid is both terrain following and time variable, we also define a new vertical flux velocity, ω, normal to the top, ζ, of finite volumes as

$$ \label{omegaveldef} \omega = w - \mathbf u \cdot \nabla \zeta - \frac{\partial \zeta}{\partial t} . $$

(36)

An important consequence of this definition is that the kinematic conditions at the surface and bottom reduce to

$$ \left.\omega\right|_\eta = 0 \;\, ; \quad \left.\omega\right|_{-H} = 0 $$

Using these definitions, along with the second-order mid-point approximation

$$ \int_{\cal V} \phi \, d{\cal V} = \phi \Delta {\cal V} + O\left(\Delta{\cal V}^2\right) , $$

we discretize Eqs. 21, 23, 25, 26, and 32–34 as

$$ \label{Eq:PEcontdisc} \int_{{\cal S}^n_{\rm lat}} \mathbf u \cdot d{\boldsymbol{\cal A}} + \int_{{\cal S}^n_{\rm TB}} \omega \cdot d{\boldsymbol{\cal A}} = 0 , $$

(37)

$$ \begin{array}{rll} \label{Eq:DiscBaroclinicPeMomentumXY} {{\hat\delta \left(\mathbf{u} \Delta {\cal V}\right)} \over \tau} + \alpha f \hat k \times \hat \delta \left(\mathbf{u} \Delta {\cal V}\right) &=& \hat{\cal F}^{n,n-1} - g \left(\Delta {\cal V} \nabla \eta\right)^{\tilde \alpha} \\&&- f \hat k \times \left(\mathbf u \Delta {\cal V}\right)^{\tilde \alpha} , \end{array} $$

(38)

$$ \label{Eq:DiscBaroclinicU} \left(\mathbf{u^\prime} \Delta {\cal V}\right)^{n+1} = \widehat{\left(\mathbf u \Delta {\cal V}\right)}^{n+1} - \frac{\Delta {\cal V}^{\rm MSL}}{H} \sum^K_{k=1} \frac{\widehat{\left(\mathbf u \Delta {\cal V}\right)}^{n+1}}{\Delta {\cal V}^{\rm MSL}} dz^{\rm MSL} , $$

(39)

$$ \label{Eq:DiscConsHeat} {{\delta \left( T \Delta {\cal V}\right)} \over \tau} = {F^T}^n \Delta{\cal V}^n - \breve{\Gamma}(T^n) , $$

(40)

$$ \label{Eq:DiscConsSalt} {{\delta \left( S \Delta {\cal V}\right)} \over \tau} = {F^S}^n \Delta{\cal V}^n - \breve{\Gamma}(S^n) , $$

(41)

$$ \label{Eq:DiscUhat} \hat \delta \mathbf U + \alpha f \tau \hat k \times \hat \delta \mathbf U = \tau \left\{{\boldsymbol{\cal F}}^{n,n-1} - g \nabla \eta^{\tilde \alpha} \right\} , $$

(42)

$$ \begin{array}{rll} \alpha \theta g \tau \nabla &\cdot& \left[ \left(H+\eta^n\right) \nabla \delta \eta \right] - \theta \nabla \cdot \left(\left.\mathbf{u^\prime}^n\right|_\eta \delta \eta \right) - {{2 \delta \eta} \over \tau} \\ = \nabla &\cdot& \left[ \left(H+\eta^n\right) \left( \theta {\hat {\bf U}}^{n+1} + \mathbf U^n + (1 - \theta) \mathbf U^{n-1} \right) \right] , \end{array} $$

(43)

$$ \label{Eq:DiscBarotropicVelocity} \mathbf U^{n+1} = {\hat {\bf U}}^{n+1} - \alpha \tau g \nabla \delta \eta + \frac{\left.\mathbf{u^\prime}^n\right|_\eta}{H+\eta^n} \delta \eta $$

(44)

where

$$ {\boldsymbol{\breve{\Gamma}}}(\mathbf u) = \left( \begin{array}{c} \breve{\Gamma}(u) \\ \breve{\Gamma}(v)\end{array} \right) ;\quad \breve{\Gamma}(\phi) = \int_{{\cal S}^n_{\rm lat}} \phi \, \mathbf u \cdot d{\boldsymbol{\cal A}} + \int_{{\cal S}^n_{\rm TB}} \phi \, \omega \cdot d{\boldsymbol{\cal A}} , $$

$$\begin{array}{lll} \hat{\cal F}^{n,n-1} = &-&{1 \over \rho_0} \int_{{\cal S}^n} p^n_h \, \hat n_h \cdot d{\boldsymbol{\cal A}} - {\boldsymbol{\breve{\Gamma}}}(\mathbf u)^n + \mathbf F^n \Delta{\cal V}^n \notag\\&+& \mathbf F^{n-1} \Delta{\cal V}^{n-1} , \end{array} $$

$$\begin{array}{lll} \overline{\hat{\cal F}^{n,n-1}} & = & \frac{1}{H_{i,j}+\eta^n_{i,j}} \int^{\eta^n_{i,j}}_{-H_{i,j}} \left\{ -{1 \over \rho_0} \int_{{\cal S}^n} p^n_h \, \hat n_h \cdot d{\boldsymbol{\cal A}} \right.\\&&\left.\phantom{\int_{{\cal S}^n}}{\kern58pt} - {\boldsymbol{\breve{\Gamma}}}(\mathbf u)^n + \mathbf F^n \Delta{\cal V}^n \right\} \, dz\\ && +\, \frac{1}{H_{i,j}+\eta^{n-1}_{i,j}} \int^{\eta^{n-1}_{i,j}}_{-H_{i,j}} \left\{ \mathbf F^{n-1} \Delta{\cal V}^{n-1} \right\} \, dz , \end{array} $$

$$ {\boldsymbol{\cal F}}^{n,n-1} = \overline{\hat{\cal F}^{n,n-1}} - f \hat k \times \mathbf U^{\tilde \alpha} , $$

${\cal S}^n_{\rm lat}$ are the lateral surfaces of a computational cell and ${\cal S}^n_{\rm TB}$ represents the top and bottom surfaces of the computational cell.

With our new choice of vertical discretization, all cell volumes are functions of time. In regions with relatively high tides (compared to the total water depth), not correctly accounting for the time dependence of the volume change can lead to large errors in the tracer and momentum fields. Focusing on the computational aspects, this time dependency of the cell volume means that we solve the tracer and baroclinic velocity fields in two steps. Using temperature as an example, we first solve for $\left(T \Delta {\cal V}\right)^{n+1}$. Then, after we have solved for η ^n + 1, we update the cell volume and compute T ^n + 1. A second computational property is that we do not maintain separate storage for $\widehat{\left(\mathbf{u} \Delta {\cal V}\right)}^{n+1}$ and ${\left(\mathbf{u^\prime} \Delta {\cal V}\right)}^{n+1}$. Instead, immediately after solving Eq. 38, we remove the vertical mean according to Eq. 39. All details of the discretization of the fluxes through the boundaries of the computational volumes are given in “Appendix 1.2”. The resultant system of discrete equations is given by Eqs. 38–44 and 64–65.

3 Fully implicit nesting scheme

In this section, we derive and discuss our new fully implicit (in space and time) two-way nesting scheme. Deriving this scheme required a detailed exploration of the choices of variables to exchange and the specific algorithms, as discussed in Section 4.

Considering first traditional “explicit” and “coarse-to-fine implicit” two-way nesting (Debreu and Blayo 2008), fields are often interpolated from a coarser resolution domain to provide boundary values for a finer resolution domain. Then fields from the finer domain are averaged to replace corresponding values in the coarser domain. This is a natural order of operations in the sense that often a refined (smaller) time step is used for the finer domain, and hence, not all refined time steps have corresponding coarse field values. However, once updated, the coarse domain fields are no longer the same fields that were interpolated for the finer domain boundaries. This results in a weakened coupling (Section 4.6) between the domains which can be rectified either with an iteration scheme or with fully implicit nesting.

In our new implicit nesting, the goal is to exchange all of the updated fields values as soon as they become available. This is analogous to an implicit time-stepping algorithm, which simultaneously solves for all unknowns. It is only analogous because here updated values are exchanged across multiple scales and nested grids within the same time step, for several fields. Hence, we refer to such schemes as being implicit in space and time; the nested solutions are intertwined. Such tightly coupled implicit nesting can, in some sense, be seen as refining grids in a single domain (e.g., 1998). However, there are some advantages to the nesting paradigm. First, the time stepping can be easily refined for the finer domains. Second, the model dynamics can be tuned for the different scales in the different domains. Most notably, different sub-gridscale physics can easily be employed in the different domains, and we have used this in several regions. Finally, fundamentally different dynamics can be employed in the different domains (e.g., Shen and Evans 2004; Maderich et al. 2008). To implement our implicit nesting, we observe that most of our prognostic variables in our free-surface PE model (Eqs. 37–44) are coded with explicit time stepping. Therefore, reversing the order of operations (updating the coarse domain fields with averages from the interior of the fine domain before interpolating to the boundaries of the fine domain) ensures that, for these fields, the updated field values are in place as soon as they are needed. For the remaining variables, such implicit nesting is more complex. The free-surface η has implicit time stepping (Eq. 43), while U is coupled to η through (Eq. 44) and boundary conditions (“Appendix 1.3”). Furthermore, additional constraints are imposed on η and U to maintain the vertically integrated conservation of mass (“Appendix 1.4”). Much of the research summarized in Section 4 was centered around these two variables. The final results are presented next, assuming a two-domain configuration (coarse and fine).

We start by defining collocated grids for the coarse and fine domains as shown in Fig. 3. Our nesting algorithm is suitable for arbitrary odd refinement ratios (r:1), subject to the known issues of scale matching (e.g., Spall and Holland 1991). In this paper, we illustrate the nesting with 3:1 examples. We denote fields evaluated at coarse grid nodes with the indices (i _c ,j _c ) and fields evaluated at fine grid nodes with (i _f ,j _f ). We distinguish two special subsets of fine grid nodes: (a) fine grid nodes collocated with coarse grid nodes (i _fc ,j _fc ) and (b) fine grid nodes at the outer boundary of the fine domain (i _fb ,j _fb ). In this presentation, we assume that we have the same number of model levels and distribution of vertical levels in both domains (i.e., no vertical refinement). However, the topography can be refined in the finer domains (it is refined in all of our examples), subject to the constraints described in “Appendix 2.1.1”. The algorithms apply to (and are coded for) both Cartesian and spherical coordinates.

Fig. 3

The basic collocated nesting finite volume domains are shown (for a 3:1 example) with the coarse domain nodal points indicated by open circles and the boundaries of the corresponding coarse domain computational cells in solid lines. The fine domain nodal points are marked with plus signs and the boundaries of the corresponding fine domain computational cells in dashed lines. a The r×r array of fine grid cells averaged to update a single coarse grid cell are highlighted. b The 4×4 stencil of coarse grid nodes bi-cubically interpolated to update boundary nodes of the fine domain are highlighted as are the updated fine grid cells

At each time step, our nesting algorithm proceeds as follows (also shown graphically in Fig. 4):

• 1. Solve Eqs. 37–42 simultaneously in each domain for (u ^{′ n + 1} Δz ^n + 1, ${\hat {\bf U}}^{n+1}$, T ^n + 1 Δz ^n + 1, S ^n + 1 Δz ^n + 1)

• 2. Replace (u ^{′ n + 1} Δz ^n + 1, $\left(H+ \eta^{n}\right){\hat {\bf U}}^{n+1}$, T ^n + 1 Δz ^n + 1, S ^n + 1 Δz ^n + 1, η ⁿ) in the coarse domain at overlap nodes with the following averages from the fine domain (u ^{′ n + 1} Δz ^n + 1, $\left(H+ \eta^{n}\right){\hat {\bf U}}^{n+1}$, T ^n + 1 Δz ^n + 1, S ^n + 1 Δz ^n + 1, η ⁿ)

  $$ \phi^{n+1}_{i_c,j_c,k} \Delta z^{n+1}_{i_c,j_c,k} = \frac{1}{\Delta {\cal A}_{i_c,j_c}} \sum^{j_{fc}+r_h}_{j=j_{fc}-r_h} \sum^{i_{fc}+r_h}_{i=i_{fc}-r_h} \phi^{n+1}_{i,j,k} \Delta {\cal V}^{n+1}_{i,j,k} , $$

  (45)
  $$ \eta^{n}_{i_c,j_c} = \frac{1}{\Delta {\cal A}_{i_c,j_c}} \sum^{j_{fc}+r_h}_{j=j_{fc}-r_h} \sum^{i_{fc}+r_h}_{i=i_{fc}-r_h} \eta^{n}_{i,j} \Delta {\cal A}_{i,j} , $$

  (46)
  $$ \begin{array}{lll} \small &&\left(H_{i_c,j_c}+ \eta^{n}_{i_c,j_c}\right){\hat {\bf U}}^{n+1}_{i_c,j_c} \\&& = \frac{1}{\Delta {\cal A}_{i_c,j_c}} \sum\limits^{j_{fc}+r_h}_{j=j_{fc}-r_h} \sum\limits^{i_{fc}+r_h}_{i=i_{fc}-r_h} \left(H_{i,j}+ \eta^{n}_{i,j}\right) {\hat {\bf U}}^{n+1}_{i,j} \Delta {\cal A}_{i,j} \end{array} $$

  (47)

  where $r_h = \lfloor r/2\rfloor$ is the greatest integer less than or equal to r/2,

  $$ \begin{array}{rll} \phi &=& \mathbf{u^\prime}, T, S ; \,\Delta {\cal V}^n_{i,j,k} = \Delta x_{i,j}\Delta y_{i,j} \Delta z^n_{i,j,k} ; \\ \Delta {\cal A}_{i,j} &=& \Delta x_{i,j}\Delta y_{i,j} . \end{array} $$

• 3. In the coarse domain, recompute U ⁿ from Eq. 44 and updated η ⁿ. When the coarse domain estimate of U ⁿ was computed from Eq. 44 in the n − 1 time step, the coarse domain estimate η ⁿ had not yet been updated from the fine domain (Eq. 46 in step 2).

• 4. In the coarse domain, solve Eqs. 43 and 44 for η ^n + 1, U ^n + 1, Δz ^n + 1, u ^{′ n + 1}, T ^n + 1, S ^n + 1.

• 5. Using piece-wise bi-cubic Bessel interpolation, $\cal B$, replace values in the fine grid boundary with values interpolated from the coarse grid

  $$ \phi^{n+1}_{i_{fb},j_{fb},k} = {\cal B}\left(\phi^{n+1}_{i_c,j_c,k}\right) , $$

  (48)
  $$ \mathbf{u^\prime}^{n+1}_{i_{fb},j_{fb},k} \Delta z^{n+1}_{i_{fb},j_{fb},k} = {\cal B}\left(\mathbf{u^\prime}^{n+1}_{i_c,j_c,k} \Delta z^{n+1}_{i_c,j_c,k}\right) ,$$

  (49)
  $$ \mathbf{U}^{n+1}_{i_{fb},j_{fb},k} = {\cal B}\left[\left( H_{i_c,j_c} + \eta^{n+1}_{i_c,j_c} \right)\mathbf{U}^{n+1}_{i_c,j_c}\right] \frac{1}{H_{i_{fb},j_{fb}} + \eta^{n+1}_{i_{fb},j_{fb}}} $$

  (50)

  where

  $$ \phi = T,\,S,\,\eta^n,\,\eta^{n+1} . $$

  Note that Eqs. 49 and 50 are written in terms of transports rather than velocities. This is done to generate a consistent mass flux as seen by both domains. We have implemented this scheme to either use the interpolated values in Eqs. 48–50 directly or to correct them to allow the outward radiation of scales unrepresented in the coarse domain. The radiation scheme is an extension of Perkins et al. (1997) and updates our previous radiation schemes (Lermusiaux 2007; Haley et al. 2009). Some more promising, recent boundary conditions that we have derived and that improve the continuity of horizontal fluxes and reduce jumps in vertical fluxes across the fine domain boundaries are presented in “Appendix 1.3”.

• 6. In the fine domain, solve Eqs. 43–44 for η ^n + 1, U ^n + 1, Δz ^n + 1, u ^{′ n + 1}, T ^n + 1, and S ^n + 1.

As written in steps 1–6, the new fully implicit nesting scheme requires that both domains be run with the same time step. This is an outgrowth of the applications we have been running, which have strong thermoclines, haloclines, and pycnoclines over shallow areas, steep shelfbreak, and/or open ocean. These applications require a relatively large number of vertical levels (e.g., from 50 to 100 or more). Satisfying the Courant–Friedrichs–Lewy (CFL; Courant et al. 1928) restrictions from the resulting vertical discretizations requires a small enough time step such that the maximum horizontal velocities only reach about 10% of their own CFL limits. Hence, decreasing the horizontal grid spacing by a factor of 3 or 5 does not affect the total CFL limitation much or require a smaller time step.

Fig. 4

Present MSEAS-nesting algorithm, two-way implicit in space and time. The nesting algorithm is shown schematically a on the discrete structured finite-volume equations (Eqs. 37–44) and b in words. Solid lines indicate averaging operators from fine domain to coarse. Dashed lines indicate interpolation operators from the coarse domain to the boundary of the fine domain

It is a straightforward problem to restructure this algorithm to handle refined time stepping. First, split the data transfer from the horizontal interpolation in step 5. Before step 2, the values from the coarse grid in the two bands outside of the overlap region (i.e., all the coarse grid points in the interpolation stencil but outside of the overlap region) would be passed to some auxiliary storage in the fine grid model. In the fine grid, these external values would be time interpolated to the current refined time step then spatially interpolated with the averaged fine grid values to the outer boundary. An advantage of our scheme over one with refined time stepping is that the fine grid fields are available to make the update in Eq. 47, which increases the coupling of the barotropic modes between the domains (see Section 4)

Our scheme is directly applicable to an arbitrary number of nonoverlapping, telescoping domains. First, iterate step 2 over all domains from finest to coarsest. Then, apply the series of steps 3–5 for all domains from coarsest to finest.

Finally, since we allow refinement in the topography, our undisturbed vertical terrain-following grid, $z^{\rm MSL}_{i,j,k}$, requires constraints to maintain consistent interpolation and averaging operations in the above nesting rules. Specifically, in the portion of the coarse domain supported by averages from the fine domain, $z^{\rm MSL}_{i_c,j_c,k}$ are computed from averages $z^{\rm MSL}_{i_f,j_f,k}$ following Eq. 46. Along the boundary of the fine domain, $z^{\rm MSL}_{i_{fb},j_{fb},k}$ are interpolated from $z^{\rm MSL}_{i_c,j_c,k}$ following Eq. 48. These restrictions, along with the nesting couplings on η, keep the computational cells consistent between domains which, in turn, keeps the averaging operations in Eq. 45 consistent (i.e., as long as the coarse cell is equivalent to the sum of the fine cells then the integral of a field over the coarse cell is conceptually the same as the sum of the integrals of the same field over the corresponding fine cells).

4 Exploring different variations of the fully implicit nesting scheme

We now present and compare a series of two-way nesting schemes that we implemented and tested. Most are simpler versions of the fully implicit nesting scheme (Section 3). All schemes were tested on many common idealized (e.g., a jet meander) and realistic test simulations, for a total of about 1,000 simulations. However, only the results of one of these tests are illustrated next, the same for each scheme. In addition, even though we tried a large number of permutations among all of these schemes, with both small and large variations among them, we only present an organized subset of all schemes tried. Our goal is to illustrate the main canonical schemes. We also limit our comparisons to two-way nesting. Cailleau et al. (2008) compared one-way nesting and two-way nesting. They found significant improvements with two-way nesting, which also reflects our experience. At the end, Section 4.7, we provide an important theoretical analysis of the order of magnitude of the dominant truncation errors of the different schemes. This analysis mathematically explains and contrasts the performance of the various schemes (Section 4.7.2).

The main realistic simulation we selected (see Fig. 5) is based on the real-time AWACS and SW06 exercises (Aug.–Sep. 2006) in the New Jersey Shelf/ Hudson Canyon region (WHOI 2006; Lermusiaux et al. 2006; Chapman and Lynch 2010; Lin et al. 2010). It uses Cartesian coordinates. The coarse domain is a 522×447-km domain, with 3-km resolution, to simulate the region of influence. The fine domain is a 172×155-km domain, with 1-km resolution, to refine the simulated dynamics in the main acoustic region just south of the Hudson Canyon. For these nesting tests, both domains employed 30 vertical levels in a double-σ configuration (see “Appendix 1.1”). The bathymetry used was a combination of the NOAA (2006) Coastal Relief Model combined with V8.2 (2000) of the Smith and Sandwell (1997) topography in the deep regions. This combined bathymetry was interpolated and conditioned to coarse 3-km and fine 1-km resolution domains. In the domains overlap, the 1-km bathymetry has sharper scales and is not an interpolation of the 3-km bathymetry (but the 3-km bathymetry is a 3-km control-volume average of the 1-km bathymetry). The estimation of the initial conditions was based on two objective analyses, one inshore and one offshore of the expected shelfbreak front, using both in situ synoptic (gliders, ship deployed conductivity–temperature– depth (CTD), autonomous underwater vehicles) and historical data (National Marine Fisheries Service, World Ocean Database, Gulf Stream Feature analyses, Buoy data, etc.). These two analyses were combined using a shelfbreak front feature model (Sloan 1996; Lermusiaux 1999; Gangopadhyay et al. 2003). The Gulf Stream was initialized based on historical CTD profiles and estimates of its position based on SST and NAVOCEANO feature analyses. The simulations were forced with atmospheric fluxes derived from weather research and forecasting (J. Evans, personal communication) and Fleet Numerical Meteorological and Oceanography Center and laterally forced with linear barotropic tides (Egbert and Erofeeva 2002; Logutov and Lermusiaux 2008). Twice-daily assimilation of the synoptic data is applied to control uncertainties. The nominal duration for this simulation was 43.5 days (two cases with incomplete implicit two-way nesting terminated early due to local CFL violations, Sections 4.2 and 4.3). This duration was chosen by considering the time scales of the dominant processes. For this representative shelfbreak region, they are on the order of 2–7 days. Thus, the simulations are of significant (six to 20 events) duration. Results next are also confirmed by our extensive set of other (not shown) idealized and realistic test simulations.

Fig. 5

Nesting domains used for the series of numerical tests we completed in the Shallow Water-06 region. The New Jersey Shelf/Hudson Canyon region of the middle Atlantic Bight is shown along with a pair of domains (3 km, 1 km resolutions) used for two-way nesting

4.1 Scheme 1: baseline nesting (mimic rigid-lid nesting)

One of the first schemes we tested was a straightforward update of the nesting scheme used for the rigid-lid dynamics (see “Appendix 3”). Comparing this scheme 1 to the consistent implicit scheme of Section 3, Scheme 1 is a five-step scheme; steps 1, 4, and 6 from Section 3 remain unchanged; step 3 is eliminated; and steps 2 and 5 are modified. As a whole, the changes are as follows

• In step 2 (replacing coarse grid values with averages of fine grid values):

  • Eliminate Eq. 46 (averaging surface elevation).

  • In Eq. 47 (averaging barotropic forcing), replace $\big(H_{i,j}+ \eta^{n}_{i,j}\big){\hat {\bf U}}^{n+1}_{i,j}$ by ${\boldsymbol{\cal F}}^{n,n-1}_{i,j}$ (i.e., move averaging of barotropic forcing one “step” back in PE algorithm).

• Eliminate step 3 (making time-lagged coarse grid barotropic velocity consistent with time-lagged fine grid averaged surface elevation).

• In step 5 (interpolating coarse grid values to boundary of the fine grid; Eq. 48), do not interpolate η ⁿ.

The net result of these differences is that there is a much weaker feedback from the fine domain barotropic fields to the coarse domain in this nesting scheme. This “baseline” scheme was first considered because the analogous rigid-lid scheme worked well.

In Fig. 6, we show the results of applying this incompletely implicit nested scheme in the middle Atlantic Bight. In the top row, we present the vector differences between the barotropic velocity computed in the fine domain with the barotropic velocity computed in the corresponding coarse domain simulation, interpolated to the fine domain. These vector differences are overlaid on a map of the magnitude of these vectors. In the bottom row, we plot the same scalar differences for the surface elevation. Going from left to right, we show these differences at 3 days (after initial adjustment), 17 days (during tropical storm Ernesto), and 35 days (post-Ernesto relaxation) into the simulation. While the coupling of the surface elevation is good, within ±3 cm everywhere, there is large and growing discrepancy in the barotropic velocity. Not only is the magnitude of the velocity difference large, O(10 cm/s), but the velocity differences become similar to (sub)-mesoscale features of the region. These differences are clearly not interpolation error features but represent growing biases between the barotropic velocities estimated on the coarse and fine domains (see Section 4.7.2).

Fig. 6

Scheme 1: baseline nesting. a Vector difference between barotropic velocity in coarse and fine domains plotted in the fine domain for 00Z on 17 Aug., 31 Aug., and 18 Sep. (overlain on magnitude of vector difference). b Difference between surface elevation in coarse and fine domains plotted in the fine domain for 00Z on 17 Aug., 31 Aug., and 18 Sep. Notice the large (sub)-mesoscale differences in the barotropic velocity

4.2 Scheme 2: average ${\hat {\bf U}}$ not ${\boldsymbol{\cal F}}$

This scheme improves the barotropic feedback from the fine domain to the coarse of scheme 1 by averaging ${\hat {\bf U}}$ instead of ${\boldsymbol{\cal F}}$ in Eq. 47. This more strongly couples the barotropic mode by pushing the exchange one step later in the nonlinear free-surface PE algorithm (Eq. 42) and making the feedback closer to the actual barotropic velocity U (Eq. 44). Comparing this scheme 2 to the consistent implicit scheme of Section 3: Scheme 2 is a five-step scheme; steps 1, 4, and 6 from Section 3 remain unchanged; step 3 is eliminated; and steps 2 and 5 are modified. As a whole, the changes are as follows

• In step 2 (replacing coarse grid values with averages of fine grid values):

  • Eliminate Eq. 46 (averaging surface elevation).

  • In Eq. 47 (averaging barotropic forcing), replace $\big(H_{i,j}+ \eta^{n}_{i,j}\big){\hat {\bf U}}^{n+1}_{i,j}$ by ${\hat {\bf U}}^{n+1}_{i,j}$ (i.e., transfer velocity instead of transport).

• Eliminate step 3 (making time-lagged coarse grid barotropic velocity consistent with time-lagged fine grid averaged surface elevation).

• In step 5 (interpolating coarse grid values to boundary of the fine grid; Eq. 48), do not interpolate η ⁿ.

In Fig. 7, we again plot vector differences between the fine and coarse estimates for U, η, but using this second scheme. For this particular nesting, a local CFL violation (see below) occurs at 4.5 days into the simulations. We therefore focus on the initial error growth and examined the differences at 0, 0.25, and 0.5 days into a half-day simulation, which is sufficient to illustrate the results. Overall, since we now feedback the barotropic velocity implicitly, the differences between them are much smaller, with no mesoscale organization and amplitudes mainly less than 0.7 cm/s with regions of 0.7–1.3 cm/s along the shelfbreak and in the Hudson canyon and an isolated spot of 10 cm/s at the intersection of the shelfbreak with the southern boundary (where large tidal signal are sensitive to bathymetry resolution). By day 4.5 (not shown), this isolated spot doubles in size and leads to the CFL violation. However, the surface elevation differences are now both large, O(0.25 m), and organized on the mesoscale. By day 4.5 (not shown), these differences grow to ±1 m. By only strengthening the coupling between the U estimates, we have simply pushed the interdomain growing bias to η (see Section 4.7.2).

Fig. 7

Scheme 2: average ${\hat {\bf U}}$ not ${\boldsymbol{\cal F}}$. a Vector difference in barotropic velocity between coarse and fine domains plotted in the fine domain for 00Z, 06Z, and 12Z on 14 Aug. (overlain on magnitude of vector difference). b Difference in surface elevation difference between coarse and fine domains plotted in the fine domain for 00Z, 06Z, and 12Z on 14 Aug. Notice the large (sub)-mesoscale differences in the surface elevation that develop within a half day

4.3 Scheme 3: exchange η ⁿ

This schemes learns from the advantages of each of the schemes 1 and 2. It further increases the coupling of scheme 2 by also exchanging the surface elevation at a lagged time step. The exchange is both in the averaging from the fine domain to the coarse domain as well as in the interpolation from the coarse domain to the fine domain. Comparing this scheme 3 to the consistent implicit scheme of Section 3: Scheme 3 is a five-step scheme; steps 1, 4, 5, and 6 from Section 3 remain unchanged; step 3 is eliminated; and step 2 is modified. As a whole, the changes are as follows:

• In step 2 (replacing coarse grid values with averages of fine grid values), Eq. 47 (averaging barotropic forcing), replace $\big(H_{i,j}+ \eta^{n}_{i,j}\big){\hat {\bf U}}^{n+1}_{i,j}$ by ${\hat {\bf U}}^{n+1}_{i,j}$ (i.e., transfer velocity instead of transport).

• Eliminate step 3 (making time-lagged coarse grid barotropic velocity consistent with time-lagged fine grid averaged surface elevation).

In Fig. 8, we again plot vector differences between the fine and coarse estimates for U, η, using this third scheme. Here too, the simulation is cut short by a local CFL violation at 14.9 days into the run. The problem takes time to develop and we thus examine the differences at 3, 8, and 14 days. In the domain as a whole, the differences in both U and η are small in magnitude and scale. The magnitude of the velocity difference is generally <0.7 cm/s with regions of 0.7–1.3 cm/s mainly near the shelfbreak and Hudson canyon. However, where the shelfbreak intersects the southern boundary, there is a growing region where velocity differences reach O(10 cm/s). This eventually leads to a local CFL violation. The difference in the η estimates remains small, in the range ±3 cm over most of the domain and bounded by ±7 cm in the region of large U differences. Taken as a whole, this indicates that this scheme produces the overall desired level of coupling between the coarse and fine domains but is overly sensitive (see Section 4.7.2).

Fig. 8

Scheme 3: exchange η ⁿ. a Vector difference between barotropic velocity in coarse and fine domains plotted in the fine domain for 00Z on 17 Aug., 22 Aug., and 28 Aug. (overlain on magnitude of vector difference). b Difference between surface elevation in coarse and fine domains plotted in the fine domain for 00Z on 17 Aug., 22 Aug., and 28 Aug. Notice the growing velocity misfit caused by an instability at the shelfbreak/southern boundary intersection

4.4 Scheme 4: update U ⁿ as function of η ⁿ

The improvement in this scheme is not in exchanging additional fields between the coarse and fine domains but in making sure that the values that are exchanged are used as consistently as possible in the free-surface PE algorithm. Specifically, we use Eq. 44 to correct the time lagged barotropic velocity in the coarse domain after receiving the averaged time lagged surface elevation from the fine domain. Comparing this scheme 4 to the consistent implicit scheme of Section 3: Scheme 4 is a six-step scheme; steps 1, 3, 4, 5, and 6 from Section 3 remain unchanged; and step 2 is modified. As a whole, the changes are as follows:

• In step 2 (replacing coarse grid values with averages of fine grid values), Eq. 47 (averaging barotropic forcing), replace $\left(H_{i,j}+ \eta^{n}_{i,j}\right){\hat {\bf U}}^{n+1}_{i,j}$ by ${\hat {\bf U}}^{n+1}_{i,j}$ (i.e., transfer velocity instead of transport).

Figure 9 shows vector differences between the fine and coarse grid estimates for U, η, using this implicit nesting scheme, at 3, 17, and 35 days into the coupled simulations. Here differences between U and η are still small in magnitude and scale. Difference magnitudes for U are <0.7 cm/s over the majority of the domain with regions of 0.7–2 cm/s generally near the shelfbreak and Hudson canyon. The intersection of the shelfbreak with the southern boundary excites an isolated spot of larger differences, O(1–10) cm/s between the coarse and fine U. However, with this scheme, these boundary differences remain confined to a small region near the boundary and bounded. Moreover, these differences are not monotonic but intermittent, growing, and fading between 4 and 10 cm/s repeatedly during the simulation: They are partly due to tidal and inertial responses that differ slightly in the fine and coarse domain. This can lead to localized small intermittent misfits. Differences in η remain small, in the range ±3 cm over most of the domain and bounded by ±7 cm in the region of larger U differences. As the velocity differences, the elevation differences in this region are intermittent, growing, and fading repeatedly during the simulation. When compared to the previous schemes, this is the first scheme that possesses sufficient coupling for consistent estimates between the coarse and fine domains and sufficient robustness for use in realistic simulations. However, it does not conserve transport (see Section 4.7.2).

Fig. 9

Scheme 4: update U ⁿ as a function of η ⁿ. a Vector difference between barotropic velocity in coarse and fine domains plotted in the fine domain for 00Z on 17 Aug., 31 Aug., and 18 Sep. (overlain on magnitude of vector difference). b Difference between surface elevation in coarse and fine domains plotted in the fine domain for 00Z on 17 Aug., 31 Aug., and 18 Sep. Velocity and elevation differences generally small with intermittent misfits at the shelfbreak/southern boundary intersection

4.5 Scheme 5: pass $\left(H+\eta^{n}\right){\hat {\bf U}}^{n+1}$ (“transport”)

This is the fully implicit two-way nesting scheme which we presented in Section 3. This scheme improves upon scheme 4 by casting Eq. 47 in terms of transport instead of velocity. This brings Eq. 47 in line with Eqs. 45, 49, and 50 which were already written in terms of transports. Averaging and interpolating transports instead of velocities was chosen to enhance the long-term stability of the simulations by ensuring the consistency of the mass flux estimates between the coarse and fine domains.

Figure 10 shows vector differences between the fine and coarse estimates for U, η, using this fully implicit nesting scheme, at 3, 17, and 35 days into the coupled simulations. Differences between the estimates of U in the coarse and fine domains are generally less than 1 cm/s. Larger differences, between 1 and 4 cm/s, mainly occur at the shelf break and in Hudson Canyon, which are due to the superior ability of the fine domain to represent these topographic features. Peak differences for U again occur where the shelfbreak intersects the southern boundary, reaching O(1–10 cm/s). They are smaller than those of scheme 4 and show the same intermittent nature. It should also be noted that differences remain small before (Aug. 17), during (Aug. 31), and after (Sep. 18) the passage of tropical storm Ernesto. This indicates that the strength of the coupling of the coarse and fine solutions is not a function of the velocity magnitude. The differences between the estimates of η are generally bounded by ±3 cm, with peak values of around ±5 cm at the intersection of the shelfbreak and the southern boundary. The small improvement in the barotropic velocity coupled with the long-term advantages of maintaining consistent estimates of mass fluxes in the two domains led to the selection of this scheme as our fully implicit two-way nesting scheme (see Section 4.7.2). Note that at the end of each time step, a perfect nesting would not lead to zero differences between the coarse and fine estimates on the fine grid (differences are only zero on the coarse grid). In perfect nesting, fine-grid differences vary at each time step due to dynamics, but they do not grow with the duration of integration.

Fig. 10

Scheme 5: pass $\left(H+\eta^{n}\right){\hat {\bf U}}^{n+1}$ (“Transport”). a Vector difference between barotropic velocity in coarse and fine domains plotted in the fine domain for 00Z on 17 Aug., 31 Aug., and 18 Sep. (overlain on magnitude of vector difference). b Difference between surface elevation in coarse and fine domains plotted in the fine domain for 00Z on 17 Aug., 31 Aug., and 18 Sep. Velocity and elevation differences small with intermittent misfits at the shelfbreak/southern boundary intersection

4.6 Coarse-to-fine implicit nesting

In this section, we compare our fully implicit two-way nesting scheme (Section 3) to a more traditionally organized coarse-to-fine implicit two-way nesting scheme. We start by first designing the coarse-to-fine implicit scheme that most closely matches our fully implicit scheme.

• 1. Solve Eqs. 37–42 simultaneously in each domain for (u ^{′ n + 1} Δz ^n + 1, ${\hat {\bf U}}^{n+1}$, T ^n + 1 Δz ^n + 1, S ^n + 1 Δz ^n + 1)

• 2. In the coarse domain, solve Eqs. 43 and 44 for η ^n + 1, U ^n + 1, Δz ^n + 1, u ^{′ n + 1}, T ^n + 1, S ^n + 1.

• 3. Using piece-wise bi-cubic Bessel interpolation, $\cal B$, replace values in the fine grid boundary with values interpolated from the coarse grid

  $$ \label{Eq:ExplicitGenNestInterp} \phi^{n+1}_{i_{fb},j_{fb},k} = {\cal B}\left(\phi^{n+1}_{i_c,j_c,k}\right) \, , $$

  (51)
  $$ \label{Eq:ExplicitBaroclinicNestInterp} \mathbf{u^\prime}^{n+1}_{i_{fb},j_{fb},k} \Delta z^{n+1}_{i_{fb},j_{fb},k} = {\cal B}\left(\mathbf{u^\prime}^{n+1}_{i_c,j_c,k} \Delta z^{n+1}_{i_c,j_c,k}\right) \, , $$

  (52)
  $$\begin{array}{rll} \label{Eq:ExplicitBarotropicNestInterp} \mathbf{U}^{n+1}_{i_{fb},j_{fb},k} &=& {\cal B}\left[\left(H_{i_c,j_c}+\eta^{n+1}_{i_c,j_c}\right)\mathbf{U}^{n+1}_{i_c,j_c}\right]\\&& \times \frac{1}{H_{i_{fb},j_{fb}}+\eta^{n+1}_{i_{fb},j_{fb}}} \end{array} $$

  (53)

  where

  $$ \phi = T,\,S,\,\eta^{n+1}. $$

• 4. In the fine domain, solve Eqs. 43 and 44 for η ^n + 1, U ^n + 1, Δz ^n + 1, u ^{′ n + 1}, T ^n + 1, and S ^n + 1.

• 5. Replace values in the coarse domain at overlap nodes with the following averages from the fine domain values

  $$\begin{array}{lll} &&\phi^{n+1}_{i_c,j_c,k} \Delta z^{n+1}_{i_c,j_c,k}\\ && {\kern6pt} = \frac{1}{\Delta {\cal A}_{i_c,j_c}} \sum\limits^{j_{fc}+r_h}_{j=j_{fc}-r_h} \sum\limits^{i_{fc}+r_h}_{i=i_{fc}-r_h} \phi^{n+1}_{i,j,k} \Delta {\cal V}^{n+1}_{i,j,k}\end{array} ,$$

  (54)
  $$ \eta^{n}_{i_c,j_c} = \frac{1}{\Delta {\cal A}_{i_c,j_c}} \sum\limits^{j_{fc}+r_h}_{j=j_{fc}-r_h} \sum\limits^{i_{fc}+r_h}_{i=i_{fc}-r_h} \eta^{n}_{i,j} \Delta {\cal A}_{i,j} $$

  (55)

  where

  $$ \phi = \mathbf{u^\prime}, T, S \quad ; \quad r_h = \lfloor \frac{r}{2} \rfloor . $$

• 6. In the coarse domain, recompute U ⁿ from Eq. 44 and updated η ⁿ.

Figure 11 shows vector differences between the fine and coarse estimates for U, at 3, 17, and 35 days into the coupled simulations. The top row shows results from the coarse-to-fine implicit scheme, the bottom row from our final fully implicit scheme. The coarse-to-fine implicit scheme leads to differences between the estimates of U in the coarse and fine domains which are generally between 1 and 2 cm/s, with peak values around 10 cm/s. These differences are organized on a smaller scale than in scheme 1. This improvement over scheme 1 is due to proper couplings maintained in the coarse-to-fine implicit scheme. However, when compared to our fully implicit scheme (bottom row), we see that the peak differences in the fully implicit scheme are bounded by 2 cm/s and most differences are less than 1 cm/s. The differences are also of smaller scales than those of the coarse-to-fine implicit scales. Overall, our final implicit scheme is much more consistent than a coarse-to-fine implicit scheme (see Section 4.7.2).

Fig. 11

Barotropic velocity differences: vector difference between barotropic velocity in coarse and fine domains plotted in the fine domain for 00Z on 17 Aug., 31 Aug., and 18 Sep. (overlain on magnitude of vector difference). a Differences for coarse-to-fine implicit nesting scheme. b Differences for fully implicit nesting scheme. Overall, our fully implicit scheme is much more consistent than a coarse-to-fine implicit scheme

Note that here we are also testing the effects of smoothing the transition between the fine and coarse resolution topographies near the boundaries of the fine domain. In the two runs of Fig. 11, we used a six coarse-grid point transition (see “Appendix 2.1.1”). Comparing row (b) of Fig. 11 (with this topography transition) to row (a) of Fig. 10 (with no transition), we find that the intermittent spot of large velocity difference at the intersection of the shelfbreak with the southern boundary is absent in Fig. 11 (i.e., absent in the case of a smooth transition between the coarse and fine resolution topographies). This indicates that one of the factors driving those large isolated differences was the proximity of an artificial topography structure (the sharp coarse-fine transition at the boundary).

4.7 Error analysis

In Sections 4.1–4.5, we derived a series of nesting schemes and compared their performance in realistic simulations. Now, we complete a theoretical error analysis of the improvements among schemes. In general, the change between successive schemes is due to the use or nonuse of averaged values from the fine domain for the estimates in the coarse domain. In going from Section 4.1 to Section 4.2, we directly averaged the ${\hat {\bf U}}$ field not the ${\boldsymbol{\cal F}}$ field. This is equivalent to saying that, in our ${\hat {\bf U}}$ estimate, we upgraded our coarse estimate of $\nabla\eta$ with averaged values from the fine domain (see Eq. 42). In going from Section 4.2 to Section 4.3, we explicitly upgrade our coarse estimate of η ⁿ with averages from the fine domain. The change from Section 4.3 to Section 4.4 uses the upgraded η ⁿ to improve the estimate of U ⁿ. Therefore, we present the truncation error analysis for the averaging update in general and then apply this general analysis to the individual schemes.

4.7.1 General error analysis

The horizontal averaging operation for these fields is the central point approximation of a 2D integral. The error in this approximation can be easily shown to be of second order (Ferziger and Perić 1996):

$$ \int^\frac{\Delta y}{2}_\frac{-\Delta y}{2} \int^\frac{\Delta x}{2}_\frac{-\Delta x}{2} \phi \, dx dy \equiv \left[ \left.\phi\right|_{(0,0)} + O\big(\Delta x^2\big) + O\big(\Delta y^2\big)\right] \, \Delta x \Delta y . $$

The r:1 fine-to-coarse averaging operation can then be written as

$$ \begin{array}{rll} \phi_{{i_c},{j_c}} &=& \frac{1}{\Delta x_c \Delta y_c} \sum\limits^{j_{fc}+r_h}_{j_f=j_{fc}-r_h} \sum\limits^{i_{fc}+r_h}_{i_f=i_{fc}-r_h} \int^\frac{\Delta y_f}{2}_\frac{-\Delta y_f}{2} \int^\frac{\Delta x_f}{2}_\frac{-\Delta x_f}{2} \phi \, dx dy \\ &=& \frac{1}{\Delta x_c \Delta y_c} \sum\limits^{j_{fc}+r_h}_{j_f=j_{fc}-r_h} \sum\limits^{i_{fc}+r_h}_{i_f=i_{fc}-r_h} \left[ \phi_{i_f,j_f} + O\big(\Delta x^2_f\big)\right.\\ && \left.+ O\big(\Delta y^2_f\big)\right] \, \Delta x_f \Delta y_f \\ &=& \frac{1}{\Delta x_c \Delta y_c} \sum\limits^{j_{fc}+r_h}_{j_f=j_{fc}-r_h} \sum\limits^{i_{fc}+r_h}_{i_f=i_{fc}-r_h} \left[ \phi_{i_f,j_f} + O\big(\Delta x^2_f\big)\right. \\&& \left.+ O\big(\Delta y^2_f\big)\right] \, \frac{1}{r^2}\Delta x_c \Delta y_c \\ &=& \langle \phi \rangle_{i_{fc}\pm r_h,j_{fc}\pm r_h} +\, \Big\langle O\big(\Delta x^2_f\big) \Big\rangle_{i_{fc}\pm r_h,j_{fc}\pm r_h} \\&&+ \Big\langle O\big(\Delta y^2_f\big) \Big\rangle_{i_{fc}\pm r_h,j_{fc}\pm r_h} . \end{array} $$

where $r_h = \lfloor r/2\rfloor$ and $\langle \phi \rangle_{i_{fc}\pm r_h,j_{fc}\pm r_h}$ is the average value of ϕ over the r×r array of fine cells. From this we see that the estimate for $\phi_{{i_c},{j_c}}$ as averaged on the fine grid is second order in the fine grid spacing, $O\big(\Delta x^2_f\big)$. The estimate for $\phi_{{i_c},{j_c}}$ based on the coarse grid primitive equations is second order in the coarse grid, $O\big(\Delta x^2_c\big)$. Even for only a 3:1 ratio in the grid spacing, this equates to an order of magnitude smaller errors obtained by averaging the fine grid estimate. Furthermore, assuming that the time step is small enough to resolve the physical processes (up to their second derivatives), then the signs of the averaged error terms will remain constant over many time steps, providing a bias on the scale of time stepping and a seed for larger-scale biases built up through nonlinear interactions.

As a side note, the above error analysis shows an unambiguous error reduction when using the averages of the fine grid values to replace the coarse grid estimates. This definitive statement is due to the fact that the averaging scheme and the discretization of the primitive equations (Section 2.4) are both second order. If one was to use higher-order methods to discretize the primitive equations, then the averaging scheme used should at least match the order of the discretization. The use of higher-order averaging schemes might require extra filtering of the smallest scales in the fine domain estimates to avoid aliasing (Debreu and Blayo 2008, Section 4.1).

4.7.2 The general error analysis applied to the specific schemes

Scheme 1, Section 4.1, and Fig. 6:

In addition to having the same errors as the later schemes, this scheme uses an estimate of $\nabla \eta$ that is entirely based on the coarse domain fields to compute ${\hat {\bf U}}$. As shown above (Section 4.7.1), this maintains $O\big(\Delta x^2_c\big)$ in $\nabla \eta$ rather than $O\big(\Delta x^2_f\big)$ errors. Moreover, these are second-order errors in $\nabla \eta$; hence, the leading order error terms will be proportional to the third derivatives in η. These are more “singular” derivatives then the second-order derivatives in our PE scheme, explaining why they would have to be larger somewhere and spawn the dominant biases in Fig. 6. The fact that these errors are directly fed into ${\hat {\bf U}}$, which in turn feeds directly into U, explains why these biases appear in the barotropic velocity.

Scheme 2, Section 4.2, and Fig. 7:

This scheme updates ${\hat {\bf U}}$ in the coarse domain with averaged values from the fine domain, thereby reducing the error in $\nabla \eta$ in Eq. 42 but provides no feedback from the fine grid estimates of η to the coarse grid. Hence, the coarse domain errors in η remain everywhere $O\big(\Delta x^2_c\big)$ rather than having $O\big(\Delta x^2_f\big)$ in the overlap region. Given direct coupling of the ${\hat {\bf U}}$ estimates between the domains and the indirect coupling of U via Eq. 44, these errors only have the freedom to excite biases in η, as shown in Fig. 7.

Scheme 3, Section 4.3, and Fig. 8:

This scheme updates η ⁿ in the coarse domain with averaged values from the fine domain. These direct couplings of ${\hat {\bf U}}$ and η ⁿ prevent the domain-wide biases seen in schemes 1 and 2 (Figs. 6 and 7). However, the coarse domain estimate of U ⁿ is still based on the values of η ⁿ that were available when the coarse domain computed U ⁿ from Eq. 44; hence, the coarse domain errors in U ⁿ remain everywhere $O\big(\Delta x^2_c\big)$ rather than having $O\big(\Delta x^2_f\big)$ errors in the overlap region. These errors can feed local instabilities, like those caused by the different coarse and fine representations of the shelfbreak topography across the southern boundary of the fine domain (Fig. 8).

Scheme 4, Section 4.4, and Fig. 9:

This scheme updates U ⁿ in the coarse domain with estimates of η ⁿ which have been updated with averaged values from the fine domain. This means that each term in Eq. 44 now has errors of $O\big(\Delta x^2_f\big)$ in the overlap region rather than $O\big(\Delta x^2_c\big)$. As seen in Fig. 9, this produces a stable scheme with small scale errors.

Scheme 5, Section 4.5, and Fig. 10:

This is the scheme we selected as the best. It updates the transport, i.e., the product $\left(H+\eta^{n}\right){\hat {\bf U}}^{n+1}$, in the coarse domain with averages from the fine domain rather than updating the coarse estimate of ${\hat {\bf U}}^{n+1}$. In doing so, we add no new averaged values from the fine grid and hence make none of the error reductions described in Section 4.7.1. This is consistent with the observation that the resulting changes (Figs. 9 and 10) are relatively small. The advantage is that scheme 5 conserves transport at $O\big(\Delta x^2_f\big)$ from the fine-to-coarse grids while scheme 4 does not.

Coarse-to-Fine Implicit Scheme, Section 4.6, and Fig. 11:

With this nesting scheme, we follow traditional coarse-to-fine implicit schemes. In doing so, we introduce two error sources of the type described in Section 4.7.1. First, when interpolating coarse domain values to the boundary of the fine domain, the coarse domain values used have errors of $O\big(\Delta x^2_c\big)$. In our fully implicit scheme, the coarse domain values in the overlap region have errors of $O\big(\Delta x^2_f\big)$. Second, we do not use fine grid averaged values of either $\left(H+\eta^{n}\right){\hat {\bf U}}^{n+1}$ or ${\hat {\bf U}}^{n+1}$ to update the corresponding coarse grid values. This directly means that ${\hat {\bf U}}^{n+1}$ and U ^n + 1 have errors of $O\big(\Delta x^2_c\big)$ in the overlap region rather than $O\big(\Delta x^2_f\big)$. Since ${\hat {\bf U}}^{n+1}$ is part of the forcing for Eq. 43, the effects of these larger errors can immediately spread outside of the overlap region due to the nonlocal nature of the Helmholtz operator (Eq. 43). Finally, we note that the computational cost of our fully implicit scheme 5 is pretty much equivalent to that of the more classic scheme 6. A major conclusion of our work is that fully implicit (space and time) nesting schemes should be used when possible.

5 Examples

5.1 The middle Atlantic Bight

We continue the study of our fully implicit scheme (Section 3) and its use (Section 4.5) by now examining the consistency of the estimates of the 3D variables between the coarse and fine domains. In Fig. 12, we show the differences between the coarse and fine domain estimates of the temperature, salinity, and total velocity (T,S,u), at a depth of 50 m. As with the barotropic fields, we see an excellent overall agreement between the estimates of the 3D fields in the two domains, in accord with their different resolutions. The temperature differences are mostly bounded by ±0.2° C, the salinity differences by ±0.02 PSU and the total velocity differences by ±1 cm/s. The larger differences occur in two main categories, the topography-driven dynamics (e.g., shelfbreak) and high-gradient dynamics (e.g., filaments). First, the fine domains better resolve the shelfbreak and the Hudson Canyon and the dynamics that these features generate. There, the differences can approach ±1.5° C for temperature, ±0.2 PSU for salinity and ±10 cm/s with intermittent peak spots around ±20 cm/s for velocity. Second, in the offshore regions where filamentation is taking place, larger differences are being generated at the edges of the filaments and eddies, which are better resolved in the fine domain. Note that these differences are not the same as the biases studies in Section 4. On the coarse grid, there would be no difference between the coarse and averaged fine grid solutions (coarse fields are replaced by averages of fine fields). On the fine grid, differences arise from the above dynamical and bathymetric reasons. Further, the coarse fields are bi-linearly interpolated to the fine grid, which cannot reproduce the real gradients on the fine grid.

Fig. 12

Tracer and total velocity differences at 50 m in the fully implicit scheme, to illustrate baroclinic aspects and increased accuracy of finer nested domain. a, b Temperature differences. c, d Salinity differences. e, f Total velocity differences. a, c, e Differences at 1 day into the nested simulation. b, d, f Differences at 24 days into the nested simulation. Main differences occur at shelfbreak/canyon and offshore at edges of filament/eddies, all in regions where resolution is important

In Fig. 13, we present a snap shot of the surface temperature fields at 11 Sep. 2006 overlaid with surface velocity vectors. Eleven days earlier, tropical storm Ernesto passed over the region, cooling the surface and advecting the shelfbreak front several kilometers offshore (Ernesto did not create any issues in nesting, see Section 4). In the relaxation which follows, filaments are being spun off of the shelfbreak front. These processes are well captured in this simulation. Additionally, Fig. 13 shows the continuity of the large-scale structures across the nesting boundary. No shocks or spurious waves are generated at the interface between the coarse and fine domains.

Fig. 13

Surface temperature, overlaid with surface velocity vectors, for 0000Z on 11 Sep. 2006 in the fully implicit two-way nested New Jersey shelf and Hudson Canyon domains

One of the most significant dynamical achievement of our new implicit nesting scheme is an increase in predictive capability. This is shown by comparing our estimates to independent acoustic Doppler current profiler (ADCP) data (T. Duda, personal communication) that were neither assimilated nor used in the initial conditions of the simulations. Results are illustrated in Fig. 14. The ADCP data from a mooring (SW30) are compared to velocity estimates from two different simulations. The first simulation (left panel) is the coarse 3-km resolution large domain run in “Stand Alone” mode, i.e., no nested subdomain. The second simulation (right panel) is the nested simulations using our new implicit scheme. The initial conditions, atmospheric and tidal forcings, assimilated data, and all model parameters are identical. The open boundary conditions for the two coarse 3-km resolution domains are also the same. The only difference is whether the 1-km resolution domain is nested in this 3 km or not. The results are dramatic. Simply including the high-resolution domain reduces the bias with respect to the mooring data from 12 to 2 cm/s and the RMS error from 15 to 8 cm/s. To assess the statistical significance of these improvements, we compute the standard deviation of subtidal signal (obtained by averaging the data with a ±1-day window) about its mean, 5 cm/s, and the standard deviation of the tidal signal about the subtidal signal, 6 cm/s. Clearly the error reductions (10 and 7 cm/s) produced by the nesting are significant when compared to the variability in the data.

Fig. 14

Hourly meridional velocities (v) at 68 m depth at the location of mooring SW30, as measured by the moored ADCP (red curves) and as estimated by re-analysis simulations (blue curves) with atmospheric and barotropic tidal forcing. No mooring data are assimilated. a Comparing mooring velocities against velocity estimates from a 3-km simulation without nesting (“Stand Alone”). b Comparing mooring velocities against velocity estimates from a two-way nested simulation. Our new nesting scheme removes an O(15 cm/s) bias, as averaged during Aug. 22–Sep. 09. Notice that this bias reaches O(30 cm/s) during the Tropical Storm Ernesto

5.2 The Philippine archipelago

Our next realistic simulation results come from our research in the Philippine archipelago as part of the Philippines Straits Dynamics Experiment (PhilEx; Gordon 2009; Lermusiaux et al. 2009a). The goal of PhilEx was to enhance our understanding of physical and biogeochemical processes and features arising in and around straits and improve our capability to predict the spatial and temporal variability of these regions. Here we used spherical coordinates and defined six two-way nested domains, in telescoping setups, ranging from a 3,267 × 3,429-km regional domain (with 27-km resolution) down to a pair of roughly 170 × 220-km strait domains with high (1-km) resolution (see Fig. 15). For physical, biogeochemical, and numerical parameter tuning and real-time forecasting, more than 1,000 simulations were run in this region, for three periods. The simulation shown here is for the Feb.–Mar. 2009 real-time experiment period, focusing on the 1,656 × 1,503 Philippine archipelago domain (9-km resolution) and the 552×519 Mindoro Strait domain (3-km resolution). Both domains have 70 vertical levels arranged in a double-σ configuration, optimized for the local steep bathymetry and depths of thermoclines/haloclines. Our bathymetry estimates merged profile data (C. Lee, personal communication) and ship data (Gordon and Tessler, personal communication) with V12.1 (2009) of the Smith and Sandwell (1997) topography. These simulations were initialized using SSH anomaly data (Colorado Center for Astrodynamics Research; Leben et al. 2002), climatological profiles (Locarnini et al. 2006), and our new mapping scheme (Agarwal and Lermusiaux 2010). Atmospheric forcing at the surface was obtained from Coupled Ocean Atmosphere Mesoscale Prediction System (COAMPS; wind stress) and Navy Operational Global Atmospheric Prediction System (NOGAPS; net heat flux, E-P) fields. For open boundary conditions (OBC), the transports from the HYCOM model were used. Our multiresolution tidal forcing was also used at the OBCs of our free-surface simulations (as well as in the initial conditions). SSH and SST are assimilated, but no in situ synoptic data are used, since one of the PhilEx goals was to evaluate if assimilating remotely sensed data in tuned models could capture some dynamics.

Fig. 15

Six spherical-grid domains in a telescoping zoom configuration for multiscale simulations in the Philippine archipelago

Figure 16 shows the surface velocity after 20 days of simulation. The Mindoro Strait domain (right panel) is used to resolve two main areas. The first is the Mindoro Strait which connects the South China Sea (northwest corner of the domain) to the Sulu Sea (southwest corner). The second is the Sibuyan Sea (interior of archipelago) which connects the Mindoro Strait to the Pacific Ocean via the San Bernardino Strait (12.5 N, 124.25 E). The higher resolution of the Mindoro Strait domain resolves the various pathways of the region. In the snapshot shown, the tides are favoring inflow from the Pacific. This inflow turns primarily northward along the island of Luzon. Even with two-way nesting, this pathway is poorly resolved in the Philippine archipelago domain (left panel). The Philippine archipelago domain provides the external forcing to the Mindoro Strait domain. Looking at the left panel, we again see the continuity of the flow across the boundary of the Mindoro Strait domain.

Fig. 16

Surface velocity at 0600Z on 22 Feb. 2009 in the Philippine archipelago, estimated by our new fully implicit two-way nesting. Left panel: the velocity in the 9-km Archipelago domain. Right panel: the surface velocity in the 3-km Mindoro Strait domain

We also compared our nested fields to independent in situ data. As an example, we utilize the results of Tessler et al. (2010) who analyzed time series from moored ADCP that were deployed around the Panay Sill (11°16′ N, 121°55′ E) in the Mindoro strait system. As in our simulations, they found that the mean velocity showed a bottom intensified southward flow (lower 170 m) into the Sulu Sea. For the Feb.–Mar. 2009 time frame, Tessler et al. (2010) estimate a mean transport of 0.35 Sv southward into the Sulu Sea, with a standard deviation of 0.07 Sv. We compare this to a time-averaged transport of the bottom 170 m through a section from (11.305 N, 121.8003 E) to (11.3746 N, 121.9275 E) taken from our nested simulation. Our model estimate is a mean transport of 0.39 Sv into the Sulu Sea. Our ensemble of simulations gives a model standard deviation of 0.2 Sv, reflecting model parameter uncertainty. To show the impact of two-way nesting, we compare these runs to stand-alone coarse Archipelago runs, with an identical setup, but without the finer nested Mindoro domain. For this coarse-domain-only case, we find that the time-averaged net transport in the bottom 170 m is close to zero and in the central simulation, it is reversed (0.28 Sv northward out of the Sulu sea). This demonstrates the impact that resolution can have on the dynamical flow structure. Our multiresolution approach is likely important also for larger basin-scale and climate studies.

5.3 The Taiwan–Kuroshio region

Our last realistic simulation results come from our research in the Taiwan–Kuroshio region (see Liang et al. 2003, Fig. 1). This research was part of the Quantifying, Predicting, and Exploiting Uncertainty initiative (Gawarkiewicz 2008; Lermusiaux et al. 2009c), which aims to integrate coupled ocean-acoustic modeling, multidisciplinary data assimilation, and autonomous ocean platforms to improve prediction and reduce uncertainties. We defined a pair of nested domains, each with Cartesian coordinates and 70 levels. The larger domain spanned 1,125 × 1,035 km with a 4.5-km resolution. This domain was designed to maintain an accurate synoptic estimate of the Kuroshio and other regional influences on the intensive survey area. The smaller domain covered a 345 × 386-km area with 1.5-km resolution. This domain was designed to resolve the intensive survey, the recurring cold dome, and the Kuroshio–shelf interactions, especially in the region of the North Mien-Hwa canyon system. Our bathymetry estimate merges high-resolution data (B. Calder, personal communication) with V10.1 (2008) of the Smith and Sandwell (1997) topography. The initial and boundary fields were created using ship initialization surveys (OR2/OR3), Sea-Glider data and SST analyses, and a background constructed from high-resolution August WOA-05 climatology with deep Summer WOA-05 climatology profiles (Locarnini et al. 2006). The simulations were forced with a combination of COAMPS (wind stress) and NOGAPS (net heat flux, E-P) atmospheric fields along with barotropic tides. The barotropic tidal forcing was computed using the Logutov and Lermusiaux (2008) model, the regional high-resolution bathymetry, in situ tidal gages, and coarser-resolution tidal simulations from the Egbert global model (Egbert and Erofeeva 2002). During the IOP09 (Lermusiaux et al. 2009c), ensembles of ESSE simulations were used for uncertainty forecasting, over a 1-month period.

Figure 17 shows the relative vorticity computed at 50 m depth, 10 days (0000Z on 28 Aug. 2009) into 1-month-long realization of the ensemble of simulations that were carried out. This is a representative simulation for which the fine domain (right panel) captures the vortex generation of the Kuroshio passing over the I-Lan ridge (starting from Taiwan at 24.5 N, 121.9 E and extending to the southeast). A well-developed vortex wake is clearly visible trailing to the northeast off of Yonaguni Island (24.45 N, 123 E). Downstream of the I-Lan ridge, the vorticity field shows an eddy trapped between the Kuroshio and the shelf. The various off-shelf vorticity wakes generally follow the Kuroshio to the northeast, out of the domain. On the shelf, the interaction of tidal currents with topography produces a tight vorticity signal along the 50-m isobath just north of Taiwan. Across the mouth of the Taiwan strait, we find another (weaker) interaction of tidal currents and bathymetry, aligned north by northeast roughly along the 80-m isobath. In the coarse domain (left panel), the averaged versions of the small domain features are maintained. The vortex wakes streaming out of the small domain are smoothly continued in the external portions of the large domain. The nesting also maintains the wake off Yonaguni Island in the large domain even though the island itself is not explicitly represented in the large domain. Outside of the small domain, similar wakes, topographic generation, and eddies are present though of necessarily larger scale. We have also compared 2 to 3 days forecasts with in situ temperature and salinity data (Newhall et al. 2010). We find that the two-way nested simulations have RMSE and biases that are on .average 10% smaller than a stand-alone run (coarse domain alone, without the nested domain). Such higher-resolutions runs are also useful for internal tide predictions and acoustic simulations (Lermusiaux and Xu 2010).

Fig. 17

Relative vorticity at 50 m in the Taiwan/Kuroshio region for 0000Z on 28 Aug. 2009, estimated by our new fully implicit two-way nesting. This is one of the ensemble simulations we have for the period 18 Aug.–10 Sep. 2009. Note the smaller scales maintained in the fine resolution, especially the topographic generation of vorticity as the Kuroshio crosses I-Lan ridge

6 Summary and conclusions

In this manuscript, we derived and applied conservative time-dependent structured discretizations and powerful two-way nesting (embedding) schemes for multiresolution, telescoping domains of primitive equation ocean models with a nonlinear free surface. The resulting schemes are suitable for realistic data-driven multiscale simulations over deep seas to very shallow coastal regions with strong tidal forcing. Starting from the primitive equations with a nonlinear free surface, cast into a control volume formulation, we introduced a second order temporal discretization, including a new time-splitting algorithm compatible with the nonlinear free-surface physics. We then derived a second-order spatial discretization that correctly accounts for the time variations in the finite volumes. It is coded for both spherical and Cartesian horizontal coordinates and for generalized vertical grids. We introduced the concepts of “implicit nesting” in space and time (exchange all of updated fields values as soon as they become available), “explicit nesting” (exchange coarse and fine domain fields only at the start of a discrete time integration or time step), “coarse-to-fine implicit” nesting (the coarse domain feeds the fine domain during its time step, usually boundary conditions, with no feedback from the fine domain), and “fine-to-coarse implicit” nesting (fine domain updates are fed to the coarse domain during its integration). We then derived a fully implicit two-way nesting scheme that is compatible with the time varying discretization of the nonlinear free-surface primitive equations. This scheme allowed us to use different parametrizations for the sub-gridscale physics in each of the nested domains. We compared this scheme to other two-way nesting schemes with modified interdomain couplings. We completed a theoretical truncation error analysis of these schemes, which confirmed and explained our simulation results. We have employed our new discretizations and nesting schemes with data assimilation in several ocean regions with multiscale dynamics around steep shelfbreaks, straits, or other complex geometries. Presently, such simulations were qualitatively and quantitatively evaluated in three regions: the middle Atlantic Bight off the east coast of the USA, the Philippine archipelago, and the Taiwan–Kuroshio region. Of course, we have used the schemes in other regions (e.g.,  Xu et al. 2008; Kaufman 2010).

Our comparisons of various two-way nesting schemes showed that for nesting with free surfaces, the most accurate schemes are those with strong implicit couplings among grids, especially for the velocity components. We showed selected results for five nesting schemes (including our fully implicit scheme) and a coarse-to-fine implicit scheme. Among the implicit schemes, providing more fine-to-coarse feedback reduces biases and other discrepancies across grids and produces more stable simulations. For the simulations shown, the scheme with the least amount of fine grid feedback has differences between the barotropic velocity estimates of O(10) cm/s, with the structures of the difference field organized on the (sub) mesoscale. Conversely, the schemes with more feedback keep these discrepancies smaller, O(1) cm/s, intermittent and organized on smaller scales, with some larger differences, 1–4 cm/s along topographic features. Among these schemes, our fully implicit one has the smallest discrepancies, much smaller than 1 cm/s except near steep topography or strong dynamical gradients where differences reach 1 cm/s. This is because the finer grid is needed there to represent this variability. The coarse-to-fine implicit scheme is shown to have much greater discrepancies between the coarse and fine estimates, generally around 1–6 cm/s organized on intermediate scales.

With our theoretical truncation error analysis, we revealed the benefits of additional feedback from the fine-to-coarse domains. The leading error terms for each nesting scheme were determined and studied. We proved that coarse domain estimates which are made up from averages of fine domain estimates retain the truncation error of the fine grid. Even for a second-order scheme with only a 3:1 refinement, this equates to an order of magnitude reduction in the truncation error at these coarse domain points. A corollary of this analysis is that the improvement from the fine grid feedback can be guaranteed only if the feedback algorithm (in our case volume averaging) has at least the same order of accuracy as that of the overall discretization.

In our three realistic simulations, we resolved large domains with multiscale dynamics, including steep bathymetries and strong tidal flows in shallow seas. In each case, we found that without our new discrete PE model, or without nested grids, predictions do not match the ocean data. Specifically, in the middle Atlantic Bight, we compared nested estimates to mooring data not assimilated in simulations. Using twin experiments between a 3-km resolution “stand-alone” domain and the same domain with a two-way nested 1-km resolution domain, we show that the addition of the nested subdomain removes large biases and RMSEs, O(10–15) cm/s, in the model velocities when compared to the mooring data. The two-way nesting scheme is found especially needed during tropical storm Ernesto. It is also required for future studies of internal tide propagation. The application to the Philippine Archipelago region is mostly striking by the complexity of the geometry, with multiple islands and passages, and by the multiscale dynamics, from very strong tides in shallow areas to the North Equatorial Current in the Pacific. This complexity required novel schemes, from our multiscale objective analyses for such regions (Agarwal and Lermusiaux 2010) to the present time-dependent spatial discretizations and fully implicit two-way nesting. In this region, we have so far implemented six two-way nested domains, in a telescoping setup, covering four-grid resolutions. Without the present schemes, such multiscale simulations were not possible. In addition, comparisons with independent ADCP data show that nesting substantially improves mean transport estimates through straits. Such results are also significant for basin-scale and climate studies. The simulations for the Taiwan–Kuroshio region focused on uncertainty, and we showed one realization of an ensemble of two-way nested simulations. The region is characterized by strong interactions near the shelfbreaks involving the Kuroshio, mesoscale features, strong atmospheric events, rivers, strong tides, internal tides, and waves. Multiresolution two-way nesting or unstructured grids are required for such dynamics and also for their impacts on acoustics (Lermusiaux and Xu 2010; Xu and Lermusiaux 2010). Quantitative comparisons with independent data confirm increased forecast skill due to nesting.

Ongoing and future research includes a study of boundary conditions (e.g., Blayo and Debreu 2005; Oddo and Pinardi 2008) for nested domains and comparisons with our current radiation-allowing conditions. Finer scales should exit the finer domains freely, but this is challenging since they are not resolved in the coarser domains. We have also applied our schemes to coupled physical–biological dynamics in two-way nested domains in the Philippines archipelago (Lermusiaux et al. 2009b), and dynamical studies in various regions are underway. Also valuable would be to merge our nesting algorithms with refined time stepping in finer domains (Section 3) and compare the results to our present algorithm. Our implicit nesting scheme, after some modifications, could also be applied to other dynamics such as nonhydrostatic regimes as well as to multidynamics, e.g., two-way nesting of nonhydrostatic and hydrostatic models; sediment, wave, and coastal models (Warner et al. 2008); and coastal and storm surge models, with wetting and drying (Bunya et al. 2010; Tanaka et al. 2010). Other research directions are the comparison and merging of our nesting scheme with unstructured grid approaches (e.g., Deleersnijder and Lermusiaux 2008b; Ueckermann 2009; Ueckermann and Lermusiaux 2010; Kleptsova et al. 2010), multiscale feature initialization (Gangopadhyay et al. 2003), and multimodel fusion (Logutov 2007; Rixen et al. 2009). We also intend to combine our schemes with uncertainty predictions based on dynamically orthogonal equations (Sapsis and Lermusiaux 2009). Even though it is only recently that realistic multiscale ocean modeling is becoming possible, the topic is so important for ocean science and societal applications that opportunities for our novel schemes are expected over a rich spectrum of needs.

Appendices

Appendix 1: Additional details of the conservative discrete equations

Our horizontal grids are structured Cartesian or spherical grids, either of which can be rotated from the standard geographic orientation (for more details, see Haley 1999, Section 2.2). To obtain the spherical representation of our Eqs. 37–44 and “Appendix  1.2”, identify x with longitude and y with latitude. Then multiply all Δx terms by the radius of the earth (R _earth) times the cosine of the latitude and all Δy terms by R _earth. Our model also includes options for atmospheric forcing, assimilation, tidal forcing, and a river forcing that employs relaxation time constants which can be tuned to reproduce the desired mass, salt, and internal energy (heat) transports. All of these options are compatible with the two-way nesting scheme.

1.1 Appendix 1.1: Vertical grid

In Section 2.4, we introduced our vertical discretization, defining first a set of terrain-following depths for the undisturbed mean sea level, $z^{\rm MSL}_{i,j,k}$. Here we present the details of $z^{\rm MSL}_{i,j,k}$. We can currently employ five different schemes for defining these vertical levels, two of which are new:

• (a) σ-Coordinates (Phillips 1957)

  $$ \label{Eq:SigmaCoords} z^{\rm MSL}_{i,j,k} = - \sigma_k H_{i,j} $$

  (56)

  where 0 ≤ σ _k  ≤ 1

• (b) Hybrid coordinates (Spall and Robinson 1989)

  $$ \label{Eq:HybridCoords} z^{\rm MSL}_{i,j,k} = \left\{ \begin{array}{lcc} \tilde{z}_k & {\rm if} & k \le k_c \\ -h_c - \sigma_k \left( H_{i,j} - h_c\right) & {\rm if} & k > k_c \end{array} \right. $$

  (57)

  where $\tilde{z}_k$ are a set of constant depths and h _c is the sum of the top k _c flat level depths

• (c) Double σ-coordinates (Lozano et al. 1994)

  $$ \label{Eq:DoubleSigmaCoords} z^{\rm MSL}_{i,j,k} = \left\{ \begin{array}{lcc} - \sigma_k \tilde{f}_{i,j} & {\rm if} & k \le k_c \\ -\tilde{f}_{i,j} - (\sigma_k - 1) \left( H_{i,j} - \tilde{f}_{i,j}\right) & {\rm if} & k > k_c \end{array} \right. $$

  (58)
  $$\begin{array}{rll} \tilde{f}_{i,j} &=& \frac{z_{c_1} + z_{c_2}}{2} + \frac{z_{c_2} - z_{c_1}}{2} \\&&\times \tanh\left[\frac{2 \alpha}{z_{c_2} - z_{c_1}} \left(H_{i,j} - h_{ref} \right)\right] \\ \sigma_k &\in& \left\{ \begin{array}{lcc} [0, 1] & {\rm if} & k \le k_c \\ {[1, 2]} & {\rm if} & k > k_c \end{array} \right. \end{array} $$

  where $\tilde{f}_{i,j}$ is the variable interface depth between the upper and lower σ-systems, $z_{c_1}$ and $z_{c_2}$ are the shallow and deep bounds for $\tilde{f}_{i,j}$, h _ref is the reference topographic depth at which the hyperbolic tangent term changes sign, and α is a nondimensional slope parameter ($|| \nabla \tilde{f} || \le \alpha || \nabla H ||$).

• (d) Multi-σ-coordinates This new system is a generalization of the double σ system in which, for Pσ-systems, we define P + 1 nonintersecting interface surfaces. Then the depths are found from

  $$ \begin{array}{rll}\label{Eq:MultiSigmaCoords} z^{\rm MSL}_{i,j,k} &=& -\tilde{f}^{p-1}_{i,j} - (\sigma_k - p + 1) \tilde{f}^p_{i,j} \quad \\&&\quad {\rm for}\quad k_{p-1} < k \le k_p \end{array} $$

  (59)
  $$ \begin{array}{lll}&&\tilde{f}^0_{i,j} = 0 ; \quad \tilde{f}^P_{i,j} = H_{i,j} \\ &&\sigma_k \in {[(p-1),\ p]} \quad {\rm for} \quad k_{p-1} < k \le k_p \end{array} $$

  The intermediate interfaces are free to be chosen from many criteria, including key σ _θ surfaces (e.g., top of mean thermocline) or large mean vertical gradients.

• (e) General coordinates For this new system, we provide a 3D field of level thicknesses, $\Delta z^{\rm MSL}_{i,j,k}$, under the constraint

  $$ \sum\limits^K_{k=1} \Delta z^{\rm MSL}_{i,j,k} = H_{i,j} \, . $$

  The unperturbed levels are then found from

  $$ \label{Eq:GeneralVerticalCoords} z^{\rm MSL}_{i,j,k} = \left\{ \begin{array}{lcc} \displaystyle\frac{-1}{2} \Delta z^{\rm MSL}_{i,j,1} & {\rm if} & k = 1 \\ z^{\rm MSL}_{i,j,k-1} - \displaystyle\frac{1}{2} \left( \Delta z^{\rm MSL}_{i,j,k-1} + \Delta z^{\rm MSL}_{i,j,k} \right) & {\rm if} & k > 1 \end{array} \right. $$

  (60)

  Note that our new general coordinate scheme contains schemes (a–d) as special cases. Hence, schemes (a–d) are now implemented by specifying $\Delta z^{\rm MSL}_{i,j,k}$ outside the model, according to their respective rules, and using the resulting $\Delta z^{\rm MSL}_{i,j,k}$ as input to the general coordinate scheme.

1.2 Appendix 1.2: Fluxes through boundaries of computational cells

To complete the conservative spatial discretizations of Section 2.4, we first establish some notation. Values taken at the centers of tracer volumes have integer indices, e.g., T _i,j,k, while values taken at the centers of velocity volumes have odd-half integer indices, e.g., $\mathbf u_{i+\frac{1}{2},j+\frac{1}{2},k}$. In the vertical, values taken at either the centers of tracer or velocity volumes have integer indices while those at the tops or bottoms of the computational volumes have odd-half integer indices, e.g., $\omega_{i,j,k+\frac{1}{2}}$. Using these rules, we define the following averaging and differencing operators:

$$ \begin{array}{rll} \label{Eq:avgop} \langle \phi \rangle^x_{i,j,k} &=& \frac{1}{2} \big(\phi_{i+\frac{1}{2},j,k} + \phi_{i-\frac{1}{2},j,k} \big) \\ \langle \phi \rangle^y_{i,j,k} &=& \frac{1}{2} \big(\phi_{i,j+\frac{1}{2},k} + \phi_{i,j-\frac{1}{2},k} \big)\\ \langle \phi \rangle^z_{i,j,k} &=& \frac{1}{2} \big(\phi_{i,j,k+\frac{1}{2}} + \phi_{i,j,k-\frac{1}{2}} \big) \\ \delta^x(\phi)_{i,j,k} &=& \phi_{i+\frac{1}{2},j,k} - \phi_{i-\frac{1}{2},j,k} \\ \delta^y(\phi)_{i,j,k} &=& \phi_{i,j+\frac{1}{2},k} - \phi_{i,j-\frac{1}{2},k}\\ \delta^z(\phi)_{i,j,k} &=& \phi_{i,j,k-\frac{1}{2}} - \phi_{i,j,k+\frac{1}{2}}. \end{array} $$

Note that in the above, i and j increase with increasing x and y while k increases with decreasing depth (negative below sea level).

Now we can define the fluxes through the sides of the computational cells. We start with the “flux velocities” evaluated at the centers of the sides. Following Dukowicz and Smith (1994, Appendix E), we define the integrated flows through the “east” and “north” lateral walls of the tracer volumes as

$$ \upsilon^n_{i+\frac{1}{2},j,k} = \Delta y_j \left\langle \Delta z^n {u^\prime} + \frac{1}{2} \Delta z^{n-1} \left(U^n + U^{n-1} \right) \right\rangle^y_{i+\frac{1}{2},j,k} \, , $$

$$ \nu^n_{i,j+\frac{1}{2},k} = \Delta x_i \left\langle \Delta z^n {v^\prime} + \frac{1}{2} \Delta z^{n-1} \left(V^n + V^{n-1} \right) \right\rangle^x_{i,j+\frac{1}{2},k} \, , $$

while at the velocity boxes, we define the integrated flows through the “east” and “north” lateral walls as

$$ \begin{array}{lll} &&{\kern-6pt} \upsilon^n_{i+1,j+\frac{1}{2},k} \\ && = \Delta y_{j+\frac{1}{2}} \Bigg\langle \Bigg\langle \Bigg\langle \Delta z^n {u^\prime} + \frac{1}{2} \Delta z^{n-1} \left(U^n + U^{n-1} \right) \Bigg\rangle^y \Bigg\rangle^x \Bigg\rangle^y_{i+1,j+\frac{1}{2},k} \, , \end{array} $$

$$\begin{array}{lll} &&{\kern-6pt} \nu^n_{i+\frac{1}{2},j+1,k} \\ &&= \Delta x_{i+\frac{1}{2}} \Bigg\langle \Bigg\langle \Bigg\langle \Delta z^n {v^\prime} + \frac{1}{2} \Delta z^{n-1} \left(V^n + V^{n-1} \right) \Bigg\rangle^x \Bigg\rangle^y \Bigg\rangle^x_{i+\frac{1}{2},j+1,k} \, . \end{array} $$

These particular spatial averagings are chosen to match the discrete transport constraint (Eq. 65 in “Appendix 1.4”). The new aspect here is the temporal evaluations. The baroclinic velocity components are evaluated at time n. However, the timings for the barotropic components are, again, chosen to match the transport constraint (Eq. 65). Also note that these timings assume θ = 1. To get the corresponding flows through the “west”(“south”) lateral walls, simply decrement i(j ) by one.

To evaluate the fluxes through the tops of the computational volumes, we use the above definitions in Eq. 37. At tracer volumes this yields

$$ \begin{array}{lll} \label{Eq:VertFluxTbox} &&{\kern-6pt} \delta^z (\omega^n)_{i,j,k} \Delta x_i \Delta y_j + \delta^x (\upsilon^n)_{i,j,k} + \delta^y(\nu^n)_{i,j,k}\\ &&{\kern2pt} + \frac{\Delta {\cal V}^n_{i,j,k}}{H_{i,j}+\eta^n_{i,j}} \frac{\delta (\eta_{i,j})^{n,n-2}}{\tau} = 0 \end{array} $$

(61)

while at velocity volumes, we get

$$ \begin{array}{lll} &&{\kern-6pt}\delta^z(\omega^n)_{i+\frac{1}{2},j+\frac{1}{2},k} \Delta x_{i+\frac{1}{2}} \Delta y_{j+\frac{1}{2}}\\ &&{\kern2pt} +\, \delta^x(\upsilon^n)_{i+\frac{1}{2},j+\frac{1}{2},k} + \delta^y(\nu^n)_{i+\frac{1}{2},j+\frac{1}{2},k}\\ \label{Eq:VertFluxVbox} &&{\kern2pt} +\, \frac{\Delta {\cal V}^n_{i+\frac{1}{2},j+\frac{1}{2},k}} {H_{i,j}+\langle\langle\eta^n\rangle^x\rangle^y_{i+\frac{1}{2},j+\frac{1}{2}}} \frac{\delta \left(\langle\langle\eta\rangle^x\rangle^y_{i+\frac{1}{2},j+\frac{1}{2}}\right)^{n,n-2}} {\tau}= 0 \, .\\ \end{array} $$

(62)

Using these definitions of the fluxes through the boundaries of the computational volumes, we can now simply write the discrete advection operator as

$$ \begin{array}{rll} \breve{\Gamma}(\phi)^n_{i,j,k} &=& \delta^x\left(\langle\phi^n\rangle^x\upsilon^n\right)_{i,j,k} + \delta^y\left(\langle\phi^n\rangle^y\nu^n\right)_{i,j,k}\\ &&+\; \delta^z\left(\langle\phi^n\rangle^z\omega^n\right)_{i,j,k} \Delta x_i \Delta y_j \, . \end{array} $$

This formulation is valid for both tracer and velocity computational volumes, with the understanding that for velocity volumes the i,j indices are shifted by one half.

We have evaluated the pressure force term, $-{1 \over \rho_0} \int_{{\cal S}^n} p^n_h \, \hat n_h \cdot d{\boldsymbol{\cal A}}$, both by directly discretizing the integrals of pressure along the cell walls (including the horizontal contributions from the sloping cell tops and bottoms) and by interpolating the pressure to the corresponding velocity depths and evaluating the differential gradient. Both give similar results, but the integral evaluation is conservative and produces less noise in the resulting velocities (especially near sloping bottoms).

1.3 Appendix 1.3: Open boundary conditions

For u ^′, T, S, and η, the application of boundary conditions is straightforward. Our options (see Haley et al. 2009; Lermusiaux 1997) include using values based on data, applying radiation conditions (Orlanski 1976; Spall and Robinson 1989), or, following Perkins et al. (1997), using radiation conditions to correct the provided values. For nested subdomains, we have first used the interpolated values directly or with Perkins et al. (1997) corrections. Some other promising options we have explored with nested subdomains include using the coarse grid values in a narrow buffer zone around the fine domain, which reduces discontinuities. Another important multiscale conservative boundary condition option is to feedback the averages of the fluxes across the boundary walls shared with the large domain (Fig. 3). These include the advective fluxes of momentum and tracers, the pressure force, and the diffusive fluxes of momentum and tracers.

We still need an additional boundary condition for $\overline{\hat{\cal F}^{n,n-1}}$ since we are unable to directly evaluate Eq. 42 at the boundaries. To derive this boundary condition, we recast Eq. 42 in the form of Eq. 24 and solve for $\overline{\hat{\cal F}^{n,n-1}}$:

$$ \label{Eq:SetUpUbarBC} \overline{\hat{\cal F}^{n,n-1}} = \frac{\delta(\mathbf{U})}{\tau} + f \hat k \times {\mathbf{U}}^\alpha + g \nabla \eta^\alpha_{i,j} \, . $$

(63)

Now, the right-hand side of Eq. 63 is made up entirely of quantities that can be directly evaluated at the boundary of the velocity grid. For the free surface, we have found that it is more stable to rewrite Eq. 63 in terms of transports:

$$ \begin{array}{rll} \label{Eq:UbarotropicBC} \overline{\hat{\cal F}^{n,n-1}} &=& \frac{1}{H+\eta^n} \left\{\frac{\delta\left[\left(H+\eta\right)\mathbf{U}\right]}{\tau} + f \hat k \times \left[\left(H+\eta\right){\mathbf{U}}\right]^\alpha\right\}\\ &&+\, g \nabla \eta^\alpha_{i,j} \, . \end{array} $$

(64)

Note: when evaluating Eq. 64, only values at time t _n + 1 are taken from the provided fields (or nesting interpolations). The fields at times t _n and t _n − 1 are both already in memory and in primitive equation balance. They are combined with the t _n + 1 fields to evaluate (Eq. 64).

Applying Perkins et al. ( 1997 ) boundary conditions:

Following the algorithm of Perkins et al. (1997), corrections to the provided values (and nesting interpolation values) are obtained by applying the Orlanski radiation algorithm to the difference between the PE model values and these provided values and using these differences to correct the boundary values.

For the barotropic transport, however, this is only done for the tangential component to the boundary. The correction to the normal component is derived from the correction obtained for the surface elevation, Δη, and the barotropic continuity equation

$$ \frac{\partial \Delta \eta}{\partial t} + \nabla \, \cdot \, \left[ (H+\eta) \Delta {\mathbf U} \right] = 0 \, . $$

1.4 Appendix 1.4: Maintaining the vertically integrated conservation of mass

To see how the free-surface algorithm maintains the vertically integrated conservation of mass, start from Eq. 44, multiply by θ(H + η ⁿ), and take the divergence of the result to get

$$ \begin{array}{lll} \nabla &\cdot& \left[ \left(H+\eta^n\right) \theta \mathbf U^{n+1}\right] = \nabla \cdot \left[ \left(H+\eta^n\right) \theta {\hat {\bf U}}^{n+1}\right]\\ &-& \alpha \theta g \tau \nabla \cdot \left[ \left(H+\eta^n\right) \nabla \delta \eta \right] + \theta \nabla \cdot \left(\left.\mathbf{u^\prime}^n\right|_\eta \frac{\delta \eta}{\tau}\right) \, . \end{array} $$

Substitute for the right-hand side of the above equation from Eq. 43 and rearrange to obtain

$$ \label{Eq:FreeSurfaceVertIntCont} \frac{\delta \eta}{\tau} {\kern-.5pt} +{\kern-.5pt} \frac{1}{2} \nabla {\kern-.5pt}\cdot{\kern-.5pt} \left[ \left(H{\kern-.5pt}+{\kern-.5pt}\eta^n\right) \left( \theta \mathbf U^{n+1} {\kern-.5pt}+{\kern-.5pt} \mathbf U^n {\kern-.5pt}+ (1 {\kern-.5pt}-{\kern-.5pt} \theta) \mathbf U^{n-1} \right) \right] {\kern-.5pt}={\kern-.5pt} 0 . $$

(65)

Equation 65 represents the discrete form of the barotropic continuity enforced by the free-surface algorithm. Imbalances in Eq. 65 produce unrealistic vertical velocities via Eqs. 61 and 62.

However, as illustrated by the above derivation, Eq. 65 is only satisfied to the same degree that Eqs. 43 and 44 are satisfied. This places restrictions on the valid avenues for nesting. For example, we can safely replace the coarse domain estimates of $(H+\eta){\hat {\bf U}}^{n+1}$ with averages from the fine domain without disturbing (Eq. 65). Moving this exchange one step later in the algorithm and trying to average $(H+\eta)[\theta{\hat {\bf U}}^{n+1} + \mathbf U^n + (1 - \theta) \mathbf U^{n-1}]$ would violate Eq. 43, in the sense that we would not be able to make the last substitution leading to Eq. 65 and hence we would violate Eq. 65. Similar to the bias argument of Section 4.7, these fields and their errors will persist over many time steps, leading to unsustainable vertical velocities.

Appendix 2: Additional details on running our fully implicit two-way nested free-surface PE model

1.1 Appendix 2.1: Setting up domains

1.1.1 Appendix 2.1.1: Topography

There are two main issues when defining topographies for nested simulations. The first is that the finer resolution grid can support finer topography scales, including sharper gradients. The bathymetry on the finer grid is not an interpolation of the coarser grid bathymetry, but the coarser grid bathymetry is a coarse-control-volume average of the finer grid bathymetry. The refinement in topographic scales can lead to abrupt artificial discontinuities in the topography where the fine and coarse domains meet. This can be exacerbated by conditioning the topography (Haley and Lozano 2001) to control the hydrostatic consistency condition (Haney 1991). For a given value of the hydrostatic consistency factor (roughly proportional to $\frac{d\mathbf{x} \times \nabla h}{h}$), the finer resolution domain can support steeper bathymetric features (e.g., shelfbreak). To ensure a smooth transition, we define a band of points around the outer edge of a fine domain (e.g., a band from the boundary to 6 points inside the boundary, see also Penven et al. 2006). In this band, we replace the fine grid topography with a blend of the coarse and fine grid topographies:

$$ \label{Eq:TopoBlending} h_{\rm blend} = \alpha h_{\rm f\/ine} + (1-\alpha) h_{\rm coarse} $$

(66)

where α varies from zero at the boundary to one at the inner edge of the band (e.g., 6 points).

The second issue comes about from the nesting algorithm itself. As mentioned in Section 3, we force the undisturbed vertical grid , $z^{\rm MSL}_{i,j,k}$, to satisfy the nesting rules of Eqs. 46 and 48. To ensure that the topographies in nested domains satisfy Eq. 46 and 48 and the blending Eq. 66 ,we usually follows these steps:

• 1. Apply the nesting constraints on the unconditioned topographies. Starting from the smallest domain, average the fine grid topographies on the successively larger topographies according to Eq. 46. Then starting from the coarsest domain, interpolate the topographies to the boundaries of the successively smaller domains according to Eq. 48.

• 2. Starting from the largest domain, apply the conditioning. After the largest domain is conditioned, apply the blending Eq. 66 to the second largest. Condition that domain and repeat the blending-conditioning cycle with the successively smaller domains.

• 3. Reapply the nesting constraints on the conditioned topography. Repeat step 1.

1.1.2 Appendix 2.1.2: Land masking

The first constraint for masking occurs at the boundaries of the finer domains. Considering any two nested domains, we want continuity of the masks across the domain boundary. In other words, a coastline that crosses the boundary of the fine domain should not have a jump or jog at the boundary of the fine domain. Enforcing this consistency, along with boundary constraints on the topography (“Appendix 2.1.1”), enforces consistent estimates of the areas of the lateral boundaries of the fine domain as measured in both the coarse and fine grids.

The second constraint is to have a certain degree of consistency in defining land and sea in the interior of the fine domain. This is a less exact statement because the fine domain supports a more detailed resolution of the land/sea boundary than the coarse domain. Because of the superior resolution, we take the view that the land mask in the interior of the fine domain is “more correct” than the coarse domain mask. Since we use collocated grids, this provides us with a simple algorithm for resetting the coarse mask. For each coarse grid point fully supported by fine grid points, we count how many of the supporting fine grid points are land and how many are sea. If at least one half the fine grid points are sea, the coarse grid point is marked as sea; otherwise, it is masked as land.

Our general procedure is to first define the land mask for the largest (coarsest) domain. Then use that mask to define a crude first guess for the mask in the fine domain. We then reset the interior nodes of the fine mask to better resolve the coasts (leaving a narrow band around the exterior untouched to ensure continuity through the boundary). If we have more then two domains, we use the current domain to initialize the mask for the next finest domain and repeat. When we finish the mask in the smallest (finest) domain, we use that mask to reset the mask in the next coarser domain, using the above sea/land counting procedure. We then examine the modified mask in that next coarser domain to eliminate any spurious artifacts that may have been created (e.g., a narrow mouth of a bay may have been closed leaving an isolated “lake” that we do not need to maintain). We repeat with the next coarser domain and so on until we get back to the coarsest domain.

1.2 Appendix 2.2: Initialization

Our common situation is to estimate the best initial synoptic state from temperature and salinity data (in situ, climatologies, satellite, etc.) but little or no direct velocity data. Our initialization scheme for this situation is described next, focusing mainly on the nesting considerations, first briefly for the rigid-lid procedures and then the extensions for initializations with a free surface.

1.2.1 Appendix 2.2.1: Rigid lid

Our procedures for rigid lid initializations in nested grids are based on (e.g., Haley et al. 2009). Starting from temperature and salinity data, climatologies, etc., we create 3D estimates of temperature and salinity, often using objective analyses (Carter and Robinson 1987; Agarwal and Lermusiaux 2010). From these 3D temperature and salinity estimates, we construct density (Eq. 6) and the hydrostatic pressure (Eq. 9). We then estimate the total velocity using the rigid lid geostrophic relation

$$ f \hat k \times (\mathbf u - \mathbf u_{\rm ref}) = \frac{1}{\rho_0} \nabla p_h = \frac{g}{\rho_0} \int^z_{Z_{\rm ref}} \nabla \rho \, d\zeta$$

where Z _ref is a suitably chosen reference level, which can be a “level of no motion”, u _ref is the absolute velocity at that depth, and we have interchanged the horizontal gradient with the vertical integral. When evaluating $\nabla \rho$ at a particular depth, if any of the ρ values used for the gradient would be below topography, we set $\nabla \rho$ to zero. To enforce no penetration of land, we find a stream function, ψ, which satisfies $\nabla^2 \psi = \nabla \times \mathbf u$ with ψ set to be constant along coasts. From this ψ, we recompute the velocity. We decompose this velocity into barotropic and baroclinic parts (Eq. 8). The baroclinic portion is fine as is, but barotropic velocities at this stage generally do not satisfy the nondivergence of transport. To enforce this, we define a transport stream function $\hat k \times \nabla \Psi = H \mathbf U$ and fit it to our estimated barotropic velocities via the Poisson equation

$$ \nabla \times \left( \frac{\hat k}{H} \times \nabla \Psi \right) = \nabla \times \mathbf U \, . $$

We derive Dirichlet boundary conditions for the above by first noting that the tangential derivative of Ψ to the boundary equals the normal component of transport, H U, through the boundary. We then integrate this relation around the boundary to obtain the Dirichlet values. For domains with islands, we also need to provide constant values for Ψ along the island coasts. We do this in a two-stage process in which we first compute Ψ assuming all the islands are open ocean. We then use that initial guess to derive constant island values that minimize the relative interisland transports using fast marching methods (Agarwal 2009).

Nesting considerations

For nesting the initial temperature, salinity, other tracers, and baroclinic velocity, we can directly enforce some conservation constraints by averaging estimates from finer to coarser grids. For the transport stream function, we go to the additional step of generating the Dirichlet boundary values for the Poisson equation in the fine domain by interpolating the stream function values from the coarse domain. This ensures that the same constant of integration is used for both domains and that the net flows through the fine domain are consistent in both the coarse and fine grids. For island values, if the island is represented in both the coarse and fine domains, the coarse domain value is used. If the island is only in the fine domain, then the procedure of the preceding paragraph is used.

1.2.2 Appendix 2.2.2: Free surface

The starting point for the free-surface initialization scheme is the above rigid-lid initialization. We start by explicitly computing the final, rigid-lid barotropic velocities from

$$ \mathbf U = \frac{\hat k}{H} \times \nabla \Psi \, . $$

We next create an equation for the initial surface elevation. We start from the geostrophic approximation with the full pressure

$$ f \hat k \times \mathbf u = g \nabla \eta + \frac{1}{\rho_0} \nabla p_h \, .$$

Integrating this equation in the vertical from − H to 0 and isolating η results in

$$ \label{Eq:FreeSurfaceGradientIC} g H \nabla \eta = f \hat k \times H \mathbf U - \frac{1}{\rho_0} \int^0_{-H} \nabla p_h dz \, . $$

(67)

Finally, we take the divergence of Eq. 67 to get

$$ \label{Eq:FreeSurfaceDivergenceIC} \nabla \cdot \left( g H \nabla \eta \right ) = \nabla \cdot \left( f H \mathbf U \right) - \frac{1}{\rho_0} \nabla \cdot \left( \int^0_{-H} \nabla p_h dz \right) \, . $$

(68)

To generate Dirichlet boundary values for Eq. 68, we integrate the tangential components of Eq. 67 around the boundary. Because the coastal boundary condition is zero normal derivative, no special action needs to be taken for islands.

Once an initial value for η is constructed, then, by Eq. 35, the initial depths are recomputed. The tracers (temperature, salinity, etc.) and baroclinic velocity are re-interpolated to these new initial depths. Finally, the barotropic velocities from the rigid-lid calculation are rescaled to preserve the transports:

$$ \mathbf U_{\rm free\ surface} = \frac{H}{H+\eta} \mathbf U_{\rm rigid\ lid} \, . $$

Nesting considerations

These are the same as for the rigid-lid case. The additional detail is that now we also interpolate the coarse grid estimate of η to generate Dirichlet boundary values for solving Eq. 68 in the fine domain.

1.3 Appendix 2.3: Tidal forcing

1.3.1 Appendix 2.3.1: Constructing the tidal forcing

When adding tidal forcing to our simulations, our underlying assumption is that our regional domains are small enough so that the tidal forcing through the lateral boundaries completely dominates the local body force effects. To model these lateral forcings, we employ the linearized barotropic tidal model (Logutov 2008; Logutov and Lermusiaux 2008). We use a shallow water spectral model and generate 2D fields for the amplitude and phase of tidal surface elevation and the barotropic tidal velocity. We dynamically balance these barotropic tidal fields with our best available topographic and coastal data along with the best exterior barotropic tidal fields (e.g., Egbert and Erofeeva 2002). Once we have constructed our tidal fields for the desired modes, we can simply evaluate them for any time.

The above procedures can provide tidal fields on different grids than used by our PEs. For example, Logutov (2008) and Logutov and Lermusiaux (2008) are formulated on a C-grid, instead of the B-grid being used here. In particular, this means that tidal fields interpolated from these grids will not, in general, exactly satisfy the same discrete continuity as in our grid. Our experience shows that satisfying the same discrete continuity leads to more robust solutions. To enforce this constraint, we solve the constrained minimization problem

$$ \begin{array}{rll} {\cal J} & = & \int \left\{ \alpha \eta^*_1 \eta_1 + \theta \beta \mathbf U^*_1 \cdot \mathbf U_1 + \phi \beta \mathbf U^* \cdot \mathbf U \right.\\ & & \left. + \lambda \Re\left[i\omega \eta + \nabla \cdot \left(H \mathbf U \right) \right] +\, \gamma \Im \left[i\omega \eta + \nabla \cdot \left(H \mathbf U \right) \right] \vphantom{\eta^*_1}\right\} d {\cal V} \nonumber \end{array} $$

where η ₀, U ₀ as the complex tidal surface elevation and barotropic tidal velocity interpolated from the original grid and η ₁, U ₁ are the additive “correction” complex tidal surface elevation and barotropic tidal velocity that minimize $\cal J$,

$$ \eta = \eta_0 + \eta_1 \; ; \quad \mathbf U = \mathbf U_0 + \mathbf U_1 $$

α and β are the weights (including nondimensionalizing factors), λ and γ are the Lagrange multipliers, the superscript ^* indicate complex conjugation, $\Re$ and $\Im$ refer to the real and imaginary parts, and θ, φ are penalty parameters to inhibit unreasonably large total velocities. Using the calculus of variations, the above minimization is equivalent to solving the following system of equations

$$ \begin{array}{rll} \omega \eta_1 - \nabla \cdot \left[ \frac{H^2}{(\theta + \phi) \omega \beta} \nabla \left( \alpha \eta_1 \right) \right] & = & - \omega \eta_0 + i \nabla \notag\\&&\cdot \left( \frac{\theta}{\theta + \phi} H \mathbf U_0 \right) \\ \left. \alpha \right|_{\rm open\ boundary} & = & 0 \\ \left.\left( i \omega \eta_1 + \sqrt{g H} \frac{\partial \eta_1}{\partial n}\right) \right|_{\rm open\ boundary} & = & 0 \\ \mathbf U_1 & = & - \frac{\phi}{\theta + \phi} \mathbf U_0 \nonumber\\&&- i \frac{H}{(\theta + \phi) \omega \beta} \nabla \left(\alpha \eta_1\right) \end{array} $$

Note that the radiation boundary condition does not come from the variations but is a useful addition we are free to make after obtaining α = 0 from the variations.

1.3.2 Appendix 2.3.2: Applying the tidal forcing

We use the barotropic tides both for initialization and for boundary forcing. For the surface elevation, we simply superimpose the tidal surface elevation with the subtidal elevation estimated in “Appendix 2.2.2”. For initialization, this superposition is done over the entire area before the final vertical interpolation of tracers and u ^′. For lateral forcing, this is done at run time in the PE model at the exterior boundaries (and also along two bands inside these boundaries for Perkins et al. (1997) boundary conditions). The resulting boundary values are used to generate Dirichlet boundary conditions for Eq. 43. A similar procedure is used for the barotropic velocities with two notable differences. First, the superposition is performed to preserve transport:

$$ \begin{array}{rll} \left(H + \eta_{\rm superimposed}\right) \mathbf U_{\rm superimposed} &=& \left(H + \eta_{\rm subtidal}\right) \mathbf U_{\rm subtidal}\\ &&+\, H \mathbf U_{\rm tidal} \, . \end{array} $$

Note that the tidal velocity is only multiplied by the undisturbed water depth. This is because we are using a linearized tidal model. The second difference is that the run-time boundary values of the barotropic velocity are used for Eq. 64, not directly applied to the final barotropic velocities.

Nesting considerations

For initialization, the process is as for the unnested case. The superpositions described above are done for the initial conditions of each domain. For the lateral forcing, however, the barotropic tidal fields are only applied at the boundaries of the coarsest domain. The reason being that applying the barotropic tidal fields at the boundary of the coarsest domain can produce the full tidal response in the interior, and hence, the barotropic tidal fields are unnecessary for the nested subdomains.

1.4 Appendix 2.4: Solving the equation for the surface elevation

Equation 43, with Dirichlet boundary conditions, represents an elliptic system of equations for the surface elevation, η. To numerically solve this system, we use a preconditioned conjugate gradient solver for sparse matrices (e.g., SPARSKIT; Saad 2009). A typical convergence test for such an iterative solver is an integrated measure of the reduction in the norm of the residual over all points. Specifically, if r is the residual of the current solver iteration and r ₀ is the residual of the initial guess, the convergence test is

$$\Vert r \Vert \le \tau_r \Vert r_0 \Vert + \tau_a$$

where τ _r is the relative tolerance and τ _a is the absolute tolerance. In practice, we tend to use very small values (10^− 12 and 10^− 25, respectively) to ensure a tight convergence. Using the results of “Appendix 3”, we also supplement this global constraint with the following point-wise constraint:

$$ \begin{array}{rll} \left\vert \frac{\partial \delta\eta^k}{\partial x} - \frac{\partial \delta\eta^{k-1}}{\partial x} \right\vert &\le& \tau^g_r \left\vert \frac{\partial \delta\eta^k}{\partial x} \right\vert + \tau_a \; ; \quad \\ \left\vert \frac{\partial \delta\eta^k}{\partial y} - \frac{\partial \delta\eta^{k-1}}{\partial y} \right\vert &\le& \tau^g_r \left\vert \frac{\partial \delta\eta^k}{\partial y} \right\vert + \tau_a\\ \left\vert \delta\eta^k - \delta\eta^{k-1} \right\vert \le \tau^g_r \left\vert \delta\eta^k \right\vert + \tau_a \end{array} $$

where the superscript k refers to the iteration number and $\tau^g_r$ is the relative tolerance for the gradient test (typically around 10^− 8). Here we test on both δη and its gradients to ensure the relative convergence of the barotropic velocities (Eq. 44).

Since we have discretized our equations on the B-grid, both Eq. 43 and, especially, Eq. 68 possess a well-known checkerboard mode in their null spaces (Deleersnijder and Campin 1995; le Roux et al. 2005; Wubs et al. 2006). For realistic geometries, we found that applying a Shapiro filter (Shapiro 1970) to the solution was sufficient to suppress the noise while maintaining the correct physical features. The one case where this approach failed was in creating an initialization for an idealized flow in a periodic channel. The lack of Dirichlet boundary values in that case and corresponding lack of structure they would have imposed allowed the checkerboard mode to suppress all other structures. To control this error, the matrix in Eq. 68 was augmented with a Laplacian filter (Deleersnijder and Campin 1995; Wickett 1999) to prevent the appearance of this mode. Again, this filter was only needed for the idealized periodic channel flow.

Appendix 3: Review of rigid-lid nesting algorithm

One of our first nesting schemes (see Section 4.1) for the nonlinear free-surface version of the PEs was built by analogy with our two-way nesting scheme (e.g., Spall and Holland 1991; Fox and Maskell 1995; Sloan 1996) for the HOPS rigid-lid formulation of the PEs. We have used this scheme in a variety of dynamical situations (Robinson et al. 2002; Leslie et al. 2008; Haley et al. 2009) and we present it next.

We start with the rigid-lid PEs:

$$ \nabla \cdot \mathbf u + \frac{\partial w}{\partial z} = 0 \, , $$

$$\frac{\partial \mathbf{u^\prime}}{\partial t} + f \hat k \times \mathbf{u^\prime} = \widehat{\cal F} - \overline{\widehat{\cal F}} \, , $$

$$\nabla \times \left( \frac{\hat k}{H} \times \nabla \delta \Psi \right) + \alpha_{\rm RL} \nabla \times \left[ f \, \hat k \times \left( \frac{\hat k}{H} \times \nabla \delta \Psi \right) \right] = \nabla \times \overline{\widehat{\cal F}} \,\, , $$

$$p_h = - \int^0_z \rho g \, d\zeta \, , $$

$$\frac{D T}{D t} = F^T \, , $$

$$\frac{D S}{D t} = F^S \, , $$

$$\rho = \rho (z,T,S) $$

where

$$ \mathbf u = \mathbf{u^\prime} + \mathbf U \; ; \quad \mathbf U = \frac{1}{H} \int^0_{-H} \mathbf u \, dz \; ; \quad H \mathbf U = \hat k \times \nabla \Psi \, , $$

$$ \widehat{\cal F} = -{1 \over \rho_0} \nabla p_h - {\boldsymbol{\Gamma}}(\mathbf u) + \mathbf F \; ; \quad \overline{\widehat{\cal F}} = \frac{1}{H} \int^0_{-H} \widehat{\cal F} \, dz $$

$$ {\boldsymbol \Gamma}(\mathbf u) = \left( \begin{array}{c} \Gamma(u) \\ \Gamma(v)\end{array}\right) \; ; \quad \Gamma(\phi) = u \frac{\partial \phi}{\partial x} + v \frac{\partial \phi}{\partial y} + w \frac{\partial \phi}{\partial z} . $$

Here we have introduced the transport stream function, Ψ, to replace the barotropic velocity as a state variable. Using this notation, we write our rigid-lid nesting algorithm as

• 1. Solve the rigid-lid PEs simultaneously in each domain for (u ^{′ n + 1}, T ^n + 1, S ^n + 1)

• 2. Replace values in the coarse domain at overlap nodes with the following averages from the fine domain values

  $$ \phi^{n+1}_{i_c,j_c,k} = \frac{1}{\Delta {\cal V}_{i_c,j_c}} \sum\limits^{j_{fc}+r_h}_{j=j_{fc}-r_h} \sum\limits^{i_{fc}+r_h}_{i=i_{fc}-r_h} \phi^{n+1}_{i,j,k} \Delta {\cal V}_{i,j,k} \, , $$

  (69)
  $$ \left(\nabla \times \overline{\widehat{\cal F}}\right)_{i_c,j_c} = \frac{1}{\Delta {\cal A}_{i_c,j_c}} \sum\limits^{j_{fc}+r_h}_{j=j_{fc}-r_h} \sum\limits^{i_{fc}+r_h}_{i=i_{fc}-r_h} \left(\nabla \times \overline{\widehat{\cal F}}\right)_{i,j} \Delta {\cal A}_{i,j}\nonumber\\ $$

  (70)

  where r is the ratio of the resolution of the coarse grid to fine grid,

  $$ \begin{array}{lll} &&{\kern-6pt} \phi = \mathbf{u^\prime}, T, S \; ; \quad \Delta {\cal V}_{i,j,k} = \Delta x_{i,j}\Delta y_{i,j} \Delta z_{i,j,k} \; ; \\ &&{\kern-6pt} \Delta {\cal A}_{i,j} = \Delta x_{i,j}\Delta y_{i,j} \; ; \quad r_h = \lfloor r/2\rfloor \; . \end{array} $$

• 3. In the coarse domain, solve the rigid-lid barotropic momentum equation for Ψ^n + 1.

• 4. Using piece-wise bi-cubic Bessel interpolation, $\cal B$, replace values in the fine grid boundary with values interpolated from the coarse grid

  $$ \begin{array}{rll} \phi^{n+1}_{i_{fb},j_{fb},k} &=& {\cal B}\left(\phi^{n+1}_{i_c,j_c,k}\right) \, , \\ \mathbf{u^\prime}^{n+1}_{i_{fb},j_{fb},k} \Delta z_{i_{fb},j_{fb},k} &=& {\cal B}\left(\mathbf{u^\prime}^{n+1}_{i_c,j_c,k} \Delta z_{i_c,j_c,k}\right) \, , \end{array} $$

  where

  $$ \phi = T,\,S,\,\Psi \, . $$

  Note that the interpolation of baroclinic velocity is written in terms of transport rather than velocity. This is done to preserve the baroclinicity of u ^′ in the fine domain.

• 5. In the fine domain, solve the barotropic momentum equation for Ψ^n + 1.

We found that this scheme maintains consistency between the estimates on the coarse and fine grids provided that a sufficiently stringent convergence criterion is used when solving for Ψ^n + 1. Only using a test on the integral of the residuals did not always maintain the consistency. Such a test is global in nature and can give different convergence results in the coarse and fine domains. Instead, we found the best results occurred when we supplemented the residual tests with the following point-wise test:

$$ \left| \frac{\frac{\partial \Psi^{k+1}}{\partial x} - \frac{\partial \Psi^k}{\partial x}} {\frac{\partial \Psi^k}{\partial x}} \right| \le \epsilon \; ; \quad \left| \frac{\frac{\partial \Psi^{k+1}}{\partial y} - \frac{\partial \Psi^k}{\partial y}} {\frac{\partial \Psi^k}{\partial y}} \right| \le \epsilon $$

where here the superscripts k refer to the iteration count in the solver and ϵ is the relative tolerance. We test the derivative of Ψ instead of Ψ so that the convergence is on the relative change in the transport, a physically more meaningful quantity than Ψ itself. This test ensures that in both domains the iterative solution proceeds at least until the specified tolerance is reached at every point, thereby ensuring at least that level of consistency between the solutions in the coarse and fine domains.