Efficient Numerical Computations of Long-Wave Run-Up and Their Sensitivity to Grid Nesting

Abstract

Computation of long-wave run-up has been of high interest in the fields of ocean sciences and geophysics—particularly for tsunami and river flood modeling. An accurate calculation of run-up and inundation requires the numerical model to account for a sequence of critical processes—each of them posing a different challenge to the numerical solution. This study presents the strategic development of a numerical solution technique for shallow water equations with a focus on accuracy and efficiency for long-wave run-up. The present model is based on an explicit second-order finite-volume scheme over a staggered grid that efficiently achieves fundamental properties. The scheme is well-balanced and preserves shock fronts without the need for computationally expensive solvers. The streamlined code serves as a foundation for the implementation of nested grids. Computations of commonly used long-wave benchmark tests showcase that accurate predictions of local extreme run-up can often be achieved with highly refined yet spatially focused nested grids. Strategic grid nesting can lead to stable and accurate solutions of run-up at locations of interest and reduce the computational load to a fraction of what is usually necessary for a comparable solution over a single grid.

1 Introduction

The estimation of run-up from long waves is crucial for the assessment and prediction of hazardous flooding scenarios associated with tsunamis and storm surges. As wave run-up is the final stage a water wave undergoes when it reaches the shore, it depends on multiple processes such as wave transformation, breaking, and interaction with dry land. Consequently, a substantial and continuous effort has been made to better understand and compute the run-up processes of long waves [1]. This includes studies with respect to the derivation of analytical solutions for simplified geometries (e.g., [2,3,4,5]), laboratory experiments (e.g., [6,7,8]), and development of new numerical methods (e.g., [9, 10]). The latter provides approximate yet valid run-up solutions in more general settings suitable for the reconstruction of past events, forecasting, and practical engineering applications.

Numerical models for long waves, such as tides, storm surges, and tsunamis, have traditionally been based on shallow-water equations (SWE). Despite their simplistic hydrostatic assumptions, the SWE provide a valid basis for many long-wave problems and are often preferred over more complete equations thanks to their hyperbolic nature in which shocks can form as part of the solution. These depth-averaged equations have proven to give a reasonable balance between the accuracy and numerical cost [11] and serve by far as the most commonly used baseline for run-up calculations (e.g., [12,13,14]). Various numerical techniques have been proposed for the discretization of the SWE, ranging from conventional mesh-based methods such as finite difference (FD), finite volume (FV), or finite element (FE) to unconventional mesh-free methods such as smooth particle hydrodynamics (SPH) [15]. The numerical solutions of SWE have been subject to many trends. Earlier solutions were based on traditional FD schemes solved on a staggered grid [16]. This approach has been successfully employed in many first-generation tsunami models (e.g., TUNAMI [17], COMCOT [18]). Several wetting–drying techniques have been proposed to achieve a reasonable representation of the run-up heights. Shuto and Goto [19] used a staggered scheme with a Lagrangian description for the moving boundaries. Another approach has been based on the Neumann-type technique, which has been used to extrapolate the velocity at the wet-dry fronts [20], while Liu et al. [21] modeled the run-up based on water-level changes through flooding and drying of the cells.

FD methods offer a simplified solution for hyperbolic equations. However, they are known to exhibit deficiencies when dealing with flow discontinuities [22, 23], which particularly require local conservation of both mass and momentum. These conservation properties are necessary for the transport of breaking waves toward the shore and, hence, are important for the accuracy of the run-up computation. FV methods, on the other hand, solve the integral form of the SWE and directly benefit from conservation and shock-capturing capabilities. For this reason, FV methods such as Godunov [24], and Roe [25] solvers, which were previously used in gas dynamics, have become increasingly popular for the solution of long-wave problems. A new generation of tsunami and flooding models has been developed [26,27,28,29] based on a finite-volume interpretation of the equations, where the in-going and out-going fluxes over a control volume are computed with approximate Riemann solvers (e.g., [30,31,32]). These solvers are designed to preserve the hyperbolicity of the governing equations to allow for the formation of discontinuities in the numerical system. However, hyperbolicity can be a source of problems for the solution of the SWE. One drawback of this property is the well-balance between flux gradient, and source terms [33]. This means that models based on the FV approach often require computationally expensive techniques to ensure the scheme is well-balanced—especially in the presence of dry cells [22, 34,35,36,37,38]. With respect to run-up and as a way to deal with the numerical problems of the moving shoreline, many FV schemes employ an artificial bed-wetting algorithm. These work through the definition of a minimum value of the water depth in the dry cells adjacent to the wet cells for computation of the numerical flux [37, 39]. Another difficulty for these schemes lies in the conservation of the non-negativity of the water depth—especially in the case of run-down [40]. Nevertheless, several operational models such as FUNWAVE ([41], COULWAVE [42], and BOSZ ([43]) successfully utilize these schemes.

Another approach for solving the SWE is linked to the use of conservative staggered schemes. These methods benefit from the efficiency and robustness of the FD approximations while achieving conservative and shock-capturing properties. Such schemes have been successfully applied to flows at high Froude numbers, including hydraulic jumps and inundation of dry areas (e.g., [44,45,46,47,48]). These schemes are based on specific FD approximations, which satisfy the Rankine–Hugoniot jump condition at a discrete level [33], and achieve valid solutions for rapidly varying flows. The concept from [45] has been widely used in many operational wave and run-up models (e.g., SWASH [49], NEOWAVE [50] and Xbeach [51]). This scheme guarantees the positivity of the water depth under the standard Courant–Friedrichs–Lewy (CFL) condition and, therefore, is very efficient for the computation of large-scale inundation problems.

The design of the numerical solutions of long-wave run-up requires taking the multi-scale nature of the problem into account, i.e., large-scale long-wave propagation in combination with the small-scale run-up and inundation processes. High spatial resolution is necessary for a detailed representation of the run-up process. However, computing a high-resolution grid over the entire domain is often unnecessarily expensive and can hinder the applicability of the model to real problems. With the objective of achieving efficient long-wave run-up computations, it is, therefore, desirable to utilize different grid sizes—each appropriate for the particular problems in the propagation and the run-up stages. Different approaches have been used to obtain local mesh refinement. For example, traditional nested grid methods have been implemented in tsunami models [17, 18, 52]. These techniques are usually built into structured grids where the refinement arises from the insertion of a sub-grid with higher resolution. The exchange of information between the grids is achieved either with one-way or two-way interactions. On the other hand, for unstructured grids, an adaptive mesh refinement technique has been successfully implemented in a number of long-wave models (e.g., [26, 53, 54]). The adaptive mesh refinement generates locally refined cells adapted to the flow condition without the need to use fixed sub-grid [55]. The refined region is, therefore, able to move with the area of interest, and unnecessary refinement is avoided. The disadvantage of these methods lies mainly in the complexity of the grid generation techniques, which require intensive data storage. In addition, the time step constraint is bound to the smallest grid cell that can hinder the efficiency of the implementation for explicit schemes [56].

This paper presents the rigorous development of a stable and accurate numerical framework for the computation of long-wave run-up. We address the details of the numerical scheme and outline the strategy for grid nesting to achieve a fast and low-cost numerical tool for run-up computations. The model is based on a conservative staggered scheme in which the shock-capturing capabilities are achieved by satisfying the Rankine–Hugoniot at a discrete level. The scheme avoids the splitting of the free surface gradient into a pressure flux and topography term, resulting in direct non-negativity preserving and well-balanced computations. The verification process checks off the fundamental properties necessary for the computation of run-up: shock-capturing capabilities, moving boundaries with bottom friction, and exchange of information across nested grids. Two standard tsunami benchmark datasets are then employed to demonstrate the sensitivity of long-wave run-up to the overall grid resolution as well as to the extent of the nested grid and the refinement factor.

2 Methodology

2.1 Governing Equations

The present study considers the two-dimensional, depth-averaged Shallow Water equations (SWE). These equations provide a powerful baseline for long-wave modeling thanks to their wave-like hyperbolic structure. Moreover, the SWE serve as the backbone for many numerical models that address nearshore wave propagation and inundation. This is the case for dispersive Boussinesq-type and non-hydrostatic models in which the governing equations contain the SWE as a subset.

The SWE are derived from the Navier–stokes equations under the following assumptions: (a) the pressure is hydrostatic, and (b) the vertical distribution of the horizontal velocity is uniform (no variation). Under these assumptions, the equations take the following differential form in Cartesian coordinates:

$$\begin{aligned}{} & {} \frac{\partial h}{\partial t} + \frac{\partial hu}{\partial x} + \frac{\partial hv}{\partial y} = 0 \end{aligned}$$

(1)

$$\begin{aligned}{} & {} \frac{\partial hu}{\partial t} + \frac{\partial hu^2}{\partial x} + \frac{\partial huv }{\partial y} + gh \frac{\partial \eta }{\partial x} = - g n^2 \frac{u\sqrt{u^2 + v^2}}{h^{1/3}} \end{aligned}$$

(2)

$$\begin{aligned}{} & {} \frac{\partial hv}{\partial t} + \frac{\partial huv }{\partial x} + \frac{\partial hv^2}{\partial y} + gh \frac{\partial \eta }{\partial y} = - g n^2 \frac{v \sqrt{u^2 + v^2}}{h^{1/3}} \end{aligned}$$

(3)

We define t as the time variable, x and y are the space variables, h is the water depth, u and v are the depth-averaged velocities in the x- and y-directions, respectively. $\eta$ refers to the free surface elevation: $\eta \left( x, y, t \right) = h \left( x, y, t \right) - d \left( x,y \right)$, where d is the positive bottom topography (Fig. 1). The constant g is the gravitational acceleration and n is the Manning roughness coefficient [s m$^{-1/3}$].

Fig. 1

Definition sketch for the free surface flow problem with key variables

We write the SWE, Eqs. (1)–(3) in a conservative form to ensure the conservation of mass and momentum across discontinuities. The conserved variables, in this case, are the total water depth h and its product with the velocity components: hu and hv. In this form of the equations, we avoid the splitting of the free surface gradient into an artificial flux gradient and a source term that includes the effect of bed slope. The free surface gradient is, therefore, computed independently of the numerical flux, and no additional treatments are required to ensure that the scheme is well-balanced. The preservation of shocks and discontinuities will consequently depend on the numerical approximations of the scheme, which have to satisfy the Rankine–Hugoniot jump condition at the discrete level [33].

We introduce the auxiliary variables p and q, which denote the mass fluxes:

$$\begin{aligned} p=hu \quad \mathrm {\,\,\,\,\,\,\,}\quad q=hv \end{aligned}$$

(4)

We rewrite the SWE in the following form:

$$\begin{aligned}{} & {} \frac{\partial h}{\partial t} + \frac{\partial p}{\partial x} + \frac{\partial q}{\partial y} = 0 \end{aligned}$$

(5)

$$\begin{aligned}{} & {} \frac{\partial hu}{\partial t} + \frac{\partial pu}{\partial x} + \frac{\partial qu }{\partial y} + gh \frac{\partial \eta }{\partial x} = - g n^2 \frac{u\sqrt{u^2 + v^2}}{h^{1/3}} \end{aligned}$$

(6)

$$\begin{aligned}{} & {} \frac{\partial hv}{\partial t} + \frac{\partial pv}{\partial x} + \frac{\partial qv}{\partial y} + gh \frac{\partial \eta }{\partial y} = - g n^2 \frac{v \sqrt{u^2 + v^2}}{h^{1/3}} \end{aligned}$$

(7)

It is worth mentioning that in the momentum equations Eqs. (6) and (7), the variables hu and hv in the local acceleration and the variables p and q in the convective acceleration play different roles. The former is a storage quantity, while the latter is a transport quantity. Consequently, these terms are approximated differently, and in order to avoid confusion, we avoid using the same symbols.

2.2 Conservative Staggered Scheme

As detailed in the introduction, a variety of numerical schemes have previously been developed for the solution of the SWE. The choice of the numerical scheme depends mainly on the problem being addressed, which defines the requirements for the scheme properties. For the computation of long-wave run-up, a conservative shock-capturing scheme is crucial for the preservation of momentum and propagation of shocks at the correct speed and height. Other important properties are the well-balanced approximations of the topography variations, along with the non-negativity of the water depth to ensure mass conservation across wet/dry transitions without parasitic waves. This adds to the stability and robustness of the numerical model—particularly over irregular bathymetry. Consequently, a scheme that provides these features is suitable for computing wave-breaking processes and, subsequently, wave run-up estimations.

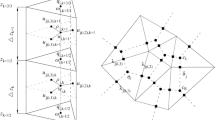
In this study, the objective is to develop a lightweight yet accurate and stable solution structure that keeps the computational expenses at a low level. For these reasons, we utilize a conservative scheme on a staggered grid where the numerical fluxes are computed with simple FD approximations instead of Riemann solvers. The SWE variables, in this case, are approximated on a staggered C-grid: the total water depth h and the bed topography d are defined at the cell center, and the depth-averaged velocities $\left( u,v \right)$ are stored at the cell interfaces (see Fig. 2).

For the discretization, we consider a 2D rectangular computational domain with a uniform grid spacing of $\Delta x$ and $\Delta y$ in the x- and y-directions, respectively. The variables stored at the cell center are expressed as $x_{i,j}$, where i and j are the spatial indices in the x- and y-directions. The variables stored at the cell interface are denoted by $x_{i \pm \frac{1}{2},j}$ or $x_{i,j \pm \frac{1}{2}}$ in the x- and y-directions, respectively. The time stepping is based on discrete, non-uniform time intervals $t^n = n \Delta t$, where n is the time index and $\Delta t$ is the adaptive time step. The value of each variable a at the time level $t^n$ is denoted with $a^n$. The water depth h is evaluated at each time step level $t=n \Delta t$, whereas, the depth-averaged velocities u and v are evaluated halfway between the present and the following time step $t = \left( n+\frac{1}{2} \right) \Delta t$. This leads to the staggering of spatial and temporal information and facilitates consistent second-order accuracy in space and time.

Fig. 2

Schematic of the 2D staggered grid

The present scheme first requires the solution of the continuity equation, which is subsequently used in the momentum equation. The discretization of the continuity equation, Eq. (5), is expressed as

$$\begin{aligned} \frac{h_{i,j}^{n+1} - h_{i,j}^{n}}{\Delta t} + \frac{ p_{i+\frac{1}{2},j}^{n} - p_{i-\frac{1}{2},j}^{n}}{\Delta x} + \frac{q_{i,j+\frac{1}{2}}^{n} - q_{i,j-\frac{1}{2}}^{n}}{\Delta y} = 0 \end{aligned}$$

(8)

where

$$\begin{aligned} p_{i+\frac{1}{2},j}^n = {\hat{h}}_{i+\frac{1}{2},j}^{n} u_{i+\frac{1}{2},j}^{n+\frac{1}{2}} \quad \mathrm {\,\,\,\,\,\,\,}\quad q_{i,j+\frac{1}{2}}^n = {\hat{h}}_{i,j+\frac{1}{2}}^{n} v_{i,j+\frac{1}{2}}^{n+\frac{1}{2}} \end{aligned}$$

(9)

${\hat{h}}_{i \pm \frac{1}{2},j}^{n}$ and ${\hat{h}}_{i,j \pm \frac{1}{2}}^{n}$ are the water depths at the cell interfaces computed with an upwind approximation:

$$\begin{aligned} {\hat{h}}_{i+\frac{1}{2},j}^{n} = {\left\{ \begin{array}{ll} h_{i,j}^{n} &{} \text {if}\ u_{i+\frac{1}{2},j}^{n+\frac{1}{2}} \ge 0 \\ h_{i+1,j}^{n} &{} \text {if}\ u_{i+\frac{1}{2},j}^{n+\frac{1}{2}}< 0 \end{array}\right. } \quad \mathrm {\,\,\,\,\,\,\,}\quad {\hat{h}}_{i,j+\frac{1}{2}}^{n} = {\left\{ \begin{array}{ll} h_{i,j}^{n} &{} \text {if}\ v_{i,j+\frac{1}{2}}^{n+\frac{1}{2}} \ge 0 \\ h_{i,j+1}^{n} &{} \text {if}\ v_{i,j+\frac{1}{2}}^{n+\frac{1}{2}} < 0 \end{array}\right. } \end{aligned}$$

(10)

The next step is the solution of the momentum equation, Eq. (6). First, we consider the momentum equation without the friction term; the approximation of this term will be detailed later. We employ the FD approximations recommended in Zijlema [33] to achieve conservation of the momentum flux across discontinuities, as

$$\begin{aligned} \begin{aligned}&\frac{{{\bar{h}}}_{i + \frac{1}{2},j}^{n+1} u_{i +\frac{1}{2},j}^{n+\frac{3}{2}} - {{\bar{h}}}_{i+\frac{1}{2},j}^{n} u_{i+\frac{1}{2},j}^{n+\frac{1}{2}}}{\Delta t} + \frac{{\hat{u}}_{i+1,j}^{n+\frac{1}{2}} {\bar{p}}_{i+1,j}^{n} - {\hat{u}}_{i,j}^{n+\frac{1}{2}} {\bar{p}}_{i,j}^{n}}{\Delta x}\\&\qquad + \frac{{\hat{u}}_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}} {\bar{q}}_{i+\frac{1}{2},j+\frac{1}{2}}^{n} - {\hat{u}}_{i+\frac{1}{2},j-\frac{1}{2}}^{n+\frac{1}{2}} {\bar{q}}_{i+\frac{1}{2},j-\frac{1}{2}}^{n} }{\Delta y}\\&\quad = - g {{\bar{h}}}_{i+\frac{1}{2},j}^{n+1} \frac{ \eta _{i+1,j}^{n+1} - \eta _{i,j}^{n+1} }{\Delta x} \end{aligned} \end{aligned}$$

(11)

Regarding the free surface gradient term, the use of the updated variable ${{\bar{h}}}_{i+\frac{1}{2},j}^{n+1}$ is necessary for the scheme to guarantee the entropy inequality as demonstrated in Doyen and Gunawan [47]. Further, it is necessary to approximate the convective acceleration with an upwind scheme, where the mass fluxes p and q are the criteria for upwinding and the velocities u and v are the upwinded quantities:

$$\begin{aligned} {\hat{u}}_{i,j}^{n+\frac{1}{2}} = {\left\{ \begin{array}{ll} u_{i-\frac{1}{2},j}^{n+\frac{1}{2}} &{} \text {if}\ {\bar{p}}_{i,j}^{n} \ge 0 \\ u_{i+\frac{1}{2},j}^{n+\frac{1}{2}} &{} \text {if}\ {\bar{p}}_{i,j}^{n}< 0 \end{array}\right. } \quad \mathrm {\,\,\,\,\,\,\,} {\hat{u}}_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}} = {\left\{ \begin{array}{ll} u_{i+\frac{1}{2},j}^{n+\frac{1}{2}} &{} \text {if}\ {\bar{q}}_{i+\frac{1}{2},j+\frac{1}{2}}^{n} \ge 0 \\ u_{i+\frac{1}{2},j+1}^{n+\frac{1}{2}} &{} \text {if}\ {\bar{q}}_{i+\frac{1}{2},j+\frac{1}{2}}^{n} < 0 \end{array}\right. }\qquad \end{aligned}$$

(12)

It is important to note, that a reversed approach where the upwinded quantities are p and q, leads to errors in the computation of the momentum fluxes across discontinuities as demonstrated in Zijlema [33].

Since the mass fluxes p and q are continuous quantities, an averaged approximation of these quantities can be applied in the computation of the convective acceleration terms:

$$\begin{aligned} {{\bar{p}}}_{i,j}^n = \frac{1}{2}\left( p_{i+\frac{1}{2},j}^{n} + p_{i-\frac{1}{2},j}^{n} \right) \quad \mathrm {\,\,\,\,\,\,\,}\quad {\bar{q}}_{i+\frac{1}{2},j+\frac{1}{2}}^{n} = \frac{1}{2}\left( {q}_{i,j+\frac{1}{2}}^{n} + {q}_{i+1,j+\frac{1}{2}}^{n} \right) \end{aligned}$$

(13)

The flow depth, originally defined at the cell centroid, is approximated at the cell interface with arithmetic averaging to be used in the computation of the local acceleration:

$$\begin{aligned} {{\bar{h}}}_{i+\frac{1}{2},j}^{n+1} = \frac{1}{2}\left( h_{i,j}^{n+1} + h_{i+1,j}^{n+1} \right) \end{aligned}$$

(14)

Finally, the momentum equation, Eq. (7), in the y-direction is solved in an analogous way as

$$\begin{aligned} \begin{aligned}&\frac{{{\bar{h}}}_{i,j+ \frac{1}{2}}^{n+1} v_{i,j+ \frac{1}{2}}^{n+\frac{3}{2}} - {{\bar{h}}}_{i,j+\frac{1}{2}}^{n} v_{i,j+\frac{1}{2}}^{n+\frac{1}{2}}}{\Delta t} + \frac{{\hat{v}}_{i,j+1}^{n+\frac{1}{2}} {\bar{q}}_{i,j+1}^{n} - {\hat{v}}_{i,j}^{n+\frac{1}{2}} {\bar{q}}_{i,j}^{n}}{\Delta y} \\&\qquad + \frac{{\hat{v}}_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}} {\bar{p}}_{i+\frac{1}{2},j+\frac{1}{2}}^{n} - {\hat{v}}_{i-\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}} {\bar{p}}_{i-\frac{1}{2},j+\frac{1}{2}}^{n} }{\Delta x}\\&\quad = - g {{\bar{h}}}_{i,j+\frac{1}{2}}^{n+1} \frac{ \eta _{i,j+1}^{n+1} - \eta _{i,j}^{n+1} }{\Delta y} \end{aligned} \end{aligned}$$

(15)

where

$$\begin{aligned} {\hat{v}}_{i,j}^{n+\frac{1}{2}} = {\left\{ \begin{array}{ll} v_{i,j-\frac{1}{2}}^{n+\frac{1}{2}} &{} \text {if}\ {\bar{q}}_{i,j}^{n} \ge 0 \\ v_{i,j+\frac{1}{2}}^{n+\frac{1}{2}} &{} \text {if}\ {\bar{q}}_{i,j}^{n}< 0 \end{array}\right. } \quad \mathrm {\,\,\,\,\,\,\,}\quad {\hat{v}}_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}} = {\left\{ \begin{array}{ll} v_{i,j+\frac{1}{2}}^{n+\frac{1}{2}} &{} \text {if}\ {\bar{p}}_{i+\frac{1}{2},j+\frac{1}{2}}^{n} \ge 0 \\ v_{i+1,j+\frac{1}{2}}^{n+\frac{1}{2}} &{} \text {if}\ {\bar{p}}_{i+\frac{1}{2},j+\frac{1}{2}}^{n\frac{1}{2}} < 0 \end{array}\right. } \end{aligned}$$

(16)

and

$$\begin{aligned} {{\bar{q}}}_{i,j}^n = \frac{1}{2}\left( q_{i,j+\frac{1}{2}}^{n} + q_{i,j-\frac{1}{2}}^{n} \right) \quad \mathrm {\,\,\,\,\,\,\,} {{\bar{p}}}_{i+\frac{1}{2},j+\frac{1}{2}}^n = \frac{1}{2}\left( p_{i+\frac{1}{2},j+1}^{n} + p_{i+\frac{1}{2},j}^{n} \right) \end{aligned}$$

(17)

The flow depth in this case is approximated as

$$\begin{aligned} {{\bar{h}}}_{i,j+\frac{1}{2}}^{n+1} = \frac{1}{2}\left( h_{i,j}^{n+1} + h_{i,j+1}^{n+1} \right) \end{aligned}$$

(18)

2.2.1 Second-Order Numerical Accuracy

Staggering of the variables both in space and time and utilization of the Leapfrog scheme lead to second-order accuracy for both the continuity and the momentum equations, except for the advection terms, [45, 49]. The flux terms are responsible for transporting the conserved quantities, and consequently, the construction of the advection terms with upwind differencing is necessary for the robustness and stability of the computed solution. However, first-order upwind methods are diffusive, and it is, therefore, useful to target second-order accuracy for all terms in the equations. One way to counter unnecessary numerical dissipation is based on extending the upwind scheme to the second order in combination with a slope limiter.

The approximations in Eqs. (10), (12), (16), and (17) can be improved by including two neighboring data points instead of only one, as is the case in the first-order upwind approach. The second-order upwind discretization is shown for Eq. (10) and applied to Eqs. (12), (16), and (17) in the same way:

$$\begin{aligned} {\hat{h}}_{i+\frac{1}{2},j}^{n} = {\left\{ \begin{array}{ll} h_{i,j}^{n} + \frac{1}{2}\psi \left( r_{i+\frac{1}{2},j}^{+} \right) \left( h_{i,j}^{n} - h_{i-1,j}^{n} \right) , &{} \text {if}\ u_{i+\frac{1}{2},j}^{n} \ge 0 \\ h_{i+1,j}^{n} + \frac{1}{2}\psi \left( r_{i+\frac{1}{2},j}^{-} \right) \left( h_{i+1,j}^{n} - h_{i+2,j}^{n} \right) , &{} \text {if}\ u_{i+\frac{1}{2},j}^{n} < 0 \end{array}\right. } \end{aligned}$$

(19)

$r_{i+\frac{1}{2},j}^{+}$ and $r_{i+\frac{1}{2},j}^{-}$ are, respectively, the left and right gradients of the flow depth:

$$\begin{aligned} r_{i+\frac{1}{2},j}^{+} = \frac{h_{i+1,j}^{n} - h_{i,j}^{n}}{h_{i,j}^{n} - h_{i-1,j}^{n}} \quad \textrm{,}\quad r_{i+\frac{1}{2},j}^{-} = \frac{h_{i+1,j}^{n} - h_{i,j}^{n}}{h_{i+2,j}^{n} - h_{i+1,j}^{n}} \end{aligned}$$

(20)

$\psi (r)$ is the slope limiter function, which locally reduces the solution from second to first order. The slope limiter is necessary to ensure the stability of the second-order upwind scheme at locations with opposite slopes, zero gradients, or sharp transitions. Here, a Generalized MinMod slope limiter is used:

$$\begin{aligned} \phi \left( r, \theta \right) = \max \left( 0, \min \left( \theta r, \frac{1 + r}{2}, \theta \right) \right) \end{aligned}$$

(21)

$\theta$ is a parameter that controls the diffusivity. The generalized MinMod limiter is most dissipative for $\theta =1$ when it reduces to the traditional MinMod limiter, and it is least diffusive for $\theta = 2$.

A predictor–corrector method can be used to improve the temporal accuracy of the advection terms to retain second-order accuracy in time. Here, we employ the Total Variation Diminishing (TVD) Runge–Kutta method. This method enhances the accuracy of the scheme in time while maintaining the strong stability property of the first-order Euler integration [57]. It is worth mentioning that other time integration methods can be combined with the above-described spatial discretization. For example, [49] used a MacCormack approach for the second-order integration in time.

We split the SWE equations into a convective acceleration term ${\mathscr {F}}$ and a free surface gradient term ${\mathscr {G}}$, which simplifies the description of the multi-step method:

$$\begin{aligned} \frac{\partial U}{\partial t} + {\mathscr {F}} \left( U \right) + {\mathscr {G}} \left( U \right) = 0 \end{aligned}$$

(22)

where

$$\begin{aligned} U = \left[ \begin{array}{c} h \\ hu\\ hv\end{array} \right] \quad \mathrm {\,\,\,\,\,\,\,}\quad {\mathscr {F}} \left( U \right) = \left[ \begin{array}{c} \frac{\partial p}{\partial x} + \frac{\partial q}{\partial y} \\ \frac{\partial pu}{\partial x} + \frac{\partial qu }{\partial y} \\ \frac{\partial pv}{\partial x} + \frac{\partial qv}{\partial y}\end{array} \right] \quad \mathrm {\,\,\,\,\,\,\,}\quad {\mathscr {G}} \left( U \right) = \left[ \begin{array}{c} 0 \\ gh \frac{\partial \eta }{\partial x}\\ gh \frac{\partial \eta }{\partial y} \end{array} \right] \end{aligned}$$

(23)

The discretization described in Eqs. (8), (11), and (15) can be summarized in the following expression:

$$\begin{aligned} U_{ij}^{n+1} = U_{ij}^{n} - \Delta t {\mathscr {F}} \left( U_{ij}^{n} \right) - \Delta t {\mathscr {G}} \left( U_{ij}^{n+1} \right) \end{aligned}$$

(24)

where

$$\begin{aligned} U_{ij}^{n} = \left[ \begin{array}{c} h_{ij}^{n} \\ {{\bar{h}}}_{i+\frac{1}{2},j}^{n} u_{i+\frac{1}{2},j}^{n+\frac{1}{2}} \\ {{\bar{h}}}_{i,j+\frac{1}{2}}^{n} v_{i,j+\frac{1}{2}}^{n+\frac{1}{2}} \end{array} \right] \end{aligned}$$

(25)

At each time step, the variables $\left( h,hu,hv\right)$ are solved using a two-stage time integration with an intermediate solution obtained by the predictor step. In the first step, we solve the equations with only the advection terms on the right-hand side:

$$\begin{aligned} U_{ij}^{*} = U_{ij}^{n} - \Delta t {\mathscr {F}} \left( U_{ij}^{n} \right) \end{aligned}$$

(26)

This leads to a predictor solution of first-order accuracy for the complete continuity equation and incomplete momentum equations due to the lack of source terms. In the second step, the surface gradient terms are added to the momentum equations, and the predicted variables are corrected to full second-order accuracy in time by

$$\begin{aligned} U_{ij}^{n+1} =\frac{\Delta t}{2} \left( U_{ij}^{n} + U_{ij}^{*} \right) - \frac{\Delta t}{2} {\mathscr {F}} \left( U_{ij}^{*} \right) - \Delta t {\mathscr {G}} \left( U_{ij}^{n+1} \right) \end{aligned}$$

(27)

It is important to emphasize that the predictor step of the time integration should only involve the convective acceleration terms. The source terms attain second-order accuracy by staggering the flow speed variables in time, and an application of Eq. (26) to the source terms would lead to inaccurate results.

The last term on the right-hand side of Eq. (27) applies only to the momentum equations and involves the corrected flow depth value $h^{n+1}$. This completes the fully explicit time integration where no system of equations with data dependencies has to be solved.

2.2.2 Flooding and Drying

The wetting and drying process requires the model’s performance for two fundamental processes. The scheme has to be well-balanced and has to preserve the positivity of the water depth across wet/dry boundaries.

The model is based on an explicit time integration. Although implicit methods lead to unconditionally stable computations with no restriction on the time step, their solution is admittedly complex and requires the solution of systems of equations [58,59,60]. This solution structure can pose a bottleneck, especially in parallelized implementations due to data dependencies.

The explicit scheme is stable under the Courant–Friedrichs–Lewy (CFL) condition given by

$$\begin{aligned} Cr = \Delta t \max \left( \frac{|u_{i + \frac{1}{2},j}^{n+ \frac{1}{2}}| + \sqrt{g{\hat{h}}_{i + \frac{1}{2},j}^{n}}}{\Delta x} , \frac{|v_{i,j+ \frac{1}{2}}^{n+ \frac{1}{2}}| + \sqrt{g{\hat{h}}_{i ,j+ \frac{1}{2}}^{n}}}{\Delta y} \right) <1 \end{aligned}$$

(28)

Under this condition, the scheme preserves the non-negativity of the water depth [33, 61]. This has the advantage that the run-up and inundation limits are inherent solutions of the numerical scheme and are not subject to additional ad-hoc flooding and drying treatments or require particular restructuring of the flux and source terms.

Since the flow depth can become arbitrarily small at the wet-dry transitions and, therefore, can lead to excessively high-velocity values, it makes sense to limit the minimum flow depth at the run-up front to a physically and numerically meaningful level. For efficiency reasons, the velocity values can be set to zero when the local water level falls below a threshold value $h_{\min }$, and the calculation of the momentum equations can be skipped:

$$\begin{aligned}{} & {} u_{i+\frac{1}{2},j}^{n+\frac{3}{2}} = 0 \quad \mathrm {\,\,\,\,}\quad \text {if} \quad \mathrm {\,}\quad \frac{h_{i,j}^{n+1} + h_{i+1,j}^{n+1}}{2} < h_{\min } \end{aligned}$$

(29)

$$\begin{aligned}{} & {} v_{i,j+\frac{1}{2}}^{n+\frac{3}{2}} = 0 \quad \mathrm {\,\,\,\,}\quad \text {if} \quad \mathrm {\,}\quad \frac{h_{i,j}^{n+1} + h_{i,j+1}^{n+1}}{2} < h_{\min } \end{aligned}$$

(30)

The value of $h_{\min }$ should be chosen as small as possible to accurately resolve the wet-dry front [37], but large enough to avoid physically questionable values in the local flow speed, which can cause excessively small time steps as shown in Eq. (28). It should be noted that the present scheme is not particularly sensitive to this threshold, and values between $10^{-8}$ and $10^{-4}$ m lead to virtually identical results. For the sake of quality verification and validation, we are using $h_{\min }$ = $10^{-8}$ m in the subsequent examples.

2.2.3 Friction Term

The friction terms added to the momentum equations are discretized as

$$\begin{aligned} g n^2 \frac{u_{i+\frac{1}{2},j}^{n+\frac{3}{2}} \sqrt{ \left( u_{i+\frac{1}{2},j}^{n+\frac{1}{2}} \right) ^2 + \left( {{\bar{v}}}_{i+\frac{1}{2},j}^{n+\frac{1}{2}} \right) ^2}}{\left( {{{\bar{h}}}_{i+\frac{1}{2},j}^{n+1}} \right) ^{1/3}} \quad \textrm{and}\quad g n^2 \frac{v_{i,j+\frac{1}{2}}^{n+\frac{3}{2}} \sqrt{ \left( {{\bar{u}}}_{i,j+\frac{1}{2}}^{n+\frac{1}{2}} \right) ^2 + \left( v_{i,j+\frac{1}{2}}^{n+\frac{1}{2}} \right) ^2}}{\left( {{{\bar{h}}}_{i,j+\frac{1}{2}}^{n+1}} \right) ^{1/3}}\nonumber \\ \end{aligned}$$

(31)

where

$$\begin{aligned} \begin{aligned} {{\bar{v}}}_{i+\frac{1}{2},j}^{n+\frac{1}{2}}&= \frac{1}{4} \left( v_{i,j-\frac{1}{2}}^{n+\frac{1}{2}} + v_{i,j+\frac{1}{2}}^{n+\frac{1}{2}} + v_{i+1,j-\frac{1}{2}}^{n+\frac{1}{2}} + v_{i+1,j+\frac{1}{2}}^{n+\frac{1}{2}} \right) \\ {{\bar{u}}}_{i,j+\frac{1}{2}}^{n+\frac{1}{2}}&= \frac{1}{4} \left( u_{i-\frac{1}{2},j}^{n+\frac{1}{2}} + u_{i+\frac{1}{2},j}^{n+\frac{1}{2}} + u_{i-\frac{1}{2},j+1}^{n+\frac{1}{2}} + u_{i+\frac{1}{2},j+1}^{n+\frac{1}{2}} \right) \end{aligned} \end{aligned}$$

(32)

and n, with units [s m$^{-1/3}$], is the Manning roughness coefficient representing the bottom property. Using the variables $\left( h_{i,j+\frac{1}{2}}^{n+1}, u_{i+\frac{1}{2},j}^{n+\frac{3}{2}} , v_{i+\frac{1}{2},j}^{n+\frac{3}{2}} \right)$ from the next time step in the friction terms improves the accuracy and the robustness of the solution [49].

Some of the following numerical tests, presented in Sect. 3, are computed with the Darcy–Weisbach formulation, which requires replacement of the term $\frac{gn^2}{h^{1/3}}$ by $\frac{f}{8}$. f is the dimensionless Darcy–Weisbach coefficient.

2.3 Nested Grid Method

The accuracy and applicability of a numerical model for free surface flows can substantially benefit from an efficient mesh refinement technique. Here, we concentrate on the nested grid method, which provides a reasonable trade-off between computational complexity and the gain in accuracy of the numerical solution for long-wave run-up. A simplified approach for mesh refinement involves the insertion of a high-resolution Child grid into a surrounding Parent grid of coarser resolution. The grids are herein fixed in space and predefined before the computation is executed. The SWE are solved independently in each grid. Consequently, the overall solution structure of the governing equations remains untouched as the exchange between the grids only requires interpolation of the key variables.

The staggered C-grid has been widely used in combination with embedded grid models due to its simplicity and conservative properties [56, 62, 63]. In this study, we build the nested grid approach on some of the techniques used and validated by several previously developed tsunami models [17, 18]. Several features are expected from a functioning grid nesting technique:

Data exchange The exchange of information between the grids occurs along the boundary of the inner grid. The Parent grid provides the boundary conditions to the Child grid in a one-way interaction. The flux variables (i.e., hu and hv) from the coarse grid are linearly interpolated in time and space and then dynamically imposed in each time step as boundary conditions to the solution of the Child grid (see Fig. 3). For a two-way interaction, the high-resolution free surface elevation from the Child grid is used to update the information in the Parent grid via an averaging operator. The update of the free surface only occurs inside the feedback interface in the Parent grid (see Fig. 3), rather than in the domain occupied by the Child grid. Several authors have proposed separating the feedback interface from the dynamic interface where the boundary values are interpolated [64,65,66]. This separation helps to avoid inconsistencies between the solutions and stability problems that often arise from forcing the solution of the Parent grid with the updated values of the inner grid [56].

Fig. 3

Schematic illustrating the two-way nesting process on a Arakawa C grid

Time synchronization The use of an explicit time integration means that the model needs to verify the CFL stability condition, and the ratio $\Delta t / \Delta x$ must be kept smaller than a given value on the whole grid hierarchy. Consequently, a temporal refinement must be applied in addition to the spatial mesh refinement. The integration algorithm for a time refinement of 3 is depicted in Fig. 4. The model is first integrated on the Parent grid $\Omega _p$ with a time step equal to $\Delta t_{p1}$, the model is then advanced multiple times on the Child grid $\Omega _c$ to reach the same physical time as the outer grid. To synchronize the two solutions, the last time step in the inner grid is imposed: $\Delta t_{c3} = \Delta t_{p1} - \sum \Delta t_{ci}$.

• 1: Model integration on the Parent grid $\Omega _p$

• 2: Model integration on the Child grid $\Omega _c$

• 3: Time and space interpolation of the boundary values

• 4: Update of the Parent Grid in feedback domain

Fig. 4

Schematic illustrating the two-way nesting process

3 Verification

A systematical analysis of a numerical solution for long-wave run-up requires benchmarking. Since the model was developed from scratch and involves a combination of adapted numerical features, it is required to first verify its performance for idealized flow problems, for which analytical solutions have been derived. These tests examine the model’s ability to handle important flow processes, such as flow discontinuities and wet/dry transitions. These features are particularly critical for the quality of the computed run-up and can often pose numerical challenges. The implementation of the nested grid approach is then verified with a 2D moving boundaries problem.

3.1 Shock-Capturing Capabilities

Shock-capturing schemes refer to numerical methods that can directly solve wave propagation with large gradients and rapid changes in the free surface and velocity regimes. Such nonlinear phenomena are present in many wave problems (e.g., wave breaking, dambreak wave propagation, and propagation of wet/dry fronts). Consequently, a lot of effort is made to compute shock waves as part of the complete solution [37]. A stable numerical solution for shock waves targets the generation and propagation of an oscillation-free discontinuity without excessive smearing across the shock front.

In the following, we examine the solution of the present model in handling discontinuities and assess the accuracy and quality of the results. Since many shock-capturing flow models are built around Riemann solvers, we compare the solution from the presented scheme, referred to as “Present Scheme”, with the solution obtained by a 1D HLLC Riemann solver (“HLLC Scheme”). The HLLC scheme used for comparison was coded based on the techniques given by Toro [37]. For consistency with the presented scheme, the first-order HLLC scheme is extended to second-order accuracy through a MUSCL reconstruction [67] combined with a generalized MinMod limiter and a predictor–corrector Runge–Kutta time integration.

The dambreak problem is a widely used test to demonstrate the shock-capturing capabilities of numerical schemes. We consider a one-dimensional dambreak over a wet bed of uniform depth. The domain is ${1}\,{\textrm{m}}$ long and the initial condition is

$$\begin{aligned} h \left( x,0 \right) = {\left\{ \begin{array}{ll} {1}\,{\textrm{m}} &{} \text {if}\ x \le {0.5}\,{\textrm{m}} \\ {0.2}\,{\textrm{m}} &{} \text {otherwise}\ \end{array}\right. } \quad \mathrm {\,\,\,\,\,\,\,}\quad u\left( x,0 \right) = {0}\,{\mathrm{m/s}} \end{aligned}$$

The analytical solution for this test was derived by Stoker [68] and consists of a shock and a rarefaction wave moving in opposite directions from the center of the domain. The solutions of the dambreak test for 100 grid cells ($\Delta x$ = ${1}\,{\textrm{cm}}$) and at $t=$ ${0.1}\,{\textrm{sec}}$ are shown in Fig. 5. For both schemes, we use a constant Courant number of $CN=0.7$ and a diffusion parameter in the generalized MinMod limiter $\theta = 1.5$.

Both numerical schemes correctly capture the rarefaction and shock waves despite small discrepancies in comparison to the analytical solution. This small mismatch can be reduced significantly with a reduction in grid size. In general, the Present scheme achieves slightly sharper solutions around the flow transitions compared to the HLLC scheme. Consequently, the Present scheme contains smaller L1-norm errors than the HLLC scheme, as listed in Table 1, albeit the fact that both solutions converge towards the exact solution with mesh refinement. The presented model is able to compute the propagation of shocks with the correct wave speed and height, proving its powerful shock-capturing capability without the need for the computationally expensive sampling of the solution as it is necessary for the HLLC scheme.

Fig. 5

Dambreak over wet bed: water height profiles from the Present and HLLC schemes at $t=$ ${0.1}\,{\textrm{s}}$ for a cell size $\Delta x$ of ${1}\,{\textrm{cm}}$

Table 1 Dambreak over a wet bed: L1-norm error

3.2 Moving Boundaries

An essential feature of shallow-water models used for flood and inundation mapping is the ability to compute wet-dry transitions and track moving boundaries. The biggest challenges are associated with the definition of the numerical fluxes and source terms in the presence of dry cells. A clean and stable representation of the moving boundary is essential for the correct description of run-up and inundation limits independent of the previous stages of wave propagation and breaking.

We investigate the performance of the present model in describing fast sheet flows induced by a dambreak over a dry bed with and without frictional resistance. This test is also used to verify the implementation of the friction term.

The test case involves a ${2000}\,{\textrm{m}}$ long horizontal channel of uniform depth with $\Delta x$ = ${5}\,{\textrm{m}}$ grid spacing and the following initial condition:

$$\begin{aligned} h \left( x,0 \right) = {\left\{ \begin{array}{ll} {6}\,{\textrm{m}} &{} \text {if}\ x \le {1000}\,{\textrm{m}} \\ {0}\,{\textrm{m}} &{} \text {otherwise}\ \end{array}\right. } \quad \mathrm {\,\,\,\,\,\,\,}\quad u\left( x,0 \right) = {0}\,{\textrm{m}} \end{aligned}$$

The test is computed with a minimum water depth of $h_{\min }$ = $10^{-8}$ m and a Courant number of 0.7. Two cases are taken into account:

• 1. Dambreak without friction: The numerical results are compared with the Ritter solution. The solution involves a wet-dry front propagating downstream and a rarefaction wave moving upstream into the reservoir.

• 2. Dambreak with friction: In this case, the Darcy–Weisbach friction law with a coefficient $f = 8g/40^2$ is utilized in the friction source term of the momentum equations. The reference solution is based on the Dressler/Whitham/Chanson conceptual model [69,70,71], which is based on the assumption that near the wavefront, frictional resistance controls the fluid motion. The exact shape of the wavefront can be found in [71]. In contrast to the process at the downstream wave, the frictional resistance in the rarefaction regime is neglected, and the solution at the front can be described by a modified Ritter’s solution as presented in Delestre et al. [72].

Fig. 6

Dambreak on dry bed: water height profiles after t = ${40}\,{\textrm{s}}$ for grid spacing $\Delta x$ = ${10}{\textrm{m}}$. The wave front around ${1250}\,{\textrm{m}}$ corresponds to the solution with a friction coefficient of $f = 8g/40^2$

In both cases, good agreement between the reference and the numerical solutions is obtained (Fig. 6). In the case of bottom friction, the model accurately captures the deceleration of the wavefront, which verifies its capability of correctly handling bottom roughness. As before, the results can be improved through mesh refinement but not through further reduction of the predefined minimum water depth $h_{\min }$.

3.3 Nested Grid Implementation

In this section, we examine the accuracy of the nested grid implementation. This step is important to scrutinize the model performance with respect to the information exchange across different grid resolutions, especially in the presence of wet/dry transitions. For applications related to long-wave run-up, the nested grid approach is expected to deal with moving boundaries and fast flows over varying topography in two-dimensional settings. A few analytical solutions of the SWE exist for problems in the 2D horizontal plane. The oscillation in a parabolic basin is one of them, as it addresses a two-dimensional run-up problem, which helps examine the validity of the numerical structure in the combined xy-directions.

The water oscillation is induced inside a $\left[ 0,L \right] \times \left[ 0,L \right]$ parabolic basin given by

$$\begin{aligned} z \left( r \right) = -h_{0} \left( 1 - \frac{r^2}{a^2} \right) \quad \textrm{where}\quad r = \sqrt{\left( x-\frac{L}{2} \right) ^2 + \left( y-\frac{L}{2} \right) ^2} \end{aligned}$$

The value of $h_{0}$ represents the still-water depth at the basin center, and a is the radius of the wetted perimeter. The exact solution for this test was derived by Thacker [4]. For a smooth bed with no friction, the analytical solution for the water depth is described as

$$\begin{aligned} h \left( r,t \right) = h_{0} \left( \frac{\sqrt{1-A^2}}{1-A \cos \left( \omega t \right) } -1 - \frac{r^2}{a^2} \left( \frac{1-A^2}{\left( 1-A \cos \left( \omega t \right) \right) ^2} -1 \right) \right) - z \left( r \right) \end{aligned}$$

where $\omega = \sqrt{8gh_{0}/ a}$ is the frequency of the oscillation, and the coefficient $A = \left( a^2 - r_{0}^2 \right) /\left( a^2 + r_{0}^2 \right)$ with $r_{0}$ the radius of the initial shoreline. For the setup of the dimensions of the parabola and the initial condition of the free surface, we use $a={1}\,{\textrm{m}}$, $r_{0}$ = ${0.8}\,{\textrm{m}}$, $h_{0}$ = ${0.1}\,{\textrm{m}}$ and L = ${4}\,{\textrm{m}}$.

The analytical solution is used to verify the symmetry and accuracy of the nested grid implementation. Here, we place a nested domain off-center, including the moving waterline, with a refinement factor of 4. The use of an off-center nested grid is critical to verifying the grid exchange for both the normal and cross fluxes. The Parent grid is computed with a quadratic cell size of ${2}\,{\textrm{cm}}$ by ${2}\,{\textrm{cm}}$. The inner Child grid is computed with $\Delta x = \Delta y = {0.5}$ cm.

The water height evolution at the center of the basin is shown in Fig. 7 after ${40}\,{\textrm{s}}$ corresponding to over 17 full cycles in the Parent grid. The present solution convinces through the maintenance of amplitude and phase over multiple oscillation cycles the quality of the second-order numerical scheme. These results confirm not only the low numerical diffusion but also the smooth transition across the wet/dry boundary inherent to the model without the need for excessively small grid sizes.

Figure 8 depicts the free surface transect across the basin center line at several stages, $t=T$, $t=T+T/4$, and $t=T+T/2$, where $T= 2 \pi / \omega$ denotes the oscillation period. The run-up is well described, and no numerical artifact arises from the exchange between the Parent and Child grid. In addition, Fig. 9 gives a visual impression of the three-dimensional problem and showcases that the definition of the run-up outline benefits from mesh refinement.

Fig. 7

Time series of water height at center point of parabolic basin $\left( x=L/2 , y=L/2 \right)$. Grid spacing $\Delta x = \Delta y = 2$ cm. The numerical solution is of low diffusion without requiring excessively fine mesh sizes

Fig. 8

Oscillation in a parabolic basin: cross-section of water height after one full oscillation. Each circle represents the solution from the numerical model at each grid cell across the transect. The solution from the nested grid is indicated with blue circles

Fig. 9

Free surface elevation of oscillation in parabolic basin with grid nesting after 4.5 cycles (9.9 s). The refined Child grid is denoted by the dashed line and shows a more detailed run-up limit than the coarse Parent grid

4 Effect of Grid Nesting on Wave Run-Up

Previous verification efforts have ensured that the present model correctly handles the fundamental features that are essential for the accurate computation of long-wave run-up. The following tests examine the sensitivity of the computed results to grid nesting for efficient computation of local run-up problems. For this purpose, we utilize two standard experimental benchmark tests that have been widely used in the tsunami community and that highlight the complexity of the local long-wave run-up. The two tests present common long-wave features such as the increase in local wave run-up from the collision of two or more waves as well as extreme run-up over highly detailed terrain. We will present an analysis of the sensitivity of the computed run-up to the general mesh size and further investigate the sensitivity of the maximum run-up extent to the size of the nested grid and the refinement factor.

4.1 Solitary Wave Run-Up Around a Conical Island

The transformation of long waves around islands has attracted a lot of attention in the past—especially among tsunami researchers. A common observation is that long waves can refract and diffract around an island from both sides and collide in the back. In some cases, the maximum run-up occurs counter-intuitively at the island’s lee side due to a superposition effect when the refracted/diffracted waves from both sides run into each other and double up. The problem of the conical island is exemplary since the high run-up and inundation at the lee side cannot be approximated with empirical formulae or computationally cheap 1D calculations. Instead, the problems require a full 2D solution that naturally exhibits a substantial computational effort.

Briggs et al. [7] conducted a large-scale laboratory experiment to investigate solitary wave transformation around a conical island. The basin is 25 m by 30 m with a circular island in the shape of a truncated cone constructed of concrete with a diameter of 7.2 m at the bottom and 2.2 m at the top. The island is 0.625 m high and has a side slope of 1:4. A 27.4-m-long directional wavemaker consisting of 61 paddles generated the input solitary waves for three laboratory tests. Wave absorbers at the three remaining sidewalls reduced reflection in the basin. Further details about the laboratory model setup, the location of the wave gauges, and the numerical setup can be found in NTHMP [73].

Fig. 10

Grid size sensitivity of maximum run-up outlines for the test with $A/h = 0.096$ of Briggs et al. [7]. Black dots denote experimental data, solid lines represent results from the present model

The present study focuses on experiments with a water depth $h = 0.32$ m and solitary wave heights of $A/h = 0.1$. Consistent with NTHMP benchmark problem 6 [73], our numerical test uses the measured wave heights of $A/h = 0.096$ from the laboratory experiment instead of the target wave heights as they better represent the recorded data and thus the incident wave conditions to the conical island. A reflective boundary condition is imposed at the lateral sides. The wave absorbers from the laboratory layout are not considered since their absorbing performance is unknown. The model is set up with a reference grid of $\Delta x = \Delta y = {5}\,{\textrm{cm}}$. A Manning roughness coefficient of n = 0.012 s/m$^{1/3}$ accounts for the smooth concrete finish according to Chaudhry [74]. The Courant number is set to Cr = 0.5. The model setup is comparable to earlier work and will be used as a reference as it is expected to return solutions of similar and comparable quality to previously published studies. The results from the free surface elevation observed at five wave gauges are omitted here as they are comparable to previously published results.

Sensitivity to grid resolution In view of sensitivity to the grid size, Fig. 10 shows the run-up limits for the reference scenario with $\Delta x = \Delta y = {5}\,{\textrm{cm}}$, as well as the solutions of the model with coarser grid sizes of $\Delta x = \Delta y = {10}\,{\textrm{cm}}$ and $\Delta x = \Delta y = {20}\,{\textrm{cm}}$, respectively. The reference mesh size of ${5}\,{\textrm{cm}}$ returns the closest agreement overall with the run-up data—particularly at the lee side of the island. Nevertheless, a numerical domain with four times fewer cells, i.e., uniform ${10}\,{\textrm{cm}}$ grid spacing, still provides a decent estimate of the run-up, albeit with less precision at the lee side. It is not really surprising that a grid size of $\Delta x = \Delta y = {20}\,{\textrm{cm}}$ is too coarse to represent the details of the run-up outline, and virtually no run-up is recorded in the lee of the island.

Careful examination of the temporal evolution of the wave field at $\Delta x = \Delta y = {5}\,{\textrm{cm}}$ resolution shows that the colliding waves in the back of the island locally and momentarily augment the water level, but then pass through each other and continue the refraction/diffraction process. The locally high run-up in the back of the island results to a great extent from the two waves that shoal and spill up on either flank of the leeward side. It often goes unnoticed that the steepened refracted waves then meet head-on over the leeward topography, i.e., the initially dry beach, from where a substantial portion of maximum run-up and inundation originates. For a relatively steep slope, this wrapping process requires rather fine resolution to properly account for the flooding process, and insufficient grid cells over the beach can lead to an under-representation of the run-up.

Sensitivity to grid nesting It is understood that any reduction in the total cell count will reduce the computational load. A nested grid approach caters to lowering the computational effort without compromising too much on the quality of the results. A question of practical interest is whether the overall wave transformation around the island could potentially be computed over a coarse grid, from which information is fed into a nested inner grid of higher resolution that is placed only over a local area of interest. Figure 10 demonstrates that a grid resolution of ${5}\,{\textrm{cm}}$ is an adequate choice for the resolution of the wave run-up along the beach of the conical island and that coarser mesh sizes, in particular the ${20}\,{\textrm{cm}}$ resolution, are insufficient to resolve most of the run-up.

The solitary input wave has a length of several meters. As shown in the previous benchmark tests, e.g. Sect. 3.3, the present model computes long waves with minimal numerical diffusion and hence is expected to handle the general processes of the solitary wave transformation around the island even over a rather coarse mesh. Inspection of the full free surface evolution has shown that even a grid of ${20}\,{\textrm{cm}}$ mesh size can account for the overall wave processes in the vicinity of the conical island and that it only fails in computing the detailed run-up.

Fig. 11

Maximum run-up outlines for the test with $A/h = 0.096$ of Briggs et al. [7]. Each model run uses a Parent grid with $\Delta x = \Delta y = {20}\,{\textrm{cm}}$ resolution and one Child grid of $\Delta x = \Delta y = {5}\,{\textrm{cm}}$. The three individual nested grid set-ups (a), (b), and (c) and their corresponding maximum run-up limits are color-coded and denoted by the dashed rectangle and the solid lines within

Figure 11 shows the results from three nested grid approaches—all with an inner grid of ${5}\,{\textrm{cm}}$ resolution placed into an outer grid of ${20}\,{\textrm{cm}}$ resolution. The individual inner domains are color-coded and of ${2}\,{\textrm{m}}$ by ${4}\,{\textrm{m}}$, ${1.2}\,{\textrm{m}}$ by ${4}\,{\textrm{m}}$ and ${0.8}\,{\textrm{m}}$ by ${1.2}\,{\textrm{m}}$. The additional computational load arising from the inner grid is associated with 3200, 1920, or 384 cells, respectively. It can be seen that the run-up outline in the nested grid (a) denoted by the cyan line in Fig. 11 is nearly identical to the outline of the uniform ${5}\,{\textrm{cm}}$ reference grid. This implies that the overall wave processes are sufficiently resolved by the coarse outer grid up to the boundary of the nested grid (a), which subsequently takes care of the detailed wave transformation and run-up processes at the back side of the conical island. The domain size of the nested grid is then reduced behind the island, as illustrated by the red dashed rectangle. The corresponding run-up limit (red line) remains nearly identical to the run-up outline from the largest nested grid setup. The run-up at the lee side, therefore, depends only minimally on the higher resolution in the area behind the island where the wave collision process occurs. The nested grid extends to a very small area just around the hotspot of run-up, as denoted by the green dashed rectangle. Surprisingly, the run-up along the center lee side remains qualitatively very similar to the run-up computed by the larger nested grids.

The effect of the nested grid approaches can be seen in Fig. 12 in more detail. Row 1 shows the free surface evolution over the ${5}\,{\textrm{cm}}$ uniform reference grid. The corresponding alternate solutions, denoted by the black dashed rectangles, illustrate the nested grid solutions. As the wave is moving around the island, the nested grid (a) (second row) picks up its energy and resolves the wrap of the run-up tongue in detail, though with slightly less steepness at the leading edge compared to the reference solution. The maximum run-up after 9.2 s in the nested grid is nearly identical to the uniform reference solution. The third row shows the free surface elevation from the red rectangle and the run-up limit from Fig. 11. The high-resolution inner grid extends only marginally over the bathymetry behind the island and mostly covers the topography. The detailed solution of the colliding waves behind the island is less critical for the maximum run-up than a high-resolution computation of the two refracted run-up tongues that meet each other over the dry slope. The last row shows that a representative run-up limit is achievable even by only using an extremely small inner grid of high resolution at the location where the refracted waves collide over the beach.

The long-wave refraction and collision processes do not necessarily require high grid resolution given that a low-diffusive coarse solution captures the main energy flux. Counter-intuitively, the locally high run-up of long waves, as illustrated in this example, is often driven by wave processes in the immediate vicinity of the shoreline and over the beach. Accurate run-up results can potentially be obtained with locally very small nested grids as long as they cover the entire run-up zone over the beach. This is particularly true for locations with steep beach slopes.

As for the results from Figs. 10, 11 and 12, the computed wave field is symmetric to machine precision with respect to the horizontal center line at 15 m in the y-direction. This supports the quality of the numerical results as any instability arising from the interface at the boundary of the nested grids would have eliminated the perfect symmetry.

Fig. 12

Free surface elevation at lee side of conical island computed over the single reference grid of $\Delta x = \Delta y = {5}\,{\textrm{cm}}$ (first row) and with three separate grid nesting approaches each combining a coarse outer grid of $\Delta x = \Delta y = {20}\,{\textrm{cm}}$ mesh size with inner fine grids of $\Delta x = \Delta y = {5}\,{\textrm{cm}}$ resolution (2nd, 3rd, 4th row). First column: refraction/diffraction of solitary wave around flank of conical island. Second column: maximum run-up from superposition of refracted/diffracted waves. The extent of the nested grid is outlined by the black dashed line in row 2 to 4

4.2 Long-Wave Run-Up at Monai Valley

The second benchmark is testing the sensitivity of the present model to the mesh size and refinement of the solution with a nested grid for the computation of nonlinear wave processes over an irregular terrain that favors extreme run-up. The 1993 Hokkaido Nansei-Oki tsunami is a well-studied event thanks to the laboratory experiments conducted by Matsuyama and Tanaka [75] at the Central Research Institute for Electric Power Industry (CRIEPI) in Japan. The down-scaled laboratory test examined the extreme run-up of over 30 m at Monai Valley, located between two headlands and sheltered by the small Muen Island. The area around Monai Valley was reconstructed with a plywood model at 1:400 scale based on bathymetric and topographic data as shown in Fig. 13.

A wave gauge near the wavemaker recorded the initial low amplitude N-wave used in the present numerical model as boundary input with the free surface elevation interpolated from the data according to the model time step. As in the previous test, we first examine the sensitivity of the numerical solution to the grid size over a single domain with uniform resolution. Again, the Courant number is kept constant at Cr = 0.5. A Manning coefficient of $n = 0.012$ $sm^{-1/3}$ accounts for the surface roughness of the plywood model [74].

Sensitivity to grid resolution Figure 14 shows the comparison between the computed and recorded data at the wave gauges placed in the numerical and experimental setup between Muen Island and Monai Valley. The computed results are of similar quality as the solutions from previous studies. The wave regime at the locations of the gauges is still reasonably well resolved with a rather coarse mesh. Even with a ${10}\,{\textrm{cm}}$ grid size, the general shape of the free surface time series is captured, and the overall energy of the wave field behind Muen island is accounted for.

Fig. 13

Outline of the bathymetry from the 1:400 scaled model used by Matsuyama and Tanaka [75]. The black dashed and dotted lines denotes the boundaries of two individual inner nested grids (a) and (b)

Fig. 14

Free surface time series at the gauges shown in the left panel from computations over the entire domain with different uniform mesh sizes

Fig. 15

Maximum run-up limits around Monai Valley. Left A Uniform grid with different resolutions. Center B Nested grid (a) with ${1.25}\,{\textrm{cm}}$ resolution and different Parent grid resolutions of ${2.5}\,{\textrm{cm}}$, ${5}\,{\textrm{cm}}$, and ${10}\,{\textrm{cm}}$ leading to refinement factors of RF = 2, RF = 4, and RF = 8. Right C Nested grid (a) and (b) with ${1.25}\,{\textrm{cm}}$ resolution and Parent grid resolution ${10}\,{\textrm{cm}}$

Figure 15A illustrates the sensitivity of the computed maximum run-up to different uniform grid sizes of 1.25 cm, 2.5 cm, 5 cm, and 10 cm. The local run-up in Monai Valley is more sensitive to the grid resolution than the nearshore wave field in front of the beach. Since the terrain is steep and narrow, the computations with the present model show that a rather fine grid of 1.25 cm is necessary to obtain a proper outline of the run-up envelope. NTHMP [73] confirms that most previous numerical studies utilized a mesh size of $\Delta$ x = $\Delta$ y $< {1.5}\,{\textrm{cm}}$ to obtain a consistent definition of the wave run-up in the narrow and steep valley. The fine grid of 1.25 cm in the second row of Fig. 16 resolves the details of wave refraction and collision in front of the steep cliff, whereas a coarser option of 10 cm resolves neither the flow details nor the small-scale flow features over the topography and consequently leads to a significant underestimation of the run-up in the Monai Valley.

Fig. 16

Free surface elevation in front of Monai Valley with single Parent grid of $\Delta x = \Delta y = {10}\,{\textrm{cm}}$ (first row) and $\Delta x = \Delta y = {1.25}\,{\textrm{cm}}$ (second row) mesh size. Results from embedded nested Child grids a and b of $\Delta x = \Delta y = {1.25}\,{\textrm{cm}}$ in a Parent grid of $\Delta x = \Delta y = {10}\,{\textrm{cm}}$ are shown in the second row and third row. The extent of the respective Child grid is outlined by the black dashed lines. First column: drawdown from leading depression of N-wave and approaching wave crest upstream of Muen island. Second column: maximum run-up from superposition of refracted and reflected waves

Sensitivity to grid nesting Similar to the previous benchmark test, the question arises whether it is possible to utilize a coarse mesh for the overall flow field in combination with a fine nested grid for the detailed run-up in an area of interest like Monai Valley. Knowing that the run-up over terrain with irregular and steep slopes requires small grid sizes, we utilize a 1.25 cm nested grid (a) inside a Parent grid as outlined in Fig. 13. The inner nested grid starts offshore of Muen island, similar to what Yamazaki et al. [52] have used. The Parent grid is of 5.5 m by 3.4 m size. It contains only 1870 cells with a 10 cm resolution. The two nested grid options (a) and (b) have dimensions of 2.3 m by 1.8 m and 1.3 m by 2.3 m and consequently add 26,496 or 14,976 grid cells, respectively, to the computation. Hence, the two nested grid options reduce the total cell count by 76% and 86% in comparison to a single grid of uniform 1.25 cm resolution with 119,680 cells.

The sensitivity of the results with respect to the refinement factor is analyzed by increasing the Parent grid resolution by factors of 2, 4, and 8 with respect to the nested grid. Consequently, the individual run-up limits of Fig. 15B refer to the results from a 1.25 cm nested grid in combination with different Parent grids of 2.5 cm, 5 cm, and 10 cm. The refinement factor hardly influences the run-up limit with a nested grid domain that covers most of the nearshore area (dashed line of the domain (a) in Fig. 13). Again, a basic requirement for the utilization of a coarse Parent grid is a low diffusivity of the numerical scheme. It is understood that the interpolation in the nesting process between the individual grids can lead to small discrepancies in comparison to a uniform grid with high resolution. This can be seen in Fig. 15. The grid nesting strategy should, therefore, always be seen as method to primarily reduce the computational load by still retaining an acceptable quality of the solution.

It is finally shown how the computed results are sensitive to the nested domain size. This is analyzed through reduction of the area covered by the nested grid (see dotted line (b) in Fig. 13). The resolutions of the Parent and Child grid are identical to the setup with nested grid (a). The two scenarios only differ in the domain size of the nested grids. Figure 15C highlights that the run-up limit from the two scenarios varies only at some locations. Though the flow details of the overtopping and refraction processes around Muen island are resolved in detail with a fine grid as shown in rows two and three of Fig. 16, they do not have a substantial influence on the run-up. It is sufficient that the outer grid resolves the overall wave energy and the inner grid accounts for the run-up process.

5 Conclusions and Perspectives

We have shown the performance of a newly developed model for long-wave run-up with respect to standard analytical solutions and laboratory experiments. The model was demonstrated to be shock-capturing, well-balanced, and water-depth positivity preserving, which are crucial properties for the correct estimation of long-wave-driven run-up. The model was proven to be stable and efficient in dealing with wet/dry transitions without the need for computationally expensive treatment of the moving boundary. The numerical scheme is based on a finite-volume staggered approximation with second-order accuracy in space and time. The accuracy in time arises from a combination of the Runge–Kutta method for the convective acceleration and the Leapfrog method for the surface gradient and friction terms. Similarly, the spatial accuracy comes from a second-order upwinded advection along with a second-order central difference scheme for the remaining terms.

The model performs consistently for shock-driven problems and compares to established Riemann solver-based TVD methods. The wet-dry interface is stable and well-defined without the need for additional treatment of the moving boundary. The model contains a two-way grid nesting scheme that allows for local refinement of the solution. The implementation has been verified and proven to be accurate and stable for moving boundaries and was shown to be applicable to long-wave run-up problems.

The performance and sensitivity of long-wave run-up was then investigated in dependence of the nested grid’s domain size and the level of its refinement. Two standard benchmark tests from the tsunami community were chosen for the investigation. Though there are no universal rules for the size, position, and refinement factor of nested grids, our results from the two benchmark tests reveal that computations of high quality can be achieved with small nested grids placed strategically at a location of interest such as in areas where locally high run-up occurs. The refinement factor was found to have only small influence on the run-up limit, if the solution in the Parent grid is representative of the wave envelope and the grid nesting method accounts for the correct exchange of the total wave energy flux.

Further, it was demonstrated that it is possible to place a nested grid rather close to the initial still-water level as long as the long-wave flow regime prevails across nested grid’s offshore boundary. Long-wave run-up is often more subject to the resolution of the local topography than it is influenced by the detailed wave processes over the bathymetry. This is line with commonly used empirical run-up formulae for swell waves where the maximum run-up envelope is controlled by the overall wave energy and the slope.

The quality of the computed results encourages to expand the development of the model with respect to frequency dispersion. This will allow for a further investigation of how grid nesting can affect the run-up from swell waves. In the same context, the model can be optimized through implementation of massive parallelization techniques commonly used to reduce the computation time associated with large flow problems. It is evident that a low overall cell count reduces the model’s computation time and that the insights gained from the present study can be used to efficiently decrease the computational load for computations of long waves by retaining accuracy and quality of the solutions.