Non-hydrostatic unified model of the ocean with application to ice/ocean interaction modeling

Abstract

The non-hydrostatic unified model of the ocean (NUMO) has been developed to advance model capability to realistically represent the dynamics and ice/ocean interactions in Greenland fjords, including an accurate representation of complex fjord geometries. To that end, NUMO uses high-order spectral element methods on unstructured grids to solve the incompressible Navier–Stokes equations complemented with heat and salinity transport equations. This paper presents the model’s description and discusses the formulation of ice/ocean Neumann boundary conditions based on the three-equation model. We validate the model on a range of test cases. The convergence study on the classical Kovasznay flow shows exponential convergence with arbitrary basis function polynomial order. The lock-exchange and density current cases show that the model results of buoyancy-driven flows solved with 2D and 3D unstructured meshes agree well with previously published findings. Finally, we show that a high-order simulation of an ice block immersed in saline water produces results that match both direct numerical simulation and laboratory experiments.

1 Introduction

Numerical modeling of ice/ocean interactions has gained significant interest in the climate modeling community due to the observed changes to Earth’s cryosphere. The most rapid of those changes occur in the Arctic, where the mass loss of the Greenland ice sheet accounts for a quarter of global sea-level rise (Jackson et al. 2014) and is the fastest-growing contributor to this metric (Slater et al. 2019). One of the dominant drivers of those changes is the melting of glacier termini by warming of the inflowing Atlantic waters (Straneo and Heimbach 2013). Accurate representation of ice-ocean interactions in regional and global ocean models is crucial, yet challenging, for accurate sea-level rise predictions (Catania et al. 2020).

In recent years, there have been several attempts to simulate ice/ocean interactions in the context of marine-terminating glaciers. A popular choice is to use a three-equation formulation (Jenkins et al. 2001) of heat and salt balance to calculate melt rate as a function of near-terminus conditions. This is often coupled with a well-established buoyant plume theory (Morton et al. 1956; MacAyeal 1985), which calculates near-terminus temperature and salinity based on the far-field properties. This parameterization is used either as a stand-alone tool to quantify melt rate (Jenkins 2011; Slater et al. 2016) or within a numerical ocean model to prescribe a boundary condition in an ocean simulation (Xu et al. 2012; Sciascia et al. 2013; Kimura et al. 2014; Cowton et al. 2015; Carroll et al. 2017). This approach, however, was shown to underestimate the observed melt rates (Jackson et al. 2017).

To avoid extensive parameterizations, some researchers use high-resolution, small-scale models to resolve the turbulent plume near the ice/ocean interface. Gayen et al. (2016) performed a direct numerical simulation (DNS) of an ice face immersed in unstratified saline water that showed excellent agreement with experiments Josberger and Martin (1981), Kerr and McConnochie (2015). Mondal et al. (2019) took a similar approach for sloping ice faces, while Ezhova et al. (2018) used DNS to simulate wall plumes and compared them with existing parameterizations. While very accurate, the DNS approach is unrealistic for fjord-scale simulations due to an excessive cost dictated by the fine resolution.

In the long term, the non-hydrostatic unified model of the ocean (NUMO) aims to bridge the gap between the parameterization-dependent models which can perform large-scale simulations and small-scale, accurate models. We believe that using adaptive unstructured meshes combined with high-order numerical methods can both realistically resolve key processes at the ice/ocean interface and represent the entire fjord circulation. In this paper, we present the details of the model using arbitrarily high-order element-based nodal Galerkin methods to discretize the three-dimensional, incompressible Navier–Stokes equations on arbitrarily unstructured meshes. We validate the model on standard test cases and compare a small-scale ice/ocean simulation with the DNS result of Gayen et al. (2016) and the laboratory experiment result in Josberger and Martin (1981).

Previous approaches to modeling non-hydrostatic interactions between a vertical ice face and ocean have used either the well-established MITgcm (Marshall et al. 1997) finite-volume model, Fluidity (Piggott et al. 2008) finite element model, or other models based on the finite difference (with spectral algorithm in the spanwise direction) for DNS simulations (Gayen et al. 2016). All of the above models use at most second order numerical methods. Examples of high-order Galerkin methods used in non-hydrostatic ocean simulations are the Thetis coastal ocean model (Kärnä et al. 2018), and NEK5000 (Fischer 1997). To the authors’ knowledge, NUMO is the first model which applies those methods for vertical ice/ocean interactions. This paper is the first publication of the NUMO model.

2 Model description

NUMO uses the incompressible Navier–Stokes equations with the Boussinesq approximation for buoyancy processes, which we write as follows

$$\begin{aligned} \frac{\partial \textbf{u}}{\partial t} + \textbf{u}\cdot \nabla \textbf{u} - \nu \Delta \textbf{u} + 2\varvec{\Omega } \times \textbf{u}&= -\frac{1}{\rho _0}\nabla p + \frac{\rho }{\rho _0} g\textbf{k}, \end{aligned}$$

(1)

$$\begin{aligned} \nabla \cdot \textbf{u}&= 0 , \end{aligned}$$

(2)

where $\textbf{u}=(u,v,w)^{\mathcal {T}}$ is a velocity vector, $\mathcal {T}$ is the transpose operator, $\nabla$ is the gradient operator, $\Delta$ the Laplacian, $\nu$ is the viscosity, $\varvec{\Omega }$ is the Earth’s angular velocity vector, $\rho = \rho _0 + \rho '$ is the density of water split into reference constant density $\rho _0$ and the variation $\rho '$, p is the pressure, g is the gravitational acceleration magnitude and $\textbf{k}$ is the unit vector of the direction along which the gravitational acceleration acts (in this paper $\textbf{k}=(0,0,1)^\mathcal {T}$).

Equations (1)–(2) are complemented with the transport equation for temperature T and salinity S

$$\begin{aligned} \frac{\partial }{\partial t} \left[ \begin{array}{c} T \\ S \end{array}\right] -\left[ \begin{array}{c} \kappa _T \Delta T\\ \kappa _S \Delta S \end{array}\right] = - \textbf{u} \cdot \nabla \left[ \begin{array}{c} T \\ S \end{array}\right] , \end{aligned}$$

(3)

where $\kappa _{T,S}$ are diffusivities of temperature and salinity. To compute the density variation in the buoyancy term in the test cases presented in the paper, NUMO uses a linearized equation of state

$$\begin{aligned} \rho ' = \rho _0 \left( \alpha _T (T-T_0) + \alpha _S (S-S_0)\right) , \end{aligned}$$

(4)

where $\alpha _{T,S}$ are temperature and salinity expansion coefficients, and $T_0 = T_0(z)$ and $S_0 = S_0(z)$ are temperature and salinity reference profiles. Another option in the model is the simplified equation of state developed by Roquet et al. (2015) to fit the UNESCO EOS for seawater Intergovernmental Oceanographic Commission (2010). The non-linear EOS is not used here to remain consistent with the reference simulations we compare against.

In Eq. (1) we split the density into a constant reference component $\rho _0$, and a perturbation $\rho '$. Let us now split the pressure

$$\begin{aligned} p = p_0 + p', \end{aligned}$$

(5)

such that

$$\begin{aligned} \nabla p_0 = \rho _0 g \textbf{k}, \end{aligned}$$

(6)

i.e., the gradient of the reference pressure, $p_0$, balances the gravity term due to the reference density, $\rho _0$. This allows us to use a simplified form of (1):

$$\begin{aligned} \frac{\partial \textbf{u}}{\partial t} + \textbf{u}\cdot \nabla \textbf{u} - \nu \Delta \textbf{u} + 2\varvec{\Omega } \times \textbf{u} = -\frac{1}{\rho _0}\nabla p' + \frac{\rho '}{\rho _0} g\textbf{k}. \end{aligned}$$

(7)

Similarly to pressure, we separate the temperature and salinity fields into reference and perturbation parts:

$$\begin{aligned} T = T_0 + T', \qquad S = S_0 + S'. \end{aligned}$$

(8)

This separation leads to the following reorganization of Eq. (3):

$$\begin{aligned} \frac{\partial }{\partial t} \left[ \begin{array}{c} T' \\ S' \end{array}\right] -\left[ \begin{array}{c} \kappa _T \Delta T'\\ \kappa _S \Delta S' \end{array}\right] = - \textbf{u} \cdot \nabla \left[ \begin{array}{c} T' + T_0\\ S' +S_0 \end{array}\right] +\left[ \begin{array}{c} \kappa _T \Delta T_0\\ \kappa _S \Delta S_0 \end{array}\right] . \end{aligned}$$

(9)

The last term on the right-hand-side represents the diffusion of the reference state. In the cases presented in this paper both $T_0$ and $S_0$ are constant, so we omit these terms.

2.1 Boundary conditions

The domain sides and ocean bottom are modeled as either no-slip ($\textbf{u}=0$) or free-slip walls ($\textbf{n}\cdot \nabla \textbf{u} = 0$, where $\textbf{n}$ is the outward pointing normal vector). Unless otherwise stated, all walls are adiabatic ($\textbf{n}\cdot \nabla T = 0$), and do not allow for salinity transport ($\textbf{n}\cdot \nabla S = 0$). One exception to this rule is the ice-ocean interface, where we compute the heat and salinity flux to the domain using balance equations for heat and salinity.

2.1.1 Heat and salinity balance

The heat conservation equation is

$$\begin{aligned} Q_i^T - Q_w^T = Q_{latent}^T, \end{aligned}$$

(10)

where $Q_i^T$ is the heat transported to the ice, $Q_w^T$ the heat transported from the water, and $Q_{latent}^T = -\rho _i V L_i$ the latent heat. V is the melt rate with units of velocity [m/s] and $L_i$ the latent heat of ice fusion. Holland and Jenkins (1999) discuss various choices for modeling $Q_i^T$. Since in the cases explored in this paper $Q^T_i$ is small compared to $Q_{latent}^T$ due to a small difference between the initial temperatures of ice and water (Kerr and McConnochie 2015), we assume no heat flux into the ice, and express the heat flux from water as

$$\begin{aligned} Q_w^T = -\rho _0 c_w \kappa _T \textbf{n} \cdot \nabla T \big |_b, \end{aligned}$$

(11)

where $c_w$ is the specific heat of water, $\kappa _T$ thermal diffusivity of water, $\textbf{n}$ the unit vector normal to the ice boundary and the symbol $|_b$ indicates that the temperature gradient is taken at the ice boundary. Equations (10) and (11) result in a Neumann condition for water temperature at the ice/ocean boundary

$$\begin{aligned} \textbf{n} \cdot \nabla T\big |_b = \frac{\rho _i L_i}{\rho _0 c_w \kappa _T} V. \end{aligned}$$

(12)

Similarly, we derive a boundary condition for salinity from the conservation equation

$$\begin{aligned} Q_i^S - Q_w^S = Q^S_{brine}, \end{aligned}$$

(13)

where $Q_w^S = -\rho _0 \kappa _S\, \textbf{n} \cdot \nabla S|_b$ is the flux of salt from the water and $Q_i^S$ the flux of salt to the ice. This is balanced by the brine salinity flux $Q_{brine}^S = \rho _0 V (S_i-S_b)$ required to maintain the ice/ocean interface salinity $S_b$, which corresponds to the melting/freezing temperature $T_b$ (see Eq. (15)). We neglect the salinity flux to the ice, and assume $S_i=0$, which leads to a Neumann condition for salinity

$$\begin{aligned} \textbf{n} \cdot \nabla S\big |_b = \frac{\rho _i}{\rho _0 \kappa _S} S_b V. \end{aligned}$$

(14)

2.1.2 Three-equation formulation

Conditions (12) and (14) are defined in terms of the melt rate V and salinity of the ice/ocean interface $S_b$. We compute those quantities using the three-equation formulation (Holland and Jenkins 1999). The three-equation formulation involves using the freezing temperature $T_b$ dependence on the interface salinity

$$\begin{aligned} T_b = a S_b + b + c p_b, \end{aligned}$$

(15)

where $p_b$ is the pressure at the interface, and a, b, c are constants. Following Gayen et al. (2016), we use a simplified version $T_b = a S_b$ with $a = -0.06$ 1/psu, where salinity is expressed in practical salinity units (psu), which are equivalent to parts per thousand ($\permille$) or [g/kg]. This simplification is valid for the test case used in this paper, where the 1m domain depth does not provide a significant variation in pressure $p_b$. For more general cases we use empirical values for a, b, c from Holland and Jenkins (1999). In addition, we use Eqs. (10), (13) with approximations to temperature and salinity gradients (Jenkins et al. 2001)

$$\begin{aligned} c_i V\left( T_i-T_b\right) + c_w\gamma _T(T_w-T_b)&= V L_i, \end{aligned}$$

(16)

$$\begin{aligned} \gamma _S(S_w-S_b)&= V S_b, \end{aligned}$$

(17)

where $T_i$ is the internal temperature of ice, $\gamma _T$ and $\gamma _S$ are thermal and salinity exchange velocities, $c_i$ and $c_w$ are the specific heats of ice and water. $T_w$ and $S_w$ are the temperature and salinity of water at a certain distance from the interface. In the results presented in this paper, we chose $T_w = T \big |_b$ and $S_w = S \big |_b$, meaning that for the purpose of Eqs. (16) and (17) we take the water properties at the ice boundary as our $T_w$ and $S_w$ and note that they are not equal to the interface properties $T_b$ and $S_b$. This approximation is only used to compute the melt-rate and interface salinity required by boundary conditions (12), (14), which will affect the near-interface conditions simulated by the Navier–Stokes equations.

2.1.3 Restoring condition

The restoring condition introduces an additional body force in the selected volume which forces a quantity q (e.g., T, S) to a prescribed profile $q_0$:

$$\begin{aligned} F_r(t) = \frac{1}{\Delta t_r}(q_{0} - q), \end{aligned}$$

(18)

where $\Delta t_r$ is the time-scale (restoring time) over which the restoring happens. The restoring term is added to the right-hand-side of Eq. (3) only for the elements which belong to the restoring volume. This condition is typically used near the outflow from the domain, either to stabilize the flow close to the no-stress outflow, or while modeling the interaction of the fjord water with the open ocean, where we prescribe restoring to the reference $T_0$ and $S_0$ profiles.

2.2 Time integration

NUMO follows the classical fractional step method with a stiffly-stable pressure correction scheme (Karniadakis et al. 1991). It consists of breaking the time-step into three sub-steps. First, we take the explicit step involving only the non-linear and forcing terms to form an intermediate variable $\hat{\textbf{q}} = [\hat{\textbf{u}}^{\mathcal {T}}, \hat{T'}, \hat{S'}]^{\mathcal {T}}$:

$$\begin{aligned} \frac{\hat{\textbf{q}} - \sum _{k=0}^{J_i}\alpha _k\textbf{q}^{n-k}}{\Delta t} = \sum _{k=0}^{J_e}\beta _k \left( -\textbf{u}^{n-k} \cdot \nabla \textbf{q}^{n-k} + \textbf{G}(\textbf{q}^{n-k})\right) \end{aligned}$$

(19)

where $\textbf{q} = [ \textbf{u}^{\mathcal {T}}, T', S']^{\mathcal {T}}$ is a vector of variables, $\Delta t$ is the time-step, constants $J_i$ and $J_e$ define the order of the integration scheme, and $\alpha _k,\ \beta _k$ are the coefficients of the stiffly-stable scheme. Throughout the paper we use $J_i = J_e = 2$ for second-order time accuracy. Superscript $^n$ symbolizes the quantity taken at a time-level $t^n$, and the values of the coefficients are given in Karniadakis et al. (1991). The source terms are defined as $\textbf{G}(\textbf{q}) = [(\frac{\rho '}{\rho _0}g\textbf{k} - 2\varvec{\Omega } \times \textbf{u})^\mathcal {T}, 0, 0]^\mathcal {T}$.

Next, we find the pressure gradient, which when applied to the preliminary velocity $\hat{\textbf{u}}$ will result in a divergence-free velocity field

(20)

where ${p'}^{n+1}$ is the solution of the Poisson equation

$$\begin{aligned} \frac{1}{\rho _0}\Delta {p'}^{n+1} = \nabla \cdot \left( \frac{\hat{\textbf{u}}}{\Delta t}\right) \end{aligned}$$

(21)

with high-order boundary conditions (Karniadakis et al. 1991)

$$\begin{aligned} \textbf{n} \cdot \nabla {p'}^{n+1} = \textbf{n} \cdot \left( \sum _{k=0}^{J_e-1}\beta _k \left( -\textbf{u}^{n-k} \cdot \nabla \textbf{u}^{n-k}+ \textbf{G}(\textbf{u}^{n-k}) +\nu \nabla \times (\nabla \times \textbf{u}^{n-k}) \right) \right) , \end{aligned}$$

(22)

where $\nu$ is the dynamic viscosity coefficient. This approach circumvents the LBB stability condition when using equal order approximations to u and p (Karniadakis et al. 1991).

To complete the time-step, we apply the diffusion term to the updated variable vector

(23)

where the $\circ$ symbol represents the Hadamard product ($(\textbf{a}\circ \textbf{b})_i = a_i b_i$), $\kappa _T,\ \kappa _S$ are the thermal and salinity diffusivities, $\varvec{\nu } = [\nu , \nu , \nu ]^T$ a vector of viscosity coefficients, and $\gamma _0$ is another coefficient of the stiffly-stable scheme. Rearranging (23) leads to a Helmholtz equations for $\textbf{q}^{n+1}$ with boundary conditions defined by the physics of the problem (see Sect. 2.1). Since the Helmholtz problems for each velocity component, temperature, and salinity are decoupled (except for some choices of velocity boundary conditions, not used in this paper), we can solve them separately rather than as one monolithic system. This means that at each time-step we solve one Poisson problem for pressure, and five Helmholtz problems for the components of $\textbf{q}$.

2.3 Spatial discretization

NUMO is part of the Galerkin Numerical Modeling Environment (GNuME) (Giraldo 2016) framework, which offers a choice of continuous Galerkin (CG) and discontinuous Galerkin (DG) methods. The details can be found in Abdi and Giraldo (2016). Here we summarize the implementation of the Neumann boundary conditions in the CG method, as it was used to model the ice/ocean boundary.

We divide the domain $\Omega \in \mathbb {R}^3$ into $N_e$ non-overlapping hexahedral elements. In the case of two dimensional simulations, we use quadrilateral elements. Within each element $\Omega _e$, we create a grid of M nodal points using Legendre–Gauss–Lobatto distribution (Giraldo 2020), and define Lagrange polynomial basis functions $\psi _j$ such that their value is 1 at the corresponding node j, and 0 on all other nodes. We use the basis functions to expand the solution $\textbf{q}(\textbf{x},t)$ inside the element $\Omega _e$:

$$\begin{aligned} \textbf{q}(\textbf{x},t) \approx \textbf{q}_N^{(e)} (\textbf{x}, t) = \sum _{j=1}^{M}\psi _j(\textbf{x})\textbf{q}_j^{(e)}(t), \end{aligned}$$

(24)

where superscript $^{(e)}$ denotes the element-based entity and $\textbf{q}_j^{(e)}$ is the expansion coefficient corresponding to node j.

We will demonstrate the CG method on the example of the Poisson equation

$$\begin{aligned} \nabla ^2 q(\textbf{x}) = f(\textbf{x}), \end{aligned}$$

(25)

which is a generic version of the pressure equation (21) and can be easily adapted to the Helmholtz Eq. (23). To complete the system, we include the boundary conditions of both Dirichlet and Neumann types prescribed at boundaries $\Gamma _D$ and $\Gamma _N$ respectively:

$$\begin{aligned} q\big |_{\Gamma _D} = g_D(\textbf{x}), \qquad \textbf{n} \cdot \nabla q\big |_{\Gamma _N} = g_N(\textbf{x}). \end{aligned}$$

(26)

We expand both the solution $q(\textbf{x})$ and the right-hand-side $f(\textbf{x})$ using approximation (24), substitute the approximations to Eq. (25), multiply by a test function $\psi _i$ and integrate within each element:

$$\begin{aligned} \int _{\Omega _e} \psi _i \nabla ^2 q^{(e)}_N d\Omega _e = \int _{\Omega _e} \psi _i f_N^{(e)} d\Omega _e. \end{aligned}$$

(27)

Next, we use integration by parts and the divergence theorem on the left-hand-side of (27) to obtain

$$\begin{aligned} \int _{\Gamma _e} \textbf{n} \cdot (\psi _i \nabla q_N^{(e)}) d\Gamma _e- \int _{\Omega _e} \nabla \psi _i \cdot \nabla q_N^{(e)} d\Omega _e = \int _{\Omega _e} \psi _i f_N^{(e)} d\Omega _e. \end{aligned}$$

(28)

The first term on the left-hand-side is used to impose Neumann boundary conditions on the element faces which are also domain boundaries

$$\begin{aligned} \int _{\Gamma _e/\Gamma _N} \textbf{n} \cdot (\psi _i \nabla q_N^{(e)}) d\Gamma _e- \int _{\Omega _e} \nabla \psi _i \cdot \nabla q_N^{(e)} d\Omega _e = \int _{\Omega _e} \psi _i f_N^{(e)} d\Omega _e - \int _{\Gamma _N} \psi _i g_N d\Gamma _N. \end{aligned}$$

(29)

The boundary term on the left-hand-side will vanish on the inter-element edges due to the direct stiffness summation operation (not shown), which enforces continuity across element interfaces and results in the global representation of the discretization. For details of the implementation of the Dirichlet condition and direct stiffness summation, we refer the reader to Giraldo (2020).

2.4 Unstructured mesh

The goal of the NUMO project is to create a model which is capable of modeling complex and relatively small-scale fjord geometries using unstructured meshes and high-order CG/DG methods. The numerical methods in GNuME are capable of supporting arbitrary unstructured meshes (Marras et al. 2015) both as static and non-conforming adaptive grids (Kopera and Giraldo 2014, 2015). The mesh connectivity and information is handled by the parallel p4est library (Burstedde et al. 2011). In this paper we focus on static unstructured meshes only. We use the GMSH (Geuzaine and Remacle 2009) mesh generator, which is capable of creating 2D quadrilateral unstructured meshes, and also 3D hexahedral meshes by subdividing tetrahedral grids, or extruding 2D quadrilateral meshes in the third dimension. We use GMSH’s ability to label physical boundaries and elements to prescribe boundary conditions and restoring zones.

3 Results

To validate the model, we present the results of several test cases. The Kovasznay flow test (Sect. 3.1) checks the convergence rates of the CG method compared with the analytic solution. The lock-exchange (Sect. 3.2) and density current (Sect. 3.3) cases compare buoyancy-driven flow in 2D and 3D domains with results in the literature. Finally, we compare the ice/ocean interaction simulation (Sect. 3.4) against a direct numerical simulation and laboratory experiment.

3.1 Kovasznay flow

The Kovasznay flow (Kovasznay 1948) is a steady-state analytic solution to the incompressible Navier–Stokes equations given by

$$\begin{aligned} u(x,y) = 1 - e^{\lambda x}\cos (2\pi y),\quad v(x,y) = \frac{\lambda }{2\pi }e^{\lambda x}\sin (2\pi y),\quad p(x,y) = \frac{1}{2}(1-e^{2\lambda x}), \end{aligned}$$

where $\lambda = \frac{Re}{2} -\sqrt{\frac{Re^2}{4} + 4\pi ^2}$ and $Re = 40$ is the Reynolds number. We run it in the domain $[-0.5, 1]\times [-0.5, 0.5]$, with the initial condition equal to the exact solution. We then take a single time-step to assess the spatial convergence error. Starting the simulation from $\textbf{u}=0$ initial condition gives the same result.

Fig. 1

Streamlines of the Kovasznay flow (a) and a sample of an unstructured mesh used in the test (b). Higher resolutions were obtained by subdividing elements of the mesh

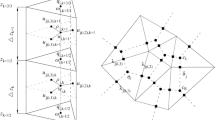
Figure 1a shows the streamlines and domain extent of this test. We run three sequences of simulations with increasing element resolution, each for different polynomial expansion order $N_p$. We repeat the same experiment on a structured mesh of square elements ($6\times 4$ elements in the least refined case) and an unstructured mesh shown in Fig. 1b. The unstructured mesh was generated such that the grid is refined near the strong gradient in the solution, located close to the left end of the domain. We have specified the element size on the left end to be three times smaller than on the right boundary.

Fig. 2

Spatial convergence of the $L_2$ error for different polynomial orders using the Kovasznay flow test with (a) structured and (b) unstructured mesh. The error is plotted against the square root of the total number of nodal points. In panel (b) the dashed lines represent the convergence lines from panel (a). The numbers by the lines are the slopes in a log-log plot

In Fig. 2, the $L_2$ error between the numerical and analytic solution for horizontal velocity is plotted against the square root of the total number of nodal points ($N_{pts}$). We use this measure for resolution to be able to directly compare the convergence on structured (panel (a)) and unstructured (panel (b)) meshes. We expect the $L_2$ error to decline at a rate of $N_p+1$ (Deville et al. 2002, sec. 2.6). The values of computed convergence rates are plotted above the lines corresponding to each $N_p$ sequence.

We obtain the convergence rates close to the theoretical expectation, except the $N_p=3$ simulation in panel (a). The important takeaway from this test is that the convergence rates for the unstructured mesh are comparable to those for the structured mesh. In fact, the values are slightly higher, which may be due to increased resolution in the left part of the domain, where the wake of the Kovasznay flow occurs.

3.2 Lock-exchange

The lock-exchange test case simulates the interaction of two bodies of water of different density initially placed next to each other in a tank of dimensions 0.8 m $\times$ 0.1 m. The density perturbation is achieved by setting the temperature difference between the fluids $\Delta T = 1 ^\circ C$. We use a Grashof number $Gr = g \Delta \rho H^3\nu ^{-2} = 1.25 \times 10^6$, where $\Delta \rho$ is the density difference corresponding to $\Delta T$, $H=0.1$ m is the height of the domain, and $\nu =10^{-6}\ m^2s^{-1}$ is the fluid viscosity. We use thermal conductivity $\alpha _T = 10^{-3}$ in the linearized equation of state (4). We run the simulations for two different choices of Prandtl number $Pr=\nu \kappa _T^{-1}=6.74$ and $Pr=0.71$.

We used a structured, uniform mesh of $512 \times 64$ elements and basis functions of order $N_p=4$, giving a total number of nodal points $N_{pts}=819,200$. Taking the average distance between nodal points as an effective resolution, we get $\Delta x = \Delta y \approx 0.0015$ m. The time-step was $\Delta t = 0.0025$ s. All the walls were modeled as free-slip adiabatic boundaries, except the bottom wall where we applied the no-slip condition.

Fig. 3

Snapshots of the temperature field of the lock-exchange test case for different times (a) $t = 250s$, (b) $t = 500s$, (c) $t = 1000s$

Figure 3 shows three snapshots of the temperature field at times 250 s, 500 s and 1000 s (panels (a), (b), (c), respectively). Blue color represents cold fluid and red represents warm fluid. Panel (a) compares well visually with similar results reported in Hiester et al. (2011). To provide a more quantitative comparison, we compared the velocities of hot/cold fronts at the top (free-slip) and bottom (no-slip) walls. Figure 4 presents a comparison of the front speeds $u_f$, reported as a non-dimensional Froude number $Fr = u_f\left( \sqrt{\frac{\Delta \rho }{\rho _0}gH}\right) ^{-1}$, as a function of the distance from the initial front position. Lines represent the NUMO results with $Pr = 6.74$ for no-slip (dashed line) and freeslip (solid line) fronts, which compare very well with the results by Hiester et al. (2011) (markers) throughout the entire length of the domain. It is worth to note that the Hiester et al. (2011) simulation was performed with no explicit thermal diffusivity, so nominally $Pr = \infty$.

Fig. 4

Front velocity Froude number for no-slip and free-slip boundary conditions as a function of the distance from $x=0$. We compare NUMO (lines) with the results reported in Hiester et al. (2011) (markers)

Table 1 Comparison of the average Froude number (Fr) in the steady front velocity regime for different Prandtl numbers (Pr)

Table 1 compares the average Fr computed for the steady front velocity regime between $x=0.2$ m and $x=0.3$ m for different settings of Pr number. NUMO compares well with the simulation by Hiester et al. (2011), even though the reference result was obtained using much higher resolution ($0.25 \times 10^{-3}$ m). The result by Fringer et al. (2006), even though run with no explicit thermal diffusivity, shows a slower front than other results, which can be attributed to relatively high numerical diffusion of the finite volume method. Our result is also quite close to the experimental study by Simpson and Britter (1979), which used a similar Pr. Higher Gr in this case explains a slightly faster front. NUMO compares well with the DNS simulation Härtel et al. (2000) for the lower value of Pr, as well as the three-dimensional simulation in Cantero et al. (2007) with slightly higher Gr.

3.3 Density current on a slope

The density current on a slope test case was previously used by Özgökmen et al. (2004) in both two- and three-dimensional configurations to investigate the overflow-induced mixing and benchmark the development of a three-dimensional non-hydrostatic ocean model capable of simulating bottom gravity currents. Here we compare NUMO against this result to further validate the model in a fully three-dimensional test with a vertically unstructured mesh, representative of a Greenland tidewater fjord.

Fig. 5

Snapshots of the salinity field of the density current case. Only salinity $S>0.1\ \permille$ is visible, with warm colors indicating more salt concentration up to $1\ \permille$. Panel a presents the initial condition, while panel b shows volume rendering of salinity at $t=8000$ s. The three-dimensional structure of the flow is triggered by a slight span-wise perturbation of the initial condition.

The domain dimensions are 10 km $\times$ 2 km in the horizontal directions x and y respectively, with the ocean depth varying linearly from 400 m at $x = 0$ to 1 km at $x=10$ km. The mesh, visible in Fig. 5, is generated initially in the vertical x-z plane, and then extruded in the span-wise (y) direction. The smallest element size is 25 m by 25 m in x-z directions and 100 m in the y direction. The largest element near the top is approximately 100 m in each direction. We used polynomial order $N_p = 4$ which results in the effective resolution varying between 6.25 m near the bottom to 25 m near the surface in the x-z plane, and is uniformly 25 m in the span-wise direction. The time-step of 0.25 s results in a Courant number not exceeding 0.39 throughout the simulation. In the reference simulation of Özgökmen et al. (2004), the smallest effective resolution in a structured mesh was approximately 16 m by 2 m by 20 m in x, y, z directions, respectively. The authors report Courant number below 1 for a time step of 0.85 s.

The initial condition (Fig. 5a, see Özgökmen et al. (2004) for details) for salinity is

$$\begin{aligned} S = \frac{1}{2}\exp \left[ - \left( \frac{x}{1+a\sin (\pi y)} \right) ^{20}\right] \times \left[ 1 - \cos \left( \pi \frac{1-z}{0.4}\right) \right] . \end{aligned}$$

The velocity is initially zero in the entire domain, however a time dependent velocity profile is prescribed at the inlet ($x=0$) boundary

$$\begin{aligned} u_{in} = 0.8 u_{max} (-1.25 + 46.875 z^2 - 244.14 z^4), \end{aligned}$$

where $u_{max}$ is the current front velocity (diagnosed as maximum velocity) in the domain, and the total net flux to the domain is zero. The outflow boundary is set as a no-stress outflow condition, the bottom is a no-slip wall, and the other boundaries are free-slip walls. This test also validates the anisotropic viscosity implementation, which is a common feature in ocean models. Following Özgökmen et al. (2004), we chose the horizontal viscosity $\nu _h = 1.17 m^2/s$ and vertical viscosity $\nu _v = 2.34 \times 10^{-2} m^2/s$. The Schmidt number is $Sc = \frac{\nu }{\kappa _S} = 1$, so salinity diffusivities are equal to viscosities in the horizontal and vertical directions. Additionally, we set the salinity expansion coefficient to $\alpha _S = 7 \times 10^{-4}$ 1/psu, which led to Rayleigh number $Ra = 5 \times 10^6$.

Fig. 6

Normalized front speed $u_f/u_B$ for the density current test. Comparison is made with the simulation of Özgökmen et al. (2004) (circles) and the experiment of Monaghan et al. (1999) (dashed line - dotted lines indicate measurement error)

To compare the results, in Fig. 6 we plot the normalized front velocity $u_f/u_B$ over time, where the front velocity is derived from the spanwise-averaged front position, obtained by finding the maximum extent of a spanwise averaged $S=0.1\ \permille$ contour. The velocity scale $u_B = (g'Q)^{1/3}$ is computed using the reduced gravity $g' = \frac{\Delta \rho }{\rho _0}$ and spanwise-averaged volume flux of salty water into the domain Q. The results are in good agreement with the reference simulation (Özgökmen et al. 2004) (circles). The dashed (orange) band is the experimental result obtained for steady-state flow (Monaghan et al. 1999). The NUMO result fits within the measurement uncertainty bands, indicating good agreement with the laboratory experiment.

3.4 Ice/ocean interface

Following Gayen et al. (2016), we constructed a simulation where an ice block is immersed in the saltwater of initially constant temperature and salinity. We set the initial T and S to the reference values $T_0 = 2.3\, ^\circ {C}$ and $S_0 =35\, \permille$. The extents of the 2-dimensional domain are $x\in [0,\ 0.5]$ m by $z \in [0,\ 1]$ m with an ice face at $x=0$ and a restoring zone at $x > 0.2$ m where we relax the temperature and salinity field to the initial values using restoring time $\Delta t_r = 10$s (see Sect. 2.1.3). Our experimentation showed, however, that the restoring condition is not necessary for such short simulation times. The velocity boundary conditions were free-slip at all domain boundaries. We prescribed no-flux for both heat and salinity ($\textbf{n}\cdot \nabla T = 0$, $\textbf{n}\cdot \nabla S = 0$) at all boundaries, except at the ice interface, where the ice/ocean boundary condition described in Sect. 2.1 was used. The viscosity $\nu = 1.8\times 10^{-6}\ m^2s^{-1}$ and thermal and salinity diffusivities $\kappa _T = 1.285\times 10^{-7}\ m^2s^{-1}$, $\kappa _S = 1.8\times 10^{-8}\ m^2s^{-1}$ resulted in Prandtl number $Pr=14$ and Schmidt number $Sc = 100$. At the ice interface, to compute the boundary conditions (12), (14), we adjusted the salinity diffusivity to $Sc=2500$, following Gayen et al. (2016). The values for transfer velocities $\gamma _T = 1.68 \times 10^{-4}\ ms^{-1}$, $\gamma _S = 5.05 \times 10^{-6} ms^{-1}$ were computed from the initial values of $T_b$, $S_b$ in Gayen et al. (2016).

Fig. 7

Temperature (left panel) and salinity (right panel) fields at time $t=72$ s. Darker colors indicate T and S below the reference values $T_0 = 2.3\ ^\circ \textrm{C}$ and $S_0 = 35\ \permille$. The minimum value of salinity on the color bar was adjusted from $20\ \permille$ to $33\ \permille$ to improve visibility of low salinity regions near the surface

The mesh consisted of 48 by 96 elements in the x and z directions, respectively, with 8th order polynomial basis functions, resulting in an effective resolution of $\Delta x = \Delta z = 0.0012$ m. The simulation was run with a time-step $\Delta t = 0.013$ s corresponding to Courant number 0.13. A plot of instantaneous T and S fields in Fig. 7 shows the main features of this test case, including the geometric extents and the presence of a turbulent plume at the ice/ocean interface. The temperature and salinity boundary layers are presented in Fig. 8, where we show time-averaged profiles of T and S as a function of the distance from the ice/ocean interface.

Fig. 8

Time averaged profiles of temperature T (a) and salinity S (b) as a function of distance from the ice face near the ice/ocean interface, comparing the results of NUMO (solid blue line) with Gayen et al. (2016) (dashed orange line). The averaging time was chosen such that it averages only the quasi-steady state after the initial transients have passed (see Fig. 9). In dot-dash green line we include a NUMO result with double the number of elements in each direction, for an effective resolution of $\Delta x = \Delta z = 0.0006$ m

NUMO presents a steeper temperature gradient in the thermal boundary layer in Fig. 8(a). The resolution of the DNS simulation is much finer in the boundary region than in our simulation. One 8th order element in NUMO has dimensions $0.01 \times 0.01$ m, with 9 nodal points in each direction inside the element. This amounts to effective resolution of 0.00125 m. The DNS simulation has about 200 points in each direction inside an 0.01 m square. Assuming the smallest spacing, and neglecting the fact that the distribution of points in the DNS simulation is not uniform, gives the resolution of 0.00005 m. Despite this difference, the salinity profiles in the boundary layer in Fig. 8(b) are similar.

The discrepancy between the temperature profiles could be caused by a possible difference in the implementation of the ice/ocean boundary condition. For the computation of interface properties in the three-equation formulation, Eq. (17), we take the water temperature $T_w$ at the domain boundary ($x=0$), and assume that $T_b$ is some temperature of the interface which is not present in the fluid domain. Gayen et al. (2016) does not provide details of the boundary condition beyond stating it is formulated as heat and salinity flux. Other researchers, however, chose to use the water temperature outside the boundary layer (Kimura et al. 2014, for example). Further analysis in Fig. 11 shows that this discrepancy does not have a significant effect on the melt rate and interface temperature computed across a range of initial water temperatures $T_0$.

To test this further, we doubled the number of elements in our simulation. The result is shown as a green dotted line in Fig. 8. Both profiles are smoother, indicating that the oscillations visible in the salinity profile in Fig. 8 are due to only a single element resolving the boundary layer and it’s transition to far-field state. In the finer resolution simulation, those oscillations are not present, but a much sharper transition to far-field than in the DNS simulation persists, similarly like in the T profile. This indicates a qualitative difference in how higher-order polynomials resolve boundary layers compared to lower-order methods.

Fig. 9

Melt rate V (a) and interface temperature $T_b$ (b) as a function of time at mid depth ($z=0.5$ m). NUMO results are shown by the solid blue line, and Gayen et al. (2016) results by the dashed orange line. In green dot-dash line we include an increased resolution simulations with twice as many elements

Figure 9 shows a time history of the melt rate V (panel (a)) and interface temperature $T_b$ (panel (b)) at mid-depth. After the initial transients, the melt rate stabilized for $t>50$ s. This is in agreement with the reference result Gayen et al. (2016), but our value of V is slightly higher than that of the DNS simulation. The interface temperature takes longer to stabilize but eventually reaches the level about 0.1 $^{\circ }\textrm{C}$ above the reference simulation. When running the finer resolution simulation we did not observe a significant change in the quasi-steady value of $T_b$, but the value of V decreased to about $2 \mu$ m/s.

The initial transients in NUMO simulation look different than for the DNS reference. Although the onset of turbulence happens in about the same time, the value of $T_b$ in NUMO is initially significantly lower. We suspect that this is due to the same reason as the discrepancy between the profiles in Fig. 8. We will explore this issue further in an upcoming paper where we will compare different formulations of the ice/ocean boundary condition, including a Robin type.

Fig. 10

Instantaneous interface temperature $T_b$ (a) and melt rate V (b) profiles at time $t = 72$ s, comparing the results of NUMO (solid blue line) with Gayen et al. (2016) (dashed orange line). The time was chosen such that the simulation is in a quasi-steady state after the initial transients have passed

The instantaneous vertical profiles in Fig. 10 confirm that the interface temperature computed in NUMO matches that of the DNS simulation at the same value of t. There is a discrepancy in the instantaneous value of the melt rate, but this difference does not show in the time and space averaged results in Fig. 11(b).

Fig. 11

Depth and time-averaged interface temperature $T_b$ (a) and melt rate $\bar{V}$ (b), comparing the results of NUMO (filled blue circles) with those in Gayen et al. (2016) (orange squares), and laboratory experiment of Josberger and Martin (1981) (green triangles). The averaging time was chosen such that we avoid the initial transients

To further validate the model, in Fig. 11 we plot the time and face averaged interface temperature and melt rates obtained for a range of initial water temperatures $T_0$. The NUMO results match well with the DNS Gayen et al. (2016) and are in good agreement with the experiment Josberger and Martin (1981). The closeness of both simulation results may be a consequence of us calculating the temperature and salinity exchange velocities $\gamma _T$ and $\gamma _S$ in Eqs. (16) and (17) based on the initial values of $T_b = T_0$ and $S_b = S_0$ in the DNS simulation. The choice of the exchange velocity values gives us room to explore possibly better fits with the experimental data in the future.

4 Conclusion and future directions

The results presented above verify the high-order convergence of the numerics used in the NUMO model and validate it on a range of test cases where the buoyancy forces are a dominant driver of the flow. We get excellent agreement with other simulations and laboratory experiments in all the tests. The ice/ocean interface test case shows that the ice/ocean boundary condition produces melt rate predictions which are in the range of the direct numerical simulation and laboratory experiment. This was achieved using significantly lower resolution than the DNS, but with high-order polynomial basis functions.

The ice/ocean boundary condition presented here is a variation of the classic three-equation formulation used by many ocean models attempting this problem. We have posed it in terms of the Neumann boundary condition with some assumptions about the thermodynamics of the ice melting. Most notably, we have assumed that the interface temperature and salinity are not the temperature and salinity of the water at the ice/ocean interface but rather some measure of properties of the ice/water mixture. In a forthcoming paper, we will discuss various possibilities of choosing the location of water temperature $T_w$ and its impact on the melt rate. We will experiment with using the Robin boundary condition to describe the ice interface more accurately.

The work in this paper was achieved using arbitrarily unstructured quadrilateral and hexahedral meshes. Although all the test cases used simplified geometries, we are now ready to try more complex cases, similar to realistic Greenland fjords. The current limitation lies in generating fully unstructured, hexahedral grids. We can use GMSH to generate a 2D unstructured grid for the ocean’s surface and extrude it in the vertical direction, which is similar to the approach presented in the density current case, except the extrusion there happened in the spanwise direction. This approach would require us to incorporate the bathymetry information in NUMO after the mesh is read. An alternative approach is a fully unstructured 3D mesh generator, but state-of-the-art software capabilities in hexahedral mesh generation are currently very limited.

At the moment, NUMO assumes a rigid lid condition at the ocean surface. We plan to continue the work on implementing Arbitrary Lagrangian Eulerian method to represent a dynamic boundary. The model also does not use any sub-grid-scale parameterizations for turbulence. The GNuME framework contains a set of LES parameterizations, but they have not been used in the test cases presented here. We will evaluate the turbulence parameterization on another set of test cases in a future publication.

The tests presented in this paper indicate significant benefits of high-order methods in NUMO for variable-scale modeling of ice/ocean interfaces. The mid-term trajectory for our model is to evaluate it in more realistic fjord geometries and in the long-term test it with and implement it in global circulation models.