On a fuzzy cash flow model with insurance applications

Abstract

We consider a discrete-time model for the cash flow of an insurance portfolio/business in which the net losses are random variables, while the return rates are fuzzy numbers. We choose the shape of these fuzzy numbers trapezoidal, Gaussian or lognormal, the last one having a more flexible shape than the previous ones. For the resulting fuzzy model, we evaluate the fuzzy present value of its wealth; then, we propose an approximation for the chance of ruin and a ranking criterion which could be used to compare different risk management strategies.

1 Introduction

The development of the fuzzy mathematics of finance started with Buckley (1987), who introduced fuzzy analogues of the future and present values of a fuzzy cash amount. Further on, in insurance, Lemaire (1990) applied Buckley’s fuzzy concepts to compute fuzzy premiums, while other applications in insurance were studied by Ostaszewski (1993), Terceno et al. (1996), Huang et al. (2009), Andrés-Sánchez and González-Vila Puchades (2012) etc.; see also references therein and the survey of Shapiro (2004).

Much of the uncertainty in risk analysis can be regarded as rooted in the fuzziness of the information. By eluding probabilistic limitations, fuzzification could be an alternative to the stochastic approach for complex problems. This explains the extent to which fuzzy theory has lately been used to approach classical insurance problems, which are traditionally studied in a stochastic context. Moreover, since sometimes the uncertainty includes both randomness and fuzziness, if possible, they should be considered simultaneously. This is why in this paper, we consider a fuzzy approach of a discrete-time model for the cash flow of an insurance business/portfolio such that within each period, the net loss is considered to be a random variable (r.v.), while the return rate is assumed to be a fuzzy number; as a consequence, the corresponding present value of the insurer’s wealth becomes a fuzzy random variable.

The idea behind our fuzzy model is based on the fact that the uncertainty in the return rates can be quantified by fuzzy numbers as an alternative to random variables, making the models more tractable. Such fuzzy cash flows were also studied by Kaufmann and Gupta (1988), Ward (1989), or Chiu and Park (1994); the last one modeled the periodic payments and the discount rates by triangular fuzzy numbers. In this paper, we go further on and work with some fuzzy numbers having a more flexible shape, while the net losses are random variables.

Therefore, in Sect. 2, we briefly summarize some basic fuzzy concepts and obtain some formulas needed in our study. In Sect. 3, we present the discrete-time model and its fuzzy form; then, we discuss its possible application to ruin theory, and we suggest a ranking criterion for such fuzzy models, mainly based on simulation. In Sect. 4, we numerically illustrate the results from previous section considering two particular loss distributions and some specific fuzzy numbers for the return rate. We end with several conclusions.

2 Some basic fuzzy concepts

We start by recalling the fuzzy concepts needed in next sections.

2.1 Fuzzy numbers

A fuzzy set $A$ can be defined by the set of ordered pairs $\left\{ \left( x;\mu _{A}\left( x\right) \right) \left| x\in U\right. \right\} ,$ where $U$ is a set of elements and $\mu _{A}:U\rightarrow [0,1]$ is the membership function; then $\hbox {Supp}(A) =\left\{ x\in U\left| \mu _{A}\left( x\right) >0\right. \right\}$ represents the support of $A$. The $\alpha$-cut, $0\le \alpha \le 1,$ of a fuzzy set $A$ is defined as

$$\begin{aligned} A_{\alpha }=\left\{ \begin{array}{ll} \left\{ x\in U\left| \mu _{A}\left( x\right) \ge \alpha \right. \right\} &{} \quad \hbox {if }\,\alpha >0 \\ \hbox {Cl}\left( \hbox {Supp}\left( A\right) \right) &{} \quad \hbox {if }\,\alpha =0 \end{array}\right. , \end{aligned}$$

where $\hbox {Cl}\left( \hbox {Supp}\left( A\right) \right)$ denotes the closure of the support of $A$.

A fuzzy set $A$ is called convex if $A_{\alpha }$ is a convex subset of $U$ for all $\alpha \in \left[ 0,1\right] .$ If there exists at least one point $x\in U$ with $\mu _{A}\left( x\right) =1,$ the fuzzy set $A$ is called normal $,$ while $x$ is a mode of $A$. If the mode exists and is unique, we will denote it by $m_{A}$.

A fuzzy number (f.n.) is a special normal, convex fuzzy set of the real line with at least piecewise continuous membership function, whose highest membership values are clustered around a given real number (the mode). Therefore, the $\alpha$-cut of a f.n. A is in fact an interval $\left[ A_{\alpha }^{L},A_{\alpha }^{R}\right]$, where $A_{\alpha }^{L}=\inf \left\{ x\in U\left| \mu _{A}\left( x\right) \ge \alpha \right. \right\}$ and $A_{\alpha }^{R}=\sup \left\{ x\in U\left| \mu _{A}\left( x\right) \ge \alpha \right. \right\}$. If $\hbox {Supp}\left( A\right) \subseteq \left( 0,\infty \right) ,$ the f.n. $A$ is called positive. Some specific fuzzy numbers will be introduced in Sect. 2.3.

For two fuzzy numbers $A$ and $B$, the arithmetic operation $A(*)B$ is defined by the membership function $\mu _{A(*)B}\left( z\right) =\sup _{z=x*y}\min \left\{ \mu _{A}\left( x\right) ,\mu _{B}\left( y\right) \right\} ,$ where $*\in \left\{ +,-,\times ,/\right\}$. The power of a f.n. $A$ is recursively defined as $A^{n}=A\otimes A^{n-1},n=2,3,\ldots ,$ while $\mu _{A^{-1}}\left( x\right) =\mu _{A}\left( \frac{1}{x}\right)$ for any $x\ne 0$. We will also use the symbols $\sum$ and $\prod$ to denote the multiple fuzzy sum and, respectively, product, i.e.,

$$\begin{aligned} \sum _{i=1}^{n}A_{i}=A_{1}\oplus \cdots \oplus A_{n}, \quad \prod _{i=1}^{n}A_{i}=A_{1}\otimes \cdots \otimes A_{n}. \end{aligned}$$

Therefore, the meaning of $\sum$ and $\prod$ will depend on the context, but this should not be a problem since crisp numbers are particular cases of fuzzy numbers.

As, e.g., in Gao and Zhang (2009), the $\alpha$-cuts can be used to easier express fuzzy arithmetic operations. More precisely, for two fuzzy numbers $A$ and $B$, we have

$$\begin{aligned} \left[ A\oplus B\right] _{\alpha }&= \left[ A_{\alpha }^{L}+B_{\alpha }^{L},A_{\alpha }^{R}+B_{\alpha }^{R}\right] , \end{aligned}$$

(1)

$$\begin{aligned} \left[ A\ominus B\right] _{\alpha }&= \left[ A_{\alpha }^{L}-B_{\alpha }^{R},A_{\alpha }^{R}-B_{\alpha }^{L}\right] , \end{aligned}$$

(2)

$$\begin{aligned} \left[ A\otimes B\right] _{\alpha }&= \left[ \min \left\{ A_{\alpha }^{L}B_{\alpha }^{L},A_{\alpha }^{R}B_{\alpha }^{L},A_{\alpha }^{L}B_{\alpha }^{R},A_{\alpha }^{R}B_{\alpha }^{R}\right\} ,\right. \nonumber \\&\left. \qquad \max \left\{ A_{\alpha }^{L}B_{\alpha }^{L},A_{\alpha }^{R}B_{\alpha }^{L},A_{\alpha }^{L}B_{\alpha }^{R},A_{\alpha }^{R}B_{\alpha }^{R}\right\} \right] . \end{aligned}$$

(3)

Based on $\alpha$-cuts, Carlsson and Fuller (2001) defined the crisp expected value of a fuzzy number $A\$as $E\left[ A\right] =\int \nolimits _{0}^{1}\left( A_{\alpha }^{L}+A_{\alpha }^{R}\right) \alpha \hbox {d}\alpha$ and also introduced the possibilistic variance $\hbox {Var}\left[ A\right] =\frac{1}{2}\int \nolimits _{0}^{1}\left( A_{\alpha }^{R}-A_{\alpha }^{L}\right) ^{2}\alpha \hbox {d}\alpha$.

Another important issue consists of extending the natural ordering of real numbers to fuzzy numbers. In this sense, several ranking methods were developed, see e.g., Bortolan and Degani (1985) or Chen and Hwang (1992). Unfortunately, these methods present some drawbacks like nonconsistency, producing different rankings for the same numbers. Among them, we recall the rankings based on comparing the mode (i.e., the most promising value), the expected value (given above), some dominance indices, etc. In this paper, we shall use the area compensation method, see Fortemps and Roubens (1996). This method is based on the defuzzification function $\mathcal {F}$, defined for a f.n. $A$ by

$$\begin{aligned} \mathcal {F}\left( A\right) =\frac{1}{2}\int \limits _{0}^{1}\left( A_{\alpha }^{L}+A_{\alpha }^{R}\right) \hbox {d}\alpha . \end{aligned}$$

Then, the crisp ordering between two fuzzy numbers $A$ and $B$ is defined as

$$\begin{aligned} \left( A>B\ \Leftrightarrow \ \mathcal {F}\left( A\right) >\mathcal {F}\left( B\right) \right) \ \ \ \text {and}\ \ \ \left( A=B\ \Leftrightarrow \ \mathcal {F}\left( A\right) =\mathcal {F}\left( B\right) \right) . \end{aligned}$$

Note that $\mathcal {F}\left( A\right)$ represents the mean of the two areas defined by the vertical axis and by the left and, respectively, the right slope of $\mu _{A}$, which makes the above ordering easy to understand in terms of areas.

2.2 Fuzzy random variables

Introduced by Kwakernaak in 1978, the concept of fuzzy random variable was further developed in several papers from which we recall Puri and Ralescu (1986), Kruse and Meyer (1987), Liu and Liu (2003), etc.; in this paper, we shall use the definition of Puri and Ralescu (1986). In this sense, we assume that $\left( \varOmega ,F,\Pr \right)$ is a probability space, and we let $\mathcal {B}$ denote the collection of all Borel subsets of $\mathbb {R}$, while $\mathcal {S}$ denotes the set of all fuzzy numbers.

A fuzzy random variable (f.r.v.) is a function $X:\varOmega \rightarrow \mathcal {S}$ such that $\forall B\in \mathcal {B},\forall \alpha \in \left[ 0,1\right] ,\left\{ \omega \in \varOmega \left| X_{\alpha }\left( \omega \right) \cap B\ne \varnothing \right. \right\} \in F$, where $X\left( \omega \right)$ is a f.n. having the $\alpha$-cut $X_{\alpha }\left( \omega \right) =\left[ X_{\alpha }^{L}\left( \omega \right) ,X_{\alpha }^{R}\left( \omega \right) \right] .$ Note that, for fixed $\alpha$, the extremes of this $\alpha$-cut, i.e., $X_{\alpha }^{L},X_{\alpha }^{R}:\varOmega \rightarrow \mathbb {R},$ become themselves random variables that we call the infima and, respectively, suprema r.v., as in Andrés-Sánchez and González-Vila Puchades (2012). Based on these r.v.’s, Huang et al. (2009) defined of the mean chance Ch of the fuzzy random event $\left\{ X<0\right\}$ as

$$\begin{aligned} \hbox {Ch}\left\{ X<0\right\} =\frac{1}{2}\int \limits _{0}^{1}\left( \Pr \left( X_{\alpha }^{L}<0\right) +\Pr \left( X_{\alpha }^{R}<0\right) \right) \hbox {d}\alpha . \end{aligned}$$

(4)

If $X$ is a r.v. and $Y$ a f.n., we define the product $Z=XY$ by $Z\left( \omega \right) =X\left( \omega \right) \otimes Y$, which makes $Z$ a f.r.v. Assuming that the f.n. $Y$ is positive, the infima and suprema of $Z$ are given from (3) by, respectively,

$$\begin{aligned} Z_{\alpha }^{L}\left( \omega \right) =\left\{ \begin{array}{c} X\left( \omega \right) Y_{\alpha }^{L},\quad X\left( \omega \right) \ge 0 \\ X\left( \omega \right) Y_{\alpha }^{R},\quad X\left( \omega \right) <0 \end{array} \right. ,\quad \ Z_{\alpha }^{R}\left( \omega \right) =\left\{ \begin{array}{c} X\left( \omega \right) Y_{\alpha }^{R},\quad X\left( \omega \right) \ge 0 \\ X\left( \omega \right) Y_{\alpha }^{L},\quad X\left( \omega \right) <0 \end{array} \right. . \end{aligned}$$

From here, denoting by $F_{X}$ the cumulative distribution function (cdf) of $X$, we easily obtain the cdf’s of $Z_{\alpha }^{L}$ and $Z_{\alpha }^{R}$ to be

$$\begin{aligned} F_{Z_{\alpha }^{L}}\left( x\right) =\left\{ \begin{array}{c} F_{X}\left( x/Y_{\alpha }^{L}\right) ,\quad x\ge 0 \\ F_{X}\left( x/Y_{\alpha }^{R}\right) ,\quad x<0 \end{array} \right. ,\quad \ F_{Z_{\alpha }^{R}}\left( x\right) =\left\{ \begin{array}{c} F_{X}\left( x/Y_{\alpha }^{R}\right) ,\quad x\ge 0 \\ F_{X}\left( x/Y_{\alpha }^{L}\right) ,\quad x<0 \end{array} \right. . \end{aligned}$$

If $X$ and $Y$ are two f.r.v.’s, then an arithmetic operation on them is straightforward defined by $\left( X(*)Y\right) \left( \omega \right) =X\left( \omega \right) (*)Y\left( \omega \right)$, where $*\in \left\{ +,-,\times ,/\right\} .$ Again, the symbols $\sum$ and $\prod$ will also denote the multiple fuzzy form of the corresponding operations on f.r.v.’s.

The following proposition will be useful in next section.

Proposition 1

Let $X_{1},\ldots ,X_{n}$ be r.v.’s and let $Y_{1},\ldots ,Y_{n}$ be positive f.n.’s, $n\ge 1$. Then the sum $S_{n}=\sum _{j=1}^{n}X_{j}Y_{j}$ is a f.r.v. whose infima and suprema are given, respectively, by

$$\begin{aligned} S_{n,\alpha }^{L}\left( w\right) =\sum _{j=1}^{n}X_{j}\left( w\right) Y_{j,\alpha }^{L_{j}},\quad S_{n,\alpha }^{R}\left( w\right) =\sum _{j=1}^{n}X_{j}\left( w\right) Y_{j,\alpha }^{R_{j}}, \end{aligned}$$

(5)

where $L_{j}=\left\{ \begin{array}{ll} L,&{} X_{j}\left( w\right) \ge 0 \\ R,&{} X_{j}\left( w\right) <0 \end{array} \right.$   and   $R_{j}=\left\{ \begin{array}{ll} R,&{} X_{j}\left( w\right) \ge 0 \\ L,&{} X_{j}\left( w\right) <0 \end{array} \right.$.

Proof

Since $X_{j}$ is a r.v. and $Y_{j}$ a f.n., it follows that for all $j,X_{j}Y_{j}$ is a f.r.v., and hence their sum $S_{n}$ is also a f.r.v. Moreover, from (1) it is clear that

$$\begin{aligned} S_{n,\alpha }^{L}\left( w\right) =\sum _{j=1}^{n}\left[ X_{j}\left( w\right) Y_{j}\right] _{\alpha }^{L},\quad S_{n,\alpha }^{R}\left( w\right) =\sum _{j=1}^{n}\left[ X_{j}\left( w\right) Y_{j}\right] _{\alpha }^{R}, \end{aligned}$$

and the corresponding formulas (5) easily result using (3) as done above for $Z$.

2.3 Particular fuzzy numbers

In the following, we present some particular fuzzy numbers that will be used in next sections. Apart the well-known trapezoidal, triangular, and Gaussian f.n.’s, we define the lognormal-type f.n., whose membership function, based on the shape of the corresponding lognormal probability density function (pdf), is very flexible. We focus mainly on the $\alpha$-cuts that are involved in our formulas.

2.3.1 Trapezoidal and triangular fuzzy numbers

Let $Q=\left( a,m_{1},m_{2},b\right) ,a<m_{1}\le m_{2}<b,$ be a trapezoidal f.n. whose membership function is defined by

$$\begin{aligned} \mu _{Q}\left( x\right) =\left\{ \begin{array}{ll} \frac{x-a}{m_{1}-a},&{}\quad a\le x\le m_{1} \\ 1,&{}\quad m_{1}\le x\le m_{2} \\ \frac{b-x}{b-m_{2}},&{}\quad m_{2}\le x\le b \\ 0,&{}\quad \hbox {otherwise} \end{array} \right. . \end{aligned}$$

Its $\alpha$-cut is given by

$$\begin{aligned} Q_{\alpha }=\left[ \left( m_{1}-a\right) \alpha +a,\left( m_{2}-b\right) \alpha +b\right] . \end{aligned}$$

(6)

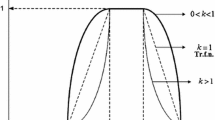
See right plot in Fig. 1 for an example of trapezoidal f.n. When $m_{1}=m_{2}=m,$ the trapezoidal f.n. becomes a triangular one having the unique mode $m$; we therefore denote this triangular f.n. by $\left( a,m,b\right)$.

Fig. 1

Left plot pdf shapes for $X$; Right plot shapes for $\mu _{Q}$

2.3.2 Gaussian fuzzy number

The Gaussian f.n. is also well known in the literature, and it is usually defined on the support $\left( -\infty ,\infty \right)$. For our purpose, its support must be $\left( 0,\infty \right)$. Therefore, we define the truncated Gaussian f.n. $Q$ by the membership function

$$\begin{aligned} \mu _{Q}\left( x\right) =\exp \left\{ -\frac{(x-m_{Q})^{2}}{2\sigma ^{2}} \right\} ,\quad x>0, \end{aligned}$$

(7)

where $m_{Q}>0$ is the mode and $\sigma >0$ is the standard deviation, which controls the shape (in Fig. 1, right plot, we present such a shape). This number could be seen as left-truncated in $x=0$. Its $\alpha$-cut has the limits

$$\begin{aligned} Q_{\alpha }^{L}=\left\{ \begin{array}{ll} m_{Q}-\sigma \sqrt{-2\ln \alpha },&{}\quad \alpha >\alpha _{\hbox {Gauss}} \\ 0,&{}\quad \alpha \le \alpha _{\hbox {Gauss}} \end{array} \right. ,\quad Q_{\alpha }^{R}=m_{Q}+\sigma \sqrt{-2\ln \alpha }, \end{aligned}$$

(8)

where $\alpha _{\hbox {Gauss}}=\mu _{Q}\left( 0\right) =\exp \left\{ -\left( m_{Q}/\sigma \right) ^{2}\big /2\right\}$. For the usual practical values of the parameters $m_{Q}$ and $\sigma$ considered in our study, $\alpha _{\hbox {Gauss}}$ is small enough to be approximated with 0.

2.3.3 Lognormal-type fuzzy number

We say that a f.n. $Q$ is of lognormal-type if its membership function is given by

$$\begin{aligned} \mu _{Q}\left( x\right) =\dfrac{\exp \left\{ c-\sigma ^{2}/2\right\} }{x} \exp \left\{ -\frac{1}{2\sigma ^{2}}\left( \ln x-c\right) ^{2}\right\} ,\ \ x>0, \end{aligned}$$

(9)

with real $c$ and positive $\sigma$. The constant $\exp \left\{ c-\sigma ^{2}/2\right\}$ insures that $\mu _{Q}\left( x\right) \le 1$ for all $x>0$ (see Fig. 1, right plot, for an example of $\mu _{Q}$). This f.n. has a unique mode $m_{Q}=\exp \left\{ c-\sigma ^{2}\right\} .$ As in Vernic and Ungureanu (2011), the $\alpha$-cut limits of $Q$ are

$$\begin{aligned} Q_{\alpha }^{L}=\exp \left\{ c-\sigma ^{2}-\sigma \sqrt{-2\ln \alpha } \right\} ,\ \ Q_{\alpha }^{R}=\exp \left\{ c-\sigma ^{2}+\sigma \sqrt{-2\ln \alpha }\right\} . \quad \end{aligned}$$

(10)

3 A fuzzy cash flow model for insurance

In the following, we obtain the fuzzy form of a discrete-time cash flow model used to evaluate the ruin probability of an insurance business/portfolio. The purpose of this fuzzification is to study the effect of some parameters of the model and to be able to compare different investment strategies and model modifications under fuzzy information.

3.1 The probabilistic model and its fuzzy form

We consider the following discrete-time model for the cash flow of an insurance business/portfolio: within period $j,j=1,2,\ldots ,n$, we denote by $X_{j}$ the net loss (i.e., total outcome minus income during period $j$, evaluated at the end of the period; this can also take negative values, which are in fact gains), and by $R_{j}$ the return rate (assuming that the company invests its surplus in both a risk-free bond and a risky stock). The initial capital put aside by the insurance company when starting this business is denoted by $u$. In a stochastic setting, $X_{j}$ and $R_{j}$ are random variables, while $u$ is constant. The present value of the insurer’s wealth corresponding to this cash flow considered over $n$ time periods in the future is

$$\begin{aligned} PV_{n}^{\hbox {stoch}.}=u-\sum _{j=1}^{n}X_{j}\prod \limits _{i=1}^{j}\left( 1+R_{i}\right) ^{-1}=u-\sum _{j=1}^{n}X_{j}\prod \limits _{i=1}^{j}Q_{i}^{-1}, \end{aligned}$$

(11)

where $Q_{i}=1+R_{i}$ represents the accumulation factor during period $i$. For this model, the usual probabilistic assumption is that the net losses are all independent, identically distributed (i.i.d.) random variables, and independent of the return rates; moreover, as it can be seen from real data, their distribution is usually asymmetric and long-tailed. For the return rates, a handy-for-calculation assumption is also i.i.d., but unfortunately, it is not very realistic. This assumption was surpassed in various ways, using approximate calculation based on extra-assumptions.

The main utility of the above model is to illustrate the cash flow of an insurance business or portfolio in order to evaluate its probability of ruin (see e.g., Tang and Tsitsiashvili 2004; for more details on the ruin probability see e.g., Asmussen and Albrecher 2010). Assuming it did not occur before, the ruin occurs at time $n$ if $PV_{n}^{\hbox {stoch}.}<0$. The probability of ruin by time $n$, also called finite time ruin probability, is defined by $\psi _{n}=\Pr \left( \min \nolimits _{1\le k\le n}PV_{k}^{\hbox {stoch}.}<0\right)$. Unfortunately, the finite time ruin probability is very difficult to evaluate and, as noted before, needs some extra-assumptions that can limit practical applications.

In the following, we restate the above model in a fuzzy framework by replacing the r.v.’s return rates with fuzzy numbers. Therefore, we keep the assumptions that the $X_{j}$s are i.i.d. r.v.’s and that $u$ and the number of time periods $n$ under study are both deterministic (crisp) values, but we now assume fuzzy return rates such that the accumulation factors $Q_{i}$ are positive fuzzy numbers. These fuzzy return rates are in fact estimates of the average periodical return rates represented as fuzzy numbers. For example, an actuary could estimate that during next year, the profitability will be around 5 %, with a minimum around 1 % and a maximum around 10 %; this could be modeled using a triangular f.n.

Buckley (1987) was the first to define the fuzzy present value of a fuzzy amount $X,$ with fuzzy return rate $R$ per period, $n$ periods in the future, as $PV(X,R,n)=X\otimes \left( 1\oplus R\right) ^{-n}$. Special attention must be paid to the case when $X$ has negative support.

Back to our model, we denote by $S_{n}=\sum _{j=1}^{n}X_{j}\prod \nolimits _{i=1}^{j}Q_{i}^{-1}=\sum _{j=1}^{n}X_{j}Y_{j}$ the fuzzy aggregate discounted losses by time $n,$ where $Y_{j}=\prod \nolimits _{i=1}^{j}Q_{i}^{-1}$. According to Proposition 1, $S_{n}$ is a f.r.v. Then, the fuzzy equivalent of (11) is

$$\begin{aligned} PV_{n}=u\ominus S_{n}. \end{aligned}$$

(12)

Note that since each $X_{j}$ can take positive values (i.e., proper losses), then the f.r.v. $PV_{n}$ might also be defined for negative values, in which case, for these negative values, the business/portfolio is considered to be in ruin at time $n$.

As already stated for our fuzzy model, the $X_{j}$s are i.i.d. as the generic variable $X$; we also assume that its mean is finite. Since $X$ represents a net loss, it is defined for both positive and negative values (i.e., proper losses and, respectively, proper gains). Moreover, it is natural to assume that $\mathbb {E}\left[ X\right] <0,$ i.e., in average, we expect to gain.

Another usual assumption in the stochastic context is that the $R_{j}$s are identically distributed. In our fuzzy model, we take the same average fuzzy return rate throughout the evaluation horizon, i.e., $R_{j}=R$ for all $j;$ from here, $Q_{j}=Q$ for all $j$, which yields $Y_{j}=Q^{-j},$ and hence $S_{n}=\sum _{j=1}^{n}X_{j}Q^{-j}$. We shall now have a closer look at the fuzzy number $Q=1\oplus R$. Since $R$ is a return rate, it is usually positive, but due to, e.g., the way crisis situations affect risky stocks, it can also become negative. Therefore, we assume that the support of $Q$ is $\left( 0,\infty \right) ,$ and from (3), it is easy to see that for a positive integer $j$, $\left[ Q^{j}\right] _{\alpha }=\left[ \left( Q_{\alpha }^{L}\right) ^{j},\left( Q_{\alpha }^{R}\right) ^{j}\right] ,$ so that $\left[ Q^{-j}\right] _{\alpha }=\left[ \left( Q_{\alpha }^{R}\right) ^{-j},\left( Q_{\alpha }^{L}\right) ^{-j}\right] .$ From Proposition 1, we obtain the infima and suprema r.v.’s of $S_{n}$ as

$$\begin{aligned} S_{n,\alpha }^{L}\left( \omega \right) =\sum _{j=1}^{n}X_{j}\left( \omega \right) \left( Q_{\alpha }^{R_{j}}\right) ^{-j},\quad S_{n,\alpha }^{R}\left( \omega \right) =\sum _{j=1}^{n}X_{j}\left( \omega \right) \left( Q_{\alpha }^{L_{j}}\right) ^{-j}, \end{aligned}$$

(13)

where $R_{j}=\left\{ \begin{array}{c} R,\ X_{j}\left( \omega \right) \ge 0 \\ L,\ X_{j}\left( \omega \right) <0 \end{array} \right.$ and $L_{j}=\left\{ \begin{array}{c} L,\ X_{j}\left( \omega \right) \ge 0 \\ R,\ X_{j}\left( \omega \right) <0 \end{array} \right.$. Moreover, using (2) into (12) yields

$$\begin{aligned} PV_{n,\alpha }^{L}=u-S_{n,\alpha }^{R},\quad PV_{n,\alpha }^{R}=u-S_{n,\alpha }^{L}. \end{aligned}$$

(14)

Remark 1

For fixed $\alpha$, consider the aggregate discounted losses r.v. given by

$$\begin{aligned} S_{n,\alpha }\left( \omega ;q_{1},\ldots ,q_{n}\right) =\sum _{j=1}^{n}X_{j}\left( \omega \right) \prod \limits _{i=1}^{j}q_{i}^{-1}, \end{aligned}$$

where $q_{i}\in \left[ Q_{\alpha }^{L},Q_{\alpha }^{R}\right] ,i=1,\ldots ,n$. Then the r.v.’s infima and suprema given in (13) represent lower and, respectively, upper approximations of the extreme values of $S_{n,\alpha }\left( \omega ;q_{1},\ldots ,q_{n}\right)$ with constraints on the $q_{i}s$, i.e.,

$$\begin{aligned} \left\{ \begin{array}{c} S_{n,\alpha }^{L}\left( \omega \right) \le \min \limits _{\begin{array}{c} q_{i}\in \left[ Q_{\alpha }^{L},Q_{\alpha }^{R}\right] \\ i=1,\ldots ,n \end{array}}S_{n,\alpha }\left( \omega ;q_{1},\ldots ,q_{n}\right) \\ S_{n,\alpha }^{R}\left( \omega \right) \ge \max \limits _{\begin{array}{c} q_{i}\in \left[ Q_{\alpha }^{L},Q_{\alpha }^{R}\right] \\ i=1,\ldots ,n \end{array}}S_{n,\alpha }\left( \omega ;q_{1},\ldots ,q_{n}\right) \end{array} \right. . \end{aligned}$$

Note that though more uncertain, $S_{n,\alpha }^{L}$ and $S_{n,\alpha }^{R}$ are easier to calculate than the solutions of the above optimization problems.

3.2 Approximating the chance of ruin and comparing risk management strategies

3.2.1 Mean chance of ruin

Starting from the f.r.v. present value (12), we construct the f.r.v. $PVm_{n}$ related to the risk of ruin at time $n$ and defined by the $\alpha$-cut $PVm_{n,\alpha }\left( \omega \right) =\left[ \min \nolimits _{1\le k\le n}PV_{k,\alpha }^{L}\left( \omega \right) ,\min \nolimits _{1\le k\le n}PV_{k,\alpha }^{R}\left( \omega \right) \right]$. Note that, since $\min \nolimits _{1\le j\le n}PV_{j,\alpha }^{L}\left( \omega \right) \le PV_{k,\alpha }^{L}\left( \omega \right) \le PV_{k,\alpha }^{R}\left( \omega \right)$ for any $k,1\le k\le n,$ it follows that

$$\begin{aligned} \min \limits _{1\le k\le n}PV_{k,\alpha }^{L}\left( \omega \right) \le \min \limits _{1\le k\le n}PV_{k,\alpha }^{R}\left( \omega \right) , \end{aligned}$$

(15)

hence the corresponding $\alpha$-cut is well defined. We then evaluate the following ruin probabilities corresponding to the infima and suprema of $PVm_{n}$

$$\begin{aligned} P_{n,\alpha }^{L}=\Pr \left( \left\{ \omega \left| \min \limits _{1\le k\le n}PV_{k,\alpha }^{R}\left( \omega \right) <0\right. \right\} \right) ,\ P_{n,\alpha }^{R}=\Pr \left( \left\{ \omega \left| \min \limits _{1\le k\le n}PV_{k,\alpha }^{L}\left( \omega \right) <0\right. \right\} \! \right) \!. \end{aligned}$$

From (15), we have $\left\{ \omega \left| \min \nolimits _{1\le k\le n}PV_{k,\alpha }^{R}\left( \omega \right) <0\right. \right\} \subseteq \left\{ \omega \left| \min \nolimits _{1\le k\le n}PV_{k,\alpha }^{L}\left( \omega \right) <0\right. \! \right\} \!$, so clearly $P_{n,\alpha }^{L}\le P_{n,\alpha }^{R}$. Therefore, these probabilities generate the f.n. $P_{n}$ defined by the $\alpha$-cut $P_{n,\alpha }=\left[ P_{n,\alpha }^{L},P_{n,\alpha }^{R}\right]$; we call $P_{n}$ chance of ruin by time n. This f.n. gives us information on the risk of ruin of the business/portfolio under study; to synthesize the ruin risk into one crisp value, the defuzzification function $\mathcal {F}$ could be used, leading to the mean chance of ruin after $n$ time periods, $\mathcal {F}\left( P_{n}\right)$. Note that

$$\begin{aligned} \mathcal {F}\left( P_{n}\right)&= \frac{1}{2}\int \limits _{0}^{1}\left( P_{n,\alpha }^{L}+P_{n,\alpha }^{R}\right) \hbox {d}\alpha \nonumber \\&= \frac{1}{2}\int \limits _{0}^{1}\left( \Pr \left( \min \limits _{1\le k\le n}PV_{k,\alpha }^{L}<0\right) +\Pr \left( \min \limits _{1\le k\le n}PV_{k,\alpha }^{R}<0\right) \right) \hbox {d}\alpha \nonumber \\&= \hbox {Ch}\left\{ PVm_{n}<0\right\} , \end{aligned}$$

(16)

where Ch is the mean chance defined by (4). Unfortunately, in general, it is not possible to find analytic expressions for $P_{n,\alpha }^{L}$ and $P_{n,\alpha }^{R}$. Therefore, we suggest using simulation to obtain an approximate shape of the membership function of $P_{n}$ that could give us information on the ruin risk and help us choose some parameters values as, e.g., a proper initial capital $u$ that generates an approximate mean chance of ruin smaller than a certain value (e.g., smaller than 0.05). The simulation algorithm consists of the following steps:

• Step 1. We set several values for $\alpha$, i.e., $0\le \alpha _{1}<\cdots <\alpha _{j}\le 1$. We repeat $m$ times the following step:

  • Step 1. l. At iteration $l$, we simulate $n$ independent realizations of the r.v. $X$, i.e., $x_{1}^{\left( l\right) },\ldots ,x_{n}^{\left( l\right) }$; using these, we obtain the simulated values $S_{k,\alpha _{i}}^{L\left( l\right) },S_{k,\alpha _{i}}^{R\left( l\right) }$ from (13); then (14) yields the simulated values $PV_{k,\alpha _{i}}^{L\left( l\right) },PV_{k,\alpha _{i}}^{R\left( l\right) },i=1,\ldots ,j,k=1,\ldots ,n.$

• Step 2. We approximate $P_{n,\alpha _{i}}^{L}$ with $\tilde{P} _{n,\alpha _{i}}^{L}=\frac{1}{m}\#\left\{ l\left| \min \nolimits _{1\le k\le n}PV_{k,\alpha _{i}}^{R\left( l\right) }<0\right. \right\}$ and $P_{n,\alpha _{i}}^{R}$ with $\tilde{P}_{n,\alpha _{i}}^{R}=\frac{1}{m} \#\left\{ l\left| \min \nolimits _{1\le k\le n}PV_{k,\alpha _{i}}^{L\left( l\right) }<0\right. \right\}$, where # denotes the cardinality of a set. Then, by joining the $\alpha$-cuts $\left[ \tilde{P}_{n,\alpha _{i}}^{L}, \tilde{P}_{n,\alpha _{i}}^{R}\right] ,i=1,\ldots ,j,$ we obtain the f.n. approximate chance of ruin by time $n$, denoted $\tilde{P}_{n}$.

For our study, we took $m=10^{6},j=11$ and $\alpha _{i+1}=0.1\cdot i,i=0,\ldots ,10.$

Remark 2

Note that, based on the values $\tilde{P}_{n,\alpha _{i}}^{L},\tilde{P} _{n,\alpha _{i}}^{R},i=1,\ldots ,j,$ the integral (16) can be numerically approximated (for example, using Simpson’s method) and then used to asses the ruin risk.

Remark 3

To obtain the value of the initial capital $u$ that yields a certain mean chance of ruin (and therefore, a certain solvency level), we can modify the above algorithm as follows:

• We consider the values $\left( u_{q}\right) _{q=0,\ldots ,m},$ where $u_{q}=u_{0}+qh,q=1,\ldots ,m,$ with step $h>0;$

• At Step 1.l we evaluate $PV_{k,\alpha _{i}}^{L\left( l\right) },PV_{k,\alpha _{i}}^{R\left( l\right) }$ for each $u_{q},q=0,\ldots ,m;$

• Similarly, at Step 2 we evaluate $\tilde{P}_{n,\alpha _{i}}^{L}$ and $\tilde{P}_{n,\alpha _{i}}^{R}$ for each $u_{q}.$ Then we plot $\mathcal {F} \left( \tilde{P}_{n}\right)$ as a function of $u$ and obtain the required $u$ by interpolation.

3.2.2 Ranking criterion

We shall now assume that the insurer can choose between several net losses and fuzzy investment strategies. More precisely, the insurer could vary the net loss $X$ by varying, e.g., the premium, or he can choose between several types of fuzzy returns rates $R$, or both. For example, the company could invest its surplus only in a risk-free bond (having a crisp return rate), or only in a risky stock, or in a combination of both. The last two cases can be modeled by different fuzzy numbers, depending on the risk level associated with each case. For such different choices, we would like to rank the resulting f.r.v.’s and choose the most promising one.

We suggest the following ranking method based on the mean chance of ruin:

• Using simulation, we obtain the f.n. approximate chance of ruin $\tilde{P} _{n}$, as described in the algorithm above.

• Based on the shape of their membership functions, we can compare these f.n.’s for different models; for example, taking $\alpha _{j}=1$ in the simulation algorithm, we obtain the modal values of $\tilde{P}_{n}$ and based on them, we choose the model having the smallest such mode. Moreover, if $j$ is large enough (say, $j\ge 10$), we can use the approximate value $\mathcal {F}\big ( \tilde{P}_{n}\big )$ to rank the models; more precisely, the smallest $\mathcal {F}\big ( \tilde{P}_{n}\big )$ is the best choice since it represents the smallest chance of ruin.

4 Numerical study

We shall now illustrate the simulation algorithm and selecting method on some particular choices of $Q\$and $X.$

For $X$, we first consider the normal distribution $N\left( \mu ,\sigma ^{2}\right)$, having pdf $f_{X}\left( x\right) =\frac{1}{\sigma \sqrt{2\pi } }e^{-\frac{\left( x-\mu \right) ^{2}}{2\sigma ^{2}}},$ $x\in \mathbb {R},\sigma >0;$ we also assume that its expected value $\mu <0,$ meaning that in average, we expect a gain rather than a proper loss. However, since the net losses are known to have asymmetric and heavy-tailed distributions, we shall also consider for $X$ the shifted lognormal distribution $\hbox {Log}N\left( \mu ,\sigma ^{2};d\right) ,\mu \in \mathbb {R},\sigma >0,d>0$, having pdf

$$\begin{aligned} f_{X}\left( x\right) =\frac{1}{\left( x+d\right) \sigma \sqrt{2\pi }}e^{- \frac{\left( \ln (x+d)-\mu \right) ^{2}}{2\sigma ^{2}}},\quad x>-d. \end{aligned}$$

For the same reason as in the normal case, we assume that the parameters satisfy the condition that the expected value of this lognormal distribution is negative, i.e., $\mathbb {E}\left[ X\right] =e^{\mu +\sigma ^{2}/2}-d<0$ yielding $\mu <\ln d-\sigma ^{2}/2.$ We also recall $\hbox {Var}\left[ X\right] =e^{2\mu +\sigma ^{2}}\left( e^{\sigma ^{2}}-1\right)$. See left plot in Fig. 1 for possible shapes of the normal and shifted lognormal pdf’s.

To model $Q,$ we chose trapezoidal, Gaussian, and lognormal f.n.’s. In the literature, triangular and trapezoidal f.n.’s were already used to model return rates, but the Gaussian shape could also be a good model for $Q$. Moreover, in, e.g., crisis situations, a lognormal f.n. seems more realistic due to its more flexible asymmetric shape that allows us to model the natural situation in which we trust more lower return values than higher ones, see for example left plot in Fig. 4. Note that the lognormal f.n. cannot be properly approximated by a triangular or trapezoidal f.n. (especially for small or large $\alpha$), since due to its $\left( 0,\infty \right)$ support, it gives us the possibility to trust—at small levels—a wider area of small and large values. While to the estimation of its parameters, it can be done by choosing its mode $m_{Q}$ and a value for $\sigma$ that controls the shape, then we immediately obtain $c_{Q}=\ln m_{Q}+\sigma ^{2}.$

Table 1 Ranking values for $u=300$ when the f.n.’s $Q$ have equal modes

In the following, we set the number of time periods $n=5$, expressed in, e.g., years.

Example 1

We start with three different investment strategies based on f.n.’s having the same mode $m_{Q}=1.1$ (i.e., the most trusted return rate per year is 10 %). The three f.n.’s are as follows: triangular $Q=\left( 0.9,1.1,1.3\right)$, Gaussian $Q$ with parameters $m_{Q}=1.1,\sigma _{Q;Ga}=0.07$ and Lognormal $Q$ with $\sigma _{Q;Ln}=0.08,c_{Q;Ln}=\ln \left( 1.1\right) +0.08^{2}=0.10171$. For these f.n.’s, we also evaluated the crisp expected value and possibilistic variance defined in Sect. 2.1, yielding

$$\begin{aligned} E\left[ Q\right] =\left\{ \begin{array}{l} 1.100,\quad \hbox {triangular}\ Q \\ 1.100,\quad \hbox {Gaussian}\ Q \\ 1.103,\quad \hbox {Lognormal}\ Q \end{array} \right. ,\ \hbox {Var}\left[ Q\right] =\left\{ \begin{array}{l} 0.0066,\quad \hbox {triangular}\ Q \\ 0.0049,\quad \hbox {Gaussian}\ Q \\ 0.0077,\quad \hbox {Lognormal}\ Q \end{array} \right. . \end{aligned}$$

For $X$, we took both distributions: the normal $N\left( -100,100^{2}\right)$ having $\mathbb {E}\left[ X\right] =-100,\hbox {Var}[X]=10,000,$ and shifted lognormal $\hbox {Log}N\left( 5.5,0.5^{2};300\right)$ having $\mathbb {E}\left[ X \right] =-90.4421,\hbox {Var}[X]=27,767.9;$ moreover, the probability of losses is $\Pr \left( X>0\right) =\left\{ \begin{array}{l} 0.15865,\text { normal case} \\ 0.34180,\text { lognormal case} \end{array}\right.$. In Table 1, we present the rankings based on the modal value $m_{ \tilde{P}_{n}}$ and on the approximate mean chance of ruin obtained by simulation for $u=300$, while in Fig. 2 we have the shapes of $Q$ and $\tilde{P}_{n}$.

First of all, note that since the shifted lognormal distribution is heavy-tailed and in our case has a larger variance than the normal one, the corresponding fuzzy model requires a larger initial value $u$; this is clearly indicated by the large values of $\mathcal {F}\big ( \tilde{P} _{5}\big )$ in last line of Table 1. To obtain a proper value of $u$ corresponding to a smaller mean chance of ruin, we used the algorithm described in Remark 3. Figure 3 shows the plot of $\mathcal {F}\big ( \tilde{P }_{5}\big )$ as a function of $u$ for lognormal $X$ (with two different scales for $u$); from here, we obtained by interpolation the values $u\simeq 875$ for a mean chance of ruin of 0.02 and $u\simeq 1,000$ for a mean chance of ruin equal to 0.01.

Regarding the rankings, they vary with the ranking criterion, which is not unexpected as already noted at the end of Sect. 2.1. Regarding the shapes of the resulting f.n.’s, clearly the modal value is not a reliable criterion, and the approximate mean chance of ruin should be calculated. Also, note that the triangular choice for $Q$ could underestimate the chance of ruin.

Fig. 2

Shapes of $Q$ (left plot) and of $\tilde{P}_{5}$ for the parameters in Example 1

Fig. 3

$\mathcal {F}\left( \tilde{P}_{5}\right)$ as a function of $u$ for the parameters in Example 1

Example 2

We also considered the situation with different modal values, i.e., triangular $Q=\left( 0.8,1.08,1.4\right)$, Gaussian $Q$ with parameters $m_{Q}=1.1,\sigma _{Q;Ga}=0.11$ and Lognormal $Q$ with $c_{Q;Ln}=0.07,\sigma _{Q;Ln}=0.11$ having the mode $m_{Q;Ln}=1.06$. The crisp expected values and possibilistic variances of these f.n.’s are

$$\begin{aligned} E\left[ Q\right] =\left\{ \begin{array}{l} 1.086,\quad \hbox {triangular}\ Q \\ 1.100,\quad \hbox {Gaussian}\ Q \\ 1.066,\quad \hbox {Lognormal}\ Q \end{array} \right. ,\ \hbox {Var}\left[ Q\right] =\left\{ \begin{array}{l} 0.0150,\quad \hbox {triangular}\ Q \\ 0.0121,\quad \hbox {Gaussian}\ Q \\ 0.0137,\quad \hbox {Lognormal}\ Q \end{array}\right. . \end{aligned}$$

For $X$, we took the same distributions as in Example 1, and we ranked the models using both criteria as in previous example. The results are presented in Table 2 for $u=100,$ and in Fig. 4.

In this case, the ranking values are quite close, and the conclusions are similar with the ones of Example 1 in what concerns the heavy-tailed shifted lognormal loss distribution; however, this time the two ranking criteria gave similar results. Moreover, looking at the shapes and expected values of the f.n.’s considered for $Q$ and at the rankings based on $\mathcal {F} \big ( \tilde{P}_{5}\big )$, it seems that the order of the $Q$’s is reversed in the order of $\mathcal {F}\big ( \tilde{P}_{5}\big ),$ which make sense since a larger return rate should generate a smaller chance of ruin. The possibilistic variance (in association with the crisp expected value) also seems to influence the rankings; e.g., in Example 1, where all three f.n.’s have the same mode and about the same expected value, the Lognormal f.n. has the largest variance and yields the worst investment strategy.

Table 2 Ranking values for $u=100$ when the f.n.’s $Q$ have different modes

Fig. 4

Shapes of $Q$ (left plot) and of $\tilde{P}_{5}$ for the parameters in Example 2

5 Conclusions

In this paper, we obtained the fuzzy form of a classical stochastic model used in insurance risk analysis by replacing the r.v. return rate with a fuzzy number representing an average return rate throughout the evaluation horizon. From the resulting present value of the insurer’s wealth, we evaluated the fuzzy quantity mean chance of ruin related to the ruin risk, and based on it, we proposed a ranking criterion for such models.

Compared with the ranking based on the modal value of the f.n. approximate chance of ruin, the method based on the approximate mean chance of ruin after $n$ time periods $\mathcal {F}\big ( \tilde{P}_{n}\big )$ seems more reliable, having also the advantage that it gives more indications on the ruin risk (e.g., when the modal values are almost equal), and also helps us to choose a proper initial capital $u$ such that the approximate mean chance of ruin is smaller than a maximum accepted value.

On the other hand, due to its flexible shape, the lognormal f.n. seems to be a good choice for the return rate in a risky financial environment, since the other choices for $Q$ having similar shapes and modal values could underestimate the mean chance of ruin.

As final conclusions, we consider that this fuzzy approach of the discrete-time stochastic model could be of interest for the following reasons:

• The fuzzification of the model appears naturally from the uncertainty of the return rate. Moreover, other quantities involved by the model can be considered to be fuzzy, like, e.g., the parameters of the distribution of the r.v. net loss $X$, or the net loss could be taken as a fuzzy r.v. Also, as in Buckley (1987), the number $n$ of time periods can be made fuzzy. These are possible subjects for future work.

• This fuzzy approach can be also adapted for complex stochastic models, like the models used in evaluating ruin probabilities.

• It can avoid some restrictive assumptions usually imposed for such stochastic models (like heavy-tailed losses or certain distributions for the return rates), and it does not involve cumbersome mathematical proofs as it is the case with, e.g., the asymptotic results obtained for ruin probabilities.