1 Introduction

Supply chains (SCs) are usually considered as networks of semi-independent firms who pool their capabilities and resources in order to deliver value to the end consumer. Costs, delays, quality, and reliability are relevant criteria in a SC [3, 11].

Supply chain management (SCM) is often considered as a distributed system involving several individual firms or participants such as manufacturers, suppliers, customers, etc. Each of these actors is faced with some economic constraints besides its own strategic preferences. Therefore, it is obvious that SC overall effectiveness may suffer, if SC members pursue their own individual preferences without considering the effect of their decisions on other partners. Such inefficiencies often creep in when rational members decide to optimize individually instead of coordinating their efforts [11]. Therefore, global optimality in the context of a supply network would be purely theoretical and inefficiency may arise due to the decentralized decision-making based upon local interests [3, 38].

A simple serial SC consists of suppliers, manufacturers, distributors, retailers and customers which are connected by flows of information and product in two opposite directions. In a linear SC, information flow from downstream echelons toward upstream echelons and product flows in opposite direction (from upstream echelons toward downstream echelons). Information and product flows (in both directions) are aligned and balanced in a healthy and efficient supply network [9]. However, because of the competitive nature of real-world markets, complete information flow occurs less frequently in SCs. These incomplete information flows lead to inaccessibility to real amounts of market demand. Therefore, replenishment demands which are received from downstream echelons will be considered as the basis of decision-making for upstream echelons [11, 27]. In other words, SC echelons tend to place orders based upon the gap between their target inventory level and their current on-hand stock, while giving insufficient weight to the supply line of unfilled orders (the stock of orders placed but not yet received) [10]. This procedure leads to increasing the variability of replenishment orders when moving up from downstream echelons of SC toward its upstream echelons, as a rational remedy for confronting with inventory shortage risks. This tendency of replenishment orders to increase in variability while moving up the SC (from retailer echelon toward the manufacturer), is named the “Bullwhip Effect” (BWE) [11, 28].

BWE affects the efficiency of SCs by imposing unnecessary inventory costs to SC echelons and intervening the production plans. Many real SCs, in particular in the automotive industry, have met serious economic problems because of inventory shortages or excessive inventories [3]. Therefore, the control of inventory and production variations through managing the BWE can be considered as a great challenge for SCs.

This paper focuses on managing BWE and inventory variations in a four-echelon serial SC. Several approaches are proposed in the literature on taming the BWE in SCs. However, sharing of relevant information among SC echelons is considered as the most effective approach for BWE management and control of its bad effects on the SC efficiency through decreasing inventory costs by the means of improving the ordering decisions [21]. We concentrate on facilitating the demand information sharing among SC echelons through a proper ordering policy, in this paper. Token-based ordering policy (TB) is selected as our main approach in order to simultaneously control the inventory levels and demand amplifications in a SC. The main strategy of token-based ordering policy is to differentiate between real market demand and replenishment orders which reflect the inventory control strategies of each SC echelon. The BWE concept can be reflected by the amounts of tokens that are ordered by each echelon to its upstream layer in every period, in this ordering policy. Therefore, a proper token-ordering procedure has a significant role in controlling the BWE and inventory levels through the use of TB ordering policy in the supply system.

After a survey on the relevant literature [9], it was concluded that there is a lack of an appropriate mechanism for token-ordering procedure in TB ordering policy. Therefore, the main contribution of the present paper is to propose a novel robust mechanism for token-ordering procedure in token-based ordering policy with the aim of controlling the BWE and inventory costs in a SC simultaneously. The main idea is to model the token-ordering mechanism based upon the imprecise and vague real decision-making process in hybrid push–pull systems using fuzzy modeling approaches.

For this purpose, two fuzzy approaches will be proposed in this paper to determine about the amount of tokens that each echelon should order to its upstream echelon (in order to manage its inventory level and coping with the risk of inventory shortages). Takagi–Sugeno–Kang (TSK) fuzzy approach which models token-ordering policy through a linear function of the system’s endogenous variables in each SC echelon and hybrid multiple-input single-output (MISO) fuzzy approach which models the token-ordering policy through an imprecise inference on the system’s endogenous variables in each SC echelon.

The rest of the paper is as following: A short literature review on BWE, its causes and remedies and token-based ordering policy are presented in the next section. After preparation a proper background for the current study, the previous token-ordering policy (that had been proposed in the literature) will be analyzed and we will discuss about its main deficiencies. TSK and MISO fuzzy models are presented to improve the efficiency of token-based ordering policy and remove the discussed shortcomings, in section three. This section will also present some numerical experiments to confirm the effectiveness of the proposed approaches in diminishing BWE, inventory costs and variations. Finally, some complementary numerical experiments with a discussion on the results and main characteristics of the proposed fuzzy approaches and conclusion will be presented respectively in the fourth and fifth sections.

2 Background

2.1 The bullwhip effect

The first formal description of the bullwhip effect (BWE) was presented by Forrester in 1958. He surveyed all the orders that were placed by different echelons of supply chain to their upstream echelons and observed that the variability of these orders is much bigger than the variation of real customer’s demand. He also discovered that these demand variations tend to increase while orders moving up the SC from downstream echelons to the upstream. He called this phenomenon “Demand Amplification” [14]. The BWE is a shorthand term for this dynamic phenomenon, and the appellation is how the severity of a lash can be increased during its movement along a whip.

Further in 1989, Sterman simulated the BWE through introducing the well-known MIT beer game [33]. He pointed out that the players tend to have a common mental model, which is making orders only according to the current inventory minus unfilled orders, without taking into account the orders on the way. He discussed that the players failed to recognize the beer SC as a system with interconnected parties, which is confronted with complex information feedbacks and delay. He believed that system-thinking trainings can help to decrease these irrationalities in decision-making [33, 39].

Briefly, the BWE refers to the tendency of the variability of order rates to increase while they are passing through the lower echelons of a SC toward the producer and raw material suppliers [11]. Figure 1 demonstrates the stream of orders in a three-echelon SC and shows how the variability of demands increases while moving to upstream echelons. The standard deviation \(\sigma \) of orders is the main indicator to measure the BWE [25].

Fig. 1
figure 1

Amplification of order variability in a three-layer SC [25]

Full size image

The BWE leads to unstable production schedules which impose a considerable range of unnecessary costs to SCs. What happens in practice is that companies invest in extra capacity to meet the highly variable demand and this extra capacity remain underutilized when the demand drops [9, 29]. Therefore, the direct consequence of the BWE in SCs is inventory backlog. This backlog may lead to high losses to the company due to the fact that it is resulted from information distortion rather than real demand variation [39]. Therefore, BWE management is a necessary task to upgrade the overall efficiency of supply networks, the customer satisfaction level and managing inventory costs.

2.1.1 Causes of the bullwhip effect

As mentioned above, the BWE is a prominent example for the negative impact of information asymmetry in supply networks [19]. Previous research attributed the BWE to both operational and behavioral causes. Operational causes are structural characteristics that lead rational agents to amplify demand variation. Lee et al. recounted five possible operational sources for BWE, including demand forecast updating, price fluctuation, rationing and shortage gaming, order batching and nonzero lead time [19, 20]. The techniques to eliminate these operational causes of BWE are now an important part of the tool kit for SCM.

Behavioral causes, in contrast, emphasize on the bounded rationality of decision makers, particularly the failure to adequate accounting for feedback effects and time delays. Corson et al. surveyed the behavioral causes of the BWE in the absence of operational causes in [10]. They examined how individuals perform when all operational causes of the BWE are eliminated in a SC. They found that order oscillation and amplification persists even in this simplified environment and a large majority of participants continue to underweight the supply line of unfilled orders, and this refers to the existence of coordinating risks in the system; in fact, they concluded that “the BWE can be mitigated by operational issues but its behavioral causes appear robust” [10]. Therefore, BWE will exist still in modern SCM systems with (almost) real-time, fully automatic data and information handling. Because, however, these modern systems can cover lack of information and technical causes of the BWE, they cannot eliminate its behavioral causes.

Some important possible causes of the BWE are as following: lead time and neglecting time delays, ordering policies, inventory control policies, number of SC echelons, price fluctuations, fear of empty stock, local optimization, multiplier effect and Lack of transparency [27].

2.1.2 Remedies for bullwhip effect

Studies on BWE were conducted in four broad classes of Behavioral, Analytical, Industrial and Dynamic approaches in the literature [30]. Behavioral studies deal with capacity adjustment studies and keeping inventory level unchanged, considering an uneven customer demand [2]. Logistic cost minimization techniques are discussed to control the BWE in analytical approaches, while quantitative and dynamic presences of the BWE are surveyed in industrial and dynamic approaches, respectively [1]. A perfect model should be able to survey the BWE in at least two of these viewpoints; in this work, we want to propose such a model.

The BWE can be diminished by reduction of demand uncertainty through additional (more accurate and relevant) information [23]. Sharing relevant information across various stages of the SC has found to be efficient in BWE reduction and controlling its negative effects on SC performance [1, 8, 9, 19]. Lee et al. discussed that information sharing (IS) can cause making better ordering decisions and lead to reducing each echelon’s inventory level and overall system’s costs [21]. However, it has been proved that some amount of BWE will always occurs in SCs even after sharing both inter- as well as intra-echelon information [1]. IS has been confronted with a variety of range of research in the SCM domain, for example, some of them have dealt with the effect of information technology in the coordination cost reduction [31]. The interested reader can pursue a comprehensive research about IS benefits on BWE if refers to [7].

The information which can be shared among SC echelons include inventory levels, sales data, demand forecasts, the status of orders, product planning, logistics and production schedules and can be grouped into three main types: product information, customer demand information and inventory information [17]. There are several researches in BWE domain that are concentrated on collaborative forecasting methods or vendor managed inventory as effective tools for BWE reduction; the works of Stubbings et al. and Sadeghi et al. can be referred as recent works in these area [29, 34].

However, our main objective in the present paper is facilitating IS among SC echelons via modeling a proper ordering policy. Ordering policy refers to the mechanism that SC echelons adopt to put their orders to the upstream echelon based upon their own preferences. Different ordering policies are presented and surveyed in the context of SCM. Among them, Lot-for-Lot ordering policy is the solution which is often suggested to reduce the BWE based upon demand information sharing [19, 20, 32]. It is known to eliminate the BWE and propagate the market consumption in the SC. Inventory variations in this policy often results in backorders. Therefore, Lot-for-Lot ordering policy eliminates the BWE but does not manage the inventory levels. This is why it is proposed to distinguish between real market demand from extra orders which are required for inventory stabilization [13, 24]. To achieve that, Porteus and Moyaux had proposed an approach based upon using tokens in ordering policy [13, 24, 26]. A summarized introduction to the token-based ordering policy is presented as following.

2.2 Token-based ordering policy

Since the advent of Kanban, pull systems have been widely studied and used in practice. Push and Pull are two different systems that are discussed in the context of production control systems. A push system schedules the release of works based on demands, while a pull system authorizes it based on the system status. An important feature of pull systems is the use of tokens. Tokens usually consist of cards that authorize certain production tasks to be performed. It can be used in various manners to control the production and can be combined with several other mechanisms [15, 16].

The combination of pull and push systems is called push–pull inventory control system that combines the best of both the push and pull strategies, and its goal is to stabilize the SC and reduce the product shortages. Several researches have confirmed that the hybrid push–pull system is more effficient and robust to cope with SC uncertainties. We will try to close token-based ordering policy to push–pull approach in order to improve its efficiency, in this work.

The token strategy is dividing orders into two streams to control demand and inventory at the same time; the first stream is the actual value of customer demand, whereas the second stream is the required adjustments to manage fluctuations and keep a stable inventory for SC echelons. Therefore, every order of a downstream echelon i to its immediate upstream \(i+1\), in period t is: \(O_{i}(t) = (X(t), Y_{i} (t)\)) where \(X(t), Y_{i}(t)\) are first and second streams of order, respectively [9, 13, 25].

The amount of tokens \((Y_i(t))\) can be used to stabilize the inventory of an echelon i \((I_{i} (t))\). The main condition for ordering tokens in this ordering policy is that an increase change should be occurred in the customer’s demand (means \({X(t)}>{X(t-1)})\) [9, 25].

Figure 2 demonstrates how streams of token and product orders are transferred between different echelons of a four-layer serial SC.

Fig. 2
figure 2

Transition of order streams between SC echelons

Full size image
Fig. 3
figure 3

Demand fulfillment procedure

Full size image

Unsatisfied demands will be backlogged in the cases of insufficient inventory (except for retailer echelon, which confronts with lost-sale). Therefore, backlogged demands composed from two different streams based upon the incoming orders: actual demand backlogs (or product backlogs) and token backlogs.

The product backlog refers to the amount of product demands (X: real demand) which could not be met and were backlogged due to the inventory shortages. The token backlog also refers to the amount of token demands (Y: token demand) which could not be met and were backlogged due to the inventory shortages.

The token-based ordering strategy (TB) suggests to differentiate between these types of backlogs by prioritizing the demand fulfillment procedure. This means while the inventory is positive the first priority of fulfillment is for product backlog, the second is for incoming product demand and the third and fourth priorities are, respectively, for token backlogs and current incoming token demand. Figure 3 depicts the demand fulfillment procedure clearly. Nomenclature of the model variables is also presented in Table 1.

Table 1 Nomenclature
Full size table

After demand fulfillment in each period, both of the backlogs and on-hand inventory will be updated. If the amount of on-hand inventory \(I_{i}(t)\) was less than the value that is determined in accordance with inventory management policies, a desired amount of \(Y_{i}(t)\) will be ordered, otherwise \(Y_{i}(t) = 0\).

Costantino et al. have proposed the following two different token-ordering policies [Eqs. (1) and (2)].

$$\begin{aligned} Y_{i} \left( t\right) =\left\{ {\begin{array}{ll} Y_{i-1} \left( t \right) +\alpha _{i} \left( {X\left( t \right) -X \left( {t-1} \right) } \right) &{} \quad \hbox {if}\,X\left( t\right) >X\left( {t-1} \right) \,\hbox {AND}\, I_{i}({t})<\hbox {mean}\left( X \right) \\ 0 &{} \quad \hbox {else} \\ \end{array}}\right. \quad \end{aligned}$$
(1)

and

$$\begin{aligned} Y_{i} \left( t \right) =\left\{ {\begin{array}{ll} Y_{i-1}\left( t \right) +\alpha _{i} \left( {X\left( t\right) -X\left( {t-1}\right) }\right) &{}\quad \hbox {if}\,X\left( t \right) >X\left( {t-1}\right) \,\hbox {AND}\,B_{i-1} ({t})< \hbox {mean}( X ) \\ 0 &{} \quad \hbox {else}\\ \end{array}} \right. \,\,\, \end{aligned}$$
(2)

They represented a simulation model for a four-echelon SC with unlimited production and inventory capacities and deterministic lead times. They tried to make an estimation for \(\alpha \) vector based upon the amount of expected backlogs, which is shown in Eq. (3) [9].

$$\begin{aligned} \sum \limits _{{i}=1}^{4} {\upalpha }_{{i}} \ge \hbox {Expected Backlog}{/}\left( {X\left( t\right) -{X}\left( {{t}-1} \right) } \right) \quad , i=1,2,3,4 \end{aligned}$$
(3)

Considering a step function for customer demand and equal elements for the \(\alpha \) vector, they concluded Eq. (4) as an estimator of \(\alpha \);

$$\begin{aligned} {\upalpha }_{i} \ge {48}/{4 \left( {{X}\left( {t} \right) -{X}\left( {t}-1 \right) } \right) } \end{aligned}$$
(4)

They then compared the results of both proposed token-ordering policies [Eqs. (1) and (2)] with two different \(\alpha \) vectors (\(\alpha =\left[ {0.5,1,2,3}\right] \) and \(\alpha ^{\prime }=\left[ 0.5,1.5,2.5,3.5\right] )\). Based upon their investigations, the inventory recovery period of the first ordering policy (Eq. 1) was considerably lower in comparison with the second policy (Eq. 2). They have reported that the main difference between these ordering policies is that the first one tends to keep a positive inventory at a higher level, while the second one tends to keep a positive inventory at a lower level but requires more time to recover the SC stability. Therefore, they believe that the best policy can be identified only through a trade-off between costs and benefits for any SC system [9]. However, the most important common feature of these two approaches is that the \({\upalpha }\) vector has a significant role in determining the amount of replenishment orders.

As discussed before, first stream of orders in the TB ordering policy is the exact amount of customer’s demand and SC echelons pursue their inventory control policies through ordering tokens. This means that the concept of the BWE is reflected by the token-ordering procedures in the TB ordering policy. Therefore, the \({\upalpha }\) vector [in Eqs. (1) and (2)] is a critical exogenous factor in the proposed token-ordering strategies and has a significant role on the amounts of inventory variation and the BWE in the supply system. Thus, representing a proper estimation for \({\upalpha }\) seems to be an effective step for increasing the efficiency of TB ordering policy. Next section provides a more detailed discussion on this important issue.

2.2.1 A discussion on previous token-ordering policies

As mentioned above, Costantino et al. have estimated the \({\upalpha }\) vector considering these essential assumptions: 1—Step function for customer demand, 2—Equal components for \({\upalpha }\) vector and 3—Deterministic lead time.

Assuming a step function customer demand leads to have a constant value for \(\left( {X\left( t \right) -X\left( {t-1} \right) } \right) \) that besides the second assumption leads to obtain a simple estimator for \({\upalpha }\) (the reader can refer to [9] for more details). However, the model’s generality can be affected by assuming a step function as customer’s demand function because it may occur rarely in the real market.

The second assumption also cannot be a strong hypothesis because the elements of \({\upalpha }\) vector should reflect the inventory control policies of each SC echelon. In other words, considering the difference between the inventory capacity and incoming orders of upstream echelons with downstream SC echelons, it is not realistic to assume equal elements for \({\upalpha }\) vector. Fazel Zarandi et al. [13] reported some numerical results that can approve this claim. They simulated a four-echelon serial SC with Costantino et al.’s initial assumptions and surveyed the numerical results for \({\upalpha }= [3, 3, 3, 3]\); the simulated model calculated the BWE as 952.8710 which is very large for a SC model with a step function for customer demand. Fazel Zarandi et al. also suggested some reformations to improve the efficiency of the TB ordering policy. They have suggested to apply fuzzy lead time to the model and determine the \({\upalpha }\) vector through a dynamic procedure. However, their attempt was to somewhat successful but is not sufficient, because their proposed token-ordering policies also depend seriously on the amount of \({\upalpha }\) vector.

This work deals with the eradication of the dependence between the performance of token-based ordering policy with the values of exogenous variable \(\alpha \) and the way of its estimation.

We have performed multiple sensitivity analyses on the all model parameters and surveyed their effects on the amount of BWE and inventory levels of each SC echelon. We found that all of following variables can affect the overall outcome of the model: \(\upmu {(t)}, I_{i}(t), D\left( {t}\right) ,\,Y_{i}(t), YB_{i-1} (t)\) and \(B_{i-1}(t)\).

Some of the mentioned variables have common effects on the system outputs or complete each other’s effects, but \(D\left( {t} \right) ,YB_{i-1}(t)\) and \(B_{i-1}(t)\) have most unique effects on the outcomes of the model.

If we define \(Y_{i}(t)\) as \(Y_{i}(t)= {\upalpha }_{i} \,\, D(t)+ Y_{i-1}(t)\), we used \(Y_{i-1}(t)\) in \(Y_{i}(t)\) modeling which propagates the perception of the BWE along the SC instead of using \(YB_{i-1}(t)\) and \(B_{i-1}(t)\) which reflect the current situation of backlogs. Therefore, Eqs. (1) and (2) cannot provide a proper function to determine about the amount of tokens that should be ordered in each period. Considering this, we determined to change the equation of \(Y_{i}(t)\) as a function of before mentioned variables. In other words, our purpose is to obtain a prominent function “f” which can be able to satisfy \(Y_{i}(t)= {f}(D(t), YB_{i-1}(t),B_{i-1}(t))\).

If we can model \(Y_{i}(t)\) as f (\(D(t), YB_{i-1}(t),B_{i-1} (t))\), the system can be considered as a push–pull system because the orders and production schedules will be set based upon both real customer demands and the system status in each period using this approach.

It is necessary to take the following notes into account:

  • All demands are rounded to the nearest integer; therefore, all input and output variables of the model are considered as integer.

  • Lead times are often fuzzy in real-world SCs, and considering deterministic lead time for a SC model will decrease its generality.Footnote 1

Regarding the mentioned notes, we are confronted with a non-deterministic model with crisp input and outputs. Therefore, it seems that a TSK fuzzy modeling may help us to model \(Y_i(t)\) as a linear function of selected input variables in each echelon.

Next section provides a short introduction about TSK fuzzy modeling, then the proposed TSK token-ordering policy is presented. Some numerical experiments have been conducted to investigate the efficiency of the proposed TSK token-ordering policy, which will be presented at the end of the section.

3 Proposed fuzzy models for improving token-based ordering policy

3.1 TSK fuzzy modeling

Fuzzy inference is the mathematical procedure to deduce model output from a given set of fuzzy rules. Mamdani and Assilian have studied one of the first real-life applications of fuzzy rule base structure on control systems [4, 22]. They used a fuzzy rule base in order to control a cement pilot plant. Today, there are many different applications of fuzzy inference systems (FIS) including financial, health care, robotics, web data mining and many more [4, 36, 37].

Takagi–Sugeno–Kang (TSK) type fuzzy inference system structure is one of the most commonly implemented and investigated FISs which is proposed by Takagi, Sugeno and Kang [4, 36, 37].

A typical fuzzy rule in TSK model has the following form:

If u isr A and v isr B then \({w} = {f}(u, v)\)

Where A and B are fuzzy sets in the antecedent and \({w}={f}(u, v)\) is a crisp function in the consequent part of the rule. f(u, v), is usually a polynomial function of the input variable u and v; thus, this approach works when inputs are given as singleton values. The final output of the rule set is a weighted mean of fired consequents of all rules of the rule set. For example, in a rule set with two rules, if \({z}_{1}\) is the fired consequent of the first rule and \({z}_{2}\) is the fired consequent of the second rule, then the output of TSK for this rule set \(({Z}_{\mathrm{TSK}})\) will be as following (Eq. 5):

$$\begin{aligned} {Z}_{\mathrm{TSK}}={w_{1} z_{1} +w_{2} z_{2}}/{w_{1} +w_{2}} \end{aligned}$$
(5)

where \({w}_{1}\) and \({w}_{2}\) are weights attributed to the consequent of each rule, in the rule set.

3.1.1 Proposed TSK fuzzy approach for token ordering

As mentioned before, variables such as \(D(t), YB_{i-1}(t)\) and \(B_{i-1}(t)\) affect the outputs of the system. Based upon our SC model assumptions, crisp amounts of all of these variables are available after inventory updating in each period when the crisp amount of \(Y_{i}(t)\) should be determined. Therefore, we want to model \(Y_{i}(t)\) as a linear function of these variables using TSK fuzzy modeling approach.

TSK determines the value of a crisp output based upon a polynomial function of crisp inputs in each rule of the rule set; therefore, the following equation (Eq. 6) can be considered as an estimator for the \(Y_{i}(t)\).

$$\begin{aligned} Y_{i} (t)={a}_{0} + {a}_{1} \,\, D(t) + {a}_{2} \,\, B_{i-1}(t) + {a}_{3}\,\, YB_{i-1} (t) \quad i=2,3,4 \end{aligned}$$
(6)

We refused to bring \(\upmu (t)\) directly in the model, so \({a}_{0}\) is defined as a multiplier of \(\upmu (t)\) (in other words \({a}_{0}={a}_{{00}^{*}}\upmu \left( t\right) , 0\le {a}_{00} \, \le 1)\).

It should be noticed that the retailer receives the customer’s demand (actual market demand) in each period, so it is confronted with lost-sales (L(t)) in the case of inventory shortages instead of backlogs. Therefore, Eq. (6) is not suitable for the retailer echelon and should be modified to the following equation [Eq. (7)] for the retailer echelon:

$$\begin{aligned} Y_{1} (t)= {b}_{0} + {b}_{1} \, \, D(t) + {b}_{2} \quad L(t) \end{aligned}$$
(7)

Here \({b}_{0}\) is a multiplier of \(\upmu (t)\) similar to \({a}_{0}\) in Eq. 6.

Input factors should be defined as fuzzy variables in order for using the TSK model; an imprecise (“fuzzy”) property (x) (such as low, fast, hot, etc.) is described by its membership function (\(MF\left( x \right) )\), in fuzzy logic. A MF associated with a given fuzzy set maps an input value to its appropriate membership value between 0 and 1; this function describes to what degree the real number (x) satisfies the desired property [5, 18, 41]. In principle, MFs can be of different shapes, but in most practical applications, trapezoidal membership functions work well and are simple to implement and fast for computation [5].

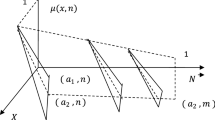
Trapezoidal MF depends on four scalar parameters; a, b, c and d. Equation 8 represents the main function of this MF.

$$\begin{aligned} \hbox {MF}(x)=\left\{ {\begin{array}{ll} 0&{}\quad x<a \\ \left( {x-a} \right) {/}\left( {b-a} \right) &{} a\ge x<b \\ 1&{}b\ge x<c \\ \left( {d-x} \right) {/}\left( {d-c} \right) &{}c \ge x\le d \\ 0&{}\quad x>d \\ \end{array}}\right. \end{aligned}$$
(8)

Considering the following issues, trapezoidal MF is selected for mapping model’s fuzzy concepts into mathematical modeling;

  • All inputs and outputs of the model are integer.

  • The domain expert believes that this MF is able to map the decision-making factors into appropriate mathematical function.

  • Considering the simplicity of calculations and the complexity of the model.

Therefore, each of \(D(t),YB_{i-1}{(t)}, B_{i-1}{(t)}\) and L(t) are considered as trapezoidal fuzzy numbers in three linguistic levels of “Low,” “Medium” and “High.” The parameters of these trapezoidal membership functions (MF) are defined based upon the mean of demand vector.Footnote 2 Sample \(B_{i-1}(t)\) MFs is depicted in Fig. 4 (for \(\hbox {MU}=6\)).

Note that \(B_{i-1}(t)\) is the backlogged amount of downstream’s X part demand in each echelon. We have assumed that each echelon orders exactly X(t) in the first part of its demand vector in each period \((O_i(t) = (X(t), Y_{i}(t))\), so MF parameters of \(B_{i-1}(t)\) can be considered the same in echelons 2, 3, 4.

But it is important to notice that each echelon orders tokens with the aim of inventory stabilization and coping with inventory shortage risks. Therefore, all replenishment policies are reflected by \(Y_{i}(t)\) through the SC; in fact, it is the BWE causative factor and increase as moving up toward upstream echelons.

In addition, the \(YB_{i-1}(t)\) is the amount of backlogged downstream token demands which are remained unmet because of the inventory shortages. Thus, the amount of \(YB_{i-1}(t)\) may increase as moving up to upstream echelons in SC, similar to the \(Y_i{(t)}\) and this means that the domain of its values may differ in different echelons. Therefore, the same fuzzy MF parameters (for defining different fuzzy levels of \(YB_{i-1}{(t)})\) cannot be considered for all echelons (at least for the “High” level).

Fig. 4
figure 4

Sample trapezoidal fuzzy membership functions for \(B_{i-1}(t)\)

Full size image

Regarding abovementioned points, we defined different MF parameters for the “High” level of \(YB_{i-1}(t)\) in each echelon of the SC. In other words, if the “High” level of \(YB_{1}(t)\) is considered as a trapezoidal fuzzy number with parameters \([a_{1} ,b_{1}, c_{1} ,d_{1}]\) and the parameters for \(YB_{2}(t), YB_{3}(t)\) respectively be \([a_{2} ,b_{2} , c_{2} ,d_{2}]\) and \([a_{3} ,b_{3} , c_{3},d_{3}]\), then it is observed that \(a_{1} <a_{2} <a_{3} , b_{1} <b_{2} <b_{3}, c_{1} <c_{2} <c_{3}\) and \(d_{1} <d_{2} <d_{3}\).

As Fazel et al. mentioned in [13], a good ordering system should have the ability to change flexibly based upon different situations which are caused by changing time horizons. The SC under consideration is a four-echelon SC with fuzzy lead time of \(\tilde{\ell }\). Therefore, as the time period becomes closer to \([[4\tilde{\ell }]]\, ([[ ]]\) indicates the bracket of \(4\tilde{\ell })\), the possibility of receiving big orders will decrease. Considering this, we add the time counter variable to our model, as well. This factor is considered in two linguistic levels; “Beginning of Period” and “End of Period” which are also considered as trapezoidal fuzzy numbers. The parameters of time counter trapezoidal MF are specified based upon their closeness to \([{[ {4\tilde{\ell }}]}]\), as mentioned before.

Considering three linguistic levels for \(D(t), YB_{i-1}(t), B_{i-1}(t)\) and L(t) and two linguistic levels for the time factor, 54 rules will be obtained for determining \(Y_i(t)\) (for \(i= 2, 3, 4\)) in the wholesaler, distributer and manufacturer echelons, also 18 rules for determining \(Y_{1}(t)\) in the retailer echelon.

General form of the jth rule of the proposed TSK model for \(Y_{i}(t)\) determination in the manufacturer, distributer and wholesaler echelons is as following:

\(\hbox {RULE}_{{j}}\): IF D(t) isr \(\hbox {U}_{{1j}}\) AND \(B_{i-1}(t)\) isr \({\hbox {U}}_{{2j}}\) AND \(YB_{i-1}(t)\) isr \(\hbox {U}_{{3j}}\) AND t isr \(\hbox {U}_{{4j}}\) THEN

$$\begin{aligned} Y_{ij} (t)={a}_{{0j}} + {a}_{{1j}} \,\, D(t) +{a}_{{2j}} \quad B_{i-1} (t) + {a}_{{3j}} \,\, YB_{i-1} (t) \quad \hbox {for} i= 2, 3, 4 \hbox {and} j= 1,\ldots , 54 \end{aligned}$$

In which \({U}_{1}, {U}_{2}, {U}_{3}\) are trapezoidal linguistic terms “Low,” “Medium” and “High” and \({U}_{4}\) refers to trapezoidal linguistic terms “Beginning of Period” and “End of Period.”

Following statement shows a general form of the jth rule of the proposed TSK model for \(Y_1(t)\) determination, in the retailer echelon:

\(\hbox {RULE}_{{j}}\) : IF D(t) isr \(\hbox {V}_{{1j}}\) AND L(t) isr \(\hbox {V}_{2j}\) AND t isr \(\hbox {V}_{3j}\) THEN

$$\begin{aligned} Y_{1j} (t)= {b}_{{0j}} + {b}_{\mathrm{1j}} \,\, D(t) + {b}_{{2j}}\,\, L(t)\quad \hbox {for} j=1,\ldots , 18 \end{aligned}$$

where \({V}_{1}, {V}_{2}\) are trapezoidal linguistic terms “Low,” “Medium” and “High” and \({V}_{3}\) refers to trapezoidal linguistic terms “Beginning of Period” and “End of Period.”

\(Y_1(t)\) rule base of the proposed TSK model is shown in Fig. 5 as an example, presentation of \(Y_{i}(t)\) rule base is skipped due to the lack of the space.

Fig. 5
figure 5

\(Y_{1}(t)\) TSK rule base

Full size image

A sample rule of the proposed TSK model for both \(Y_1(t)\) and \(Y_{i}(t)\) is presented in Fig. 6 in order to have a graphical view of the proposed TSK model rules.

Fig. 6
figure 6

a, b Graphical representation of a sample rule of proposed TSK model. a Graphical representation of a sample rule of proposed TSK model for \(Y_{1}(t)\), b Graphical representation of a sample rule of proposed TSK model for \(Y_{i}(t)\)

Full size image

As mentioned above, TSK approach determines outputs of the model as a linear function of inputs. Therefore, we should obtain the coefficient matrix of the linear function which is used in fuzzy rule base (\({a}_{ij}\) s and \({b}_{{ij}}\) s). The proposed TSK model for obtaining \({Y}_{i}(t)\) had 54 rules and 4 input variables so its coefficient matrix has 54 rows and 5 columns, and the proposed TSK model for obtaining \({Y}_1(t)\) had 18 rules and 3 input variables so its coefficient matrix has 18 rows and 4 columns. These coefficient matrixes should be determined before using TSK fuzzy modeling approach; we have selected neighborhood search method for obtaining them. A start point for the search is developed by random normal generation command of MATLAB, and the overall amount of BWE was selected as the objective function. If we call the target matrix with C, then the new matrix will be obtained as following in each iteration of the search:

$$\begin{aligned} C_{\mathrm{new}} =C+Z. \partial \end{aligned}$$

in which Z is a random normal distributed number which is generated in MATLAB and the \(\partial \) is a multiplier of C. The search algorithm is encoded in MATLAB, and the pseudocode is represented in Fig. 7:

Fig. 7
figure 7

Pseudocode of neighborhood search algorithm for obtaining coefficient matrix of proposed TSK models

Full size image

After parameter tuning, we will investigate the performance of proposed TSK models in determination of \({Y}_{i}(t)\) and \({Y}_1(t)\) in next section via some numerical examples.

3.1.2 Simulation model assumptions

In order to survey some comparisons on mitigating the BWE in SCM and the effects of the discussed ordering policies on it, we have considered a four-echelon SC and modeled its dynamics using MATLAB.

Model initial assumptions have been tried to be similar to the main assumptions of the “Beer Game” and the work of Costantino et al. in order to providing better comparisons.

The SC has four echelons including manufacturer, distributer, wholesaler and retailer with unlimited production and inventory capacities, similar to the well-known MIT beer game. Unlimited production capacity refers to the possibility of production incensement based upon demand changes, considering the lead times. Initial inventory of 12 and initial shipment of MU (MU is the mean of the customer’s demand vector) are assumed. Lost-sale is assumed just for the retailer echelon in the case of inventory shortage and other echelons can backlog their unsatisfied demands. Inventory costs increase as moving down to the retailer echelon.

It is assumed that all echelons observe any conditions of each ordering strategy that is implemented to the SC. We supposed that customer demand follows the normal distribution with mean of MU and standard deviation of \({\varvec{\sigma }}\). The generated values for demand vector rounded to the nearest integer; thus, all the variables of the model assumed to be integer.

The SC model and all its related ordering strategies are encoded in MATLAB R2012a over a timeline of 52 weeks (\(T=52\)). We have considered the product delivery lead time as a triangular fuzzy number of (0, 3, 5).

In order to have sufficient numerical basis for comparison, we also ran both of the Costantino et al.’s token-based ordering policy (TB) and the fuzzy lead time token-based ordering policy (FTB) which Fazel Zarandi et al. have suggested to modify the Francesco et al.’s proposed policy in [13], besides the proposed approaches.

3.1.3 Performance measures

As mentioned before, demand amplification imposes vast inventory variations and costs to SCs; thus, we evaluated the numerical experiments based upon these performance measures: The amount of BWE, costs and inventory variation in each echelon and overall SC.

The costs refer to the sum of the lost-sale and inventory costs in each period for the retailer and the sum of the inventory costs in each period for other echelons.

Equations (9) and (10) which are custom in literature are used to quantify the BWE and comparison of results [9].

$$\begin{aligned} \hbox {BWE}_{{i}}= & {} {\hbox {Var}\left( {\hbox {O}_{{i}} \left( {t} \right) } \right) }/{\hbox {Var}\left( {{X}\left( {t} \right) } \right) } \end{aligned}$$
(9)
$$\begin{aligned} \hbox {Overall BWE}= & {} \sum \nolimits _{{i}=1}^{4} \hbox {BWE}_{i} \end{aligned}$$
(10)

where “Var” is the short term of variance and \(i= 1, 2, 3, 4\) refers to the retailer, wholesaler, distributer and manufacturer echelons respectively.

3.1.4 Numerical results for the proposed TSK fuzzy approach

Numerical results of TB, FTB and our proposed TSK fuzzy token-based ordering policy (TSK-FTB) for two random demand vectors are shown in Table 2.

Table 2 Comparison of numerical results of TB, FTB and the proposed TSK fuzzy token-based ordering policy (TSK-FTB) for two random demand vectors
Full size table

Figure 8 has prepared a good summarized graphical view of Table 2.

Inventory graphs related to the first and second numerical experiments are presented in Figs. 9 and 10, respectively.

Fig. 8
figure 8

Graphical view of Table 2. a Chart of BWE amounts for TB, FTB and TSK-FTB token-ordering policies in numerical experiments 1, 2. b Chart of cost and inventory variation amounts for TB, FTB and TSK-FTB token-ordering policies in numerical experiments 1, 2

Full size image
Fig. 9
figure 9

Graph of inventory status for all SC echelons related to the TB, FTB and TSK-FTB ordering policies in the first numerical experiment

Full size image
Fig. 10
figure 10

Graph of inventory status for all SC echelons related to the TB, FTB and TSK-FTB ordering policies in the second numerical experiment

Full size image

As shown in Table 2, the TSK-FTB ordering policy presented lower amounts of BWE, cost and inventory variation compared to the TB and FTB ordering policies.

Figures 9 and 10 confirm that the TSK-FTB ordering policy can decrease the inventory gap between echelons and diminish the inventory variation of echelons considerably, especially for the manufacturer stage.

As seen before, using TSK model in determination of \(Y_i(t)\) resulted in better outcomes compared to the ordering policies which were already proposed in the literature. However, in order to achieve \(Y_i(t)\) as a linear function of input variables the values of \({a}_{{i}}\) s and \({b}_{{i}}\) s should be determined in each rule; the way of obtaining these coefficients can affect the performance of TSK approach. It should be noted that obtaining the optimal matrix may lead to increase in the complexity of the system, in cases with large coefficient matrix.

In fact, in TSK method the output is characterized based upon some certain coefficients in each rule, whereas the decision-making process in real world is not so exact and bounded. When a person wants to minimize the future costs and shortages by making a near-optimal ordering decision, he/she decides based upon some inexact experiences and forecasts considering available information. A part of these experiences and rule of thumb policies that are used in an approximate decision-making process can be transferred to the knowledge base of a MISO system as a fuzzy rule base. The fuzzy inference mechanism of MISO models can mimic the complex procedure of approximate decision-makings well, using this rule set. In a fuzzy MISO model, the system tries to make a near-optimal decision for the output variable based upon its rule set and fuzzy inputs. Therefore, we determine to examine the performance of MISO fuzzy modeling in token-ordering policy as well.

Next section represents a short introduction about MISO fuzzy systems. Then, the proposed MISO token-ordering policy and some numerical examples are presented, in following.

3.2 MISO fuzzy modeling

A knowledge base of a system is often represented by the form of “fuzzy rule base.” The fuzzy rule base consists of several fuzzy if-then rules. In many cases, the fuzzy reasoning on the fuzzy rule base is based on one-level forward data-driven inference (GNP: generalized modus ponens). The rule base sometimes has the form of a MISO system as following [6, 12].

\({R}=[R_{\mathrm{MISO}}^1 ,R_{\mathrm{MISO}}^2 ,\ldots ,R_{\mathrm{MISO}}^n]\) where \(R_{\mathrm{MISO}}^{j}\) represents the following rule:

IF X isr \({A}_{{j}}\) AND Y isr \(\hbox {B}_{{j}}\) THEN Z isr \({C}_{{j}}\)

In which X and Y are input variables and Z is the output variable of the system. \({A}_{{j}}\) and \({B}_{{j}}\) indicate fuzzy sets that define input variables in antecedent part of the jth rule and \({C}_{{j}}\) is also the fuzzy set which defines output variable in the consequent part of jth rule in the rule set.

The fuzzy inference approach which is selected in this paper is a combination of Mamdani and Logical modeling systems (it is named also unified or hybrid approach) with standard form of all operators.

General forms of jth linguistic fuzzy if-then rules for Mamdani and Logical linguistic fuzzy modeling approaches are as following [6, 12]:

  • Mamdani approach: IF \({X}_{1}\) isr \({U}_{{1j}}\) AND... \({X}_{i}\) isr \({U}_{{ij}}\) THEN Y isr \({V}_{{j}}\)    (\(i= 1, 2,\ldots , n\))

  • Logical approach: IF \({X}_{1}\) isr \(\bar{{ U}}_{1j}\) AND ... \({X}_{{i}}\) isr \(\bar{{U}}_{{ ij}}\) THEN Y isr \({V}_{{j}}\)    \((i= 1, 2,\ldots , n)\)

where \({X}_{i}\) indicates input variables of the system (for \(i= 1, 2,\ldots ,n\) in which, n is the number of input variables) and Y is the consequent variable of the system. \({U}_{{ij}}\) and \({V}_{{j}}\) are linguistic terms (fuzzy sets) which define input and output variables in antecedent and consequent parts of jth rule, respectively. \(\bar{U}{ij}\) is also the complement fuzzy set of the \({U}_{{ij}}\) fuzzy sets. Final result is calculated based upon a specific set of fuzzy operations on the all fired consequents in each approach (see [4] for more detailed information).

The final output of the Hybrid inference approach (Yager Unified approach) is a linear combination of the final results of both Mamdani and Logical methods as displayed in Eq. 11 [6, 12]:

$$\begin{aligned} \hbox {Result}_{\mathrm{Unified}}={\upbeta }. \,\hbox {Result}_{\mathrm{Logical}} + (1-{\upbeta }). \hbox { Result}_{\mathrm{Mamdani}} \end{aligned}$$
(11)

where \({\upbeta }\) is determined by the system analyst depending on to what extent he/she prefers to use Mamdani or Logical approaches. If \({\upbeta }=1\), the system uses only Logical approach and if \({\upbeta }=0\), the Mamdani approach is used for the system’s inference.

3.2.1 Proposed hybrid MISO fuzzy approach for token ordering

Here \(Y_1(t)\) and \(Y_i(t)\) \((i= 2, 3, 4)\), respectively, will be modeled, respectively, by \(D(t),L(t), \upmu (t)\) and \(D(t), YB_{i-1}(t), B_{i-1}(t), \upmu (t)\) and also time factor using MISO fuzzy modeling according to the descriptions mentioned in previous section. In MISO approach, inputs should be fuzzified to obtain a fuzzy value for \(Y_i(t)\) using MISO rule base. Then, this fuzzy outcome will be defuzzified by the system in order to achieve a crisp intelligible output.

Similar to what was discussed in the previous section, three linguistic levels for \(D(t),YB_{i-1}(t), B_{i-1}(t)\) and L (t) and two linguistic levels for time factor are considered. Thus, there are 54 rules for determining \(Y_i(t)\) in the manufacturer, distributer and wholesaler echelons, and 18 rules for determining \(Y_1(t)\) in the retailer echelon.

All MFs are determined as trapezoidal, and its MF parameters have been specified based upon the mean of demand vector (MU). MF parameters for \(YB_{i-1}(t)\) in “High” level are considered different for different echelons, too (as discussed before for the proposed TSK model).

In this approach, the output is obtained from a pre-specified area of the weighted mean of inputs instead of the polynomial function which was used by TSK model. In other words, the consequent (then part) of rules is defined as one of the following seven statements:

“Much more than W”, “More than W”, “Slightly more than W”, “Around W”, “Slightly less than W”, “Less than W”, “Much less than W”, in which W is the weighted mean of input variables.

Therefore, an instance of the jth rule of MISO rule set for obtaining \(Y_{i}(t)\) (\(i= 2, 3, 4\)) can be written as following:

RULE j: IF D(t) isr \({U}_{{1j}}\) AND \(B_{i-1}(t)\) isr \({U}_{{2j}}\) AND \(YB_{i-1}(t)\) isr \({U}_{3j}\) AND t isr \({U}_{{4j}}\) THEN

\(Y_{i}(t)\) isr \({V}_{{j}}\) for \(j= 1: 54\)

\({V}_{{j}}\) is one of the seven statements related to W which have mentioned above.

Also, an instance of the jth rule of MISO rule set for obtaining \(Y_{1}(t)\) can be consdered as following:

RULE j: IF D(t) isr \({U}_{{1j}}\) AND L(t) isr \({U}_{{2j}}\) AND t isr \({U}_{3j}\) THEN \(Y_{1}(t)\) isr \({V}_{{j}}\) for \(j=1: 18\)

The MISO rule set of \(Y_{1}(t)\) is shown in Fig. 11 as an example, and we skipped the presentation of the \(Y_{i}(t)\) MISO rule set due to the lack of space.

Fig. 11
figure 11

\({Y}_{1}(t)\) MISO rule base

Full size image

A sample rule of the proposed hybrid MISO model for both \(Y_{1}(t)\) and \(Y_{i}(t)\) are presented in Fig. 12 in order to have a graphical view of proposed hybrid MISO model rules.

Fig. 12
figure 12

a, b Graphical representation of a sample rule of the proposed hybrid MISO model. a Graphical representation of a sample rule of the proposed hybrid MISO model for \(Y_{1}(t)\), b Graphical representation of a sample rule of the proposed hybrid MISO model for \(Y_{i}(t)\)

Full size image

3.2.2 Numerical results for the proposed hybrid MISO fuzzy approach

The same experiments which were mentioned in previous section were repeated for this policy again in order to enable us to compare the results of the MISO fuzzy token-based (MISO-FTB) policy with TB, FTB and TSK-FTB policies.

Table 3 shows the numerical results of MISO-FTB for the random demand vectors of experiments 1, 2 that mentioned before in TSK model numerical examples.

Table 3 Numerical results of MISO-FTB for experiments 1, 2
Full size table

Figure 13 represents a good summarized graphical view of Table 3 versus the results of TB, FTB and TSK-FTB which were presented in previous section.

Fig. 13
figure 13

Graphical view of Table 3. a Chart of BWE amounts for TB, FTB, TSK-FTB and MISO-FTB token-ordering policies in numerical experiments 1, 2. b Chart of cost and inventory variation amounts for TB, FTB, TSK-FTB and MISO-FTB token-ordering policies in numerical experiments 1, 2

Full size image

Table 3 and Fig. 13 obviously confirm that the MISO-FTB strategy has presented better results for all considered SC performance measures, in comparison with the other three approaches. Therefore, it can be concluded that MISO-FTB is able to make better decisions about token-ordering values.

4 Discussion

In order to make sure about the accuracy of the results, similar experiments have been done on fifty different random demand vectors. The results are shown in Fig. 14. These experiments have also confirmed previous results. Therefore, the strategies can be sorted as following according to their results for SC performance measures: (1) MISO-FTB, (2) TSK-FTB, (3) FTB and (4) TB.

Note that the hybrid MISO model is more flexible vs TSK model in decision-making and improved it by closing the token-ordering decisions to the process of human approximate reasoning and enhanced its robustness, thus according to its better outcomes it seems to be rational to use MISO-FTB. However, it should be noticed that hybrid MISO inference mechanism is more complex and requires more computations which can lead to increasing the system’s runtime.

So in the cases in which runtime and complexity are critical factors for the system, it may be preferred not to use hybrid MISO, and in such cases using simple Mamdani approach is more reasonable.

The Mamdani MISO approach has less complexity in comparison with hybrid MISO approach, but it is more complex than TSK model. Therefore, our proposed approaches were certified to be better from previous approaches, a trade-off between the degree of importance of the SC measures or system constraints such as runtime or complexity can determine the best selection among hybrid MISO, Mamdani MISO and TSK models.

Fig. 14
figure 14

a–c Scatter plots of overall BWE, cost and inventory variation values for TB, FTB, TSK-FTB and MISO-FTB token-ordering policies with fifty different random demand vectors. a Overall BWE values for TB, FTB and proposed fuzzy ordering policies with 50 different random demand vectors. b Overall cost values for TB, FTB and proposed fuzzy ordering policies with 50 different random demand vectors. c Overall inventory variation values TB, FTB and proposed fuzzy ordering policies with 50 different random demand vectors

Full size image

5 Conclusion

The term BWE refers to a dynamical phenomenon, which is able to affect the efficiency of SCs and cause the increase in inventory costs as a result of the existence of information asymmetry in supply chains (SCs). Several remedies have been presented for BWE management up to now, but none of them has been able to eliminate it completely. Information sharing (IS) policies are known as an effective theoretical approach to managing BWE in SCs. An effective IS technique which is recently used to facilitate sharing demand information in SCs is the token-based ordering policy (TB). The strategy is dividing orders into two streams: the first stream is actual value of customer demand, whereas the second one is adjustments which are required to manage fluctuations and keep a stable inventory in each echelon of SC.

This work concentrated on improving the efficiency of token-based ordering policy through proposing a robust push–pull policy for the token-ordering procedure. Token-ordering procedure is the procedure of obtaining the optimal amount of tokens which should be ordered in every period by different SC echelons. Two new fuzzy approaches were proposed to improve this procedure: the TSK and hybrid MISO fuzzy approaches. The main characteristic of the proposed approaches is that they can eliminate the dependence between the efficiency of TB ordering policy and exogenous and constant variables. In other words, proposed fuzzy approaches are able to determine the amount of tokens that each SC echelon should order to manage its inventory control policies through a push–pull approach and using the endogenous variables of the supply system.

Numerical examples showed that both of the proposed fuzzy models improved the SC performance criteria, but the hybrid MISO fuzzy model presented better outputs and prepared more robust modeling. Finally, the advantages and disadvantages of the proposed approaches were discussed to provide a basis for decision-making trade-offs.

Two main approaches are pursued in future works; applying type 2 fuzzy logic for improvement of the power of the proposed model in coping with uncertainties (regarding the capabilities of type 2 fuzzy logic in uncertainty modeling) and survey of the incentive of the echelons for participation in information sharing (IS) through an automated negotiation in an agent-based supply platform.