Fast classification of univariate and multivariate time series through shapelet discovery

Abstract

Time-series classification is an important problem for the data mining community due to the wide range of application domains involving time-series data. A recent paradigm, called shapelets, represents patterns that are highly predictive for the target variable. Shapelets are discovered by measuring the prediction accuracy of a set of potential (shapelet) candidates. The candidates typically consist of all the segments of a dataset; therefore, the discovery of shapelets is computationally expensive. This paper proposes a novel method that avoids measuring the prediction accuracy of similar candidates in Euclidean distance space, through an online clustering/pruning technique. In addition, our algorithm incorporates a supervised shapelet selection that filters out only those candidates that improve classification accuracy. Empirical evidence on 45 univariate datasets from the UCR collection demonstrates that our method is 3–4 orders of magnitudes faster than the fastest existing shapelet discovery method, while providing better prediction accuracy. In addition, we extended our method to multivariate time-series data. Runtime results over four real-life multivariate datasets indicate that our method can classify MB-scale data in a matter of seconds and GB-scale data in a matter of minutes. The achievements do not compromise quality; on the contrary, our method is even superior to the multivariate baseline in terms of classification accuracy.

1 Introduction

Classification of time-series data has attracted considerable interest in the recent decades, which is not surprising given the numerous domains where time series are collected. A recent paradigm has emerged into the perspective of classifying time series, the notion of shapelets. Shapelets are supervised segments of series that are highly descriptive of the target variable [23]. In the recent years, shapelets have achieved a high momentum in terms of research focus [17, 18, 23, 25].

Distances of time series to shapelets can be perceived as new classification predictors, also called “the shapelet-transformed data” [14]. It has been shown by various researchers that shapelet-derived predictors boost the classification accuracy [17, 24]. In particular, shapelets are efficient in datasets where the class discrimination is attributed to local variations of the series content, instead of the global structure [23]. Even though not explicitly mentioned by the related work, the discovery of shapelets can be categorized as a supervised dimensionality reduction technique. In addition, shapelets also provide interpretive features that help domain experts understand the differences between the target classes.

In contrast to the high classification accuracy, discovering shapelets remains challenging in terms of runtime. The current discovery methods need to search for the most predictive shapelets from all the possible segments of a time-series dataset [17, 23]. Since the number of possible candidates is high, the required time for evaluating the prediction quality of each candidate is prohibitive for large datasets. Therefore, the time-series research community has proposed several speedup techniques [17, 18, 23], aiming at making shapelet discovery feasible in terms of time.

This paper proposes a novel method that discovers time-series shapelets considerably faster than the fastest existing method. Our method follows the knowledge that time-series instances contain lots of similar segments. Often inter-class variations of time series depend on differences within small segments, with the remaining parts of the series being similar. Therefore, we hypothesize that the time needed to discover shapelets can be scaled up by pruning candidate segments that are similar in Euclidean distance space. We introduce a fast distance-based clustering approach to pruning future segments that result similar to previously considered ones. In addition, we propose a fast supervised selection of shapelets that filters out the qualitative shapelets using an incremental nearest-neighbor classifier. Extensive experiments conducted on real-life data demonstrate a large reduction (3–4 orders of magnitude) in the discovery time, by even gaining prediction accuracy with respect to baselines. The contributions of this paper can be short-listed as follows:

• 1. A fast pruning strategy for similar shapelets in Euclidean space involving a distance-based clustering approach;

• 2. A fast supervised selection of qualitative shapelets using an incremental nearest-neighbor classifier, conducted jointly with the pruning;

• 3. Extensive experimental results against the fastest existing univariate shapelet discovery methods on a large set of 45 time-series datasets.

• 4. Extension to multivariate time-series datasets showing that our method scales to GB-sized data.

2 Related work

Shapelets were introduced by Ye and Keogh [23] as a new primitive representation of time series that is highly predictive of the target. A large pool of candidates from all segments of a dataset were assessed as potential shapelet candidates, while the minimum distance of series to shapelets was used as a predictive feature. The best performing candidates were ranked using the information gain criteria over the target. Successively, other prediction quality metrics were also proposed such as the Kruskal–Wallis or Mood’s median [14], as well as F stats [16]. The minimum distance of the time series to a set of shapelets can be understood as a data transformation (dimensionality reduction) and is called shapelet-transformed data [14]. Certain classifiers, such as SVMs or rotation forests, have been shown to perform competitively over the shapelet-transformed predictors [14].

The excessive amount of potential candidates makes brute-force (exhaustive) shapelet discovery intractable for large datasets. Therefore, researchers have come up with various approaches for speeding up the search. Early abandoning of the Euclidean distance computation combined with an entropy pruning of the information gain metric is an early pioneer in that context [23]. Additional papers emphasize the reuse of computations and the pruning of the search space [17], while the projection of series to SAX representation was also elaborated [18]. Furthermore, the discovery time of shapelets has been minimized by mining infrequent shapelet candidates [13]. Speedups have also been attempted by using hardware-based implementations, such as the usage of the processing power of GPUs for reducing search time [7].

In terms of applicability, shapelets have been utilized in a battery of real-life domains. Unsupervised shapelet discovery, for instance, has been shown useful in clustering time series [25]. Shapelets have been used in classifying/identifying humans through their gait patterns [19]. Gesture recognition is another application domain where the discovery of shapelets has played an instrumental role in improving the prediction accuracy [11, 12]. In the realm of medical and health informatics, interpretable shapelets have been shown to help in early classification of time series [21, 22].

In contrast to the state-of-the-art methods, we propose a fast novel method that discovers shapelets by combining a direct similarity-based pruning strategy of candidates with an incremental classification technique.

3 Scalable shapelet discovery

3.1 Distances of shapelets to series as classification features

Throughout this paper, we denote a time-series dataset having N series of Q points each, as $T \in {{\mathbb {R}}}^{N \times Q}$. While our method can work with series of arbitrary lengths, we define a single length Q for ease of mathematical formalism. The distances of shapelets to series can be used as classification features, also known as shapelet-transformed features [14]. The distance of a candidate shapelet to the closest segment of a series can be perceived as a membership degree for that particular shapelet. Equations 1 and 2 formalize the minimum distances between a shapelet s and the dataset T as a vector of the Euclidean distances $({\mathcal {D}})$ between the shapelet and the closest segment of each series. (The notation $V_{a:b}$ denotes a subsequence of vector V from the ath element to the bth element.)

$$\begin{aligned} \mathbf{MinDist }(s,T):= & {} \begin{bmatrix} {\mathcal {D}}(s,T_1) \\ {\mathcal {D}}(s,T_2) \\ \vdots \\ {\mathcal {D}}(s,T_N) \end{bmatrix} \end{aligned}$$

(1)

$$\begin{aligned} {\mathcal {D}}(s,T_i):= & {} \min _{j = 1,\ldots ,Q-|s|+1} \left\| T_{i,j:j+|s|-1} - s \right\| ^2 \end{aligned}$$

(2)

Fig. 1

TwoLeadECG dataset: aligning shapelets to the closest series segments, and in right the resulting two-dimensional shapelet-transformed training data

Table 1 Summary of notations

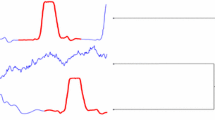
An illustration of the minimum distances between shapelets and series is shown in Fig. 1 for the TwoLeadECG dataset. Two shapelets (purple) are matched to four time series of two different classes (red and blue). Following the principle that Eq. 2 states, the distance of a shapelet is computed to the closest series segment. The distances between training time series and the two shapelets can project the dataset to a two-dimensional shapelet-transformed space, as shown in the right subplot. A nearest-neighbor classifier and the corresponding classification decision boundary are also illustrated (Fig. 1). The notation conventions of this paper are presented in Table 1.

3.2 Quantification of similarity using a distance threshold

A time-series dataset generally contains lots of similar patterns spread over various instances. Since series from the same class generally follow a similar structure, similar patterns repeat over time series of the same class. Similarities can also be observed among time series of different classes, because often classes are discriminated by differences in small subsequences rather than the global structure. As a result, we raise the hypothesis that existing state-of-the-art techniques, which exhaustively search all candidates, inefficiently consider lots of very similar patterns.

Fig. 2

a Distribution of distances among random pairs of candidates. b Illustration of similar segments from the SwedishLeaf dataset with pairwise distances $<$25th percentile of the distribution in a

Figure 2 illustrates the distribution of distances among arbitrary pairs of candidate segments from various time series of the UCR collection of datasets [15]. As can be seen from subfigure a, the distribution of distances is highly skewed toward zero, which indicates that most candidates are very similar to each other. However, a threshold separation on the similarity distance is required to judge segments as being similar or not. We propose to use a threshold over the percentile on the distribution of distances. For instance, Fig. 2b displays pairs of similar segments whose pairwise distances are within the 25th percentile of the distance distribution.

The procedure of determining a distance threshold value, denoted as $\epsilon$ and belonging to the pth percentile of the distance distribution, is described in Algorithm 1. The algorithm selects a pair of random segments starting at indices $(i,j), (i^{\prime },j^{\prime })$ and having random shapelet lengths $\varPhi _r$. Then a distribution is built by accumulating the distances of random pairs of segments, and the distance value that corresponds to the desired percentile p is computed from the sorted list of distance values. For instance, in case all the distance values are sorted from smallest to largest, then the 25th percentile is the value at the index that belongs to 25 % of the total indices.

In total, there are ${\mathcal {O}}(\textit{NQR})$ segments in a time-series dataset, and the total number of pairs is $\frac{1}{2} (\textit{NQR})(\textit{NQR}-1)$. However, in order to estimate the distribution of a set of values (here distances), one does not need to have access to the full population of values. On the contrary, a sample of values are sufficient for estimating the distribution. In order to balance between a fast and accurate compromise, we choose to select $\textit{NQ}$-many random segment pairs for estimating the distance distributions. The runtime speedup success in Sect. 4.3 indicates that the distance threshold estimation is accurate.

3.3 Main method: scalable discovery of time-series shapelets

The scalable discovery of time-series shapelets follows the two primary principles of this paper: (i) pruning of similar candidates and (ii) on-the-fly supervised selection of shapelets. The rationale of these principles is based on the knowledge that the majority of patterns from any specific time series are similar to patterns in other series of the same dataset. Therefore, it is computationally non-optimal to measure the quality of lots of very similar candidates. Instead, we aim at considering only a small nucleus of non-redundant candidates.

3.3.1 Taxonomy of the terms

The fate of any candidate shapelet will be one of refused, considered, accepted and rejected. The decision tree below helps clarifying those terms.

The similarity of a candidate is first evaluated by looking up whether a close candidate has been previously considered, i.e., has been previously flagged as either accepted or rejected. The considered non-redundant (non-similar to previous) candidates are subsequently checked on whether they improve the classification accuracy of previously selected candidates, and are either marked as accepted or rejected.

We are presenting our method as Algorithm 2 and incrementally walking the reader through the steps. The algorithm is started by compressing the time series via the piecewise aggregate approximation (PAA) technique, to be detailed in Sect. 3.4. In order to prune similar candidates, the threshold distance $\epsilon$ is computed using Algorithm 1. Our method operates by populating two lists of accepted and rejected shapelets, denoted as ${\mathcal {A}}$ and ${\mathcal {R}}$, and storing a distance matrix X for distances between series in the shapelet-transformed space.

3.3.2 Pruning similar candidates

Random shapelet candidates, denoted as s, are drawn from the training time series, and a similarity search is conducted by looking up whether similar candidates have been previously considered (lines 4–8). Equation 3 formalizes the procedure as a similarity search over a list ${\mathcal {L}}$ (e.g., ${\mathcal {A}}$ or ${\mathcal {R}}$), considering candidates having same length [length()]. Please note that in the concrete implementation, we use a pruning of the Euclidean distance computations, by stopping comparisons exceeding the threshold $\epsilon$.

$$\begin{aligned} \mathbf{LookUp }(s, {\mathcal {L}},\epsilon ) := \exists q \in {\mathcal {L}}\,\, |\,\,|| s - q ||^2 < \epsilon \wedge |s| = |q| \end{aligned}$$

(3)

3.3.3 Incremental nearest-neighbor distances

In case a candidate is found to be novel (not similar to previously considered), then the distance of the candidate to training series is computed using Eq. 1 and stored as $d^s$. Our approach evaluates the joint accuracy of accepted shapelets, so far, using a nearest-neighbor classifier over the shapelet-transformed data, i.e., distances of series to accepted shapelets.

When checking how does a new $(|{\mathcal {A}}|+1)$st candidate influence the accuracy of $|{\mathcal {A}}|$ currently accepted candidates, an important speedup trick can be used. We can pre-compute the distances among shapelet-transformed features in an incremental fashion. The distances among series in the shapelet-transformed space are stored in a distance matrix, denoted as X, as shown in Eq. 4.

$$\begin{aligned} X_{i,m}\left( D\right)= & {} \sum _{j=1}^{|{\mathcal {A}}|} \left( D_{i,j} - D_{m,j} \right) ^2, \quad \forall i \in \{1,\ldots ,N\},\quad \forall m \in \{1,\ldots ,N\} \end{aligned}$$

(4)

We propose a novel trick, which can add the distance contribution of a new candidate to the distance matrix in an incremental manner. When adding one more attribute $d^s$ to the shapelet-transformed data D, we can use the previously computed pairwise distances to incrementally update the new pairwise distances as shown in Eq. 5.

$$\begin{aligned} X_{i,m}\left( D \cup d^s \right)= & {} \sum _{j=1}^{|{\mathcal {A}}|} \left( D_{i,j} - D_{m,j} \right) ^2 + \left( d^s_i - d^s_m \right) ^2 \nonumber \\= & {} X_{i,m}\left( D\right) + \left( d^s_i - d^s_m \right) ^2 \end{aligned}$$

(5)

Those steps correspond to lines 10–12 and 19–21 in Algorithm 2. It is trivial to verify that this technique can improve the runtime of a nearest neighbor from $\mathcal {O}({N^2 |{\mathcal {A}}|})$ to $\mathcal {O}({ N^2}),$ which means that we can avoid recomputing distances among previously accepted $|{\mathcal {A}}|$-many shapelets, yielding a speedup factor $|{\mathcal {A}}|$ for every considered shapelet candidate.

3.3.4 Supervised shapelet selection

In case the contribution of a unique candidate improves the classification accuracy of a nearest-neighbor classifier, then the shapelet is added to the accepted list and the distance vector is stored in a shapelet-transformed data representation ${\mathcal {D}}$, in order to be later on used for classifying the test instances. Otherwise, the shapelet is inserted to the rejected list and the contribution of the candidate to the distance matrix X is rolled back. The classification accuracy of the distances between series and a set of shapelets is measured by the nearest-neighbor accuracy of the cumulative distance matrix X. The accuracy over the training data is formalized in Eq. 6.

$$\begin{aligned} \mathbf{Accuracy }(X,Y) := \frac{1}{N} \left| \left\{ i \in \{1,\ldots ,N\} |Y_i = Y_{ {{\mathrm{{\text {argmin}}}}}_{m, m \ne i } X_{i,m} } \right\} \right| \end{aligned}$$

(6)

The mechanism described in Sects. 3.3.3 and 3.3.4 consists of a supervised variable selection for shapelet-transformed features [10]. The strategy is a “Forward greedy selection” where shapelets are Accepted incrementally if they improve the accuracy [10].

3.3.5 Number of sampled candidates

Algorithm 2 samples shapelet candidates randomly, and however, the total number of sampled candidates is $\textit{NQR}$, which upper-bounds the total possible series segments of a dataset. Our method could perform competitively even if we would sample a subset of the total possible candidates, as indicated by Fig. 3c. That plot illustrates that the train and test accuracy on the StarLightCurves dataset converges well before trying out all the candidates. However, since the state-of-the-art methods try out all the series segments as candidates, we also opted for the same approach. In that way, the runtime comparison against the baselines provides an isolated hint on the impact of the pruning strategy.

Fig. 3

a–c Relations of refused, rejected and accepted candidate shapelets, and the resulting accuracy, for the Starlight dataset; d–f histograms of refused, accepted and rejected candidate percentages over all 45 UCR datasets

3.3.6 An illustration of the process

We present the main idea of our method with the aid of Fig. 3. Subfigures a–c display the progress of the method on the StarLightCurves dataset, the largest dataset from the UCR collection [15]. The fraction of considered (accepted $+$ rejected) shapelets are shown in a with respect to the total candidates in the X-axis. As can be seen, the first few candidates are considered until the accepted and rejected lists are populated with patterns from the dataset. Afterward, the algorithm starts refusing (pruning/not considering) previously considered candidates within the 25th percentile threshold, while in the end, an impressive 99.97 % of candidates are pruned. In fact, this behavior is not special to the StarLightCurves dataset. We ran the algorithm over all the 45 datasets of the UCR collection and measured the fraction of refused candidates as displayed in the histogram of subfigure d. In average, 99.14 % of candidates can be pruned, with cross-validated values p, r on the training data for each dataset.

Among the considered candidates, a supervised selection of shapelets is carried on by accepting only those candidates that improve the classification accuracy. Subfigure b shows that the number of rejections overcomes the number of acceptances as candidates are evaluated, which validates the current belief that very few shapelets can accurately classify a dataset [23]. As a consequence of the accepted shapelets, the train and test accuracy of the method on the dataset is improved as testified by subfigure c. With respect to all datasets of the UCR collection, histograms of subfigures d, e show that on average, only 0.06 % of candidates are accepted and 0.81 % are rejected.

3.3.7 A further intuition

The similarity-based pruning of candidates can be compared to a particular type of clustering where the considered candidates represent centroids. In principle, the mechanism resembles fast online clustering methods [1]. Figure 4 illustrates how the considered shapelets (blue) can be perceived as an $\epsilon$ threshold clustering of the refused candidates (gray). Each cluster is represented by a hyper-ball of radius $\epsilon$ in a $\varPhi _r$-dimensional space, for $\varPhi _r$ being the shapelet length. For the sake of illustration, we selected random points of the shapelets and printed two-dimensional plots of the six considered candidates and 7036 refused candidates from the MALLAT dataset.

Fig. 4

Refused (gray) candidates versus considered ones (blue), together with the distance threshold circles, are shown for MALLAT dataset. Considered shapelets are displayed in the right. Parameters: $r=0.125$, $p=25$ (i.e., radius is $\epsilon =1.26$) $\varPhi _r=25$ (color figure online)

Fig. 5

Impact of alternating the distance threshold’s percentile (p) value on accuracy, discovery time and the fraction of refused candidates

The threshold distance used for pruning similar candidates has a significant effect on the quantity of refused candidates. Figure 5 shows that an increase in the percentile parameter both deteriorates the classification accuracy (subfigure a) and significantly shortens the running time (subfigure b). The higher the distance threshold percentile, the more the distant segments will be considered similar and subsequently the more the candidates will be refused. In order to avoid a severe accuracy deterioration, the percentile parameter p needs to be fixed by cross-validating over the training accuracy.

3.4 Piecewise aggregate approximation (PAA)

The PAA is a dimensionality reduction technique that shortens time series by averaging consecutive values [6]. Algorithm 3 illustrates how the time series of a dataset can be compressed by a ratio r. For instance, if $r=\frac{1}{4}$, then every four consecutive points are replaced by their average values.

PAA significantly reduces the discovery time of shapelets as shown in Fig. 6b for selected datasets. Moreover, subfigure a shows that the classification accuracy does not deteriorate significantly because time-series data can be compressed without undermining the series pattern.

The exact amount of PAA reduction and the percentile of the pruning similarity threshold are hyper-parameters that need to be fixed per each dataset using the training data. For instance, Fig. 6c illustrates the accuracy heatmap on the 50 words dataset as a result of alternating both parameters. As shown, the best accuracy is achieved for moderate values of percentile threshold and compression. In contrast, (i) excessive compression and (ii) high threshold percentiles can deteriorate accuracy by (i) destroying informative local patterns by compression and (ii) pruning qualitative variations of shapelet candidates.

Fig. 6

a, b Consequence of PAA into accuracy and running time; c grid sensitivity of the impact of PAA and the percentile distance threshold over accuracy

3.5 Algorithmic analysis of the runtime speedup

The runtime of shapelet discovery algorithms, which explore candidates among series segments, is upper-bounded by the number of candidates in a dataset. Given N-many training series of length Q, the total number of shapelet candidates has an order of $\mathcal {O}({\textit{NQ}^2})$, while the time needed to find the best shapelet is $\mathcal {O}({N^2 Q^4})$. Please note that the discovery time is quadratic in terms of the number of candidates. Applying PAA, in order to reduce the length of time series by a ratio $r \in \left\{ \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \ldots , \right\}$, does alter the runtime complexity into $\mathcal {O}({N^2 (r \,Q)^4})$ translated to $\mathcal {O}({\mathbf{r^4} N^2 Q^4})$. In other words, PAA reduces the running time by a factor of $\mathbf r^4$. Furthermore, similarity pruning of candidates has a determinant role in reducing the runtime complexity. Let us denote the fraction of considered candidates as $f := \frac{\# \text {accepted} + \# \text {rejected}}{\textit{NQ}^2}$. Therefore, if executed after a PAA reduction, our algorithm reduces the number of candidates to $\mathcal {O}({\textit{fN} (\textit{rQ})^2})$ and impacts the total runtime complexity by $\mathcal {O}({\textit{fN} (\textit{rQ})^2 \times ( N ( \textit{rQ})^2 + 2N^2)})$, which is upper-bounded by $\mathcal {O}({f r^4 N^2 Q^4})$, since usually $(\textit{rQ})^2 \gg 2N$. Ultimately, the expected runtime reduction factor achieved by this paper is upper-bounded by $\mathbf f r^4$.

There is an additional term that adds up into the runtime complexity: the time needed to check whether any sampled candidate has been previously considered. Such a complexity is $\mathcal {O}({N(\textit{rQ}^2) \times f|r \varPhi _{*}|})$, in other words, all candidates times the time needed to search for $\epsilon$ similarity on the accepted and rejected lists (f-considered candidates having length $|r \varPhi _{*}|$). Since $|r \varPhi _{*}| \sim \mathcal {O}({\textit{rQ}})$, then the whole operation has a final complexity of $\mathcal {O}({fr^3 NQ^3})$. Such a complexity is smaller than the time needed to evaluate the accuracy of the candidates ($\mathcal {O}({f r^4 N^2 Q^4}$)), which, therefore, does not alter the big-O complexity.

Let us illustrate the theoretically expected speedup via an example. Assume that we compress time series into a quarter of the original lengths, i.e., $r = \frac{1}{4}$. The average fraction of considered shapelets in the UCR datasets is $f = 0.0086$, as previously displayed in Fig. 3. Therefore, a runtime reduction factor of $f r^4 = (0.0086) (0.065) \approx 5.3 \times 10^{-4}$ is expected. As shown, the expected theoretic runtime speedup can be four orders of magnitude compared to the exhaustive shapelet discovery. A detailed analysis of the effects of the dimensionality reduction (PAA compression) and pruning on the runtime performance is provided in Sect. 4.6. Furthermore, in Sect. 4.3, we will empirically demonstrate that our method is faster than existing shapelet discovery methods.

3.6 Effect analysis of supervised shapelet selection

In this subsection, we analyze the effects of the supervised shapelet selection mechanism. In particular, one could ask whether the incremental nearest-neighbor (NN) method in Sect. 3.3.3 is better than not pruning based on accuracy. Stated alternatively, would accepting all considered candidates (no rejection as per the taxonomy in Sect. 3.3.1) be equally preferable?

Fig. 7

Comparing an incremental NN against a full NN in terms of accuracy, model complexity and classification time on 45 datasets from the UCR collection

There are two primary reasons why an incremental NN is needed: interpretability and classification time. Meanwhile, Fig. 7 helps clarifying both points. One of the motivations for shapelets is interpretability; therefore, visual comprehension demands a small set of shapelets [23]. As is seen in Fig. 7b), a full NN (no rejected candidates) ends up having on average 1477 % more accepted candidates than our incremental approach. As a form of variable subset selection, our incremental NN is expected to achieve comparable accuracy compared to an NN with a full set of features. As Fig. 7a) indicates, the full NN has slightly higher accuracy values, and however, the differences are way insignificant according to a Wilcoxon signed-rank test indicating a p value of $p=0.65272$ with a significance level of $p \le 0.05$. The last argument in favor of an incremental NN approach is the classification time, which is a trivial consequence of having more features (i.e., more accepted shapelets). Figure 7c) shows the comparisons of classification times between the two approaches, with the full NN being on average 1566 % slower.

4 Experimental results

4.1 Baselines

In order to evaluate the efficiency of the proposed method scalable shapelet discovery (denoted by SD), the fastest state-of-the-art shapelet discovery methods were selected, being:

• 1. Logical shapelet [17] (denoted as LS) advances the original shapelet discovery method [23] by one order of magnitude, via: (i) caching and reusing computations, and (ii) applying an admissible pruning of the search space [17].

• 2. Fast shapelet [18] (denoted as FS) is a recent state-of-the-art method that proposes a random projection technique on the SAX representation by filtering potential candidates [18]. FS has been shown to reduce the shapelet discovery time of LS by two to three orders of magnitude [18].

• 3. Improved fast shapelet (denoted as FS++) is a variation of FS that we created for the sake of being fair to the FS baseline. The original FS paper iterates through all the shapelet lengths from one to the length of the series. In comparison, our method SD iterates through a subset of the possible lengths ($\varPhi$) as mentioned in Sect. 4.2. In order to be fair (with respect to runtime), we created a variant of the FS, named FS++, that also iterates through the same subsets of shapelet lengths that SD does.

The comparison against the listed state-of-the-art methods will testify the efficiency of our method in terms of runtime scalability. When proposing a faster solution to a supervised learning task, it is crucial to also demonstrate that the speedup does not deteriorate the prediction accuracy. For this reason, we payed attention to additionally compare the classification accuracy against the baselines.

4.2 Setup and reproducibility

In order to demonstrate the speedup achievements of the proposed shapelet discovery method, we use the popular collection of time-series datasets from the UCR collection [15]. The collection includes 45 univariate time-series datasets of different number of instances, different number of classes and lengths, found on [15].

Our scalable shapelet discovery method, denoted as SD, requires the tuning of two parameters, the aggregation ratio r and the threshold percentile p. The parameters were searched for each dataset via cross-validation using only the training data. The combination (r, p) that yielded the highest accuracy on the training set was selected. A grid search was conducted with parameter ranges being $r \in \left\{ 1, \frac{1}{2}, \frac{1}{4}, \frac{1}{8} \right\}$ and $p \in \{15,25,35 \}$. We start with the fastest configuration $r=\frac{1}{8}$ and $p=35$. Subsequently we increase r and decrease p with the values of the range, one at a time. The selection stops when there is no more increase in accuracy as a result of relaxing the dimensionality reduction r and threshold p. Finally, the winning combination of parameters was applied over the test data. We would like to note that we used three shapelet lengths for all our experiments, i.e., $L=3$ and $\varPhi =\{0.2Q,0.4Q,0.6Q \}$. In order to neutralize the randomness effect, all the results of our method represent the averages over five different repetitions.

We used the Java programming language to implement our method (SD), while the other baselines (LS, FS, FS++) are implemented in C++. We decided to use the C++ source codes provided and optimized by the respective baseline paper authors [17, 18], in order to avoid typical allegations on inefficient re-implementations. Finally, we are presenting the exact number of accepted shapelets per each dataset and the respective percentages of the accepted, rejected and refused candidates in the columns merged under “SD Performance.” All experiments (both our method and the baselines) were conducted in a Sun Grid Engine distributed cluster with 40 node processors, each being Intel Xeon E5-2670v2 with speed 2.50 GHz and 64 GB of shared RAM for all nodes. The operating system was Linux CentOS 6.3. All the experiments were launched using the same cluster parameters.

The authors are committed to promote experimental reproducibility. For this reason, the source code, all the datasets, the executable file and instructions are provided unconditionally.¹

Table 2 Parameters of SD and runtime results of SD and state-of-the-art baselines over 45 UCR datasets (n/a denotes a 24-h time-out)

4.3 Highly qualitative runtime results

The empirical results include both the discovery time and the classification accuracy of our method SD against baselines for 45 UCR datasets. Table 2 contains a list of results per dataset, where the discovery time is measured in seconds. A time-out threshold of 24 h was set for the discovery of shapelets of a single dataset. As can be seen, the logical shapelet (LS) exceeded the time-out threshold in a considerable number of datasets. The reader is invited to notice that 24 h (86,400 s) is a very large threshold, given that our method SD often finds the shapelets within a fraction of 1 s, as for instance in the 50 words dataset.

It can be clearly deduced that our method SD is faster than the fastest existing baselines LS [17] and FS [18]. There is no dataset where any of the baselines is faster. Even, our modification of FS, i.e., the FS++, is considerably slower than SD. For instance, it took only 3.19 s for our method to find the shapelets of the StarLightCurves dataset, which has 1000 training instances each having 1024 points. The high-level conclusion from the discovery time results is: “Since the introduction of shapelets in 2009, time-series community believed shapelets are very useful classification patterns, but finding them is slow. This paper demonstrates that shapelets can be discovered very fast.”

The discovery time measurements do not include the time needed by a practitioner to tune the parameters of the methods. While our method has two parameters (p and r, totaling $3\times 4=12$ combinations, see Sect. 4.2), the strongest baseline fast shapelet (FS) has more parameters, concretely four: the reduced dimensionality and cardinality of SAX, the random projection iterations and the number of SAX candidates (denoted as d, c, r, k in the original paper [18]).

Fig. 8

Time and accuracy comparison of our method (denoted as SD) against state-of-the-art methods in terms of both discovery time and classification accuracy for all the 45 UCR datasets

Table 3 Parameters of SD and classification accuracy results of SD and SOTA baselines over 45 UCR datasets (n/a denotes a 24-h time-out)

4.4 Competitive prediction accuracy

In addition, our results are atypical in another positive aspect. Most scalability papers propose speedups of the learning time by sacrificing a certain fraction of the prediction accuracy. The results of Table 3 show that our method is both faster and more accurate than the baselines. The winning method that achieves the highest accuracy on each dataset (on each row) is distinguished in bold. Our method has more wins than the baselines (21 wins against 13 of the second best method) and also a better rank (1.889 against 2.178 of the second best method). The accuracy improvement arises from the joint interaction of accepted shapelets as predictors (distance matrix X in Algorithm 2), while the baselines measure the quality of each shapelet separately, without considering their interactions during the discovery phase [17, 18, 23]. Incorporating the interactions among shapelets into the prediction model has been recently shown to achieve high classification accuracy [9].

Table 4 Modular decomposition of the performance of our method (SD); n/a denotes a 24-h time-out

4.5 Speedup analysis

In order to show the speedup factor of our method with respect to the (former) state of the art, we provide another presentation of the results in Fig. 8. The three plots on the left side show the discovery time of SD in x-axis and the logarithm of the discovery time of each baseline as the y-axis. As can be easily observed from the illustrative order lines, SD is 4–5 orders of magnitude faster than the LS and 3–4 orders of magnitude faster than the FS. The datasets where LS exceeds the 24-h threshold are depicted in light blue. In addition, FS++ is faster than FS because it iterates over less shapelet length sizes, yet it is still 1–2 orders of magnitude slower than SD (Fig. 8).

The plots on the right represent scatter plots of the classification accuracy of SD against the baselines. While generally better than LS and FS, our method SD is largely superior to FS++. Such a finding indicates that the accuracy of the FS is dependent on trying shapelet candidates from a fine-grained set of lengths, while our method is very accurate even though it iterates over few shapelet lengths.

4.6 A modular decomposition of the performance

We have already seen that our proposed method, SD, outperforms significantly the state of the art in terms of runtime and produces even better prediction accuracy. Nevertheless, there are a couple of questions that can be addressed to our method, such as:

• 1. What fraction of SD’s runtime reduction is attributed to the novel candidate pruning and what fraction to the PAA compression?

• 2. To what extent does pruning deteriorate the prediction accuracy?

In order to address those analytic questions, we will decompose our method in a modular fashion. Our method, SD, conducts both a PAA approximation and a pruning by the parameters r, p provided in Table 2. In order to isolate the effect of compression and pruning, we are creating four variants of our method, namely all the permutations “With/Without PAA compression” and “With/Without Pruning” (w.r.t. p, r from Table 2). All the decomposed results of the SD variants are shown in Table 4. Note that “No pruning” means $p=0$, while “no PAA” means $r=1$. The variant with both pruning and PAA is the same as SD from Sect. 4.3, which already was shown to be superior to the state of the art.

Looking into the results in Table 4, it is important to observe that the variant with PAA compression alone is significantly faster than the variant without compression (column 4 vs column 3). However, using pruning without compression is much faster than the exhaustive approach and also much faster than compression alone (column 5 vs. columns 3 and 4). When pruning and compression are combined (column 6), then the runtime reduction effect multiplies. More concretely, Fig. 9 analyzes the runtime reduction in SD variants: that use pruning (X-axis) against variants without pruning (Y-axis) for both scenarios with PAA (plot a) or without PAA (plot b) compression. As can be clearly deduced, pruning alone has a significant effect on the runtime reduction by 3–4 orders of magnitude, compared to the cases where no pruning is employed. While PAA helps our method to be even faster, it is clear that the lion’s share of the speedup arises from the proposed pruning mechanism.

Fig. 9

Runtime comparison (s) plots among variants of SD with and without pruning

There is still a concern on how does pruning affect the classification accuracy. The prediction accuracy results are demonstrated in Table 4 for all the datasets, with the winning variant emphasized in bold. The total wins and the ranks of the variants indicate that the best prediction performance is attributed to the exhaustive methods (no pruning, columns 7 and 8). Such a finding is natural because exhaustive approaches consider all the candidate variants and can extract more qualitative minimum distance features. Yet, are the results of the exhaustive variants better with a statistical significance margin? Table 5 illustrates the p values of a Wilcoxon signed-rank test of statistical significance, for a two-tailed hypothesis with a significance level of 5 % $(\alpha =0.05).$

Table 5 Wilcoxon statistical significance test: p values (significance level 5 %, two-tailed hypothesis)

The p values which compare variants that use pruning against variants that do not use pruning are shown in bold and correspond to $p=0.119, p=0.112$. Therefore, the prediction quality using pruning is not significantly (significance means $p < 0.05$) worse than the exhaustive approach. The final message of this section is: “Pruning of candidates provides 3–4 orders of runtime speedup without any statistically significant deterioration in terms of classification accuracy.”

4.7 Comparison to other state-of-the-art shapelet discovery methods

One would categorize the methods focusing on shapelet discovery into “speed-oriented” and “accuracy-oriented” approaches. The method proposed in this paper SD and the baselines LS and FS were focused on reducing the runtime of shapelet discovery. On the other hand, there are other methods which prioritize on achieving the highest classification accuracy. The most prominent methods on accurate shapelet discovery are “Shapelet Transformation” [14] (denoted as ST) and the recently more accurate method “Learning Time-Series Shapelet” [9] (denoted as LTS).

Table 6 Comparison of the proposed method SD against LTS and ST

In this section, we aim at showing that while those methods are more accurate, their runtime is much slower than the proposed method SD. For this reason, we selected the three largest datasets of the UCR collection as shown in Table 6 and ran SD, ST and LTS on those datasets. In order to be fair to the baselines, LTS and ST were also run on a subset of shapelet lengths $\{0.2Q, 0.4Q, 0.6Q\}$. For both LTS and ST, we used the source code provided by the authors. Since those methods are known to be slow, we violated the 24-h time-out in Sect. 4.2 and instead gave the methods a very large time-out deadline of 20 days to complete the execution over the three datasets. The results in Table 6 indicate that LTS is more accurate than SD in all the dataset; however, it took LTS from 18.2 h to 17.7 days to compute. Furthermore, ST could not finish learning on any of the three datasets within 20 days (time-out denoted by *). On the other hand, SD needs 3.19–7.03 s to compute the shapelets of those datasets, for a speedup of up to 346,293 times faster. On the other hand, the deterioration in accuracy varies only between 3.3 and 6.2 % worse than LTS.

5 Extension to multivariate time series

Multivariate time series has become increasingly popular in the data mining research community. Part of the popularity is attributed to the widespread of affordable motion sensor devices. In fact, multivariate (synonym: multidimensional) time series are a generalization of univariate series. In the multivariate case, a single time-series instance is composed of different streams measured at the same time. An example of multivariate series is recordings of wearable body sensors, where signal measuring devices are positioned at different parts of the body [2, 3].

We can formalize a time-series dataset having N instances and V many dimensions as $T \in {{\mathbb {R}}}^{N \times V \times Q*}$, where each series has a different length $T_{i,:,:} \in {{\mathbb {R}}}^{Q_i}, \forall i \in \{1,\ldots ,N\}$. While the lengths of different instances vary, we assume that the different dimensions within one instance have the same length. In this section, we will demonstrate that it is trivial to extend the method proposed in this paper to multivariate time-series datasets. All is needed is to sample shapelet candidates from random dimensions and accept them based on their joint accuracy.

5.1 Addressing challenges of multivariate series

Different series lengths are a common reality for multivariate series. The time-series research community has worked extensively on the UCR collection of datasets, where the time-series instances were preprocessed to have the same lengths. In reality, this is rarely the case; however, different lengths pose no concrete problem for shapelet-based methods. The minimum distance between a candidate and various series segments is independent on the number of segments. There is, however, a small problem, the case when a series is shorter than a shapelet. In order to overcome this concern, we propose to slid the series over the shapelet, i.e., to measure the minimum distance of a series to all the segments of the shapelet candidate. Equation 7 formalizes the distance between the vth dimension of the ith series $T_{i,v,:}$ and a shapelet candidate s.

$$\begin{aligned} {\mathcal {D}}(s,T_{i,v,:}) := {\left\{ \begin{array}{ll} \underset{j = 1,\ldots ,|T_{i,v,:}|-|s|+1}{\min } \left\| T_{i,v,j:j+|s|-1} - s \right\| ^2 &{} |T_{i,v,:}| \ge |s| \\ \underset{j = 1,\ldots ,|s|-|T_{i,v,:}|+1}{\min } \left\| s_{j:j+|T_{i,v,:}|-1} - T \right\| ^2 &{} |s| > |T_{i,v,:}| \end{array}\right. } \end{aligned}$$

(7)

Features from different dimensions are known to improve the classification accuracy; however, related works take diverse approaches in how series of different dimensions are incorporated. In terms of shapelets, an early approach extended the concept of univariate shapelets into multivariate shapelets [8]. However, a label might not be associated with certain dimensions, or there might be shifts of the starting time of a pattern across dimensions. As a result, a recent work [5] proposed to learn a shapelet-based classifier on each dimension and use a majority voting over the predictions of the per-dimension models.

In contrast, we propose a simple and novel technique to incorporate features from different dimensions. The principle relies on sampling random candidates from random dimensions. Roughly speaking, we will harvest accepted and rejected candidates per each dimensions. Distance features from each dimensions will be jointly integrated into the same incremental nearest neighbor and filtered by classification accuracy. This mechanism will allow to fuse features of candidates from different dimensions into a joint feature set.

5.2 Algorithm for multivariate shapelet discovery

The concrete implementation of our multivariate method is described in Algorithm 4. Our method selects NMLV-many random candidates, from random series i, random dimension v, random length $\varPhi _r$ and starting at random time index j (lines 4–8). Each random candidate is looked up for similarity to previously considered (accepted or rejected) candidates within that dimension (line 9). If a shapelet candidate is not found to be similar to previous candidates, then its feature vector is computed (line 10) and the pairwise distance matrix X is updated (line 11–13). In case the candidate improves the overall accuracy (line 14), then it is accepted (lines 15–17), otherwise it is rejected (lines 19–23). In the end, we are going to have lists of accepted shapelets for each dimension, such that the features of those accepted shapelets achieve the highest classification accuracy.

5.3 Experimental results

In order to test our method, we compared against the most recent and relevant method which elaborates shapelets for multivariate classification [5]. Furthermore, we are going to experiment on four multivariate datasets, whose statistics are displayed in Table 7. Three of them (“HMP,” “M-Health,” “REALDISP”) are related to human action recognition using wearable sensors, while “Characters” represents pen tip trajectories of handwritten characters. The instances of all datasets were randomly divided into train and test sets. It is interesting to note that those datasets are diverse in terms of number of dimensions (V from 3 to 117), number of instances (63–1429), number of classes (‘Cls.’ from 12 to 33) and lengths (109–5643).

Table 7 Results of scalable shapelet discovery on multivariate datasets, n/a denotes a 24-h time-out

Another aspect worth consideration is the size of the datasets. For instance, REALDISP has a training set size of 889 MB and a total size of 1.75 GB, which is considerably large for labeled time-series data. As a comparison, the largest univariate dataset from the UCR collection is “StarLightCurves,” which has a train set of 16 MB and a total size of 144 MB. In order to address this size challenge, we opted for the single fastest parameter configuration for all datasets, with respect to the ranges in Sect. 4.2, concretely $r=\frac{1}{8}$, $p=35$. In order to aggregate the randomness effect, we present the average figures of five different executions of our method. The runtimes in Table 7 include the classification time. We would like to point out that dataset characters are retrieved from [20], HMP from [4] and M-Health from [2], while REALDISP is retrieved from [3].

The results in Table 7 indicate great achievements in terms of runtime. Our method can classify the MB-scale datasets in matters of seconds and the GB-scale dataset in matter of minutes. Concretely, our method needs $<$5 min to classify the 1.75 GB dataset. Compared to the baseline method [5], our method is $322.8\times$ to $2494.93\times$ faster on the MB-scale datasets. Unfortunately, the baseline could not complete on the GB-scale dataset under the 24-h time-out specified in Sect. 4.3. On the other hand, our method is more accurate than the baseline on all the datasets. We believe that such a superiority comes from the joint interactions of features from different dimensions, as opposed to learning isolated per-dimension classifiers.

6 Conclusion

Shapelets represent discriminative segments of a time-series dataset, and the distances of time series to shapelets are shown to be successful features for classification. The discovery of shapelets is currently conducted by trying out candidates from the segments (subsequences) of the time series. Since the number of candidate segments is large, the time-series community has spent efforts on speeding up the discovery time of shapelets. This paper proposed a novel method that prunes the candidates based on a distance threshold to previously considered other similar candidates. In a joint fashion, a novel supervised selection filters those shapelets that boost classification accuracy. We empirically showed that our method is 3–4 orders of magnitude faster than the fastest existing shapelet discovery methods, while providing a better prediction accuracy. In addition, we extended our method to multivariate datasets. Results indicate that our approach is able to classify MB-scale datasets in a matter of seconds and GB-scale datasets in a matter of minutes, therefore transporting shapelet discovery to the Big Data era.