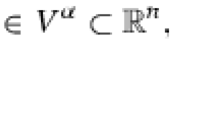A tractable approach for designing piecewise affine policies in two-stage adjustable robust optimization

Abstract

We consider the problem of designing piecewise affine policies for two-stage adjustable robust linear optimization problems under right-hand side uncertainty. It is well known that a piecewise affine policy is optimal although the number of pieces can be exponentially large. A significant challenge in designing a practical piecewise affine policy is constructing good pieces of the uncertainty set. Here we address this challenge by introducing a new framework in which the uncertainty set is “approximated” by a “dominating” simplex. The corresponding policy is then based on a mapping from the uncertainty set to the simplex. Although our piecewise affine policy has exponentially many pieces, it can be computed efficiently by solving a compact linear program given the dominating simplex. Furthermore, we can find the dominating simplex in a closed form if the uncertainty set satisfies some symmetries and can be computed using a MIP in general. We would like to remark that our policy is an approximate piecewise-affine policy and is not necessarily a generalization of the class of affine policies. Nevertheless, the performance of our policy is significantly better than the affine policy for many important uncertainty sets, such as ellipsoids and norm-balls, both theoretically and numerically. For instance, for hypersphere uncertainty set, our piecewise affine policy can be computed by an LP and gives a $O(m^{1/4})$-approximation whereas the affine policy requires us to solve a second order cone program and has a worst-case performance bound of $O(\sqrt{m})$.

1 Introduction

Addressing uncertainty in problem parameters in an optimization problem is a fundamental challenge in most real world problems where decisions often need to be made in the face of uncertainty. Stochastic and robust optimization are two approaches that have been studied extensively to handle uncertainty. In a stochastic optimization framework, uncertainty is modeled using a probability distribution and the goal is to optimize an expected objective [18]. We refer the reader to Kall and Wallace [25], Prekopa [27], Shapiro [28], Shapiro et al. [29] for a detailed discussion on stochastic optimization. While it is a reasonable approach in certain settings, it is intractable in general and suffers from the “curse of dimensionality”. Moreover, in many applications, we may not have sufficient historical data to estimate a joint probability distribution over the uncertain parameters.

Robust optimization is another paradigm where we consider an adversarial model of uncertainty using an uncertainty set and the goal is to optimize over the worst-case realization from the uncertainty set. This approach was first introduced by Soyster [30] and has been extensively studied in recent past. We refer the reader to Ben-Tal and Nemirovski [4,5,6], El Ghaoui and Lebret [19], Bertsimas and Sim [15, 16], Goldfarb and Iyengar [23], Bertsimas et al. [8] and Ben-Tal et al. [2] for a detailed discussion of robust optimization. Robust optimization leads to a tractable approach where an optimal static solution can be computed efficiently for a large class of problems. Moreover, in many cases, designing an uncertainty set is significantly less challenging than estimating a joint probability distribution for high-dimensional uncertainty. However, computing an optimal adjustable (or dynamic) solution for a multi-stage problem is generally hard even in the robust optimization framework.

In this paper, we consider two-stage adjustable robust (AR) linear optimization problems with covering constraints and uncertain right-hand side. In particular, we consider the following model:

$\varPi _{\textsf {AR}}(\mathcal{U})$:

$$\begin{aligned} \begin{aligned} z_{\textsf {AR}}(\mathcal{U}) = \min \;&\varvec{c}^T \varvec{x} + \max _{\varvec{h}\in \mathcal{U}} \min _{\varvec{y}(\varvec{h})} \varvec{d}^T \varvec{y}(\varvec{h}) \\&\varvec{A}\varvec{x} + \varvec{B}\varvec{y}(\varvec{h}) \; \ge \; \varvec{h}\quad \forall \varvec{h} \in \mathcal{U} \\&\varvec{x} \; \in \; {{\mathbb {R}}}^{n_1}_+\\&\varvec{y}(\varvec{h}) \; \in \; {{\mathbb {R}}}^{n_2}_+, \end{aligned} \end{aligned}$$

(1.1)

where $\varvec{A} \in {{\mathbb {R}}}_+^{m {\times } n_1}, \varvec{c}\in {{\mathbb {R}}}^{n_1}_+, \varvec{d}\in {{\mathbb {R}}}^{n_2}_+, \varvec{B} \in {{\mathbb {R}}}^{m {\times } n_2}$, and $\mathcal{U}\subseteq {{\mathbb {R}}}^m_+$ is the uncertainty set. The goal in this problem is to select the first-stage decision $\varvec{x}$, and the second-stage recourse decision, $\varvec{y}(\varvec{h})$, as a function of the uncertain right hand side realization, $\varvec{h}$ such that the worst-case cost over all realizations of $\varvec{h} \in \mathcal{U}$ is minimized. We assume without loss of generality that $n_1 = n_2 = n$ and that the uncertainty set $\mathcal{U}$ satisfies the following assumption.

Assumption 1

$\mathcal{U}\subseteq [0,1]^m$ is convex, full-dimensional with $\varvec{e}_i \in \mathcal{U}$ for all $i =1,\ldots ,m$, and down-monotone, i.e., $\varvec{h}\in \mathcal{U}$ and $\varvec{0}\le \varvec{h}' \le \varvec{h}$ implies that $\varvec{h}' \in \mathcal{U}$.

We would like to emphasize that the above assumption can be made without loss of generality since we can appropriately scale the uncertainty set, and consider a down-monotone completion, without affecting the two-stage problem (1.1). Note that in the model $\varPi _{\textsf {AR}}(\mathcal{U})$ the objective coefficients $\varvec{c}$, $\varvec{d}$, the first-stage constraint matrix $\varvec{A}$, and the decision variables $\varvec{x}, \varvec{y}(\varvec{h})$ are all non-negative. This is restrictive as compared to general two-stage linear programs but the above model still captures many important applications including set cover, facility location and network design problems under uncertain demand. Here the right-hand side, $\varvec{h}$ models the uncertain demand and the covering constraints capture the requirement of satisfying the uncertain demand.

The worst case scenario of problem (1.1) occurs on extreme points of $\mathcal{U}$. Therefore, given an explicit list of the extreme points of the uncertainty set $\mathcal{U}$, the adjustable robust optimization problem (1.1) can be solved efficiently by including the second-stage decisions and the covering constraints only for the extreme points of $\mathcal{U}$. Some approaches have been developed to generate dynamically the required extreme points, e.g. Zeng and Zhao [31], Ayoub and Poss [1]. However, in general the adjustable robust optimization problem (1.1) is intractable; for example, when the number of extreme points is large or due to other structural complexities of $\mathcal{U}$. In fact, Feige et al. [22] show that problem $\varPi _{\textsf {AR}}(\mathcal{U})$ is hard to approximate within any factor that is better than $\varOmega (\log m)$, even in the case of budget uncertainty set and $\varvec{A}$, $\varvec{B}$ being 0–1 matrices. This motivates us to consider approximations for the problem. Static robust and affinely adjustable solution approximations have been studied in the literature for this problem. In a static robust solution, we compute a single optimal solution $(\varvec{x},\varvec{y})$ that is feasible for all realizations of the uncertain right hand side. Bertsimas et al. [13] relate the performance of static solution to the symmetry of the uncertainty set and show that it provides a good approximation to the adjustable problem if the uncertainty is close to being centrally symmetric. However, the performance bound of static solutions can be arbitrarily large for a general convex uncertainty set with the worst case performance being $\varOmega (m)$. El Housni and Goyal [21] consider piecewise static policies for two-stage adjustable robust problem with uncertain constraint coefficients. These are a generalization of static policies where the uncertainty set is divided into several pieces and a static solution specified for each piece. However, they show that, in general, there is no piecewise static policy with a polynomial number of pieces that has a significantly better performance than an optimal static policy.

Ben-Tal et al. [3] introduce an affine adjustable solution (also known as affine policy) to approximate adjustable robust problems. Affine policy restricts the second-stage decisions, $\varvec{y}(\varvec{h})$ to being an affine function of the uncertain right-hand side $\varvec{h}$, i.e., $\varvec{y}(\varvec{h})=\varvec{P}\varvec{h}+\varvec{q}$ for some $\varvec{P}\in {{\mathbb {R}}}^{n\times m}$ and $\varvec{q}\in {{\mathbb {R}}}^m$, which are decision variables on top of $\varvec{x} \in {{\mathbb {R}}}_+^n$. An optimal affine policy can be computed efficiently for a large class of problems and has a strong empirical performance. For a class of multistage problems where there is a single uncertain parameter in each period, Bertsimas et al. [14] and Iancu et al. [24] show that affine policies are optimal. Bertsimas and Goyal [12] show that affine policies are optimal if the uncertainty set $\mathcal{U}$ is a simplex. They prove a worst case bound of $O(\sqrt{m})$ on the performance of affine policy for general uncertainty sets. Moreover, they show that this bound is tight for an uncertainty set quite analogous to the intersection of the unit $\ell _2$-norm ball and the non-negative orthant, i.e.,

$$\begin{aligned} \mathcal{U}=\{\varvec{h}\in {{\mathbb {R}}}^m_+\;|\;||\varvec{h}||_2\le 1\}. \end{aligned}$$

(1.2)

Bertsimas and Bidkhori [7] provide improved approximation bounds for affine policies for $\varPi _{\textsf {AR}}(\mathcal{U})$ that depend on the geometric properties of the uncertainty set. More general decision rules have been considered in the literature and tested numerically; extended affine decision rules (Chen et al. [17]), binary decision rules (Bertsimas and Georghiou [11]) and adjustable solutions via iterative splitting of uncertainty sets, (Postek and Den Hertog [26]). More recently, Bertsimas and Dunning [10] give an MIP-based algorithm to adaptively partition the uncertainty set. However, no theoretical guarantees on the performance, or the number of partitions, are known.

Piecewise affine policies (PAP) have been studied earlier. In a PAP, we consider pieces $\mathcal{U}_i, i\in [k]$ of $\mathcal{U}$ such that $\mathcal{U}_i \subseteq \mathcal{U}$ and $\mathcal{U}$ is covered by the union of all pieces. For each $\mathcal{U}_i$, we have an affine solution $\varvec{y} ( \varvec{h})$ where $\varvec{h} \in \mathcal{U}_i$. PAP are significantly more general than static and affine policies. For problem $\varPi _{\textsf {AR}}(\mathcal{U})$, with $\mathcal{U}$ being a polytope, a PAP is known to be optimal. However, the number of pieces can be exponentially large. Moreover, finding the optimal pieces is, in general, an intractable task. In fact, Bertsimas and Caramanis [9] prove that it is NP-hard to construct the optimal pieces, even for pieceiwse policies with two pieces, for two-stage robust linear programs.

1.1 Our contributions

Our main contributions in this paper are as follows.

New framework for piecewise affine policy We present a new framework to efficiently construct a “good” piecewise affine policy for the adjustable robust problem $\varPi _{\textsf {AR}}(\mathcal{U})$. As we mentioned earlier, one of the significant challenges in designing a piecewise affine policy arises from the need to construct “good pieces” of the uncertainty set. We suggest a new approach where instead of directly finding an explicit partition of $\mathcal U$, we approximate $\mathcal U$ with a “simple” set $\hat{\mathcal{U}}$ satisfying the following two properties:

• 1. the adjustable robust problem (1.1) over $\hat{\mathcal{U}}$ can be solved efficiently,

• 2. $\hat{\mathcal{U}}$ “dominates” $\mathcal{U}$, i.e., for any $\varvec{h}\in \mathcal{U}$, there exists $\hat{\varvec{h}}\in \hat{\mathcal{U}}$ such that $\varvec{h}\le \hat{\varvec{h}}$.

Using the uncertainty set $\hat{\mathcal{U}}$ instead of $\mathcal{U}$, the domination property of $\hat{\mathcal{U}}$ preserves the feasibility of the adjustable robust problem. Specifically, we choose $\hat{\mathcal{U}}$ to be a simplex dominating $\mathcal{U}$. Therefore, the adjustable robust problem (1.1) over $\hat{\mathcal{U}}$ can be solved efficiently since $\hat{\mathcal{U}}$ only has $m+1$ extreme points. We construct a piecewise affine mapping between the uncertainty set $\mathcal{U}$ and the dominating set $\hat{\mathcal{U}}$, i.e. we use a piecewise affine function to map each point $\varvec{h} \in \mathcal{U}$ to a point $\hat{\varvec{h}}$ that dominates $\varvec{h}$. This mapping leads to our piecewise affine policy which is constructed from an optimal adjustable solution over $\hat{\mathcal{U}}$. We show that the performance of our policy is significantly better than the affine policy for many important uncertainty sets both theoretically and numerically.

We elaborate on the two ingredients of designing our piecewise affine policy below, namely, constructing $\hat{\mathcal{U}}$ and the corresponding piecewise map below.

• (a) Constructing a dominating uncertainty set Our framework is based on choosing an appropriate dominating simplex $\hat{\mathcal{U}}$ based on the geometric structure of $\mathcal{U}$. Specifically, $\hat{\mathcal{U}}$ is taken to be a simplex of the following form

  $$\begin{aligned} \hat{\mathcal{U}} = \beta \cdot {\textsf {conv}} \left( \varvec{e}_1,\ldots ,\varvec{e}_m, \varvec{v} \right) , \end{aligned}$$

  where $\beta >0$ and $\varvec{v} \in \mathcal{U}$ are chosen appropriately so that $\hat{\mathcal{U}}$ dominates $\mathcal{U}$. Solving the adjustable robust problem over $\hat{\mathcal{U}}$ gives a feasible solution for problem $\varPi _{\textsf {AR}}(\mathcal{U})$ due to the domination property. Moreover, the optimal adjustable solution over $\hat{\mathcal{U}}$ gives a $\beta$-approximation for problem $\varPi _{\textsf {AR}}(\mathcal{U})$, since $\hat{\mathcal{U}} = \beta \cdot {\textsf {conv}} \left( \varvec{e}_1,\ldots ,\varvec{e}_m, \varvec{v} \right) \subseteq \beta \cdot \mathcal{U}$. The approximation bound $\beta$ is related to a geometric scaling factor that represents the Banach–Mazur distance between $\mathcal{U}$ and $\hat{\mathcal{U}}$. We note that $\hat{\mathcal{U}}$ does not necessarily contain $\mathcal{U}$.

• (b) The piecewise affine mapping We employ the following piecewise affine mapping $\varvec{ \hat{h}}(\varvec{h}) = \beta \varvec{v} + \left( \varvec{h} - \beta \varvec{v}\right) ^+$ that maps any $\varvec{h} \in \mathcal{U}$ to a dominating point $\hat{\varvec{h}}$ such that $\varvec{h} \le \hat{\varvec{h}}$. For any $\varvec{h} \in \mathcal{U}$, $\varvec{{\hat{h}}}(\varvec{h})$ is contained in the down-monotone completion of $2 \cdot \hat{\mathcal{U}}$. The piecewise affine policy is based on the above piecewise affine mapping and gives a $2\beta$-approximation for problem $\varPi _{\textsf {AR}}(\mathcal{U})$. In this policy, $\beta \varvec{v}$ is covered by the static component and $\left( \varvec{h} - \beta \varvec{v}\right) ^+$ is covered by the piecewise linear component of our policy. This is quite analogous to threshold policies that are widely used in dynamic optimization. Note that $\hat{\varvec{h}}$ does not necessarily belong to $\hat{\mathcal{U}}$ but is contained in the down-monotone completion of $2 \cdot \hat{\mathcal{U}}$ and therefore, we get an approximation factor of $2 \beta$ instead of $\beta$. We can construct a set-dependent piecewise affine map between $\mathcal{U}$ and $\hat{\mathcal{U}}$ that allows us to construct a piecewise affine policy with a performance bound of $\beta$. This bound $\beta$ is not affected by the scaling introduced in Assumption 1.

Given the dominating set, $\hat{\mathcal{U}}$, our piecewise affine policy can be computed efficiently; in fact, it can be computed even more efficiently than an affine solution over $\mathcal{U}$ in many cases because the adjustable problem over $\hat{\mathcal{U}}$ is a simple LP with only $m+1$ constraints while the affine problem over $\mathcal{U}$ is a general convex program for general convex uncertainty sets.

Results for scaled permutation invariant (SPI) sets The uncertainty set $\mathcal{U}$ is SPI if $\mathcal{U} = \text{ diag } ( \varvec{\lambda }) \cdot \mathcal{V}$ where $\varvec{\lambda }\in {\textsf {R}}_+^m$ and $\mathcal{V}$ is an invariant set, i.e., if $\varvec{v} \in \mathcal{V}$, then any permutation of the components of $\varvec{v}$ are also in $\mathcal{V}$. SPI sets include ellipsoids, weighted norm-balls, intersection of norm-balls with budget uncertainty sets and more. SPI sets are commonly used in Robust Optimization literature and in practice.

We show that for SPI uncertainty set $\mathcal{U}$, it is possible to construct the dominating set $\hat{\mathcal{U}}$ and compute the scaling factor $\beta$. In particular, we give an efficiently computable closed-form expression for $\beta$ and $\varvec{v} \in \mathcal{U}$ that are needed to construct $\hat{\mathcal{U}}$. Consequently, we can efficiently construct our piecewise affine decision rule, having a performance bound $2\beta$.

Using this framework, we provide approximation bounds for the piecewise affine policy that are significantly better than those of the optimal affine policy in [7] for many SPI uncertainty sets. For instance, we show that our policy gives a $O (m^{1/4})$-approximation for the two-stage adjustable robust problem (1.1) with hypersphere uncertainty set as in (1.2), compared to the affine policy in [7] that has an approximation bound of $O(\sqrt{m})$. More generally, the performance bound for our policy for the p-norm ball is $O ( m^{\frac{p-1}{p^2}} )$ as opposed to $O ( m^\frac{1}{p} )$ given by the affine policy in [7].¹ Table 1 summarizes the above comparisons. We also present computational experiments and observe that our policy also outperforms affine policy in computation time on several examples of uncertainty sets considered in our experiments including hypersphere, norm-balls and certain polyhedral uncertainty sets. However, we would like to note that our piecewise affine policy does not a generalize affine policy and there are instances where affine policy performs better than our policy. For instance, we observe in our computational experiments that the performance of affine policy is better than our policy for budget of uncertainty sets.

Results for general uncertainty sets While the dominating set $\hat{\mathcal{U}}$ is given in an efficiently computable closed-form expression for SPI sets, the construction of $\hat{\mathcal{U}}$ for general uncertainty sets requires solving a sequence of MIPs which is computationally much harder than for the case of SPI sets. In Sect. 4, we give an algorithm for constructing the dominating set $\hat{\mathcal{U}}$, and a piecewise affine policy for general uncertainty set $\mathcal{U}$. Our framework is not necessarily computationally more appealing than computing optimal affine policies. However, we would like to note that in practice these MIPs can be solved efficiently. Moreover, the construction of the dominating set $\hat{\mathcal{U}}$ is independent of the parameters of the adjustable problem and depends only on the uncertainty set, $\mathcal{U}$. Therefore, $\hat{\mathcal{U}}$ can be computed offline and then used to construct the piecewise affine policy efficiently.

We show that our policy gives a $O(\sqrt{m})$-approximation for general uncertainty sets which is same as the worst-case performance bound for affine policy. We also show that the bound of $O(\sqrt{m})$ is tight. In particular, for the budget uncertainty set

$$\begin{aligned} \mathcal{U}= \left\{ \varvec{h} \in {\mathbb {R}}^{m}_+ \; \bigg \vert \; \sum _{i=1}^m h_i = \sqrt{m} , \; 0 \le h_i \le 1 \ \; \forall i \in [m] \right\} , \end{aligned}$$

the performance bound of our piecewise affine policy is $\varTheta (\sqrt{m})$. Furthermore, the bound of $\varTheta (\sqrt{m})$ holds even if we consider dominating sets with a polynomial number of extreme points that are significantly more general than a simplex. While this example shows that the worst-case performance of our policy is the same as the worst-case performance of the affine policy, we would like to emphasize that our policy still gives a significantly better approximation than affine policies for many important uncertainty sets, and does so in a fraction of computing time (see Sect. 6.2).

Table 1 Comparison with performance bounds for affine policies in Bertsimas and Bidkhori [7]. The ellipsoid in Example 3 is assumed to be a permutation invariant set. There is no specialized bound for this Ellipsoid in [7]. For intersection of norm-balls (Example 4 in the table), we assume $m^{\frac{1}{q}-\frac{1}{p}} \ge r \ge 1$

Outline In Sect. 2, we present the new framework for approximating the two-stage adjustable robust problem (1.1) via dominating uncertainty sets and constructing piecewise affine policies. In Sect. 3, we provide improved approximation bounds for (1.1) for scaled permutation invariant sets. We present the case of general uncertainty sets in Sect. 4. In Sect. 5, we present a family of lower-bound instances where our piecewise affine policy has the worst performance bound and finally in Sect. 6, we present a computational study to test our policy and compare it to an affine policy over $\mathcal{U}$.

2 A new framework for piecewise affine policies

We present a piecewise affine policy to approximate the two-stage adjustable robust problem (1.1). Our policy is based on approximating the uncertainty set $\mathcal{U}$ with a simple set $\hat{\mathcal{U}}$ such that the adjustable problem (1.1) can be efficiently solved over $\hat{\mathcal{U}}$. In particular, we select $\hat{\mathcal{U}}$ such that it dominates$\mathcal{U}$ and it is close to $\mathcal{U}$. We make these notions precise with the following definitions.

Definition 1

(Domination) Given an uncertainty set $\mathcal{U}\subseteq {{\mathbb {R}}}^{m}_+$, $\hat{\mathcal{U}}\subseteq {{\mathbb {R}}}^{m}_+$ dominates $\mathcal{U}$ if for all $\varvec{h}\in \mathcal{U}$, there exists $\hat{\varvec{h}}\in \hat{\mathcal{U}}$ such that $\hat{\varvec{h}}\ge \varvec{h}$.

Definition 2

(Scaling factor) Given a full-dimensional uncertainty set $\mathcal{U}\subseteq {{\mathbb {R}}}^{m}_+$ and $\hat{\mathcal{U}}\subseteq {{\mathbb {R}}}^{m}_+$ that dominates $\mathcal{U}$. We define the scaling factor $\beta (\mathcal{U},\hat{\mathcal{U}})$ as following

$$\begin{aligned} \beta (\mathcal{U},\hat{\mathcal{U}})= \min \left\{ \beta >0 \; |\;\hat{\mathcal{U}} \subseteq \beta \cdot \mathcal{U} \right\} . \end{aligned}$$

For the sake of simplicity, we denote the scaling factor $\beta (\mathcal{U},\hat{\mathcal{U}})$ by $\beta$ in the rest of this paper. The scaling factor always exists since $\mathcal{U}$ is full-dimensional. Moreover, it is greater than one because $\hat{\mathcal{U}}$ dominates $\mathcal{U}$. Note that the dominating set $\hat{\mathcal{U}}$ does not necessarily contain $\mathcal{U}$. We illustrate this in the following example.

Example Consider the uncertainty set $\mathcal{U}$ defined in (1.2) which is the intersection of the unit $\ell _2$-norm ball and the non-negative orthant. We show later in this paper (Proposition 1) that the simplex $\hat{\mathcal{U}}$ dominates $\mathcal{U}$ where

$$\begin{aligned} \hat{\mathcal{U}}= m^{\frac{1}{4}}\cdot {\textsf {conv}} \left( \varvec{e}_1,\ldots ,\varvec{e}_m, \frac{1}{\sqrt{m}}\varvec{e} \right) . \end{aligned}$$

(2.1)

Figures 1 and 2 illustrate the sets $\mathcal{U}$ and $\hat{\mathcal{U}}$ for $m=3$. Note that $\hat{\mathcal{U}}$ does not contain $\mathcal{U}$ but only dominates $\mathcal{U}$. This is an important property in our framework.

Fig. 1

The uncertainty set (1.2)

Fig. 2

The dominating set $\hat{\mathcal{U}}$ (2.1)

The following theorem shows that solving the adjustable problem over the set $\hat{\mathcal{U}}$ gives a $\beta$-approximation to the two-stage adjustable robust problem (1.1).

Theorem 1

Consider an uncertainty set $\mathcal{U}$ that verifies Assumption 1 and $\hat{\mathcal{U}}\subseteq {{\mathbb {R}}}^m_+$ that dominates $\mathcal{U}$. Let $\beta$ be the scaling factor of $(\mathcal{U},\hat{\mathcal{U}})$. Moreover, let $z_{\textsf {AR}}(\mathcal{U})$ and $z_{\textsf {AR}}(\hat{\mathcal{U}})$ be the optimal values for (1.1) corresponding to $\mathcal U$ and $\hat{\mathcal{U}}$, respectively. Then,

$$\begin{aligned} z_{\textsf {AR}}(\mathcal{U}) \le z_{\textsf {AR}}(\hat{\mathcal{U}}) \le \beta \cdot z_{\textsf {AR}}(\mathcal{U}). \end{aligned}$$

The proof of Theorem 1 is presented in “Appendix A”.

2.1 Choice of $\hat{\mathcal{U}}$

Theorem 1 provides a new framework for approximating the two-stage adjustable robust problem $\varPi _{\textsf {AR}}(\mathcal U)$ (1.1). Note that we require $\hat{\mathcal{U}}$ to be such that it dominates $\mathcal{U}$ and that $\varPi _{\textsf {AR}}(\hat{\mathcal{U}})$ can be solved efficiently over $\hat{\mathcal{U}}$. In fact, the latter is satisfied if the number of extreme points of $\hat{\mathcal{U}}$ is small and is explicitly given (typically polynomial of m). In our framework, we choose the dominating set to be a simplex of the following form

$$\begin{aligned} \hat{\mathcal{U}} = \beta \cdot {\textsf {conv}} \left( \varvec{e}_1,\ldots ,\varvec{e}_m, \varvec{v} \right) , \end{aligned}$$

(2.2)

for some $\varvec{v} \in \mathcal{U}$. The coefficient $\beta$ and $\varvec{v} \in \mathcal{U}$ are chosen such that $\hat{\mathcal{U}}$ dominates $\mathcal{U }$. For a given $\hat{\mathcal{U}}$ (i.e., $\beta$ and $\varvec{v} \in \mathcal{U}$), the adjustable robust problem, $\varPi _{\textsf {AR}}(\hat{\mathcal{U}})$ (1.1) can be solved efficiently as it can be reduced to the following LP:

$$\begin{aligned} \begin{aligned} z_{\textsf {AR}}(\hat{\mathcal{U}}) = \min \;&\varvec{c}^T\varvec{x}+z \\&z\ge \varvec{d}^T\varvec{y}_i,\;\forall i\in [m+1] \\&\varvec{A}\varvec{x}+\varvec{B}\varvec{y}_i\ge \beta \varvec{e}_i,\;\forall i\in [m] \\&\varvec{A}\varvec{x}+\varvec{B}\varvec{y}_{m+1}\ge \beta \varvec{v} \\&\varvec{x}\in {{\mathbb {R}}}^{n}_+, \; \varvec{y}_i\in {{\mathbb {R}}}^{n}_+, \;\forall i\in [m+1] .\\ \end{aligned} \end{aligned}$$

2.2 Mapping points in $\mathcal{U}$ to dominating points

Consider the following piecewise affine mapping for any $\varvec{h} \in \mathcal{U}$:

$$\begin{aligned} \forall \varvec{h} \in \mathcal{U}, \qquad \varvec{ \hat{h}}(\varvec{h}) = \beta \varvec{v} + ( \varvec{h} - \beta \varvec{v} )_+. \end{aligned}$$

(2.3)

We show that this maps any $\varvec{h} \in \mathcal{U}$ to a dominating point contained in the down-monotone completion of $2 \cdot \hat{\mathcal{U}}$. First, the following structural result is needed.

Lemma 1

(Structural result) Consider an uncertainty set $\mathcal{U}$ that verifies Assumption 1.

• (a) Suppose there exists $\beta$ and $\varvec{v} \in \mathcal{U}$ such that $\; \hat{\mathcal{U}} = \beta \, \cdot \, {\textsf {conv}} \left( \varvec{e}_1,\ldots ,\varvec{e}_m, \varvec{v} \right)$ dominates $\mathcal U$. Then,

  $$\begin{aligned} \frac{1}{\beta } \sum _{i=1}^m \left( h_i -\beta v_i \right) ^{+} \le 1, \; \forall \varvec{h} \in \mathcal{U}. \end{aligned}$$

  (2.4)

• (b) Moreover, if there exists $\beta$ and $\varvec{v} \in \mathcal{U}$ satisfying (2.4), then $2\beta \, \cdot \, {\textsf {conv}} \left( \varvec{e}_1,\ldots ,\varvec{e}_m, \varvec{v} \right)$ dominates $\mathcal{U}$.

The proof of Lemma 1 is presented in “Appendix B”.

The following lemma shows that the mapping in (2.3) maps any $\varvec{h} \in \mathcal{U}$ to a dominating point that belongs to the down-monotone completion of $2 \cdot \hat{\mathcal{U}}$.

Lemma 2

For all $\varvec{h} \in \mathcal{U}$, $\varvec{ \hat{h}}(\varvec{h})$ as defined in (2.3) is a dominating point that belongs to the down-monotone completion of $2 \cdot \hat{\mathcal{U}}$.

Proof

It is clear that $\varvec{ \hat{h}}(\varvec{h})$ dominates $\varvec{h}$ because $\varvec{ \hat{h}}(\varvec{h}) \ge \beta \varvec{v} + ( \varvec{h} - \beta \varvec{v} ) = \varvec{h}$. Moreover, for all $\varvec{h} \in \mathcal{U}$, we have

$$\begin{aligned} \hat{\varvec{h}}(\varvec{h})&= \beta \varvec{v} + \frac{1}{\beta } \sum _{i=1}^m ( h_i - \beta v_i )^+ \beta \varvec{e}_i \\&\le \underbrace{ \beta \varvec{v} }_{\in \hat{\mathcal{U}} }+ \underbrace{\frac{1}{\beta } \sum _{i=1}^m ( h_i - \beta v_i )^+ \beta \varvec{e}_i + \left( 1- \frac{1}{\beta }\sum _{i=1}^m ( h_i - \beta v_i )^+ \right) \beta \varvec{v} }_{\in \hat{\mathcal{U}} } \in 2 \cdot \hat{\mathcal{U}} \end{aligned}$$

where the inequality

$$\begin{aligned} 1- \frac{1}{\beta } \sum _{i=1}^m ( h_i - \beta v_i )^+ \ge 0. \end{aligned}$$

follows from part a) of Lemma 1. Therefore, $\varvec{ \hat{h}}(\varvec{h})$ belongs to the down-monotone completion of $2 \cdot \hat{\mathcal{U}}$. $\square$

2.3 Piecewise affine policy

We construct a piecewise affine policy over$\mathcal{U}$ from the optimal solution of $\varPi _{\textsf {AR}}(\hat{\mathcal{U}})$ based on the piecewise affine mapping in (2.3). Let $\varvec{\hat{x}}, \varvec{\hat{y}(\hat{h})}$ for $\varvec{\hat{h}} \in \hat{\mathcal{U }}$ be an optimal solution of $\varPi _{\textsf {AR}}(\hat{\mathcal{U}})$. Since $\hat{\mathcal{U}}$ is a simplex, we can compute this efficiently.

The piecewise affine policy (PAP)

$$\begin{aligned} \begin{aligned} \varvec{x}&= 2 \hat{\varvec{x}} \\ \varvec{y}( \varvec{h} )&= \frac{1}{\beta } \sum _{i=1}^m \left( h_i -\beta v_i \right) ^+ \hat{\varvec{y} }( \beta \varvec{e}_i)+\hat{\varvec{y} }(\beta \varvec{v}), \quad \forall \varvec{h} \in \mathcal U. \end{aligned} \end{aligned}$$

(2.5)

The following theorem shows that the above PAP gives a $2\beta$-approximation for $\varPi _{\textsf {AR}}(\mathcal{U})$ (1.1).

Theorem 2

Consider an uncertainty set $\mathcal{U}$ that verifies Assumption 1 and $\hat{\mathcal{U}} = \beta \cdot {\textsf {conv}} \left( \varvec{e}_1,\ldots ,\varvec{e}_m, \varvec{v} \right)$ be a dominating set where $\varvec{v} \in \mathcal{U}$. The piecewise affine solution in (2.5) is feasible and gives a $2\beta$-approximation for the adjustable robust problem, $\varPi _{\textsf {AR}}(\mathcal{U})$ (1.1).

Proof

First, we show that the policy (2.5) is feasible. We have,

$$\begin{aligned} \varvec{A} \varvec{x} + \varvec{B} \varvec{y} ( \varvec{h} )&= 2 \varvec{A} \hat{\varvec{x}} + \varvec{B} \left( \frac{1}{\beta } \sum _{i=1}^m\left( h_i -\beta v_i \right) ^+ \hat{\varvec{y} }( \beta \varvec{e}_i)+ \hat{\varvec{y} }(\beta \varvec{v}) \right) \\&= \left( \varvec{A} \hat{\varvec{x}}+\varvec{B} \hat{\varvec{y} }( \beta \varvec{v} ) \right) + \varvec{A} \hat{\varvec{x}} + \frac{1}{\beta } \sum _{i=1}^m \left( h_i -\beta v_i \right) ^+ \varvec{B} \hat{\varvec{y} }( \beta \varvec{e}_i)\\&\ge \left( \varvec{A} \hat{\varvec{x}}+\varvec{B} \hat{\varvec{y} }( \beta \varvec{v} ) \right) + \frac{1}{\beta } \sum _{i=1}^m \left( h_i -\beta v_i \right) ^+ \left( \varvec{B} \hat{\varvec{y} }( \beta \varvec{e}_i) + \varvec{A} \hat{\varvec{x}} \right) \\&\ge \beta \varvec{v}+ \sum _{i=1}^m \left( h_i -\beta v_i \right) ^+ \varvec{e}_i \\&\ge \beta \varvec{v} + \sum _{i=1}^m \left( h_i -\beta v_i \right) \varvec{e}_i = \varvec{h}, \end{aligned}$$

where the first inequality follows from part a) of Lemma 1 and the non-negativity of $\hat{\varvec{x}}$ and $\varvec{A}$. The second inequality follows from the feasibility of $\varvec{\hat{x}}, \varvec{\hat{y}(\hat{h})}$.

To compute the performance of (2.5), we have for any $\varvec{h} \in \mathcal{U},$

$$\begin{aligned} \varvec{c}^{T} \varvec{x} + \varvec{d}^{T} \varvec{y} ( \varvec{h} )&= 2 \left( \varvec{c}^{T} \hat{\varvec{x}} + \varvec{d}^{T} \left( \frac{1}{2\beta } \sum _{i=1}^m \left( h_i -\beta v_i \right) ^+ \hat{\varvec{y} }( \beta \varvec{e}_i)+\frac{1}{2}\hat{\varvec{y} }( \beta \varvec{v}) \right) \right) \\&\le 2 \left( \varvec{c}^{T} \hat{\varvec{x}} + \underset{ \varvec{{\hat{h}}} \in {\hat{\mathcal{U}}}}{\max }\; \varvec{d}^T \hat{\varvec{y}}( \hat{\varvec{h}}) \left( \frac{1}{2 \beta } \sum _{i=1}^m \left( h_i -\beta v_i \right) ^+ +\frac{1}{2} \right) \right) \\&\le 2 \left( \varvec{c}^{T} \hat{\varvec{x}} + \underset{ \varvec{{\hat{h}}} \in {\hat{\mathcal{U}}}}{\max }\; \varvec{d}^T \hat{\varvec{y}}( \hat{\varvec{h}}) \right) \\&= 2 \cdot z_{\textsf {AR}}( {\hat{\mathcal{U}}}), \end{aligned}$$

where the second last inequality follows from part a) of Lemma 1. From Theorem 1, $z_{\textsf {AR}}( {\hat{\mathcal{U}}}) \le \beta \cdot z_{\textsf {AR}}\left( \mathcal{U} \right)$. Therefore, the cost of the piecewise affine policy for any $\varvec{h} \in \mathcal{U}$

$$\begin{aligned} \varvec{c}^{T} \varvec{x} + \varvec{d}^{T} \varvec{y} ( \varvec{h} ) \le 2 \beta \cdot z_{\textsf {AR}}\left( \mathcal{U} \right) , \end{aligned}$$

which implies that the piecewise affine solution (2.5) gives a $2 \beta$-approximation for the adjustable robust problem, $\varPi _{\textsf {AR}}(\mathcal{U})$ (1.1). $\square$

The above proof shows that it is sufficient to find $\beta$ and $\varvec{v} \in \mathcal{U}$ satisfying (2.4) in Lemma 1 to construct a piecewise affine policy that gives a $2 \beta$-approximation for (1.1). In particular, we summarize the main result in the following theorem.

Theorem 3

Let the uncertainty set $\mathcal{U}$ satisfy Assumption 1. Consider any $\beta$ and $\varvec{v} \in \mathcal{U}$ satisfying (2.4). Then, the piecewise affine solution in (2.5) gives a $2\beta$-approximation for the adjustable robust problem, $\varPi _{\textsf {AR}}(\mathcal{U})$ (1.1).

We would like to note that our piecewise affine policy in not necessarily an optimal piecewise policy. However, for a large class of uncertainty sets, we show that our policy is significantly better than affine policy and can even be computed more efficiently than an affine policy.

3 Performance bounds for scaled permutation invariant sets

In this section, we present performance bounds of our policy for the class of scaled permutation invariant sets. This class includes ellipsoids, weighted norm-balls, intersection of norm-balls and budget of uncertainty sets. These are widely used uncertainty sets in theory and in practice.

Definition 3

(Scaled permutation invariant sets (SPI))

• 1. $\mathcal{U}$ is a permutation invariant set if $\varvec{x}\in \mathcal{U}$ implies that for any permutation $\tau$ of $\{1,2,\ldots ,m\}$, $\varvec{x}^{\tau }\in \mathcal{U}$ where $x^\tau _i= x_{\tau (i)}$.

• 2. $\mathcal{U}$ is a scaled permutation invariant set if there exists $\varvec{\lambda }\in \mathbb {R}^m_+$ and $\mathcal{V}$ a permutation invariant set such that $\mathcal{U}= {\textsf {diag}} (\varvec{\lambda }) \cdot \mathcal{V}$

For a given SPI set $\mathcal{U}$, it is possible to scale the two-stage adjustable problem (1.1) and get a new problem where the uncertainty set is permutation invariant (PI). Indeed, suppose $\mathcal{U}= {\textsf {diag}} (\varvec{\lambda }) \cdot \mathcal{V}$ where $\mathcal{V}$ is a permutation invariant set; by multiplying the constraint matrices $\varvec{A}$ and $\varvec{B}$ by ${\textsf {diag}} (\varvec{\lambda }) ^{-1}$, we get a new problem where the uncertainty set now is PI. The performance of our policy is not affected by this scaling. Therefore, without loss of generality, we consider in the rest of this section, the case of permutation invariant uncertainty sets.

We first introduce some structural properties of PI sets. Let $\mathcal{U}$ be PI satisfying Assumption 1. For all $k={1,\ldots ,m}$, let

$$\begin{aligned} \gamma (k)=\frac{1}{k} \cdot \max \left\{ \sum _{i=1}^k h_i \; \Big \vert \ \varvec{h} \in \mathcal{U} \right\} . \end{aligned}$$

(3.1)

The coefficients, $\gamma (k)$ for all $k=1,\ldots ,m$ affect the geometric structure of $\mathcal{U}$. In particular, we have the following lemma.

Lemma 3

Le $\mathcal{U}$ be a permutation invariant set and $\gamma (\cdot )$ be as defined in (3.1). Then,

$$\begin{aligned} \gamma (k) \cdot \sum _{i=1}^k \varvec{e}_i \in \mathcal{U}, \; \forall k=1,\ldots ,m \end{aligned}$$

We present the proof of Lemma 3 in “Appendix C”. For the sake of simplicity, we denote $\gamma (m)$ by $\gamma$ in the rest of the paper. From the above lemma, we know that $\gamma \cdot \varvec{e} \in \mathcal{U}$.

3.1 Piecewise affine policy for permutation invariant sets

For any PI set $\mathcal{U}$, we consider the following dominating uncertainty set, $\hat{\mathcal{U}}$ of the form (2.2) with $\varvec{v} = \gamma \varvec{e}$, i.e.,

$$\begin{aligned} \hat{\mathcal{U}} = \beta \cdot {\textsf {conv}}\left( \varvec{e}_1,\varvec{e}_2, \ldots ,\varvec{e}_m, \gamma \varvec{e}\right) \end{aligned}$$

(3.2)

where $\beta$ is the scaling factor guaranteeing that $\hat{\mathcal{U}}$ dominates $\mathcal{U}$. This dominating set $\hat{\mathcal{U}}$ is motivated by the symmetry of the permutation invariant set $\mathcal U$. In this section, we show that one can efficiently compute the minimum $\beta$ such that $\hat{\mathcal{U}}$ in (3.2) dominates $\mathcal{U}$. In particular, we derive an efficiently computable closed-form expression for $\beta$, for any PI set $\mathcal{U}$.

From Theorem 3 we know that to construct a piecewise affine policy with an approximation bound of $2 \beta$, it is sufficient to find $\beta$ such that

$$\begin{aligned} \frac{1}{\beta } \max _{ \varvec{h} \in \mathcal{U }} \sum _{i=1}^m \left( h_i -\beta \gamma \right) ^{+} \le 1 \end{aligned}$$

(3.3)

and any $\beta$ implies that $2\beta \cdot {\textsf {conv}}\left( \varvec{e}_1,\varvec{e}_2, \ldots ,\varvec{e}_m, \gamma \varvec{e}\right)$ dominates $\mathcal{U}$ (see Lemma 1b). Finding the minimum $\beta$ that satisfies (3.3) requires solving:

$$\begin{aligned} \min \left\{ \beta \ge 1 \; \Big \vert \; \frac{1}{\beta } \max _{ \varvec{h} \in \mathcal{U }} \sum _{i=1}^m \left( h_i -\beta \gamma \right) ^{+} \le 1 \right\} . \end{aligned}$$

(3.4)

The following lemma characterizes the structure of the optimal solution for the maximization problem in (3.3) for a fixed $\beta$.

Lemma 4

Consider the maximization problem in (3.3) for a fixed $\beta$. There exists an optimal solution $\varvec{h}^*$ such that

$$\begin{aligned} \varvec{h}^* = \gamma (k) \cdot \sum _{i=1}^k \varvec{e}_i, \end{aligned}$$

for some $k=1,\ldots ,m$.

We present the proof of Lemma 4 in “Appendix D”. The following lemma characterizes the optimal $\beta$ for (3.4).

Lemma 5

Let $\mathcal{U}$ be a permutation invariant uncertainty set satisfying Assumption 1. Then the optimal solution for (3.4) is given by

$$\begin{aligned} \beta = \max _{ k=1,\ldots ,m} \frac{\gamma (k)}{\gamma +\frac{1}{k}}. \end{aligned}$$

(3.5)

Proof

Using Lemma 4, we can reformulate (3.4) as follows.

$$\begin{aligned} \min \left\{ \beta \ge 1 \; \Big \vert \; \frac{1}{\beta } \max _{ k=1,\ldots ,m } \sum _{i=1}^k \left( \gamma (k) -\beta \gamma \right) \le 1 \right\} , \end{aligned}$$

i.e.,

$$\begin{aligned} \min \left\{ \beta \ge 1 \; \Big \vert \; \beta \ge \frac{\gamma (k)}{\gamma +\frac{1}{k}}, \; \; \forall k=1,\ldots ,m \right\} . \end{aligned}$$

Therefore,

$$\begin{aligned} \beta = \max _{ k=1,\ldots ,m} \frac{\gamma (k)}{\gamma +\frac{1}{k}}. \end{aligned}$$

$\square$

The above lemma computes the minimum $\beta$ that satisfies (3.3). Therefore, from Theorem 3, we have the following theorem.

Theorem 4

Let $\mathcal{U}$ be a permutation invariant set satisfying Assumption 1. Let $\gamma = \gamma (m)$ be as defined in (3.1) and $\beta$ be as defined in (3.5), and

$$\begin{aligned} \hat{\mathcal{U}} = \beta \cdot {\textsf {conv}} \left( \varvec{e}_1,\ldots ,\varvec{e}_m, \gamma \varvec{e} \right) . \end{aligned}$$

Let $\varvec{\hat{x}}, \varvec{\hat{y}(\hat{h})}$ for $\varvec{\hat{h}} \in \hat{\mathcal{U }}$ be an optimal solution for $\varPi _{\textsf {AR}}(\hat{\mathcal{U}})$ (1.1). Then the following piecewise affine solution

$$\begin{aligned} \begin{aligned} \varvec{x}&= 2 \hat{\varvec{x}} \\ \varvec{y}( \varvec{h} )&= \frac{1}{\beta }\sum _{i=1}^m \left( h_i -\beta \gamma \right) ^+ \hat{\varvec{y} }( \beta \varvec{e}_i)+ \hat{\varvec{y} }( \beta \gamma \varvec{e}) \quad \forall \varvec{h} \in \mathcal U, \end{aligned} \end{aligned}$$

(3.6)

gives a $2 \beta$-approximation for $\varPi _{\textsf {AR}}(\mathcal{U})$ (1.1). Moreover, the set $2 \cdot \hat{\mathcal{U}}$ dominates $\mathcal{U}$.

The last claim that $2 \cdot \hat{\mathcal{U}}$ dominates $\mathcal{U}$ is a straightforward consequence of part (b) of Lemma 1.

As a consequence of Theorem 4, for any permutation invariant uncertainty set, $\mathcal{U}$, we can compute the piecewise-affine policy for $\varPi _{\textsf {AR}}(\mathcal{U})$(1.1) efficiently. In fact, for many cases, even more efficiently than an affine policy.

3.2 Examples

We present the approximation bounds for several permutation invariant uncertainty sets that are commonly used in the literature and in practice, including norm balls, intersection of norm balls and budget of uncertainty sets. In particular, it follows that for these sets, the performance bounds of our piecewise affine policy are significantly better than the best known performance bounds for affine policy.

Proposition 1

(Hypersphere) Consider the uncertainty set $\mathcal{U}=\{\varvec{h}\in {{\mathbb {R}}}^{m}_+\;|\;||\varvec{h}||_2 \le 1\}$ which is the intersection of the unit hypersphere and the nonnegative orthant. Then,

$$\begin{aligned} \hat{\mathcal{U}}=m^{\frac{1}{4}} \cdot {\textsf {conv}}\left( \varvec{e}_1, \varvec{e}_2,\ldots , \varvec{e}_m, \frac{1}{\sqrt{m}}\varvec{e} \right) , \end{aligned}$$

dominates $\mathcal{U}$ and our piecewise affine solution (3.6) gives $O ( m^{\frac{1}{4}} )$ approximation to (1.1).

Proof

We have for $k=1,\ldots ,m$,

$$\begin{aligned} \gamma (k) = \frac{1}{k} \cdot \max \left\{ \sum _{i=1}^k h_i \vert \ \varvec{h} \in \mathcal{U} \right\} = \frac{1}{\sqrt{k}}. \end{aligned}$$

In particular, $\gamma = \frac{1}{\sqrt{m}}$. From Lemma 5 we get,

$$\begin{aligned} \beta&= \max _{ k=1,\ldots ,m} \frac{\gamma (k)}{\gamma (m) +\frac{1}{k}} \\&= \max _{ k=1,\ldots ,m} \frac{\frac{1}{\sqrt{k}}}{\frac{1}{\sqrt{m}} +\frac{1}{k}}. \end{aligned}$$

The maximum of this problem occurs for $k = \sqrt{m}$. Then, $\beta = \frac{m^{\frac{1}{4}}}{2}$. We conclude from Theorem 4 that $\hat{\mathcal{U}}$ dominates $\mathcal{U}$ and our piecewise affine policy gives $O ( m^{\frac{1}{4}} )$ approximation to the adjustable problem (1.1). $\square$

Remark Consider the following ellipsoid uncertainty set

$$\begin{aligned} \left\{ \varvec{h} \ge \varvec{0} \; \left| \; \sum _{i=1}^m r_i h_i^ 2 \le 1 \right. \right\} . \end{aligned}$$

(3.7)

This is widely used to model uncertainty in practice and is just a diagonal scaling of the hypersphere uncertainty set. For instance, scaled ellipsoid sets has been considered by Ben-Tal and Nemirovski in [3,4,5]. In particular, Ben-Tal and Nemirovski [5] consider ellipsoids of the form (3.7) to model uncertainty in a portfolio optimizaiton problem. As we mention before, the performance of our policy is not affected by scaling. Hence, our piecewise affine policy gives an $O ( m^{\frac{1}{4}} )$-approximation to the adjustable problem (1.1) for ellipsoid uncertainty sets (3.7) similar to hypersphere. We analyze the case of more general ellipsoids in Proposition 4.

Proposition 2

(p-norm ball) Consider the p-norm ball uncertainty set $\mathcal{U}= \left\{ \varvec{h} \in {\mathbb {R}}^{m}_+ \; \big \vert \; \Vert \varvec{h}\Vert _p \le 1 \right\}$ where $p \ge 1$. Then

$$\begin{aligned} \hat{ \mathcal U} = 2 \beta \cdot {\textsf {conv}} \left( \varvec{e_1}, \varvec{e_2},\ldots , \varvec{e_m},m^{-\frac{1}{p}} \varvec{e} \right) \end{aligned}$$

dominates $\mathcal{U}$ with

$$\begin{aligned} \beta = \frac{1}{p} (p-1)^{\frac{p-1}{p}} \cdot m^{\frac{p-1}{p^2}} = O \left( m^{\frac{p-1}{p^2}} \right) . \end{aligned}$$

Our piecewise affine solution (3.6) gives $O ( m^{\frac{p-1}{p^2}} )$ approximation to (1.1).

Proof

We have for $k=1,\ldots ,m$,

$$\begin{aligned} \gamma (k) = \frac{1}{k} \cdot \max \left\{ \sum _{i=1}^k h_i \vert \ \varvec{h} \in \mathcal{U} \right\} = k^{\frac{-1}{p}}. \end{aligned}$$

In particular, $\gamma =m^{\frac{-1}{p}}$. From Lemma 5 we get,

$$\begin{aligned} \beta&= \max _{ k=1,\ldots ,m} \frac{\gamma (k)}{\gamma (m) +\frac{1}{k}} = \max _{ k=1,\ldots ,m} \frac{k^{\frac{-1}{p}}}{m^{\frac{-1}{p}} +\frac{1}{k}} \\&= \frac{1}{p} (p-1)^{\frac{p-1}{p}} \cdot m^{\frac{p-1}{p^2}} = O \left( m^{\frac{p-1}{p^2}} \right) . \end{aligned}$$

We conclude from Theorem 4 that $\hat{\mathcal{U}}$ dominates $\mathcal{U}$ and our piecewise affine policy gives $O ( m^{\frac{p-1}{p^2}} )$ approximation to the adjustable problem (1.1). $\square$

Proposition 3

(Intersection of two norm balls) Consider $\mathcal{U}$ the intersection of the norm balls $\mathcal{U}_1= \left\{ \varvec{h} \in {\mathbb {R}}^{m}_+ \; \big \vert \; \Vert \varvec{h}\Vert _p \le 1 \right\}$ and $\mathcal{U}_2= \left\{ \varvec{h} \in {\mathbb {R}}^{m}_+ \; \big \vert \; \Vert \varvec{h}\Vert _q \le r \right\}$ where $p > q \ge 1$ and $m^{\frac{1}{q}-\frac{1}{p}} \ge r \ge 1$. Then,

$$\begin{aligned} \hat{ \mathcal U} = \beta \cdot {\textsf {conv}} \left( \varvec{e_1}, \varvec{e_2},\ldots , \varvec{e_m}, \left( r m^{-\frac{1}{q}}\right) \varvec{e} \right) , \end{aligned}$$

where

$$\begin{aligned} \beta = \min ( \beta _1, \beta _2), \; \beta _1= r^{\frac{1-p}{p}}m^{\frac{p-1}{pq}}, \text{ and } \beta _2=r^{\frac{1}{q}}m^{\frac{q-1}{q^2}}. \end{aligned}$$

Our piecewise affine solution (3.6) gives a $2 \beta$ approximation to (1.1).

Proof

To prove that $\hat{ \mathcal U}$ dominates $\mathcal{U}_1 \cap { \mathcal U}_2$, it is sufficient to consider $\varvec{h}$ in the boundary of $\mathcal{U}_1$ or ${ \mathcal U}_2$ and find $\alpha _1, \alpha _2,\ldots ,\alpha _{m+1} \ge 0$ with $\alpha _1+ \ldots +\alpha _{m+1} =1$ such that for all $i \in [m],$

$$\begin{aligned} h_i \le \beta \left( \alpha _i + rm^{-\frac{1}{q}}\alpha _{m+1}\right) . \end{aligned}$$

Case 1$\beta = \beta _1.$

Let $\varvec{h} \in \mathcal{U}_1$ such that $\Vert \varvec{h}\Vert _p=1$, we take $\alpha _i = \frac{h_i^p}{p}$ for $i \in [m]$ and $\alpha _{m+1}= \frac{p-1}{p}.$ First, we have $\sum _{i=1}^{m+1} \alpha _i =1$ and for all $i \in [m]$,

$$\begin{aligned} \beta \left( \alpha _i +rm^{-\frac{1}{q}}\alpha _{m+1}\right)&= \beta _1 \left( \frac{h_i^p}{p}+ \frac{p-1}{p} rm^{-\frac{1}{q}} \right) \\&\ge \beta _1 \left( h_i^p \right) ^{\frac{1}{p}} \left( r m^{-\frac{1}{q}}\right) ^{\frac{p-1}{p}} = h_i, \end{aligned}$$

where the inequality follows from the weighted inequality of arithmetic and geometric means (known as Weighted AM-GM inequality). Therefore $\hat{ \mathcal U}$ dominates $\mathcal{U}_1 \cap { \mathcal U}_2$.

Case 2 $\beta = \beta _2.$

Let $\varvec{h} \in \mathcal{U}_2$ such that $\Vert \varvec{h}\Vert _q=r$, we take $\alpha _i = \frac{h_i^q}{r^q q}$ for $i \in [m]$ and $\alpha _{m+1}= \frac{q-1}{q}.$ First, we have $\sum _{i=1}^{m+1} \alpha _i =1$ and for all $i \in [m]$,

$$\begin{aligned} \beta \left( \alpha _i +rm^{-\frac{1}{q}}\alpha _{m+1}\right)&= \beta _2 \left( \frac{h_i^q}{r^q q}+ \frac{q-1}{q} rm^{-\frac{1}{q}} \right) \\&\ge \beta _2 \left( \frac{h_i^q}{r^q} \right) ^{\frac{1}{q}} \left( r m^{-\frac{1}{q}}\right) ^{\frac{q-1}{q}} = h_i, \end{aligned}$$

where the inequality followed from the weighted AM-GM inequality. Therefore, $\hat{ \mathcal U}$ dominates $\mathcal{U}_1\cap { \mathcal U}_2$. $\square$

We also consider a permutation invariant uncertainty set that is the intersection of an ellipsoid and the non-negative orthant , i.e.,

$$\begin{aligned} \mathcal{U}=\left\{ \varvec{h}\in {{\mathbb {R}}}^{m}_+\;|\; \varvec{h}^T \varvec{\varSigma }\varvec{h} \le 1\right\} \end{aligned}$$

(3.8)

where $\varvec{\varSigma }\succeq \varvec{0}$. For $\mathcal{U}$ to be a permutation invariant set satisfying Assumption 1, $\varvec{\varSigma }$ must be of the following form

$$\begin{aligned} \varvec{\varSigma }= \left( \begin{matrix} 1 &{}\quad a &{}\quad \ldots &{}\quad a\\ a &{}\quad 1 &{}\quad \ldots &{}\quad a\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ a &{}\quad a &{}\quad \ldots &{}\quad 1 \end{matrix} \right) \end{aligned}$$

(3.9)

where $0\le a \le 1$.

Proposition 4

(Permutation invariant ellipsoid) Consider the uncertainty set $\mathcal{U}$ defined in (3.8) where $\varvec{\varSigma }$ is defined in (3.9). Then

$$\begin{aligned} \hat{\mathcal{U}}=\beta \cdot {\textsf {conv}}\left( \varvec{e}_1, \varvec{e}_2,\ldots , \varvec{e}_m, \gamma \varvec{e} \right) , \end{aligned}$$

dominates $\mathcal{U}$ with

$$\begin{aligned} \beta = \left( \frac{a}{2}+ \frac{(1-a)^{\frac{1}{2}}}{\left( am^2+(1-a)m\right) ^{\frac{1}{4}}}\right) ^{-1}= O \left( m^{\frac{2}{5}} \right) \end{aligned}$$

and

$$\begin{aligned} \gamma = \frac{1}{ \sqrt{\left( am^2+(1-a)m \right) } } . \end{aligned}$$

Our piecewise affine policy (3.6) gives $O \left( m^{\frac{2}{5}} \right)$ approximation to the adjustable robust problem (1.1).

The proof of Proposition 4 is presented in “Appendix E”.

Proposition 5

(Budget of uncertainty set) Consider the budget of uncertainty set

$$\begin{aligned} { \mathcal{U}= \left\{ \varvec{h} \in [0,1]^{m} \; \big \vert \; \sum _{i=1}^m h_i \le k \right\} .} \end{aligned}$$

(3.10)

Then,

$$\begin{aligned} \hat{ \mathcal U} = \beta \cdot {\textsf {conv}} \left( \varvec{e_1}, \varvec{e_2},\ldots , \varvec{e_m}, \frac{k}{m} \varvec{e} \right) \end{aligned}$$

where $\beta = \min \left( k, \frac{m}{k}\right)$. In particular, our piecewise affine policy (3.6) gives $2 \beta$ approximation to the adjustable problem (1.1).

The proof of Proposition 5 is presented in “Appendix F”.

3.3 Comparison to affine policy

Table 1 summarizes the performance bounds for our piecewise affine policy and the best known performance bounds in the literature for affine policies [7]. As can be seen, our piecewise affine policy performs significantly better than the known bounds for affine policy for many interesting sets, including hypersphere, ellipsoid and norm-balls. For instance, our policy gives $O ( m^{\frac{1}{4}})$-approximation for the hypersphere and $O(m^{\frac{p-1}{p^2}})$-approximation for the p-norm ball, while affine policy gives $O(m^{\frac{1}{2}})$-approximation for hypersphere and $O(m^{\frac{1}{p}})$-approximation for the p-norm ball [7], respectively. However, as we mentioned before, our policy is not a generalization of affine policies and, in fact, affine policies may perform better for certain uncertainty sets. However, we present a family of examples where an optimal affine policy gives an $\varOmega (\sqrt{m})$-approximation, while our policy is near-optimal for the adjustable robust problem (1.1). In particular, we consider the following instance motivated from the worst-case examples of affine policy in [12, 20].

$$\begin{aligned} \begin{aligned}&n=m, \; \; r= \lceil m- \sqrt{m} \rceil ,\; \; N= \left( {\begin{array}{c}m\\ r\end{array}}\right) \\&{B}_{ij}= \left\{ \begin{array}{ll} 1 &{}\quad \text{ if } \quad i=j \\ \frac{1}{\sqrt{m}} &{}\quad \hbox {if} \quad i \ne j \\ \end{array} \right. \\&\varvec{A}= \varvec{B}, \; \; \varvec{c}=\frac{1}{15}\varvec{e}, \; \; \varvec{d} = \varvec{e} \\&\mathcal{U} = {\textsf {conv}} \left( \varvec{0}, \varvec{e}_1 , \ldots ,\varvec{e}_m, \varvec{\nu }_1, \ldots , \varvec{\nu }_N \right) \\&\text { where } \varvec{\nu }_1 = \frac{1}{\sqrt{m}} \cdot [ \underbrace{1,\ldots ,1}_r ,0\ldots ,0 ] ; \end{aligned} \end{aligned}$$

(3.11)

$\varvec{\nu }_1$ has exactly r non-zero coordinates, each equal to $\frac{1}{\sqrt{m}}$. The extreme points $\varvec{\nu }_i$ of $\nu _1$, are permutations of the non-zero coordinates of $\varvec{\nu }_{1}$. Therefore, $\mathcal{U}$ has exactly $\left( {\begin{array}{c}m\\ r\end{array}}\right) + m + 1$ extreme points.

Lemma 6

Our piecewise affine policy (2.5) gives an $O (1+ \frac{1}{\sqrt{m}})$-approximation for the adjustable robust problem (1.1) for instance (3.11).

We can prove Lemma 6 by constructing a dominating set within a scaling factor $O (1+ \frac{1}{\sqrt{m}})$ from $\mathcal{U}$. We present the complete proof of Lemma 6 in “Appendix G”.

Lemma 7

Affine policy gives an $\varOmega ({\sqrt{m}})$-approximation for the adjustable robust problem (1.1) for instance (3.11). Moreover, for any optimal affine solution, the cost of the first-stage solution $\varvec{x}^*_{\textsf {Aff}}$ is $\varOmega ({\sqrt{m}})$ away from the optimal adjustable problem  (1.1), i.e. $\varvec{c}^T \varvec{x}^*_{\textsf {Aff}} = \varOmega (m^{1/2}) \cdot z_{\textsf {AR}}(\mathcal{U})$.

We present the proof of Lemma 7 in “Appendix H”. From Lemma 7 and 6, we conclude that our policy is near-optimal whereas affine policy is $\varOmega ( \sqrt{m})$ away from the optimal adjustable solution for the instance (3.11). Hence our policy provides a significant improvement. We would like to note that since $\hat{\mathcal{U}}$ is a simplex, an affine policy is optimal for $\varPi _{\textsf {AR}}(\hat{\mathcal{U}})$. In particular, we have the following

$$\begin{aligned} z_{\textsf {AR}}(\mathcal{U}) \le z_{\textsf {AR}}(\hat{\mathcal{U}}) = z_{\textsf {Aff}}(\hat{\mathcal{U}}) \le O \left( 1+\frac{1}{\sqrt{m}}\right) \cdot z_{\textsf {AR}}(\mathcal{U}), \end{aligned}$$

where the first inequality follows as $\hat{\mathcal{U}}$ dominates $\mathcal{U}$ and the last inequality follows from Lemma 6. Moreover, from Lemma 7, we know that for instance (3.11),

$$\begin{aligned} z_{\textsf {Aff}}(\mathcal{U}) = \varOmega (\sqrt{m}) \cdot z_{\textsf {AR}}(\mathcal{U}). \end{aligned}$$

Therefore,

$$\begin{aligned} z_{\textsf {Aff}}(\mathcal{U}) = \varOmega (\sqrt{m}) \cdot z_{\textsf {Aff}}(\hat{\mathcal{U}}), \end{aligned}$$

which is quite surprising since $\hat{\mathcal{U}}$ dominates $\mathcal{U}$. We would like to emphasize that $\hat{\mathcal{U}}$ only dominates $\mathcal{U}$ and does not contain it and this is crucial to get a significant improvement for our piecewise affine policy constructed through the dominating set.

Comparison to re-solving policy In many applications, a practical implementation of affine policy only implements the first stage solution $\varvec{x}^*_{\textsf {Aff}}$ and re-solve (or recompute) the second-stage solution once the uncertainty is realized. The performance of such a re-solving policy is at least as good as affine policy and in many cases significantly better. Lemma 7 shows that for instance (3.11), such a re-solving policy is $\varOmega (\sqrt{m})$ away from the optimal adjustable policy whereas we show in Lemma 6 that our piecewise affine policy is near-optimal. Hence, our piecewise affine policy for instance (3.11) is performing significantly better not only than affine policy but also the re-solving policy.

4 General uncertainty set

In this section, we consider the case of general uncertainty sets. The main challenge in our framework of constructing the piecewise affine policy is the choice of the dominating simplex, $\hat{\mathcal{U }}$. More specifically, the choice of $\beta$ and $\varvec{v} \in \mathcal{U}$ such that $\beta \cdot {\textsf {conv}} \left( \varvec{e}_1,\ldots ,\varvec{e}_m, \varvec{v} \right)$ dominates $\mathcal{U }$. For a permutation invariant set, $\mathcal{U}$, we choose $\varvec{v}= \gamma \varvec{e}$ and we can efficiently find $\beta$ using Lemma 5 to construct the dominating set. However, this does not extend to general sets and we need a new procedure to find those parameters.

Theorem 3 shows that to construct a good piecewise affine policy over $\mathcal{U}$, it is sufficient to find $\beta$ and $\varvec{v} \in \mathcal{U}$ such that for all $\varvec{h} \in \mathcal{U}$

$$\begin{aligned} \frac{1}{\beta } \sum _{i=1}^m \left( h_i -\beta v_i \right) ^{+} \le 1 . \end{aligned}$$

(4.1)

In this section, we present an iterative algorithm to find such $\beta$ and $\varvec{v} \in \mathcal{U}$ satisfying (4.1). In each iteration t, the algorithm maintains a candidate solution, $\beta ^t$ and $\varvec{v}^t \in \mathcal{U}$. Let $\varvec{u}^t = \beta ^t \cdot v^t$. The algorithm solves the following maximization problem:

$$\begin{aligned} \max _{\varvec{h} \in \mathcal{U}} \sum _{i=1}^m \left( h_i - u^t_i \right) ^{+} \end{aligned}$$

(4.2)

The algorithm stops if the optimal value is at most $\beta ^t$ in which case, Condition (4.1) is verified for all $h \in \mathcal{U}$. Otherwise, let $\varvec{h}^t$ be an optimal solution of problem  (4.2). The current solutions are updated as follows:

$$\begin{aligned} \begin{aligned} \beta ^{t+1}&= \beta ^t + 1 \\ u^{t+1}_i&= \min \left( 1, u^t_i + h^t_i\right) . \end{aligned} \end{aligned}$$

This corresponds to updating $\varvec{v}^{t+1} = \frac{1}{\beta ^{t+1}} \cdot \varvec{u}^{t+1}$. Algorithm 1 presents the steps in detail.

The number of $\beta$-iterations is finite since $\mathcal{U}$ is compact. The following theorem shows that $\varvec{v}$ returned by the algorithm belongs to $\mathcal{U}$ and the corresponding piecewise affine policy is a $O(\sqrt{m})$-approximation for the adjustable problem (1.1).

Theorem 5

Suppose Algorithm 1 returns $\beta$, $\varvec{v}$. Then $\varvec{v} \in \mathcal{U}$. Furthermore, the piecewise affine policy (2.5) with parameters $\beta$ and $\varvec{v}$ gives a $O(\sqrt{m})$-approximation for the adjustable problem (1.1).

Proof

Suppose Algorithm 1 returns $\beta , \varvec{v}$. Note that $\beta$ is the number of iterations in Algorithm 1. First, we have

$$\begin{aligned} \varvec{u}^{\beta } \le \sum _{t=0}^{\beta -1} \varvec{h}^t . \end{aligned}$$

Moreover $\frac{1}{\beta }\cdot \sum _{t=0}^{\beta -1} \varvec{h}^t \in \mathcal{U}$ since $\mathcal{U}$ is convex. Therefore $\varvec{v} = \frac{\varvec{u}^{\beta }}{\beta } \in \mathcal{U}$ by down-monotonicity of $\mathcal{U}$.

Let us prove that $\beta =O ( \sqrt{m} )$. First, note that, when we set $h_i^t=0$ for $u_i^t=1$, the objective of the maximization problem in the algorithm does not change and $\varvec{h}^t$ still belongs to $\mathcal{U}$ by down-monotonicity. Then, for any $t=0, \ldots , \beta -1$

$$\begin{aligned} \sum _{i=1}^m \left( h_{i}^t- u_i^t \right) ^+ > t . \end{aligned}$$

Moreover, $h_i^t \ge 0$ and $u_i^t \ge 0$, hence $h_i^t \ge (h_i^t - u_i^t )^+$ and therefore for all $t= 0,\ldots ,\beta -1$

$$\begin{aligned} \sum _{i=1}^m h_i^t > t. \end{aligned}$$

Then,

$$\begin{aligned} \sum _{t=0}^{\beta -1} \sum _{i=1}^m h_i^t > \sum _{t=0}^{\beta -1} t = \frac{1}{2} \beta ( \beta -1 ) . \end{aligned}$$

(4.3)

Note that, if $u_i^t=1$ at some iteration t, then $h_i^{t'}=0$ for any $t' \ge t$. Hence, for any $i\in [m]$,

$$\begin{aligned} \sum _{t=0}^{\beta -1} h_i^t \le u_i^{\beta } +1 \le 2 . \end{aligned}$$

(4.4)

Hence, from (4.3) and from (4.4) we get, $2m > \frac{1}{2} \beta ( \beta -1 )$, i.e., $\beta \cdot (\beta -1) \le 4m ,$ which implies, $\beta = O ( \sqrt{m} ).$$\square$

We note that the maximization problem (4.2) that Algorithm 1 solves in each iteration t is not a convex optimization problem. However,  (4.2) can be formulated as the following MIP:

$$\begin{aligned} \begin{aligned} \max \;&\sum _{i=1}^m z_i \\&z_i \le (h_i-u_i^t) +(1-x_i) \; \; \forall i \in [m], \\&z_i \le x_i \; \; \forall i \in [m] \\&z_i \ge 0, \; \; \forall i \in [m] \\&x_i \in \{0,1\} \; \; \forall i \in [m] \\&\varvec{h} \in \mathcal{U} . \end{aligned} \end{aligned}$$

(4.5)

Therefore, for general uncertainty set $\mathcal{U}$, the procedure to find $\beta$ and $\varvec{v} \in \mathcal{U}$ is computationally more challenging than for the case of permutation invariant sets.

Remark Since the computation of $\beta$ and $\varvec{v}$ depends only on $\mathcal{U}$, and not on the problem parameters (i.e., the parameters $\varvec{A}, \varvec{B}, \varvec{c}$ and $\varvec{d}$), one can compute them offline and then use them to efficiently construct a good piecewise affine policy.

Connection to Bertsimas and Goyal [12] We would like to note that Algorithm 1 is quite analogous to the explicit construction of good affine policies in [12]. The analysis of the $O(\sqrt{m})$-approximation bound for affine policies is based on the following projection result (which is a restatement of Lemma 8 and Lemma 9 in [12]).

Theorem 6

(Bertsimas et al. [13]) Consider any uncertainty set $\mathcal{U}$ satisfying Assumption 1. There exists $\beta \le \sqrt{m}$, $\varvec{v} \in \mathcal{U}$ such that

$$\begin{aligned} \sum _{ j : \beta v_j < 1} \; h_j \le \beta , \; \forall \varvec{h} \in \mathcal{U}. \end{aligned}$$

Suppose $J = \{ j \; |\; \beta v_j < 1\}$. The affine solution in [12] covers $\beta \varvec{v}$ using the static component and the components J using a linear solution. The linear solution does not exploit the coverage of $\beta v_i$ for $i \in J$ from the static solution. The approximation factor is $O(\beta )$ since for all $\varvec{h} \in \mathcal{U}$, $\sum _{j \in J} h_j \le \beta$.

Our piecewise affine solution given by Algorithm 1 finds analogous $\beta$, $\varvec{v} \in \mathcal{U}$ such that

$$\begin{aligned} \sum _{i=1}^m ( h_i - \beta v_i) _+ \le \beta , \quad \forall \varvec{h} \in \mathcal{U}. \end{aligned}$$

In the piecewise affine solution, the static component covers $\beta \varvec{v}$ and the remaining part $( \varvec{h} - \beta \varvec{v})_+$ is covered by a piecewise-linear function that exploits the coverage of $\beta \varvec{v}$. This allows us to improve significantly as compared to the affine policy for a large family of uncertainty sets. We would like to note again that our policy is not necessarily an optimal one and there can be examples where affine policy is better than our policy.

5 A worst case example for the domination policy

From Theorem 5, we know that our piecewise affine policy gives an $O(\sqrt{m})$-approximation for the adjustable robust problem (1.1). In this section, we show that this bound is tight for the following budget of uncertainty set:

$$\begin{aligned} \mathcal{U}= \left\{ \varvec{h} \in {\mathbb {R}}^{m}_+ \; \bigg \vert \; \sum _{i=1}^m h_i= \sqrt{m} , \; 0 \le h_i \le 1 \quad \forall i \in [m] \right\} . \end{aligned}$$

(5.1)

We show that our dominating simplex based piecewise affine policy gives an $\varOmega (\sqrt{m})$-approximation to the adjustable robust problem (1.1). The lower bound of $\varOmega (\sqrt{m})$ holds even when we consider more general dominating sets than simplex. We show that for any $\epsilon > 0$, there is no polynomial number of points in $\mathcal{U}$ such that the convex hull of those points scaled by $m ^{\frac{1}{2}-\epsilon }$ dominates $\mathcal{U}$. In particular, we have the following theorem.

Theorem 7

Given any $0< \epsilon < 1/2$, and $k \in {{\mathbb {N}}}$, consider the budget of uncertainty set, $\mathcal{U}$ (5.1) with m sufficiently large. Let $P(m) \le m^k$. Then for any $\varvec{z}_1,\varvec{z}_2,\ldots \varvec{z}_{P(m)} \in \mathcal{U}$, the set

$$\begin{aligned} {\hat{\mathcal{U}}}= m^{\frac{1}{2}-\epsilon } \cdot {\textsf {conv}} \left( \varvec{z}_1,\varvec{z}_2,\ldots \varvec{z}_{P(m))}\right) , \end{aligned}$$

does not dominate $\mathcal{U}$.

Proof

Suppose for a sake of contradiction that there exists $\varvec{z}_1,\varvec{z}_2,\ldots ,\varvec{z}_{P(m)} \in \mathcal{U}$ such that ${\hat{\mathcal{U}}}= m^{\frac{1}{2}-\epsilon } \cdot {\textsf {conv}} \left( \varvec{z}_1,\varvec{z}_2,\ldots \varvec{z}_{P(m)}\right)$ dominates $\mathcal{U}$.

By Caratheodory’s theorem, we know that any point in $\mathcal{U}$ can be expressed as a convex combination of at most $m+1$ extreme points of $\mathcal{U}$. Therefore

$$\begin{aligned} {\hat{\mathcal{U}}} \subseteq m^{\frac{1}{2}-\epsilon } \cdot {\textsf {conv}} \left( \varvec{y}_1,\varvec{y}_2,\ldots , \varvec{y}_{Q(m))}\right) , \end{aligned}$$

where $\varvec{y}_1,\varvec{y}_2,\ldots ,\varvec{y}_{Q(m)}$ are extreme points of $\mathcal{U}$ and

$$\begin{aligned} Q(m) \le (m+1) \cdot P(m) = O(m^{k+1}). \end{aligned}$$

Consider any $I \subseteq \{1,2,\ldots ,m\}$ such that $\vert I \vert = \sqrt{m}$. Let ${\varvec{h}}$ be an extreme point of $\mathcal{U}$ corresponding to I, i.e., $h_i= 1$ if $i \in I$ and $h_i= 0$ otherwise. Since we assume that $\hat{\mathcal{U}}$ dominates $\mathcal U$, there exists ${\hat{\varvec{h}}} \in {\hat{\mathcal{U}}}$ such that $\varvec{h} \le \hat{\varvec{h}}$. Let

$$\begin{aligned} {\hat{\varvec{h}}}=m^{\frac{1}{2}-\epsilon } \sum _{j=1}^{Q(m)} { \alpha }_j \varvec{y}_j, \end{aligned}$$

where $\sum _{j=1}^{Q(m)} { \alpha }_j=1$ and ${ \alpha }_j \ge 0$ for all $j=1,2,\ldots ,Q(m)$. We have

$$\begin{aligned} 1= h_i \le \hat{h}_i \quad \forall i \in I \end{aligned}$$

i.e.

$$\begin{aligned} 1 \le m^{\frac{1}{2}-\epsilon } \sum _{j=1}^{Q(m)} { \alpha }_j {y_{ji}}, \quad \forall i \in I. \end{aligned}$$

Summing over $i \in I$, we have,

$$\begin{aligned} \sqrt{m}= \vert I \vert \le m^{\frac{1}{2}-\epsilon } \sum _{i \in I} \sum _{j=1}^{Q(m)} { \alpha }_j {y_{ji}}. \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{aligned} m^{\epsilon }&\le \sum _{j=1}^{Q(m)} { \alpha }_j \sum _{i \in I} {y_{ji}}, \\&\le \left( \sum _{j=1}^{Q(m)} { \alpha }_j \right) \cdot \underset{ j=1,2,\ldots ,Q(m)}{\max }\sum _{i \in I} {y_{ji}}\\&= \underset{ j=1,2,\ldots ,Q(m)}{\max }\sum _{i \in I} {y_{ji}} = \sum _{i \in I} {y_{j^*i}}, \end{aligned} \end{aligned}$$

where the second inequality follows from taking the max of the inner sum over indices j and $j^*$ is the index corresponding to the maximum sum.

Therefore, for any $I \subseteq \{1,2,\ldots ,m\}$ with cardinality $\vert I \vert = \sqrt{m}$, there exists $j=1,2,\ldots , Q(m)$ such that

$$\begin{aligned} \sum _{i \in I} {y_{ji}} \ge m^{\epsilon }. \end{aligned}$$

Denote $\mathcal{F} = \left\{ I \subseteq \{1,2,\ldots ,m\} \; \big \vert \; \vert I \vert =\sqrt{m} \right\}$ which represents the set of all subsets of $\{1,2,\ldots ,m\}$ with cardinality $\sqrt{m}$. Note that the cardinality of $\mathcal F$ is

$$\begin{aligned} \vert \mathcal{F} \vert = \left( {\begin{array}{c}m\\ \sqrt{m}\end{array}}\right) . \end{aligned}$$

We know that for any $I \in \mathcal{F}$ there exists $\varvec{y} _j \in \{ \varvec{y}_1,\varvec{y}_2,\ldots \varvec{y}_{Q(m)} \}$ such that

$$\begin{aligned} \sum _{i \in I} {y_{ji}} \ge m^{\epsilon }. \end{aligned}$$

We have $\left( {\begin{array}{c}m\\ \sqrt{m}\end{array}}\right)$ possibilities for I and Q(m) possibilities for $\varvec{y}_j$, hence by the pigeonhole principle, there exists a fixed $\varvec{y} \in \{ \varvec{y}_1,\varvec{y}_2,\ldots \varvec{y}_{Q(m)} \}$ and $\tilde{\mathcal{F}} \subseteq \mathcal{F}$ such that

$$\begin{aligned} \vert \tilde{\mathcal{F}} \vert\ge & {} \frac{1}{Q(m)} \left( {\begin{array}{c}m\\ \sqrt{m}\end{array}}\right) , \text{ and } \nonumber \\ \sum _{i \in I} {y_{i}}\ge & {} m^{\epsilon }, \; \forall I \in \tilde{\mathcal{F}}. \end{aligned}$$

(5.2)

Note that $\varvec{y}$ is an extreme point of $\mathcal U$. Hence, $\varvec{y}$ has exactly $\sqrt{m}$ ones and the remaining components are zeros. The maximum cardinality of subsets $I \subseteq [m]$ that can be constructed to satisfy $\sum _{i \in I} {y_{i}} \ge m^{\epsilon }$ is

$$\begin{aligned} \sum _{k=m^{\epsilon }}^{k=\sqrt{m}} \left( {\begin{array}{c}\sqrt{m}\\ k\end{array}}\right) \cdot \left( {\begin{array}{c}m-\sqrt{m}\\ \sqrt{m}-k\end{array}}\right) . \end{aligned}$$

By over counting, the above sum can be upper-bounded by

$$\begin{aligned} \left( {\begin{array}{c}\sqrt{m}\\ m^{\epsilon }\end{array}}\right) \cdot \left( {\begin{array}{c}m-m^{\epsilon }\\ \sqrt{m}-m^{\epsilon }\end{array}}\right) . \end{aligned}$$

Therefore, cardinality of $\tilde{\mathcal{F}}$ should be less that the above upper bound, i.e.

$$\begin{aligned} \left( {\begin{array}{c}\sqrt{m}\\ m^{\epsilon }\end{array}}\right) \cdot \left( {\begin{array}{c}m-m^{\epsilon }\\ \sqrt{m}-m^{\epsilon }\end{array}}\right) \ge \vert \tilde{\mathcal{F}} \vert \ge \frac{1}{Q(m)} \left( {\begin{array}{c}m\\ \sqrt{m}\end{array}}\right) \end{aligned}$$

Then,

$$\begin{aligned} \frac{\left( {\begin{array}{c}\sqrt{m}\\ m^{\epsilon }\end{array}}\right) \cdot \left( {\begin{array}{c}m-m^{\epsilon }\\ \sqrt{m}-m^{\epsilon }\end{array}}\right) }{\left( {\begin{array}{c}m\\ \sqrt{m}\end{array}}\right) } \ge \frac{1}{Q(m)}. \end{aligned}$$

(5.3)

which is a contradiction. The contradiction is derived by analyzing the order of the fractions in (5.3) (see “Appendix I”). $\square$

6 Computational study

In this section, we present a computational study to compare the performance of our policy with affine policies both in terms of objective function value of problem $\varPi _{\textsf {AR}}(\mathcal{U})$ (1.1) and computation times. We explore both cases of permutation invariant sets and non-permutation invariant sets.

6.1 Experimental setup

Uncertainty sets We consider the following classes of uncertainty sets for our computational experiments.

• 1. Hypersphere We consider the following unit hypersphere defined in (1.2),

  $$\begin{aligned} \mathcal{U}=\{\varvec{h}\in {{\mathbb {R}}}^m_+\;|\;||\varvec{h}||_2\le 1\}. \end{aligned}$$

• 2. p-norm balls We consider the following sets defined in Proposition 2.

  $$\begin{aligned} \mathcal{U}= \left\{ \varvec{h} \in {\mathbb {R}}^{m}_+ \; \big \vert \; \Vert \varvec{h}\Vert _p \le 1 \right\} . \end{aligned}$$

  For our numerical experiments, we consider the cases of $p=3$ and $p=3/2$.

• 3. Budget of uncertainty set We consider the following set defined in (3.10),

  $$\begin{aligned} \mathcal{U}= \left\{ \varvec{h} \in [0,1]^{m} \; \Bigg \vert \; \sum _{i=1}^m h_i \le k \right\} . \end{aligned}$$

  Here, k denotes the budget. For our numerical experiments, we choose $k=c \sqrt{m}$ where c is a random uniform constant between 1 and 2.

• 4. Intersection of budget of uncertainty sets We consider the following intersection of L budget of uncertainty sets:

  $$\begin{aligned} \mathcal{U}= \left\{ \varvec{h} \in [0,1]^m \; \Bigg \vert \; \sum _{j=1}^m \alpha _{ij} h_j \le 1, \; \forall i=1,\ldots ,L \right\} . \end{aligned}$$

  (6.1)

  Here, $\alpha _{ij}$ are non-negative scalars. Note that the intersection of budget of uncertainty sets are not permutation invariant. For our numerical experiments, we generate $\alpha _{ij}$ i.i.d. according to absolute value of standard Gaussians and we normalize $\vert \vert \varvec{\alpha }_i \vert \vert _2$ to 1 for all i (i.e. $\varvec{\alpha }_{i} = \vert \varvec{G}_i \vert / \vert \vert \varvec{G}_i \vert \vert _2$ where $\varvec{G}_i$ are i.i.d. according to $\mathcal{N}(0, \varvec{I}_m )$). We consider $L=2$ and $L=5$ for our experiments.

• 5. Generalized budget of uncertainty set We consider the following set

  $$\begin{aligned} \mathcal{U}= \left\{ \varvec{h} \in [0,1]^m \; \Bigg \vert \; \sum _{\ell =1}^m h_{\ell } \le 1 + \theta ( h_i +h_j) \; \; \forall i \ne j \right\} . \end{aligned}$$

  (6.2)

  This is a generalized version of the budget of uncertainty set (3.10) where the budget is not a constant but depends on the uncertain parameter $\varvec{h}$. In particular, the budget in the set (6.2) depends on the sum of the two lowest components of $\varvec{h}$. For our numerical experiments, we choose $\theta = O(m)$.

Instances We construct test instances of the adjustable robust problem (1.1) as follows. We choose $n=m$, $\varvec{c}= \varvec{d} = \varvec{e}$ and $\varvec{A}= \varvec{B}$ where $\varvec{B}$ is randomly generated as

$$\begin{aligned} \varvec{B} = \varvec{I}_m + \varvec{G}, \end{aligned}$$

where $\varvec{I}_m$ is the identity matrix and $\varvec{G}$ is a random normalized gaussian. In particular, for the hypersphere uncertainty set, the budget of uncertainty set, the intersection of budget of uncertainty sets and the generalized budget, we conisder $G_{ij} = |Y_{ij}|/ \sqrt{m}$. For the 3-norm ball, $G_{ij} = |Y_{ij}|/ m^{\frac{1}{3}}$ and for the $\frac{3}{2}$-norm ball, $G_{ij} = |Y_{ij}|/ m^{\frac{2}{3}},$ where $Y_{ij}$ are i.i.d. standard gaussian. We consider values of m from $m=10$ to $m=100$ in increments of 10 and consider 50 instances for each value of m.

Our piecewise affine policy We construct the piecewise affine policy based on the dominating simplex $\hat{\mathcal{U}}$ as follows. For permutation invariant sets, we use the dominating simplex that can be computed in closed form. In particular, for the hypersphere uncertainty set, we use the dominating set $\hat{\mathcal{U}}$ in Proposition 1. For the p-norm balls, we use the dominating set $\hat{\mathcal{U}}$ in Proposition 2. For the budget of uncertainty set, we use the dominating set $\hat{\mathcal{U}}$ in Proposition 5 and for the generalized budget of uncertainty set (6.2), we use the dominating set ${\hat{\mathcal{U}}}$ in Proposition 7 (see “Appendix K”).

For non-permutation invariant sets, we use Algorithm 1 to compute the dominating simplex. In particular, we get $\beta$ and $\varvec{v}$ that satisfies (2.4) and $2 \beta \cdot {\textsf {conv}} \left( \varvec{e}_1,\ldots ,\varvec{e}_m, \varvec{v} \right)$ is a dominating set (see Lemma 1b). We can also show that the following set (6.3) is a dominating set (see Proposition 6 in “Appendix J”),

$$\begin{aligned} {\hat{\mathcal{U}}} = \beta \cdot {\textsf {conv}} \left( \varvec{v}, \varvec{e}_1 + \varvec{v}, \ldots , \varvec{e}_m + \varvec{v} \right) . \end{aligned}$$

(6.3)

While the worst case scaling factor for the above dominating set can be $2 \beta$ and therefore the theoretical bounds do not change, computationally (6.3) can provide a better policy and we use this in our numerical experiments for the intersection of budget of uncertainty sets (6.1).

6.2 Results

Let $z_{\textsf {p-aff}}(\mathcal{U})$ denote the worst-case objective value of our piecewise affine policy. Note that the piecewise affine policy over $\mathcal{U}$ is computed by solving the adjustable robust problem over $\hat{\mathcal{U}}$ and $z_{\textsf {p-aff}}(\mathcal{U}) = z_{\textsf {AR}}(\hat{\mathcal{U}})$. For each uncertainty set we report the ratio $r = \frac{z_{\textsf {Aff}} (\mathcal{U}) }{z_{\textsf {p-aff}} (\mathcal{U}) }$ for $m=10$ to 100. In particular, for each value of m, we report the average ratio (${\textsf {Avg}}$), the maximum ratio (${\textsf {Max}}$), the minimum ratio (${\textsf {Min}}$), the quantiles $95\%, 90\% , 75\%, 50\%$ for the ratio r, the running time of our policy ($T_{\textsf {p-aff}}(s)$) and the running time of affine policy ($T_{\textsf {aff}}(s)$). In addition, for the intersection of budget of uncertainty sets, we also report the computation time to construct $\hat{\mathcal{U}}$ via Algorithm 1 ($T_{\textsf {Alg1}}(s)$). The numerical results are obtained using Gurobi 7.0.2 on a 16-core server with 2.93 GHz processor and 56 GB RAM.

Table 2 Comparison on the performance and computation time of affine policy and our piecewise affine policy for the hypersphere uncertainty set. For 50 instances, we compute $\frac{z_{\textsf {Aff}} (\mathcal{U}) }{z_{\textsf {p-aff}} (\mathcal{U})}$ and present the average, $\min$, $\max$ ratios and the quantiles $95\%, 90\%, 75\%, 50\%$. Here, $T_{\textsf {p-aff}}(s)$ denotes the running time for our piecewise affine policy and $T_{\textsf {aff}}(s)$ denotes the running time for affine policy in seconds

Table 3 Comparison on the performance and computation time of affine policy and our piecewise affine policy for the 3-norm ball uncertainty set

Table 4 Comparison on the performance and computation time of affine policy and our piecewise affine policy for the 3 / 2-norm ball uncertainty set

Table 5 Comparison on the performance and computation time of affine policy and our piecewise affine policy for the budget of uncertainty set with a budget $k=c\sqrt{m}$ where for each instance we generate c uniformly from [1, 2]

Table 6 Comparison on the performance and computation time of affine policy and our piecewise affine policy for the intersection of 2 budget of uncertainty sets (6.1)

Table 7 Comparison on the performance and computation time of affine policy and our piecewise affine policy for the intersection of 5 budget of uncertainty sets (6.1)

Table 8 Comparison on the performance and computation time of affine policy and our piecewise affine policy for the generalized budget of uncertainty set (6.2)

Hypersphere and Norm-balls. We present the results of our computational experiments in Tables 2, 3 and 4 for the hypersphere and norm-ball uncertainty sets. We observe that the piecewise affine policy performs significantly better than affine policy for our family of test instances. In Tables 2, 3 and 4, we observe that the ratio $r= \frac{z_{\textsf {Aff}} (\mathcal{U}) }{z_{\textsf {p-aff}} (\mathcal{U}) }$ increases significantly as m increases which implies that our policy provides a significant improvement over affine policy for large values of m. We also observe that the ratio for the hypersphere is larger than the ratio for norm-balls. This matches the theoretical bounds presented in Table 1 which suggests that the improvement over affine policy is the highest for $p=2$ for p-norm balls.

We note that for the smallest values of m ($m =10$), the performance of affine policy is better than our policy. However, for $m > 10$, the performance of our policy is significantly better for all these three uncertainty sets: hypersphere, 3-norm ball and 3/2-norm ball.

Furthermore, our policy scales well and the average running time is less than 0.1 s even for large values of m. On the other hand, computing the optimal affine policy over $\mathcal{U}$ becomes computationally challenging as m increases. For instance, the average running time for computing an optimal affine policy for $m=100$ is around 9 min for the hypersphere uncertainty set, around 17 min for the 3-norm ball and around 16 min for the 3 / 2-norm ball.

Budget of uncertainty sets We present the results of our computational experiments in Tables 5, 6, 7 and 8 for the single budget of uncertainty set, the intersection of budget sets and the generalized budget.

For the budget of uncertainty set (3.10), we observe that affine policy performs better than our piecewise affine policy for our family of test instances. Note that as we mention earlier, our policy is not a generalization of affine policies and therefore is not always better. For our experiments, we use $k=c \sqrt{m}$ which gives the worst case theoretical bound for our policy (see Theorem 7), but the performance of our policy is still reasonable and the average ratio $r= \frac{z_{\textsf {Aff}} (\mathcal{U}) }{z_{\textsf {p-aff}} (\mathcal{U}) }$ over all instances is around 0.88 as we can observe in Table 5. On the other hand, as in the case of conic uncertainty sets, our policy scales well with an average running time less than 0.1 s even for large values of m, whereas affine policy takes for example more than 6 min on average for $m=100$.

Tables 6 and 7 present the results for intersection of budget of uncertainty sets. We observe that affine policy outperforms our policy as in the case of a single budget. This confirms that affine policy performs very well empirically for this class of uncertainty sets. We also observe that the performance of our policy improves when we increase the number of budget constraints. For example, for $m=100$, the average ratio $r= \frac{z_{\textsf {Aff}} (\mathcal{U}) }{z_{\textsf {p-aff}} (\mathcal{U}) }$ increases from 0.79 in the case of $L=2$ to 0.88 for $L=5$. This suggests that the performance of our policy gets closer to the one of affine policy as long as we add more budgets constraints. While affine policy performs better than our policy for budget of uncertainty sets, we would like to note that this is not necessarily true for any polyhedral uncertainty set. In particular, we also test our policy with the generalized budget (6.2) and observe that our policy is significantly better than affine even when the set is polyhedral.

Table 8 presents the results for the generalized budget set (6.2). We observe that our piecewise affine policy outperforms affine policy both in terms of objective value and computation time. The gap increases as m increases which implies a significant improvement over affine policy for large values of m. Furthermore, unlike the piecewise affine policy, computing an affine solution becomes challenging for large values of m.

For the intersection of budget of uncertainty sets (6.1) that are not permutation invariant, we compute the dominating set (in particular $\beta$ and $\varvec{v}$) using Algorithm 1. We report the average running time, $T_{\textsf {Alg1}}$ of Algorithm 1 which solves a sequence of MIPs in Tables 6 and 7. We note that there is no need to solve MIPs optimally in Algorithm 1; one can stop when a feasible solution with an objective value greater than t is found. We observe that the running time of Algorithm 1 is reasonable as compared to that of affine policy. For example, the average running time of Algorithm 1 for $m=100$ and $L=5$ is 7 min whereas affine policy takes 10 min in average. For large values of m and a large number of budget constraints, the running time of Algorithm 1 might increase significantly and exceed the computation time of affine policy. However, we would like to emphasize that $\beta$ and $\varvec{v}$ given by Algorithm 1 do not depend on the parameters $(\varvec{A}, \varvec{B}, \varvec{c}, \varvec{d})$ and only depend on the uncertainty set. Therefore, they can be computed offline and can be used to solve many instances of the problem parameters for the same uncertainty set.

7 Conclusion

This paper introduces a new framework for designing piecewise affine policies (PAP) for two-stage adjustable robust optimization with right-hand side uncertainty. The framework is based on approximating the uncertainty set $\mathcal{U}$ by a dominating simplex and constructing a PAP using the map from $\mathcal{U}$ to the dominating simplex. For the class of conic uncertainty sets including ellipsoids and norm-balls, our PAP performs significantly better, theoretically and computationally than affine policy. For general uncertainty sets (particularly a “budgeted” $\mathcal{U}$ or intersection of a small number of “budget of uncertainty sets”), our PAP does not necessarily outperform affine policies, but while the latter may fail for large dimensional $\mathcal{U}$, the PAP scales well given the dominating set.

It is an interesting open question whether a PAP can be designed that significantly improves over affine policy for budgeted uncertainty sets.

Appendices

Proof of Theorem 1

Proof

Let $(\hat{\varvec{x}},\varvec{\hat{y}}(\hat{\varvec{h}}), \hat{\varvec{h}}\in \hat{\mathcal{U}})$ be an optimal solution for $z_{\textsf {AR}}(\hat{\mathcal{U}})$. For each $\varvec{h}\in \mathcal{U}$, let $\tilde{\varvec{y}}(\varvec{h})= \hat{\varvec{y}}(\hat{\varvec{h}})$ where $\hat{\varvec{h}}\in \hat{\mathcal{U}}$ dominates $\varvec{h}$. Therefore, for any $\varvec{h}\in \mathcal{U}$,

$$\begin{aligned} \varvec{A}\hat{\varvec{x}}+\varvec{B}\tilde{\varvec{y}}(\varvec{h}) = \varvec{A}\hat{\varvec{x}}+\varvec{B}\hat{\varvec{y}}(\hat{\varvec{h}})\ge \hat{\varvec{h}}\ge \varvec{h}, \end{aligned}$$

i.e., $(\hat{\varvec{x}},\tilde{\varvec{y}}(\varvec{h}),\varvec{h}\in \mathcal{U})$ is a feasible solution for $z_{\textsf {AR}}(\mathcal{U})$. Therefore,

$$\begin{aligned} z_{\textsf {AR}}(\mathcal{U})\le \varvec{c}^T\hat{\varvec{x}}+\max _{\varvec{h}\in \mathcal{U}}\varvec{d}^T\tilde{\varvec{y}}(\varvec{h})\le \varvec{c}^T\hat{\varvec{x}}+\max _{\hat{\varvec{h}}\in \hat{\mathcal{U}}}\varvec{d}^T\hat{\varvec{y}}(\hat{\varvec{h}})=z_{\textsf {AR}}(\hat{\mathcal{U}}). \end{aligned}$$

Conversely, let $(\varvec{x}^*, \varvec{y}^*(\varvec{h}), \varvec{h}\in \mathcal{U})$ be an optimal solution of $z_{\textsf {AR}}(\mathcal{U})$. Then, for any $\hat{\varvec{h}}\in \hat{\mathcal{U}}$, since $\frac{\hat{\varvec{h}}}{\beta } \in \mathcal{U}$, we have,

$$\begin{aligned} \varvec{A}\varvec{x}^*+\varvec{B}\varvec{y}^*\left( \frac{\hat{\varvec{h}}}{\beta }\right) \ge \frac{\hat{\varvec{h}}}{\beta }, \end{aligned}$$

Therefore, $(\beta \varvec{x}^*, \beta \varvec{y}^*\left( \frac{\hat{\varvec{h}}}{\beta }\right) , \hat{\varvec{h}} \in \mathcal{U})$ is feasible for $\varPi _{\textsf {AR}}(\hat{\mathcal{U}})$. Therefore,

$$\begin{aligned} z_{\textsf {AR}}(\hat{\mathcal{U}})\le \varvec{c}^T \beta \varvec{x}^* + \underset{ \varvec{\hat{h}} \in \hat{\mathcal{U}}}{\max }\; \varvec{d}^T \beta \varvec{y^*}\left( \frac{\varvec{\hat{h}}}{\beta }\right) \le \beta \cdot \left( \varvec{c}^T \varvec{x}^* + \underset{ \varvec{h} \in \mathcal{U}}{\max }\; \varvec{d}^T \varvec{y^*(h)} \right) = \beta \cdot z_{\textsf {AR}}(\mathcal U). \end{aligned}$$

$\square$

Proof of Lemma 1

Proof

(a) Suppose there exists $\beta$ and $\varvec{v} \in \mathcal{U}$ such that $\; \hat{\mathcal{U}} = \beta \cdot {\textsf {conv}} \left( \varvec{e}_1,\ldots ,\varvec{e}_m, \varvec{v} \right)$ dominates $\mathcal U$. Consider $\varvec{h} \in \mathcal{U }$. Since $\hat{\mathcal{U}}$ dominates $\mathcal{U}$, there exists $\alpha _1, \alpha _2,\ldots ,\alpha _{m+1} \ge 0$ with $\alpha _1 + \cdots + \alpha _{m+1} =1$ such that

$$\begin{aligned} h_i \le \beta \left( \alpha _i + \alpha _{m+1} v_i \right) , \; \forall i =1,\ldots ,m. \end{aligned}$$

(B.1)

Let

$$\begin{aligned} I (\varvec{h} )= \left\{ i \in [m] \; \bigg \vert \; h_i - \beta v_i \ge 0 \right\} . \end{aligned}$$

Then,

$$\begin{aligned} \sum _{i=1}^m \left( h_i -\beta v_i \right) ^{+}&= \underset{i \in I (\varvec{h} ) }{\sum }h_i - \beta \underset{i \in I (\varvec{h} ) }{\sum }v_i\\&\le \sum _{i\in I (\varvec{h} )} \beta \left( \alpha _i + \alpha _{m+1} v_i \right) - \beta \underset{i \in I (\varvec{h} )}{\sum }v_i\\&= \beta \sum _{i\in I (\varvec{h} )} \alpha _i + \left( \alpha _{m+1} -1\right) \beta \underset{i \in I (\varvec{h} ) }{\sum }v_i\\&\le \beta , \end{aligned}$$

where the first inequality follows from (B.1) and the last inequality holds because $\alpha _{m+1} -1 \le 0$, $v_i \ge 0$ , $\beta \ge 0$ and $\sum _{i\in I (\varvec{h} )} \alpha _i \le 1$. We conclude that

$$\begin{aligned} \frac{1}{\beta } \sum _{i=1}^m \left( h_i -\beta v_i \right) ^{+} \le 1. \end{aligned}$$

(b) Now, suppose there exists $\beta$ and $\varvec{v} \in \mathcal{U}$ such that $\; \hat{\mathcal{U}} = \beta \cdot {\textsf {conv}} \left( \varvec{e}_1,\ldots ,\varvec{e}_m, \varvec{v} \right)$ dominates $\mathcal U$. For any $\varvec{h} \in \mathcal{U}$, let

$$\begin{aligned} \varvec{{\hat{h}}} = \sum _{i=1}^m \left( h_i -\beta v_i \right) ^{+} \varvec{e}_i + \beta \varvec{v}. \end{aligned}$$

Then for all $i=1,\ldots ,m$,

$$\begin{aligned} \hat{h}_i&= \left( h_i -\beta v_i \right) ^{+} + \beta v_i \\&\ge \left( h_i -\beta v_i \right) + \beta v_i \ge h_i . \end{aligned}$$

Therefore, $\varvec{{\hat{h}}}$ dominates $\varvec{h}$. Moreover,

$$\begin{aligned} \varvec{{\hat{h}}} = 2\beta \left( \sum _{i=1}^m \frac{\left( h_i -\beta v_i \right) ^{+}}{2 \beta } \varvec{e}_i + \frac{1}{2}\varvec{v} \right) \in 2\beta \cdot {\textsf {conv}} \left( \varvec{0}, \varvec{e}_1,\ldots ,\varvec{e}_m, \varvec{v} \right) , \end{aligned}$$

because

$$\begin{aligned} \frac{1}{\beta } \sum _{i=1}^m \left( h_i - \beta v_i \right) ^{+} \le 1. \end{aligned}$$

Therefore, $2\beta \cdot {\textsf {conv}} \left( \varvec{0}, \varvec{e}_1,\ldots ,\varvec{e}_m, \varvec{v} \right)$ dominates $\mathcal{U}$ and consequently $2\beta \cdot {\textsf {conv}} \left( \varvec{e}_1,\ldots ,\varvec{e}_m, \varvec{v} \right)$ dominates $\mathcal{U}$ as well. $\square$

Proof of Lemma 3

Proof

Suppose $k \in [m]$. Let us consider

$$\begin{aligned} \varvec{h} \in \underset{\varvec{h} \in \mathcal{U}}{\textsf {argmax}} \sum _{i=1}^k h_i . \end{aligned}$$

Without loss of generality, we can suppose that $h_i =0$ for $i =k+1,\ldots , m$. Denote, $\mathcal{S}_k$ the set of permutations of $\{ 1,2,\ldots ,k\}$. We define $\varvec{h} ^{\sigma } \in \mathbb {R}_+^m$ such that $h^{\sigma }_i = h_{\sigma (i) }$ for $i=1, \ldots ,k$ and $h^{\sigma }_i =0$ otherwise. Since $\mathcal{U}$ is a permutation invariant set, we have $\varvec{h} ^{\sigma } \in \mathcal{U}$ for any $\sigma \in \mathcal{S}_k$. The convexity of $\mathcal{U}$ implies that

$$\begin{aligned} \frac{1}{k!} \sum _{ \sigma \in \mathcal{S}_k} \varvec{h}^{\sigma } \in \mathcal{U}. \end{aligned}$$

We have,

$$\begin{aligned} \sum _{ \sigma \in \mathcal{S}_k} h^{\sigma }_i = \left\{ \begin{array}{ll} (k-1)! \cdot \sum _{j=1}^k h_j &{}\quad \hbox {if } i=1,\ldots ,k \\ 0 &{}\quad \text{ otherwise, } \end{array} \right. \end{aligned}$$

and $\sum _{j=1}^k h_j = k \cdot \gamma (k)$ by definition. Therefore,

$$\begin{aligned} \frac{1}{k!} \sum _{ \sigma \in \mathcal{S}_k} \varvec{h}^{\sigma } = \gamma (k) \cdot \sum _{i=1}^k \varvec{e}_i \in \mathcal{U}. \end{aligned}$$

$\square$

Proof of Lemma 4

Proof

Consider, $\tilde{\varvec{h}} \in \mathcal{U}$ an optimal solution for the maximization problem in (3.3) for fixed $\beta$. We will construct $\varvec{h}^* \in \mathcal{U}$ another optimal solution of (3.3) that verifies the properties in the lemma. First, denote $I = \{ i \; \vert \; {\tilde{h}}_i > \beta \gamma \}$ and $\vert I\vert =k$. Since, $\mathcal{U}$ is permutation invariant, we can suppose without loss of generality that $I =\{1,2,\ldots ,k \}$. We define,

$$\begin{aligned} h^*_i = \left\{ \begin{array}{ll} \gamma (k) &{}\quad \hbox {if } i=1,\ldots ,k \\ 0 &{}\quad \hbox {otherwise.} \end{array} \right. \end{aligned}$$

From Lemma 3, we have $\varvec{h}^* \in \mathcal{U}$. Moreover,

$$\begin{aligned} \sum _{i=1}^m ( \tilde{h}_i - \beta \gamma )^+&= \sum _{i=1}^k \tilde{h}_i - \beta \gamma k \le k \cdot \gamma (k) - \beta \gamma k \\&= \sum _{i=1}^k ( \gamma (k) - \beta \gamma ) = \sum _{i=1}^k ( h^*_i- \beta \gamma ) \\&\le \sum _{i=1}^k ( h^*_i- \beta \gamma )^+ = \sum _{i=1}^m ( h^*_i- \beta \gamma )^+\\ \end{aligned}$$

where the first inequality follows from the definition of the coefficients $\gamma (.)$. Therefore, $\varvec{h}^*$ and $\tilde{\varvec{h}}$ have the same objective value in (3.3) and consequently $\varvec{h}^*$ is also optimal for the maximization problem (3.3). Moreover, from the first inequality, we have $\gamma (k) - \beta \gamma >0$, i.e., $\big \vert \{ i \; \vert \; h_i^* > \beta \gamma \} \big \vert =k.$ Therefore, $\varvec{h}^*$ verifies the properties of the lemma. $\square$

Proof of Proposition 4

Proof

To prove that $\hat{\mathcal{U}}$ dominates $\mathcal{U}$, it is sufficient to take $\varvec{h}$ in the boundaries of $\mathcal{U}$, i.e.,

$$\begin{aligned} a \sum _{i=1}^m h_i \sum _{j=1}^m h_j + (1-a) \sum _{i=1}^m h_i^2 =1 , \end{aligned}$$

(E.1)

and find $\alpha _1, \alpha _2,\ldots ,\alpha _{m+1}$ nonnegative reals with $\sum _{i=1}^{m+1} \alpha _i =1$ such that for all $i \in [m],$

$$\begin{aligned} \; h_i \le \beta \left( \alpha _i + \gamma \alpha _{m+1}\right) . \end{aligned}$$

By taking all $h_i$ equal in (E.1), we get

$$\begin{aligned} \gamma = \frac{1}{ \sqrt{\left( am^2+(1-a)m \right) } } . \end{aligned}$$

We choose for $i \in [m]$,

$$\begin{aligned} \alpha _i = \frac{1}{2} \left( (1-a)h_i^2+ a h_i \sum _{j=1}^m h_j \right) \end{aligned}$$

and $\alpha _{m+1}= \frac{1}{2}.$ First, we have $\sum _{i=1}^{m+1} \alpha _i =1$ and for all $i \in [m]$,

$$\begin{aligned} \beta \left( \alpha _i + \gamma \alpha _{m+1}\right)&= \frac{\beta }{2} \left( (1-a)h_i^2+ a h_i \sum _{j=1}^m h_j + \frac{1}{ \sqrt{am^2+(1-a)m} } \right) \\&\ge \frac{\beta }{2} \left( (1-a)h_i^2 + \frac{1}{ \sqrt{am^2+(1-a)m} } + a h_i \right) \\&\ge \frac{\beta }{2} \left( 2 \left( \frac{(1-a)}{\sqrt{am^2+(1-a)m}} \right) ^{\frac{1}{2}}h_i+ a h_i \right) =h_i \end{aligned}$$

where the first inequality holds because $\sum _{j=1}^m h_j \ge 1$ which is a direct consequence of $\varvec{h}^T \varSigma \varvec{h} =1$ and $a \le 1$. The second one follows from the inequality of arithmetic and geometric means (AM-GM inequality). Finally, we can verify by case analysis on the values of a that

$$\begin{aligned} \left( \frac{a}{2}+ \frac{(1-a)^{\frac{1}{2}}}{\left( am^2+(1-a)m\right) ^{\frac{1}{4}}}\right) ^{-1}= O \left( m^{\frac{2}{5}} \right) . \end{aligned}$$

In fact, denote $H(m)= \left( \frac{a}{2}+ \frac{(1-a)^{\frac{1}{2}}}{\left( am^2+(1-a)m\right) ^{\frac{1}{4}}}\right) ^{-1} = O \left( a+ \frac{1}{\left( am^2+m\right) ^{\frac{1}{4}}}\right) ^{-1}$

Case 1$a=O(\frac{1}{m})$. We have $\left( am^2+m \right) ^{\frac{1}{4}} = O(m^{\frac{1}{4}})$. Then $H(m)=O(m^{\frac{1}{4}})=O(m^{\frac{2}{5}})$.

Case 2$a=\varOmega (m^{\frac{-2}{5}})$. We have $H(m)=O(a^{-1})=O(m^{\frac{2}{5}})$.

Case 3$a=O(m^{\frac{-2}{5}} )$and$a=\varOmega (\frac{1}{m})$. We have $\left( am^2+m \right) ^{\frac{1}{4}} = O(m^{\frac{2}{5}})$. Then,

$$\begin{aligned} a+ \frac{1}{\left( am^2+m\right) ^{\frac{1}{4}}}= \varOmega \left( \frac{1}{m}\right) +\varOmega \left( m^{\frac{-2}{5}}\right) =\varOmega \left( m^{\frac{-2}{5}}\right) . \end{aligned}$$

Therefore, $H(m)=O(m^{\frac{2}{5}})$. $\square$

Proof of Proposition 5

Proof

To prove that $\hat{ \mathcal U}$ dominates ${ \mathcal U}$, it is sufficient to take $\varvec{h}$ in the boundaries of $\mathcal{U}$, i.e., $\sum _{i=1}^m h_i =k$ and find $\alpha _1, \alpha _2,\ldots ,\alpha _{m+1}$ non-negative reals with $\sum _{i=1}^{m+1} \alpha _i =1$ such that for all $i \in [m],$

$$\begin{aligned} \; h_i \le \beta \left( \alpha _i + \frac{k}{m}\alpha _{m+1}\right) . \end{aligned}$$

First case If $\beta =k$, we choose $\alpha _i = \frac{h_i}{k}$ for $i \in [m]$ and $\alpha _{m+1}= 0.$ We have $\sum _{i=1}^{m+1} \alpha _i =1$ and for all $i \in [m]$,

$$\begin{aligned} \beta \left( \alpha _i + \frac{k}{m}\alpha _{m+1}\right) = k \frac{h_i}{k} \ge h_i . \end{aligned}$$

Second case If $\beta =\frac{m}{k}$, we choose $\alpha _i = 0$ for $i \in [m]$ and $\alpha _{m+1}= 1.$ We have $\sum _{i=1}^{m+1} \alpha _i =1$ and for all $i \in [m]$,

$$\begin{aligned} \beta \left( \alpha _i + \frac{k}{m}\alpha _{m+1}\right) = 1 \ge h_i . \end{aligned}$$

$\square$

Proof of Lemma 6

Proof

Consider the following simplex

$$\begin{aligned} \hat{\mathcal{U}} = {\textsf {conv}} \left( \varvec{e}_1 , \ldots ,\varvec{e}_m, \frac{1}{\sqrt{m}} \varvec{e} \right) \end{aligned}$$

It is clear that $\hat{\mathcal{U}}$ dominates $\mathcal{U}$ since $\frac{1}{\sqrt{m}} \varvec{e}$ dominates all the extreme points $\varvec{\nu }_j$ for $j \in [N]$. Moreover, by the convexity of $\mathcal U$, we have $\frac{1}{N} \sum _{j=1}^N \varvec{\nu }_j = \frac{\left( {\begin{array}{c}m-1\\ r-1\end{array}}\right) }{\sqrt{m}\left( {\begin{array}{c}m\\ r\end{array}}\right) } \varvec{e} = \frac{r}{m\sqrt{m}} \varvec{e} \in \mathcal{U}$. Denote $\beta = \frac{m}{r }$. Hence, for all $i \in [m]$

$$\begin{aligned} \varvec{e}_i = \beta \underbrace{\left( \frac{1}{\beta } \cdot \varvec{e}_i + \left( 1- \frac{1}{\beta }\right) \cdot \varvec{0}\right) }_{\in \mathcal{U}} \qquad \text {and} \qquad \frac{1}{\sqrt{m}} \varvec{e} = \beta \cdot \underbrace{\frac{r}{m\sqrt{m}} \varvec{e}}_{\in \mathcal U}. \end{aligned}$$

Therefore, $\hat{\mathcal{U}} \subseteq \beta \cdot \mathcal{U}$ and from Theorem 1, we conclude that our policy gives a $\beta$-approximation to the adjustable problem  (1.1) where $\beta = \frac{m}{\lceil m- \sqrt{m \rceil } }=O (1+ \frac{1}{\sqrt{m}})$. $\square$

Proof of Lemma 7

Proof

First, let us prove that $z_{\textsf {AR}}(\mathcal{U}) \le 1$. It is sufficient to define an adjustable solution only for the extreme points of $\mathcal{U}$ because the constraints are linear. We define the following solution for all $i=1,\ldots ,m$ and for all $j=1,\ldots ,N$

$$\begin{aligned} \varvec{x} = \varvec{0} , \quad \varvec{y} ( \varvec{0}) = \varvec{0}, \quad \varvec{y} ( \varvec{e}_i) = \varvec{e}_i, \quad \varvec{y} ( \varvec{\nu }_j) = \frac{1}{m} \varvec{e}. \end{aligned}$$

We have $\varvec{B} \varvec{y} ( \varvec{0}) = \varvec{0}$. For $i \in [m]$

$$\begin{aligned} \varvec{B} \varvec{y} ( \varvec{e}_i) = \varvec{e}_i + \frac{1}{\sqrt{m}} ( \varvec{e} - \varvec{e}_i) \ge \varvec{e}_i \end{aligned}$$

and for $j \in [N]$

$$\begin{aligned} \varvec{B} \varvec{y} (\varvec{\nu }_j) = \frac{1}{m} \varvec{B} \varvec{e} = \left( \frac{1}{m}+ \frac{m-1}{m \sqrt{m}} \right) \varvec{e} \ge \frac{1}{\sqrt{m}} \varvec{e} \ge \varvec{\nu }_j. \end{aligned}$$

Therefore, the solution defined above is feasible. Moreover, the cost of our feasible solution is 1 because for all $i \in [m]$ and $j \in [N]$, we have

$$\begin{aligned} \varvec{d}^T \varvec{y} ( \varvec{e}_i)= \varvec{d}^T \varvec{y} ( \varvec{\nu }_j)= 1. \end{aligned}$$

Hence, $z_{\textsf {AR}}(\mathcal{U}) \le 1.$ Now, it is sufficient to prove that $z_{\textsf {Aff}}(\mathcal{U})= \varOmega ( \sqrt{m})$. First, $\tilde{\varvec{x}}= \frac{1}{\sqrt{m}} \varvec{e}$ and $\varvec{y}( \varvec{h})= \varvec{0}$ for any $\varvec{h} \in \mathcal{U}$ is a feasible static solution (which is a special case of an affine solution). In fact,

$$\begin{aligned} \varvec{A} \tilde{\varvec{x}}= \frac{1}{\sqrt{m}} \varvec{A} \varvec{e} = \left( \frac{1}{\sqrt{m}}+ \frac{m-1}{m} \right) \varvec{e} \ge \varvec{e} \ge \varvec{h} \quad \forall \varvec{h} \in \mathcal{U} \end{aligned}$$

where the last inequality holds because $\mathcal{U} \subseteq [0,1]^m$. Moreover, the cost of this static solution is

$$\begin{aligned} \varvec{c}^T \tilde{\varvec{x}} = \frac{\sqrt{m}}{15}. \end{aligned}$$

Hence,

$$\begin{aligned} z_{\textsf {Aff}}(\mathcal{U}) \le \frac{\sqrt{m}}{15}. \end{aligned}$$

(H.1)

Our instance is “a permuted instance”, i.e. $\mathcal{U}$ is permutation invariant, $\varvec{A}$ and $\varvec{B}$ are symmetric and $\varvec{c}$ and $\varvec{d}$ are proportional to $\varvec{e}$. Hence, from Lemma 8 and Lemma 7 in Bertsimas and Goyal [12], for any optimal solution $\varvec{x}^*_{\textsf {Aff}}, \varvec{y}^*_{\textsf {Aff}}( \varvec{h})$ of the affine problem, we can construct another optimal affine solution that is “symmetric” and have the same stage cost. In particular, there exists an optimal solution for the affine problem of the following form $\varvec{x}= \alpha \varvec{e}$, $\varvec{y}( \varvec{h}) = \varvec{P} \varvec{h} + \varvec{q}$ for $\varvec{h} \in \mathcal{U}$ where

$$\begin{aligned} \varvec{P}= \left( \begin{matrix} \theta &{}\quad \mu &{}\quad \ldots &{}\quad \mu \\ \mu &{}\quad \theta &{}\quad \ldots &{}\quad \mu \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ \mu &{}\quad \mu &{}\quad \ldots &{}\quad \theta \end{matrix} \right) \end{aligned}$$

(H.2)

$\varvec{q} = \lambda \varvec{e}$, $\varvec{c}^T \varvec{x}= \varvec{c}^T \varvec{x}^*_{\textsf {Aff}}$ and $\max _{ \varvec{h} \in \mathcal{U}} \varvec{d}^T \varvec{y}(\varvec{h})= \max _{ \varvec{h} \in \mathcal{U}} \varvec{d}^T \varvec{y}^*_{\textsf {Aff}}(\varvec{h})$. We have $\varvec{x} \ge \varvec{0}$ and $\varvec{y}(\varvec{0}) = \lambda \varvec{e} \ge \varvec{0}$ hence

$$\begin{aligned} \lambda \ge 0 \qquad \text {and} \qquad \alpha \ge 0. \end{aligned}$$

(H.3)

Claim

$\alpha \ge \frac{1}{24 \sqrt{m}}$ For a sake of contradiction, suppose that $\alpha > \frac{1}{24 \sqrt{m}}$. We know that

$$\begin{aligned} z_{\textsf {Aff}}(\mathcal{U}) \ge \varvec{c}^T \varvec{x} + \varvec{d}^T \varvec{y}( \varvec{0}) = \frac{\alpha }{15} m + \lambda m. \end{aligned}$$

(H.4)

Case 1 If $\lambda \ge \frac{1}{12 \sqrt{m}}$, then from (H.4) and $\alpha \ge 0$, we have $z_{\textsf {Aff}}(\mathcal{U}) \ge \frac{\sqrt{m}}{12}$. Contradiction with (H.1).

Case 2 If $\lambda \le \frac{1}{12 \sqrt{m}}$. We have

$$\begin{aligned} \varvec{y}( \varvec{e}_1) = ( \theta + \lambda ) \varvec{e}_1 + ( \mu + \lambda ) ( \varvec{e} - \varvec{e}_1). \end{aligned}$$

By feasibility of the solution, we have $\varvec{A} \varvec{x}+ \varvec{B} \varvec{y} ( \varvec{e}_1) \ge \varvec{e}_1$, hence

$$\begin{aligned} \theta + \lambda + \alpha \left( \frac{m-1}{\sqrt{m}} +1 \right) +\frac{1}{\sqrt{m}} (m-1)(\mu + \lambda ) \ge 1 \end{aligned}$$

Therefore $\theta + \lambda + \alpha \left( \frac{m-1}{\sqrt{m}} +1 \right) \ge \frac{1}{2}$ or $\frac{1}{\sqrt{m}} (m-1)(\mu + \lambda ) \ge \frac{1}{2}$.

Case 2.1 Suppose $\frac{1}{\sqrt{m}} (m-1)(\mu + \lambda ) \ge \frac{1}{2}$. Therefore,

$$\begin{aligned} z_{\textsf {Aff}}(\mathcal{U}) \ge \varvec{d}^T \varvec{y} (\varvec{e}_1) = \theta + \lambda + (m-1)(\mu + \lambda ) \ge \frac{\sqrt{m}}{2}. \; \; [\text {Contradiction with } (\hbox {H.1})] \end{aligned}$$

where the last inequality holds because $\theta + \lambda \ge 0$ as $\varvec{y}( \varvec{e}_1) \ge \varvec{0}$.

Case 2.2 Now suppose we have the other inequality i.e. $\theta + \lambda + \alpha \left( \frac{m-1}{\sqrt{m}} +1 \right) \ge \frac{1}{2}$. Recall that we have $\lambda \le \frac{1}{12\sqrt{m}}$ and we know that $\alpha < \frac{1}{24 \sqrt{m}}$. Therefore,

$$\begin{aligned} \theta \ge \frac{1}{2}- \frac{1}{12\sqrt{m}} - \frac{1}{24\sqrt{m}}\left( \frac{m-1}{\sqrt{m}} +1 \right) = \frac{11}{24} - \frac{3}{24 \sqrt{m}} + \frac{1}{24m} \ge \frac{11}{24} - \frac{3}{24 }= \frac{1}{3}. \end{aligned}$$

We have,

$$\begin{aligned} \varvec{y} ( \varvec{\nu }_1 ) = \frac{1}{\sqrt{m}} \left( ( \theta + (r-1) \mu ) ( \varvec{e}_1+ \cdots \varvec{e}_r) + r \mu ( \varvec{e} -( \varvec{e}_1+ \cdots \varvec{e}_r)) \right) + \lambda \varvec{e}. \end{aligned}$$

In particular we have ,

$$\begin{aligned} z_{\textsf {Aff}}(\mathcal{U}) \ge \varvec{d}^T \varvec{y} (\varvec{\nu }_1)&= \frac{r}{\sqrt{m}} ( \theta +(m-1) \mu ) + \lambda m \nonumber \\&\ge \frac{r}{\sqrt{m}} \left( \frac{1}{3} + (m-1) \mu \right) . \end{aligned}$$

(H.5)

where the last inequality follows from $\lambda \ge 0$ and $\theta \ge \frac{1}{3}.$

Case 2.2.1 If $\mu \ge 0$ then from (H.5)

$$\begin{aligned} z_{\textsf {Aff}}(\mathcal{U}) \ge \frac{r}{3\sqrt{m}} \ge \frac{m-\sqrt{m}}{3\sqrt{m}} \ge \frac{\sqrt{m}}{6} \; \; \text {for } m \ge 4 \; \; [\text {Contradiction with } (\hbox {H.1})] \end{aligned}$$

Case 2.2.2 Now suppose that $\mu < 0$, by non-negativity of $\varvec{y} ( \varvec{\nu }_1)$ we have

$$\begin{aligned} \frac{r}{\sqrt{m}} \mu + \lambda \ge 0 \end{aligned}$$

i.e.

$$\begin{aligned} \mu \ge \frac{-\lambda \sqrt{m}}{r} \end{aligned}$$

and from (H.5)

$$\begin{aligned} z_{\textsf {Aff}}(\mathcal{U})&\ge \frac{r}{\sqrt{m}} \left( \frac{1}{3} + (m-1) \mu \right) \\&\ge \frac{r}{\sqrt{m}}\left( \frac{1}{3} - \lambda \sqrt{m}\frac{m-1}{r} \right) \\&\ge \frac{r}{\sqrt{m}}\left( \frac{1}{3} - \frac{1}{12} \frac{m-1}{r} \right) \ge \frac{r}{\sqrt{m}} \left( \frac{1}{3} - \frac{1}{6} \right) \; \; \text {for } m \ge 4 . \\&\ge \frac{\sqrt{m}}{12} \; \; [\text {Contradiction with } (\hbox {H.1})]\\ \end{aligned}$$

We conclude that $\alpha \ge \frac{1}{24 \sqrt{m}}$ and consequently

$$\begin{aligned} z_{\textsf {Aff}}(\mathcal{U}) \ge \varvec{c}^T \varvec{x} = \frac{\alpha m}{15} \ge \frac{\sqrt{m}}{360} = \varOmega ( \sqrt{m}). \end{aligned}$$

Hence,

$$\begin{aligned} z_{\textsf {Aff}}(\mathcal{U})= \varOmega ( \sqrt{m}) \cdot z_{\textsf {AR}}(\mathcal{U}). \end{aligned}$$

$\varvec{c}^T \varvec{x}= \varvec{c}^T \varvec{x}^*_{\textsf {Aff}}$ Moreover, for any optimal affine solution, the cost of the first-stage affine solution $\varvec{x}^*_{\textsf {Aff}}$ is $\varOmega ({\sqrt{m}})$ away from the optimal adjustable problem  (1.1), i.e. $\varvec{c}^T \varvec{x}^*_{\textsf {Aff}} =\varvec{c}^T \varvec{x} =\varOmega ( \sqrt{m})\cdot z_{\textsf {AR}}(\mathcal{U})$. $\square$

Proof of Theorem 7

Proof

Let us find the order of the left hand side ratio in inequality (5.3). We have,

$$\begin{aligned} \frac{\left( {\begin{array}{c}\sqrt{m}\\ m^{\epsilon }\end{array}}\right) \cdot \left( {\begin{array}{c}m-m^{\epsilon }\\ \sqrt{m}-m^{\epsilon }\end{array}}\right) }{\left( {\begin{array}{c}m\\ \sqrt{m}\end{array}}\right) }&= \frac{ (\sqrt{m})! \times (m-{m^{\epsilon }})! \times (m-\sqrt{m})! \times (\sqrt{m})! }{ ( \sqrt{m} - m^{\epsilon } )!\times ( m^{\epsilon } )! \times m! \times ( \sqrt{m} - m^{\epsilon } )! \times (m-\sqrt{m})! } \\&= \left( \frac{ (\sqrt{m})! }{ ( \sqrt{m} - m^{\epsilon } )! } \right) ^2 \cdot \frac{ (m-{m^{\epsilon }})! \ }{ ( m^{\epsilon } )! \times m! } .\\ \end{aligned}$$

By Stirling’s approximation, we have

$$\begin{aligned} \left( \sqrt{m}\right) !&= \varTheta \left( m^{\frac{1}{4}} \left( \frac{\sqrt{m}}{e} \right) ^{\sqrt{m}} \right) . \\ \left( \sqrt{m}-m^{\epsilon }\right) !&= \varTheta \left( ( \sqrt{m}-m^{\epsilon })^{\frac{1}{2}} \left( \frac{\sqrt{m}-m^{\epsilon }}{e} \right) ^{\sqrt{m}-m^{\epsilon }} \right) . \\ \left( m-m^{\epsilon }\right) !&= \varTheta \left( ( m-m^{\epsilon })^{\frac{1}{2}} \left( \frac{m-m^{\epsilon }}{e} \right) ^{m-m^{\epsilon }} \right) . \\ \left( m\right) !&= \varTheta \left( m^{\frac{1}{2}} \left( \frac{m}{e} \right) ^{m} \right) .\\ \left( m^{\epsilon }\right) !&= \varTheta \left( m^{\frac{1}{2} \epsilon }\left( \frac{m^{\epsilon }}{e} \right) ^{m^{\epsilon }} \right) . \end{aligned}$$

All together,

$$\begin{aligned} \frac{\left( {\begin{array}{c}\sqrt{m}\\ m^{\epsilon }\end{array}}\right) \cdot \left( {\begin{array}{c}m-m^{\epsilon }\\ \sqrt{m}-m^{\epsilon }\end{array}}\right) }{\left( {\begin{array}{c}m\\ \sqrt{m}\end{array}}\right) }= \varTheta \left( \frac{ \left( \sqrt{m} \right) ^{2 \sqrt{m}} \cdot \left( m-m^{\epsilon } \right) ^{ \left( m-m^{\epsilon }\right) } }{ m^{\frac{1}{2} \epsilon } \cdot \left( \sqrt{m}-m^{\epsilon } \right) ^{2 \left( \sqrt{m}-m^{\epsilon }\right) } \cdot m^m \cdot m^{ \epsilon m^{\epsilon }} } \right) . \end{aligned}$$

We have

$$\begin{aligned} \left( m-m^{\epsilon } \right) ^{ \left( m-m^{\epsilon }\right) } = \varTheta \left( m ^{ \left( m-m^{\epsilon }\right) } \cdot e^{-m^{\epsilon }+ \frac{m^{2\epsilon }}{m}} \right) , \end{aligned}$$

and

$$\begin{aligned} \left( \sqrt{m}-m^{\epsilon } \right) ^{ 2 \left( \sqrt{m}-m^{\epsilon }\right) } = \varTheta \left( \left( \sqrt{m} \right) ^{2 \left( \sqrt{m}-m^{\epsilon }\right) } \cdot e^{- 2m^{\epsilon }+ 2 \frac{m^{2\epsilon }}{\sqrt{m}}}\right) , \end{aligned}$$

WLOG, we can suppose that $\epsilon < \frac{1}{4}$, therefore

$$\begin{aligned} \frac{\left( {\begin{array}{c}\sqrt{m}\\ m^{\epsilon }\end{array}}\right) \cdot \left( {\begin{array}{c}m-m^{\epsilon }\\ \sqrt{m}-m^{\epsilon }\end{array}}\right) }{\left( {\begin{array}{c}m\\ \sqrt{m}\end{array}}\right) }&= \varTheta \left( \frac{ e^{ m^{\epsilon } - 2 \frac{m^{2\epsilon }}{\sqrt{m}} + \frac{m^{2\epsilon }}{m} } }{ m^{ \epsilon m^{\epsilon } +\frac{1}{2}\epsilon } } \right) \\&=\varTheta \left( \frac{ e^{ m^{\epsilon } } }{ m^{ \epsilon m^{\epsilon } +\frac{1}{2}\epsilon } } \right) . \\ \end{aligned}$$

We have,

$$\begin{aligned} \varTheta \left( \frac{ Q(m)e^{ m^{\epsilon } } }{ m^{ \epsilon m^{\epsilon } +\frac{1}{2}\epsilon }} \right) \ge 1, \end{aligned}$$

but the later inequality contradicts

$$\begin{aligned} \lim _{m\rightarrow \infty } \frac{ Q(m)e^{ m^{\epsilon } } }{ m^{ \epsilon m^{\epsilon } +\frac{1}{2}\epsilon }} = 0. \end{aligned}$$

$\square$

Domination for non-permutation invariant sets

Proposition 6

Suppose Algorithm 1 returns $\beta$ and $\varvec{v}$ for some uncertainty set $\mathcal{U}$. Then the set (6.3) is a dominating set for $\mathcal U$.

Proof

Suppose Algorithm 1 returns $\beta$ and $\varvec{v}$,then the inequality (2.4) is verified, namely,

$$\begin{aligned} \frac{1}{\beta } \sum _{i=1}^m \left( h_i -\beta v_i \right) ^{+} \le 1, \quad \forall \varvec{h} \in \mathcal{U}. \end{aligned}$$

Recall the dominating point (2.3)

$$\begin{aligned} \varvec{ \hat{h}}(\varvec{h}) = \beta \varvec{v} + ( \varvec{h} - \beta \varvec{v} )_+. \end{aligned}$$

We have

$$\begin{aligned} \varvec{ \hat{h}}(\varvec{h}) = \beta \left( \sum _{i=1}^m \frac{( h_i -\beta v_i )^{+} }{\beta } ( \varvec{e}_i + \varvec{v} ) + \underbrace{\left( 1- \sum _{i=1}^m \frac{( h_i -\beta v_i )^{+} }{\beta } \right) }_{ \ge 0} \varvec{v} \right) \in {\hat{\mathcal{U}}} \end{aligned}$$

where

$$\begin{aligned} {\hat{\mathcal{U}}} = \beta \cdot {\textsf {conv}} \left( \varvec{v}, \varvec{e}_1 + \varvec{v}, \ldots , \varvec{e}_m + \varvec{v} \right) \end{aligned}$$

Hence ${\hat{\mathcal{U}}}$ is a dominating set. $\square$

Domination for the generalized budget set

Proposition 7

Let consider

$$\begin{aligned} {\hat{\mathcal{U}}}= {\textsf {conv}} \left( \varvec{e}_1, \ldots , \varvec{e}_m, \frac{1}{m-1-2\theta } \varvec{e} \right) \end{aligned}$$

(K.1)

The set (K.1) dominates the uncertainty set (6.2).

Proof

Consider the uncertainty set (6.2) given by

$$\begin{aligned} \mathcal{U}= \left\{ \varvec{h} \in [0,1]^m \; \Bigg \vert \; \sum _{i=1}^m h_i \le 1 + \theta ( h_i +h_j) \quad \forall i \ne j \right\} \end{aligned}$$

and

$$\begin{aligned} {\hat{\mathcal{U}}}= {\textsf {conv}} \left( \varvec{e}_1, \ldots , \varvec{e}_m, \frac{1}{m-1-2\theta } \varvec{e} \right) . \end{aligned}$$

Note that in our setting we choose $\theta > \frac{m-1}{2}$. Take any $\varvec{h} \in \mathcal{U}$. Suppose WLOG that

$$\begin{aligned} h_1 \le h_2 \le \cdots \le h_m \end{aligned}$$

Hence, by definition of $\mathcal{U}$

$$\begin{aligned} \varvec{e}^T \varvec{h} \le 1+ \theta ( h_1+h_2) \end{aligned}$$

To prove that $\hat{ \mathcal U}$ dominates ${ \mathcal U}$, it is sufficient to find $\alpha _1, \alpha _2,\ldots ,\alpha _{m+1}$ non-negative reals with $\sum _{i=1}^{m+1} \alpha _i \le 1$ such that for all $i \in [m],$

$$\begin{aligned} \; h_i \le \alpha _i + \frac{1}{m-1-2\theta }\alpha _{m+1}. \end{aligned}$$

We choose $\alpha _{m+1} = (m-1-2\theta ) \cdot \frac{h_1+h_2}{2}$, $\alpha _1=h_1$ and for $i \ge 2$, $\alpha _i = h_i - \frac{h_1+h_2}{2}$. We can verify that

$$\begin{aligned} \alpha _1+ \frac{1}{m-1-2\theta } \alpha _{m+1} \ge \alpha _1 =h_1 \end{aligned}$$

and for $i \ge 2$,

$$\begin{aligned} \alpha _i + \frac{1}{m-1-2\theta } \alpha _{m+1} =h_i \end{aligned}$$

Moreover, $\alpha _{m+1} \ge 0$, $\alpha _1 \ge 0$ and for $i \ge 2$, $\alpha _i \ge 0$ since $h_1+h_2= min_{i\ne j} (h_i+h_j)$. Finally,

$$\begin{aligned} \sum _{i=1}^{m+1} \alpha _i&= \sum _{i=1}^{m} h_i - (m-1)\cdot \frac{h_1+h_2}{2}+ (m-1-2\theta ) \cdot \frac{h_1+h_2}{2}\\&\le 1+ \theta ( h_1+h_2) - (m-1)\cdot \frac{h_1+h_2}{2}+ (m-1-2\theta ) \cdot \frac{h_1+h_2}{2} =1. \end{aligned}$$

Note that the construction of this dominating set is slightly different from the general approach in Sect. 3 since we do not scale the unit vectors $\varvec{e}_i$ in ${\hat{\mathcal{U}}}$. $\square$