Stationarity conditions and constraint qualifications for mathematical programs with switching constraints

Abstract

In optimal control, switching structures demanding at most one control to be active at any time instance appear frequently. Discretizing such problems, a so-called mathematical program with switching constraints is obtained. Although these problems are related to other types of disjunctive programs like optimization problems with complementarity or vanishing constraints, their inherent structure makes a separate consideration necessary. Since standard constraint qualifications are likely to fail at the feasible points of switching-constrained optimization problems, stationarity notions which are weaker than the associated Karush–Kuhn–Tucker conditions need to be investigated in order to find applicable necessary optimality conditions. Furthermore, appropriately tailored constraint qualifications need to be formulated. In this paper, we introduce suitable notions of weak, Mordukhovich-, and strong stationarity for mathematical programs with switching constraints and present some associated constraint qualifications. Our findings are exploited to state necessary optimality conditions for (discretized) optimal control problems with switching constraints. Furthermore, we apply our results to optimization problems with either-or-constraints. First, a novel reformulation of such problems using switching constraints is presented. Second, the derived surrogate problem is exploited to obtain necessary optimality conditions for the original program.

1 Introduction

This paper is devoted to the study of optimization problems of the form

$$\begin{aligned} \begin{aligned} f(x)&\,\rightarrow \,\min&\\ g_i(x)&\,\le \,0&\qquad&i=1,\ldots ,m&\\ h_j(x)&\,=\,0&\qquad&j=1,\ldots ,p&\\ G_k(x)H_k(x)&\,=\,0&\qquad&k=1,\ldots ,l,&\end{aligned} \end{aligned}$$

(MPSC)

where all functions $f,g_1,\ldots ,g_m,h_1,\ldots ,h_p,G_1,\ldots ,G_l,H_1,\ldots ,H_l:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ are assumed to be continuously differentiable. For brevity of notation, $g:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^m$, $h:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^p$, $G:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^l$, and $H:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^l$ are the mappings which possess the component functions $g_i$ ($i=1,\ldots ,m$), $h_j$ ($j=1,\ldots ,p$), $G_k$ ($k=1,\ldots ,l$), and $H_k$ ($k=1,\ldots ,l$), respectively. Due to the appearence of the last l constraints which force $G_k(x)$ or $H_k(x)$ to be zero for all $k=1,\ldots ,l$ at any feasible point $x\in {\mathbb {R}}^n$ of (MPSC), we call it a mathematical program with switching constraints.

Recently, in the context of optimal control, the concept of control switching became very popular, see [7, 8, 19, 22, 28, 32, 36, 38, 40] and the references therein as well as Sect. 2. In the presence of multiple control functions, it demands that at most one of them is nonzero at any instance of the underlying domain. This way, control cost might be reduced while the practical realization of the optimal control strategy becomes easier to implement. On the other hand, switching structures naturally appear via modelling of certain real-world applications as presented in e.g. [19, 22, 36]. Such models can be interpreted as mixed-integer optimal control problems, see [22, 32] and the references therein. Disclaiming the use of discrete control variables, penality approaches for the solution of such problems are derived in Clason et al. [7, 8]. To the best of our knowledge, optimization problems with switching constraints have not yet been considered in the finite-dimensional framework. This, however, is desirable in order to establish a solid theory for the numerical treatment of switching constraints in optimal control.

Another possible application of switching structures in optimization theory appears in the context of either-or-constraints, see e.g. [9, Section 3.2.2] and [33, Section 5.3]. Let the functions $c^1,c^2:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ be continuously differentiable. In order to model that at least one of the constraints $c^1(x)\le 0$ or $c^2(x)\le 0$ shall hold, one generally introduces a binary variable y as well as some sufficiently large constant $M>0$ and states

$$\begin{aligned} \begin{aligned} c^1(x)&\,\le \,My\\ c^2(x)&\,\le \,M(1-y)\\ y&\,\in \,\{0,1\}. \end{aligned} \end{aligned}$$

Hence, if $y=0$ holds, $c^1(x)\le 0$ must be satisfied while $c^2(x)\le 0$ needs to hold for $y=1$. Clearly, the use of a binary variable induces a mixed-integer regime which makes the numerical treatment of this so-called either-or-constraint challenging. Furthermore, a reasonable value for M has to be computed a priori in order to apply this technique. Another possible way to model the described situation is given by

$$\begin{aligned} \min \{c^1(x);c^2(x)\}\,\le \,0. \end{aligned}$$

An obvious drawback of this constraint is its inherent nonsmoothness. However, introducing continuous variables $z^1,z^2\in {\mathbb {R}}$ and postulating

$$\begin{aligned} \begin{aligned} (c^1(x)-z^1)(c^2(x)-z^2)&\,=\,0\\ z^1,z^2&\,\le \,0, \end{aligned} \end{aligned}$$

this situation can be modeled in a different way exploiting the idea of switching systems. Since all appearing variables are now continuous while all involved functions are continuously differentiable, this system might be easier to handle than its mixed-integer or nonsmooth counterpart from above.

Problem (MPSC) is closely related to mathematical programs with complementarity constraints, MPCCs for short, see [29, 30], and mathematical programs with vanishing constraints, MPVCs for short, see [1, 24]. By definition, any MPCC is a switching-constrained optimization problem of special structure. Vice versa, it is easily seen that (MPSC) can be stated as an equivalent MPCC or MPVC. One possible (but, obviously, lightheaded) way in order to carry out this transformation is to square $G_1,\ldots ,G_k,H_1,\ldots ,H_k$ while adding superflous nonnegativity constraints on some of these square functions. It is easy to check that problem-tailored constraint qualifications for MPCCs, see [39], and MPVCs, see [24, 25], are likely to fail at all feasible points of the resulting problems, respectively. Moreover, the respective weak stationarity conditions, see [39, Definition 2.3] and [23, Definition 6.1.12], of the transformed problem do not comprise any information on the actual switching constraints. Similar problems may appear when more enhanced transformation techniques are used since some of the inherent structural properties of the switching constraints are annihilated during the transfer. Thus, a direct treatment of (MPSC) seems to be more promising.

One could write $\left\| G(x)\bullet H(x)\right\| _{0}=0$ in order to state the switching constraints in compact form. Here, $\bullet$ denotes the Hadamard product (i.e. the componentwise product of two vectors) while $\left\| \cdot \right\| _{0}:{\mathbb {R}}^l\rightarrow {\mathbb {N}}$ represents the mapping which counts the nonzero entries of a vector. That is why (MPSC) seems to be related to mathematical programs with cardinality constraints as well, see [5, 6]. Defining

$$\begin{aligned} {\mathcal {C}}:=\{(a,b)\in {\mathbb {R}}^2\,|\,ab=0\} \end{aligned}$$

(1)

which is the union of two convex polyhedrons, one can represent (MPSC) in the form

$$\begin{aligned} \begin{aligned} f(x)&\,\rightarrow \,\min&\\ g_i(x)&\,\in \,{\mathbb {R}}^0_-&\qquad&i=1,\ldots ,m&\\ h_j(x)&\,\in \,\{0\}&\qquad&j=1,\ldots ,p&\\ (G_k(x),H_k(x))&\,\in \,{\mathcal {C}}&\qquad&k=1,\ldots ,l.&\end{aligned} \end{aligned}$$

(2)

Here, ${\mathbb {R}}^0_-\subset {\mathbb {R}}$ denotes the set of all nonpositive reals. Consequently, (MPSC) is an instance of disjunctive programming as well, see e.g. [4, 14, 15].

As it turns out, standard constraint qualifications like MFCQ, the so-called Mangasarian–Fromovitz constraint qualification, and, thus, LICQ, the linear independence constraint qualification, do not hold at the feasible points of (MPSC) in several situations. Thus, the associated Karush–Kuhn–Tucker (KKT for short) conditions do not provide a necessary optimality criterion in general. This phenomenon is well known from the rich theory on MPCCs and MPVCs as well. In order to overcome this shortcoming, applicable stationarity notions for (MPSC) and compatible constraint qualifications need to be introduced. This is the central purpose of this paper.

The remaining part of the article is structured as follows: in Sect. 2, we motivate the study of (MPSC) by means of an optimal control problem with switching constraints. Afterwards, we recall some basics from variational analysis and nonlinear programming in Sect. 3. In Sect. 4, we first show that reasonable constraint qualifications from nonlinear programming may easily fail to hold at the feasible points of (MPSC). Thus, we study weaker stationarity notions which are suited for the investigation of switching constraints. Particularly, we derive notions of weak, Mordukhovich-, and strong stationarity. Furthermore, MPSC-tailored versions of MFCQ and LICQ are introduced. Section 5 is dedicated to the study of MPSC-tailored versions of the Abadie and Guignard constraint qualification which are some of the weakest regularity conditions from nonlinear programming. Our findings are applied to state necessary optimality conditions for (discretized) optimal control problems with switching constraints in Sect. 6. In Sect. 7, we study a switching-constrained reformulation of mathematical programs with either-or-constraints. First, we interrelate the local and global minimizers of the original program and its surrogate. Afterwards, the developed theory on switching-constrained programs is used to derive necessary optimality conditions for the either-or-constrained optimization problem. Some final comments on the paper’s results and aspects of future research are presented in Sect. 8.

2 A motivating example

For some bounded domain $\varOmega \subset {\mathbb {R}}^d$ with sufficiently smooth boundary $\varGamma$ and some time interval $I:=(0,T)$, we consider the optimal control of a non-stationary heat source with switching constraints on the controls. More precisely, two control functions $u,v:I\rightarrow {\mathbb {R}}$ are used to model whether heating/cooling elements $\varOmega _u,\varOmega _v\subset \varOmega$ are active or not while at most one heating/cooling element is allowed to be active at any time instance from I. Moreover, an initial heat distribution $y_0\in L^2(\varOmega )$ shall be given. The overall aim of optimization is to find controls and the resulting state function ${\bar{y}}:I\times \varOmega \rightarrow {\mathbb {R}}$, such that the terminal heat distribution ${\bar{y}}(T,\cdot ):\varOmega \rightarrow {\mathbb {R}}$ fits a desirable heat distribution $y_\text{ d }\in L^2(\varOmega )$ as best as possible while the overall control cost has to be minimized. In order to guarantee the existence of optimal solutions, $L^2$-regularity of control functions is in general not enough, see [8, Section 2]. Instead, we choose the Sobolev space $H^1(I)$ for the control space. A suitable space for the state functions is given by $W(I;H^1(\varOmega ))$. The latter set contains all functions from $L^2(I;H^1(\varOmega ))$ which possess a weak derivative in $L^2(I;H^1(\varOmega )^\star )$, see [37, Section 3] for a precise definition of these function spaces.

For brevity, let $Q:=I\times \varOmega$ be the time-space-cylinder and let $\varSigma :=I\times \varGamma$ be its lateral boundary. A potential formulation of the problem described above is given as stated below:

(3)

Here, $\sigma _u,\sigma _v>0$ are regularization parameters, $\varDelta _\omega =\sum _{i=1}^d\partial ^2_{\omega _i\omega _i}$ is the Laplacian w.r.t. space variables, $\mathbf {{\mathbf {n}}}:\varGamma \rightarrow {\mathbb {R}}^d$ denotes the unit vector pointing out of $\varOmega$, and $\nabla _\omega$ represents the weak gradient w.r.t. space variables. Furthermore, for any measurable set $A\subset \varOmega$, $\chi _A\in L^\infty (\varOmega )$ is the characteristic function of A which equals 1 on A and vanishes otherwise. Noting that the embedding $H^1(I)\hookrightarrow L^2(I)$ is continuous, the control-to-state-operator, which assigns to any pair of controls $(u,v)\in H^1(I)\times H^1(I)$ the (uniquely determined) weak solution $y\in W(I;H^1(\varOmega ))$ of the state equation, is affine and continuous, see [37, Section 3.6.4]. Due to the demanded Sobolev-regularity of the control functions, the set of feasible controls of (3) is weakly sequentially closed. Now, it is possible to exploit standard arguments in order to see that (3) possesses an optimal solution.

In practice, the control functions often need to be bounded in order to ensure their technical feasibility. Thus, it is reasonable to state additional control constraints of the form

$$\begin{aligned} \begin{aligned} \underline{u}(t)&\,\le \,u(t)\,\le \,\overline{u}(t)&\qquad&\text {a.e. on}\; I&\\ \underline{v}(t)&\,\le \,v(t)\,\le \,\overline{v}(t)&\qquad&\text {a.e. on}\; I.&\end{aligned} \end{aligned}$$

(4)

Here, the functions $\underline{u},\overline{u},\underline{v},\overline{v}\in H^1(I)$ shall satisfy the following requirements:

$$\begin{aligned}\begin{aligned} \underline{u}(t)&\,<\,0\,<\,\overline{u}(t)&\qquad&\text {everywhere on}\; I&\\ \underline{v}(t)&\,<\,0\,<\,\overline{v}(t)&\qquad&\text {everywhere on}\; I.&\end{aligned}\end{aligned}$$

It is easily seen that in the presence of the additional control constraints (4), (3) still possesses an optimal solution. Similarly, one could consider the situation where only upper or only lower bounds on u or v are postulated, or the setting where only u (or v, respectively) has to satisfy additional control constraints.

Using a tessellation of $\varOmega$ as well as a suitable finite element space, (3) can be transferred into an optimal control problem of ordinary differential equations. Afterwards, one can fix a partition of the interval I and use e.g. the implicit Euler scheme in order to discretize (3) completely. For simplicity, we denote the variables of the resulting finite-dimensional optimal control problem with switching constraints by $y\in {\mathbb {R}}^n$ and $u,v\in {\mathbb {R}}^l$ again. In abstract form, this program looks as stated below:

$$\begin{aligned} \begin{aligned} \tfrac{1}{2}\left| {\mathbf {Q}}{{y}}-{\mathbf {y}}_\text{ d }\right| _{2}^2+\tfrac{\sigma _u}{2}\left| {\mathbf {M}} u\right| _{2}^2+\tfrac{\sigma _v}{2}\left| {\mathbf {M}} v\right| _{2}^2&\,\rightarrow \,\min \limits _{y,u,v}&\\ {\mathbf {A}} y-{\mathbf {B}}{{u}}-{\mathbf {C}}{{v}}&\,=\,{\mathbf {d}}&\\ u_kv_k&\,=\,0&\qquad&k=1,\ldots ,l&\\ \underline{{\mathbf {u}}}_k\,\le \,u_k&\,\le \,\overline{{\mathbf {u}}}_k&\qquad&k=1,\ldots ,l&\\ \underline{{\mathbf {v}}}_k\,\le \,v_k&\,\le \,\overline{{\mathbf {v}}}_k&\qquad&k=1,\ldots ,l.&\end{aligned} \end{aligned}$$

(OCSC)

Here, we already included the discretized control constraints associated with (4). It will be assumed that the data satisfies

$$\begin{aligned} \begin{aligned} \underline{{\mathbf {u}}}_k&\,<\,0\,<\,\overline{{\mathbf {u}}}_k&\qquad&k=1,\ldots ,l&\\ \underline{{\mathbf {v}}}_k&\,<\,0\,<\,\overline{{\mathbf {v}}}_k&\qquad&k=1,\ldots ,l.&\end{aligned} \end{aligned}$$

(5)

Due to the properties of the control-to-state-operator associated with the constraining partial differential equation in (3), we can assume that the matrix ${\mathbf {A}}\in {\mathbb {R}}^{n\times n}$ is regular. Above, bold matrices and vectors indicate that these objects result from the original data of (3) as well as the precise choice of the finite element space and the time discretization.

In this paper, we will derive necessary optimality conditions for (OCSC). It is shown that local minimizers of (OCSC) satisfy strong stationarity-type conditions, see Theorem 6.1.

3 Preliminaries

In this section, we provide the necessary background for the investigation of (MPSC). Therefore, we first review some essentials from variational analysis, see e.g. [31], before we recall some constraint qualifications from nonlinear programming, see e.g. [2].

For some nonempty set $A\subset {\mathbb {R}}^n$, we call

$$\begin{aligned} A^\circ :=\left\{ y\in {\mathbb {R}}^n\,|\,\forall x\in A:\,x\cdot y\le 0\right\} \end{aligned}$$

the polar cone of A. Here, $x\cdot y$ denotes the Euclidean inner product of the two vectors $x,y\in {\mathbb {R}}^n$. It is well known that $A^\circ$ is a nonempty, closed, convex cone. If $C\subset {\mathbb {R}}^n$ is a cone, then $C^{\circ \circ }={\overline{{\mathrm{conv}}}}C$ is valid. This relation is called bipolar theorem in the literature. Supposing that $U,V\subset {\mathbb {R}}^n$ are nonempty sets, we obtain the polarization rule $(U\cup V)^\circ =U^\circ \cap V^\circ$ directly from the definition. For polyhedral cones, the following duality relation is a straightforward consequence of e.g. Motzkin’s lemma.

Lemma 3.1

For matrices ${\mathbf {C}}\in {\mathbb {R}}^{m\times n}$ and ${\mathbf {D}}\in {\mathbb {R}}^{p\times n}$, let ${\mathcal {K}}\subset {\mathbb {R}}^n$ be the closed, convex cone defined below:

$$\begin{aligned} {\mathcal {K}}:=\left\{ d\in {\mathbb {R}}^n\,\big |\,{\mathbf {C}}{{d}}\le 0,\,{\mathbf {D}}{{d}}=0\right\} . \end{aligned}$$

Then, we have

$$\begin{aligned} {\mathcal {K}}^\circ =\left\{ {\mathbf {C}}^\top \lambda +{\mathbf {D}}^\top \rho \,\big |\,\lambda \in {\mathbb {R}}^m,\,\lambda \ge 0,\,\rho \in {\mathbb {R}}^p\right\} . \end{aligned}$$

Now, suppose that $A\subset {\mathbb {R}}^n$ is closed and choose ${\bar{x}}\in A$ arbitrarily. The tangent (or Bouligand) cone, the Fréchet (or regular) normal cone, and the limiting (or basic, Mordukhovich) normal cone to A at ${\bar{x}}$ are defined as stated below:

$$\begin{aligned} \begin{aligned} {\mathcal {T}}_A({\bar{x}})&:=\left\{ d\in {\mathbb {R}}^n\,\big | \begin{aligned}&\exists \{d_s\}_{s\in {\mathbb {N}}}\subset {\mathbb {R}}^n\,\exists \{t_s\}_{s\in {\mathbb {N}}}\subset {\mathbb {R}}_{+}:\\&\qquad d_s\rightarrow d,\,t_s\rightarrow 0,\,{\bar{x}}+t_sd_s\in A\,\forall s\in {\mathbb {N}}\end{aligned}\right\} ,\\ \widehat{{\mathcal {N}}}_A({\bar{x}})&:={\mathcal {T}}_A({\bar{x}})^\circ ,\\ {\mathcal {N}}_A({\bar{x}})&:=\left\{ \eta \in {\mathbb {R}}^n\,\big | \begin{aligned}&\exists \{x_s\}_{s\in {\mathbb {N}}}\subset A\,\exists \{\eta _s\}_{s\in {\mathbb {N}}}\subset {\mathbb {R}}^n:\\&\qquad \,x_s\rightarrow {\bar{x}},\,\eta _s\rightarrow \eta ,\,\eta _s\in \widehat{{\mathcal {N}}}_A(x_s)\,\forall s\in {\mathbb {N}}\end{aligned}\right\} . \end{aligned} \end{aligned}$$

Note that ${\mathbb {R}}_+\subset {\mathbb {R}}$ denotes the set of all positive real numbers. All these cones are closed. Additionally, the Fréchet normal cone is a convex subset of the limiting normal cone. Note that the Fréchet and the limiting normal cone coincide with the normal cone in the sense of convex analysis provided A is a convex set.

For later use, we compute the Fréchet and limiting nomal cones to the set ${\mathcal {C}}$ defined in (1). The proof of the subsequent result directly follows by definition of these variational objects.

Lemma 3.2

Let $(a,b)\in {\mathcal {C}}$ be arbitrarily chosen where ${\mathcal {C}}$ is the set defined in (1). Then, the following formulas are valid:

$$\begin{aligned}\begin{aligned} \widehat{{\mathcal {N}}}_{\mathcal {C}}(a,b)&={\left\{ \begin{array}{ll} {\mathbb {R}}\times \{0\} &{}\text {if }a=0\,\wedge \,b\ne 0,\\ \{0\}\times {\mathbb {R}}&{}\text {if }a\ne 0\,\wedge \,b=0,\\ \{(0,0)\} &{}\text {if }a=0\,\wedge \,b=0, \end{array}\right. } \\ {\mathcal {N}}_{\mathcal {C}}(a,b)&={\left\{ \begin{array}{ll} {\mathbb {R}}\times \{0\} &{}\quad \text {if }\;a=0\,\wedge \,b\ne 0,\\ \{0\}\times {\mathbb {R}}&{}\quad \text {if }\;a\ne 0\,\wedge \,b=0,\\ {\mathcal {C}} &{}\quad \text {if }\;a=0\,\wedge \,b=0. \end{array}\right. } \end{aligned} \end{aligned}$$

Let us consider the standard nonlinear program

$$\begin{aligned} \begin{aligned} {\tilde{f}}(x)&\,\rightarrow \,\min&\\ {\tilde{g}}_i(x)&\,\le \,0&\qquad&i=1,\ldots ,m&\\ {\tilde{h}}_j(x)&\,=\,0&\qquad&j=1,\ldots ,p&\end{aligned} \end{aligned}$$

(P1)

for continuously differentiable functions ${\tilde{f}},{\tilde{g}}_1,\ldots ,{\tilde{g}}_m,{\tilde{h}}_1,\ldots ,{\tilde{h}}_p:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$. Let $X\subset {\mathbb {R}}^n$ be the feasible set of (P1) and choose ${\bar{x}}\in X$ arbitrarily. Then, the linearization cone to X at ${\bar{x}}$ is defined as follows:

$$\begin{aligned} {\mathcal {L}}_X({\bar{x}}):=\left\{ d\in {\mathbb {R}}^n\,\big | \begin{aligned} \nabla {\tilde{g}}_i({\bar{x}})\cdot d&\,\le \,0&i\in I^{{\tilde{g}}}({\bar{x}})\\ \nabla {\tilde{h}}_j({\bar{x}})\cdot d&\,=\,0&j\in I^{{\tilde{h}}} \end{aligned} \right\} . \end{aligned}$$

Here, we used

$$\begin{aligned} \begin{aligned} I^{{\tilde{g}}}({\bar{x}})&:=\{i\in \{1,\ldots ,m\}\,|\,{\tilde{g}}_i({\bar{x}})=0\},\\ I^{{\tilde{h}}}&:=\{1,\ldots ,p\}. \end{aligned} \end{aligned}$$

Below, we recall some constraint qualifications which are applicable to (P1).

Definition 3.1

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a feasible point of (P1). Then, ${\bar{x}}$ is said to satisfy

• 1. the linear independence constraint qualification, LICQ for short, provided the following condition is valid:

  $$\begin{aligned} 0=\sum \limits _{i\in I^{{\tilde{g}}}({\bar{x}})}\lambda _i\nabla {\tilde{g}}_i({\bar{x}}) +\sum \limits _{j\in I^{{\tilde{h}}}}\rho _j\nabla {\tilde{h}}_j({\bar{x}})\;\Longrightarrow \;\lambda =0,\,\rho =0, \end{aligned}$$

• 2. the Mangasarian–Fromovitz constraint qualification, MFCQ for short, provided the following condition is valid:

  $$\begin{aligned} \left. \begin{aligned}&0=\sum \limits _{i\in I^{{\tilde{g}}}({\bar{x}})}\lambda _i\nabla {\tilde{g}}_i({\bar{x}}) +\sum \limits _{j\in I^{{\tilde{h}}}}\rho _j\nabla {\tilde{h}}_j({\bar{x}}),\\&\forall i\in I^{{\tilde{g}}}({\bar{x}}):\,\lambda _i\ge 0 \end{aligned}\right\} \;\Longrightarrow \;\lambda =0,\,\rho =0, \end{aligned}$$

• 3. the Abadie constraint qualification, ACQ for short, if ${\mathcal {T}}_X({\bar{x}})={\mathcal {L}}_X({\bar{x}})$ holds, and

• 4. the Guignard constraint qualification, GCQ for short, if $\widehat{{\mathcal {N}}}_X({\bar{x}})={\mathcal {L}}_X({\bar{x}})^\circ$ holds.

Note that in the above definition, we stated the dual representations of LICQ and MFCQ. Primal versions of these constraint qualifications can be found in the literature and are easily derived via Motzkin’s lemma. It is well known from the literature, see e.g. [2], that the following relations hold between the aforementioned constraint qualifications:

$$\begin{aligned} \text {LICQ}\;\Longrightarrow \;\text {MFCQ}\;\Longrightarrow \;\text {ACQ}\;\Longrightarrow \;\text {GCQ}. \end{aligned}$$

Since the validity of GCQ at a local minimizer ${\bar{x}}\in {\mathbb {R}}^n$ of (P1) implies that the KKT conditions

$$\begin{aligned} \begin{aligned}&0=\nabla {\tilde{f}}({\bar{x}}) +\sum \limits _{i\in I^{{\tilde{g}}}({\bar{x}})}\lambda _i\nabla {\tilde{g}}_i({\bar{x}}) +\sum \limits _{j\in I^{{\tilde{h}}}}\rho _j\nabla {\tilde{h}}_j({\bar{x}}),\\&\forall i\in I^{{\tilde{g}}}({\bar{x}}):\,\lambda _i\ge 0 \end{aligned} \end{aligned}$$

provide a necessary criterion for optimality, the same holds true for the stronger constraint qualifications LICQ, MFCQ, and ACQ, respectively.

Finally, we take a short look at the more abstract nonlinear program

$$\begin{aligned} \begin{aligned} {\tilde{f}}(x)&\,\rightarrow \,\min \\ F(x)&\,\in \,D \end{aligned} \end{aligned}$$

(P2)

where $F:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^q$ is continuously differentiable while $D\subset {\mathbb {R}}^q$ is a nonempty, closed set. Clearly, (P1) is a specific instance of (P2) for $F:=({\tilde{g}},{\tilde{h}})$, $q:=m+p$, and $D:=\{z\in {\mathbb {R}}^m\,|\,z\le 0\}\times \{0\}$. A feasible point ${\bar{x}}\in {\mathbb {R}}^n$ of (P2) is said to satisfy the no nonzero abnormal multiplier constraint qualification, NNAMCQ for short, provided the following condition is valid:

$$\begin{aligned} \left. \begin{aligned}&0=\nabla F({\bar{x}})^\top \eta ,\\&\eta \in {\mathcal {N}}_D(F({\bar{x}})) \end{aligned}\right\} \;\Longrightarrow \;\eta =0. \end{aligned}$$

In [14], this condition is referred to as generalized Mangasarian–Fromovitz constraint qualification since it equals MFCQ when applied to (P1). If NNAMCQ is valid at a locally optimal solution ${\bar{x}}\in {\mathbb {R}}^n$ of (P2), then the following necessary optimality condition holds:

$$\begin{aligned} \begin{aligned}&0=\nabla {\tilde{f}}({\bar{x}})+\nabla F({\bar{x}})^\top \eta ,\\&\eta \in {\mathcal {N}}_D(F({\bar{x}})), \end{aligned} \end{aligned}$$

see e.g. [31, Section 6.D]. Due to the appearence of the limiting normal cone, this condition is called the system of Mordukhovich–stationarity, M-stationarity for short. We note that M-stationarity of local minimizers associated with (P2) can be guaranteed under much weaker conditions like metric subregularity of the induced feasibility map $x\rightrightarrows \{F(x)\}-D$ at $({\bar{x}},0)$ which is implied by validity of NNAMCQ at ${\bar{x}}$, see [17, Section 2] for details.

If we replace the limiting normal cone ${\mathcal {N}}_D(F({\bar{x}}))$ by the smaller Fréchet normal cone $\widehat{{\mathcal {N}}}_D(F({\bar{x}}))$, then the system of strong stationarity, S-stationarity for short, is obtained. Cleary, S-stationarity is a more restrictive condition than M-stationarity in general. For (P1), however, the systems of M- and S-stationarity are both equivalent to the KKT conditions. It is well known from the literature, see e.g. [31, Exercise 6.7, Theorem 6.12], that whenever $\nabla F({\bar{x}})$ possesses full row rank q at a locally optimal solution ${\bar{x}}\in {\mathbb {R}}^n$ of (P2), then the S-stationarity conditions are satisfied. A slightly weaker but far more technical constraint qualification implying local minimizers of (P2) to be S-stationary is provided in [16, Theorem 4].

In the case where D is the union of finitely many polyhedral sets, we call (P2) a disjunctive program. We note that under a problem-tailored version of GCQ called generalized Guignard constraint qualification, local minimizers of disjunctive programs are M-stationary, see [14, Theorem 7]. There exist other reasonable stationarity notions which may serve as necessary optimality conditions for disjunctive programs, see [3, 4, 15].

4 MPSC-tailored stationarity conditions

In this section, we derive three different stationarity notions for (MPSC) which are not stronger than the associated KKT conditions which will be stated later on as well. Therefore, we introduce some index sets which depend on a feasible point ${\bar{x}}\in {\mathbb {R}}^n$ of (MPSC) first:

$$\begin{aligned} \begin{aligned} I^G({\bar{x}})&:=\{k\in \{1,\ldots ,l\}\,|\,G_k({\bar{x}})=0\,\wedge \,H_k({\bar{x}})\ne 0\},\\ I^H({\bar{x}})&:=\{k\in \{1,\ldots ,l\}\,|\,G_k({\bar{x}})\ne 0\,\wedge \,H_k({\bar{x}})=0\},\\ I^{GH}({\bar{x}})&:=\{k\in \{1,\ldots ,l\}\,|\,G_k({\bar{x}})=0\,\wedge \,H_k({\bar{x}})=0\}. \end{aligned} \end{aligned}$$

Note that $\left\{ I^G({\bar{x}}),I^H({\bar{x}}),I^{GH}({\bar{x}})\right\}$ is a disjoint partition of $\{1,\ldots ,l\}$. We will also exploit the set $I^g({\bar{x}})$ of all indices associated with active inequality constraints as well as $I^h:=\{1,\ldots ,p\}$, see Sect. 3.

The necessity of considering weaker stationarity notions than the KKT conditions is motivated by the following observation.

Lemma 4.1

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a feasible point of (MPSC) where $I^{GH}({\bar{x}})\ne \varnothing$ is valid. Then, MFCQ and, thus, LICQ are violated at ${\bar{x}}$.

Proof

For the proof, we define the function $K_k:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ by

$$\begin{aligned} \forall x\in {\mathbb {R}}^n:\quad K_k(x):=G_k(x)H_k(x) \end{aligned}$$

for any $k\in \{1,\ldots ,l\}$. Note that its gradient at ${\bar{x}}$ is given by

$$\begin{aligned} \nabla K_k({\bar{x}})=H_k({\bar{x}})\nabla G_k({\bar{x}})+G_k({\bar{x}})\nabla H_k({\bar{x}}) ={\left\{ \begin{array}{ll} H_k({\bar{x}})\nabla G_k({\bar{x}})&{}\quad \text {if }k\in I^G({\bar{x}}),\\ G_k({\bar{x}})\nabla H_k({\bar{x}})&{}\quad \text {if }k\in I^H({\bar{x}}),\\ 0&{}\quad \text {if }k\in I^{GH}({\bar{x}}). \end{array}\right. } \end{aligned}$$

Thus, if $I^{GH}({\bar{x}})\ne \varnothing$ holds true, then at least one of the gradients associated with the equality constraints in (MPSC) is zero. Consequently, MFCQ and, thus, LICQ cannot hold at the point ${\bar{x}}$.$\square$

In the setting $I^{GH}({\bar{x}})=\varnothing$, the standard constraint qualifications MFCQ and LICQ are reasonably applicable to (MPSC), i.e. the KKT conditions may turn out to be necessary optimality conditions in this situation. Clearly, the KKT conditions provide a necessary optimality criterion under the weaker regularity condition GCQ as well, see Sect. 3. However, the latter might be more difficult to check than MFCQ or LICQ.

Corollary 4.1

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a local minimizer of (MPSC) where GCQ is valid. Then, the following system possesses a solution:

$$\begin{aligned} \begin{aligned}&0=\nabla f({\bar{x}}) +\sum \limits _{i\in I^g({\bar{x}})}\lambda _i\nabla g_i({\bar{x}}) +\sum \limits _{j\in I^h}\rho _j\nabla h_j({\bar{x}})\\&\qquad +\,\sum \limits _{k\in I^G({\bar{x}})}\mu _k\nabla G_k({\bar{x}}) +\sum \limits _{k\in I^H({\bar{x}})}\nu _k\nabla H_k({\bar{x}}),\\&\forall i\in I^g({\bar{x}}):\,\lambda _i\ge 0. \end{aligned} \end{aligned}$$

(6)

Proof

Exploiting the definition of $K_1,\ldots ,K_l:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ and the computation of their respective derivatives in the proof of Lemma 4.1, we find multipliers $\lambda _i$ ($i\in I^g({\bar{x}})$), $\rho _j$ ($j\in I^h$), and $\xi _k$ ($k=1,\ldots ,l$) which solve the KKT system of (MPSC) which is given as stated below:

$$\begin{aligned} \begin{aligned}&0=\nabla f({\bar{x}}) +\sum \limits _{i\in I^g({\bar{x}})}\lambda _i\nabla g_i({\bar{x}}) +\sum \limits _{j\in I^h}\rho _j\nabla h_j({\bar{x}})\\&\qquad +\,\sum \limits _{k\in I^G({\bar{x}})}\xi _kH_k({\bar{x}})\nabla G_k({\bar{x}}) +\sum \limits _{k\in I^H({\bar{x}})}\xi _kG_k({\bar{x}})\nabla H_k({\bar{x}}),\\&\forall i\in I^g({\bar{x}}):\,\lambda _i\ge 0. \end{aligned} \end{aligned}$$

(7)

Thus, we define $\mu _k:=\xi _kH_k({\bar{x}})$ ($k\in I^G({\bar{x}})$) and $\nu _k:=\xi _kG_k({\bar{x}})$ ($k\in I^H({\bar{x}})$) in order to show the claim.$\square$

Remark 4.1

The proof of Corollary 4.1 shows that any KKT point of (MPSC) solves the system (6). However, the converse statement is also true. Namely, if ${\bar{x}}\in {\mathbb {R}}^n$ is a feasible point of (MPSC) such that there exist multipliers $\lambda _i$ ($i\in I^g({\bar{x}})$), $\rho _j$ ($j\in I^h$), $\mu _k$ ($k\in I^G({\bar{x}})$), and $\nu _k$ ($k\in I^H({\bar{x}})$) which solve the system (6), then setting

$$\begin{aligned} \forall k\in \{1,\ldots ,l\}:\quad \xi _k:={\left\{ \begin{array}{ll} \mu _k/H_k({\bar{x}}) &{}\quad \text {if }k\in I^G({\bar{x}}),\\ \nu _k/G_k({\bar{x}}) &{}\quad \text {if }k\in I^H({\bar{x}}),\\ 0 &{} \quad \text {if }k\in I^{GH}({\bar{x}}), \end{array}\right. } \end{aligned}$$

we easily see that (7) possesses a solution, i.e. ${\bar{x}}$ is a KKT point of (MPSC).

In the situation where $I^{GH}({\bar{x}})$ is nonempty, the reasoning from Corollary 4.1 is not longer possible. Thus, we may have to rely on weaker stationarity notions than the KKT conditions of (MPSC). In order to find such stationarity systems, we apply the concepts of M- and S-stationarity mentioned in Sect. 3 to (2). Therefore, Lemma 3.2 is helpful. We also state a natural definition of so-called weak stationarity.

Definition 4.1

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a feasible point of (MPSC). Then, ${\bar{x}}$ is called

• 1. weakly stationary, W-stationary for short, if there exist multipliers which solve the following system:

  $$\begin{aligned} \begin{aligned}&0=\nabla f({\bar{x}}) +\sum \limits _{i\in I^g({\bar{x}})}\lambda _i\nabla g_i({\bar{x}}) +\sum \limits _{j\in I^h}\rho _j\nabla h_j({\bar{x}})\\&\qquad +\,\sum \limits _{k=1}^l\bigl [\mu _k\nabla G_k({\bar{x}}) +\nu _k\nabla H_k({\bar{x}})\bigr ],\\&\forall i\in I^g({\bar{x}}):\,\lambda _i\ge 0,\\&\forall k\in I^H({\bar{x}}):\,\mu _k=0,\\&\forall k\in I^G({\bar{x}}):\,\nu _k=0, \end{aligned} \end{aligned}$$

  (8)

• 2. Mordukhovich–stationary, M-stationary for short, if there exist multipliers which satisfy the conditions (8) and

  $$\begin{aligned} \forall k\in I^{GH}({\bar{x}}):\,\mu _k\nu _k=0, \end{aligned}$$

• 3. strongly stationary, S-stationary for short, if there exist multipliers which satisfy the conditions (8) and

  $$\begin{aligned} \forall k\in I^{GH}({\bar{x}}):\,\mu _k=0\,\wedge \,\nu _k=0. \end{aligned}$$

By definition, we easily see that the following relations hold between the introduced stationarity notions:

$$\begin{aligned} \text {S-stationarity}\;\Longrightarrow \;\text {M-stationarity}\;\Longrightarrow \;\text {W-stationarity.} \end{aligned}$$

Furthermore, consulting Remark 4.1, we obtain that the S-stationarity conditions of (MPSC) equal its KKT conditions in a certain sense. This behavior of switching-constrained problems is similar to MPCCs and MPVCs. Finally, it has to be mentioned that the W-stationarity conditions of (MPSC) at one of its feasible points ${\bar{x}}\in {\mathbb {R}}^n$ are equivalent to the KKT conditions of the subsequently stated tightened nonlinear problem at ${\bar{x}}$:

$$\begin{aligned} \begin{aligned} f(x)&\,\rightarrow \,\min&\\ g_i(x)&\,\le \,0&\qquad&i=1,\ldots ,m&\\ h_j(x)&\,=\,0&\qquad&j=1,\ldots ,p&\\ G_k(x)&\,=\,0&\qquad&k\in I^G({\bar{x}})\cup I^{GH}({\bar{x}})&\\ H_k(x)&\,=\,0&\qquad&k\in I^H({\bar{x}})\cup I^{GH}({\bar{x}}).&\end{aligned} \end{aligned}$$

(TNLP)

Note that the feasible set of (TNLP) is a subset of the feasible set of (MPSC).

Let ${\mathcal {P}}(I^{GH}({\bar{x}}))$ be the set of all (disjoint) bipartitions of $I^{GH}({\bar{x}})$. For fixed $(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))$, we define

Again, its feasible set is included in the feasible set of (MPSC). Note that locally around ${\bar{x}}$, the union of all the feasible sets of (NLP$(\beta _1,\beta _2)$) over $(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))$ corresponds to the feasible set of (MPSC). This allows to apply a so-called local decomposition approach in order to derive weak constraint qualifications for (MPSC) in Sect. 5.

In the following lemma, we show a close relationship between the M-stationary points of (MPSC) and the KKT points of (NLP$(\beta _1,\beta _2)$).

Lemma 4.2

A feasible point ${\bar{x}}\in {\mathbb {R}}^n$ of (MPSC) is M-stationary if and only if there exists a partition $(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))$ such that ${\bar{x}}$ is a KKT point of (NLP$(\beta _1,\beta _2)$).

Proof

“$\Longrightarrow$” Let ${\bar{x}}$ be an M-stationary point of (MPSC) and let $(\lambda ,\rho ,\mu ,\nu )$ be the vector of associated multipliers which solve the system of M-stationarity. Then, the sets

$$\begin{aligned} \beta _1:=\left\{ k\in I^{GH}({\bar{x}})\,\big |\,\mu _k\ne 0\right\} , \qquad \beta _2:=\left\{ k\in I^{GH}({\bar{x}})\,\big |\,\mu _k=0\right\} \end{aligned}$$

are well-defined and $(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))$ holds true. By definition of M-stationarity, we have

$$\begin{aligned} \begin{aligned}&0=\nabla f({\bar{x}})+\sum \limits _{i\in I^g({\bar{x}})}\lambda _i\nabla g_i({\bar{x}})+\sum \limits _{j\in I^h}\rho _j\nabla h_j({\bar{x}})\\&\qquad +\,\sum \limits _{k\in I^G({\bar{x}})\cup \beta _1}\mu _k\nabla G_k({\bar{x}}) +\sum \limits _{k\in I^H({\bar{x}})\cup \beta _2}\nu _k\nabla H_k({\bar{x}}),\\&\forall i\in I^g({\bar{x}}):\,\lambda _i\ge 0, \end{aligned} \end{aligned}$$

i.e. ${\bar{x}}$ is a KKT point of (NLP$(\beta _1,\beta _2)$).

“$\Longleftarrow$” Let ${\bar{x}}$ be a KKT point of (NLP$(\beta _1,\beta _2)$) for $(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))$. Then, we find multipliers $\lambda _i$ ($i\in I^g({\bar{x}})$), $\rho _j$ ($j\in I^h$), $\eta _k$ ($k\in I^G({\bar{x}})\cup \beta _1$), as well as $\theta _k$ ($k\in I^H({\bar{x}})\cup \beta _2$) which satisfy

$$\begin{aligned} \begin{aligned}&0=\nabla f({\bar{x}})+\sum \limits _{i\in I^g({\bar{x}})}\lambda _i\nabla g_i({\bar{x}})+\sum \limits _{j\in I^h}\rho _j\nabla h_j({\bar{x}})\\&\qquad +\,\sum \limits _{k\in I^G({\bar{x}})\cup \beta _1}\eta _k\nabla G_k({\bar{x}}) +\sum \limits _{k\in I^H({\bar{x}})\cup \beta _2}\theta _k\nabla H_k({\bar{x}}),\\&\forall i\in I^g({\bar{x}}):\,\lambda _i\ge 0. \end{aligned} \end{aligned}$$

Defining

$$\begin{aligned} \mu _k:= {\left\{ \begin{array}{ll} \eta _k &{}\quad k\in I^G({\bar{x}})\cup \beta _1,\\ 0 &{}\quad k\in I^H({\bar{x}})\cup \beta _2, \end{array}\right. } \qquad \nu _k:= {\left\{ \begin{array}{ll} 0 &{}\quad k\in I^G({\bar{x}})\cup \beta _1,\\ \theta _k &{}\quad k\in I^H({\bar{x}})\cup \beta _2, \end{array}\right. } \end{aligned}$$

the multipliers $(\lambda ,\rho ,\mu ,\nu )$ solve the M-stationarity system, i.e. ${\bar{x}}$ is an M-stationary point of (MPSC).$\square$

We would like to remark that a similar result as the above lemma can be obtained for MPCCs if the associated M-stationarity condition is replaced by the weaker Abadie-stationarity notion, see [10, Section 3.3] for details.

The upcoming corollary follows immediately.

Corollary 4.2

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a locally optimal solution of (MPSC). Furthermore, assume that there exists a partition $(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))$ such that GCQ holds for (NLP$(\beta _1,\beta _2)$) at ${\bar{x}}$. Then, ${\bar{x}}$ is an M-stationary point of (MPSC).

Next, we introduce some MPSC-tailored constraint qualifications. Here, we proceed in a similar way as it is well known from the theory of MPCCs and MPVCs.

Definition 4.2

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a feasible point of (MPSC). Then, ${\bar{x}}$ is said to satisfy

• 1. MPSC-LICQ, provided LICQ holds for (TNLP) at ${\bar{x}}$,

• 2. MPSC-MFCQ, provided MFCQ holds for (TNLP) at ${\bar{x}}$, and

• 3. MPSC-NNAMCQ, provided NNAMCQ holds for (2) at ${\bar{x}}$, i.e. we have

  $$\begin{aligned} \left. \begin{aligned}&0=\sum \limits _{i\in I^g({\bar{x}})}\lambda _i\nabla g_i({\bar{x}})+\sum \limits _{j\in I^h}\rho _j\nabla h_j({\bar{x}})\\&\qquad +\,\sum \limits _{k=1}^l\bigl [\mu _k\nabla G_k({\bar{x}})+\nu _k\nabla H_k({\bar{x}})\bigr ],\\&\forall i\in I^g({\bar{x}}):\,\lambda _i\ge 0,\\&\forall k\in I^{H}({\bar{x}}):\,\mu _k=0,\\&\forall k\in I^{G}({\bar{x}}):\,\nu _k=0,\\&\forall k\in I^{GH}({\bar{x}}):\,\mu _k\nu _k=0 \end{aligned}\right\} \, \Longrightarrow \; \begin{aligned}&\lambda =0,\,\rho =0,\\&\mu =0,\,\nu =0. \end{aligned} \end{aligned}$$

Due to the above definition and the dual representations of LICQ and MFCQ stated in Definition 3.1, we find

$$\begin{aligned} \text {MPSC-LICQ}\;\Longrightarrow \;\text {MPSC-MFCQ}\;\Longrightarrow \;\text {MPSC-NNAMCQ.} \end{aligned}$$

Clearly, if $I^{GH}({\bar{x}})=\varnothing$ holds true, then MPSC-LICQ and MPSC-MFCQ are equivalent to the classical constraint qualifications LICQ and MFCQ for (MPSC), respectively. Furthermore, MPSC-NNAMCQ equals MPSC-MFCQ and, thus, MFCQ in this situation. Obviously, all the introduced stationarity notions for (MPSC) equal its KKT conditions whenever $I^{GH}({\bar{x}})$ is empty.

Mimicing classical ideas from the theory of MPCCs, see e.g. [34], the following result is easily obtained.

Theorem 4.1

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a locally optimal solution of (MPSC) where MPSC-LICQ is valid. Then, ${\bar{x}}$ is an S-stationary point of (MPSC).

Proof

Clearly, ${\bar{x}}$ is a locally optimal solution of the program (NLP$(\beta _1,\beta _2)$) for the partitions $(\beta _1,\beta _2)\in \{(I^{GH}({\bar{x}}),\varnothing ),(\varnothing ,I^{GH}({\bar{x}}))\}$ as well. Since the validity of MPSC-LICQ for (MPSC) at ${\bar{x}}$ implies the validity of LICQ for (NLP$(\beta _1,\beta _2)$) at ${\bar{x}}$ for arbitrary partitions $(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))$, we find two sets of multipliers satisfying

$$\begin{aligned} \begin{aligned}&0=\nabla f({\bar{x}})+\sum \limits _{i\in I^g({\bar{x}})}\lambda _i^1\nabla g_i({\bar{x}})+\sum \limits _{j\in I^h}\rho _j^1\nabla h_j({\bar{x}})\\&\qquad +\,\sum \limits _{k\in I^G({\bar{x}})\cup I^{GH}({\bar{x}})}\mu ^1_k\nabla G_k({\bar{x}})+\sum \limits _{k\in I^H({\bar{x}})}\nu _k^1\nabla H_k({\bar{x}}),\\&\forall i\in I^g({\bar{x}}):\,\lambda ^1_i\ge 0 \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&0=\nabla f({\bar{x}})+\sum \limits _{i\in I^g({\bar{x}})}\lambda _i^2\nabla g_i({\bar{x}})+\sum \limits _{j\in I^h}\rho _j^2\nabla h_j({\bar{x}})\\&\qquad +\,\sum \limits _{k\in I^G({\bar{x}})}\mu ^2_k\nabla G_k({\bar{x}})+\sum \limits _{k\in I^H({\bar{x}})\cup I^{GH}({\bar{x}})}\nu _k^2\nabla H_k({\bar{x}}),\\&\forall i\in I^g({\bar{x}}):\,\lambda ^2_i\ge 0, \end{aligned} \end{aligned}$$

respectively. Thus, we obtain

$$\begin{aligned} \begin{aligned}&0=\sum \limits _{i\in I^g({\bar{x}})}(\lambda _i^1-\lambda _i^2)\nabla g_i({\bar{x}}) +\sum \limits _{j\in I^h}(\rho ^1_j-\rho ^2_j)\nabla h_j({\bar{x}})\\&\qquad +\,\sum \limits _{k\in I^G({\bar{x}})}(\mu ^1_k-\mu ^2_k)\nabla G_k({\bar{x}}) +\sum \limits _{k\in I^H({\bar{x}})}(\nu ^1_k-\nu ^2_k)\nabla H_k({\bar{x}})\\&\qquad +\,\sum \limits _{k\in I^{GH}({\bar{x}})}\mu ^1_k\nabla G_k({\bar{x}}) -\sum \limits _{k\in I^{GH}({\bar{x}})}\nu ^2_k\nabla H_k({\bar{x}}). \end{aligned} \end{aligned}$$

Due to the validity of MPSC-LICQ, $\lambda ^1_i=\lambda ^2_i$ ($i\in I^g({\bar{x}})$), $\rho ^1_j=\rho ^2_j$ ($j\in I^h$), $\mu ^1_k=\mu ^2_k$ ($k\in I^G({\bar{x}})$), $\nu ^1_k=\nu ^2_k$ ($k\in I^H({\bar{x}})$), and $\mu ^1_k=\nu ^2_k=0$ ($k\in I^{GH}({\bar{x}})$) are obtained. This shows

$$\begin{aligned} \begin{aligned}&0=\nabla f({\bar{x}})+\sum \limits _{i\in I^g({\bar{x}})}\lambda _i^1\nabla g_i({\bar{x}})+\sum \limits _{j\in I^h}\rho _j^1\nabla h_j({\bar{x}})\\&\qquad +\,\sum \limits _{k\in I^G({\bar{x}})}\mu ^1_k\nabla G_k({\bar{x}})+\sum \limits _{k\in I^H({\bar{x}})}\nu _k^1\nabla H_k({\bar{x}}),\\&\forall i\in I^g({\bar{x}}):\,\lambda ^1_i\ge 0, \end{aligned} \end{aligned}$$

i.e. the S-stationarity conditions are satisfied. $\square$

Under the assumptions of Theorem 4.1 it is easy to show that the associated S-stationarity multipliers $(\lambda ,\rho ,\mu ,\nu )$ are uniquely determined.

The next theorem is a direct consequence of the abstract theory on Mordukhovich’s stationarity concept provided in Sect. 3.

Theorem 4.2

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a locally optimal solution of (MPSC) where MPSC-NNAMCQ is valid. Then, ${\bar{x}}$ is an M-stationary point of (MPSC).

Due to the relations between the introduced constraint qualifications, we infer the following corollary from Theorem 4.2.

Corollary 4.3

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a locally optimal solution of (MPSC) where MPSC-MFCQ is valid. Then, ${\bar{x}}$ is an M-stationary point of (MPSC).

The upcoming example indicates, that local minimizers of (MPSC) where MPSC-MFCQ is valid do not generally satisfy the S-stationarity conditions, i.e. the assertion of Corollary 4.3 cannot be strengthened without additional assumptions.

Example 4.1

We consider the following optimization problem:

$$\begin{aligned}\begin{aligned} (x_1-2)^2+(x_2-1)^2+(x_3-2)^2&\,\rightarrow \,\min \\ x_1^2+x_2^2+x_3^2&\,\le \,3\\ x_3&\,\le \,1\\ (x_1-x_2^2)(x_2-x_1^2)&\,=\,0. \end{aligned}\end{aligned}$$

On can check that ${\bar{x}}:=(1,1,1)$ is a globally optimal solution of this program. Since $I^g({\bar{x}})=\{1,2\}$ and $I^{GH}({\bar{x}})=\{1\}$ hold, MPSC-LICQ is trivially violated at ${\bar{x}}$. On the other hand, one can check that MPSC-MFCQ is satisfied at ${\bar{x}}$. The associated M-stationarity system reads as

$$\begin{aligned} \begin{aligned}&0=-2+2\lambda _1+\mu _1-2\nu _1,\\&0=2\lambda _1-2\mu _1+\nu _1,\\&0=-2+2\lambda _1+\lambda _2,\\&\lambda _1\ge 0,\,\lambda _2\ge 0,\,\mu _1\nu _1=0. \end{aligned} \end{aligned}$$

It possesses the solutions $\lambda ^1_1=\lambda ^1_2=\mu ^1_1=\tfrac{2}{3}$, $\nu ^1_1=0$ and $\lambda ^2_1=\tfrac{1}{3}$, $\lambda ^2_2=\tfrac{4}{3}$, $\mu ^2_1=0$, $\nu ^2_1=-\tfrac{2}{3}$. Note that none of these multipliers solves the associated S-stationarity system since the multipliers $\mu ^i_1$ and $\nu ^i_1$, $i=1,2$, do not vanish at the same time.

5 Abadie- and Guignard-type constraint qualifications

5.1 Derivation of MPSC-ACQ and MPSC-GCQ

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a feasible point of (MPSC) and let ${\mathcal {T}}_X({\bar{x}})$ be the tangent cone to the feasible set X of (MPSC) at ${\bar{x}}$. The associated linearization cone is given by

$$\begin{aligned} \begin{aligned} {\mathcal {L}}_X({\bar{x}})&=\left\{ d\in {\mathbb {R}}^n\,\big |\, \begin{aligned} \nabla g_i({\bar{x}})\cdot d&\,\le \,0&i\in I^g({\bar{x}})\\ \nabla h_j({\bar{x}})\cdot d&\,=\,0&j\in I^h\\ (H_k({\bar{x}})\nabla G_k({\bar{x}})+G_k({\bar{x}})\nabla H_k({\bar{x}}))\cdot d&\,=\,0&k=1,\ldots ,l \end{aligned} \right\} \\&=\left\{ d\in {\mathbb {R}}^n\,\big |\, \begin{aligned} \nabla g_i({\bar{x}})\cdot d&\,\le \,0&i\in I^g({\bar{x}})\\ \nabla h_j({\bar{x}})\cdot d&\,=\,0&j\in I^h\\ \nabla G_k({\bar{x}})\cdot d&\,=\,0&k\in I^G({\bar{x}})\\ \nabla H_k({\bar{x}})\cdot d&\,=\,0&k\in I^H({\bar{x}}) \end{aligned} \right\} . \end{aligned} \end{aligned}$$

Obviously, ${\mathcal {L}}_X({\bar{x}})$ is a polyhedral and, thus, convex cone. In the situation $I^{GH}({\bar{x}})\ne \varnothing$, however, the set X is likely to behave in a nonconvex way in a neighborhood of ${\bar{x}}$ which is why ${\mathcal {T}}_X({\bar{x}})$ might be nonconvex as well. Consequently, the constraint qualification ACQ may turn out to be too selective for (MPSC). The constraint qualification GCQ, on the other hand, might be applicable even if $I^{GH}({\bar{x}})\ne \varnothing$ holds.

Example 5.1

Let us consider the program

$$\begin{aligned}\begin{aligned} (x_1-1)^2+x_2^2&\,\rightarrow \,\min \\ x_1&\,\le \,0\\ -x_2&\,\le \,0\\ x_1x_2&\,=\,0, \end{aligned}\end{aligned}$$

which is actually an MPCC, at its unique global minimizer ${\bar{x}}:=(0,0)$. We easily check

$$\begin{aligned} \begin{aligned} {\mathcal {T}}_X({\bar{x}})&=\{d\in {\mathbb {R}}^2\,|\,d_1\le 0,\,d_2\ge 0,\,d_1d_2=0\},\\ \widehat{{\mathcal {N}}}_X({\bar{x}})&=\{\eta \in {\mathbb {R}}^2\,|\,\eta _1\ge 0,\,\eta _2\le 0\},\\ {\mathcal {L}}_X({\bar{x}})&=\{d\in {\mathbb {R}}^2\,|\,d_1\le 0,\,d_2\ge 0\},\\ {\mathcal {L}}_X({\bar{x}})^\circ&=\{\eta \in {\mathbb {R}}^2\,|\,\eta _1\ge 0,\,\eta _2\le 0\}. \end{aligned} \end{aligned}$$

Consequently, GCQ is valid at ${\bar{x}}$ while ACQ is violated there. Note that MPSC-NNAMCQ and, thus, MPSC-MFCQ as well as MPSC-LICQ do not hold at ${\bar{x}}$.

Clearly, any locally optimal solution of (MPSC) where GCQ is valid must be an S-stationary point since this stationarity notion equals the KKT conditions of (MPSC), see Corollary 4.1, Remark 4.1, and Definition 4.1.

Here, we want to introduce MPSC-tailored versions of ACQ and GCQ, respectively. Therefore, we follow ideas from [10, 12, 25] where a similar approach is used to tackle MPCCs and MPVCs, respectively. First, an MPSC-tailored linearization cone is defined:

$$\begin{aligned} {\mathcal {L}}_X^MPSC ({\bar{x}}):= \left\{ d\in {\mathbb {R}}^n\,\big |\, \begin{aligned} \nabla g_i({\bar{x}})\cdot d&\,\le \,0&i\in I^g({\bar{x}})\\ \nabla h_j({\bar{x}})\cdot d&\,=\,0&j\in I^h\\ \nabla G_k({\bar{x}})\cdot d&\,=\,0&k\in I^G({\bar{x}})\\ \nabla H_k({\bar{x}})\cdot d&\,=\,0&k\in I^H({\bar{x}})\\ (\nabla G_k({\bar{x}})\cdot d)(\nabla H_k({\bar{x}})\cdot d)&\,=\,0&k\in I^{GH}({\bar{x}}) \end{aligned} \right\} . \end{aligned}$$

Clearly, ${\mathcal {L}}_X^MPSC ({\bar{x}})\subset {\mathcal {L}}_X({\bar{x}})$ is valid. The relation ${\mathcal {T}}_X({\bar{x}})\subset {\mathcal {L}}_X^\text {MPSC}({\bar{x}})$, however, does not follow directly from the definition of these cones. For the proof of the correctness of this inclusion, we want to exploit the following lemma which is similar to [10, Lemma 3.1] for MPCCs and [25, Lemma 2.4] which addresses MPVCs.

Lemma 5.1

For a fixed feasible point ${\bar{x}}\in {\mathbb {R}}^n$ of (MPSC), the following formulas hold true:

$$\begin{aligned} \begin{aligned} {\mathcal {T}}_X({\bar{x}})&=\bigcup \limits _{(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))} {\mathcal {T}}_{NLP (\beta _1,\beta _2)}({\bar{x}}),\\ {\mathcal {L}}_X^MPSC ({\bar{x}})&=\bigcup \limits _{(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))} {\mathcal {L}}_{NLP (\beta _1,\beta _2)}({\bar{x}}). \end{aligned} \end{aligned}$$

For any partition $(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))$, ${\mathcal {T}}_{NLP (\beta _1,\beta _2)}({\bar{x}})$ and ${\mathcal {L}}_{NLP (\beta _1,\beta _2)}({\bar{x}})$ denote the tangent cone and the linearization cone to the feasible set of the program (NLP$(\beta _1,\beta _2)$) at ${\bar{x}}$, respectively.

Proof

Let us start with the proof of the formula for the tangent cone. We show both inclusions separately.

$[\subset ]$ Choose a direction $d\in {\mathcal {T}}_X({\bar{x}})$ arbitrarily. By definition, we find sequences $\{d_s\}_{s\in {\mathbb {N}}}\subset {\mathbb {R}}^n$ and $\{t_s\}_{s\in {\mathbb {N}}}\subset {\mathbb {R}}_{+}$ such that $d_s\rightarrow d$, $t_s\rightarrow 0$, and ${\bar{x}}+t_sd_s\in X$ for all $s\in {\mathbb {N}}$ hold true. Particularly, $G_k({\bar{x}}+t_sd_s)H_k({\bar{x}}+t_sd_s)=0$ is valid for all $s\in {\mathbb {N}}$ and $k=1,\ldots ,l$. Due to continuity of G and H, we obtain $I^G({\bar{x}})\subset I^{G}({\bar{x}}+t_sd_s)$ and $I^H({\bar{x}})\subset I^H({\bar{x}}+t_sd_s)$ for all sufficiently large $s\in {\mathbb {N}}$. Let us define

$$\begin{aligned} \begin{aligned} \beta ^s_1&:=\left\{ k\in I^{GH}({\bar{x}})\,\big |\,G_k({\bar{x}}+t_sd_s)= 0\right\} ,\\ \beta ^s_2&:=\left\{ k\in I^{GH}({\bar{x}})\,\big |\,G_k({\bar{x}}+t_sd_s)\ne 0\right\} \end{aligned} \end{aligned}$$

for all $s\in {\mathbb {N}}$. Clearly, $(\beta ^s_1,\beta ^s_2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))$ holds true for all $s\in {\mathbb {N}}$. Since there are only finitely many bipartitions in ${\mathcal {P}}(I^{GH}({\bar{x}}))$, there is a partition $(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))$ and an infinite set $N\subset {\mathbb {N}}$ such that $\beta ^s_1=\beta _1$ and $\beta ^s_2=\beta _2$ hold true for all $s\in N$. Particularly, ${\bar{x}}+t_sd_s$ is feasible to (NLP$(\beta _1,\beta _2)$) for all $s\in N$. By definition, we obtain $d\in {\mathcal {T}}_{\text {NLP}(\beta _1,\beta _2)}({\bar{x}})$.

$[\supset ]$ For $(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))$, choose $d\in {\mathcal {T}}_{\text {NLP}(\beta _1,\beta _2)}({\bar{x}})$ arbitrarily. Then, there exist sequences $\{d_s\}_{s\in {\mathbb {N}}}\subset {\mathbb {R}}^n$ and $\{t_s\}_{s\in {\mathbb {N}}}\subset {\mathbb {R}}_{+}$ such that $d_s\rightarrow d$, $t_s\rightarrow 0$, and ${\bar{x}}+t_sd_s$ is feasible to (NLP$(\beta _1,\beta _2)$) for all $s\in {\mathbb {N}}$. Noting that the feasible set of (NLP$(\beta _1,\beta _2)$) is a subset of X, we already have $d\in {\mathcal {T}}_X({\bar{x}})$.

Next, we show the formula for the linearization cone. Therefore, observe that

$$\begin{aligned} {\mathcal {L}}_{\text {NLP}(\beta _1,\beta _2)}({\bar{x}}) = \left\{ d\in {\mathbb {R}}^n\,\big | \begin{aligned} \nabla g_i({\bar{x}})\cdot d&\,\le \,0&i\in I^g({\bar{x}})\\ \nabla h_j({\bar{x}})\cdot d&\,=\,0&j\in I^h\\ \nabla G_k({\bar{x}})\cdot d&\,=\,0&k\in I^G({\bar{x}})\cup \beta _1\\ \nabla H_k({\bar{x}})\cdot d&\,=\,0&k\in I^H({\bar{x}})\cup \beta _2 \end{aligned} \right\} \end{aligned}$$

(9)

is valid for any partition $(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))$. Thereby, the inclusion $[\supset ]$ follows trivially.

For a fixed $d\in {\mathcal {L}}^{\text {MPSC}}_X({\bar{x}})$, let us define

$$\begin{aligned} \begin{aligned} \beta _1&:=\left\{ k\in I^{GH}({\bar{x}})\,\big |\,\nabla G_k({\bar{x}})\cdot d=0\right\} ,\\ \beta _2&:=\left\{ k\in I^{GH}({\bar{x}})\,\big |\,\nabla G_k({\bar{x}})\cdot d\ne 0\right\} . \end{aligned} \end{aligned}$$

Then, $d\in {\mathcal {L}}_{\text {NLP}(\beta _1,\beta _2)}({\bar{x}})$ follows by definition, i.e. the inclusion $[\subset ]$ holds as well.$\square$

Clearly, the formula for the tangent cone also follows from the fact that the family of all problems (NLP$(\beta _1,\beta _2)$), $(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))$, provides a local decomposition of (MPSC) around ${\bar{x}}$.

Corollary 5.1

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a feasible point of (MPSC). Then, ${\mathcal {T}}_X({\bar{x}})\subset {\mathcal {L}}_X^MPSC ({\bar{x}})$ holds.

Proof

For any partition $(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))$, we obtain the trivial inclusion ${\mathcal {T}}_{\text {NLP}(\beta _1,\beta _2)}({\bar{x}})\subset {\mathcal {L}}_{\text {NLP}(\beta _1,\beta _2)}({\bar{x}})$ since (NLP$(\beta _1,\beta _2)$) is a standard nonlinear program. That is why Lemma 5.1 yields

$$\begin{aligned} \begin{aligned} {\mathcal {T}}_X({\bar{x}})&= \bigcup \limits _{(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))} {\mathcal {T}}_{\text {NLP}(\beta _1,\beta _2)}({\bar{x}})\\&\subset \bigcup \limits _{(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))} {\mathcal {L}}_{\text {NLP}(\beta _1,\beta _2)}({\bar{x}}) ={\mathcal {L}}^MPSC _X({\bar{x}}). \end{aligned} \end{aligned}$$

This completes the proof. $\square$

Exploiting a more abstract definition of linearization cones which applies to (P2) and, thus, to (2), the statement of Corollary 5.1 would follow from [31, Theorem 6.31] as well.

The result of Corollary 5.1 justifies the following definition.

Definition 5.1

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a feasible point of (MPSC). Then, ${\bar{x}}$ is said to satisfy

• 1. MPSC-ACQ, provided ${\mathcal {T}}_X({\bar{x}})={\mathcal {L}}_X^MPSC ({\bar{x}})$ holds,

• 2. MPSC-GCQ, provided $\widehat{{\mathcal {N}}}_X({\bar{x}})={\mathcal {L}}_X^MPSC ({\bar{x}})^\circ$ holds.

By definition, we obtain

$$\begin{aligned} \text {MPSC-ACQ}\;\Longrightarrow \;\text {MPSC-GCQ}. \end{aligned}$$

Invoking Corollary 5.1, we have ${\mathcal {T}}_X({\bar{x}})\subset {\mathcal {L}}^MPSC _X({\bar{x}})\subset {\mathcal {L}}_X({\bar{x}})$ and, using polarization, ${\mathcal {L}}_X({\bar{x}})^\circ \subset {\mathcal {L}}^MPSC _X({\bar{x}})^\circ \subset \widehat{{\mathcal {N}}}_X({\bar{x}})$. Particularly, the validity of GCQ implies the validity of MPSC-GCQ. The converse relation, which holds in the context of cardinality-constrained programming, see [6, Corollary 3.8], does not hold true in general.

Example 5.2

Let us consider the optimization problem

$$\begin{aligned} \begin{aligned} x_1+x_2^2&\,\rightarrow \,\min \\ -x_1+x_2&\,\le \,0\\ x_1x_2&\,=\,0. \end{aligned} \end{aligned}$$

Clearly, its unique global minimizer is given by ${\bar{x}}:=(0,0)$. We easily check

$$\begin{aligned} \begin{aligned} {\mathcal {T}}_X({\bar{x}})&=\{d\in {\mathbb {R}}^2\,|\,d_1\ge 0,\,d_2\le 0,\,d_1d_2=0\},\\ \widehat{{\mathcal {N}}}_X({\bar{x}})&=\{\eta \in {\mathbb {R}}^2\,|\,\eta _1\le 0,\,\eta _2\ge 0\},\\ {\mathcal {L}}_X({\bar{x}})&=\{d\in {\mathbb {R}}^2\,|\,d_2\le d_1\},\\ {\mathcal {L}}^MPSC _X({\bar{x}})&=\{d\in {\mathbb {R}}^2\,|\,-d_1+d_2\le 0,\,d_1d_2=0\},\\ {\mathcal {L}}_X({\bar{x}})^\circ&={\text {cone}}\{(-1,1)\}. \end{aligned} \end{aligned}$$

Thus, MPSC-ACQ is valid which implies that MPSC-GCQ holds true as well. On the other hand, neither ACQ nor GCQ are satisfied in the present situation.

By means of this example, we also see that MPSC-MFCQ is generally stronger than MPSC-NNAMCQ since the latter is valid at ${\bar{x}}$ while the former fails to hold there.

One can easily check that ${\bar{x}}$ is an M- but not an S-stationary point of the program.

5.2 Relations to other constraint qualifications

First, we would like to mention a sufficient condition for the validity of standard GCQ. This result parallels [12, Theorem 4.6] for MPCCs and [25, Theorem 4.3] for MPVCs.

Lemma 5.2

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a feasible point of (MPSC) where MPSC-LICQ is valid. Then, GCQ holds at ${\bar{x}}$ as well.

Proof

For the proof, we note that under validity of MPSC-LICQ, ${\bar{x}}$ is an S-stationary point of (MPSC) provided it is a local minimizer, see Theorem 4.1. Now, the desired result follows from [18, Section 3] observing that the S-stationarity conditions and the KKT conditions of (MPSC) coincide, see Remark 4.1.$\square$

Exploiting Lemma 5.1 once more, the upcoming result follows immediately. The subsequent corollary can be derived easily.

Lemma 5.3

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a feasible point of (MPSC). Assume that ACQ is valid at ${\bar{x}}$ for (NLP$(\beta _1,\beta _2)$) for all partitions $(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))$. Then, MPSC-ACQ is valid at ${\bar{x}}$.

Corollary 5.2

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a feasible point of (MPSC) where all the functions g, h, G, and H are affine. Then, MPSC-ACQ is valid at ${\bar{x}}$.

Proof

By assumption, for any partition $(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))$, (NLP$(\beta _1,\beta _2)$) is a standard nonlinear program with affine constraints. Thus, ACQ holds for (NLP$(\beta _1,\beta _2)$) at ${\bar{x}}$, see [2, Lemma 5.1.4]. Thus, the corollary’s assertion follows from Lemma 5.3.$\square$

Next, we aim to study the relationship between MPSC-NNAMCQ and MPSC-ACQ.

Lemma 5.4

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a feasible point of (MPSC) where the constraint qualification MPSC-NNAMCQ is valid. Then, MPSC-ACQ holds at ${\bar{x}}$ as well.

Proof

Clearly, we only need to show that the validity of MPSC-NNAMCQ at ${\bar{x}}$ implies that MFCQ holds at ${\bar{x}}$ for the program (NLP$(\beta _1,\beta _2)$) for all partitions $(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))$. Afterwards, the lemma’s assertion would follow immediately by Lemma 5.3.

Thus, choose a partition $(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))$ arbitrarily and fix multipliers $\lambda _i$ ($i\in I^g({\bar{x}})$), $\rho _j$ ($j\in I^h$), $\mu _k$ ($k\in I^G({\bar{x}})\cup \beta _1$), and $\nu _k$ ($k\in I^H({\bar{x}})\cup \beta _2$) which satisfy

$$\begin{aligned} \begin{aligned}&0=\sum \limits _{i\in I^g({\bar{x}})}\lambda _i\nabla g_i({\bar{x}})+\sum \limits _{j\in I^h}\rho _j\nabla h_j({\bar{x}})\\&\qquad +\,\sum \limits _{k\in I^G({\bar{x}})\cup \beta _1}\mu _k\nabla G_k({\bar{x}}) +\sum \limits _{k\in I^H({\bar{x}})\cup \beta _2}\nu _k\nabla H_k({\bar{x}}),\\&\forall i\in I^g({\bar{x}}):\,\lambda _i\ge 0. \end{aligned} \end{aligned}$$

Defining $\mu _k:=0$ ($k\in I^H({\bar{x}})\cup \beta _2$) and $\nu _k:=0$ ($k\in I^G({\bar{x}})\cup \beta _1$), we obtain

$$\begin{aligned} \begin{aligned}&0=\sum \limits _{i\in I^g({\bar{x}})}\lambda _i\nabla g_i({\bar{x}})+\sum \limits _{j\in I^h}\rho _j\nabla h_j({\bar{x}})+\sum \limits _{k=1}^l\bigl [\mu _k\nabla G_k({\bar{x}})+\nu _k\nabla H_k({\bar{x}})\bigr ],\\&\forall i\in I^g({\bar{x}}):\,\lambda _i\ge 0,\\&\forall k\in I^H({\bar{x}}):\,\mu _k=0,\\&\forall k\in I^G({\bar{x}}):\,\nu _k=0,\\&\forall k\in I^{GH}({\bar{x}}):\,\mu _k\nu _k=0 \end{aligned} \end{aligned}$$

from $\beta _1\cap \beta _2=\varnothing$ and $\beta _1\cup \beta _2=I^{GH}({\bar{x}})$. Since MPSC-NNAMCQ holds at ${\bar{x}}$, we deduce that all these multipliers need to vanish. As a consequence, MFCQ is valid for (NLP$(\beta _1,\beta _2)$) at ${\bar{x}}$. Due to the above arguments, this completes the proof.$\square$

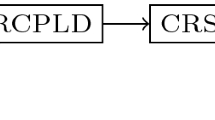
In Fig. 1, the relations between all the introduced constraint qualifications for (MPSC) are visualized. This summarizes the above results.

Fig. 1

Relations between constraint qualifications

Consulting the rich literature on MPCCs, see [39], there might exist even more regularity conditions like MPSC-tailored versions of Slater’s or Zangwill’s constraint qualification which are applicable to (MPSC). A detailed study of such conditions is, however, beyond the scope of this paper.

5.3 Necessary optimality conditions

In this section, we will show that the validity of MPSC-GCQ at a locally optimal solution of (MPSC) implies that this point is M-stationary. This result parallels [13, Theorem 3.1] for MPCCs.

Theorem 5.1

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a locally optimal solution of (MPSC) where MPSC-GCQ is valid. Then, ${\bar{x}}$ is an M-stationary point of (MPSC).

Proof

Since ${\bar{x}}$ is a local minimizer of (MPSC), we obtain

$$\begin{aligned} \forall d\in {\mathcal {T}}_X({\bar{x}}):\quad \nabla f({\bar{x}})\cdot d\ge 0 \end{aligned}$$

from [31, Theorem 6.12]. The above condition is equivalent to $-\nabla f({\bar{x}})\in \widehat{{\mathcal {N}}}_X({\bar{x}})$. Then, $-\nabla f({\bar{x}})\in {\mathcal {L}}^{\text {MPSC}}_X({\bar{x}})^\circ$ follows by validity of MPSC-GCQ. This yields

$$\begin{aligned} \forall d\in {\mathcal {L}}^{\text {MPSC}}_X({\bar{x}})^{\circ \circ }:\quad \nabla f({\bar{x}})\cdot d\ge 0. \end{aligned}$$

Since we have ${\mathcal {L}}^{\text {MPSC}}_X({\bar{x}})^{\circ \circ }={\overline{{\mathrm{conv}}}}{\mathcal {L}}^{\text {MPSC}}_X({\bar{x}})\supset {\mathcal {L}}^{\text {MPSC}}_X({\bar{x}})$ by the bipolar theorem,

$$\begin{aligned} \forall d\in {\mathcal {L}}_{X}^MPSC ({\bar{x}}):\quad \nabla f({\bar{x}})\cdot d\ge 0 \end{aligned}$$

holds true. Next, we invoke Lemma 5.1 in order to obtain

$$\begin{aligned} \forall d\in {\mathcal {L}}_{\text {NLP}(\beta _1,\beta _2)}({\bar{x}}):\quad \nabla f({\bar{x}})\cdot d\ge 0 \end{aligned}$$

for any partition $(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))$. Let us fix a particular partition $(\beta _1,\beta _2)\in {\mathcal {P}}(I^{GH}({\bar{x}}))$. Then, the above condition and (9) imply that ${\bar{d}}:=0$ solves the linear program

$$\begin{aligned} \begin{aligned} \nabla f({\bar{x}})\cdot d&\,\rightarrow \,\min&\\ \nabla g_i({\bar{x}})\cdot d&\,\le \,0&\qquad&i\in I^g({\bar{x}})&\\ \nabla h_j({\bar{x}})\cdot d&\,=\,0&\qquad&j\in I^h&\\ \nabla G_k({\bar{x}})\cdot d&\,=\,0&\qquad&k\in I^G({\bar{x}})\cup \beta _1&\\ \nabla H_k({\bar{x}})\cdot d&\,=\,0&\qquad&k\in I^H({\bar{x}})\cup \beta _2.&\end{aligned} \end{aligned}$$

Since ACQ is valid at all feasible points of this program, see [2, Lemma 5.1.4], we find $\lambda _i$ ($i\in I^g({\bar{x}})$), $\rho _j$ ($j\in I^h$), $\mu _k$ ($k\in I^G({\bar{x}})\cup \beta _1$), and $\nu _k$ ($k\in I^H({\bar{x}})\cup \beta _2$) which satisfy

$$\begin{aligned} \begin{aligned}&0=\nabla f({\bar{x}}) +\sum \limits _{i\in I^g({\bar{x}})}\lambda _i\nabla g_i({\bar{x}}) +\sum \limits _{j\in I^h}\rho _j\nabla h_j({\bar{x}})\\&\qquad +\,\sum \limits _{k\in I^G({\bar{x}})\cup \beta _1}\mu _k\nabla G_k({\bar{x}}) +\sum \limits _{k\in I^H({\bar{x}})\cup \beta _2}\nu _k\nabla H_k({\bar{x}}),\\&\forall i\in I^g({\bar{x}}):\,\lambda _i\ge 0. \end{aligned} \end{aligned}$$

Particularly, ${\bar{x}}$ is a KKT point of (NLP$(\beta _1,\beta _2)$). Now, we can invoke Lemma 4.2 in order to obtain that ${\bar{x}}$ is an M-stationary point of (MPSC).$\square$

Interpreting (MPSC) as a disjunctive program, the statement of the above theorem follows from [14, Theorem 7] as well. However, the proof we presented is completely elementary and only exploits the specific switching structure as well as the characterization of M-stationarity we derived in Lemma 4.2. Particularly, we do not need to rely on the calmness property of polyhedral multifunctions which is indispensable in order to derive necessary optimality conditions of M-stationartity-type for general disjunctive programs, see [14, 15].

Clearly, if ${\bar{x}}\in {\mathbb {R}}^n$ is a locally optimal solution of (MPSC) where MPSC-ACQ holds, then ${\bar{x}}$ is an M-stationary point of (MPSC) by means of Theorem 5.1 since the validity of MPSC-ACQ implies that MPSC-GCQ is satisfied as well. Thus, the subsequent corollary is an immediate consequence of the above result and Corollary 5.2. On the other hand, it follows directly from Corollary 4.2. It parallels similar results for MPCCs, see [11, Theorem 3.5, Proposition 3.8], and MPVCs, see [24, Theorems 3.4, 4.2].

Corollary 5.3

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a locally optimal solution of (MPSC) where all the functions g, h, G, and H are affine. Then, ${\bar{x}}$ is an M-stationary point of (MPSC).

Taking a look at the proof of Theorem 5.1, the condition

$$\begin{aligned} \widehat{{\mathcal {N}}}_X({\bar{x}})\subset \left\{ \eta \in {\mathbb {R}}^n\,\big |\, \begin{aligned}&\eta =\sum \limits _{i\in I^g({\bar{x}})}\lambda _i\nabla g_i({\bar{x}})+\sum \limits _{j\in I^h}\rho _j\nabla h_j({\bar{x}})\\&\qquad +\,\sum \limits _{k=1}^l\bigl [\mu _k\nabla G_k({\bar{x}})+\nu _k\nabla H_k({\bar{x}})\bigr ]\\&\forall i\in I^g({\bar{x}}):\,\lambda _i\ge 0\\&\forall k\in I^H({\bar{x}}):\,\mu _k=0\\&\forall k\in I^G({\bar{x}}):\,\nu _k=0\\&\forall k\in I^{GH}({\bar{x}}):\,\mu _k\nu _k=0 \end{aligned} \right\} \end{aligned}$$

(10)

is sufficient to guarantee that a local minimizer ${\bar{x}}\in {\mathbb {R}}^n$ of (MPSC) is an M-stationary point. Moreover, one can mimic the proof of [20, Theorem 3.3] in order to show that the validity of MPSC-GCQ at ${\bar{x}}$ implies that (10) holds as well. The final example of this section visualizes that (10) might be strictly weaker than MPSC-GCQ in some situations. Consequently, MPSC-GCQ is not the weakest constraint qualification which implies local minimizers of (MPSC) to be M-stationary. This contrasts classical results for standard nonlinear programming problems where it is well known that GCQ is the weakest available constraint qualification which guarantees that a local minimizer is a KKT point as well, see e.g. [18]. However, it has to be noted that checking the validity (10) might be rather difficult in practice.

Example 5.3

Let us investigate the switching-constrained optimization problem

$$\begin{aligned} \begin{aligned} x_1+x_2&\,\rightarrow \,\min \\ x_1^2-x_2&\,\le \,0\\ x_1x_2&\,=\,0. \end{aligned} \end{aligned}$$

Its uniquely determined global minimizer is given by ${\bar{x}}:=(0,0)$. One can check that it is an M-stationary point of this program. We compute

$$\begin{aligned} {\mathcal {T}}_X({\bar{x}})&={\text {cone}}\{(0,1)\},\\ \widehat{{\mathcal {N}}}_X({\bar{x}})&=\{\eta \in {\mathbb {R}}^2\,|\,\eta _2\le 0\},\\ {\mathcal {L}}_X^MPSC ({\bar{x}})&=\{d\in {\mathbb {R}}^2\,|\,d_2\ge 0,\,d_1d_2=0\},\\ {\mathcal {L}}_X^MPSC ({\bar{x}})^\circ&={\text {cone}}\{(0,-1)\} \end{aligned}$$

which shows that MPSC-GCQ is violated at ${\bar{x}}$. On the other hand, we have

$$\begin{aligned} \widehat{{\mathcal {N}}}_X({\bar{x}})&={\text {cone}}\{(0,-1)\}+{\mathrm{span}}\{(1,0)\}\\&\subset \left\{ \lambda (0,-1)+\mu (1,0)+\nu (0,1)\in {\mathbb {R}}^2\,|\,\lambda \ge 0,\,\mu \nu =0\right\} , \end{aligned}$$

i.e. the constraint qualification (10) holds at ${\bar{x}}$.

6 Necessary optimality conditions for discretized optimal control problems with switching constraints

In this section, we apply the results obtained for (MPSC) to the discretized optimal control problem with switching constraints (OCSC). In order to do so, we have to clarify some notation first. Choose a feasible point ${\bar{x}}:=({\bar{y}},{\bar{u}},{\bar{v}})\in {\mathbb {R}}^n\times {\mathbb {R}}^l\times {\mathbb {R}}^l$ of (OCSC). We set

$$\begin{aligned} I^G({\bar{x}})&:=\{k\in \{1,\ldots ,l\}\,|\,{\bar{u}}_k=0\,\wedge \,{\bar{v}}_k\ne 0\},\\ I^H({\bar{x}})&:=\{k\in \{1,\ldots ,l\}\,|\,{\bar{u}}_k\ne 0\,\wedge \,{\bar{v}}_k=0\},\\ I^{GH}({\bar{x}})&:=\{k\in \{1,\ldots ,l\}\,|\,{\bar{u}}_k= 0\,\wedge \,{\bar{v}}_k=0\},\\ I_u^\uparrow ({\bar{x}})&:=\{k\in \{1,\ldots ,l\}\,|\,{\bar{u}}_k=\overline{{\mathbf {u}}}_k\},\\ I_u^\downarrow ({\bar{x}})&:=\{k\in \{1,\ldots ,l\}\,|\,{\bar{u}}_k=\underline{{\mathbf {u}}}_k\},\\ I_v^\uparrow ({\bar{x}})&:=\{k\in \{1,\ldots ,l\}\,|\,{\bar{v}}_k=\overline{{\mathbf {v}}}_k\},\\ I_v^\downarrow ({\bar{x}})&:=\{k\in \{1,\ldots ,l\}\,|\,{\bar{v}}_k=\underline{{\mathbf {v}}}_k\}. \end{aligned}$$

By definition and the additional requirement (5), we obtain $I^\uparrow _u({\bar{x}})\cup I^\downarrow _u({\bar{x}})\subset I^H({\bar{x}})$ and $I^\uparrow _v({\bar{x}})\cup I^\downarrow _v({\bar{x}})\subset I^G({\bar{x}})$.

First, we check that MPSC-LICQ is valid at all feasible points of (OCSC).

Lemma 6.1

Let ${\bar{x}}:=({\bar{y}},{\bar{u}},{\bar{v}})\in {\mathbb {R}}^n\times {\mathbb {R}}^l\times {\mathbb {R}}^l$ be a feasible point of (OCSC). Then, MPSC-LICQ is valid at ${\bar{x}}$.

Proof

Suppose that there are multipliers $\rho \in {\mathbb {R}}^{n}$ and $\alpha ,\beta ,\gamma ,\delta ,\mu ,\nu \in {\mathbb {R}}^l$ which solve the system

$$\begin{aligned}&0={\mathbf {A}}^\top \rho ,\\&0=-{\mathbf {B}}^\top \rho +\mu +\alpha -\beta ,\\&0=-{\mathbf {C}}^\top \rho +\nu +\gamma -\delta ,\\&\forall k\in I^{H}({\bar{x}}):\,\mu _k=0,\\&\forall k\in I^{G}({\bar{x}}):\,\nu _k=0,\\&\forall k\in \{1,\ldots ,l\}{\setminus } I^\uparrow _u({\bar{x}}):\,\alpha _k=0,\\&\forall k\in \{1,\ldots ,l\}{\setminus } I^\downarrow _u({\bar{x}}):\,\beta _k=0,\\&\forall k\in \{1,\ldots ,l\}{\setminus } I^\uparrow _v({\bar{x}}):\,\gamma _k=0,\\&\forall k\in \{1,\ldots ,l\}{\setminus } I^\downarrow _v({\bar{x}}):\,\delta _k=0. \end{aligned}$$

Since ${\mathbf {A}}\in {\mathbb {R}}^{n\times n}$ is regular, the same holds true for its transpose and, thus, $\rho =0$ follows. Excluding all trivially vanishing multipliers, the above system reduces to

$$\begin{aligned} \begin{aligned}&0=\sum \limits _{k\in I^G({\bar{x}})\cup I^{GH}({\bar{x}})}\mu _ke^l_k+\sum \limits _{k\in I^\uparrow _u({\bar{x}})}\alpha _ke^l_k-\sum \limits _{k\in I^\downarrow _u({\bar{x}})}\beta _ke^l_k,\\&0=\sum \limits _{k\in I^H({\bar{x}})\cup I^{GH}({\bar{x}})}\nu _ke^l_k+\sum \limits _{k\in I^\uparrow _v({\bar{x}})}\gamma _ke^l_k-\sum \limits _{k\in I^\downarrow _v({\bar{x}})}\delta _ke^l_k. \end{aligned} \end{aligned}$$

Here, $e^l_k\in {\mathbb {R}}^l$ denotes the kth unit vector in ${\mathbb {R}}^l$ for all $k=1,\ldots ,l$. Noting that $I^\uparrow _u({\bar{x}}),I^\downarrow _u({\bar{x}})\subset I^H({\bar{x}})$ are disjoint, we obtain $\mu _k=0$ ($k\in I^{G}({\bar{x}})\cup I^{GH}({\bar{x}})$), $\alpha _k=0$ ($k\in I^\uparrow _u({\bar{x}})$), and $\beta _k=0$ ($k\in I^\downarrow _u({\bar{x}})$) from the trivial linear independence of the vectors in $\{e^l_k\,|\,k\in \{1,\ldots ,l\}\}$. Similarly, we derive $\nu _k=0$ ($k\in I^{H}({\bar{x}})\cup I^{GH}({\bar{x}})$), $\gamma _k=0$ ($k\in I^\uparrow _v({\bar{x}})$), and $\delta _k=0$ ($k\in I^\downarrow _v({\bar{x}})$). Thus, all multipliers vanish and, particularly, MPSC-LICQ is valid at all feasible points of the program (OCSC). $\square$

Due to the inherent validity of MPSC-LICQ at the feasible points of (OCSC), the associated S-stationarity conditions provide a necessary optimality criterion, see Theorem 4.1.

Theorem 6.1

Let ${\bar{x}}:=({\bar{y}},{\bar{u}},{\bar{v}})\in {\mathbb {R}}^n\times {\mathbb {R}}^l\times {\mathbb {R}}^l$ be a locally optimal solution of (OCSC). Then, there exist multipliers $\rho \in {\mathbb {R}}^n$ and $\phi ,\psi \in {\mathbb {R}}^l$ which solve the following system:

$$\begin{aligned}&0={\mathbf {Q}}^\top ({\mathbf {Q}}{\bar{y}}-{\mathbf {y}}_d )+{\mathbf {A}}^\top \rho ,\\&0=\sigma _u{\mathbf {M}}^\top {\mathbf {M}}{\bar{u}}-{\mathbf {B}}^\top \rho +\phi ,\\&0=\sigma _v{\mathbf {M}}^\top {\mathbf {M}}{\bar{v}}-{\mathbf {C}}^\top \rho +\psi ,\\&\forall k\in I^\uparrow _u({\bar{x}}):\,\phi _k\ge 0,\\&\forall k\in I^\downarrow _u({\bar{x}}):\,\phi _k\le 0,\\&\forall k\in I^{GH}({\bar{x}})\cup \bigl [I^H({\bar{x}}){\setminus }(I^\uparrow _u({\bar{x}})\cup I^\downarrow _u({\bar{x}}))\bigr ]:\,\phi _k= 0,\\&\forall k\in I^\uparrow _v({\bar{x}}):\,\psi _k\ge 0,\\&\forall k\in I^\downarrow _v({\bar{x}}):\,\psi _k\le 0,\\&\forall k\in I^{GH}({\bar{x}})\cup \bigl [I^G({\bar{x}}){\setminus }(I^\uparrow _v({\bar{x}})\cup I^\downarrow _v({\bar{x}}))\bigr ]:\,\psi _k= 0. \end{aligned}$$

Proof

We apply Theorem 4.1 in order to find $\rho \in {\mathbb {R}}^n$ and $\alpha ,\beta ,\gamma ,\delta ,\mu ,\nu \in {\mathbb {R}}^l$ which solve the system

$$\begin{aligned}&0={\mathbf {Q}}^\top ({\mathbf {Q}}{\bar{y}}-{\mathbf {y}}_\text{ d })+{\mathbf {A}}^\top \rho ,\\&0=\sigma _u{\mathbf {M}}^\top {\mathbf {M}}{\bar{u}}-{\mathbf {B}}^\top \rho +\mu +\alpha -\beta ,\\&0=\sigma _v{\mathbf {M}}^\top {\mathbf {M}}{\bar{v}}-{\mathbf {C}}^\top \rho +\nu +\gamma -\delta ,\\&\forall k\in I^{H}({\bar{x}})\cup I^{GH}({\bar{x}}):\,\mu _k=0,\\&\forall k\in I^{G}({\bar{x}})\cup I^{GH}({\bar{x}}):\,\nu _k=0,\\&\alpha \ge 0,\,\forall k\in \{1,\ldots ,l\}{\setminus } I^\uparrow _u({\bar{x}}):\,\alpha _k=0,\\&\beta \ge 0,\,\forall k\in \{1,\ldots ,l\}{\setminus } I^\downarrow _u({\bar{x}}):\,\beta _k=0,\\&\gamma \ge 0,\,\forall k\in \{1,\ldots ,l\}{\setminus } I^\uparrow _v({\bar{x}}):\,\gamma _k=0,\\&\delta \ge 0,\,\forall k\in \{1,\ldots ,l\}{\setminus } I^\downarrow _v({\bar{x}}):\,\delta _k=0. \end{aligned}$$

Now, we only need to define $\phi :=\mu +\alpha -\beta$ and $\psi :=\nu +\gamma -\delta$ in order to show the theorem’s assertion.$\square$

Invoking Lemmas 5.2 and 6.1, we find that GCQ is valid at any feasible point of (OCSC), i.e. any local minimizer is a KKT point already, cf. Remark 4.1. We note, however, that due to the inherently nonconvex geometry of the feasible set of (OCSC), it might be technically challenging to verify the validity of GCQ directly without exploiting the obtained results for switching-constrained optimization problems.

7 Necessary optimality conditions for mathematical programs with either-or-constraints

Next, we are going to investigate the following mathematical program with either-or-constraints:

$$\begin{aligned} \begin{aligned} f(x)&\,\rightarrow \,\min&\\ g_i(x)&\,\le \,0&\qquad&i=1,\ldots ,m&\\ h_j(x)&\,=\,0&\qquad&j=1,\ldots ,p&\\ c^1_k(x)\,\le \,0\,\vee \,c^2_k(x)&\,\le \,0&\qquad&k=1,\ldots ,l.&\end{aligned} \end{aligned}$$

(MPEOC)

Therein, the functions $c^1_1,\ldots c^1_l,c^2_1,\ldots ,c^2_l:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ are assumed to be continuously differentiable. Let $c^1,c^2:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^l$ be the mappings which possess the component functions $c^1_1,\ldots ,c^1_l$ and $c^2_1,\ldots ,c^2_l$, respectively. Let us emphasize that $\vee$ denotes the logical OR. For simplicity of notation, the standard nonlinear parts of (MPEOC) are modeled by the continuously differentiable functions $f:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$, $g:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^m$, and $h:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^p$ again.

For further investigations, we fix an arbitrary point ${\bar{x}}\in {\mathbb {R}}^n$ which is feasible to (MPEOC) and introduce the following index sets:

$$\begin{aligned} I^{0-}({\bar{x}})&:=\{k\in \{1,\ldots ,l\}\,|\,c^1_k({\bar{x}})=0\,\wedge \,c^2_k({\bar{x}})<0\},\\ I^{-0}({\bar{x}})&:=\{k\in \{1,\ldots ,l\}\,|\,c^1_k({\bar{x}})<0\,\wedge \,c^2_k({\bar{x}})=0\},\\ I^{0+}({\bar{x}})&:=\{k\in \{1,\ldots ,l\}\,|\,c^1_k({\bar{x}})=0\,\wedge \,c^2_k({\bar{x}})>0\},\\ I^{+0}({\bar{x}})&:=\{k\in \{1,\ldots ,l\}\,|\,c^1_k({\bar{x}})>0\,\wedge \,c^2_k({\bar{x}})=0\},\\ I^{-+}({\bar{x}})&:=\{k\in \{1,\ldots ,l\}\,|\,c^1_k({\bar{x}})<0\,\wedge \,c^2_k({\bar{x}})>0\},\\ I^{+-}({\bar{x}})&:=\{k\in \{1,\ldots ,l\}\,|\,c^1_k({\bar{x}})>0\,\wedge \,c^2_k({\bar{x}})<0\},\\ I^{00}({\bar{x}})&:=\{k\in \{1,\ldots ,l\}\,|\,c^1_k({\bar{x}})=0\,\wedge \,c^2_k({\bar{x}})=0\},\\ I^{--}({\bar{x}})&:=\{k\in \{1,\ldots ,l\}\,|\,c^1_k({\bar{x}})<0\,\wedge \,c^2_k({\bar{x}})<0\}. \end{aligned}$$

Note that these index sets form a disjoint partition of $\{1,\ldots ,l\}$.

In order to avoid the introduction of binary variables or the appearance of nonsmooth constraints (which are possible drawbacks connected to the elimination of the logical OR as depicted in Sect. 1), it is reasonable to consider the following associated optimization problem with switching constraints:

$$\begin{aligned} \begin{aligned} f(x)&\,\rightarrow \,\min \limits _{x,z}&\\ g_i(x)&\,\le \,0&\qquad&i=1,\ldots ,m&\\ h_j(x)&\,=\,0&\qquad&j=1,\ldots ,p&\\ z^1_k,z^2_k&\,\le \,0&\qquad&k=1,\ldots ,l&\\ (c^1_k(x)-z^1_k)(c^2_k(x)-z^2_k)&\,=\,0&\qquad&k=1,\ldots ,l.&\end{aligned} \end{aligned}$$

(SC-MPEOC)

In the remaining part of this section, we aim for the derivation of necessary optimality conditions for (MPEOC) via its surrogate (SC-MPEOC).

7.1 On the switching-constrained reformulation of an either-or-constrained problem

In this section, we interrelate the local and global minimizers of the programs (MPEOC) and (SC-MPEOC). Let us start with the consideration of locally optimal solutions.

Lemma 7.1

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a locally optimal solution of (MPEOC). Furthermore, define ${\bar{z}}^1,{\bar{z}}^2\in {\mathbb {R}}^l$ as stated below for any $k\in \{1,\ldots ,l\}$:

$$\begin{aligned} \begin{aligned} {\bar{z}}^1_k&:= {\left\{ \begin{array}{ll} c^1_k({\bar{x}}) &{}\quad \text {if}\;k\in I^{-0}({\bar{x}})\cup I^{-+}({\bar{x}})\cup I^{--}({\bar{x}}),\\ -1 &{}\quad \text {if}\;k\in I^{0-}({\bar{x}}),\\ 0 &{}\quad \text {if}\;k\in I^{0+}({\bar{x}})\cup I^{+0}({\bar{x}})\cup I^{+-}({\bar{x}})\cup I^{00}({\bar{x}}), \end{array}\right. } \\ {\bar{z}}^2_k&:= {\left\{ \begin{array}{ll} c^2_k({\bar{x}}) &{}\quad \text {if}\;k\in I^{0-}({\bar{x}})\cup I^{+-}({\bar{x}})\cup I^{--}({\bar{x}}),\\ -1 &{}\quad \text {if}\;k\in I^{-0}({\bar{x}}),\\ 0 &{}\quad \text {if}\;k\in I^{0+}({\bar{x}})\cup I^{+0}({\bar{x}})\cup I^{-+}({\bar{x}})\cup I^{00}({\bar{x}}). \end{array}\right. } \end{aligned} \end{aligned}$$

(11)

Then, $({\bar{x}},{\bar{z}}^1,{\bar{z}}^2)$ is a locally optimal solution of (SC-MPEOC).

Proof

Clearly, we have ${\bar{z}}^1,{\bar{z}}^2\le 0$. Furthermore, one obtains

$$\begin{aligned} (c^1_k({\bar{x}})-{\bar{z}}^1_k)(c^2_k({\bar{x}})-{\bar{z}}^2_k) = {\left\{ \begin{array}{ll} 1\cdot 0 &{}\quad \text {if}\; k\in I^{0-}({\bar{x}}),\\ 0\cdot 1 &{}\quad \text {if}\; k\in I^{-0}({\bar{x}}),\\ 0\cdot c^2_k({\bar{x}}) &{}\quad \text {if}\; k\in I^{0+}({\bar{x}})\cup I^{-+}({\bar{x}}),\\ c^1_k({\bar{x}})\cdot 0 &{}\quad \text {if}\; k\in I^{+0}({\bar{x}})\cup I^{+-}({\bar{x}}),\\ 0\cdot 0 &{}\quad \text {if}\; k\in I^{00}({\bar{x}})\cup I^{--}({\bar{x}}) \end{array}\right. } \end{aligned}$$

(12)

for any $k\in \{1,\ldots ,l\}$, i.e. $({\bar{x}},{\bar{z}}^1,{\bar{z}}^2)$ is feasible to (SC-MPEOC).

Suppose on the contrary that $({\bar{x}},{\bar{z}}^1,{\bar{z}}^2)$ is no local minimizer of (SC-MPEOC). Then, we find a sequence $\{(x_s,z^1_s,z^2_s)\}_{s\in {\mathbb {N}}}\subset {\mathbb {R}}^n\times {\mathbb {R}}^l\times {\mathbb {R}}^l$ of points which are feasible to (SC-MPEOC) such that $x_s\rightarrow {\bar{x}}$, $z^1_s\rightarrow {\bar{z}}^1$, and $z^2_s\rightarrow {\bar{z}}^2$ as well as $f(x_s)<f({\bar{x}})$ for all $s\in {\mathbb {N}}$ hold true. By construction, $c^1_k(x_s)\le 0$ or $c^2_k(x_s)\le 0$ is valid for all $k\in \{1,\ldots ,l\}$ and $s\in {\mathbb {N}}$. Thus, $x_s$ is feasible to (MPEOC) for all $s\in {\mathbb {N}}$. From $x_s\rightarrow {\bar{x}}$ and the local optimality of ${\bar{x}}$ for (MPEOC) we infer a contradiction.$\square$

We note that formula (11) provides only one possible construction which assigns to a feasible point of (MPEOC) a feasible point of (SC-MPEOC). Particularly, if ${\bar{x}}\in {\mathbb {R}}^n$ is a local minimizer of (MPEOC), then there exist several locally optimal solutions of (SC-MPEOC) associated with ${\bar{x}}$. However, the particular point we considered in the above lemma will be beneficial for our investigations in Sect. 7.2.

The following example depicts that local minimizers of (SC-MPEOC) do not generally need to correspond to locally optimal solutions of (MPEOC).

Example 7.1

Let us consider the simple program

$$\begin{aligned} \begin{aligned} (x_1-1)^2&\,\rightarrow \,\min \\ x_1\,\le \, 0\,\vee \,x_2&\,\le \,0 \end{aligned} \end{aligned}$$

(13)

as well as its continuous reformulation

$$\begin{aligned} \begin{aligned} (x_1-1)^2&\,\rightarrow \,\min \limits _{x,z}\\ z^1,z^2&\,\le \,0\\ (x_1-z^1)(x_2-z^2)&\,=\,0. \end{aligned} \end{aligned}$$

(14)

The set of global minimizers associated with (13) is given by $\{(1,t)\,|\,t\le 0\}$. There do not exist local minimizers of (13) which are different from its globally optimal solutions. Consider the point $({\bar{x}}_1,{\bar{x}}_2,{\bar{z}}^1,{\bar{z}}^2):=(0,-\,1,0,-\,2)$ which is feasible to (14). We show that this point is a local minimizer of this program. Note that its associated objective value can only decrease if the $x_1$-component enlarges to some $\varepsilon \in (0,1]$. Thus, if $(\varepsilon ,x_2,z^1,z^2)$ is feasible to (14), we have $\varepsilon -z^1>0$ and, thus, $x_2=z^2$ due to the presence of the switching constraint. This, however, shows

$$\begin{aligned} \begin{aligned} \left\| ({\bar{x}}_1,{\bar{x}}_2,{\bar{z}}^1,{\bar{z}}^2)-(\varepsilon ,x_2,z^1,z^2)\right\| _{2}^2&\ge \varepsilon ^2+(x_2+1)^2+(z^2+2)^2\\&\ge (x_2+1)^2+(x_2+2)^2\ge \tfrac{1}{2}. \end{aligned} \end{aligned}$$

Thus, $({\bar{x}}_1,{\bar{x}}_2,{\bar{z}}^1,{\bar{z}}^2)$ is a local minimizer of (14) while $({\bar{x}}_1,{\bar{x}}_2)$ is no locally optimal solution of (13). Similarly, one can show that $({\tilde{x}}_1,{\tilde{x}}_2,{\tilde{z}}^1,{\tilde{z}}^2):=(0,0,0,-\,2)$ is a local minimizer of (14) while $({\tilde{x}}_1,{\tilde{x}}_2)$ does not provide a local minimizer of (13). Note that in these situations, the respective index sets $I^{0-}({\bar{x}}_1,{\bar{x}}_2)$ and $I^{00}({\tilde{x}}_1,{\tilde{x}}_2)$ are nonempty.

Despite the above example, it can be shown that locally optimal solutions associated with (SC-MPEOC) correspond to local minimizers of (MPEOC) under additional assumptions.

Lemma 7.2

Let $({\bar{x}},{\bar{z}}^1,{\bar{z}}^2)\in {\mathbb {R}}^n\times {\mathbb {R}}^l\times {\mathbb {R}}^l$ be a locally optimal solutions of the problem (SC-MPEOC). Furthermore, assume that the index sets $I^{-0}({\bar{x}})$, $I^{0-}({\bar{x}})$, and $I^{00}({\bar{x}})$ are empty. Then, ${\bar{x}}$ is a local minimizer of (MPEOC).

Proof

Assume on the contrary that ${\bar{x}}$ is no local minimizer of (MPEOC). Then, there exists a sequence $\{x_s\}_{s\in {\mathbb {N}}}\subset {\mathbb {R}}^n$ of points feasible to (MPEOC) which converges to ${\bar{x}}$ such that $f(x_s)<f({\bar{x}})$ holds true for all $s\in {\mathbb {N}}$. Below, we construct sequences $\{z^1_s\}_{s\in {\mathbb {N}}},\{z^2_s\}_{s\in {\mathbb {N}}}\subset {\mathbb {R}}^l$ such that $z^1_s\rightarrow {\bar{z}}^1$, $z^2_s\rightarrow {\bar{z}}^2$, and $(x_s,z^1_s,z^2_s)$ is feasible to (SC-MPEOC) for sufficiently large $s\in {\mathbb {N}}$. This yields a contradiction to the local optimality of $({\bar{x}},{\bar{z}}^1,{\bar{z}}^2)$ for (SC-MPEOC).

Due to continuity of $c^1$ and $c^2$, we note that the inclusions

$$\begin{aligned} \begin{aligned} I^{--}({\bar{x}})&\subset I^{--}(x_s),\\ I^{0+}({\bar{x}})\cup I^{-+}({\bar{x}})&\subset I^{0+}(x_s)\cup I^{-+}(x_s),\\ I^{+0}({\bar{x}})\cup I^{+-}({\bar{x}})&\subset I^{+0}(x_s)\cup I^{+-}(x_s) \end{aligned} \end{aligned}$$

(15)

hold true for sufficiently large $s\in {\mathbb {N}}$. Fix $k\in \{1,\ldots ,l\}$.

If $k\in I^{--}({\bar{x}})$ is valid, then we have $0>c^1_k({\bar{x}})={\bar{z}}^1_k$ or $0>c^2_k({\bar{x}})={\bar{z}}^2_k$. W.l.o.g. we assume $c^1_k({\bar{x}})={\bar{z}}^1_k$ and set

$$\begin{aligned} \forall s\in {\mathbb {N}}:\quad z^1_{s,k}:=c^1_k(x_s),\qquad z^2_{s,k}:={\bar{z}}^2_k. \end{aligned}$$

On the other hand, if $k\in I^{0+}({\bar{x}})\cup I^{-+}({\bar{x}})$ is valid, then we infer $c^1_k({\bar{x}})={\bar{z}}^1_k$ from $c^2_k({\bar{x}})-{\bar{z}}^2_k\ge c^2_k({\bar{x}})>0$. In this case, we set

$$\begin{aligned} \forall s\in {\mathbb {N}}:\quad z^1_{s,k}:=c^1_k(x_s),\qquad z^2_{s,k}:={\bar{z}}^2_{k}. \end{aligned}$$

Finally, $k\in I^{+0}({\bar{x}})\cup I^{+-}({\bar{x}})$ is possible. Due to $c^1_k({\bar{x}})-{\bar{z}}^1_k\ge c^1_k({\bar{x}})>0$, we have $c^2_k({\bar{x}})={\bar{z}}^2_k$. Let us set

$$\begin{aligned} \forall s\in {\mathbb {N}}:\quad z^1_{s,k}:={\bar{z}}^1_k,\qquad z^2_{s,k}:=c^2_{k}(x_s). \end{aligned}$$

By construction, the convergences $z^1_s\rightarrow {\bar{z}}^1$ and $z^2_s\rightarrow {\bar{z}}^2$ hold true. Furthermore, by means of (15), the points $(x_s,z^1_s,z^2_s)$ are feasible to (SC-MPEOC) for sufficiently large $s\in {\mathbb {N}}$. As mentioned above, this completes the proof.$\square$

Finally, let us take a look at globally optimal solutions. Here, the situation is much more comfortable.

Lemma 7.3

• 1. Let ${\bar{x}}\in {\mathbb {R}}^n$ be a globally optimal solution of (MPEOC). Furthermore, define ${\bar{z}}^1,{\bar{z}}^2\in {\mathbb {R}}^l$ as stated in (11). Then, $({\bar{x}},{\bar{z}}^1,{\bar{z}}^2)$ is a globally optimal solution of (SC-MPEOC).

• 2. Let $({\bar{x}},{\bar{z}}^1,{\bar{z}}^2)\in {\mathbb {R}}^n\times {\mathbb {R}}^l\times {\mathbb {R}}^l$ by a globally optimal solution of (SC-MPEOC). Then, ${\bar{x}}$ is a globally optimal solution of (MPEOC).

Proof

The proof of this result directly follows from the following observations: If $x\in {\mathbb {R}}^n$ is feasible to (MPEOC), then we find $z^1,z^2\in {\mathbb {R}}^l$ such that $(x,z^1,z^2)$ is feasible to (SC-MPEOC) [e.g. via construction (11)]. If, on the other hand, the point $({\tilde{x}},{\tilde{z}}^1,{\tilde{z}}^2)\in {\mathbb {R}}^n\times {\mathbb {R}}^l\times {\mathbb {R}}^l$ is feasible to (SC-MPEOC), then ${\tilde{x}}$ is feasible to (MPEOC).$\square$

Again, we need to remark that there exist several globally optimal solutions of (SC-MPEOC) which correspond to a particular global minimizer of (MPEOC).

7.2 Necessary optimality conditions and constraint qualifications

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a feasible point of (MPEOC). If it is a locally optimal solution of this problem, then, due to Lemma 7.1, $({\bar{x}},{\bar{z}}^1,{\bar{z}}^2)$ is a locally optimal solution of the switching-constrained problem (SC-MPEOC) where ${\bar{z}}^1$ and ${\bar{z}}^2$ are defined as in (11). Thus, the W-, M-, or S-stationarity conditions of (SC-MPEOC) may provide necessary optimality conditions for (MPEOC) provided suitable constraint qualifications are valid.

In order to state these stationarity conditions, we first recall that for any feasible point $(x,z^1,z^2)\in {\mathbb {R}}^n\times {\mathbb {R}}^l\times {\mathbb {R}}^l$ of (SC-MPEOC), the sets $I^G(x,z^1,z^2)$, $I^H(x,z^1,z^2)$, and $I^{GH}(x,z^1,z^2)$ are given by

$$\begin{aligned} \begin{aligned} I^{G}(x,z^1,z^2)&=\{k\in \{1,\ldots ,l\}\,|\,c^1_k(x)=z^1_k\,\wedge \,c^2_k(x)\ne z^2_k\},\\ I^{H}(x,z^1,z^2)&=\{k\in \{1,\ldots ,l\}\,|\,c^1_k(x)\ne z^1_k\,\wedge \,c^2_k(x)= z^2_k\},\\ I^{GH}(x,z^1,z^2)&=\{k\in \{1,\ldots ,l\}\,|\,c^1_k(x)=z^1_k\,\wedge \,c^2_k(x)= z^2_k\}. \end{aligned} \end{aligned}$$

For the particular point $({\bar{x}},{\bar{z}}^1,{\bar{z}}^2)$ constructed in (11), we obtain

$$\begin{aligned} \begin{aligned} I^{G}({\bar{x}},{\bar{z}}^1,{\bar{z}}^2)&=I^{-0}({\bar{x}})\cup I^{0+}({\bar{x}})\cup I^{-+}({\bar{x}}),\\ I^{H}({\bar{x}},{\bar{z}}^1,{\bar{z}}^2)&=I^{0-}({\bar{x}})\cup I^{+0}({\bar{x}})\cup I^{+-}({\bar{x}}),\\ I^{GH}({\bar{x}},{\bar{z}}^1,{\bar{z}}^2)&=I^{00}({\bar{x}})\cup I^{--}({\bar{x}}) \end{aligned} \end{aligned}$$

from (12). Taking the precise definition of ${\bar{z}}^1$ and ${\bar{z}}^2$ into account, the associated W-stationarity system of (SC-MPEOC) is given by

$$\begin{aligned}&0=\nabla f({\bar{x}})+\sum \limits _{i\in I^g({\bar{x}})}\lambda _i\nabla g_i({\bar{x}})+\sum \limits _{j\in I^h}\rho _j\nabla h_j({\bar{x}})\\&\qquad +\,\sum \limits _{k=1}^l\bigl [\mu _k\nabla c^1_k({\bar{x}})+\nu _k\nabla c^2_k({\bar{x}})\bigr ],\\&0=\alpha -\mu ,\\&0=\beta -\nu ,\\&\forall i\in I^g({\bar{x}}):\,\lambda _i\ge 0,\\&\forall k\in I^{0-}({\bar{x}})\cup I^{-0}({\bar{x}})\cup I^{-+}({\bar{x}})\cup I^{--}({\bar{x}}):\,\alpha _k=0,\\&\forall k\in I^{0+}({\bar{x}})\cup I^{+0}({\bar{x}})\cup I^{+-}({\bar{x}})\cup I^{00}({\bar{x}}):\,\alpha _k\ge 0,\\&\forall k\in I^{0-}({\bar{x}})\cup I^{-0}({\bar{x}})\cup I^{+-}({\bar{x}})\cup I^{--}({\bar{x}}):\,\beta _k=0,\\&\forall k\in I^{0+}({\bar{x}})\cup I^{+0}({\bar{x}})\cup I^{-+}({\bar{x}})\cup I^{00}({\bar{x}}):\,\beta _k\ge 0,\\&\forall k\in I^{0-}({\bar{x}})\cup I^{+0}({\bar{x}})\cup I^{+-}({\bar{x}}):\,\mu _k=0,\\&\forall k\in I^{-0}({\bar{x}})\cup I^{0+}({\bar{x}})\cup I^{-+}({\bar{x}}):\,\nu _k=0. \end{aligned}$$

We eliminate the multipliers $\alpha$ and $\beta$ in order to come up with the following natural definitions.

Definition 7.1

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a feasible point of (MPEOC). Then, ${\bar{x}}$ is called

• 1. weakly stationary, W-stationary for short, if there exist multipliers which solve the following system:

  $$\begin{aligned} \begin{aligned}&0=\nabla f({\bar{x}})+\sum \limits _{i\in I^g({\bar{x}})}\lambda _i\nabla g_i({\bar{x}})+\sum \limits _{j\in I^h}\rho _j\nabla h_j({\bar{x}})\\&\qquad +\,\sum \limits _{k\in I^{0+}({\bar{x}})\cup I^{00}({\bar{x}})}\mu _k\nabla c^1_k({\bar{x}}) +\sum \limits _{k\in I^{+0}({\bar{x}})\cup I^{00}({\bar{x}})}\nu _k\nabla c^2_k({\bar{x}}),\\&\forall i\in I^g({\bar{x}}):\,\lambda _i\ge 0,\\&\forall k\in I^{0+}({\bar{x}})\cup I^{00}({\bar{x}}):\,\mu _k\ge 0,\\&\forall k\in I^{+0}({\bar{x}})\cup I^{00}({\bar{x}}):\,\nu _k\ge 0. \end{aligned} \end{aligned}$$

  (16)

• 2. Mordukhovich–stationary, M-stationary for short, if there exist multipliers which satisfy the conditions (16) and

  $$\begin{aligned} \forall k\in I^{00}({\bar{x}}):\,\mu _k\nu _k=0. \end{aligned}$$

• 3. strongly stationary, S-stationary for short, if there exist multipliers which satisfy the conditions (16) and

  $$\begin{aligned} \forall k\in I^{00}({\bar{x}}):\,\mu _k=0\,\wedge \,\nu _k=0. \end{aligned}$$

Next, we apply the MPSC-tailored constraint qualifications to the surrogate problem (SC-MPEOC) at the point $({\bar{x}},{\bar{z}}^1,{\bar{z}}^2)$ in order to ensure that a locally optimal solution ${\bar{x}}\in {\mathbb {R}}^n$ of (MPEOC) satisfies the M- or S-stationarity conditions from Definition 7.1. Here, we first present a result which addresses the S-stationarity conditions. It directly follows from Theorem 4.1.

Theorem 7.1

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a locally optimal solution of (MPEOC) and assume that the following vectors are linearly independent:

$$\begin{aligned} \begin{aligned}&\nabla g_i({\bar{x}})&i\in I^g({\bar{x}}),\\&\nabla h_j({\bar{x}})&j\in I^h,\\&\nabla c^1_k({\bar{x}})&k\in I^{0+}({\bar{x}})\cup I^{00}({\bar{x}}),\\&\nabla c^2_k({\bar{x}})&k\in I^{+0}({\bar{x}})\cup I^{00}({\bar{x}}). \end{aligned} \end{aligned}$$

Then, ${\bar{x}}$ is an S-stationary point of (MPEOC).

Proof

Let ${\bar{z}}^1,{\bar{z}}^2\in {\mathbb {R}}^l$ be the vectors defined in (11). Then, due to Lemma 7.1, $({\bar{x}},{\bar{z}}^1,{\bar{z}}^2)$ is a locally optimal solution of (SC-MPEOC).

Next, we show that the only multipliers which satisfy

are constantly zero. Recall that $e^l_k\in {\mathbb {R}}^l$ denotes the kth unit vector in ${\mathbb {R}}^l$ for all $k=1,\ldots ,l$. From the obvious equalities $\alpha =\mu$ and $\beta =\nu$, we deduce $\mu _k=0$ for all $k\in I^{0-}({\bar{x}})\cup I^{-0}({\bar{x}})\cup I^{+0}({\bar{x}})\cup I^{-+}({\bar{x}})\cup I^{+-}({\bar{x}})\cup I^{--}({\bar{x}})$ as well as $\nu _k=0$ for all $k\in I^{0-}({\bar{x}})\cup I^{-0}({\bar{x}})\cup I^{0+}({\bar{x}})\cup I^{-+}({\bar{x}})\cup I^{+-}({\bar{x}})\cup I^{--}({\bar{x}})$. Now, we only take a look at the first component, i.e. the derivatives w.r.t. x. The constraint qualification postulated in the theorem’s assumptions implies $\lambda _i=0$ ($i\in I^g({\bar{x}})$), $\rho _j=0$ ($j\in I^h$), $\mu _k=0$ ($k\in I^{0+}({\bar{x}})\cup I^{00}({\bar{x}})$), and $\nu _k=0$ ($k\in I^{+0}({\bar{x}})\cup I^{00}({\bar{x}})$). This finally yields $\alpha =\mu =0$ and $\beta =\nu =0$.

Thus, MPSC-LICQ is valid at $({\bar{x}},{\bar{z}}^1,{\bar{z}}^2)$ for (SC-MPEOC). By means of Theorem 4.1, $({\bar{x}},{\bar{z}}^1,{\bar{z}}^2)$ is an S-stationary point of (SC-MPEOC), i.e. ${\bar{x}}$ is an S-stationary point of (MPEOC).$\square$

Using a local decomposition approach, the above result can be obtained in a completely different way which is related to the proof strategy we used to validate Theorem 4.1.

Remark 7.1

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a locally optimal solution of (MPEOC) where the constraint qualification of Theorem 7.1 holds and set

$$\begin{aligned} \begin{aligned} I^{-}_1({\bar{x}})&:=I^{-0}({\bar{x}})\cup I^{-+}({\bar{x}})\cup I^{--}({\bar{x}}),\\ I^{-}_2({\bar{x}})&:=I^{0-}({\bar{x}})\cup I^{+-}({\bar{x}})\cup I^{--}({\bar{x}}). \end{aligned} \end{aligned}$$

Then, for any partition $(\beta _1,\beta _2)\in {\mathcal {P}}(I^{00}({\bar{x}}))$, ${\bar{x}}$ is a locally optimal solution of

as well since the feasible set of (MPEOC$(\beta _1,\beta _2)$) is a subset of the feasible set of (MPEOC) and ${\bar{x}}$ is feasible to (MPEOC$(\beta _1,\beta _2)$). Let us consider the particular partitions $(\beta _1,\beta _2)\in \{(I^{00}({\bar{x}}),\varnothing ),(\varnothing ,I^{00}({\bar{x}}))\}$. Since the constraint qualification of Theorem 7.1 is valid, standard LICQ holds for the associated problems (MPEOC$(\beta _1,\beta _2)$) at ${\bar{x}}$. Consequently, the associated respective KKT conditions hold. Let $\lambda ^1_i$ ($i\in I^g({\bar{x}})$), $\rho ^1_j$ ($j\in I^h$), $\mu ^1_k$ ($k\in I^{0+}({\bar{x}})\cup I^{00}({\bar{x}})$), $\nu ^1_k$ ($k\in I^{+0}({\bar{x}})$) and $\lambda ^2_i$ ($i\in I^g({\bar{x}})$), $\rho ^2_j$ ($j\in I^h$), $\mu ^2_k$ ($k\in I^{0+}({\bar{x}})$), $\nu ^2_k$ ($k\in I^{+0}({\bar{x}})\cup I^{00}({\bar{x}})$) be the respective Lagrange multipliers. Then, we obtain

$$\begin{aligned}&0=\sum \limits _{i\in I^g({\bar{x}})}(\lambda ^1_i-\lambda ^2_i)\nabla g_i({\bar{x}}) +\sum \limits _{j\in I^h}(\rho ^1_j-\rho ^2_j)\nabla h_j({\bar{x}})\\&\qquad +\,\sum \limits _{k\in I^{0+}({\bar{x}})}(\mu ^1_k-\mu ^2_k)\nabla c^1_k({\bar{x}}) +\sum \limits _{k\in I^{+0}({\bar{x}})}(\nu ^1_k-\nu ^2_k)\nabla c^2_k({\bar{x}})\\&\qquad +\,\sum \limits _{k\in I^{00}({\bar{x}})}\mu ^1_k\nabla c^1_k({\bar{x}}) -\sum \limits _{k\in I^{00}({\bar{x}})}\nu ^2_k\nabla c^2_k({\bar{x}}). \end{aligned}$$

Exploiting the linear independence of all appearing vectors, we easily obtain the relation $\mu ^1_k=\nu ^2_k=0$ for all $k\in I^{00}({\bar{x}})$. It follows that the multipliers $\lambda ^1_i$ ($i\in I^g({\bar{x}})$), $\rho ^1_j$ ($j\in I^h$), $\mu ^1_k$ ($k\in I^{0+}({\bar{x}})\cup I^{00}({\bar{x}})$), and $\nu ^2_k$ ($k\in I^{+0}({\bar{x}})\cup I^{00}({\bar{x}})$) solve the S-stationarity system of (MPEOC).

We note that the derivation of the W-, M-, and S-stationarity conditions of (MPEOC) via the construction from Lemma 7.1 heavily relies on the particular point from (11). The above remark, however, justifies that this choice was well founded since the obtained results are of reasonable strength, i.e. they parallel those results one would obtain via standard local decomposition.

Below, situations are presented where M-stationarity is an inherent necessary optimality condition for (MPEOC).

Theorem 7.2

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a locally optimal solution of (MPEOC) where the data functions g, h, $c^1$, and $c^2$ are affine. Then, ${\bar{x}}$ is an M-stationary point of (MPEOC).

Proof

Due to the assumptions of the theorem, the data functions which model the constraints of the surrogate switching-constrained problem (SC-MPEOC) are affine as well. By means of Corollary 5.3, $({\bar{x}},{\bar{z}}^1,{\bar{z}}^2)$, where ${\bar{z}}^1,{\bar{z}}^2\in {\mathbb {R}}^l$ are defined in (11), is an M-stationary point of (SC-MPEOC). Thus, ${\bar{x}}$ is an M-stationary point of (MPEOC) and the proof is completed.$\square$

Theorem 7.3

Let ${\bar{x}}\in {\mathbb {R}}^n$ be a locally optimal solution of (MPEOC). Furthermore, assume that there exists a partition $(\beta _1,\beta _2)\in {\mathcal {P}}(I^{00}({\bar{x}}))$ such that standard GCQ is valid for (MPEOC$(\beta _1,\beta _2)$) at ${\bar{x}}$. Then, ${\bar{x}}$ is an M-stationary point of (MPEOC).

Proof

Noting that ${\bar{x}}$ is a locally optimal solution of (MPEOC$(\beta _1,\beta _2)$) where GCQ holds, it is a KKT point of the latter program. Particularly, there exist multipliers $\lambda _i$ ($i\in I^g({\bar{x}})$), $\rho _j$ ($j\in I^h$), $\mu _k$ ($k\in I^{0+}({\bar{x}})\cup \beta _1$), and $\nu _k$ ($k\in I^{+0}({\bar{x}})\cup \beta _2$) which solve the system

$$\begin{aligned}&0=\nabla f({\bar{x}})+\sum \limits _{i\in I^g({\bar{x}})}\lambda _i\nabla g_i({\bar{x}})+\sum \limits _{j\in I^h}\rho _j\nabla h_j({\bar{x}})\\&\qquad +\,\sum \limits _{k\in I^{0+}({\bar{x}})\cup \beta _1}\mu _k\nabla c^1_k({\bar{x}}) +\sum \limits _{k\in I^{+0}({\bar{x}})\cup \beta _2}\nu _k\nabla c^2_k({\bar{x}}),\\&\forall i\in I^g({\bar{x}}):\,\lambda _i\ge 0,\\&\forall k\in I^{0+}({\bar{x}})\cup \beta _1:\,\mu _k\ge 0,\\&\forall k\in I^{+0}({\bar{x}})\cup \beta _2:\,\nu _k\ge 0. \end{aligned}$$

Setting $\mu _k:=0$ ($k\in \beta _2$) as well as $\nu _k:=0$ ($k\in \beta _1$), we obtain that ${\bar{x}}$ is an M-stationary point of (MPEOC).$\square$

Finally, we present an example which shows that the assertions of Theorems 7.2 and 7.3 cannot be strengthened in general.

Example 7.2

We consider the optimization problem

$$\begin{aligned} \begin{aligned} (x_1+1)^2+x_2^2&\,\rightarrow \,\min \\ -x_1+x_2&\,\le \,0\\ -x_1\,\le \,0\,\vee \,-x_2&\,\le \,0. \end{aligned} \end{aligned}$$

Its unique globally optimal solution is given by ${\bar{x}}=(0,0)$ and $I^{00}({\bar{x}})=\{1\}$ holds true. Due to Theorems 7.2 or 7.3, ${\bar{x}}$ satisfies the M-stationarity conditions. Indeed, the multipliers $\lambda ^1_1=0$, $\mu ^1_1=2$, $\nu ^1_1=0$ and $\lambda ^2_1=2$, $\mu ^2_1=0$, $\nu ^2_1=2$ solve the associated M-stationarity system. Note that these multipliers do not solve the associated S-stationarity system since $\mu ^i_1$ and $\nu ^i_1$, $i=1,2$, do not vanish at the same time. Clearly, the constraint qualification from Theorem 7.1 is violated.

8 Final remarks

In this paper, we derived necessary optimality conditions as well as constraint qualifications for the abstract nonlinear model problem (MPSC), inferred that locally optimal solutions of discretized optimal control problems with switching constraints are S-stationary without additional requirements, and presented a novel reformulation as well as reasonable necessary optimality conditions for optimization problems with either-or-constraints. The derivation of second-order optimality conditions for (MPSC) should be possible taking into account that such results are available for the related classes of MPCCs, see [21, 34, 39], and MPVCs, see [23]. Moreover, using second-order information, it seems to be possible to discuss genericity properties of (MPSC) as it has been done for MPCCs, see e.g. [35]. Due to the special structure of (MPEOC), a separate analysis of this problem class seems to be a nearby topic of future research.

Relying on the First-Discretize-Then-Optimize approach for the numerical treatment of optimal control problems with switching constraints like (3), efficient computational solution methods for (MPSC) need to be developed in the future. Here, it might be possible to adapt well-known relaxation techniques for the numerical handling of MPCCs, see [27], or MPVCs, see [26], for that purpose. Taking into account that the comparatively strong regularity condition MPSC-LICQ is valid at all feasible points of problem (OCSC), see Lemma 6.1, these relaxation methods should be applicable to the setting of switching control. On the other hand, numerical methods for the computational solution of (MPSC) might be applicable to problems of type (MPEOC) as well. This is a promising approach in order to tackle either-or-constraints without the aid of tools from mixed-integer or nonsmooth optimization.