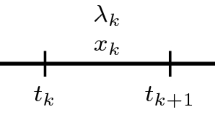A numerical study of transformed mixed-integer optimal control problems

Abstract

Time transformation is a ubiquitous tool in theoretical sciences, especially in physics. It can also be used to transform switched optimal control problems into control problems with a fixed switching order and purely continuous decisions. This approach is known either as enhanced time transformation, time-scaling, or switching time optimization (STO) for mixed-integer optimal control. The approach is well understood and used widely due to its many favorable properties. Recently, several extensions and algorithmic improvements have been proposed. We use an alternative formulation, the partial outer convexification (POC), to study convergence properties of (STO). We introduce the open-source software package ampl_mintoc (Sager et al., czeile/ampl_mintoc: Math programming c release, 2024, https://doi.org/10.5281/zenodo.12520490). It is based on AMPL, designed for the formulation of mixed-integer optimal control problems, and allows to use almost identical implementations for (STO) and (POC). We discuss and explain our main numerical result: (STO) is likely to result in more local minima for each discretization grid than (POC), but the number of local minima is asymptotically identical for both approaches.

1 Introduction

In this study, we consider mixed-integer optimal control problems. The integer aspect results from time-dependent control functions that are restricted to take values in a finite set. Prominent examples include gear switches, compressors and valves, the applicability of laws and regulations, combinations of administered drugs, performing measurements yes or no, or general on/off controls. See [49] for an online benchmark library. There are various mathematically equivalent ways to formulate such control problems. The choice of formulation usually has a large impact on solution algorithms, though. A convenient formulation is based on switched optimal control problems, where at any given point t of time exactly one of ${n_\omega }$ different right-hand sides $f_{j(t)}(x(t))$ is active. In practice, often a common drift term $f_0(x(t))$ is present, such that the ordinary differential equation reads as

$$\dot{x}(t) = f_0(x(t)) + f_{j(t)}(x(t))$$

where j(t) is the active mode at time $t \in {\mathcal {T}}:= [0,t_{N }]$. Note, that the interval starts at 0 without loss of generality. For example, $f_0$ could comprise the dynamics that are independent of a gear choice, such as the effect of steering or air friction, whereas the gear-specific dynamics $f_{j(t)}$ could be calculated using different transmission ratios and degrees of efficiency, e.g., [27].

In this study, we assume Lipschitz-continuity of the right-hand side functions $f_0$ and $f_{j(t)}$ for guaranteeing the existence of a (unique) ODE solution by the Picard-Lindelöf theorem [44]. Throughout the paper, we use the notation $[N] = \{1, 2, \ldots , N\}$ and $[N]_0 = \{0, 1, 2, \ldots , N\}$. Also, we use the exclusive-or operator $\bigoplus$ for choosing exactly one active mode for all time points and on the same time all other modes are inactive. We define the problem class of interest as follows.

Definition 1

(Mixed-integer optimal control problem) We refer to

$$\begin{aligned} \begin{array}{lrlll} \displaystyle \inf _{x(\cdot ), j(\cdot )} & {\phi (x(t_{N }))} & & & \\ {{\hbox {subject to}}} & & & & \\ {\displaystyle \bigoplus _{j(t) \in [{n_\omega }]}} & \dot{x}(t) & = f_0(x(t)) + f_{j(t)}(x(t)) & \quad \text {for } \; t \in {\mathcal {T}}\text { a.e.}, \\ & x(0) & = x_0, & & \end{array} \end{aligned}$$

(MIOCP)

as a mixed-integer optimal control problem (MIOCP) on a fixed time horizon ${\mathcal {T}}= [0,t_{N }]$ with differential states $x: {\mathcal {T}}\mapsto \mathbb {R}^{n_x}$, fixed initial values $x_0~\in ~\mathbb {R}^{n_x}$, and a continuous objective function $\phi :~\mathbb {R}^{n_x}~\mapsto ~\mathbb {R}$ of Mayer type. The degrees of freedom are switching decisions, i.e., the selection of the active mode j almost everywhere on ${\mathcal {T}}$.

In the following, we omit the time dependency of $f_{j(t)}$ and write $f_j$ instead for a more compact notation. There are a variety of different approaches to solve (MIOCP) to local or global optimality. They comprise indirect methods based on the global maximum principle, dynamic programming, moment relaxations, or direct first-discretize then-optimize methods which result in mixed integer nonlinear programs. A survey is beyond the scope of this paper and we refer to [6, 16, 17, 23, 27, 50, 52, 58] for further references.

Note that the modeling of practical problems may result in more general formulations than Problem (MIOCP), e.g., using additional continuous control functions $u: [0,t_{N }] \mapsto \mathbb {R}^{n_u}$, additional path constraints $0 \le c(x(t), u(t))$ (mode-specific or for all modes), a Lagrange term $\int _{0}^{t_{N }} L(x(\tau ))\textrm{d}\tau$ in the objective, non-fixed terminal time $t_{N }$, more general boundary conditions, path-control, combinatorial, dwell time, or vanishing constraints, multi-stage problems with changes in dynamics or even in the dimension, differential algebraic equations, or semi-discretized partial differential equations. In the interest of a clear presentation of the convergence properties, which are likely to carry over to the more general cases, and because above formulation covers our benchmark problems, we work in the following with Problem (MIOCP).

In this paper, we are going to numerically study convergence properties of two established approaches to (approximately) solve (MIOCP): switching time optimization (STO) [58] and partial outer convexification (POC) [50]. To our knowledge this is the first comparison of this type. In the interest of understanding the main differences between the two approaches, we use comparable implementations within a new open-source software package, similar notation and discretization grids, and two benchmark problems from the literature. The paper is organized as follows.

In Sect. 2, we survey a semi-discretization of the state equations of (MIOCP), namely (STO), and the relaxation of another semi-discritization of the state equations (POC). Thereby, in both cases the solution space is reduced to a finite-dimensional subspace of the feasible set. In the following, we will use the term ’approximation’ instead of (relaxation) of a semi-discretization, whenever we compare the two approaches. Both are formulated in a way such that the small, but fundamental difference between them is clearly visible. We also discuss their relation to problem (MIOCP). We derive approximation properties of the two approaches in Sect. 3. In Sect. 4, two test problems are presented. In Sect. 5, we describe the novel open-source software package ampl_mintoc. It is placed on top of AMPL [13] and allows to formulate finite-dimensional approximations of (mixed-integer) optimal control problems in a compact way. In Sect. 6, we present simulation- and optimization-based numerical results for comparing the two approaches. In Sect. 7 we discuss these results, focusing on nonconvexity, algorithmic properties and number of local minima. A summary concludes the paper.

2 Switching time optimization and partial outer convexification

In this paper, we focus on two approximations (MIOCP) that have received increasing attention in the last years. In the following, let

$$\mathcal {G}_N:= \{t_0, t_1, t_2, \ldots , t_{N}\}$$

be an ordered set of equidistant time points $t_i = i \Delta t$ for all $i\in [N]_0$ and grid size $\Delta t > 0$. We remark that the number of discretization intervals N is assumed to be fixed in the remainder.

2.1 Switching time optimization

The first one is referred to as enhanced time transformation or as switching time optimization in the literature. The underlying idea is fundamental in many sciences, particularly in physics, e.g., [7]. A dynamic process with differential states $x: [0,t_{N }] \mapsto \mathbb {R}^{n_x}$ specified via $f: \mathbb {R}^{n_x} \mapsto \mathbb {R}^{n_x}$ and

$$\begin{aligned} \dot{x}(t) = f(x(t)) \quad t \in [0,t_{N }] \end{aligned}$$

(1)

can be written equivalently as

$$\begin{aligned} \dot{x}(\tau ) = t_{N }\; f(x(\tau )) \quad \tau \in [0,1], \end{aligned}$$

(2)

exploiting that $t=t_{N }\tau$ implies $\textrm{d} t = t_{N }\textrm{d} \tau$ (in a slightly abused Leibniz’s notation). The advantage is obvious if the terminal time $t_{N }$ is unknown. Formulation (2) allows the treatment of $t_{N }$ as an optimization variable, while the integration horizon is fixed. By gluing several horizons with fixed horizon lengths together, this idea can also be applied to several interior time points, e.g.,

$$\begin{aligned} \dot{x}(t) = \left\{ \begin{array}{ll} f_1(x(t)) & \text { if } t \in [0,t_1), \\ f_2(x(t)) & \text { if } t \in [t_1,t_2], \end{array} \right. \end{aligned}$$

(3)

can be written equivalently as

$$\begin{aligned} \dot{x}(\tau ) = \left\{ \begin{array}{rl} t_1 \; f_1(x(\tau )) & \text { if } \tau \in [0,1), \\ (t_2-t_1) \; f_2(x(\tau )) & \text { if } \tau \in [1,2]. \end{array} \right. \end{aligned}$$

(4)

Applying this idea to transform problem (MIOCP) needs only three more ingredients. First, we define two time grids in Definition 2. The second step is to assume an order in which the switches occur. The corresponding switching sequence is introduced in Definition 3. Finally, in Definition 4 we make sure that the variables indicating the duration of the active modes, denoted by $w_{ij}$, are normalized to get an equivalence to the outer grid time points of the original time horizon.

Definition 2

(Equidistant grids) Let numbers $N \in \mathbb {N}$ and $n_\sigma \in \mathbb {N}$ be given and let $\Delta t$ be the equidistant outer grid size. We write

$${{\mathcal {T}}_i}:=[t_{i-1}, t_i), \quad i\in [N], t_i \in \mathcal {G}_N, $$

for a coarse grid partition ${\mathcal {T}}=\cup _{i\in [N]} {{\mathcal {T}}_i}$. Furthermore, let

$$\begin{aligned} {\mathcal {T}}_{ij}:=[t_{i-1,j-1}, t_{i-1,j}), \quad i \in [N], \ j \in [n_\sigma ] \end{aligned}$$

for a fine grid partition ${{\mathcal {T}}_i}= \cup _{j \in [n_\sigma ]} {\mathcal {T}}_{ij}$ with equidistant inner grid points $t_{ij} := t_i + j \frac{\Delta t}{n_\sigma }$ and inner grid size $\Delta _{\textrm{in}} t := \frac{\Delta t}{n_\sigma }$. We include $t_N$ in the last outer and inner intervals $\mathcal {T}_{N}$ and $\mathcal {T}_{N,n_\sigma }$, respectively.

We stress that despite fixed inner and outer grids, we still optimize the duration of mode activations based on the control variables defined in Definition 4. For this, we specify the sequence of active control modes.

Definition 3

(Switching sequence) Let $n_\sigma \in \mathbb {N}$ be the maximum number of control mode activations per outer grid interval. We define a switching sequence as a surjective mapping $\sigma : [n_{\sigma }] \mapsto [n_\omega ]$ on ${{\mathcal {T}}_i}$ and, repeated N times, also on ${\mathcal {T}}$.

The above definition implies that at most $n_\sigma -1$ switches are possible per outer interval. The choice $n_\sigma =n_\omega$ allows to activate each control mode once on every interval, in a specific order. With larger choices of $n_\sigma$ arbitrary switching sequences can be generated by shrinking the duration of specific mode activations to zero.

Definition 4

(Feasible control set) For a given number of intervals N and maximum number of control mode activations $n_\sigma$, we define the feasible set of controls $\mathcal {W}$ as:

$$\mathcal {W} := \left\{ w \in \mathbb {R}^{N \times n_\sigma }: w_{ij} \in [0,1] \;\forall \; i \in [N], j \in [n_\sigma ], \; \sum _{j=1}^{n_\sigma } w_{ij} = 1 \;\forall \; i \in [N] \right\} .$$

The variables $w_{ij}$ indicate how the time points of the inner grid move and can thus be interpreted as the fraction of the duration $w_{ij}\Delta t$ of the activated mode $\sigma (j)$ on the interval ${{\mathcal {T}}_i}$. The condition $\sum _{j=1}^{n_\sigma } w_{ij} = 1$, which is often referred to as one-hot condition, ensures that the outer grid points $t_i$ are not moved by the time-transformation.

We consider the differential equation with a transformed time $\tau$ on time intervals of unit length as in (4), with time scaling depending on $w_{ij}$ for all $i\in [N]$ and $j\in [n_\sigma ]$:

$$\begin{aligned} \dot{x}(\tau ) = w_{ij} \Delta t \; (f_0(x(\tau )) + f_{\sigma (j)}(x(\tau ))), \,\,\, \tau \in [(i-1)n_{\sigma }+j-1, (i-1)n_{\sigma }+j]. \nonumber \\ \end{aligned}$$

(5)

For comparability of the problem formulations, we scale the total length of the intervals for $\tau$ to the length of $\mathcal {T}$. This is equivalent to scaling the individual intervals for $\tau$ of length 1 to the length of $\mathcal {T}_{ij}$ via multiplication with $\frac{1}{\Delta _{\textrm{in}}t}$. Exploiting $n_\sigma = \frac{\Delta t}{\Delta _{\textrm{in}}t}$ according to Definition 2 and using t again instead of $\tau$ to denote the time variable, we introduce the problem (P-STO):

Definition 5

(Switching time optimization) With the definitions from above we refer to

$$\begin{aligned} \begin{array}{lrlll} \displaystyle \min _{x, w \in \mathcal {W}} & {\phi (x(t_{N }))} & & & \\ {{\hbox {subject to}}} & & & & \\ & \dot{x}(t) & =& w_{ij} \; n_\sigma (f_0(x(t)) + f_{\sigma (j)}(x(t))), & \quad t \in {\mathcal {T}}_{ij}, \\ & x(0) & =& x_0, & \end{array} \end{aligned}$$

(P-STO)

for $i \in [N]$ and $j \in [n_\sigma ]$ as the switching time optimization (P-STO) (or the enhanced time or time-scaling) transformation of (MIOCP).

Please note that the way in which we define the switching time optimization transformation differs from the literature, e.g., [58], although we use the same algorithmic approach. The definition above enables us to highlight the major difference to the partial outer convexification formulation introduced below. The switching time optimization is well-posed: assume a solution $\tilde{x}, \tilde{w}$ of (P-STO). Noting that $n_\sigma = \frac{\Delta t}{\Delta _{\textrm{in}}t}$ indicates the time transformation factor from the equidistant inner to the outer grid, we obtain a feasible trajectory x of (MIOCP) via

$$\begin{aligned} x(t(\tau ))&= \tilde{x}(\tau ) \quad \text {for } \tau \in {\mathcal {T}}_{ij}\text { and}\\ t(\tau )&= t_{i-1} + \sum _{k=1}^{j-1} w_{ik} \Delta t + (\tau -t_{i-1,j-1}) w_{ij} n_\sigma \ \ \in {\mathcal {T}}_{ij}^* \end{aligned}$$

for time transformed intervals

$${\mathcal {T}}_{ij}^* := \left[ t_{i-1} + \sum _{k=1}^{j-1} w_{ik} \Delta t, \; t_{i-1} + \sum _{k=1}^{j} w_{ik} \Delta t \right] $$

that also partition ${\mathcal {T}}$. Note that $\tilde{x}$ may be constant on certain time periods (i.e., whenever $w_{ij}=0$), whereas the corresponding intervals ${\mathcal {T}}_{ij}^*$ vanish. This is illustrated in the following short example.

Example 6

(Illustration of the time transformation) Consider an outer grid with $N=3$ intervals. Let $n_\sigma =3$ and the switching sequence $\sigma$ be the identity. Then the inner grid consists in total of 9 intervals. Consider the values

$$w_1 := \left( 0,1,0\right) , \ w_2:= \left( \frac{3}{5}, 0, \frac{2}{5}\right) , \ w_3 := \left( \frac{1}{5}, \frac{4}{5}, 0\right) \in [0,1]^{n_\sigma }.$$

Figure 1 illustrates the corresponding switches and the transformation in time.

Fig. 1

Illustration of the time transformation with the control values $w_{ij}$ for Example 6, adapted from [17]. Top: The control values indicate the percentage of control mode activation for the corresponding outer interval and for the three control modes. Center plot: Corresponding progress of the transformed time variable $t \in {\mathcal {T}}_{ij}^*$ as a function of $\tau \in {\mathcal {T}}_{ij}$. Bottom: Resulting activated control modes in (MIOCP) over time that correspond to the values $w_{ij}$. The mode switches occur at $\tilde{t}_1=t_1+w_{21}(t_2-t_1)$ and $\tilde{t}_2=t_2+w_{31}(t_3-t_2)$

For optimal control, time transformations have been used intensively. In indirect approaches the unknown time points of structural changes have to be determined, e.g., when a bang-bang arc becomes a singular arc or a path constraint becomes active. Also, the potential to avoid the discrete decision of which mode to activate at time t in problem (MIOCP) by continuous decisions when to switch from one mode $f_{j_1}$ to another mode $f_{j_2}$ was already discovered in the 1960 s. Dubovitskii and Milyutin used a time transformation to transform (MIOCP) into an equivalent optimal control problem without discrete control variables, [9, 10, 18, p. 95], [24, p. 148]. Necessary optimality conditions were obtained by applying suitable local maximum principles to the transformed problem. Gerdts used the time transformation to prove a global maximum principle that can be applied to mixed-integer optimal control problems [16, 17]. An STO formulation was also used for discretized dynamical systems [12], the numerical solution of free end-time [28], bi-objective [38, 39], multiple model stages [63], constrained MIOCPs [47, 60], or real-time problems [36, 37], and was studied concerning specific numerical aspects [33,34,35, 56]. The method has been investigated with respect to second-order sufficient conditions [42] and recently been extended to include vanishing constraints [43] and time delays [64]. An efficient structure exploiting way to calculate functions and derivatives was proposed in [58]. The mapping $\sigma$, which in our setting is assumed to be identical on all intervals ${{\mathcal {T}}_i}$ for notational convenience, also has an impact. As stated in [17], the order is irrelevant for (P-STO) to be an equivalent reformulation of (MIOCP) if we assume that (MIOCP) admits a unique optimal solution with finitely many switches and N is large enough and hence no more than one switching point of the optimal bang-bang solution occurs per interval ${{\mathcal {T}}_i}$. However, $\sigma$ may have an impact on computational performance as discussed in [46]. An efficient way to determine optimal sequences has been proposed in [1, 11].

2.2 Partial outer convexification

An alternative approximation of (MIOCP) is the following, using the same outer time grid ${{\mathcal {T}}_i}$ as in (P-STO) for control discretization and relaxation of the integrality constraints.

Definition 7

(Partial outer convexification) With the definitions from above (using $n_\sigma =n_\omega$ in Definition 4 of $\mathcal {W}$) we refer to

$$\begin{aligned} \begin{array}{lrlll} \displaystyle \min _{x, w \in \mathcal {W}} & {\phi (x(t_{N }))} & & & \\ {{\hbox {subject to}}} & & & & \\ & \dot{x}(t) & =& \sum _{j=1}^{n_\omega } w_{ij} \; (f_0(x(t)) + f_j(x(t))), & \quad t \in {{\mathcal {T}}_i}\text { for } i \in [N] \\ & x(0) & =& x_0, & \\ \end{array} \end{aligned}$$

(P-POC)

as the partial outer convexification (P-POC) approximation of (MIOCP).

Note that partial refers to the fact that the dynamics are only convexified with respect to the switching decision, but the $f_j$ may still be nonconvex. Outer is in contrast to an inner convexification as suggested, e.g., in [15], and compared in [25]. The formulation itself is well-known in many areas. In integer programming it is usually referred to as a one-row or one-hot relaxation. The usage in mixed-integer optimal control and the name itself were initiated by [47, 50]. In the control engineering community, the term embedding transformation was introduced [2] for the same reformulation idea and led to various subsequent publications [45, 61, 62]. As discussed in the next subsection, (P-POC) only provides relaxed solutions for a discretized version of (MIOCP). Methods for the generation of integer solutions have been proposed in [47, 48, 50, 54]. Extensions comprise the explicit treatment of combinatorial [26, 40, 53, 65] and vanishing constraints [27, 29], of differential-algebraic equations [17], and of partial differential equations [19,20,21,22, 31, 41].

To highlight the similarities and differences to formulation (P-STO), we have defined (P-POC) in a first-discretize, then-optimize way with finitely many degrees of freedom. Here, the controls w can be interpreted as piecewise constant functions $\omega _j(t) = w_{ij}$ for $t\in {{\mathcal {T}}_i}$ almost everywhere.

We recapitulate two methods that round the optimal solution of (P-POC). We use these methods in the numerical experiments for a fair comparison with the STO approach, which directly constructs binary-feasible solutions for (MIOCP).

Definition 8

(Sum-up rounding) Let the optimal $w^*$ for (P-POC) be given. Sum-up rounding computes for $i\in [N]$ the binary control values $b_{i,j}$:

$$\begin{aligned} b_{i,j}:= {\left\{ \begin{array}{ll} 1, & \text { if } j=\arg \max \limits _{l=1,\ldots ,{n_\omega }} \left\{ \sum \limits _{k=1}^i w_{k,l}^* - \sum \limits _{k=1}^{i-1} b_{k,l} \right\} , \\ 0, & \text { else, } \end{array}\right. } \quad \text {for } j\in [{n_\omega }]. \end{aligned}$$

We break ties arbitrarily in the above $\arg \max$.

One option to limit the number of switches in the binary solution is to impose total variation (TV) constraints as part of a mixed-integer linear program.

Definition 9

((CIA) with TV constraints) Let the optimal $w^*$ for (P-POC) and the number of maximal allowed number of switches $n_s$ be given. The combinatorial integral approximation (CIA) problem with TV constraints is defined by

$$\begin{aligned} \begin{array}{ll} \underset{ b\in \mathcal {W}, \ b_{i,j} \in \{0,1\}, \, \theta \ge 0 }{\textrm{min}} \hspace{0.2cm} & \theta \\ \mathrm {s.\,t.} \hspace{0.4cm} & \theta \ge \pm \sum \limits _{l\in [i]} (w_{l,j}^*-b_{l,j}), \qquad \text { for } i\in [N], \, j\in [{n_\omega }]. \\ \qquad \hspace{0.4cm} & n_s \ge \frac{1}{2} \sum \limits _{i\in [N-1] } \sum \limits _{j\in [{n_\omega }]}|b_{i+1,j}-b_{i,j}|. \end{array} \end{aligned}$$

Adding the TV constraints to the problem can be seen as regularization technique, which might prevent us from reaching the infimum of (MIOCP) in the constructed solution since we assume $n_s$ to be given and fixed.

2.3 Relations to the original problem formulation

Both problem formulations (P-STO) and (P-POC) are approximations of (MIOCP). Both are discretizing (MIOCP), which is usually modeled with $\mathcal {L}^\infty ({\mathcal {T}},\{0,1\}^{n_\omega })$ control functions, with finitely many decision variables w. In addition to this finite-dimensional approximation which depends on N, the formulation (P-POC) additionally relaxes the decision variables, as $\mathcal {W}$ is defined with $w_{ij} \in [0,1]$ instead of $w_{ij} \in \{0,1\}$.

The optimal solution of (P-STO) is a feasible solution $\omega (\cdot )$ of the original problem (MIOCP) (compare $\omega$ in the proof of Corollary 12). Depending on the number and location of switches in the optimal solution of (MIOCP), the numbers N and $n_\sigma$ need to be chosen sufficiently large to ensure that the optimal switching points of (MIOCP) can be realized within (P-STO). In the case that the optimal solution shows chattering behavior (i.e., an infinite number of switches as in the famous example of Fuller [14]), the optimal objective function value can be approximated arbitrarily well with increasing N or $n_\sigma$.

There is a bijection between feasible solutions of formulations (P-POC) and (MIOCP) if one replaces $w_{ij} \in [0,1]$ by $\omega _j(t) \in \{0,1\}$ and one uses the same discretization on (MIOCP). Formulated for continuous variables $w_{ij}$, (P-POC) only provides a relaxed solution for the control discretization grid $\mathcal {G}_N$, however with strong theoretical properties and tailored algorithms like Combinatorial Integral Approximation, Sum Up Rounding (SUR), or Next Forced Rounding to derive binary solutions with error bounds, see [47, 48, 50, 54]. The need to derive $\omega _j(t) \in \{0,1\}$ from $w_{ij} \in [0,1]$ seems like a big disadvantage at first sight. However, the aforementioned rounding strategies have excellent asymptotic behavior with respect to the integrality gap and a runtime which is often negligible compared to the solution of (P-POC). The need to transform the solution back even offers advantages, e.g., to take a penalization of switches or dwell time constraints into account [3, 4, 65].

2.4 A first comparison

Comparing (P-STO) and (P-POC), one observes a small, but important difference in the dynamics. For $i \in [N]$ and $j \in [n_\omega ]$ we have within (P-STO)

$$\begin{aligned} \dot{x}(t) = w_{ij} \; n_\sigma \; (f_0(x(t)) + f_{\sigma (j)}(x(t))), \quad t \in {\mathcal {T}}_{ij}, \quad x(0) = x_0 \end{aligned}$$

(STO-f)

while due to the one-hot condition in $\mathcal {W}$ we have within (P-POC)

$$\begin{aligned} \dot{x}(t) = f_0(x(t)) + \sum _{j=1}^{n_\omega } w_{ij} \; f_j(x(t)), \quad t \in {{\mathcal {T}}_i}, \quad x(0) = x_0. \end{aligned}$$

(POC-f)

The way the control variables w enter the right-hand sides look very similar in (STO-f) and (POC-f). Figure 2 gives an example to visualize how they differ in their impact on the original dynamic system.

Fig. 2

Shown is the impact of the controls on the mode selection in (MIOCP) for STO and POC controls $w^{\text {STO}}_{i1} = w^{\text {POC}}_{i1} = 0.1 (i-1)$ for $i\in [11]$. The values of $w^{\text {STO}}_{i1}$ are reflected by the duration of the mode selections (width), whereas the values of $w^{\text {POC}}_{i1}$ are reflected by the relative share of mode 1 on the current time interval (height). The other $n_\sigma -1$ modes would fill the diagram vertically P-POC or horizontally P-STO, if they were also plotted

Problems (P-STO) and (P-POC) optimize the same objective function over the finite-dimensional set $\mathcal {W}$. For both, the accuracy of the approximation of (MIOCP) depends on the grid $\mathcal {G}_N$.

3 Approximation properties

Behind this asymptotic analysis an approximation theorem from [50] will be useful. It also can be used for the study of how far optimal objective function values of (P-STO) and (P-POC) may differ from one another depending on N. We repeat it here for convenience and use it in the discussion in Sect. 7.

Assumption 10

(Properties of the switched system) Let measurable functions $\alpha , \omega : [0, t_{N }] \rightarrow [0,1]^{n_\omega }$ be given and let $x(\cdot )$ and $y(\cdot )$ be solutions of the initial value problems on ${\mathcal {T}}= [0, t_{N }]$

$$\begin{aligned} \dot{x}(t)= & f_0(x(t)) + \sum _{j=1}^{n_\omega } \alpha _j(t) \; f_j(x(t)), \;\;\; x(0) = x_0, \end{aligned}$$

(6)

$$\begin{aligned} \dot{y}(t)= & f_0(y(t)) + \sum _{j=1}^{n_\omega } \omega _j(t) \; f_j(y(t)), \;\;\; y(0) = x_0. \end{aligned}$$

(7)

Let all $f_j: \mathbb {R}^{n_x} \mapsto \mathbb {R}^{n_x}$ be differentiable for $j \in [n_\omega ]_0$ and their sum be essentially bounded by $M \in \mathbb {R}^+$ on $[0, t_{N }]$, and positive numbers $C, L \in \mathbb {R}^+$ exist such that for $t \in [0, t_{N }]$ almost everywhere and a vector norm $\left\| \cdot \right\|$ we have

$$\begin{aligned} \left\| \frac{\textrm{d}}{\textrm{d}t}(f_0, f_1, f_2, \ldots , f_{n_\omega }) (x(t))\right\|\le & C, \\ \left\| \left( f_1(y(t))-f_1(x(t)), \ldots ,f_{n_\omega }(y(t))-f_{n_\omega }(x(t)) \right) \right\|\le & L \left\| y(t)-x(t)\right\| . \end{aligned}$$

Theorem 11

If Assumption 10 holds and if there exists $\varepsilon \in \mathbb {R}^+$ such that for all $t~\in ~[0, t_{N }]$

$$\begin{aligned} \left\| \int _{0}^t \alpha (\tau ) - \omega (\tau ) \; \textrm{d} \tau \right\| \le \varepsilon , \end{aligned}$$

(8)

then, also for all $t \in [0, t_{N }]$, we have

$$\begin{aligned} \left\| y(t)-x(t)\right\| \le (M + Ct) e^{Lt} \; \varepsilon . \end{aligned}$$

To understand the asymptotic behavior of the optimal objective function values of (P-STO) and (P-POC), the following corollaries will be helpful. Theorem 11 allows to a priori bound the difference of the optimal objective function values of (P-STO) and (P-POC) by a constant multiple (depending on properties of $f_j$) of the grid size $\Delta t$.

Corollary 12

(Difference in objective and constraints 1) Let $n_\sigma \in \mathbb {N}$, a map $\sigma : [n_\sigma ] \mapsto [{n_\omega }]$, and $w^{\text {STO}} \in \mathcal {W}$ be given and differential states $x^{\text {STO}}: [0,t_{N }] \mapsto \mathbb {R}^{n_x}$ be the solution of (STO-f) with $w = w^{\text {STO}}$.

Under Assumption 10, there exist a constant $C_1$ and a vector $w^{\text {POC}} \in \mathcal {W}$ such that for the solution $x^{\text {POC}}: [0,t_{N }] \mapsto \mathbb {R}^{n_x}$ of (POC-f) with $w = w^{\text {POC}}$ we have

$$ \begin{array}{rcl} \left| \phi (x^{\text {STO}}(t_{N })) - \phi (x^{\text {POC}}(t_{N })) \right| \le C_1 \Delta t. \end{array} $$

Proof

As already observed above, we have an $x^{\text {STO}}=x$ equivalence

$$\begin{array}{rll} \dot{x}^{\text {STO}}(\tau ) & = w^{\text {STO}}_{ij} \; n_\sigma \; (f_0(x^{\text {STO}}(\tau )) + f_{\sigma (j)}(x^{\text {STO}}(\tau ))), \quad & \tau \in {\mathcal {T}}_{ij}\\ \Leftrightarrow \quad \dot{x}(t) & = f_0(x(t)) + f_{\sigma (j)}(x(t)), & t \in {\mathcal {T}}_{ij}^* \end{array} $$

between (P-STO) and (MIOCP) solutions for transformed time intervals

$${\mathcal {T}}_{ij}^* := \left[ t_{i-1} + \sum _{k=1}^{j-1} w^{\text {STO}}_{ik} \Delta t, \; t_{i-1} + \sum _{k=1}^{j} w^{\text {STO}}_{ik} \Delta t \right] .$$

The functions

$$\omega _k(t):= \left\{ \begin{array}{ll} 1 & \text { if } t \in {\mathcal {T}}_{ij}^* \text { for } j \in [n_\sigma ] \text { and } k=\sigma (j) \in [{n_\omega }] \\ 0 & \text { else} \end{array} \right. $$

are obviously well-defined and have the one-hot property, such that

$$\begin{array}{lll} \dot{x}(t) & = f_0(x(t)) + \omega _{\sigma (j)}(t) f_{\sigma (j)}(x(t)), & t \in {\mathcal {T}}_{ij}^* \\ & = f_0(x(t)) + \sum _{k=1}^{n_\omega } \omega _k(t) f_k(x(t)), & t \in {\mathcal {T}}_{ij}^*. \end{array} $$

Defining

$$\alpha _j(t):= w^{\text {POC}}_{ij} \text { for } t \in {{\mathcal {T}}_i}$$

we have two measurable functions $\alpha , \omega : [0,t_{N }] \mapsto [0,1]^{n_\omega }$ and differential equations of the form (6–7) such that Assumption 10 is satisfied.

To apply Theorem 11, we choose $w^{\text {POC}}$ in a particular way. With

$$w^{\text {POC}}_{ij}:= \int _{t_{i-1}}^{t_i} \omega _j(\tau ) \; \textrm{d} \tau $$

it follows $\left\| \int _{0}^{t_i} \alpha (\tau ) - \omega (\tau ) \; \textrm{d} \tau \right\| = 0$ for all $i \in [N]$. The maximum over all $t \in [0,t_{N }]$ can hence not exceed the integral of length $\Delta t$ over extreme cases such as $\alpha \equiv 1$ and $\omega \equiv 0$, thus

$$\displaystyle \max _{t \in {\mathcal {T}}} \left\| \int _{0}^t \alpha (\tau ) - \omega (\tau ) \; \textrm{d} \tau \right\| \le \varepsilon := \Delta t.$$

Theorem 11 now gives a bound $\Vert x^{\text {POC}}(t) - x^{\text {STO}}(t) \Vert \le \hat{C} \Delta t$ for all $t \in {\mathcal {T}}$ which carries over to the objective function via assumed continuity. This concludes the proof. $\square$

Given the symmetry of Theorem 11, the reverse is also true.

Corollary 13

(Difference in objective and constraints 2) Let $w^{\text {POC}} \in \mathcal {W}$, $x^{\text {POC}}: [0,t_{N }] \mapsto \mathbb {R}^{n_x}$ be the solution of (POC-f) with $w = w^{\text {POC}}$.

Under Assumption 10, there exist a constant $C_1$, a number $n_\sigma$, a switching order $\sigma : [n_\sigma ] \mapsto [{n_\omega }]$, and a vector $w^{\text {STO}} \in \mathcal {W}$ such that for the solution $x^{\text {STO}}: [0,t_{N }] \mapsto \mathbb {R}^{n_x}$ of (STO-f) with $w = w^{\text {STO}}$ we have

$$ \begin{array}{rcl} \left| \phi (x^{\text {STO}}(t_{N })) - \phi (x^{\text {POC}}(t_{N })) \right| \le C_1 \Delta t. \end{array} $$

Proof

The claim can be proved analogously to the proof of Corollary 12. Here $n_\sigma$, $\sigma$, and $w^{\text {STO}}$ can be constructed with the well-known bound that is linear in $\Delta t$ using SOS1 Sum Up Rounding [47, 50]. $\square$

Both corollaries together show that the optimal objective function values of (P-STO) and (P-POC) are close with respect to $\Delta t$. Therefore, one can expect that for larger N the objective function landscapes look very similar for the approximations (P-STO) and (P-POC).

Moreover, from Theorem 11 in conjunction with Corollaries 12 and 13, it can be deduced that the (local) optima of (P-STO) and (P-POC) are $\varepsilon$-optima with respect to the modified problem (P-POC) in which $w_{ij}$ is replaced by the non-discretized $w_j(t)$. Since this modified (P-POC) with non-discretized controls $w_j(t)$ is a true relaxation of (MIOCP), this implies the minima of (P-STO) and the rounded minima of (P-POC) are also $\varepsilon$-optima of (MIOCP).

4 Two test problems

We are going to compare numerical properties of (P-STO) and (P-POC) in Sect. 6, using the new software package ampl_mintoc [55] introduced in Sect. 5. The numerical results are obtained for two test mixed-integer optimal control problems that we shortly present in this section. In this study, we limit ourselves to two benchmark problems, since a more detailed analysis of other problems is beyond the scope of this paper. We have specifically chosen two structurally different problems. The optimal solution of the first problem consists of singular and bang-bang arcs, which renders its solution to be challenging, while the other involves only bang-bang arcs. Moreover, the problems have different convexity properties. One problem is convex over a large part of the domain and, thus, in this sense relatively easy to solve, while the other problem is very nonconvex and raises numerically more difficulties. The Lotka-Volterra fishing benchmark problem was first formulated in [51]. The numerically constructed optimal relaxed solution has bang-bang and singular arcs, which can be derived using Pontryagin’s maximum principle [51]. The (P-POC) formulation is convex on large parts of the domain and for many choices of the discretization grid, initial values, and bounds, as we will show in the numerical results in Sect. 6 in Fig. 7. The second problem, a calcium signaling pathway inhibition, was formulated in [32]. The numerically constructed optimal relaxed solution consists of three bang-bang arcs. Both the (P-POC) and the (P-STO) formulation are nonconvex. Both problems have oscillatory dynamics and only use one binary control function. Further references and details can be found in [49]. Here, we only state and use the mathematical formulations of these problems.

Definition 14

(Lotka problem) We refer to

$$\begin{aligned} \begin{array}{lrll} \displaystyle \min _{x, \omega } & { x_3(t_{N }) } & & \\ \text{ s.t. } & \dot{x_1}(t) & = & x_1(t) - x_1(t) x_2(t) - \; c_1 x_1(t) \; \omega (t) \\ & \dot{x_2}(t) & = & - x_2(t) + x_1(t) x_2(t) - \; c_2 x_2(t) \; \omega (t) \\ & \dot{x_3}(t) & = & \sum _{i=1}^{2} (x_i(t) - \tilde{x}_i)^2 \\ & x(t_0) & =& (0.5, 0.7, 0.0), \quad \tilde{x}=(1,1) \\ & \omega (t) & \in & \{0,1\} \end{array} \end{aligned}$$

(Lotka)

as the Lotka-Volterra fishing control problem with $c_1 = 0.4$, $c_2 = 0.2$ and $t_{N }=12$ on ${\mathcal {T}}= [0,12]$.

Definition 15

(Calcium problem) We refer to

$$\begin{aligned} \begin{array}{lr} \displaystyle \min _{x, \omega } x_5(t_{N }) \end{array} \end{aligned}$$

(Calcium)

$$\begin{aligned} \begin{array}{lrll} \text{ s.t. } & \dot{x_1}(t) & = & k_1 + k_2 x_1(t) - \frac{k_3 x_1(t) x_2(t)}{x_1(t) + K_4} - \frac{k_5 x_1(t) x_3(t)}{x_1(t) + K_6} \\ & \dot{x_2}(t) & = & k_7 x_1(t) - \frac{k_8 x_2(t)}{x_2(t) + K_9} \\ & \dot{x_3}(t) & = & \frac{k_{10} x_2(t) x_3(t) x_4(t)}{x_4(t) + K_{11}} + k_{12} x_2(t) + k_{13} x_1(t) - \frac{k_{16} x_3(t)}{x_3(t) + K_{17}} + \frac{x_4(t)}{10} \nonumber \\ & & & - \omega \frac{k_{14} x_3(t)}{ \bar{u}^{\textrm{max}} \; x_3(t) + K_{15}} - (1-\omega (t)) \frac{k_{14} x_3(t)}{ \bar{u}^{\textrm{min}} \; x_3(t) + K_{15}} \\ & \dot{x_4}(t) & = & - \frac{k_{10} x_2(t) x_3(t) x_4(t)}{x_4(t) + K_{11}} + \frac{k_{16} x_3(t)}{x_3(t) + K_{17}} - \frac{x_4(t)}{10} \\ & \dot{x_5}(t) & = & \sum _{i=1}^4 \left( \frac{x_i(t) - \tilde{x}_i}{\tilde{x}_i} \right) ^2 + 100 \; \omega (t) \\ & x(t_0) & =& (0.03966, 1.09799, 0.00142, 1.65431, 0) \\ & \omega (t) & \in & \{0,1\} \end{array} \end{aligned}$$

as the Calcium control problem with $t_{N }=22$ on ${\mathcal {T}}= [0,t_{N }]$ with data $\bar{u}^{\textrm{min}}=1$, $\bar{u}^{\textrm{max}}=1.3$, $k_1=0.09, k_2=2.30066, k_3=0.64, K_4=0.19, k_5=4.88, K_6=1.18, k_7=2.08, k_8=32.24, K_9=29.09, k_{10}=5.0, K_{11}=2.67, k_{12}=0.7, k_{13}=13.58, k_{14}=153.0, K_{15}=0.16, k_{16}=4.85, K_{17}=0.05$, and reference unstable steady state $\tilde{x}_1=6.78677, \tilde{x}_2=22.65836, \tilde{x}_3=0.38431, \tilde{x}_4=0.28977$.

Both control problems can be cast (easily) into the formulation of (MIOCP), where the $n_\omega =2$ different modes correspond to values $\omega (t)=0$ and $\omega (t)=1$, respectively. They use a single binary control, as the second control was eliminated via the one-hot constraint.

5 The software package ampl_mintoc

We have designed the AMPL [13] code ampl_mintoc for the formulation of Mixed INTeger Optimal Control problems, in particular for problems of type (MIOCP). The package ampl_mintoc is available as open-source on GitHub.¹ We explain the concept and idea of the software in Sect. 5.1. In Sect. 5.2, we first describe the most relevant problem-independent files and explain the different algorithmic options and discretizations. We then dedicate the remaining section to the implementation of the approximations (P-STO) and (P-POC). We also provide an explanation of how optimal control problems can be formulated and solved with ampl_mintoc in Appendix 9.1.

5.1 Conceptual description

ampl_mintoc consists of a set of code files that allow the user to efficiently formulate control problems. These are solved by off-the-shelf NLP or MINLP solvers interfaced by AMPL. In particular, problem-independent code exists to apply (P-STO) as well as (P-POC) formulations to problem-dependent functions.

The application of ampl_mintoc is illustrated in Fig. 3. The goal of this software is to be able to formulate and solve optimal control problems easily. For this purpose, there is a set of problem-independent code files that define generic parameters, variables, problems, and approximations that can be used by the user depending on the application. For formulation of an MIOCP, the user needs to specify files problem.mod and problem.dat to define the objective function and constraints as well as parameter values, respectively. In the file problem.run algorithmic choices are set, such as the choice of the solver, the integrator, and the problem approximation. To this end, problem-independent files, e.g. mintocPre.mod, mintocPost.mod, and solve.run, are included in this file to reuse generic structures.

After applying the numerical solver interfaced via AMPL, the constructed optimal solution can be visualized with plot routines from the software package and gnuplot. The obtained solution can also be used for further optimization steps as specified in problem.run. For instance, after solving (P-POC), one could be interested in computing a rounded solution via SUR or Combinatorial Integral Approximation [53].

Fig. 3

Flowchart overview of the application of ampl_mintoc. The user can formulate an MIOCP in this code by creating problem-specific files, as listed in the lower box. ampl_mintoc provides a set of problem-independent files that implement generic routines and which simplify the problem formulation, as listed in the upper box. The modeling language is AMPL, which facilitates to interface a wide range of numerical solvers. The constructed optimal solution can be visualized or used for further optimization steps by using ampl_mintoc code routines. The dashed lines mark the software related area without input and output

The advantage of using AMPL is that the syntax remains close to the mathematical formulation. Due to the chosen direct approach for the solution of the OCPs, the implementation is done directly in a discretized setting. As a disadvantage, the usage of AMPL implies that functions cannot be implemented in a straightforward manner, complicating the implementation of adaptive numerical integrators. However, the discretized problem formulation can also be beneficial, since the program’s preprocessor can eliminate variables and constraints from discretized functions before the solution process.

We note that there are other AMPL packages for optimal control, such as TACO [30] that interfaces a multiple shooting code for optimal control. The novel feature of ampl_mintoc is the possibility for rapid prototyping of transformation and decomposition algorithms and to facilitate the formulation and solution of MIOCPs, by using the flexibility of solver choice provided with AMPL.

5.2 Details on problem-independent files

In order to save implementation effort, problem-independent variables and generic problem structures are outsourced to dedicated AMPL files. The file mintocPre.mod contains the declaration of general parameters such as the time discretization and the number of differential states and controls. It also defines the variables for the ODE model function, the control values, differential states, and discretized constraint functions. In mintocPost.mod, we define different objectives, constraints, numerical integration schemes for the ODEs, and the formulation of NLPs and Combinatorial Integral Approximation [66] problems.

The files mintocPre.mod and mintocPost.mod can be considered as the core of ampl_mintoc. Both files need to be included in the problem-specific run file and reduce the effort to formulate the optimal control problems significantly.

Currently available numerical integrator schemes are the Radau collocation and explicit and implicit Euler methods, which can be set via the variable integrator. Various problem variants can be solved via setting the variable mode. For instance, in the Simulate mode, all control variables are fixed and in the Relaxed mode the optimization problem is solved with relaxed integer variables. The file solve.run contains the commands to interface and run the NLP solver based on the chosen algorithmic options. Thus, one needs to use include ../solve.run in the problem-specific run file to let the problem at hand be solved. The files solveMILP.run and solveRound.run work similarly as solve.run, but interface MILP solvers for specific combinatorial integral approximation problems [53] and contain specific rounding algorithms, respectively, as part of the Combinatorial Integral Approximation decomposition [66]. The declaration of default settings for solvers, problem classes, and integrators are outsourced in the file set.run, while checkConsistency.run verifies if valid options/modes have been chosen for solver, integrator, and discretization.

Standardized routines are implemented in the ampl_mintoc code to postprocess, store, and restore problem solutions. These can be retrieved via the file problem.run and the AMPL command include. For instance, by calling the script printOutput.run, detailed solution results can be output, such as the objective function value, constraint violation metrics, and the run time. If the user includes the script plot.run, the determined solution is stored in a file problem.plot, which in turn can be used by gnuplot to plot result data such as the state or control trajectories. Furthermore, one can use the scripts storeTrajectory.run and readTrajectory.run to save or read problem solutions in order to solve a problem again later in a modified form. The problem-independent files do not need to be modified by users, but can be extended by algorithm developers.

We illustrate the implementation of the problem-independent formulations of the ODE constraints for STO and POC in the Listing 1. The presented implementation is done in mintocPost.mod and is based on a discretization with an explicit Euler scheme. We note that the (discretized) ODE equations in ampl_mintoc closely resemble the corresponding mathematical ODE equations from (P-STO) and (P-POC).

6 Numerical experiments

We are going to investigate the two test problems from Sect. 4 numerically. Special focus is given on nonconvexity of the objective functions over $\mathcal {W}$. We present first simulation-based analyses. To be able to plot results, we consider low dimensions, projections, and the concept of mid-point convexity, respectively. We complement the findings with optimization-based analyses, comparing the number of optimal solutions that are found for random initial values. An interesting approach is to initialize (P-STO) with the binary solution determined from (P-POC), which we test as part of this investigation. We also use different algorithms to compare integer solutions, that can be derived using the solution of (P-POC). In the following, we are only inspecting local optimality up to the precision of the numerical method.

6.1 Discretization and numerical integration

All numerical results were produced using a machine with 160 Intel CPU cores (2 GHz each) and 1 TB of RAM running Ubuntu 18.04.5 LTS. We implemented the Problems (P-STO) and (P-POC) in ampl_mintoc and used IPOPT 3.12.13 to solve the resulting NLPs. In the following, we refer to the determined optima of IPOPT as local minima, neglecting the fact that in theory the determined stationary points can also be saddle points. The underlying motivation was to get as close to objective comparability as possible, ignoring issues of efficacy. Thus, the absolute computational times are irrelevant and only a relative comparison between them will play a role. Our main focus will be the impact of the different dynamics on the objective function values. To this end, we used the same discretization grids. For both test problems, an explicit Euler scheme with equidistant step sizes was used. We tested different numbers of grid points $n_t$ for the evaluation of differential states, with control values arbitrarily fixed to 1, compare Table 1. Then, we chose $n_t=48000$ since the objective function values hardly change (less than $0.05\%$) with finer discretizations.

Table 1 Simulated objective function values for the two test problems and fixed controls $w^{\text {STO}}_{i1} = w^{\text {POC}}_{i1} = 1$ for all i and an equidistant explicit Euler scheme with $n_t$ discretization points

We also qualitatively compared the simulation results to those of an implicit Euler scheme and of a Gauß Radau collocation of order 3. These approaches are more efficient in the sense of computational speed, but we experienced also additional numerical issues such as convergence issues in IPOPT. The results for the explicit Euler scheme are hence easier to compare and might always serve as an initialization of the more involved schemes.

Unfortunately, even for this simplistic numerical scheme, a fair comparison with the same number of integration intervals for STO and POC is not straightforward because the discretization grid depends on the values in $w^{\text {STO}}$. If $w^{\text {STO}}_{ij} \in \{0,1\}$ for all i, j, then for the overall number of state discretization time points $n_t^{\text {STO}}$ it holds that $n_t^{\text {STO}} =n_\sigma n_t^{\text {POC}}$ since $n_\sigma -1$ sub-intervals on each discretization interval will not be used for integration in the STO approach. However, if $w^{\text {STO}}_{ij} \in (0,1)$ for all i, j, then $n_t^{\text {STO}} = n_t^{\text {POC}}$. As these values $w^{\text {STO}}_{ij}$ are going to change during the optimization, there is no perfect choice. In the interest of getting an idea about the numerical effort, we chose $n_t$ identical for (STO-f) and (POC-f). Also in the interest of simplicity, we focused on $n_\sigma =2$ and a switching order $\sigma (1)=1, \sigma (2)=0$ on each sub-interval. As we consider cases with only two possible modes $\omega (t) \in \{0,1\}$, we can omit the second index, such that $w_i = w_{i1}$ and $1-w_i = w_{i2}$.

6.2 Measuring convexity

We would like to evaluate the constructed solutions by STO and POC in terms of (non-)convexity. One quantitative measure of nonconvexity is the nonconvex ratio [59], a measure of the nonconvexity of black-box functions. It can be easily applied to our ampl_mintoc implementation via outer simulation loops. The approach uses the midpoint convexity as an indicator for convexity. We repeat the definitions here for convenience.

Definition 16

(Midpoint convexity) The continuous function $f:~\mathbb {R}^n~\supset ~\mathbb {M}~\rightarrow ~\mathbb {R}$ is called midpoint convex on the convex domain $\mathbb {M}$, if and only if

$$\begin{aligned} f(x_1) + f(x_2) \ge 2f\left( \frac{x_1 + x_2}{2}\right) \quad \forall x_1, x_2 \in \mathbb {M}. \end{aligned}$$

(9)

The following definition already takes the practical calculation of the nonconvex ratio into account. Details of the development of the method can be found in [59].

Definition 17

(Nonconvex ratio $R^*$) Let $\zeta : \mathbb {M}^2 \rightarrow \{0,1\}$ denote a function with $\zeta (x_1,x_2)=1$ if and only if $x_1$ and $x_2$ fulfill (9) and let S denote the number of samples. For uniformly chosen $x_{1i},x_{2i}$, $i \in \left[ S\right]$, the nonconvex ratio $R^*$ can be computed as

$$\begin{aligned} R^*:= 1 - \frac{1}{S} \displaystyle \sum _{i=1}^{S} \zeta \left( x_{1i},x_{2i}\right) \quad \left( \{x_{1i},x_{2i}\} \sim \mathcal {U}(\mathbb {M}^2) \right) . \end{aligned}$$

(10)

Note, that a value of $R^*=1$ corresponds to a concave function. Please also note that $R^*$ is only an approximation of the ratio of the number of points fulfilling the midpoint convexity property to the number of pairs of points in $\mathbb {M}$. Thus, the parameter S has to be chosen sufficiently large. Due to the fact that each function evaluation in our setting comes at the cost of solving a discretized ODE, we restricted the sample size S to 1000 in this study, still resulting in an overall computation time of approximately one week.

6.3 Simulation-based analysis

We start with visualizations of the objective function landscapes for two-dimensional problems. For both problems (Lotka) and (Calcium) we performed simulations with $N=2$ and varied the controls $w_1, w_2$ between 0 and 1 with an increment of 0.01.

Fig. 4

Comparison of simulated objective function landscapes for (Lotka) example using two degrees of freedom $w_1$ and $w_2$. Left: (P-STO), i.e., $\dot{x} = w_1 (f_0 + f_1)$ for $t \in [0, 6 w_1]$, $\dot{x} = (1-w_1) f_0$ for $t \in [6 w_1, 6]$ and $\dot{x} = w_2 (f_0 + f_1)$ for $t \in [6, 6 + 6 w_2]$, $\dot{x} = (1-w_2) f_0$ for $t \in [6 + 6 w_2, 12]$. Right: (P-POC), i.e., $\dot{x} = f_0 + w_i f_1$ for $t \in {{\mathcal {T}}_i}$ with $t_0=0, t_1=6, t_2=12$. The (P-STO) formulation has at least 3 local minima, see Table 2

Figure 4 shows a comparison for (Lotka) and the case $N=2$. The switching time optimization approximation on the left appears to be nonconvex, while the partial outer convexification approximation on the right is much more convex. This is also reflected in the nonconvex ratios (see Definition 17). While $R^*_{STO} = 0.849$ is indicating a very nonconvex objective landscape, $R^*_{POC} = 0.188$. Note, that the nonconvexity of the results is presumably mainly attributed to the very small number of controls ($N=2$). At least, this behavior was experienced in further numerical trials for our test problems. If this generally holds true might be an interesting question for further research.

Fig. 5

Same setting as Fig. 4, but for problem (Calcium). Both formulations are nonconvex. The objective function landscapes are dominated by a bifurcation

Figure 5 shows a comparison for (Calcium) and the case $N=2$. Both approximations result in nonconvex objective function landscapes, which is also reflected in the high nonconvex ratios $R^*_{STO} = 0.472$ and $R^*_{POC} = 0.707$.

To get an impression of the nonconvexity in higher dimensions we performed another simulation. Here we used a one-dimensional parameterization

$$w_i = \beta , \quad i \in [N],$$

with $\beta$ running from 0 to 1 in steps of 0.01. The resulting control for (P-POC) is simply a constant function with the value $\beta$ and hence independent of N. However, in the case of (P-STO), each value of N results in different dynamics (cf. Fig. 2). Figure 6 shows a comparison of the resulting one-dimensional slices through the N-dimensional objective function landscapes for (Lotka) and for (Calcium).

Fig. 6

Simulated objective function values for fixed $w_i = \beta$. The x-axis reflects the fixed values $w_i = \beta$. We show the values based on the transformed problem (P-STO) for (Lotka) and $N \in \{1,2,3,4,8,16\}$ (left) and for (Calcium) and $N \in \{16,32,64,128\}$ (right). Note that (P-POC) has identical results for all values of N due to the constant choice of $w_i$. STO-N converges to POC as N increases

Comparing the resulting objective function values for (Lotka) on the left of Fig. 6, one gets an idea of the nonconvexity of the different approximations of the optimization problem depending on N. For each N, the formulation (P-STO) is less convex than the (P-POC) formulation. For $N=2$ one sees two of the local minima that we observed already in Fig. 4 (left). When looking at the objective functions for increasing N, one sees a convergence of the (P-STO) objective function values to the (P-POC) objective function values.

A similar picture emerges from the right plot of Fig. 6. Here, however, the objective function landscape is also visibly nonconvex for formulation (P-POC). Again, for small values of N more local minima can be seen in (P-STO), and for large N the objective functions look similar.

We considered the $R^*$ values also in higher dimensions. Figure 7 illustrates the values of $R^*$ as a function of N. For (Lotka), the (P-STO) formulation produces higher nonconvexities, which approaches that of (P-POC) for large N. For (Calcium), we have a similar result in the sense that (P-STO) appears to be more convex than (P-POC) with the exception of $N \in \{1,2,64\}$. Note, that because of our relatively small sample size, the results suffer from high uncertainty and need to be interpreted with care. Also, deviating from the rest of this section, we used $n_t=51200$ in this case. Otherwise, the larger values of N would have resulted in a corresponding non-integer value for $n_\sigma$.

Fig. 7

Nonconvex ratios $R^*$ for different discretizations N for (Lotka) on the left and (Calcium) on the right-hand side for sample size $S=1000$. Here, only the x axes are logarithmic. One observes higher $R^*$ values for (P-STO) compared to (P-POC) for small N and similar values for larger N

6.4 Optimization-based analysis

We performed an additional study to understand the convergence behavior for (P-STO) and (P-POC). We calculated local minima for $n_t = 48000$ and different values of N using IPOPT. For both formulations, we used random initializations for the controls w by means of AMPL’s Uniform01 function. For (P-STO) and (P-POC) we used the same random seed via option randseed, such that the starting values $w^{\text {STO}}_0 = w^{\text {POC}}_0$ were uniformly randomly distributed in $[0,1]^N$ and identical. Also for the corresponding state variables $x(\cdot )$, initial values were provided. We used the initializations STOa and POCa where we initialized x discontinuously, but possibly close to an optimal solution via

$$\begin{aligned} x_{ki} = \left\{ \begin{array}{cc} \tilde{x}_k & \text { if } k < n_x \\ 0 & \text { if } k = n_x \end{array} \right. \end{aligned}$$

for $i \in [n_t]$. Here, we used the special structure of the control problems (Lotka) and (Calcium) and their (steady-state $\tilde{x}$ seeking) Mayer terms in $x_3$ and $x_5$, respectively. As a second scenario, we considered initializations STOb and POCb, respectively, for values $x(\cdot )$ that were obtained from a (single shooting) forward solution based on the fixed initial values x(0) and $w^{\text {STO}}_0 = w^{\text {POC}}_0$.

To obtain an idea about the distribution of local minima for the two approaches we performed 100 optimization runs for each of the four approximations plus initializations STOa, STOb, POCa, and POCb, and for different values of N. An upper limit of 60 min CPU time was imposed via an AMPL and IPOPT option and additionally via a system timeout command. The latter was necessary because often IPOPT got stuck in the linear system solves. Hence, the category “no convergence” in the tables is composed of several different numerical phenomena, such as too large number of iterations or problems with dual variables in the range of $10^{12}$ in the linear system solves. As stated before, the implementations are by no means efficient and the CPU times shall only give a hint on how the different approximations relate to one another. Iteration counts and CPU times (and their standard deviations) are only calculated from the instances that converged within the time limit.

The numbers of times (out of 100 each) that IPOPT converged to a local minimum are shown in Tables 2 and 3. Stationary points are clustered with a tolerance of $10^{-3}$ for (Lotka) and 1 for (Calcium), comparing objective function values (not the values of w).

We observe that for small numbers of N the number of local minima are larger for (P-STO) than for (P-POC), e.g., 3 : 1 for (Lotka) and $N=2$ (compare also Fig. 4 left for this special case) or 11 : 6 for (Calcium) and $N=3$. For $N=100$ the behavior is almost identical for (P-STO) and (P-POC): converging to only one local minimum for (Lotka) and to a comparable amount of five to six local minima for (Calcium).

Table 2 Convergence results for different numbers N of controls, the approximations and initializations STOa, STOb, POCa, and POCb introduced in Sect. 6.4, and for problem (Lotka)

Table 3 As Table 2, but for problem (Calcium)

One can also see differences for state initialization a (i.e., setting $x^0=\tilde{x}$) and b (i.e., calculating $x^0_i$ from $x_0$ and $w^0$). While STOa and POCa have a tendency to converge to better local minima, they also have a tendency to not converge at all.

Finally, to provide an idea of how local minima differ in the space of the corresponding controls and differential states, Fig. 8 shows exemplary solutions for (Calcium). All four plots correspond to results calculated for $N=100$ as shown in Table 3. Comparing the first two and the last two rows, respectively, one sees how the activations of mode 1 in the (P-STO) and (P-POC) formulations are very similar in the state space. The corresponding trajectories are almost identical, which is also reflected in the objective function values (1597.61 versus 1596.66 and 4225.18 versus 4223.89). In control space, the solutions are only similar in a weak topology and look different to the eye. A comparison of rows 1 and 2 on the one hand, and rows 3 and 4 on the other hand, gives a comparison between two different local minima also in state space. One state remains in the steady state after time $t\approx 7$, while the other state continues to oscillate. A second control activation at $t\approx 15$ is necessary to bring the system into the unstable steady state.

Fig. 8

Exemplary stationary points for (Calcium) and $N=100$, corresponding to the objective function values 1597.61, 1596.66, 4225.18, and 4223.89 (top to bottom)

6.5 Initialization of STO with solution of POC

As a remedy to avoid bad local minima and the also observed convergence issues, it seems a logical choice to use (P-POC) in a first phase to derive an initialization for (P-STO), as first suggested and implemented in [47].

We thus investigated the behavior of (P-STO), when being initialized with the optimal solution of (P-POC). For this purpose, we simply performed a "hot-start" of the STOa and STOb methods after running POCa and POCb, respectively. Other than that, the experimental setup remained unchanged. We also did some computations with an additional run of SUR for the solutions of POCa and POCb to use integer solution for the initialization. The results with respect to convergence properties and objective values were much worse than for the original initializations of STOa and STOb. We omit detailed results here and instead focus on the experiments without this additional algorithm.

Looking again at the results for (Lotka) in Table 2, in all cases but one (POCa and $N=3$) the methods POCa and POCb converged to the same objective function value and correspondingly to the same optimal controls. Thus, it is sufficient to inspect one run of STOa and one run of STOb for each N for this problem. In Table 4 the objective function values and numbers of STO-iterations for the four combinations of initializations are presented. As in the case of STOb without POC-initialization, all instances could be solved in this scenario. Also, the number of iterations until convergence is close to the results of STOb. In the cases of $N=2$ and $N=3$, only the smaller objective function values were achieved. In comparison with STOa without POC-initialization, the hot-start gave an advantage in numbers of iterations and stability, but was not able to capture the best objective in the case of $N=2$.

Table 4 Objective function values and numbers of iterations of STOa and STOb for (Lotka) after hot-starting the problems with the results of POCa and POCb, respectively

Very similar results can be observed in the calcium example in Fig. 9. Here, we chose a graphical representation due to the much higher number of local minima. Again, the initialization of the method with the results of POCa and POCb can help by means of more successful runs for STOa. As a drawback, again, the best results for $N=4$ could not be achieved. In comparison to STOb without POC-initialization, the number of solved instances is lower for each combination, but one.

Fig. 9

Results of initialization of STOa and STOb with the optimal solutions from POCa and POCb as described in Sect. 6.4 for $N\in \{2,3,4,100\}$. The upper bar shows the number of local minima, where the number of instances with no convergence is presented in black. The black lower bar represents the ratio of the median number of iterations for each of the 16 categories to the maximum median number of iterations over all categories. The maximal median number of iterations is assumed in the category N=2, POCb, STOa. In the case of no success for all instances, the bars are empty

6.6 Comparison of constructed (MIOCP) solutions

To fairly compare the two approaches STO and POC, it is useful to also construct and analyze the resulting integer (MIOCP) solutions. For this, we used the Lotka-Volterra problem with $N=100$ intervals and investigated both, the number of switches and the corresponding (MIOCP) objective function values of the constructed solutions. We note that, in contrast to the optimal solution of (P-POC), the (P-STO) solution is already feasible for (MIOCP). Based on the (P-POC) solution $w^*$, we used the CIA problem from Def. (9) to compute solutions with a limited number of switches, where we varied the bound on the number of switches $n_s$ between 2 and 20. Focusing on the (MIOCP) objective function value, we also applied SUR on $w^*$. The approximation Theorem 11 implies that for a given $\varepsilon >0$, we can construct a binary control via SUR with a corresponding (MIOCP) objective value that is $\varepsilon$-close to the optimal solution by refining the discretization grid. For this purpose, we created refined (P-POC) solutions $\tilde{w}$ with $2^k N, \ k=0,1,2,3,$ discretization intervals, where the $w^*$ value on the unrefined interval is used for definition of $\tilde{w}$ values on the refined intervals:

$$\begin{aligned} \tilde{w}_{i,j}:= w_{l,j}^*, \quad \text {for } i\in \{2^k(l-1)+1,\ldots , 2^k l\}. \end{aligned}$$

Then, we applied SUR on these relaxed control solutions $\tilde{w}$ with $2^k N$ discretization intervals.

Fig. 10

Comparison of number of switches and (MIOCP) objective values for the solution of different approaches and the Lotka-Volterra problem with $N=100$. The (P-STO) solution is depicted with the black star. The (P-POC) solution is not integer-feasible and therefore shown as green line (without a meaningful switching value). Based on the (P-POC) solution, we used the CIA-TV approach from Def. (9) and SUR as explained in the text with refined grid levels k for constructing integer-feasible (MIOCP) solutions. Please note, that grid refinement was applied only in the case of SUR. With increasing $n_s$, the CIA-TV solution converges to the unrefined SUR solution. The same convergence behavior could be demonstrated for each refined grid with CIA-TV towards the corresponding SUR solution

We illustrate the numerical result in Fig. 10, where the x-axis depicts the number of switches and the y-axis shows the deviation of the objective value of the constructed solution from the (P-POC) in percentage. The (P-STO) solution is in terms of the objective function value very close to the (P-POC) solution, at the expense of a large number of switches. Since the (P-POC) solution is fractional and therefore has no meaningful switching value, we represent it as a line in the plot.

If we permit only a small number of switches in the CIA problem, the corresponding (MIOCP) solution deviates more than $7\%$ from the (P-POC) objective value. The more switches we allowed, the better the (MIOCP) objective function value became. This holds up to $n_s=14$. For larger $n_s$ values, the determined binary control still involves only 14 switches, since more switches result in no improvement in the objective on the unrefined grid. We remark, however, that this method would result in the same convergence behavior to the optimal objective value of (P-POC) as the SUR method when applied on the refined discretization grid and with sufficiently large chosen $n_s$.

The determined solution from SUR on the unrefined grid, i.e. $k=0$, has a small number of switches compared to the (P-STO) solution but yields a larger objective value. By refining the discretization grid, the constructed SUR solutions converged to the optimal objective value of (P-POC) or even reached smaller values for large k, which is possible as (P-POC) was solved on the unrefined grid. The improved objective values come at the expense of frequent switching.

7 Discussion

We are going to discuss the most important results of the previous section, looking for plausibility of the observations. We start with some considerations concerning the computational costs, before we address the main finding: the different numbers of local minima in the two formulations.

7.1 Computational costs

The computational costs of iterative algorithms are determined by the number of iterations, and the computational costs per iteration. In the previous section, and in particular in Tables 2 and 3 we observed

Numerical Result 18

(Number of Iterations) There is an increased number of iterations and of convergence issues for (P-STO) compared to (P-POC).

A closer look at (STO-f) and (POC-f) reveals one detail: in (STO-f) the drift term $f_0$ is multiplied with the optimization variables w. In (POC-f), this is not the case owing to the one-hot property of $w \in \mathcal {W}$. It is well known that higher nonlinearities, e.g., measured via Lipschitz constants, typically lead to increased regions of fast local convergence and to worse convergence rate constants, e.g., [5, 8, 57]. Thus we think that Numerical Result 18 is due to the augmented nonlinearity of the differential equations that appear in function and derivative evaluations in (P-STO).

One may possibly construct cases in which this multiplication does not increase nonlinearity, because $f_0(x) \approx 1/w$, or the effect might be negligible compared to the nonlinearities in the other $f_j$. However, for most practically relevant cases we can assume that the multiplication of $f_0$ with w increases nonlinearity of the optimization problem. There might be ways to reduce this nonlinearity again via a lifting procedure and usage of big M or McCormick-type constraints. Since this would involve case-specific upper bounds on the right-hand sides and a further level of approximation, we did not pursue this direction here, but worked with the formulation that is usually used in the STO literature.

A second observation in Tables 2 and 3 was

Numerical Result 19

(Computational Costs) The computational costs per iteration are roughly similar for (P-STO) and (P-POC).

For our numerical approach and test problems the computational costs per iteration were mainly governed by the evaluation of the differential equations and the sensitivity differential equations. Thus, the computational effort to evaluate the right-hand sides in (STO-f) and in (POC-f) for the whole time horizon ${\mathcal {T}}$ are important, as they carry over in a more or less straightforward way to the effort of derivative calculation. For many practical optimal control problems the evaluation of function and derivatives dominates the computational costs. Evaluating (POC-f) for a fixed $t \in {\mathcal {T}}$ needs more function evaluations, as all ${n_\omega }+1$ functions $f_j$ need to be evaluated, whereas for (STO-f) only two evaluations are necessary. However, if we assume that the computational effort to evaluate (STO-f) on ${\mathcal {T}}_{ij}$ is approximately constant (this certainly depends on the numerical integration scheme), then the evaluation on all $n_\sigma$ subintervals ${\mathcal {T}}_{ij}$ increases the overall effort by a factor of $n_\sigma$. This would then give advantage to (POC-f), because the drift term $f_0$ needs to be evaluated only once for each $t \in {\mathcal {T}}$ and multiple times for STO (because it is evaluated at different times). Another interesting question is the one about situations in which $w^{\text {STO}}_{ij} = 0$. While it is clear that in this case no integration on ${\mathcal {T}}_{ij}$ would be necessary, an implementation of this is rather tricky to realize, especially as also derivatives are needed to determine whether the search direction of the optimization algorithm is positive for $w^{\text {STO}}_{ij} = 0$ or not.

For (P-STO) a speedup by two orders of magnitude was achieved for test problems based on a linearization of the dynamics [58]. The approach benefits from the usage of an exponential integrator and closed-form analytical derivatives. The main idea should also carry over to POC approximations, with the main difficulty of deriving analytical formulas for the derivatives of the matrix exponential for non-commutative matrices, though.

As a summary, we see reasons that in many cases the computational costs for (P-STO) might be higher than for (P-POC) because of more iterations of a generic iterative optimization algorithm, with similar costs per iteration.

In Table 4 and Fig. 9, the experiments of initializing (P-STO) with the optimal solution of (P-POC) led to ambiguous results. For some problem sizes, the number of converging instances could be increased; however, for few others, the opposite was the case. The same holds true with respect to the constructed best objective values. This non-intuitive behavior can have several reasons. An interior-point solver like IPOPT is not well suited for restarts, and active-set based approaches could rather be used. Also, efficient schemes like the one proposed in [58] could be taken into account, possibly exploiting additional structures in a hot-start. The transfer of differential states from one time grid to another has to be carefully implemented unless one uses a single shooting initialization with the controls resulting from the first phase, as we did in this study. This initialization led overall to better convergence properties than using only the optimal control values of (P-POC).

7.2 Nonconvexity of the objective function

There were three main observations in the previous section for the two benchmark problems, which might carry over to other mixed-integer optimal control problems. We are somewhat sloppy with our formulations concerning “small” or “large” values of N, as this is certainly problem-specific. In Fig. 7 we got indications that

Numerical Result 20

(Nonconvexity Evaluation) Quantified measures of nonconvexity such as $R^*$ are higher for (P-STO) compared to (P-POC) for small N, and identical for large N.

Almost as a corollary, but also from Figs. 4, 5, and 6 as well as from Tables 2 and 3 we obtained

Numerical Result 21

(Number of Local Minima) For fixed N, there are typically at least as many local minima for (P-STO) as for (P-POC).

The case $N=100$ in Table 3 indicated that

Numerical Result 22

(Asymptotic Objective Function Values) The number of $\varepsilon$-optimal local minima is asymptotically, i.e. for $N\rightarrow \infty$, identical for (P-STO) and (P-POC).

The additional nonconvexity in (P-STO) is again due to the additional multiplication of the drift term $f_0$ by w, as discussed above. Therefore, it is not surprising that there are instances in which the number of local minima of (P-POC) is dominated by the number corresponding to (P-STO), e.g., the case $N=3$ in Table 3.

Numerical Result 22 is less intuitive. The asymptotic behavior of the number of local minima can be explained by the fact that the optimal objective function values of (P-STO) and (P-POC) are converging to the same value for increasing N as derived in Corollaries 12 and 13 and discussed at the end of Sect. 3.

Thus, the effect of the increased nonconvexity on the number of local minima can only be observed for coarse control discretizations (large $\Delta t$). We summarize that (P-STO) is likely to have more local minima for each discretization grid than (P-POC); however, the number of local minima is asymptotically identical.

7.3 Obtaining (MIOCP)-feasibility

While the STO approach constructs integer-feasible solutions for (MIOCP) and can be viewed as a primal heuristic, the main motivation of the POC approach is to provide a relaxed solution of (MIOCP). The necessary postprocessing of the (P-POC) solution for determining an integer solution can be considered as a drawback, in particular since the rounded solution can result in relatively large objective values compared with the relaxed one. However, we showed in Sect. 6.6 that the rounded (P-POC) solution converges to the optimal solution of (MIOCP) by applying refinement of the discretization grid. Moreover, rounding methods such as SUR are computationally inexpensive. Regardless of whether we use STO or POC as solution approach for (MIOCP), a trade-off between objective quality and the number of used switches can be observed. The more switches we allow by means of control discretization or as part of CIA, the better the optimal objective value.

8 Conclusion

In this paper, we compared the (P-STO) and the (P-POC) approximations of Problem (MIOCP). We have demonstrated with numerical simulation and optimization results that (P-STO) tends to result in more local minima than (P-POC) for few degrees of freedom (small N), whereas both problem formulations show similar behavior for large N. We explained theoretically the underlying reasons. The additional nonconvexities and nonlinearities are due to a multiplication of the drift term $f_0(\cdot )$ with the control w in (P-STO). However, asymptotically in $N \rightarrow \infty$, i.e., for $\Delta t \rightarrow 0$, every solution of (P-STO) can be approximated arbitrarily close by a solution of (P-POC), and vice versa. The initialization of (P-STO) with optimal solutions of (P-POC) led to ambiguous results with respect to convergence properties but could be investigated further in the future. Another future research direction could be an investigation if singular, path-constrained, and bang-bang arcs in optimal solutions of (P-POC) have an impact in this context. Also, a broader numerical investigation with more control problems, more instances, various switching orders $\sigma$, more efficient implementations, additional underlying constraints, and aspects of global and/or robust optimization could shed additional light on the question of how the two approximations can be combined to solve Problem (MIOCP).

Appendix

1.1 How to set up and solve an MIOC with ampl_mintoc

Following AMPL standards, a problem-specification usually involves one data file, one model file and one run file. An optimal control problem prob can be formulated using ampl_mintoc via the problem-specific files prob.dat, prob.mod, and prob.run. First, problem dimensions (e.g. of the differential states and controls), parameters (e.g. the number of discretization intervals), and initial values are specified in prob.dat. In the prob.mod file, model-specific functions can be defined (in the discretized sense). This includes the model function f, mixed state-control constraints, path constraints c, and vanishing constraints. Listings 2 and 3 show the AMPL implementations for the (Lotka) and (Calcium) problems from Sect. 4 as examples of how to formulate f and, hence, the problems’ dynamics.

Note that we use the time index i to define the functions. These discretized definitions allow the user to easily specify piecewise functions on different sub-domains.

Finally, algorithmic choices can be provided in prob.run, such as the integration scheme, the problem reformulation, the simulation or optimization algorithm, relaxation of integer variables, or postprocessing of results.