1 Introduction

In this work, let us consider the multiobjective optimization problem where a set a objective functions must be minimized simultaneously

$$\begin{aligned} \min _{x \in {{{\mathbb {R}}}}^{n}} F(x), \quad F: {{{\mathbb {R}}}}^{n}\rightarrow {{{\mathbb {R}}}}^{m}. \end{aligned}$$

Since there is not a single point which minimize all the functions simultaneously the concept of optimality is established in terms of Pareto optimality or efficiency. Let us recall that a point is said to be Pareto optimal or efficient, if there does not exist a different point with the same or smaller objective function values such that there is a decrease in at least one objective function value. Applications of this type of problems can be found in different areas. For instance [14, 17, 18] to mention some of them.

Among the strategies for multiobjective optimization problems we can mention the scalarization approach [11, 12]. The idea is to solve one or several parameterized single-objective problems, resulting in a corresponding number of Pareto optimal points. One of the drawbacks of this approach is the choice of the parameters that are not known in advance (see [9, sect. 7]).

Algorithms that do not scalarize the problem have recently been developed. Some of these techniques are extensions of well known scalar algorithms [9, 10], while others take ideas developed in heuristic optimization [13]. For the latter, no convergence proofs are known, and empirical results show that convergence generally is, as in the scalar case, quite slow [20].

In this paper, we focus on some a priori parameter-free optimizations problems developed in [9, 10]. In such methods there is a scalarization procedure that does not set parameters before solving the problem. The main idea of it consists in replacing, at each iteration, each objective function with a quadratic model for it, as in the scalar Newton’s method. With these local models they minimize the max-scalarization of the variations of the quadratic approximations and obtain a descent direction for the convex case. For globalization purposes [9, 10] use a line search strategy and obtain convergence to Pareto points in the convex case. In the present work we consider a trust region algorithm for the nonconvex case by using some ideas of these works.

According to our knowledge there is not too much activity on this subject. In 2006, Ashry [2] converts the multiobjective optimization problem in a scalar one and uses a TR-algorithm for solving the general nonlinear porgramming problem. He uses an algorithm based on the Byrd theory for equality constrained minimization. Recently Qu et al. [16] have developed a TR-algorithm for the unconstrained vector optimization case which has some points in common with ours. For instance, they apparently were inspired by the work of Fliege et. al. [9] like us, but they focus the discussion on the non differentiable case that is not our case. Finally, it is also interesting the work of Villacorta et. al. [19] where they propose a TR-algorithm for the same problem with a different subproblem and a different way to evaluate the step.

This work is organized as follows: the next section is devoted to state the optimality condition, the subproblem involved and some properties about its solution. The algorithm is presented in the third section and the fourth one is dedicated to its global convergence properties. The fifth section is dedicated to the analysis of the local q-quadratic rate of convergence of the algorithm. Numerical tests are presented in the sixth section and in the last one some conclusions are established.

2 The subproblem and the optimality conditions

The problem under discussion consists to find an efficient point or Pareto optimum of \(F:{{{\mathbb {R}}}}^{n}\rightarrow {{{\mathbb {R}}}}^{m}\), i.e. a point \(x^\star \in {{{\mathbb {R}}}}^{n}\) such that

$$\begin{aligned} \not \exists y \in {{{\mathbb {R}}}}^{n}, F (y) \le F (x^\star ), F (y) \ne F (x^\star ), \end{aligned}$$

where the inequality sign \(\le \) between vectors must be understood in the componentwise sense. This means that one is seeking to minimize F in the partial order induced by the positive orthant \({\mathbb {R}}_+^m\).

A point \(x^\star \) is weakly efficient or weak Pareto optimum if

$$\begin{aligned} \not \exists y \in {{{\mathbb {R}}}}^{n}, F (y) < F (x^\star ), \end{aligned}$$

where the vector strict inequality \(F (y) < F (x^\star )\) has to be understood componentwise too.

Locally efficient points are also called local Pareto optimal, and locally weakly efficient points are also called local weak Pareto optimal. Note that if F is \({{{\mathbb {R}}}}^{m}\)-convex (i.e., if F is componentwise-convex), then each local Pareto optimal point is globally Pareto optimal. Clearly, every locally efficient point is locally weakly efficient.

Throughout this paper, unless explicitly mentioned, we will assume that \( F \in {\mathcal {C}}^2 \left( {{{\mathbb {R}}}}^{n}, {{{\mathbb {R}}}}^{m}\right) , \) i.e., F is twice continuously differentiable on \( {{{\mathbb {R}}}}^{n}\), \(F(x)=\left( f_1(x),\dots ,\right. \left. f_m(x)\right) ^T\). For \(x\in {{{\mathbb {R}}}}^{n}\), denote by \(\nabla F \left( x\right) \in {{{\mathbb {R}}}}^{m \times n}\) the Jacobian matrix of the vectorial function F at x, by \(\nabla f_j (x) \in {\mathbb {R}}^n\) the gradient vector of the scalar function \(f_j\) at x, and by \(\nabla ^2 f_j (x) \in {{{\mathbb {R}}}}^{n \times n}\) the Hessian matrix of \(f_j\) at x.

Denoting the column space of the Jacobian matrix by \({\mathcal {R}}\left( \nabla F\left( x\right) \right) \), a point is \(x^\star \in {{{\mathbb {R}}}}^{n}\) is critical for F if

$$\begin{aligned} {\mathcal {R}}\left( \nabla F\left( x\right) \right) \cap \left( - {\mathbb {R}}_{++}^m\right) =\emptyset . \end{aligned}$$

This is necessary condition for Pareto optimality [15].

Clearly, if \(x^\star \) is critical for F, then for all \(s\in {{{\mathbb {R}}}}^{n}\) there exists an index \(j_0 = j_0(s)\in \left\{ 1,\dots ,m\right\} \) such that

$$\begin{aligned} \nabla f_{j_0} \left( x^\star \right) ^T s \ge 0. \end{aligned}$$

We observe that if \(x\in {{{\mathbb {R}}}}^{n}\) is noncritical, then there exists \(s\in {{{\mathbb {R}}}}^{n}\) such that \(\nabla f_j(x)^T s < 0\) for all \(j=1,\dots ,m\). As F is continuously differentiable,

$$\begin{aligned} \lim _{t\rightarrow 0} \frac{f_j\left( x+ts\right) -f_j\left( x\right) }{t}=\nabla f_j^T \left( x\right) s<0, \ j=1,\dots ,m. \end{aligned}$$

Thus, s is a descent direction for F at x; i.e., there exists \(t_0 > 0\) such that

$$\begin{aligned} F\left( x + t s\right) < F(x) \hbox { for all } t\in \left( 0, t_0\right] . \end{aligned}$$

The next proposition due to Fliege et. al. [9] establishes the relationship between the properties of being a critical and an optimal point.

Proposition 1

Let F is continuously differentiable on \({{{\mathbb {R}}}}^{n}\), i.e. \(F\in {\mathcal {C}}^1\left( {{{\mathbb {R}}}}^{n}, {\mathbb {R}}^m\right) \).

  1. (i)

    If \(x^\star \) is locally weak Pareto optimal, then \(x^\star \) is a critical point for F.

  2. (ii)

    If F is \({\mathbb {R}}^m\)-convex and \(x^\star \) is critical for F, then \(x^\star \) is weak Pareto optimal.

  3. (iii)

    If \(F\in {\mathcal {C}}^2({{{\mathbb {R}}}}^{n}, {\mathbb {R}}^m)\), and the Hessians matrices are positive definite for all x and for all j, and if \(x^\star \) is critical point for F, then \(x^\star \) is Pareto optimal.

With the purpose to obtain a descent direction for F at x, in [10] the problem

$$\begin{aligned} \begin{array}{l@{\quad }l} \displaystyle { \min _{s. t.}} &{} \alpha + \frac{1}{2} \left\| s \right\| ^2 \\ &{} \left( \nabla F\left( x\right) s \right) _j \le \alpha , \ j=1,\dots ,m, \end{array} \end{aligned}$$
(1)

is solved. In this problem \(\alpha \) is an auxiliar variable and s is used in order to obtain a step for the iterations. If a point x is a critical point then the minimum of (1) is 0 (see Lemma 1 of [10]). In this way the authors obtain a steepest descent direction.

In [9] a Newton direction is defined as the solution of

$$\begin{aligned} \displaystyle {\min _{s\in {\mathbb {R}}^n}} \displaystyle {\max _{j=1,\dots ,m}} \left[ \nabla f_j \left( x\right) ^T s+\frac{1}{2} s^T \nabla ^2f_j\left( x\right) s \right] . \end{aligned}$$
(2)

Because the problem (2) is not differentiable, the following problem is introduced

$$\begin{aligned} \begin{array}{c@{\quad }l} \displaystyle { \min _{s. t.}} &{} t \\ &{} \nabla f_j \left( x\right) ^T s+\frac{1}{2} s^T \nabla ^2f_j\left( x\right) s -t \le 0, \quad j=1,\dots ,m,\\ &{} \left( t,s \right) \in {\mathbb {R}}\times {\mathbb {R}}^n, \end{array} \end{aligned}$$

which is differentiable and has the same solution as (2). In [9] the convex case is considered and the direction s, solution of the problem, is a descent direction. Unfortunately, in the nonconvex case can not be guaranteed that the direction s given by this subproblem will be a descent direction, It can be seen in the next example.

Example 1

Consider \(F\left( x_1,x_2 \right) =\left[ e^{x_1-1}+e^{x_2-1}, \ \frac{x_1^2-x_2^2}{2} -10x_1+x_2 \right] ^T\). Clearly \(f_1\) is convex and \(f_2\) is not. For this, the associated subproblem (2) at the point \(x=\left( 1,\ 1 \right) \) is

$$\begin{aligned} \begin{array}{c@{\quad }l} \displaystyle { \min _{s. t.}} &{} t \\ &{} \frac{1}{2} s^T \left[ \begin{matrix} 1 &{}\quad 0\\ 0&{}\quad -1 \end{matrix} \right] s + \left[ -10 \ 1 \right] s-t \le 0, \\ &{} \frac{1}{2} s^T \left[ \begin{matrix} 1 &{}\quad 0\\ 0&{}\quad 1 \end{matrix} \right] s + \left[ 1 \ 1 \right] s-t \le 0. \end{array} \end{aligned}$$

The approximate solution is \(t=-0.6024\) and \(s=\left( -0.1284, \ -1.1883 \right) ^T\). This direction is a descent direction for \(f_1\) but is not for \(f_2\).

Therefore, to overcome this difficulty in the nonconvex case, to obtain a descent direction we add the linear inequality constraints \(\nabla f_j(x)^Ts-t\le 0\), \(j=1, \ldots , m\),

$$\begin{aligned} \begin{array}{c@{\quad }l} \displaystyle { \min _{s. t.}} &{} t \\ &{} \nabla f_j \left( x\right) ^T s+\frac{1}{2} s^T \nabla ^2f_j\left( x\right) s -t \le 0, \quad j=1,\dots ,m,\\ &{}\nabla f_j \left( x\right) ^T s-t \le 0, \quad j=1,\dots ,m,\\ &{} \left( t,s \right) \in {{\mathbb {R}}}\times {{{\mathbb {R}}}}^{n}. \end{array} \end{aligned}$$

The resulting problem could be not bounded, so we introduce a trust region, \(\Vert s\Vert \le \Delta \):

$$\begin{aligned} \begin{array}{c@{\quad }l} \displaystyle { \min _{s. t.}} &{} t \\ &{} \nabla f_j \left( x\right) ^T s+\frac{1}{2} s^T \nabla ^2f_j\left( x\right) s -t \le 0, \quad j=1,\dots ,m,\\ &{}\nabla f_j \left( x\right) ^T s-t \le 0, \quad j=1,\dots ,m,\\ &{}\left\| s\right\| \le \Delta , \\ &{} \left( t,s \right) \in {{\mathbb {R}}}\times {{{\mathbb {R}}}}^{n}, \end{array} \end{aligned}$$
(3)

where \(\Delta >0\).

Remark 1

The trust region is applied only to the original variables of the problem \(s \in {{{\mathbb {R}}}}^{n}\) and not to the variable t which has been introduced only to avoid the nondifferentiability of the problem.

The problem (3) is the key in our development, so we will analyze some of its properties. Let us define \(\theta (x)\) as the optimal value of problem (3) and s (x) as the value of s in an optimal solution of (3).

Is important to note that \(s\left( x\right) \) could not be a function because the problem (3) is not convex, therefore has no unique solution. The relation among a critical point \(x^\star \), the Newton step \(s(x^\star )\) and the value \(\theta (x^\star )\) is established in the next lemma,

Lemma 1

Let \(\theta (x)\) be as above, then:

  1. (a)

    For any \(x\in {{{\mathbb {R}}}}^{n}\), \(\theta (x)\) is well defined, continuous and \(\theta (x)\le 0\).

  2. (b)

    s(x) is bounded.

  3. (c)

    The following statements:

    1. (i)

      \(x^\star \) is not a critical point.

    2. (ii)

      \(\theta \left( x^\star \right) <0\).

    3. (iii)

      \(s\left( x^\star \right) \ne 0\).

    satisfy \((i) \Leftrightarrow (ii) \Rightarrow (iii)\). Moreover, if the vectorial function F is \({{{\mathbb {R}}}}^{m}\)-convex, then (i), (ii) and (iii) are equivalents.

Proof

It’s clear that

$$\begin{aligned} \theta (x)= \displaystyle {\min _{\Vert s\Vert \le \Delta }} \; \displaystyle {\max _{ j=1,\dots ,m}} \left\{ \nabla f_j \left( x\right) ^T s+\frac{1}{2} s^T \nabla ^2f_j\left( x\right) s, \nabla f_j \left( x\right) ^T s \right\} \end{aligned}$$

is well defined because it is the maximum of continuous functions over a compact set, the feasible set of the subproblem. Then \(\theta \left( x\right) \) is well defined.

Due to \(\left( t,s \right) =\left( 0,\mathbf{0} \right) \) is feasible a point, from (3), \(\theta (x)\le 0\).

Now, we prove the continuity of \(\theta \left( x\right) \). As any point in \({{{\mathbb {R}}}}^{n}\) is in the interior of a compact subset of \({{{\mathbb {R}}}}^{n}\), it is enough to show continuity of \(\theta \) on an arbitrary compact set \(W\subseteq {{{\mathbb {R}}}}^{n}\). For each \(x\in W\) and \(j=1,\dots ,m\), we define

$$\begin{aligned} \phi _{x, j} \left( z\right) =\nabla f_j \left( z\right) ^T s(x)+ \frac{1}{2} s(x)^T \nabla ^2f_j \left( z\right) s(x) \end{aligned}$$

and

$$\begin{aligned} \psi _{x,j} \left( z\right) =\nabla f_j \left( z\right) ^T s(x). \end{aligned}$$

The family \(\left\{ \phi _{x,j} , \psi _{x,j} \right\} _{x\in W, j=1,\dots ,m }\) is equicontinuous. Therefore, the family

$$\begin{aligned} \varPhi _x (z)= \max _{j=1,\dots ,m} \left\{ \varphi _{x,j}(z), \psi _{x,j}(z)\right\} , \end{aligned}$$

where the maximum is over \(\varphi _{x,1}(z),\dots ,\varphi _{x,m}(z), \psi _{x,1}(z),\dots , \psi _{x,m}(z)\), is equicontinuous too.

Given \(\epsilon >0\); there exists \(\delta >0\) such that \(\forall y,z\in W\)

$$\begin{aligned} \left\| z-y\right\| < \delta \Rightarrow \left| \varPhi _x(z)-\varPhi _x(y)\right| <\epsilon , \ \forall x\in W. \end{aligned}$$

Hence, for \(\left\| z-y\right\| < \delta \),

$$\begin{aligned} \theta (z)\le & {} \max _{j=1,\dots , m} \left\{ \nabla f_j \left( z\right) ^T s(y)+ \frac{1}{2} s(y)^T \nabla ^2 f_j \left( z\right) s(y), \nabla f_j \left( z\right) ^T s(y) \right\} \\= & {} \varPhi _y (z) \\\le & {} \varPhi _y (y) + \left| \varPhi _y (z) - \varPhi _y (y) \right| \\< & {} \theta (y) + \epsilon . \end{aligned}$$

i.e. \(\theta (z)-\theta (y)<\epsilon \). Interchanging the roles of z and y, we conclude that \(\left| \theta (y)-\theta (z) \right| <\epsilon \). Therefore (a) has been proved.

The values of \(s\left( x\right) \) are clearly bounded because of the trust region.

To prove the implications of (c):

\((i)\Rightarrow (ii)\) If \(x^\star \) is not critical

$$\begin{aligned} {\mathcal {R}}\left( \nabla F\left( x^\star \right) \right) \cap \left( -{\mathbb {R}}_{++}^m\right) \ne \emptyset , \end{aligned}$$

so \(\exists \tilde{s} \in {\mathbb {R}}^n\) such that \(\nabla f_j\left( x^\star \right) ^T \tilde{s} <0\) for all \(j=1,\dots ,m\).

Then there exists \(\tilde{t}< 0\) such that

$$\begin{aligned} \nabla f_j\left( x^\star \right) ^T \tilde{s} - \tilde{t} < 0 \ j=1,\dots ,m. \end{aligned}$$

If \(\tilde{s}^T \nabla ^2 f_j\left( x^\star \right) \tilde{s} \le 0\) for all \(j=1,\dots ,m\), then

$$\begin{aligned} \nabla f_j\left( x^\star \right) ^T \tilde{s} + \frac{1}{2} \tilde{s}^T \nabla ^2f_j\left( x^\star \right) \tilde{s} < \tilde{t} < 0 . \end{aligned}$$
(4)

If \(\tilde{s}^T \nabla ^2 f_j\left( x^\star \right) \tilde{s} > 0\) for some \(j=1,\dots ,m\), then choosing \(l\tilde{s}\), with l small enough, we have that there exists \(\widehat{t}<0\)

$$\begin{aligned} \nabla f_j\left( x^\star \right) ^T \tilde{s} l + \frac{1}{2} l^2 \tilde{s}^T \nabla ^2f_j\left( x^\star \right) \tilde{s} < \widehat{t}< 0, \ j=1,\dots ,m . \end{aligned}$$
(5)

Then, for (4), (5) and the fact that s is a descent direction for F at \(x^\star \), \( \theta \left( x^\star \right) < 0. \)

\((ii)\Rightarrow (i)\) If \(\theta \left( x^\star \right) <0\) then \(\exists (t, s)\), feasible for (3), with \(x=x^\star \), such that

$$\begin{aligned} \nabla f_j\left( x^\star \right) ^T s\le t <0 \ j=1,\dots ,m, \end{aligned}$$

so \({\mathcal {R}}\left( \nabla F\left( x^\star \right) \right) \cap \left( -{\mathbb {R}}_{++}^m\right) \ne \emptyset \), i.e. \(x^\star \) is not critical.

\((ii)\Rightarrow (iii)\) Assume that \(s\left( x^\star \right) =0\), then

This contradicts \(\theta \left( x^\star \right) <0\). Then \(s(x^\star )\ne 0\).

Finally, assuming that F is \({{{\mathbb {R}}}}^{m}\)-convex we prove \((iii)\Rightarrow (i)\). Due to \(\nabla ^2 f_j\left( x^\star \right) \) are positive definite for \(j=1,\dots ,m\), and \(s=s\left( x^\star \right) \ne 0\) we have

$$\begin{aligned} \nabla f_j\left( x^\star \right) ^T s < \nabla f_j\left( x^\star \right) ^T s +\frac{1}{2} s\left( x^\star \right) ^T \nabla ^2 f_j \left( x^\star \right) s\left( x^\star \right) \le \theta \left( x^\star \right) \le 0, \end{aligned}$$

for \(j=1,\dots ,m\), then \({\mathcal {R}}\left( \nabla F\left( \bar{x} \right) \right) \cap \left( -{\mathbb {R}}_{++}^m\right) \ne \phi \), therefore, \(x^\star \) is not critical. \(\square \)

The relation \((iii)\Rightarrow (ii)\) is not true in the nonconvex case, as it can be seen in the next example.

Example 2

Consider \( \displaystyle { \min _{s. t.}} \left[ \begin{array}{c@{\quad }c} cos(x_1)+e^{x_2}-x_2&-cos(x_2)-e^{x_1}-x_1 \end{array} \right] ^T \).

The associate TR-subproblem (3) at the point \(x=(0 \ 0)^T\) is

$$\begin{aligned} \begin{array}{c@{\quad }l} \displaystyle { \min _{s. t.}} &{} t \\ &{} \left[ 0 \ \quad 0 \right] s+ \frac{1}{2} s^T \left[ \begin{array}{c@{\quad }c} -1 &{} 0\\ 0&{} 1 \end{array} \right] s -t \le 0, \\ &{}\left[ 0 \ \quad 0 \right] s-t \le 0, \\ &{}\left\| s\right\| \le \Delta , \\ &{} \left( t,s \right) \in {{\mathbb {R}}}\times {\mathbb {R}}^2. \end{array} \end{aligned}$$

Clearly, the solutions are \(t=0\) and \(s\in {\mathbb {R}}^2\) such that \(\left| s_2\right| \le \left| s_1\right| \). Thus, there are solutions with \(s\ne 0\) and \(t=0\).

3 The trust region algorithm

Algorithms which use trust regions establish a quadratic model around the current iterate and later solve a subproblem. This subproblem consists in finding the minimizer of the quadratic model in a compact set, the trust region. We will propose an algorithm defining a quadratic model for each objective function:

$$\begin{aligned}\displaystyle q_k^j\left( s\right) =\nabla f_j\left( x_k\right) ^T s +\frac{1}{2} s^T\nabla ^2 f_j\left( x_k\right) s . \end{aligned}$$

In contrast to the scalar case we do not minimize the quadratic models but the maximun of them in a descent direction. In each iterate \(x_k\), the next algorithm solve the trust region subproblem (3), whose solution allows us to define the next iterate \(x_{k+1}\). The trial step \(s_k\) is obtained like the component s from the solution of the subproblem (3) in \(x=x_k\). In the steps 3 and 4 of the next algorithm a criterion for evaluating and accepting the step is presented, and, in the step 5, a rule for updating the trust region radius is established.

Algorithm 1

Set \(x_0\in {{{\mathbb {R}}}}^{n}\), \(\Delta _0>0\), \(0<\eta _1<\eta _2<1\), \(0<\gamma _1<\gamma _2<1\), \(tol>0\) and \(k=0\)

  1. 1.

    Evaluate \(\nabla f_j\left( x_k\right) \), \(\nabla ^2 f_j\left( x_k\right) , \; j=1, \ldots , m\), and solve the subproblem (3) with \(x=x_k\) and \(\Delta =\Delta _k\), in order to obtain \(\left( t_k,\ s_k \right) \).

  2. 2.

    If \(\left| t_k\right| <tol\), stop.

  3. 3.

    Set

    $$\begin{aligned} \rho _k^j =\frac{f_j\left( x_k\right) -f_j\left( x_k+s_k\right) }{q_k^j\left( 0\right) -q_k^j\left( s_k\right) } . \end{aligned}$$
  4. 4.

    If \(\rho _k^j\ge \eta _1 \ \forall j\), \(x_{k+1}=x_k+s_k\); otherwise \(x_{k+1}=x_k\).

  5. 5.

    Update the trust region radius:

    $$\begin{aligned} \Delta _{k+1} \in \left\{ \begin{array}{l@{\quad }l@{\quad }l} \left( \Delta _k , \infty \right) &{}\hbox {if}&{} \eta _2\le \rho _k^j \ \forall j. \\ \left( \gamma _2 \Delta _k , \Delta _k \right] &{}\hbox {if}&{} \eta _1\le \rho _k^j \ \forall j \hbox { and } \exists l \ \hbox { such that } \rho _k^l< \eta _2. \\ \left[ \gamma _1 \Delta _k , \gamma _2 \Delta _k \right] &{}\hbox {if}&{} \exists l \ \hbox { such that } \rho _k^l\le \eta _1. \\ \end{array}\right. \end{aligned}$$
  6. 6.

    \(k \leftarrow k+1\).

In scalar trust region algorithms, at each iteration, the trial step is evaluated using the agreement between the functional and the model reduction around \(x_k\), (i.e: \(\rho _k\)). In our algorithm m quotients: \(\rho _k^j\), \(j=1,\dots ,m\), one for each objective function, were used. We said that the k-th iteration is very successful if \(\rho _k^j\ge \eta _2\) for all \(j=1,\dots ,m\), and, in such case, we increase the trust region radius, i.e. \(\Delta _{k+1}\in \left( \Delta _k , \infty \right) \). We say that the k-th iteration is successful if \(\rho _k^j\ge \eta _1\) for all \(j=1,\dots ,m\), and there are some index l such that \(\rho _k^l\le \eta _2\), in such case, we update the new trust region radius taking \(\Delta _{k+1}\in \left( \gamma _2 \Delta _k , \Delta _k \right] \). In other case, we said that the k-th iteration is unsuccessful and we reduce the trust region radius, i.e. \(\Delta _{k+1}\in \left[ \gamma _1 \Delta _k , \gamma _2 \Delta _k \right] \).

It is important to note that, due to \(\theta (x)\le 0\), if \(x_k\) is not a critical point, the direction \(s_k\) obtained by the subproblem (3) is a descent direction for F at \(x_k\). Moreover, the stoping criteria established in the 2nd step is suiteable due to the continuity of \(\theta (x)\). Furthermore, we have shown that the subproblem (3) is well defined.

To establish the well-definedness of the algorithm it is necessary to choose the step \(s_k\) among the vectors s such that \(\left( \theta \left( x_k\right) ,s\right) \) be a solution of (3). After that, \(q_k^j\left( 0\right) -q_k^j\left( s_k\right) >0\) for all \(j=1,\dots ,m\), has to be proved at every noncritical \(x_k\) and itis necessary to prove that Algorithm 1 will accept a step in a finite number of inner iterations. This will be discussed in the Remarks 6 and 7.

4 Global convergence analysis

The global convergence analysis shares characteristics from the analysis developed for the scalar case and the hypothesis also are similar, see [4]. Assuming second order information, we will suppose uniformerly boundness of the first and second order derivatives of F:

  1. (A1)

    \(F\in {\mathcal {C}}^2({{{\mathbb {R}}}}^{n},{{{\mathbb {R}}}}^{m})\).

  2. (A2)

    The Hessian matrices are uniformely bounded:

    $$\begin{aligned} \left\| \nabla ^2 f_j\left( x\right) \right\| \le \kappa _{H} \ \ \forall x\in {\mathbb {R}}^n,\ \hbox { for } j=1,\dots ,m. \end{aligned}$$
  3. (A3)

    \(f_j(x)\) is lower bounded for \(j=1,\dots ,m\).

  4. (A4)

    Exists \(\Delta _{\max }>0\) such that

    $$\begin{aligned} \Delta _k \le \Delta _{\max }, \quad \forall k\ge 0. \end{aligned}$$
  5. (A5)

    Exists \(\kappa _{G}>0\) such that

    $$\begin{aligned} \left\| \nabla f_j\left( x\right) \right\| \le \kappa _{G} \ \ \forall x\in {\mathbb {R}}^n,\ \hbox { for } j=1,\dots ,m. \end{aligned}$$

Remark 2

The hypothesis (A3) can be asummed without loss of generality. See [19].

Remark 3

The hypothesis (A4) is an algorithmic assumption: it allows us to have an bound for all quadratics models \(q_k^j\), \(j=1,\dots ,m\). This assumption is necessary in order to the ratios \(\rho _k^j\), \(j=1,\dots ,m\), result to be well defined.

Remark 4

The hypothesis (A2) and (A5) might seem too strong but if we consider that the level sets of the functions \(f_j\), \(j=1,\dots ,m\), are bounded, this requirement is automatically satisfied because the continuity of \(\nabla f_j\) and \(\nabla ^2 f_j\), \(j=1,\dots ,m\), and the fact that our method is a descent method [4].

In the scalar case, the strategy consists in obtaining that the reduction produced by a step be at least a fraction of the reduction produced by the Cauchy step. In the vectorial case, since it does not have a Cauchy step with the optimal length for all the functionals, the strategy consists in estimating the optimal reduction for each of the models with a descent direction different of the steepest descent for it. The bound for the reduction predicted by a quadratical model \(q_k^j\) at \(x_k\) in a descent direction for F is given by the next lemma.

Lemma 2

Let \(v\in {\mathbb {R}}^n\) a descent direction for F at \(x_k\), a noncritical point. For each \(j=1,\dots ,m\), there exists \(\overline{t}>0\), such that \(\left\| \overline{t} v \right\| \le \Delta _k\) and

$$\begin{aligned} q^j_k\left( \overline{t} v \right) \le q^j_k\left( t v \right) , \ \forall t>0 \ \hbox {such that} \ \left\| t v\right\| \le \Delta _k. \end{aligned}$$
(6)

Furthermore

$$\begin{aligned} q_k^j(0)-q_k^j( \overline{t} v)\ge & {} - \frac{1}{2} \frac{\nabla f_j\left( x_k\right) ^T v }{\left\| v\right\| } \min \left\{ -\frac{\nabla f_j(x_k)^T v}{\left\| v\right\| \kappa _H} , \Delta _k \right\} . \end{aligned}$$

Proof

The existence of \(\overline{t}>0\) is straightforward. Let us consider the function \(\phi (t):\left[ 0, \ \Delta _k /\left\| v\right\| \right] \rightarrow {\mathbb {R}}\) defined as

$$\begin{aligned} \phi (t) = q_k^j(t v). \end{aligned}$$

The function \(\phi \) is continuous in a compact set, \(\left[ 0, \ \Delta _k /\left\| v\right\| \right] \), then there exists \(\overline{t}\in \left[ 0, \ \Delta _k /\left\| v\right\| \right] \) such that

$$\begin{aligned} q^j_k\left( \overline{t} s \right) \le q^j_k\left( t s \right) , \ \forall t>0 \ \hbox {such that} \ \left\| t v\right\| \le \Delta _k. \end{aligned}$$

Furthermore, \(\overline{t}>0\) because \(\phi ^\prime (0)= \nabla f_j(x_k)^T v<0\), due to v is a descent direction for \(f_j\) at \(x_k\).

In the second part, for each quadratic model let us consider the cases in which the curvature along the line defined by v is positive or not. If v is a direction such that

$$\begin{aligned} v^T \nabla ^2 f_j(x_k) v > 0, \end{aligned}$$
(7)

the model has a minimizer on the line tv:

$$\begin{aligned} t^\star = \frac{-\nabla f_j(x_k)^T v}{v^T \nabla ^2 f_j(x_k) v}>0. \end{aligned}$$

Then, if the minimizer is inside the trust region (\(\left\| t^\star v \right\| \le \Delta _k\)), we took \(\overline{t}=t^\star \), then

$$\begin{aligned} q_k^j\left( \overline{t} v \right)= & {} \frac{-\nabla f_j\left( x_k\right) ^T v}{v^T \nabla ^2 f_j\left( x_k\right) v} \nabla f_j\left( x_k\right) ^T v + \frac{1}{2} \left( \frac{-\nabla f_j\left( x_k\right) ^T v}{v^T \nabla ^2 f_j\left( x_k\right) v}\right) ^2 v^T\nabla ^2 f_j\left( x_k\right) v \\= & {} -\frac{1}{2} \frac{\left( \nabla f_j\left( x_k\right) ^T v\right) ^2}{v^T \nabla ^2 f_j\left( x_k\right) v} .\\ \end{aligned}$$

Now, using the hypothesis (A2) and the fact \(q_k^j(0)=0\), we obtain

$$\begin{aligned} q_k^j\left( 0\right) -q_k^j\left( \overline{t} v \right)= & {} \frac{1}{2} \frac{\left( \nabla f_j\left( x_k\right) ^T v\right) ^2}{v^T \nabla ^2 f_j\left( x_k\right) v} \ge \frac{1}{2} \frac{\left( \nabla f_j\left( x_k\right) ^T v\right) ^2}{\left\| v\right\| ^2 \kappa _H} . \end{aligned}$$
(8)

On the other hand, if \(\left\| t^\star v \right\| > \Delta _k\), the minimizer along the line t v is outside the trust region, then \(\overline{t}\) is defined as \(\overline{t}= \frac{\Delta _k}{\left\| v\right\| }\), then

$$\begin{aligned} q_k^j\left( \overline{t} v \right)= & {} \frac{\Delta _k}{\left\| v\right\| } \nabla f_j\left( x_k\right) ^T v + \frac{1}{2} \left( \frac{\Delta _k}{\left\| v\right\| }\right) ^2 v^T\nabla ^2 f_j\left( x_k\right) v . \end{aligned}$$
(9)

From \(\left\| t^\star v \right\| > \Delta _k\), we have \({\displaystyle \frac{-\nabla f_j\left( x_k\right) ^T v}{v^T \nabla ^2 f_j\left( x_k\right) v} \left\| v \right\| = \left\| t^\star v \right\| > \Delta _k= \overline{t}\left\| v\right\| } \) and, for (7),

$$\begin{aligned} \frac{\nabla f_j\left( x_k\right) ^T v}{\overline{t}} < - v^T \nabla ^2 f_j\left( x_k\right) v. \end{aligned}$$

Therefore, using the last inequality, (9), the hypothesis and the fact \(\left\| \overline{t}v \right\| = \Delta _k \),

$$\begin{aligned} q_k^j\left( 0\right) -q_k^j\left( \overline{t} v \right)> & {} - \frac{\Delta _k}{\left\| v\right\| } \nabla f_j\left( x_k\right) ^T v + \frac{1}{2} \left( \frac{\Delta _k}{\left\| v\right\| }\right) ^2 \frac{\nabla f_j\left( x_k\right) ^T v}{\overline{t}} \nonumber \\= & {} - \frac{\Delta _k}{\left\| v\right\| } \nabla f_j\left( x_k\right) ^T v + \frac{1}{2} \frac{\Delta _k}{\left\| v\right\| } \nabla f_j\left( x_k\right) ^T v \nonumber \\= & {} - \frac{1}{2} \frac{\Delta _k}{\left\| v\right\| } \nabla f_j\left( x_k\right) ^T v . \end{aligned}$$
(10)

If it happens that \(v^T \nabla ^2 f_j\left( x_k\right) v\le 0\), the minimum value of the model in the trust region is reached at its border, then we take \(\overline{t}=\frac{\Delta _k }{\left\| v \right\| }\) and

$$\begin{aligned} q_k^j\left( \overline{t} v \right)= & {} \frac{\Delta _k}{\left\| v\right\| } \nabla f_j\left( x_k\right) ^T v + \frac{1}{2} \frac{\Delta ^2}{\left\| v\right\| ^2} v^T \nabla ^2 f_j\left( x_k\right) v \le \frac{\Delta _k}{\left\| v\right\| } \nabla f_j\left( x_k\right) ^T v. \end{aligned}$$
(11)

Then, since v is a descent direction for F at \(x_k\),

$$\begin{aligned} q_k^j\left( 0\right) -q_k^j\left( \overline{t} v \right)\ge & {} -\frac{\Delta _k}{\left\| v\right\| } \nabla f_j\left( x_k\right) ^T v \ge - \frac{1}{2} \frac{\Delta _k}{\left\| v\right\| } \nabla f_j\left( x_k\right) ^T v , \end{aligned}$$
(12)

where the first inequality due to (11).

Summarizing, for (8), (10), (12), and using again that v is a descent direction for F at \(x_k\),

$$\begin{aligned} q_k^j\left( 0\right) -q_k^j\left( \overline{t} v \right)\ge & {} - \frac{1}{2} \frac{\nabla f_j\left( x_k\right) ^T v }{\left\| v\right\| } \min \left\{ -\frac{\nabla f_j\left( x_k\right) ^T v}{\left\| v\right\| \kappa _H} , \Delta _k\right\} . \end{aligned}$$

\(\square \)

It is important to note that the previous lemma is true for each \(f_j\), \(j=1,\dots ,m\), because v is a descent direction for F at \(x_k\), but, naturally, at first glance, the value of \(\overline{t}\) will be different for each function \(f_j\), \(j=1,\dots ,m\).

Remark 5

The reduction obtained in the quadratic models \(q_k^j\) using the direction \(s_k\) given by the solution of the subproblem (3) can be bounded below using the bound given by the previous lemma. For that, let us observe \(q_k^j(s_k)\le t_k\), for \(j=1,\dots ,m\), for the definition of the subproblem (3). If Algorithm 1 does not terminate at the second step, \(-t_k=\left| t_k \right| \ge tol\)

$$\begin{aligned} q_k^j(0)-q_k^j(s_k)\ge -t_k \ge tol, \ \hbox {for } j=1,\dots ,m. \end{aligned}$$
(13)

On the other hand, the assumptions (A2), (A4) and (A5) allow us to obtain the bound

$$\begin{aligned} q_k^j(0)- q_k^j(\overline{t}s_k)= & {} -\overline{t} \nabla f_j\left( x_k\right) ^T s_k-\frac{1}{2}\overline{t}^2 s_k^T\nabla ^2 f_j\left( x_k\right) s_k\nonumber \\\le & {} \left\| \nabla f_j\left( x_k\right) \right\| \left\| \overline{t} s_k\right\| +\frac{1}{2} \left\| \overline{t}s_k\right\| ^2 \kappa _H\nonumber \\\le & {} \kappa _{G} \Delta _{\max }+\frac{1}{2} \Delta _{\max }^2 \kappa _H, \end{aligned}$$
(14)

where \(\overline{t}=\overline{t_j}\) satisfies (6).

So, using (13) and (14), we obtain

$$\begin{aligned} \frac{q_k^j(0)- q_k^j(s_k)}{q_k^j(0)- q_k^j(\overline{t}s_k)} \ge \frac{tol}{\kappa _{G} \Delta _{\max }+\frac{1}{2} \Delta _{\max }^2 \kappa _H} =\beta . \end{aligned}$$

Using Lemma 2, we can claim that for every \(x_k\) and \(s_k\) generated by Algorithm 1, we have

$$\begin{aligned} q_k^j(0)- q_k^j(s_k)\ge - \beta \frac{1}{2} \frac{\nabla f_j\left( x_ k\right) ^T s }{\left\| s\right\| } \min \left\{ -\frac{\nabla f_j\left( x_ k\right) ^T s}{\left\| s\right\| \kappa _H} , \Delta _k \right\} > 0 , \end{aligned}$$
(15)

for \(j=1,\dots ,m\), except when \(x_k\) is a critical point.

Remark 6

It is important to observe that the bound (15) is greater than zero then the ratios \(\rho _k^j\) are well defined.

The next result establishes the conditions to accept a step and enlarge the trust region radius.

Lemma 3

Assuming (A2), if \(s_k\) is solution of (3) such that \(\left| \nabla f_j\left( x_k\right) ^T s_k\right| \ne 0\) and

$$\begin{aligned} \Delta _k \le \frac{\beta \left| \nabla f_j\left( x_k\right) ^T s_k\right| \left( 1-\eta _2\right) }{2 \kappa _H \left\| s_k\right\| }, \end{aligned}$$
(16)

for all \(j=1,\dots ,m\), then the k-th iteration is successful and \( \Delta _{k+1}\ge \Delta _k . \)

Proof

From the fact that \(0< \eta _2 <1\), \( \frac{1}{2} \left( 1-\eta _2\right) <1, \) and, for (16), we have

$$\begin{aligned} \Delta _k < \frac{\beta \left| \nabla f_j\left( x_k\right) ^T s_k\right| }{ \kappa _H \left\| s_k\right\| }. \end{aligned}$$

Then, it is possible to rewrite the bound for the decreased observed in the models (15):

$$\begin{aligned} q_k^j\left( 0\right) -q_k^j\left( s_k \right)\ge & {} - \beta \frac{1}{2} \frac{\nabla f_j\left( x_k\right) ^T s_k }{\left\| s_k\right\| } \Delta _k . \end{aligned}$$
(17)

On the other hand

$$\begin{aligned} \left| \rho _k^j -1\right|= & {} \left| \frac{f_j\left( x_k\right) -f_j\left( x_k+s_k\right) }{-q_k^j\left( s_k\right) } -1\right| =\left| \frac{f_j\left( x_k\right) -f_j\left( x_k+s_k\right) +q_k^j\left( s_k\right) }{-q_k^j\left( s_k\right) } \right| . \end{aligned}$$

Expanding \(f_j\) by Taylor series around \(x_k\); there exists \(\xi =x_k+\lambda s_k\), with \(\lambda \in \left( 0 , 1 \right) \) so that

$$\begin{aligned} \left| \rho _k^j -1\right|= & {} \left| \frac{f_j\left( x_k\right) -f_j\left( x_k\right) -\nabla f_j\left( x_k\right) ^T s_k - \frac{1}{2} s_k^T \nabla ^2 f_j\left( \xi \right) s_k +q_k^j\left( s_k\right) }{ -q_k^j\left( s_k\right) } \right| \\= & {} \left| \frac{ - \frac{1}{2} s_k^T \nabla ^2 f_j\left( \xi \right) s_k + \frac{1}{2} s_k^T\nabla ^2 f_j\left( x_k\right) s_k}{-q_k^j\left( s_k\right) } \right| \\= & {} \frac{1}{2}\frac{ \left| s_k^T \left( \nabla ^2 f_j\left( \xi \right) - \nabla ^2 f_j\left( x_k\right) \right) s_k\right| }{\left| -q_k^j\left( s_k\right) \right| } . \end{aligned}$$

Finally, by the Cauchy-Schwartz inequality:

$$\begin{aligned} \left| \rho _k^j -1\right| \le \frac{1}{2}\frac{ \left\| s_k \right\| ^2\left\| \nabla ^2 f_j\left( \xi \right) - \nabla ^2 f_j\left( x_k\right) \right\| }{\left| q_k^j\left( 0 \right) -q_k^j\left( s_k\right) \right| } . \\ \end{aligned}$$

The numerator can be bounded by using the assumption (A2) and since \(s_k\) is a descent direction and it is inside of the trust region, by (17):

$$\begin{aligned} \left| \rho _k^j -1\right| \le \frac{1}{2}\frac{ \Delta _k^2 2 \kappa _H}{\left| q_k^j\left( 0\right) -q_k^j\left( s_k\right) \right| } \le \frac{ \Delta _k^2 \kappa _H}{- \beta \frac{1}{2} \frac{\nabla f_j\left( x_k\right) ^T s_k }{\left\| s_k\right\| } \Delta _k }, \end{aligned}$$

then by using again the fact that \(s_k\) is a descent direction it is possible to write

$$\begin{aligned} \left| \rho _k^j -1\right|\le & {} \frac{ 2 \Delta _k \left\| s_k\right\| \kappa _H}{- \beta \nabla f_j\left( x_k\right) ^T s_k } =\frac{ 2 \Delta _k \left\| s_k\right\| \kappa _H}{ \beta \left| \nabla f_j\left( x_k\right) ^T s_k\right| } \\< & {} 1-\eta _2 , \end{aligned}$$

where the last inequality due to (16). Therefore we obtain \(\rho _k^j > \eta _2\) for \(j=1,\dots ,m\), then, considering the 5th. step of Algorithm 1, the step is accepted and the trust radius is increased, except in case that \(\Delta _k = \Delta _{\max }\), so \( \Delta _{k+1}\ge \Delta _k. \) \(\square \)

Remark 7

From this lemma we can claim that a step will be accepted in a finite number of inner iterations; Let’s observe that if \(x_k\) is not critical, then \(\left\{ \frac{\left| \nabla f_j \left( x_k\right) ^T s_k\right| }{\left\| s_k\right\| } : \ j=1,\dots ,m \right\} \), will be bounded below by \(\min _{ j=1,\dots ,m } \left\{ \left\| \nabla f_j\left( x_k\right) \right\| \right\} >0\). Therefore, after a finite numbers of inner iterations, in which the step is rejected and the trust radius reduced, the inequality (16) will be satisfied and the step accepted.

Lemma 4

Assuming that there exists \( \sigma >0\) such that \(\frac{\left| \nabla f_j\left( x_k\right) ^T s_k \right| }{\left\| s_k\right\| } >\sigma \) for all indices k and j, then there exists \(\Delta _{\min }\) so that \( \Delta _k > \Delta _{\min }\) for all k.

Proof

Let us suppose a subsequence of trust region radius \(\left\{ \Delta _{k_i} \right\} \) such that \(\Delta _{k_i} \rightarrow 0\) where the kth iterate is the first one such that

$$\begin{aligned} \Delta _{k+1} \le \frac{\gamma _1 \sigma \beta \left( 1-\eta _2\right) }{2\kappa _H} . \end{aligned}$$
(18)

Since k is the the first index satisfying the inequality \(\gamma _1\Delta _k \le \Delta _{k+1}\), we have

$$\begin{aligned} \Delta _k\le & {} \frac{ \sigma \beta \left( 1-\eta _2\right) }{2\kappa _H} \le \frac{ 1-\eta _2}{2\kappa _H} \frac{\beta \left| \nabla f_j\left( x_k\right) ^T s_k \right| }{\left\| s_k\right\| }, \end{aligned}$$

where the second inequality due to the hypothesis of this lemma. Then, for Lemma 3, the previous iteration was very successful and the radius must increase, which is a contradiction with the assumption that k is the first index that satisfies (18). Therefore there does not exist k which satisfies (18) so that

$$\begin{aligned} \Delta _{k+1} > \frac{\gamma _1 \sigma \beta \left( 1-\eta _2\right) }{2\kappa _H} = \Delta _{\min } \quad \forall {k}. \end{aligned}$$

\(\square \)

Theorem 1

Assuming there are a finite number of successful iterations, then \(x_k=x^\star \) for all k large enough and \(x^\star \) is a critical point.

Proof

Following the algorithm \(x^\star =x_{k}=x_{k+l}\) for all \(l>0\) where k is the last index of a successful iterate then, since the next iterations are rejected \(\Delta _k\rightarrow 0\).

If for all \(j=1,\dots ,n,\; \left| \nabla f_j\left( x_k\right) ^T s_k \right| \ne 0\), by Lemma 4, some future iterate must be successful, contradicting the fact that \(x_k\) was the last successful iterate, hence \(\left| \nabla f_j\left( x_k\right) ^T s_k \right| = 0\), and this implies that \(x_k\) is a critical point. \(\square \)

Theorem 2

Let \(\left\{ x_k\right\} \) and \(\left\{ s_k\right\} \) generated by Algorithm 1, then

$$\begin{aligned} {\displaystyle \liminf _{k\rightarrow \infty } \max _{j=1,\dots ,m} \left\{ \frac{\left| \nabla f_j\left( x_k\right) ^T s_k\right| }{\left| s_k\right| }\right\} = 0}. \end{aligned}$$

Proof

Let us suppose that exists \(\epsilon \), such that \(\forall k\) there exist \(j\in \left\{ 1,\dots ,m\right\} \) such that

$$\begin{aligned} \frac{\left| \nabla f_j\left( x_k\right) ^T s_k\right| }{\left\| s_k\right\| }\ge \epsilon . \end{aligned}$$
(19)

Let \({\mathcal {S}}\) be the index set of successful iterations, then, for \(k\in {\mathcal {S}}\),

$$\begin{aligned} f_j\left( x_k\right) -f_j\left( x_{k+1}\right)\ge & {} \eta _1\left( q_k^j\left( 0\right) -q_k^j\left( s_k\right) \right) \\\ge & {} \eta _1 \beta \left( - \frac{1}{2} \frac{\nabla f_j\left( x_k\right) ^T s_k }{\left\| s_k\right\| } \min \left\{ - \frac{\nabla f_j\left( x_k\right) ^T s_k}{\left\| s_k\right\| \kappa _H} , \Delta _k\right\} \right) , \end{aligned}$$

where the first inequality due to the iteration was successful and the second to the bound for the expected descent (15). Then, due to \(s_k\) being a descent direction and by (19)

$$\begin{aligned} f_j\left( x_k\right) -f_j\left( x_{k+1}\right)\ge & {} \eta _1 \epsilon \beta \frac{1}{2} \min \left\{ - \frac{\nabla f_j\left( x_k\right) ^T s_k}{\left\| s_k\right\| \kappa _H} , \Delta _k\right\} \\\ge & {} \eta _1 \epsilon \beta \frac{1}{2} \min \left\{ \frac{\epsilon }{ \kappa _H} , \Delta _{\min }\right\} , \end{aligned}$$

for \(k\in {\mathcal {S}}\).

Then, summing over all the successful iterations up to the k-th index,

$$\begin{aligned} f_j\left( x_0\right) -f_j\left( x_{k+1}\right)= & {} \sum _{l=0, l\in {\mathcal {S}}}^k \left( f_j\left( x_l\right) -f_j\left( x_{l+1}\right) \right) \\\ge & {} \sum _{l=0, l\in {\mathcal {S}}}^k \eta _1 \epsilon \beta \frac{1}{2} \min \left\{ \frac{\epsilon }{ \kappa _H} , \Delta _{\min }\right\} \\\ge & {} \sigma _k \eta _1 \epsilon \beta \frac{1}{2} \min \left\{ \frac{\epsilon }{ \kappa _H} , \Delta _{\min }\right\} , \end{aligned}$$

where \(\sigma _k\) is the number of successful iterations up to the k-th. Then if

$$\begin{aligned} \lim _{k\rightarrow \infty , k\in {\mathcal {S}}} \sigma _k < +\infty , \end{aligned}$$

the Theorem 1 implies the first result. If

$$\begin{aligned} \lim _{k\rightarrow \infty } \sigma _k=\infty , \end{aligned}$$

the difference \(f_j\left( x_0\right) -f_j\left( x_{k+1}\right) \) goes to infinite for (19) and Lemma 4, and \(f_j\) will not be bounded contradicting (A3). Therefore does not exist \(\epsilon >0\) that satisfies (19) for some \(j\in \left\{ 1,\dots ,m\right\} \). Then

$$\begin{aligned} {\displaystyle {\liminf }_{k\rightarrow \infty }} \max _{j=1,\dots ,m} \left\{ \frac{\left| \nabla f_j\left( x_k\right) ^T s_k\right| }{\left| s_k\right| }\right\} = 0. \end{aligned}$$

\(\square \)

Finally, if we assume bounded level sets for the function F we can claim the next corollary.

Corollary 1

Let \(\left\{ x_k\right\} \) be generated by Algorithm 1, and assume that the level sets of the functions \(f_j\), \(j=1,\dots ,m\), are bounded, then \(\left\{ x_k\right\} \) converges to a Pareto critical point.

Proof

Set \(A=\left\{ x\in {\mathbb {R}}^n : \ f_j\left( x\right) \le f_j\left( x_0\right) ,\ j=1,\dots ,m\right\} \). Due to the fact that the level sets of \(f_j\), \(j=1,\dots ,m\), are bounded, A is bounded. Furthermore, the set A is closed because \(f_j\), \(j=1,\dots ,m\), are continuous functions. Then A is compact. Therefore, the sequence \(\left\{ x_k \right\} \) generated by Algorithm 1 has an acumulation point \(x^\star \). Later, due to the Theorem 2, \(x^\star \) is a critical point. \(\square \)

5 The convex case and the local convergence analysis

In the convex case, obviously it is possible to obtain better results: at first glance the subproblem involves a convex feasible set, which makes it easier. Furthermore the theoretical results for the multiobjective problem are stronger.

In the local discussion we need to add the following assumption:

  1. (A6)

    There exists \(U\subseteq {{{\mathbb {R}}}}^{n}\) such that the sequence generated by Algorithm 1 \(\{x_k\} \subset U\) and there exists \(a>0\) such that

    $$\begin{aligned} a\left\| v\right\| ^2 \le v^T \nabla ^2 f_j(x) v, \ \ j=1,\dots ,m, \end{aligned}$$

    for all \(x\in U\) and \(v\in {{{\mathbb {R}}}}^{n}\).

This condition, clearly, implies the local strict convexity of the quadratical models \(q_k^j\) of the subproblem (3) for \(j=1,\dots ,m\).

For solving nonlinear programs there are several optimality conditions [3] based on the Lagrangian function associated to the problem and many of them are established for the differentiable problem, so we will consider the problem

$$\begin{aligned} \begin{array}{c@{\quad }l} \min &{} t \\ s.t. &{} \nabla f_j \left( x\right) ^T s+\frac{1}{2} s^T \nabla ^2f_j\left( x\right) s -t \le 0, \quad j=1,\dots ,m\\ &{}\nabla f_j \left( x\right) ^T s-t \le 0, \quad j=1,\dots ,m\\ &{}\frac{\left\| s\right\| ^2}{2}- \frac{\Delta ^2}{2}\le 0, \\ &{} \left( t,s \right) \in {{\mathbb {R}}}\times {{{\mathbb {R}}}}^{n}, \end{array} \end{aligned}$$
(20)

which is differentiable and equivalent to (3).

For the subproblem (20) the associated Lagrangian function is

$$\begin{aligned} {\mathcal {L}} \left( t, s, \lambda ^1, \lambda ^2, \lambda \right)= & {} t+\sum _{j=1}^m \lambda _j^1 \left( \nabla f_j(x)^T s+\frac{1}{2} s^T \nabla ^2f_j(x) s -t\right) \nonumber \\&+ \sum _{j=1}^m \lambda _j^2 \left( \nabla f_j(x)^T s -t\right) +\lambda \left( \frac{\left\| s \right\| ^2}{2}-\frac{\Delta ^2}{2}\right) , \end{aligned}$$
(21)

with \(\lambda ^1,\lambda ^2\in {\mathbb {R}}^n\), \(\lambda \in {\mathbb {R}}\).

Due to the convexity of the quadratical models \(q_k^j\), the subproblem (20) satisfies the Slater constraint qualification [3], then, for the optimal value of (20) there exist the multipliers \(\lambda _j^1, \lambda _j^2, \lambda \), with \(j=1,\dots ,m\), satisfying the first order necessary conditions: The gradient of the Lagrangian function vanishes, the point is feasifle and satisfies the complementary condition for the multipliers.

Remark 8

If x is not a critical point, from Lemma 1, \(s(x)\ne 0\), and, from the strict convexity of the functionals \(f_j\), \(j=1,\dots ,m\), the Hessian matrices \(\nabla ^2 f_j\), \(j=1,\dots ,m\), are positive definite. Then the linear constraints never will be active and, from the complementarity condition, the multipliers \(\lambda _j^2=0\), for all \(j=1,\dots ,m\).

The relationship between the variables and the multipliers occurs from the previous remark and the fact that the gradient vector of Lagrangian function vanishes at the optimal solution of (20).

$$\begin{aligned} \left[ \begin{array}{c} 1 \\ 0 \end{array} \right] + \sum _{j=1}^m \lambda _j^1 \left( \left[ \begin{array}{c@{\quad }c} 0 &{} 0 \\ 0 &{} \nabla ^2 f_j(x) \end{array} \right] \left[ \begin{array}{c} 0 \\ s \end{array} \right] + \left[ \begin{array}{c} 0 \\ \nabla f_j(x) \end{array} \right] - \left[ \begin{array}{c} 1 \\ 0 \end{array} \right] \right) +\lambda \left[ \begin{array}{c} 0 \\ s \end{array} \right] = 0 , \end{aligned}$$

which it can be written

$$\begin{aligned} 1-\sum _{j=1}^m \lambda _j^1&=0, \\ \sum _{j=1}^m \lambda _j^1 \nabla ^2 f_j(x) s + \sum _{j=1}^m \lambda _j^1 \nabla f_j(x) + \lambda s= & {} 0. \end{aligned}$$

Since \(\nabla ^2 f_j(x)\), \(j=1,\dots ,m\) are positive definite for all \(x\in U\), after arithmetic calculations, we obtain

$$\begin{aligned} s= - \left[ \sum _{j=1}^m \lambda _j^1 \nabla ^2 f_j(x) + \lambda I\right] ^{-1} \sum _{j=1}^m \lambda _j^1 \nabla f_j(x) . \end{aligned}$$
(22)

Therefore, we have obtained expressions of s and t as function of \(x, \lambda \) and \(\lambda ^1\).

Remark 9

Let us observe that for obtaining (22) is enough that \(\lambda ^1_j>0\) for some \(j=1,\dots ,m\), but this equation is valid if and only if \(\lambda _j^2=0\) for all \(j=1,\dots ,m\). Assuming strict convexity of \(f_j(x)\) we can ensure that \(\lambda _j^2=0\) for all \(j=1,\dots ,m\). If the strict convexity assumption is dropped, it is not possible to ensure the uniqueness of the multipliers \(\lambda ^1_j\), \(j=1,\dots ,m\), and the solution as well.

In order to discuss the rate of convergence of Algorithm 1 we establish some technical lemmas.

Lemma 5

Let us assume that for any \(\epsilon ,\delta >0\) such that \(\left\| x-y \right\| <\delta \) then

$$\begin{aligned} \left\| \nabla ^2 f_j(x)-\nabla ^2 f_j(y)\right\| < \epsilon \quad j=1,\dots ,m. \end{aligned}$$

Then \(\forall x,y\) such that \(\left\| x-y \right\| <\delta \) the following inequalities hold

$$\begin{aligned} \left\| \nabla f_j(y)-\left( \nabla f_j(x) + \nabla ^2 f_j(x) (y-x) \right) \right\| \le \epsilon \left\| y-x\right\| , \end{aligned}$$

and

$$\begin{aligned} \left| f_j(y)\!- \!\left( f_j (x) \!+\! \nabla f_j (x)^T \left( y\!-\!x\right) \!+\! \frac{1}{2} \left( y-x\right) ^T \nabla ^2 f_j (x)\left( y-x\right) \right) \right| \le \frac{\epsilon }{2} \left\| y-x \right\| ^2, \end{aligned}$$

for all \(j=1,\dots ,m\). If \(\nabla ^2 f_j\) is Lipschitz continuous with constant L for \(j=1,\dots ,m\), then

$$\begin{aligned} \left\| \nabla f_j(y)- \left( \nabla f_j (x)+\nabla ^2 f_j(x)(y-x)\right) \right\| \le \frac{L}{2} \left\| y-x \right\| ^2 \end{aligned}$$

for all \(j=1,\dots ,m\).

Proof

This is easy applying Lemmas 4.1.10 and 4.1.12 from [8]. \(\square \)

The next lemma establishes the relationship between the absolute value of the solution of the subproblem, \(|\theta (x)|\), and the size of the step, \(\Vert s(x)\Vert \).

Lemma 6

Let \(U\subseteq {{{\mathbb {R}}}}^{n}\) and \(a>0\) satisfying (A6), then

$$\begin{aligned} \frac{a}{2} \left\| s(x) \right\| ^2 \le \left| \theta (x) \right| . \end{aligned}$$

Proof

We should analyze two different cases according to the trust region constraint being active or not. In both cases, the term associated to the trust region in the Lagrangian function (21) vanishes, for this reason we develop only the case when the trust region is inactive. The another case is analogous.

Let us consider the case \(\left\| s \right\| <\Delta \). The complementarity conditions and Remark 8 implies:

$$\begin{aligned} {\mathcal {L}} \left( t, s, \lambda ^1, \lambda ^2, \lambda \right)= & {} t + \sum _{j=1}^m \lambda _j^1 \left( \nabla f_j(x)^T s + \frac{1}{2} s^T \nabla ^2 f_j(x) s -t \right) \\= & {} t. \end{aligned}$$

From (22) and \(\lambda =0\), we obtain

$$\begin{aligned} \sum _{j=1}^m \lambda _j^1 \nabla f_j(x) = - \left[ \sum _{j=1}^m \lambda _j^1 \nabla ^2 f_j(x) \right] s . \end{aligned}$$

Then, using the last two equalities,

$$\begin{aligned} {\mathcal {L}} \left( t, s, \lambda ^1, \lambda ^2, \lambda \right)= & {} \left( - \left[ \sum _{j=1}^m \lambda _j^1 \nabla ^2 f_j(x) \right] s \right) ^T s +\frac{1}{2} \sum _{j=1}^m \lambda _j^1 s^T \nabla ^2 f_j(x) s \nonumber \\= & {} - \frac{1}{2} \sum _{j=1}^m \lambda _j^1 s^T \nabla ^2 f_j(x) s \nonumber \\= & {} t, \end{aligned}$$
(23)

where the equality (23) due to \(\nabla ^2 f_j(x)\) is symmetric, because \(f_j\in {\mathcal {C}}^2\left( {\mathbb {R}}^n\right) \) for every \(j=1,\dots ,m\).

Then \( t= - \frac{1}{2} s^T \left( \sum _{j=1}^m \lambda _j^1 \nabla ^2 f_j\right) s < 0 , \) therefore, using the assumption (A6),

$$\begin{aligned} \left| t\right|\ge & {} \frac{1}{2} s^T \left( \sum _{j=1}^m \lambda _j^1 \nabla ^2 f_j\right) s \ge \frac{a}{2} \left\| s \right\| ^2 . \end{aligned}$$

\(\square \)

The following lemma gives a bound to the subproblem in term of the gradients of the objective functions.

Lemma 7

Let \(x\in U\) and \(a>0\) satisfying (A6), then

$$\begin{aligned} \left| \theta (x) \right| \le \frac{1}{2a} \left\| \sum _{j=1}^m \lambda _j \nabla f_j(x) \right\| ^2 \end{aligned}$$

for every \(\lambda _j\ge 0\), \(j=1,\dots ,m\), such that \(\sum _{j=1}^m \lambda _j =1\), and for all \(x\in U\).

Proof

For this lemma, it is useful to consider the dual problem of (3)

$$\begin{aligned} \begin{array}{rl} \begin{array}{r} \displaystyle { \max } \\ \end{array}&{} \begin{array}{rl} \displaystyle {\inf _{ (t,s) }} &{} \left\{ t + \sum _{j=1}^m \lambda _j^1 \left( \nabla f_j(x)^T s + \frac{1}{2} s^T \nabla ^2 f_j(x) s - t \right) \right. \\ &{} \left. +\sum _{j=1}^m \lambda _j^2 \left( \nabla f_j(x)^T s- t \right) + \lambda \left( \frac{\left\| s\right\| ^2}{2} - \frac{\Delta ^2}{2}\right) \right\} . \end{array} \end{array} \end{aligned}$$

For (A6), we have that all the constraints of (20) are convex and the Slater constraint qualification is satisfied, therefore, there is not duality gap. It allows us to ensure that the optimal value of the primal problem \(\theta (x)\) is the optimal value of the dual problem

$$\begin{aligned} \begin{array}{rl} \begin{array}{r} \theta (x)=\displaystyle { \max } \\ \ \end{array}&{} \begin{array}{rl} \displaystyle {\inf _{ (t,s) }} &{} \left\{ t + \sum _{j=1}^m \lambda _j^1 \left( \nabla f_j(x)^T s + \frac{1}{2} s^T \nabla ^2 f_j(x) s - t \right) \right. \\ &{} \left. +\sum _{j=1}^m \lambda _j^2 \left( \nabla f_j(x)^T s- t \right) + \lambda \left( \frac{\left\| s\right\| ^2}{2} - \frac{\Delta ^2}{2}\right) \right\} . \end{array}\\ \end{array}\\ \end{aligned}$$

If we add the constraint \(\sum _{j=1}^m \lambda _j^1=1\), \(\lambda _j^1,\lambda \ge 0\) and \(\lambda _j^2=0\), we have

$$\begin{aligned} \begin{array}{rl} \begin{array}{r} \theta (x)\ge \displaystyle { \max _{s. a}} \\ \end{array}&{} \begin{array}{rl} \displaystyle {\inf _{ (t,s) }} &{} \left\{ t + \sum _{j=1}^m \lambda _j^1 \left( \nabla f_j(x)^T s + \frac{1}{2} s^T \nabla ^2 f_j(x) s - t \right) + \right. \\ &{} \left. + \lambda \left( \frac{\left\| s\right\| ^2}{2} - \frac{\Delta ^2}{2}\right) \right\} \end{array}\\ &{} \lambda _j^1,\lambda \ge 0, \\ &{}\sum _{j=1}^m \lambda _j^1=1. \end{array} \end{aligned}$$

Now, using the constraint that we impose and the infimum properties we have

The minimum in the second term is obtained taking \(s=0\),

$$\begin{aligned} \theta (x)\ge & {} \begin{array}{cll} \sup &{}\ \left\{ \displaystyle {\inf _{s}} \right. &{}\left. \left\{ \sum _{j=1}^m \lambda _j^1 \left( \nabla f_j(x)^T s + \frac{1}{2} s^T \nabla ^2 f_j(x) s \right) \right\} - \lambda \frac{\Delta ^2}{2} \right\} \\ \tiny { \begin{array}{c} \lambda _j^1,\lambda \ge 0, \\ \sum _{j=1}^m \lambda _j^1=1 \end{array}}&\,&\end{array} \end{aligned}$$

Because \(-\frac{\Delta ^2}{2}<0\), the supremum must be \(\lambda =0\), then

$$\begin{aligned} \theta (x)\ge & {} \begin{array}{cll} \sup &{} \displaystyle {\inf _{s}} &{}\left\{ \sum _{j=1}^m \lambda _j^1 \left( \nabla f_j(x)^T s + \frac{1}{2} s^T \nabla ^2 f_j(x) s \right) \right\} \\ \tiny { \begin{array}{c} \lambda _j^1\ge 0, \sum _{j=1}^m \lambda _j^1=1. \end{array}}&\,&\end{array}\\ \end{aligned}$$

Using the hypothesis (A6),

$$\begin{aligned} \theta (x)\ge & {} \sup _{\tiny { \begin{array}{c} \lambda _j^1 \ge 0, \sum _{j=1}^m \lambda _j^1=1. \end{array}} } \inf _{s} \sum _{j=1}^m \lambda _j^1 \frac{1}{2} a\left\| s\right\| ^2 + \sum _{j=1}^m \lambda _j^1 \nabla f_j(x)^T s . \end{aligned}$$
(24)

Note that the last infimum is, actually, a minimum at the zero of the gradient, because is taken over a convex function. Then, we obtain the gradient and find such value of s

$$\begin{aligned}&\sum _{j=1}^m \lambda _j^1 a s + \sum _{j=1}^m \lambda _j^1 \nabla f_j =0,\\&s= - \frac{\sum _{j=1}^m \lambda _j^1 \nabla f_j}{\sum _{j=1}^m \lambda _j^1 a}. \end{aligned}$$

Replacing it in (24)

$$\begin{aligned} \theta (x)\ge & {} \sup _{\tiny { \begin{array}{c} \lambda _j^1\ge 0,\\ \sum _{j=1}^m \lambda _j^1 =1. \end{array}} } \sum _{j=1}^m \lambda _j^1 \frac{1}{2} a\left\| \frac{\sum _{j=1}^m \lambda _j^1 \nabla f_j(x)}{\sum _{j=1}^m \lambda _j^1 a}\right\| ^2 \\&- \left( \sum _{j=1}^m \lambda _j^1 \nabla f_j(x) \right) ^T \frac{\sum _{j=1}^m \lambda _j^1 \nabla f_j(x)}{\sum _{j=1}^m \lambda _j^1 a} \\= & {} \sup _{\tiny { \begin{array}{c} \lambda _j^1,\ge 0, \\ \sum _{j=1}^m \lambda _j^1=1. \end{array}} } - \frac{1}{2} \frac{ \left\| \sum _{j=1}^m \lambda _j^1 \nabla f_j(x)\right\| ^2}{\sum _{j=1}^m \lambda _j^1 a}. \\\ge & {} - \frac{1}{2} \frac{ \left\| \sum _{j=1}^m \lambda _j^1 \nabla f_j(x)\right\| ^2}{a}, \end{aligned}$$

where the last inequality is due to \(\sum _{j=1}^m \lambda _j^1 =1\).

Finally, taking in account that \(\theta (x)\le 0\) and with \(\lambda _j^1=\lambda _j\), we obtain

$$\begin{aligned} \left| \theta (x)\right| \le \frac{1}{2a} \left\| \sum _{j=1}^m \lambda _j \nabla f_j(x)\right\| ^2, \end{aligned}$$

\(\forall \lambda _j \ge 0\), \(j=1,\dots ,m\), such that \(\sum _{j=1}^m \lambda _j =1\). \(\square \)

Remark 10

The bound giving by the previous lemma is valid not only for the multipliers associated to the subproblem but also to any convex combination.

Lemma 8

Let \(U\subseteq {\mathbb {R}}^n\), \(\widehat{x}\) and \(\widehat{x_+}=\widehat{x}+s\left( \widehat{x}\right) \), \(a,r,\delta ,\epsilon >0\) such that

  1. (a)

    \(U\subseteq {\mathbb {R}}^n\) and \(a>0\) satisfies (A6),

  2. (b)

    \(B\left( \widehat{x},r\right) \subset U\),

  3. (c)

    \(\left\| \nabla ^2 f_j(x) - \nabla ^2 f_j(y) \right\| \le \epsilon \) \(\forall x,y\in B\left( \widehat{x},r\right) \) such that \(\left\| x-y\right\| <\delta \),

  4. (d)

    \(\left\| s\left( \widehat{x_+}\right) \right\| < \min \left\{ \delta ,r \right\} \),

then

$$\begin{aligned} \left\| s\left( \widehat{x_+}\right) \right\| \le \frac{\epsilon }{a} \left\| \widehat{s}\right\| . \end{aligned}$$

Moreover, if \(\nabla ^2 f_j\) are Lipschitz continuous with constant L in \(B\left( \widehat{x},r\right) \):

$$\begin{aligned} \left\| \nabla ^2 f_j(x) - \nabla ^2 f_j(y) \right\| \le L \left\| x-y\right\| \ \ \forall x,y\in B\left( \widehat{x},r\right) , \end{aligned}$$

then

$$\begin{aligned} \left\| s\left( \widehat{x_+}\right) \right\| \le \frac{L}{2 a} \left\| \widehat{s}\right\| ^2. \end{aligned}$$

Proof

Let \(\widehat{\lambda _j^1}, \widehat{\lambda _j^2}, \widehat{\lambda } >0\), \(j=1,\dots ,m\), the multipliers associated to the subproblem (3) with \(x=\widehat{x}\).

From the convexity of the functionals \(f_j\), \(j=1,\dots ,m\), and since the trust region constraint is inactive, the multipliers associated to them are all zero but \(\widehat{\lambda _j^1}\), then \(\displaystyle \sum \nolimits _{j=1}^m\widehat{\lambda _j^1} =1.\)

The Lemma 7 allows to write

$$\begin{aligned} \left| \theta (\widehat{x_+}) \right| \le \frac{1}{2a} \left\| \sum _{j=1}^m \widehat{\lambda _j^1} \nabla f_j\left( \widehat{x_+}\right) \right\| ^2 . \end{aligned}$$
(25)

On the other hand, let us define

$$\begin{aligned} G(x)= \sum _{j=1}^m \widehat{\lambda _j^1} f_j\left( x\right) , \end{aligned}$$

then

$$\begin{aligned} \nabla G\left( \widehat{x_+}\right)= & {} \nabla G\left( \widehat{x}+s\left( \widehat{x}\right) \right) =\sum _{j=1}^m \widehat{\lambda _j^1} \nabla f_j\left( \widehat{x}+s\left( \widehat{x}\right) \right) , \end{aligned}$$

and also

$$\begin{aligned} \nabla ^2 G\left( \widehat{x}\right) =\sum _{j=1}^m \widehat{\lambda _j^1} \nabla ^2 f_j\left( \widehat{x}\right) . \end{aligned}$$
(26)

From (22) with \(x=\hat{x}\) and the fact \(\lambda =0\), we can write

$$\begin{aligned} \widehat{s}= & {} s\left( \hat{x}\right) = - \left[ \sum _{j=1}^m \widehat{\lambda _j^1} \nabla ^2 f_j\left( \widehat{x}\right) \right] ^{-1} \sum _{j=1}^m \widehat{\lambda _j^1} \nabla f_j\left( \widehat{x}\right) =-\nabla ^2 G\left( \widehat{x}\right) ^{-1} \nabla G\left( \widehat{x}\right) . \end{aligned}$$

Since \(\nabla ^2 G\) is a convex combination of the \(\nabla ^2 f_j\), \(j=1,\dots ,m\), it inherits the uniform continuity, therefore Lemma 5 can be used having in mind the last equation,

$$\begin{aligned} \left\| \nabla G\left( \widehat{x}+\widehat{s}\right) - \left[ \nabla G\left( \widehat{x}\right) +\nabla ^2 G\left( \widehat{x}\right) \widehat{s} \right] \right\| \le \epsilon \left\| \widehat{s}\right\| , \end{aligned}$$

thus, by (26),

$$\begin{aligned} \left\| \nabla G\left( \widehat{x_+}\right) \right\| \le \epsilon \left\| \widehat{s}\right\| . \end{aligned}$$

Now, relating the last inequality with (25) and Lemma 6, we have

$$\begin{aligned} \frac{a}{2} \left\| \widehat{s_+}\right\| ^2 \le \left| \theta \left( \widehat{x_+} \right) \right| \le \frac{1}{2 a} \left( \epsilon \left\| \widehat{s}\right\| \right) ^2, \end{aligned}$$

then

$$\begin{aligned} \left\| \widehat{s_+}\right\| \le \frac{\epsilon }{ a}\left\| \widehat{s}\right\| . \end{aligned}$$

If in addition \(\nabla ^2 f_j\), \(j=1,\dots ,m\), are Lipschitz continuous with constant L, also \(\nabla ^2 G\) is Lipschitz continuous with the same constant. Then, once again Lemma 5 and (25) allow us to write,

$$\begin{aligned} \left| \theta \left( \widehat{x_+} \right) \right|\le & {} \frac{1}{2 a} \left\| \nabla G\left( \widehat{x_+}\right) \right\| ^2 = \frac{1}{2 a} \left\| \nabla G\left( \widehat{x}+\widehat{s}\right) - \left[ \nabla G\left( \widehat{x}\right) +\nabla ^2 G\left( \widehat{x}\right) \widehat{s} \right] \right\| ^2 \\\le & {} \frac{1}{4 a} L^2 \left\| \widehat{s} \right\| ^4, \end{aligned}$$

where the inequality follows from (26).

Then, using Lemma 6,

$$\begin{aligned} \frac{a}{2} \left\| \widehat{s_+}\right\| ^2 \le \frac{1}{2 a} \frac{L^2}{4} \left\| \widehat{s} \right\| ^4, \end{aligned}$$

meaning

$$\begin{aligned} \left\| \widehat{s_+}\right\| \le \frac{L}{2 a} \left\| \widehat{s} \right\| ^2. \end{aligned}$$

\(\square \)

The next theorem guarantees the convergence to an optimal Pareto point in a neighborhood of any starting point. No assuming the existence of such a point is an interesting characteristic of the result which has the flavor of the Kantorovich’s theorem for the scalar case.

Theorem 3

Let be \(\left\{ x_k\right\} \) the sequence generated by Algorithm 1, and let be \(U\subseteq {\mathbb {R}}^m\), \(a,r,\delta ,\epsilon >0\) such that

  1. (a)

    \(U\subseteq {\mathbb {R}}^n\) and \(a>0\) satisfies the assumption (A6),

  2. (b)

    \(\left\| \nabla ^2 f_j (x) -\nabla ^2 f_j (y) \right\| \le \epsilon \), \(\forall x,y\in U\), such that \(\left\| x-y \right\| <\delta \),

  3. (c)

    \(\frac{\epsilon }{a} < 1-\eta _2\), where \(\eta _2\) is the parameter to consider very successful an iteration in Algorithm 1,

  4. (d)

    \(B\left( x_0,r\right) \subseteq U\),

  5. (e)

    \( \left\| s\left( x_0\right) \right\| \le \min \left\{ \delta , r \left( 1-\frac{\epsilon }{a}\right) \right\} \),

then

  1. (i)

    \(\left\| x_k -x_0 \right\| \le \displaystyle { \left\| s\left( x_0\right) \right\| \frac{1-\left( \frac{\epsilon }{a}\right) ^k}{1- \frac{\epsilon }{a}}}\) \(\forall k\ge 0\).

  2. (ii)

    \(\left\| s\left( x_k\right) \right\| \le \left\| s\left( x_0\right) \right\| \left( \frac{\epsilon }{a}\right) ^k\) \(\forall k\ge 0\).

  3. (iii)

    \(\Delta _{k+1}\ge \Delta _k\) \(\forall k\ge 0\).

  4. (iv)

    \(\left\| s\left( x_{k+1}\right) \right\| \le \left\| s\left( x_k\right) \right\| \left( \frac{\epsilon }{a}\right) \) \(\forall k\ge 0\).

Moreover the sequence \(\left\{ x_k\right\} \) converges to some local Pareto point.

Proof

First we show that if items (i) and (ii) hold for some k, then items (iii) and (iv) also hold for that k.

Let us assume that (i) and (ii) hold for k and together with the triangular inequality,

$$\begin{aligned} \left\| x_{k+1}-x_0 \right\|= & {} \left\| x_k+s\left( x_k\right) -x_0 \right\| \le \left\| x_k-x_0 \right\| +\left\| s\left( x_k\right) \right\| \\\le & {} \left\| s\left( x_0\right) \right\| \frac{1-\left( \frac{\epsilon }{a}\right) ^k}{1- \frac{\epsilon }{a}} +\left\| s\left( x_0\right) \right\| \left( \frac{\epsilon }{a}\right) ^k \\= & {} \left\| s\left( x_0\right) \right\| \frac{1-\left( \frac{\epsilon }{a}\right) ^{k+1}}{1- \frac{\epsilon }{a}}. \end{aligned}$$

Then, by the hypothesis (c) and, \(0<\eta _2< 1\), we have \(0\le \frac{\epsilon }{a} \le 1\), therefore, by (e)

$$\begin{aligned} \left\| x_{k+1}-x_0 \right\|\le & {} r \left( 1- \frac{\epsilon }{a} \right) \frac{1-\left( \frac{\epsilon }{a}\right) ^{k+1}}{1- \frac{\epsilon }{a}} = r \left( 1-\left( \frac{\epsilon }{a}\right) ^{k+1}\right) \le r . \end{aligned}$$
(27)

In the same way, using (e) and (i),

$$\begin{aligned} \left\| x_k - x_0 \right\| \le r. \end{aligned}$$
(28)

Moreover, from (ii) and the definition of \(x_{k+1}\) (4th step of Algorithm 1)

$$\begin{aligned} \left\| x_{k+1}-x_k \right\|= & {} \left\| s\left( x_k\right) \right\| \le \left\| s\left( x_0\right) \right\| \left( \frac{\epsilon }{a}\right) ^{k}\le \left\| s\left( x_0\right) \right\| \le \delta , \end{aligned}$$

where the last inequality is due to (e).

Then, by (27) and (28), \(x_k, x_k+s\left( x_k\right) \in B\left( x_0,r\right) \) and \(\left\| x_{k+1}-x_k\right\| \le \delta \).

Let us prove that (iii) holds, proving that \(\rho _k^j\) is greater than \(\eta _2\) for \(j=1,\dots ,m\).

Using Lemma 5

$$\begin{aligned} f_j\left( x_k+s_k\right) - f_j\left( x_k\right)\le & {} \nabla f_j\left( x_k\right) ^T s_k + \frac{1}{2} s_k^T \nabla f_j\left( x_k\right) ^T s_k +\frac{\epsilon }{2} \left\| s_k\right\| ^2 \nonumber \\= & {} q_k^j\left( s_k\right) + \frac{\epsilon }{2} \left\| s_k\right\| ^2 \nonumber \\= & {} \eta _1 q_k^j\left( s_k\right) + \left( 1-\eta _1\right) q_k^j\left( s_k\right) +\frac{\epsilon }{2} \left\| s_k\right\| ^2 , \end{aligned}$$
(29)

where, naturally, \(s_k=s\left( x_k\right) \).

Let us check that the sum of the two last terms is not positive, because the definition of \(\theta \left( x_k\right) \) and from Lemmas 5 and 7,

$$\begin{aligned} \left( 1-\eta _2\right) q^j_k\left( s_k\right) +\frac{\epsilon }{2} \left\| s_k\right\| ^2\le & {} \left( 1-\eta _2\right) \theta \left( x_k\right) +\frac{\epsilon }{2} \left\| s_k\right\| ^2 \\\le & {} -\left( 1-\eta _2\right) \frac{a}{2} \left\| s_k\right\| ^2 +\frac{\epsilon }{2} \left\| s_k\right\| ^2 \\= & {} a\frac{\left\| s_k\right\| ^2}{2} \left( \frac{\epsilon }{a} - \left( 1-\eta _2\right) \right) \le 0 , \end{aligned}$$

where the last inequality is consequence of (c).

Then (29) becomes, \( f_j\left( x_k+s_k\right) - f_j\left( x_k\right) \le \eta _2 q_k^j \left( s_k\right) \). Since \(q_k^j \left( s_k\right) <0\) and \(q_k^j(0)=0\),

$$\begin{aligned} \frac{f_j\left( x_k\right) -f_j\left( x_k+s_k\right) }{q_k^j(0)-q^j_k \left( s_k\right) } \ge \eta _2 , \end{aligned}$$

thus

$$\begin{aligned} \Delta _{k+1}\ge \Delta _k . \end{aligned}$$

The item (iv) is true from Lemma 8 and from the fact that, satisfied (iii), the step is accepted.

Now let us prove by the induction principle the items (i) and (ii) for all \(k\ge 0\).

Clearly they hold for \(k=0\) by the assumptions. Let us suppose that they are valid up to k. Since (iii) holds, \(x_{k+1}=x_k+s_k\), then

$$\begin{aligned} \left\| x_{k+1}-x_0\right\|\le & {} \left\| x_{k}-x_0\right\| +\left\| s_{k}\right\| \le \left\| s\left( x_0\right) \right\| \frac{1-\left( \frac{\epsilon }{a}\right) ^k}{1- \frac{\epsilon }{a}} +\left\| s\left( x_0\right) \right\| \left( \frac{\epsilon }{a}\right) ^k\\= & {} \left\| s\left( x_0\right) \right\| \frac{1-\left( \frac{\epsilon }{a}\right) ^{k+1}}{1- \frac{\epsilon }{a}} , \end{aligned}$$

therefore (i) holds for \(k+1\).

Using (iv) y (ii) for k we obtain

$$\begin{aligned} \left\| s_{k+1} \right\|\le & {} \left\| s_{k} \right\| \frac{\epsilon }{a} \le \left\| s_{0} \right\| \left( \frac{\epsilon }{a}\right) ^{k+1}, \end{aligned}$$

then (ii) is true for \(k+1\), and since (iii) and (iv) are derived from (i) and (ii), the four statements hold for k.

Now, from (i) and (ii),

$$\begin{aligned} \sum _{k=0}^\infty \left\| x_{k+1}-x_k\right\|= & {} \sum _{k=0}^\infty \left\| s_k\right\| \le \left\| s_0\right\| \sum _{k=0}^\infty \left( \frac{\epsilon }{a}\right) ^k <\infty , \end{aligned}$$

then the sequence \(\left\{ x_k\right\} \) is a Cauchy sequence, then there exists \(x^\star \) such that \(x_k\rightarrow x^\star \).

Since \(\left\| s_k \right\| \rightarrow 0\) then \(\theta \left( x_k\right) \rightarrow 0\), by Lemma 5, \(q_k^j(s_k)\le \theta (x_k)\le 0\), and by continuity of \(\theta (x)\), \(\theta \left( x^\star \right) =0\). Thus \(x^\star \) is a local optimal Pareto point, because of Lemma 5 and the Theorem 3.1 of [9]. \(\square \)

From the result and considering the Lipschitz continuity condition of the Hessian matrices of the objective functions, the local q-quadratic rate of convergence is obtained.

Theorem 4

Under the assumptions of Theorem 3 and assuming that \(\nabla ^2 f_j\) is Lipschitz continuous with constant L in U, let

$$\begin{aligned} \tau _k =\left( \frac{L}{2 a}\right) \left\| s_k\right\| \end{aligned}$$

and \(\xi \in \left( 0 , \frac{1}{2}\right) \) then there exists \(k_0\) such that \(\forall k\ge k_0\), \(\tau _k < \xi \) and

$$\begin{aligned} \left\| x^\star -x_{k+1}\right\|\le & {} \frac{L}{a} \frac{1-\tau _k}{\left( 1-2 \tau _k\right) ^2} \left\| x^\star -x_k\right\| ^2 \le \frac{L}{a} \frac{1-\xi }{\left( 1-2 \xi \right) ^2} \left\| x^\star -x_k\right\| ^2 ,\\ \end{aligned}$$

where \(x^\star \) is an accumulation point of \(\left\{ x_k\right\} \) and a local optimal Pareto point.

Proof

From Theorem 3, we have \( \left\| s_k\right\| \le \left\| s_0 \right\| \left( \frac{\epsilon }{a} \right) ^k, \) then

$$\begin{aligned} \tau _k \le \frac{L}{2 a} \left\| s_0 \right\| \left( \frac{\epsilon }{a}\right) ^k, \end{aligned}$$

so, because \(\frac{\epsilon }{a}<1\), there exists \(k_0\) such that \(\forall k\ge k_0\)

$$\begin{aligned} \tau _k < \xi , \end{aligned}$$
(30)

From Lemma 8

$$\begin{aligned} \left\| s_{k+1} \right\| \le \frac{L}{2 a} \left\| s_k \right\| ^2. \end{aligned}$$
(31)

Let \(i>k\ge k_0\) then

$$\begin{aligned} \left\| x_i - x_{k+1}\right\|\le & {} \sum _{j=k+2}^i \left\| x_j -x_{j-1}\right\| \le \sum _{j=k+2}^i \left\| s_{j-1}\right\| , \end{aligned}$$

and, if i goes to \(\infty \),

$$\begin{aligned} \left\| x^\star - x_{k+1}\right\|\le & {} \sum _{j=k+1}^\infty \left\| s_{j}\right\| . \end{aligned}$$

Applying the inequality (31)

$$\begin{aligned} \left\| x^\star - x_{k+1}\right\|\le & {} \frac{L}{2 a} \left\| s_{k}\right\| ^2 \sum _{j=0}^\infty \left( \frac{L}{2 a} \left\| s_{k}\right\| \right) ^{2^j} \le \frac{L}{2 a} \left\| s_{k}\right\| ^2 \sum _{j=0}^\infty \left( \tau _k \right) ^{2^j} . \end{aligned}$$

Since (30), \(\tau _k < \frac{1}{2}\), a convergent geometric series is obtained, thus

$$\begin{aligned} \left\| x^\star - x_{k+1}\right\|\le & {} \frac{L}{2 a} \left\| s_{k}\right\| ^2 \sum _{j=0}^\infty \tau _k^j= \frac{L}{2 a} \left\| s_{k}\right\| ^2 \frac{1}{1-\tau _k}. \end{aligned}$$
(32)

Therefore

$$\begin{aligned} \left\| x^\star -x_k \right\|\ge & {} \left\| x_{k+1} -x_k \right\| -\left\| x^\star -x_{k+1} \right\| \ge \left\| s_k\right\| - \left\| s_k\right\| ^2 \frac{\frac{L}{2 a}}{1-\tau _k} \\= & {} \left\| s_k\right\| \frac{1-2\tau _k}{1-\tau _k}, \end{aligned}$$

where the last equality occurs because the definition of \(\tau _k\); then, because \(\tau _k<\frac{1}{2}\),

$$\begin{aligned} \left\| s_k\right\| \le \left\| x^\star -x_k \right\| \frac{1-\tau _k}{1-2\tau _k} . \end{aligned}$$

Connecting the last inequality and (32)

$$\begin{aligned} \left\| x^\star - x_{k+1}\right\|\le & {} \frac{L}{2 a} \left\| s_{k}\right\| ^2 \frac{1}{1-\tau _k} \\= & {} \frac{L}{2 a} \left\| x^\star -x_k \right\| ^2 \frac{1-\tau _k}{\left( 1-2\tau _k\right) ^2} \\\le & {} \frac{L}{2 a} \left\| x^\star -x_k \right\| ^2 \frac{1-\xi }{\left( 1-2\xi \right) ^2} , \end{aligned}$$

because \(\phi (t)=\frac{1-t}{(1-2 t)^2}\) is monotonically increasing (its derivative is positive) in \(\left( 0,\frac{1}{2}\right) \). This proves the local q-quadratic convergence of Algorithm 1. \(\square \)

6 Numerical results

In order to exhibit the behavior of the algorithm we consider a set of ten problem from the literature [6, 7, 9], one of this with variable size [9] and a new nonconvex problem proposed in [5]. Each problem has been considered with different starting points generated at random. The points have been clustered in three regions: the small region is the set \(\left[ -1, \ 1\right] \times \dots \times \left[ -1, \ 1\right] \subset {\mathbb {R}}^n\), the medium region is \(\left[ -10, \ 10\right] \times \dots \times \left[ -10, \ 10\right] \subset {\mathbb {R}}^n\), and the big region is \(\left[ -100, \ 100\right] \times \dots \times \left[ -100, \ 100\right] \subset {\mathbb {R}}^n\); and the problems that originally were box constrained were tested with random points in that region too. The algorithm has been coded in FORTRAN 95 in double precision using GFortran compiler. The code has been executed on a personal computer with a processor INTEL Core I3 with 3 Gb of memory RAM using Ubuntu 10.04 Linux operation system.

We establish the maximum number of iterations as \(maxiter = 500\), and the tolerance for the stopping criterion as \(\varepsilon = 10^{-8}\). The parameters in the algorithm are chosen as follows: \(\eta _1 = 10^{-1},\eta _2 = 0.9\). The trust region subproblem has been solved by means the routine ALGENCAN [1].

To show the behavior of Algorithm 1 we compare it with the procedure proposed by Qu, Goh and Lian [16] and the proposed by Villacorta, Oliveira and Souberyran [19], using the problem proposed in [9]. For the algorithm proposed in [19] many features, such as the parameters to update the trust region radius and to evaluate the steps for acceptances as well as the election of the matrix for the second order term, are not specified and should be chosen by the user. We consider \(B_k= \left( \nabla ^2 f_1 \left( x_k\right) + \nabla ^2 f_2 \left( x_k\right) + \nabla ^2 f_3 \left( x_k\right) \right) /3\). The parameters to evaluate the steps and to update the trust region radius were established the same as our algorithm in order to run both methods under the same conditions. The algorithm of [16] was coded with the parameters suggested by the authors.

To visualize the whole behavior of the algorithm we present tables for each cluster points. In Table 1 we show the average of iterations needed for each problem in each region and the source of the problem. In Table 2, we present the number of iterations for the problem proposed in [9] for Algorithm 1, [16] and [19]. In this table we can observe a better performance of Algorithm 1 than the algorithm of [16], in a similar way that Newton’s method is better than secant methods. The poor performance of the algorithm of [19] is attributed to the fact that the subproblem can provide long steps even when the current iterate is near to a Pareto critical point.

Table 1 Average of iterations needed for convergence in each region
Full size table
Table 2 FGS problem [9]
Full size table

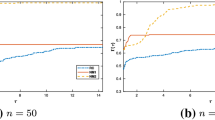
Moreover, in Fig. 1, we can observe the performance profile with the problems clustered by the region where the starting point was located. Considering this graphic, it is possible to observe that Algorithm 1 had a good performance independently of the starting point. The good performance of the some of test problems for initial points in the small region is due to have their Pareto frontier near zero.

Fig. 1
figure 1

Performance profile of Algorithm 1 according with the location of the starting points

Full size image

7 Conclusions

A trust region algorithm for the nonconvex unconstrained multiobjective optimization problem has been presented. From a theoretical point of view the proposed algorithm exhibits a similar behavior to the scalar case. We remark that the notion of fraction of Cauchy decrease has been adapted to the multiobjective problem. The algorithm provides a sequence which has at least a subsequence converging to a weak Pareto point. Moreover, under convexity assumptions the limit point of this subsequence is a Pareto point. In this case, the locally q-quadratic rate of convergence of the algorithm is proved.

An interesting local convergence result was obtained, where the information is related to the staring point, not to the solution. In that sense it is possible to consider Theorem 3 as similar to Kantorovich’s theorem [8].

From a practical point of view, the algorithm shows a good behavior in a set of problems. With respect to the problem FGS we observe that our algorithm behave better than the proposed by Qu, Goh and Lian [16] and, according with ours test, we can not establish a good comparison with the algorithm [19].

In the future, following this line of research we consider to implement an algorithm where the Hessian matrices be updated via a secant approximation. In order to obtain q-superlinear rate of convergence we are trying to introduce a Dennis-More type condition. On the other side we believe that the algorithm can be easily extended if nonlinear constraints are added to the problem.