Adaptive trust region scheme for multi-objective optimization problem using Geršgorin circle theorem

Abstract

In this article, a trust region algorithm is proposed to solve multi-objective optimization problem. A sequence of points is generated using Geršgorin Circle theorem with a modified secant equation. This sequence converges to a critical point of the problem. At every iteration, a common positive definite matrix is considered to take care of all the objective functions simultaneously and the radius of the trust region is obtained in an explicit form. Global convergence of the method is established with numerical support using a set of test problems.

1 Introduction

A general unconstrained multi-objective optimization problem is stated as

$$\begin{aligned} (MOP)~~\underset{x\in {\mathbb {R}}^n}{\min }~F(x), \end{aligned}$$

where $m\ge 2$, $F(x)=(f_1(x),f_2(x)\ldots ,f_m(x))^T$, $f_j:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$, $j=1,2,\ldots ,m$. A point $x\in {\mathbb {R}}^n$ that minimizes all the objective functions simultaneously is an ideal minimum point of (MOP). This type of solution exists in rare cases when all the objective functions have the same local minimum point. In general, improvement in one objective function at any point results in other objective functions, causing trade-off among various objectives. Visualizing and resolving this trade-off is a key issue of (MOP). Due to the conflicting nature of the objective functions, the concept of optimality is replaced by the concept of Pareto optimality or efficiency. Scalarization methods and heuristic methods are traditional approaches to solve (MOP). The scalarization processes (see [6, 16]) transform (MOP) to a single objective optimization problem with the help of pre-determined parameters. So these methods are user dependent, and often have difficulties in finding an approximation to the Pareto front. Heuristic methods [5] provide approximate Pareto front but do not guarantee the convergence property.

In recent years, many researchers have developed numerical approximation algorithms for (MOP) to overcome these difficulties and proved convergence property under different assumptions. The first few numerical approximation techniques for (MOP) are steepest descent method by Fliege and Svaiter [9], Newton’s method by Fliege et al. [8]. The first one uses the linear approximation and the latter one uses the quadratic approximation of all objective functions. Newton’s method requires the convexity assumption of each objective function. To avoid the convexity criterion, Qu et al. [17] proposed an extension of Quasi-Newton method for multi-objective optimization and Ansary and Panda ( [1,2,3]) proposed a modified Quasi-Newton method for vector optimization.

Each of these algorithms is based on the line search techniques. Line search techniques and trust region techniques generate steps with the help of a subproblem in which the quadratic approximations of the objective functions are considered in different ways. Line search techniques generate a search direction by solving the subproblem, and then search for a suitable step length along this direction. In the trust region techniques, a region around the current iterate is defined within which one may trust the approximations as the sufficient depiction of the objective functions. This region is called the trust region. Then the step is chosen to be the approximate minimizer in this region. If a step is not acceptable, the size of the region is reduced and a new step is computed by solving the subproblem within the reduced region.

Recently, the classical trust region method for single objective optimization problems is extended to the multi-objective case by Qu, Goh, and Liang [18], in which a sequence $\{x^k\}$ is generated in ${\mathbb {R}}^n$, where $x^{k+1}=x^k+d^k,~d^k\in {\mathbb {R}}^n$ with $\vert \vert d^k\vert \vert \le \varDelta ^k$, $\varDelta ^k$ is the radius of trust region, and $\{x^k\}$ converges to a critical point of (MOP). In this iterative process, the initial trust region radius is independent of Hessian of the objective functions. At every $x^k$, m number of positive definite matrices are computed corresponding to m objective functions using the BFGS update formula. As a result, there is a chance of an increase in the computational difficulty in the case of a very large number of objective functions. In this article, the following improvements are made to address these issues.

A common positive definite matrix is constructed at every $x^k$ in place m positive definite matrices in the light of the concept of the author’s previous work [1] in a different scenario. The BFGS update formula is modified accordingly and Geršgorin Circle theorem is used to ensure the positive definiteness of the common matrix, which is a new concept. The trust region radius at $x^k$ is derived in explicit form. This does not depend on the trust region radius of the previous step directly.

This article is organized as follows: Some preliminaries on (MOP) are discussed in the next section. The methodology is developed and an algorithm is proposed in Sect. 3. In Sect. 4, global convergence of the algorithm is established. Numerical illustrations of the algorithm is provided in Sects. 5 and 6 has some concluding remarks. The differences and advantages of this methodology over the existing method are discussed towards the end of this section.

2 Preliminaries

In this section, some notations and preliminaries which will be used in the rest of the article are introduced. Denote ${\mathbb {R}}$ and ${\mathbb {R}}_+$ as the set of real numbers and the set of non-negative real numbers respectively. For $p,q\in {\mathbb {R}}^m,$ the vector inequalities are considered as:

$$\begin{aligned}&p=q\Leftrightarrow p_i=q_i~\forall i\in \varLambda _m,\\&p\le q\Leftrightarrow p_i\le q_i~\forall ~i\in \varLambda _m,~p\ne q,\\&p<q\Leftrightarrow p_i<q_i~\forall i\in \varLambda _m. \end{aligned}$$

Denote the non-negative orthant and the positive orthant of ${\mathbb {R}}^m$ as

$$\begin{aligned} {\mathbb {R}}_{++}^m:=\{p\in {\mathbb {R}}^m|~p>0\}~\text {and}~ {\mathbb {R}}_{+}^m:=\{p\in {\mathbb {R}}^m|~p\ge 0\}, \end{aligned}$$

respectively and the index set as $\varLambda _m:=\{1,2,\ldots ,m\}$. For $x\in {\mathbb {R}}^n$, $\vert \vert x\vert \vert$ is the Euclidean norm of x and $\vert \vert A\vert \vert =\underset{x\in {\mathbb {R}}^n}{\max }~\frac{\vert \vert Ax\vert \vert }{\vert \vert x\vert \vert },~x\ne 0$ is the norm of the matrix A of order $m\times n$. Throughout the article, assume that $F\in C^2({\mathbb {R}}^n,{\mathbb {R}}^m)$, that is, F is twice continuously differentiable on ${\mathbb {R}}^n$. The symbols $\nabla f_j(x)\in {\mathbb {R}}^m$, $JF(x)\in {\mathbb {R}}^{m\times n}$ and $\nabla ^2 f_j(x)\in {\mathbb {R}}^{n\times n}$ are used to denote the gradient of $f_j$, the Jacobian of F and the Hessian of $f_j$ respectively at x. Associated with (MOP), some definitions and theorems that are used in this article are provided below.

Definition 1

A vector $d\in {\mathbb {R}}^n$ is said to be a descent direction of F at x if for any $j\in \varLambda _m,~f_j^{'}(x;d)<0$, where $f_j^{'}(x;d)$ is the directional derivative of $f_j$ in the direction d, defined as $f_j^{'}(x;d)=\lim _{h\rightarrow 0}\frac{f_j(x+hd)-f_j(x)}{h}$

Since $F\in C^2({\mathbb {R}}^n,{\mathbb {R}}^m)$, so it follows from the above definition that d is a descent direction of F at x if $\nabla {f_j(x)}^Td<0~~\forall j.$

Definition 2

(Ehrgott [6]) A point $x^*$ is called (weak)Pareto optimal solution of (MOP) if there does exist any other x such that $F(x)\le F(x^*)$ and $F(x)\ne F(x^*)(F(x)< F(x^*))$.

If E is the set of all Pareto optimal solutions then F(E) is said to be the Pareto front of (MOP). Most of the numerical algorithms search for a local solution. The following definition deals with the local (weak)Pareto optimal.

Definition 3

(Fleige et al. [8]) A point $x^*$ is said to be a local (weak)Pareto optimal solution of (MOP) if there is a neighborhood N of $x^*$ such that there does not exist any other point $x\in N$ satisfying $F(x)\le F(x^*)$ and $F(x)\ne F(x^*)(F(x)<F(x^*))$.

A necessary condition for x to be a local weak Pareto optimal solution of (MOP) is $Range(JF(x))\cap (-{\mathbb {R}}^m_{++})=\phi$. The following definition is motivated from this fact.

Definition 4

(Fleige et al. [8, 9]) A point $x^*$ is said to be a critical point of F if $Range(JF(x))\cap (-{\mathbb {R}}^m_{++})=\phi$

From the above definition, it is clear that if $x^*$ is not a critical point of F then there exists a direction $d\in {\mathbb {R}}^n$ such that $JF(x^*)d\in (-{\mathbb {R}}^m_{++})$. In other words, $\nabla {f_j(x^*)}^Td<0$ for every $j\in \varLambda _m$ ensures the existence of a descent direction at $x^*$. If $x^*$ is critical point of F then $\forall ~ d\in {\mathbb {R}}^n$, there exists at least one $j\in \varLambda _m$ such that $\nabla {f_j(x^*)}^Td\ge 0$.

Note that criticality does not imply Pareto optimality (see [8]). There is a relation between criticality and local (weak) Pareto optimality, which is presented in the following theorem.

Theorem 1

(Fleige et al. [8]) Let $F\in C^1(Q,{\mathbb {R}}^m)$, where $Q\subseteq {\mathbb {R}}^n$

• 1. If $x^*$ is a locally weak Pareto optimal, then $x^*$ is a critical point for F.

• 2. If Q is convex, F is ${\mathbb {R}}^m$- convex and $x^*\in Q$ is critical for F, then $x^*$ is weak Pareto optimal.

• 3. If Q is convex, $F\in C^2(Q,{\mathbb {R}}^m)$, $\nabla ^2 f_j(x)$ are positive definite for all $j\in \varLambda _m$ and for all $x\in Q$, and if $x^*\in Q$ is critical for F, then x is Pareto optimal.

Theorem 2

(Gordan’s Theorem of alternative) Let A be an $m\times n$ matrix. Then exactly one of the following two systems has a solution:

• 1. $Ax<0$ for some $x\in {\mathbb {R}}^n$

• 2. $A^Ty=0,~y\ge 0$ for some non zero y.

3 Methodology

In this section, a methodology is developed to generate an iterative sequence of the form $x^{k+1}=x^k+d^k$, which will converge to a critical point. The direction vector $d^k$ is determined through a subproblem, associated with a region of trust.

3.1 Determination of a trial step

To compute a trust region trial step d, the following subproblem is considered at every iteration.

$$\begin{aligned}&\underset{d}{\min }~~\underset{j\in \varLambda _m}{\max }~\nabla f_j(x)^Td+\frac{1}{2}d^TB(x)d\nonumber \\&\text {subject to}~~\vert \vert d\vert \vert \le \varDelta , \end{aligned}$$

(1)

where $g_j(x)=\nabla f_j(x)$, B(x) is assumed to be a symmetric positive definite matrix and $\varDelta >0$ is the trust region radius. This subproblem is equivalent to

$$\begin{aligned}&P_{TR}(x,\varDelta ):~~\underset{d,t}{\min }~~ t+\frac{1}{2}d^TB(x)d\\&\text {subject to}~g_j(x)^Td\le t,~j\in \varLambda _m\\&\vert \vert d \vert \vert \leqslant \varDelta , \end{aligned}$$

Let $(t(x,\varDelta );d_{TR}(x,\varDelta ))$ be the optimal solution of $P_{TR}(x,\varDelta )$ with optimal value $\theta (x,\varDelta )$,

$$\begin{aligned} \theta (x,\varDelta )= & {} \underset{t,d}{\min }~~ \{t+\frac{1}{2}d^TB(x)d~|~g_j(x)^Td\le t,~\vert \vert d\vert \vert \le \varDelta \}\\= & {} \underset{\vert \vert d\vert \vert \le \varDelta }{\min }~\underset{j\in \varLambda _m}{\max }~ g_j(x)^Td+\frac{1}{2}d^TB(x)d \end{aligned}$$

Since B(x) is a positive definite matrix, so $P_{TR}(x,\varDelta )$ is a convex programming problem with a unique solution. This implies that there exist Lagrange multipliers $\lambda \in {\mathbb {R}}_{+}^m, ~\alpha \in {\mathbb {R}}_{+}$ satisfying Karush-Kuhn-Tucker(KKT) optimality conditions. The Lagrange function of this problem is given by

$$\begin{aligned} L(t,d;\lambda ,\alpha )=t+\frac{1}{2}d^TB(x)d+\underset{j\in \varLambda _m}{\sum }{\lambda _j(g_j(x)^Td-t)}+\alpha (d^Td-\varDelta ^2) \end{aligned}$$

The KKT optimality conditions for $P_{TR}(x,\varDelta )$ are

$$\begin{aligned}&\underset{j\in \varLambda _m}{\sum }{\lambda _jg_j(x)}+ B(x)d+2\alpha d=0, \end{aligned}$$

(2)

$$\begin{aligned}&\quad \underset{j\in \varLambda _m}{\sum }{\lambda _j}=1, \end{aligned}$$

(3)

$$\begin{aligned}&\quad \lambda _j\ge 0,~~ g_j(x)^Td\leqslant t, \end{aligned}$$

(4)

$$\begin{aligned}&\quad \lambda _j({g_j(x)}^Td-t)=0~~\forall j\in \varLambda _m, \end{aligned}$$

(5)

$$\begin{aligned}&\quad \alpha \ge 0,~ d^Td\le \varDelta ^2,\alpha (d^Td-\varDelta ^2)=0. \end{aligned}$$

(6)

For the sake of simplicity the following notations are used for developing theoretical results.

$$\begin{aligned} t:= t(x,\varDelta ),~d:= d_{TR}(x,\varDelta ),~\theta := \theta (x,\varDelta ) \end{aligned}$$

Next two lemmas provide some properties of $P_{TR}(x,\varDelta )$.

Lemma 1

Suppose (t, d) be a solution of $P_{TR}(x,\varDelta )$. If $d=0$, then x is a critical point of (MOP).

Proof

Let $d=0$. Then from (2) and (3) we have,

$$\begin{aligned} \underset{j\in \varLambda _m}{\sum }{\lambda _jg_j(x)}=0,~\underset{j\in \varLambda _m}{\sum }{\lambda _j}=1 \end{aligned}$$

Now consider a matrix A of order $m\times n$, whose row vectors are $g_j(x),~j\in \varLambda _m$. Then from the above relation, one can say that there exists $\lambda \in {\mathbb {R}}^m$ with $\lambda \ge 0$ such that $A^T\lambda =0$ holds. Hence by Gordan’s theorem of alternative, $Ad<0$ has no solution d. This implies that for all $d\in {\mathbb {R}}^n$, $g_j(x)^Td\ge 0$ holds. Therefore $x^*$ is a critical point of (MOP). $\square$

Lemma 2

Suppose (t, d) is a solution of $P_{TR}(x,\varDelta )$ and there exists $a>0$ such that $z^TBz\ge a\vert \vert z\vert \vert ^2$ holds for every $z\in {\mathbb {R}}^n.$ Then $t\le -(a+2\alpha )\vert \vert d\vert \vert ^2,$ where $\alpha$ is a Lagrange multiplier. If $d\ne 0,$ then d is a descent direction of F.

Proof

Since (t, d) is a solution of $P_{TR}(x,\varDelta )$, the KKT optimality conditions (2)-(6) hold at (t, d). Taking the sum of (5) over j and using (3),

$$\begin{aligned} \underset{j\in \varLambda _m}{\sum }\lambda _j{g_j(x)}^Td-t=0. \end{aligned}$$

Operating both sides of (2) with d and then using $t=\underset{j\in \varLambda _m}{\sum }\lambda _j{g_j(x)}^Td$,

we have $d^TBd+2\alpha d^Td+t=0$.

Since $z^TBz\ge a\vert \vert z\vert \vert ^2~~\forall z$, so $t=-d^TBd-2\alpha d^Td \le -(a+2\alpha )\vert \vert d\vert \vert ^2$. In this expression if $d\ne 0$ then $t<0.$ Hence from (4), ${g_j(x)}^Td<0~\forall j$, which ensures that d is a descent direction. $\square$

3.2 Adaptive BFGS Update using Geršgorin Circle Theorem

Here, a sequence of positive definite matrices $\{B(x^k)\}$ is generated with an initial symmetric positive definite matrix $B(x^0)$ starting at the initial point $x^0$. At the $k^{th}$ iteration, denote

$$\begin{aligned}&{x^k:=(x_1^k,x_2^k,\ldots ,x_n^k)^T},~d^k:= d_{TR}(x^k,\varDelta ^k) \\&\quad B^k:= B(x^k),~g_j^k:= g_j(x^k),~f_j^k:= f_j(x^k) \end{aligned}$$

Consider the following quadratic form in x.

$$\begin{aligned} {f_j}^{k+1}+\nabla {f_j^{k+1}}^Td+\frac{1}{2}d^TB^{k+1}d,~~j\in \varLambda _m \end{aligned}$$

From (3) we have $\underset{j\in \varLambda _m}{\sum }{\lambda _j}=1$. Consider the summation over j in the above form. Denote

$$\begin{aligned} m^{k+1}(x)\triangleq \underset{j\in \varLambda _m}{\sum }{\lambda _j}{f_j}^{k+1}+(x-x^{k+1})^T{g_j}^{k+1} +\frac{1}{2}(x-x^{k+1})^TB^{k+1}(x-x^{k+1}) \end{aligned}$$

Instead of $f_j,~j\in \varLambda _m$, consider the function ${f_j}^k=f_j(x)+\frac{1}{2}(x-x^k)^TA^k(x-x^k)$ for all j at the $k^{th}$ iteration, where $A^k$ is some symmetric positive definite matrix. Taking the summation over j in ${f_j}^k$ and denote

$$\begin{aligned} m^k(x)\triangleq \underset{j\in \varLambda _m}{\sum }{\lambda _j}(f_j(x)+\frac{1}{2}(x-x^k)^TA^k(x-x^k))~(\text {using} (3) ) \end{aligned}$$

As in general BFGS update concept, $B^{k+1}$ is a good approximation when $\nabla m^k(x^k)=\nabla m^{k+1}(x^k)$ and $\nabla m^k(x^{k+1})=\nabla m^{k+1}(x^{k+1})$ These two relations can be simplified to

$$\begin{aligned} B^{k+1}(x^{k+1}-x^k)=\underset{j\in \varLambda _m}{\sum }{\lambda _j}(\nabla f_j^{k+1}-\nabla f_j^k) \end{aligned}$$

and

$$\begin{aligned} \underset{j\in \varLambda _m}{\sum }{\lambda _j}\nabla f_j^{k+1}=\underset{j\in \varLambda _m}{\sum }{\lambda _j}\nabla f_j^{k+1}+A^k(x^{k+1}-x^k) \end{aligned}$$

respectively. Hence

$$\begin{aligned} B^{k+1}d^k=v^k+A^kd^k={\gamma ^k}~(\text {say}), \end{aligned}$$

(7)

where $d^k=x^{k+1}-x^k$, $v^k=\underset{j\in \varLambda _m}{\sum }{\lambda _j}(\nabla f_j^{k+1}-\nabla f_j^k)$. This is a new modified secant equation for (MOP). Suppose ${d^k}^T{\gamma ^k}>0$. Then using new modified secant equation (7) and following the steps of BFGS update formula for single objective optimization problem, a BFGS-type update formula is obtained as follows:

$$\begin{aligned} B^{k+1}=B^k-\frac{B^kd^k{d^k}^TB^k}{{d^k}^TB^kd^k}+\frac{{\gamma ^k}{\gamma ^k}^T}{{d^k}^T{\gamma ^k}} \end{aligned}$$

At the k th iteration, the functions $f_j^k$ for all $j\in \varLambda _m$ are used with the following nice properties.

• (i) At $x^k$, for all $j\in \varLambda _m$, ${f_j}^k(x^k)=f_j(x^k)$ and $\nabla {f_j}^k(x^k)=\nabla f_j(x^k)$. Hence $\nabla f_j(x^k)^Td^k<0$ for all $j\in \varLambda _m$ implies $\nabla {f_j}^k(x^k)^Td^k<0$. That is, if $d^k$ is a descent direction of $f_j$ for all j, then $d^k$ is also a descent direction of ${f_j}^k$ for all $j\in \varLambda _m$ at $x^k$.

• (ii) If $f_j\in C^2({\mathbb {R}}^n,{\mathbb {R}}^m)$ and $A^k$ is a symmetric positive definite matrix then for any $z\in {\mathbb {R}}^n$ with $z\ne 0$ we have $z^T(\nabla ^2 {f_j}^k(x^k)-\nabla ^2 f_j(x^k))z=z^TA^kz>0$ for all j. Thus, at the iterative point $x^k$, ${f_j}^k$ has better curvature than that of $f_j$ for every j.

Next, it is necessary to select a suitable matrix $A^k$ so that the new matrix $B^{k+1}$ is positive definite. Using the Taylor series expansion for each $f_j$ about $x^{k+1}$

$$\begin{aligned} f_j(x)\simeq f_j^{k+1}+(x-x^{k+1})^Tg_j^{k+1}+\frac{1}{2}(x-x^{k+1})^T\nabla ^2{f_j}^{k+1}(x-x^{k+1}). \end{aligned}$$

At $x^k$,

$$\begin{aligned} f_j(x^k)=f_j^k\simeq f_j^{k+1}+(x^k-x^{k+1})^Tg_j^{k+1}+\frac{1}{2}(x^k-x^{k+1})^T\nabla ^2{f_j}^{k+1}(x^k-x^{k+1}). \end{aligned}$$

That is, ${d^k}^T\nabla ^2{f_j}^{k+1}d^k \simeq 2(f_j^k-f_j^{k+1})+2{d^k}^Tg_j^{k+1}$, where $d^k=x^{k+1}-x^k$. Hence using (3), we get

$$\begin{aligned} {d^k}^T\underset{j\in \varLambda _m}{\sum }\lambda _j^k \nabla ^2{f_j}^{k+1}d^k \simeq 2\underset{j\in \varLambda _m}{\sum }{\lambda _j^k(f_j^k-f_j^{k+1})}+2\underset{j\in \varLambda _m}{\sum }{\lambda _j^k{d^k}^Tg_j^{k+1}} \end{aligned}$$

(8)

Operating both sides of (7) by ${d^k}^T$,

$$\begin{aligned} {d^k}^TB^{k+1}d^k ={d^k}^T{\gamma ^k} ={d^k}^T\underset{j\in \varLambda _m}{\sum }{\lambda _j^k(g_j^{k+1}-g_j^k)}+{d^k}^TA^kd^k.\end{aligned}$$

(9)

Both (8) and (9) indicate that a reasonable choice for $A^k$ should satisfy the following relation.

$$\begin{aligned} {d^k}^TA^kd^k=2\underset{j\in \varLambda _m}{\sum }{\lambda _j^k(f_j^k-f_j^{k+1})}+\underset{j\in \varLambda _m}{\sum }\lambda _j^k{d^k}^T(g_j^{k+1}+g_j^k)=u^k~(say). \end{aligned}$$

At the k th iteration, if $x^k$ is not the critical point then $x^k$ can be updated to $x^{k+1}$. So $d^k=x^{k+1}-x^k\ne 0.$ In that case, one possible solution of ${d^k}^TA^kd^k=u^k$ is $A^k=\frac{u^k}{{d^k}^Td^k}I$, where I is the identity matrix.

The positive definite condition ${d^k}^T{\gamma ^k}>0$ holds if ${d^k}^Tv^k>0$ and $A^k$ is positive definite. $A^k=\frac{u^k}{{d^k}^Td^k}I$ is positive definite if $u^k>0,$ which is not always true. For $u^k\le 0$, a matrix is constructed using Geršgorin Circle theorem so that $B^{k+1}$ is positive definite.

Theorem 3

(Geršgorin Circle theorem [19]) Let G be a complex matrix of order n,  with entries $a_{ij}.$ For $i\in \{ 1,2,3,\ldots ,n\} ,$ let $R_i={\sum }_{j\ne i} \vert a_{ij}\vert$ and $D(a_{ij},R_i)$ be the closed disc centered at $a_{ii}$ with radius $R_i$. Such a disc is known as Geršgorin disc. Every eigenvalue $\lambda$ of G lies within at least one of the Geršgorin disc $D(a_{ij},R_i),$ that is, $\vert \lambda -a_{ii}\vert \leqslant R_i$ for some i.

Lemma 3

At the k th iteration consider the matrix $G^k=~{(a_{ij})}_{n\times n},$ where $\delta >0$ a small number,

$$\begin{aligned} a_{ij}= {\left\{ \begin{array}{ll} \frac{u^k}{\vert \vert d^k\vert \vert ^2}, &{} \text{ if } i\ne j~and~\vert i-j\vert =1 \\ 2\frac{\vert u^k\vert }{\vert \vert d^k\vert \vert ^2}+\delta , &{} \text{ if } i=j \\ 0, &{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$

(10)

Then $G^k$ is positive definite.

Proof

Let $R_i {=}{\sum }_{j\ne i}\vert a_{ij}\vert ,\forall i,j=1,2,\ldots ,n.$ From the construction of $G^k$, we have, $a_{ii}-R_i>0$. Therefore by Geršgorin Circle theorem, the eigenvalues (say $\lambda$) of the matrix $G^k$ satisfies the condition $\vert \lambda -a_{ii}\vert \leqslant R_i,$ which implies $-(\lambda - a_{ii})\leqslant R_i$. This implies that $\lambda \geqslant a_{ii}-R_i> 0$. Therefore all the eigenvalues of $G^k$ are positive. Hence $G^k$ is positive definite. $\square$

Using this new positive definite matrix $G^k$, the updated matrix $B^{k+1}$ can be determined as follows.

$$\begin{aligned} B^{k+1}= {\left\{ \begin{array}{ll} B^k-\frac{B^kd^k{d^k}^TB^k}{{d^k}^TB^kd^k}+\frac{{\gamma ^k}{{\gamma ^k}}^T}{{d^k}^T{\gamma ^k}} , &{} \text{ if } {d^k}^Tv^k>0~\text {and}~ u^k>0 \\ (1-c_k)G^k+c_kB^k, &{} \text{ otherwise }, \end{array}\right. } \end{aligned}$$

(11)

where $\{c_k\}$ is a real positive monotonically convergent sequence such that $\{ c_k\}\rightarrow 1$ and $0<c_0<1$.

3.3 Determination of trust region radius

Consider the sub-problem $P_{TR}(x,\varDelta ).$ If $P_{TR}(x,\varDelta )$ is free from the restriction on trust region radius, that is, if $\vert \vert d\vert \vert <\varDelta$ is replaced by $d\in {\mathbb {R}}^n$, then condition (2) becomes $\underset{j\in \varLambda _m}{\sum }{\lambda _jg_j(x)}+ B(x)d=0$. So at the $k^{th}$ iteration, $d^k=-{B^k}^{-1}\underset{j\in \varLambda _m}{\sum }{\lambda _j^kg_j^k}$. In that case,

$$\begin{aligned} \vert \vert d^k\vert \vert\le & {} \vert \vert {B^k}^{-1}\vert \vert \vert \vert \underset{j\in \varLambda _m}{\sum }\lambda _j^kg_j^k\vert \vert \\\le & {} \vert \vert {B^k}^{-1}\vert \vert (\underset{j\in \varLambda _m}{\max }\vert \vert g_j^k\vert \vert )\underset{j\in \varLambda _m}{\sum }\lambda _j^k\\= & {} \vert \vert {B^k}^{-1}\vert \vert (\underset{j\in \varLambda _m}{\max }\vert \vert g_j^k\vert \vert ) \end{aligned}$$

This relation provides information about an upper bound of $\vert \vert d^k\vert \vert .$ So we may consider $\varDelta ^k=\vert \vert {B^k}^{-1}\vert \vert (\underset{j\in \varLambda _m}{\max }\vert \vert g_j^k\vert \vert )$.

The trust region trial step $d^k$ is a solution to the subproblem $P_{TR}(x,\varDelta )$. After the computation of $d^k$, the improvement on the objective function can be measured through its actual reduction and predicted reduction from the subproblem. At the $k^{th}$ iteration, the actual reduction is given by

$$\begin{aligned} Ared(d^k)=\underset{j\in \varLambda _m}{\max }\{f_j(x^k)-f_j(x^k+d^k)\}. \end{aligned}$$

Let $\phi ^k(d^k)=\underset{j\in \varLambda _m}{\max }~{g_j^k}^Td^k+\frac{1}{2}{d^k}^TB^kd^k$. Then the predicted reduction, that is, the reduction according to our sub-problem $P_{TR}(x,\varDelta )$ is

$$\begin{aligned} Pred(d^k) =\phi ^k(0)-\phi ^k(d^k)=-(\underset{j\in \varLambda _m}{\max }~{g_j^k}^Td^k+\frac{1}{2}{d^k}^TB^kd^k). \end{aligned}$$

Let $\rho _k(d^k)=\frac{Ared(d^k)}{Pred(d^k)}$. If $\rho _k(d^k)$ is close to 1,  there is a good agreement between $Ared^k$ and $Pred^k$ over this step. In this situation, it is safe to expand the trust region for the next iteration. If $\rho _k(d^k)$ is positive but significantly smaller than 1,  then the trust region remains unaltered. But if it is close to zero or negative then the trust region can be shrunk by reducing $\varDelta ^k$ at the next iteration. Using this logic, the trust region radius $\varDelta ^k$ can be updated, which is explained in the algorithm of the next subsection.

Lemma 4

Suppose $F\in C^2({\mathbb {R}}^n,{\mathbb {R}}^m)$, for all $j\in \varLambda _m$, $g_j(x)$ and B(x) are bounded, then at the $k^{th}$iteration, $\vert Ared(d^k)-Pred(d^k)\vert \le \delta _1\vert \vert {d^k}\vert \vert +\delta _2\vert \vert {d^k}\vert \vert ^2$ for some $\delta _1,~\delta _2>0$.

Proof

$$\begin{aligned} Ared(d^k) - Pred(d^k)= & {} \underset{j\in \varLambda _m}{\max }(f_j(x^k)-f_j(x^k+d^k))+\underset{j\in \varLambda _m}{\max }~ {g_j^k}^Td^k\nonumber \\&+\frac{1}{2}{d^k}^TB^kd^k\nonumber \\ \Rightarrow \vert Ared(d^k)-Pred(d^k)\vert= & {} \vert \underset{j\in \varLambda _m}{\max }(f_j(x^k)-f_j(x^k+d^k))\vert +\vert \underset{j\in \varLambda _m}{\max }~ ({g_j^k}^Td^k)\vert \nonumber \\&+\frac{1}{2}\vert \vert B^k\vert \vert \vert \vert d^k\vert \vert ^2\nonumber \\\le & {} \underset{j\in \varLambda _m}{\max }~\vert (f_j(x^k)-f_j(x^k+d^k))\vert +\underset{j\in \varLambda _m}{\max }~\vert ({g_j^k}^Td^k)\vert \nonumber \\&+\frac{1}{2}\vert \vert B^k\vert \vert \vert \vert d^k\vert \vert ^2 \end{aligned}$$

(12)

Using Taylor series expansion of first order, we have,

$$\begin{aligned} f_j(x^k+d^k)=f_j(x^k)+{g_j(\xi )}^Td^k, \end{aligned}$$

where $\xi$ is an interior point in the line segment joining $x^k$ and $x^k+d^k$. Hence from (12), we get,

$$\begin{aligned} \vert Ared(d^k)-Pred(d^k)\vert\le & {} \underset{j\in \varLambda _m}{\max }~\vert {g_j(\xi )}^Td^k\vert +\underset{j\in \varLambda _m}{\max }~\vert {g_j^k}^Td^k\vert +\frac{1}{2}\vert \vert B^k\vert \vert \vert \vert d^k\vert \vert ^2\\\le & {} (\underset{j\in \varLambda _m}{\max }~\vert \vert g_j(\xi )\vert \vert +\underset{j\in \varLambda _m}{\max }~\vert \vert g_j^k\vert \vert )\vert \vert d^k\vert \vert +\frac{1}{2}\vert \vert B^k\vert \vert \vert \vert d^k\vert \vert ^2 \end{aligned}$$

Hence the lemma follows, since $g_j(x)$ and B(x) are bounded for all $j\in \varLambda _m$. $\square$

Define

$$\begin{aligned} v(x,\varDelta )=\underset{\vert \vert d\vert \vert \le \varDelta }{\sup }~\{-\underset{j\in I_m}{\max }~g_j(x)^Td\} \end{aligned}$$

(13)

Then the following lemma holds.

Lemma 5

• 1. $v(x,\cdot )$ is non negative.

• 2. x is a critical point of (MOP) if and only if $v(x,\varDelta )=0$ for some $\varDelta >0$.

Proof

• 1. From the definition of $v(x,\varDelta )$, the result is obvious.

• 2. Let $v(x,\varDelta )= \underset{\vert \vert d\vert \vert \le \varDelta }{\sup }~\underset{j\in \varLambda _m}{\max }~g_j(x)^Td=0$. Then for all d satisfying $\vert \vert d\vert \vert \le \varDelta$, $\underset{j\in \varLambda _m}{\max }~g_j(x)^Td=0$. This implies that there exists a $j\in \varLambda _m$ such that $g_j(x)^Td=0$. Hence x is a critical point. Conversely let x is a critical point of (MOP). Then by the definition of critical point, there exists a $j\in \varLambda _m$ such that $g_j(x)^Td\ge 0$ for all d. This implies that there exists some $\varDelta$ such that $\underset{\vert \vert d\vert \vert \le \varDelta }{\sup }~\{-\underset{j\in I_m}{\max }~g_j(x)^Td\}\le 0$. That is, $v(x,\varDelta )\le 0$. But from the first part, we have, $v(x,\varDelta )\ge 0$. Hence the result follows.

$\square$

Lemma 6

Suppose there is a constant $M>0$ such that $\vert \vert B(x)\vert \vert \le M$. Then at the $k^{th}$ iteration $Pred(d^k)\ge \frac{1}{2}\frac{\{v(x^k,\varDelta ^k)\}^2}{M{\varDelta ^k}^2}$.

Proof

From the definition of predicted reduction, we have at the $k^{th}$ iteration,

$$\begin{aligned} Pred(d^k)= & {} -\underset{j\in \varLambda _m}{\max }~{g_j^k}^Td^k-\frac{1}{2}{d^k}^TB^kd^k\\\ge & {} -\underset{j\in \varLambda _m}{\max }~{g_j^k}^Td^k-\frac{M\vert \vert d^k\vert \vert ^2}{2} \end{aligned}$$

Let $\bar{d^k}$ be the maximum in (13). Then for any $\eta \in [0,1]$, we have that

$$\begin{aligned} Pred(d^k)\ge & {} \underset{\eta \in [0,1]}{\max }[-\underset{j\in \varLambda _m}{\max }~ g_j(x^k)^T(\eta \bar{d^k})-\frac{M\vert \vert \eta \bar{d^k}\vert \vert ^2}{2}]\\\ge & {} \underset{\eta \in [0,1]}{\max }[\eta (-\underset{j\in \varLambda _m}{\max }~ g_j(x^k)^T\bar{d^k})-\eta ^2\frac{M{\varDelta ^k}^2}{2}]\\\ge & {} \underset{\eta \in [0,1]}{\max }[\eta v(x^k,\varDelta ^k)-\frac{\eta ^2}{2}M{\varDelta ^k}^2]\\\ge & {} \frac{1}{2}\frac{\{v(x^k,\varDelta ^k)\}^2}{M{\varDelta ^k}^2} \end{aligned}$$

Hence the lemma. $\square$

3.4 Algorithm

The concepts developed in Subsections 3.1 to 3.3 are summarized in the following steps.

Step 1. Let $x^0\in {\mathbb {R}}^n$, $0<c_0<1$, error of tolerance $\epsilon >0$. Choose the parameters $0<\alpha _1\leqslant \alpha _2<1, 0<\beta _1< 1< \beta _2$, a positive definite matrix. Set $k=0$. Compute $\varDelta ^k$

Step 2. Solve the sub-problem $P_{TR}(x^k,\varDelta ^k)$. Find the value of $d^k$, $t^k$.

Step 3. If $\vert \vert d^k\vert \vert <\epsilon$ then stop. Otherwise compute

$$\begin{aligned} \rho _k(d^k))=\frac{Ared(d^k)}{Pred(d^k)}=\frac{\underset{j\in \varLambda _m}{\max }\left\{ f_j(x^k)-f_j(x^k+d^k\right\} }{\phi ^k(0)-\phi ^k(d^k)} \end{aligned}$$

Step 4. If $\rho _k(d^k)<\alpha _1$, set $\varDelta ^{k}=\beta _1\varDelta ^k$ and go to Step 2. Otherwise set $x^{k+1}=x^k+d^k$.

Step 5. Generate a positive definite matrix $B^{k+1}$ using the formula (11). Compute $\varDelta ^k$ as

$$\begin{aligned} \varDelta ^{k+1}= {\left\{ \begin{array}{ll} \beta _1\vert \vert {B^{k+1}}^{-1}\vert \vert \underset{j\in \varLambda _m}{\max }\vert \vert {g_j}^{k+1}\vert \vert , &{} \text{ if } \alpha _1\le \rho _k(d^k)\le \alpha _2 \\ \beta _2\vert \vert {B^{k+1}}^{-1}\vert \vert \underset{j\in \varLambda _m}{\max }\vert \vert {g_j}^{k+1}\vert \vert , &{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$

(14)

Set $k=k+1$, compute $c_{k+1}$, Go to Step 2.

4 Convergence analysis

The following theorem guarantees that Algorithm 3.4 does not cycle infinitely in the inner cycle.

Theorem 4

Suppose that $\lbrace B^k\rbrace$ is bounded and the sequence $\lbrace x^k\rbrace$ is generated by Algorithm 3.4. Then Algorithm 3.4 does not cycle infinitely in the inner cycle Step 2-Step 3-Step 4-Step 2.

Proof

Suppose at the k th iteration, the inner cycle of the algorithm goes infinitely. Then the algorithm will not terminate at $x^k$, that is, $v(x^k,\varDelta ^k)>0$. Let $n_k$ be the number of iterative steps of the inner iteration. Then $\rho _k(d^k_{n_k})<\alpha _1$. In this situation, $\varDelta ^k_{n_k}$ is updated by Step 5 of the algorithm. Since at every step in the inner cycle, the trust region is shrinking, so $\varDelta ^k_{n_k}\rightarrow 0$ as $n_k\rightarrow \infty .$ Hence $\vert \vert d^k_{n_k}\vert \vert \le \varDelta ^k_{n_k}\rightarrow 0~~~as~~ n_k\rightarrow \infty$.

From Lemma 4 and Lemma 6,

$$\begin{aligned} \vert \rho _k(d^k_{n_k})-1)\vert =\vert \frac{Ared^k-Pred^k}{Pred^k}\vert \le \frac{ \delta _1\vert \vert d^k_{n_k}\vert \vert +\delta _2\vert \vert d^k_{n_k}\vert \vert ^2}{\frac{1}{2}\frac{\{v(x^k,\varDelta ^k)\}^2}{M{\varDelta ^k}^2}} \end{aligned}$$

As $n_k\rightarrow \infty$, $\vert \rho _k(d^k_{n_k})-1)\vert \rightarrow 0.$ Hence $\rho _k(d^k_{n_k})\rightarrow 1.$ This implies that there exists $\alpha _1$ such that for sufficiently large $n_k,$ $\rho _k(d^k_{n_k})\ge \alpha _1$. This contradicts the relation $\rho _k(d^k_{n_k})<\alpha _1$. Hence the lemma follows. $\square$

Theorem 5

Suppose that $\varOmega _0=\{x\in {\mathbb {R}}^n | F(x)\le F(x^0)\}$ is bounded, $x^0\in {\mathbb {R}}^n$ is the initial point, and $F\in C^1({\mathbb {R}}^n,{\mathbb {R}}^m)$. $\{x^k\}$ is generated by Algorithm 3.4 and the sequence $\{B^k\}$ is bounded. Then every accumulation point of $\{x^k\}$ is a critical point of (MOP).

Proof

Let $d^k$ be the accepted step at the k th iteration. Then from Algorithm 3.4, we have $\rho _k(d^k)\ge \alpha _1$. Denote $\varGamma =\{k\mid \rho _k(d^k)\ge \alpha _1\}$.

Since $\varOmega _0$ is a bounded set, $\{x^k\}$ has at least one accumulation point. Without loss of any generality, suppose that the subsequence $\{x^k\}_{k\in \varGamma }$ converges to $x^*$.

Since $\rho _k(d^k)\ge \alpha _1$, so

$$\begin{aligned} \alpha _1Pred(d^k)\le Ared(d^k)=\underset{j\in \varLambda _m}{\max }\{f_j(x^k)-f_j(x^k+d^k)\}. \end{aligned}$$

Hence

$$\begin{aligned} \underset{k\in \varGamma }{\sum }\alpha _1Pred(d^k)\le & {} \underset{k\in \varGamma }{\sum }\underset{j\in \varLambda _m}{\max }\{f_j(x^k)-f_j(x^{k+1})\}\nonumber \\= & {} \underset{k\in \varGamma }{\sum }~(f_{j_0}(x^k)-f_{j_0}(x^{k+1}))~(\text {for some}~j_0\in \varLambda _m)\nonumber \\= & {} f_{j_0}(x^0)-f_{j_0}(x^{1}))+f_{j_0}(x^1)-f_{j_0}(x^{2})+\ldots +f_j(x^k)\nonumber \\- & {} f_j(x^{k+1})\}+\ldots \nonumber \\\le & {} \underset{j\in \varLambda _m}{\max }[f_j(x^0)-f_j(x^*)]< +\infty \end{aligned}$$

(15)

From Lemma 6, we have for all $\varDelta >\varDelta ^k$, $k\in \varGamma$,

$$\begin{aligned} \underset{k\in \varGamma }{\sum }\frac{1}{2}\frac{\{v(x^k,\varDelta )\}^2}{M{\varDelta }^2}\le \underset{k\in \varGamma }{\sum }~Pred(d^k) \end{aligned}$$

Using the above inequality along with (15) we get,

$$\begin{aligned} \underset{k\in \varGamma }{\sum }\frac{\alpha _1}{2}\frac{\{v(x^k,\varDelta )\}^2}{M{\varDelta }^2}<+\infty \end{aligned}$$

(16)

Lemma 5 indicates that it is enough if we show that $x^*$ is a solution of $v(x,\varDelta )$ for some $\varDelta >0$. If possible let $v(x^*,\varDelta )>0$. This implies, there exists $\mu ,\varepsilon _0>0$ such that for all $0<\varepsilon \le \varepsilon _0$ and for all $\vert \vert x^k-x^*\vert \vert _{k\in \varGamma }\le \varepsilon$, $v(x^k,\varDelta )\ge \mu >0$.

Therefore

$$\begin{aligned} \underset{k\in \varGamma }{\sum }\frac{\{v(x^k,\varDelta )\}^2}{M{\varDelta }^2}\ge \underset{k\in \{k|\vert \vert x^k-x^*\vert \vert _{k\in \varGamma }\le \varepsilon \}}{\sum }\frac{\mu ^2}{M\varDelta ^2}=+\infty \end{aligned}$$

This contradicts (16). Therefore $v(x^*,\varDelta )=0$, and $x^*$ is a critical point. $\square$

5 Numerical experiment and result analysis

In this section, MATLAB implementation of Algorithm 3.4 is executed on many test problems with bound constraints $lb\le x\le ub$, where $lb,~ub\in {\mathbb {R}}^n$. Details of these test problems are summarized in Table 1. In that table, m and n denote the number of objective functions and number of variables respectively. The results obtained by Algorithm 3.4(in short term ATRMO) are compared with the Algorithm 1(in short TRMO)of [18]. Solution of (MOP) is a well-distributed set of Pareto optimal solutions. Spreading out an approximation to a Pareto set is a difficult problem. There is no single spreading technique that can work in a satisfactory manner for (MOP). In this article, a set of initial points is selected with the strategy rand to generate an approximated Pareto front. In this strategy, 100 random initial point are selected, which are uniformly distributed in lb and ub. Every test problem of Table 1 is executed 10 times with these random initial points.

Table 1 Multi-objective test problems with bound constraints

Table 2 Computation details of the test problems

The number of iterations, number of function counts, and number of gradient counts are recorded to compare ATRMO with TRMO, which are summarized in Table 2. Comparison between the performance of the algorithms is done using these factors.

Performance profiles Performance profiles are defined by a cumulative function $\bar{\rho }_s(\tau )$ representing a performance ratio with respect to a given metric, for a given set of algorithms. Given a set of problems P and a set of algorithms S, let the metric $\zeta _{p,s}$ be the performance of solver s on solving problem p. The performance ratio is then defined as $r_{p,s}=\zeta _{p,s}/\underset{s\in S}{\min }~\zeta _{p,s}$. The cumulative function $\bar{\rho }_s(\tau )~(s\in S)$ is defined as the percentage of problems whose performance ratio is less than or equal to $\tau$, that is,

$$\begin{aligned} \bar{\rho }_s(\tau )=\frac{\vert \{p\in P:r_{p,s}\le \tau \}\vert }{\vert P\vert }. \end{aligned}$$

In multi-objective optimization, the output is a set of non-dominated points providing as an approximation of the full Pareto set. In this article, the following metrics are considered to compare between ATRMO and TRMO: the Purity metric, two Spread metrics.

Purity metric The purity metric is used to measure how many non-dominated points an algorithm is able to compute. The approximated Pareto front of problem p obtained by algorithm s is denoted by $F_{p,s}$. By considering the union of all individual Pareto approximation $\underset{s\in S}{\cup }~F_{p,s}$, where the dominated points are removed, an approximation to the Pareto front $F_p$ is achieved. The purity metric for algorithm s and problem p is defined by the ratio ${\tilde{r}}_{p,s}=\frac{\vert F_{p,s}\cap F_p\vert }{\vert F_{p}\vert }$. When computing the performance profiles for the purity metric it is required to set $r_{p,s}=1/{\tilde{r}}_{p,s}$, since higher values of ${\tilde{r}}_{p,s}$ indicates that the algorithm gives a higher percentage of non-dominated points for problem p.

Spread metric In order to examine whether the points generated by algorithm s for problem p are well distributed over the approximated Pareto front, two spread metrics $\varGamma$ and $\varDelta$ are considered. The largest gap in the approximated Pareto front is measured by the $\varGamma$ metric, while the scaled deviation from the average gap in the approximated Pareto front is measured by the $\varDelta$ metric. In the following, how to compute these metrics is described. Let the set of N points $x^1,x^2,\ldots ,x^N$ forms the approximated Pareto front obtained by algorithm s for problem p. Furthermore, let $x^0$ and $x^{N+1}$ be the extreme points for objective j, computed over all the approximated Pareto fronts obtained by different algorithms. Suppose that those N points are sorted by the $j^{th}$ objective function, that is, $f_j(x^i)\le f_j(x^{i+1})~(i=1,2,\ldots ,N)$. Define $\delta _{i,j}=\vert f_j(x^{i+1})-f_j(x^i)\vert$, and suppose that $\tilde{\delta _j}(j\in \varLambda _m)$ be the average of the distances $\delta _{i,j}$. Then $\varGamma >0$ and $\varDelta >0$ spread metrics are defined as

$$\begin{aligned} \varGamma _{p,s}=\underset{j\in \varLambda _m}{\max }~\underset{i\in \{0,1,\ldots N\}}{\max }~\delta _{i,j} \end{aligned}$$

and

$$\begin{aligned} \varDelta _{p,s}=\underset{j\in \varLambda _m}{\max }~(\frac{\delta _{0,j}+\delta _{N,j}+\sum _{i=1}^{N-1}~\vert \delta _{i,j}-\tilde{\delta _j}}{\delta _{0,j}+\delta _{N,j}+(N-1)\tilde{\delta _j}}) \end{aligned}$$

Implementation details MATLAB(2016a) code is developed for both the algorithms ATRMO and TRMO. Implementation of the algorithms are described below:

• Initial points selection strategy rand is used for every test problem. An initial matrix $B^0=I$, parameters $c_0=0.5$, $\alpha _1=0.2$, $\alpha _2=0.5$, $\beta _1=0.5$, $\beta _2=1.2$ are accepted and the sequence $\{c_k\}$, where $c_{k+1}=1-c_k^i,~i$ is the number iteration, is considered.

• Subproblems of both the algorithms are solved using MATLAB function ‘fmincon’ with -‘Algorithm’,‘interior-point’, -‘initial guess’,$0^{n+1}$.

• For both the algorithms, stopping criteria is used as $\vert \vert d^k\vert \vert \le 10^{-5}$ or maximum 200 iterations.

• Every test problem is executed 10 times with random initial points and average is considered for performance profile. Computational details of these average values for both algorithms are presented in Table 2. In this table, ‘It’ corresponds to the number of iterations, ‘$F_c$’ corresponds to the number of function counts and ‘$G_c$’ corresponds to the number of gradient counts.

• The gradient is computed using forward difference formula, which needs n additional function evaluations. Therefore the total function evaluations($F_e$) for 100 initial points for a test problem of m objective functions are obtained as $F_e=m F_c+mnG_c$.

Explanation with one test problem Steps of Algorithm 3.4 are explained in one numerical example. Consider the following bi-objective optimization problem in two dimensions.

$$\begin{aligned} \underset{x\in {\mathbb {R}}^n}{\min }~\{f_1(x),f_2(x)\}, \end{aligned}$$

where

$$\begin{aligned} f_1(x)=\frac{1}{4}[(x_1-1)^4+2(x_2-2)^4],~~f_2(x)=(x_2-x_1^2)^2+(1-x_1)^2. \end{aligned}$$

Here $f_2$ is not a convex function.

Consider the initial point $x^0=(0,5)^T$, the initial matrix $B^0=I_2$, parameters $c_0=0.5$, $\alpha _1=0.2$, $\alpha _2=0.5$, $\beta _1=0.5$, $\beta _2=1.2$. Stopping condition is $\vert \vert d^k\vert \vert <10^{-5}$. $f(x^0)=(40.75,26.00)$ and $\varDelta ^0=\max \{\vert \vert g_1(x^0)\vert \vert ,\vert \vert g_2(x^0)\vert \vert \}=54.0095$. Now clearly assumptions of Theorem 5 are satisfied at $x^0=(0,5)^T$. So the sub-problem $P_{TR}(x^0,\varDelta ^0)$ is solved using MATLAB (R2016a) function “fmincon” with -‘Algorithm’, ‘interior-point’, -‘initial guess’,$0^{n+1}$, and the solution is obtained as $t^0=-104.0006$, $d^0=(2.0001,-10.0000)^T$. Since $\vert \vert d^0\vert \vert >10^{-5}$, so $\rho _0(d^0)=\frac{Ared(d^0)}{Pred(d^0)}=-1.0770$ is computed, which is less than $\alpha _2$. So according to Algorithm 3.4, the subproblem is solved again with $\varDelta ^0=27.0048$. After solving the subproblem three times, $\rho _0(d^0)=0.3152$ is obtained. So we proceed to Step 5. Hence the matrix $B^1$ is computed using (11).

$$\begin{aligned} B^1=\begin{pmatrix} 3.6891 &{} -2.4898 \\ -2.4898 &{} 2.6758 \end{pmatrix} \end{aligned}$$

Since $\rho _0(d^0)=0.3152<\alpha _2$, so trust region radius is updated as

$$\begin{aligned} \varDelta ^1=\beta _1\vert \vert {B^1}^{-1}\vert \vert \max \{\vert \vert g_1(x^1)\vert \vert ,\vert \vert g_2(x^1)\vert \vert \}=30.7087. \end{aligned}$$

Then the sub-problem $P_{TR}(x^1,\varDelta ^1)$ is solved. Repeating the above process, the critical point of this problem is obtained after 15th iteration and the solution is $(1,1)^T$.

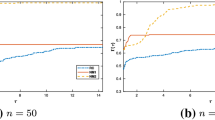
Comparison using performance profiles Comparison of ATRMO and TRMO using performance profiles for the number of iterations(It) and the number of function evaluations($F_e$) are provided in Figs. 1 and 2. In rand, an average of 10 purity metric values, obtained in 10 different runs is denoted by the average purity metric value. Similarly, average $\varGamma$ and $\varDelta$ metric values are computed. The average purity performance profile between ATRMO and TRMO is provided in Fig. 3. Figures 4 and 5 represent the average $\varGamma$ and $\varDelta$ performance profile respectively between ATRMO and TRMO.

Fig. 1

Performance profile for It

Fig. 2

Performance profile for $F_e$

Fig. 3

Average purity performance profile between ATRMO and TRMO

Fig. 4

Average $\varGamma$ performance profile between ATRMO and TRMO

Fig. 5

Average $\varDelta$ performance profile between ATRMO and TRMO

Result Analysis Figures 1-4 indicate that the proposed scheme ATRMO provides better performance than TRMO in most test problems. Also one may observe from Table 2 that ATRMO takes fewer iterations and function evaluations and gradient evaluations than TRMO in the most number of cases.

6 Conclusion

In this article, a new algorithm is proposed for (MOP) and the global convergence of the proposed algorithm is proved. The differences and advantages of this method over the previous existing method are summarized below.

• (i) In the existing method [18], the positive definite matrix $B_j^k$ is computed for every objective function, whereas the proposed scheme computes a common positive definite matrix $B^k$ at every iteration for all objective functions. This provides a new BFGS-type update formula.

• (ii) Geršgorin Circle theorem is used to ensure the positive definiteness of the matrix in BFGS update formula, which is a new concept in multi-objective programming.

• (iii) The trust region radius of this method is explicitly expressed at each iterative point, which contains both first and second order information, whereas in [18] the trust region radius is independent of first and second order information.

From the numerical illustrations, one may observe the numerical advantages from performance profiles and computation table. Application of this concept in constrained multi-objective optimization problems is the future scope of this article.