A solution algorithm for chance-constrained problems with integer second-stage recourse decisions

Abstract

We study a class of chance-constrained two-stage stochastic optimization problems where the second-stage recourse decisions belong to mixed-integer convex sets. Due to the nonconvexity of the second-stage feasible sets, standard decomposition approaches cannot be applied. We develop a provably convergent branch-and-cut scheme that iteratively generates valid inequalities for the convex hull of the second-stage feasible sets, resorting to spatial branching when cutting no longer suffices. We show that this algorithm attains an approximate notion of convergence, whereby the feasible sets are relaxed by some positive tolerance $\epsilon$. Computational results on chance-constrained resource planning problems indicate that our implementation of the proposed algorithm is highly effective in solving this class of problems, compared to a state-of-the-art MIP solver and to a naive decomposition scheme.

1 Introduction

We study two-stage chance-constrained mathematical optimization problems formulated as

$$\begin{aligned} \min \{cx : \Pr (x \in C_x(\omega )) \ge 1-\alpha , x \in X \}, \end{aligned}$$

(CCP)

where $\omega$ is a random variable with sample space $\varOmega$, $\alpha \in [0,1]$, $X \subseteq \mathbb {R}^{n_x}$ is compact, and $C_x(\omega ) = \textrm{Proj}_x C_{x,y}(\omega ) \subseteq \mathbb {R}^{n_x}$ is the projection onto the x-space of a higher-dimensional set $C_{x,y}(\omega ) \subseteq \mathbb {R}^{n_x + n_y(\omega )}$, whose dimension might depend on the realization $\omega$. An algorithmic approach for optimizing over this problem class is a powerful tool for decision making under uncertainty: the problem class models situations where we want to make decisions that are feasible with high probability, as determined by $1-\alpha$, and depending on the realization of uncertainty, we are allowed to take recourse actions (the y variables) to amend the initial decision x. Unlike two-stage stochastic programs [4], problem (CCP) does not require the first-stage solution to be feasible for all second-stage problems, but only for enough realizations to satisfy the chance constraint.

Chance-constrained problems are difficult to solve in general due to nonconvexity of the feasible region, and additional assumptions are often imposed in order to make the problem tractable. The importance of establishing conditions that guarantee existence of an equivalent deterministic problem has been identified since the early days of stochastic programming [7, 31]. In this paper we make a few assumptions that are common in the literature and guarantee the existence of a deterministic equivalent formulation; the most notable assumptions are that X is a bounded set and $\omega$ is a discrete random variable with finite support. The realizations of $\omega$ are called scenarios. For more general random variables, sample-average approximation provides a possible way to reduce to the case studied in this paper [28].

There are many ways to construct deterministic equivalent problems, under suitable conditions. A recent survey on reformulations of chance-constrained mixed-integer linear programs that arise from finite discrete distribution optimization can be found in [20]. The approach used in this paper leads to a mixed-integer program with one binary variable for each scenario, and big-M inequalities to describe the sets $C_x(\omega )$. The drawback of this approach is that the big-M inequalities could lead to poor bounds for the continuous relaxation. Strong valid inequalities for similar formulations under right-hand side uncertainty are discussed in [19, 29] and combine inequalities that are valid for single scenarios into so-called mixing inequalities. The idea is extended in [18], where aggregated mixing inequalities, incorporating lower bounds on the continuous variables in the original inequalities, are introduced. An alternative reformulation for the same class of problems can be constructed using the concept of $(1-\alpha )$-efficient points, see [3, 8, 32, 34]. Problem-specific algorithms can also be devised, e.g., the algorithm for chance-constrained packing problems developed in [39] using probabilistic covers.

For problems of the form (CCP) that admit a deterministic equivalent formulation including all scenarios, the direct solution of the deterministic equivalent quickly becomes intractable as the size of the problem and number of scenarios increase. Decomposition strategies that deal with each scenario separately have been shown to be very effective in this context and in multi-stage programming general, but their applicability depends on the structure of the problem at hand. If the second-stage feasible sets $C_{x,y}(\omega )$ are polyhedra with an explicitly known description (i.e., linear programs), we can apply Benders decomposition [2] or the L-shaped method [42]; Benders decomposition is at the heart of effective branch-and-cut algorithms for chance-constrained two-stage problems [1, 25, 27, 40, 43]. This approach cannot be applied, in general, if the second-stage sets $C_{x,y}(\omega )$ are not polyhedra, because finding an appropriate outer approximation of these sets is no longer as simple as applying linear programming duality. If the second-stage sets are convex, generalized Benders decomposition provides a possible solution strategy [16, 23, 24, 41], and so does outer approximation [10, 11], see, e.g., [26]. The convexification of second-stage problems containing binary variables only is studied in [35], using disjunctive programming and the facial property of 0–1 programs. Along the same lines, [36, 38] describe convergent Benders decomposition approaches if the second stage is mixed-binary, relying on sequential convexification. For the linear case in which the first-stage problem contains binary variables only and the second stage includes integer variables, [12] proposes a decomposition algorithm that relies on parametric Gomory cuts, while [44] extends the approach to deal with first-stage general integer variables. The case with mixed-integer first and second-stage variables is considered in [33], where the solution algorithm combines branch-and-bound, interval partitioning and polyhedral approximations; see also the tutorial [21]. The L-shaped method has been extended to accommodate for integer variables with linear constraints in the second stage, when the first-stage problem is a pure binary problem [22], or, more in general, by incorporating dual cuts based on integer programming duality [6]. A very general approach, that can in principle deal with mixed-integer as well as nonlinear problems, is the stochastic branch-and-bound algorithm presented in [30]; the main obstacle to its implementation is the design of efficient upper and lower bounding procedures for the subproblems created by branching, and this ultimately determines the effectiveness of the algorithm.

In this paper we address the solution of problem (CCP) when the first-stage problem is a (potentially mixed-integer) linear program, and the second-stage problems are convex mixed-integer nonlinear programs (i.e., the sets $C_{x,y}(\omega )$ are described by convex constraints and integrality requirements on some or all of the variables). This very general class of problems encompasses all the ones discussed in the previous paragraph and is considered to be very difficult to solve in practice. The main ingredient of our algorithm is a sequential convexification procedure that generates valid inequalities for the convex hull of the second-stage problems. To generate an inequality, we use a conditional gradient (Frank–Wolfe) algorithm that requires the solution of several (small) mixed-integer programs. These inequalities are integrated within a branch-and-cut framework that acts in the space of the x variables, as well as additional binary variables used to determine which scenarios are feasible to satisfy the chance constraint. Branching is undertaken to ensure integrality of the x variables, if any, and feasibility for the second-stage problems, which may require spatial branching, in general.

We show that the proposed algorithm converges in finite time to a point that is optimal for a relaxation of the original problem, where the relaxation amount can be chosen arbitrarily close to zero. Proving convergence in finite time requires a careful analysis of the different steps of the algorithm. We first analyze our sequential convexification procedure based on generating feasible points for the second-stage problems. While the analysis is straightforward in the linear case, in the nonlinear case the procedure may fail to produce a valid cut in finite time, as we show with an example. To overcome this obstacle, we show that introducing a relaxation step for the inequality suffices to guarantee a valid cut with any desired precision in finite time even in the nonlinear case. Second, we show that the convexification procedure, combined with a spatial branch-and-bound framework where branching occurs on the x variables, is sufficient for convergence in finite time. We remark that our spatial branch-and-bound algorithm creates children nodes with branching constraints $x_j \le b, x_j \ge b$ for some index j and value b; that is, we do not eliminate any region by branching, in contrast to the simplest scheme that eliminates a strip of width $\epsilon > 0$ at each branching to ensure finiteness when the feasible set is compact. Therefore, convergence of our algorithm is not based on subdivision of the feasible region into a finite number of hyperrectangles: rather, it is based on the ability of the convexification procedure to eventually separate every infeasible point while making “sufficient progress”. A key step of our proof is to generalize the convergence of Kelley’s cutting plane algorithm [17] to inequalities that may not be supporting for the epigraph of the constraints at the points in the usual cut-then-reoptimize sequence.

From a computational point of view, we propose several practical enhancements of the algorithm to increase its numerical performance: primal heuristics, warm-starts of the convexification procedure, and solution of the deterministic equivalent of partially-fixed branch-and-bound nodes to close them immediately. We show that all these components contribute to the effectiveness of our implementation, and allow us to solve instances of a mixed-integer two-stage chance-constrained resource allocation problem, with hundreds of scenarios, that are out of reach for a commercial solver applied to the deterministic equivalent formulation.

The rest of this paper is organized as follows. In Sect. 2 we formally introduce the considered problem, present the general scheme of our decomposition approach, and give results about its finite convergence. Section 3 gives some algorithmic details and enhancements, while Sect. 4 presents the outcome of a comprehensive computational analysis of the performance of the algorithm on two stochastic problems. Finally, we draw some conclusions in Sect. 5.

2 Decomposition algorithm for (CCP)

Recall that our goal is to solve problem (CCP), restated here for convenience:

$$\begin{aligned} \min \{cx : \Pr (x \in C_x(\omega )) \ge 1-\alpha , x \in X \}. \end{aligned}$$

(CCP)

We denote by $\textrm{Proj}_x$ the projection of a set onto the space of the x variables, by $\textrm{Conv}$ the convex hull, and by $\textrm{Cont}$ the continuous relaxation (i.e., the set obtained by relaxing any integrality requirements on the variables defining the set). Given $S \subset \mathbb {R}^n$ and $\epsilon \ge 0$, we denote $S + \epsilon := \{ x \in \mathbb {R}^n: \Vert x - y \Vert \le \epsilon \text { for some } y \in S\}$, where we use $\Vert \cdot \Vert$ to indicate $\ell _2$-norm. If S is the feasible set of a problem, we denote any point in $S + \epsilon$ as $\epsilon$-feasible for that problem. To obtain a deterministic reformulation for (CCP), we make the following assumptions:

• 1. The sample space $\varOmega$ is discrete and finite, and in particular $\varOmega = \{\omega ^k: k = 1, \ldots , h \}$;

• 2. $C_{x}(\omega ^k) = \textrm{Proj}_x(C_{x,y}(\omega ^k)) {\ne \emptyset }$, where $C_{x,y}(\omega ^k) = \{(x,y): x \in \mathbb {R}^{n_x}, y \in \mathbb {R}^{n_y(\omega ^k)}, g^k(x, y) \le 0, {y} \in Y^k\}$, $Y^k = \{y \in \mathbb {R}^{n_y(\omega ^k)}: y_j \in \mathbb {Z}\; \forall j \in \mathcal{I}_k\}$, and $g^k(x, y)$ is a vector of convex functions $(g^k_1, \ldots , g^k_m)$;

• 3. X is closed and $X \subseteq [-U, U]^{n_x}$ for some constant U.

We discussed the first assumption in the introduction. The second assumption states that the feasible set for each scenario is a non-empty mixed-integer convex set. The motivation for the third assumption will be apparent shortly. Using the first assumption, and denoting $p_k = \Pr (\omega = \omega ^k)$, we introduce a set of indicator variables $z_k$ and rewrite the problem as

$$\begin{aligned} \begin{array}{rrcl} \min &{} cx \\ \text {s.t.:} &{} x&{}\in &{} X \\ k=1,\ldots ,h &{} z_k = 0 \; \Rightarrow x &{}\in &{} C_x(\omega ^k) \\ &{} \sum _{k=1}^h p_k z_k &{}\le &{} \alpha \\ k=1,\ldots ,h &{} z_k &{}\in &{} \{0,1\}. \end{array} \end{aligned}$$

(CCP-R)

Using the second and third assumption, the problem can be modeled as the mixed-integer nonlinear program (MINLP)

$$\begin{aligned} \begin{array}{{r}*{9}{c}} \min &{} cx &{} &{} &{} &{} &{} &{} &{} &{} \\ \text {s.t.:} &{} Ax &{} &{} &{} &{} &{} &{} &{}\ge &{} b \\ &{} g^1(x, &{} &{} y^1) &{} &{} &{} &{} &{}\le &{} M^1z_1\\ &{} \vdots &{} &{} &{} &{} \ddots &{} &{} &{}\vdots &{} \\ &{} g^h(x, &{} &{} &{} &{} &{} &{} y^h) &{}\le &{} M^h z_h\\ &{} &{} &{} p_1 z_1 &{}+&{}\dots &{}+&{} p_h z_h &{}\le &{} \alpha \\ &{} &{} &{} y^1 &{} &{} &{} &{} &{} \in &{} Y^1 \\ &{} &{} &{} &{} &{} \dots &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} y^h &{} \in &{} Y^h \\ &{} &{} &{} z_1, &{} &{} \dots &{} &{} z_h &{}\in &{} \{0,1\} \end{array} \end{aligned}$$

(CCP-MINLP)

In this formulation, we assume that $M^k$ are vectors of constants large enough to deactivate the corresponding constraints if $z_k = 1$. Such constants exist thanks to the third assumption. Since there is no objective function contribution associated with variables y, the second stage problems are feasibility problems; alternative models with second-stage objective function contributions can be considered, e.g., by enlarging the vector of first-stage variables, developing specialized optimality cuts, or even introducing a “recovery mode” for violated scenarios, see [25]. One motivation for the third assumption can now be properly explained: it ensures that the recession cone of (CCP-MINLP) and the one of (CCP-R) are the same, as they coincide with the set $\{0\}$. The assumption that the recession cones are the same is necessary for mixed-integer representability [15]. A further motivation is technical: we need the third assumption for our convergence proof. We remark that, although we discuss the case in which all x variables are continuous, our approach is based on a branch-and-cut framework in the x-space, therefore from a theoretical point of view it can be easily extended to handle integrality requirements on some x variables. The implementation of the algorithm would however be more complex, therefore we do not explicitly consider this case.

Formulation (CCP-MINLP) is the deterministic equivalent of (CCP), under the three assumptions stated above. It can be solved with a convex MINLP solver, or, in case the constraints $g^1,\ldots ,g^h$ are linear, with a MILP solver. However, such formulation has two main drawbacks: its size, and its weak continuous relaxation. The size is an issue because (CCP-MINLP) includes all variables and constraints for the second-stage problems: since the problem is then solved via branch and cut, increasing the size linearly with the number of scenarios generally leads to exponential growth of the running time in practice. The weak continuous relaxation is due to the presence of many big-M constraints, which can lead to large gaps between the original problem and its relaxation.

Several decomposition algorithms for problems with a structure similar to (CCP-MINLP) have been proposed, see also the discussion in Sect. 1. The algorithm that we propose is inspired, most notably, by [26, 27], both of which employ a similar branch-and-bound scheme, and generate valid inequalities for second-stage feasible sets $C_{x,y}(\omega )$ that are linear and nonlinear convex, respectively. We follow a decomposition approach whereby we define a master problem with first-stage variables x only, and h subproblems, one for each scenario, involving the respective scenario-dependent constraints. The master problem is a relaxation of the original problem, as all the constraints depending on second-stage variables have been eliminated. Therefore, whenever the solution of the master problem does not satisfy the constraints of some active scenario ($z_k=0$), we want to generate cuts for the corresponding set $C_{x,y}(\omega ^k)$, and add them to the master problem. This scheme, originally proposed by [37], has been later used in [26, 27], but the task in this paper is complicated by the integrality restrictions on the second-stage variables $y^1,\ldots ,y^h$, so that the generation of valid inequalities for $C_{x,y}(\omega ^k)$ is considerably more involved. Although we add these cuts as big-M constraints, they only involve x variables, therefore we need smaller values of the big-M coefficients than in CCP-MINLP.

To develop intuition, let us consider the case in which we want all scenarios to be satisfied, i.e., (CCP-MINLP) with $\alpha = 1$. At a high level, the problem that we need to solve can then be stated in terms of the following simpler question: given a point ${\hat{x}}$ from the master problem and a scenario index k, is ${\hat{x}}$ feasible for scenario $\omega ^k$, i.e., does there exist ${\hat{y}}$ such that $({\hat{x}},{\hat{y}}) \in C_{x,y}(\omega ^k)$, and if not, can we somehow exclude ${\hat{x}}$ from the master? A systematic procedure for this task can be used to solve the original problem: the master is a relaxation of the original problem, and with the above procedure we could exclude every candidate solution until we find one that is feasible for all $C_{x,y}(\omega ^k)$, $k=1,\ldots ,h$ (if we do not require all scenarios to be satisfied, i.e., $\alpha < 1$, then the algorithm must be modified to eliminate only those ${\hat{x}}$ that are not feasible for a number of scenarios sufficient to satisfy the chance constraint). Notice that if ${\hat{x}}$ is infeasible for scenario $\omega ^k$, the nonconvexity of $C_{x,y}(\omega ^k)$ (due to integrality) may prevent us from deriving a valid linear inequality that cuts off ${\hat{x}}$, so cutting may not be sufficient by itself. We now discuss in more detail how to eliminate ${\hat{x}}$ when it is not feasible for a scenario $\omega ^k$.

By definition of the second-stage feasible sets $C_{x,y}(\omega ^k)$, a point ${\hat{x}}$ is feasible for $C_{x,y}(\omega ^k)$ if and only if ${\hat{x}} \in \textrm{Proj}_x(C_{x,y}(\omega ^k))$. For simplicity, we consider a fixed scenario and therefore temporarily drop the symbol $\omega ^k$: the discussion applies in the same way to all scenarios. There are three notable cases in which ${\hat{x}}$ is not feasible and we want to exclude it, leading to three different procedures of increasing computational cost:

• 1. ${\hat{x}} \not \in \textrm{Proj}_x \textrm{Cont}(C_{x,y})$;

• 2. ${\hat{x}} \in \textrm{Proj}_x \textrm{Cont}(C_{x,y})$ and ${\hat{x}} \not \in \textrm{Proj}_x \textrm{Conv}(C_{x,y})$;

• 3. ${\hat{x}} \in \textrm{Proj}_x \textrm{Conv}(C_{x,y})$.

In the first case, it is sufficient to find an inequality valid for the projection of the continuous relaxation of $C_{x,y}$; this can be done with standard techniques, such as Benders or generalized Benders [13] cuts for linear and nonlinear convex sets, respectively. We use the outer approximation procedure of [26]. In the second case, we need a valid inequality for $\textrm{Proj}_x \textrm{Conv}(C_{x,y})$, which in turn requires knowledge of $\textrm{Conv}(C_{x,y})$; note that such an inequality exists, because we are separating from a convex set. We will generate a valid inequality with a sequential convexification procedure described subsequently. In both cases, the derived cuts can be interpreted as so-called “Fenchel cuts” (see [5]), i.e., deep cuts that separate a point ${\hat{x}}$ from a given set ($\textrm{Proj}_x \textrm{Cont}(C_{x,y})$ in the first case, $\textrm{Proj}_x \textrm{Conv}(C_{x,y})$ in the second case) by exploiting the equivalence between separation and optimization over this set. Finally, in the third case, a separating inequality does not exist, therefore to separate ${\hat{x}}$ we perform spatial branching.

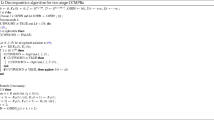
The pseudo-code of our decomposition approach is provided in Algorithm 2.0.1. Since the master problem involves the x variables only, the separation routines must find a cut in the x space. In the remainder of this section, we provide the separation algorithms for cases 1 and 2 and we specify how branching is performed when case 3 occurs.

2.1 Case 1: separation when ${\hat{x}} \not \in \textrm{Proj}_x\textrm{Cont}(C_{x,y})$

In order to check whether ${\hat{x}} \in \textrm{Proj}_x\textrm{Cont}(C_{x,y})$ and, when this is not the case, determine a cut to separate ${\hat{x}}$, let us define the problem

It it clear that the optimal solution value of (PROJ$^1$) is strictly positive if and only if ${\hat{x}} \not \in \textrm{Proj}_x\textrm{Cont}(C_{x,y})$. In this case, Theorem 1 of [26], adapted to our case, allows us to compute a valid cut to separate ${\hat{x}}$:

Theorem 1

Let $\textrm{Cont}(C_{x,y})$ be a closed set such that $\textrm{Proj}_x\textrm{Cont}(C_{x,y})$ is convex, and ${\hat{x}} \not \in \textrm{Proj}_x\textrm{Cont}(C_{x,y})$. Let ${\bar{x}}^{*}$ be the optimal solution to (PROJ$^1$) with positive objective function value. Then, the hyperplane

$$\begin{aligned} ({\hat{x}} - {\bar{x}}^{*})^T (x - {\bar{x}}^{*}) \le 0 \end{aligned}$$

separates ${\hat{x}}$ from $\textrm{Proj}_x\textrm{Cont}(C_{x,y})$. This hyperplane is the deepest valid cut that separates ${\hat{x}}$ from $\textrm{Proj}_x\textrm{Cont}(C_{x,y})$, if depth is computed in $\ell _2$-norm.

We refer to [26] for a proof of this result.

2.2 Case 2: separation when ${\hat{x}} \not \in \textrm{Proj}_x\textrm{Conv}(C_{x,y})$

Let us assume that ${\hat{x}} \in \textrm{Proj}_x\textrm{Cont}(C_{x,y})$, because otherwise we would fall under Case 1. Our approach for Case 2 is (i) to check if ${\hat{x}}$ lies in $\textrm{Proj}_x\textrm{Conv}(C_{x,y})$ and, if not, (ii) to define a supporting hyperplane for $\textrm{Proj}_x\textrm{Conv}(C_{x,y})$ separating ${\hat{x}}$. To this aim, we solve the following problem:

by using an adaptation of the conditional gradient (also known as Frank–Wolfe) algorithm, in its fully corrective variant. The finite convergence of such a procedure is well established in the linear case [14]. In the nonlinear convex case, only asymptotic convergence is guaranteed [14], but we show that with the introduction of proper numerical tolerances we can obtain convergence in finite time with any desired level of accuracy.

The procedure is initialized with the feasible point in $C_{x,y}$ closest to ${\hat{x}}$, obtained by solving the following convex MINLP:

$$\begin{aligned} x^1 \leftarrow \arg _x \min _{(x,y) \in C_{x,y}} \Vert {\hat{x}} - x\Vert . \end{aligned}$$

(FINDX1)

If the distance between this point and ${\hat{x}}$ is 0 (or lower than a fixed tolerance $\epsilon$, see the discussion surrounding Algorithm 2.2.2), ${\hat{x}}$ is feasible (or we consider it feasible within the tolerance) and the procedure stops; no cut is generated. Otherwise, an iterative process starts, where at each iteration we solve two problems: a (continuous) nonlinear problem, and an MINLP with convex continuous relaxation, with the aim of finding a new point in $C_{x,y}$ that decreases the distance from ${\hat{x}}$.

Let S be a set of points in $\textrm{Proj}_x C_{x,y}$; initially, $S = \{x^1\}$. The first problem minimizes the distance from the convex combination of the points in the current set S to ${\hat{x}}$, and is defined as follows:

$$\begin{aligned} \begin{array}{rrcl} \min &{} \Vert {\hat{x}} - \sum _{i=1}^{|S|} \lambda _i x^i \Vert &{}&{} \\ \text {s.t.:} &{} \sum _{i=1}^{|S|} \lambda _i &{} = &{} 1 \\ i=1,\ldots ,|S| &{} \lambda _i &{}\ge &{} 0. \end{array} \end{aligned}$$

(MINDIST)

In this model, a continuous variable $\lambda _i$ is associated with each point $x^i \in S$; note that the $x^i$ here are data. Given an optimal solution ${\bar{\lambda }}_i$ of (MINDIST), let us define ${{\bar{x}}}= \sum _{i=1}^{|S|} {\bar{\lambda }}_i x^i$. If the distance between ${\hat{x}}$ and ${{\bar{x}}}$ is 0, then ${\hat{x}} \in \textrm{Proj}_x\textrm{Conv}(C_{x,y})$, and the procedure stops. Otherwise, we define a second problem to determine a new point $x^{|S|+1}$ to be added to S, with the goal of decreasing the objective function value of (MINDIST). This is equivalent to identifying a descent direction from ${{\bar{x}}}$ that decreases the distance to ${\hat{x}}$, as follows:

$$\begin{aligned} \begin{array}{rrcl} \max &{} ({\hat{x}} - {{\bar{x}}})^T(x^{|S|+1} - {{\bar{x}}}) &{}&{} \\ \text {s.t.:} &{} (x^{|S|+1}, y)&{}\in &{} C_{x,y}. \end{array} \end{aligned}$$

(NEWPOINT)

Here, the only (vector-valued) decision variable is the point $x^{|S|+1}$. As shown below, if the optimal solution value of this problem is larger than zero, adding the new point $x^{|S|+1}$ to S decreases the objective function value of (MINDIST). Otherwise, the iterative procedure stops, returning the point ${\bar{x}}^{*}$. If the distance between ${\hat{x}}$ and ${\bar{x}}^{*}$ is still strictly positive, we can conclude that ${\hat{x}} \not \in \textrm{Proj}_x\textrm{Conv}(C_{x,y})$, finding an inequality to separate ${\hat{x}}$. The inequality is the hyperplane orthogonal to ${\hat{x}}$ at ${\bar{x}}^{*}= \sum _{i=1}^{|S|} \lambda _i x^i$. The entire procedure is described in Algorithm 2.2.1. For now, let us assume that we are working with infinite precision, i.e., all calculations can be carried out exactly.

The result below follows from the convergence properties of the conditional gradient algorithm when applied to our setting.

Proposition 1

The sequence ${{\bar{x}}}$ of points generated by Algorithm 2.2.1 as solutions to the problem (MINDIST) converges to ${\hat{x}}$ or to a point ${\bar{x}}^{*}=\sum _{i=1}^{|S|} \lambda _i^* x^i \in \textrm{Proj}_x \textrm{Conv}(C_{x,y})$ that has minimum distance from ${\hat{x}}$, i.e., to an optimal solution of (PROJ$^2$).

Because Algorithm 2.2.1 is equivalent to fully corrective Frank–Wolfe, it exhibits linear convergence rate on problem (PROJ$^2$) for which the objective function is strongly convex; the exact rate of convergence depends on geometric properties of the underlying set [14, Thm. 1]. Although Proposition 1 shows that Algorithm 2.2.1 converges to an optimal solution for problem (PROJ$^2$), it is known that convergence may be obtained only asymptotically in case $C_{x,y}$ is a mixed-integer nonlinear (convex) set, as can be seen from the following example.

Example 1

Let us consider the example depicted in Fig. 1, where the two circles represent the feasible set, and the (sub)sequence of feasible points $x^1,x^2,x^3$ and $x^4$ returned by (NEWPOINT) is reported. At every iteration, the facet of the convex hull of S generated by Algorithm 2.2.1 is not perfectly horizontal; as a consequence, the vector from the solution ${{\bar{x}}}$ of (MINDIST) to ${\hat{x}}$ is not vertical. Hence, at every iteration the next feasible point generated by (NEWPOINT) lies on the outer arc of one of the two circles (outside the dashed lines), and the sequence of generated points does not reach the top of the circles in finite time. However, the optimal solution to (PROJ$^2$) can only be obtained when both points at the top of the two circles belong to S.

In the above nonlinear example, the algorithm is unable to generate the (exact) convex hull in finite time. This behavior cannot occur when $C_{x,y}$ is a mixed-integer linear set: in that case, convergence is ensured in finite time, although the algorithm may explore all the (exponentially-many) extreme points of the convex hull.

Fig. 1

Two-dimensional example showing that Algorithm 2.2.1 may not converge in a finite number of steps

We now show how to guarantee finite convergence of Algorithm 2.2.1 in the nonlinear case, by introducing numerical tolerances. The resulting approximate procedure, detailed in Algorithm 2.2.2, returns a point ${{\bar{x}}}$ that is close (although possibly not the closest) to ${\hat{x}}$. Note that, as opposed to Algorithm 2.2.1, for convenience we now assume that the initial point $x^1$ is given as an input.

Proposition 2

Given two values of tolerance $\epsilon > 0$ and $\zeta > 0$, Algorithm 2.2.2 terminates in a finite number of iterations.

Proof

At each iteration of Algorithm 2.2.2, either the distance of ${{\bar{x}}}$ from ${\hat{x}}$ is reduced by a value larger than $\zeta$, or it is not. The former case can only happen a finite number of times, because the distance between ${\hat{x}}$ and $\textrm{Proj}_x \textrm{Conv}(C_{x,y})$ is finite; in the latter case, the algorithm stops. Thus, the algorithm runs for a finite number of steps. $\square$

When Algorithm 2.2.2 stops with $d_{|S|} > \epsilon$, not only the computed point ${{\bar{x}}}$ may be in the strict interior of $\textrm{Proj}_x\textrm{Conv}(C_{x,y})$, but we also have no upper bound on the distance of ${{\bar{x}}}$ from the boundary of $\textrm{Proj}_x\textrm{Conv}(C_{x,y})$. Hence, the inequality $({\hat{x}} - {{\bar{x}}})^{\top }(x - {{\bar{x}}}) \le 0$ may not be valid (i.e., it may cut some feasible solution), and needs to be relaxed before it can be added to (MASTER) (line 14 of Algorithm 2.0.1). We relax the inequality by increasing its r.h.s. to a value that makes it supporting to $\textrm{Conv}(C_{x,y})$. However, if the tolerances $\epsilon$ and $\zeta$ are large, the relaxed cut may not cut ${\hat{x}}$ off, as shown in the left part of Fig. 2, where the dashed line represents the “ideal” cut (associated with ${\bar{x}}^{*}$), the dotted line is the invalid cut (through ${{\bar{x}}}$), and the solid line corresponds to its valid relaxed counterpart. The right part of the figure shows that reducing the numerical tolerances, which leads to performing additional iterations of the repeat-until loop of Algorithm 2.2.2, allows convergence to a point closer to ${\bar{x}}^{*}$ than in the previous case: this yields a relaxed cut that now separates ${\hat{x}}$.

Fig. 2

Early termination of Algorithm 2.2.3 produces an invalid cut, whose relaxation is unable to cut ${\hat{x}}$ (left). Reducing tolerance $\zeta$ yields a relaxed cut that separates ${\hat{x}}$ (right)

Hence, in case the relaxed cut does not separate ${\hat{x}}$, our approach is to reduce the tolerance $\zeta$ (that controls the repeat-until loop), and execute Algorithm 2.2.2 with the new tolerance. The resulting scheme, described in Algorithm 2.2.3, generates a sequence of points ${\bar{x}}^{j}$, until we get to a point that allows us to compute a valid inequality to separate ${\hat{x}}$, or to conclude that ${\hat{x}}$ is optimal within an $\epsilon$ tolerance, provided that the sequence of the $\zeta$ values is such that $\lim _{j \rightarrow \infty } \zeta ^j \rightarrow 0$. The next proposition shows that Algorithm 2.2.3 always terminates in a finite number of iterations.

Proposition 3

Given a value of tolerance $\epsilon > 0$ and an initial value $\zeta ^0 > 0$, Algorithm 2.2.3 (with a sequence $\zeta ^j$ such that $\lim _{j \rightarrow \infty } \zeta ^j \rightarrow 0$) terminates in a finite number of iterations by either returning a valid inequality to separate ${\hat{x}}$, or “${\hat{x}} \in \textrm{Proj}_x \textrm{Conv}( C_{x,y}) + \epsilon$”, or “${\hat{x}}$ is $\epsilon$-feasible for $C_{x,y}$”.

Proof

First, observe that in lines 1–4 of the algorithm we check if a feasible point $x^1$ whose distance from ${\hat{x}}$ is not larger than $\epsilon$ exists. In this case, the algorithm immediately returns “${\hat{x}}$ is $\epsilon$-feasible for $C_{x,y}$”.

When this is not the case, we know from Proposition 1 that, if tolerances $\epsilon$ and $\zeta$ were set to 0, the sequence ${\bar{x}}^{j}$ generated at step 7 of Algorithm 2.2.3 would converge to either (i) ${\hat{x}}$, when ${\hat{x}} \in \textrm{Proj}_x\textrm{Conv}(C_{x,y})$, or (ii) a point, say ${\bar{x}}^{*}$, on the boundary of $\textrm{Proj}_x\textrm{Conv}(C_{x,y})$.

Assume now that the tolerances are set to strictly positive values. Note that the main loop of Algorithm 2.2.1 is the same as in Algorithm 2.2.2, except that Algorithm 2.2.2 terminates early whenever it reaches the desired convergence criterion $\epsilon$, or if the most recent iteration improved the distance from ${\hat{x}}$ only by a small amount $\zeta$, and this amount $\zeta$ is progressively decreased in Algorithm 2.2.3. In case (i) we have that for each $\epsilon >0$ there is a finite index ${\bar{\jmath }}$ such that $\Vert {\hat{x}} - {\bar{x}}^{j}\Vert <\epsilon$ for $j \ge {\bar{\jmath }}$; the exact algorithm would reach ${\bar{\jmath }}$ in a finite number of iterations, therefore so does the approximate algorithm when executed with tolerance $\epsilon$ and a small enough value $\zeta$, and then returns “${\hat{x}} \in \textrm{Proj}_x \textrm{Conv}( C_{x,y}) + \epsilon$”. In case (ii), when ${\hat{x}} \notin \textrm{Proj}_x\textrm{Conv}(C_{x,y})$, we have that for every $\delta >0$, there exists a finite index ${\bar{\jmath }}$ such that $\Vert {\bar{x}}^{*}- {\bar{x}}^{j}\Vert <\delta$ for $j \ge {\bar{\jmath }}$. Now, we distinguish two sub-cases of (ii): when $0< \Vert {\hat{x}} - {\bar{x}}^{*}\Vert <\epsilon$, for small enough $\delta >0$, we have $\Vert {\hat{x}} - {\bar{x}}^{j}\Vert <\epsilon$ for $j \ge {\bar{\jmath }}$, and the algorithm returns “${\hat{x}} \in \textrm{Proj}_x \textrm{Conv}( C_{x,y}) + \epsilon$”. When $\Vert {\hat{x}} - {\bar{x}}^{*}\Vert >\epsilon$, we claim (see Prop. 4) that there exists a small enough $\delta >0$ such that if $\Vert {\bar{x}}^{*}- {\bar{x}}^{j}\Vert <\delta$, a (not valid) inequality $({\hat{x}} - {\bar{x}}^{j})^{\top }(x - {\bar{x}}^{j}) \le 0$ can be relaxed to a valid inequality that separates ${\hat{x}}$. This inequality is obtained in finite time, i.e., we can compute it at iteration ${\bar{\jmath }}$. This concludes the proof. $\square$

It still remains to show that for ${\bar{x}}^{j}$ close enough to ${\bar{x}}^{*}$, we can relax the inequality returned by Algorithm 2.2.3 and separate ${\hat{x}}$. This is our next result.

Proposition 4

For every $\epsilon > 0$ and ${\hat{x}} \not \in \textrm{Proj}_x \textrm{Conv}(C_{x,y}) + \epsilon$, there exists $\delta > 0$ such that if $\Vert {\bar{x}}^{{\bar{\jmath }}} - {\bar{x}}^{*}\Vert < \delta$, the inequality $({\hat{x}} - {\bar{x}}^{{\bar{\jmath }}})^{\top }(x - {\bar{x}}^{{\bar{\jmath }}}) \le 0$ can be relaxed to be valid for $\textrm{Proj}_x \textrm{Conv}(C_{x,y})$ while still cutting off ${\hat{x}}$. The relaxation amount is upper bounded by $\epsilon ^2$.

Proof

Notice that by convexity and the fact that ${\bar{x}}^{*}\in \textrm{Proj}_x \textrm{Conv}(C_{x,y})$, we have

$$\begin{aligned} \max _{x \in \textrm{Proj}_x \textrm{Conv}(C_{x,y})} ({\hat{x}} - {\bar{x}}^{*})^{\top } (x -{\bar{x}}^{*}) = 0. \end{aligned}$$

(1)

To find the tightest relaxation that makes the inequality $({\hat{x}} - {\bar{x}}^{{\bar{\jmath }}})^{\top }(x - {\bar{x}}^{{\bar{\jmath }}}) \le 0$ valid, we compute

$$\begin{aligned} b := \max _{x \in \textrm{Proj}_x \textrm{Conv}(C_{x,y})} ({\hat{x}} - {\bar{x}}^{\bar{\jmath }})^{\top } (x - {\bar{x}}^{{\bar{\jmath }}}) = \max _{(x, y) \in C_{x,y}} ({\hat{x}} - {\bar{x}}^{{\bar{\jmath }}})^{\top } (x - {\bar{x}}^{\bar{\jmath }}), \end{aligned}$$

(2)

where the second equality follows from the fact that optimizing a linear function over a bounded set or over its convex hull yields the same value because there is at least one optimal extreme point. Thus, we obtain the inequality $({\hat{x}} - {\bar{x}}^{\bar{\jmath }})^{\top }(x - {\bar{x}}^{{\bar{\jmath }}}) \le b$. Now, let us expand (2) as

$$\begin{aligned} \max _{(x,y) \in C_{x,y}} ({\hat{x}} - {\bar{x}}^{{\bar{\jmath }}})^{\top }(x - {\bar{x}}^{{\bar{\jmath }}})&= \max _{(x,y) \in C_{x,y}} ({\hat{x}} - {\bar{x}}^{*}+ {\bar{x}}^{*}- {\bar{x}}^{\bar{\jmath }})^{\top }(x - {\bar{x}}^{*}+ {\bar{x}}^{*}- {\bar{x}}^{{\bar{\jmath }}}) \\&\le \max _{(x,y) \in C_{x,y}} ({\hat{x}} - {\bar{x}}^{*})^{\top }({\bar{x}}^{*}- {\bar{x}}^{{\bar{\jmath }}}) + ({\bar{x}}^{*}- {\bar{x}}^{{\bar{\jmath }}})^{\top } (x - {\bar{x}}^{{\bar{\jmath }}}), \end{aligned}$$

where we used (1). Since $\Vert ({\hat{x}} - {\bar{x}}^{*})\Vert \le 2U$ and $\Vert (x - {\bar{x}}^{{\bar{\jmath }}})\Vert \le 2U$, and $\Vert ({\bar{x}}^{*}- {\bar{x}}^{{\bar{\jmath }}})\Vert < \delta$ by assumption, we can upper bound the above expression by $4U\delta$. Thus, as long as $\delta \le \frac{\epsilon ^2}{4U}$, $b < \epsilon ^2$, we have

$$\begin{aligned} ({\hat{x}} - {\bar{x}}^{{\bar{\jmath }}})^{\top }({\hat{x}} - {\bar{x}}^{\bar{\jmath }}) = \Vert {\hat{x}} - {\bar{x}}^{{\bar{\jmath }}}\Vert ^2 \ge \epsilon ^2 > b, \end{aligned}$$

showing that the relaxed inequality cuts off ${\hat{x}}$. $\square$

2.3 Case 3: spatial branching on variable x

When ${\hat{x}} \in \textrm{Proj}_x\textrm{Conv}(C_{x,y})$ there is no way to separate this point through a valid cut expressed in terms of the first-stage variables x only. Hence, in this case we perform spatial branching on (MASTER), by selecting a variable $x_j$ that is neither at its lower nor at its upper bound in ${\hat{x}}$, and splitting the feasible set by imposing $x_j \le {\hat{x}}_j$ and $x_j \ge {\hat{x}}_j$, respectively. As discussed in the proof of Theorem 2, whenever ${\hat{x}} \in \textrm{Proj}_x\textrm{Conv}(C_{x,y})$, such a variable exists.

2.4 Convergence of the decomposition Algorithm 2.0.1

We are now ready to state the main theoretical result of our paper, namely, the finite convergence of the Decomposition Algorithm 2.0.1 for any tolerance $\epsilon >0$.

Theorem 2

Consider a problem of the form (CCP) satisfying Assumptions A1-A3. Let $\epsilon > 0$. Let $\mathcal{C}$ be the cut generation procedure of Algorithm 2.2.3. Assume that the branching procedure is such that we always branch on a fractional variable z, if any, and on a first-stage variable $x_j$ whose current value ${\hat{x}}_j$ is neither at its lower nor at its upper bound, otherwise.

Then, the algorithm terminates after a finite number of nodes and a finite number of calls to $\mathcal{C}$ with the following outcome: if (CCP) is feasible, Algorithm 2.0.1 returns a point $({\hat{x}}^*, {\hat{z}}^*)$ that is feasible for

$$\begin{aligned} \begin{array}{rrcl} \min &{} cx \\ \text {s.t.:} &{} x&{}\in &{} X \\ k=1,\ldots ,h &{} z_k = 0 \; \Rightarrow x &{}\in &{} C_x(\omega ^k) + \epsilon \\ &{} \sum _{k=1}^h p_k z_k &{}\le &{} \alpha \\ k=1,\ldots ,h &{} z_k &{}\in &{} \{0,1\}, \end{array} \end{aligned}$$

(3)

i.e., a version of (CCP) where each second-stage feasible set is relaxed by $\epsilon$, and that has objective value at least as good as an optimal solution to (CCP). If model (3) does not admit a feasible solution, Algorithm 2.0.1 returns “infeasible”. Finally, when (CCP) is infeasible while its relaxation (3) is feasible, Algorithm 2.0.1 can either return a feasible point for (3), or return “infeasible”.

Proof

Since $z \in \{0,1\}^h$ and branching decisions (i.e., binary variables fixed at some value) are never relaxed in children nodes, we can branch on a z variable at most $O(2^h)$ times. Therefore, we now discuss the convergence of the algorithm assuming a fixed vector ${\hat{z}}$. If we can show that when (CCP) is feasible the algorithm returns a point feasible for (3), the fact that this point has objective value at least as good as an optimal solution to (CCP) immediately follows because the returned point is a minimizer of the objective function of (CCP) over a relaxation of its feasible set.

The proof is in two steps: first, we prove finite convergence of the cutting plane procedure at a given node; second, we show that the number of nodes generated by spatial branching is finite for the given ${\hat{z}}$.

Finite cutting plane convergence. Let B be the set defined by the branching decisions accumulated at node N and let $K_B$ be the set of scenarios k such that ${\hat{z}}_k = 0$.

We claim that, if $\cap _{k \in K_B} \textrm{Conv}(C_{x}(\omega ^k) \cap B) + \epsilon \not = \emptyset$, after a finite number of calls to $\mathcal{C}$ with tolerance $\sqrt{\epsilon }$, we have ${\hat{x}} \in \textrm{Conv}(C_{x}(\omega ^k) \cap B) + \epsilon$ for every $k \in K_B$. Then, for any fixed $k \in K_B$, we generalize the proof of [17] to allow for the cut relaxation step described in Algorithm 2.2.3; this requires some modifications in the proof. Define $G(x):= \min _{x' \in \textrm{Conv}(C_{x}(\omega ^k)\cap B)} \Vert x - x'\Vert$, i.e., the distance between x and the set that we aim to converge to. Notice that with the cutting plane method, with the goal of separating a solution ${\hat{x}}$ from $\textrm{Conv}(C_{x}(\omega ^k)\cap B)$, we are solving a sequence of problems of the form $\min _{x \in X, x \in R} c x$, where R is a relaxation of $\textrm{Conv}(C_{x}(\omega ^k)\cap B)$, and we iteratively add inequalities to R. Let $t_i$ be the sequence of points generated by this algorithm, and assume that the i-th inequality is of the form

$$\begin{aligned} G(t_i) + \nabla G (t_i)^{\top } (x - t_i) \le 0, \end{aligned}$$

(4)

where $\nabla G (t_i)$ is a subgradient of G at $t_i$. By convexity of function G, this inequality is valid for the set $\{x: G(x) \le 0\}$. Let ${{\bar{x}}}^{\rho }:= \arg \min _{x' \in \textrm{Conv}(C_{x}(\omega ^k)\cap B)} \Vert t_i - x'\Vert$. Then, $G(t_i) = \Vert t_i - {{\bar{x}}}^{\rho }\Vert$, and a subgradient of G at $t_i$ is given by $\frac{t_i - {{\bar{x}}}^{\rho }}{\Vert t_i - {{\bar{x}}}^{\rho }\Vert }$. Writing $x - t_i$ as $x - {{\bar{x}}}^{\rho } + {{\bar{x}}}^{\rho } - t_i$ and carrying out algebraic manipulations, (4) can be rewritten as

$$\begin{aligned} (t_i - {{\bar{x}}}^{\rho })^{\top }(x - {{\bar{x}}}^{\rho }) \le 0, \end{aligned}$$

which is precisely the type of inequality generated by our exact cut generation algorithm, Algorithm 2.2.1. As discussed in the previous section, because the exact cut generation algorithm is not guaranteed to converge, we instead use inequalities

$$\begin{aligned} (t_i - {\bar{x}}^{{\bar{\jmath }}})^{\top }(x - {\bar{x}}^{{\bar{\jmath }}}) \le b, \end{aligned}$$

where $\Vert {\bar{x}}^{{\bar{\jmath }}} - {{\bar{x}}}^{\rho }\Vert \le \delta$. With algebraic manipulations, we rewrite this as

$$\begin{aligned} \Vert t_i - {\bar{x}}^{{\bar{\jmath }}}\Vert + \frac{(t_i - {\bar{x}}^{\bar{\jmath }})^{\top }}{\Vert t_i - {\bar{x}}^{{\bar{\jmath }}}\Vert }(x - t_i) \le b, \end{aligned}$$

showing that the inequalities generated by Algorithm 2.2.3 can be written as

$$\begin{aligned} G(t_i) + L(t_i)^{\top } (x-t_i) \le b + \Vert t_i - {{\bar{x}}}^{\rho }\Vert - \Vert t_i - {\bar{x}}^{{\bar{\jmath }}}\Vert , \end{aligned}$$

where $L(t_i):= \frac{(t_i - {\bar{x}}^{{\bar{\jmath }}})^{\top }}{\Vert t_i - {\bar{x}}^{{\bar{\jmath }}}\Vert }$ is a function of $t_i$. We now show that the sequence $\{t_i\}_{i=1,\ldots ,\infty }$ converges to a point $x^c$ such that $G(x^c) \le \epsilon$. Suppose not. At any iteration r, by construction the point $t_k$ must satisfy all previous inequalities

$$\begin{aligned} G(t_i) + L(t_i)^{\top } (t_r-t_i) \le b + \Vert t_i - {{\bar{x}}}^{\rho }\Vert - \Vert t_i - {\bar{x}}^{{\bar{\jmath }}}\Vert , \quad \text {for all}\quad 1 \le i < r. \end{aligned}$$

Then, there must exist some $\epsilon ' > 0$, independent of r, such that

$$\begin{aligned} \epsilon + \epsilon ' \le G(t_i)&\le b + \Vert t_i - {{\bar{x}}}^{\rho }\Vert - \Vert t_i - {\bar{x}}^{{\bar{\jmath }}}\Vert + L(t_i)^{\top } (t_i-t_r) \\&\le b + \delta + L(t_i)^{\top } (t_i-t_r) <\epsilon + \delta + L(t_i)^{\top } (t_i-t_r), \end{aligned}$$

where we used the triangle inequality and the fact that $b < \sqrt{\epsilon }^2$ if Algorithm 2.2.3 is executed using tolerance $\sqrt{\epsilon }$. Assume that in Algorithm 2.0.1 we reduce $\zeta$ (and hence, as a by-product, $\delta$) every fixed number of iterations of Algorithm 2.2.3 at the same node.¹ If we are generating many cuts at a node without converging to a point $x^c$ such that $G(x^c) \le \epsilon$, the iteration index r grows until we have $\delta < \epsilon '$. Therefore, the above equation shows

$$\begin{aligned} \epsilon ' - \delta < L(t_i)^{\top } (t_i-t_r) \le \Vert L(t_i)\Vert \Vert t_i-t_r\Vert = \Vert t_i - t_r\Vert , \end{aligned}$$

because $\Vert L(t_i)\Vert =1$ by definition of L. In the above equation, for large r we have that $\epsilon ' - \delta$ is strictly positive because $\delta$ gets progressively reduced. This implies that $\{t_i\}_{i=1,\ldots ,\infty }$ does not contain a Cauchy subsequence, which is impossible because X is compact. It follows that $\{t_i\}_{i=1,\ldots ,\infty }$ converges to a point $x^c$ such that $G(x^c) \le \epsilon$, i.e., $x^c \in \textrm{Conv}(C_{x}(\omega ^k) \cap B) + \epsilon$, as desired.

The above discussion shows that for fixed $\epsilon$, the number of calls to the cutting plane routine is finite before ${\hat{x}} \in \textrm{Conv}(C_{x}(\omega ^k) \cap B) + \epsilon$ for every $k: {\hat{z}}_k = 0$.

Finite number of spatial branchings. We now show that the number of nodes in the branch-and-bound tree before the algorithm returns “infeasible”, or a solution $({\hat{x}}^*, {\hat{z}}^*)$, is also finite. Note that whenever a candidate solution, say (${\hat{x}}, {\hat{z}}$), is found such that ${\hat{x}} \in \textrm{Conv}(C_{x}(\omega ^k) \cap B) + \epsilon$ for every selected scenario (i.e., such that ${\hat{z}}_k = 0$), $\epsilon$-feasibility for ${\hat{x}}$ is checked for all such scenarios. Hence, only $\epsilon$-feasible solutions are accepted as incumbents. We now need to prove that the branching process is finite. Our argument is as follows. First, we show that only a finite number of branching steps can take place between two consecutive calls to the cutting plane procedure that generate a valid cut. Then, we show that we cannot alternate between cutting and branching an infinite number of times. Since we already know that after a finite number of cutting planes, we have ${\hat{x}} \in \textrm{Conv}(C_{x}(\omega ^k) \cap B) + \epsilon$ for every $k: {\hat{z}}_k = 0$, this implies that the entire process terminates in a finite number of steps. We now prove these claims.

If ${\hat{x}}$ is $\epsilon$-feasible, it is accepted and because we are solving a relaxation, it is optimal for the corresponding node. Suppose now that ${\hat{x}}$ is $\epsilon$-infeasible; then Algorithm 2.0.1 branches on some component of ${\hat{x}}$. Let us analyze how many branching steps can take place before a valid inequality cutting off ${\hat{x}}$ is generated. Recall that we do not allow branching on components of ${\hat{x}}$ that are at one of their bounds, by assumption; thus, after at most $O(n_x)$ branches (along each branching path) the point ${\hat{x}}$ will be a corner point of the hyperrectangle defined by the branching decisions B. When this happens, there are only two possibilities:

• if ${\hat{x}} \in \textrm{Conv}(C_{x}(\omega ^k) \cap B) + \epsilon$ for all the selected scenarios, then ${\hat{x}}$ is an $\epsilon$-feasible solution for these scenarios. Indeed, otherwise ${\hat{x}}$ would be the combination of at least two points in $(C_{x}(\omega ^k) \cap B) + \epsilon$, which contradicts the fact that ${\hat{x}}$ is extreme for B;

• if ${\hat{x}} \not \in \textrm{Conv}(C_{x}(\omega ^k) \cap B) + \epsilon$ for some scenario k that has ${\hat{z}}_k = 0$, we are able to generate a separating inequality (by assumption).

This shows that there is only a finite number of branching steps that can occur between the generation of cutting planes. We still need to show that we cannot switch between cutting and branching an infinite number of times; for this, we show that if we perform spatial branching at some node $N_1$, when a cutting plane is generated at a child node $N_2$ for a scenario k with ${\hat{z}}_k = 0$, we made “sufficient progress” with respect to $N_1$. Suppose that after solving the relaxation of node $N_1$, with branching decisions $B_1$, and obtaining the candidate solution ${\hat{x}}$, $\mathcal{C}$ does not return a cut and we are forced to branch. Because $\mathcal{C}$ fails to return a cut, $\Vert {\hat{x}} - {\bar{x}}\Vert \le \epsilon$, where ${\bar{x}} = \sum _{i} \bar{\lambda }_i x^i$ for some $x^i \in C_{x}(\omega ^k) \cap B_1$, i.e., a nontrivial convex combination of feasible points. Since ${\hat{x}}$ is $\epsilon$-infeasible, $\Vert {\hat{x}} - x^i\Vert > \epsilon$ for all i. At node $N_2$, associated with branching decisions $B_2$, we are able to separate ${\hat{x}}$. Thus, there exists a point $x^i \notin C_{x}(\omega ^k) \cap B_2$, i.e., the point is no longer feasible for $N_2$, since otherwise ${\bar{x}} \in \textrm{Conv}(C_{x}(\omega ^k) \cap B_2)$, a contradiction as a cut through ${\bar{x}}$ was unable to separate ${\hat{x}}$ at node $N_1$. This shows that, after reconvexification, we have removed at least a ball of diameter $\epsilon$. Since all sets are compact, this shrinking process can only occur a finite number of times (upper bounded by the number of balls with diameter $\epsilon$ necessary to cover the set). Thus, along each branching path, our algorithm can switch between branching and cutting only a finite number of times. This, together with standard arguments regarding the correctness of branch-and-bound, concludes the proof for the case where (CCP) is feasible.

When (3) is infeasible, then (CCP) is also infeasible and Algorithm 2.0.1 returns “infeasible” by standard branch-and-bound arguments. Finally, if (CCP) is infeasible but (3) is feasible, the value returned by the algorithm is undetermined: the cutting planes that we generate are only guaranteed to distinguish $\epsilon$-approximate feasibility, therefore they may or may not be able to prove that the feasible region of (CCP) is empty (the algorithm still terminates in a finite number of nodes). $\square$

3 Algorithmic details and enhancements

In this section we complete the description of Algorithm 2.0.1 providing some additional details on the method, in particular concerning the branching strategy, cutting planes acceleration, and heuristics. The computational effectiveness of all these elements will be evaluated in Sect. 4.

3.1 Branching strategy

Our branching strategy is based on the observation that the problem reduces to a deterministic one (i.e., without the chance constraint) whenever all z variables attain an integer value. For this reason, we first perform a standard branching on these variables, if some of them are not integer. Otherwise, we execute the separation procedure for the current point ${\hat{x}}$ and resort to spatial branching on an $x_j$ variable only in Case 3, i.e., there is at least one active scenario for which ${\hat{x}}$ is infeasible though ${\hat{x}} \in \textrm{Proj}_x\textrm{Conv}(C_{x,y})$. In this case, let $\ell _j$ and $u_j$ denote the lower and upper bounds, respectively, for each variable $x_j$ in the current subproblem. For branching, we consider as candidates all those variables such that $\ell _j< {\hat{x}}_j < u_j$. For each candidate variable and for each violated active scenario, we execute the separation procedure for the two nodes that would be generated by branching on that variable. All violated inequalities associated with a candidate variable are stored in a pool, and possibly added to the corresponding node subproblems whenever that variable is used for branching. The procedure selects for branching the first variable (if any) that would allow separation of ${\hat{x}}$ in both the generated nodes. If such a variable does not exist, the procedure arbitrary selects a branching variable that allows separation of ${\hat{x}}$ in at least one of the two descendant nodes. If such a variable does not exist either, the procedure selects an arbitrary branching variable among the candidates.

3.2 Cut generation

Recall that cut generation is possibly executed only in case all the z variables are integer. In this case, we check whether a master solution ${\hat{x}}$ can be separated from the continuous relaxation of some active scenario (Case 1), or from its convex hull (Case 2). Notice that explicitly handling the former case (Sect. 2.1) is not necessary for the correctness of the decomposition algorithm. Nevertheless, we include the generation of the corresponding inequalities because their separation typically requires a negligible effort compared with separation from the convex hull.

When some scenario k produces a valid separating cut, there are two natural alternatives to add it to the master problem. The first option is to directly add inequality $\gamma x \le \beta _k + M_k z_k$ to the master problem, where the coefficient $M_k$ can be computed as $M_k = \sum _{j: \gamma _j > 0} \gamma _j u_j - \beta _k$, and $u_j$ is the upper bound associated with non-negative variable $x_j$. The second option, as suggested by [27], is to compute, for each scenario i, the minimum value $\beta _i$ that makes inequality $\gamma x \le \beta _i$ valid for that scenario. By sorting scenarios according to non-decreasing values of the associated $\beta _i$ coefficients, one can derive the $p = \lfloor \alpha h \rfloor$ inequalities

$$\begin{aligned} \gamma x + (\beta _i - \beta _{p+1}) z_i \le \beta _i \quad i = 1, \ldots , p \end{aligned}$$

(5)

to be added to the master problem. Instead of directly adding (5) to the master problem, one could consider mixing these inequalities so as to obtain an exponentially large family of stronger inequalities, each one possibly including more than one z variable (see [27] for details). However, when separating points with an integer-valued z vector, the inequality (5) with the smallest i such that $z_i=0$ already has the maximum violation among the class of mixing inequalities (as the corresponding right-hand side is the smallest value for which the inequality is valid). Additional inequalities might be obtained, at the cost of a larger computational effort, by using a separation procedure that does not return only one most violated inequality, or by separating solutions that are fractional in the z variables, and then applying the mixing procedure (as done, e.g., in [27]). Those inequalities could dominate inequalities (5). In this paper, we use a simpler approach in which separation is carried out only when z is integral, and all inequalities (5) are added to the master problem. It is possible that a more sophisticated and computationally-intensive approach would improve the performance of our branch-and-cut scheme.

It is worth mentioning that any cut that is generated at a node of the branching tree whose feasible region has not been affected by spatial branching is globally valid. Conversely, in case some branching on x variables has been imposed, the resulting cut is only locally valid. After an initial round of experiments, we observed that the effort required to compute (5) leads to a performance improvement only when these cuts are added as global cuts. If instead the cuts are only locally valid, directly adding an inequality with coefficient $M_k$ (first option) is empirically more effective.

As the cut generation process may be time consuming, we halt it as soon as a valid inequality separating ${\hat{x}}$ is found for some active scenario. Thus, the order in which the active scenarios are processed may affect the overall performance of Algorithm 2.0.1. We apply the same strategy as in [27], i.e., we give a priority to each scenario according to the number of violated inequalities it produced in the previous iterations (the higher, the better).

3.3 Storing feasible points

At each execution, Algorithm 2.0.1 produces a collection of feasible points, whose convex combination includes ${\hat{x}}$ or defines a point minimizing the distance from ${\hat{x}}$. The procedure can be sped up by storing, for each scenario, a list of feasible points computed at any iteration. In addition, we use these points to check the feasibility of ${\hat{x}}$ for the active scenarios: if, for some scenario, the associated list contains a feasible point whose distance from ${\hat{x}}$ is smaller than $\epsilon$, then ${\hat{x}}$ is feasible for that scenario; this approach avoids solving an optimization problem to check feasibility. In our implementation, we store up to 10,000 points per scenario.

4 Application and computational experiments

In this section, we evaluate the computational performance of our base algorithm and of the computational enhancements described in Sect. 3 on two problems derived from the literature. Specifically, we extend the linear problem addressed in [27], in which all variables are continuous, to define two new problems with binary and general integer variables, respectively. In both cases the objective function and the constraints are linear. Although our method applies to sets whose continuous relaxation is defined by general (not necessarily linear) convex constraints, we mainly focus on the linear case. Indeed, solving nonlinear problems with our algorithm requires the use of nonlinear convex MINLP solvers that are typically less stable than MILP solvers from a numerical point of view, making the computational analysis less reliable. Thus, most of our computational experiments focus on the linear case. However, we provide a short analysis of the performance for the nonlinear case in Sect. 4.7.

The scope of our computational experiments is twofold: first, we are interested in assessing the effectiveness of the proposed computational enhancements, and to understand what is the limit of the methodology we propose. Second, we want to compare the performance of the proposed methodology with an alternative solution approach consisting in the direct application of a general-purpose solver to the formulation (CCP-MINLP).

All algorithms are implemented in C++ and use the CPLEX 12.7.1 framework to implement our branch-and-cut algorithm. The experiments are performed on a computer equipped with an AMD 3960X processor clocked at 3.8 GHz, 128 GB RAM, running Linux. The master problem and each scenario subproblem are solved in single-threaded mode, imposing, for the master problem, a tree-size limit to 16 GB and disabling its heuristic procedures; heuristics are disabled because in a preliminary computational evaluation they were found ineffective, leading to an overall slowdown of the proof of optimality. All the remaining CPLEX parameters, including tolerances, are left to their default values.

4.1 Application: resource planning

In [27], the author considers a continuous resource planning problem inspired by a call center staffing application. The input consists of a set of resources used to meet demands for a set of customer types, and the objective is to determine the quantity of each resource to activate to satisfy the demands. We consider two variants of this application that have binary and integer variables. Both problems consider a set $I = \{1, \ldots , n\}$ of resources and a set $J:= \{1, \ldots , m\}$ of customer types. Given the unit cost $c_i$ of each resource i, the demand $\lambda _{j}$ of each customer type j, and the service rate $\mu _{ij}$ of resource i for customer type j, the first problem is to decide the activation level of each resource and the assignment of customers to resources, in such a way that the demand of the customers is satisfied at minimum cost. In the first problem (denoted as INT), we introduce variables $x_i,~i \in I,$ and $y_{ij},~i \in I,~j \in J$ to define the activation level of resource i and the amount of resource i allocated to customer type j, respectively. The y variables are imposed to be integer, i.e., resources must be assigned to customers in integer multiples, producing the following formulation:

$$\begin{aligned} \begin{array}{rrclr} \min &{} \sum \limits _{i \in I} c_i x_i \\ \text {s.t.:} &{} \sum \limits _{i \in I} \mu _{ij} y_{ij} &{} \ge &{} \lambda _{j} &{} j = 1,\ldots , m \\ &{} \sum \limits _{j \in J} y_{ij} &{} \le &{} x_i &{} i = 1,\ldots ,n \\ &{} {x_i} &{} {\ge } &{} {0} &{} {i=1,\ldots ,n}\\ &{} y_{ij} &{} \in &{} {\mathbb {N}}&{} i = 1 \ldots n, \quad j = 1,\ldots , m \end{array} \end{aligned}$$

(INT)

In the second problem (denoted as BIN), the y variables are imposed to be binary, so that each customer type is assigned exactly one resource. The continuous variables $x_i,~i \in I$ denote the activation level of each resource i as in the first problem. For each customer type j and resource i, the amount of resource used by the customer type if the assignment is performed is given by $\Big \lceil \frac{\lambda _{j}}{\mu _{ij}} \Big \rceil$. The formulation reads as

$$\begin{aligned} \begin{array}{rrclr} \min &{} \sum \limits _{i \in I} c_i x_i \\ \text {s.t.:} &{} \sum \limits _{i \in I} y_{ij} &{} = &{} 1 &{} j=1,\ldots ,m \\ &{} \sum \limits _{j \in J : \mu _{ij} > 0} \Big \lceil \frac{\lambda _{j}}{\mu _{ij}} \Big \rceil y_{ij} &{} \le &{} x_i &{} i=1,\ldots ,n\\ &{} {x_i} &{} {\ge } &{} {0} &{} {i=1,\ldots ,n}\\ &{} y_{ij} &{} \in &{} \{0, 1\} &{} i=1 \ldots n, \quad j=1,\ldots ,m \end{array} \end{aligned}$$

(BIN)

In the stochastic version of the two problems, we assume the demand of each customer type to be a random parameter with discrete probability distribution over a set $K = \{1, \ldots , h\}$ of scenarios. Hence, we denote by $\lambda _{jk}$ the demand of customer type j in case scenario $k \in K$ materializes. The problems are approached in two stages; in the first one, the activation of the resources is decided, before the actual demands are revealed, whereas in the second stage customer types are assigned to activated resources. Both problems have a chance-constraint as in (CCP-MINLP), and feasibility of each scenario $k \in K$ is achieved if it is possible to assign all demands (in problem INT) or all customer types (in problem BIN) to the resources activated in the first stage.

4.2 Test instances

We define our benchmark for problems INT and BIN starting from the original instances introduced in [27] together with a large set of distinct scenarios. Given an original instance and a number h of scenarios, we use the cost coefficients $c_i$ from the original data, whereas demands are derived by considering the first h scenarios, dividing each entry by 10 and rounding down the resulting values. Accordingly, for the service rates, we replace each non-zero entry in the base instance with a random value between 1 and 10.

We evaluate each of the five original instances with $n=20$ resources and $m=30$ customer types with different values for the number h of scenarios ($h \in \{10, 20, 50, 100, 200 \}$ for INT and $h \in \{10, 20, 50, 100 \}$ for BIN) and for the risk level ($\alpha \in \{0.05, 0.10, 0.20\}$). Observe that there are no instances with $h=10$ and $\alpha =0.05$ as this would correspond to the deterministic case in which no scenario can be violated. Thus, our benchmark includes 70 instances for problem INT and 55 instances for problem BIN.²

4.3 Problem-specific primal heuristics

We design a problem-specific primal heuristic, referred to as Fast, to compute an initial feasible solution. The heuristic works as follows. Initially, it solves each scenario, one at a time, and sorts the scenarios according to non-increasing values of their optimal solution. Then, it processes the scenarios in the same order, and solves each of them while, iteratively, the lower bound of each first stage variable $x_j$ is set to the optimal value attained by that variable in the solution of the previous scenario. Since in the application we consider, the x variables represent resources that do not have an upper bound, the Fast heuristic defines a feasible solution.

4.4 Algorithm tuning

In the first set of experiments, we investigate the effectiveness of the components embedded in our branch-and-cut algorithm that we will denote as DEC. The algorithm includes all the enhancements described in Sect. 3, and the problem-specific heuristic Fast, applied at the root node.

In the following, we deactivate each component of algorithm DEC, one at a time, in order to assess its contribution to the algorithm performance. In particular, we consider the following variants:

• NoPoint corresponds to the version in which feasible points are not stored for later use;

• BigM is obtained by disabling the use of inequalities (5) and directly adding a single inequality $\gamma x \le \beta _k + M_k z_k$ for each scenario k;

• RandSB replaces the spatial branching selection strategy with a random selection of the variable used for spatial branching;

• Basic is the version of the algorithm in which all the features above are deactivated at the same time.

We execute each variant of the algorithm on the instances of problems INT and BIN with 50 scenarios, with a time limit of 5 h for each run. Table 1 reports, for each problem and set of 5 instances with the same value of $\alpha$, the number of proven optimal solutions and the average computing time (over instances solved to optimality) of each algorithm tested.

Table 1 Comparison of the performance of different variants of the algorithm on instances with 50 scenarios

The results show that algorithm DEC is able to solve all instances for problem INT in less than 20 mins, on average. For problem BIN, it solves to optimality four instances for each value of $\alpha$, outperforming all the remaining algorithms when solving this problem. Algorithm NoPoint fails in solving one instance of problem INT and, for problem BIN, its performance gets worse when $\alpha$ increases: for $\alpha =0.20$ it only solves one instance in more than 4 h. Algorithm BigM solves all the instances of problem INT and it is faster than DEC for $\alpha =0.05$, while it requires a larger computing time for $\alpha =0.10$ and $\alpha =0.20$. Furthermore, BigM solves to optimality only 9 instances of problem BIN. The role of our refined strategy in spatial branching is clear comparing algorithms DEC and RandSB. Indeed, the latter solves all instances of problem INT, though being slower than DEC, and is able to solve only 7 instances (out of 15) of problem BIN. The last considered variant, obtained by disabling all features of DEC, displays very weak performance: algorithm Basic is up to one order of magnitude slower than DEC for problem INT, for which it fails to solve 2 instances. For problem BIN this method solves to optimality only 5 instances out of 15. Summing up, the results reported in Table 1 show that each component of algorithm DEC gives a valuable contribution to the computational performance of the method. In addition, the table shows that a naive implementation of Algorithm 2.0.1, similar to our Basic variant, is far from being effective on these problems.

4.5 Performance of spatial branching

As already mentioned, a careful spatial branching strategy contributes significantly to the effectiveness of our algorithm DEC. Here, we present some additional results aimed at evaluating the relevance of spatial branching in more detail, by comparing with a version of the algorithm in which spatial branching is not implemented at all. In this scheme, denoted as NoSB in the following, a node of the branching tree is fathomed if the solution of the continuous relaxation of the node is infeasible after the separation on the continuous relaxation and on the convex hull. In this case, the incumbent is updated, i.e., this scheme returns the value of the lower bound, say L, obtained optimizing over the intersection of the convex hulls of the selected scenarios. Comparing this lower bound with the optimal solution value provides a measure of the gap that has to be closed by spatial branching.

Table 2 reports the results for algorithms NoSB and DEC on the instances of our benchmark. Each row of the table addresses the 5 instances of the same problem defined by the same values for h and $\alpha$. For both algorithms, columns “Cont” and “Conv” report the number of cuts generated on the continuous relaxation and on the convex hull, respectively. In addition, for NoSB we report the corresponding gap percentage, computed as gap = $100 \times (z^* - L)/L$, where $z^*$ is the optimal (or the best known) solution value. For algorithm DEC, we also report the number of times that spatial branching is performed (“# Bra”) and the total number of branch-and-bound nodes explored (“# Nodes”). All entries report averages (rounded to the closest integer) computed over all the instances solved to optimality by algorithm DEC.

Table 2 Computational details of algorithm DEC

The results confirm that problem INT is easier to solve than BIN. Indeed, even without spatial branching, a few thousand cuts in total are sufficient to obtain very small gaps. Algorithm DEC rarely has to resort to spatial branching: it takes place, on average, only 63 times on the most difficult instances ($h=200$ and $\alpha =0.20$). For this group of instances, the average number of generated branch-and-bound nodes is below one thousand.

Concerning problem BIN, without spatial branching we still attain fairly small residual percentage gaps for instances with $h \le 50$, the largest average gap being 0.61. The residual percentage gap slightly increases when $h = 100$, and it is equal to 2.21 in the worst case. Observe that the number of cuts that are generated on the continuous relaxation is relatively small, and that no cuts are generated on the convex hull. Indeed, the continuous relaxation of problem BIN always admits an optimal solution that is integral, corresponding to the assignment of each customer type j to the resource i for which $c_i \Big \lceil \frac{\lambda _{j}}{\mu _{ij}} \Big \rceil$ is a minimum. Hence, extreme points of the continuous relaxation are integer, and the continuous relaxation coincides with the convex hull of the integer solutions; this is the case at the root node, before any spatial branching takes place. When active, spatial branching changes the bounds of the x variables; as a consequence, the continuous relaxation of the problem does not necessarily admit optimal integer solutions after branching. In this setting, the number of spatial branchings and the generation of cuts increase considerably (up to one order of magnitude) when considering the largest instances.

4.6 Computational comparison with a CPLEX-heavy variant

In this section, we study the possibility to further enhance the performance of algorithm DEC. To this end, we implement a hybrid strategy, denoted DEC+, that combines DEC with the use of a MIP solver for computing the initial feasible solution at the root node and for solving deterministic subproblems at the subsequent nodes. We call Complete the heuristic procedure that algorithm DEC+ executes for computing the initial solution. This procedure: (i) orders the scenarios with the same rule used by the heuristic Fast (see Sect. 4.3); (ii) defines a deterministic problem by selecting the scenarios (i.e., fixing the associated z variables) in the given order, until the chance constraint is satisfied; and (iii) solves this deterministic problem using a MIP solver as a black box. Notice that procedure Complete can be applied to any problem instance, but it can be quite slow in practice, as the deterministic problem must enforce feasibility for all the selected scenarios and may thus include a very large number of variables and constraints. In addition, algorithm DEC+ fully solves (defining a sub-MIP) branch-and-bound nodes in which all the z variables are fixed because of branching. Indeed, each such node induces a deterministic problem, and we can immediately close the node if the deterministic problem is solved, after possibly updating the incumbent.

We compare the performance of DEC and DEC+ with the direct application of a MIP solver (the same solver that is used by our algorithm, i.e., IBM-ILOG CPLEX 12.7.1) on formulation (CCP-MINLP). The solver, denoted as CPLEX in the reminder of this section, is executed in single-thread mode with all the remaining parameters to their default values.

Table 3 reports the outcome of our experiments on all instances introduced in Sect. 4.2 for problems INT and BIN. As in previous experiments, we use a time limit of 5 h per run. Each row of the table refers to 5 instances of the same problem, having the same number h of scenarios and the same risk parameter $\alpha$. For each solution method, the table reports the number of optimal solutions, the average computing time (with respect to instances solved to optimality only) and the average percentage optimality gap, computed as gap = $100 \times (U - L)/L$. In 5 of the 15 instances of problem BIN with $h=100$, DEC+ reaches the time limit during the execution of the heuristic procedure Complete. Because the method is unable to compute a lower bound in these cases, we calculated the average optimality gap with respect to the remaining instances only (and put the number of instances used to calculate the gap in brackets).

Table 3 Comparison of the performance of different solution approaches

Both DEC and DEC+ are able to solve all the instances of problem INT. Solving the deterministic subproblems proved to be effective, as DEC+ is always, on average, faster that DEC. Not surprisingly, CPLEX is the fastest method for small instances ($h \in \{10, 20\}$) whose associated (CCP-MINLP) MIP formulation is manageable. Increasing the number h of scenarios produces larger number of variables in the model that make the direct use of the solver impractical. Indeed, CPLEX is not able to solve to optimality all the instances with $h=50, 100$, and no instance is solved for $h=200$ and $\alpha =0.20$.

Problem BIN is more challenging for all solution methods. Comparing DEC and DEC+, the latter seems to have a better performance: it solves to optimality all the instances with $h \le 50$, whereas DEC is unable to solve 3 of these instances for $h=50$. As for the computing time when $h \le 50$, DEC+ is in general much faster than DEC, but there is a single instance with $h=10$ and $\alpha =0.10$, for which it takes more than 6000 s. In addition, DEC+ also solves 1 instance more than DEC with $h=100$. However, for this latter group of instances, algorithm DEC is always able to compute a feasible solution, with corresponding percentage optimality gaps ranging from 1.06 to 1.93. Instead, there are 5 instances for which algorithm DEC+ hits the time limit during the search for an initial solution, and no feasible solution is available. Concerning CPLEX, it is very fast for $h = 10$, as it requires, on average, less than 20 s to solve all instances. Moreover, it solves all but one instance with $h \in \{20, 50\}$, though being one order of magnitude slower than DEC+. Results get worse for $h=100$, as no instance is solved in this case: the corresponding percentage optimality gap ranges from 3.63 to 8.92, confirming that the direct application of the solver to formulation CCP-MINLP leads to gaps that can be unsatisfactory when the number of scenarios is large.

One may wonder if the solution of nodes with fixed z variables is the main workhorse of the DEC+ algorithm, or in other words, if the cutting planes valid for the convex hull of the scenario subproblems are still beneficial in the setting of DEC+. We experimentally verified that, on problem INT, where these cuts are used starting from the root node, disabling the cut generation procedure on the convex hull leads to a significant worsening of the algorithm’s performance. Indeed, in this setting, the resulting algorithm is able to solve, within the time limit, only 5 instances with $h = 50$ and no instance with $h = 100$, indicating that the cuts are very impactful even in the setting of DEC+.

We also executed DEC and CPLEX with a looser value of the optimality tolerance (equal to 1%) on the subset of instances considered in Table 1. For both INT and BIN, CPLEX solves one additional instance in class $h=50$ and $\alpha =0.20$. Regarding the other instances solved to optimality, the computing times are similar. Conversely, DEC solves one additional instance only (problem BIN with $h=50$ and $\alpha =0.20$) though its computing time for solved instances is halved on average. This shows that the value of the optimality tolerance is not a critical issue in determining the performance of both methods.

4.7 Experiments with nonlinear constraints

In this section, we consider a variant of problem INT to analyze the performance of our solution method in the nonlinear setting. Specifically, we model a congested situation in which, for each resource i, the activation level is lower bounded by a quadratic function of the overall demand (as, for example, in [9]), i.e.,

$$\begin{aligned} \left( \sum _{j \in J} y_{ij}\right) ^2 \le x_i \quad i = 1 \ldots n. \end{aligned}$$

The resulting mixed-integer quadratically-constrained problem can be handled by CPLEX and therefore allows us a direct comparison with our implementation. For this nonlinear setting, we reduced the scenario size to $n=8$ and $m=12$, and we used a tolerance $\epsilon = 10^{-4}$ for all the tested algorithms. Table 4 has the same structure as Table 3. The results show that our branch-and-cut algorithm DEC performs remarkably well as the problem size increases. For small instances ($h \le 20$), all methods solve all instances and CPLEX is on average the fastest solution method. For $h \ge 50$, DEC is on average the fastest and the best performing algorithm: it solves all instances with $h=200$ except one for which the execution prematurely stops due to a numerical error occurring while solving problem (NEWPOINT). In addition, DEC is the only method solving all the instances with $h = 100$. Finally, the “tailored” version of our algorithm DEC+ has worse performance than DEC. Letting CPLEX do more work on some subproblems does not seem to pay off in the nonlinear setting.

Table 4 Comparison of the performance of different solution approaches on a nonlinear problem

5 Conclusions and future work

In this work, we considered chance constrained mathematical problems in which the second-stage variables are integer and uncertainty is modeled via a discrete set of scenarios. The feasible regions of the second-stage problems are not convex sets, as they are defined by convex constraints and by the integrality of the second-stage variables. To the best of our knowledge, this is the first attempt to solve this class of problems with general integer second-stage variables, which are known to be difficult in practice and tend to complicate the solution algorithm. We introduced a decomposition approach based on a branch-and-cut framework. In this framework, we possibly generate cutting planes based on outer approximation of the convex hull of the integer points, and resort to spatial branching when the current infeasible solution cannot be separated using a linear cut. We analyzed the theoretical convergence of the algorithm both in case of infinite precision and when some numerical tolerances are used. Finally, we performed an extensive computational analysis on two problems derived from a test-case addressed in the recent literature, showing that our algorithm is able to solve medium-sized instances in a reasonable amount of time, and much more effectively than a state-of-the-art solver applied to the deterministic equivalent of the chance-constrained problem. To achieve this performance we used many computational enhancements, all of which were empirically shown to be beneficial in improving the performance of the algorithm.