A preference-based multi-objective evolutionary algorithm R-NSGA-II with stochastic local search

Abstract

Incorporation of a decision maker’s preferences into multi-objective evolutionary algorithms has become a relevant trend during the last decade, and several preference-based evolutionary algorithms have been proposed in the literature. Our research is focused on improvement of a well-known preference-based evolutionary algorithm R-NSGA-II by incorporating a local search strategy based on a single agent stochastic approach. The proposed memetic algorithm has been experimentally evaluated by solving a set of well-known multi-objective optimization benchmark problems. It has been experimentally shown that incorporation of the local search strategy has a positive impact to the quality of the algorithm in the sense of the precision and distribution evenness of approximation.

1 Introduction

Many real-world problems are multi-objective. Due to conflicting objectives usually there is no solution which would be the best by all objectives. However, a set of solutions optimal in a multi-objective sense exists. Such a set of solutions is called the Pareto set, and the corresponding set of objective vectors—the Pareto front. Determination of the Pareto front is the main goal of multi-objective optimization, however for some problems it is impossible to identify the exact Pareto front due to reasons such as continuity of the front, nonexistence of analytical expression or complexity of the problem being solved. On the other hand in practical situations usually it is not necessary to find the whole Pareto front, but rather its approximation. Moreover, the decision maker (DM) commonly is interested in a certain part of the Pareto front and prefers to analyse that part deeper. Therefore, algorithms for approximation of the Pareto front are useful to tackle real-world multi-objective optimization problems.

A well-known class of such algorithms are Evolutionary Multi-objective Optimization (EMO) algorithms. The main target of a classic EMO is to find a set of well-distributed points on objective space that precisely approximate the entire Pareto front (Deb 2001; Lančinskas et al. 2013; Talbi 2009). The obtained set is presented to the DM for consideration and selection of the most preferable solutions. Some well-known EMO algorithms should be mentioned regarding to such a kind of approaches: PAES (Knowles and Corne 2000), SPEA2 (Zitzler et al. 2001), NSGA-II (Deb et al. 2002), IBEAZ (Zitzler and Künzli 2004), etc. The EMO algorithms have gained their popularity because they do not require deep knowledge about the problem to solve and are easy to implement. However, most of the EMO approaches are not suitable to problems with a big number of objectives (Knowles and Corne 2000). Recently several EMO algorithms have been developed that are suitable for solving many objective problems: MOEA/D (Ray et al. 2013; Zhang and Li 2007) and NSGA-III (Jain and Deb 2014). However, the problem of large computational cost arises here as big amount of solutions must be found to represent the entire Pareto front. Moreover, a reasonable number of solutions should be provided for the DM so that he/she could make an adequate decision avoiding complex analysis of large amount of information. Therefore, optimization methods based on DM’s preferences must be used in which only the region of interest of the Pareto front is approximated.

During the last decade incorporation of DM’s preference information into evolutionary approaches has become a new trend. So-called preference-based EMO algorithms are being actively developed that focus on only some parts of the Pareto front. Such algorithms aim to find an approximation of the Pareto front which elements are scattered regarding to the preference information provided by the DM. The well-known EMO algorithms of this kind have been proposed: the reference point-based (R-NSGA-II) (Deb et al. 2006; Siegmund et al. 2012), the light beam approach based EMO (Deb and Kumar 2007), the weighted hypervolume based EMO (Auger et al. 2009), achievement scalarizing function based EMOs—PIBEA (Thiele et al. 2009) and interactive EMO-based technique (López-Jaimes and Coello Coello 2014), interactive MOEA/D (Gong et al. 2011), Preference-based Interactive Evolutionary (PIE) algorithm (Sindhya et al. 2011), the Weighting Achievement Scalarizing Function based EMO (WASF-GA) (Ruiz et al. 2015). The comprehensive survey is given in Purshouse et al. (2014).

The preference-based EMO algorithms have been applied for solving different real-world optimization problems: R-NSGA-II was used for solving industrial-scale simulation-based optimization problem (Siegmund et al. 2012) and for deregulated power system in transmission expansion planning problem (Mohammadpour et al. 2013); PIBEA and PIE were applied for locating a pollution monitoring station in a two-dimensional decision space (Sindhya et al. 2011; Thiele et al. 2009); interactive MOEA/D was applied for airfoil design optimization problem (Gong et al. 2011), etc.

As preference-based algorithms are applied to different practical multi-objective problems, improvement of efficiency of such algorithms is undisputed. The one of the most common ways to enhance the EMO algorithm is to incorporate a local search procedure. Such hybrid algorithms, also called memetic, have gained a big attention as they converge faster and more precisely approximate the Pareto front (Zavala et al. 2014). Different strategies of local search have been applied for improvement of EMO algorithms: the fitness function based on weighted sum of multiple objectives was utilized when selecting solution for generating a new solution by crossover and mutation operations (Ishibuchi and Murata 1998); a similar idea was investigated in Goel and Deb (2002); local search procedure based on neighbourhood search was incorporated into the cellular multi-objective genetic algorithm (Murata et al. 2002); a memetic algorithm based on the cross dominant adaptation was proposed in Caponio and Neri (2009); a hybrid with achievement scalarizing function that can be solved with any appropriate local search method was presented in Sindhya et al. (2009); a gradient based sequential quadratic programming method was used in a local search for optimization of a scalarized objective function (Sindhya et al. 2013); Multi-Objective Single Agent Stochastic Search (MOSASS) (Lančinskas et al. 2011) was incorporated into NSGA-II (Lančinskas et al. 2013). More works related to memetic multi-objective optimization algorithms can be found in EMO survey (Zhou et al. 2011). Hence, hybridization of classic EMO algorithms with local search procedures was sufficiently deeply investigated, however to our knowledge, the preference-based EMO has not received great attention yet.

A memetic algorithm that integrates the Directed Search method into the most widely used preference-based EMO algorithm—R-NSGA-II has been proposed in Mejía et al. (2014). However, the algorithm involves Jacobian calculation that leads to specific requirements for a problem being solved or/and to additional computations for numerical estimation of gradients. In this paper, we propose to enhance R-NSGA-II by incorporating the heuristic local search technique MOSASS (Lančinskas et al. 2013, 2011) which does not require any gradient information. The proposed R-NSGA-II with MOSASS improves the quality of approximation of the Pareto front in a limited number of function evaluations, taking into account DM’s preference information.

The rest of this paper is organized as follows. In Sect. 2 the description of the multi-objective problem is provided, as well as the preference-based EMO algorithm R-NSGA-II and the local search strategy MOSASS are described. Section 3 is devoted to proposition of a memetic algorithm derived by incorporating MOSASS into R-NSGA-II, and to adaptation of the performance metrics for evaluating the preference-based algorithms. The experimental investigation of the proposed algorithm and the obtained results are discussed in Sect. 4. Finally, conclusions are drawn in Sect. 5.

2 Background concepts

2.1 Multi-objective optimization problem

Here a formulation of a multi-objective optimization problem is introduced. Let us have $k\ge 2$ conflicting objectives, described by the functions $f_1(\mathbf x ), f_2(\mathbf x ), \ldots , f_k(\mathbf x )$, where $\mathbf x =(x_1, x_2, \ldots , x_n)$ is a vector of variables (decision vector), n is the number of variables. A multi-objective minimization problem is formulated as follows (Miettinen 1999):

$$\begin{aligned}&\text {minimize }&\mathbf f (\mathbf x )=[f_1(\mathbf x ), f_2(\mathbf x ), \ldots , f_k(\mathbf x )], \end{aligned}$$

(1)

$$\begin{aligned}&\text { subject to }&\mathbf x \in \mathbf S . \end{aligned}$$

(2)

where $\mathbf z = \mathbf f (\mathbf x ) \in \mathbb {R}^k$ is objective vector, and $\mathbf S \subset \mathbb {R}^n$ is an n-dimensional Euclidean space, called feasible region, which defines all feasible decision vectors.

In terms of multi-objective optimization, two decision vectors $\mathbf x$ and $\mathbf x '$ can be related with each other by dominance relation: the decision vector $\mathbf x$ can dominate the decision vector $\mathbf x '$ and vice versa, as well as none of the decision vectors dominate each other.

It is said that the decision vector $\mathbf x$ dominates the decision vector $\mathbf x '$ (denoted by $\mathbf x \succ \mathbf x '$) if

• (1) the decision vector $\mathbf x$ is not worse than $\mathbf x '$ by all objectives, and

• (2) the decision vector $\mathbf x$ is strictly better than $\mathbf x '$ by at least one objective.

If the conditions above are satisfied, then the decision vector $\mathbf x '$ is called a dominator of $\mathbf x '$. If none of the decision vectors can be identified as a dominator of the other, then both decision vectors are assumed to be indifferent (denoted by $\mathbf x \sim \mathbf x '$). Analogically, it is said that the objective vector $\mathbf z = (z_1, z_2, \ldots , z_k)$ dominates $\mathbf z ' = (z'_1, z'_2, \ldots , z'_k)$, if each component of $\mathbf z$ is not worse than the corresponding component of $\mathbf z '$ and there exists at least one component of $\mathbf z$ which is strictly better than the corresponding component of $\mathbf z '$.

Decision vectors which have no dominators in the whole search space $\mathbf S$ are called non-dominated or Pareto-optimal (optimal in Pareto sense). The set of all non-dominated decision vectors is called the Pareto set, and the corresponding set of non-dominated objective vectors is called the Pareto front.

Furthermore, two more objective vectors that describe the ranges of the Pareto front are usually used—the ideal objective vector and the nadir objective vector. Lower bounds of the Pareto front constitute the ideal objective vector, its components are obtained by minimizing each of the objective functions individually in the feasible region. The upper bounds of the Pareto front are the components of the nadir objective vector.

2.2 Preference-based EMO algorithms

As it was mentioned in Sect. 1 the classic EMO algorithms aim to approximate the whole Pareto front and to distribute the obtained non-dominated objective vectors evenly. On contrary, the objective vectors obtained by preference-based algorithms are concentrated on a particular region(s) of the Pareto front approximated according to the preference information expressed by the DM. This information can be expressed in different ways: using reference direction, reference points, aspiration levels, weights or other (Miettinen 1999). Wide range of the preference-based EMO algorithms use reference points that consist of desirable aspiration levels for each objective function. Such a way of expressing preference is easy to implement and incorporate into EMO approach. Moreover, other types of information (as aspiration levels or reference directions) can be easily transformed into reference points. The differences between results obtained by the classic EMO and preference-based EMO algorithms are demonstrated using the popular test problem ZDT1 in Fig. 1. We see that the points of the Pareto front approximation are distributed evenly enough on the whole Pareto front in Fig. 1a, while the points are concentrated on one region in Fig. 1b.

Fig. 1

Non-dominated objective vectors of ZDT1 problem, obtained by: a classic EMO algorithm, b preference-based EMO algorithm

Among the preference-based EMO algorithms R-NSGA-II (Deb et al. 2006; Siegmund et al. 2012) is the most commonly used one. It is an extension of the well-known classic EMO approach NSGA-II (Deb et al. 2002), where the crowding distance is changed to the Euclidean distance from the reference point which expresses the DM’s preference. The general idea of R-NSGA-II is that the parents with smaller Euclidean distances to the reference point are preferred. R-NSGA-II can be described as follows:

• 1. A random initial population consisting of decision vectors is randomly generated in the feasible region.

• 2. A new offspring population is created by applying genetic operators (crossover and mutation) to the individuals of the parent population. The crossover is related to the recombination of two selected parent individuals by taking some values of elements from the first parent, while the remaining values are taken from the second one. The selected individuals are recombined with a predefined probability; if recombination is not performed, then better of the parents is used to represent an offspring. The derived offspring is mutated by adding a small random change to the values of some variables. Each variable is mutated with a predefined (usually small) probability; all variables usually have equal probabilities to be mutated.

• 3. The parent and offspring populations are combined into one joint population.

• 4. The new population is sorted into different non-domination levels (so-called fronts) by a non-dominated sorting procedure.

• 5. Each front of the joint population is clustered, and representatives of clusters are identified.

• 6. The obtained joint population is reduced to the size of the parent population by leaving the representatives of the clusters starting from the best non-domination level. If not all representatives can be selected to the next generation, then ones with the smaller Euclidean distance to the reference point are preserved.

• 7. If the termination condition is not satisfied, then the reduced population is used as a parent population in the next generation (go to Step 2).

It should be noted that the clustering performed in Step 5 is required in order to control the diversity of the obtained solutions. The clustering parameter value $\delta (0 < \delta \leqslant 1$) (Deb et al. 2006) defines the size of clusters and in such a way controls the extent of the population.

2.3 MOSASS

The local search strategy Multi-Objective Single Agent Stochastic Search (MOSASS) (Lančinskas et al. 2011, 2013) has been developed by modifying a random search strategy for single-objective optimization, called Single Agent Stochastic Search (SASS) (Solis and Wets 1981), in order to make it suitable for multi-objective optimization.

The MOSASS iterative algorithm begins with an initial decision vector $\mathbf x = (x_1, x_2, \ldots , x_n)$, which is assumed to be locally optimized, and an empty archive A for storing non-dominated decision vectors which are expected to be found during runtime of the algorithm. A new decision vector $\mathbf x '$ is generated by changing values of some variables of $\mathbf x$. Each variable $x_i (i=1,2,\ldots ,n$) is modified with probability 1 / n by adding a random value $\xi _i$ generated following Gaussian distribution. In general, the new decision vector can be expressed mathematically as

$$\begin{aligned} \mathbf x ' \leftarrow \mathbf x + \mathbf {\xi }, \end{aligned}$$

(3)

where $\mathbf {\xi } = (\xi _1, \xi _2, \ldots , \xi _n)$ and

$$\begin{aligned} \xi _i \leftarrow {\left\{ \begin{array}{ll} \mathcal {N}(b_i, \sigma ), &{} \text {if} \quad r_i \le 1/n, \\ 0, &{} \text {if} \quad r_i > 1/n. \end{array}\right. } \end{aligned}$$

(4)

Here $\mathcal {N}(b_i, \sigma )$ is a random number generated following Gaussian distribution with the bias $b_i$ and the standard deviation $\sigma$, $r_i$ is a random number uniformly generated within interval [0, 1]. Such a probabilistic approach for generation of a new decision vector leads to the change of a single variable in average; see Lančinskas et al. (2013) for details.

The generated decision vector $\mathbf x '$ is compared with its precursor $\mathbf x$ in the sense of dominance relation. If the new decision vector dominates its precursor, then $\mathbf x$ is changed to the newly generated one. If $\mathbf x '$ is indifferent with $\mathbf x$, then $\mathbf x '$ is compared with all non-dominated decision vectors found so far and stored in the archive A. If $\mathbf x '$ is non-dominated in A, then the archive is supplemented by $\mathbf x '$. If $\mathbf x '$ is used either to change $\mathbf x$ or to supplement the archive, all decision vectors in A dominated by $\mathbf x '$ are removed in order to keep the archive of non-dominated decision vectors only.

If the newly generated decision vector is either dominated by its precursor or a decision vector from A, then $\mathbf x '$ is rejected and an opposite decision vector

$$\begin{aligned} \mathbf x '' \leftarrow \mathbf x - \mathbf {\xi } \end{aligned}$$

(5)

is investigated following the same strategy.

If the decision vector $\mathbf x$ is updated or the archive A is supplemented by $\mathbf x '$, then the iteration is assumed to be successful and the biases of Gaussian perturbation are updated:

$$\begin{aligned} b_i \leftarrow 0.2 b_i + 0.4 \xi _i, \quad i=1,2,\ldots ,n. \end{aligned}$$

(6)

If the decision vector $\mathbf x$ is updated or the archive A is supplemented by $\mathbf x ''$, then iteration is assumed to be successful and the biases of Gaussian perturbation are updated by

$$\begin{aligned} b_i \leftarrow b_i - 0.4 \xi _i, \quad i=1,2,\ldots ,n. \end{aligned}$$

(7)

If both $\mathbf x '$ and $\mathbf x ''$ are rejected, then the iteration is assumed to be failed and the biases of Gaussian perturbation are updated by

$$\begin{aligned} b_i \leftarrow 0.5 b_i, \quad i=1,2,\ldots ,n. \end{aligned}$$

(8)

The standard deviation $\sigma$ of the Gaussian perturbation is dynamically adjusted with respect to the repetitive successful and failed iterations. If the number scnt of repetitive successful iterations reaches the predefined number Scnt, then the standard deviation is increased twice. Analogically, if the number fcnt of repetitive failed iterations reaches the predefined number Fcnt, then the standard deviation is reduced by a half. If the standard deviation becomes smaller than the predefined value $\sigma _{min}$, then $\sigma$ is set to $\sigma _{min}$.

The iterative process is continued while a stopping criterion is not satisfied, which is usually based on the maximum number of functions evaluations. The algorithm returns a set $A \cup \lbrace \mathbf x \rbrace$ of non-dominated decision vectors found during the runtime of the algorithm. The detailed MOSASS algorithm is given in Algorithm 1.

3 Memetic preference-based EMO algorithm

Fig. 2

Approximations of the Pareto fronts of different test problems obtained by MOSASS

The original R-NSGA-II algorithm aims to provide the points concentrated on the Pareto front region considering the DM’s preferences. When solving real-world multi-objective optimization problems, the results should be provided to DM for his/her analysis in appropriate amount of time, therefore the number of function evaluations must be limited. In such a case, the widely-used R-NSGA-II algorithm is faced with difficulties when obtaining in the well-distributed points that approximate a part of the Pareto front.

The local search strategy MOSASS uses a single decision vector $\mathbf x$ to generate a new decision vector, therefore it is likely that newly generated non-dominated decision vector will be in the neighborhood of $\mathbf x$. Examples of the Pareto front approximations obtained by 400 function evaluations of MOSASS are presented in Fig. 2. One can see, non-dominated decision vectors determined by the algorithm are concentrated around the initial decision vectors x, denoted by the squares.

Such a generation of non-dominated vectors in the neighbourhood of an initial decision vector meets the concept of preference-based approaches. Moreover, the latter process is much quicker comparing to the genetic operators used in EMO. Therefore, it is reasonable to incorporate the local search strategy MOSASS into the preference-based R-NSGA-II algorithm to improve the quality of approximation of the Pareto front in the limited number of function evaluations. In next subsection, we will describe the proposed memetic algorithm which we call R-NSGA-II with MOSASS.

3.1 The proposed R-NSGA-II with MOSASS algorithm

The memetic R-NSGA-II with MOSASS algorithm begins with initial parent population $P_0$ consisting of N decision vectors (see Algorithm 2). A value of clustering parameter $\delta$ ($0 < \delta \leqslant 1$) and the number of function evaluations $E_L$ dedicated for the local search are also predefined. The algorithm runs while the termination criterion is not satisfied (for example the number of generations or the number of function evaluations is not reached). After sorting the population into different non-domination levels (fronts) and calculating rank for each individual an offspring population is created using local search procedure MOSASS or using standard genetic operators (recombination and mutation). MOSASS procedure is activated if condition for the local search is satisfied, i.e. after every predefined number of function evaluations $E_G$ (see Row 6 of Algorithm 2). Individual $\mathbf x$ with the best rank of the population $P_t$ is passed to MOSASS procedure (see Algorithm 1) and local search runs till the number of function evaluations reaches the value $E_L$. The result of MOSASS procedure is the offspring population $Q_t$.

After the joint population is created and sorted, a new population is started to be formed (see Row 14 of Algorithm 2). Each front $\bar{F}_i$ of the joint population is clustered in such a way: the individuals which difference of the Euclidean distance to the reference point is less than $\delta$ are assigned to one cluster, where $\bar{R}_t$ ($\bar{R}_t \subset R_t$) is a set of representatives of each cluster, $\bar{R}_{ti}$ ($\bar{R}_{ti} \in \bar{R}_{t}$) are representatives in front $\bar{F}_i$. The representatives of each cluster are added to the new population (see Row 19). If all representatives in the front cannot be added to the population, only representatives with the smallest rank are selected (see Rows 24–25). In the case when there are not enough representatives from all the fronts to form the population of size N, clustering is performed again after removing the individuals already added to a new population. The result of the algorithm is the population $P_t$, which consists of decision vectors, and their corresponding objective vectors approximate the Pareto front.

3.2 Performance metrics for preference-based EMO

The EMO algorithms are usually measured on two aspects: the accuracy (how close the obtained approximation is to the Pareto front), and the evenness of distribution of the points in approximation.

The following performance metrics are commonly used to evaluate the performance of the EMO algorithms:

• Generational Distance measures the accuracy of the approximation of the Pareto front. The generational distance for an obtained set of points $\tilde{P}$ in objective space is calculated by the formula (Deb 2001):

  $$\begin{aligned} \textit{GD} = \frac{1}{|\tilde{P}|}\sum _{j=1}^{|\tilde{P}|} \min _{l=1, \dots , |P^*|}\Big (\sum _{i=1}^{k}||\tilde{P}_{ji}-P_{li}^{*}|| \Big ), \end{aligned}$$

  (9)

  Here we sum the Euclidean distances between the jth objective vector of $\tilde{P}$ and the nearest objective vector of the Pareto front $P^*$. It is aimed to find approximating points as close as possible to the Pareto front, therefore lower value of Generational Distance means better quality of the approximation.

• Spread metric measures the distribution of the points in approximation. For a set $\tilde{P}$ obtained by a classic EMO algorithm Spread is calculated by the formula (Deb 2001):

  $$\begin{aligned} \textit{SP} = \frac{\sum _{i=1}^{k}d_i^e+\sum _{j=1}^{|\tilde{P}|}|d_j-\hat{d}|}{\sum _{i=1}^{k}d_i^e+|\tilde{P}|\hat{d}}, \end{aligned}$$

  (10)

  where

  $$\begin{aligned} d_j= & {} \min _{l=1, \dots , |\tilde{P}|, ~ l \ne j}||\tilde{P}_{l}-\tilde{P}_{j}||, \end{aligned}$$

  (11)
  $$\begin{aligned} \hat{d}= & {} \frac{1}{|\tilde{P}|}\sum _{j=1}^{|\tilde{P}|}d_j, \end{aligned}$$

  (12)
  $$\begin{aligned} d_i^e= & {} ||\tilde{P}_{i}^{e}-{P}_{i}^{*e}||. \end{aligned}$$

  (13)

  Thus, $d_j$ is Euclidean distance between neighbouring objective vectors, $\hat{d}$ is an average of these distances, $d_i^e$ is a distance between the extreme objective vectors $\tilde{P}_{i}^{e}$ and $P_{i}^{*e}$. In the case when the points of the approximated Pareto front are well-distributed, the Spread value is close to 0.

• Hypervolume (HV) metric measures the volume of the dominated region made by the obtained objective vectors approximating Pareto front and the given point R (Zitzler and Thiele 1998). The larger hypervolume value means the better quality of the Pareto front approximation and distribution.

These metrics have been developed for evaluation performance of classical EMO algorithms. In this paper, we investigate preference-based EMO algorithms where the DM’s preferences are expressed by reference points, therefore we must consider them when evaluating performance of the algorithms. Hence, we introduce one new metric and adapt the aforementioned metrics for evaluation of the preference-based EMO algorithms.

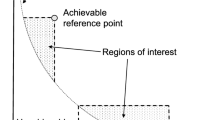
In the case of a preference-based EMO algorithm, the DM is interested only in the objective vectors that dominate the achievable reference points, i.e. they get into the region of the DM’s interest (see Fig. 3). Therefore, we propose a PR metric (14) for evaluation the preference-based EMO algorithms according to percentage of solutions that get into the region of the DM’s interest.

$$\begin{aligned} {\textit{PR}} = \frac{|\tilde{P}^{r}|}{|\tilde{P}|}\times 100. \end{aligned}$$

(14)

Here $\tilde{P}^{r}$ is a set of solutions that get into the region of the DM’s interest, $\tilde{P}$ is a set of all the solutions, obtained by the EMO algorithm. The metric evaluates performance of the algorithm in sense of an ability to obtain the concentrated solutions satisfying the DM’s preferences.

Fig. 3

Region of interest of the DM

As it is mentioned before, evaluation of hypervolume metric is already based on a given point. In this investigation for hypervolume metric evaluation, we consider the reference point provided by the DM instead of the nadir point that is commonly used for classical EMO algorithms.

Moreover, we have proposed to modify Spread metric (Filatovas et al. 2015), because incorporation of $d_i^e$ distances in the metric [Formula (10)] can distort representation of diversity of the objective vectors obtained. We propose to eliminate $d_i^e$ distance, and to calculate the Spread metric by the following formula:

$$\begin{aligned} \textit{SP}_p = \frac{\sum _{j=1}^{|\tilde{P}|}|d_j-\hat{d}|}{|\tilde{P}|\hat{d}}. \end{aligned}$$

(15)

In classical EMO algorithms all the obtained solutions are considered when evaluating GD and Spread metrics. Here we propose to consider only solutions from the region of the DM’s interest when evaluating GD (9) and Spread (15) metrics.

4 Investigation of the proposed memetic algorithm

In this section the performed computational experiments with the proposed memetic algorithm R-NSGA-II with MOSASS as well as the obtained results are described. The comparative analysis with the original R-NSGA-II algorithm is carried out. The performance of the algorithms is evaluated by metrics, described in Sect. 3.2.

Table 1 Test problems and reference points used in the evaluated algorithms

A set of well-known test problems has been considered: two-objective problems ZDT1–ZDT4, ZDT6, and three-objective problems DTLZ1–DTLZ7 (Deb et al. 2002). It should be noted, that these benchmark problems has different complexity and characteristics as convexity, concavity, discontinuity, non-uniformity. Moreover, some of them have many local Pareto fronts. A definition of the local Pareto front is introduced in Deb (1999).

Each experiment has been performed for 100 independent runs using different initial populations and average results have been evaluated. We selected a population size of 100 individuals and 100 generations for the problems with two objectives, and a population size of 150 individuals and 150 generations for the three-objective problems, as such population sizes are enough to sufficiently represent an approximation of a region of the Pareto front. We select relative small number of generation in order to find good enough approximation in reasonable computation time.

The value of the clustering parameter $\delta =0.0001$ was fixed as it ensures both diversity and concentration of the obtained solutions (Siegmund et al. 2012). Several trials has been performed for different combinations of parameters ($E_G, E_L$): (1000, 100), (1000, 200), (1000, 400), (2000, 100), (2000, 200), (2000, 400). The value $E_G$ defines the number of function evaluations after which local search MOSASS is performed, and $E_L$ sets the number of function evaluations to be performed during each local search.

Preference information provided by the DM that is expressed as a reference point is required for the evaluated algorithms, therefore various reference points were selected. The used reference points, the numbers of objectives and variables for each test problem considered are presented in Table 1. All the reference points are achievable—it means that all objectives can be improved at the same time without having to impair any of them.

After the final population has been obtained, the number of the objective vectors that get into the region of the DM’s interest is calculated and its percentage of the whole final population, i.e. value of PR metric (14) is evaluated. The mean values of PR for all performed runs with each test problem are presented in Table 2 for the original R-NSGA-II algorithm and for each trial of the memetic R-NSGA-II with MOSASS algorithm. The best average values of PR metric are presented in Italic and Bold italic. The values obtained by the proposed R-NSGA-II with MOSSAS algorithm which are better than obtained by original R-NSGA-II are marked in bold. One can see that the majority of the final population solutions get into the region of the DM’s interest for all the test problems except DTLZ1, DTLZ3, and DTLZ7. It means that the fixed number of function evaluations is enough to find crowded set of solutions when running the investigated algorithms. DTLZ1, DTLZ3, and DTLZ7 problems are hard to approximate in limited number of function evaluations, therefore PR values are low in these cases. However, in the case of DTLZ1 problem, the proposed R-NSGA-II with MOSSAS algorithm manages to obtain some solutions in the region of the DM’s interest unlike the original R-NSGA-II algorithm. For further performance evaluation of the algorithms we will not consider the DTLZ1, DTLZ3, and DTLZ7 problems.

Table 2 Values of PR metric

Table 3 Mean and confidence intervals of generational distance metric

Table 4 Mean and confidence intervals of Spread metric

Table 5 Mean and confidence intervals of HV metric

The mean values of Generational Distance (9), Spread (15) and Hypervolume metrics and their confidence intervals (95 % confidence level) for each test problem are presented in Tables 3, 4 and 5, respectively. The best average values (lowest for Generational Distance and Spread, highest for Hypervolume) of the calculated metrics are presented with italics. The values obtained by the proposed R-NSGA-II with MOSSAS algorithm which are better than obtained by original R-NSGA-II are marked in bold. Table 3 shows that the proposed R-NSGA-II with MOSSAS algorithm approximates the Pareto front of two-objective problems ZDT2, ZDT3, ZDT4, ZDT6, and three-objective problems DTLZ2, DTLZ4 better. The proposed algorithm is superior in cases of almost all combinations of parameters $E_G, E_L$ for problems ZDT2, ZDT3, DTLZ2, DTLZ4. Moreover, for problems ZDT2, ZDT3, ZDT6, DTLZ2, confidence intervals are not overlapped comparing with the original R-NSGA-II algorithm. Although the results obtained by the original algorithm are better in the case of ZDT1 and DTLZ5 problems, however for these problems the confidence intervals for some combinations of parameters $E_G, E_L$ are overlapping, hence the difference between the obtained results is not essential.

The mean values of Spread metric (see Table 4), obtained by the proposed algorithm are lower for all problems except of DTLZ5. It means that the non-dominated objective vectors are more evenly distributed on the part of the Pareto front covered by the region of the DM’s interest. For problem DTLZ5 the original algorithm has better performance considering the Spread metric, however Spread values are small enough in the investigated algorithms, hence sufficient distribution of the obtained objective vectors is ensured in both cases.

HV metric estimates both precision of the Pareto front approximation and distribution of the objective vectors. Reference points are selected as the points R for HV estimation (see Table 1). Table 5 shows that in almost all cases the proposed algorithm has better performance considering HV value, and higher $E_L$ value enables obtaining a higher HV value.

5 Conclusions

The memetic preference-based evolutionary multi-objective algorithm has been proposed in this paper. It is an extension of the R-NSGA-II algorithm where the local search strategy based on single agent stochastic search MOSASS is incorporated. The proposed memetic algorithm enables improving of quality of the Pareto front approximation and obtaining more even distribution of the approximating objective vectors.

The proposed memetic R-NSGA-II with MOSASS algorithm has been experimentally compared with the original R-NSGA-II algorithm by solving the widely-used benchmark test problems with the limited number of function evaluations. To evaluate the preference-based EMO algorithms we have proposed a new PR metric and adapted the well-known performance metrics—Generational Distance, Spread and Hypervolume, where only solutions from the region of the DM’s interest are considered.

Experimental investigation has shown that, in most of the analysed cases, the proposed algorithm approximates the Pareto front better than the original R-NSGA-II algorithm by measuring the approximation quality using the Generational Distance. The values of Spread metric has shown that the solutions obtained by the proposed memetic algorithm are more evenly distributed. In the sense of Hypervolume metric, that estimates both approximation quality and distribution, the proposed algorithm is superior for all analysed test problems.