1 Introduction

Civil engineering is a discipline that deals with the design, construction, and maintenance of the physical and naturally built environment, which includes works such as bridges, roads, canals, dams, and buildings (Institution of Civil Engineers 2012). By determining the stability of structures, it can materialize, among others, works for the shelter, protection, a livability of the society and its goods against inclement weather and environmental phenomena.

In this field, as in other disciplines (e.g, industrial engineering, telecommunications, economics, etc.), optimization problems appear everywhere and they bring a constant challenge, not only because of the appearance of new materials that may be used along with traditional ones, but also because this leads to cutting-edge methodologies that enable to realize complex designs in unexpected places.

When considering civil structures there are many issues to take into consideration, but there is always a common denominator for the concretion of a project: getting the minimum investment cost and the maximum safety of the final design. These are opposite goals indeed, because enhancing one of them involves worsening the other one. An example, is the design of a bridge, in which it is normally desirable to minimize cost, but with the aim of simultaneously maximizing safety. These are two conflicting goals, since a higher safety implies a higher economical cost. As a consequence, multi-objective optimization techniques are a highly valuable tool in this context. Compared to single-objective optimization, where a single objective function \(f(x)\) has to be optimized and a single optimal solution \(x^{*}\) is searched for, in multi-objective optimization a set of so-called non-dominated solutions, known as the Pareto optimal set, is the goal of the search (Coello et al. 2007; Deb 2001). Non-dominated solutions represent the best possible trade-offs among the objectives of the problem (i.e., these are solutions for which no improvement can be obtained for one objective without worsening another). Such non-dominated solutions are provided to the decision maker (e.g., the designer of a bridge) so that he/she can select a single one that best fits his/her particular needs and requirements (i.e., his/her user preferences). Among the available computational methods that can be used to solve multi-objective optimization problems, we focus on metaheuristics (Blum and Roli 2003), which are high level strategies governing a set of underlying techniques (usually, heuristics) in the search of optimal or quasi-optimal solutions of a given optimization problem. Metaheuristics are considered as particularly useful algorithms in structural engineering because, being randomized black box algorithms, they are able to handle problems with non-linear, non-differentiable, or noisy objectives, which are features normally found in structural engineering. Also, as opposed to traditional mathematical programming techniques used for solving multiobjective optimization problems (Miettinen 1999), metaheuristics are able to generate several elements of the Pareto optimal set in a single run.

The main goal of this paper is to provide both regular users and newcomers with a comprehensive survey of multi-objective metaheuristic techniques applied to structural design, along with a review of applications. To the best of our knowledge, this is the first attempt in the literature devoted to analyzing these two topics together. One can find an extensive study of evolutionary computing approaches in Kicinger et al. (2005), but no non-evolutionary metaheuristics are not considered in that study and the attention paid to multi-objective optimizations is limited to a section whose length is only of one page. A survey of multi-objective optimization methods for engineering was presented in Marler and Arora (2004), where only genetic algorithms, a particular type of metaheuristic, were included. However, since 2005 (the publication date of such survey), the multi-objective research community has developed numerous and major algorithmic advances, many of which have been applied to structural design problems. Thus, we consider that it is worth reviewing such research work and such is the motivation for this work. This paper aims to provide an overall view of the work conducted on the use of multi-objective metaheuristics for solving structural optimization problems, thus facilitating the exploration of the literature for those interested in pursuing research in this area. It is worth mentioning that we provide not only a fairly comprehensive list of the different metaheuristics that have been used to address structural design problems, but also details about each particular problem in which they have been applied (namely, type and domain, number of decision variables, objectives, and constraints, number of nodes, elements and groups) as well as details of the specific type of algorithm adopted (i.e., algorithm type, population size, termination condition, operators, type of local search (if adopted)).

The remainder of this paper is structured as follows. Section 2 introduces basic concepts about multi-objective optimization. Basic concepts about metaheuristics, their main features, and the implications of dealing with multi-objective optimization problems are issues dealt with in Section 3. The next section is devoted to presenting a classification of the different types of structural design problems. The survey of solved problems and used techniques is provided in Section 5, and an analysis is included in Section 6. Finally, we present our conclusions as well as some open research lines in this area in Section 7.

2 Multi-objective optimization background

In this section, we provide some background on multi-objective optimization fundamentals. We define first basic concepts such as multi-objective optimization problem, Pareto optimality, Pareto dominance, Pareto optimal set, and Pareto front. Then, the goals of multi-objective optimization are discussed. We will assume, without loss of generality, that all the objective functions are to be minimized.

A general multi-objective optimization problem (MOP) can be formally defined as follows:

Definition 1

(MOP) Find a vector \(\textbf {x}^*= \left [x_{1}^*, x_{2}^*, \ldots ,x_{n}^* \right ]\) which satisfies the m inequality constraints \(g_{i}\left (\textbf {x}\right ) \geq 0, i= 1,2,\ldots ,m\), the p equality constraints \(h_{i}\left (\textbf {x}\right ) = 0, i= 1,2,\ldots ,p\), and minimizes the vector function \(\textbf {f}\left (\mathbf {x}\right ) = \left [f_{1}(\mathbf {x}),f_{2}(\mathbf {x}), \ldots , f_{k}(\mathbf {x}) \right ]^{T}\), where \(\mathbf {x} = \left [x_{1},x_{2},\ldots ,x_{n} \right ]^{T}\) is the vector of decision variables.

The set of all the values satisfying the constraints defines the feasible region \(\Omega \) and any point \(\mathbf {x} \in \Omega \) is a feasible solution. In order to determine those points that are solutions to a given MOP, the concept of Pareto optimality has to be introduced:

Definition 2

(Pareto Optimality) A point \(\mathbf {x}^* \in \Omega \) is Pareto Optimal if for every \(\mathbf {x} \in \Omega \) and \(I = \left \{1,2,\ldots ,k \right \}\) either \(\forall _{i \in I} \left ( f_{i} \left ( \mathbf {x} \right ) = f_{i}(\mathbf {x}^*) \right )\) or there is at least one \(i \in I\) such that \(f_{i}\left (\mathbf {x}\right ) > f_{i}\left (\mathbf {x}^*\right )\).

This definition states that \(\mathbf {x}^*\) is Pareto optimal if no feasible vector \(\mathbf {x}\) exists which would improve some criteria without causing a simultaneous worsening in at least one other criterion. A related definition associated with Pareto optimality is Pareto dominance:

Definition 3

(Pareto Dominance) A vector \(\mathbf {u} = \left (u_{1}, \ldots , u_{k} \right )\) is said to dominate \(\mathbf {v} = \left (v_{1}, \ldots , v_{k} \right )\) (denoted by \(\mathbf {u}\) \( \preccurlyeq \) \(\mathbf {v}\)) if and only if \(\mathbf {u}\) is partially less than \(\mathbf {v}\), i.e., \(\forall i \in \left \{1, \ldots , k \right \}, \; u_{i} \leq v_{i} \;\wedge \; \exists i \in \left \{1, \ldots , k \right \}: \; u_{i} < v_{i}.\)

This way, a Pareto optimal point is that which is not dominated by any other point in \(\Omega \). Pareto dominance relates two solutions and it can be used as a binary operator. Thus, the application of this operator to two solutions in objective space returns that one solution dominates another or that the solutions do not dominate each other (i.e., they are non-dominated solutions).

The optimization of a MOP consequently will be aimed at finding the set of all the Pareto optimal solutions. This is the so-called Pareto optimal set, or simply Pareto set, and it is defined as follows:

Definition 4

(Pareto Optimal Set) For a given MOP \(\mathbf {f}(\mathbf {x})\), the Pareto optimal set is defined as \(\mathcal {P^*} = \{\mathbf {x} \in \Omega | \neg \exists \mathbf {x'} \in \Omega , \mathbf {f}(\mathbf {x'}) \preccurlyeq \mathbf {f}(\mathbf {x})\}\).

Each vector in the Pareto optimal set has a correspondence in objective function space, leading to the so-called Pareto front:

Definition 5

Pareto Front For a given MOP \(\mathbf {f}(\mathbf {x})\) and its Pareto optimal set \(\mathcal {P^*}\), the Pareto front is defined as \(\mathcal {PF^*} = \{\mathbf {f}(\mathbf {x}) | \mathbf {x} \in \mathcal {P^*} \}\).

Let us take into consideration as an example the four-bar plane truss design problem depicted in Fig. 1. It is a bi-objective optimization problem, in which two objectives are to be minimized: the volume of the truss \((f_{1})\)) and its joint displacement \(\Delta \) (\((f_{2})\)). This problem can be formulated as follows:

$$\begin{array}{@{}rcl@{}} Min F & = & (f_{1}(\mathbf{x}), f_{2}(\mathbf{x})) \\ f_{1}(\mathbf{x}) & = & L(2x_{1} + \sqrt{2}x_{2} + \sqrt{x_{3}} + x_{4}) \\ f_{2}(\mathbf{x}) & = & \frac{FL}{E} \left(\frac{2}{x_{1}}+\frac{2\sqrt{2}}{x_{2}}-\frac{2\sqrt{2}}{x_{3}}\frac{2}{x_{4}}\right) \end{array} $$

such that:

$$\begin{array}{@{}rcl@{}} (F/\sigma) \leq x_{1},x_{4} \leq 3(F/\sigma) \\ \sqrt{2}(F/\sigma) \leq x_{2},x_{3} \leq 3(F/\sigma) \\ \end{array} $$

where:

$$\begin{array}{@{}rcl@{}} F=10 kN, E=2 \times 10^{5} kN/cm^{2}, \\ L=200 cm, \sigma=10kN/cm^{2} \end{array} $$
Fig. 1
figure 1

Four-bar plane truss problem

Full size image

This problem has four decision variables \(\mathbf {x}= \left [x_{1}, x_{2}, x_{3}, x_{4} \right ]\), and its true Pareto front is shown in Fig. 2.

Fig. 2
figure 2

Pareto front of the four-bar plane truss

Full size image

The main goal of multi-objective optimization algorithms is to obtain an approximation of the true Pareto front of a given MOP. In general, multi-objective optimization problems can have a Pareto front composed by a huge (possibly infinite) number of solutions. When using stochastic techniques, such as metaheuristics, the goal is thus to obtain a Pareto front approximation (also called approximation set), i.e., a subset of solutions that represents the true Pareto front. We want to emphasize here that we are approaching multi-objective optimization using a posteriori techniques, that is, we produce first an approximation of the Pareto front and then, we pass the solutions obtained to the decision maker (the civil engineer in the case of structural design problems), so that he/she can choose the most appropriate solution to be implemented, based on his/her own preferences. There are multi-objective optimization approaches that can be used in an a priori or in interactive form (Coello et al. 2007), but they will not be discussed here.

In general, it does not make sense to search for a huge number of Pareto optimal solutions, since normally a reasonably low number of solutions is enough. Thus, multi-objective metaheuristics normally aim to obtain a limited set of Pareto optimal solutions (typically, around 100), although this is clearly a user-defined parameter and other values (e.g., 50, 200, or any other value) can be adopted as well, depending on the specific requirements from the user (Das 1999; Gobbi et al. 2013; di Pierro et al. 2007).

When producing an approximation of the Pareto optimal set using multi-objective metaheuristics, two main properties are normally aimed for: (1) convergence (i.e., we want to produce solutions as close as possible to the true Pareto front) and (2) diversity (i.e., we want to produce solutions that are spread along the entire Pareto set, and not only clustered around a few specific parts of it).

These concepts are illustrated in Fig. 3. The Pareto front approximation in the top left is on the true Pareto front, but there are some regions in which no solutions were found; this means that the decision maker would not know whether or not there are any useful solutions in this region. The example in the top right of Fig. 3 shows a Pareto front with an excellent distribution of points along the Pareto front, but they have not converged to the true Pareto front. This is evidently undesirable, since a good distribution of solutions is relevant only when having a good convergence. Finally, the approximation set shown in the bottom of the figure shows a desirable result which has both a good convergence and a good diversity.

Fig. 3
figure 3

Pareto front approximations: good convergence (top left), good diversity (top right), good convergence and diversity (bottom)

Full size image

It is important to indicate that, in practice, other goals may also be desirable. For example, it may be required to obtain more solutions only on a specific part of the Pareto front. This may be particularly relevant when dealing with computationally expensive objective functions (e.g., in aeronautical engineering problems). In such cases, it may happen, for example, that the solutions shown in the top left part of Fig. 3 are preferred if they can be reached in a significantly shorter time than that required to obtain the solutions shown at the bottom of the figure.

3 Metaheuristics and multi-objective optimization

In the previous section we provided a background of basic multi-objective optimization concepts. Here we include a complement of that information by presenting some fundamentals of multi-objective metaheuristics. First, we define the concept of metaheuristic and how this family of solvers can be classified. Second, we describe Evolutionary Algorithms, which are, by far the most well-known metaheuristic techniques. Third, a number of issues that are particular to multi-objective optimization algorithms are highlighted. Finally, we elaborate on the solution encoding, which is an important feature because of its influence in the algorithms than can be chosen to solve a specific problems.

3.1 Definition of metaheuristic and classification

Metaheuristics are a broad family of non-deterministic optimization methods aimed at finding accurate solutions to complex optimization problems when exact methods are not applicable. Metaheuristics cannot, in general, guarantee to find optimal solutions but they tend to produce near-optimal solutions with a reasonably low computational effort. This class of approaches includes, among others, Evolutionary Algorithms (by far, the most well-known metaheuristic), Ant Colony Optimization, Scatter Search, Simulated Annealing, and Particle Swam Optimization. In fact, many metaheuristics have been designed in the last 20 years, and a number of approaches to classify them according to some criteria have been proposed (see for example Blum and Roli (2003)). One of the most accepted taxonomies is that distinguishing between nature-inspired and non-nature inspired metaheuristics. Table 1 contains a list of metaheuristic algorithms according to this classification.

Table 1 Classification of metaheuristics in Nature-inspired and Non-nature-inspired techniques
Full size table

Of the many definitions of metaheuristics that can be found in the literature, a number of basic properties of them can be stated (Blum and Roli 2003):

  • They are general strategies or templates that guide the search process.

  • Their goal is to provide an efficient exploration of the search space to find (near-) optimal solutions.

  • They are not exact algorithms and their behavior is generally nondeterministic (stochastic).

  • They may incorporate mechanisms to avoid visiting non promising regions of the search space.

  • Their basic scheme has a predefined structure.

  • They may use specific problem knowledge for the problem at hand, by using some specific heuristic controlled by the high level strategy.

This way, metaheuristics can be considered as high level strategies for exploring search spaces by using different low level search operators. From an algorithmic point of view, the provided templates can be instantiated or tuned to perform an efficient search of any given optimization problem. Algorithm 1 shows the pseudocode of a generic metaheuristic, where a set A of some initial solutions (A may be eventually initialized to \(\emptyset \)), is iteratively updated by generating a set S of new solutions from it until a stopping condition is met.

3.2 Evolutionary algorithms

As an example, we describe next an evolutionary algorithm (EA), the most popular and widely used member of the metaheuristics family. A typical EA follows the pseudocode included in Algorithm 2.

In EAs, candidate solutions are called individuals, which are composed of a chromosome (the representation of the variables of the problem) and a fitness (an indicator of the quality of the solution in the context of the problem being solved). Groups of individuals are referred to as populations. As in real life, some selected individuals from a population mate (i.e., are selected) for reproduction, generating new child or offspring individuals which, according to the natural selection process, can replace some other individuals. Whenever a new solution is created, it is evaluated to be assigned its corresponding fitness value. When the current population is replaced by a new one, a generation has taken place. The process of iterating through successive generations is called evolution, and ends when a termination condition is fulfilled.

The pseudocode in Algorithm 2 can be instantiated also to yield particular EA variants. Thus, if the reproduction is based on crossover and mutation operators, the resulting EA is a Genetic Algorithm (GA), which, by the way, is the best-known EA. Other EA variants are Evolution Strategies (ESs) and Genetic Programming (GP). It is important to note that some parameters, such as the population size or the probability of applying the crossover and mutation operators, have to be carefully tuned so that the EA can have a good performance. In fact, this topic has been subject of a considerable amount of research in the evolutionary computation literature (see for example Lobo et al. (2007)).

Most metaheuristics, single and multi-objective, follow a pattern similar to the one used by EAs, i.e., the algorithms consist of a loop where a number of tentative solutions are combined and modified in a certain way, in order to produce new solutions, and at each iteration the loop tries to improve the managed solutions towards the optimum of the problem to be solved. All of these techniques have control parameters whose values have an important influence in the search capabilities of the algorithm.

3.3 Issues when solving multi-objective optimization problems

When the goal is to solve a multi-objective optimization problem (MOP) with metaheuristics, there are new issues to consider due to the fact that we aim to produce a set of solutions (i.e., our approximation of the Pareto set) rather than a single value. Comparisons between solutions are required in many selection operators used within metaheuristics (e.g., binary tournament within an EA) and in replacing policies. When dealing with single-objective optimization problems, the relationship “is better than” between two solutions is trivial: the one with the lower or higher fitness value, depending whether function has to be minimized or maximized, is better. In the case of MOPs, this relationship has to be redefined, because when comparing two solutions which are non-dominated there is no a way to assess which of them is better, unless we impose certain user’s preferences. The consequence is that a new kind of fitness measurement is needed. On the other hand, as commented in Section 2, the set of solutions that we aim to produce has to have at the same time satisfactory convergence and diversity properties. This means that not only Pareto optimal solutions are sought for, which would guarantee a high degree of convergence, but also that such solutions must be evenly distributed along the Pareto front. Again, and in order to illustrate these issues, we will analyze next an example using the Nondominated Sorting Genetic Algorithm-II (NSGA-II), which is the most popular multi-objective evolutionary algorithm (MOEA) in current use.

The NSGA-II (Deb et al. 2002) is a multi-objective genetic algorithm that is characterized by two features: the use of a Pareto ranking mechanism to classify solutions and a density estimator known as crowding distance. The ranking of solutions classifies a population in ranks (1, 2, ...) in such a way that the non-dominated solutions are assigned a rank equal to 1; then, they are removed and the procedure is successively applied yielding to solutions with ranks 2, 3, and so on. By selecting the solutions with best ranking, NSGA-II tries to converge towards the true Pareto front. However, when choosing the best ranked solutions it is possible that only a subset of solutions of a given rank be needed. In this case, it is necessary to carefully select the most promising solutions in order to promote diversity, and the approach taken in NSGA-II is to define a density estimator. The idea of a density estimator is to assign to a set of non-dominated solutions a value indicating in some way the degree of proximity (or density) of nearby solutions in the set. This way, solutions in sparse regions are preferred compared to those in most crowded regions. As indicated before, the density estimator in NSGA-II is called crowding distance, and it is detailed in Deb et al. (2002). NSGA-II has become de de facto multi-objective optimization metaheuristic, and it has influenced many other techniques proposed in the last ten years (Coello et al. 2007).

Another popular MOEA is the Strength Pareto Evolutionary Algorithm 2 (SPEA2) (Zitzler et al. 2001). As the NSGA-II, SPEA2 is a genetic algorithm based on Pareto dominance. SPEA2 adopts a scheme known as strength, that takes into account, for each solution in the population, not only the number of solutions that dominate it, but also the number of solutions by which it is dominated. This provides a finer grained estimation of the actual ranking of a solution. The density estimator adopted in SPEA2 is based on measuring the distance to the k-th nearest neighbor (i.e., it is a clustering approach).

NSGA-II, SPEA2 and most of the multi-objective metaheuristics developed in the last ten years conform the so-called second generation of multi-objective metaheuristics (characterized for adopting some form of elitism to retain the globally non-dominated solutions that they generate), leading to the period when research in this field grew in a very important manner, thus becoming a hot research topic. A set of representative multi-objective metaheuristics is depicted in Table 2.

Table 2 Examples of representative multi-objective metaheuristics
Full size table

A popular scheme to deal with multi-objective optimization problems before the raising of the second-generation algorithms was the use of aggregating functions. Under this sort of approach, a multi-objective optimization problem is transformed into a single-objective one, thus allowing to apply single-objective metaheuristics. However, this sort of approach has a number of drawbacks, from which the main one is that it cannot generate non-convex portions of the Pareto front (Das and Dennis 1997). Scalarizing functions are a better choice if one is interested in using single-objective optimizers for solving multi-objective optimization problems, since they don’t have the same limitations of aggregating functions and can be very effective when dealing with complicated Pareto sets. When using scalarizing functions, the solution of a multi-objective optimization problem is decomposed into a set of single-objective optimizations (a set of weights are used for this sake). This idea is indeed the basis of the Multiobjective Evolutionary Algorithm Based on Decomposition (MOEAD, Zhang and Li (2008)), in which the several single-objective optimization problems generated are solved at the same time. By combining this idea with the definition of neighborhood relations among the subproblems that are being solved, MOEA/D (and, particularly, its MOEA/D-DE variant (Li and Zhang 2009)), is considered as one of the most powerful MOEAs currently available.

3.4 The influence of solution encoding

A key point when using metaheuristics (both for single- and multi-objective optimization) to solve a given problem is the encoding of the solutions. To illustrate this issue, the four-bar plane truss depicted in Fig. 2 will be used. This problem has four real variables, so a natural encoding in this case is to use an array of real values (i.e., real numbers encoding), but it is also possible to use a binary encoding, where each decision variable is encoded as a binary string. Choosing between these two representation has two consequences. First, many reproduction operators are applicable only to a given encoding; for example, single point crossover (SPX) and bit-flip mutation are used with binary strings, while simulated binary crossover (SBX) and polynomial-based mutation are operators intended for real numbers encoding. Given that each operator has a different behavior, the performance of the algorithm using it, gets affected. Second, some metaheuristics are designed to work with a given type of encoding. Differential Evolution (DE) and Particle Swarm Optimization (PSO) are typically adopted for solving continuous optimization problems, while other such as Ant Colony Optimization (ACO) or Tabu Search (TS) are intended mainly to work with combinatorial problems. Thus, encoding is an important feature that will be included in the survey (see Tables 6 and 7 in Section 5).

4 Structural design optimization problems

It is difficult to determine when was the first time that optimization was applied to structural design, but we can say as a historical review that in the ancient times, before the Roman aqueducts, there were stone arches and curved bar structures aimed at covering long spans by reducing the weight or the amount of material.

Ohsaki and Swan included a historical review in Ohsaki and Swan (2003) about a number of optimization techniques applied to discrete structural topology. There periods were stated as follows:

  • Initial period where J.C. Maxwell (in 1894) and A.G.M. Michel (in 1904) made their pioneering studies in the field.

  • Second period in the 1960s and 1970s, when the use of computers began to arise.

  • Third period, during the 1980s and 1990s, characterized by the extremely dramatic grown in computer technologies.

The first applications of metaheuristics to structural optimization problems can be found in works developed in the 1970s and the begin of the 1980s, as it was pointed out in Kicinger et al. (2005). If we focus in multi-objective approaches, we can trace back works in the mid-1980s (Goldberg and Samtani 1986) and the beginning of the 1990s (Hajela 1990). Surveys about structural optimization including both single- and multi-objective optimization techniques were published in Andersson (2000) and in Kicinger et al. (2005). These techniques and others were discussed in Saitou et al. (2005).

The problems analyzed in these surveys can be divided in two main categories:

  • Bar or element design: it is a local optimization process that affects the shapes and sizes of the elements of a structure. It is addressed by finding the measures of a pre-defined geometry transverse to the main axis of the structure, or determining the variables that lead to the optimum geometric shapes.

  • Topological design: It is a global optimization process aimed at defining the entire topology (layout) of a structure. It is known as topological optimum design (TOD), and it can be applied to discrete and continuous structures. TOD takes into account the number of elements and the links or continuities among them in order to determine the optimum distribution of masses in the considered domain, with the goal of obtaining the stability of the structure. In this process, while new elements are incorporated or existing ones are removed, the shape and/or size of each element is also optimized.

4.1 Bar or element design

In this section, bar design problems (Chapman 1994) are classified. These problems are related to structures composed of flat and spatial bars, such as trusses and frames.

Truss structures are composed of bar elements that are linked by articulated joints. The calculation of the equilibrium requires to determine the areas of the cross section of each bar, with no information about shape and sizes. A frame structure is a more complex problem because, besides the areas, the flexural inertia must be calculated, so the cross shape and sizes must be previously defined in order to determine the stability of the structure. The problem complexity might increase in case of three dimensional structures, because there are four variables for the design: the area, two inertia moments, and a torsional inertia.

So, in this category, the cross geometry of each bar of the structure must be calculated, which defines the decision variables of the problem that is to be optimized. Four sub-categories can be distinguished, as illustrated in Fig. 4:

  1. 1.

    Area optimization: The decision variables represent the areas of the bars without considering the sizes nor the shapes of the cross sections (Fig. 4(1)).

  2. 2.

    Size optimization: As shown in Fig. 4(2), the shape is pre-defined, so the problem to optimize is related to finding the values that define the size of each part of the shape.

  3. 3.

    Shape optimization: The goal is to find the geometry and dimensions of a closed polygon inscribed within a known frame or border (Fig. 4(3)) by the discretization of the shape into lines or curves linked together by nodes.

  4. 4.

    Topological optimization of cross-section. The fourth sub-category is illustrated in Fig. 4(4). Starting from a known elemental section, it must be discretized into small elements having triangular or square sections. The optimization process is then based on removing pieces and re-arranging the linked elements with their neighbors by their sides. Empty spaces can appear inside.

Fig. 4
figure 4

Bar dimensioning or geometrical design problem variants: (1) Area without sizing, (2) sizing, (3) shape, and (4) topology cross-section

Full size image

4.2 Topological design

As commented before, TOD comprises the distribution of internal elements, the links, and the external shape of the structure to optimize, and it basically relies on distributing the resistant masses of material where required as well as defining their size. The optimization process starts from an initial state and the final shape, trying to find the optimum design satisfying the objective functions and constraints.

Three categories can be established to classify this type of problems. The issues to consider are the type of the used element or the way in which the subdivisions are made (bars or elements components interconnected by nodes, sides, or surfaces). The categories are the following:

  1. 1.

    No topological optimization (pre-defined topological design): the topology of the structure is defined by the designer, and it is fixed and remains unchanged during the optimization process concerning the number of elements, links, restriction of movements, etc. This category is considered because it allows to classify those TOD problems in which only bar design issues and continuous structures are considered, as illustrated in Fig. 5(1a) and (1b) respectively. In the first case, the problems are composed of 2D or 3D bar structures where one of the measures stands of the other two (length on the measures of the cross section), using a linear representation of the bar element that matches the centroid of the cross section describing a longitudinal axis; each element is linked to the others through its nodes. Examples are truss and frame structures. The second kind of problems include continuous structures in which there is no variation of shape, and the optimization is limited to the thickness equal for all elements of the structure or the suitability of the main lengths of the structure.

  2. 2.

    Discrete topological optimization: this case is similar to the previous one, but the design of the structure is not defined in advance, i.e., it is unknown (see Fig. 5(2)). The starting point is the design domain, which is the zone of study, and consists of a figure or wire body, containing the boundary conditions, which can be in the 2D or 3D domain. It is divided internally by grids in which the coordinates of the vertices are known. The design of the structure shall be defined by the required unions of these points, allowing the links among the longitudinal elements to represent the bars.

  3. 3.

    Continuous topological optimization: Depicted in Fig. 5(3) it is applied to plate-like structures or continuous 2D and 3D structures. The thickness can be constant or not, so the decision variables of the optimization problem take values between the limits of the exploration space and boundary conditions. The starting point is a figure or basic body with pre-established peripheral measures and with excess material known as design domain. In both cases, 2D and 3D, the design domain is discretized in small elements. The final result will be a different figure depending on the grouping obtained with the optimization of the resistance and distribution of the material, discarding the decking material on the strength of the assembly. In general, these kinds of structures evolve to adopt bar shapes through the discrete elements linked among them by the adjacent sides between neighbors. When the problems are in 3D, the design is a spatial one and evolves by varying the sizes in the three dimensions, coupling and uncoupling volumetric finite elements attached to their neighbors through the contact surfaces. After the optimization, the required conditions of shape and size to meet the stability of the structure will be obtained.

Fig. 5
figure 5

Topological design classification: No topological optimization with two variants, (1a) bars and (1b) continuous structures; (2) bar topology optimization; (3) continuous topological optimization

Full size image

5 The survey

After doing an in-depth analysis of the literature, we have selected more than 50 references related to multi-objective optimization applied to structural design problems, which we have found to be the most representative of the work that has been done in this area. Even though we have tried to encompass a wide and thorough review, it is important to clarify that the aim was not to be comprehensive, and there may be other relevant works that are not included here.

The analysis of this published material is divided in two parts. First, Section 5.1 provides all the details about the particular structural design problem tackled by the analyzed works. Then, an in-depth review based on the particular algorithmic details such as the algorithm used, the encoding of the tentative solutions, the search operators adopted, the number of solutions managed, etc., is provided.

5.1 Structural design problems addressed by multi-objective metaheuristics

Tables 3, 4 and 5 summarize the main features of the structural design problems that have been addressed with multi-objective metaheuristics in the analyzed papers. We use n/a for those cases in which we did not find the required information as well as in cases when that feature is not applicable. The entries in these tables include the following information:

  • Cite: Bibliographic reference. The citations are arranged according to their publication year and, in a given year, they are presented alphabetically considering the first author name.

  • Mat.: Material used in the structure, e.g., steel, wood, reinforced concrete (RF), prestressed concrete (PC), etc. If the material is not available, this field will include its mechanical feature such as (Elastic), when a linear relation exists between tension and distortion, or (Plastic), when this relation is not linear.

  • Dom.: Domain of the problem. It can be either (2D) or (3D) if the analysis of the structure is carried out in the plane or the space, respectively.

  • Calc.: Calculation method used to determine the effects of loads in the structure and stability. We have used the acronyms and names detailed next. SDC: Seismic Design Criteria (for problems related to seismic analysis of structures), DNV-CSR: Det Norske Veritas - Common Structural Rules (certification relating to calculus and quality of ships), DGV-CPH and NBE AE-88: Spanish construction regulations, Damage: identification of damaged members and estimation of severity, FEM: Finite Element Method, FEM-P: FEM and parallel processing, FEM-NRH: Nonlinear Response History FEM, SRSM: Stochastic Response Surface Method, CFDM: Constrained Force Density Method, Equ: Algebraic Equations, Ad Hoc: other method, different from the ones previously mentioned.

  • Type: type of structure. We consider here Truss, Frame, SMRF: Special Moment-Resisting Frame, Cantilever plate, Tall building frame, etc.

  • Nodes: number of nodes used in bar structures. Additionally, we use the \(\vartriangle \) (triangular cell) and \(\square \) (quadrilateral cell) symbols to represent the shape of the discrete structure forming a grid of continuous real problem 2D, and solid45 and solid95 to represent linear and quadratic hexahedral solid elements, respectively.

  • Elem.: number of finite elements that form the structure.

  • Gr.: Number of groups of bars with similar mechanical and geometrical features. Grouping bars means simplifying the problem size with the goal of making it more affordable to be solved.

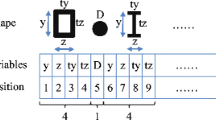
  • Design: Size, shape and topology optimization problem. An \(X.Y\) encoding of two variables has been used only for structures with bars, where X indicates the kind of structural component design (1: area, 2: size, 3: shape, 4: topology), as presented in Section 4.1, and Y represents the type of topology design of the structure (1: no optimization, 2: discrete, 3: continuous), as described in Section 4.2. For example, an 1.1 code in this column means optimizing the cross section area without taking into account shape or size, while the entire design of the structure remains the same (number of trusses and bars, external topology, etc.).

    Table 3 Synthesis of the problems solved with MOPs
    Full size table
    Table 4 Synthesis of the problems solved with MOPs (cont)
    Full size table
    Table 5 Synthesis of the problems solved with MOPs (cont)
    Full size table

    In the case of continuous structures, it is enough to identify the type of optimization with one single value, which is pointed by the Y variable. Bearing in mind the classification of Section 4.2), \(Y=1\) means a size type design optimization and it corresponds only to a plate thickness optimization (not the geometry of the other two dimensions, which are fixed and predefined). The value 3 indicates a design change in the size and shape of the structure (topology design). In the 2D domain, the optimization is targeted to the main axis of the structure, being the constant the thickness or depth. In the 3D domain, the optimization is global, considering all the design variables.

  • Obj.: Objective functions to be optimized.

  • Const.: Constraints used to define a feasible structure.

  • No Var.: Number of decision variables of the problem.

We have used the following symbols, names, and acronyms to refer to the different objectives and side constraints that are considered in the analyzed works:

  • \(\alpha \), \(\beta \): function of the geometrical parameters

  • \(\delta \): displacement of node or point

  • \(\delta _{ave}\): deviation between the actual output path of the mechanism and the desired path

  • \(\gamma \): safety

  • \(\lambda \): compressive slenderness or buckling factor

  • \(\omega _{i}\): \(i^{th}\) natural frequency

  • \(\sigma \): axil stress limits (or allowable); in case the values of stress (+) and compression (-) are different, the corresponding sign will appear

  • \(\sigma {_{A}}\): stress in the anchorages

  • \(\sigma _{B}\): Euler buckling stress

  • \(\sigma _{VM}\): Von Misses stress

  • \(\vartheta \): allowable values for rotation

  • \(a_{1}=e_{1}\): restriction associated with the dimensions of each group

  • A: cross sectional area

  • c: structural compliance

  • CMA: constrained mass average

  • Cost: cost of material, design, analysis, execution, etc.

  • Da: boundary constraints of the numerical values of damage that are acceptable

  • Dcb: distance away from the constraint boundary

  • DI: diversity index

  • Dist: Euclidean distance considering the loading point, desired support point and actual support

  • DR: interstory drift ratio among all stories corresponding to all the seismic motions for the initial Peak Ground Velocity (PGV) level

  • DS: diversity of structure

  • DyR: dynamic response

  • Ei: input energy

  • Ec: equations which take into account the allowable stresses of materials and other features

  • Env: counts the environmental impact of the structure

  • Ep: dissipated energy

  • \(E_{rh}\): hysteretic energy dissipation ratios

  • EVS: first mode eigenvalue of the structure

  • \(f^{v}\): vulnerability function (VF) of robust multi-objective and multi-level optimization (RMOL)

  • \(f^{v}_{M}\): VF for mass of the structure

  • \(f^{v}_{\delta }\) VF to the maximum displacement at a specific point

  • F: force or load

  • Fr: frequency

  • \(F_{b}\): bound on the applied load needed to cause the mechanism to achieve the desired path

  • FEV: first eigen period

  • FRF(\(\omega _{i}\)): frequency response function crest parameter with respect to the \(\omega _{i}\)

  • \(\overline {FRF}\): mean value of FRF crest parameters at \(\omega {_{1}}, \omega {_{2}}, \omega {_{3}}\)

  • FT(\(\omega _{i}\)): force transmissibility crest parameter with respect to \(\omega _{i}\)

  • \(\overline {FT}\): mean value of FT crest parameters at \(\omega {_{1}}, \omega {_{2}}, \omega {_{3}}\)

  • \(g_{BDS}\): constraint requirement that each member meets the AASHTO LRFD Bridge Design Specifications (BDS) throughout opening

  • GAM: geometric advantage of the mechanism.

  • GC: geometric constraints related to the position of nodes which support the distributed loads acting on the deck

  • HMAWV: hybrid mode aerial working vehicle

  • L: length

  • LSDC: life time seismic damage cost

  • M: mass

  • MD: modal damage

  • MF: modal flexibility

  • n: number of transversely stiffening flat bars which expresses in a simple way the complexity of design or workmanship expenses

  • n/a: not available

  • \(n^{t}\): dynamical and recursive constraint

  • NCST: number of different cross-section type

  • NEC: number of elements within this area that contains material

  • \(N_{s}\): constructability through the number of longitudinal bars

  • p: lateral pressure

  • PAS: prescribed area must be fully solid

  • q: maximum non-dimensional ratio under a combination of axial force and bending moments

  • r: normalized mass or the ratio of structural mass to the maximum mass

  • SDCV: standard deviation of the constraints violation

  • SDL: standard deviation of ultimate load carrying capacity taken as a measures of robustness of a structure

  • SIE: supplied input energy

  • Sust: environmental cost of the most sustainable solution

  • t: plating of thickness

  • \(t/h\): ratio between flat bars of thickness t and height h

  • V: volume

  • \(V_{r}\): volume ratio

  • W: weight

  • WS: allowable modulus section

5.2 Algorithms and parameter settings

This section aims at analyzing the literature from the point of view of the components of the multiobjective metaheuristic used for addressing structural design problems.

The columns in the tables are the following ones:

  • Algorithms: name of the multiobjective algorithm used to solve the structural design problem. The algorihtms in parentheses are included for comparison purposes in the cited work.

  • Fam.: metaheuristic family to which the algorithm belongs (GA: Genetic Algorithm, SA: Simulated Annealing, ES: Evolution Strategy, GP: Genetic Programming, AIS: Artificial Immune System, PSO: Particle Swarm Optimization, EDA: Estimation of Distribution Algorithm, TS: Tabu Search).

  • PS: this column shows the number of solutions (PS = Population Size) used by the algorithm (if applicable).

  • Encod.: representation used for the solutions manipulated by the multiobjective metaheuristics. The values that may appear in this column are: B: Binary encoding; BG: Binary Gray, IN: Integer, FP: Floating Point, DV: Discrete Values.

  • Sel.: selection operator used (RW: Roulette Wheel, T: Tournament, BT: Binary Tournament, UST: Uniform Stochastic and Truncation, IS: Interval Selection, SS: Sequential Selection, RS: Random Selection). This method is the one in charge of providing (either explicitly or implicitly) an ordering for the solutions managed by the multiobjective metaheuristic.

  • Rec.: recombination operator used (SBX: Simulated Binary Crossover, UX: Uniform crossover, IX: Intermediate Crossover, DPX: Two-points crossover). When more than one operator is used, we use the label “Mult.”.

  • Mut.: mutation operator (BF: Bit Flip, UM: Uniform Mutation, PM: Polynomial Mutation, DM: Displacement Mutation, SM: Shift Mutation, RM: Random Mutation). When more than one operator is used, we use the label “Mult.”.

  • FA-DP (Fitness Assignment and Diversity Preservation): these are the two most important design issues when proposing a new multiobjective metaheuristic. It is worth noting that in some cases, these two components are merged into a single measure that translates the vector of objective functions of a multiobjective problem into one single scalar value which is used to rank solutions properly. We consider here the following techniques: UIS: Uniform Interval Selection, St.: Strength, PR: Pareto Ranking, CD: Crowding Distance (density estimator of NSGA-II), WS: Weighted sum, G: Grid, AG: Adaptive Grid, SD: SPEA2’s Density estimator, FS: Fitness Sharing, Cl.: Clustering

It must be noted that the columns including the selection, recombination, and mutation operators are mainly applicable to EAs (such as GA and ES). However, we can find in the literature that, for example, several PSO algorithms employ mutation as a perturbation operator. The choice of considering these three operators has its rationale in that more than the 90 % of the found works are about EAs, and the information about the used operators is, therefore, relevant. Detailing the operators used by non-EA algorithms (e.g., PSO, SA, AIS) would make the tables very complex to understand and, therefore, we omitted such details.

Whenever an item is not applicable to a given algorithm, or the paper does not report information to infer it, we write ‘n/a’ in the corresponding cell.

6 Analysis

In this section, we perform an analysis of the table contents presented in the previous section. We use bar plots to summarize the most relevant issues that can be extracted from all the collected data. We have considered: the number of publications per year, the type of problems addressed within each design category, and the multi-objective metaheuristics used to tackle these problems.

The total number of papers finally included in the survey is 51. Figure 6 includes the number of publications per year. The first conclusion that can be drawn from this figure is that, up to 2004, very few papers (oscillating between 1 and 3 per year, and only one before 2000) had been published. This makes sense because the use of multi-objective metaheuristics became popular at the beginning of the last decade, when the first two monographs on evolutionary multi-objective optimization were published (Deb (2001) and the first edition of Coello et al. (2007), which became available in 2002). From 2005 onwards (with the exception of 2006, in which no papers were found), the tendency increases up to 2011, where 11 papers appeared in the specialized literature. Regarding 2012, 4 papers have been considered for the survey. Our guess is that more papers are expected in the following years due to the evident benefits that multi-objective metaheuristics have produced in structural optimization. We want to remark here that this survey is intended to serve to both expert practitioners and newcomers as the basis of cutting edge ideas and state-of-the-art algorithms to further improve this field.

Fig. 6
figure 6

Number of reviewed publications per year

Full size image

We focus now on the 84 problems tackled according to the design categories established in Section 4, which are summarized in Fig. 7 and Table 6. The most studied problems fit into the categories with keys 1.1 (area optimization, no topological optimization) where 26 problems have been considered, and 2.1 (size optimization, no topological optimization), with 17 problems addressed. Continuous topological optimization (labelled as 3 in Table 7) has received also a lot interest, with 17 problems. A second group is formed by the 8 and 12 problems belonging to area/size optimization plus discrete topological optimization (categories 1.2 and 2.2 respectively). Finally, no problems have been found related to the 3.1 and 4.1 types (shape/cross-section topology plus discrete no topological optimization), and 4 problems belongs to the class labelled as 1.

Fig. 7
figure 7

Number of problems in each design category

Full size image
Table 6 Algorithms and parameter settings
Full size table
Table 7 Algorithms and parameter settings (cont)
Full size table

Front the point of view of the algorithms that have been applied, Fig. 8 clearly confirms that NSGA-II is the most widely used technique (it appears in 20 publications), as it could be expected a priori given the popularity of this algorithm. The second metaheuristic most frequently used is SPEA2 (7 occurrences), being the following ones different variants of MOPSO and MOSA algorithms. The rest of algorithms include a mix of techniques including PAES, PBIL, NSGA, SPEA, etc.

Fig. 8
figure 8

Multi-objective algorithms used in the reviewed papers

Full size image

7 Conclusions and perpectives

Multi-objective optimization with metaheuristics has become a hot research topic in the last decade mainly because metaheuristics have shown to be an easy and effective approach for solving real-world problems. The survey carried out in this paper confirms this fact in the field of structural design. Our purpose has been to provide the reader with a comprehensive review of relevant papers with the goal of offering a source of useful information about the most salient studies in this area.

From the analyzed information, a summary of issues and a number of open research lines can be indicated. We can subdivide them in two classes: (1) those related to structural design problems and (2) those having to do with the multi-objective techniques.

Design problems

From the analyzed papers in Tables 3, 4, and 5 and Fig. 7, we can conclude that most of the studied engineering problems related to area dimensioning with no structural topology design (1.1) have been chosen because they are typically adopted as benchmarks to test multi-objective algorithms. In these problems, the use of static loads and truss structures is common (e.g., truss bridges). Somewhat more complex studies are those of class 2.2, e.g., tall building frames, which include the design of bar sizes as well as structural topological design. Similarly, problems of designs 1.2 (trusses), 2.1 (frames), 1 (slab, cantilever plate, etc.) and 3 (cantilever plate, beam, etc.) have been addressed in the specialized literature. Among the problems that have not been studied yet, we have the optimization of the cross sections of bars defining the shape of the boundary (design 3.1) and the transversal topology (design 4.1).

Multi-objective metaheuristics

A rather quick look at the tables and figures suggests that, from an algorithmic point of view, there are many open research lines which can be largely exploited. For example, many of the problems reported in the specialized literature are encoded using floating point representation (i.e., real numbers are used for all the decision variables), and we found no study in which differential evolution was used to solve any of these problems. This is rather surprising if we consider that differential evolution is a very powerful approach for solving problems in which all the decision variables are real numbers. Some of the multi-objective metaheuristics based on differential evolution that could be used for these problems are GDE3 (Kukkonen and Lampinen 2005) and MOSADE (Huang et al. 2009).

Another interesting finding is that NSGA-II and SPEA2 are still the most commonly used multi-objective metaheuristics in the literature on structural optimization. This is a bit surprising considering that these two MOEAs were introduced more than 10 years ago. Remarkably, the use of other, more recent, MOEAs such as those based on decomposition (e.g., MOEA/D by Zhang and Li (2008) and Li and Zhang (2009)), MOEAs based on structuring the populations into a grid (Nebro et al. 2009b), indicator-based MOEAs (e.g., SMS-EMOA by Beume et al. (2007) and HyPE by Bader and Zitzler (2011)), algorithms based on local approximations (e.g., ANC by Gobbi et al. (2013), NBI by Das and Dennis (1998), UPS-MOEA by Aittokoski and Miettinen (2010)), and non-evolutionary metaheuristics such as scatter search (Nebro et al. 2008a), has not been reported yet in structural optimization problems. The use of coevolution and game theory (Sim and Kim 2004; Tan and Teo 2009) in structural optimization would also be an interesting choice. In fact these approaches may be quite useful in some applications (Barbosa 1997). For example, coevolutionary approaches are known to be very effective for dealing with large-scale optimization problems (i.e., problems having a very large number of decision variables) (see for example the work of Li and Yao (2012)). However, its use in large-scale multi-objective optimization has been very rare until now.

The use of parallel MOEAs (Nebro et al. 2005), surrogate methods (Ray et al. 2009), fitness approximation (Reyes Sierra and Coello Coello 2005) and incorporation of domain knowledge during the search (Landa-Becerra et al. 2008) could also bring important savings in terms of CPU time when solving multi-objective structural optimization problems. However, the use of these techniques has been very relatively scarce until now in multi-objective optimization problems (Ray and Smith 2006).

Finally, another aspect that has been only scarcely explored in multi-objective structural optimization using metaheuristics, is the incorporation of user’s preferences in the search engine (Sanchis et al. 2008). These preferences allow, for example, to focus the search into a specific region of the Pareto front, and also helps the decision maker to choose one (or very few) solution from the many that a multi-objective metaheuristic normally generates (Thiele et al. 2009).

Evidently, more work in these directions is expected to appear in the next few years, as we expect that the use of multi-objective metaheuristics becomes more common not only in structural optimization, but also in engineering in general.