Recovering the Initial Distribution for a Time-Fractional Diffusion Equation

Abstract

We consider the inverse problem of reconstructing the initial condition of a one-dimensional time-fractional diffusion equation from measurements collected at a single interior location over a finite time-interval. The method relies on the eigenfunction expansion of the forward solution in conjunction with a Tikhonov regularization scheme to control the instability inherent in the problem. We show that the inverse problem has a unique solution provided exact data is given, and prove stability results regarding the regularized solution. Numerical realization of the method and illustrations using a finite-element discretization are given at the end of this paper.

1 Introduction

Fractional partial differential equations are extensions of the classical models for which the usual time and/or space derivatives are replaced by fractional-order ones. In recent years, such equations (and fractional calculus in general) have gained increasing currency in the field of mathematical modeling due to a promising wide range of applications in physics, engineering, hydrology, polymer sciences, finance, and many other disciplines; see for example [7, 13, 15, 20, 23].

In this paper, we consider the one-dimensional time-fractional diffusion equation

$$ \partial^{\alpha }_{t}u(x,t) =\partial_{xx}u(x,t)+f(x), \quad x\in I,\ 0< t< T, $$

(1)

subject to the initial and boundary conditions

$$ \begin{aligned} u(x,0) &=\psi_{u}(x), \quad x\in I, \\ u(0,t)&=0, \quad 0< t\leq T, \\ u(l,t)&=0, \quad 0< t\leq T, \end{aligned} $$

(2)

where $I=(0,l)$, and $\partial^{\alpha }_{t}u(x,t)$ stands for the Caputo fractional derivative of $u(x,t)$ with respect to the time variable $t$ of order $\alpha \in (0,1)$. Such equations can be used, for example, to model a sub-diffusion process that takes place in a straight pipe (such as a column experiment) of finite length $l$ over the time period $0\leq t\leq T$. See also [2, 10, 12, 18] for more details and concrete examples.

Finding the density $u$ from a given source $f$ and initial distribution $\psi_{u}$ is usually termed as a forward problem. Here we are concerned with the following inverse problem:

• Given $f(x)$ and a measurement $g_{m}(t)$ of $g(t)=u(x_{0},t)$ , $t\in [0,T]$ , estimate the spatially varying function $\psi_{u}(x)$ .

Such inverse problem can be used to recover the initial concentration of a contaminant (or the initial temperature profile in the case of a heat conduction problem) in a sub-diffusive media which is important for example in environmental engineering, hydrology, and physics. Here we regard $x_{0}$ as a fixed interior location at which the measurements are to be taken.

Nowadays, it can be noticed that one of the most successful and concrete applications of fractional diffusion equations is to adequately describe anomalous diffusion in a complex media such as the sub-diffusion (slow propagation) and super-diffusion (fast propagation) phenomena which have been observed in transport processes in porous media, protein diffusion within cells, transport of ions in column experiments, movement of a material along fractals, etc., see [2, 10, 12, 15, 18, 23].

Equation (1) and its variations have been extensively examined in the last few decades from both theoretical and scientific applications points of view. In [22] Sakamoto and Yamamoto established the unique existence of the weak solution and they gave regularity results and representation formulas for the solution based on the eigenfunction expansion. Murio [19] developed an implicit finite difference approximation and showed that it is unconditionally stable. Agrawal [1] obtained an explicit form of the solution using a finite sine transform. We also mention [2, 7, 17, 20, 27] and references therein for a non-exhaustive list of publications in this area.

Several inverse problems related to (1)–(2) have been proposed. We mention briefly some of the publications in this area. Wang and Liu [25] considered the inverse problem of the determination of the initial distribution from internal measurements of $u(\cdot ,T)$, their problem is in 2D and they used total variation regularization to obtain stable approximations of the backward problem. They presented some examples in image de-blurring. In [6], Deng and Yang proposed a numerical method based on the idea of reproducing kernel approximation to reconstruct the unknown initial heat distribution from a finite set of scattered measurements of transient temperature at a fixed final time. Ye and Xu [26] formulated the inverse problem as an optimal control problem to obtain a space-time spectral method. They derived optimality conditions and some error bounds based on the weak formulation of the forward problem. Zhang and Xu [28] considered the problem of identifying the time-independent source term $f$ from the additional boundary data $u(0,\cdot )$. They established uniqueness results and deduced analytical solution based on the method of eigenfunction expansion. See also [4, 14, 16, 21, 24] for other related inverse problems and their mathematical treatment.

Our proposed method relies on the eigenfunction expansion of the forward solution which can be deduced from the work by [22]. Then we handle the instability of the inverse problem using a Tikhonov regularization scheme; the precise formulation will be given in Sect. 3. We prove existence and stability theorems concerning the resulted infinite-dimensional optimization problem. Besides giving theoretical results, we also present numerical examples to show the efficiency of the proposed approach.

This paper is organized as follows. In Sect. 2 we present some definitions and results, in Sect. 3 we introduce the main problem and results, numerical illustrations using a finite-element discretization are contained in Sect. 4.

2 Preliminaries

In this section, we present some results and definitions pertaining to this paper. We use $(\cdot ,\cdot )$ to denote the scalar product on $L^{2}(I)$, and $H^{1}_{0}(I)$, $H^{1}(I)$, $H^{2}(I)$ the usual Sobolev spaces, e.g. [3], and [9] for other spaces appearing in this paper.

The Caputo fractional derivative of order $\alpha$ of a function $u$ with respect to $t$ is defined as

$$\begin{aligned} \partial^{\alpha }_{t}u(x,t)=\dfrac{1}{\varGamma (1-\alpha )} \int_{0} ^{t}(t-\tau )^{-\alpha } \dfrac{\partial u(x,\tau )}{\partial \tau }\,d \tau , \end{aligned}$$

where $\varGamma (\cdot )$ is the Gamma function. More about fractional calculus can be found in [7, 15].

The Mittag-Leffler function of index $(\alpha ,\beta )$ is the complex function defined as

$$\begin{aligned} E_{\alpha ,\beta }(z)=\sum_{k=0}^{\infty } \dfrac{z^{k}}{\varGamma ( \alpha k+\beta )},\quad\alpha >0,\ \beta \in \mathbb{R},\ z\in \mathbb{C}. \end{aligned}$$

The function $E_{\alpha ,\beta }(z)$ is an entire function, and so the function $E_{\alpha ,\beta }(t)$ is real analytic for $t\in \mathbb{R}$, see [15, 20]. For brevity, we write $E_{\alpha }(\cdot )$ to denote $E_{\alpha ,1}(\cdot )$. We have the following lemmas:

Lemma 1

Suppose that $\alpha \in (0,2)$, $\beta \in \mathbb{R}$, and $\mu$ satisfies $\alpha \pi \leq 2\mu \leq 2\min \{\pi ,\alpha \pi \}$, then there exits a positive constant $C=C(\alpha ,\beta , \mu )$ such that

$$ \bigl|E_{\alpha ,\beta }(z)\bigr|\leq \dfrac{C}{1+|z|}, \quad z\in \mathbb{C},\ \mu \leq \bigl|\arg (z)\bigr|\leq \pi . $$

(3)

Lemma 2

Let $k$ be a nonnegative integer, then

$$\begin{aligned} \int_{0}^{\infty }e^{-zt}t^{\alpha k+\beta -1}E^{(k)}_{\alpha ,\beta } \bigl(\pm a t^{\alpha }\bigr)dt=\dfrac{k! z^{\alpha -\beta }}{ ( z^{\alpha }\mp a ) ^{k+1}},\quad\Re (z)>|a|^{1/\alpha }. \end{aligned}$$

The proofs of the above two lemmas can be found in [20]. From Lemmas 1 and 2, and the analytic continuation we conclude the following corollary concerning the Laplace transform of the M-L function $E_{\alpha }(-a t^{\alpha })$.

Corollary 1

For $a>0$ and $\alpha \in (0,1)$ we have

$$ \int_{0}^{\infty }e^{-zt}E_{\alpha }\bigl(-a t^{\alpha }\bigr)dt=\dfrac{z^{ \alpha -1}}{z^{\alpha }+ a}, \quad \Re (z)>0. $$

(4)

We conclude with the following result which shows that problem (1)–(2) has a unique (weak) solution and gives a representation formula in terms of the eigenfunctions of the operator $-\partial_{xx}$.

Corollary 2

Assuming that $\alpha \in (0,1)$, $\psi_{u}\in H_{0}^{1}(I)$, and $f\in L^{2}(I)$, then there exists a unique solution $u\in L^{2}(0,T;H ^{2}(I)\cap H^{1}_{0}(I))$ to (1). Moreover, the solution $u$ has the representation

$$\begin{aligned} u(x,t)=\sum_{n=1}^{\infty }(\varphi_{n}, \psi_{u})E_{\alpha }\bigl(-\lambda _{n} t^{\alpha } \bigr) \varphi_{n}(x) + \sum_{n=1}^{\infty } \lambda_{n} ^{-1}(\varphi_{n},f) \bigl( 1-E_{\alpha }\bigl(-\lambda_{n} t^{\alpha }\bigr) \bigr) \varphi_{n}(x) \end{aligned}$$

in $L^{2}(0,T;H^{2}(I)\cap H^{1}_{0}(I))$, where $\varphi_{n}(x)= \sqrt{2/l}\,\sin (\sqrt{\lambda_{n}}\,x)$ and $\lambda_{n}=(n \pi /l)^{2}$.

Proof

From [22, Theorem 2.1], we deduce that problem (1)–(2) with $f=0$ has the unique solution

$$\begin{aligned} \sum_{n=1}^{\infty }(\varphi_{n}, \psi_{u})E_{\alpha }\bigl(-\lambda_{n} t ^{\alpha } \bigr) \varphi_{n}(x)\quad\text{in}\ L^{2} \bigl(0,T;H^{2}(I)\cap H ^{1}_{0}(I)\bigr), \end{aligned}$$

and from [22, Theorem 2.2], we see that problem (1)–(2) with $\psi_{u}=0$ has the unique solution

$$\begin{aligned} \sum_{n=1}^{\infty }\lambda_{n}^{-1}( \varphi_{n},f) \bigl( 1-E_{\alpha }\bigl(-\lambda_{n} t^{\alpha }\bigr) \bigr) \varphi_{n}(x)\quad\text{in}\ L ^{2}\bigl(0,T;H^{2}(I)\cap H^{1}_{0}(I) \bigr), \end{aligned}$$

and consequently the result follows. □

3 Main Results

Next we formulate and analyze a regularization method for the aforementioned inverse problem. Throughout the sequel we regard $C$ as a generic constant which may vary in different places. We shall assume that $f\in L^{2}(I)$ and $x_{0}$ is a fixed point in $I$ and satisfying the conditions $\varphi_{n}(x_{0})\neq 0$ for all positive integers $n$.

To present our optimization approach for handling the inverse problem, consider the operator $A_{t}:[0,T]\times H^{1}_{0}(I)\rightarrow \mathbb{R}$ given by

$$\begin{aligned} A_{t} \psi =\sum_{n=1}^{\infty } \varphi_{n}(x_{0})E_{\alpha }\bigl(-\lambda _{n} t^{\alpha }\bigr) (\varphi_{n},\psi ) + \sum _{n=1}^{\infty }\lambda _{n}^{-1}( \varphi_{n},f) \bigl( 1-E_{\alpha }\bigl(-\lambda_{n} t^{\alpha }\bigr) \bigr) \varphi_{n}(x_{0}). \end{aligned}$$

Since for exact data $g$ we have $A_{t} \psi_{u} = g(t)$, we want to choose the approximation $\psi$ of $\psi_{u}$ such that the residual $\|A_{t} \psi - g_{m}\|$ is small. But since inverse diffusion problems are known to be ill-posed [8], we expect instability in the fractional inverse problem. One possible remedy to this issue is to use regularization. To this end, we instead consider the optimization problem

$$ \min_{\psi \in H_{0}^{1}(I)} \|A_{t}\psi -g_{m}\|^{2}_{L^{2}(0,T)}+ \beta \|\psi \|^{2}_{H^{1}(I)}, $$

(5)

where $\beta >0$ is the regularization parameter and $\|\psi \|^{2} _{H^{1}(I)}$ is the regularizing term. We note that problem (5) can be identified as a Tikhonov regularized version of the familiar output least-squares approach.

First we show that the proposed inverse problem has a unique solution provided exact data is given.

Theorem 1

Suppose that $u$ and $w$ are the solutions of (1) with initial conditions $\psi_{u}\in H_{0}^{1}(I)$ and $\psi_{w}\in H_{0}^{1}(I)$, respectively. If $u(x_{0},t)=w(x_{0},t)$ for all $0\leq t\leq T$, then $\psi_{u}=\psi_{w}$ in $L^{2}(I)$.

Proof

Since $u(x_{0},t)=w(x_{0},t)$, from Corollary 2 we can conclude that

$$\begin{aligned} \sum_{n=1}^{\infty } ( \varphi_{n}, \psi_{u} ) E_{\alpha }\bigl(- \lambda_{n} t^{\alpha }\bigr) \varphi_{n}(x_{0}) = \sum _{n=1}^{\infty } ( \varphi_{n}, \psi_{w} ) E_{\alpha }\bigl(-\lambda_{n} t^{\alpha } \bigr) \varphi_{n}(x_{0}),\quad0\leq t\leq T. \end{aligned}$$

Let $a>0$ be a fixed constant, and consider the series

$$\begin{aligned} \sum_{n=1}^{\infty } ( \varphi_{n}, \psi_{u} ) E_{\alpha }\bigl(- \lambda_{n} z^{\alpha }\bigr) \varphi_{n}(x_{0}),\quad |z|\geq a. \end{aligned}$$

By bound (3), the fact that $|z|\geq a$, and Schwarz inequality we have

$$\begin{aligned} \bigl\vert ( \varphi_{n},\psi_{u} ) E_{\alpha } \bigl(-\lambda_{n} z^{ \alpha }\bigr) \varphi_{n}(x_{0}) \bigr\vert \leq \dfrac{C\|\psi_{u}\|_{L^{2}(I)}}{1+ \lambda_{n} a^{\alpha }}\leq C \dfrac{1}{n^{2}}, \end{aligned}$$

and consequently, the series is uniformly convergent to an analytic function. Hence, the series $\sum_{n=1}^{\infty } ( \varphi_{n}, \psi_{u} ) E_{\alpha }(-\lambda_{n} t^{\alpha }) \varphi_{n}(x _{0})$ is real analytic in $t>0$. By real analytic continuation, we see that

$$\begin{aligned} \sum_{n=1}^{\infty } ( \varphi_{n}, \psi_{u} ) E_{\alpha }\bigl(- \lambda_{n} t^{\alpha }\bigr) \varphi_{n}(x_{0}) = \sum _{n=1}^{\infty } ( \varphi_{n}, \psi_{w} ) E_{\alpha }\bigl(-\lambda_{n} t^{\alpha } \bigr) \varphi_{n}(x_{0}),\quad t\geq 0. \end{aligned}$$

Multiplying both sides by $e^{-zt}$, and then integrating from 0 to $\infty$ we get

$$\begin{aligned} &\int_{0}^{\infty } \sum_{n=1}^{\infty }e^{-zt} ( \varphi _{n},\psi_{u} ) E_{\alpha }\bigl(- \lambda_{n} t^{\alpha }\bigr) \varphi_{n}(x _{0})dt \\ & \quad= \int_{0}^{\infty } \sum_{n=1}^{\infty }e^{-zt} ( \varphi_{n}, \psi_{w} ) E_{\alpha }\bigl(- \lambda_{n} t^{\alpha }\bigr) \varphi_{n}(x _{0})dt. \end{aligned}$$

Since the function $t^{-\alpha } e^{-\beta t}$ is integrable on the interval $0< t<\infty$ for $\beta >0$, and

$$\begin{aligned} \bigl\vert e^{-t\Re ( z)} ( \varphi_{n},\psi_{u} ) E_{\alpha }\bigl(- \lambda_{n} t^{\alpha }\bigr) \varphi_{n}(x_{0})\bigr\vert \leq e^{-t\Re ( z)} \dfrac{C _{0}\|\psi_{u}\|_{L^{2}(I)}}{1+ \lambda_{n} t^{\alpha }}\leq C t^{- \alpha } e^{-t\Re (z)}, \end{aligned}$$

the Lebesgue dominated convergence theorem and (4) imply

$$\begin{aligned} \sum_{n=1}^{\infty }\dfrac{ ( \varphi_{n},\psi_{u} ) \varphi _{n}(x_{0})}{z^{\alpha }+\lambda_{n}} =\sum _{n=1}^{\infty }\dfrac{ ( \varphi_{n},\psi_{w} ) \varphi_{n}(x_{0})}{z^{\alpha }+ \lambda_{n}},\quad\Re (z)>0, \end{aligned}$$

or equivalently

$$\begin{aligned} \sum_{n=1}^{\infty }\dfrac{ ( \varphi_{n},\psi_{u} ) \varphi _{n}(x_{0})}{\xi +\lambda_{n}} =\sum _{n=1}^{\infty }\dfrac{ ( \varphi_{n}, \psi_{w} ) \varphi_{n}(x_{0})}{\xi +\lambda_{n}},\quad\Re (\xi )>0. \end{aligned}$$

But since each term in this series is analytic, and

$$\begin{aligned} \biggl\vert \dfrac{ ( \varphi_{n},\psi_{u} ) \varphi_{n}(x_{0})}{ \xi +\lambda_{n}}\biggr\vert \leq \dfrac{\|\psi_{u}\|_{L^{2}(I)}}{\Re ( \xi )+\lambda_{n}} \leq C \dfrac{1}{n^{2}}, \end{aligned}$$

it follows from the Weierstrass M-test that the series converges uniformly to an analytic function for $\Re (\xi )>0$. Now since

$$\begin{aligned} \biggl\vert \dfrac{ ( \varphi_{n},\psi_{u} ) \varphi_{n}(x_{0})}{ \xi +\lambda_{n}}\biggr\vert \leq \dfrac{\|\psi_{u}\|_{L^{2}(I)}}{\Re ( \xi )+\lambda_{n}}\leq C \dfrac{1}{n^{2}-3} \end{aligned}$$

for $n\geq 2$ and $\Re (\xi )>\lambda_{1}-\lambda_{2}$, and the series $\sum_{n=2}^{\infty }(n^{2}-3)^{-1}$ is convergent, we conclude that

$$\begin{aligned} \sum_{n=2}^{\infty }\dfrac{ ( \varphi_{n},\psi_{u} ) \varphi _{n}(x_{0})}{\xi +\lambda_{n}} \end{aligned}$$

is analytic for $\Re (\xi )>\lambda_{1}-\lambda_{2}$. By continuation, we have

$$\begin{aligned} \dfrac{ ( \varphi_{1},\psi_{u} ) \varphi_{1}(x_{0})}{\xi + \lambda_{1}}+\sum_{n=2}^{\infty } \dfrac{ ( \varphi_{n},\psi_{u} ) \varphi_{n}(x_{0})}{\xi +\lambda_{n}} = \dfrac{ ( \varphi_{1},\psi _{w} ) \varphi_{1}(x_{0})}{\xi +\lambda_{1}}+\sum_{n=2}^{\infty } \dfrac{ ( \varphi_{n},\psi_{w} ) \varphi_{n}(x_{0})}{\xi + \lambda_{n}} \end{aligned}$$

on the set $A_{1}=\{\xi \in \mathbb{C}\,:\,\Re (\xi )>\lambda_{1}- \lambda_{2},\,\xi \neq -\lambda_{1} \}$. Integrating both sides over any circle contained in $A_{1}$ and containing the point $z=-\lambda_{1}$ in its interior, then applying the Cauchy integral theorem, we get

$$\begin{aligned} -2\pi ( \varphi_{1},\psi_{u} ) i=-2\pi ( \varphi_{1},\psi _{w} ) i, \end{aligned}$$

that is, $( \varphi_{1},\psi_{u} ) = ( \varphi_{1},\psi _{w} )$. Repeating the above argument, we inductively conclude that

$$\begin{aligned} ( \varphi_{n},\psi_{u} ) = ( \varphi_{n}, \psi_{w} ) , \quad n=2,3,\dots . \end{aligned}$$

Hence, $\psi_{u}=\psi_{w}$ in $L^{2}(I)$, which ends the prove. □

The next task is to show that the optimization problem (5) has a unique solution. To this end, we need the following lemma:

Lemma 3

For a fixed $\beta >0$, the functional $J_{\beta }:H_{0}^{1}(I)\rightarrow \mathbb{R}$ given by

$$\begin{aligned} J_{\beta }(\psi )=\|A_{t}\psi -g_{m} \|^{2}_{L^{2}(0,T)}+\beta \| \psi \|^{2}_{H^{1}(I)} \end{aligned}$$

is weakly lower semicontinuous and strictly convex.

Proof

Let $\psi \in H_{0}^{1}(I)$, and let $\{\psi_{n}\}$ be any sequence in $H_{0}^{1}(I)$ with $\psi_{n}\rightharpoonup \psi$ in $H_{0}^{1}(I)$. In view of (3) and the Cauchy-Schwarz inequality we have

$$ \begin{aligned} \|A_{t}\psi_{n}-A_{t}\psi \|^{2}_{L^{2}(0,T)} &\leq C \int_{0}^{T} \sum_{k=1}^{\infty } \bigl( 1+k^{2} t^{\alpha } \bigr) ^{-2} \sum _{j=1} ^{\infty }\bigl\vert ( \varphi_{j}, \psi_{n}-\psi )\bigr\vert ^{2} dt \\ &\leq C \int_{0}^{T} t^{-\alpha } dt\sum _{k=1}^{\infty }k^{-2} \sum _{j=1}^{\infty }\bigl\vert ( \varphi_{j}, \psi_{n}-\psi )\bigr\vert ^{2} \\ &\leq C \|\psi_{n}-\psi \|^{2}_{L^{2}(I)}, \end{aligned} $$

where the last inequality follows from Bessel’s inequality. But since (e.g. Evans [9]) the space $H^{1}(I)$ is compactly embedded in $L^{2}(I)$, we have $\psi_{n}\rightarrow \psi$ in $L^{2}(I)$, and consequently

$$\begin{aligned} \lim_{n\rightarrow \infty } \|A_{t}\psi_{n}-A_{t} \psi \|_{L^{2}(0,T)}=0. \end{aligned}$$

From the reverse triangle inequality and simple manipulations we see that

$$\begin{aligned} \lim_{n\rightarrow \infty } \|A_{t}\psi_{n}-g_{m} \|_{L^{2}(0,T)}=\|A _{t}\psi -g_{m}\|_{L^{2}(0,T)}. \end{aligned}$$

Thus, since $\|\cdot \|$ is weakly lower semicontinuous, it follows that

$$ \begin{aligned} J_{\beta }(\psi ) &=\|A_{t}\psi -g_{m} \|^{2}_{L^{2}(0,T)}+\beta \| \psi \|^{2}_{H^{1}(I)} \\ &\leq \lim_{n\rightarrow \infty } \|A_{t}\psi_{n}-g_{m} \|^{2}_{L^{2}(0,T)}+ \beta \varliminf_{n\rightarrow \infty } \| \psi_{n}\|^{2}_{H^{1}(I)} \\ &\leq \varliminf_{n\rightarrow \infty } J_{\beta }(\psi_{n}), \end{aligned} $$

showing that $J_{\beta }$ is weakly lower semicontinuous.

Next, we show that $J_{\beta }$ is strictly convex. In view of the fact that $\|\cdot \|^{2}_{H^{1}(I)}$ is strictly convex, it suffices to show that the functional $J$ given by

$$\begin{aligned} J(\psi )=\|A_{t}\psi -g_{m}\|^{2}_{L^{2}(0,T)} \end{aligned}$$

is convex. For all $\varphi ,\psi \in H_{0}^{1}(I)$ and $\lambda \in [0,1]$ we have

$$\begin{aligned} J\bigl(\lambda \varphi +(1-\lambda )\psi \bigr) &=\bigl\| \lambda (A_{t} \varphi -g_{m})+(1- \lambda ) (A_{t}\psi -g_{m}) \bigr\| ^{2}_{L^{2}(0,T)} \\ &\leq \bigl( \lambda \|A_{t}\varphi -g_{m}\|_{L^{2}(0,T)} + (1- \lambda )\|A_{t}\psi -g_{m}\|_{L^{2}(0,T)} \bigr) ^{2} \\ &\leq \lambda J(\varphi )+(1-\lambda ) J(\psi ), \end{aligned}$$

where the last inequality follows from the fact that $|\cdot |^{2}$ is convex (on ℝ). Thus $J$ is convex, and so the functional $J_{\beta }$ is strictly convex. □

Now we are ready to prove the existence and uniqueness results for the minimization problem given in (5).

Theorem 2

The optimization problem (5) has a unique solution $\psi_{\beta} \in H_{0}^{1}(I)$.

Proof

Let $\varepsilon =\inf_{\psi \in H_{0}^{1}(I)} J_{\beta }(\psi )$. By definition of infimum, there exists a sequence $\{\psi_{n}\}\subset H _{0}^{1}(I)$ such that $J_{\beta }(\psi_{n})\rightarrow \varepsilon$. Clearly $\{\psi_{n}\}$ is bounded in the Hilbert space $H_{0}^{1}(I)$, and so, there exists a subsequence of $\{\psi_{n}\}$, which we still denote by $\{\psi_{n}\}$, and a $\tilde{\psi }\in H^{1}_{0}(I)$ such that $\psi_{n}\rightharpoonup \tilde{\psi }$ in $H^{1}_{0}(I)$. Since $J_{\beta }$ is weakly lower semicontinuous we have

$$\begin{aligned} J_{\beta }(\tilde{\psi }) &\leq \varliminf_{n\rightarrow \infty } J _{\beta }(\psi_{n})=\varepsilon , \end{aligned}$$

showing that $\tilde{\psi }$ is a solution of the optimization problem (5). The uniqueness follows from the strict convexity of $J_{\beta }$, which ends the proof. □

We conclude this section with the following stability result.

Theorem 3

Suppose that $\psi_{u} \in H_{0}^{1}(I)$ and $g\in L^{2}(0,T)$. Let $\{ g_{n} \} \subset L^{2}(0,T)$ be a sequence of observations of $g$, and let $\{ \epsilon_{n} \}$ and $\{ \beta_{n} \}$ be two sequences of real numbers such that

• 1. $\epsilon^{2}_{n}\leq \beta_{n}\leq \epsilon_{n}$ $\forall n\in \mathbb{N}$,

• 2. $\Vert g_{n}-g\Vert_{L^{2}(0,T)}\leq \epsilon_{n}$ $\forall n \in \mathbb{N}$,

• 3. $\epsilon_{n}\rightarrow 0$ as $n\rightarrow \infty$.

For each $n\in \mathbb{N}$, let $\psi_{n}\in H_{0}^{1}(I)$ be the unique solution of the optimization problem

$$\begin{aligned} \min_{\psi \in H_{0}^{1}(I)}\Vert A_{t}\psi -g_{n} \Vert^{2}_{L^{2}(0,T)}+ \beta_{n}\Vert \psi \Vert^{2}_{H^{1}(I)}. \end{aligned}$$

Then $\psi_{n}\rightarrow \psi_{u}$ in $L^{2}(I)$.

Proof

From the definition of $\psi_{n}$, for all $n\in \mathbb{N}$ we have

$$\begin{aligned} \beta_{n}\Vert \psi_{n}\Vert^{2}_{H^{1}(I)} &\leq \Vert A_{t}\psi_{u}-g _{n} \Vert^{2}_{L^{2}(0,T)}+\beta_{n}\Vert \psi_{u} \Vert^{2}_{H^{1}(I)} \\ &= \Vert g-g_{n}\Vert^{2}_{L^{2}(0,T)}+ \beta_{n}\Vert \psi_{u}\Vert ^{2}_{H^{1}(I)} \\ &\leq \beta_{n}+\beta_{n}\Vert \psi_{u} \Vert^{2}_{H^{1}(I)}. \end{aligned}$$

Therefore $\{\psi_{n}\}$ is bounded in $H_{0}^{1}(I)$, and so, there exists a subsequence of $\{\psi_{n}\}$, which we still denote by $\{\psi_{n}\}$, and a vector $\tilde{\psi }\in H_{0}^{1}(I)$ such that $\psi_{n}\rightharpoonup \tilde{\psi }$ in $H_{0}^{1}(I)$. We have

$$ \begin{aligned} \Vert A_{t}\psi_{n}-g \Vert^{2}_{L^{2}(0,T)} &\leq 2 \bigl( \Vert A_{t} \psi_{n}-g_{n}\Vert^{2}_{L^{2}(0,T)}+\Vert g_{n}-g\Vert^{2}_{L^{2}(0,T)} \bigr) \\ &\leq 2 \bigl( \Vert A_{t}\psi_{u}-g_{n} \Vert^{2}_{L^{2}(0,T)}+\beta _{n} \Vert \psi_{u} \Vert^{2}_{H^{1}(I)}+\epsilon^{2}_{n} \bigr) \\ & \leq 2 \bigl( \epsilon^{2}_{n}+\beta_{n} \Vert \psi_{u}\Vert^{2}_{H^{1}(I)}+ \epsilon^{2}_{n} \bigr) , \end{aligned} $$

and so from the proof of Lemma 3 we see that

$$\begin{aligned} \Vert A_{t}\tilde{\psi }-g\Vert_{L^{2}(0,T)}=\lim _{n\rightarrow \infty }\Vert A_{t}\psi_{n}-g \Vert_{L^{2}(0,T)}=0. \end{aligned}$$

Now the fact that $\psi_{u}$ is unique implies $\tilde{\psi }=\psi _{u}$, and since $\psi_{n}\rightarrow \tilde{\psi }$ in $L^{2}(I)$, we also have $\psi_{n}\rightarrow \psi_{u}$ in $L^{2}(I)$, which ends the proof. □

4 Numerical Illustration

In this section we will demonstrate how to implement the proposed method in a practical algorithm. We present several examples to evaluate the proposed algorithm.

4.1 Implementation

In the actual computations we compute the minimizer of (5) from a finite-dimensional subspace $X_{N}$ of $H^{1}_{0}(I)$. That is, the solution of the continuous optimization problem (5) is approximated by the solution of the discretized optimization problem

$$ \min_{\psi \in X_{N}} J^{N}_{\beta }(\psi ):=\|A_{t}\psi -g_{m}\|^{2} _{L^{2}(0,T)}+\beta \|\psi \|^{2}_{H^{1}(I)}. $$

(6)

Since $X_{N}$ is finite-dimensional, it is convex and closed. Thus, from the fact that $J_{\beta }$ is weakly lower semicontinuous, strictly convex, and coercive it follows that the optimization problem (6) admits a unique solution, which we shall denote by $\psi_{\beta }$.

Let $\{\psi_{1},\psi_{2},\dots ,\psi_{N}\}$ be a basis for $X_{N}$, and write the solution $\psi_{\beta }$ of (6) as

$$\begin{aligned} \psi_{\beta }=\sum_{i=1}^{N}A_{i} \psi_{i}. \end{aligned}$$

Define the matrices $\textbf{P},\textbf{B}\in \mathbb{R}^{N\times N}$, the vector $\textbf{K}\in \mathbb{R}^{N}$, and the constant $C\in \mathbb{R}$ by

$$\begin{gathered} (\textbf{B})_{i,j}=(\gamma_{i},\gamma_{j})_{L^{2}(0,T)}, \qquad(\textbf{P})_{i,j}=(\psi_{i},\psi_{j})_{H^{1}(I)}, \\ (\textbf{K})_{i}= ( \gamma_{i},g_{m} -F ) _{L^{2}(0,T)}, \qquad C=\|F-g_{m}\|^{2}_{L^{2}(0,T)}, \end{gathered}$$

where the functions $\gamma_{i}$ and $F$ are defined as

$$\begin{gathered} \gamma_{i}(t)=\sum_{k=1}^{\infty }( \varphi_{k},\psi_{i}) E_{\alpha } \bigl( - \lambda_{k} t^{\alpha } \bigr) \varphi_{k}(x_{0}), \\ F(t)=\sum_{k=1}^{\infty }\lambda^{-1}_{k}( \varphi_{k},f) \bigl( 1-E_{ \alpha } \bigl( -\lambda_{k} t^{\alpha } \bigr) \bigr) \varphi_{k}(x_{0}). \end{gathered}$$

Then by simple manipulations, one can show that

$$\begin{aligned} J^{N}_{\beta }(\textbf{A})=\textbf{A}^{T}\textbf{B} \textbf{A}-2 \textbf{A}^{T} \textbf{K}+C+\beta \textbf{A}^{T} \textbf{P} \textbf{A}. \end{aligned}$$

Since the objective functional $J^{N}_{\beta }$ is convex, a necessary and sufficient condition for $\textbf{A}\in \mathbb{R}^{N}$ to be a global minimizer is

$$\begin{aligned} \nabla J^{N}_{\beta }(\textbf{A})=2\textbf{B}\textbf{A}-2 \textbf{K}+2 \beta \textbf{P}\textbf{A}=0, \end{aligned}$$

and hence, the vector of coefficients $\textbf{A}$ is obtained by solving the linear system of equations

$$\begin{aligned} (\textbf{B}+\beta \textbf{P}) \textbf{A}=\textbf{K}. \end{aligned}$$

4.2 Examples

In the following examples the approximating subspace $X_{N}$ of $H_{0}^{1}(I)$ is chosen to be the space of continuous piecewise linear polynomials with respect to the regular mesh

$$\begin{aligned} 0=x_{0}< x_{1}< \cdots < x_{N+1}=l \end{aligned}$$

and having zero boundary values. We use the standard basis functions of $X_{N}$ which are defined by the conditions

$$\begin{aligned} \psi_{i}(x_{j})=\delta_{i,j},\quad i=1,\dots ,N, \ j=0,\dots ,N+1, \end{aligned}$$

where $\delta_{i,j}$ is the Kronecker delta function.

Remark 1

It can be shown that $X_{N}$ is in fact a subspace of $H_{0}^{1}(I)$, and the set $\{\psi_{1},\dots ,\psi_{N}\}$ is indeed a basis for $X_{N}$; see for example [3, 5]. Instead, one can also use the approximating subspace

$$\begin{aligned} X_{N}=\text{span} \bigl\{ \sin (\pi x/l),\sin (2\pi x/l),\dots ,\sin (N \pi x/l) \bigr\} , \end{aligned}$$

which we shall not consider in the experiments below.

In these experiments we assume that the measurement $g_{m}$ of $u(x_{0},\cdot )$ is contaminated by an additive Gaussian noise satisfying

$$\begin{aligned} \frac{\|g_{m}-u(x_{0},\cdot )\|_{L^{2}(0,T)}}{\|u(x_{0},\cdot )\|_{L ^{2}(0,T)}}= \epsilon , \end{aligned}$$

where $\epsilon$ represents the noise level in the data. Furthermore, the observation time and position are taken to be $T=0.1$ and $x_{0}=1/\sqrt{2}$, respectively.

The regularization parameter $\beta$ is chosen using the L-curve strategy which is an a priori rule that chooses the parameter $\beta$ that corresponds to the corner (point of maximum curvature) of the parametrized curve

$$\begin{aligned} \bigl( \|A_{t}\psi_{\beta }-g_{m}\|_{L^{2}(0,T)},\| \psi_{\beta }\| _{L^{2}(I)} \bigr) . \end{aligned}$$

We refer the reader to [8, 11] for more detailed discussion. In the sequel, we designate the symbol $\beta_{O}$ to denote optimal choice of the regularization parameter $\beta$ (using the knowledge of the exact solution), and $\beta_{L}$ to denote the parameter obtained by the L-curve criterion.

We note that the ill-posedness of the considered inverse problem is reflected by the large condition number of the matrix $B$ which was somewhere between $10^{9}$ and $10^{13}$ for most of the experiments below.

Example 1

In this first example, we consider the fractional order diffusion equation

$$ \begin{aligned} \partial^{1/2}_{t}u &=\partial_{xx}u+x^{2} - x, \quad 0< x< 1,\ 0< t< 0.1, \\ u(x,0)&=\sin (2\pi x) -\bigl(x^{4}-2x^{3}+x\bigr)/12, \\ u(0,t)&=0, \\ u(1,t)&=0. \end{aligned} $$

The forward solution is

$$\begin{aligned} u(x,t)=\exp \bigl( 16\pi^{4} t \bigr) \operatorname{Erfc} \bigl( 4 \pi^{2} \sqrt{t} \bigr) \sin (2\pi x) + \frac{x^{3}}{6} - \frac{x^{4}}{12} - \frac{x}{12}. \end{aligned}$$

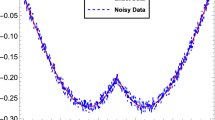
In Table 1 we compare the relative $L^{2}$-errors for several noise levels using optimal regularization parameter and the L-curve method. The exact solution versus the recovered initial concentrations are shown in Fig. 1. A plot for the L-curve is shown in Fig. 3(a).

Fig. 1

Comparison between the exact initial condition $\psi_{u}$ and the recovered approximations for different noise levels

Table 1 Relative $L^{2}$ errors for several noise levels using optimal regularization parameter and the L-curve method

Example 2

In this example we consider the equations:

$$ \begin{aligned} \partial^{3/4}_{t}u &=\partial_{xx}u+ \pi^{2}\sin (\pi x), \quad 0< x< 1,\ 0< t< 0.1, \\ u(x,0)&=2\sin (\pi x), \\ u(0,t)&=0, \\ u(1,t)&=0. \end{aligned} $$

The forward solution is

$$\begin{aligned} u(x,t)=E_{3/4}\bigl(-\pi^{2} t^{3/4}\bigr) \sin (\pi x) +\sin (\pi x). \end{aligned}$$

In Table 2 we compare the relative $L^{2}$-errors for several noise levels using optimal regularization parameter and the L-curve method. The exact solution versus the recovered initial concentrations are shown in Fig. 2. A plot for the L-curve is shown in Fig. 3(b).

Fig. 2

Comparison between the exact initial condition $\psi_{u}$ and the recovered approximations for different noise levels

Fig. 3

L-curves corresponding to noise level $\epsilon =0.005$. The graphs are plotted in a log-log scale

Table 2 Relative $L^{2}$ errors for several noise levels using optimal regularization parameter and the L-curve method.

5 Conclusions and Future Work

We have investigated the possibility of recovering initial distribution in a time-fractional diffusion equation. We proposed a regularized output least-square method and give existence results and a stability analysis. The numerical experiments showed encouraging results.

Our analysis does not contain any convergence rates which we hope to obtain in a future work. Furthermore, we look to generalize the results for problems with higher spatial domains which are more realistic to scientific applications.