Introduction

Many engineering problems, such as the uneven settlement of foundations, the deformation of underground structures, and casing damage, are caused by the strong creep behavior of weakly cemented soft rock (WCSR) (Xu and Chen 2013; Xu and Jiang 2017). The weakly cemented soft rock shows significant rheological characteristics under long-term loading and exposure to water (Roedder and Bassett 1981; Sun and Wang 2000). The physicochemical interaction between water and rock not only reduces the friction angle and cohesion of WCSR but alters the mineral composition and microstructure of the rock, thereby aggravating crack initiation and propagation (Jiang et al. 2014; Matthess 1988). These changes lead to deterioration of the strength and rigidity of WCSR, which can result in engineering disasters.

The effect of the water content on the mechanical properties of rock is a particularly prominent topic among researchers. Chenevert (1970) studied the decrease in strength experienced by mudstone through water absorption; Ajalloeian and Lashkaripour (2000) utilized the exponential relationship between mudstone strength and water content to predict the uniaxial compressive strength at different water contents. Işık (2010) concluded that even a very small increase in the water content can cause considerable loss of the uniaxial compressive strength of gypsum. Shi et al. (2016) studied rock strength data at various water contents and demonstrated that sand-stone strength and water content have a negative exponential relationship. In addition, research has also shown that the water content has a significant effect on the creep behavior of rock (Hong et al. 2015; Wei et al. 2018). A series of shear creep tests on the weak structural plane of sandstone at different water contents has also been conducted (Li et al. 2008). Huang and Liu (2011) studied the effect of changes in the moisture content on the creep properties of siltite and proposed a mathematical relationship between the creep modulus and moisture content. Liu et al. (2015) analyzed the creep properties of rock with different moisture contents and the relationship between the moisture content and creep mechanical properties. The research results showed that the ratio of the creep strain and instantaneous strain, the initial, steady, and ultimate accelerated creep rates increased, while the long-term strength of the red bed mudstone decreased with an increase in the water content (Ju et al. 2016). The creep test result of loess show that the creep strain increases with an increase of moisture content and decreases with an increase in confining pressure (Tang et al. 2020). In general, water content and stress are important factors affecting rock creep characteristics (Deng et al. 2016; Feng et al. 2020; Yang et al. 2007; Zhang et al. 2013). Therefore, it is necessary to consider the effect of the water content conditions on the creep behavior of weakly cemented soft rock.

Creep behavior is one of the most important mechanical properties of rock, and creep modeling is the main characterization technique for this property (Duan et al. 2013; Hou et al. 2019; Li et al. 2013; Wu et al. 2014, 2015). Thus, to establish a reasonable creep model, a quantitative description of the influence of creep effects, strain rate, and stress relaxation on the strength and deformation characteristics of WCSR is necessary. In recent decades, numerous creep models have been proposed to simulate the behavior of rock creep (e.g., the Maxwell, Kelvin, and Nishihara models) (Chen et al. 2015; Ofoegbu et al. 2017; Tomanovic 2006). At present, creep constitutive models for WCSR mainly include empirical models, element models, and the viscoelastic–plastic mechanical model (Zhou et al. 2011, 2013; Liao et al. 2016; Liu et al. 2016; Metzler and Nonnenmacher 2003). As such, the element combination models, which have strong theoretical properties, a strict mechanics deduction process, and parameters with clear physical meaning, have been widely employed to study the creep characteristics of geotechnical materials. However, accelerated creep has not yet been well described by the integral order component model. Fractional calculus theory can be employed to study the differential of any order and can describe the creep behavior of geotechnical materials in addition to the evolution of structural characteristics (Arikoglu 2014; Heymans and Bauwens 1994; Papoulia et al. 2010; Pu et al. 2018). Fractional calculus has been considered as one of the best tools for modeling the physical responses of materials owing to its flexibility. Moreover, many creep models have been established. For example, Yuan (2014) proposed a creep model to describe the creep damage characteristics of mudstone using fractional calculus theory, while Tang et al. (2017) proposed a new four-element rock creep model based on the variable-order fractional derivative and continuum damage mechanics. In addition, Chen et al. (2014) proposed a fractional-order theological model to describe the creep behavior of fractured mudstone based on the fractional calculus and three-parameter theological models, while Li established a fractional derivative of the Burgers model based on strain energy theory, where the model parameters were obtained using the particle swarm optimization method (Li et al. 2018). Furthermore, Zhang established a new three-element nonlinear stress relaxation model for Nanning expansive soils based on fractional calculus theory (Zhang et al. 2014).

However, despite the recent improvements in creep models of geotechnical materials, the majority of universal models cannot fully describe the accelerated creep characteristics of soft rock, and the relationship between creep properties and experimental conditions remains unclear (Bouras et al. 2018; Xu and Jiang 2017; Zhou et al. 2013). Thus, we herein report our study involving multi-stage loading creep tests of weakly cemented soft rock under different water content conditions. A novel four-element fractional-order creep model was developed using the Abel dashpot instead of the Kelvin clay pot element, in addition to taking the plastic element instead of the elastic element. The model parameters of the four-element creep model were obtained using the trust-region method. Finally, the reliability of the four-element model was verified.

Creep tests and results analysis

Rock samples

The rock samples employed in the multi-stage loading creep tests were taken from the Jurassic mudstone strata in the main inclined shaft of the Hongqingliang Coal Mine, in Erdos City, Inner Mongolia. The rock sample density (ρ) was 2.41 g/cm3, and the natural water content (w) was 7.9%.

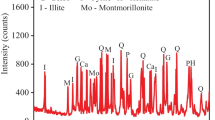
X-Ray diffraction measurements showed that the mineral composition of the rock samples was as follows: quartz, 31.6%; montmorillonite, 18.9%; albite, 15.9%; illite, 15.4%; and kaolinite, 18.2%. It should be noted that the hydrophilic viscous minerals present in the rock (i.e., montmorillonite, illite, and kaolinite) are responsible for the facile disintegration of soft rock in water. This rock adopts a block structure exhibiting porosity cementation and belongs to the group of medium expansive WCSR.

The rock was prepared in cylindrical samples, which diameter (φ) is 50 mm and height (h) is 100 mm, using a YBZS-100 rock coring machine and cutting apparatus according to test procedures reported by the ISRCSC. Four groups of WCSR samples with water contents of 0% (dry state), 7.9% (natural state), 14.5%, and 21.6% (saturated state) were prepared using drying and natural immersion methods, as appropriate. The processed samples exhibited good integrity.

Creep test scheme

The multi-stage loading creep tests of the WCSR samples were performed using the GDS HPTAS creep triaxial apparatus, which is shown in Fig. 1. The axial loaded value of the apparatus can reach 250 kN, and its lowest loading rate is 0.01 mm/min. This apparatus can be employed for stress or strain control tests.

Fig. 1
figure 1

Triaxial rheometer apparatus (GDS HPTAS)

Full size image

The uniaxial compressive strength (σc) obtained from the uniaxial compression test was used as the loading basis for the creep tests, where the confining pressure was 6 MPa, and the maximum loading stress was about 0.7σc times the uniaxial strength.

The majority of the creep tests performed showed that the geotechnical materials exhibited a memory effect for the loading history. According to the principle of linear superposition, the creep curves of WCSR under different stress levels and water contents can be obtained. Therefore, multi-stage loading creep tests of the WCSR were performed. The creep experiment was divided into three stages: (1) The advanced loading module was used to apply the confining pressure and axial pressure at a loading rate of 0.05 MPa/s until a pressure of 6 MPa was reached, which was a preset value set according to the actual working environment of weakly cement soft rock. The specimen was in an initial isotropic stress state after confining pressure loading (Su et al. 2019). (2) A loading rate of 0.1 MPa/s was then employed until the deviator stress reached the predicted value while the confining pressure was kept constant. (3) Multi-stage loading creep tests of the WCSR were performed and a loading time of 50 h was employed for each stage. When the creep rate became less than or equal to 0.01 mm/min (i.e., a stable creep stage), the subsequent level of load was stopped. The test was stopped when the deformation rate exceeded 0.05%·h−1 of the accelerated creep stage. All of the creep test data were recorded during the test and the multi-stage loading scheme are outlined in Table 1.

Table 1 Multi-stage loading scheme employed for the rheology tests
Full size table

Analysis of creep test results

Creep deformation

The soft rock samples were found to exhibit obvious creep behavior characteristics during the various creep tests, but no significant brittle failure was observed. The results of the axial strain and radial strain under different deviator stresses and water contents were obtained, as shown in Fig. 2.

Fig. 2
figure 2

Creep test results. (a) w = 0%; (b) w = 7.9%; (c) w = 14.5%; (d) w = 21.6%

Full size image

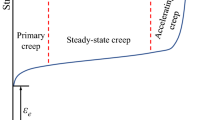
The results show that the deformation of WCSR increases with the load time. The total deformation includes instantaneous deformation and creep deformation. However, the creep curves present in different forms with different water content and deviator stress. More specifically, attenuation creep and constant rate creep behavior were observed when the deviator stress (σ0) was relatively small, and accelerated creep behavior occurred only for larger deviator stress (σ0) values. In addition, the creep curves of WCSR indicate typical creep characteristics, including attenuation creep, constant rate creep, and accelerated creep. An increase in the deviator stress leads to damage and destruction of the internal structure of the soft rock specimen, thereby increasing the creep deformation. A higher deviator stress will lead to the rock sample reaching a steady state or accelerated state more rapidly.

Figure 2 also shows that accelerated creep behavior occurs when the water content (w) is 0% and the deviator stress (σ0) is 14.5 MPa. More specifically, We also note that the deviator stress (σ0) which correspond to the occurrence of accelerated creep were 10.5, 8.0, and 6.0 MPa when the water content was 7.9%, 14.5%, and 21.6%, respectively. Therefore, the water content has a significant effect on the creep behavior of WCSR. This occurs mainly due to the presence of expansive minerals, such as montmorillonite, illite, and kaolinite, which expand through water absorption with increasing water content. This also reduces the bonding structure potential between particles and increases the damage to the rock mass. Furthermore, the lubrication caused by the water film leads to a decrease in the internal friction structure potential of the rock, which in turn reduces the friction strength between the rock structures and causes a transition from steady-state creep to unsteady creep, until accelerated creep occurs.

The radial creep curves were found to be similar to the axial creep curves. More specifically, the radial creep was negative due to the lateral expansion deformation of the soft rock specimen. In addition, the radial creep deformation was significantly smaller than the axial creep deformation because the confining pressure effectively limited the lateral deformation.

Creep rate

The creep rate is an important index that reflects the behavior of creep curves. The creep rate can be obtained according to the first derivation of the creep test results, as shown in Fig. 3.

Fig. 3
figure 3

Creep rate curves. (a) w = 0%; (b) w = 7.9%; (c) w = 14.5%; (d) w = 21.6%

Full size image

Figure 3 shows that the creep rate curve shows two forms. More specifically, each steady-state creep rate curves include a steeply descending stage and stationary holding stage, while except these two stages, each unsteady creep rate curves also include the sharply increasing stage. However, the creep rate curves fluctuate to some extent due to the differences between samples caused by the inhomogeneity of the geomaterial components.

The initial creep rate and steady creep rate are important for the creep properties of weakly cement soft rock. Therefore, the initial creep rate and steady creep rate under different water content conditions can be obtained according to creep rate curves of Fig. 3, as shown in Fig. 4.

Fig. 4
figure 4

Creep rate curves: (a) initial creep rate, (b) steady creep rate

Full size image

Figure 4 shows that the creep rate is significantly affected by water content and deviator stress. Figure 4a shows that the axial initial creep rate increases with deviator stress and water content increase. However, influence of water content on the radial initial creep rate curves is not consistent. For example, when water content is 14.5%, the radial initial creep rate is 0.0325, 0.0445, 0.0695, and 0.11125%·h−1, corresponding to deviator stress is 2, 4, 6, and 8 MPa of water, respectively. Nevertheless,when water content is 7.9%, the radial initial creep rate is 0.05438, 0.09493, 0.11152, 0.14793, and 0.18435%·h−1, corresponding to deviator stress is 3, 5, 7, 9 and 10.5 MPa, respectively. This indicates that the radial initial creep rate of water content (7.9%) is larger than that of water content (14.5%). In addition, the other experimental results are consistent with the viewpoint that the initial creep rate increases with the increase of water content and deviator stress.

We also note that the axial initial creep rate is larger than radial initial creep rate when water content is larger than 14.5%. At the same time, the axial initial creep rate is considerably close to the radial initial creep rate when water content is smaller than 7.9% (natural water content). This can be explained as that the internal structure of rock mass is softened and the strength is weakened seriously with higher water content, while the radial initial creep rate is restrained by confining pressure in the initial stage.

Figure 4b shows that the steady creep rate increases with water content and deviator stress increase, which indicates that a higher water content and deviator stress will enhance the occurrence of creep deformation. The axial steady creep rate is always larger than the radial steady creep rate. The axial steady creep rate ranges from 0.00132%·h−1 to 0.04227%·h−1 and the radial steady creep rate ranges from 0.00017%·h−1 to 0.0181%·h−1. This indicates that the axial creep deformation is more intense than the radial creep deformation. The failure mode of the weakly cemented soft rock specimen had also been shown to be dominated by longitudinal crack generation, expansion, and penetration. Therefore, it is necessary to pay particular attention to the creep deformation corresponding to the direction of the major principal stress to avoid deformation failure as part of the long-term stability evaluation process of underground engineering.

Instantaneous deformation and creep deformation

The creep test curves of the WCSR include instantaneous deformation and creep deformation. It should be noted that instantaneous deformation is an important index for the modulus characteristics of rock samples and the creep deformation is mainly employed to measure the long-term stability of underground engineering surrounding rock. The initial deformation values, which were obtained at the time when the deviator stress was just constant, were taken as the instantaneous deformation. The creep deformation was obtained by differentiating the instantaneous deformation with respect to the total deformation at the end of the creep tests. The instantaneous deformation and the creep deformation under different water content and deviator stress conditions are shown in Table 2. The strain ratio in Table 2 refers to the ratio of the instantaneous strain to the creep strain of the WCSR under this level of load.

Table 2 Instantaneous strain and creep strain
Full size table

Table 2 shows that the instantaneous deformation and creep deformation increases with an increase in the deviator stress and water content. The ratio of the axial instantaneous deformation to the creep deformation is approximately 0.01–0.15, while the ratio of the radial deformation to the creep deformation is approximately 0.09–0.92. This indicates that the creep deformation of WCSR is dominant. The ratio is larger when the deviator stress is lower and the creep curves indicate long-term steady creep. The ratio of the radial instantaneous deformation to the creep deformation is larger than that of the axial deformation. This result can be accounted for by the expansion deformation of WCSR specimens under the combined actions of an applied load and a specific water content. Moreover, as the degree of expansion deformation decreases gradually with time, more time is required to complete the expansion deformation process. This part of the deformation process plays an important role in the creep test; however, the expansion deformation of soft rock cannot be removed from the test data.

In addition, the ratio of the axial instantaneous deformation to the radial instantaneous deformation is approximately 0.35–1.11, while the creep ratio is approximately 1.94–5.54. This can be explained by the fact that instantaneous deformation occurred in the initial loading stage, radial expansion deformation occurred rapidly, and axial deformation was limited. In addition, the axial creep deformation increased with increasing loading time in the creep stage, but radial creep deformation was limited due to the confining pressure effect.

Long-term strength

Long-term strength is an important index for evaluating the long-term stability of underground engineering structures and estimating whether accelerated creep occurs. Stress–strain isochronous curves are the main method used to determine the long-term strength of rock. However, it is difficult to describe the regularity of the inflection point of stress–strain isochronous curves accurately, which results in a certain amount of uncertainty when determining the long-term strength. The operation of this method is also complex when there are many data. The reciprocal of the steady creep rate method was used to determine the long-term strength of weakly cemented soft rock in this study according to Wang et al. (2018). Two linear functions were used to fit the curve between the reciprocal of the steady creep rate and the deviator stress when the stress was high and low, respectively. The intersection of the two fit curves was taken as the long-term strength of the soft rock. The long-term strength results are shown in Fig. 5, where Fig. 5a was obtained by using the reciprocal of the axial steady creep rate and Fig. 5b was obtained by using the reciprocal of the radial steady creep rate.

Fig. 5
figure 5

Long-term strength of rock determined with the reciprocal of steady creep rate: (a) axial; (b) radial

Full size image

Figure 5 shows that the long-term strength of the rock decreases with an increase of the water content. The long-term strengths of the rock were 8.402, 5.241, 4.381, and 4 MPa via the reciprocal of the axial steady creep rate, and 8.052, 5.614, 4.105, and 4 MPa via the reciprocal of the radial steady creep rate when the water content was 0%, 7.9%, 14.5%, and 21.6%, respectively. However, the long-term strength difference between the axial and radial creep rates is insignificant. Therefore, the average values were taken to describe the relationship between the long-term strength and water content of the weakly cemented soft rock, as shown in Fig. 6.

Fig. 6
figure 6

Long-term strength with water content

Full size image

Figure 5 illustrates the negative exponential function relationship between the long-term strength and the water content.

Fractional order creep model

Fractional calculus theory

Fractional calculus is derived from the development of the traditional integral calculus theory, and it is able to describe the derivatives or integrals of arbitrary order (Chen et al. 2014; Liao et al. 2016). Fractional order calculus is defined in the form of an integral. The most well-known forms include the Riemann–Liouville fractional differential operator and the Caputo operator (Zhang et al. 2014).

In this case, the Riemann–Liouville definition of the calculus operator was employed, as shown in Eq. (1):

$$ {{}_a{}^{\mathrm{RL}}D}_t^{\alpha }f(t)={\left(\frac{\mathrm{d}}{\mathrm{d}t}\right)}^n{I}_{a^{+}}^{n-\alpha }f(t)=\frac{1}{\Gamma \left(n-\alpha \right)}{\left(\frac{\mathrm{d}}{\mathrm{d}t}\right)}^n{\int}_a^t\frac{f\left(\tau \right)\mathrm{d}\tau }{{\left(t-\tau \right)}^{\alpha -n-1}},\kern0.5em \left(n-1\le \alpha <n,\kern0.5em t>\alpha \right) $$
(1)

The Riemann–Liouville fractional integral operator is shown in Eq. (2):

$$ {I}_{a^{-}}^{\alpha}\mathrm{f}(t)=\frac{1}{T\left(\upalpha \right)}{\int}_a^t\frac{\mathrm{f}\left(\uptau \right)\mathrm{d}\uptau}{{\left(t-\uptau \right)}^{1-\upalpha}},\left(\upalpha >0,t>a\right) $$
(2)

where Γ(α) is the Gamma function, \( \Gamma \left(\upalpha \right)={\int}_0^{\infty }{t}^{\upalpha -1}{e}^{-t}\mathrm{d}t\operatorname{Re}\left(\upalpha \right)>0 \); D and I are differential and integral symbols, respectively; t is the upper limit of the integral; and α is the fractional order.

Fractional derivative Abel dashpot

The stress versus strain characteristics of the geotechnical materials between an ideal rigid body and an ideal fluid body can be expressed in the fractional differential form of the Abel dashpot, as shown in Fig. 7 (Zhou et al. 2011).

Fig. 7
figure 7

Abel dashpot

Full size image

The stress versus strain relationship of the Abel dashpot can be calculated according to Eq. (3):

$$ \upsigma (t)=\upxi \frac{{\mathrm{d}}^{\upalpha}\upvarepsilon (t)}{\mathrm{d}{t}^{\upalpha}} $$
(3)

where ξ is the viscosity coefficient of the Abel dashpot and α is the fractional order. Equation (3) can be reduced to Hooke’s elastic law when α is 0 and similarly to Newton’s fluid law when α is 1. The Abel dashpot can describe stress versus strain characteristics between ideal elastic and fluid materials.

The deviator stress σ(t) was considered to have a constant value in the creep constitutive model. The creep constitutive equation of the Abel dashpot can be obtained using the Riemann–Liouville fractional differential operator theory, as shown in Eq. (4):

$$ \upvarepsilon (t)=\frac{\upsigma_0}{\upxi}\frac{t^{\upalpha}}{\Gamma \left(1+\upalpha \right)} $$
(4)

The creep curves for different fractional orders (α) can then be obtained as shown in Fig. 8 through the dimensionless treatment of Eq. (4).

Fig. 8
figure 8

Creep strain curves of Abel dashpot. (a) α ≤ 1; (b) α ≥ 1

Full size image

Figure 8 shows that for an α value between 0 and 1 (Fig. 8a), the stress versus strain curves gradually increase, although the growth rate slows gradually, which describes the steady-state creep characteristics of the geomaterials. In addition, the growth rate of the creep curves increases significantly when α is greater than 1 (Fig. 8b), which in turn describes the accelerated creep characteristics.

The creep rate of the Abel dashpot can be obtained from the derivation of Eq. (4), as shown in Eq. (5):

$$ \dot{\upvarepsilon (t)}=\frac{\upsigma_0}{\upxi}\frac{\upalpha \cdotp {t}^{\upalpha -1}}{\Gamma \left(1+\upalpha \right)}\mathrm{d}t $$
(5)

Equation (5) is a descending function when α is between 0 and 1, i.e., the strain rate decreases continuously during the creep process, thereby describing the attenuation creep characteristics of the rock materials. In contrast, Eq. (5) is an increasing function when α is greater than or equal to 1, which describes the accelerated creep characteristics. We can transform Eq. (5) into Eq. (6) when α is 1:

$$ \dot{\upvarepsilon (t)}=\frac{\upsigma_0}{\upxi} $$
(6)

This equation indicates that the strain rate of Eq. (4) is constant when α is 1, thereby describing the equal velocity creep characteristics of the geomaterials.

Similarly, we assume that ε(t) is a constant value (ε0) in the stress relaxation constitutive model, and so the stress relaxation equation of the Abel dashpot is given by.

$$ \upsigma (t)=\upxi {\upvarepsilon}_0\frac{t^{-\upalpha}}{\Gamma \left(1-\upalpha \right)} $$
(7)

As such, the stress relaxation curves for different α values can be obtained by the dimensionless treatment of Eq. (7), as shown in Fig. 9.

Fig. 9
figure 9

Stress relaxation curves

Full size image

As shown in Fig. 9, when α is less than 1, the stress decreases gradually over time. The reduction rate of the stress relaxation is larger in the initial stages, prior to becoming relatively stable at a later point. Thus, the relaxation is enhanced with increasing α. It is therefore evident that the Abel dashpot can clearly describe the nonlinear relaxation process of the geomaterials.

Fractional-order creep model

The creep theory of soft rock has been thoroughly studied with common creep models including the Burgers model, Bingham model, and Nishihara model, the latter of which is widely used in the creep model research of geomaterials (see Fig. 10).

Fig. 10
figure 10

Nishihara model

Full size image

The creep formula of the Nishihara model can be defined according to Eqs. (8, 9) and (10):

$$ \varepsilon (t)=\frac{\sigma }{E_0}+\frac{\sigma }{E_1}\left(1-{e}^{-\frac{E_1}{\eta_1}t}\right)\kern0.5em \left(\sigma <{\sigma}_{\mathrm{s}}\right) $$
(8)
$$ \varepsilon (t)=\frac{\sigma }{E_0}+\frac{\sigma }{E_1}\left(1-{e}^{-\frac{E_1}{\eta_1}t}\right)+\frac{\sigma -{\sigma}_{\mathrm{s}}}{\eta_2}t\kern0.5em \left(\sigma \ge {\sigma}_{\mathrm{s}}\right) $$
(9)

where E0 and E1 are the elastic moduli of the Hooke body, η1 and η2 are the viscosity coefficients of the Newton body, and σs is the stress threshold for accelerated creep.

According to Fig. 10 and Eqs. (8) and (9), the Nishihara model can be used to describe the instantaneous elastic strain, stress relaxation, constant-rate creep, and residual elasticity. However, it is unable to describe the accelerated creep properties of soft rock accurately. So many studies have increasingly focused on improving the creep constitutive model (Cao et al. 2002; Tomanovic 2006; Xu and Chen 2013).

Fractional calculus theory has been increasingly applied in studies of the constitutive modeling of geomaterials. Thus, we herein proposed a four-element fractional-order constitutive model of WCSR based on fractional calculus theory and the Abel dashpot, as shown in Fig. 11.

Fig. 11
figure 11

Modified fractional-order model

Full size image

In addition, the Hooke body was employed to describe the instantaneous deformation of soft rock, while the Abel dashpot was used to describe the stress versus strain characteristics between ideal elastic and ideal fluid geomaterials (α1 ≤ 1). In addition, the Abel dashpot, which is parallel to the plastic body, was used to characterize the accelerated creep characteristics of soft rock when the deviator stress exceeded the stress threshold (α2 > 1).

Thus, the fractional-order creep constitutive model of the four elements (see Fig. 10) can be deduced as follows according to the series and parallel rules of the element model. In Eq. (10), σ0 is the deviator stress and ε1 is the strain of the Hooke body.

$$ {\upvarepsilon}_1=\frac{\upsigma_0}{E_1} $$
(10)

In addition,ε2 is the strain of the Abel dashpot, and can be expressed as follows:

$$ \frac{{\mathrm{d}}^{\alpha_1}{\varepsilon}_2(t)}{\mathrm{d}{t}^{\alpha_1}}=\frac{\sigma_0}{\xi_1} $$
(11)

Furthermore, σ3 and ε3 are the stress and strain of the parallel combined model of the plastic element and Abel dashpot. The constitutive model can therefore be represented by Eq. (12):

$$ \left\{\begin{array}{ll}{\varepsilon}_3=0& {\sigma}_0<{\sigma}_{\mathrm{s}}\\ {}\frac{{\mathrm{d}}^{\alpha_2}{\varepsilon}_3(t)}{\mathrm{d}{t}^{\alpha_2}}=\frac{\sigma_0-{\sigma}_{\mathrm{s}}}{\xi_2}& {\sigma}_0\ge {\sigma}_{\mathrm{s}}\end{array}\right. $$
(12)

where ξ1 and ξ2 are the viscosity coefficients of the attenuation and accelerated creep of the Abel dashpot, and α1 and α2 are the fractional orders of the creep model, where α1 ≤ 1 and α2 > 1.

Assuming that the α2-order derivative exists for a continuous function f(t), Riemann–Liouville fractional calculus can satisfy the following properties:

$$ {}_{\alpha }{}^{\mathrm{RL}}D\left[\mathrm{f}(t)+\mathrm{g}(t)\right]={}_{\alpha }{}^{\mathrm{RL}}D\mathrm{f}(t)+{}_a{}^{\mathrm{RL}}{D}_t^{\alpha}\mathrm{g}(t) $$
(13)

The combined model formula can therefore be expressed as follows:

$$ {{}_{\alpha }{}^{\mathrm{RL}}D}_t^{\alpha_1}\varepsilon (t)={{}_{\alpha }{}^{\mathrm{RL}}D}_t^{\alpha_1}{\varepsilon}_1(t)+{{}_{\alpha }{}^{\mathrm{RL}}D}_t^{\alpha_1}{\varepsilon}_2(t)\kern0.5em {\alpha}_1\le 1\;\mathrm{for}\ {\sigma}_0<{\sigma}_{\mathrm{s}} $$
(14)
$$ {{}_{\alpha }{}^{\mathrm{RL}}D}_t^{\alpha_2}\varepsilon (t)={{}_{\alpha }{}^{\mathrm{RL}}D}_t^{\alpha_1}{\varepsilon}_1(t)+{{}_{\alpha }{}^{\mathrm{RL}}D}_t^{\alpha_1}{\varepsilon}_2(t)+{{}_{\alpha }{}^{\mathrm{RL}}D}_t^{\alpha_2}{\varepsilon}_3(t)\kern0.5em \left({\alpha}_1\le 1,{a}_2>1\right)\;\mathrm{for}\;{\sigma}_0\ge {\sigma}_{\mathrm{s}} $$
(15)

According to Eqs. (10), (11), and (14), we can deduce the following:

$$ {{}_{\alpha }{}^{\mathrm{RL}}D}_t^{\alpha_1}{\varepsilon}_1(t)=\frac{1}{E_1}\frac{{\mathrm{d}}^{\alpha_1}\sigma (t)}{\mathrm{d}{t}^{\alpha_1}} $$
(16)
$$ {{}_{\alpha }{}^{\mathrm{RL}}D}_t^{\alpha_1}{\varepsilon}_1(t)=\frac{1}{E_1}\frac{{\mathrm{d}}^{\alpha_1}\sigma (t)}{\mathrm{d}{t}^{\alpha_1}} $$
(17)

Assuming that the fractional derivative function \( {{}_a{}^{\mathrm{RL}}D}_t^{\lambda -\beta }f(t) \) exists, it has the following properties:

$$ {{}_{\alpha }{}^{\mathrm{RL}}D}_t^{\lambda }{{}_a{}^{\mathrm{RL}}D}_t^{-\beta }f(t)={{}_a{}^{\mathrm{RL}}D}_t^{\lambda -\beta }f(t)\kern0.5em \left(\lambda >0,\beta >0\right) $$
(18)

In particular, when λ = α, we have

$$ {{}_{\alpha }{}^{\mathrm{RL}}D}_t^{\lambda }{{}_a{}^{\mathrm{RL}}D}_t^{-\lambda }f(t)={{}_a{}^{\mathrm{RL}}D}_t^0f(t)-f(t) $$
(19)

So,

$$ {{}_a{}^{\mathrm{RL}}D}_t^{\alpha_2}{\varepsilon}_2(t)=\frac{{\mathrm{d}}^{\left({\alpha}_2+{\alpha}_1\right)}\left(\frac{\sigma (t)}{\xi_1}\right)}{\mathrm{d}{t}^{\left({\alpha}_2+{\alpha}_1\right)}} $$
(20)
$$ {{}_{\alpha }{}^{\mathrm{RL}}D}_t^{\alpha_2}{\varepsilon}_3(t)=\frac{{\mathrm{d}}^{\alpha_2}{\varepsilon}_3(t)}{\mathrm{d}{t}^{\alpha_2}}=\frac{\sigma (t)-{\sigma}_{\mathrm{s}}}{\xi_2} $$
(21)

Thus:

$$ {{}_{\alpha }{}^{\mathrm{RL}}D}_t^{\alpha_2}\varepsilon (t)=\frac{1}{E_1}{{}_a{}^{\mathrm{RL}}D}_t^{\alpha_2}\sigma (t)+\frac{1}{\xi }{{}_a{}^{\mathrm{RL}}D}_t^{\left({\alpha}_2+{\alpha}_1\right)}\sigma (t)\kern0.5em \left({\alpha}_1\le 1\right)\;\mathrm{for}\;{\sigma}_0\le {\sigma}_{\mathrm{s}} $$
(22)
$$ {{}_{\alpha }{}^{\mathrm{RL}}D}_t^{\alpha_2}\varepsilon (t)=\frac{1}{E_1}{{}_a{}^{\mathrm{RL}}D}_t^{\alpha_2}\sigma (t)+\frac{1}{\xi_1}{{}_a{}^{\mathrm{RL}}D}_t^{\left({\alpha}_2+{\alpha}_1\right)}\sigma (t)+\frac{\sigma (t)-{\sigma}_{\mathrm{s}}}{\xi_2}\left({\alpha}_1\le 1,{\alpha}_2>1\right)\kern0.5em \mathrm{for}\;{\sigma}_0\ge {\sigma}_{\mathrm{s}} $$
(23)
  1. (1)

    Creep equation

The H-Fox function is then introduced to obtain the creep model and relaxation expression.

Assuming σ(t) = σ0H(t), then Eq. (22) can be transformed as follows:

$$ {\tilde{D}}_t^{\alpha_1}\varepsilon =\frac{\sigma_0}{E_1}{{}_a{}^{\mathrm{RL}}D}_t^{\alpha_1}\tilde{H}(t)+\frac{\sigma_0}{\xi_1}{{}_a{}^{\mathrm{RL}}D}_t^{\alpha_1}\tilde{H}(t)\kern0.5em \left({\alpha}_1\le 1\right)\kern0.5em \mathrm{for}{\sigma}_0<{\sigma}_{\mathrm{s}} $$
(24)
$$ {\tilde{D}}_t^{\alpha_2}\varepsilon =\frac{\sigma_0}{E_1}{{}_a{}^{\mathrm{RL}}D}_t^{\alpha_2}\tilde{H}(t)+\frac{\sigma_0}{\xi_1}{{}_a{}^{\mathrm{RL}}D}_t^{\left({\alpha}_2+{\alpha}_1\right)}\tilde{H}(t)+\frac{\sigma_0\tilde{H}(t)-{\sigma}_{\mathrm{s}}}{\xi_2}\left({\alpha}_1\le 1,{\alpha}_2>1\right)\kern0.5em \mathrm{for}\kern0.5em {\sigma}_0\ge {\sigma}_{\mathrm{s}} $$
(25)

Taking Eqs. (24, 25) for the fractional Laplace transform:

$$ {s}^{\alpha_1}=\frac{\sigma_0}{E_1}{s}^{\alpha_1-1}+\frac{\sigma_0}{\xi_1}{s}^{\alpha_1} $$
(26)
$$ {s}^{\alpha_2}=\frac{\sigma_0}{E_1}{s}^{\alpha_2-1}+\frac{\sigma_0}{\xi_1}{s}^{\alpha_2+{\alpha}_1-1}+\frac{\sigma_0-s{\sigma}_{\mathrm{s}}}{s{\xi}_2} $$
(27)

Subsequently, taking the inverse Laplace transform of Eqs. (26) and (27), the four-element fractional order model can be expressed as follows:

$$ \upvarepsilon (t)=\frac{\upsigma_0}{{\mathrm{E}}_1}+\frac{\upsigma_0{\mathrm{t}}^{\upalpha_1}}{\upxi_1}{\mathrm{H}}_{1,2}^{1,1}\left[\frac{1}{\Gamma \left(1+{\upalpha}_1\right)}{\mathrm{t}}^{\upalpha_1}|\begin{array}{cc}\left[0,1\right]& \\ {}\left[0,1\right]& \left(\upalpha, \upalpha \right)\end{array}\right]\kern0.5em \left({\alpha}_1\le 1\right)\;\mathrm{for}\;{\sigma}_0<{\sigma}_{\mathrm{s}}\;\mathrm{for}\;{\sigma}_0<{\sigma}_{\mathrm{s}} $$
(28)
$$ \upvarepsilon (t)=\frac{\upsigma_0}{{\mathrm{E}}_1}+\frac{\upsigma_0{\mathrm{t}}^{\upalpha_1}}{\upxi_1}{\mathrm{H}}_{1,2}^{1,1}\left[\frac{1}{\Gamma \left(1+{\upalpha}_1\right)}{\mathrm{t}}^{\upalpha_1}|\begin{array}{cc}\left[0,1\right]& \\ {}\left[0,1\right]& \left(\upalpha, \upalpha \right)\end{array}\right]+\frac{\left[{\upsigma}_0-{\upsigma}_{\mathrm{s}}\right]{\mathrm{t}}^{\upalpha_2}}{\upxi_2}{\mathrm{H}}_{1,2}^{1,1}\left[\frac{1}{\Gamma \left(1+{\upalpha}_2\right)}{\mathrm{t}}^{\upalpha_2}|\begin{array}{cc}\left(0,1\right)& \\ {}\left(0,1\right)& \left(\upalpha, \upalpha \right)\end{array}\right]\kern0.5em \left({\alpha}_1\le 1,{\alpha}_2>1\right)\;\mathrm{for}\kern0.33em {\sigma}_0\ge {\sigma}_{\mathrm{s}} $$
(29)

where the special function is defined by the Mellin–Barnes integral as follows:

$$ {\mathrm{H}}_{\mathrm{p},\mathrm{q}}^{\mathrm{m},\mathrm{n}}\left[\mathrm{z}|\begin{array}{cc}\left({\mathrm{a}}_1,{\upalpha}_1\right)\cdots & \left({\mathrm{a}}_{\mathrm{p}},{\upalpha}_{\mathrm{p}}\right)\\ {}\left({\mathrm{b}}_1,{\upalpha}_1\right)\cdots & \left({\mathrm{b}}_{\mathrm{q}},{\upalpha}_{\mathrm{q}}\right)\end{array}\right]=\frac{1}{2\uppi \mathrm{i}}\int \frac{\prod_{\mathrm{j}=1}^{\mathrm{n}}\Gamma \left(1-{\mathrm{a}}_{\mathrm{j}}+{\mathrm{a}}_{\mathrm{j}}\mathrm{s}\right){\prod}_{\mathrm{j}=1}^{\mathrm{m}}\Gamma \left({\mathrm{b}}_{\mathrm{j}}-{\upbeta}_{\mathrm{j}}\mathrm{s}\right)}{\prod_{\mathrm{j}=\mathrm{m}+1}^{\mathrm{q}}\Gamma \left(1-{\mathrm{b}}_{\mathrm{j}}+{\upbeta}_{\mathrm{j}}\mathrm{s}\right){\prod}_{\mathrm{j}=1}^{\mathrm{p}}\Gamma \left({\upalpha}_{\mathrm{j}}-{\upalpha}_{\mathrm{j}}\mathrm{s}\right)}{\mathrm{z}}^{\mathrm{s}}\mathrm{ds} $$
(30)
  1. (2)

    Relaxation equation

Assuming ε = ε0H(t), then Eq. (22) can be transformed as follows:

$$ {\tilde{D}}_t^{\alpha_2}{\varepsilon}_0H(t)=\frac{1}{E_1}{{}_a{}^{\mathrm{RL}}D}_t^{\alpha_2}\sigma +\frac{1}{\xi_1}{{}_a{}^{\mathrm{RL}}D}_t^{\left({\alpha}_2+{\alpha}_1\right)}\sigma $$
(31)

Taking the Laplace transform of Eq. (31), we obtain:

$$ {s}^{\alpha_2-1}=\tilde{\sigma}\left(\frac{1}{E_1}{s}^{\alpha_2}+\frac{1}{\xi_1}{s}^{\alpha_2+{\alpha}_1}\right) $$
(32)

The creep equation, H-fox special function, and Laplace inverse transform were used to obtain the relaxation functions as follows:

$$ \sigma (t)=\frac{E_1{\xi}_1{t}^{-{\alpha}_1}}{E_1+{\xi}_1}{H}_{1,2}^{1,1}\left[\frac{1}{\varGamma \left(1-{\alpha}_1\right)}{t}^{-{\alpha}_1}|\begin{array}{cc}\left[0,1\right]& \\ {}\left[0,1\right]& \left(-\alpha, \alpha \right)\end{array}\right]{\varepsilon}_0\kern0.5em {\alpha}_1\le 1\kern0.5em \mathrm{for}\;{\sigma}_0<{\sigma}_{\mathrm{s}} $$
(33)
$$ \sigma (t)={\sigma}_{\mathrm{s}}+\frac{E_1{\xi}_1{t}^{-{\alpha}_1}}{\xi_1+{\xi}_2}{H}_{1,2}^{1,1}\left[\frac{1}{\varGamma \left(1-{\alpha}_1\right)}{t}^{-{\alpha}_1}|\begin{array}{cc}\left[0,1\right]& \\ {}\left[0,1\right]& \left(-\alpha, \alpha \right)\end{array}\right]{\varepsilon}_0+\frac{E_1{\xi}_2{t}^{-{\alpha}_2}}{\xi_1+{\xi}_2}{H}_{1,2}^{1,1}\left[\frac{1}{\varGamma \left(1-{\alpha}_2\right)}{t}^{-{\alpha}_2}|\begin{array}{cc}\left[0,1\right]& \\ {}\left[0,1\right]& \left(-\alpha, \alpha \right)\end{array}\right]{\varepsilon}_0{\displaystyle \begin{array}{cc}& {\alpha}_1\le 1,{\alpha}_2>1\end{array}}\kern0.5em \mathrm{for}\;{\sigma}_0\ge {\sigma}_{\mathrm{s}} $$
(34)

Equation (33, 34) is the stress–strain relationship of the four-element fractional model under stress relaxation conditions.

The aforementioned fractional-order constitutive model can then be employed to describe the characteristics of instantaneous deformation, steady-state creep, accelerated creep, and stress relaxation of WCSR.

Parameter solution and verification of the fractional creep model

Model parameter solution

The ant colony algorithm (ACA) is a swarm intelligence algorithm with good robustness that characterizes positive feedback and allows for a parallel search. The parameters of the four-element fractional creep constitutive model are regarded as a group of optimization problems. Therefore, the ant colony optimization algorithm is employed to search the optimal objective function value to obtain the appropriate combination parameter values.

The specific algorithm steps are shown in Fig. 12 (Yao et al. 2016; Zhuang et al. 2011).

Fig. 12
figure 12

The flow chart of procedure of ACA

Full size image

In Fig. 12, X = {E1, ξ1, α1, ξ2, α2} are the creep model parameters that are randomly assigned to each ant. Range of parameters are E1∈[0,1000], ξ1∈[0,200], ξ2∈[103,106], α1∈[0,1], and α2∈[1,20]. Δt(i) is the error of the creep model, β is the basic parameter, and β = 3. “Error” represents the error index function, where \( Error(i)={\left[{\varepsilon}_{\mathrm{j}}^{\ast }(i)-{\varepsilon}_t(i)\right]}^2 \) and \( {\varepsilon}_{\mathrm{j}}^{\ast }(i) \) is the calculated value of the deformation using the creep model equations, Eqs. (28) and (29).εt(i) is the test results. “BIndex” is the ant with the largest pheromone, δ is the pheromone volatilization factor, K = 0.1. “Echo” represents the current evolutionary algebra of the ant colony, and “Echomax” represents the largest evolutionary algebra of the ant colony, where Echomax is 100.

We assume the ant number (m) is 30 and calculate \( {e}^{-{T}_0(i)} \), i = 1,2,…,m. The calculated results are arranged in ascending order as T1(j), where j = 1,2,…, m. The dynamic transfer factor can be calculated as Eq. (35).

$$ \left\{\begin{array}{cc}{p}_0={t}_1\left(\frac{2}{3}m\right),& Echo<\left(\frac{Echo_{\mathrm{max}}}{2}\right)\\ {}{p}_0={t}_1\left(\frac{1}{2}m\right),& else\end{array}\right. $$
(35)

A local search is performed if p(i) < p0, otherwise a global search is performed. In this way, a better solution will obtain at the beginning, and the search will avoid falling into a local optimum during the search process.

Then, the pheromone of the creep model parameters is update and the largest pheromone is saved. The error value is calculated according to the error model. Then the process returns to the parameter initialization to carry out the iteration cycle. The search ends when the number of iterations reaches the initial setting. The optimization creep model parameters are obtained from the best ants.

The parameters of the Nishihara model and four-element fractional creep constitutive model were obtained by using the above method, as shown in Tables 3 and 4.

Table 3 Parameters of Nishihara’s model
Full size table
Table 4 Parameters of four-element fractional-order model
Full size table

Model verification

Substituting the aforementioned model parameters into Eqs. (28) and (29), the calculated values of the model could be compared with the experimental results, as shown in Fig. 13.

Fig. 13
figure 13

Test and model verification results. (a) w = 0%; (b) w = 7.9%; (c) w = 14.5%; (d) w = 21.6%

Full size image

As shown in Fig. 13, the tests were performed in the stable creep stage, and the Nishihara model and four-element fractional-order creep model give higher values than those obtained in the tests. In addition, the correlation coefficients are satisfactory (i.e., R2 ≥ 0.85); however, a higher value was obtained for the fractional creep model correlation coefficient (i.e., R2 ≥ 0.93). As such, both models can reasonably describe the steady-state creep characteristics of WCSR. However, the Nishihara model cannot describe the accelerated creep characteristics of the specimen, as a large error was obtained in this case (correlation coefficient R2 ≥ 0.93). Moreover, the calculation results obtained using this model suggests a trend of constant velocity growth, which is inconsistent with the trend of an accelerated creep rate increase. We also found that the four-element fractional creep model can reasonably describe the instantaneous deformation, decay rheology, constant velocity rheology, and accelerated rheology of WCSR, in particular when describing the accelerated creep curves with R2 = 0.924–0.991. These results therefore indicate that the four-element fractional creep model proposed herein can reasonably reflect the creep variation of weakly cemented soft rock.

Conclusions

In this study, a series of triaxial creep tests were performed to study the creep properties of weakly cemented soft rock. Then, a four-element fractional creep constitutive model was established basing on the fractional calculus theory. The main conclusions are as follows:

1. Test results show that moisture content and deviator stress have significant influence on creep behavior of weakly cemented soft rock. The creep curves gradually change from two-stage steady-state creep to three-stage unsteady-state creep and accelerated creep occurs, eventually. The instantaneous deformation, creep deformation, axial initial creep rate, and steady creep rate increase with the water content and deviator stress increase, while the influence of water content on the radial initial creep rate curves is not consistent.

2. The total deformation increases with the water content and deviator stress increase. And the ratio of the creep deformation to instantaneous deformation also increases, which indicates that the WCSR with water content perform obvious creep characteristics under the action of long-term load. The long-term strength of weakly cemented soft rock was obtained by using the reciprocal of steady creep rate method. The long-term strength decreases with the increase of water content and the relationship between long-term strength and water content shows a good negative exponential function.

3. A four-element fractional creep constitutive model of weakly cement soft rock was proposed basing on fractional calculus theory. The specific creep equation and relaxation equation of the model were obtained by introducing the H-Fox special function. The constructed model can describe the steady creep, unsteady creep, and stress relaxation of soft rock. In addition, it only contains only five parameters, which could be easily acquired.

4. The model parameters were obtained by trust-region method and optimized by the ant colony optimization algorithm method. The parameters were taken into the four-element fractional creep constitutive model to calculate the creep deformation with different water and deviator stress conditions. Comparison results show that the four-element fractional creep constitutive model can accurately simulate the steady and unsteady creep characteristics of weakly cemented soft rock, especially for accelerated creep behavior.

These research results will be helpful for studying the stability of weakly cemented soft rock mine engineering.