Introduction

Determining how to describe the creep process for rock remains a challenging problem, while it is essential to research the rock creep property in rock engineering (Xu et al. 2014a, b; Wang et al. 2014; Yang et al. 1999; Wu et al. 2009, 2014; Hou et al. 2012). As a result, during several decades much effort has been directed toward the study of creep behavior of rock, most of which was devoted to modeling the rock creep. Consequentially, various creep constitutive models of rock have been proposed (Munson 1997; Chan et al. 1997; Wang 2004; Fabre and Pellet 2006; Zhou et al. 2008).

In addition, the fractional derivative has long history dependence or the so-called memory effects. It has been found that fractional calculus is a powerful tool for modeling the viscoelastic behaviors and particularly suited for building the time-dependent constitutive model (Yin et al. 2012). In addition, an increasing effort has been devoted to the application of fractional calculus to viscoelastic and viscoplastic constitutive models. The contributions of Bagley and Torvik (1983, 1986), and Koeller (1984) are remarkable and they established a solid foundation in fractional derivative models. The use of fractional-derivative-based constitutive models is motivated, to some extent, by the fact that fewer parameters are required to represent material creep behavior than in the classical component models (Welch et al. 1999). Most recently, Zhou et al. (2011) proposed a new creep constitutive model of salt rock on the basis of time-based fractional derivative by replacing a Newtonian dashpot in the classical Nishihara model with the fractional-derivative Abel dashpot, and found that the predicted results are in a good agreement with the experimental data. Furthermore, by replacing the Newtonian dashpot in the classical Nishihara model with the variable-viscosity Abel dashpot, a damage-mechanism-based creep constitutive model was proposed on the basis of time-based fractional derivative (Zhou et al. 2013). Considering the damage and time-dependent characteristics of the rock’s yield strength, Chen et al. (2014) proposed a time-dependent damage constitutive model of the marble based on fractional calculus theory and damage variables.

But in fact, the property of material is time-dependent under loading, which means that the order of fractional derivative should be variable. Recently the constitutive model based on variable-order fractional derivatives has been getting attention (Ramirez and Coimbra 2007). In a sense, the variable-order fractional calculus is the extension of fractional calculus. Theoretically, the change of the order can exhibit the evolution of mechanical properties of materials.

This paper suggests a new model based on variable-order fractional derivatives in order to precisely describe the creep failure process for rock.

Basic theory of fractional derivative

Definition 1

Let L 1 = L 1 (I) be the class of Lebesgue integral functions on the interval I = [0, ∞], and \(f\left( t \right) \in\) L 1, \(\alpha \in [0,{ + }\infty ]\), for \(t > 0\), \(\text{Re} \left( \alpha \right) > 0\), the Riemann–Liouville integration with the order \(\alpha\) is defined by (Podlubny 1999; Zhou et al. 2011)

$${}_{0}I_{t}^{\alpha } f\left( t \right) = \frac{1}{\varGamma \left( \alpha \right)}\int_{0}^{t} {\left( {t - \tau } \right)^{\alpha - 1} f\left( \tau \right)d\tau ,} \quad 0 < t,\,0 < \alpha ,$$
(1)

where Γ is the Gamma function.

Definition 2

The Caputo derivative is defined as (Podlubny 1999)

$${}_{0}^{C} D{}_{t}^{\alpha } f\left( t \right) = I_{0}^{n - \alpha } f^{\left( n \right)} \left( t \right) = \frac{1}{{\varGamma \left( {n - \alpha } \right)}}\int_{0}^{t} {\frac{{f^{\left( n \right)} \left( \tau \right)d\tau }}{{\left( {t - \tau } \right)^{\alpha - n + 1} }}} ,\quad 0 < t,\,0 < \alpha ,\,n = \left\lfloor \alpha \right\rfloor + 1,$$
(2)

where \(n\) is the minimum positive integer greater than \(\alpha\), the function \(f\left( t \right)\) must be \(n\) times continuously differentiable.

For \(0 \le \alpha \le 1,\) the above definition can be simplified as

$${}_{0}^{C} D{}_{t}^{\alpha } f\left( t \right) = \frac{1}{{\varGamma \left( {1 - \alpha } \right)}}\int_{0}^{t} {\frac{{f^{\prime } \left( \tau \right)d\tau }}{{\left( {t - \tau } \right)^{\alpha } }}} ,\quad 0 < t,0 \le \alpha \le 1.$$
(3)

The constitutive relationship of Abel dashpot is given in (Smit and De Vries 1970)

$$\sigma (t) = \eta_{0} \,_{0}^{C} D_{t}^{\beta } \varepsilon \left( t \right),\,0 \le \beta \le 1,$$
(4)

where \(\eta_{0}\) is viscosity coefficient, \(\beta\) is the order of fractional derivative.

If the stress is constant, the element will describe change of creep behavior. Taking the fractional integral to both sides of Eq. (4), we can get

$$\varepsilon \left( t \right) = \frac{{\sigma_{0} }}{{\eta_{0} }}\frac{{t^{\beta } }}{{\varGamma \left( {1 + \beta } \right)}},\quad 0 \le \beta \le 1,$$
(5)

where \(\sigma_{0}\) denotes the constant stress level.

The Maxwell creep model based on variable-order fractional derivatives

Figure 1 shows the common fractional derivative Maxwell model composed by the Hooke body and the Abel dashpot. Suppose the strain of the Hooke body is ε 1, that of the Abel dashpot is ε 2. The stress–strain relationship of the Hooke body (H) is

Fig. 1
figure 1

Fractional derivative Maxwell model

Full size image
$$\varepsilon_{1} = \frac{\sigma }{{E_{0} }},$$
(6)

where E 0 stands for elastic modulus of the Hooke body.

The stress–strain relationship of the Abel dashpot reads

$$\varepsilon_{2} \left( t \right) = \frac{\sigma }{{\eta_{0} }}\frac{{t^{\beta } }}{{\varGamma \left( {1 + \beta } \right)}}, \quad 0 \le \beta \le 1.$$
(7)

In this way, the order of the fractional derivative can be regarded as a function of time, i.e. \(\beta = \alpha \left( t \right),\,0 \le \alpha \left( t \right) \le 1.\) \(\alpha \left( t \right)\) is given as follows.

Then

$$\sigma \left( t \right) = \eta_{\alpha \left( t \right)} \,_{{t_{k - 1} }}^{C} D_{t}^{\alpha \left( t \right)} \varepsilon_{2} \left( t \right),\quad 0 \le \alpha \left( t \right) \le 1,t_{k - 1} \le t < t_{k} ,$$
(8)

where α(t) representing the fractional derivative order is a function of time and varies according to Table 1, and \(\eta_{\alpha \left( t \right)}\) is the corresponding viscosity coefficient.

Table 1 Value of \(\alpha \left( t \right)\) versus time
Full size table

Let the stress be constant, we can obtain

$$\varepsilon_{2} \left( t \right) = \sum\limits_{k = 1}^{n} {\frac{\sigma }{{\eta_{{\alpha_{k} }} }}} \frac{{\left( {t - t_{k - 1} } \right)^{{\alpha_{k} }} }}{{\varGamma \left( {\alpha_{k} + 1} \right)}},\quad 0 \le \alpha \left( t \right) = \alpha_{k} \le 1,\,t_{k - 1} \le t < t_{k} ,$$
(9)

where σ stands for normal stress, \(\alpha_{k}\) denotes the value of \(\alpha \left( t \right)\) at a given moment.

Considering the two parts of strain, and combining (6) and (9), the constitutive equation of variable-order fractional derivatives creep model can be represented as

$$\varepsilon \left( t \right) = \varepsilon_{1} + \varepsilon_{2} \left( t \right) = \frac{\sigma }{{E_{0} }} + \sum\limits_{k = 1}^{n} {\frac{\sigma }{{\eta_{{\alpha_{k} }} }}\frac{{\left( {t - t_{k - 1} } \right)}}{{\varGamma \left( {\alpha_{k} + 1} \right)}},\quad 0 \le \alpha \left( t \right) \le 1,\,t_{k - 1} \le t < t_{k} ,}$$
(10)

Equation (10) is the theoretical expression of the variable-order fractional derivative Maxwell model.

Creep experiment and method

Experiment equipment

Creep experiment is the foundation of creep property investigation on salt rock, determining the parameters in creep constitutive models. The current experiments were conducted in Sichuan University using a computer-controlled creep test system possessing a high accuracy (Fig. 2), with uniaxial load in the range of 0–600 kN and confining pressure in the range of 0–30 MPa, and the indoor temperature and humidity was controlled by air conditioning. All the salt rock samples were drilled from Pingding Shan in Henan province, Central China, at the depth of about 1,800 m from ground surface. XRD analysis showed the samples consist mainly of sodium chloride. The specimens were prepared with a required dimension of 75 mm in diameter and 150 mm in height.

Fig. 2
figure 2

Experiment set-up for creep test

Full size image

Experiment method and results

The specimens of salt rock were tested under uniaxial loading. Figure 3 shows the detail of one salt rock specimen for creep experiment.

Fig. 3
figure 3

Sample in creep testing

Full size image

From the creep experiment lasting for 27 days or so, we obtained the experimental creep curve of salt rock shown in Fig. 4. By further processing, the creep rate curve of salt rock is acquired as illustrated in Fig. 5.

Fig. 4
figure 4

Creep curve of salt rock under axial load of 13 MPa

Full size image
Fig. 5
figure 5

Creep rate of salt rock under axial load of 13 MPa

Full size image

Parameter determination for the new creep model by fitting analysis

As shown in the above two figures, the creep curve exhibits only deceleration creep and steady-state creep, without an apparent accelerating creep stage. Therefore, the creep curve can be divided into two segments, and the segment point of time is comprehensively determined in accordance with creep curve and creep rate curve, i.e., t 1 = 8.428472.

From Eq. (10), the curve form of the first stage can be expressed as follows:

$$\varepsilon \left( t \right)\, = \,\frac{\sigma }{{E_{0} }} + \frac{\sigma }{{\eta_{{\alpha_{1} }} }}\frac{{\left( {t - t_{0} } \right)^{{\alpha_{1} }} }}{{\varGamma \left( {\alpha_{1} + 1} \right)}}\, = \,\frac{\sigma }{{E_{0} }} + \frac{\sigma }{{\eta_{{\alpha_{1} }} }}\frac{{t^{{\alpha_{1} }} }}{{\varGamma \left( {\alpha_{1} + 1} \right)}},\quad 0 \le 1,\,0 = t_{0} \le t < t_{1} .$$
(11)

where \(\varepsilon \left( {t_{0} } \right) = \frac{\sigma }{{E_{0} }}\), thus

$$E_{0} = \frac{\sigma }{{\varepsilon \left( {t_{0} } \right)}}.$$
(12)

Taking the logarithmic operation on both sides of Eq. (11), we can obtain

$$\lg \left( {\varepsilon \left( t \right) - \frac{\sigma }{{E_{0} }}} \right) = \lg \left( {\frac{\sigma }{{\eta_{{\alpha_{1} }} }}\frac{{t^{{\alpha_{1} }} }}{{\varGamma \left( {\alpha_{1} + 1} \right)}}} \right),\quad 0 \le \alpha_{1} \le 1,\,0 = t_{0} \le t_{1} .$$
(13)
$$\lg \left( {\varepsilon \left( t \right) - \varepsilon \left( {t_{0} } \right)} \right) = \alpha_{1} \lg t - \lg \frac{{\eta_{{\alpha_{1} }} \varGamma \left( {\alpha_{1} + 1} \right)}}{\sigma },\,0 \le \alpha_{1} \le 1,\quad 0 \le t < t_{1} .$$
(14)

Might as well suppose

$$\left. \begin{gathered} y = \lg \left( {\varepsilon (t) - \varepsilon (t_{0} )} \right) \hfill \\ x = \lg \,t \hfill \\ \end{gathered} \right\} .$$
(15)

Then Eq. (14) becomes a linear equation about x and y

$$y = a_{1} x + b_{1} .$$
(16)

By dealing with the creep experimental data of the first stage, we can calculate to get the data set about x and y. Hence, whether x and y is a linear correlation can be determined by linear fitting analysis of the date set about x and y. If x and y are linearly related, one can further get α 1 and \(\eta_{{\alpha_{1} }}\), derived from the fitting coefficients a 1 and b 1.

$$\left. \begin{gathered} \alpha _{1} = a_{1} \hfill \\ \eta \alpha _{1} = 10^{{ - b_{1} }} \frac{\sigma }{{\Gamma (a_{1} + 1)}} \hfill \\ \end{gathered} \right\}$$
(17)

From the analysis results shown as Fig. 6, it is obvious that the correlation coefficient of the equation \(R^{2} > 0.99\), indicating the predicted date by the fractional derivative model proposed in the paper is in good agreement with the creep experimental data of the first stage. Then the coefficients both α 1 and \(\eta_{{\alpha_{1} }}\) can be obtained.

Fig. 6
figure 6

Deceleration creep region data with linear fitting equation after logarithmic processing

Full size image

Similarly according to Eq. (10), the creep curve in the second stage can be given by

$$\varepsilon \left( t \right)\, = \,\frac{\sigma }{{E_{0} }} + \frac{\sigma }{{\eta_{{\alpha_{1} }} }}\frac{{t_{1}^{{\alpha_{1} }} }}{{\varGamma \left( {\alpha_{1} + 1} \right)}} + \frac{\sigma }{{\eta_{{\alpha_{2} }} }}\frac{{\left( {t - t_{1} } \right)^{{\alpha_{2} }} }}{{\varGamma \left( {\alpha_{2} + 1} \right)}},\quad 0 \le \alpha_{2} \le 1,\,t_{1} \le t < t_{2} .$$
(18)

Taking the logarithmic operation on both sides of Eq. (18), then

$$\lg \left( {\varepsilon \left( t \right) - \varepsilon \left( {t_{1} } \right)} \right) = \alpha_{2} \lg t - \lg \frac{{\eta_{{\alpha_{2} }} \varGamma \left( {\alpha_{2} + 1} \right)}}{\sigma }, \quad 0 \le \alpha_{2} \le 1,t_{1} \le t < t_{2} .$$
(19)

where \(\varepsilon \left( {t_{1} } \right) = \frac{\sigma }{{E_{0} }} + \frac{\sigma }{{\eta_{{\alpha_{1} }} }}\frac{{t_{1}^{{\alpha_{1} }} }}{{\varGamma \left( {\alpha_{1} + 1} \right)}}\)

Similarly, we can assume:

$$\left. \begin{gathered} y = \lg \left( {\varepsilon (t) - \varepsilon (t_{1} )} \right) \hfill \\ x = \lg \,t \hfill \\ \end{gathered} \right\} .$$
(20)

Then Eq. (19) establishes another linear relationship between x and y

$$y = a_{2} x + b_{2} .$$
(21)

Analyzing the creep experimental data of the second stage, the data set about x and y can be calculated and whether x and y is a linear correlation can be confirmed by linear fitting analysis of the date set. If x and y are linearly related, one can further get α 2 and \(\eta_{{\alpha_{2} }}\), derived from the fitting coefficients a 2 and b 2.

$$\left. \begin{gathered} \alpha _{2} = a_{2} \hfill \\ \eta \alpha _{2} = 10^{{ - b_{2} }} \frac{\sigma }{{\Gamma (a_{2} + 1)}} \hfill \\ \end{gathered} \right\}.$$
(22)

From the analysis results shown below (Fig. 7), it can be seen that the correlation coefficient \(R^{2} > 0.99\), indicating the fractional derivative model proposed in the paper is in good agreement with the creep experimental data of the second stage. Eventually we can further determine the coefficients \(\alpha_{2}\) and \(\eta_{{\alpha_{2} }}\).

Fig. 7
figure 7

Steady-state creep region data with linear fitting equation after logarithmic processing

Full size image

By segmentation treatment based on the creep experimental data, Fig. 8 demonstrates the fact that the variable order of fractional derivatives regarded as a step function is reasonable and reliable, and the fitting correlation coefficients of experimental data in respective stages are pretty good, which helps us to determine all the parameters (Table 2).

Fig. 8
figure 8

Values of the step function α(t)

Full size image
Table 2 Parameters determined by fitting analysis based on creep tests of salt rock
Full size table

Figure 9 describes the theoretical creep curve according to the parameters given in Table 2. As shown in the figure, the variable-order fractional derivative constitutive model presented in the paper has good consistency with the experimental data, which further proves that the improved creep model is reliable.

Fig. 9
figure 9

Comparison of experimental results and predicted date obtained from the constitutive equation

Full size image

Through the segmentation treatment, according to different creep stages, of the above two experimental results, it is shown that the predicted date by the new creep model in the respective stages agrees with the experimental data, and the fitting correlation coefficients are greater than 0.99. It is also verified that the variable order of fractional derivatives as a step function is reasonable and reliable.

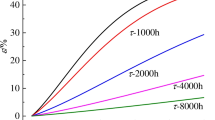
Normally, we find that the order of fractional derivatives of the primary creep is lower than 1; that of the secondary creep is very close to 1. According to the previous studies, the secondary creep deformation of most empirical models is proportional to time. By analyzing the predicted creep curves with two different orders of Abel dashpot derived from the empirical models and the improved model based on variable-order fractional derivatives, respectively, it is obvious that the two curves are extremely similar as illustrated in Fig. 10. Consequently, for the secondary creep, the empirical models are also feasible within the range of allowable error.

Fig. 10
figure 10

Creep curve of the Abel dashpot with different fractional derivative orders (parameters: σ = 13 MPa, η = 53.6547; when α = 1, it represents the empirical model)

Full size image

Discussion and conclusion

The physics significance of the Abel dashpot has been a research hotspot. The commonly accepted interpretation regards the Abel dashpot as a constitutive element describing the material state between ideal solid and Newton fluid. In a sense, the fractional derivative seems an extension of the integer order derivative, which can reveal the mechanical properties in nature closer to viscoelastic materials properties.

In order to describe the mechanical property of rock is time-dependent during the creep, a new method was presented to build the constitutive model. The Maxwell creep model for salt rock based on variable-order fractional derivatives was proposed, and the creep constitutive equations were concluded in an explanatory manner.

Through the segmentation of the experimental results according to different creep stages, it was found that the creep model based on variable-order fractional derivatives agrees well with the experimental data. It was also verified that the fact the variable order of fractional derivatives is a step function. And through further piecewise fitting, the parameters in the model were determined. The theoretical curves according to the parameters were consistent well with the experimental data.

Summing up the above experimental results, it was found that the order of fractional derivatives of the primary creep is lower than 1; that of the secondary creep is very close to 1. So, for the secondary creep, it was verified the empirical models are also feasible within the range of allowable error. In the primary creep stage, the order of fractional derivative is close to zero, meaning that the mechanical property of salt rock is analog to elastic body. While in the steady creep stage, the mechanical property of salt rock behaves like viscous material with the order of fractional derivative nearly equal to one. As we can see, the improved Maxwell creep model proposed in this paper, based on variable-order fractional derivatives, can thorough reveal the gradual transformation process of salt rock creep from elastic state to viscous state.

The Maxwell creep model based on variable-order fractional derivatives proposed in the paper not only highly agrees with the experimental results but also shows the evolution of mechanical properties of materials with the change of the order during whole process. All above, we hope such research can arouse interests of other researchers in the constitutive model based on variable-order fractional derivatives.