Introduction

Landslides are common phenomena in mountainous regions worldwide. During the past two decades, catastrophic landslides in mountainous regions, such as the 1999 Chiu-fen-erh-shan landslide (Wang et al. 2003) and Tsaoling landslide (Yang et al. 2014) in Taiwan and the 2008 Daguangbao landslide (Zhang et al. 2013a, b, 2015c) and Donghekou landslide (Zhang et al. 2014b, 2015b) in Sichuan, have caused serious damage and fatalities. To develop effective preventive countermeasures, it is important to analyze the stability of a slope before failure and estimate the kinematic behavior of the displaced masses after failure, such as the velocity, run-out distance, and extent. Traditional continuum-based approaches (e.g., Savage and Hutter 1989; McDougall and Hungr 2004; Chen et al. 2006; Griffiths and Marquez 2007; Zhang et al. 2013a, b; Troncone et al. 2014; Han et al. 2015, 2016; Wang et al. 2016b) are generally suitable for flow-like landslides, such as earthflows, mudflows, debris flows, and lahars. Simplified approaches based on the sliding-block model (e.g., Miao et al. 2001; Conte and Troncone 2012; Conte et al. 2016) neglect the contacts between rocks, which prevents them from tracing the position or trajectory of individual rocks during a landslide. In contrast, discontinuum-based approaches, such as the commonly used distinct element method (DEM) (Cundall 1971) and discontinuous deformation analysis (DDA) (Shi 1988), are appropriate tools to account for the kinematic behavior of individual displaced rocks in a rockfall, rockslide, or rock avalanche.

DDA has several basic advantages over the DEM, such as using an unconditionally stable time integration scheme (Doolin and Sitar 2004), having a larger time interval and no overlapping contacts, and being compatible with the finite element method (Jing 1998). With continuous modifications, two-dimensional (2-D) DDA has been accepted for analyzing rockslide problems, such as the design of fences to intercept falling rocks (Ohnishi et al. 1996), the fragmentation due to rock-slope impacts (Lin et al. 1996), the energy dissipation considering friction, collision and vegetation (Ma et al. 2007) and the run-out distance (Beyabanaki et al. 2016). In particular, Sasaki et al. (2004), Wu et al. (2009), Wu (2010) and Zhang et al. (2013a, b) proposed several input schemes of dynamic loading for 2-D DDA to simulate the dynamic behavior of blocks in seismically induced rockslides. Although practical applications of DDA have focused on 2-D rockslide problems, three-dimensional (3-D) kinematic analysis is still desirable because 2-D analysis cannot quantitatively estimate (i) the effect of rock shape and terrain on the lateral dispersion process, (ii) the effect of vegetation and fences on the trajectory of the displaced rocks, and (iii) the run-out extent of the displaced rocks. In conclusion, 2-D analysis cannot supply sufficient information for rockslide disaster prevention and mitigation.

Since Shi (2001) first derived the basic formulations of 3-D DDA, much effort has focused on more extensive and efficient analyses of practical rock engineering problems. For example, Yeung et al. (2003) investigated the wedge failure problem in terms of both the effective failure mode and block displacement history. Hwang et al. (2004) developed a 3-D DDA program to simulate the slope toppling failure process at a site in Japan. Beyabanaki et al. (2009a, b) enhanced the blocks’ deformability by introducing finite element meshes into 3-D DDA, and Beyabanaki et al. (2010) achieved the same goal by employing high-order displacement functions in 3-D DDA. Liu et al. (2012) studied the wedge failure mode and the Jiweishan rockslide using 3-D DDA combined with tetrahedral finite elements. Shi (2014) used a simple version of 3-D DDA to perform a stability analysis of a major key block. Wu (2015) introduced a local frame into each block to overcome the false volume expansion and stress distortion problems that occur with large rotations in rockslide simulations. Zhang et al. (2014a) coupled the smoothed particle hydrodynamics (SPH) model into 3-D DDA to investigate rockslide-generated impulse waves (Wang et al. 2016a). Zhang et al. (2016a) extended 3-D DDA to analyze the frictional-cohesive failure behavior of a slope. Beyabanaki and Bagtzoglou (2012, 2015) and Jiao et al. (2015) developed preliminary 3-D spherical DDA models to simulate the kinematic behavior of rockslide problems. However, these spherical models are more suitable for applications to particulate media, and the terrain model is too ideal and simple to be used for practical cases. To address this problem, Chen et al. (2013) and Zheng et al. (2014) developed the contact face element (CFE) model for realistic slope terrain, on which the 3-D trajectories of rockfalls were investigated. However, the preliminary CFE model can only handle the independent movement of individual blocks, i.e., the interaction between the blocks is not considered. In addition, it only accounts for vertex-to-face contacts between the block and the slope model and could not prevent inter-penetration when the edges of a rock block contact the edges of the slope model. Therefore, it cannot be used to model the kinematic behavior of a large number of rocks on complex terrain.

This study developed a new 3-D DDA model to analyze the kinematic behavior of rockslides on complex 3-D terrain. Including the introduction, this paper consists of six sections. Section 2 introduces the fundamental theory of 3-D DDA. Section 3 presents an extension to the original 3-D DDA for the analysis of rockslides on complex 3-D terrain. Section 4 verifies the accuracy of the new model with the benchmark tests on the four basic types of block motion, including parabolic motion, sliding, rolling and bouncing on 3-D terrain. Section 5 shows the simulation results of a designed rockslide on complex 3-D terrain and provides a detailed discussion of the results to demonstrate the model’s practical applicability. Finally, Sect. 6 presents the main conclusions.

Fundamental theory of 3-D DDA

Block displacements and deformations

For a 3-D DDA formulation, the linear system has twelve degrees of freedom for each individual block with an arbitrary polyhedral shape:

$$D_{i} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {u_{0} } & {v_{0} } & {\omega_{0} } \\ \end{array} } & {\begin{array}{*{20}c} {r_{x} } & {r_{y} } & {r_{z} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varepsilon_{x} } & {\varepsilon_{y} } & {\varepsilon_{z} } \\ \end{array} } & {\begin{array}{*{20}c} {\gamma_{yz} } & {\gamma_{zx} } & {\gamma_{xy} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]^{T}$$
(1)

where (u 0, v 0, w 0) are the rigid body translations of a specific point (x 0, y 0, z 0) of Block i, (r x , r y , r z ) are the rigid body rotations of Block i with the center of rotation at (x 0, y 0, z 0), and (ε x , ε y , ε z ), and (γ yz , γ zx , γ xy ) are the normal and shear strains on Block i, respectively. The displacement of an arbitrary point (x, y, z) in Block i is:

$$\left[ {\begin{array}{*{20}c} u & v & w \\ \end{array} } \right]^{T} = \left[ {{\mathbf{T}}_{i} \left( {x,y,z} \right)} \right]{\mathbf{D}}_{i}$$
(2a)

where [T i (x, y, z)] is the formula for the displacement function of Block i, which is given by:

$$\left[ {{\mathbf{T}}_{i} \left( {x,y,z} \right)} \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & {z - z_{0} } & { - \left( {y - y_{0} } \right)} & {x - x_{0} } & 0 & 0 & 0 & {\frac{{z - z_{0} }}{2}} & {\frac{{y - y_{0} }}{2}} \\ 0 & 1 & 0 & { - \left( {z - z_{0} } \right)} & 0 & {x - x_{0} } & 0 & {y - y_{0} } & 0 & {\frac{{z - z_{0} }}{2}} & 0 & {\frac{{x - x_{0} }}{2}} \\ 0 & 0 & 1 & {y - y_{0} } & { - \left( {x - x_{0} } \right)} & 0 & 0 & 0 & {z - z_{0} } & {\frac{{y - y_{0} }}{2}} & {\frac{{x - x_{0} }}{2}} & 0 \\ \end{array} } \right]$$
(2b)

Equations of motion

The total potential energy is the summation over all of the potential energy sources from the block stiffness, the initial stress, the point loads, the body loads, the inertia forces, the constraint springs of fixed points or measured displacements, and the contact forces between the blocks.

The equations of motion for a system of n blocks is derived by minimizing the total potential energy:

$$\left[ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {{\mathbf{K}}_{11} } & {{\mathbf{K}}_{12} } \\ {} & {{\mathbf{K}}_{22} } \\ \end{array} } & {\begin{array}{*{20}l} \cdots & {{\mathbf{K}}_{1n} } \\ \cdots & {{\mathbf{K}}_{2n} } \\ \end{array} } \\ {\begin{array}{*{20}l} {} & {} \\ {{\text{Sym}}.} & {} \\ \end{array} } & {\begin{array}{*{20}l} \ddots & \vdots \\ {} & {{\mathbf{K}}_{nn} } \\ \end{array} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {{\mathbf{D}}_{1} } \\ {{\mathbf{D}}_{2} } \\ \end{array} } \\ {\begin{array}{*{20}l} \vdots \\ {{\mathbf{D}}_{n} } \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {{\mathbf{F}}_{1} } \\ {{\mathbf{F}}_{2} } \\ \end{array} } \\ {\begin{array}{*{20}l} \vdots \\ {{\mathbf{F}}_{n} } \\ \end{array} } \\ \end{array} } \right]$$
(3)

where K ij and F i are 12 × 12 stiffness submatrices and 12 × 1 loading vectors, respectively. The submatrices K ii depend on the material properties of Block i, and K ij (i ≠ j) is defined by the contacts between Blocks i and j. For additional details, the interested reader is referred to Shi (1988, 2001).

Limitations of the original 3-D DDA for kinematic analysis of rockslides

A rigorous contact theory that allows 3-D DDA to address contact problems for systems of arbitrarily shaped polyhedral blocks is still under development. The contact theory must account for the geometrical and mechanical relationships between the blocks; i.e., contact detection and contact mechanics treatment, respectively. Contact detection and resolution is important because (i) it is the most time-consuming part of discrete analyses and can take up 80% of the total computation time (Horner et al. 2000), and (ii) the types of contacts determine the mechanical response of the contacts (Cundall 1988).

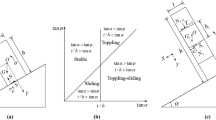
In the original 3-D DDA, the terrain of a slope is generated as the boundaries of a single large block or the combination of several artificial column blocks. In practice, the blocky slope model is not applicable because of the following factors: (i) no effective tools have been developed to automatically generate a large-scale, complex polyhedral slope model to be used in 3-D DDA; (ii) if the 3-D slope is reconstructed as a single large polyhedral block (Fig. 1a), difficulty will arise from the treatment of the contacts between blocks with significantly different sizes; and (iii) if the slope is discretized into several artificial column blocks (Fig. 1b), the computational cost for these extra blocks will increase significantly.

Fig. 1
figure 1

Three types of slope models: a a single block; b artificial column blocks; c TRN terrain

Full size image

Extensions of the original 3-D DDA for kinematic analyses of rockslides on complex 3-D terrain

Triangulated regular network for the terrain of a slope

Kinematic analyses of rockslides only consider the kinematic behavior of the displaced rocks, and the slope merely serves as the boundary for these rocks to interact with. Moreover, the ground motion and deformation that are induced by the rockslide are neglected due to their small values; for example, the velocities induced by a 2.5 × 106 m3 rockslide are on the order of 10−6 m/s (Favreau et al. 2010). Therefore, it is not necessary to generate a slope as blocks. A simpler slope model for the terrain of a slope (Fig. 1c), such as a triangulated regular network (TRN), can play a similar role as the boundary of the blocky slope.

In practice, the terrain of a slope is usually prepared in a geographical information system (GIS) in the form of a contour map, which is represented by extracted polylines (Fig. 2a). The polylines are a straightforward description of the terrain, but they cannot be used directly as the slope model in 3-D DDA because they do not intersect with each other and cannot form polyhedral faces. To solve this problem, the polyline file is first transformed into a triangulated irregular network (TIN) map (Fig. 2b), which is then converted into a raster format (Fig. 2c). The terrain of the slope in the raster format is represented mathematically by a set of elevation points in the form of an m × n matrix (where m and n are the rows and columns of the matrix, respectively) of elevations. Physically, the terrain of the slope is composed of equally sized cells (Δ denotes the cell size) in rows and columns. As shown in Fig. 3a, the coordinates are contained in the ordering of the matrix; i.e., the x- (or y-)coordinate of each point is calculated by multiplying the cell size and its x- (or y-)index, and the elevation in the z-direction can be directly accessed from the elevation matrix according to its x- and y-indices.

Fig. 2
figure 2

Representations of the terrain of a slope

Full size image
Fig. 3
figure 3

Representations of the terrain of a slope by a TRN map: a a raster dataset; b the TRN generated from the raster dataset

Full size image

However, the raster slope model also cannot be used directly in 3-D DDA because the faces in 3-D DDA are defined as plane polygons. Therefore, it is necessary to divide each cell into two triangles (Fig. 3b). If the indices of the upper left point of a cell are (i, j), then the lower left triangle consists of three points that are indexed as (i, j), (i + 1, j), and (i + 1, j + 1), and the upper right triangle consists of three points that are indexed as (i, j), (i + 1, j + 1), and (i, j + 1) (Fig. 3). All of these triangles are stored in sequence in an array. Accordingly, a lower left triangle is always indexed in the array with an even number, whereas an upper right triangle is always indexed with an odd number (Fig. 3). Assuming that a TRN slope model is represented by an m × n matrix, the indices of the upper left point of a cell are (i, j), and the indices of the lower left and upper right triangles of this cell in the array can be directly obtained as 2 × [(n − 1) × i + j] and 2 × [(n − 1) × i + j] + 1, respectively, according to the regular arrangement, which is useful in searching for possible contacts.

Contact detection scheme

Search for possible contacting TRN elements

A TRN slope model that is represented by an m × n matrix contains v a (=m × n) vertices, e a edges (including (n − 1) × m edges along the x-axis, (m − 1) × n edges along the y-axis, and (m − 1) × (n − 1) edges that separate the cells), and f a faces (including (m − 1) × (n − 1) lower left and upper right triangles, respectively). If a block contains v b vertices, e b edges, and f b faces, the number of discrete contact combinations between the block and the slope model is given by (Cundall 1988):

$$N = \left( {v_{a} + e_{a} + f_{a} } \right) \cdot \left( {v_{b} + e_{b} + f_{b} } \right)$$
(4)

For example, if a slope model is represented by a 570 × 455 matrix, it contains 2,59,350 vertices, 7,76,001 edges and 5,16,652 faces. Even if only one cuboid moves on the slope, the total number of possible contacts would be 4,03,52,078 per time step. Clearly, the number of contact elements is too large to allow for an exhaustive search. However, this drawback can be overcome in the TRN slope model due to its regular element arrangement. A brief procedure of the new program is presented in Fig. 4.

Fig. 4
figure 4

Flow chart of the extended 3-D DDA program

Full size image

To improve the computational efficiency, the contact detection begins by searching for possible contacting TRN elements of the slope model. In this step, it should be sufficient to confine each block to a relatively rough axis-aligned bounding box (AABB) (Wu et al. 2005, 2014) (Fig. 5a). Let x min, y min, z min, x max, y max, and z max be the minimum and maximum coordinates of a block, and limit the block within its AABB. The possible contact territory for the block can be determined by enlarging its AABB with a relatively small tolerance ctol that is the maximum allowable vertex displacement within a single time step. The possible contacting TRN elements of the slope can be restricted within the region that is contained by the projection of the block’s contact territory on the xy-plane (Fig. 5b, c). The range of the region can be indexed by Eq. (5a–d):

Fig. 5
figure 5figure 5

Global search between a block and a TRN slope

Full size image
$$i_{ \hbox{min} } = {\text{INT}}\left( {\frac{{x_{ \hbox{min} } - ctol}}{\Delta }} \right)$$
(5a)
$$i_{ \hbox{max} } = {\text{INT}}\left( {\frac{{x_{ \hbox{max} } + ctol}}{\Delta }} \right)$$
(5b)
$$j_{ \hbox{min} } = {\text{INT}}\left( {\frac{{y_{ \hbox{min} } - ctol}}{\Delta }} \right)$$
(5c)
$$j_{ \hbox{max} } = {\text{INT}}\left( {\frac{{y_{ \hbox{max} } + ctol}}{\Delta }} \right)$$
(5d)

where Δ is the cell size, and INT means taking the integer portion of the value; that is, the triangles whose upper left point’s indices (i, j) satisfy the condition:

$$\left\{ {\left( {i,j} \right)|i \in \left[ {i_{ \hbox{min} } ,i_{ \hbox{max} } } \right],j \in \left[ {j_{ \hbox{min} } ,j_{ \hbox{max} } } \right]} \right\}$$
(6)

are the possible contacting TRN elements for the block.

Furthermore, local contact detection can be avoided if Eq. (7) is satisfied:

$$z_{ \hbox{min} } - ctol \ge Z_{ \hbox{max} }$$
(7)

where Z max is the maximum elevation of the possible contacting TRN elements (Fig. 5d). Consequently, the number of possible contacting TRN elements is dramatically decreased, and the efficiency of the contact detection is greatly improved.

Examination of dominant contact types

In this step, the blocks and corresponding possible contacting TRN elements are examined in more detail for the dominant contact types (Fig. 4). Blocks contact these possible TRN elements at their boundaries (i.e., vertices, edges and faces). In general, seven contact types must be addressed in 3-D cases, including vertex-to-vertex (V–V), vertex-to-edge (V–E), vertex-to-face (V–F), crossing edge-to-edge (E–E), parallel E–E, edge-to-face (E–F), and face-to-face (F–F) (Cundall 1988; Liu and Lemos 2001; Keneti et al. 2008). However, as indicated by Shi (2015), only four dominant contact types need to be examined in 3-D DDA, including V–V, V–E, V–F and crossing E–E (hereinafter referred to as “E–E” for short if not otherwise specified) (Fig. 6), because the others can be converted to combinations of these four dominant contact types.

Fig. 6
figure 6

Contact types

Full size image

Contact pairs of these dominant contacts can be in contact when their distances are close enough to be within ctol. Some contact pairs may belong to multiple types. For example, Vertex A in the V–E contact (Fig. 6b) actually matches Edge B and Faces B 1 and B 2 at the same time. These cases follow the rule of “complex to simple” (He et al. 2014), which is V–V > V–E > V–F = E–E. The purpose is to avoid misjudgment of complex situations. Additional details of dominant contact examination can be found in Zhang et al. (2016b).

Identification of the entrance plane and contact point pair

According to the entrance plane (EP) method (Zhang et al. 2015a), all dominant contacts will be converted to one or two entrance modes; i.e., V–F and E–E entrance modes. A V–F contact can occur between a vertex and a face. An E–E contact can occur between two edges. A V–E contact (denoted as Vertex A and Edge B) can occur between Vertex A and either face that contains Edge B (i.e., V–F entrance) or between Edge B and the edge that contains Vertex A (i.e., E–E entrance). A V–V contact (denoted as Vertices A and B) can occur between Vertex A and either face that contains Vertex B (i.e., V–F entrance), between Vertex B and either face that contains Vertex A (i.e., V–F entrance) or between two edges that contain Vertices A and B (i.e., E–E entrance).

For a V–F entrance, the face is the EP, and all of the faces that contain the vertex should be on the outer side of the EP. For an E–E entrance, the plane that contains one edge and is parallel to the other edge is the EP, and the two faces that contain one edge should be on one side of the EP, while the two faces that contain the other edge should be on the other side of the EP. General entrance formulas (Zhang et al. 2015a) are used to determine if these entrance candidates can physically occur.

Finally, each dominant contact between a block and a TRN slope model may occur in three modes: a block vertex and a slope face (Mode 1), a slope vertex and a block face (Mode 2), and a block edge and a slope edge (Mode 3) (Fig. 7). A solution to real entrance modes and contact point pairs can be determined using a “trial-and-error” procedure. Hence, “open-close” iterations (Jiang and Yeung 2004) were employed to locate all closed entrances and contact point pairs and to apply the most suitable contact force patterns for contact computation in each time step.

Fig. 7
figure 7

Three modes of contacts between a block and a TRN slope

Full size image

Contact mechanics treatment

Submatrix of a normal contact spring

The relevant formulation for the V–F entrance between polyhedral blocks was provided by Shi (2001), and the counterpart for the E–E entrance can be found in Zhang et al. (2016c). In the following sections, the formulation for the entrances of the contacts between a block and a TRN slope model are derived in a uniform way based on the previous work of Shi (2001) and Zhang et al. (2016c).

Let P a and P b be a contact point pair that belong to Block i and the slope model, respectively. The coordinates and displacement increments of Point P m (m = 1, 2, 3, 4) are assumed to be (x m , y m , z m ), and (u m , v m , w m ), respectively. The submatrices of normal contact springs, shear contact springs and friction force are derived as follows.

The normal distance between P a and P b can be approximately calculated by Eq. (8a):

$$d_{\text{n}} = d_{0} + \frac{{\mathop \sum \nolimits_{r = 1}^{4} \left\{ {\left[ {\begin{array}{*{20}c} {A_{r2} } & {A_{r3} } & {A_{r4} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {u_{r} } \\ {v_{r} } \\ {w_{r} } \\ \end{array} } \right]} \right\}}}{{A_{0} }}$$
(8a)

where

$$d_{0} = \frac{{\mathop \sum \nolimits_{r = 1}^{4} A_{r1} }}{{A_{0} }}$$
(8b)

and

$$A_{0} = \left\{ {\begin{array}{*{20}c} {\sqrt {\left| {\begin{array}{*{20}c} {y_{3} - y_{2} } & {z_{3} - z_{2} } \\ {y_{4} - y_{2} } & {z_{4} - y_{2} } \\ \end{array} } \right|^{2} + \left| {\begin{array}{*{20}c} {z_{3} - z_{2} } & {x_{3} - x_{2} } \\ {z_{4} - z_{2} } & {x_{4} - x_{2} } \\ \end{array} } \right|^{2} + \left| {\begin{array}{*{20}c} {x_{3} - x_{2} } & {y_{3} - y_{2} } \\ {x_{4} - x_{2} } & {y_{4} - y_{2} } \\ \end{array} } \right|^{2} } ,} & {{\text{for the V}}{-}{\text{F entrance}}} \\ {\sqrt {\left| {\begin{array}{*{20}c} {y_{3} - y_{2} } & {z_{3} - z_{2} } \\ {y_{4} - y_{2} } & {z_{4} - y_{2} } \\ \end{array} } \right|^{2} + \left| {\begin{array}{*{20}c} {z_{3} - z_{2} } & {x_{3} - x_{2} } \\ {z_{4} - z_{2} } & {x_{4} - x_{2} } \\ \end{array} } \right|^{2} + \left| {\begin{array}{*{20}c} {x_{3} - x_{2} } & {y_{3} - y_{2} } \\ {x_{4} - x_{2} } & {y_{4} - y_{2} } \\ \end{array} } \right|^{2} } ,} & {{\text{for the V}}{-}{\text{F entrance}}} \\ \end{array} } \right.$$
(8c)

A rs is obtained through Eqs. (9–11):

Denote

$$V_{0} = \left| {\begin{array}{*{20}c} 1 & {x_{1} } & {y_{1} } & {z_{1} } \\ 1 & {x_{2} } & {y_{2} } & {z_{2} } \\ 1 & {x_{3} } & {y_{3} } & {z_{3} } \\ 1 & {x_{4} } & {y_{3} } & {z_{3} } \\ \end{array} } \right| = \left| {\begin{array}{*{20}c} {a_{11} } & {a_{12} } & {a_{13} } & {a_{14} } \\ {a_{21} } & {a_{22} } & {a_{23} } & {a_{24} } \\ {a_{31} } & {a_{32} } & {a_{33} } & {a_{34} } \\ {a_{41} } & {a_{42} } & {a_{43} } & {a_{44} } \\ \end{array} } \right|$$
(9)

and M rs as the cofactor of the determinant V 0 about the element a rs in Eq. (9). For example,

$$M_{23} = \left| {\begin{array}{*{20}c} 1 & {x_{1} } & {y_{1} } & {z_{1} } \\ 1 & {x_{2} } & {y_{2} } & {z_{2} } \\ 1 & {x_{3} } & {y_{3} } & {z_{3} } \\ 1 & {x_{4} } & {y_{3} } & {z_{3} } \\ \end{array} } \right| = \left| {\begin{array}{*{20}c} 1 & {y_{1} } & {z_{1} } \\ 1 & {y_{3} } & {z_{3} } \\ 1 & {y_{4} } & {z_{4} } \\ \end{array} } \right|$$
(10)

Denote A rs as the algebraic complement of the determinant V 0 about the element a rs ; i.e.,

$$A_{rs} = \left( { - 1} \right)^{r + s} \cdot M_{rs}$$
(11)

In Mode 1, Vertex P 1 belongs to Block i, and Vertices P 2, P 3, and P 4 belong to the base of the slope. Let:

$${\mathbf{G}}_{i} = \frac{{\left[ {\begin{array}{*{20}c} {A_{12} } & {A_{13} } & {A_{14} } \\ \end{array} } \right]\left[ {{\mathbf{T}}_{i} \left( {x_{1} , y_{1} , z_{1} } \right)} \right]}}{{A_{0} }}$$
(12)

In Mode 2, Vertices P 2, P 3, and P 4 belong to Block i, and Vertex P 1 belongs to the base of the slope. Let:

$${\mathbf{G}}_{i} = \frac{{\mathop \sum \nolimits_{r = 2}^{4} \left\{ {\left[ {\begin{array}{*{20}c} {A_{r2} } & {A_{r3} } & {A_{r4} } \\ \end{array} } \right]\left[ {{\mathbf{T}}_{i} \left( {x_{r} , y_{r} , z_{r} } \right)} \right]} \right\}}}{{A_{0} }}$$
(13)

In Mode 3, Vertices P 1 and P 2 belong to Block i, and Vertices P 3 and P 4 belong to the base of the slope. Let:

$${\mathbf{G}}_{i} = \frac{{\mathop \sum \nolimits_{r = 1}^{2} \left\{ {\left[ {\begin{array}{*{20}c} {A_{r2} } & {A_{r3} } & {A_{r4} } \\ \end{array} } \right]\left[ {{\mathbf{T}}_{i} \left( {x_{r} , y_{r} , z_{r} } \right)} \right]} \right\}}}{{A_{0} }}$$
(14)

Equation (8a) can be rewritten as:

$$d_{n} = d_{0} + {\mathbf{G}}_{i} {\mathbf{D}}_{i}$$
(15)

The potential energy of the normal contact spring is:

$$\prod\nolimits_{n} { = \frac{1}{2}k_{n} d_{n}^{2} }$$
(16)

where k n is the stiffness of the normal contact spring.

By minimizing Π n , the submatrix of the normal contact spring is formed as:

$$k_{n} {\mathbf{G}}_{i}^{T} {\mathbf{G}}_{i} \to {\mathbf{K}}_{ii}$$
(17a)
$$- k_{n} d_{0} {\mathbf{G}}_{i}^{T} \to {\mathbf{F}}_{i}$$
(17b)

Submatrix of a shear contact spring

The shear distance between P a and P b is:

(18)

where n = (n x , n y , n z ) is the unit normal vector of the EP, and \({\mathbf{N}} = \left[ {\begin{array}{*{20}c} {1 - n_{x}^{2} } & 0 & 0 \\ 0 & {1 - n_{y}^{2} } & 0 \\ 0 & 0 & {1 - n_{z}^{2} } \\ \end{array} } \right].\)

The potential energy of the shear contact spring is:

$$\prod\nolimits_{s} { = \frac{1}{2}k_{\text{s}} d_{\text{s}}^{2} }$$
(19)

where k s is the stiffness of the shear contact spring.

By minimizing Π s , the submatrix of the shear contact spring is formed as:

$$k_{s} \left[ {{\mathbf{T}}_{i} \left( {x_{a} , y_{a} , z_{a} } \right)} \right]^{T} {\mathbf{N}}\left[ {{\mathbf{T}}_{i} \left( {x_{a} , y_{a} , z_{a} } \right)} \right] \to {\mathbf{K}}_{ii}$$
(20a)
$$- k_{s} \left[ {{\mathbf{T}}_{i} \left( {x_{a} , y_{a} , z_{a} } \right)} \right]^{T} {\mathbf{N}}\left[ {\begin{array}{*{20}c} {x_{a} - x_{b} } \\ {y_{a} - y_{b} } \\ {z_{a} - z_{b} } \\ \end{array} } \right] \to {\mathbf{F}}_{i}$$
(20b)

Submatrix of the friction force

A normal contact spring and friction force will be added to P a and P b to account for the sliding motion, which is controlled by the Coulomb friction law:

$${\mathbf{f}} = - k_{n} d_{n} { \tan }\phi \cdot {\mathbf{e}}_{s}$$
(21)

where ϕ is the friction angle, and e s  = (e x , e y , e z ) is the unit vector of the relative shear displacement from P b to P a . The relative shear displacement at this iteration step is:

(22)

The potential energy due to the friction forces is:

$$\prod\nolimits_{f} { = - {\mathbf{f}} \cdot {\mathbf{d}}_{f} }$$
(23)

By minimizing Π f , the submatrix of the friction force is formed as:

$$- k_{n} d_{n} { \tan }\phi \left[ {{\mathbf{T}}_{i} \left( {x_{a} , y_{a} , z_{a} } \right)} \right]^{T} \left[ {\begin{array}{*{20}c} {e_{x} } \\ {e_{y} } \\ {e_{z} } \\ \end{array} } \right] \to {\mathbf{F}}_{i}$$
(24)

As shown above, the submatrices that depend on the TRN slope itself can be excluded from Eq. (3), and the stiffness submatrices that are defined by the contacts between the block and the TRN slope are only located in the main diagonal of the global stiffness matrix. Thus, the efficiency of the matrix solutions is enhanced considerably.

Determination of the contact force pattern

Depending on the normal and shear components of the contact force (Fig. 8), three patterns of the contact force are determined by the following criteria (Shi 1988):

Fig. 8
figure 8

Mechanical models of a contact

Full size image
  1. 1.

    If d n  ≤ 0, the contact status is “open”, and neither spring nor a friction force is added to the contact points;

  2. 2.

    If d n  > 0 and k s d s  > k n d n tanϕ + cA c , the contact status is “slip”, and a normal spring and a friction force are applied at the contact points;

  3. 3.

    If d n > 0 and k s d s  ≤ k n d n tanϕ + cA c , the contact status is “stick”, and both normal and shear springs are placed at the contact points.

Benchmark tests

To investigate the accuracy of the new model, the benchmark tests on the four basic types of block motion (i.e., parabolic motion, sliding, rolling, and bouncing of blocks on 3-D terrain) are presented. The value of the gravitational acceleration g is taken as 10 m/s2.

Parabolic motion

An example of a projectile with an initial speed is used to numerically investigate the accuracy of the parabolic motion when a block is detached from the slope. In this example, the block moves with a constant speed of v y (10 m/s) in the y-direction and falls freely in the z-direction. Hence, the analytical solutions of the displacements in the y- and z-directions at the centroid of the block after time t, d y , and d z , are:

$$d_{y} = v_{y} t$$
(25a)
$$d_{z} = - \frac{1}{2}gt^{2}$$
(25b)

As shown in Fig. 9, the 3-D DDA results exhibit satisfactory agreement with the analytical solutions, which validates the precision of the new 3-D DDA model for parabolic motion of a block.

Fig. 9
figure 9

Verification of the 3-D DDA solution for parabolic motion

Full size image

Sliding motion

An example of a block sliding on an inclined plane due to gravity with interface friction is used to numerically investigate sliding motion. The parameters θ and ϕ are the inclination of the slope and friction angle, respectively, and ϕ < θ. The analytical solution for the downslope displacement of the block is:

$$d = \frac{1}{2}g\left( {{ \sin }\theta - { \tan }\phi { \cos }\theta } \right)t^{2}$$
(26)

As shown in Fig. 10, the 3-D DDA results agree with the analytical solutions. The block remains stable on the inclined plane when ϕ ≥ θ (θ = 30° in this example). Thus, the new 3-D DDA model is able to capture essential aspects of sliding motion.

Fig. 10
figure 10

Verification of the 3-D DDA solution for sliding motion

Full size image

Rolling motion

An example of the so-called “critical rolling initiation angle” (CRIA) is used to numerically investigate the rolling motion of a block. The CRIA of a regular prism with n equilateral edges (Fig. 11a) is defined as:

Fig. 11
figure 11

Verification of the 3-D DDA solution for rolling motion

Full size image
$$\alpha = \frac{180}{n}$$
(27)

In 3-D DDA simulations, the friction angle ϕ is assigned a greater value than the inclination of the slope θ to avoid sliding failure; then, θ is gradually increased until rolling motion occurs when θ = α. Thus, the value of θ when rolling motion occurs in the 3-D DDA simulation can be used as the CRIA of the block.

As shown in Fig. 11b, the DDA results are nearly identical to the analytical solutions, which confirms the precision of the results of rolling motion from the new 3-D DDA model.

Bouncing motion

The existing DDA model assumes completely elastic deformation without energy dissipation during block collision, so the rebounding rock will travel faster and further than is observed in experiments or measured in the field.

From the perspective of contact mechanics, the TRN slope model that was developed in this study is similar to the completely fixed, rigid blocky slope model that was used in the original 3-D DDA. This condition in a blocky slope model can be approximately obtained when (i) the slope block is fixed with springs of very large stiffness and is not subjected to gravity, and (ii) the slope block has a very large value of Young’s modulus and a Poisson’s ratio of zero. As shown in Fig. 12a, the bouncing solutions using a TRN slope model and a completely fixed, rigid blocky slope model are nearly the same, in which Young’s modulus E = 1.0 × 1010 Pa, Poisson’s ratio υ = 0.25, and the normal spring stiffness k n  = 1.0 × 1010 N/m.

Fig. 12
figure 12

Verification of the 3-D DDA solution for bouncing motion

Full size image

The bouncing height in Fig. 12a is reduced because some of the gravitational potential energy of the upper colliding block is converted into elastic strain energy of the block. The mechanical properties, including E and υ, and the computational parameter k n are the main factors that affect the energy conversion during block collision. As shown in Fig. 12b, the coefficient of restitution (COR) approaches 1.0 when E and k n are sufficiently large.

However, the phenomenon of energy dissipation during a collision has been observed in many experiments, but it is not fully understood and thus requires further studies. Hence, bouncing motion is difficult to simulate because it depends on the kinetic energy that is absorbed as plastic deformation of the soft layer of the slope surface or converted into thermal energy.

To account for the energy dissipation due to the collision, a so-called post-adjustment method similar to Chen’s (2003) was employed. The velocities of a rock immediately before and after the collision are denoted v b and v a , respectively, and the initial velocity of the rock immediately after the collision is modified to:

$$v_{a} = {\text{COR}} \cdot v_{b}$$
(28)

Estimating the value of the COR requires laboratory or in situ tests, which were carried out by Zhu et al. (2016b). According to the observed data cited by Chen (2003), the COR in rockslides ranges from 0.6 to 0.8.

Applications to the kinematic analysis of a designed large-scale rockslide

Model setup

Figure 13 shows the geometry of a model of a large-scale rockslide. The TRN slope model consists of 2240 triangles with a cell size of 0.5 m. The rockslide mass on the slope is composed of 39 arbitrarily shaped polyhedral blocks with a minimum volume of 50.833 m3 and a minimum edge length of 1.670 m.

Fig. 13
figure 13

Geometry of the model

Full size image

The blocks are allowed to move freely under gravity from the resting state. The mechanical properties and computational parameters used in the simulations are: density ρ = 2500 kg/m3, Young’s modulus E = 5.0 × 1010 Pa, Poisson’s ratio υ = 0.25, gravitational acceleration g = 10 m/s2, friction angle ϕ = 25°, zero cohesion (because the cohesion is too sensitive to sliding stability (Shi 2014)), normal spring stiffness k n  = 5.0 × 1010 N/m, rebound velocity ratio COR = 0.7, time interval Δt = 0.0001 s, and the total computational time is 20 s. A normal contact spring stiffness value of E is used to obtain reasonable displacements and stresses because the ratio of the normal contact spring stiffness to the Young’s modulus should range between 1/100 and 100 (Shi 1988; Wu 2008).

The computations were executed on a desktop computer with an Intel(R) Core(TM) i7-4790 CPU (3.60 GHz, 8 cores) and 24 GB of RAM.

Results and discussion

Figure 14 shows the velocity, run-out distance and extent of the example. The results show that:

Fig. 14
figure 14

Comparisons of the velocity, run-out distance and distribution of the landslide deposit before (a, b) and after (c, d) construction of a fence

Full size image
  1. 1.

    The terrain has a strong influence on the run-out distance and extent because of lateral dispersion (Fig. 13a–d). These results indicate that using a 2-D DDA model to describe the spatial motion along a prescribed 2-D path may result in large errors. The results predicted by the 3-D simulation, such as the velocity (or kinetic energy depending on the mass and the velocity of an individual block), run-out distance, and extent, provide more straightforward information than a 2-D model, which is useful in rockslide disaster prevention and mitigation, such as the design of fences to prevent a potential rockslide from destroying structures (Fig. 14c, d).

  2. 2.

    The velocity of the rockslide masses greatly depends on the slope angle (Ritchie 1963). The kinematic process of the rockslide can be divided into two main stages. In the first stage, the rockslide accelerates to a high speed in a short period of time (Fig. 14a). In the second stage, the rockslide decelerates to a stationary state (Fig. 14b). This is due to the effect of the inclination of the slope on the type of block motion. For gentle slopes, the most commonly observed phenomena are rolling and sliding (Volkwein et al. 2011). For intermediate slopes, rocks propagate as a succession of parabolic motions and bouncing, whereas for steep slopes, parabolic motion is the dominant mode of block motion. Sliding motion clearly plays a primary role in energy dissipation in the form of friction.

  3. 3.

    The run-out distance appears to be related to the slope angle. The friction angle (25°) is approximately equal to the angle of reach (approximately 23.4°), which is calculated by:

    $$\beta = { \tan }^{ - 1} \left( {\frac{H}{L}} \right)$$
    (29)

    where H is the elevation difference between the top of the source area and the toe of the deposit, and L is the length of the horizontal projection of the streamline that connects these two points (Fig. 14b). This relationship is consistent with the results that were obtained from methods based on regression models (Heim and Skermer 1989).

  4. 4.

    In this example, the computational time for 1000 steps using the TRN slope model is approximately 53 s, whereas the counterpart using the blocky slope model is up to 880 s; that is, the new model increased the computational efficiency by 17 times. Because of the regular arrangement of elements, the computation time using the TRN slope model will remain the same as in the example even if the size of the slope is greatly increased; however, for the blocky slope model, the computational cost will increase significantly due to the contact detection between the blocks and the extra elements of the blocky slope when it is expanded to a larger-scale problem. In other words, the larger the problem is, the more significantly the efficiency will be improved using the TRN slope model.

Conclusions

This paper proposes a new TRN slope model for 3-D DDA to analyze rockslides on complex 3-D terrain. The main merits of the new model are as follows:

  1. 1.

    Large-scale slope models with complex terrain can be created easily and efficiently using GIS tools.

  2. 2.

    The computational efficiency of the contact detection is greatly improved because the total number of possible contacts is dramatically reduced due to the regular element arrangement of the TRN slope model.

  3. 3.

    The computational efficiency of the treatment of contact mechanics is enhanced considerably because all of the submatrices that are related to the TRN slope are excluded from the matrix assembly.

To investigate the accuracy of the new model, the benchmark tests on the four basic types of block motion, including parabolic motion, sliding, rolling, and bouncing, were verified. Finally, applications to large-scale rockslides with complex terrain were provided to demonstrate the practical applicability of the model. The results indicate that the new 3-D DDA model is an effective tool to analyze large-scale rockslides.

However, modeling three dimensional multi-block systems in 3D-DDA is a complex and challenging task because the block cutting code (Shi 2006) in 3D-DDA does not have a graphical interface and does not accept 3-D blocks as input; rather, it uses 2-D triangles to build the blocks. A more complex case study will be provided in the future after incorporating more user-friendly techniques, such as binocular photogrammetry (Zhu et al. 2016a) and computer-aided design (CAD) techniques (Yagoda-Biran and Hatzor 2016).

Moreover, this study addressed the energy dissipation due to a collision using a so-called post-adjustment method, which is somewhat empirical and artificial. Further development of a more physical elastic–plastic model instead of the current completely elastic model is a way to address the problem of energy dissipation due to a collision.

Finally, the dynamic analysis of large-scale rockslides on complex 3-D terrain under seismic loading remains an interesting topic for further study. This problem requires additional effort to incorporate dynamic loading input schemes into the current 3-D DDA model for dynamic analyses.