1 Introduction

In mountainous areas and along engineered slopes, rockfalls are one of the most frequently occurring geological hazards, potentially threatening lives, settlements, facilities, and transportation corridors within their runout (Agliardi and Crosta 2003). Generally, a rockfall event consists of three distinct phases: (1) the preparatory phase in which the bedrock is gradually deteriorated and a potentially unstable rock mass is formed on the upper part of the slope; (2) the initial failure phase in which the potential unstable rock mass detaches from its parent rock; and (3) the post-failure phase in which the detached rock volume moves downward along the slope (Matsuoka 2019; Asteriou et al. 2012). The first two phases are controlled and triggered by multiple internal (e.g., topography, stratum lithology, geological structure, and rock mass discontinuities) and external (e.g., weathering, freezing–thawing, rainfall, earthquake, vegetation, and human activities) factors (Hungr et al. 1999; Wang et al. 2020). During the post-failure phase, a single block, boulder, or a small group of independent blocks move rapidly downward by a combination of freefalling, bouncing, rolling, or sliding under the effect of gravity and finally come to rest at a gentle zone or near obstacles (Asteriou et al. 2012; Descoeudres and Zimmermann 1987). The initial and post-failure phases are dynamic processes involving large deformations and movements of rock masses. The failure mechanisms and subsequent movement characteristics are particularly essential for rockfall risk assessment, prediction, and prevention (Azzoni et al. 1995).

The post-failure phase involves complicated movement processes that are active near the slope surface, and rock masses often exhibit very high velocities with a broad area of debris coverage (Geniş et al. 2017). The evolutions of the runout trajectory, velocity, and kinetic energy are the key parameters for representing the rockfall movement characteristics, which are directly related to the design of countermeasures against rockfalls (Volkwein et al. 2011; Zheng et al. 2014). The lateral deviations, jumping heights, runout distances, and deposition positions of the blocks can be obtained from the motion trajectories. Essentially, the motion trajectories of the blocks are the external manifestation of their total kinetic energies. The total kinetic energy (including translational and rotational) can be increased owing to the transformation of gravitational potential energy during the downward movement of the block, or can be dissipated through collisions between the block and the slope, and among blocks (Li et al. 2016; Zhu et al. 2019). It can be said that the kinetic energy and motion trajectory are the main basis for determining the strength as well as the location and scale of rockfall protection structures. Thus, many methods, such as analytical calculations (Azzoni et al. 1995; Zambrano 2008; Irfan and Chen 2017), laboratory model tests (Asteriou et al. 2012; Asteriou and Tsiambaos 2016; Nagendran and Ismail 2019), field experiments (Giacomini et al. 2009; Ma et al. 2011; Spadari et al. 2012), and numerical simulations (Stevens 1998; Jones et al. 2000; Guzzetti et al. 2002), have been used to study the movement characteristics of rockfalls. However, only a few studies have analysed the failure mechanisms and dynamic characteristics during the initial failure phase of rockfalls. If the initial failure mechanisms of rockfalls can be recognised and prevention measures can be developed accordingly, rockfall disasters may be eliminated in the early stage. Therefore, it is necessary to systematically study the entire dynamic process of rockfalls from their initial to post-failure stages.

With the advancement of computational mechanics and computer technology, the use of computer programs for rockfall simulations has become popular over the past decades (Chau et al. 2002; Peng et al. 2020). Discontinuous deformation analysis (DDA) is a discrete numerical method pioneered by Shi (1988), which has received considerable attention from researchers and engineers in recent years. With its effective use of block kinematics in dealing with the complicated interaction between discrete blocks under general loading and boundary conditions, it is very capable of treating the problems of both rigid body movements and large deformations of discrete block systems (Chen 2003). In addition, DDA can consider the actual shape and geological and mechanical properties of both slope and falling rocks (Chen et al. 2013). Hence, it is probably the most suitable numerical simulation method for rockfall analysis (Koo and Chern 1998).

DDA has been proved to be highly accurate through a large number of examples (Yagoda-Biran and Hatzor 2016), and it has been successfully used in the engineering of slopes experiencing rockfalls. For instance, Ohnishi et al. (1996) first applied DDA to rockfall computations to design protective fences. Ma et al. (2011) and Chen (2003) introduced models of energy loss originating from friction, collision, and vegetation into DDA, and applied the developed DDA to a rockfall simulation. Koo and Chern (1998) and Wu et al. (2010) implemented a post-contact adjustment method into the original DDA to overcome the false volume expansion due to the large rotation of blocks, and the movement processes of an actual rockfall were analysed. However, these applications of DDA to rockfalls have concentrated thus far on the two-dimensional (2D) problem and are not very useful for investigating rockfalls in three dimensions (Wang et al. 2017b). A 2D model shows, at best, a crude approximation of rock engineering. Therefore, a three-dimensional (3D) DDA simulation is required for two reasons. First, the effect of the 3D spatial distribution (e.g., orientation and geometry) of rock discontinuities is very significant for the initial failure of rockfalls. Second, the 3D spatial effects of the rock block shape and topography on the rockfall movement in lateral directions should be considered.

The theory of 3D DDA, originally published by Shi (2001), shares the same basic principles as 2D DDA. A series of developments have been achieved in recent years, and most of the studies focus on the basic theory. For example, a compatible simplex integration algorithm (Wu 2010) was presented for a 3D DDA block domain of any shape, and the integration of convex and concave polyhedrons was performed. The 3D DDA formulas with higher order (second- and third-order) displacement functions (Beyabanaki et al. 2010) or finite-element meshed blocks (Liu et al. 2012) were deduced, and the 3D DDA capabilities for modelling a deformable block were enhanced. Smoothed particle hydrodynamics (Wang et al. 2017a) and a distinct lattice spring model (Zhao et al. 2017) were coupled with 3D DDA to simulate landslide dam behaviours as well as rock cutting and rock penetration. The dynamic deformation formulation based on the strain-rotation decomposition theorem was implemented in 3D DDA to eliminate the error caused by rotation (Fan et al. 2018). In addition, the elastic distortion problem with large rotation in 3D DDA was solved by coordinate-transformation calculations in the vertex coordinate, stress, and velocity update (Wu 2015). A damped contact model based on the linear spring-dashpot assumption was incorporated into the 3D DDA to address the energy loss in collisions (Yu et al. 2020). Compared to 2D DDA, the contact mechanism between 3D blocks is more complicated, which is a difficulty that is restricting the development of 3D DDA. To date, the common plane method (Liu et al. 2004), the closest points algorithm (Beyabanaki et al. 2008), and the main plane method (Keneti et al. 2008) have been introduced to address 3D mechanical interactions between convex blocks. Moreover, many contact models, such as vertex-to-face (V–F) contact (Jiang and Yeung 2004; Wu et al. 2005a) and edge-to-edge (E–E) contact (Yeung et al. 2007; Wu 2008; Zhang et al. 2016), associated with 3D DDA have been developed to deal with contact problems in 3D discrete blocky systems. Particularly, Shi (2015) recently developed a new entrance block contact theory that can solve the contacts between 3D general blocks with arbitrary convex or concave shapes using uniform mathematical equations. With the use of the entrance block model, the geometrical and topological computations of 3D contacts can be transformed into algebraic operations, and the relationship between two general blocks reduces to the relationship between a reference point and the entrance block, thus considerably simplifying the complexity of contact computation. It can be said that the above fundamental studies have made the rapid development of 3D DDA possible.

Nevertheless, the application of 3D DDA for rockfall simulations is still very rare in the literature. Wu et al. (2005b) employed a developed 3D DDA code to analyse the complex failure process of the Amatoribashi-nishi rockfall, and the phenomena of lateral migration and rotation of blocks can be observed, which agree well with the field observations recorded on videotape. Recently, Liu and Li (2019, 2020) studied the effect of slope geometrical characteristics and tree barriers on rockfall movement using 3D DDA and put forward some suggestions on disaster prevention of rockfalls. These few applications demonstrate the applicability of 3D DDA to slope rockfall simulations. However, the slope topography and block shape of the present 3D DDA models are generally regular and the number of falling block elements is small. In addition, the research on large-scale rockfall volumes is insufficient. Liu et al. (2021) and Ma et al. (2021) have combined 3D DDA with outdoor experiments to conduct preliminary studies on the movement characteristics of rockfalls. Nevertheless, more studies are required to verify the 3D DDA simulation of slope failure and rockfall movement and calibrate the physical parameters using laboratory tests to facilitate the application of the approach presented.

In this study, we use the 3D DDA method to study the failure mechanisms and movement characteristics of slope rockfalls, such as single boulders and large-scale rockfalls, and provide detailed insights into the entire kinematic process of rockfall disasters. The fundamentals of 3D DDA are explained, and its accuracy is verified by the results of existing laboratory experiments. Moreover, a typical slope subjected to rockfalls, namely K4580 in the Tibetan Plateau, is taken as an example. Subsequently, the initiation and failure of a large-scale dangerous rock mass at the source area are simulated by 3D DDA, and the movement characteristics of the formed boulder and massive collapsing rocks along slopes of different geometrical characteristics are investigated.

2 Engineering Background

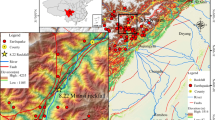
The K4580 typical slope, on the left bank of the Lhasa River, is located at the junction of Lamu Village and Zunmucai Village in Dazi County (district), Lhasa City, Tibet Autonomous Region (Fig. 1a). The altitude is 3762 m, the longitude is 91°59′28ʺ, and the latitude is 29°36′59ʺ. The G318 national road and Lhasa–Nyingchi highway (viaduct) pass through the leading edge of the slope, as illustrated in Fig. 1b, c. Figure 1d shows a field photograph of the slope. The landslide trend is evident, and a clear landslide wall is formed on the upper part of the landslide mass. The entire slope is composed of an upper soil layer and a lower rock layer. The upper part is broken stone soil with silty clay, whereas the lower part is metamorphic massive granodiorite. The potential landslide is rocky. Over the years, the slope has been continuously deformed and the surface rock (and soil) has been gradually peeled off. The length of the threatened road is approximately 160 m.

Fig. 1
figure 1

K4580 typical slope along the G318 national road in Tibetan Plateau. a Studied area, b landslide location, c photo of the scene, and d photo of the slope

Full size image

On the top of the slope, an exposed bedrock with joint development forms a large-scale, potentially unstable rock mass, as displayed in Fig. 2a. In the past decades, especially during summer rainfall and seasonal changes, local rockfall failures have occurred occasionally owing to the weakening of the structural planes inside the potential unstable rock mass of the slope. Some of the rock blocks may reach or even be deposited on the highway, which constitute a major geological hazard in this section of the G318 national road. A large number of rock blocks (Fig. 2b) are also found on the slope as a result of rockfalls, especially in the gentle area below the top of the slope, and many rock blocks or boulders have accumulated.

Fig. 2
figure 2

Potential unstable rock mass and rock blocks originating from rockfalls. a Potential unstable rock mass and b rock blocks deposited on the slope surface

Full size image

The existing monitoring data show that the slope is in an unstable state with very slow deformation under natural conditions (Liu 2019). Under the condition of a large amount of rainfall, the landslide mass has a certain deformation, indicating the possibility of slope deformation and instability. Because of the steep slope and long-term influence of weathering, freezing–thawing, rainfall, earthquakes, and other complex environmental conditions, the slope is prone to landslides. After a landslide, a large number of rock and soil masses slid to the slope bottom. Compared with that before the landslide, the slope topography has changed significantly.

3 Fundamental Principles of 3D DDA

The 3D DDA method is a displacement-based and an implicit method. It has some unique features, such as complete block kinematics and its numerical realisation, perfect first-order displacement approximation, strict postulate of equilibrium, accurate energy consumption, and high computing efficiency (Shi 1988, 2001). Because the implicit solution scheme used in 3D DDA is unconditionally stable for any time step, a large time step size can be used. The larger the time step size, the fewer the time steps required for analysis, indicating that less computing time is required for 3D DDA (Tang et al. 2015). In this method, a practical rock slope is modelled as an assemblage of blocks of any convex or concave shape, and all blocks are physically isolated and bounded by pre-existing discontinuities. The interactions between blocks are simulated by contact springs at the contacting positions. The simultaneous equilibrium equations are established by minimising the total potential energy, which originates from the potential energies of single blocks and contacts between two blocks, and the unknowns in the equilibrium equations are displacement-based variables. The large displacements are the accumulation of incremental displacements and deformations at each time step. Within each time step, the incremental displacements of all blocks are small; hence, the block displacements can be reasonably represented by the first-order approximations (Shi 1988, 2001).

3.1 Block Displacement Function

The displacement function, similar to the shape function of the finite-element method, calculates the displacement of all blocks using the displacement of each block centroid. By applying the first-order displacement approximations, 3D DDA assumes that each block has a constant strain and stress throughout. There are 12 basic degrees of freedom for block i of an arbitrary shape

$$ \left[ {D_{i} } \right]^{T} = \left[ {\begin{array}{*{20}c} {u_{c} } & {v_{c} } & {w_{c} } & {r_{x} } & {r_{y} } & {r_{z} } & {\varepsilon_{x} } & {\varepsilon_{y} } & {\varepsilon_{z} } & {\gamma_{yz} } & {\gamma_{zx} } & {\gamma_{xy} } \\ \end{array} } \right]_{i} , \, \left( {i = 1, \, 2, \ldots , \, n} \right), $$
(1)

where (uc, vc, wc) are the translations of the centroid (xc, yc, zc) of the block along the x, y, and z axes, respectively; (rx, ry, rz) are the rotations of the block around the x, y, and z axes, respectively; and (εx, εy, εz, γyz, γzx, γxy) are the three normal strains and three shear strains of the block, respectively. The displacement [u v w]T of any point (x, y, z) of the block can be expressed in the following form:

$$ \left[ {\begin{array}{*{20}c} u & v & w \\ \end{array} } \right]^{T} = \left[ {T_{i} (x, \, y, \, z)} \right]\left[ {D_{i} } \right], \, \left( {i = 1, \, 2, \ldots , \, n} \right), $$
(2)

where [Ti(x, y, z)] is the displacement transformation matrix defined by

$$ \left[ {T_{i} \left( {x, \, y, \, z} \right)} \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & {\hat{z}} & { - \hat{y}} & {\hat{x}} & 0 & 0 & 0 & {\frac{{\hat{z}}}{2}} & {\frac{{\hat{y}}}{2}} \\ 0 & 1 & 0 & { - \hat{z}} & 0 & {\hat{x}} & 0 & {\hat{y}} & 0 & {\frac{{\hat{z}}}{2}} & 0 & {\frac{{\hat{x}}}{2}} \\ 0 & 0 & 1 & {\hat{y}} & { - \hat{x}} & 0 & 0 & 0 & {\hat{z}} & {\frac{{\hat{y}}}{2}} & {\frac{{\hat{x}}}{2}} & 0 \\ \end{array} } \right], $$
(3)

where \(\hat{x} = x - x_{c}\), \(\hat{y} = y - y_{c}\), and \(\hat{z} = z - z_{c}\).

Block rotation is common in both the initial and post-failure phases of rockfalls. Because the first-order linear displacement approximation in Eq. (2) is employed in DDA, an unreasonable change in block size, called the free expansion phenomenon, may result because of the treatment of large rigid rotation of the block (Wu et al. 2010). This false expansion may lead to contact identification errors if the rotating blocks are close to each other. To overcome the block volume expansion, a post-correction of the displacement of all relevant points in the x, y, and z directions is performed at the end of each time step (Jiang and Yeung 2004; Wang et al. 2017b), namely

$$ \begin{gathered} \left[ {\begin{array}{*{20}c} {u^{\prime}} & {v^{\prime}} & {w^{\prime}} \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} u & v & w \\ \end{array} } \right]^{T} - \left[ {\begin{array}{*{20}c} 0 & {\hat{z}} & { - \hat{y}} \\ { - \hat{z}} & 0 & {\hat{x}} \\ {\hat{y}} & { - \hat{x}} & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {r_{x} } \\ {r_{y} } \\ {r_{z} } \\ \end{array} } \right] \hfill \\ + \left[ {\begin{array}{*{20}c} {\cos r_{y} + \cos r_{z} - 2} & { - \sin r_{z} } & {\sin r_{y} } \\ {\sin r_{z} } & {\cos r_{x} + \cos r_{z} - 2} & { - \sin r_{x} } \\ { - \sin r_{y} } & {\sin r_{x} } & {\cos r_{x} + \cos r_{y} - 2} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\hat{x}} \\ {\hat{y}} \\ {\hat{z}} \\ \end{array} } \right]. \hfill \\ \end{gathered} $$
(4)

3.2 Simultaneous Equilibrium Equations

A block system is formed by individual blocks through contacts among blocks and displacement constraints on single blocks. Assuming that there are n blocks in the defined block system, the simultaneous equilibrium equations are derived using the principle of minimum total potential energy and they are established as follows (Yagoda-Biran and Hatzor 2016; Liu et al. 2019b):

$$ \left[ M \right]\left[ {\ddot{D}} \right] + \left[ K \right]\left[ D \right] = \left[ F \right], $$
(5)

where [M] and [K] represent the mass and stiffness matrices, respectively, whereas \(\left[ {\ddot{D}} \right]\), [D], and [F] denote the acceleration, displacement, and external force vectors, respectively.

Assume that the velocity vector at the beginning of time step (t = t0) is \(\left[ {\dot{D}_{0} } \right]\), which can be obtained from the previous time step, and that the time step size is Δt. Based on Newmark’s β and γ methods using β = 0.5 and γ = 1.0, the acceleration vector \(\left[ {\ddot{D}} \right] = \left[ {\ddot{D}\left( {t_{{0}} + {\Delta }t} \right)} \right]\) and velocity vector \(\left[ {\dot{D}} \right] = \left[ {\dot{D}\left( {t_{{0}} + {\Delta }t} \right)} \right]\) at the current time step (t = t0 + ∆t) can be represented by

$$ \left[ {\ddot{D}} \right]{ = }\frac{2}{{\Delta t^{2} }}\left( {\left[ D \right] - \Delta t\left[ {\dot{D}_{0} } \right]} \right), $$
(6)
$$ \left[ {\dot{D}} \right]{ = }\frac{2}{\Delta t}\left[ D \right] - \left[ {\dot{D}_{0} } \right]. $$
(7)

Substituting Eq. (6) into Eq. (5), we obtain

$$ \left[ {\hat{K}} \right]\left[ D \right] = \left[ {\hat{F}} \right], $$
(8)

where \(\left[ {\hat{K}} \right]\) is the equivalent global stiffness matrix, and \(\left[ {\hat{F}} \right]\) is the equivalent force vector. Equation (8) can be rewritten in a sub-matrix form as follows:

$$ \left[ {\begin{array}{*{20}c} {\left[ {K_{11} } \right]} & {\left[ {K_{12} } \right]} & \cdots & {\left[ {K_{1n} } \right]} \\ {\left[ {K_{21} } \right]} & {\left[ {K_{22} } \right]} & \cdots & {\left[ {K_{2n} } \right]} \\ \vdots & \vdots & \ddots & \vdots \\ {\left[ {K_{n1} } \right]} & {\left[ {K_{n2} } \right]} & \cdots & {\left[ {K_{nn} } \right]} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\left[ {D_{1} } \right]} \\ {\left[ {D_{2} } \right]} \\ \vdots \\ {\left[ {D_{n} } \right]} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left[ {F_{1} } \right]} \\ {\left[ {F_{2} } \right]} \\ \vdots \\ {\left[ {F_{n} } \right]} \\ \end{array} } \right], $$
(9)

where [Kij] (i, j = 1, 2, …, n) is a stiffness sub-matrix, which is a 12 × 12 matrix calculated for a single block and its contact with other blocks. [Di] and [Fi] (i = 1, 2, …, n) represent the 12 × 1 displacement vector and 12 × 1 force vector corresponding to block i, respectively. More detailed descriptions of the derivation of the 3D DDA formulas can be found in Shi’s paper (Shi 2001).

3.3 Block Contact Mechanism

Arbitrarily shaped polyhedral blocks in a block system can be represented by their boundary vertices, edges, and faces. The blocks are in contact only along the block boundaries (Wang et al. 2017b). The 3D contact forms can be geometrically classified as vertex-to-vertex (V–V), vertex-to-edge (V–E), V–F, crossing E–E, parallel E–E, edge-to-face (E–F), and face-to-face (F–F). Because DDA follows small time step sizes and the step displacements are sufficiently small, all contacts are independent and local in computation, and all contact forms can be equivalent to V–V, V–E, V–F, and crossing E–E contacts (Shi 2015). Thus, only the first four basic contact forms are involved in the 3D DDA contact computations. For example, the F–F contact between blocks i and j in Fig. 3a can be solved as four V–F contacts, as illustrated in Fig. 3b.

Fig. 3
figure 3

Contacts between blocks i and j in 3D DDA. a F-F contact and a typical contact model

Full size image

For 3D contact judgement, Shi (2015) proposed a global contact theory to detect when and where contacts occur between blocks with arbitrary shapes. The entrance block theory is a key component of the new contact theory, which provides complete algebraic formulas and is rigorously proved in algebraic and geometrical ways. Based on this entrance block theory, contacts between two blocks can be simplified into contacts between a reference point and an entrance block; thus, the complexity of the contact calculation is greatly simplified. The entrance block can be represented by its boundaries, and its solution procedure involves establishing and solving inequality equations that employ point sets. Within each time step, the possible contact times, positions, and degrees of freedom can be identified by the entrance block and its contact covers (Shi 2015). Therefore, the judgement of where and when to apply possible and suitable contact springs or penalties can be realised.

DDA uses a penalty technique to treat the contact constraints between blocks. When the blocks contact each other, the block boundary follows the maximum tensile strength criteria, and the corresponding shear resistance conforms to the Mohr–Coulomb failure criterion. If penetration occurs at the contact, contact springs should be added in normal or/and sliding direction(s) to prevent penetration, and the penetrated point will be pushed back along the shortest path by the spring. The contact force depends on the contact spring stiffness and penetration distance. When the blocks are separated, the contact springs should be removed, and the contact force is neglected. Within each time step, the contact springs (open-close iteration) are added or removed to satisfy the compatibility conditions of no-tension and no-penetration between any two blocks, which is achieved by iteratively solving Eq. (9).

A typical contact model is depicted in Fig. 3b. The stiffnesses of the normal and shear springs are kn and ks, respectively. The penetration distances in the normal and shear directions are dn and ds, respectively. According to the relative normal component Fn = kndn and shear component Fs = ksds of the contact force, a block contact may have three states, i.e., locked, sliding, and open. These contact states can be determined by the conditions listed in Table 1, and the corresponding contact interactions based on Eq. (9). The details of the implementation of the 3D DDA program, including the implementation of the contact treatment in 3D DDA, can be found in the studies by Liu and Li (2019), Liu et al. (2019b), and Zhang et al. (2016), who also provided a flowchart of the 3D DDA method.

Table 1 Block contact states in 3D DDA
Full size table

4 Validation of 3D DDA

4.1 Failure of a Dangerous Rock Mass

A rock mass at risk of a rockfall may be cut by structural planes to form a block system. If the system reaches a certain geometrical or physical condition, it will become unstable or fail. In this section, a laboratory experiment conducted by the authors (Liu et al. 2019b) is used to verify the accuracy of 3D DDA in simulating the failure of a dangerous rock mass of a slope. As displayed in Fig. 4a, a large aluminium block with dimensions of 10 × 10 × 15 cm is cut into 14 sub-blocks. There are four cubes of the same size with an edge length of 5 cm at the top and bottom layers, respectively, and six cuboids of the same size (2.5 × 5 × 5 cm) in the middle layer. The aluminium block system is placed on a slope with an aluminium surface painted by reference grids, each of which has a size of 5 × 5 cm. A flat panel is arranged on one side of the slope, on which the coordinate paper is pasted and grids of the same size as the slope grids are drawn. A microelectromechanical system accelerometer is attached to the monitoring point of the key block of the block system. As indicated in Fig. 4a, the red block located at the top of the block system and likely to take the lead in the destabilisation and movement is selected as the key block, and a black point on its top is chosen as the monitoring point. Six accelerations, namely three translational and three rotational accelerations, of the monitoring point during the instability and movement of the block system are collected. Based on these accelerations, the displacement of the monitoring point is then obtained through transformation computation. Two high-speed digital cameras capable of 545 frames per second are used to record the process of instability and movement of the block system. One is installed on one side of the slope to capture the movement projection of the block system along the slope, such as sliding, toppling, and bouncing. The other is mounted above the slope and vertically downward to capture the movement states of the blocks, such as lateral deflections and translations.

Fig. 4
figure 4

Laboratory experiment for the failure of a dangerous rock mass. a Experimental model, b resultant displacement-time curves of the monitoring point (dotted lines represent experimental results, while solid lines represent 3D DDA results), and c lateral displacement curves of the monitoring point along the slope

Full size image

Tilting table tests were conducted, and the sliding properties of the aluminium sub-blocks were determined. The results show that the average friction angle is approximately 24°, and the cohesion of the interface is sufficiently small to be neglected. In addition, the Young’s modulus and Poisson’s ratio of the blocks for the experimental model are E = 68 GPa and 0.34, respectively. The 3D DDA numerical parameters are as follows: Δt = 0.00001 s, kn = 1.1 × 105 kN/m, and ks = 1.0 × 104 kN/m. The slope angle was adjusted and increased from 20° to 50°, and the increment of each adjustment was 5°. In other words, the failure characteristics and movement process of the dangerous rock mass under the conditions of θ = 20°, 25°, 30°, 35°, 40°, 45°, and 50° were analysed. Figure 4b illustrates the resultant displacement–time curves of the monitoring point under different slope angles, and correspondingly, the lateral displacement curves along the slope are displayed in Fig. 4c. Here, the solid and dashed lines of the same colour represent the displacement evolution under the same slope angle. The direction of the lateral movements is perpendicular to the aspect of the slope. The lateral displacement in the same direction as the y-axis is positive, while the lateral displacement opposite to the y-axis is negative (Fig. 4a). As can be seen from Fig. 4b, c, these displacement curves have the same evolution trends, and the results of the 3D DDA are almost consistent with those of the experiment.

Tables 2 and 3 present the movement processes of the block system obtained by the experiment and 3D DDA under θ = 30°, respectively, which indicate that the failure and movement states at several different moments from these two methods are basically the same. For the initial failure of the block system, the entire system topples first accompanied by dislocation between blocks. With the deformation and failure of the block system, the upper blocks fall on the slope, and collision, bouncing, and rolling along the slope subsequently occur. In addition, the processes of failure and movement show 3D spatial characteristics of the blocks, which also indicates the necessity of 3D numerical simulation of DDA.

Table 2 Failure and movement process of the block system obtained from the experiment (θ = 30°)
Full size table
Table 3 Failure and movement process of the block system obtained from the 3D DDA (θ = 30°)
Full size table

4.2 Motion Trajectory and Kinetic Energy of the Rockfall

In the subsequent movement of the rockfall after its instability, a variety of motion modes coexist and transform into each other, most of which are mainly rolling and bouncing. For example, when rolling or sliding blocks encounter obstacles such as rock outcrops, they may bounce owing to contact and collision, fall back to the slope surface after moving in the air, and then rebound and jump. In this process, the motion trajectories and kinetic energies of the blocks change drastically, which is one of the emphases of the study of block movement characteristics. Therefore, the existing laboratory model experiment by Zhu (2010) was used to verify the effectiveness of the 3D DDA simulation.

Taking a rockall slope along the Wanzhou highway in Chongqing as an example, a laboratory slope model was built using a scale based on the actual measured slope topography and geometrical dimensions (Zhu 2010), as depicted in Fig. 5a. The slope model is made of concrete, and the experimental rock block is a hard cobblestone of nearly spherical shape with a mass of 44.8 g and a density of 2610 kg/m3. The interfacial friction angle is 10°. In the experiment, the exact position of the rockfall at every moment was captured by a digital image processing technology (Irfan and Chen 2017). The block was released 50 times, and the corresponding motion trajectories were obtained (Fig. 5b) and compared with the 50 motion trajectories simulated by the numerical software RocFall (Fig. 5c). The motion trajectories from the experiments and RocFall simulations are similar. RocFall (Stevens 1998) is a rockfall simulation software based on a lumped mass and hybrid model, and it is commonly used to calculate the impact energy and trajectory of rockfalls. In the RocFall simulation, a falling block is always reduced to a particle, and the trajectories of a block are described using a statistical analysis method (Guzzetti et al. 2002). By default, RocFall may generally form 50 trajectories of block movement per simulation, which is equivalent to the trajectories where the same block falls 50 times (Zhu 2010).

Fig. 5
figure 5figure 5

Experimental model of a rockfall slope along Wanzhou highway. a Scaled geometrical size (Zhu 2010), b motion trajectories obtained from the experiment (Zhu 2010), c motion trajectories obtained from the RocFall simulation (Zhu 2010), d 3D model of the slope and blocks, e motion trajectories obtained from the 3D DDA simulation, and f comparison of kinetic energies

Full size image

To verify the correctness of the 3D DDA in the simulation of rockfall motion trajectory, six blocks of three different shapes, namely regular dodecahedron, regular icosahedron, and approximate spheres, were used. Among them are four approximate spheres with the number of longitude and latitude lines (m × n) of 4 × 4, 5 × 5, 6 × 6, and 7 × 7. The first step of 3D DDA numerical modelling is establishing the corresponding mathematical models. The mathematical models of the approximate spheres were established using AutoCAD, involving both longitudinal and latitudinal lines. The greater the number of longitudinal and latitudinal lines, the closer the block to a sphere. The modelling process of the approximate spheres can be referred to the study by Liu (2019). The 2D slope model in Fig. 5a was extended to 3D, as illustrated in Fig. 5d, for the 3D DDA simulation. The computational parameters are as follows: Young’s modulus E = 54 GPa, Poisson’s ratio υ = 0.13, gravitational acceleration g = 9.8 m/s2, time step size Δt = 0.0001 s, and normal and shear spring stiffnesses kn = 1.0 GN/m and ks = 0.5 GN/m, respectively. As depicted in Fig. 5e, six trajectories of the six moving blocks (centroids) are obtained by 3D DDA, and each of them agrees well with several trajectories in the experiment and RocFall simulation. However, these six trajectories differ from each other. The main reason is the difference in the shapes of these blocks, because the shape of the block is one of the factors affecting its motion trajectory. The blocks simulated above are regular and ideal in shape. Thus, blocks that are more general in shape should be studied to better understand the actual block movement. As displayed in Fig. 5d, there are two arbitrarily convex and concave blocks with the same mass and density as the above simulated regular blocks. Their motion trajectories are presented in Fig. 5e. In contrast to numerical software such as RocFall, 3D DDA can consider the shape of blocks, instead of simplifying them into mass points. This is one of the advantages of 3D DDA in simulating rockfall movements.

In addition, the kinetic energy evolution of the moving block was analysed. As presented by Zhu (2010), the dimensions of the slope model in Fig. 5d are enlarged ten times, and the mass of the falling block is increased to 10 kg. As depicted in Fig. 5f, the evolution trends of the total kinetic energy of the block obtained by the 3D DDA and RocFall software are essentially the same. Figure 5f also illustrates the evolutions of the translational and rotational kinetic energies of the block calculated using 3D DDA. It can be observed that the translational kinetic energy and total kinetic energy are close in numerical value and have the same change trend, while the proportion of the rotational kinetic energy to the total kinetic energy is very small. The kinetic energy of a block corresponds to its motion trajectory, and each attenuation of the kinetic energy represents a collision between the block and the slope surface. For example, when the block moves to the platform at the slope bottom and collides with it, the kinetic energy of the block definitely decreases.

In the existing studies, 3D DDA validations, such as failure, motion trajectory, and kinetic energy of blocks, have been achieved using the cases presented in Sects. 4.1 and 4.2. On this basis, the authors will try to conduct more 3D experiments to verify the accuracy of 3D DDA in simulating rockfall movements in the future.

5 Numerical Simulation of Slope Rockfalls

5.1 3D DDA Numerical Model and Parameters

According to the slope site situation, slope topography, and potential landslide trend, a 3D geometrical model of a rockfall slope was established, as displayed in Fig. 6a. From the analysis of the slope landslide trend, it was inferred that there are two possible situations of slope landslides: shallow landslide with approximate plane sliding and deep landslide with arc sliding. The sliding surfaces of these two types of landslides are illustrated in Fig. 6a and a potentially unstable rock area can be observed. In his Ph.D. thesis, Liu (2019) simulated shallow and deep landslides using 3D DDA. The failure mechanisms of rockfalls and their subsequent movement characteristics along the slope surface before and after shallow and deep landslides were studied.

Fig. 6
figure 6

3D model of the rockfall slope. a Geometrical model, b DDA model, c slope shape after the shallow landslide, and d slope shape after the deep landslide

Full size image

To ensure the constraint conditions of the slope surface on the rockfall movement, i.e., blocks should move within the range of the slope surface, the slope model shown in Fig. 6a was widened on both sides by 38 m. Obviously, the slope model can be expanded to a larger width on both sides. Here, the width expansion was selected as 38 m, which not only satisfies the movement of the blocks within the range of the slope surface, but also reduces the modelling workload. The slope surface was simplified into several triangular sub-faces. According to the terrain data, topological data, such as dip direction, dip angle, and position of each sub-face, were obtained and input into the 3D block cutting program. After the cutting calculation, the geometrical information required for 3D DDA computation was obtained, and then, a 3D DDA model of the slope before the landslide was established, as shown in Fig. 6b. Thus, the 3D block cutting calculation is the pre-processing program for 3D DDA. Correspondingly, the 3D DDA models of the slope after the shallow and deep landslides are presented in Fig. 6c, d, respectively. For a detailed introduction and implementation of the 3D block cutting algorithm, the reader can refer to the studies by Liu and Li (2019) and Shi (2005). In the 3D DDA model, the fixed points are generally arranged at the vertices of the boundary surfaces, such as the lateral boundaries and the bottom of the slope, as depicted in Fig. 6b. The boundary surface can be constrained by limiting its vertices, and the entire slope model can then be constrained. Table 4 lists the common mechanical and numerical parameters used in 3D DDA simulations. Incidentally, the value of the normal spring stiffness was set as ten times that of the Young’s modulus for blocks according to Shi’s suggestion (Shi 1988). The values of the contact spring stiffness may also need to be adjusted and considered to be reasonable until there are no abnormal phenomena such as obvious intrusion and jumping of blocks (Liu et al. 2019a). In the authors’ past research (Liu et al. 2021; Ma et al. 2021), the value criteria of the contact spring stiffnesses are also discussed.

Table 4 Mechanical and numerical parameters used in 3D DDA simulation
Full size table

5.2 Rockfall Analysis of a Single Boulder

There are many groups of structural planes in the potential unstable rock area at the top of the slope, among which the occurrences (dip directions/dip angles) of the most typical ones are 2°∠29° (Joint 1), 3°∠89° (Joint 2), 267°∠87° (Joint 3), and 92°∠88° (Joint 4), respectively, as shown in Figs. 2a and 6a. A single boulder with a volume of approximately 115 m3 is formed in a potentially unstable rock area, which may be the first to fail. The movement characteristics of the rockfall along three different types of slope surfaces, i.e., before the landslide (non-landslide), after the shallow landslide, and after the deep landslide, were investigated after falling of the boulder. The failure processes and motion trajectories of the boulder along these different slope surfaces, including the elevation and planform, are illustrated in Fig. 7. The failure of a dangerous rock mass can be described as follows: first, the interfacial friction between the dangerous rock mass and its parent rock becomes insufficient to resist its driving force, and the failure mode is sliding, forming a boulder. With the continuous increase in slippage, the movement mode of the boulder changes from sliding to toppling–sliding, and then to toppling. Finally, the boulder falls while overturning, moves to, and collides with a gentle slope surface.

Fig. 7
figure 7

Motion trajectories (elevations and planforms) of the boulder along the slopes of different shapes. a Before the landslide, b after the shallow landslide, and c after the deep landslide

Full size image

The movement of the boulder along the slope is manifested as colliding, bouncing, flying, rolling, and sliding, which threatens the operation of the G318 national road and Lhasa–Nyingchi highway (viaduct). The rockfall movement along these three different slope surfaces can be summarised as follows: (1) along the non-landslide slope, the boulder finally leaps from the slope surface, jumps over the viaduct, and moves to the slope bottom. At this stage, the boulder collides with the edge of the viaduct. Then, after colliding, bouncing, rolling, and sliding, it enters the Lhasa River, collides with its bank slope and rebounds, and finally stops in the Lhasa River (Fig. 7a). (2) Along the slope after the shallow landslide, the boulder slides into and passes through the bottom of the viaduct after colliding with the slope. At this stage, the boulder collides with the piers of the viaduct. Finally, it slides and rolls into and stabilises in the Lhasa River (Fig. 7b). (3) Along the slope after the deep landslide, the boulder moves into and stabilises at the bottom of the viaduct. At this stage, it collides with the piers of the viaduct many times (Fig. 7c). From the entire movement process, it can be observed that the boulder movement is affected by its own shape and slope shape, and lateral deviations and deflections occur.

The spatial position coordinates of the centroid of the boulder in Fig. 7 when the boulder is in contact with the different slope surfaces, including colliding, rolling, and sliding along the slopes as well as final stillness, were extracted. Subsequently, the position information of the falling points of the boulder at the moment when the movement forms change was described, as shown in Fig. 8. Corresponding to the movement of the boulder along the different slope surfaces in Fig. 7, the contact occurrences between the boulder and the slopes before the landslide, after the shallow landslide, and after the deep landslide are 7, 8, and 5 times, respectively, and the corresponding centroid numbers of the boulder are W1–W7, S1–S8, and D1–D5, respectively. In addition, Fig. 8 presents the spatial positions of the centroid (C1–C4) of the boulder in the four movement forms of sliding, toppling, falling, and colliding, from boulder collapse and instability to the first collision with the slope. The lateral deviation–time curves of the boulder moving along these three different slope surfaces are displayed in Fig. 9a, which indicates that the lateral deviation of the boulder along the slopes before the landslide (d1), after the shallow landslide (d2), and after the deep landslide (d3) can be generally compared as d1 > d2 > d3. When the boulder tends to be stable, d1 = 40.69 m, d2 = 14.16 m, and d2 = 11.87 m. Therefore, the lateral deviation of the boulder before the landslide is the most significant, which is approximately 2.87 and 3.23 times the lateral deviations of the boulder after the shallow and deep landslides, respectively. The kinetic energy–time curves of the boulders are depicted in Fig. 9b. For these three different slope surfaces, the time when the boulder moves to and collides with the bottom of the slope is recorded as t1, t2, and t3, respectively, and is compared as follows: t1 > t2 > t3. Thus, after the landslide, the moving time of the boulder to the slope bottom is significantly reduced. Combining Fig. 9a, b, the comparison of the final stabilisation time of the boulder before the landslide (ts1), after the shallow landslide (ts2), and after the deep landslide (ts3) can be expressed as ts1 > ts2 > ts3. Under the non-landslide condition, the kinetic energy of the same boulder is relatively large and is difficult to stabilise. After the boulder moves along the slope after the deep landslide and enters the viaduct bottom, the kinetic energy changes many times, indicating that the boulder collides with the bridge body or piers many times, which may cause obvious energy dissipation of the boulder and serious damage to the viaduct.

Fig. 8
figure 8

Spatial positions of the centroid of the boulder when the boulder is in contact with different slopes

Full size image
Fig. 9
figure 9

Time curves of the lateral deviation and kinetic energy of the boulder along the slopes of different shapes. a Lateral deviation and b kinetic energy

Full size image

5.3 Rockfall Analysis of a Large-Scale Dangerous Rock Mass

Actually, the potentially unstable rock area has several groups of structural planes that can form a large-scale, dangerous rock mass. Two joint sets with occurrences (dip directions/dip angles) of 267°∠87° and 92°∠88° mentioned above are mainly distributed inside the rock mass, which is cut into a large number of sub-blocks. Their average joint spacing is approximately 3.84 m and 2.17 m, respectively. The 3D DDA model was established, as shown in Fig. 10a. Several fixed points were imposed at the boundary surface of the slope model to constrain the entire slope model. All numerical tests were executed on a desktop computer with an Intel(R) Core(TM) i7 CPU (3.40 GHz) and 16 GB of RAM. Each test in this section lasted approximately 4 h. The failure process of the dangerous rock mass, including the enlarged elevations and planforms of the failure positions at some moment, is depicted in Fig. 10b–d. First, the dangerous rock mass slides as a whole. Then, a tensile crack appears between its trailing edge and the parent rock, and the front edge tends to topple. Many cracks form at the top of the rock mass, and the interlayers between the blocks are staggered owing to shear failure (Fig. 10b). Subsequently, the deformation of the dangerous rock mass increases, and the sliding displacements, toppling displacements, and interlayer tension cracks of the internal blocks increase significantly, while the blocks with a toppling trend at the front edge show a falling trend (Fig. 10c). Finally, the blocks in the front edge of the dangerous rock mass fall away from the parent rock, and the falling process is accompanied by overturning and projectile motion (Fig. 10d). In summary, the failure mode of the dangerous rock mass is mainly sliding, local toppling, falling, and overturning, which occur simultaneously when the rocks detach from the parent rock, and a rockfall ejection phenomenon exists.

Fig. 10
figure 10

Failure process of the dangerous rock mass. a Time = 0.0 s, b time = 3.0 s, c time = 5.0 s, and d time = 7.0 s

Full size image

Figures 11,12,13 display the movement processes of the rockfall along the slopes before the landslide, after the shallow landslide, and after the deep landslide, respectively. With the sliding and toppling of the internal blocks and the opening and staggering between blocks, the deformation of the dangerous rock mass is increasing. The number of blocks falling on the slope from the parent rock is increasing and moving down the slope one after another, with sliding, rolling, colliding, bouncing, and oblique throwing (or projectile). Among them, the ‘rolling’ includes lateral deflection, and the ‘colliding’ includes collision of the blocks with their surrounding ones and the slope surface. A large number of blocks move along the slope to form a movement range, the magnitude of which along the slopes before the landslide (r1), after the shallow landslide (r2), and after the deep landslide (r3) can be compared as follows: r1 > r2 > r3. In other words, the distribution of the moving blocks along the slope without landslide is the most dispersed, the range of influence and threat is the widest, and the impact on the highway and viaduct at the foot of the slope is also the most scattered. For the slopes after the shallow and deep landslides, the rockfall has a concentrated impact on the highway and viaduct, and the impact damage is more intense, which may destroy the viaduct. After the massive collapse, the blocks left over from the dangerous rock area at the top of the slope fall to the bottom of the slope intermittently, impacting the highway and viaduct and forming a secondary rockfall disaster. With the decrease in the number of blocks in the dangerous rock area, the time interval between the successive falling blocks increases. This may give pedestrians the illusion that the unstable blocks have completely fall down and the highway is passable, which may be very dangerous. Therefore, after occurrence of a large-scale rockfall disaster, it is necessary to make a detour to avoid accidental falling blocks that may cause casualties.

Fig. 11
figure 11

Movement process of the rockfall along the slope before the landslide. a Time = 8.0 s, b time = 9.5 s, c time = 14.0 s, d time = 21.0 s, e time = 27.5 s, and f time = 38.0 s

Full size image
Fig. 12
figure 12

Movement process of the rockfall along the slope after the shallow landslide. a Time = 8.5 s, b time = 10.0 s, c time = 15.0 s, d time = 21.5 s, e time = 27.5 s, and f time = 37.0 s

Full size image
Fig. 13
figure 13

Movement process of the rockfall along the slope after the deep landslide. a Time = 8.8 s, b time = 10.5 s, c time = 13.0 s, d time = 20.5 s, e time = 27.5 s, and f time = 36.5 s

Full size image

The rock blocks have migrated to the slope bottom and they are mostly deposited near the viaduct and in the Lhasa River. For the non-landslide slope, some of the blocks are dispersed along the viaduct, and the deposited range is strip-shaped (Fig. 11f). For the slopes after the shallow and deep landslides, some of the blocks are concentrated near the viaduct, and the deposited range is oval (Figs. 12f, 13f). Among them, the deposited range of the blocks of the slope after the deep landslide is more concentrated and smaller. The blocks are not only distributed on the road and under the viaduct, but also on the viaduct deck. The other blocks have migrated into the Lhasa River, which may cause the river to rise. In particular, the slope after the deep landslide has the largest volume of blocks falling into the river, which may lead to blockage of the river. The deposited position and range of rockfall indicate that this section of the road and viaduct is completely impassable. Owing to the large overall volume of the rockfall, it is difficult to clean up the area in a short time; therefore, detour countermeasures should be implemented timely.

To analyse the movement characteristics of the large rockfall event more quantitatively, block #1 was taken as the key block in the large-scale dangerous rock mass (Fig. 10a) to study its displacement and kinetic energy evolution. The lateral displacement–time curves of the monitoring point on block #1 are plotted in Fig. 14a. The magnitude of the lateral deviation of block #1 when it tends to be stable along the slopes before the landslide (db1), after the shallow landslide (db2), and after the deep landslide (db3) can be compared as follows: db1 > db2 > db3. Accordingly, the kinetic energy–time curves of block #1 are plotted in Fig. 14b. Combining Fig. 14a, b, the comparison of the final stabilisation time of block #1 before the landslide (ts1), after the shallow landslide (ts2), and after the deep landslide (ts3) can be expressed as ts1 > ts2 > ts3. For the kinetic energy–time curves of block #1 along the slopes after the shallow and deep landslides, there are many violent swings between approximately 10 s and 15 s, showing that block #1 collides with the bridge body or piers many times. The positions of block #1 along the different slopes at different moments are depicted in Figs. 10,11,12,13. It is worth noting that block #1 in Fig. 13c–f moves under the bridge and is buried. The present study does not consider the destruction of the bridge by a rockfall event at such a scale. The damage of the bridge is a process of deformation and failure from continuous to discontinuous, and it is difficult to solve this problem using a simple DDA method. Hence, it may be advisable to couple 3D DDA with other methods, such as finite-element method and numerical manifold method, to conduct research on the failure of the bridge by rock block impact.

Fig. 14
figure 14

Time curves of the lateral deviation and kinetic energy of block #1 along the slopes of different shapes. a Lateral deviation and b kinetic energy

Full size image

It should be noted that there are still four blocks in the dangerous rock area at the slope top in an under-stable state. Under rainfall conditions, these blocks may further deform and become unstable. Therefore, they should be cleaned up in time to prevent secondary rockfall disasters. After a rockfall of a large volume of dangerous rock mass, joints may develop in other positions at the slope top because of unloading, which makes the originally stable rock mass tend to be unstable and induce a new rockfall disaster. Therefore, it is necessary to check whether there is a risk of rockfalls in other positions of the slope top again. Furthermore, it is essential to examine whether there are large blocks remaining on the slope surface, and the retained blocks should be cleaned up. Recently, some scholars (Chen and Wu 2018; Wu and Hsieh 2021) found the possibility of rock mass erosion during a slope failure and recommended to consider it in numerical simulations. It may be necessary to use 3D DDA to determine the impact of erosion on the slope failure behaviour to completely consider all possible slope failure scenarios.

6 Conclusions

In this study, the failure mechanisms and movement characteristics of slope rockfalls along the G318 national highway in Tibet are investigated using the 3D DDA method. The entire process and phenomenon of rockfalls along slopes with different geometrical characteristics are analysed, and the disaster prediction for a boulder and massive rockfall is realised. By comparing with the results of laboratory experiments, the ability of 3D DDA to simulate the rockfall failure and movement characteristics, such as motion trajectory and kinetic energy, is validated.

For the rockfall of a single boulder, the initial failure is usually because the interface friction is less than the driving force, and the failure mode is mainly sliding. Before falling from the source area, the sliding, toppling–sliding, and toppling modes of the boulder occur successively. The subsequent movements of the boulder along the three slope surfaces, i.e., before the landslide, after the shallow landslide, and after the deep landslide, are manifested as colliding, bouncing, flying, rolling, and sliding, which are affected by the rock and slope shapes, and lateral deviations and deflections can be observed. The lateral deviation, time of moving to the slope bottom, and final stabilised time of the boulder have the following relations: before the landslide > after the shallow landslide > after the deep landslide. Along these three slopes, the boulder collides with either the edge or the piers of the viaduct, and its kinetic energy significantly changes many times, threatening the transportation safety of the G318 national road and Lhasa–Nyingchi highway (viaduct).

For the rockfall of a large-scale dangerous rock mass, the initial failure mode is mainly sliding, local toppling, falling, and overturning, which occur simultaneously when the rocks detach from the parent rock, and a rockfall ejection phenomenon is presented. The blocks fall gradually and move rapidly downward, and a movement range is formed. The movement ranges of the rockfall along the three slopes can be ranked as follows: before the landslide > after the shallow landslide > after the deep landslide. The impact area of the rockfall along the non-landslide slope is the largest, and some of the blocks are dispersed along the viaduct. Along the slope after the shallow and deep landslides, the impact area of the rockfall is concentrated, and many blocks are deposited intensively near the viaduct, which may destroy the viaduct. The rockfall volume is mainly deposited near the viaduct and in the Lhasa River, and the deposition after the deep landslide is the most concentrated.

The 3D DDA simulation provides comprehensive information on the 3D failure and movement characteristics of rockfalls. It can analyse not only the failure mode in the initial failure phase of a rockfall, but also the velocity (or kinetic energy), trajectory, and process of the rockfall movement. Moreover, it can predict the movement range, deposition position, and affected area of the rockfall. Therefore, it is of great significance for predicting slope disasters and formulating disaster prevention countermeasures to reduce casualties.