Introduction

Oceanic forces such as waves and tides can influence the movement of water-table waves in the aquifers. The propagation of water-table waves plays an important role in many coastal processes like mixing seawater and freshwater (e.g. Li et al. 1999; Robinson et al. 2006; Xin et al. 2010) and also beach sediment transport (e.g. Elfrink and Baldock 2002; Xin et al. 2010; Bakhtyar et al. 2011). The water-table propagation can be described in terms of a complex water-table wave number (k = k r + k i i) where k i is the imaginary part of the water-table wave number, k r is the real part of the water-table wave number, and i is an imaginary number; k r and k i show the decay rate of water-table wave amplitude and the rate of increase in phase lag respectively. Many studies have been done to extract theoretical water-table wave dispersion relationship considering different physical influences such as vertical flows (non-hydrostatics pressure; e.g. Nielsen et al. 1997), horizontal flows in the unsaturated zone (e.g. Kong et al. 2013) and capillary effects (Barry et al. 1996; Li et al. 2000). A summary of the existing analytical dispersion relationships can be found in Shoushtari et al. (2016).

Shoushtari et al. (2016) presented an extensive laboratory sand flume dataset on the propagation of groundwater waves in an unconfined sandy aquifer with a vertical boundary subject to simple harmonic forcing with a wide range of oscillation period from 10.7 to 909 s. Their data showed a monotonic increase in both amplitude decay rate and rate of increase in phase lag of the water-table waves with increasing oscillation frequency (increasing nωd/K sat, where n is the porosity, ω is the angular frequency, d is the aquifer depth and K sat is the saturated hydraulic conductivity) which was in contrast to existing theories which predict (1) zero phase lag or standing wave behaviour and (2) an asymptotic decay rate as the frequency increases. Shoushtari et al. (2016) considered possible influences like sand packing, measurement location, finite amplitude wave effects, unsaturated zone truncation and multiple wave mode effects but none of them can explain the observed discrepancy. They also compared laboratory data against numerical solutions of hysteresis and non-hysteresis Richards’ equation (Richards 1931) and in both cases, the same qualitative behaviour as the analytic solutions described in the aforementioned was found.

In this paper, the hypothesis was tested that the deformation of porous media due to periodic water-table motion is the cause of the model-data discrepancy of Shoushtari et al. (2016). To examine the influence of porous media deformation on water-table wave dispersion, a model was developed that considers saturated-unsaturated water flow in elastic porous solids. Biot’s poro-elastic theory (Biot 1941, 1955, 1962) is adopted which combines Darcy’s law with solid mechanics and describes the interaction between fluids and deformation in porous media. Numerous studies have been carried out to derive analytical (e.g. Madsen 1978; Yamamotom et al. 1978; Okusa 1985; Zienkiewicz et al. 1980; Yamamoto 1981; Yamamoto and Schuckman 1984; Mei and Foda 1981; Rahman et al. 1994; Cha et al. 2002; Jeng and Cha 2003) and numerical (e.g. Thomas 1989, 1995; Jeng and Lin 1996, 1997) solutions to Biot’s theory. Biot’s theory has been also used to analyse different physical systems such as wave-induced stresses and pore pressure in a porous seabed (e.g. Jeng and Hsu 1996; Jeng 2003) and wave-seabed-submarine structures interactions (e.g. Shabani et al. 2009; Zhang et al. 2011a, b). There has been no previous investigation of the influence of porous media deformation on water-table wave propagation in an unconfined aquifer. This paper addresses this gap in knowledge and in doing so tests the hypothesis that the deformation of porous media due to periodic water-table motion is the cause of the model-data discrepancy of Shoushtari et al. (2016). In this paper, a brief description is given of the experimental data of Shoushtari et al. (2016) used for model-data comparison, after which a description of the numerical model and boundary conditions are given, and the model results are compared with the laboratory data.

Experimental setup and procedures

In this section, a brief outline of the sand flume experiments of Shoushtari et al. (2016) is presented for ease of reference. Shoushtari et al. (2016) conducted a series of laboratory tests in the sand flume which is 9 m long, 1.5 m high and 0.15 m wide. A simple harmonic wave was applied across a vertical interface,

$$ {H}_{\mathrm{o}}=d+A \cos \left(\omega t\right) $$
(1)

where H o is the driving head [L], d is the mean driving head [L], A is the driving head amplitude [L], ω = 2π/T is the oscillation frequency [T−1] and T is the oscillation period [T]. Table 1 summarises the driving head parameters used in this study noting that the two periods examined were selected in accordance with the shortest and longest periods examined in the experiments of Shoushtari et al. (2016).

Table 1 Driving head parameters
Full size table

The flume had no-flow boundaries at the ‘landward’ end and at the bottom. The top of the flume was covered in loose plastic sheeting which allowed free connection of the aquifer with the surrounding atmospheric pressure but can be considered a no flow boundary in terms of moisture transport. The sand in the flume was well-sorted quartz sand whose properties were examined in detail by Nielsen and Perrochet (2000a, b; Table 2). Horizontal piezometers inside the sand at different locations along the sand flume were used to measure the hydraulic head.

Table 2 Physical and hydraulic characteristics of the sand (Nielsen and Perrochet 2000a, b)
Full size table

Numerical modeling

To consider the water flow in elastic porous solids, Biot’s poro-elastic theory (Biot 1941, 1955, 1962) is used. This theory is the combination of Darcy’s law with solid mechanics and describes the interaction between fluids and deformation in porous media.

Fluid flow

The Richards’ equation (Richards 1931) is used to estimate the flow field in the poro-elastic model as follows

$$ {\rho}_{\mathrm{f}}\left(\frac{C_{\mathrm{m}}}{\rho_{\mathrm{f}}g}+{S}_{\mathrm{e}}S\right)\frac{\partial {p}_{\mathrm{f}}}{\partial t}+\nabla .{\rho}_{\mathrm{f}}\left[-{K}_{\mathrm{sat}}{\kappa}_{\mathrm{r}}\left(\nabla {p}_{\mathrm{f}}+{\rho}_{\mathrm{f}}g\nabla z\right)\right]=-{\rho}_{\mathrm{f}}{\alpha}_{\mathrm{B}}\frac{\partial }{\partial t}{\varepsilon}_{\mathrm{vol}} $$
(2)

where ρ f is the fluid density [ML−3], p f is the fluid pore pressure [MT−2L−1], C m represents the specific moisture capacity [L−1], S e denotes the effective saturation [−], κ r is the relative permeability [−]. S is the storage coefficient [L−1], K sat is the saturated hydraulic conductivity [LT−1], g is the acceleration of the gravity [LT−2], z is the elevation [L], ∂ε vol/∂t is the rate of change in volumetric strain of the porous matrix [T−1].

The analytical formulas of van Genuchten (1980) are used to define the C m, S e and κ r as follows

$$ {S}_{\mathrm{e}}=\frac{\theta -{\theta}_{\mathrm{r}}}{\theta_{\mathrm{s}}-{\theta}_{\mathrm{r}}}=\left\{\begin{array}{lll}\frac{1}{{\left[1+{\left|\alpha \psi \right|}^{\beta}\right]}^m}\hfill & \hfill & \psi <0\hfill \\ {}1\hfill & \hfill & \psi \ge 0\hfill \end{array}\right. $$
(3)

where ψ is the pressure head [L], θ is the volumetric moisture content [−], θ s and θ r are saturated and residual moisture contents [−], respectively.

The relative permeability is the ratio of the unsaturated hydraulic conductivity relative to the saturated value and for the van Genuchten (1980) model is given by

$$ {\kappa}_{\mathrm{r}}=\left\{\begin{array}{lll}{S}_{\mathrm{e}}^l{\left[1-{\left(1-{S}_{\mathrm{e}}^{1/m}\right)}^m\right]}^2\hfill & \hfill & \psi <0\hfill \\ {}1\hfill & \hfill & \psi \ge 0\hfill \end{array}\right. $$
(4)

The specific moisture capacity is defined as

$$ {C}_{\mathrm{m}}=\frac{d\theta }{dh}=\left\{\begin{array}{lll}\frac{\alpha m}{1-m}\left({\theta}_{\mathrm{s}}-{\theta}_{\mathrm{r}}\right){S}_{\mathrm{e}}^{1/m}{\left(1-{S}_{\mathrm{e}}^{1/m}\right)}^m\hfill & \hfill & \psi <0\hfill \\ {}0\hfill & \hfill & \psi \ge 0\hfill \end{array}\right. $$
(5)

where α [L−1], β [−], l = 0.5 [−] and m = 1 – 1/β [−] are empirical curve fitting parameters, and ψ = 0 corresponds to the water-table position.

The Biot-Willis coefficient α B [−], which relates the volume of fluid expelled by (or sucked into) a porous material element to the volumetric changes of the same element, is defined in terms of the drained and solid bulk moduli as

$$ {\alpha}_{\mathrm{B}}={\left.\frac{\partial {p}_{\mathrm{m}}}{\partial {p}_{\mathrm{f}}}\right|}_{\varepsilon }=1-\frac{K_{\mathrm{d}}}{K_{\mathrm{s}}} $$
(6)

where p m is the total mean pressure for the porous matrix-fluid system [MT−2L−1], ε is the strain tensor [−], and K d and K s are the drained and the solid bulk modulus [MT−2L−1], respectively. The drained bulk modulus (K d) is always smaller than the solid bulk modulus (K s); therefore, Biot-Willis coefficient is always bounded to ε p ≤ α B ≤1 (where ε p is the porosity [−]). The α B does not depend on the properties of the porous matrix. A soft porous matrix has a Biot-Willis coefficient close to 1 (since K d << K s), while for a stiff matrix, it is close to the porosity (since K d ≈ (1 – ε p) K s).

Porous matrix deformation

The governing equation for the poro-elastic material model is

$$ -\nabla .\sigma ={\rho}_{\mathrm{av}}g=\left({\rho}_{\mathrm{f}}{\varepsilon}_{\mathrm{p}}+{\rho}_{\mathrm{d}}\right)g $$
(7)

where σ is the total stress tensor [MT−2L−1], and ρ av, ρ f and ρ d are the average, fluid and drained densities [ML−3], respectively. The total stress tensor, σ, can be calculated by

$$ \sigma =\mathbf{C}\varepsilon -{\alpha}_{\mathrm{B}}{p}_{\mathrm{f}}\mathbf{I} $$
(8)

where C is the elasticity matrix [MT−2L−1], ε is the strain tensor [−] and I is the identity matrix. For an isotropic porous material under plane strain condition which is common for two-dimensional (2D) poro-elasticity problems (i.e. the normal strain to the xz-plane equals zero), this can be simplified to

$$ \left[\begin{array}{c}\hfill {\sigma}_{\mathrm{xx}}\hfill \\ {}\hfill {\sigma}_{\mathrm{zz}}\hfill \\ {}\hfill {\sigma}_{\mathrm{xz}}\hfill \end{array}\right]=\frac{E}{\left(1+\nu \right)\left(1-2\nu \right)}\left[\begin{array}{ccc}\hfill 1-\nu \hfill & \hfill \nu \hfill & \hfill 0\hfill \\ {}\hfill \nu \hfill & \hfill 1-\nu \hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 1-2\nu \hfill \end{array}\right]\left[\begin{array}{c}\hfill {\varepsilon}_{\mathrm{xx}}\hfill \\ {}\hfill {\varepsilon}_{\mathrm{zz}}\hfill \\ {}\hfill {\varepsilon}_{\mathrm{xz}}\hfill \end{array}\right]-\left[\begin{array}{ccc}\hfill {\alpha}_{\mathrm{B}}{p}_{\mathrm{f}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill {\alpha}_{\mathrm{B}}{p}_{\mathrm{f}}\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill {\alpha}_{\mathrm{B}}{p}_{\mathrm{f}}\hfill \end{array}\right] $$
(9)

where E is the Young’s modulus [MT−2L−1] and ν is the Poisson’s ratio for the drained porous matrix [−]. The poro-elastic material model uses Eq. (7) to describe changes in the total stress tensor σ and porous matrix displacement u [L] due to boundary conditions and changes in pore pressure. The α B p f term is often described as the fluid-to-structure coupling expression which counts the fluid pressure contribution.

For small deformation with the plane strain condition, the normal strains (ε xx, ε yy, ε zz) and shear strains (ε xy, ε yz, ε xz) relate to displacements as

$$ \begin{array}{llll}{\varepsilon}_{\mathbf{xx}}=\frac{\partial u}{\partial x},\hfill & {\varepsilon}_{\mathbf{zz}}=\frac{\partial v}{\partial z},\hfill & {\varepsilon}_{\mathbf{xz}}={\varepsilon}_{\mathbf{zx}}=\frac{1}{2}\left(\frac{\partial u}{\partial z}+\frac{\partial v}{\partial x}\right),\hfill & {\varepsilon}_{\mathbf{xy}}={\varepsilon}_{\mathbf{yx}}={\varepsilon}_{\mathbf{yz}}={\varepsilon}_{\mathbf{zy}}={\varepsilon}_{\mathbf{zz}}=0\hfill \end{array} $$
(10)

where u and v are the displacement components in x and z direction [L], respectively.

Equations (9) and (10) are substituted into Eq. (7) which is then solved simultaneously with the time-dependent flow model (Eq. 2) through the time rate of change in strain (∂ε vol/∂t). In this paper, the finite element method is applied using the COMSOL 4.3b (COMSOL 2013) software package.

Model domain and boundary conditions

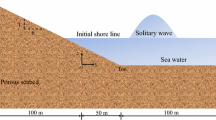
The model domain and boundary conditions of the sand flume using the poro-elastic model are shown in Fig. 1.The no-flow boundary condition in the fluid flow model is given by

$$ \mathbf{n}.{K}_{\mathbf{sat}}\nabla {p}_{\mathbf{f}}=0 $$
(11)

where n is the vector normal to the boundary.

The Cauchy boundary condition has been used to implement the periodic seepage face boundary in the fluid flow model. The Cauchy boundary condition can be expressed by

$$ \mathbf{n}.{\rho}_{\mathbf{f}}{K}_{\mathbf{sat}}\nabla {p}_{\mathbf{f}}={\rho}_{\mathbf{f}}{R}_{\mathbf{b}}\left[\left(\frac{p_{\mathbf{b}}-{p}_{\mathbf{f}}}{\rho_{\mathbf{f}}g}\right)+\left({z}_{\mathbf{b}}-z\right)\right] $$
(12)

where p b and z b are the pressure [MT−2L−1] and elevation of the distant fluid source [L], respectively, and R b is the conductance of the material between the source and the model domain [T−1].

Fig. 1
figure 1

The model domain and boundary conditions used in the poro-elastic model. MWL is the mean water level and d is the aquifer depth

Full size image

By applying appropriate logical statements, the Cauchy boundary condition can be switched between a Dirichlet boundary condition and a Neumann boundary condition. For full details of implementation of the seepage face boundary condition in the numerical model, the reader is referred to Shoushtari et al. (2015a) and Chui and Freyberg (2009).

The boundary conditions for the porous matrix deformation model are a series of constraints on the displacement which are including:

  • Free constraint at the surface (the upper surface is free to move in horizontal and vertical directions)

  • Roller constraint at the bottom, left and right hand sides—the displacement is zero in the direction perpendicular (normal) to the boundary, but it is free to move in the tangential direction.

Model parameters

The coefficients and parameters used in the poro-elastic model are summarized in Table 3. Depending on the degree of compaction in the sand, Young’s modulus (E) and Poisson’s ratio (ν) range between 10 < E (MPa) < 69 and 0.25 < ν < 0.4 respectively. Hence a sensitivity analysis was conducted (see section ‘Results and discussion’) to examine the influence of these model parameters on the water-table wave propagation.

Table 3 Parameters used in the poro-elastic model
Full size table

Results and discussion

To analyse the water-table wave propagation, the water-table wave number has been calculated from a linear regression of water-table wave amplitude and phase profiles which were extracted using harmonic analysis on the simulated pore-pressure time series (e.g. Nielsen 1990; Cartwright et al. 2003).

Model sensitivity analysis

Figures 3 and 4 show the predicted water-table wave number components for T = 16.4 s and T = 908.6 s respectively and their dependence on Young’s modulus (E) and Poisson’s ratio (ν).

For the short period (T = 16.4 s), the real part of the water-table wave number k r d (Fig. 2a) is seen to be insensitive to E and ν with a maximum of k r d = 1.248 obtained for E = 10 MPa and ν = 0.25 and a minimum of k r d = 1.21 for E = 69 MPa and ν = 0.40, i.e. less than 4 % changes in the value of the k r d. In terms of the imaginary part of the water-table wave number k i d (Fig. 2b), the maximum value is 0.396 for E = 10 MPa and ν = 0.25 and a minimum value of 0.092 for E = 69 MPa and ν = 0.40, i.e. 76 % reduction, indicates that the k i d (the rate of increase in phase lag) is sensitive to E and ν.

Fig. 2
figure 2

Water-table wave number components for T = 16.4 s extracting from the poro-elastic model with different values of Young’s modulus (E) and Poisson’s ratio (ν) of the sand—a the real part of the water-table wave number (k r d) for ν = 0.25 (open circle) and ν = 0.40 (closed circle); b the imaginary part of the water-table wave number (k i d) for ν = 0.25 (open triangle) and ν = 0.40 (closed triangle)

Full size image

For the long period (T = 908.6 s, Fig. 3), both real and imaginary parts of the water-table wave number are essentially insensitive to E and ν. The maximum value for k r d is 0.929 for E = 35 MPa and ν = 0.25, which is reduced by 2 % to a minimum value of 0.908 for E = 10 MPa and ν = 0.25. In terms of k i d, the maximum value is 0.276 for E = 35 MPa and ν = 0.25 and the minimum value is 0.250 which indicates 9 % reduction.

Fig. 3
figure 3

Water-table wave number components for T = 908.6 s extracting from the poro-elastic model with different values of Young’s modulus (E) and Poisson’s ratio (ν) of the sand—a the real part of the water-table wave number (k r d) for ν = 0.25 (open circle) and ν = 0.40 (closed circle); b the imaginary part of the water-table wave number (k i d) for ν = 0.25 (open triangle) and ν = 0.40 (closed triangle)

Full size image

The results of the maximum total displacement [√(u 2 + v 2)] where u and v are the displacement components in x and z direction respectively) are summarized in Table 4. As it can be seen in this table, there is a trend that the deformation increases with decreasing Young’s modulus (E) and decreasing Poisson’s ratio (ν). However, with the exception of the E = 10 MPa results, the deformation is less than 1 mm in all cases. This negligible response of the porous media is likely due the fact that the water-table fluctuations in the experimental data are not large enough to induce a significant deformation; hence, overall the water-table wave numbers are generally insensitive to Young’s modulus (E) and Poisson’s ratio (ν) due to the negligible deformation of the sand body.

Table 4 The summary of the maximum total displacement
Full size table

In comparing the trends seen in Table 4 with the wave numbers shown in Figs. 2 and 3, an interesting relationship is found which, whilst perhaps not important under the present experimental parameters (since maximum deformation is <1 mm in almost all cases), may become important under more energetic fluctuations. Figure 2 shows a clear trend of increasing wave numbers with decreasing Young’s modulus (E) which correlates with the predicted increase in deformation with decreasing Young’s modulus (E) for T = 16.4 s (cf. Table 4). The increase in maximum displacement for T = 908.6 s is very similar to that of the T = 16.4 s results; however, Fig. 3 shows no obvious trend with E, which indicates that, if the influence of porous media deformation on water-table wave dispersion was to become more significant under more energetic fluctuations, this would be more likely to occur at shorter oscillation periods than longer ones.

Comparison with existing laboratory data and non-elastic model results

The comparisons of the present poro-elastic model results with the existing laboratory data and non-elastic (hysteretic and non-hysteretic) Richards’ equation model results of Shoushtari et al. (2016) are presented in Figs. 4 and 5 and are also summarised in Table 5. The non-hysteretic Richards’ equation model employed the van Genuchten (1980) parameters α = 1.7 m−1 and β = 9 and the hysteretic model used α w = 3.4 m−1, α d = 1.7 m−1 and β = 9. Full details of non-hysteretic and hysteretic Richards’ model can be found in Shoushtari et al. (2015b).

Fig. 4
figure 4

Model-data comparison of the water-table wave number components for T = 16.4 s. Circles show the poro-elastic model results for different values of Young’s modulus (E) for ν = 0.25 (open circle) and ν = 0.40 (closed circle). The plus sign (+) denotes the non-hysteretic Richards’ model with α = 1.7 m−1 and β = 9; the cross sign (×) shows the hysteretic Richards’s model with α w = 3.4 m−1, α d = 1.7 m−1 and β = 9; the asterisk (∗) denotes the laboratory data of Shoushtari et al. (2016)

Full size image
Fig. 5
figure 5

Model-data comparison of the water-table wave number components for T = 908.6 s. Circles show the poro-elastic model results for different values of Young’s modulus (E) for ν = 0.25 (open circle) and ν = 0.40 (closed circle). The plus sign (+) denotes the non-hysteretic Richards’ model with α = 1.7 m−1 and β = 9; the cross sign (×) shows the hysteretic Richards’s model with α w = 3.4 m−1, α d = 1.7 m−1 and β = 9; the asterisk (∗) denotes the laboratory data of Shoushtari et al. (2016)

Full size image
Table 5 Summary of water-table wave number components
Full size table

In terms of k r d for the short period (T = 16.4 s, Fig. 4), the poro-elastic model results (solid and open circles with an average of k r d = 1.218) are very close to non-hysteretic Richards’ model (plus sign with k r d = 1.151) which is almost 20 % less than laboratory data (asterisk with k r d = 1.499). The hysteretic Richards’ model (cross sign with k r d = 1.426) predicts k r d better than the other two models (poro-elastic and non-hysteretic model) with only <5 % underestimation with respect to laboratory data.

In terms of k i d for the short period (Fig. 4), the non-hysteretic Richards’ model results (plus sign with k i d = 0.101) is similar to the poro-elastic model with E = 69 MPa and ν = 0.40 (open circle with k i d = 0.099), which is 87 % less than laboratory data (asterisk with k r d = 0.751). The result of hysteretic Richards’ model (cross sign with k i d = 0.160) is close to poro-elastic model with E = 35 MPa and ν = 0.25 (open circles with k i d = 0.170), which is 78 % less than the laboratory data. The closest result to the laboratory data is obtained from the poro-elastic model with E = 10 MPa and ν = 0.25 (open circles with k i d = 0.395), but this is still 47 % less than the laboratory data.

For the long period (T = 908.6 s, Fig. 5), the values of k r d and k i d predicted by the poro-elastic model (solid and open circles, average values of 0.919 and 0.263 respectively), are very close to the non-hysteretic Richards’ model with k r d = 0.870 and k i d = 0.231 as compared to the laboratory data (0.471 and 0.295 for k r d and k i d respectively). The closest result to the laboratory data has been obtained with the hysteretic Richards’ model which underestimates k r d and k i d as 17 and 24 % less than laboratory data respectively.

Conclusion

This paper has disproved the hypothesis that porous media deformation can explain the observed model-data discrepancy of Shoushtari et al. (2016) in which the experimental data showed large amounts water-table wave dispersion that their models were unable to predict.

The present study used a numerical model to solve Biot’s poro-elastic equation coupled to Richards’ saturated-unsaturated flow equation to examine the influence of porous media deformation on the water-table wave dispersion which was quantified using the complex water-table wave number.

The poro-elastic model results were found to be generally insensitive to the Young’s modulus (E) and Poisson’s ratio (ν) of the sand with maximum displacements generally less than 1 mm with the exception of the E = 10 MPa results, which indicate maximum displacements >2 mm. This is likely due to the fact that the experimental water-table fluctuations are not energetic enough to induce a significant deformation response.

A sensitivity analysis shows that the only model result which was sensitive to these parameters was the imaginary part of the water-table wave number (k i d) for the short period oscillation (T = 16.4 s). In this case, there was a 76 % change over the range of acceptable values for E and ν. Correspondingly, the real part of the water-table wave number (k r d) only changed about 4 % for the short period and for the long period (T = 908.6 s), k r d and k i d varied by only 2 and 9 % respectively.

The poro-elastic model results were compared with both the laboratory data and rigid medium model results of Shoushtari et al. (2016). For the short period (T = 16.4 s), the difference in predicted k r d between the poro-elastic and rigid medium model results was negligible; however, both model predictions were almost 20 % less than the laboratory data. Decreasing the values of E and ν in the poro-elastic model resulted in some small improvement in the prediction of k i d compared to the rigid media results although it was still 47 % less than the laboratory data. For the long period (T = 908.6 s), the results of poro-elastic and rigid media models were almost the same for both k r d and k i d with both models over-predicting k r d by 94 % relative to the laboratory data.

Whilst the poro-elastic model was unable to reproduce the experimental results, the model results suggest that, if porous media deformation was to become more significant under more energetic fluctuations, the influence of the deformation on water-table wave dispersion is likely to be more significant at shorter oscillation periods than longer ones.