Keywords

1 Introduction

Various types of porous breakwaters are being built as pilot projects in coastal zones in Mekong delta in Vietnam (Nguyet-Minh et al. 2019). These porous breakwaters are placed at a distance from 150 m to 200 m away from sea dikes system to dissipate waves energy or reduce waves attacking on sea dikes directly and to trap sediment behind the breakwaters. After being sedimented, the area between the breakwaters and the sea dikes will be covered with mangrove vegetation (Halide et al. 2004; Schmitt et al. 2013; Nguyet-Minh et al. 2019). There are two types of breakwaters being built in Mekong delta: hollow breakwaters and porous breakwaters. The former dissipates the wave energy when waves pass through some hollows fabricated at front and back faces of the breakwater. The empty space inside the breakwater would also help to damp the wave energy. Sizes of the holes are different from each other and depend on specific purposes, e.g., wave heights behind breakwaters, sedimentation (Fig. 1a). A pilot project of this hollow breakwater type was built in Ca Mau province with 180 m in length (Tran et al. 2019). These projects show the efficiency of hollow breakwater in attenuating wave energy. The latter is a porous breakwater. There are two types of porous breakwater being built in Mekong Delta coastal area: reinforced concrete piles filled with rock and bamboo breakwater (Fig. 1b). The reinforced concrete piles filling with rocks breakwater named CM porous breakwater showed its effect on reducing wave energy and alluvial accumulation (Nguyen and Nguyen 2018; Nguyen and Vu 2019). The bamboo breakwater type or wooden breakwater type was constructed in Thailand (Phansri 2011) and in a pilot project at Bac Lieu province, Vietnam (Schmitt et al. 2013). This is an environment-friendly and effective breakwater in protecting land for mid-slope coastal profile.

Fig. 1.
figure 1

Popular breakwaters built in coastal zone in Mekong delta area: a) hollow breakwater (Tran et al. 2019); b) porous breakwater (Schmitt et al. 2013).

Full size image

The effectiveness of bamboo breakwater in dissipating wave energy has been studied in various ways such as pilot projects, field experiments, physical experiments and numerical simulations. Halide et al. (2004) evaluated the degree of wave attenuation for several bamboo densities and diameters. In their research, bamboo poles were pushed into the sediment offshore from the coastal mangrove plant. They concluded that the bamboo barrier was an economical method in reducing waves. However, they did not mention the impact of the breakwater porosity.

Dao et al. (2018) and Mai et al. (2019) applied SWASH model to simulate waves propagating through a bamboo breakwater with various conditions of breakwater widths, porosities and incoming waves characteristics. Their numerical results evaluated the effectiveness of bamboo breakwater in damping waves when increasing breakwater width and decreasing the porosity of the breakwater. However, their numerical results did not consider the affection of the nonlinearity of waves on wave transmission coefficients.

Albers et al. (2013), Schmitt et al. (2013), Thieu and Mai (2020) show pilot project results and numerical simulations of waves propagating through bamboo breakwaters, Fig. 2. The field experiment data from these studies show the primary effects of the crest height of the breakwater. Thieu and Mai (2020) applied the IH2-VOF model combined with a volume of fluid method to simulate waves and to track the surface elevation. Turbulence effects were modeled by means of a k-ε model. The numerical results show the influences of the fence parameters (i.e. width, freeboard and porosity) on wave attenuation.

In this research, the extended Boussinesq model for waves in porous media of Vu et al. (2018) is applied to evaluate the damped waves effectiveness of bamboo breakwater due to the width of the breakwater and the porosities of the breakwater also. The research results are well compared with the results from Mai et al. (2019).

Fig. 2.
figure 2

a) Designed cross section of bamboo breakwater; b) bamboo breakwater in reality. Mai and Ngo (2018).

Full size image

The first Section of the paper gives some introduction about some types of breakwater being built in the south west coastal zone of Vietnam, especially the bamboo breakwater. The second Section of the paper introduces the governing equations used in this research. The numerical results from this research are analyzed in Sect. 3. The final Section shows some concluding remarks.

2 Governing Equations for Waves in Porous Media

In this research, the bamboo breakwater is considered as a porous media and is not submerged. Thus, the extended Boussinesq equations for waves in porous media of Vu et al. (2018) is applied. The continuity and momentum equations are given by

$$\frac{\partial \eta }{{\partial t}} + \nabla \cdot \left[ {\left( {h + \eta } \right)\,{\text{u}}} \right] = 0$$
(1)
$$\begin{gathered} \left( {\beta \frac{\partial }{\partial t} + \alpha } \right){\text{u}} + g\nabla \eta + \beta \,{\text{u}} \cdot \nabla {\text{u}} + \frac{1}{6}\left( {\beta \frac{\partial }{\partial t} + \alpha } \right)h^{2} \nabla \left( {\nabla \cdot {\text{u}}} \right) - \left( {\frac{1}{2} + \gamma } \right) \times \hfill \\ \left( {\beta \frac{\partial }{\partial t} + \alpha } \right)h\nabla \left[ {\nabla \cdot \left( {h{\text{u}}} \right)} \right] - \gamma \,gh\nabla \left[ {\nabla \cdot \left( {h\nabla \eta } \right)} \right] = 0 \hfill \\ \end{gathered}$$
(2)

where \(\nabla \equiv \left( {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}},\,{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} \right)\,\) is the gradient operator; \({\text{u = }}\left( {u,v} \right)\) is the depth integrated horizontal velocity; \(h\) is the water depth; \(\eta\) is the water surface elevation; \(\gamma\) is the tunning parameter of the extended Boussinesq model, \(\gamma = 1/18\); \(\lambda\) is the porosity; \(\alpha\) and \(\beta\) are the inertial and drag coefficients, respectively. Porosity is the ratio of the void volume over the total volume. It ranges from 0 to unity, the value of 0 for rigid media and unity for clean water media. The inertial and drag coefficients are given by

$$\alpha = \alpha_{l} \left( {\frac{1 - \lambda }{\lambda }} \right)^{2} \frac{\nu }{{d^{2} }} + \alpha_{t} \frac{1 - \lambda }{\lambda }\frac{1}{d}\left| {\text{u}} \right|$$
(3)
$$\beta = 1 + \left( {1 - \lambda } \right)\kappa$$
(4)

where \(\alpha_{l}\) are \(\alpha_{t}\) laminar and turbulent drag coefficients, respectively; \(\nu\) is the dynamic viscosity; \(d\) is the gravel diameter and \(\kappa\) is the added mass coefficient.

3 Waves Propagating Through a Bamboo Breakwater

3.1 Model Setup

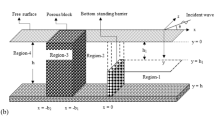
Mai et al. (2019) applies a non-hydrostatic wave-flow model called SWASH to simulate waves propagating through a bamboo breakwater. It should be noted that SWASH is not a Boussinesq-type wave model (Zijlema et al. 2011). The computational domain can be divided into a fixed number of vertical terrain-following layers which would be complicated. In this work, an extended Boussinesq model is used to compare with the results from Mai et al. (2019). A source term addition method is applied to generate waves in 1 dimensional domain (Fig. 3). The length of the computational domain is 45 m. The bamboo breakwater is placed at 20 m. There are two wave gauges placed in front of and behind the bamboo breakwater with G1 at 19.5 m and G2 at 22.5 m. Two sponge layers are fixed at two ends of the computational domain to avoid re-reflection effects back to the computational domain. The sponge layer is specified by a damping coefficient

$$D_{s} = \omega \frac{{\exp \left[ {\left( {d/Sp} \right)^{2.5} } \right] - 1}}{\exp \left( 1 \right) - 1}$$
(5)

where \(\omega\) is the wave angular frequency, \(d\) is the distance from the starting point of the sponge layer, \(Sp\) is the width of the sponge layer. In this research, \(Sp\) is determined as 4 times of a wave length (Vu et al. 2015).

Waves with the height of \(H = 0.3\,{\text{m}}\) are generated in a constant water depth \(h = 0.6\,{\text{m}}\). The horizontal step size is chosen with \(dx = 0.02\,{\text{m}}\) (\(L/dx = 100\), \(L\) is the wave length), the time step is chosen in order to make the model stable with a Courant number \(Cr < 0.2\). The wave source is placed on the left side of the computational domain.

Fig. 3.
figure 3

One-dimensional computational domain.

Full size image

The widths of the bamboo breakwater are fixed with the research of Mai et al. (2019) as 0.4 m and 0.8 m. The porosity characteristics of the Boussinesq model are matched with SWASH as \(\alpha_{l} = 1100\), \(\alpha_{t} = 1.5\), \(\kappa = 0.4\), \(\lambda = 0.5,\,0.9\), \(\nu = 1.004 \times 10^{ - 6} \,{\text{m}}^{{2}} {\text{/s}}\). The widths and porosities of the bamboo breakwater are combined in four cases which are given in the following Table 1.

Table 1. Cases of simulation.
Full size table

3.2 Influence of Porosity and Bamboo Breakwater Width on Transmission Coefficient

Figure 4 shows the comparison between the numerical results of the present work and the numerical results using SWASH of Mai et al. (2019) for 4 cases. The present results are almost the same with Mai et al. (2019)’s results. Figure 4 illustrates the influence of the relative width (\(B_{f} /L\)) and the porosity (\(\lambda\)) of the bamboo breakwater on the transmission coefficient which is given in Eq. (6). When the porosity decreases and the breakwater’s width increases, the transmission coefficient decreases. The numerical results present that the influence of the porosity on the transmission coefficient is dominant. When the porosity keeps small, i.e. \(\lambda = 0.5\), the breakwater width increases from 0.4 m to 0.8 m, the transmission coefficient reduces largely from 0.9 to 0.55. However, with a greater value of porosity, i.e. \(\lambda = 0.9\), when the breakwater width increases with the same amount as the previous case, the transmission coefficient does not reduce much. For field cases, small porosity is conducted by putting bundles of small-size branches inside bamboo breakwaters.

The transmission coefficient \(K_{t}\) in conventional form is given by

$$K_{t} = \frac{{H_{t} }}{{H_{i} }}$$
(6)

where \(H_{t}\) is the transmission wave height and \(H_{i}\) is the incident wave height.

Fig. 4.
figure 4

Comparison between the numerical results of the present research and the results of Mai et al. (2019).

Full size image
Fig. 5.
figure 5

Time series of water surface elevations at Gauge 1 (solid lines) and Gauge 2 (dashed lines) for 4 cases: a) case 1; b) case 2; c) case 3; d) case 4.

Full size image

Figure 5 (a, b, c, d) show more detail about the influence of porosity on transmission coefficient when comparing water surface elevations in front of the bamboo breakwater (at gauge G1) with ones behind the bamboo breakwater (at gauge G2) for 4 cases. The water surface elevations are recorded in 12 periods, from the 36th period to the 48th period. Figure 5 (a, b) shows a large reduction of waves behind the breakwater while Fig. 5 (c, d) show a small variance. It should be noted that the porosities in cases 1 and 2 (Fig. 5 a, b) are smaller than those in cases 3 and 4 (Fig. 5 c, d).

3.3 Effectiveness of Wave Nonlinearity on Wave Transmission Coefficient

This part shows the effectiveness of wave nonlinearity (\(H/h\), \(H\) is the incident wave height and \(h\) is the water depth) on wave height behind the bamboo breakwater in 4 cases. The nonlinearity increases from 0.1 to 0.58. Figure 6 shows the transmission coefficient in a downward trend when increasing the wave nonlinearity. It can be seen clearly that when the porosity is small (\(\lambda = 0.5\), cases 1 & 2) the affection of the nonlinearity is large and when the porosity is large (\(\lambda = 0.9\), cases 3 & 4) the affection of the nonlinearity is small. Thus, the porosity of the bamboo breakwater is significant. It is interesting to find that the similarity trend of nonlinearity effect on transmission coefficient through porous breakwater can be found in literature (Liu and Wen 1997; Lynett et al. 2000; Vu et al. 2018).

Fig. 6.
figure 6

Effectiveness of wave nonlinearity on wave transmission coefficient.

Full size image

4 Concluding Remarks

Most of the previous works on bamboo breakwaters have focused on waves attenuating by changing the breakwater width, porosity, crest height and waves nonlinearity. However, the importance of the breakwater porosity was unclear. This work proves the effectiveness of the breakwater width, porosity and waves nonlinearity on waves height behind the bamboo breakwater. It is concluded that the breakwater porosity is the most dominant factor.

The numerical results applying extended Boussinesq equations for waves in porous media of Vu et al. (2018) show a very good agreement with the numerical results from Mai et al. (2019) applying SWASH. The research results prove small porosities give significant effect on dissipating wave energy.