Introduction

Non-Darcian flow, which describes a non-linear relationship between the specific discharge and hydraulic gradient, often occurs for cases with high flow velocities, or in low-permeability media under very low velocities (e.g. Sen 1989, 1990, 2000; Moutsopoulos and Tsihrintzis 2005; Mathias et al. 2008; Wen et al. 2011; Houben 2015a). Obviously, the flow near a pumping well is likely to be non-Darcian when the pumping rate is relatively large and Darcy’s law becomes invalid. The Forchheimer (1901) equation and Izbash (1931) equation are most commonly used to quantify the relationship between the specific discharge and hydraulic gradient for non-Dracian flow, and it was found that both equations can describe non-Darcian flow very well (Bordier and Zimmer 2000; Chen et al. 2003; Moutsopoulos et al. 2009; Sedghi-Asl et al. 2014; Chen et al. 2015; Houben 2015a). Up to now, a series of (semi-)analytical solutions for non-Darcian flow to a pumping well have been conducted on the basis of these two equations. For instance, Sen (1989, 1990) obtained analytical solutions on the basis of Forchheimer flow for an infinitesimal well or a large diameter well in confined aquifers by using the Boltzmann transform method. Sen (2000) also derived a transient drawdown solution for Izbash flow toward a fully penetrating well of infinitesimal radius in a confined aquifer by using Boltzmann transform as well. Recently, Wen et al. (2008a, 2008b, 2013) have done much work on Izbash non-Darcian flow to a fully penetrating pumping well in different aquifer systems and some approximate solutions have been obtained by using the Laplace transform associated with a linearization approximation. It has been proven that the linearization procedure can lead to an underestimation of the drawdown at early times, but works quite well at late times (Wen et al. 2008a, b). A careful review of the existing (semi-)analytical solution for the non-Darcian flow to a pumping well indicates that the analytical methods of the Boltzmann transform and the linearization procedure have been used to solve such non-Darcian flow models. However, it has been proven that the Boltzmann transform is not mathematically rigorous (Mathias et al. 2008; Wen et al. 2011). The linearization procedure might be a good choice for such non-Darcian problems, although it has some limitations for the early-time solutions (Wen et al. 2009, 2013).

For Darcian flow to a partially penetrating well with a constant rate, a variety of (semi-) analytical solutions are available to analyze the effect of partial penetration on the drawdown in different aquifer systems. For instance, Yang et al. (2006) developed an analytical solution for the constant-flux pumping test in a confined aquifer with a partially penetrating well. Malama et al. (2008) derived a semi-analytical solution for flow toward a partially penetrating well pumped at a constant rate in a leaky unconfined aquifer. Feng and Zhan (2015) derived a semi-analytical solution for flow toward a partially penetrating well pumped at a constant rate in a leaky confined aquifer. Most of the previous studies about groundwater flow to a partially penetrating well are based on the flow being Darcian. Although Wen et al. (2013, 2014) derived approximate analytical solutions for Izbash non-Darcian flow to a partially penetrating well of an infinitesimally small radius or a large diameter in a confined aquifer, research related to non-Darcy flow to a partially penetrating well is still quite limited.

In addition to the non-Darcian effect, another issue which should be considered for the groundwater flow to a pumping well is the skin effect. The well skin is usually developed outside the wellbore because of the well construction (Novakowski 1989; Park and Zhan 2002; Chang and Chen 2002; Yeh and Yang 2006; Yeh and Chang 2013; Houben 2015b). In general, the well skin can be classified into two types, the infinitesimal skin and finite thickness skin. The thickness of the well skin cannot be neglected (Novakowski 1989; Yang and Yeh 2007; Pasandi et al. 2008; Yang et al. 2014). In this case, the skin zone should be treated as a different formation zone with individual hydrodynamic properties and thickness. The flow to a constant-flux pumping well in an aquifer, considering finite thickness skin, has been extensively investigated (Yeh et al. 2003; Perina and Lee 2006; Pasandi et al. 2008; Chiu et al. 2007). For instance, Yeh et al. (2003) developed a closed-form analytical solution for a fully penetrating constant-flux pumping well in a two-zone confined aquifer. Chiu et al. (2007) derived an analytical solution of the drawdown for flow toward a partially penetrating well in a confined aquifer system while treating the skin as a finite thickness zone. Wen and Wang (2013) developed an approximate analytical solution for radial non-Darcian flow to a fully penetrating well in a leaky aquifer with wellbore storage and skin effect, and also developed a finite difference solution to compare with the approximate analytical solution.

A careful check of the previous literature easily determines that most of the research focused on the non-Darcian flow to a fully penetrating well, while research on the non-Darcian flow to a partially penetrating well is quite limited. Meanwhile, note that most of the studies on groundwater flow towards a constant-rate pumping well in an aquifer while considering the finite-thickness skin, were based on the assumption of Darcian flow. Only a few researchers (Wen and Wang 2013) studied the non-Dracian flow to a well considering the effect of finite thickness skin. In reality, all of the non-Darcian flow effect, well partial penetration, and the skin effect are of vital importance and should be considered when analyzing the non-Darcian flow to a partially penetrate well pumped at a constant rate. The purpose of this study is to extend previous work (Wen et al. 2013) and obtain an available analytical solution, taking simultaneously the effects of non-Darcian flow, partial penetration, skin type and skin thickness into account in a confined aquifer system.

In this study, a new mathematical model is developed. The flow in the horizontal direction is assumed to be non-Darcian. The flow velocity in the vertical direction is relatively small and the vertical flow is assumed to be Darcian (Wen et al. 2013). The Laplace domain approximate solution is derived by using the linearization approximation proposed by Wen et al. (2008a), associated with the Laplace transforms and the finite Fourier cosine transform. The effects of the power index in the Izbash equation, well partial penetration, skin type and skin thickness on the drawdowns were analyzed in this study. Additionally, a sensitivity analysis was made to study the degree of sensitivity of the drawdown to the major parameters of the aquifer and well configuration.

Mathematical model and solution

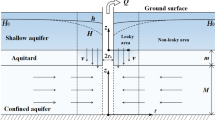
A schematic diagram summarizing the parameters of this study is shown in Fig. 1. The horizontal flow near the pumping well is assumed to non-Darcian. Both the horizontal flow and the vertical flow should be considered in partially penetrating wells and a finite-thickness skin is assumed to exist around the wellbore. The other assumptions are: (1) both the skin zone and the formation are homogeneous and isotropic, the formation zone is of infinite-extent and with a constant thickness, and the skin zone has uniform finite thickness around the wellbore; (2) the pumping well is partially penetrating the aquifer with a finite radius; (3) the pumping rate is constant; and (4) the whole system is hydrostatic before the pumping starts.

Fig. 1
figure 1

Schematic diagram of the partially penetrating well and aquifer configurations (r is the distance from the center of the pumping well, r w is the radius of the pumping well; r s is the radius of the skin zone. Q is the pumping rate, L is the thickness of the confined aquifer, and d and l denote the top and bottom vertical coordinates of the screen, respectively.)

Full size image

Based on the aforementioned assumptions, the governing equations for the skin and formation zones can be established as follows (Sen 1989; Wen et al. 2013):

$$ \frac{\partial {q}_{\mathrm{r}1}\left(r,z,t\right)}{\partial r}+\frac{q_{\mathrm{r}1}\left(r,z,t\right)}{r}+\frac{\partial {q}_{\mathrm{z}1}\left(r,z,t\right)}{\partial z}={S}_{\mathrm{s}1}\frac{\partial {s}_1\left(r,z,t\right)}{\partial t},\kern1em {r}_{\mathrm{w}}\le r\le {r}_{\mathrm{s}} $$
(1)
$$ \frac{\partial {q}_{\mathrm{r}2}\left(r,z,t\right)}{\partial r}+\frac{q_{\mathrm{r}2}\left(r,z,t\right)}{r}+\frac{\partial {q}_{\mathrm{z}2}\left(r,z,t\right)}{\partial z}={S}_{\mathrm{s}2}\frac{\partial {s}_2\left(r,z,t\right)}{\partial t},\kern1em {r}_{\mathrm{s}}\le r<\infty $$
(2)

in which the subscripts 1 and 2 denote the skin and formation zones, respectively; r is the distance from the center of the pumping well [m]; t is the pumping time [h]; z is the vertical coordinate [m]; S s is the specific storage of the aquifer [m−1], q r(r, z, t) and q z(r, z, t) are the specific discharge in the horizontal and vertical plane [m h−1], respectively; s(r, z, t) is the drawdown; r w is the radius of pumping well [m]; r s is the outer radius of the skin [m].

The initial conditions can be expressed as:

$$ {s}_1\left(r,z,0\right)={s}_2\left(r,z,0\right) $$
(3)

The outer boundary condition for the formation at an infinite distance is:

$$ {s}_2\left(\infty, z,t\right)=0 $$
(4)

The boundary conditions at the top and bottom of the aquifer in the vertical direction are:

$$ \frac{\partial {s}_1\left(r,0,t\right)}{\partial z}=\frac{\partial {s}_2\left(r,0,t\right)}{\partial z}=\frac{\partial {s}_1\left(r,L,t\right)}{\partial b}=\frac{\partial {s}_2\left(r,L,t\right)}{\partial z}=0 $$
(5)

The boundary condition for the horizontal specific discharge along the screen is assumed uniform and can be written as:

$$ {q}_{r1}\left({r}_{\mathrm{w}},z,t\right)=-\frac{Q}{2\pi {r}_{\mathrm{w}}\left(l-d\right)}\left[U\left(z-d\right)-U\left(z-l\right)\right],0\le z\le L $$
(6)

where Q is the pumping rate [m3 h−1], d and l denote the top and bottom vertical coordinates of the screen [m], respectively, L is the thickness of confined aquifer [m], U (·) is the unit step function, and U (z – d) equals one when z is larger than d, otherwise, U (z – d) is zero.

The drawdown and the flux at the interface between the formation zone and the skin zone are continuous, respectively. This requires that:

$$ {s}_1\left({r}_{\mathrm{s}},z,t\right)={s}_2\left({r}_{\mathrm{s}},z,t\right) $$
(7)

and

$$ {q}_{\mathrm{r}1}\left({r}_{\mathrm{s}},z,t\right)={q}_{\mathrm{r}2}\left({r}_{\mathrm{s}},z,t\right) $$
(8)

In order to make the problem mathematically tractable, the Izbash equation is employed to describe the horizontal flow in the skin and formation zones:

$$ {q}_{\mathrm{r}1}{\left|{q}_{\mathrm{r}1}\right|}^{n_1-1}=-{\left(-{q}_{\mathrm{r}1}\right)}^{n_1}={K}_{\mathrm{r}1}\frac{\partial {s}_1\left(r,z,t\right)}{\partial r} $$
(9)

and

$$ {q}_{\mathrm{r}2}{\left|{q}_{\mathrm{r}2}\right|}^{n_2-1}=-{\left(-{q}_{\mathrm{r}2}\right)}^{n_2}={K}_{\mathrm{r}2}\frac{\partial {s}_2\left(r,z,t\right)}{\partial r} $$
(10)

where, n 1, n 2, K r1 and K r2 are empirical parameters, which are treated as constants here. n is used to reflect the effect of non-Darcian flow, and the range of n is from 1 to 2 for non-Darcian flow with relatively high velocities, demonstrating both the viscous flow regime and the inertial flow regime (Bordier and Zimmer 2000; Moutsopoulos et al. 2009). Obviously, the Izbash equation agrees with Darcy’s law in the case of n 1 = n 2 = 1, and K r1 and K r2 become the hydraulic conductivity. Thus, K r1 and K r2 can be considered as the apparent radial hydraulic conductivity of the skin and formation zone, respectively. In this study, the variable γ is defined to reflect the ratio between the apparent radial hydraulic conductivity of the formation zone and the quasi radial hydraulic conductivity of the skin zone. If the apparent radial hydraulic conductivity of the skin zone is smaller than that of the formation zone, the well skin is defined as a positive skin under non-Darcian flow conditions, which is similar to the studies about the skin effect under Darcian flow conditions, and in this case, γ is larger than one. The reverse case is defined as a negative skin with γ smaller than one. In addition, it should be noted that the negative sign is shown in Eqs. (9) and (10) because the direction of the radial flow and the r-axis is opposite.

Darcy’s law is used to describe the vertical direction flow in the skin and formation zones, and can be written as:

$$ {q}_{\mathrm{z}1}={K}_{\mathrm{z}1}\frac{\partial {s}_1\left(r,z,t\right)}{\partial z} $$
(11)

and

$$ {q}_{\mathrm{z}2}={K}_{\mathrm{z}2}\frac{\partial {s}_1\left(r,z,t\right)}{\partial z} $$
(12)

where K z1 and K z2 are the vertical hydraulic conductivity of the skin and formation zone [m h−1], respectively.

Substituting Eq. (9) and (11) into Eq. (1), one can obtain:

$$ \frac{K_{\mathrm{r}1}}{n_1{\left(-{q}_{\mathrm{r}1}\right)}^{n_1-1}}\frac{\partial^2{s}_1\left(r,z,t\right)}{\partial {r}^2}+\frac{K_{\mathrm{r}1}}{r{\left(-{q}_{\mathrm{r}1}\right)}^{n_1-1}}\frac{\partial {s}_1\left(r,z,t\right)}{\partial r}+{K}_{\mathrm{z}1}\frac{\partial^2{s}_1\left(r,z,t\right)}{\partial {z}^2}={S}_{s1}\frac{\partial {s}_1\left(r,z,t\right)}{\partial t}\kern2em {r}_{\mathrm{w}}\le r\le {r}_{\mathrm{s}} $$
(13)

Notably, the term \( {\left(-{q}_{\mathrm{r}1}\right)}^{n_1-1} \) makes Eq. (13) non-linear. However, the linearization procedure proposed by Wen et al. (2008a) can be used to approximate the non-linear term efficiently, which has been proven to work extremely well at late times and it will underestimate the drawdowns at early times (Wen et al. 2009). With the similar linearization approximation, the nonlinear term can be approximated as follows:

$$ {\left(-{q}_{\mathrm{r}1}\right)}^{n_1-1}\approx {\left[\frac{Q}{2\pi rL}\right]}^{n_1-1} $$
(14)

This approximation means the flow rate at any cylindrical cross section is regarded as the pumping rate Q. Obviously, this assumption is valid unless the flow approaches steady state, indicating that the storage release is completed. At early times, the fact is that the flow rate at any cylindrical cross section is less than the pumping rate Q. In other words, such a linearization procedure ignores the storage release of the aquifer, consequently, it will underestimate the drawdowns at early times as found by Wen et al. (2009). Many studies (e.g. Wen et al. 2008a, b, 2013) have proven the error might be acceptable or negligible under some circumstances especially for the relative large pumping time. With this, Eq. (1) reduces to:

$$ \frac{\partial^2{s}_1\left(r,z,t\right)}{\partial {r}^2}+\frac{n_1}{r}\frac{\partial {s}_1\left(r,z,t\right)}{\partial r}+\frac{K_{\mathrm{z}1}{n}_1}{K_{\mathrm{r}1}}{\left(\frac{Q}{2\pi rL}\right)}^{n_1-1}\frac{\partial^2{s}_1\left(r,z,t\right)}{\partial {z}^2}=\frac{S_{\mathrm{s}1}{n}_1}{K_{\mathrm{r}1}}{\left(\frac{Q}{2\pi rL}\right)}^{n_1-1}\frac{\partial {s}_1\left(r,z,t\right)}{\partial t},\kern1em {r}_{\mathrm{w}}\le r\le {r}_{\mathrm{s}} $$
(15)

Similarly, Eq. (2) can be simplified as:

$$ \frac{\partial^2{s}_2\left(r,z,t\right)}{\partial {r}^2}+\frac{n_2}{r}\frac{\partial {s}_1\left(r,z,t\right)}{\partial r}+\frac{K_{\mathrm{z}2}{n}_2}{K_{\mathrm{r}2}}{\left(\frac{Q}{2\pi rL}\right)}^{n_2-1}\frac{\partial^2{s}_2\left(r,z,t\right)}{\partial {z}^2}=\frac{S_{\mathrm{s}2}{n}_2}{K_{\mathrm{r}2}}{\left(\frac{Q}{2\pi rL}\right)}^{n_2-1}\frac{\partial {s}_2\left(r,z,t\right)}{\partial t},\kern1em {r}_{\mathrm{s}}\le r<\infty $$
(16)

Applying Eqs. (9) and (14) to Eq. (6), and then utilizing the Laplace transform, the Fourier cosine transform and the linearization method to deal with it, the boundary condition Eq. (6) can be expressed as:

$$ \frac{\partial {\overline{s}}_1\left({r}_{\mathrm{w}},{\omega}_{\mathrm{N}},p\right)}{\partial r}=-\frac{1}{p{K}_{\mathrm{r}1}}{\left[\frac{Q}{2\pi {r}_{\mathrm{w}}\left(l-d\right)}\right]}^{n_1}F\left(d,l\right),\kern1em 0\le z\le L $$
(17)

in which p is the Laplace variable, F (d, l) = [sin(ω N l) – sin(ω N d)]/ω N, and ω N is the Fourier variable (ω N = Nπ/L, N = 1,2,3,…). Similarly, the continuity conditions required at the interface between the skin zone and the formation in Laplace domain can be written as:

$$ {\overline{s}}_1\left({r}_{\mathrm{s}},{\omega}_{\mathrm{N}},p\right)={\overline{s}}_2\left({r}_{\mathrm{s}},{\omega}_{\mathrm{N}},p\right) $$
(18)

and

$$ \frac{\partial {\overline{s}}_1\left({r}_{\mathrm{s}},{\omega}_{\mathrm{N}},p\right)}{\partial r}=\gamma {\left[\frac{Q}{2\pi {r}_{\mathrm{s}}\left(l-d\right)}\right]}^{n_1-{n}_2}\frac{\partial {\overline{s}}_2\left({r}_{\mathrm{s}},{\omega}_{\mathrm{N}},p\right)}{\partial r} $$
(19)

Applying the Laplace transform and the finite Fourier cosine transform to Eqs. (15) and (16) while considering the initial condition Eq. (3), the governing flow equation in the skin zone and formation zone can be rewritten as:

$$ \frac{\partial^2{\overline{s}}_1\left(r,{\omega}_{\mathrm{N}},p\right)}{\partial {r}^2}+\frac{n_1}{r}\frac{\partial {\overline{s}}_1\left(r,{\omega}_{\mathrm{N}},p\right)}{\partial r}={\delta}_1{r}^{1-{n}_1}{\overline{s}}_1\left(r,{\omega}_{\mathrm{N}},p\right),\kern1em {r}_{\mathrm{w}}\le r\le {r}_{\mathrm{s}}, $$
(20)

and

$$ \frac{\partial^2{\overline{s}}_2\left(r,{\omega}_{\mathrm{N}},p\right)}{\partial {r}^2}+\frac{n_2}{r}\frac{\partial {\overline{s}}_2\left(r,{\omega}_{\mathrm{N}},p\right)}{\partial r}={\delta}_2{r}^{1-{n}_2}{\overline{s}}_2\left(r,{\omega}_{\mathrm{N}},p\right),\kern1em {r}_{\mathrm{w}}\le r\le {r}_{\mathrm{s}}, $$
(21)

where \( \begin{array}{ccc}\hfill {\delta}_1=\left({K}_{\mathrm{z}1}{n}_1{\omega}_{\mathrm{N}}^2+{S}_{\mathrm{s}1}{n}_1p\right){\left[Q/2\pi \left(l-d\right)\right]}^{n_1-1}/{K}_{\mathrm{r}1}\hfill & \hfill \mathrm{and}\hfill & \hfill {\delta}_2=\left({K}_{\mathrm{z}2}{n}_2{\omega}_{\mathrm{N}}^2+{S}_{\mathrm{s}2}{n}_2p\right){\left(Q/2\pi \left(l-d\right)\right)}^{n_2-1}/{K}_{\mathrm{r}2}\hfill \end{array} \). After a series of mathematical derivations, one can obtain the solutions in the Laplace domain, which can be expressed as:

$$ {\overline{s}}_1\left(r,{\omega}_{\mathrm{N}},p\right)={r}^{\frac{1-{n}_1}{2}}\frac{1}{p{K}_{\mathrm{r}1}}{\left[\frac{Q}{2\pi {r}_{\mathrm{w}}\left(l-d\right)}\right]}^{n_1}F\left(d,l\right)\left[\frac{\phi_1}{\phi_0}{I}_{\frac{1-{n}_1}{3-{n}_1}}\left(\frac{2}{3-{n}_1}{r}^{\frac{3-{n}_1}{2}}\sqrt{\delta_1}\right)+\frac{\phi_2}{\phi_0}{K}_{\frac{1-{n}_1}{3-{n}_1}}\left(\frac{2}{3-{n}_1}{r}^{\frac{3-{n}_1}{2}}\sqrt{\delta_1}\right)\right] $$
(22)

and

$$ {\overline{s}}_2\left(r,{\omega}_{\mathrm{N}},p\right)={r}^{\frac{1-{n}_2}{2}}\frac{1}{p{K}_{\mathrm{r}1}}{\left[\frac{Q}{2\pi {r}_{\mathrm{w}}\left(l-d\right)}\right]}^{n_1}\frac{\phi }{\phi_0}\frac{K_{\frac{1-{n}_2}{3-{n}_2}}\left(\frac{2}{3-{n}_2}{r}^{\frac{3-{n}_2}{2}}\sqrt{\delta_2}\right)}{K_{\frac{1-{n}_2}{3-{n}_2}}\left(\frac{2}{3-{n}_2}{r_{\mathrm{s}}}^{\frac{3-{n}_2}{2}}\sqrt{\delta_2}\right)}F\left(d,l\right) $$
(23)

with

$$ {\phi}_1=\sqrt{\delta_1}{K}_{\frac{2}{3-{n}_1}}\left(\frac{2}{3-{n}_1}{r}_{\mathrm{s}}^{\frac{3-{n}_1}{2}}\sqrt{\delta_1}\right){K}_{\frac{1-{n}_2}{3-{n}_2}}\left(\frac{2}{3-{n}_2}{r}_{\mathrm{s}}^{\frac{3-{n}_2}{2}}\sqrt{\delta_2}\right)-\gamma {r}_{\mathrm{s}}^{\frac{n_1-{n}_2}{2}}\sqrt{\delta_2}\times {\left(\frac{Q}{2\pi \left(l-d\right)}\right)}^{n_1-{n}_2}{K}_{\frac{2}{3-{n}_2}}\left(\frac{2}{3-{n}_2}{r}_{\mathrm{s}}^{\frac{3-{n}_2}{2}}\sqrt{\delta_2}\right){K}_{\frac{1-{n}_1}{3-{n}_1}}\left(\frac{2}{3-{n}_1}{r}_{\mathrm{s}}^{\frac{3-{n}_1}{2}}\sqrt{\delta_1}\right) $$
(24)
$$ {\phi}_2=\sqrt{\delta_1}{I}_{\frac{-2}{3-{n}_1}}\left(\frac{2}{3-{n}_1}{r}_{\mathrm{s}}^{\frac{3-{n}_1}{2}}\sqrt{\delta_1}\right){K}_{\frac{1-{n}_2}{3-{n}_2}}\left(\frac{2}{3-{n}_2}{r}_{\mathrm{s}}^{\frac{3-{n}_2}{2}}\sqrt{\delta_2}\right)+\gamma {r}_{\mathrm{s}}^{\frac{n_1-{n}_2}{2}}\sqrt{\delta_2}\times {\left(\frac{Q}{2\pi \left(l-d\right)}\right)}^{n_1-{n}_2}{K}_{\frac{2}{3-{n}_2}}\left(\frac{2}{3-{n}_2}{r}_{\mathrm{s}}^{\frac{3-{n}_2}{2}}\sqrt{\delta_2}\right){I}_{\frac{1-{n}_1}{3-{n}_1}}\left(\frac{2}{3-{n}_1}{r}_{\mathrm{s}}^{\frac{3-{n}_1}{2}}\sqrt{\delta_1}\right) $$
(25)
$$ {\phi}_0={r}_{\mathrm{w}}^{1-{n}_1}\sqrt{\delta_1}\left[{\phi}_2{K}_{\frac{2}{3-{n}_1}}\left(\frac{2}{3-{n}_1}{r}_{\mathrm{w}}^{\frac{3-{n}_1}{2}}\sqrt{\delta_1}\right)-{\phi}_1{I}_{\frac{-2}{3-{n}_1}}\left(\frac{2}{3-{n}_1}{r}_{\mathrm{w}}^{\frac{3-{n}_1}{2}}\sqrt{\delta_1}\right)\right] $$
(26)
$$ \phi ={r_{\mathrm{s}}}^{\frac{n_2-{n}_1}{2}}\left[{\phi}_1{I}_{\frac{1-{n}_1}{3-{n}_1}}\left(\frac{2}{3-{n}_1}{r_{\mathrm{s}}}^{\frac{3-{n}_1}{2}}\sqrt{\delta_1}\right)+{\phi}_2{K}_{\frac{1-{n}_1}{3-{n}_1}}\left(\frac{2}{3-{n}_1}{r_{\mathrm{s}}}^{\frac{3-{n}_1}{2}}\sqrt{\delta_1}\right)\right] $$
(27)

Furthermore, applying the inverse finite Fourier transform to Eqs. (22) and (23), the drawdown in the Laplace domain solutions for skin and formation zones can be obtained as

$$ {\overline{s}}_1\left(r,z,p\right)={r}^{\frac{1-{n}_1}{2}}\frac{l-d}{p{K}_{\mathrm{r}1}L}{\left[\frac{Q}{2\pi {r}_{\mathrm{w}}\left(l-d\right)}\right]}^{n_1}\left[\frac{\phi_1^{\prime }}{\phi_0^{\prime }}{I}_{\frac{1-{n}_1}{3-{n}_1}}\left(\frac{2}{3-{n}_1}{r}^{\frac{3-{n}_1}{2}}\sqrt{\delta_1^{\prime }}\right)+\frac{\phi_2^{\prime }}{\phi_0^{\prime }}{K}_{\frac{1-{n}_1}{3-{n}_1}}\left(\frac{2}{3-{n}_1}{r}^{\frac{3-{n}_1}{2}}\sqrt{\delta_1^{\prime }}\right)\right]+{r}^{\frac{1-{n}_1}{2}}\frac{2}{p{K}_{\mathrm{r}1}L}\times {\left[\frac{Q}{2\pi {r}_{\mathrm{w}}\left(l-d\right)}\right]}^{n_1}{\displaystyle \sum_{\mathrm{N}=1}^{\infty}\left[\frac{\phi_1^{\prime }}{\phi_0^{\prime }}{I}_{\frac{1-{n}_1}{3-{n}_1}}\left(\frac{2}{3-{n}_1}{r}^{\frac{3-{n}_1}{2}}\sqrt{\delta_1}\right)+\frac{\phi_2^{\prime }}{\phi_0^{\prime }}{K}_{\frac{1-{n}_1}{3-{n}_1}}\left(\frac{2}{3-{n}_1}{r}^{\frac{3-{n}_1}{2}}\sqrt{\delta_1}\right)\right]F\left(d,l\right) \cos \left({\omega}_{\mathrm{N}}z\right)} $$
(28)

and

$$ {\overline{s}}_2\left(r,z,p\right)={r}^{\frac{1-{n}_2}{2}}\frac{l-d}{p{K}_{\mathrm{r}1}L}{\left[\frac{Q}{2\pi {r}_{\mathrm{w}}\left(l-d\right)}\right]}^{n_1}\frac{\phi^{\prime }}{\phi_0^{\prime }}\frac{K_{\frac{1-{n}_2}{3-{n}_2}}\left(\frac{2}{3-{n}_2}{r}^{\frac{3-{n}_2}{2}}\sqrt{\delta_2^{\prime }}\right)}{K_{\frac{1-{n}_2}{3-{n}_2}}\left(\frac{2}{3-{n}_2}{r_{\mathrm{s}}}^{\frac{3-{n}_2}{2}}\sqrt{\delta_2^{\prime }}\right)}+{r}^{\frac{1-{n}_2}{2}}\frac{2}{p{K}_{\mathrm{r}1}L}\times {\left[\frac{Q}{2\pi {r}_{\mathrm{w}}\left(l-d\right)}\right]}^{n_1}{\displaystyle \sum_{\mathrm{N}=1}^{\infty}\frac{\phi^{\prime }}{\phi_0^{\prime }}\frac{K_{\frac{1-{n}_2}{3-{n}_2}}\left(\frac{2}{3-{n}_2}{r}^{\frac{3-{n}_2}{2}}\sqrt{\delta_2}\right)}{K_{\frac{1-{n}_2}{3-{n}_2}}\left(\frac{2}{3-{n}_2}{r_{\mathrm{s}}}^{\frac{3-{n}_2}{2}}\sqrt{\delta_2}\right)}F\left(d,l\right) \cos \left({\omega}_{\mathrm{N}}z\right)} $$
(29)

in which F (d, l) = [sin(ω N l) – sin(ω N d)]/ω N, K v(·) and I v(·) is the second kind of modified Bessel function with order of v; the superscript ′ shown in variables δ ′1 , δ ′2 , ϕ′, ϕ ′0 , ϕ ′1 , ϕ ′2 represents the condition of ω N =0 for the related variables. The numerical Laplace inversion method of Stehfest (1970a, b) is employed in this study to obtain the solutions in the time domain, which has been successfully applied in similar studies such as Wen et al. (2008a, b, 2013) for non-Darcian flow in confined aquifers.

If the pumping well is fully penetrating (l 1 = L and d 1 = 0), Eqs. (28) and (29) become

$$ {\overline{s}}_1\left(r,z,p\right)={r}^{\frac{1-{n}_1}{2}}\frac{1}{p{K}_{\mathrm{r}1}}{\left[\frac{Q}{2\pi {r}_{\mathrm{w}}L}\right]}^{n_1}\left[\frac{{{\overline{\phi}}^{\prime}}_1}{{{\overline{\phi}}^{\prime}}_0}{I}_{\frac{1-{n}_1}{3-{n}_1}}\left(\frac{2}{3-{n}_1}{r}^{\frac{3-{n}_1}{2}}\sqrt{{{\overline{\delta}}^{\prime}}_1}\right)+\frac{{{\overline{\phi}}^{\prime}}_2}{{{\overline{\phi}}^{\prime}}_0}{K}_{\frac{1-{n}_1}{3-{n}_1}}\left(\frac{2}{3-{n}_1}{r}^{\frac{3-{n}_1}{2}}\sqrt{{{\overline{\delta}}^{\prime}}_1}\right)\right] $$
(30)

and

$$ {\overline{s}}_2\left(r,z,p\right)={r}^{\frac{1-{n}_2}{2}}\frac{1}{p{K}_{\mathrm{r}1}}{\left[\frac{Q}{2\pi {r}_{\mathrm{w}}L}\right]}^{n_1}\frac{{\overline{\phi}}^{\prime }}{{{\overline{\phi}}^{\prime}}_0}\frac{K_{\frac{1-{n}_2}{3-{n}_2}}\left(\frac{2}{3-{n}_2}{r}^{\frac{3-{n}_2}{2}}\sqrt{{{\overline{\delta}}^{\prime}}_2}\right)}{K_{\frac{1-{n}_2}{3-{n}_2}}\left(\frac{2}{3-{n}_2}{r_s}^{\frac{3-{n}_2}{2}}\sqrt{{{\overline{\delta}}^{\prime}}_2}\right)} $$
(31)

the superscript — shown in variables \( {{\overline{\delta}}^{\prime}}_1 \), \( {{\overline{\delta}}^{\prime}}_2 \), \( {\overline{\phi}}^{\prime } \), \( {{\overline{\phi}}^{\prime}}_0 \), \( {{\overline{\phi}}^{\prime}}_1 \), \( {{\overline{\phi}}^{\prime}}_2 \) represents the condition of l 1 = L and d 1 = 0 for the related variables. Equations. (30) and (31) are the same as the solution obtained by Wen and Wang (2013) for non-Darcian flow to a fully penetrating well in a confined aquifer considering the effect of the finite-thickness skin.

When n 1 and n 2 are equal to one, the flow becomes Darcian, then the solution Eqs. (28) and (29) can be reduced to:

$$ \begin{array}{c}\hfill {\overline{s}}_1\left(r,z,p\right)=\frac{Q}{4\pi {T}_2}\frac{1}{p}\frac{2{T}_2}{r_{\mathrm{w}}{T}_1}\left[\frac{\varphi_1^{\prime }}{\varphi_0^{\prime }}{I}_0\left(r\sqrt{\delta_3^{\prime }}\right)+\frac{\varphi_2^{\prime }}{\varphi_0^{\prime }}{K}_0\left(r\sqrt{\delta_3^{\prime }}\right)\right]+\frac{Q}{4\pi {T}_2}\frac{1}{p}\frac{4{T}_2}{\left(l-d\right){r}_{\mathrm{w}}{T}_1}\hfill \\ {}\hfill \times {\displaystyle \sum_{n=1}^{\infty}\left[\frac{\varphi_1}{\varphi_0}{I}_0\left(r\sqrt{\delta_3}\right)+\frac{\varphi_2}{\varphi_0}{K}_0\left(r\sqrt{\delta_3}\right)\right]F\left(d,l\right) \cos \left({\omega}_{\mathrm{N}}z\right)}\hfill \end{array} $$
(32)

and

$$ {\overline{s}}_2\left(r,z,p\right)=\frac{Q}{4\pi {T}_2}\left[\frac{1}{p}\frac{2\pi {T}_2}{r_{\mathrm{w}}{T}_1}\frac{\varphi^{\prime }}{\varphi_0^{\prime }}\frac{K_0\left(r\sqrt{\delta_4^{\prime }}\right)}{K_0\left({r}_{\mathrm{s}}\sqrt{\delta_4^{\prime }}\right)}\right]+\frac{Q}{4\pi {T}_2}\frac{1}{p}\frac{4{T}_2}{\left(l-d\right){r}_{\mathrm{w}}{T}_1}{\displaystyle \sum_{n=1}^{\infty}\frac{\varphi^{\prime }}{\varphi_0^{\prime }}\frac{K_0\left(r\sqrt{\delta_4}\right)}{K_0\left({r}_{\mathrm{s}}\sqrt{\delta_4}\right)}F\left({d}_1,{l}_1\right) \cos \left({\omega}_{\mathrm{N}}z\right)} $$
(33)

in which δ 3 = α 1 ω 2N  + β 1 p, δ 4 = α 2 ω 2N  + β 2 p, δ ′3  = β 1 p and δ ′4  = β 2 p ; the Greek letter φ replaces the Greek letter ϕ in variables ϕ, ϕ 0, ϕ 1, ϕ 2, ϕ′, ϕ ′0 , ϕ ′1 , ϕ ′2 under the condition of n 1 = n 2 = 1 for the related variables. Equations (32) and (33) are the same as the solutions obtained by Chiu et al. (2007) for Darcian flow to a partially penetrating well in a confined aquifer with a finite thickness skin.

Results and discussion

The default values are given as n 1 = n 2 = n, r w = 0.2 m, K z1 = K z2 = 0.01 m/h, K r2 = 0.1 (m/h)1/n, S s1 = S s2 = 0.001 m−1, Q = 100 m3/h and L = 20 m. These values are reasonable for aquifers which are composed of coarse sand (Bear 2007; Wen et al. 2013). In order to check whether non-Darcian flow occurs or not near the pumping well under such flow conditions, the Reynolds number was calculated approximately. According to Bear (2007), the Reynolds number can be expressed as:

$$ \mathrm{R}\mathrm{e}=\frac{Vd}{\nu } $$
(34)

in which V is the velocity [m h−1], d is the average size of the media [m] and v is the kinematic viscosity of water [m2 h−1]. The flow velocity at the face of the well screen can be approximated by V = Q/(2πr w w) = 78. 5 m/h. From Eq. (34), where the value of v is chosen to be 3.6 × 10−3 m2/h (Sen 1989) and the average size of the media is chosen to be 4.55 mm (Moutsopoulos et al. 2009), one can obtain a Reynolds number of 99.2 at the face of the well. Such a large Reynolds number indicates that non-Darcian flow is likely to occur in the vicinity of the pumping well (Bear 2007).

Effect of aquifer and well configuration parameters on drawdown

In this section, mainly the influence of the power index n, well partial penetration, the skin type and the skin thickness on the drawdown are discussed. Firstly, the impacts of the power index n value and the length of well screen w on the drawdown for the positive skin case are shown in Fig. 2. The other parameters used in Fig. 2 are r s = 0.6 m, t =100 h, z = 15 m, w = 10 m, 15 m and 20 m, and n = 1, 1.2 and 1.5, respectively. Note that the case of n =1 corresponds to the solution for the Darcian flow case, and the case of w = 20 m for a fully penetrating well with (non-)Darcian flow are included in this figure. As shown in Fig. 2, the drawdowns nearby the pumping well for the non-Darcian case are larger than those for the Darcian case; and the effect of n is gradually decreasing from the skin zone to formation zone and disappears at the region where the distances are relatively far away from the pumping well. It was also found that a larger n leads to a smaller drawdown at late times and results in a smaller influence zone of pumping. A large n might lead to a greater recharge from the area where drawdowns are far away from the pumping well at late times when the flow approaches a quasi steady state; thus, a smaller drawdown is seen at late times. Similar results were also found and explained in detail by Wen et al. (2013). In addition, from Fig. 2, one can see that the drawdowns for the fully penetrating well case are smaller than those of the partially penetrating well at the same distance at the region where they are close to the pumping well. This is because a longer well screen can transmit water more powerfully; thus, a smaller drawdown will be found at late times.

Fig. 2
figure 2

The effect of power index n and well partial penetration w on the drawdown for negative skin with γ = 0.5

Full size image

Figure 3 shows the effect of different skin cases on the drawdown with r s = 0.6 m, t =100 h, n = 1.2, l = 15 m, d = 5 m, z = 15 m, and γ = 0.2, 0.5, 1, 2 and 5, respectively. Note that the case of γ = 1 refers to the solution without the skin; the drawdown curves for the system with a positive skin are represented by γ = 2 and 5, while γ = 0.2 and 0.5 f refer to a system with a negative skin. As shown in Fig. 3, the drawdown in the skin zone for the positive skin case is remarkably larger than that for the no skin case, while the drawdown in the skin zone for a negative skin case is smaller than that for a no skin case. This is because the positive skin has smaller hydraulic conductivity than that of the original formation zone, and the recharge from the formation zone is slower; thus, a larger drawdown was found. In contrast, the hydraulic conductivity of a negative skin is larger than without skin, and a smaller drawdown will occur inside the well at late times, as reflected in Fig. 3. Furthermore, it can be seen clearly that the drawdowns in the formation zone are the same whatever the skin type, so the effect of skin type on the drawdown in the formation zone can almost be neglected; the sensitivity analysis in the following section illustrates this point.

Fig. 3
figure 3

The effect of different skin cases on the drawdown with γ = 0.2, 0.5, 1, 2 and 5 when t = 100 h

Full size image

The effect of the skin thickness on the drawdown for negative skin (γ = 0.5) is depicted in Fig. 4. The other parameters are given as n = 1.2, l = 15 m, d = 5 m, z = 15 m, and r s = 0.4 m and 0.8 m. The case for no skin has also been depicted in this figure as a reference. It is shown in Fig. 4a that the drawdown in the skin zone is smaller than that of the no skin case when t = 10 h, and a thicker skin results in a smaller drawdown in the skin zone for the negative skin case than that of no skin case. For the negative skin case, the hydraulic conductivity of the skin zone is larger than that of a formation zone. A larger thickness of the negative skin case means the water can pass through more quickly, so a smaller drawdown can be seen in Fig. 4a. A reverse result for the positive skin case can be found in Fig. 4b. In addition, the effect of skin thickness on drawdown in the formation zone can also be neglected.

Fig. 4
figure 4

The effect of skin thickness on the drawdown for different pumping time: a negative skin with γ = 0.5; b positive skin with γ = 2

Full size image

Sensitivity analysis

Sensitivity analysis is often used to evaluate the influence of aquifer parameters on aquifer drawdown. A method of the normalized sensitivity analysis proposed by Huang and Yeh (2007) is adopted in this study. For a given parameter, the normalized sensitivity of the parameter can be defined as:

$$ {X}_{i,j}^{\prime }={P}_j\frac{\partial {O}_i}{\partial {P}_j}, $$
(35)

in which X ′ i,j respects the normalized sensitivity of the j-th parameter (P j ) at the i-th time and O i respects the dependent variable of the drawdown. In order to approximate the partial derivative in Eq. (35), a finite difference formula adopted by Huang and Yeh (2007) is used as:

$$ {X}_{i,j}^{\prime }={P}_j\frac{\partial {O}_i}{\partial {P}_j}={P}_j\frac{O_i\left({P}_j+\Delta {P}_j\right)-{O}_i\left({P}_j\right)}{\Delta {P}_j}, $$
(36)

in which ΔP j is a small increment and ΔP j =10−2 ×  P j in this study.

Figures 5 and 6 show the drawdown in the formation zone (r = 6 m) sensitivity to parameters n, w, K z1, K r1, S s1, r s, K z2, K r2, S s2, and r w for the negative skin case (γ = 0.5) and the positive skin case (γ = 2), respectively. The other parameters used in Figs. 5 and 6 are n = 1.5, l = 15 m, d = 5 m, r s = 0.6 m. The features of these two figures are almost the same. It was found that the drawdown is not sensitive to K z1, K r1, S s1 and r w no matter what the skin type is, whereas in contrast, the drawdown is sensitive to n, w, K r2, and S s2 at early times; and it is very sensitive to the parameters n, w, and K r2 at late times, especially to the power index n. Moreover, the skin thickness r s has little impact on drawdown in the formation zone during the entire pumping period.

Fig. 5
figure 5

The drawdown in the formation zone sensitivity to parameters n, w, K z1, K r1, S s1, r s, K z2, K r2, S s2, and r w for the negative skin case

Full size image
Fig. 6
figure 6

The drawdown in the formation zone sensitivity to parameters n, w, K z1, K r1, S s1, r s, K z2, K r2, S s2, and r w for the positive skin case

Full size image

Conclusions

A new semi-analytical solution for non-Darcian flow toward a partially penetrating constant rate pumping well taking account of the finite-thickness skin effect has been developed via a lineation method in combination with the Laplace transform and the finite Fourier cosine transform. The solution is different from similar investigations by previous researchers in considering the jointed effects of non-Darcian flow, well partial penetration, skin type and skin thickness. Both the drawdowns within the skin zone and formation zone are analyzed under different conditions; furthermore, the sensitivity analysis is applied to help in assessing how the drawdowns respond to the change in aquifer and well configuration parameters. The main conclusions of this study are:

  1. 1.

    The depression cone induced by pumping had a larger spread for the Darcian flow than that for non-Darcian flow. The drawdowns within the skin zone for a fully penetrating well are smaller than those for the partially penetrating well.

  2. 2.

    The skin type and skin thickness have great impact on the drawdown in the skin zone, while they have little influence on drawdown in the formation zone.

  3. 3.

    The parameters r s and r w have little influence on drawdown compared to the other parameters no matter what the skin type is.

  4. 4.

    The drawdown within the formation zone is sensitive to n, w, K r2, and S s2 at early times and it is very sensitive to the parameters n, w, and K r2 at late times, both for the negative skin case and positive skin case.