Introduction

The slug test is a popular field method to evaluate in-situ aquifer parameters in low permeability aquifers. The test involves a sudden withdrawal from or injection into a test well, resulting in an instantaneous raising or lowering of the water level in the well. An instantaneous head change is thus imposed within a wellbore and the recovery (or falloff) of the water level in the well is measured, often by means of a pressure transducer. The aquifer parameters, e.g., transmissivity and storativity, can then be obtained from the analysis of test data. For engineering applications, the slug test is a simple, quick, and economical approach.

An aquifer is considered a radial two-zone or composite system if the formation properties near the wellbore are apparently changed due to drilling or development of the well. Drilling may create a wellbore skin between the wellbore and formation. The invasion of drilling mud into the aquifer may produce a positive wellbore skin that has lower hydraulic conductivity than that of the undisturbed formation. On the other hand, the extensive well development and/or substantial fracturing of the borehole wall may increase the hydraulic conductivity as a negative wellbore skin.

The objectives of this work are to give a numerical approach for evaluating the Moench and Hsieh (1985b) Laplace-domain solution and compare this with the numerical results obtained from the Yang and Gates (1997) finite-element model. The numerical approach includes the modified Crump approach (IMSL 1997) for performing the numerical inversion for the Moench and Hsieh (1985b) solution (hereinafter referred to as MHS), the series expansion for approximating the Bessel functions in MHS, and the Shanks method (Shanks 1955; Yeh et al. 2003; Yang and Yeh 2005) for accelerating the convergence when evaluating the series of the Bessel functions. It is also proven that MHS satisfies the mathematical model of the slug test in a well with a finite-thickness skin. In addition, two new formulae related the modified zero-order Bessel functions of the first and second kinds to their first and second derivatives, and these formulae may be of use in future studies.

Literature review

Faust and Mercer (1984) provided an infinite-aquifer solution on the response of slug tests in wells containing a finite-thickness skin. They assumed that the skin has a much lower permeability than the adjacent formation does. Under this condition, the skin effect can lead to very low estimates of hydraulic conductivity if using the type-curve fitting method of Cooper et al. (1967). Moench and Hsieh (1985a) commented on the evaluation of slug tests in a finite-thickness skin by Faust and Mercer (1984). They stated that when the specific storage of the skin is negligibly small, the finite-thickness skin solution becomes equivalent to the infinitesimally thin skin solution published by Ramey et al. (1975). Under a finite-thickness skin condition, the skin properties in the test interval control the early time response, whereas the formation properties relate to the late time response. This causes the well response to depart significantly from the conventional type curves. Moench and Hsieh (1985b) provided a Laplace-domain solution for the mathematical model representing a drill-stem test in a well surrounded by a finite-thickness skin. They found that the standard methods of test-data analysis are adequate for open-well slug tests and may differ markedly in the pressure response for pressurized slug tests. Further, Sageev (1986) investigated the effects of well storage and wellbore skin in a confined aquifer system. He obtained a similar result to that of Moench and Hsieh (1985b). Karasaki et al. (1988) developed the various models of slug-tests and related solutions for linear flow, radial flow with boundaries, two zones, and concentric composite aquifer systems with different flow geometricies between the inner and outer regions; they provided type curves for each solution and stated that slug tests suffer the problems of non-uniqueness in matching the test data to type curves. Karasaki (1990) used the time convolution method of Duhamel’s theorem to derive the analytical solution of Moench and Hsieh (1985b). The systematized procedure and analysis method were proposed for a drill-stem test.

Recently, Yang and Gates (1997) constructed a finite-element model for a slug test in a confined aquifer system containing a finite-thickness skin. Their analysis shows that the effect of a low-permeability skin on the estimates of hydraulic conductivity could be minimized by the use of late-time test data. Butler and Healey (1998) investigated the estimate of hydraulic conductivities obtained through pumping or slug tests; they simply noted that the hydraulic conductivity estimate from pumping-test data is, on average, larger than that from a series of slug-test data in the same formation. Zlotnik and McGuire (1998a,b) and Hemker (1999) developed the analytical solutions of the transient well inflow in a multi-layered aquifer system. McElwee (2002) examined and used four techniques, including an extended capability nonlinear model, sensitivity analysis, correction for acceleration and velocity effects, and multiple slug tests to improve the analyses of slug tests.

Mathematical model

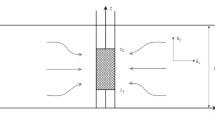
The governing equations describing the hydraulic head distributions within the skin and formation zones can respectively be written as (Moench and Hsieh 1985a,b)

$$\frac{{\partial ^{2} h_{1} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial h_{1} }}{{\partial r}} = \frac{{S_{1} }}{{T_{1} }}\frac{{\partial h_{1} }}{{\partial t}},\;r_{{\text{w}}} < r < r_{{\text{s}}} $$
(1)

and

$$\frac{{\partial ^{2} h_{2} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial h_{2} }}{{\partial r}} = \frac{{\partial h_{2} }}{{\partial t}},\;r > r_{{\text{s}}} $$
(2)

where the subscripts 1 and 2 respectively denote the skin and formation zones, T is the transmissivity, and S is the storativity. The symbol h is the hydraulic head within the skin or formation zone, r is the radial distance from center of well, r s is the distance from center of well to outer boundary of skin zone, t is the test time, and r w is the well radius.

The hydraulic heads are initially assumed to be zero within both the skin and formation zones, that is

$$h_{1} = h_{2} = 0,\;t = 0$$
(3)

The initial condition for a head in a well, h w, is

$$h_{{\text{w}}} = h_{0} ,\;t = 0$$
(4)

where h 0 is the initial head. The conservation of mass at a well requires that

$$r^{2}_{{\text{c}}} \frac{{dh_{{\text{w}}} }}{{dt}} = 2K_{1} br_{{\text{w}}} {\left( {\frac{{\partial h_{1} }}{{\partial r}}} \right)}_{{r = r_{{\text{w}}} }} ,\;r = r_{{\text{w}}}$$
(5)

and the outer boundary condition at infinitity is

$$h_{2} = 0,\,\,\,\,\,r \to \infty $$
(6)

where r c is the radius of the well casing in the region of changing water level, K is the hydraulic conductivity, and b is the aquifer thickness. The continuity conditions required at the interface between the skin and formation zones are

$$h_{1} = h_{2} ,\;r = r_{{\text{s}}}$$
(7)

and

$$K_{1} \frac{{\partial h_{1} }}{{\partial r}} = K_{2} \frac{{\partial h_{2} }}{{\partial r}},\;r = r_{{\text{s}}}$$
(8)

Applying the dimensionless transforms and the Laplace transforms to Eqs. (1) and (2) and using the initial condition, Eq. (3), gives the following subsidiary equations:

$$\frac{{d^{2} \overline{{h^{\prime }_{1} }} }}{{dr^{{\prime 2}} }} + \frac{1}{{r^{\prime } }}\frac{{d\overline{{h^{\prime }_{1} }} }}{{dr^{\prime } }} = {\left( {\beta q} \right)}^{2} \overline{{h^{\prime }_{1} }} ,\;1 < r^{\prime } < r^{\prime }_{{\text{s}}} $$
(9)

and

$$\frac{{d^{2} \overline{{h^{\prime }_{2} }} }}{{dr^{{\prime ^{2} }} }} + \frac{1}{{r^{\prime } }}\frac{{d\overline{{h^{\prime }_{2} }} }}{{dr^{\prime } }} = q^{2} \overline{{h^{\prime }_{2} }} ,\;r^{\prime } > r^{\prime }_{{\text{s}}}$$
(10)

where \(\overline{{h^{\prime } }}\) is the transform dimensionless hydraulic head, p is the Laplace transform variable of dimensionless time, \(q = p^{{1/2}} \), \(\beta = {\left( {\alpha \delta } \right)}^{{1/2}} \), α = K 1 /K 2, δ = S s1 /S s2, \(\gamma = {r^{2}_{{\text{c}}} } \mathord{\left/{\vphantom {{r^{2}_{{\text{c}}} } {{\left( {2r^{2}_{{\text{w}}} S_{{{\text{s2}}}} b} \right)}}}} \right.\kern-\nulldelimiterspace} {{\left( {2r^{2}_{{\text{w}}} S_{{{\text{s2}}}} b} \right)}}\), r′=r/r w, and \(r^{\prime }_{{\text{s}}} = {r_{{\text{S}}} } \mathord{\left/{\vphantom {{r_{{\text{S}}} } {r_{{\text{w}}} }}} \right.\kern-\nulldelimiterspace} {r_{{\text{w}}} }\). The transform boundary and continuity conditions of Eqs. (5–8) are respectively,

$$\alpha \gamma (p\overline{{h^{\prime }_{{\text{w}}} }} - 1) = {\left( {\frac{{d\overline{{h^{\prime }_{1} }} }}{{dr^{\prime } }}} \right)}_{{{\text{r}}^{\prime } = 1}}$$
(11)
$$\overline{{h^{\prime }_{2} }} = 0,\;r^{\prime } \to \infty$$
(12)
$$\overline{{h^{\prime }_{1} }} = \overline{{h^{\prime }_{2} }} ,\;r^{\prime } = r^{\prime }_{{\text{s}}}$$
(13)

and

$$\frac{{d\overline{{h^{\prime }_{1} }} }}{{dr^{\prime } }} = \alpha \frac{{d\overline{{h^{\prime }_{2} }} }}{{dr^{\prime } }},\;r^{\prime } = r^{\prime }_{{\text{s}}}$$
(14)

The Laplace-domain solutions for dimensionless hydraulic heads within both the skin and formation zones given by Moench and Hsieh (1985b) are respectively

$$\overline{{h^{\prime }_{1} }} = \frac{{\alpha \gamma {\left[ {\Delta _{1} K_{0} {\left( {q\beta r^{\prime } } \right)} - \Delta _{2} I_{0} {\left( {q\beta r^{\prime } } \right)}} \right]}}} {{c_{1} \Delta _{1} - c_{2} \Delta _{2} }}$$
(15)

and

$$\overline{{h^{\prime }_{2} }} = \frac{{\alpha \gamma {\left[ {\Delta _{1} K_{0} {\left( {q\beta r^{\prime }_{{\text{s}}} } \right)} - \Delta _{2} I_{0} {\left( {q\beta r^{\prime }_{{\text{s}}} } \right)}} \right]}K_{0} {\left( {qr^{{\prime }} } \right)}}} {{{\left[ {c_{1} \Delta _{1} - c_{2} \Delta _{2} } \right]}K_{0} {\left( {qr^{\prime }_{{\text{s}}} } \right)}}}$$
(16)

where the variables Δ1, Δ2, c 1, and c 2 are respectively defined as

$$\Delta _{1} = \alpha I_{0} {\left( {q\beta r^{\prime }_{{\text{s}}} } \right)}K_{1} {\left( {qr^{\prime }_{{\text{s}}} } \right)} + \beta I_{1} {\left( {q\beta r^{\prime }_{{\text{s}}} } \right)}K_{0} {\left( {qr^{\prime }_{{\text{s}}} } \right)}$$
(17)
$$\Delta _{2} = \alpha K_{0} {\left( {q\beta r^{\prime }_{{\text{s}}} } \right)}K_{1} {\left( {qr^{\prime }_{{\text{s}}} } \right)} - \beta K_{1} {\left( {q\beta r^{\prime }_{{\text{s}}} } \right)}K_{0} {\left( {qr^{\prime }_{{\text{s}}} } \right)}$$
(18)
$$c_{1} = \alpha \gamma pK_{0} {\left( {q\beta } \right)} + \beta qK_{1} {\left( {q\beta } \right)}$$
(19)

and

$$c_{2} = \alpha \gamma pI_{0} {\left( {q\beta } \right)} - \beta qI_{1} {\left( {q\beta } \right)}$$
(20)

When r′=1, the dimensionless head in a well obtained from Eq. (15) is

$$\overline{{h^{\prime }_{{\text{w}}} }} = \frac{{\alpha \gamma {\left[ {\Delta _{1} K_{0} {\left( {q\beta } \right)} - \Delta _{2} I_{0} {\left( {q\beta } \right)}} \right]}}}{{c_{1} \Delta _{1} - c_{2} \Delta _{2} }}$$
(21)

Moench and Hsieh Solution (1985b)

As shown in this section, the MHS satisfies the governing equations, boundary conditions, and continuity requirements at the interface of the skin and formation zones.

Taking the derivatives of Eq. (15) with respect to r and letting r′=1 yields

$$\frac{{d\overline{{h^{\prime }_{1} }} }}{{dr^{\prime } }}\left| {_{{r^{\prime } = 1}} = \frac{{ - q\beta \alpha \gamma {\left[ {\Delta _{1} K_{1} {\left( {q\beta } \right)} + \Delta _{2} I_{1} {\left( {q\beta } \right)}} \right]}}}{{c_{1} \Delta _{1} - c_{2} \Delta _{2} }}} \right.$$
(22)

Substituting Eq. (21) into the left-hand side (LHS) of Eq. (11) and using simple algebraic manipulation, one can obtain Eq. (22). Thus, the boundary condition at a wellbore, Eq. (11), is satisfied.

With K 0(∞)=0 as r′→∞, Eq. (16) yields \(\overline{{h^{\prime }_{2} }} = 0\). Therefore, the solution satisfies the outer boundary condition, Eq. (12).

Letting \(r^{\prime } = r^{\prime }_{{\text{s}}}\), Eqs. (15) and (16) become

$$ \overline{{h^{\prime }_{1} }} = \frac{{\alpha \gamma {\left[ {\Delta _{1} K_{0} {\left( {q\beta r^{\prime }_{{\text{s}}} } \right)} - \Delta _{2} I_{0} {\left( {q\beta r^{\prime }_{{\text{s}}} } \right)}} \right]}}} {{c_{1} \Delta _{1} - c_{2} \Delta _{2} }} = \overline{{h^{\prime }_{2} }} $$
(23)

This shows the continuity of dimensionless hydraulic head at the interface of the skin and formation zones.

Taking the derivatives of Eqs. (15) and (16), respectively, with respect to r′ and letting \(r^{\prime } = r^{\prime }_{{\text{s}}}\) gives

$$\frac{{d\overline{{h^{\prime }_{1} }} }} {{dr^{\prime } }}\left| {_{{r^{\prime } = r^{\prime }_{{\text{s}}} }} = \frac{{ - \alpha ^{2} \gamma K_{1} {\left( {qr^{\prime }_{{\text{s}}} } \right)}}} {{r^{\prime }_{{\text{s}}} {\left[ {c_{1} \Delta _{1} - c_{2} \Delta _{2} } \right]}}}} \right.$$
(24)

and

$$\frac{{d\overline{{h^{\prime }_{2} }} }}{{dr^{\prime } }}\left| {_{{r^{\prime } = r^{\prime }_{{\text{s}}} }} = \frac{{ - \alpha \gamma K_{1} {\left( {qr^{\prime }_{{\text{s}}} } \right)}}}{{r^{\prime }_{{\text{s}}} {\left[ {c_{1} \Delta _{1} - c_{2} \Delta _{2} } \right]}}}} \right.$$
(25)

Furthermore, Eq. (24) equals the product of Eq. (25) multiplied by α on both sides. Accordingly, this proves the continuity of flow rate between the skin and formation zones, i.e., Eq. (14).

Following steps similar to those demonstrated above by taking the first and second derivatives with respect to r′ for Eqs. (15) and (16) will prove that MHS satisfies the governing equations, Eqs. (9) and (10). McLachlan (1955, pp 192–197) provided the formulae

$$\frac{{dI_{0} {\left( {q\beta r^{\prime } } \right)}}}{{dr^{\prime } }} = {\left( {q\beta } \right)}I_{1} {\left( {q\beta r^{\prime } } \right)}$$
(26)
$$\frac{{dI_{1} {\left( {q\beta r^{\prime } } \right)}}}{{dr^{\prime } }} = \frac{1}{{q\beta r^{\prime } }}I_{1} {\left( {q\beta r^{\prime } } \right)} + I_{0} {\left( {q\beta r^{\prime } } \right)}$$
(27)

and

$$\frac{2}{{q\beta r^{\prime } }}I_{1} {\left( {q\beta r^{\prime } } \right)} = I_{0} {\left( {q\beta r^{\prime } } \right)} - I_{2} {\left( {q\beta r^{\prime } } \right)}$$
(28)

Based on Eqs. (26–28), one can obtain

$$\frac{{d^{2} }}{{dr^{{\prime 2}} }}{\left[ {I_{0} {\left( {q\beta r^{\prime } } \right)}} \right]} + \frac{1}{{r^{\prime } }}\frac{d}{{dr^{\prime } }}{\left[ {I_{0} {\left( {q\beta r^{\prime } } \right)}} \right]} = {\left( {q^{2} \beta ^{2} } \right)}I_{0} {\left( {q\beta r^{\prime } } \right)}$$
(29)

Likewise,

$$\frac{{d^{2} }}{{dr^{{\prime 2}} }}{\left[ {K_{0} {\left( {q\beta r^{\prime } } \right)}} \right]} + \frac{1}{{r^{\prime } }}\frac{d}{{dr^{\prime } }}{\left[ {K_{0} {\left( {q\beta r^{\prime } } \right)}} \right]} = {\left( {q^{2} \beta ^{2} } \right)}K_{0} {\left( {q\beta r^{\prime } } \right)}$$
(30)

After taking the first and second derivatives with respect to r′ for Eq. (15) and using Eqs. (29) and (30), one can get

$$\frac{{d^{2} \overline{{h^{\prime }_{1} }} }}{{dr^{{\prime ^{2} }} }} + \frac{1}{{r^{\prime } }}\frac{{d\overline{{h^{\prime }_{1} }} }}{{dr^{\prime } }} = {\left( {q\beta } \right)}^{2} \overline{{h^{\prime }_{1} }} $$
(31)

Similarly, one can obtain

$$\frac{{d^{2} \overline{{h^{\prime }_{2} }} }}{{dr^{{\prime 2}} }} + \frac{1}{{r^{\prime } }}\frac{{d\overline{{h^{\prime }_{2} }} }}{{dr^{\prime } }} = {\left( {q^{2} } \right)}\overline{{h^{\prime }_{2} }}$$
(32)

According to Eqs. (31) and (32), the solutions of Eqs. (15) and (16) respectively satisfy Eqs. (9) and (10).

Numerical evaluation

Bessel functions

Equations (15), (16), and (21) include the Bessel functions I 0(u), I 1(u), K 0(u), and K 1(u). These functions are approximated here by the formulae given in Watson (1958) and Abramowitz and Stegun (1964). The argument u in these formulae may be divided into two ranges; (0, 10) and (10, ∞) for I 0(u) and I 1(u), and (0, 2) and (2, ∞) for K 0(u) and K 1(u) in order to achieve better accuracy. In addition,, the formulae are essentially composed of infinite series and may converge slowly, especially when u is small. Therefore, the Shanks method (Shanks 1955; Yeh et al. 2003; Yang and Yeh 2005) is employed to accelerate the convergence when evaluating the series of the Bessel functions. Each function in Eqs. (15), (16), and (21) is calculated to ten decimal places, and thus they bear the same degree of accuracy as those listed in Abramowitz and Stegun (1964).

The Bessel functions of I 0(u), I 1(u), K 0(u), and K 1(u) may be evaluated by the formulae given in Abramowitz and Stegun (1964). For 0 ≤ u ≤ 10, the asymptotic expansions for I 0(u) and I 1(u) may be expressed respectively as (Abramowitz and Stegun 1964, p 375)

$$I_{0} {\left( u \right)} = 1 + \frac{{\frac{1}{4}u^{2} }}{{{\left( {1!} \right)}^{2} }} + \frac{{{\left( {\frac{1}{4}u^{2} } \right)}^{2} }}{{{\left( {2!} \right)}^{2} }} + \frac{{{\left( {\frac{1}{4}u^{2} } \right)}^{3} }}{{{\left( {3!} \right)}^{2} }} + \cdots $$
(33)

and

$$I_{1} {\left( u \right)} = {\left( {\frac{u}{2}} \right)}{\left[ {1 + \frac{{\frac{1}{4}u^{2} }}{{{\left( {1!} \right)}{\left( {2!} \right)}}} + \frac{{{\left( {\frac{1}{4}u^{2} } \right)}^{2} }}{{{\left( {2!} \right)}{\left( {3!} \right)}}} + \frac{{{\left( {\frac{1}{4}u^{2} } \right)}^{3} }}{{{\left( {3!} \right)}{\left( {4!} \right)}}} + \cdots } \right]}$$
(34)

The Bessel functions of I 0(u) and I 1(u) for 10< u< ∞ are respectively approximated as (Abramowitz and Stegun 1964, p 377)

$$I_{0} {\left( u \right)} = \frac{{e^{u} }}{{{\sqrt {2\pi u} }}}{\left\{ {1 + \frac{{1^{2} }}{{{\left( {1!} \right)}{\left( {8u} \right)}}} + \frac{{1^{2} \cdot 3^{2} }}{{{\left( {2!} \right)}{\left( {8u} \right)}^{2} }} + \frac{{1^{2} \cdot 3^{2} \cdot 5^{2} }}{{{\left( {3!} \right)}{\left( {8u} \right)}^{3} }} + \cdots } \right\}}$$
(35)

and

$$I_{1} {\left( u \right)} = \frac{{e^{u} }}{{{\sqrt {2\pi u} }}}{\left\{ {1 - \frac{{4 - 1^{2} }}{{{\left( {1!} \right)}{\left( {8u} \right)}}} + \frac{{{\left( {4 - 1^{2} } \right)} \cdot {\left( {4 - 3^{2} } \right)}}}{{{\left( {2!} \right)}{\left( {8u} \right)}^{2} }} - \frac{{{\left( {4 - 1^{2} } \right)} \cdot {\left( {4 - 3^{2} } \right)} \cdot {\left( {4 - 5^{2} } \right)}}}{{{\left( {3!} \right)}{\left( {8u} \right)}^{3} }} + \cdots } \right\}}$$
(36)

For 0 ≤ u ≤ 2, the asymptotic expansions for K 0(u) and K 1(u) may be written respectively as (Abramowitz and Stegun 1964, p 375)

$$K_{0} {\left( u \right)} = - {\left[ {\ln {\left( {\frac{u}{2}} \right)} + \psi } \right]}I_{0} {\left( u \right)} + \frac{{\frac{1}{4}u^{2} }}{{{\left( {1!} \right)}^{2} }} + {\left( {1 + \frac{1}{2}} \right)}\frac{{{\left( {\frac{1}{4}u^{2} } \right)}^{2} }}{{{\left( {2!} \right)}^{2} }} + {\left( {1 + \frac{1}{2} + \frac{1}{3}} \right)}\frac{{{\left( {\frac{1}{4}u^{2} } \right)}^{3} }}{{{\left( {3!} \right)}^{2} }} + \cdots $$
(37)

and

$$ \begin{aligned} & K_{1} {\left( u \right)} = {\left[ {{\text{ln}}{\left( {\frac{{\text{u}}} {{\text{2}}}} \right)} + \psi } \right]}I_{1} {\left( u \right)} + \frac{1} {u} \\ & - \frac{u} {4}{\left\{ \begin{aligned} & {\left[ {\frac{{\frac{1} {4}u^{2} }} {{{\left( {1!} \right)}{\left( {2!} \right)}}} + {\left( {1 + \frac{1} {2}} \right)}\frac{{{\left( {\frac{1} {4}u^{2} } \right)}^{2} }} {{{\left( {2!} \right)}{\left( {3!} \right)}}} + {\left( {1 + \frac{1} {2} + \frac{1} {3}} \right)}\frac{{{\left( {\frac{1} {4}u^{2} } \right)}^{3} }} {{{\left( {3!} \right)}{\left( {4!} \right)}}} + \cdots } \right]} \\ & + {\left[ {1 + {\left( {1 + \frac{1} {2}} \right)}\frac{{\frac{1} {4}u^{2} }} {{{\left( {1!} \right)}{\left( {2!} \right)}}} + {\left( {1 + \frac{1} {2} + \frac{1} {3}} \right)}\frac{{{\left( {\frac{1} {4}u^{2} } \right)}^{2} }} {{{\left( {2!} \right)}{\left( {3!} \right)}}} + \cdots } \right]} \\ \end{aligned} \right\}} \\ \end{aligned} $$
(38)

where \(\psi = \,0.577215664901533\) is the Euler’s constant. For 2< u< ∞, K 0(u) and K 1(u) are respectively taken as (Abramowitz and Stegun 1964, p 378)

$$K_{0} {\left( u \right)} = \frac{{e^{u} }}{{{\sqrt {2\pi u} }}}{\left\{ {1 - \frac{{1^{2} }}{{{\left( {1!} \right)}{\left( {8u} \right)}}} + \frac{{1^{2} \cdot 3^{2} }}{{{\left( {2!} \right)}{\left( {8u} \right)}^{2} }} - \frac{{1^{2} \cdot 3^{2} \cdot 5^{2} }}{{{\left( {3!} \right)}{\left( {8u} \right)}^{3} }} + \cdots } \right\}}$$
(39)

and

$$K_{1} {\left( u \right)} = \frac{{e^{u} }}{{{\sqrt {2\pi u} }}}{\left\{ {1 + \frac{{4 - 1^{2} }}{{{\left( {1!} \right)}{\left( {8u} \right)}}} + \frac{{{\left( {4 - 1^{2} } \right)} \cdot {\left( {4 - 3^{2} } \right)}}}{{{\left( {2!} \right)}{\left( {8u} \right)}^{2} }} + \frac{{{\left( {4 - 1^{2} } \right)} \cdot {\left( {4 - 3^{2} } \right)} \cdot {\left( {4 - 5^{2} } \right)}}}{{{\left( {3!} \right)}{\left( {8u} \right)}^{3} }} + \cdots } \right\}}$$
(40)

Shanks method

The Shanks method, which is also called the ε-algorithm (Kahaner 1972), is a non-linear sequence-to-sequence transformation. Shanks (1955) introduced a family of non-linear transforms designated as e k, \(e^{m}_{{\text{k}}}\), \(\widetilde{e}_{{\text{k}}}\), and e d. Theorems are provided to show the effectiveness of this transform both in accelerating the convergence of slowly convergent sequences and inducing convergence in divergent sequences. The Shanks transform is an iterative algorithm based on the directly summing series. The operator of the ith order transform of S n is defined as (Shanks 1955)

$$e_{m} {\left( {S_{n} } \right)} = {\left| {\begin{array}{*{20}c} {{S_{n} }} & {{S_{{n + 1}} }} & { \cdots } & {{S_{{n + m}} }} \\ {{\Delta S_{n} }} & {{\Delta S_{{n + 1}} }} & { \cdots } & {{\Delta S_{{n + m}} }} \\ { \vdots } & { \vdots } & { \vdots } & { \vdots } \\ {{\Delta S_{{n + m - 1}} }} & {{\Delta S_{{n + m}} }} & { \cdots } & {{\Delta S_{{n + 2m - 1}} }} \\ \end{array} } \right|}{\left| {\begin{array}{*{20}c} {1} & {1} & { \cdots } & {1} \\ {{\Delta S_{n} }} & {{\Delta S_{{n + 1}} }} & { \cdots } & {{\Delta S_{{n + m}} }} \\ { \vdots } & { \vdots } & { \vdots } & { \vdots } \\ {{\Delta S_{{n + m - 1}} }} & {{\Delta S_{{n + m}} }} & { \cdots } & {{\Delta S_{{n + 2m - 1}} }} \\ \end{array} } \right|}^{{ - 1}} $$
(41)

where \(\Delta S_{n} = S_{{n + 1}} - S_{n} \) with n = 1, 2,... ∞ as the number of series and m = 0, 1, 2,... n-2k as the number of iterations.

Wynn (1956) derived a mathematical expression from the Shanks transform. This transform for the first and second iterations can then be expressed for computation as follows

$$e_{0} {\left( {S_{n} } \right)} = S_{n} $$
(42)

and

$$e_{1} {\left( {S_{n} } \right)} = {\left[ {\Delta S_{n} } \right]}^{{ - 1}} $$
(43)

where n = 1, 2,.... The third and remaining iterations are expressed as

$$e_{{i + 1}} {\left( {S_{{n - i}} } \right)} = e_{{i - 1}} {\left( {S_{{n - i + 1}} } \right)} + {\left[ {e_{i} {\left( {\Delta S_{{n - i}} } \right)}} \right]}^{{ - 1}}$$
(44)

where i = 1, 2,... (n – 2).

The Shanks transform requires use of the even-order terms when approximating the sum of S n ; the odd-order terms are purely intermediate quantities in the numerical computations. Applying the Shanks transform to evaluate a given series requires setting a convergence criterion, ERR, defined as

$${\left| {\frac{{e_{{2{\text{r}} + 2}} {\left( {S_{{n - 1}} } \right)} - e_{{2{\text{r}}}} {\left( {S_{n} } \right)}}}{{e_{{2{\text{r}} + 2}} (S_{{n - 1}} )}}} \right|} \leqslant ERR,{\text{ for}}\;n = 3,4, \ldots $$
(45)

Shanks (1955) indicated that the series converges if three successive values of n satisfy the criterion. However, such a suggestion may be too strict. For comparing the implementation of the Shanks transform with the other methods to the same problem, the convergence criterion is to terminate the summing process. When applying the Shanks transform to a given series, it is defined as (Huang et al. 2000)

$${\left| {e_{{2i}} {\left( {S_{{n - 2i}} } \right)} - e_{{2(i - 1)}} {\left( {S_{{n - 2i + 1}} } \right)}} \right|} \leqslant ERR,{\text{ for}}\;n = 3,4, \ldots $$
(46)

where r = 1, 2,... (n–2)/2 when n is even and r = 1, 2,... (n–1)/2 when n is odd.

Numerical inversion

The Laplace transforms are commonly used to solve the differential and integral equations. In many engineering problems, the Laplace–domain solutions for mathematical models are tractable, yet the corresponding solutions in the time domain may be difficult or impossible to solve. Under such circumstances, the methods of numerical Laplace inversion such as the Stehfest method (Stehfest 1970), the Crump method (Crump 1976), or the Talbot method (Talbot 1979) may be used. de Hoog et al. (1982) mentioned that the different numerical methods of inversion give accurate answers for various cases.

The Laplace transform of a real-valued function f(t),t≥0, is defined as

$$F{\left( p \right)} = {\int_0^\infty {\exp {\left( { - pt} \right)}f{\left( t \right)}dt} }$$
(47)

and the inversion of F(p) is given by

$$f{\left( t \right)} = \frac{1}{{2\pi i}}{\int_{\kappa - i\infty }^{\kappa + i\infty } {\exp {\left( {pt} \right)}F{\left( p \right)}dp} }$$
(48)

where κ is to the right of any singularities of F(p).

Using the trapezoidal rule with step size \(\pi \mathord{\left/{\vphantom {\pi {T_{{\text{p}}} }}} \right.\kern-\nulldelimiterspace} {T_{{\text{p}}} }\), Crump (1976) proposed the Laplace inversion formula using an infinite series as follows

$$f{\left( t \right)} = {\left( {\frac{1}{{T_{{\text{p}}} }}\exp {\left( {\xi t} \right)}} \right)}{\left\{ {\frac{{F{\left( \xi \right)}}}{2} + {\sum\limits_{k = 1}^\infty {\operatorname{Re} } }{\left[ {F{\left( {\xi + \frac{{ik\pi }}{{T_{{\text{p}}} }}} \right)}\exp {\left( {\frac{{ik\pi t}}{{T_{{\text{p}}} }}} \right)}} \right]}} \right\}}$$
(49)

in which F(·) is constructed to be an infinite set of even and odd period functions, each with a period of 2T p, the parameter \(\xi\) is an estimate of the maximum of the real parts of singularity functions, and the symbol Re represents the real part of the function. In fact, the Crump method approximates the Laplace inversion by expressing the transform function in a Fourier series.

Crump (1976) used the ε-algorithm of Wynn (1956) (also called the Shanks method) to accelerate the convergence of the sum in Eq. (49) and gave the convergence of the sequence of partial sums as

$$S_{n} = S_{{n - 1}} + \operatorname{Re} {\left[ {F{\left( {\xi + \frac{{in\pi }}{{T_{{\text{p}}} }}} \right)}\exp {\left( {\frac{{in\pi t}}{{T_{{\text{p}}} }}} \right)}} \right]},n = 1,2, \ldots ,2M$$
(50)

The Crump’s accelerated estimate of f(t) is defined as

$$\widehat{f}{\left( t \right)} = {\left( {\frac{1}{{T_{{\text{p}}} }}\exp {\left( {\xi t} \right)}} \right)}e_{{2M}} {\left( {S_{0} } \right)}$$
(51)

where \(S_{0} = {F{\left( \xi \right)}} \mathord{\left/ {\vphantom {{F{\left( \xi \right)}} 2}} \right. \kern-\nulldelimiterspace} 2\) and the transform e j(S n ) is defined as Eq. (44).

de Hoog et al. (1982) applied the Pade approximations to improve the acceleration procedure to the transform sequence in Eq. (51). The Pade approximations represent a function as the quotient of two polynomials

$$f{\left( t \right)} \cong R_{N} {\left( t \right)} = \frac{{a_{0} + a_{1} t + a_{2} t^{2} + \cdots + a_{n} t^{n} }}{{1 + b_{1} t + b_{2} t^{2} + \cdots + b_{m} t^{m} }},N = n + m$$
(52)

where the parameters, a 0, a 1,... and b 1, b 2,... b m , are available for the approximation of f(t), by R N (t). The Pade approximations are related to Maclaurin expansions in that the coefficients are determined in a similar fashion to make \(\widehat{f}{\left( t \right)}\) and R N (t) agree at t = 0 and the first N derivatives agree at t = 0 (Gerald and Wheatley 1989). de Hoog et al. (1982) also applied the Shanks method to accelerate the running sums of infinite series.

The dimensionless hydraulic head and water level of a well are determined by inverting Eqs. (15), (16), and (21) with an appropriate numerical algorithm (e.g., Stehfest 1970; Crump 1976; or Talbot 1979). Herein, the modified Crump algorithm (Crump 1976; de Hoog et al. 1982) is adopted to invert the Laplace-domain solutions, Eqs. (15), (16), and (21), to an accuracy of five decimal places. This routine was developed based on an algorithm originally proposed by Crump (Crump 1976) and modified by de Hoog et al. (de Hoog et al. 1982). A double-precision format is used for all evaluations and the convergence criterion for the Shanks method is set as 10−7. Then, the numerical inversion results are compared with the values obtained from those given by Yang and Gates (1997). The effect of dimensionless hydraulic head distribution is also discussed for a composite aquifer system.

Numerical results and discussion

Based on a composite (two-zone) aquifer model, Yang and Gates (1997) used a finite-element method to simulate the dimensionless head distribution for a slug test. In their simulations, the hydraulic conductivity and storativity are respectively 1.8 × 10−6 cm/sec and 0.01 for a positive skin, 1.8 × 10−5 cm/sec and 0.01 for an undisturbed formation, and 1.8 × 10−4 cm/sec and 0.1 for a negative skin. Initially, MHS is evaluated using a numerical inversion routine INLAP (IMSL 1997). Table 1 gives the values of dimensionless heads in a tested well calculated using the parameters provided by Yang and Gates (1997) for r c=5.08 cm, r w=9.15 cm, and r s=30.5 cm when α (conductivity ratio)=0.1, 1, or 10. Note that the formation has a negative skin if α = 0.1 and a positive skin if α = 10; when the formation has only a single zone, α = 1. The differences of the tabular values for dimensionless heads between MHS and Yang and Gates simulation results are significant for all cases, especially for a large t and/or a small α. Figure 1 shows the curves of dimensionless head versus time obtained by MHS and those given by Yang and Gates (1997) when α = 0.1, 1, or 10. Obviously, the curves of Yang and Gates (1997) are significantly different from those of MHS. In fact, their mass balance equation—Yang and Gates (1997); Eq. (4)—and interface condition—Yang and Gates (1997), Eq. (5)—are questionable. The LHS term of Eq. (5) is set r = r w in this paper to represent the mass balance equation at the wellbore. However, Yang and Gates (1997) neglected the well radius of the test well; in other words, they treated the well as a line source. Consequently, the estimated hydraulic heads near the well may have significant errors. In addition, the partial derivative of dimensionless hydraulic head in Eq. (8) was taken with respect to dimensionless time t, instead of r, as used in Yang and Gates (1997). Physically, Eq. (8) should be used to preserve the continuity of the flow rate at the interface of the skin and formation zones.

Table 1 Dimensionless water level in a well, estimated by MHS and given in Yang and Gates (1997) for r c=5.08 cm, r w=9.15 cm, and r s=30.5 cm when α = 0.1, 1, or 10
Full size table
Fig. 1
figure 1

Curves of dimensionless head versus time obtained by MHS and those given by Yang and Gates (1997) when α = 0.1, 1 or 10

Full size image

The dimensionless well water levels estimated from MHS are compared with those given by Yang and Gates (1997) based on a finite-element modeling. The result indicates that the Yang and Gates tabular values have very poor accuracy. This problem is mainly attributed to the problem that the interface condition for the flow rate in their mathematical model is incorrect.

Figure 2 displays the curves of dimensionless hydraulic head versus dimensionless distance for r c=5.08 cm, r w=9.15 cm, r s=30.5 cm, and t = 103 sec when α = 0.1, 1 or 10. The storativity of the skin and formation zones is assumed as the same to simplify the problems and is set as 0.01. For the case without a skin zone, the dimensionless hydraulic head gradually decreases with increasing radial distance as shown in Fig. 2. If a finite-thickness skin is present, the relation of dimensionless hydraulic head versus dimensionless distance exhibits two curves with different slope joined at the interface \({\left( {r^{\prime }_{{\text{s}}} = 3.33} \right)}\). A negative skin, which has a higher transmissivity than the formation, has a curve with relative mild slope in the skin zone and with steeper slope in the formation zone. In contrast, a positive skin has a very steep slope in the skin zone due to the lower transmissivity and a relative flat slope in the formation zone. In addition, the difference of dimensionless hydraulic head between the skin and formation zones for an aquifer with a positive skin is larger obviously than that with a negative skin. This indicates that the dimensionless hydraulic head distribution depends on the hydraulic properties of both the skin and formation zones. If ignoring the skin zone, the dimensionless hydraulic head in a composite aquifer system may be apparently overestimated or underestimated and the error of the test-data analysis will be inducted.

Fig. 2
figure 2

Curves of dimensionless hydraulic head versus dimensionless distance obtained by MHS for r c=5.08 cm, r w=9.15 cm, r s=30.5 cm, and t = 103 sec when α = 0.1, 1 or 10

Full size image

Conclusions

A detailed derivation has been presented as proof that MHS for a slug test in a well surrounded by a finite-thickness skin satisfies the governing equations, boundary conditions, and continuity equations for hydraulic head and flow. Two new formulae relating the modified zero-order Bessel functions of the first and second kinds to their first and second derivatives are established. An efficient numerical approach is proposed to evaluate MHS. The numerical values of finite-element simulation given in Yang and Gates (1997) are apparently different from those evaluated based on the MHS. The problems in the mass balance equation and interface condition presented by Yang and Gates (1997) make their simulation results differ from the values of MHS. The plots for the spatial and temporal distributions of dimensionless hydraulic head demonstrate the dependence of the head on the hydraulic properties of both the skin and formation zones. In addition, the effect for an aquifer with a positive skin is significantly larger than that with a negative skin.

Notation

b :

Thickness of aquifer

h :

Hydraulic head in the skin or formation zone

h′:

Dimensionless hydraulic head in the skin or formation zone

h w :

Water level in a well

h′w :

Dimensionless water level in a well

I 0(·), K 0(·):

Modified Bessel function of the first and second kinds and order zero, respectively

I 1(·), K 1(·):

Modified Bessel function of the first and second kinds and order one, respectively

K :

Hydraulic conductivity

P :

Laplace transform variable of dimensionless time

q :

=p 1/2

r :

Radial distance from center of well

r c :

Standpipe radius

r s :

Distance from center of well to outer boundary of skin

r w :

Test well radius

r′:

=r/r w Dimensionless radial distance from center of well

r′s :

=r s/r w Dimensionless distance from center of well to outer boundary of skin

S s :

Specific storage

t :

Test time

t′:

=K 2 t/(r w)2 S s2

α :

=K 2/K 1

β :

=(δα)1/2

γ :

=r c 2/(2r w 2 S s2 b)

δ :

=S s1/S s2