Zur optimalen Auslegung von rotierenden zylindrischen Zweischicht-Behältern unter interner Erhitzung oder Innendruck

List of Symbols

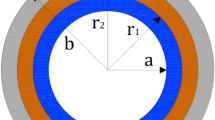
a Inner surface radius of the tube

b Interface radius between the layers

c Outer surface radius of the tube

\(A,B,C_{ki}\) Constants of integration

\(E_{i}\) Young’s modulus of material i

\(k_{i}\) Thermal conductivity of material i

\(\overline{p}\) Non-dimensional internal pressure

P Internal pressure

r Radius

\(s_{i},t\) Boundaries of integrals

T Difference of absolute and reference

temperature

\(T_{0}\) Inner surface temperature

u Displacement in radial direction

( \(\overline{\frac{{}}{{}}}\;)\) Non-dimensional quantity

Greek Symbols

\(\alpha _{i}\) Coefficient of thermal expansion of

material i

δ Thickness of a layer very thin as

compared to the wall-thickness

\(\varepsilon _{r},\varepsilon _{\theta},\varepsilon _{z}\left( =\varepsilon _{0}\right)\) Strain in radial, circumferential, and

axial direction, respectively

ν Poisson’s ratio

\(\rho _{i}\) Density of material i

\(\sigma _{M}\) Equivalent stress according to von

Mises

\(\sigma _{r},\sigma _{\theta},\sigma _{z}\) Stress in radial, circumferential, and

axial direction, respectively

\(\sigma _{y,i}\) Uniaxial yield limit of material i

ω Angular speed

Ω Non-dimensional angular speed

1 Introduction

Thick-walled long hollow cylinders are structural elements found frequently in various industrial fields like power engineering and chemical engineering, where pressure vessels, fluid conveying tubes or centrifuges, e.g., are widely used devices; another example are flywheels. Typically, these elements are loaded by rotation, by a radial temperature gradient or by internal pressure, and often also by a combination thereof. In some cases, it is advantageous not to use a homogeneous tube, but a layered one consisting of two or more materials; reasons for this might be, among others, different chemical and/or thermal requirements at the inner and outer surface, improved strength or the demand for a reduction of the weight of the device.

Hence, composite circular hollow cylinders under various loading conditions have been the subject of continuing research interest, for both elastic and inelastic behavior; an early numerical study on the latter was performed by Yalch and McConnelee [1]. Later on, thermal stresses in composite tubes were investigated for a variety of materials, boundary/end conditions and temperature fields by Takeuti et al. [2], Yang and Chen [3], Suhir and Sullivan [4], Ootao et al. [5], Tutuncu and Winckler [6], Tzeng and Chien [7], Vasilenko and Pankratova [8], Katsuo et al. [9], Kim et al. [10], Lee et al. [11], and Huang et al. [12]; some of these authors also took a pressure difference between inner and outer surface into account. The special case of heat generation in the structure itself was the subject of papers by Goshima and Miyao [13], Eraslan [14], and Eraslan et al. [15], and rotating composite/layered tubes were considered by Tutuncu [16] and Tzeng [17]. Furthermore, a particular investigation of advanced composite pressure vessels was performed by Underwood et al. [18]. Quite recently, layered tubular structures with special components like filament-wound cylinders [19] or carbon nano-tube reinforced cylinders [20] were studied, and there are applications even in the field of biomechanics [21].

For completeness, it shall be mentioned that similar investigations for functionally graded hollow cylinders are available, too: a recent paper on this topic is the one by Sharma and Yadav [22]. Moreover, the related problem of solid cylinders composed of different materials was a subject of investigations also; for example, Pardo et al. [23] considered a two-layered cylinder subject to a thermal shock, and Ozturk and Gulgec [24] studied a heat-generating compound cylinder.

Whereas there exist many investigations for the calculation of the stress fields in layered tubes for given material data and geometry, in particular for given ratios of the thicknesses of the layers, the problem of finding the optimum composition for given (maximum) load was rarely addressed, however (e.g. [12], for FGM-materials, and the related studies of shrink-fitted multi-layer cylinders without rotation by Jahed et al. [25] and Yuan et al. [26]). Indeed, not only various optimality criteria may be defined (e.g. maximum thermal and/or chemical resistance, minimum weight, minimum production costs, etc.), but also a large—and theoretically even infinite - variety of materials, layer thicknesses and number of layers may be combined, so that developing a quite general optimization algorithm seems not feasible.

Nevertheless, if two-layered tubes are presupposed and some restrictions on the materials to be used are imposed, it is possible to give a concise procedure for determining the optimum radii ratio for minimizing the weight of the device under a certain (maximum) load. This objective becomes increasingly important in engineering design, and it can be reached in an easy-to-implement way for a wide class of loading conditions. In particular, topic of the present study is a two-layered circular tube under generalized plane strain subject not only to rotation but also to either an elevated temperature at the inner surface (corresponding to the conveyance of a hot medium; Arslan et al. [27]) or to internal pressure. Since the centrifugal forces are proportional to material density and radius, it is presupposed that the inner cylindrical layer consists of the heavier material, while the outer layer is made of a material with lower density (compare also, e.g., the FGM-study by Arslan and Mack [28]). Specifically, the problem will be studied for a steel/aluminum composite hollow cylinder, but the procedure is applicable for any material combination with similar ratio of the material data, of course. Although in some applications partial plasticization of a structure is admissible (and was discussed for homogeneous rotating tubes, e.g., by Mack [29–30], and Eraslan and Mack [31]), plasticization should be avoided in general: as criterion for the maximum permissible stresses the yield criterion by von Mises is considered. (Since a thick-walled structure is treated, possible instability phenomena remain out of the scope of this study.) Thus, the present investigation not only provides a comprehensive overview of the elastic limits of composite tubes of the above type but also gives flow charts for the optimum design, which allow the practicing engineer a fast and straightforward choice of the radii ratio.

The paper is organized as follows: in Sect. 2, the mathematical statement of the problem is given, and the governing equations are derived. In Sect. 3, the stress distribution is studied, and particularly the elastic limits and the procedure for optimum design are discussed. Finally, some concluding remarks are made in Sect. 4.

2 Statement of the problem, temperature field, and governing equations

Abb. 1
figure 1

Sketch of the composite tube

Full size image

2.1 Statement of the problem

The mathematical formulation of the problem is as follows: subject of the investigation is a thick-walled tube composed of two perfectly bonded hollow cylinders of different (metallic) materials with (slowly varying) angular speed ω. The inner surface radius is a, the interface radius is b, and the outer surface radius is c (see Fig. 1); here and in the following, the inner cylinder is denoted by the index 1, the outer one by the index 2. If at the inner surface there acts a pressure P and the outer surface is stress-free, then

$$\begin{aligned}\sigma _{r,1}\left( a\right) &=&-P, \end{aligned}$$
(1)
$$\begin{aligned}\sigma _{r,2}\left( c\right) &=&0.\end{aligned}$$
(2)

At the interface radius the radial displacement u and the radial stress must be continuous,

$$\begin{aligned}u_{1}\left( b\right) &=&u_{2}\left( b\right), \end{aligned}$$
(3)
$$\begin{aligned}\sigma _{r,1}\left( b\right) &=&\sigma _{r,2}\left( b\right).\end{aligned}$$
(4)

Moreover, the tube is presupposed to be in a state of generalized plane strain, i.e. \(\varepsilon _{z}=\varepsilon _{0}\) with

$$ 2\pi \int_{a}^{b}\sigma _{z,1}\left( r\right) rdr+2\pi \int_{b}^{c}\sigma _{z,2}\left( r\right) rdr=0;$$
(5)

note that the axial strain \(\varepsilon _{0}\) depends on the temperature field, the pressure, and the angular speed, of course. Since cylindrical symmetry is presumed, the principal directions of stress and strain are the radial, circumferential, and axial directions. The stresses are subject to the equation of motion for the radial direction,

$$ \frac{d\sigma _{r}}{dr}+\frac{\sigma _{r}-\sigma _{\theta}}{r}=-\rho _{i}\omega^{2}r$$
(6)

with \(i=1,2\). As the treatment is restricted to small deformations, the geometric relations read

$$ \varepsilon _{r}=\frac{du}{dr},\varepsilon _{\theta}=\frac{u}{r}.$$
(7)

Furthermore, the generalized Hooke’s law,

$$\begin{aligned}\varepsilon _{r,i} &=&\frac{1}{E_{i}}\left[ \sigma _{r}-\nu \left( \sigma _{\theta}+\sigma _{z}\right) \right] +\alpha _{i}T, \end{aligned}$$
(8)
$$\begin{aligned}\varepsilon _{\theta,i} &=&\frac{1}{E_{i}}\left[ \sigma _{\theta}-\nu \left( \sigma _{z}+\sigma _{r}\right) \right] +\alpha _{i}T, \end{aligned}$$
(9)
$$\begin{aligned}\varepsilon _{z,i} &=&\varepsilon _{0}=\frac{1}{E_{i}}\left[ \sigma _{z}-\nu \left( \sigma _{r}+\sigma _{\theta}\right) \right] +\alpha _{i}T,\end{aligned}$$
(10)

with \(i=1,2\), holds for both of the components; T denotes the difference of absolute and reference temperature.

In the above equations, different values of density ρ, Young’s modulus E, and the coefficient of thermal expansion α for both materials are taken into account, whereas Poisson’s ratio ν does not differ too much for the most usual metals, and therefore a single value is assumed. Moreover, the influence of an elevated temperature on the material properties is disregarded, since their variation with temperature for the common operating conditions under consideration is small [32].

2.2 Temperature field

If conveyance of a hot medium is considered, the tube is presumed to have attained a steady state with the boundary and interface conditions

$$T_{1}(a)=T_{0},T_{2}(c)=0,$$
(11)
$$ T_{1}(b)=T_{2}(b),k_{1}\frac{\partial T_{1}(r)}{\partial r}\left\vert _{r=b}\right. =k_{2}\frac{\partial T_{2}(r)}{\partial r}\left\vert _{r=b}\right.$$
(12)

where the \(k_{i}\) denote the thermal conductivities. The general expression for a radially symmetric steady-state temperature field in the cylindrical coordinate system is [33]

$$ T(r)=A\ln (r)+B$$
(13)

with constants A and B, and applying Eqs.(11) and (12) one obtains

$$\begin{aligned}T_{1}(r) &=&T_{0}\frac{k_{2}\ln \left( r/b\right) +k_{1}\ln \left( b/c\right) }{k_{2}\ln \left( a/b\right) +k_{1}\ln \left( b/c\right) },a\leq r\leq b, \end{aligned}$$
(14)
$$\begin{aligned}T_{1}(r) &=&T_{0}\frac{k_{2}\ln \left( r/b\right) +k_{1}\ln \left(b/c\right) }{k_{2}\ln \left( a/b\right) +k_{1}\ln \left( b/c\right) },\text{\ \ }a\leq r\leq b, \label{T1} \\&& \notag \\T_{2}(r) &=&T_{0}\frac{k_{1}\ln \left( r/c\right) }{k_{2}\ln \left(a/b\right) +k_{1}\ln \left( b/c\right) },\text{ \ \ }b\leq r\leq c.\end{aligned}$$
(15)
$$\begin{aligned}T_{2}(r) &=&T_{0}\frac{k_{1}\ln \left( r/c\right) }{k_{2}\ln \left( a/b\right) +k_{1}\ln \left( b/c\right) },b\leq r\leq c.\end{aligned}$$
(16)

The integrals occurring in the subsequent Subsection can be given in closed form and read

$$\begin{aligned} &\int_{s}^{t}\xi T_{1}\left( \xi \right) d\xi =\frac{T_{0}}{4}\nonumber\\ &\frac{2k_{1}\left( t^{2}\!\!-\!\!s^{2}\right) \ln \left( b/c\right)\!\! +\!\!k_{2}\left[ s^{2}\left( 1\!\!-\!\!2\ln \left( s/b\right) \right) \!\!-\!\!t^{2}\!\left( 1\!\!-\!\!2\ln \left( t/b\right) \right)\! \right] }{k_{2}\ln \left( a/b\right) +k_{1}\ln \left( b/c\right) },\end{aligned}$$
(17)
$$\begin{aligned} &\int_{s}^{t}\xi T_{2}\left( \xi \right) d\xi =\nonumber\\ &\frac{T_{0}}{4}\frac{k_{1}\left[ s^{2}\left( 1-2\ln \left( s/c\right) \right) -t^{2}\left( 1-2\ln \left( t/c\right) \right) \right] }{k_{2}\ln \left( a/b\right) +k_{1}\ln \left( b/c\right) }\end{aligned}$$
(18)

2.3 Governing equations

From Eqs. (6)–(10) there follows a differential equation for the displacement in each of the components (that is, \(i=1,2\))

$$ r^{2}u_{i}^{\prime \prime}+ru_{i}^{\prime}-u_{i}=-\frac{1+\nu}{1-\nu}\left[ \frac{\left( 1-2\nu \right)}{E_{i}}\rho _{i}\omega^{2}r^{3}-\alpha _{i}r^{2}T_{i}^{\prime}\right]$$
(19)

where a prime denotes a derivative with respect to r. Its solution reads

$$\begin{aligned} &u_{i}\left( r\right) =\frac{C_{1i}}{r}+C_{2i}r-\frac{\left( 1+\nu \right) \left( 1-2\nu \right) \rho _{i}\omega^{2}}{8\left( 1-\nu \right) E_{i}}r^{3}\nonumber\\ &+\frac{\alpha _{i}\left( 1+\nu \right) }{r\left( 1-\nu \right)}\int_{s_{i}}^{r}\xi T_{i}\left( \xi \right) d\xi,\end{aligned}$$
(20)

and therefrom one obtains

$$\begin{aligned}&&\sigma _{r,i}\left( r\right) =\frac{E_{i}}{\left( 1+\nu \right) \left( 1-2\nu \right)}\left( \nu \varepsilon _{0}-\frac{C_{1i}\left( 1-2\nu \right) }{r^{2}}+C_{2i}\right) \notag \end{aligned}$$
(21)
$$\begin{aligned}&&-\frac{\rho _{i}\left( 3-2\nu \right) \omega^{2}}{8\left( 1-\nu \right)}r^{2} -\frac{E_{i}\alpha _{i}}{r^{2}\left( 1-\nu \right) }\int_{s_{i}}^{r}\xi T_{i}\left( \xi \right) d\xi,\end{aligned}$$
(22)
$$\begin{aligned} \sigma _{\theta,i}\left( r\right) &=&\frac{E_{i}}{\left( 1+\nu \right) \left( 1-2\nu \right)}\left( \nu \varepsilon _{0}+\frac{C_{1i}\left( 1-2\nu \right) }{r^{2}}+C_{2i}\right) \notag \end{aligned}$$
(23)
$$\begin{aligned} &&-\frac{\rho _{i}\left( 1+2\nu \right) \omega^{2}}{8\left( 1-\nu \right)}r^{2} -\frac{E_{i}\alpha _{i}}{r^{2}\left( 1-\nu \right) }\notag\end{aligned}$$
(24)
$$\begin{aligned} &&\left( r^{2}T_{i}\left( r\right) -\int_{s_{i}}^{r}\xi T_{i}\left( \xi \right) d\xi \right).\end{aligned}$$
(25)

For \(T_{i}=0\) the corresponding expressions in [29] are recovered, and the terms containing the temperature coincide with those in [34], e.g., thus validating the derivations.

In the above equations, \(C_{1i}\) and \(C_{2i}\) denote constants of integration, and the lower boundaries of the integrals are \(s_{1}=a\), \(s_{2}=b\). Finally, the axial stress follows from Eq. (10),

$$\sigma _{z,i}=E_{i}\varepsilon _{0}+\nu \left( \sigma _{r,i}+\sigma _{\theta,i}\right) -E_{i}\alpha _{i}T_{i}.$$
(26)

In the governing equations, the four constants of integration and the axial strain must be determined. For the calculation of these unknowns, the conditions (1)–(4) and the relation (5) are available. Since the equations are linear in the unknowns, the latter can be given in explicit form; for a tube loaded by rotation and internal pressure the expressions are given in the Appendix, in case of an internally heated rotating tube they are quite lengthy and omitted here.

The aim of the treatment is not the general solution, however, but the optimum design. This means an additional requirement, and, as a consequence, one of the parameters becomes an unknown variable. If a and c and the (maximum) values of the load parameters are kept fixed, this variable is the interface radius b. Thus, since the material of the inner layer is the one with higher density, the additional requirement is finding the minimum permissible value \(b_{\min}\) so that plasticization is avoided; the latter occurs if at some radius the equivalent stress according to von Mises reaches the yield limit [35], i.e., \(\sigma _{M}\left( r\right) =\sigma _{y,i}\) with

$$\sigma _{M}\left( r\right) =\sqrt{\frac{1}{2}\left[ \left( \sigma _{r}-\sigma _{\theta}\right)^{2}+\left( \sigma _{r}-\sigma _{z}\right)^{2}+\left( \sigma _{z}-\sigma _{\theta}\right)^{2}\right] }$$
(27)

where \(\sigma _{y,i}\) denotes the uniaxial yield limit of material i \(\left( i=1,2\right)\). While for moderate load the composite tube behaves elastically for any value of b and hence the inner layer can be chosen arbitrarily thin, one finds in a certain higher range of the load one or two solutions for b so that the yield condition is fulfilled at some radius. In the case of two solutions, the smaller value of b is \(b_{\min}\) sought for, of course. Above this load range, no solution exists for the chosen material combination; all these cases are discussed comprehensively in the next Section.

For a tube subject to rotation and an elevated temperature of the inner surface the equivalent stress reads

$$\begin{aligned}&&\sigma _{M,i}\left( r\right) =\frac{1}{8}\left( \frac{7r^{4}\left( 1-2\nu \right)^{2}\rho _{i}^{2}\omega^{4}}{\left( \nu -1\right)^{2}}+\frac{192E_{i}^{2}C_{1i}^{2}}{r^{4}\left( 1+\nu \right)^{2}}\right. \notag \end{aligned}$$
(28)
$$\begin{aligned}&&+\frac{ 64E_{i}^{2}\left( C_{2i}-\varepsilon _{0}\right)^{2}}{\left( 1+\nu \right)^{2}} +\frac{48E_{i}C_{1i}}{r^{4}\left( \nu^{2}-1\right) } \notag \end{aligned}$$
(29)
$$\begin{aligned}&&\left(\! r^{4}\left( 2\nu -1\right) \rho _{i}\omega^{2}\!-\!8E_{i}\alpha _{i}\int_{s_{i}}^{r}\xi T_{i}\left( \xi \right) d\xi\! +\!4E_{i}\alpha _{i}r^{2}T_{i}\left( r\right) \!\right) \notag \end{aligned}$$
(30)
$$\begin{aligned}&&-\frac{32E_{i}\left( C_{2i}-\varepsilon _{0}\right) \left( r^{2}\left( 2\nu -1\right) \rho _{i}\omega^{2}+2E_{i}\alpha _{i}T_{i}\left( r\right) \right) }{\nu^{2}-1} \notag \end{aligned}$$
(31)
$$\begin{aligned}&&+\frac{64E_{i}^{2}\alpha _{i}^{2}\left( 3\left( \int_{s_{i}}^{r}\xi T_{1}\left( \xi \right) d\xi \right)^{2}-3r^{2}T_{i}\left( r\right) \int_{s_{i}}^{r}\xi T_{i}\left( \xi \right) \right. }{r^{4}\left( \nu -1\right)^{2}}\notag\end{aligned}$$
(32)
$$\begin{aligned}&&\quad\frac{d\xi +r^{4}T_{i}^{2}\left( r\right)\Bigg)}{} \notag\end{aligned}$$
(33)
$$\begin{aligned}&&\left. +\frac{8E_{i}\alpha _{i}\left( 2\nu -1\right) \left(\! 5r^{2}T_{i}\left( r\right)\! -\!6\int_{s_{i}}^{r}\xi T_{i}\left( \xi \right)\! d\xi \right) \rho _{i}\omega^{2}}{\left( \nu -1\right)^{2}}\right)^{1/2}\end{aligned}$$
(34)

with \(i=1,2\) and \(s_{1}=a\), \(s_{2}=b\). Analogously, one obtains for loading by rotation and internal pressure

$$\begin{aligned}\sigma _{M,i}\left( r\right) =&&\frac{1}{8}\left( 64E_{i}^{2}\frac{3C_{1i}^{2}+\left( C_{2i}-\varepsilon _{0}\right)^{2}r^{4}}{r^{4}\left( 1+\nu \right)^{2}}\right. \notag \end{aligned}$$
(35)
$$\begin{aligned}&&+7\frac{\left( 2\nu -1\right)^{2}\rho _{i}^{2}\omega^{4}}{\left( \nu -1\right)^{2}}r^{4} +16E_{i}\notag\end{aligned}$$
(36)
$$\begin{aligned}&&\left.\frac{\left( 2\nu -1\right) \left( 3C_{1i}-2r^{2}\left( C_{2i}-\varepsilon _{0}\right) \right) }{\nu^{2}-1}\rho _{i}\omega^{2}\right)^{1/2}\end{aligned}$$
(37)

with \(i=1,2\), again.

3 Stress distribution, elastic limit loads, and optimum design

Prior to a discussion of the stress distribution and the optimization procedure it is convenient to introduce for the numerical calculations the following non-dimensional quantities:

$$\begin{aligned}\overline{p} &=&\dfrac{P}{\sigma _{y,1}},\overline{r}=\dfrac{r}{c},\overline{u}=\dfrac{uE_{1}}{c\sigma _{y,1}}, \end{aligned}$$
(38)
$$\begin{aligned}\overline{\alpha} &=&\dfrac{\alpha _{1}E_{1}T_{0}}{\sigma _{y,1}},\overline{\sigma}_{i}=\dfrac{\sigma _{i}}{\sigma _{y,1}},\Omega^{2}=\dfrac{\rho _{1}\omega^{2}c^{2}}{\sigma _{y,1}}.\end{aligned}$$
(39)

As was pointed out above, the inner component is presumed to consist of the material with higher density, and for the following discussions a layered tube of steel and aluminum is considered in particular; the parameter values for these materials are given in Table 1 [36].

Tab. 1 Material parameters of the layers
Full size table
Fig. 2
figure 2

Stresses and displacement for \(a/c=0.60\) and different combinations of \(b/c,\) \(T_{0}\) and Ω: elastic limit reached at a inner surface (case ); b interface (case ); c outer surface (case

Full size image

Case A: Rotation and elevated temperature of the inner surface

First, Fig. 2 provides three examples of the stress distribution and the displacement in a rotating tube with \(a/c=0.6\) and elevated inner surface temperature (in the following, the latter will be denominated shortly as ‘temperature’). As one can see, the dominating stress essentially is the circumferential stress in the steel layer. However, since the yield limits are different in steel and aluminum, for the onset of plasticization not merely the equivalent stress is decisive, but the ratio \(\sigma _{M,i}/\sigma _{y,i}\) which is also plotted in Fig. 2. Therefrom, one observes that for the chosen parameter values and load combinations - depending on the relative layer thicknesses - three different cases may occur: the equivalent stress may reach the yield limit either in the steel layer at the inner surface (case , like in homogeneous tubes, see [29], where Tresca’s yield criterion was applied however) or in the aluminum layer at the interface (case ), or plasticization even may start in the aluminum layer at the outer surface (case ). Extensive numerical calculations revealed that these three cases are the only ones which may occur in the subsequently considered range of \(a/c\) and temperature, and a comprehensive overview of the elastic limit loads for four different wall-thicknesses in the range \(0.25\leq a/c\leq 0.70\) and temperatures up to \(90^{\circ}C\) is given in Fig. 3. Prior to a discussion of these limit loads, three remarks are appropriate: Firstly, since—for the operating conditions under consideration—the effects of using a composite tube are especially pronounced for thick- to medium-walled tubes, the upper limit of \(a/c\) is chosen as 0.70. Secondly, as a composite hollow cylinder is presumed and the governing system of equations has been derived for such a cylinder, the cases of a homogeneous tube of pure aluminum or pure steel are excluded, and the dashed lines at \(a/c\) and 1 are to be understood as limits for very thin layers of steel and aluminum, respectively. Thirdly, at the intersections of the surfaces the elastic limits are reached with prescribed temperature and increasing angular speed at two radii simultaneously, of course, and although these singular cases will not be discussed specifically, they also can be treated by the procedure given below. Bearing these remarks in mind, one can draw several conclusions from the inspection of Fig. 3 (note the different \(\Omega -\) scales!).

Abb. 3
figure 3

Elastic limits for rotating composite tubes with elevated temperature of the inner surface (in \(^{\circ}C\)); a \(a/c=0.25\); b \(a/c=0.40\); c \(a/c=0.60\); d \(a/c=0.70\)

Full size image
Abb. 4
figure 4

Stresses in the inner part of a thick-walled composite tube with \(a/c=0.25\) and \(b/c=0.266\) at \(T_{0}=80^{\circ}C\) and a \(\Omega =0\) (stand-still); b \(\Omega =0.5\); c \(\Omega =0.970\)

Full size image
Abb. 5
figure 5

Stresses in a composite tube with \(a/c=0.70\) and \(b/c=0.708\) at \(T_{0}=90^{\circ}C\) and a \(\Omega =0\) (stand-still); b \(\Omega =0.5\); c \(\Omega =0.612\) (note the different abscissa scales)

Full size image

To begin with, it reveals that above a critical temperature \(T_{0}^{\ast}\) of about \(60^{\circ}C-70^{\circ}C\) a steel layer with a certain thickness is necessary even without rotation. A most remarkable fact is that for temperatures \(T_{0}>T_{0}^{\ast}\) and \(\Omega =0\) yielding would start at the interface in the aluminum (line I corresponds to case ), but that in very thick-walled tubes rotation at moderate angular speeds diminishes the von Mises equivalent stress at the interface whereas at a certain higher angular speed it reaches the yield limit at the interface again. This behavior can be seen clearly from Fig. 4 (the stresses in the outer part of the aluminum layer remain far below the yield limit). However, while in such tubes the yield limit is reached with increasing angular speed at the same radius again, the behavior is different for tubes with smaller wall-thickness: Fig. 5 demonstrates that in such tubes after an intermediate decrease of the equivalent stress the yield limit then is reached at the outer surface (case ).

Moreover, one recognizes from Fig. 3 that in thick-walled tubes only cases and occur, that is, the yield limit is reached either at the inner surface or at the interface, whereas for smaller wall-thickness an onset of plasticization at the outer surface (case ) can occur, too.

Here, a remark on the (almost straight) line I in Fig. 3 is appropriate. Since a purely elastically designed tube must not pass the yield limit at stand-still, of course, the necessary minimum interface radius is given by this line, even if at low angular speed then the equivalent stress remains below the yield limit. Hence, line I defines a vertical (limit) surface , the upper boundary of which is given by the intersection with surface or . It should be emphasized that a parameter combination corresponding to an arbitrary point of surface does not mean beginning of yield contrarily to points on surfaces , , and . Left of surface , i.e. for \(T_{0}\leq T_{0}^{\ast}\), for not too high angular speeds the interface radius is limited only by the fact that at least an arbitrarily thin steel layer is presupposed (vertical plane ).

Generally, it can be observed from Fig. 3 that—roughly speaking—the dependence of the elastic limit on the interface radius in tubes with moderate wall-thickness is less pronounced than in very thick-walled tubes, and on the whole in case of temperature and rotation somewhat less pronounced than in case of internal pressure and rotation (see the next Subsection).

Abb. 6
figure 6

Schematic of finding the optimum composition of the tube

Full size image
Tab. 2 Flow chart for finding the optimum interface radius \(b_{opt}\) for rotating composite tubes with elevated temperature of the inner surface
Full size table

To obtain now the optimum interface radius, one can proceed as sketched schematically in Fig. 6. That is, for given wall-thickness and given (maximum) temperature and (maximum) angular speed, one has to find the intersection point of load line h with the elastic limit surfaces or the vertical surfaces defined above; as a matter of course, it is presumed that the angular speed increases from stand-still. In case that there exist two intersection points, the first one has to be taken, since the smaller value of b is associated with the smaller percentage of steel. The corresponding flow chart is given in Table 2, and it allows a straightforward calculation of the optimum interface radius \(b_{opt}\). Nevertheless, a remark must be made on this flow chart: Since a layered tube is presupposed, the cases of homogeneous tubes of either pure steel or pure aluminum are - as already mentioned above—not included, and hence the admissible interval for b is \(a+\delta \leq b\leq c-\delta\) where δ denotes the (chosen) thickness of a layer very thin as compared to the wall-thickness.

Tab. 3 Examples of the optimum composition of rotating tubes with elevated inner surface temperature or internal pressure
Full size table

Eventually, the upper part of Table 3 provides several examples for the optimum interface radii of tubes subject to rotation and internal heating, determined by applying the above flow chart; as a matter of course, the values of \(\overline{b}_{opt}\) thus found coincide with the ones that can be seen from Fig. 3. Case B: rotation and internal pressure

This case is less intricate than the previous one. Fig. 7 shows two examples of the stress distribution and the displacement in a rotating tube with \(a/c=0.6\) subject to internal pressure. As one observes, here the dominating stresses are the circumferential and the radial stresses near the inner surface. From the ratio \(\sigma _{M,i}/\sigma _{y,i}\) one can see that for the wall-thickness and load combinations under consideration two cases may occur for different compositions of the tube: the equivalent stress may reach the yield limit either at the inner steel surface (case ) or in the aluminum layer at the interface (case ). Again, comprehensive numerical calculations showed that in the parameter range under consideration this are the only cases which may occur, and Fig. 8 provides an overview of the elastic limit loads for different wall-thicknesses. Of course, the remark in the previous Subsection on the dashed lines at \(a/c\) and 1 applies here, too.

figure 7

Stresses and displacement for \(a/c=0.60\) and different combinations of \(b/c,\) \(\overline{p}\) and Ω: elastic limit reached at a inner surface (case ); b interface (case )

Abb. 8
figure 8

Elastic limits for rotating composite tubes subject to internal pressure; a \(a/c=0.25\); b \(a/c=0.40\); c \(a/c=0.60\); d \(a/c=0.70\)

Full size image

As one can see, above a certain value of the internal pressure a steel layer of considerable thickness is necessary even at stand-still, and rotation further increases the necessary percentage of steel. On the other hand, in a certain range of small values of (maximum) pressure and (maximum) angular speed this layer may be arbitrarily small (plane like in case A).

Table 4 provides the flow chart for finding the optimum interface radius \(b_{opt}\) in the load case under consideration (the remark on the interval for b in the previous Subsection should be kept in mind here, too). Finally, in the lower part of Table 3 several examples for the optimum interface radii of tubes subject to rotation and internal pressure calculated by application of this flow chart can be found.

4 Concluding remarks

In the above, a rotating two-layered composite hollow cylinder subject to an elevated inner surface temperature or to internal pressure has been investigated, and special attention has been given to the optimum composition with respect to minimum weight at a certain maximum load; as criterion for the maximum permissible stresses the yield criterion of von Mises has been applied. In particular, the elastic limits and the procedure for finding the optimum composition for steel/aluminum tubes have been discussed in detail, and the most relevant features for this case can be summarized as follows:

(i) Depending on the composition and the combinations of the loads the equivalent stresses may reach the yield limit either at the inner surface or at the interface radius in the outer layer or at the outer surface (or simultaneously at two of these radii), thus showing a comparatively complex behavior.

(ii) In case of rotation and internal pressure the dependence of the maximum permissible load on the relative thicknesses of the layers is generally more pronounced than in case of rotation and elevated inner surface temperature. Moreover, in both cases it is found that particularly for higher angular speeds there may exist two different compositions of the tube for which it reaches the yield limit at the same load.

(iii) Although in an internally heated tube which is at stand–still just at the yield limit an intermediate decrease of the equivalent stress with increasing angular speed can be observed, the minimum permissible interface radius is nevertheless the one determined at stand-still, of course.

(iv) For all loads and wall-thicknesses in the considered parameter range flow charts can be given which allow a straightforward calculation of the optimum composition of the tube, based on analytical expressions. Furthermore, the values of the respective optimum interface radii for several cases are provided explicitly.

skip

Although the numerical results correspond to a steel/aluminum composite tube, it must be emphasized again that the equations derived in Sect. 2 are universally valid, and the procedure for finding the optimum composition given in Sect. 3 will be applicable to any material combination with similar ratios of the material data.

Moreover, it shall be pointed out that the above results could be obtained by purely analytical means, and hence they may serve as a countercheck for numerical studies on the same topic, too. Furthermore, the optimum interface radius determined with the procedures given in this paper also may provide a sound basis for refined studies by FE-methods if in engineering applications e.g. end effects or somewhat more complex geometrical properties shall be taken into account.

Tab. 4 Flow chart for finding the optimum interface radius \(b_{opt}\) for rotating composite tubes with internal pressure
Full size table

Finally, one might ask for possible generalizations of the present study. On the one hand, tubes with three or more layers might be considered, of course, but then straightforward analytical optimization procedures like in the present paper—at least if all the material properties are different from layer to layer and a well-proven yield criterion as the one of von Mises is applied—do not seem readily achievable; in this case rather an iterative optimization by numerical methods is to be recommended (compare [25]). On the other hand, an analytical optimization including additional details like temperature dependence of material properties or thermal resistance between the layers [34] seems feasible, in principle. However, apart from extremely intricate equations, very pronounced effects thereof are in the temperature range under consideration not likely.

Appendix

Constants of integration and axial strain for case B: rotation and internal pressure:

$$\begin{aligned} C_{11}& =\frac{a^{2}b^{2}\left( 1+\nu \right) }{b^{2}M_{1}+M_{2}}\left[ \frac{M_{1}P}{E_{1}}\right.\notag\end{aligned}$$
(40)
$$\begin{aligned} &+\frac{\left( b^{2}-c^{2}\right) \left\{ c^{2}\left( 2\nu -3\right) +b^{2}\left( 2\nu -1\right) \right\} }{4}\rho _{2}\omega^{2} \notag \end{aligned}$$
(41)
$$\begin{aligned} & \left.+\frac{\rho _{1}\omega^{2}}{8\left( \nu -1\right)}\left\{ \frac{E_{2}}{E_{1}}\left( 1-2\nu \right) L_{1}-\left( 2\nu -3\right) L_{2}\right\} \right], \end{aligned}$$
(42)
$$\begin{aligned}C_{21} =&\frac{1}{\left( b^{2}M_{1}+M_{2}\right) M_{3}}\left[ \frac{a^{2}P}{E_{1}}\left\{ -E_{1}^{2}\left( \nu -1\right) \right. \right. \notag \\ &L_{2}+E_{2}^{2}\left( b^{2}-c^{2}\right)^{2}\left( 1-2\nu \right) \left( 1+\nu \right) +\notag\\ & \left. E_{1}E_{2}\left( b^{2}-c^{2}\right) \left[ a^{2}\left( 1-\nu \right) +\left( 1-2\nu \right.\right.\right) \notag\\ &\left.\left.\left( c^{2}\left( 1+\nu \right) -2\nu b^{2}\right) \right] \right\} +\frac{\rho _{1}\omega^{2}}{8E_{1}\left( \nu -1\right) } \notag \\ & \left\{ E_{1}^{2}\left( a^{4}-b^{4}\right) \left( 5\nu -3\right) L_{2}+E_{2}^{2}\left( b^{2}-c^{2}\right)^{2} \right. \notag\\ &\left[ b^{4}\left( 1-3\nu +4\nu^{3}\right) +a^{4}\right. \notag\\ & \left. \left( 3-5\nu -4\nu^{2}+4\nu^{3}\right) \right] +E_{1}E_{2}\left( a^{2}-b^{2}\right) \notag \\ &\left( c^{2}-b^{2}\right) \left[ a^{4}\left( 5\nu -3\right) -b^{2}\left( 2\nu -1\right) \right.\end{aligned}$$
$$\begin{aligned} & \left. \left\{ 2b^{2}\left( 3\nu +\nu^{2}-2\right) -c^{2}\left( \nu -2\nu^{2}+3\right) \right\} \right. \notag\end{aligned}$$
(43)
$$\begin{aligned} &+a^{2}\left\{ c^{2}\left( 5\nu +4\nu^{2}-4\nu^{3}-3\right) +b^{2}\right. \notag \end{aligned}$$
(44)
$$\begin{aligned} & \left. \left. \left. \left( 11\nu -14\nu^{2}+4\nu^{3}-3\right) \right\} \right] \right\} +\frac{\left( b^{2}-c^{2}\right) }{4}\rho _{2}\omega^{2}\notag\end{aligned}$$
(45)
$$\begin{aligned} &\left\{ E_{1}\left( b^{2}-a^{2}\right) \left[ b^{2}c^{2}\left( 3-5\nu \right) \right. \right. \notag \end{aligned}$$
(46)
$$\begin{aligned} & \left. +2c^{4}\nu^{2}+b^{4}\left( 1-3\nu +2\nu^{2}\right) \right] +E_{2}\left( c^{2}-b^{2}\right) \notag\end{aligned}$$
(47)
$$\begin{aligned} &\left[ 2a^{2}c^{2}\nu^{2}+b^{4}\left( 1-3\nu +2\nu^{2}\right) +\right. \notag \end{aligned}$$
(48)
$$\begin{aligned} & \left. \left. b^{2}\left. \left( 2a^{2}\nu^{2}+c^{2}\left( 3-5\nu -2\nu^{3}\right) \right) \right] \right\} \right], \end{aligned}$$
(49)
$$\begin{aligned} C_{12}& =\frac{b^{2}c^{2}\left( 1+\nu \right) }{b^{2}M_{1}+M_{2}}\left[ 2\left( 1-\nu \right) a^{2}P\right. \notag\end{aligned}$$
(50)
$$\begin{aligned} &+\frac{a^{4}\left( 2\nu -3\right) +b^{4}\left( 1-2\nu \right) +2a^{2}b^{2}}{4}\rho _{1}\omega^{2} \notag \end{aligned}$$
(51)
$$\begin{aligned} & \left. -\frac{E_{1}}{E_{2}}\frac{\left( 2\nu -3\right) L_{4}}{8\left( \nu -1\right)}\rho _{2}\omega^{2}+\frac{\left( 2\nu -3\right) L_{3}}{8\left( \nu -1\right)}\rho _{2}\omega^{2}\right] \end{aligned}$$
(52)
$$\begin{aligned} C_{22}& =\frac{1}{\left( b^{2}M_{1}+M_{2}\right) M_{3}}\left[ 2a^{2}P\left\{ E_{2}\left( b^{2}-c^{2}\right) \right. \right. \notag\end{aligned}$$
(53)
$$\begin{aligned} &\left( a^{2}\nu^{2}-b^{2}\left( 2\nu -1\right) \right) +E_{1}\left( a^{2}-b^{2}\right) \left( c^{2}\nu^{2}-b^{2}\right. \notag \end{aligned}$$
(54)
$$\begin{aligned} & \left. \left. \left( 2\nu -1\right) \right) \right\} +\frac{\rho _{1}\omega^{2}\left( a^{2}-b^{2}\right) }{4}\left\{ E_{2}\left( c^{2}-b^{2}\right) \left[ a^{2}b^{2}\right] \right. \notag\end{aligned}$$
(55)
$$\begin{aligned} &\left( 3-5\nu \right) +2a^{4}\nu^{2}+b^{4}\left( 1-3\nu +2\nu^{2}\right) \notag \end{aligned}$$
(56)
$$\begin{aligned} & \left. -E_{1}\left( a^{2}-b^{2}\right) \left[ 2b^{2}c^{2}\nu^{2}+b^{4}\left( 1-3\nu +2\nu^{2}\right) \right.\right.\notag\end{aligned}$$
(57)
$$\begin{aligned} &\left.\left.+a^{2}\left( 2c^{2}\nu^{2}-b^{2}\left( 5\nu +2\nu^{2}-3\right) \right) \right] \right\} + \notag \end{aligned}$$
(58)
$$\begin{aligned} & \frac{\rho _{2}\omega^{2}}{8\left( 1-\nu \right)}\left\{ E_{2}L_{3}\left( b^{4}-c^{4}\right) \left( 5\nu -3\right) +\frac{E_{1}^{2}}{E_{2}}\right.\notag\end{aligned}$$
(59)
$$\begin{aligned} &\left( a^{2}-b^{2}\right)^{2}\left( 1+\nu \right) \left( 2\nu -1\right) \left[ c^{4}\left( 2\nu -3\right) \right. \notag \end{aligned}$$
(60)
$$\begin{aligned} & \left. b^{4}\left( 2\nu -1\right) \right] -E_{1}\left( a^{2}-b^{2}\right) \left( b^{2}-c^{2}\right) \left[ c^{4}\left( 3-5\nu \right) \right. \notag\end{aligned}$$
(61)
$$\begin{aligned} &+b^{2}c^{2}\left( 3-11\nu +14\nu -4\nu^{3}\right) \notag \end{aligned}$$
(62)
$$\begin{aligned} & +2b^{4}\left( 2-7\nu +5\nu^{2}+2\nu^{3}\right) +a^{2}\left( b^{2}+c^{2}\right)\notag\end{aligned}$$
(63)
$$\begin{aligned} & \left. \left. \left.\left( 3-5\nu -4\nu^{2}+4\nu^{3}\right) \right] \right\} \right], \end{aligned}$$
(64)
$$\varepsilon _{0}=\frac{\nu}{2M_{3}}\left[ 4a^{2}P+\omega^{2}\left( \left( b^{4}-a^{4}\right) \rho _{1}+\left( c^{4}-b^{4}\right) \rho _{2}\right) \right], $$
(65)

where

$$ M_{1}=b^{2}\left( E_{1}-E_{2}\right) \left( 1-2\nu \right) +c^{2}\left( E_{2}\left( 1-2\nu \right) +E_{1}\right), $$
(66)
$$ M_{2}=a^{2}\left[ c^{2}\left( E_{2}-E_{1}\right) +b^{2}\left( E_{2}\left( 1-2\nu \right) +E_{1}\right) \right], $$
(67)
$$ M_{3}=a^{2}E_{1}-b^{2}\left( E_{2}-E_{1}\right) -c^{2}E_{2}, $$
(68)
$$L_{1}=\left( b^{2}-c^{2}\right) \left( a^{2}\left( 2\nu -3\right) +b^{2}\right), $$
(69)
$$ L_{2}=\left( a^{2}-b^{2}\right) \left( b^{2}\left( 1-2\nu \right) +c^{2}\right),$$
(70)
$$ L_{3}=\left( b^{2}-c^{2}\right) \left( b^{2}\left( 1-2\nu \right) +a^{2}\right), $$
(71)
$$ L_{4}=\left( b^{2}-a^{2}\right) \left( c^{2}\left( 2\nu -3\right) +b^{2}\right). $$
(72)