Metaheuristic Optimization of Rotating Multilayer Composite Tubes Under Internal Heating and Pressure

Abstract

Although analysis/design of multilayer assemblies has been always an active field of research, works on the optimal design of rotating multilayer composite tubes are very limited. This paper addresses the design optimization of rotating multilayer composite tubes under internal heating and pressure. For determining the structural responses, analytical solutions are provided based on different boundary conditions. The automated selection of optimal material as well as thickness optimization of pressurized multilayer assemblies is carried out under different angular speed and internal heating conditions using a metaheuristic algorithm. The corresponding optimum design for each angular speed as well as internal heating condition is sought, and the numerical results are discussed. The study provides general guidelines for conceptual design of rotating multilayer composite tubes subjected to internal heating and pressure.

1 Introduction

Optimization has long been recognized as an efficient process for improving the desirable properties of structural and mechanical engineering systems. Among the numerous optimization objectives, reducing the total design cost/weight is one of the common primary goals in practical engineering applications. For optimization of multilayer composite tubes, in general, the main goal is to achieve a minimum weight or cost-efficient assembly, which satisfies the pre-specified design constraints (Sharifi et al. 2014; Apatay and Mack 2015). For this purpose, the optimum arrangement of material layers as well as the optimal thickness of each layer should be sought using a suitable design optimization algorithm. Indeed, structural response computations of multilayer composite tubes should also be accomplished as a part of the design process.

Many recent studies have focused on the analysis and design of multilayer composite assemblies under various loading, interface, and boundary conditions. Ootao et al. (1991), Lee et al. (2001), and Eraslan et al. (2003) investigated the thermal stresses in composite tubes under different thermal loading conditions. The studies performed by Tutuncu (1995) and Tzeng (2002) were based on the investigation of the stress response of rotating composite tubes. Akış and Eraslan (2005) investigated the yielding behavior of pressurized two-layer tightly fitted concentric tubes based on von Mises yield criterion. They in particular addressed the yielding of pressurized two-layer shrink-fitted composite tubes in Eraslan and Akis (2005). Moreover, Jahed et al. (2006) tackled the design optimization problem of multilayer cylinders for maximum fatigue life expectancy under the combined effects of autofrettage and shrink fit. Considering Tresca criterion, Sharifi et al. (2012) developed an analytical method for optimal design of shrink-fitted multilayer compound cylinders. The authors deduced that in the case of larger ratios of outer to inner radii, increasing the number of layers becomes more advantageous. Later, Sharifi et al. (2014) proposed an analytical method for optimum design of multilayer cylinders with respect to different objective functions including weight and cost. Miraje and Patil (2012) studied the thickness optimization of three-layer shrink-fitted compound cylinders. Zhou et al. (2012) addressed the stress analysis as well as optimal design of a three-layer composite tube subjected to thermomechanical loads. In a closely related study, Apatay and Mack (2015) studied the optimization of rotating two-layered hollow cylinder subjected to internal heating or internal pressure. Recently, the effect of shrink-fitting on the optimum design of multilayer composite tubes has been studied in Kazemzadeh Azad and Akış (2019). The design optimization results obtained for multilayer composite tubes indicated that more economical solutions could be found if shrink-fitting parameters are considered as additional design variables. Although numerous studies have been conducted on the analysis/design of multilayer assemblies, limited work has been conducted so far on the design optimization of rotating multilayer composite tubes (Apatay and Mack 2015). Accordingly, the present paper is devoted to the design optimization of rotating multilayer composite tubes under internal heating and pressure.

Typically, the first step in an optimization process is to select a suitable algorithm considering the nature of solution variables, objective function, and problem constraints. It is generally known that conventional structural optimization methods, i.e., mathematical programming (Erbatur and Al-Hussainy 1992) and optimality criteria (Tabak and Wright 1981; Saka 1991) have been originally proposed for handling continuous optimization problems and basically depend on gradient information of objective functions. Accordingly, it is generally conceived that the aforementioned classical techniques are not suitable for handling discrete or non-differentiable problems. In the past few decades, many researchers employed non-traditional stochastic search algorithms, i.e., metaheuristics as alternative tools to the conventional optimization methodologies. Generally, metaheuristic approaches, such as genetic algorithms (Goldberg and Samtani 1986), particle swarm optimization (Kennedy and Eberhart 1995), ant colony optimization (Colorni et al. 1991), harmony search algorithm (Lee and Geem 2004), big bang-big crunch algorithm (Erol and Eksin 2006), etc., follow non-deterministic search strategies to locate the optimum or a reasonably near-optimum solution. The advantageous attributes of metaheuristic or evolutionary algorithms can be outlined as: global search features, derivative-free characteristics, ease of implementation, and capability of dealing with both discrete, continuous, or mixed-integer optimization problems. Considering the discrete nature of the design variables associated with the optimal design of rotating multilayer composite tubes, metaheuristic search techniques could be efficiently employed for handling such combinatorial optimization problems.

This paper investigates the weight and cost minimization of rotating multilayer composite tubes under internal heating and pressure based on von Mises yield criterion. In order to calculate the structural responses, analytical solutions are presented based on two different tube end conditions, namely generalized plane strain case (free ends), which assumes a uniform extension in the axial direction, and plane strain case (fixed ends) in which axial displacement is prevented. The optimum material selection and thickness optimization of one-, two-, and three-layer assemblies are carried out under different angular speed and internal heating conditions using a metaheuristic optimization algorithm. The optimum designs associated with different values of angular speed as well as internal heating are sought, and the obtained results are discussed. The numerical experiments, performed under different loading and tube end conditions, provide some general guidelines for preliminary or conceptual design of rotating multilayer composite tubes.

The present work is organized as follows: In the second section, the analytical solutions of rotating multilayer composite tubes under internal heating and pressure are described. The formulation of the optimization problem is stated in the third section. The fourth section briefly outlines the utilized metaheuristic algorithm. The numerical instances as well as the obtained results are given in the fifth section. Finally, the concluding remarks are summarized in the last section.

2 Analysis of Rotating Multilayer Assemblies

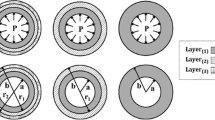
In this section, the analytical solutions developed to estimate the response of rotating one-, two-, and three-layer thick-walled tubes subjected to elevated temperature and pressure at the inner surface are presented. Here, cylindrical polar coordinates (r, θ, z) are employed and small deformations are presumed in the derivations. In addition, the multilayer assemblies are assumed to be tightly fitted and perfectly bonded. In derivations, the generalized plane strain solution is obtained first and reduced to plane strain state by equating the axial strain to zero.

2.1 Temperature Distribution

The assemblies are subjected to an elevated temperature of the inner surface and assumed to be in steady state. The temperature distribution for a long single-layer tube is governed by the following equation (Noda et al. 2003):

$$\frac{{{\text{d}}^{2} T}}{{{\text{d}}r^{2} }} + \frac{1}{r}\frac{{{\text{d}}T}}{{{\text{d}}r}} = 0$$

(1)

where r is the radial coordinate and T is the temperature distribution (i.e., difference of absolute and reference temperature). The general solution is

$$T(r) = A\ln r + B$$

(2)

where A and B are the integration constants calculated based on the following boundary conditions:

$$T(a) = T_{0} \;{\text{and}}\;T(b) = 0$$

(3)

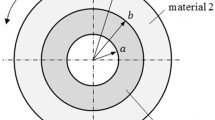
Here, a and b are the inner and outer surface radii of the tube (see Fig. 1), respectively, and $T_{0}$ is the constant inner surface temperature. The temperature of the outer surface is assumed to be zero. Application of the boundary conditions gives

Fig. 1

Typical cross section of rotating multilayer composite tube

$$A = \frac{{T_{0} }}{{\ln \left( {a/b} \right)}}\;{\text{and}}\;B = - \frac{{T_{0} \ln b}}{{\ln \left( {a/b} \right)}}$$

(4)

For the two-layer assemblies, the same temperature distribution obtained for a single-layer tube in Eq. (2) is valid for both inner and outer layers and can be written as

$$T_{1} (r) = A_{1} \ln r + B_{1} ,\quad T_{2} (r) = A_{2} \ln r + B_{2}$$

(5)

where $T_{1}$ and $T_{2}$ are the temperature distributions in the inner (a ≤ r ≤ $r_{1}$) and outer ($r_{1}$ ≤ r ≤ b) layers, respectively. The following boundary conditions are valid for the two-layer tubes:

$$T_{1} (a) = T_{0} \;{\text{and}}\;T_{2} (b) = 0$$

(6)

In addition, at the interface radius ($r = r_{1}$), both the temperatures and heat fluxes are equal, which gives

$$T_{1} (r_{1} ) = T_{2} (r_{1} )\;{\text{and}}\;\left. {k_{1} \frac{{{\text{d}}T_{1} (r)}}{{{\text{d}}r}}} \right|_{{r = r_{1} }} = \left. {k_{2} \frac{{{\text{d}}T_{2} (r)}}{{{\text{d}}r}}} \right|_{{r = r_{1} }}$$

(7)

where $k_{1}$ and $k_{2}$ denote the thermal conductivity of the inner and outer layers, respectively. Using these conditions, the integration constants are determined as

$$A_{1} = \frac{{k_{2} T_{0} }}{{k_{1} \ln (r_{1} /b) + k_{2} \ln (a/r_{1} )}}$$

(8)

$$B_{1} = T_{0} - \frac{{k_{2} T_{0} \ln a}}{{k_{1} \ln (r_{1} /b) + k_{2} \ln (a/r_{1} )}}$$

(9)

$$A_{2} = \frac{{k_{1} T_{0} }}{{k_{1} \ln (r_{1} /b) + k_{2} \ln (a/r_{1} )}}$$

(10)

$$B_{2} = - \frac{{k_{1} T_{0} \ln b}}{{k_{1} \ln (r_{1} /b) + k_{2} \ln (a/r_{1} )}}$$

(11)

Akin to the two-layer composite tubes, for the three-layer tubes, the temperature distributions in the inner (a ≤ r ≤ $r_{1}$), middle ($r_{1}$ ≤ r ≤ $r_{2}$) and outer ($r_{2}$ ≤ r ≤ b) layers can be stated as

$$T_{1} (r) = A_{1} \ln r + B_{1} ,\,T_{2} (r) = A_{2} \ln r + B_{2} \;{\text{and}}\;T_{3} (r) = A_{3} \ln r + B_{3}$$

(12)

The boundary conditions are

$$T_{1} (a) = T_{0} \;{\text{and}}\;T_{3} (b) = 0$$

(13)

and the interface conditions at the two interface radii (at $r = r_{1}$ and $r = r_{2}$) can be written as

$$T_{1} (r_{1} ) = T_{2} (r_{1} ),\quad T_{2} (r_{2} ) = T_{3} (r_{2} )$$

(14)

$$\left. {\left. {k_{1} \frac{{{\text{d}}T_{1} (r)}}{{{\text{d}}r}}} \right|_{{r = r_{1} }} = \left. {k_{2} \frac{{{\text{d}}T_{2} (r)}}{{{\text{d}}r}}} \right|_{{r = r_{1} }} ,\quad k_{2} \frac{{dT_{2} (r)}}{dr}} \right|_{{r = r_{2} }} = \left. {k_{3} \frac{{dT_{3} (r)}}{dr}} \right|_{{r = r_{2} }}$$

(15)

where $k_{1}$, $k_{2}$ and $k_{3}$ are the thermal conductivity of the inner, middle and outer layers, respectively. Application of these conditions yields

$$A_{1} = \frac{{k_{2} k_{3} T_{0} }}{{k_{2} k_{3} \ln (a/r_{1} ) + k_{1} k_{3} \ln (r_{1} /r_{2} ) + k_{1} k_{2} \ln (r_{2} /b)}}$$

(16)

$$B_{1} = T_{0} - \frac{{k_{2} k_{3} T_{0} \ln a}}{{k_{2} k_{3} \ln (a/r_{1} ) + k_{1} k_{3} \ln (r_{1} /r_{2} ) + k_{1} k_{2} \ln (r_{2} /b)}}$$

(17)

$$A_{2} = \frac{{k_{1} k_{3} T_{0} }}{{k_{2} k_{3} \ln (a/r_{1} ) + k_{1} k_{3} \ln (r_{1} /r_{2} ) + k_{1} k_{2} \ln (r_{2} /b)}}$$

(18)

$$B_{2} = \frac{{k_{1} T_{0} \left[ {k_{2} \ln (r_{2} /b) - k_{3} \ln r_{2} } \right]}}{{k_{2} k_{3} \ln (a/r_{1} ) + k_{1} k_{3} \ln (r_{1} /r_{2} ) + k_{1} k_{2} \ln (r_{2} /b)}}$$

(19)

$$A_{3} = \frac{{k_{1} k_{2} T_{0} }}{{k_{2} k_{3} \ln (a/r_{1} ) + k_{1} k_{3} \ln (r_{1} /r_{2} ) + k_{1} k_{2} \ln (r_{2} /b)}}$$

(20)

$$B_{3} = - \frac{{k_{1} k_{2} T_{0} \ln b}}{{k_{2} k_{3} \ln (a/r_{1} ) + k_{1} k_{3} \ln (r_{1} /r_{2} ) + k_{1} k_{2} \ln (r_{2} /b)}}$$

(21)

2.2 Elastic Solution

2.2.1 Generalized Plane Strain Case (Free Ends)

For a single-layer tube, using the common notation for the stresses and strains (Timoshenko and Goodier 1970), the generalized Hooke’s law reads

$$\varepsilon_{r} = \frac{1}{E}\left[ {\sigma_{r} - \nu (\sigma_{\theta } + \sigma_{z} )} \right] + \alpha T$$

(22)

$$\varepsilon_{\theta } = \frac{1}{E}\left[ {\sigma_{\theta } - \nu (\sigma_{r} + \sigma_{z} )} \right] + \alpha T$$

(23)

$$\varepsilon_{z} = \frac{1}{E}\left[ {\sigma_{z} - \nu (\sigma_{r} + \sigma_{\theta } )} \right] + \alpha T$$

(24)

Here, $\varepsilon_{i}$ are the strain components, $E$ the modulus of elasticity, $\nu$ the Poisson’s ratio, $\alpha$ the coefficient of thermal expansion, $\sigma_{i}$ the stress components in radial, circumferential, and axial directions, and $T$ the temperature difference between the absolute and the reference temperatures. The strain–displacement relations ($\varepsilon_{r} = {\text{d}}u / {\text{d}}r$ and $\varepsilon_{\theta } = u/r$), and the equation of equilibrium in the radial direction

$$\frac{{{\text{d}}\sigma_{r} }}{{{\text{d}}r}} + \frac{{\sigma_{r} - \sigma_{\theta } }}{r} = - \rho \omega^{2} r$$

(25)

form the basic elastic equations together with Eqs. (22) to (24). In Eq. (25) $\rho$ and $\omega$ are the material density and angular speed, respectively. In case of generalized plane strain ($\varepsilon_{z} = \varepsilon_{0} =$ constant), the axial stress becomes

$$\sigma_{z} = E\varepsilon_{0} + \nu (\sigma_{r} + \sigma_{\theta } ) - E\alpha T$$

(26)

Combining the equations of the generalized Hooke’s law with the strain displacement relations, substituting the axial stress into radial and circumferential stress expressions, and putting these two stress expressions into the equation of equilibrium (25), the governing differential equation for the single-layer tube can be obtained as

$$r^{2} \frac{{{\text{d}}{}^{2}u}}{{{\text{d}}r^{2} }} + r\frac{{{\text{d}}u}}{{{\text{d}}r}} - u = - \frac{(1 + \nu )(1 - 2\nu )}{E(1 - \nu )}\rho \omega^{2} r^{3} + \frac{(1 + \nu )}{(1 - \nu )}\alpha r^{2} \frac{{{\text{d}}T}}{{{\text{d}}r}}$$

(27)

The solution of the foregoing equation gives the radial displacement in a single-layer elastic tube. Here, the general solution can be stated as

$$u\left( r \right) = \frac{{C_{1} }}{r} + C_{2} r - \frac{{\rho \omega^{2} r^{3} (1 + \nu )(1 - 2\nu )}}{8E(1 - \nu )} + \frac{\alpha (1 + \nu )}{r(1 - \nu )}\int\limits_{a}^{r} {\lambda T(\lambda ){\text{d}}\lambda }$$

(28)

where $C_{1}$ and $C_{2}$ are arbitrary integration constants. The stresses in radial and circumferential directions are then computed as

$$\sigma_{r} = \frac{E}{(1 + \nu )(1 - 2\nu )}\left[ { - \frac{{C_{1} (1 - 2\nu )}}{{r^{2} }} + C_{2} + \varepsilon_{0} \nu } \right] - \frac{{r^{2} \omega^{2} (3 - 2\nu )\rho }}{8(1 - \nu )} - \frac{E\alpha }{{r^{2} (1 - \nu )}}\int\limits_{a}^{r} {\lambda T(\lambda ){\text{d}}\lambda }$$

(29)

$$\sigma_{\theta } = \frac{E}{(1 + \nu )(1 - 2\nu )}\left[ {\frac{{C_{1} (1 - 2\nu )}}{{r^{2} }} + C_{2} + \varepsilon_{0} \nu } \right] - \frac{{r^{2} \omega^{2} (1 + 2\nu )\rho }}{8(1 - \nu )} - \frac{E\alpha }{{r^{2} (1 - \nu )}}\left[ {r^{2} T(r) - \int\limits_{a}^{r} {\lambda T(\lambda ){\text{d}}\lambda } } \right]$$

(30)

The above expressions for the radial displacement and radial and circumferential stresses are also given in Ref. (Apatay and Mack 2015). The stress in the axial direction can be calculated using Eqs. (26), (29), and (30) which yields

$$\sigma_{z} = \frac{E}{(1 + \nu )(1 - 2\nu )}\left[ {2C_{2} \nu + \varepsilon_{0} (1 - \nu )} \right] - \frac{{r^{2} \omega^{2} \nu \rho }}{2(1 - \nu )} - \frac{E\alpha T(r)}{(1 - \nu )}$$

(31)

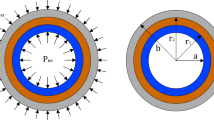
The solution is completed by calculating the integration constants and the axial strain $\varepsilon_{0}$. The boundary conditions for internally pressurized inner surface and stress-free outer surface can be written as

$$\sigma_{r} (a) = - P\;{\text{and}}\;\sigma_{r} (b) = 0$$

(32)

where P is the pressure at the inner surface. In addition, in case of generalized plane strain, the net force in the axial direction vanishes since the ends of the tube are free. This gives the following equation:

$$2\pi \int\limits_{a}^{b} {\sigma_{z} (r)r{\text{d}}r} = 0$$

(33)

Using these conditions, the integration constants and the axial strain are obtained as

$$C_{1} = \frac{{a^{2} b^{2} P(1 + \nu )}}{{(b^{2} - a^{2} )E}} + \frac{{a^{2} b^{2} \omega^{2} \rho (1 + \nu )(3 - 2\nu )}}{8E(1 - \nu )} + \frac{{a^{2} \alpha (1 + \nu )}}{{(b^{2} - a^{2} )(1 - \nu )}}\int\limits_{a}^{b} {\lambda T(\lambda ){\text{d}}\lambda }$$

(34)

$$C_{2} = \frac{{a^{2} P(1 - \nu )}}{{(b^{2} - a^{2} )E}} + \frac{{(a^{2} + b^{2} )\omega^{2} \rho (3 - 5\nu )}}{8E(1 - \nu )} + \frac{\alpha (1 - 3\nu )}{{(b^{2} - a^{2} )(1 - \nu )}}\int\limits_{a}^{b} {\lambda T(\lambda ){\text{d}}\lambda }$$

(35)

$$\varepsilon_{0} = \frac{{2a^{2} P\nu }}{{(b^{2} - a^{2} )E}} - \frac{{(a^{2} + b^{2} )\omega^{2} \rho \nu }}{2E} + \frac{2\alpha }{{b^{2} - a^{2} }}\int\limits_{a}^{b} {\lambda T(\lambda ){\text{d}}\lambda }$$

(36)

For the two-layer composite tubes with free ends, the same displacement and stress expressions given in Eqs. (28) to (31) are valid, and these expressions include four unknown integration constants: $C_{1}$, $C_{2}$ for the inner tube, and $C_{3}$, $C_{4}$ for the outer tube. In addition, the axial strain $\varepsilon_{0}$ should also be determined. In the derivations, the subscripts 1 and 2 are employed to represent material properties ($\alpha$,$E$,$\nu$ and $\rho$) of the inner and outer tubes, respectively, and superscripts I and II stand for the inner and outer tubes. The boundary conditions for the two-layer composite tubes under internal pressure are $\sigma_{r}^{I} (a) = - P^{{}}_{{}}$ and $\sigma_{r}^{II} (b) = 0^{{}}_{{}}$. In addition, at the interface of the two tubes (at $r = r_{1}$) the radial stress and radial displacement must be continuous, and thus, one can write $\sigma_{r}^{I} (r_{1} ) = \sigma_{r}^{II} (r_{1} )$ and $u_{{}}^{I} (r_{1} ) = u_{{}}^{II} (r_{1} )$. Moreover, for the generalized plane strain case one can write

$$2\pi \int\limits_{a}^{{r_{1} }} {\sigma_{z}^{I} (r)r{\text{d}}r + 2\pi \int\limits_{{r_{1} }}^{b} {\sigma_{z}^{II} (r)r{\text{d}}r} = 0}$$

(37)

Substituting the stresses and displacements into these conditions, the following system of equations is obtained:

$$\left[ {\begin{array}{*{20}c} {\frac{1}{{r_{1} }}} & {r_{1} } & { - \frac{1}{{r_{1} }}} & { - r_{1} } & 0 \\ { - \frac{{E_{1} }}{{r_{1}^{2} (1 + \nu_{1} )}}} & {\frac{{E_{1} }}{{(1 + \nu_{1} )(1 - 2\nu_{1} )}}} & {\frac{{E_{2} }}{{r_{1}^{2} (1 + \nu_{2} )}}} & { - \frac{{E_{2} }}{{(1 + \nu_{2} )(1 - 2\nu_{2} )}}} & {K_{25} } \\ { - \frac{{E_{1} }}{{a^{2} (1 + \nu_{1} )}}} & {\frac{{E_{1} }}{{(1 + \nu_{1} )(1 - 2\nu_{1} )}}} & 0 & 0 & {\frac{{E_{1} \nu_{1} }}{{(1 + \nu_{1} )(1 - 2\nu_{1} )}}} \\ 0 & 0 & { - \frac{{E_{2} }}{{b^{2} (1 + \nu_{2} )}}} & {\frac{{E_{2} }}{{(1 + \nu_{2} )(1 - 2\nu_{2} )}}} & {\frac{{E_{2} \nu_{2} }}{{(1 + \nu_{2} )(1 - 2\nu_{2} )}}} \\ 0 & {\frac{{2(r_{1}^{2} - a^{2} )E_{1} \nu_{1} }}{{(1 + \nu_{1} )(1 - 2\nu_{1} )}}} & 0 & {\frac{{2(b^{2} - r_{1}^{2} )E_{2} \nu_{2} }}{{(1 + \nu_{2} )(1 - 2\nu_{2} )}}} & {K_{55} } \\ \end{array} } \right]\;\left[ {\begin{array}{*{20}c} {C_{1} } \\ {C_{2} } \\ {C_{3} } \\ {C_{4} } \\ {\varepsilon_{0} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {B_{1} } \\ {B_{2} } \\ {B_{3} } \\ {B_{4} } \\ {B_{5} } \\ \end{array} } \right]$$

(38)

where

$$K_{25} = \frac{{E_{1} \nu_{1} }}{{(1 + \nu_{1} )(1 - 2\nu_{1} )}} - \frac{{E_{2} \nu_{2} }}{{(1 + \nu_{2} )(1 - 2\nu_{2} )}}$$

(39)

$$K_{55} = \frac{{(r_{1}^{2} - a^{2} )E_{1} (1 - \nu_{1} )}}{{(1 + \nu_{1} )(1 - 2\nu_{1} )}} + \frac{{(b^{2} - r_{1}^{2} )E_{2} (1 - \nu_{2} )}}{{(1 + \nu_{2} )(1 - 2\nu_{2} )}}$$

(40)

$$ \begin{aligned}B_{1}& = \frac{{r_{1}^{3} \omega^{2} }}{8}\left[ {\frac{{(1 + \nu_{1} )(1 - 2\nu_{1} )\rho_{1} }}{{E_{1} (1 - \nu_{1} )}} - \frac{{(1 + \nu_{2} )(1 - 2\nu_{2} )\rho_{2} }}{{E_{2} (1 - \nu_{2} )}}} \right]\\ &\quad - \frac{{\alpha_{1} (1 + \nu_{1} )}}{{r_{1} (1 - \nu_{1} )}}\int\limits_{a}^{{r_{1} }} {\lambda T_{1} (\lambda ){\text{d}}\lambda }\end{aligned} $$

(41)

$$B_{2} = \frac{{r_{1}^{2} \omega^{2} }}{8}\left[ {\frac{{(3 - 2\nu_{1} )\rho_{1} }}{{1 - \nu_{1} }} - \frac{{(3 - 2\nu_{2} )\rho_{2} }}{{1 - \nu_{2} }}} \right] + \frac{{E_{1} \alpha_{1} }}{{r_{1}^{2} (1 - \nu_{1} )}}\int\limits_{a}^{{r_{1} }} {\lambda T_{1} (\lambda ){\text{d}}\lambda }$$

(42)

$$B_{3} = \frac{{a^{2} \omega^{2} (3 - 2\nu_{1} )\rho_{1} }}{{8(1 - \nu_{1} )}} - P$$

(43)

$$B_{4} = \frac{{b^{2} \omega^{2} (3 - 2\nu_{2} )\rho_{2} }}{{8(1 - \nu_{2} )}} + \frac{{E_{2} \alpha_{2} }}{{b^{2} (1 - \nu_{2} )}}\int\limits_{{r_{1} }}^{b} {\lambda T_{2} (\lambda ){\text{d}}\lambda }$$

(44)

$$B_{5} = \frac{{\omega^{2} }}{4}\left[ {\frac{{(r_{1}^{4} - a^{4} )\nu_{1} \rho_{1} }}{{1 - \nu_{1} }} + \frac{{(b^{4} - r_{1}^{4} )\nu_{2} \rho_{2} }}{{1 - \nu_{2} }}} \right] + \frac{{2E_{1} \alpha_{1} }}{{1 - \nu_{1} }}\int\limits_{a}^{{r_{1} }} {\lambda T_{1} (\lambda )d\lambda } + \frac{{2E_{2} \alpha_{2} }}{{1 - \nu_{2} }}\int\limits_{{r_{1} }}^{b} {\lambda T_{2} (\lambda ){\text{d}}\lambda }$$

(45)

The integration constants and the axial strain can be obtained by solving Eq. (38).

Similar to two-layer composite tubes, the same displacement and stress expressions [Eqs. (28)–(31)] are valid for the three-layer tubes. The foregoing expressions contain six unknown integration constants ($C_{1}$,$C_{2}$ for the inner tube, $C_{3}$, $C_{4}$ for the middle tube, and $C_{5}$, $C_{6}$ for the outer tube) and the axial strain $\varepsilon_{0}$. The subscripts 1, 2, and 3 are employed to represent material properties of the inner, middle, and outer tubes, respectively. Moreover, superscripts I, II, and III are used to determine the displacements and stresses developed in the inner, middle, and outer tubes. The boundary conditions for the three-layer composite tubes under internal pressure are $\sigma_{r}^{I} (a) = - P^{{}}_{{}}$ and $\sigma_{r}^{III} (b) = 0^{{}}_{{}}$. In addition, at the interfaces of the tubes the radial stresses and radial displacements must be continuous, and one can write $\sigma_{r}^{I} (r_{1} ) = \sigma_{r}^{II} (r_{1} )$, $u_{{}}^{I} (r_{1} ) = u_{{}}^{II} (r_{1} )$, $\sigma_{r}^{II} (r_{2} ) = \sigma_{r}^{III} (r_{2} )$ and $u_{{}}^{II} (r_{2} ) = u_{{}}^{III} (r_{2} )$. Finally, for the generalized plane strain state, one can write

$$2\pi \int\limits_{a}^{r1} {\sigma_{z}^{I} (r)r{\text{d}}r} + 2\pi \int\limits_{r1}^{r2} {\sigma_{z}^{II} (r)r{\text{d}}r} + 2\pi \int\limits_{r2}^{b} {\sigma_{z}^{III} (r)r{\text{d}}r = 0}$$

(46)

Using the above equation and the boundary and interface conditions, the following system of equations can be obtained:

$$\left[ {\begin{array}{*{20}c} {\frac{1}{{r_{1} }}} & {r_{1} } & { - \frac{1}{{r_{1} }}} & { - r_{1} } & 0 & 0 & 0 \\ 0 & 0 & {\frac{1}{{r_{2} }}} & {r_{2} } & { - \frac{1}{{r_{2} }}} & { - r_{2} } & 0 \\ { - \frac{{E_{1} }}{{r_{1}^{2} (1 + \nu_{1} )}}} & {K_{32} } & {\frac{{E_{2} }}{{r_{1}^{2} (1 + \nu_{2} )}}} & {K_{34} } & 0 & 0 & {K_{37} } \\ 0 & 0 & { - \frac{{E_{2} }}{{r_{2}^{2} (1 + \nu_{2} )}}} & {K_{44} } & {\frac{{E_{3} }}{{r_{2}^{2} (1 + \nu_{3} )}}} & {K_{46} } & {K_{47} } \\ {\frac{{E_{1} }}{{a^{2} (1 + \nu_{1} )}}} & {K_{52} } & 0 & 0 & 0 & 0 & {K_{57} } \\ 0 & 0 & 0 & 0 & { - \frac{{E_{3} }}{{b^{2} (1 + \nu_{3} )}}} & {K_{66} } & {K_{67} } \\ 0 & {K_{72} } & 0 & {K_{74} } & 0 & {K_{76} } & {K_{77} } \\ \end{array} } \right]\;\left[ {\begin{array}{*{20}c} {C_{1} } \\ {C_{2} } \\ {C_{3} } \\ {C_{4} } \\ {C_{5} } \\ {C_{6} } \\ {\varepsilon_{0} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {B_{1} } \\ {B_{2} } \\ {B_{3} } \\ {B_{4} } \\ {B_{5} } \\ {B_{6} } \\ {B_{7} } \\ \end{array} } \right]$$

(47)

where $K_{32} = K_{52} = \frac{{E_{1} }}{{(1 + \nu_{1} )(1 - 2\nu_{1} )}}$, $K_{34} = K_{44} = \frac{{E_{2} }}{{(1 + \nu_{2} )(1 - 2\nu_{2} )}}$, $K_{37} = K_{32} \nu_{1} - K_{34} \nu_{2}$, $K_{46} = - K_{66} = - \frac{{E_{3} }}{{(1 + \nu_{3} )(1 - 2\nu_{3} )}}$, $K_{47} = K_{34} \nu_{2} + K_{46}$, $K_{57} = K_{32} \nu_{1}$, $K_{67} = - K_{46} \nu_{3}$, $K_{72} = \frac{{2(r_{1}^{2} - a^{2} )E_{1} \nu_{1} }}{{(1 + \nu_{1} )(1 - 2\nu_{1} )}}$, $K_{74} = \frac{{2(r_{2}^{2} - r_{1}^{2} )E_{2} \nu_{2} }}{{(1 + \nu_{2} )(1 - 2\nu_{2} )}}$, $K_{76} = \frac{{2(b^{2} - r_{2}^{2} )E_{3} \nu_{3} }}{{(1 + \nu_{3} )(1 - 2\nu_{3} )}}$,

$$K_{77} = \frac{{(r_{1}^{2} - a^{2} )E_{1} (1 - \nu_{1} )}}{{(1 + \nu_{1} )(1 - 2\nu_{1} )}} + \frac{{(r_{2}^{2} - r_{1}^{2} )E_{2} (1 - \nu_{2} )}}{{(1 + \nu_{2} )(1 - 2\nu_{2} )}} + \frac{{(b^{2} - r_{1}^{2} )E_{3} (1 - \nu_{3} )}}{{(1 + \nu_{3} )(1 - 2\nu_{3} )}}$$

(48)

and

$$B_{1} = \frac{{r_{1}^{3} \omega^{2} }}{8}\left[ {\frac{{(1 + \nu_{1} )(1 - 2\nu_{1} )\rho_{1} }}{{E_{1} (1 - \nu_{1} )}} - \frac{{(1 + \nu_{2} )(1 - 2\nu_{2} )\rho_{2} }}{{E_{2} (1 - \nu_{2} )}}} \right] - \frac{{\alpha_{1} (1 + \nu_{1} )}}{{r_{1} (1 - \nu_{1} )}}\int\limits_{a}^{{r_{1} }} {\lambda T_{1} (\lambda ){\text{d}}\lambda }$$

(49)

$$B_{2} = \frac{{r_{2}^{3} \omega^{2} }}{8}\left[ {\frac{{(1 + \nu_{2} )(1 - 2\nu_{2} )\rho_{2} }}{{E_{2} (1 - \nu_{2} )}} - \frac{{(1 + \nu_{3} )(1 - 2\nu_{3} )\rho_{3} }}{{E_{3} (1 - \nu_{3} )}}} \right] - \frac{{\alpha_{2} (1 + \nu_{2} )}}{{r_{2} (1 - \nu_{2} )}}\int\limits_{{r_{1} }}^{{r_{2} }} {\lambda T_{2} (\lambda ){\text{d}}\lambda }$$

(50)

$$B_{3} = \frac{{r_{1}^{2} \omega^{2} }}{8}\left[ {\frac{{(3 - 2\nu_{1} )\rho_{1} }}{{1 - \nu_{1} }} - \frac{{(3 - 2\nu_{2} )\rho_{2} }}{{1 - \nu_{2} }}} \right] + \frac{{E_{1} \alpha_{1} }}{{r_{1}^{2} (1 - \nu_{1} )}}\int\limits_{a}^{{r_{1} }} {\lambda T_{1} (\lambda ){\text{d}}\lambda }$$

(51)

$$B_{4} = \frac{{r_{2}^{2} \omega^{2} }}{8}\left[ {\frac{{(3 - 2\nu_{2} )\rho_{2} }}{{1 - \nu_{2} }} - \frac{{(3 - 2\nu_{3} )\rho_{3} }}{{1 - \nu_{3} }}} \right] + \frac{{E_{2} \alpha_{2} }}{{r_{2}^{2} (1 - \nu_{2} )}}\int\limits_{{r_{1} }}^{{r_{2} }} {\lambda T_{2} (\lambda ){\text{d}}\lambda }$$

(52)

$$B_{5} = \frac{{a^{2} \omega^{2} (3 - 2\nu_{1} )\rho_{1} }}{{8(1 - \nu_{1} )}} - P$$

(53)

$$B_{6} = \frac{{b^{2} \omega^{2} (3 - 2\nu_{3} )\rho_{3} }}{{8(1 - \nu_{3} )}} + \frac{{E_{3} \alpha_{3} }}{{b^{2} (1 - \nu_{3} )}}\int\limits_{{r_{2} }}^{b} {\lambda T_{3} (\lambda ){\text{d}}\lambda }$$

(54)

$$\begin{aligned} B_{7} & = \frac{{\omega^{2} }}{4}\left[ {\frac{{(r_{1}^{4} - a^{4} )\nu_{1} \rho_{1} }}{{1 - \nu_{1} }} + \frac{{(r_{2}^{4} - r_{1}^{4} )\nu_{2} \rho_{2} }}{{1 - \nu_{2} }} + \frac{{(b^{4} - r_{2}^{4} )\nu_{3} \rho_{3} }}{{1 - \nu_{2} }}} \right] \\ & \quad + \frac{{2E_{1} \alpha_{1} }}{{1 - \nu_{1} }}\int\limits_{a}^{{r_{1} }} {\lambda T_{1} (\lambda ){\text{d}}\lambda } + \frac{{2E_{2} \alpha_{2} }}{{1 - \nu_{2} }}\int\limits_{{r_{1} }}^{{r_{2} }} {\lambda T_{2} (\lambda ){\text{d}}\lambda } + \frac{{2E_{3} \alpha_{3} }}{{1 - \nu_{3} }}\int\limits_{{r_{2} }}^{b} {\lambda T_{3} (\lambda ){\text{d}}\lambda } \\ \end{aligned}$$

(55)

2.2.2 Plane Strain Case (Fixed Ends)

The solution for a single-layer tube with axially constrained ends is obtained through setting $\varepsilon_{z} = 0$. The stress components in radial, circumferential, and axial directions can be obtained as

$$\sigma_{r} = \frac{E}{(1 + \nu )(1 - 2\nu )}\left[ { - \frac{{C_{1} (1 - 2\nu )}}{{r^{2} }} + C_{2} } \right] - \frac{{r^{2} \omega^{2} (3 - 2\nu )\rho }}{8(1 - \nu )} - \frac{E\alpha }{{r^{2} (1 - \nu )}}\int\limits_{a}^{r} {\lambda T(\lambda ){\text{d}}\lambda }$$

(56)

$$\sigma_{\theta } = \frac{E}{(1 + \nu )(1 - 2\nu )}\left[ {\frac{{C_{1} (1 - 2\nu )}}{{r^{2} }} + C_{2} } \right]\frac{{r^{2} \omega^{2} (1 + 2\nu )\rho }}{8(1 - \nu )} - \frac{E\alpha }{{r^{2} (1 - \nu )}}\left[ {r^{2} T(r) - \int\limits_{a}^{r} {\lambda T(\lambda ){\text{d}}\lambda } } \right]$$

(57)

$$\sigma_{z} = \frac{{2EC_{2} \nu }}{(1 + \nu )(1 - 2\nu )} - \frac{{r^{2} \omega^{2} \nu \rho }}{2(1 - \nu )} - \frac{E\alpha T(r)}{(1 - \nu )}$$

(58)

On the other hand, the radial displacement is the same as the expression given in Eq. (28). By using the boundary conditions given in Eq. (32), the integration constants $C_{1}$ and $C_{2}$ can be determined as

$$C_{1} = \frac{{a^{2} b^{2} P(1 + \nu )}}{{(b^{2} - a^{2} )E}} + \frac{{a^{2} b^{2} \omega^{2} \rho (1 + \nu )(3 - 2\nu )}}{8E(1 - \nu )} + \frac{{a^{2} \alpha (1 + \nu )}}{{(b^{2} - a^{2} )(1 - \nu )}}\int\limits_{a}^{b} {rT(r){\text{d}}r}$$

(59)

$$C_{2} = \frac{{a^{2} P(1 - \nu )(1 - 2\nu )}}{{(b^{2} - a^{2} )E}} + \frac{{(a^{2} + b^{2} )\omega^{2} \rho (1 + \nu )(3 - 2\nu )(1 - 2\nu )}}{8E(1 - \nu )} + \frac{\alpha (1 + \nu )(1 - 2\nu )}{{(b^{2} - a^{2} )(1 - \nu )}}\int\limits_{a}^{b} {rT(r){\text{d}}r}$$

(60)

For the two-layer tubes, the same stress and displacement expressions for axially constrained single-layer tubes are valid and the integration constants can be determined by the boundary and interface conditions formerly expressed for the two-layer tubes having free ends. Using these conditions, they can be determined by solving the following system of equations:

$$\left[ {\begin{array}{*{20}c} {\frac{1}{{r_{1} }}} & {r_{1} } & { - \frac{1}{{r_{1} }}} & { - r_{1} } \\ { - \frac{{E_{1} }}{{r_{1}^{2} (1 + \nu_{1} )}}} & {\frac{{E_{1} }}{{(1 + \nu_{1} )(1 - 2\nu_{1} )}}} & {\frac{{E_{2} }}{{r_{1}^{2} (1 + \nu_{2} )}}} & { - \frac{{E_{2} }}{{(1 + \nu_{2} )(1 - 2\nu_{2} )}}} \\ { - \frac{{E_{1} }}{{a^{2} (1 + \nu_{1} )}}} & {\frac{{E_{1} }}{{(1 + \nu_{1} )(1 - 2\nu_{1} )}}} & 0 & 0 \\ 0 & 0 & { - \frac{{E_{2} }}{{b^{2} (1 + \nu_{2} )}}} & {\frac{{E_{2} \nu_{2} }}{{(1 + \nu_{2} )(1 - 2\nu_{2} )}}} \\ \end{array} } \right]\;\left[ {\begin{array}{*{20}c} {C_{1} } \\ {C_{2} } \\ {C_{3} } \\ {C_{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {B_{1} } \\ {B_{2} } \\ {B_{3} } \\ {B_{3} } \\ \end{array} } \right]$$

(61)

where $B_{2}$, $B_{3}$ and $B_{4}$ are given in Eqs. (41)–(44).

Finally, for the three-layer fixed-ended tubes, similar to the two-layer tubes with fixed ends, the six integration constants are to be determined using the following system of equations:

$$\left[ {\begin{array}{*{20}c} {\frac{1}{{r_{1} }}} & {r_{1} } & { - \frac{1}{{r_{1} }}} & { - r_{1} } & 0 & 0 \\ 0 & 0 & {\frac{1}{{r_{2} }}} & {r_{2} } & { - \frac{1}{{r_{2} }}} & { - r_{2} } \\ { - \frac{{E_{1} }}{{r_{1}^{2} (1 + \nu_{1} )}}} & {K_{32} } & {\frac{{E_{2} }}{{r_{1}^{2} (1 + \nu_{2} )}}} & {K_{34} } & 0 & 0 \\ 0 & 0 & { - \frac{{E_{2} }}{{r_{2}^{2} (1 + \nu_{2} )}}} & {K_{44} } & {\frac{{E_{3} }}{{r_{2}^{2} (1 + \nu_{3} )}}} & {K_{46} } \\ {\frac{{E_{1} }}{{a^{2} (1 + \nu_{1} )}}} & {K_{52} } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & { - \frac{{E_{3} }}{{b^{2} (1 + \nu_{3} )}}} & {K_{66} } \\ \end{array} } \right]\;\left[ {\begin{array}{*{20}c} {C_{1} } \\ {C_{2} } \\ {C_{3} } \\ {C_{4} } \\ {C_{5} } \\ {C_{6} } \\ \end{array} } \right]\left[ { = \begin{array}{*{20}c} {B_{1} } \\ {B_{2} } \\ {B_{3} } \\ {B_{4} } \\ {B_{5} } \\ {B_{6} } \\ \end{array} } \right]$$

(62)

where $K_{32}$, $K_{34}$, $K_{44}$, $K_{46}$, $K_{52}$, $K_{66}$, $B_{1}$, $B_{2}$, $B_{3}$, $B_{4}$, $B_{5}$ and $B_{6}$ are already given in Eqs. (48)–(54).

2.3 Onset of Yield

Monitoring the commencement of yielding for a tube with fixed or free ends is quite important in order to perform a reliable design. For an internally pressurized single-layer tube, typically, the yielding begins at the inner surface ($r$ = $a$). It is also known that for the fixed-ended two-layer tubes, depending on material properties and tube dimensions, the yielding may occur in the inner surface or at the interfaces of tube layers (Akis and Eraslan 2005; Eraslan and Akis 2005). On the other hand, when the temperature load and rotation are considered, the plasticization may also start at the outer surface of the tube assemblies with free ends (Apatay and Mack 2015). Therefore, all these locations, together with the inner parts of the layers, should be checked for yielding. To do this, the well-known von Mises yield criterion is used in this work. The von Mises yield stress $\sigma_{Y}$ can be stated as

$$\sigma_{Y} = \sqrt {\frac{1}{2}[(\sigma_{r} - \sigma_{\theta } )^{2} + (\sigma_{r} - \sigma_{z} )^{2} + (\sigma_{\theta } - \sigma_{z} )^{2} ]} .$$

(63)

The yielding takes place once the yield stress $\sigma_{Y}$ becomes higher than the uniaxial yield limit $\sigma_{0}$ of the material. For determining the yielding at the layers of the assemblies, the following non-dimensional yield variable is expressed with respect to the von Mises yield stress:

$$\varphi = \sqrt {\frac{1}{2}[(\bar{\sigma }_{r} - \bar{\sigma }_{\theta } )^{2} + (\bar{\sigma }_{r} - \bar{\sigma }_{z} )^{2} + (\bar{\sigma }_{\theta } - \bar{\sigma }_{z} )^{2} ]} ,$$

(64)

where $\bar{\sigma }_{i}$ are the non-dimensional stress components determined by

$$\bar{\sigma }_{i} = \frac{{\sigma_{i} }}{{\sigma_{0} }}$$

(65)

It is worth noting that for the values of $\varphi < 1$, the assembly is in elastic stress state, whereas for $\varphi = 1$, the yielding begins at that location. In the computations, the yield variable is calculated throughout the assemblies where yielding may occur.

3 Optimal Design Problem Formulation

The present section provides the mathematical formulation of the considered combinatorial optimization problem. The weight minimization problem of a multilayer composite tube with nl material layers and nv number of solution variables, including thickness and material variables, can be formulated as follows.

$${\text{Find}}\;{\mathbf{X}}^{T} = \left[ {x_{1} ,x_{2} , \ldots ,x_{nv} } \right]$$

(66)

such that X minimizes the following weight objective function:

$$W(X) = \sum\limits_{i = 1}^{nl} {\rho_{i} } A_{i}$$

(67)

where $W(X)$ is the weight per unit length of the tube. In the above equation, ρ_i and A_i are weight per unit of volume and cross-sectional area of the i-th material layer, respectively. On the other hand, for cost optimization, minimization of the following cost objective function is considered:

$$C(X) = \sum\limits_{i = 1}^{nl} {c_{i} \rho_{i} } A_{i}$$

(68)

where $C(X)$ is the cost per unit length of the tube. Here, ρ_i, c_i, and A_i are weight per unit of volume, cost per unit weight, and cross-sectional area of the i-th material layer, respectively. In the present study, both the minimum weight and cost design of rotating multilayer tubes are subjected to the following design constraint:

$$\phi_{\,i} - 1 < 0\,\,\,$$

(69)

where $\varphi_{\,i} \,\,$ is non-dimensional stress variable defined by Eq. (64). During the optimization process, weight and cost objective function values of the feasible designs are directly calculated by Eqs. (67) and (68), respectively. However, infeasible designs are penalized as follows.

$$f_{p} (X) = f(X)\left[ {1 + K\left( {\sum\limits_{i} {g_{i} } } \right)} \right]$$

(70)

where $f(X)$ is the associated weight/cost objective function,$f_{p} (X)$ denotes the penalized objective function, $g_{i}$ is the i-th constraint violation, and K is the penalty constant, which is taken as 100 in this study.

4 Metaheuristic Optimization Algorithm

Selection of a suitable algorithm to solve a particular design optimization problem basically depends on the nature of design variables, objective function, and imposed constraints. Metaheuristic or evolutionary algorithms are generally perceived as efficient numerical optimization methods for engineering design applications (Akbulut et al. 2020; Kazemzadeh Azad 2019). The popularity of these algorithms in practical applications (Koç 2017; Alkayem et al. 2018; Gen et al. 2017) can be attributed to their ease of implementation, derivative-free features, global search properties, and capability of dealing with both discrete and continuous solution variables.

Considering the discrete nature of the problem tackled in the present study, a reformulation of the big bang-big crunch algorithm (Erol and Eksin 2006), recently proposed by Kazemzadeh Azad and Akış (2018), is adopted for design optimization of rotating multilayer composite tubes. Akin to other metaheuristic algorithms, optimization via big bang-big crunch algorithm begins with an initial population of candidate solutions that are uniformly sampled from the design space. Next, evaluation, selection, and generation processes are carried out successively to create a new population of candidate solutions. As shown in the flowchart of the optimization method (Fig. 2), the algorithm entails an iterative process to obtain the optimum thickness and material of each layer for a given composite tube under the imposed design constraints. It is worth mentioning that, to satisfy the fabrication requirements, the thickness of each material layer is rounded to the nearest available value in the course of optimization. The algorithm is coded in MATLAB (MATLAB 2019), and the optimization runs are performed using a regular personal computer with Intel Core i5-8250U, 1.6 GHz CPU, and 8 GB RAM. Further details for the implementation of the employed big bang-big crunch algorithm can be found in Ref. (Kazemzadeh Azad and Akış 2018) and are not repeated here.

Fig. 2

Flowchart of the metaheuristic optimization algorithm

5 Numerical Experiments

This section presents the weight and cost optimization instances of rotating multilayer composite tubes under internal heating and pressure. Table 1 gives the set of available steel and aluminum alloys used for material selection of the composite tube layers. This set of steel and aluminum alloys was formerly adopted in Ref. (Kazemzadeh Azad and Akış 2018) for the optimal design of internally pressurized tightly fitted multilayer composite tubes with axially constrained ends. In the present work, both weight and cost optimization examples of internally pressurized multilayer composite tubes are investigated for different angular speed and inner surface temperature values, and the obtained results are presented and discussed. The numerical instances are studied in two different cases, i.e., Case A and Case B, as follows.

Table 1 Material properties and costs of the available steel (S) and aluminum (A) alloys

In Case A, it is aimed to examine the effect of internal heating on the final designs. For this purpose, angular speed and internal pressure of the composite tubes are set to ω = 150 rad/s and P = 150 MPa, respectively, while the internal temperature of the assemblies, T, is gradually increased from 0 to 100 °C. Here, using the aforementioned metaheuristic optimization algorithm the corresponding optimum design for each temperature value is sought and the obtained solutions are compared. In Case B, it is attempted to investigate the effect of angular speed of the assemblies on the final results. To this end, internal temperature and pressure are set to T = 50 °C and P = 150 MPa, respectively, while the angular speed of the assemblies, ω, is gradually increased from 0 to 200 rad/s. The optimum design associated with each angular speed value is sought, and the final designs are reported.

Moreover, all the numerical examples are further investigated under two different end conditions already described in Sect. 2. The optimization of assemblies with axially constrained ends (fixed-end assumption) is denoted by Case I, whereas the optimal design of composite tubes considering the generalized plane strain formulation (free-end assumption) is denoted by Case II. To investigate the effect of number of material layers on the final solutions, the numerical experiments are carried out for all the one-, two-, and three-layer tubes. For each design case, a discrete optimization problem is tackled where the employed metaheuristic algorithm attempts to select the optimal material type from Table 1 and thickness of each layer from multiples of 0.002 m. For the optimization process, the maximum number of iterations is set to 500, and a population of 50 individuals is employed to search the solution space. In all the investigated instances, the inner radius of the assemblies is set to a = 0.15 m. It is also worthwhile to note that due to the stochastic nature of the algorithm, in each design optimization case, the algorithm is executed 25 times and the details of the achieved best solution as well as the statistical results of all runs are tabulated.

Cost optimization of rotating one-, two-, and three-layer tubes is studied under different internal temperature values in Cases A-I and A-II, and the minimum cost results are presented in Fig. 3a, b. The corresponding detailed cost optimization results for rotating three-layer tubes are also presented in Tables 2 and 3. It is worth mentioning that in these tables Φ_(c) denotes the most critical value of the non-dimensional yield variable over the tube layers.

Fig. 3

Optimum costs for rotating one-, two-, and three-layer tubes: a Case A-I; b Case A-II; c Case B-I; and d Case B-II

Table 2 Cost minimization results of rotating three-layer tube in Case A-I

Table 3 Cost-minimization results of rotating three-layer tube in Case A-II

For the sake of clarity, the comparison of results is first carried out between the primary cases, i.e., Cases A and B, and discussions related to the fixed- and free-end assumptions (Cases I and II) are provided afterward. Here, angular speed and internal pressure of the tubes are set to ω = 150 rad/s and P = 150 MPa, respectively, and the effect of the inner temperature is examined. The cost optimization results obtained in Cases A-I and A-II reveal that, on the one hand, by increasing the inner temperature from 0 to 100 °C, the optimum cost of all the one-, two- and three-layer assemblies decreases. On the other hand, it is apparent from the figures that by increasing the inner temperature, the difference between the optimum results of one-, two-, and three-layer tubes diminishes. Thus, it can be inferred that in the foregoing two cases fabricating two- and three-layer tubes instead of one-layer tubes would be more profitable under lower inner temperatures. Nevertheless, it should be noted that the conclusions drawn here are valid only for the investigated set of materials as well as considered loading and boundary conditions. For instance, as can be seen from Fig. 3a, b that for T = 100 °C the results of rotating three-layer tube are same as one- and two-layer tubes. Tables 2 and 3 present the numerical results for the above-mentioned three-layer tube under T = 100 °C for which three layers of A-5 aluminum alloy are found to be the most cost-efficient solution (i.e., the same solution of the associated one-layer tube). Contrary to the design found here using the set of steel and aluminum alloys given in Table 1, superior solutions for the same rotating three-layer tube could be achieved by increasing the size of material set, which entails further research.

Figure 3c, d depicts the minimum cost results of rotating one-, two-, and three-layer tubes in Cases B-I and B-II. The corresponding cost optimization results for rotating three-layer tubes are also tabulated in Tables 4 and 5. Here, internal temperature and pressure are set to T = 50 °C and P = 150 MPa, respectively, and the effect of angular speed of the assemblies is investigated. Although for different angular speeds, the two- and three-layer tubes produce more economical solutions compared to the one-layer designs, it can be deduced from the figures that increasing the angular speed of the assemblies from 0 to 200 rad/s results in relatively slight fluctuations in the optimum costs for all the investigated one-, two- and three-layer tubes. In Cases B-I and B-II, it is observed that the angular speed parameter does not play a governing role in the minimum cost design of the investigated assemblies.

Table 4 Cost-minimization results of rotating three-layer tube in Case B-I

Table 5 Cost-minimization results of rotating three-layer tube in Case B-II

Sometimes minimizing the total weight of an assembly could be the main objective of the optimization process. In this regard, Fig. 4a, b shows the weight optimization results for rotating one-, two-, and three-layer tubes in Cases A-I and A-II. The corresponding optimum designs for rotating three-layer tubes are given in Tables 6 and 7. As can be seen from Fig. 4a, b, by increasing the inner temperature from 0 to 100 °C, mostly—if not always—the optimum weight of all the one-, two- and three-layer assemblies decreases. Moreover, it is apparent from the figures that by increasing the inner temperature, the difference between the results of one-, two-, and three-layer tubes decreases. Hence, it can be deduced that in the above-mentioned two cases fabricating minimum weight two- and three-layer tubes instead of one-layer tubes would be more advantageous only for lower inner temperatures.

Fig. 4

Optimum weights for rotating one-, two-, and three-layer tubes: a Case A-I; b Case A-II; c Case B-I; and d Case B-II

Table 6 Weight-minimization results of rotating three-layer tube in Case A-I

Table 7 Weight-minimization results of rotating three-layer tube in Case A-II

Weight minimization of rotating one-, two-, and three-layer tubes is also carried out in Cases B-I and B-II, and the results are shown in Fig. 4c, d. The obtained minimum weight solutions for rotating three-layer tubes are also presented in Tables 8 and 9. As already noted, in these cases, internal temperature and pressure are set to T = 50 °C and P = 150 MPa, respectively, and the effect of angular speed of the assemblies is examined. It can be seen from the figures that increasing the angular speed of the assemblies from 0 to 200 rad/s yields slight fluctuations in the optimum weights for all the studied one-, two-, and three-layer tubes. Similar to the cost optimization results, it is observed that in Cases B-I and B-II the angular speed parameter does not play a governing role in the minimum weight design of the investigated assemblies.

Table 8 Weight-minimization results of rotating three-layer tube in Case B-I

Table 9 Weight-minimization results of rotating three-layer tube in Case B-II

To further demonstrate the performance of the employed algorithm, Tables 10, 11, 12, and 13 show a comparison of the big bang-big crunch (BB-BC) algorithm versus the recently developed adaptive dimensional search (ADS) technique (Hasançebi and Kazemzadeh Azad 2015). The statistical results of 25 independent optimization runs presented in the above-mentioned tables show an acceptable level of comparability between the results of the BB-BC and ADS algorithms. Moreover, in order to quantify the consistency of the investigated optimization algorithms, the concept of practical reliability (Rama Mohan Rao et al. 2013) is used. The practical reliability indicates the ratio of successful solutions to the total number of independent executions of the optimization algorithm. In the present study, a successful solution is defined as a solution with a maximum difference of 5% from the best solution found by the algorithm over 25 independent runs.

Table 10 Cost-minimization results of BB-BC versus ADS in Case A-I (T = 50 °C)

Table 11 Cost-minimization results of BB-BC versus ADS in Case B-I (ω = 100 rad/s)

Table 12 Weight-minimization results of BB-BC versus ADS in Case A-I (T = 50 °C)

Table 13 Weight-minimization results of BB-BC versus ADS in Case B-I (ω = 100 rad/s)

As already mentioned, in this study, optimization of rotating one-, two-, and three-layer tubes is performed based on two different tube-end conditions (Cases I and II). For the sake of clarity, the cost and weight optimization results are separately compared for these two cases in Figs. 5, 6, 7, 8, 9, and 10. As can be seen from the figures, in all the investigated instances the obtained results in Case I (fixed-end assumption) are lighter/profitable than those achieved in Case II (free-end assumption). The presented results quantify and highlight the effect of assumptions made for structural response computations on the final designs. Average optimization histories of 25 independent runs are plotted in Figs. 11 and 12. It is worth mentioning that Figs. 11a and 12a are depicted up to 250 iterations since there is no significant improvement in the remaining iterations. Figure 13 shows the variations of non-dimensional stress variable $\varphi$ in radial direction for typical rotating one-layer, two-layer, and three-layer tubes. As can be seen from the figure, the final designs satisfy the stipulated design constraint based on the von Mises yield criterion. The presented numerical results could provide some general guidelines for practical applications, especially in the preliminary design stage of rotating multilayer composite assemblies. Yet, it is noteworthy that although the present study is limited to optimization of rotating multilayer composite tubes under internal heating and pressure, the employed methodology can be further extended to handle optimization problems of rotating solid and annular disks as well. There is also scope for further research to include other set of materials as well as different loading and boundary conditions in the optimization process.

Fig. 5

Optimum cost for rotating one-layer tube: a Case A-I versus Case A-II; and b Case B-I versus Case B-II

Fig. 6

Optimum weight for rotating one-layer tube: a Case A-I versus Case A-II; and b Case B-I versus Case B-II

Fig. 7

Optimum cost for rotating two-layer tube: a Case A-I versus Case A-II and b Case B-I versus Case B-II

Fig. 8

Optimum weight for rotating two-layer tube: a Case A-I versus Case A-II and b Case B-I versus Case B-II

Fig. 9

Optimum cost for rotating three-layer tube: a Case A-I versus Case A-II and b Case B-I versus Case B-II

Fig. 10

Optimum weight for rotating three-layer tube: a Case A-I versus Case A-II and b Case B-I versus Case B-II

Fig. 11

Cost versus iterations plot of rotating a two-layer, and b three-layer tubes in Case A-I (T = 50 °C)

Fig. 12

Cost versus iterations plot of rotating a two-layer, and b three-layer tubes in Case B-I (ω = 100 rad/s)

Fig. 13

Variations of non-dimensional stress variable in radial direction for minimum cost rotating a one-layer, b two-layer, and c three-layer tubes in Case A-I (T = 50 °C)

6 Conclusions

In the present work, both weight and cost minimization problems of rotating multilayer composite tubes are studied under internal heating and pressure. In order to determine the structural responses, analytical solutions are presented based on two different boundary conditions. The automated material selection and thickness optimization of pressurized one-, two-, and three-layer assemblies are performed under different angular speed and internal heating conditions using a contemporary metaheuristic optimization algorithm. The corresponding optimum solution for each angular speed as well as internal heating condition is sought, and the obtained designs are discussed. In Case A, where the effect of the inner temperature is examined, it is shown that by increasing the inner temperature from 0 to 100 °C, the difference between the results of one-, two-, and three-layer tubes decreases. Thus, it can be deduced that, in this case, fabricating minimum weight/cost two- and three-layer tubes instead of one-layer tubes would be more advantageous only for lower inner temperatures. Furthermore, in Case B, where the effect of angular speed of the assemblies is investigated, it is observed that increasing the angular speed of the assemblies from 0 to 200 rad/s yields slight fluctuations in the optimum weight/cost for all the investigated one-, two- and three-layer tubes. Moreover, considering the two different tube-end conditions, it is noticed that the obtained results in Case I (fixed-end assumption) are lighter/profitable than those achieved in Case II (free-end assumption) for all the test cases. The results quantify and highlight the effect of assumptions made for structural response computations on the optimality of final solutions. The foregoing results provide general guidelines for preliminary/conceptual design of rotating multilayer composite tubes under internal heating and pressure.